Research on the Design of a Priority-Based Multi-Stage Emergency Material Scheduling System for Drone Coordination

Abstract

Emergency material scheduling (EMS) is a core component of post-disaster emergency response, with its efficiency directly impacting rescue effectiveness and the satisfaction of affected populations. However, due to severe road damage, limited availability of resources, and logistical challenges after disasters, current EMS practices often suffer from uneven resource distribution. To address these issues, this paper proposes a priority-based, multi-stage EMS approach with drone coordination. First, we construct a three-level EMS network “storage warehouses–transit centers–disaster areas” by integrating the advantages of large-scale transportation via trains and the flexible delivery capabilities of drones. Second, considering multiple constraints, such as the priority level of disaster areas, drone flight range, transport capacity, and inventory capacities at each node, we formulate a bilevel mixed-integer nonlinear programming model. Third, given the NP-hard nature of the problem, we design a hybrid algorithm—the Tabu Genetic Algorithm combined with Branch and Bound (TGA-BB), which integrates the global search capability of genetic algorithms, the precise solution mechanism of branch and bound, and the local search avoidance features of Tabu search. A stage-adjustment operator is also introduced to better adapt the algorithm to multi-stage scheduling requirements. Finally, we designed eight instances of varying scales to systematically evaluate the performance of the stage-adjustment operator and the Tabu search mechanism within TGA-BB. Comparative experiments were conducted against several traditional heuristic algorithms. The experimental results show that TGA-BB outperformed the other algorithms across all eight test cases, in terms of both average response time and average runtime. Specifically, in Instance 7, TGA-BB reduced the average response time by approximately 52.37% compared to TGA-Particle Swarm Optimization (TGA-PSO), and in Instance 2, it shortened the average runtime by about 97.95% compared to TGA-Simulated Annealing (TGA-SA).These results fully validate the superior solution accuracy and computational efficiency of TGA-BB in drone-coordinated, multi-stage EMS.

1. Introduction

In recent years, various types of disaster events, such as earthquakes, floods, wildfires, and diseases, have occurred frequently around the world, significantly impacting people’s happiness, the stability of their lives, and even their safety [1]. Emergency material scheduling (EMS) is a crucial part of post-disaster response. It involves allocating various medical supplies and daily necessities to disaster areas, in order to meet the basic living requirements of the affected population and mitigate the risks associated with the disaster [2,3]. Inefficient EMS can not only delay rescue operations, but also result in unmet needs for many victims, further worsening the disaster situation and causing more serious casualties [4,5]. For example, in the 2008 Wenchuan earthquake, due to the damage to the road network in the disaster area, a large number of materials donated by the public could not be delivered to the affected villages in time. The 2023 Turkey–Syria earthquake caused severe damage to aging roads and ports in southern Turkey and Syria, hindering the timely delivery of emergency supplies and resulting in a large number of casualties. In addition, in the wake of the Noto earthquake in 2024, many survivors had to survive without heat and water due to a lack of rescue resources, which shows the limitations of relief supplies in the aftermath of disasters [6]. Furthermore, the unfair distribution of aid following the 2015 earthquake in Pakistan sparked widespread criticism and protests among survivors, further exacerbating social unrest. And in the 2025 magnitude—6.8 earthquake in Xigaze City, Tibet, the initial EMS was mainly concentrated in Dingri County, while the surrounding Lazi County, despite being more severely affected, faced a shortage of supplies [7]. This case reflects an imbalance in the regional distribution of emergency supplies caused by asymmetric information and a lagging coordination mechanism under the limited ability of EMS.

It can be seen that research on EMS is of great significance and needs to be effectively promoted, and current research mainly covers rescue network design [8], optimization of transit center location selection [9,10,11], and optimization of EMS, with the main focus on planning the EMS schemes for each disaster area from a global perspective, in order to lay the foundation for the subsequent material scheduling work [12,13]. This paper primarily investigates EMS based on drone coordination. From the aforementioned cases, it is evident that the deterioration and damage of road networks in disaster-stricken areas pose significant challenges to EMS. Utilizing drones for material delivery, as opposed to traditional ground-based emergency logistics, can overcome road conditions and save human resources, thereby significantly enhancing the efficiency of EMS. Murray and Chu [14] first proposed the concept of drone collaborative distribution, and established a truck–drone collaborative optimization model. Subsequently, scholars from various countries have carried out a lot of research on drone collaborative EMS [15,16,17]. In terms of models and methodologies, current research has developed models and methods that aim to minimize total response time [12,13] and minimize the cost of EMS [18], as well as multi-objective optimization that combines both aspects [19], further improving the efficiency of EMS and reducing disaster losses. Additionally, some studies have introduced evaluation dimensions such as fairness [20], urgency [1,21], Gini coefficient [22], and deprivation costs [23], providing important theoretical support and methodological guidance for research on EMS. However, given the high complexity of disaster scenarios and the diversity of real-world conditions, many issues still urgently need to be addressed.

In summary, this paper considers the limited transportation resources and material resources after a disaster and the priority of different disaster areas, and in order to effectively ensure the distribution of materials to the people in need, this paper proposes a priority-based multi-stage EMS method for drone coordination.

Firstly, this paper intends to form a three-level EMS network with the structure of “storage warehouses–transit centers–disaster areas”. In this network, storage warehouses are responsible for storing emergency supplies, transit centers handle the distribution and transfer of materials, drones deliver supplies from the transit centers to the disaster areas, and trains are used for large-scale transportation of materials from the storage warehouses to the transit centers. This approach enables efficient EMS under the harsh conditions and challenging transportation circumstances following a disaster. This three-level EMS network improves the efficiency of EMS optimization but also increases the complexity of post-disaster EMS. The question is how to find an appropriate model and method to formulate an appropriate EMS plan based on this three-level EMS network, and to realize the fastest response to the material demands in the disaster area? This is a bilevel programming problem [24,25,26], characterized by its complex NP-Hard nature [27,28,29].

Secondly, this paper introduces the concept of priority, where “priority” refers to the assessment of the importance and urgency of different disaster areas, based on the different levels of response order that are assigned. A higher priority indicates that an area requires earlier delivery of emergency supplies. In scenarios involving multi-stage, three-level EMS, efficiency-oriented scheduling strategies may lead to delayed supply delivery to remote and severe disaster areas, exacerbating disaster losses; whereas overemphasizing priority assurance can disrupt overall strategic deployment, reduce total scheduling efficiency, and cause resource allocation imbalances and stockpiling. Thus, how to ensure the basic needs of residents in severely disaster areas, while also considering overall EMS efficiency and choosing appropriate scheduling methods, constitutes a significant topic requiring in-depth research.

Finally, this paper intends to implement multi-stage EMS, which is an extension of the traditional EMS problem. Considering the limited availability of materials and transportation capacity after a disaster, when the number of disaster areas is large, it becomes necessary to divide the EMS process into multiple stages. This approach improves the efficiency of post-disaster rescue operations and ensures that the material needs of all disaster areas are effectively met. It is particularly important to emphasize the dynamism inherent in multi-stage EMS problems [30]. How to comprehensively consider the dynamic changes during the multi-stage scheduling process and formulate reasonable and efficient EMS schemes according to real-time situations is an important issue that needs urgent resolution in current research.

Considering these critical issues, this paper takes the actual scheduling environment of post-disaster emergency materials as its background, taking into account the transport capacity constraints of each node and the demand priorities of disaster areas, conducting systematic research on multi-stage bilevel EMS problems. The innovations of this paper are as follows:

• A three-level EMS network was constructed, which combines the advantages of large-scale transportation by train and flexible delivery by drones, effectively addressing the challenges of EMS in complex post-disaster environments.
• Proposing a multi-stage EMS method based on the priority of disaster areas achieves synergistic optimization between supply guarantees for heavily disaster areas and overall scheduling efficiency.
• Designing a hybrid intelligent optimization algorithm (Tabu Genetic Algorithm–Branch and Bound, TGA-BB), combining the generality and global search ability of GA, the exact solving capability of BB, and the memory-based search features of tabu search (TS), while a stage-adjustment operator is designed based on real-world problems, significantly improving the efficiency in solving priority-based, multi-stage, bilevel EMS problems.
• Through extensive experiments and algorithm comparisons, the effectiveness and superiority of the proposed method was validated, and practical recommendations for post-disaster EMS are provided based on the experimental results.

The remaining structure of the article is organized as follows: Section 2 reviews relevant literature in the field; Section 3 provides a detailed analysis of multi-stage EMS optimization problems and constructs a multi-stage bilevel EMS model; Section 4 designs a hybrid optimization algorithm model combining GA and BB, inspired by TS; Section 5 builds problem instances based on real situations, conducts comparative experiments, and analyzes the experimental results; Section 6 summarizes the research work of this paper and proposes future research directions.

2. Literature Review

This section will provide a literature review from three perspectives: the application of bilevel programming in EMS, multi-stage EMS problems, and priority.

2.1. Drone Cooperative Three-Tier EMS Network

With the development of unmanned technology, drones have been widely applied in various fields such as aerial photography, logistics, agriculture, and disaster relief [31]. In post-disaster EMS, drones can play a crucial role due to the limitations imposed by damaged roads and harsh post-disaster environments. While drone dispatching offers strong flexibility and high efficiency, it is constrained by their limited payload capacity, making them unsuitable for large-scale material transportation. To address this challenge, in the case of insufficient road resources, trains are prioritized for the large-scale and long-distance transportation of emergency supplies, enabling efficient delivery to transit centers. At the stage from transit centers to the disaster areas, roads are often damaged or traffic is disrupted due to the impact of the disaster. In such scenarios, drones are deployed to conduct small-scale, flexible, and precise deliveries, ensuring access to supplies for each affected location. This strategy fully leverages the efficiency advantages of trains for long-distance and large-volume logistics, while also incorporating the flexibility and rapid response capability of drones in traffic-constrained environments. Together, they form a complementary and highly efficient three-tier EMS network. Based on this network framework, EMS is transformed into a multi-level optimization problem with strong correlation between levels. Considering the complexity inherent in multi-level optimization problems, developing an appropriate algorithm to effectively solve the proposed problem becomes a key focus of this study.

A multi-level optimization problem [32] is generated in a real work scenario. As the scale of an objective practical problem becomes larger and larger, the structure becomes more and more complex, and more and more people are involved, and a kind of complex large system with many practical factors is formed; that is, a complex large system with multiple personal, hierarchical structure, and multiple objectives. Multi-level optimization problems have thus emerged. Multi-level theory was developed to study the hierarchical nature of systems, and every multi-level decision-making problem can be composed of several bilevel problems [1]. In theory, each level has its own independent optimization objective. In practice, however, there are real interdependencies between levels. The challenge in solving multi-level optimization problems is how to coordinate the overall situation, achieving global optimality while striving to reach local optimality at each level.

Multi-level theory was first introduced by Stackelberg [24] in the field of game theory, representing a two-person leader–follower game problem. In 1973, Bracken and McGill [25,26] studied this as a mathematical programming problem and proposed a mathematical model for bilevel optimization. Jeroslow [27] pointed out that the bilevel optimization problem is an NP-hard problem, and Ben-Ayed [28] and Bard [29] provided brief proofs of this conclusion. Hansen [33] gave a rigorous proof that the bilevel optimization problem is strongly NP-hard. Later, Vicente [34] noted that the bilevel optimization problem is indeed a very complex issue. Due to its NP-hard nature, there are currently no effective polynomial-time algorithms to solve it under various circumstances.

In the context of EMS problems, Song et al. [35] pointed out that post-disaster rescue operations do not consist of just one layer, but exist in double or even multiple layers. They established a bilevel EMS model consisting of disaster areas, transit centers, and storage warehouses, demonstrating the feasibility of multi-level networks in emergency scheduling, which provided a valuable reference for designing our multi-layer EMS network. Wang et al. [36], against the backdrop of significant public health events, expanded on the three-level network architecture, implementing dynamic demand prediction by combining the SEIR infectious disease model. The introduction of chaotic reverse learning and non-linear convergence factors into the improved grey wolf algorithm effectively balanced the objectives of economic efficiency and timeliness in multi-period scheduling. Fan [37] innovatively combined the CRITIC method with minimax functions, constructing a mixed-integer programming model through a “storage warehouse–transit center–disaster area” three-level structure, which inspired us to design a coordinated dispatching network that leverages the complementary characteristics of drones and trains in transportation. Matej [38] proposed a bilevel adaptive EMS system for microgrid scheduling that organically combines profit-maximizing upper-level scheduling with real-time correction lower-level control through a rolling horizon strategy. The BESS model verified the advantages of a bilevel structure in dealing with uncertainties in renewable energy. Ghaffarpour et al. [39] solved a bilevel energy supply system problem using the Karush–Kuhn–Tucker (KKT) conditions method. Li et al. [40] designed a hybrid solving framework for material transportation problems, utilizing exact algorithms in the upper model and GA in the lower model. Olivares-Aguila et al. [41] proposed the Hooke–Jeeves (HJ) algorithm and a hybrid scatter search method (Scatter Search Nelder–Mead, SSNM) to solve the bilevel resource allocation problem.

Currently, solving multi-level optimization scheduling problems mainly involves the improvement of intelligent optimization algorithms towards a fusion of multiple strategies. This paper plans to further expand research in this area by integrating real practical problems.

2.2. Multi-Stage EMS Problem

Currently, numerous studies have been conducted on the efficient scheduling of emergency materials following a disaster, based on real disaster scenarios. The EMS problem after a disaster can be divided into two categories: static and dynamic. The multi-stage material scheduling framework belongs to the dynamic scheduling model and has received widespread attention due to its flexibility and adaptability [42]. Extensive and in-depth research has been carried out on the application of both models and algorithms.

In the construction of multi-stage material scheduling models, researchers have proposed a variety of solutions for different disaster scenarios. Liu et al. [43] applied the Petri net approach to an emergency response model under resource constraints and temporal uncertainty, demonstrating the applicability of dynamic scheduling in complex scenarios. Wang et al. [44] developed a dynamic multi-stage allocation model for a three-level distribution network, aiming to minimize the shortage delay loss and total cost. By employing proportional-shortage-based fairness metrics, the model ensures equitable allocation across multiple disaster areas, highlighting the need to balance efficiency and fairness in multi-stage emergency scheduling. Wang et al. [45] proposed an EMS model for multiple rescue points, multiple affected points, and multiple periods, which allows decision-makers to balance efficiency, effectiveness, and fairness. Li et al. [46], targeting urban rainstorm and flood disasters, innovatively introduced the entropy weight-TOPSIS method to establish a two-stage material allocation framework, effectively coordinating multiple objectives, such as scheduling time, social cost, and fairness. These studies provided valuable insights for the design of dynamic scheduling frameworks.

In terms of algorithm application, due to the complexity of the multi-stage EMS problem, hybrid optimization algorithms have shown significant advantages. Wang et al. [47] addressed the dynamic scheduling problem of emergency materials under large-scale emergencies by combining mixed-integer programming with GA, solving the vehicle routing optimization problem under limited transportation capacity, demonstrating the effectiveness of hybrid algorithms in solving multi-stage vehicle routing challenges. Zhan et al. [48] proposed a dynamic distribution strategy driven by a Bayesian updating mechanism based on the demand evolution pattern in typhoon disasters. Guo et al. [49] developed a two-stage multi-objective integer programming model for earthquake disaster scenarios and optimized the supply chain network using the ant colony optimization (ACO), verifying the model’s effectiveness in post-disaster material allocation. Liu et al. [50] designed an integrated optimization algorithm and encoding adjustment strategy for multi-stage allocation and scheduling of relief materials, improving the NSGA-II algorithm and validating the proposed method through simulation experiments. Zhu et al. [51] combined behavioral operations research with inequity aversion theory to propose a multi-objective scheduling model based on disaster victims’ psychological perception, simultaneously optimizing the risk perception of emergency material arrival time and the fairness satisfaction of material quantity, and designed an ACO for solving. Liu et al. [52] improved the NSGA-II algorithm to address convergence and distribution issues, meeting the dual objectives of the shortest scheduling time and the lowest transportation cost. These studies provided insights into solving scheduling problems through multi-objective optimization.

However, the aforementioned studies still have some limitations. In terms of model construction, there is a certain discrepancy between the models and actual post-disaster EMS scenarios. Regarding algorithm solving, most studies adopted hybrid optimization algorithms to address the complex problem of multi-stage EMS. However, there is still a gap between the solution results and the optimal solution. Considering real-world situations, finding suitable models and methods to solve the multi-stage EMS problem remains a hot topic in current research.

2.3. Priority

Research on EMS has gradually incorporated non-traditional evaluation indicators such as fairness, urgency, and priority to further ensure the rationality of post-disaster material distribution and reduce the occurrence of conflicts and social instability in the aftermath of disasters. To effectively address this issue, it is crucial to first deepen our understanding of fairness. Since absolute fairness does not exist, in our view, achieving fair emergency material distribution requires solving the problem of need-based allocation. This means distributing materials according to the priority of needs in different disaster areas and ensuring comprehensive coordination.

Long et al. [20] introduced the Gini coefficient to address the equitable allocation of heterogeneous resources in the aftermath of disasters. Wei et al. [53] utilized relative deprivation cost to measure the psychological stress experienced by disaster victims in each disaster area, ensuring a fair distribution of supplies. Lee et al. [54] innovatively combined fairness with the efficiency of material scheduling, investigating resilience assessment methods and improvement strategies under emergency lockdown scenarios. These studies highlighted the importance of considering fairness and priority balance in scheduling.

Zhao et al. [55] developed a vehicle optimal path planning method based on the urgency of material demand to enhance emergency management capabilities, thereby meeting the needs of disaster areas more efficiently. Zhang et al. [21] applied the entropy weight method to determine the urgency of each demand point and adopted an improved particle swarm optimization (PSO) algorithm to optimize delivery routes, aiming to minimize path lengths, while prioritizing high-urgency demand points. Fan [37] introduced the CRITIC method to measure the volatility and conflict of demands for limited supplies in each disaster area and proposed a quantification method for demand urgency. These findings provided insights into how to quantify and apply priority in scheduling.

Chen et al. [56] proposed a multi-objective optimization model based on a utility-first economic allocation strategy that incorporates priority considerations to optimize the distribution of emergency materials. Weng et al. [57] focused on the psychological distress cost caused by shortages in relief supplies during public health emergencies, proposing an improved GA to balance demand prioritization and fairness. Wang et al. [58] optimized the calculation of priority coefficients and time windows by investigating differences in satisfaction with rescue efficiency and fairness across various disaster areas, thereby constructing a new material distribution route planning model. These studies demonstrated the application pathways for priority in optimization models and inspired us to explore how to more effectively embed priority into scheduling models.

The abovementioned literature collectively indicates that by introducing metrics such as fairness, urgency, and priority, the efficiency of EMS and resource utilization can be significantly improved, enhancing the satisfaction of disaster victims. Current research trends focus on integrating various heuristic and exact algorithms to solve complex multi-stage EMS optimization problems, thereby better addressing real-world challenges. Building on this foundation, this paper is dedicated to exploring a priority-based multi-stage EMS optimization problem, aiming to provide more scientifically effective solutions.

2.4. Research Gaps and Objectives

Extensive and in-depth research has been conducted in the existing literature on post-disaster EMS, providing a solid theoretical foundation and methodological support for practical emergency logistics operations. However, several research gaps still exist, as summarized in the following

Table 1. Comparison between existing literature and this study.

Dimension	Existing Works	Boundedness	This Study
Problem	Rescue network design [8]; optimization of transit center location selection [9,10,11]; optimization of emergency material scheduling [12,13]; drone collaborative distribution [14]	Insufficient consideration of realistic disaster scenarios, such as road disruptions and resource constraints	Designed a three-level network architecture with the cooperation of drones and trains and a multi-stage scheduling strategy based on the priority of disaster areas, which is more in line with the needs of actual material scheduling scenarios
Model	dynamic uncertain scheduling model [43]; dynamic multi-stage and multi-objective scheduling model [44]; material scheduling model considering fairness and urgency [1,20,21]; bilevel material scheduling model [37,38]	Static or single-stage assumptions, weak cross-level coordination mechanisms, unable to reflect the association relationship between upper and lower layers	A multi-stage bilevel mixed-integer nonlinear programming model based on priority, considering multi-dimensional constraints such as node inventory, warehouse capacity, and drone transportation capacity
Algorithm	A Bayesian update mechanism-driven dynamic distribution approach [48]; NSGA-II for multi-stage and multi-objective material scheduling [50,52]; Ant Colony Algorithm, etc. [49,51]	Reliance on single or rudimentary hybrid algorithms that are susceptible to converging to suboptimal solutions	Tabu Genetic Algorithm–Branch and Bound (TGA-BB), integrating GA global search, BB precision solution, and TS local obstacle avoidance, designing a stage-adjustment operator to meet multi-stage scheduling needs based on priority

:

In summary, this paper addresses the issues of the limitations of transportation modes and resources and the uneven resource distribution in post-disaster EMS by constructing a priority-based multi-stage bilevel EMS model for drone coordination. The model aims to ensure that people in urgent demand areas receive material support preferentially and promptly, thereby alleviating the spread of disaster and its negative social impacts to the greatest extent. Considering the characteristics of practical problems and model complexity, this paper further designs an efficient solution method to generate reasonable and feasible optimization plans for post-disaster EMS, effectively supporting scheduling decisions, improving overall disaster relief efficiency, and improving resource utilization levels.

3. Multi-Stage EMS Optimization Problem

This study addresses multi-stage drone-coordinated EMS based on priority levels in post-disaster scenarios, following a methodology framework of “problem modeling–algorithm design–experimental validation”. First, a multi-stage EMS model was developed based on a three-tier network incorporating coordination between drones and trains, with disaster area priorities assessed using the fuzzy comprehensive evaluation method. Second, the TGA-BB algorithm was designed to address the complex constraints of the model. Finally, the effectiveness of the proposed approach was verified through simulation experiments.

This section first introduces the problem of EMS, then constructs a bilevel programming model for multi-stage EMS based on the priority of disaster areas, and finally explains the evaluation method for priority and its role.

3.1. Problem Description

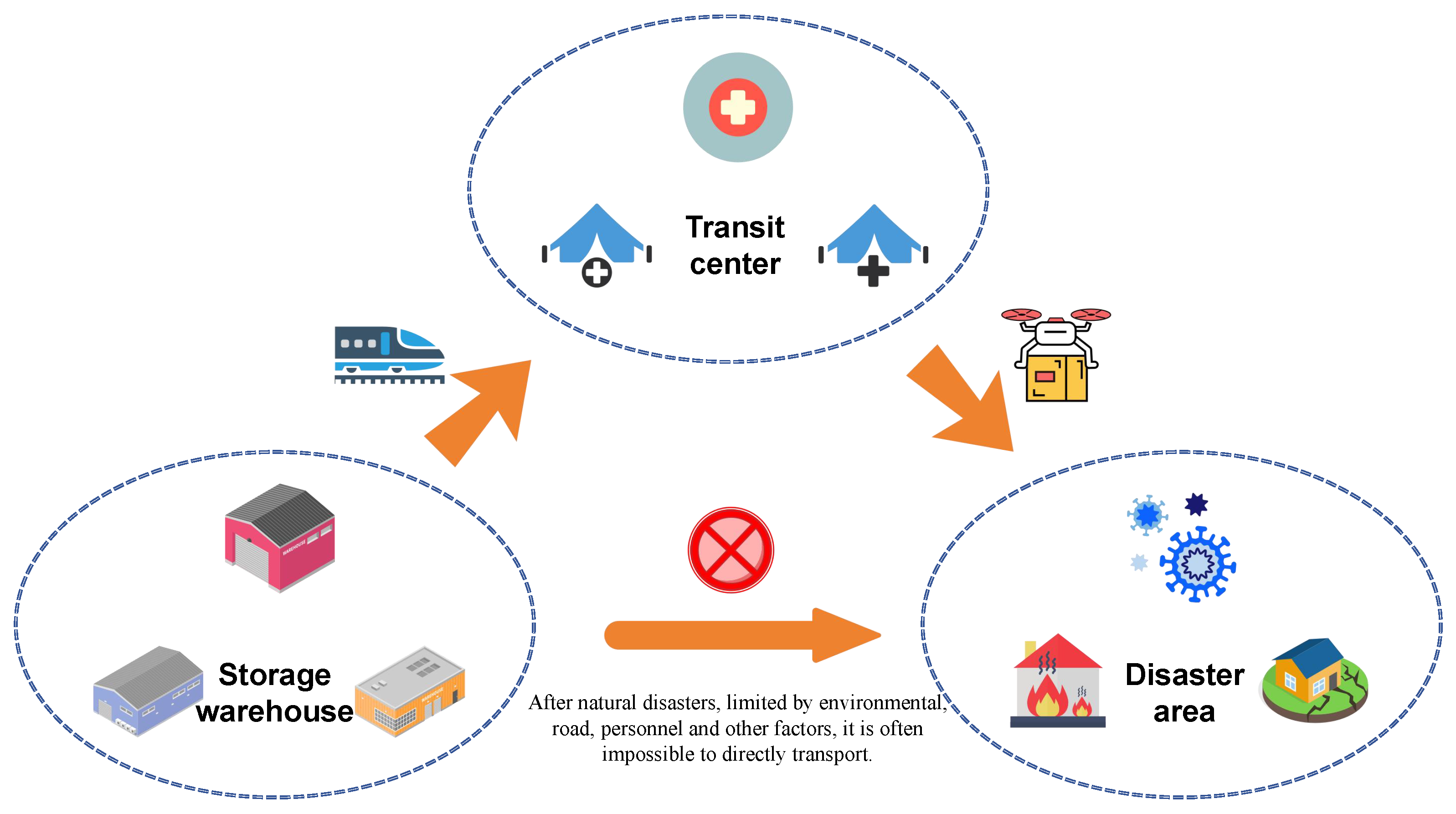
After a disaster, various living resources are severely damaged, posing a serious threat to the daily life of the people. The government urgently needs to allocate essential living security materials to meet the basic living needs of the affected people. However, in reality, storage warehouses are usually far from disaster areas, and roads are often seriously damaged after a disaster, making it impossible to directly transport large quantities of materials to the disaster areas from the storage warehouses via large trucks, trains, etc. Therefore, building transit centers in areas with relatively convenient transportation was considered, utilizing the efficiency and flexibility of drones to distribute emergency materials from the transit center to the disaster area, while large quantities are transported by trains at a large scale. 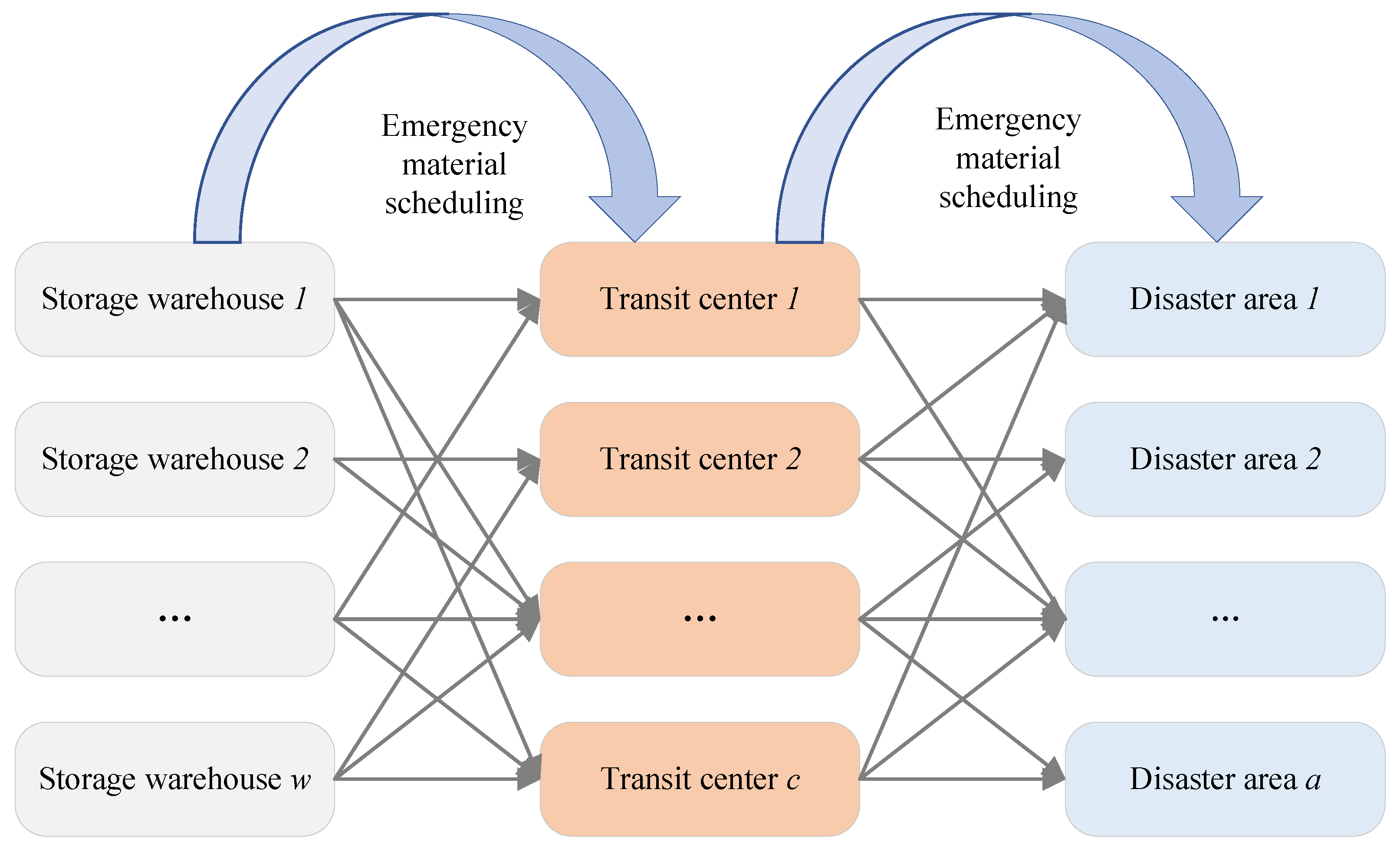This forms a coordinated drone–train three-level EMS network consisting of “storage warehouses–transit centers–disaster areas”, as illustrated in Figure 1. It should be noted that the practical deployment of drones must align with local regulatory requirements. Furthermore, the interdependencies among nodes within the three-level EMS network are examined, and an associated interaction mechanism is constructed, as shown in Figure 2.

In the abovementioned drone cooperative three-level EMS network of “storage warehouse–transit center–disaster area”, the transit center serves as a key hub, mainly undertaking the functions of material allocation and transshipment. Considering practical constraints such as the inventory capacity at both the storage warehouses and the transit centers and the transportation capability of trains and drones, and aiming to achieve the goal of the optimal response time for EMS after disasters, this paper establishes a bilevel programming model for EMS based on real-world conditions. Based on actual scenarios and the requirements of model solving, the following assumptions are made in this study:

(1)

Emergency materials are standardized in their packaging according to demand, meaning that for different disaster scenarios, the demand ratios of various types of materials (e.g., medical supplies, food, etc.) are predicted based on historical data and disaster type. These materials are then packed into fixed combinations and formed into uniform delivery units, enabling rapid and efficient scheduling and distribution;

(2)

The material needs of a transit center can be supplied jointly by multiple storage warehouses;

(3)

The assumption that the material demands of an disaster area can only be supplied by a single transit center is applicable to emergency situations in the early stages of a disaster, when resources are limited and the scheduling system has not yet been fully established. However, in large-scale disasters, it is common, and often more efficient, for multiple transit centers to collaboratively deliver supplies to the same disaster area. Therefore, this assumption has certain limitations and may underestimate, to some extent, the system’s flexibility and efficiency in resource allocation. Future research will explore more complex scenarios, to further investigate this issue and develop more realistic and adaptable models.

Related symbol descriptions are shown in

Table 2. Notations and definitions.

Notations	Definitions
Sets
W	Storage warehouses
C	Transit centers
A	Disaster areas
S	Scheduling stages
P	Priority disaster areas
Indices
w	Index for storage warehouses
c	Index for transit centers
a	Index for disaster areas
k	Index for scheduling stages
Parameters
$I_w^k$	The quantity of materials in storage warehouse at each stage
$I_c^k$	The storage capacity of transit center at each stage
$L_w^k$	The transport capacity of storage warehouse at each stage
$L_c^k$	The transport capacity of transit center at each stage
$R_a$	The need for supplies in the disaster areas
$A_k$	The disaster area for scheduling in stage k
$D_{wc}$	The shortest distance between storage warehouse w and transit center c
$D_{ca}$	The shortest distance between the transit center c and the disaster area a
$V_{wc}$	Average speed of trains from storage warehouse w to transit center c
$V_{ca}$	Average speed of drones from transit center c to the disaster area a
$D_{drones}$	The maximum distance traveled by the drones
Decision variable
$x_{wca}^k$	The quantity of supplies delivered by the storage warehouse w in stage k to the disaster area a via the transit center c

.

3.2. Multi-Stage EMS Optimization Model

In the context of post-disaster EMS, emergency management departments need to develop scientific and rational scheduling plans based on the extent of damage and material requirements in the disaster areas, thereby achieving effective coordination of the overall emergency material distribution and preventing further expansion of post-disaster negative impacts. Based on the aforementioned problem characteristics and constraints, this optimization problem can be formulated as follows:

On the premise of meeting the inventory capacity of storage warehouses and transit centers, as well as the transport capacity of trains and drones, and ensuring timely protection of high-priority disaster areas, the optimal global emergency material distribution scheme of “storage warehouses–transit centers–disaster areas” was determined, so as to minimize the total response time. Therefore, a priority-based bilevel EMS model was proposed, with the following optimization objectives:

$$MinT=T_{WC}+T_{CA}$$

(1)

In Equation (1), T represents the global total response time, while $T_{WC}$ and $T_{CA}$, respectively, represent the total response time of each level for EMS by train transportation in “storage storehouse–transit center” and drones transportation in “transit center–disaster area”.

During the EMS process, materials are first transported from storage warehouses to transit centers by train, and then distributed from the transit centers to the disaster areas by drones. Therefore, this study defines the scheduling process from “storage warehouse–transit center” as the upper-level model of the bilevel programming model, and the process from “transit center–disaster area” as the lower-level model. Although the upper- and lower-level models are structurally independent, they are highly interdependent in terms of scheduling decisions.

In summary, this study constructs a priority-based bilevel EMS model, which is specifically formulated as follows:

Upper-level model:

$$Min{T}_{sc}=\sum _{k=1}^K\sum _{c=1}^{C}Bool(x_{wca}^k)\ast ({\displaystyle \frac{D_{wc}}{V_{wc}}})$$

(2)

$$s.t.\sum _{c=1}^C\sum _{a=1}^A{x}_{wca}^k\le I_w^k,\forall w\in W,\forall k\in K$$

(3)

$$\sum _{c=1}^C\sum _{a=1}^A{x}_{wca}^k\le L_w^k,\forall w\in W,\forall k\in K$$

(4)

Equation (2) represents the optimization objective of the upper-level model, which aims to minimize the sum of the maximum response times for scheduling emergency materials from each storage warehouse w to transit centers c across all stages by train. Equation (3) is the capacity constraint at the warehouse level, ensuring that the total amount of materials scheduled from storage warehouse w to all transit centers c does not exceed the inventory capacity. Equation (4) represents the train transportation capacity constraint of each storage warehouse w, limiting the quantity of materials transported from the warehouse to each transit center, so that this does not exceed the corresponding transportation capability.

Lower-level model:

$$Min{T}_{ca}=\sum _{k=1}^K\sum _{a=1}^{A}Bool(x_{wca}^k)\ast ({\displaystyle \frac{D_{ca}}{V_{ca}}}).$$

(5)

$$s.t.\sum _{w=1}^W\sum _{a=1}^A{x}_{wca}^k\le I_c^k,\forall c\in C,\forall k\in K.$$

(6)

$$\sum _{w=1}^W\sum _{a=1}^A{x}_{wca}^k\le L_c^k,\forall c\in C,\forall k\in K.$$

(7)

$$\sum _{w=1}^W\sum _{c=1}^C{x}_{wca}^k\ge R_a,\forall a\in A,\forall k\in K.$$

(8)

$$\sum _{w=1}^W\sum _{a=1}^{A}bool\left(x_{wca}^k\right)\ast 2D_{ca}\le D_{drones},\forall c\in C,\forall k\in K.$$

(9)

Equation (5) is the optimization objective of the lower-level model, which aims to minimize the sum of the maximum response times for scheduling emergency materials from each transit center c to the disaster area a across all stages by drones. Equation (6) is the receiving capacity constraint of each transit center c, ensuring that the total amount of materials received does not exceed their storage capacity. Equation (7) specifies the drone transportation capacity constraint of each transit center c, limiting the amount of materials that can be scheduled from the transit center to disaster areas based on its drone transportation capabilities. Equation (8) is the demand satisfaction constraint, which guarantees that the quantity of materials delivered to each disaster area a is no less than the minimum required demand threshold. Equation (9) represents the flight distance limit of the drones for EMS.

3.3. Priority Analysis

The problem of priority-based EMS has long been studied, with the focus mainly centered on balancing priority and scheduling efficiency. Generally, methods for handling this balance can be categorized into three types: (1) Multi-objective Integration Method: treating priority as an objective incorporated into the model, transforming the original single-objective optimization problem into a multi-objective optimization problem; (2) Performance Evaluation Method: measuring priority separately as a performance standard; and (3) Constraint Modeling Method: solving the problem by incorporating priority as a constraint in the model, which can be further divided into soft constraints and hard constraints. This study adopts method (3) for modeling and optimization for the following reasons: (1) Compared to the Multi-objective Integration Method, the Constraint Modeling Method is less computationally complex and avoids the complexity involved in comparing Pareto solution sets in multi-objective optimization; (2) although the Performance Evaluation Method can consider fairness and scheduling efficiency to a certain extent, it struggles to guarantee actual fairness in resource allocation outcomes; (3) the Constraint Modeling Method allows flexible adjustment of the constraint space, achieving a dynamic balance between priority and scheduling efficiency and enabling differentiated responses to varying levels of priority demand.

Therefore, this paper introduces the priority of disaster areas as a constraint in the EMS optimization model, effectively ensuring that severely affected disaster areas receive priority access to supplies. To ensure the validity of the solution space after introducing priority constraints, this paper selects only those disaster areas that have urgent needs as priority scheduling targets, dividing priorities into two evaluation levels: “high” and “low”. Priority assessment uses the fuzzy comprehensive evaluation, with the calculation formula as follows:

(1) Select key evaluation indicators U according to the characteristics of different disasters. Taking the 2025 Tibet earthquake as a case example, we constructed an evaluation index system consisting of four key dimensions: “population density in disaster-stricken areas”, “casualty status”, “level of infrastructure destruction”, and “medical resource scarcity”:

$$U=\{u_1,u_2,u_3,u_4\}$$

(10)

(2) According to the priority resolution requirements of the multi-stage EMS model, the evaluation set V is determined as follows:

$$V=\{v_1,v_2\}=\{\mathrm{high}\mathrm{priority},\mathrm{low}\mathrm{priority}\}$$

(11)

(3) The weights of each indicator were obtained by collecting expert scores from multiple professionals in emergency management, calculating their average values, and subsequently normalizing the results to derive the weight vector W:

$$W=\{w_1,w_2,w_3,w_4\},\sum _{i=1}^4{w}_i=1$$

(12)

(4) Each indicator was evaluated by domain experts with relevant expertise. For instance, hospital administrators were recommended to assess the scarcity of medical resources. Based on these evaluations, the membership degrees of each indicator to the predefined evaluation levels were calculated, and the corresponding membership matrix R was constructed:

$$R=\left[\begin{array}{cc}{r}_{11}& r_{12}\\ ⋮& ⋮\\ r_{41}& r_{42}\end{array}\right]$$

(13)

(5) Perform the fuzzy synthetic operation using the weight vector W and the membership matrix R:

$$B=W\circ R=(b_1,b_2)$$

(14)

(6) Each level in the evaluation set is assigned a numerical value (e.g., High = 1, Low = 0), based on which the comprehensive score S for each disaster area is computed:

$$S=\sum _{i=1}^2(b_j\ast v_j)$$

(15)

(7) Based on the comprehensive score S, the priority levels of disaster areas are determined. It should be noted that the evaluation criteria must be adaptively calibrated in accordance with the specific disaster conditions of each affected region to ensure fairness and responsiveness in EMS:

$$P=\left\{\begin{array}{c}1,S\ge 0.8\hfill \\ 0,S<0.8\hfill \end{array}\right.$$

(16)

It should be noted that after integrating priority as a constraint into the bilevel programming model for EMS, disaster areas with a priority level of 1 will be scheduled in the first stage by drones. If insufficient supplies or lack of drones make it impossible to complete deliveries in the first stage, the scheduling for these areas will be carried over to subsequent stages. However, their priority must be maintained throughout the entire scheduling process, ensuring they receive precedence over regions with normal (lower) priority. In addition, after completing one stage of EMS, the system can incorporate real-time disaster data (e.g., newly reported needs, progress of rescue operations) to dynamically reassess the priorities of disaster areas. Based on this updated information, the global scheduling plan can be re-optimized, enabling real-time updates to the current priority settings. At present, this process still relies on manual intervention for re-evaluating priorities and adjusting the scheduling strategy. Future research could further integrate a priority evolution mechanism into the scheduling system, allowing it to automatically and adaptively update the priority levels of disaster areas after each stage of assessment. This would enable dynamic optimization of the EMS plan not only for subsequent stages, but also across the entire disaster response cycle.

4. A Priority-Based Multi-Stage EMS Optimization Method

In order to quickly and efficiently solve the multi-stage EMS optimization problem based on priority, we have designed a hybrid optimization method that combines GA with BB, TS, and stage-adjustment operators. First, the overall framework of the TGA-BB is introduced in detail. Next, the solutions for the heuristic algorithms are presented. Subsequently, the process of generating initial solutions is described. Then, the applications of BB, TS, and stage-adjustment operators in the designed hybrid optimization algorithm model are introduced in sequence. Finally, combining the problem model and the algorithm model, the computational complexity of the algorithm is analyzed.

4.1. Overview of TGA-BB

The GA, as an intelligent optimization method based on the principles of biological evolution, was first proposed in 1967 by a research team led by Professor Holland at the University of Michigan. Its core concept is derived from Darwin’s theory of evolution and Mendel’s principles of genetics [59,60]. By simulating natural selection mechanisms, the GA performs efficient stochastic searches within the solution space, making it particularly suitable for solving complex optimization problems.

The multi-stage EMS optimization model constructed in this study, which is based on priority considerations, exhibits NP-hard characteristics. Traditional exact algorithms struggle to obtain satisfactory solutions within a reasonable time frame, while conventional heuristic algorithms often face limitations such as slow convergence and a tendency to fall into local optima when dealing with such complexity. Given the strong adaptability of GAs in addressing complex optimization tasks, as well as their excellent compatibility with other optimization approaches, this paper designs a hybrid optimization algorithm, TGA–BB, which integrates GA, BB, TS, and stage-wise optimization techniques to solve the aforementioned model. This hybrid approach fully leverages the strengths of each individual optimization method, aiming to overcome the performance bottlenecks associated with using single-method algorithms in complex scheduling problems, thereby enhancing the overall solution quality.

Algorithm 1 outlines the overall framework of TGA-BB. Initially, an initial population composed of individuals is generated. The initial solutions are based on the determined priority levels of the disaster areas, allocating those urgently needing emergency materials to the initial stages, while the scheduling stages for the other ordinary disaster areas are randomly generated according to the number of schedulable areas in each stage and encoded into genes as described in Section 4.2 and Section 4.3. Subsequently, the fitness function calculation is performed. In the first step, based on the set number of schedulable disaster areas in each stage, the genes within individuals are divided into stages. In the second step, it is determined whether BB solving should be applied to the genes of each stage. If solving has been completed, the fitness function values stored in the Tabu dictionary are directly retrieved. If not, after performing BB solving, the material scheduling information and solving results for that stage are stored in the Tabu dictionary. In the third step, the objective function values of each stage are summed up to calculate the fitness function value corresponding to the individual. Following this, the optimal objective function value of the current generation is calculated based on the fitness function values of the population. Afterwards, elite individuals are selected to be retained for the next generation’s population based on the fitness function values of the population. Then, parent individuals are chosen using Tournament selection methods, and crossover and mutation operations are performed using a designed stage-selection algorithm, detailed in Section 4.6. Finally, a new population is generated, and these processes are repeated until the maximum number of iterations is reached.

4.2. Expression of Material Scheduling Scheme

Representation of scheduling solutions for disaster areas: Each candidate solution is a vector, which is essentially a decimal array whose length equals the number of disaster areas. The index of each gene represents the order in which the corresponding disaster areas will be scheduled materials. The scheduling stages are evenly divided according to the predefined number of stages specified by the problem settings. The encoding of individuals is as follows:

$$I=\{a_1,a_2,,a_p,a_{p+1},...,a_i\},a_p\in P,a_i\in A$$

(17)

$$s=\lceil index\left(a_i\right)/len\left(A\right)\ast len\left(S\right)\rceil ,a_i\in A,s\in S$$

(18)

Algorithm 1: Tabu Genetic Algorithm–Branch and Bound

Input:  Population size $Pop\_Size$, adjustment rate $\mu$, max Gens $G_{max}$, tournament size $Tourment\_Size$, elite size E, max tabu size $Max\_Tabu\_Size$ Output:  Best EMS plan and fitness value. 1: procedure  TGA-BB 2:       Initialize global parameters (W, C, A, S, etc.) 3:       Initialize tabu dictionary $tabu\_dict$ as OrderedDict 4:       $populationP\leftarrow InitializePopulation\left(\right)$ 5:       $best\_fitness\leftarrow \infty$, $best\_individual\leftarrow \varnothing$ 6:       for $gen\leftarrow 1$ to $G_{max}$ do 7:             $fitness\_values\leftarrow Fitness\left(\right)$ 8:             Update $best\_fitness$ and $best\_individual$ if improved 9:             Stage adjustment was performed using Algorithm 2 10:       end for 11:       Store results for current experiment 12:       Output results to Excel file 13: end procedure 14: function $Fitness\left(\right)$ 15:       for $stage\leftarrow 1$ to S do 16:             Call Algorithm 4 17:             if The stage disaster areas in the Tabu dictionary then 18:                    $f_i\leftarrow Algorithm4$ 19:             else 20:                    $f_i\leftarrow Algorithm3$ 21:             end if 22:             $F\leftarrow F+f_i$ 23:             return $fitness\_values$ 24:       end for 25: end function

In Equation (17), $a_i$ represents the gene, indicating the serial number of the disaster area. $a_p$ denotes the priority of the disaster area. In Equation (18), s represents the scheduling stage in which the disaster area is located. This clarifies the set of disaster areas scheduled in each stage.

The scheduling plan for disaster areas in a single stage is represented as follows: Within a single stage, given the limitation of available emergency rescue resources, the model scale is relatively small, making it feasible to use the BB for an exact solution, and the decision variable is defined as $x_{wca}$, which indicates the emergency materials are scheduled from the storage warehouse w through the transit center c to the disaster area a. Finally, the scheduling plans for the disaster areas in each stage are aggregated.

4.3. Population Initialization

In the priority-based multi-stage EMS process, it is required that the material demands of disaster areas with priority level 1 are first. Random initialization of the population makes it difficult to guarantee the precedence of high-priority disaster areas in the scheduling plan. To address this issue, this paper introduces a priority-based classification strategy during the population initialization stage: first, based on the priority information of the disaster areas, all regions are divided into two sets, the high-priority disaster area set and the normal-priority disaster area set, and the number of areas in each set is recorded; then, in the chromosome encoding, a segmented approach is adopted, with the front portion fixed for the high-priority disaster areas and the latter portion allocated to the normal-priority areas; finally, within each set, a random permutation is applied to complete the population initialization.

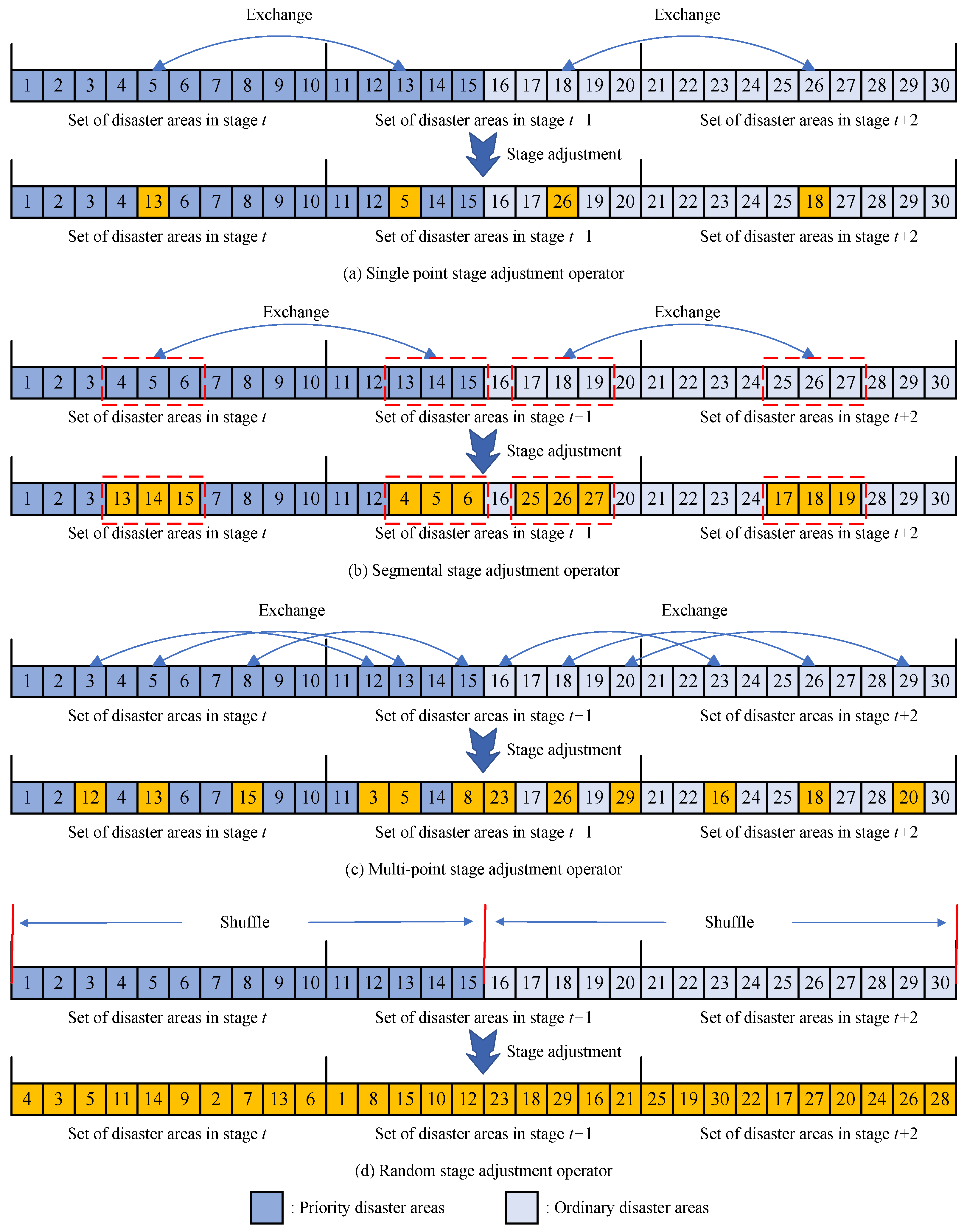
4.4. Stage-Adjustment Operator

Traditional crossover and mutation operations can disrupt the chromosome structure designed in Section 4.3, leading to a violation of the priority scheduling constraints and affecting the feasibility of solutions. To address this issue, this paper designs a stage-adjustment operator based on the GA. This algorithm ensures that chromosomes still meet priority scheduling requirements after crossover and mutation operations by performing stage adjustments within the high-priority disaster area set and the normal-priority disaster area set separately, as shown in Algorithm 2. To meet the practical requirements of the multi-stage EMS optimization problem, this paper designs four stage-adjustment operators: a single-point stage-adjustment operator, a segment-based stage-adjustment operator, a multi-point stage-adjustment operator, and a random stage-adjustment operator. Each type of operator provides a different stage-adjustment strategy to handle disturbances in chromosome structures caused by crossover and mutation operations during the scheduling process. This helps maintain solution feasibility, while enhancing population diversity and the global search capability of the algorithm. The specific mechanisms of each stage-adjustment operator are illustrated in Figure 3.

Algorithm 2: Stage adjustment operator

Input:  Initial population $P_0$, max Gens $G_{max}$, adjustment rate $\mu$, elite size E Output:  Optimal solution $S^{*}$, total cost $C^{*}$ 1: procedure  SAO 2:       Initialize population $P\leftarrow InitializePopulation\left(\right)$ 3:       $S^{*}\leftarrow \perp$, $C^{*}\leftarrow \infty$ 4:       for $g\leftarrow 1$ to $G_{max}$ do 5:             Compute fitness values $\mathcal{F}\leftarrow \left[Fitness\right(x)\mid x\in P]$ 6:             $S_g\leftarrow arg{min}_{x\in P}\mathcal{F}\left(x\right)$, $C_g\leftarrow min\mathcal{F}$ 7:             if $C_g<C^{*}$ then 8:                    $S^{*}\leftarrow S_g$, $C^{*}\leftarrow C_g$ 9:             end if 10:           Select elites $E_{\mathrm{elite}}\leftarrow SelectElites(P,\mathcal{F},E)$ 11:           Generate offspring $O\leftarrow \varnothing$ 12:           while $\left|O\right|+|E_{\mathrm{elite}}|<|P|$ do 13:                  $p\leftarrow TournamentSelection(P,\mathcal{F})$ 14:                  $Apply\mu \leftarrow StageAdjustment(p,\mu )$ 15:                  $O\leftarrow O\cup \left\{c\right\}$ 16:            end while 17:            $P\leftarrow E_{\mathrm{elite}}\cup O$ 18:      end for 19:      $\mathbf{return}{S}^{*},C^{*}$ 20: end procedure

Single-point Stage-Adjustment Operator: The EMS problem is divided into s stages. The algorithm performs single-point stage adjustment separately for the priority disaster area set and the ordinary disaster area set, with a total of $s-1$ pairs of adjacent stage-adjustment targets. This process is illustrated in Figure 3a. Within the priority disaster area set, an object is randomly selected from stage t, and another disaster area is arbitrarily chosen from stage $t+1$. Then, a point-to-point swap is performed between the two to complete the stage adjustment. The same approach is applied within the ordinary disaster area set for point-to-point exchanges. This operator is suitable for small-scale EMS problems, as it searches for high-quality stage scheduling combinations for disaster areas with minimal perturbation.

Segment-based Stage-Adjustment Operator: The segment-based stage-adjustment operator also selects target sets of adjacent stages in a random manner, but the adjustment between different stages involves more than just small-scale “point-to-point” adjustments. As shown in Figure 3b, within the set of priority disaster areas, a randomly sized segment of disaster areas is selected from the sequence of stage t as the object for exchange. Simultaneously, an equal-length sequence of disaster areas is arbitrarily chosen from stage $t+1$, and a segment-to-segment swap is performed between them to achieve stage adjustment. The same process is applied within the set of ordinary disaster areas for segment-to-segment exchanges.

Multi-Point Stage-Adjustment Operator: The multi-point stage adjustment operator integrates the characteristics of both the single-point stage-adjustment operator and the segment-based stage-adjustment operator, addressing the limitations of the former’s restricted adjustment capability and the latter’s fixed sequence combination adjustments. As shown in Figure 3c, the algorithm introduces the concept of an adjustment probability. Within the set of priority disaster areas, the algorithm traverses the sequence of disaster areas in stage t. Based on the adjustment probability, it determines whether to adjust the current disaster area. If an adjustment is made, an disaster area is arbitrarily selected from stage $t+1$, and a point-to-point swap is performed between them to complete the stage adjustment. The same approach is applied within the set of ordinary disaster areas for multi-point stage adjustments.

Random Stage-Adjustment Operator: The random stage-adjustment operator builds upon the aforementioned stage-adjustment operators by thoroughly shuffling the sequence of disaster areas to achieve a complete stage reorganization. As illustrated in Figure 3d, within the set of priority disaster areas, every stage-adjustment involves randomly rearranging all the disaster areas within the set and then generating new chromosome sequences based on this fresh arrangement. The same procedure is applied to the set of ordinary disaster areas for sequence reorganization, with these areas being arranged after the priority disaster areas to form a new chromosome.

4.5. Branch and Bound

After clarifying the disaster areas covered by each scheduling stage, it is necessary to select appropriate storage warehouses in each stage and efficiently allocate and transport emergency materials through transfer centers. This process can be abstracted as a medium-scale-integer linear programming problem. Considering the efficiency and stability of the BB in solving such problems, this paper establishes an optimization model based on the BB to determine the optimal matching relationship between each disaster area and its corresponding storage warehouse and transfer center within each stage. The specific solution procedure is shown in Algorithm 3.

The BB technique first constructs a 0-1 integer programming model for the EMS problem. It generates an initial linear programming problem by introducing slack variables and constraints. The algorithm maintains a priority queue to store active nodes, where each node represents the state of the problem under a specific variable branching condition. In each iteration, the node with the smallest lower bound is selected for expansion. Through branching operations, fractional variables are forced to take binary values (0 or 1), generating subproblems. For each subproblem, its linear programming relaxation model is solved: if the relaxed solution value exceeds the current global upper bound, the branch is pruned; if a feasible integer solution is obtained, the global upper bound is updated. This iterative process continues until the upper and lower bounds converge or all possible branches have been explored. The algorithm ultimately outputs a scheduling plan that minimizes transportation time, while satisfying all transportation constraints. By employing an intelligent pruning strategy, the BB significantly reduces the search space, ensuring solution optimality, while improving computational efficiency.

Algorithm 3: Branch and bound

Input:  Current stage area ${\mathcal{A}}_s$, need ${\mathbf{R}}_{\mathbf{as}}$, time $\mathbf{T}$ Output:  Optimal cost C, routing decisions $\mathbf{x}$ 1: procedure  BB 2:       Initialize priority queue $\mathcal{Q}$ with root node 3:       $best\_solution\leftarrow \infty$ 4:       $incumbent\leftarrow \varnothing$ 5:       while $\mathcal{Q}\ne \varnothing$ do 6:             Select node N with minimal lower bound from $\mathcal{Q}$ 7:             Solve LP relaxation of N to get solution ${\mathbf{x}}^{*}$ and bound $LB$ 8:             if Infeasible or $LB\ge best\_solution$ then 9:                    Prune node N 10:                   continue 11:            end if 12:            if ${\mathbf{x}}^{*}$ is integer-feasible then 13:                   $best\_solution\leftarrow LB$ 14:                   $incumbent\leftarrow {\mathbf{x}}^{*}$ 15:                   Prune node N 16:            else 17:                   Select fractional variable $x_{wca}$ using most infeasible branching 18:                   Create child nodes: 19:                   $N_0$: Add constraint $x_{wca}=0$ 20:                   $N_1$: Add constraint $x_{wca}=1$ 21:                   Add $N_0$ and $N_1$ to $\mathcal{Q}$ 22:            end if 23:       end while 24:       return $best\_solution$ 25: end procedure

4.6. Tabu Dictionary Algorithm

Given that the elite selection strategy and stage-adjustment operator may introduce a certain level of randomness during computation, potentially leading to repeated calculations of some solutions and thus affecting overall optimization efficiency, this paper designs a Tabu dictionary checking algorithm based on the concept of TS. By maintaining a dynamically updated Tabu dictionary, the algorithm effectively prevents redundant exploration of the solution space, thereby improving the computational efficiency and search quality of the TGA-BB algorithm. The detailed solution procedure is presented in Algorithm 4.

Algorithm 4: Tabu dictionary algorithm

Input:  Current stage area ${\mathcal{A}}_s$, need ${\mathbf{R}}_{\mathbf{as}}$, time $\mathbf{T}$ Output:  Cached cost C, or compute new solution 1: procedure  TDA 2:       Convert area indices to key $k\leftarrow Hash\left({\mathcal{A}}_s\right)$ 3:       if $k\in Tabu\_Dict$ then 4:             $C\leftarrow Tabu\_Dict\left[k\right]$ 5:       else 6:             Compute new solution $C\leftarrow BB({\mathcal{A}}_s,{\mathbf{R}}_{\mathbf{as}},\mathbf{T})$ 7:             Store result $Tabu\_Dict\left[k\right]\leftarrow C$ 8:             if $|Tabu\_Dict|>Max\_Tabu\_Size$ then 9:                  $Tabu\_Dict.popitem(last=False)$ 10:            end if 11:      end if 12:      return C 13: end procedure

The Tabu Dictionary Algorithm was designed within the GA framework. When generating new individuals using the stage-adjustment operator, the system first encodes each individual into a rounded feature vector, which serves as a unique identifier key. If this key already exists in the Tabu dictionary, the corresponding objective function value is retrieved directly, avoiding redundant calls to the BB solver. If the solution is new, its objective value is computed precisely, and the result is updated in the Tabu dictionary. To balance storage efficiency and computational resource usage, this paper employs a First-In-First-Out (FIFO) strategy to dynamically manage the dictionary capacity. Furthermore, to preserve potentially high-quality solutions, an aspiration criterion is introduced, allowing certain superior solutions to override the Tabu restrictions. This mechanism achieves a dynamic balance between resource utilization and the retention of promising solutions. The proposed algorithm significantly reduces the number of calls to the BB solver, which constitutes the most computationally expensive part of the hybrid algorithm. It effectively improves the solution efficiency for multi-stage EMS, while maintaining solution quality.

4.7. Computational Complexity

The computational complexity of the TGA-BB approach mainly includes population initialization, fitness evaluation, the Tabu dictionary algorithm, BB, tournament selection, and stage-adjustment operator. The computational complexity of TGA-BB is primarily influenced by the fitness evaluation, as its complexity is significantly higher than that of the other operations. The computational complexity of fitness evaluation mainly stems from the Tabu dictionary algorithm and BB. Considering the complexity of one iteration of the entire algorithm, the basic operations and their worst-instance complexity are as follows:

(1)

population initialization is $O(P·A)$;

(2)

fitness evaluation is $O(S·(O\left(TD\right))·(O\left(BB\right)\left)\right)$;

(3)

tabu dictionary is $O\left(1\right)$;

(4)

branch and bound is $O\left(2^{(W·C·\left(A_k\right))}\right)$;

(5)

tournament selection is $O(P·E)$;

(6)

stage-adjustment operator is $O(P·T)$;

The complexity of one iteration of the algorithm is $O(P·S·2^{(W·C·\left(A_k\right))}+P·A+P·E+P·T)$. And in practical computations, $2^{(W·C·\left(A_k\right))}\gg P$. Therefore, the overall complexity of TGA-BB is $O(G·P·S·2^{(W·C·\left(A_k\right))})$, with the computational bottleneck focusing on the repeated solving of integer linear programming problems. By introducing a local optimization strategy through TS, the algorithm effectively reduces redundant calculations, while maintaining its global search capability. This significantly improves the solution efficiency in large-scale EMS.

In summary, this study proposes a priority-based, multi-stage, bilevel EMS optimization model built upon a three-tier network structure of “storage warehouses–transit centers–disaster areas”. The model integrates the advantages of large-scale transportation by train and flexible delivery by drones, with the primary objective of minimizing the total response time. The upper-level model focuses on scheduling train transportation from storage warehouses to transit centers, while the lower-level model optimizes drone delivery routes from transit centers to disaster areas. Disaster area priorities are quantified using the fuzzy comprehensive evaluation method based on four dimensions—population density, casualties, and others—and are embedded into the model as hard constraints. This ensures that high-priority areas receive emergency supplies during earlier stages. To solve the model efficiently, we designed a hybrid optimization algorithm, TGA-BB, which combines the global search capability of the GA, the exact solving ability of BB, and the local search avoidance capability of TS. A stage-adjustment operator is introduced to better adapt to multi-stage scheduling requirements and improve computational efficiency.

5. Experimental Instance Study

This section presents a systematic instance study to validate the scientific rigor and effectiveness of the proposed method. First, the dataset and relevant parameter settings used in the experiments were defined. Subsequently, comparative experiments on algorithm performance were conducted, and the results were analyzed in depth. Finally, through a specific instance study, the practicality and feasibility of the proposed method in real-world application scenarios were further evaluated.

5.1. Dataset and Experimental Setup

The disaster areas, transfer centers, and storage warehouses were randomly generated within the ranges of 0–500 km, −100–600 km, and −500–1000 km, respectively. According to the practical requirements of the problem, different scheduling stages were defined. Eight test instances were designed to evaluate the performance of the TGA-BB algorithm. The scales and parameter settings of each instance are presented in

Table 3. Instance scale.

Instance	Problem Scale (W*C*A*S)
1	5*3*10*1
2	5*3*10*1
3	5*5*30*2
4	5*5*30*3
5	5*10*60*3
6	5*10*60*4
7	5*15*120*4
8	5*15*120*5

and

Table 4. Algorithm parameters.

Parameter Name	Notations	Value
Population Size	P	50
Adjustment Probability	M	0.5
Number of Generations	G	50
Tournament Selection Size	T	5
Elite Selection Size	E	5
Tabu List Length	L	1000

.

5.2. Comparison of Experiments

This section systematically validates the effectiveness of the proposed TGA-BB algorithm from three perspectives. First, it analyzes the impact of different stage-adjustment operators on algorithm performance. Second, it examines the influence of introducing the tabu dictionary on the solution results. Finally, it conducts a comparative analysis between TGA-BB and other typical heuristic algorithms.

5.2.1. Stage-Adjustment Operator Comparison

This section aims to analyze the runtime and solution quality of TGA-BB under different problem scales when using various stage-adjustment operators, providing guidance for the selection of an appropriate stage-adjustment operator in subsequent applications.

Table 5. Experimental results of different stage-adjustment operators.

	Average Response Time/h				Average Running Time/s
Operators Instances	Single Point	Segmental	Multiple Points	Random	Single Point	Segmental	Multiple Points	Random
1	70.02	70.02	70.02	70.02	0.56	0.56	0.57	19.51
2	66.29	66.29	66.29	66.29	10.31	6.77	14.01	17.36
3	149.33	149.48	149.34	149.42	89.60	172.56	307.10	212.34
4	147.18	147.18	147.18	147.19	33.66	37.97	63.42	40.71
5	276.78	276.88	276.86	277.10	134.56	143.59	216.57	123.34
6	277.83	278.46	278.57	279.23	170.17	184.80	308.23	171.02
7	525.40	525.75	525.81	526.35	371.86	406.49	653.12	391.32
8	526.50	528.00	527.88	529.09	543.79	601.97	939.75	487.31

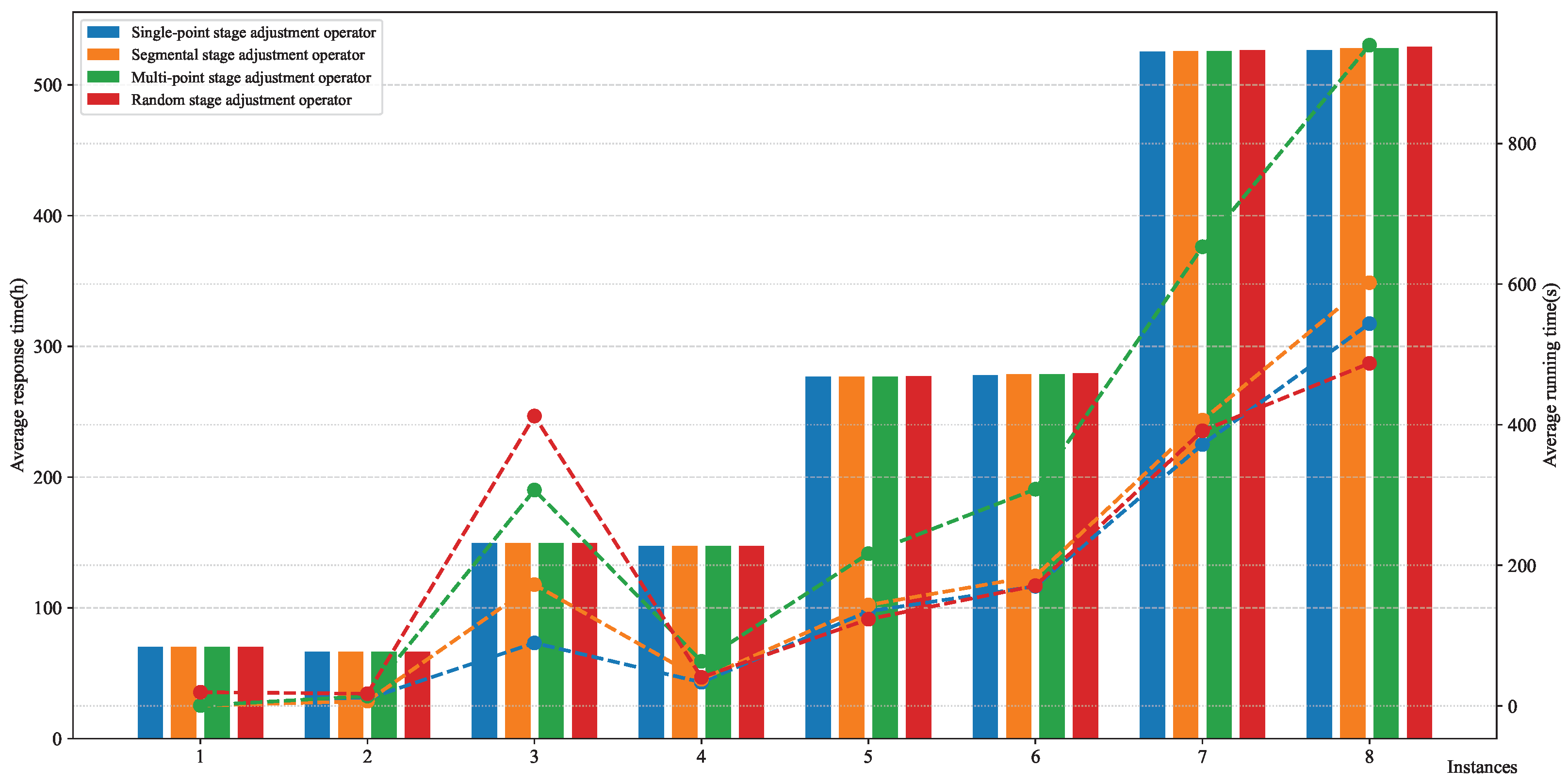
Note: The bold content represents the minimum value among all comparative experiments under the current instance.The implementation of the TGA-BB algorithm designed in this paper took the stage-adjustment operator as the only experimental variable.

lists the average solution results and average runtime obtained from 30 repeated experiments for different stage-adjustment operators on various test sets. Figure 4 shows a bar chart comparison of the average EMS response time and comparisons of algorithm runtime under different instances. Through experimental analysis, it was found that the single-point operator had an average running time of 543.79 s in instance 8, which was only 57.9% of that of the multi-point operator (939.75 s). Moreover, its average response time was 2.59 h shorter than that of the random operator, demonstrating its balanced advantages in efficiency and solution quality. The details were as follows:

In terms of the objective function value, the performance of the different stage-adjustment operators showed little overall difference. For example, in instances 1 to 8, the objective function values of the single-point stage-adjustment operator, segment stage-adjustment operator, and multi-point stage-adjustment operator were essentially consistent or had only minor deviations. However, the random stage-adjustment operator performed relatively poorly, especially in larger-scale instances (such as instances 7 and 8), where its objective function value was significantly higher than that of the other operators. This indicates that the random stage-adjustment operator, due to its large-scale genetic recombination operations in each iteration, failed to effectively preserve high-quality solutions, resulting in less-than-ideal final solutions. Further analysis reveals that, as the problem scale increased, the objective function values of all operators rose slightly, but the changes were minimal. This phenomenon demonstrates that the designed TGA-BB had a strong robustness in dealing with problems of different scales and could maintain high solution accuracy. Moreover, the single-point stage-adjustment operator consistently achieved solution effects comparable to or even better than those of the segment and multi-point operators in various instances, laying a foundation for its subsequent applications.

Regarding runtime, there was an overall upward trend as the instance scale increased, and the performance of the different stage-adjustment operators showed significant differences. Specifically, the single-point stage-adjustment operator had the shortest or nearly the shortest runtime in all instances. For example, in instance 3, its runtime was 89.60 s, much lower than the 307.10 s of the multi-point stage-adjustment operator. This is because the single-point stage-adjustment operator only performs single-step adjustment operations, resulting in lower computational complexity. The segment stage-adjustment operator had a slightly longer runtime than the single-point stage-adjustment operator but generally performed stably. Although its adjustment method involves segment operations, the limited range of segment adjustments keeps its computational complexity within a manageable range. The multi-point stage-adjustment operator had the longest runtime, especially in the large-scale problems. For example, in instance 8, its runtime reached 939.75 s, nearly twice that of the single-point stage-adjustment operator. This is because the multi-point stage-adjustment operator needs to perform adjustment operations point by point, and its computational complexity increases rapidly with the problem scale. The random stage-adjustment operator, although its runtime was similar to that of the single-point stage-adjustment operator in some instances, had poor solution effects and could not meet practical requirements. It is worth noting that the runtime of instance 4 was lower than that of instance 3. This is mainly because, although the increase in scheduling stages raises the algorithm’s computational complexity, the reduction in the number of single-stage solutions actually decreases the overall computational burden, offsetting the impact of the increased complexity.

Considering both solution quality and runtime performance, among the eight instances with different scales, the single-point operator performed the best in terms of average response time, was optimal or nearly optimal in terms of average running time, and could stably maintain priority constraints (solution fluctuation amplitude ≤ 2.3%). In comparison, although the segment-based and multi-point stage-adjustment operators performed similarly to the single-point operator in terms of solution quality, they required longer computation times. The random stage-adjustment operator, on the other hand, delivered inferior solution quality and thus failed to meet the requirements of practical applications. Therefore, the single-point stage-adjustment operator was selected for use in the subsequent experiments as the stage-adjustment strategy for TGA-BB, ensuring the algorithm’s efficiency and stability across problems of different scales, and providing a practically viable solution for real-world EMS scenarios.

However, this paper did not conduct combined tests on operators or research mixed operator strategies involving the coexistence of multiple operators. In future work, we will focus on verifying the performance of combinations such as “single-point + segment-based” and “single-point + multi-point” in dynamic priority scenarios, and explore the coordination mechanism of different operators in global search and local fine-tuning.

5.2.2. Influence of Using a Tabu Dictionary

This section is designed to systematically validate the impact of the Tabu search mechanism proposed in Section 4.6 on the solution efficiency of hybrid optimization algorithms through comparative experiments. Using the method of controlled variables, five groups of parallel comparative experiments were conducted based on the five hybrid GA frameworks constructed in Section 5.2.3, namely GA-ACO, GA-BB (the algorithm proposed in this paper), GA-GA, GA-PSO, and GA-Simulated Annealing (SA), under two conditions: with and without the inclusion of the Tabu search mechanism. The parameter settings for these experiments are provided in Table 4. The single-point stage-adjustment operator, validated in Section 5.2.1, was applied as the strategy for scheduling stage adjustments. Based on the test instance sets designed in Table 3, each algorithm combination was run independently 30 times to eliminate the influence of random factors. By comparing the average runtime of each algorithm under the two conditions (results shown in

Table 6. Experimental results with and without Tabu dictionary.

Algorithm	GA-ACO		GA-BB		GA-GA		GA-PSO		GA-SA
Instances	With	Without	With	Without	With	Without	With	Without	With	Without
1	1.90	182.56	0.56	53.76	4.88	489.24	5.30	523.16	12.23	1203.09
2	49.69	207.56	10.31	48.77	159.71	781.97	115.24	840.40	502.71	1998.57
3	190.60	263.49	89.60	286.30	411.33	581.98	445.10	617.67	190.60	263.49
4	173.15	274.09	33.66	56.80	456.43	729.80	495.77	811.21	1113.35	1800.15
5	378.01	527.59	134.56	217.59	737.78	1026.55	786.65	1096.61	1750.63	2400.52
6	365.53	532.11	170.17	251.55	794.21	1170.42	859.43	1250.52	1897.86	2811.85
7	792.70	1096.30	371.88	475.91	1136.63	1558.21	1254.49	1669.71	2675.50	3643.96
8	713.71	1086.27	543.79	713.71	1110.40	1698.88	1155.18	1846.34	2489.03	4118.53

Note: Genetic Algorithm (GA), Branch and Bound (BB), Ant Colony Optimization (ACO), Particle Swarm Optimization (PSO), Simulated Annealing (SA). The bold content represents the minimum value among all comparative experiments under the current instance. The terms “With” and “Without” represent the presence or absence of the Tabu dictionary in the respective algorithms.

), this study quantitatively evaluated the practical effectiveness of the Tabu dictionary in improving algorithmic efficiency and further explored its applicability across different hybrid algorithmic frameworks.

As shown in Table 6 and Figure 5, the introduction of the Tabu dictionary had a significant positive impact on algorithm performance, especially in small-scale problems. For example, in Instance 1, the average runtime of TGA-BB decreased from 53.76 s to 0.56 s after incorporating the Tabu dictionary, and that of GA-SA dropped from 1203.09 s to 12.23 s, both of which achieved an efficiency improvement of approximately 99%. These results indicate that in small-scale instances, the Tabu dictionary effectively prevented the algorithm from getting trapped in local optima and significantly accelerated the solution process.

As the problem scale increased, the relative performance gain from using the Tabu dictionary diminished somewhat, but the overall solution efficiency remained notably improved. Taking the large-scale instance 8 as an example, after introducing the Tabu dictionary, the running time was reduced from 713.71 s to 543.79 s, with a decrease of 23.8%. This further demonstrates that the Tabu dictionary not only provides clear advantages in small-scale problems, but also effectively reduces redundant search and repeated computations when handling complex and large-scale scheduling tasks, thereby improving overall solution efficiency.

The experimental results show that introducing the Tabu dictionary mechanism into the hybrid optimization algorithm framework proposed in this study significantly improved the solution efficiency across EMS problems of various scales. Through comparative evaluations involving multiple algorithms, this improved strategy demonstrated strong generalization performance, consistently enhancing algorithmic efficiency under different framework configurations. This study confirms the crucial role of the Tabu dictionary mechanism in hybrid optimization algorithms. On the one hand, the mechanism effectively reduces computational redundancy by avoiding repeated searches in previously explored solution spaces. On the other hand, its local avoidance characteristics significantly accelerate the convergence speed of the algorithm. These benefits not only provide reliable technical support for rapid response in EMS, but also offer new insights for the design and innovation of hybrid optimization algorithms.

5.2.3. Comparison with Other Heuristics

This section aims to systematically validate the effectiveness of the BB model proposed in Section 4.5 in achieving accurate solutions within hybrid optimization frameworks, through the designed comparative experiments. Using a controlled variable approach, the experiments retained the GA-based upper-level guiding framework unchanged, while replacing the lower-level local search modules with five commonly used algorithms for solving EMS problems, ACO, GA, PSO, SA, and BB, to form comparative experimental groups. Based on the hybrid genetic algorithm parameter settings presented in Table 4, all experiments consistently employed the single-point stage-adjustment operator and the Tabu search mechanism, with only the lower-level search module being varied, ensuring fairness of comparison. Using the test instance set constructed in Table 3, each algorithm combination was independently executed 30 times. By comparing key performance indicators, including average response time (

Table 7. Experimental results of different algorithms.

	Average Response Time/h					Average Running Time/s
Algorithm Instances	TGA-ACO	TGA-BB	TGA-GA	TGA-PSO	TGA-SA	TGA-ACO	TGA-BB	TGA-GA	TGA-PSO	TGA-SA
1	58.20	58.18	67.92	74.70	58.18	1.90	0.56	4.88	5.30	12.23
2	52.81	52.81	52.81	57.83	52.81	49.69	10.31	159.71	115.24	502.71
3	160.49	149.35	230.29	241.07	149.95	190.60	89.60	411.33	445.10	190.60
4	147.53	147.19	182.79	205.31	147.19	173.15	33.66	456.43	495.77	1113.35
5	307.08	278.34	490.87	510.78	280.10	378.01	134.56	737.78	786.65	1750.63
6	289.35	276.86	437.52	474.53	276.87	365.53	170.17	794.21	859.43	1897.86
7	663.43	527.99	1046.91	1108.44	535.03	792.70	371.86	1136.63	1254.49	2675.50
8	593.52	525.96	974.85	1034.77	528.02	713.71	543.79	1110.40	1155.18	2489.03

Note: Tabu Genetic Algorithm (TGA). The bold content represents the minimum value among all comparative experiments under the current instance.The experimental setup was built upon the hybrid optimization algorithm framework developed in this work, where only the local search module was varied across the different configurations.

), average runtime (Figure 6), and solution space distribution (Figure 7), this study systematically evaluated the effectiveness of the BB algorithm in accurately solving multi-stage EMS problems.

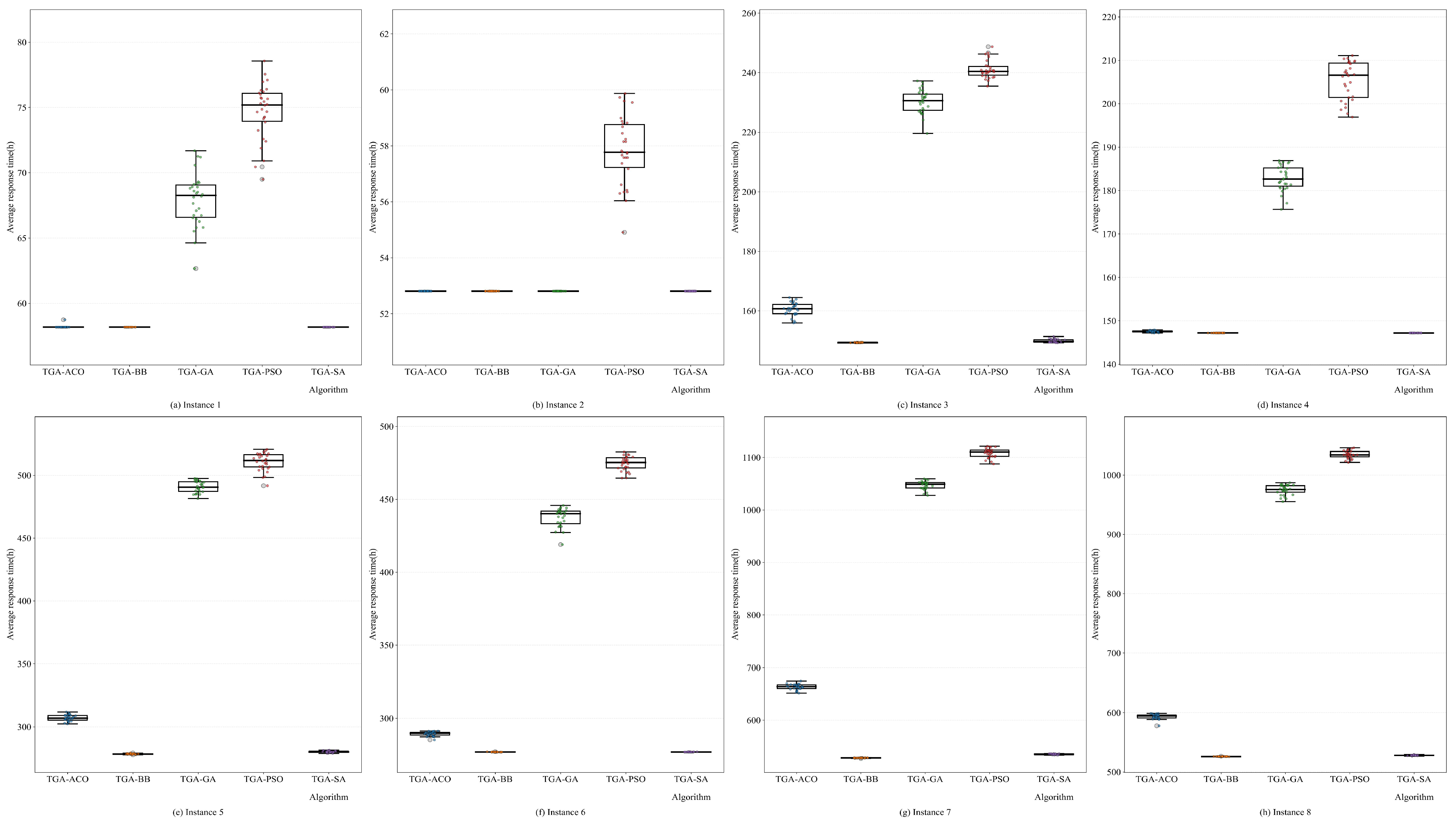
As shown by the experimental results, TGA-BB demonstrated significant advantages over other heuristic algorithms such as TGA-ACO, TGA-GA, TGA-PSO, and TGA-SA in solving EMS problems. For example, in instance 7, the average response time of TGA-BB was 527.99 h, which was more than 50% shorter than that of TGA-GA (1046.91 h), and its running time (371.86 s) was only 29.6% of that of TGA-PSO (1254.49 s). The details are as follows:

Computational Efficiency. As presented in Table 7 and Figure 6, TGA-BB achieved the shortest runtime across all test instances, significantly outperforming the traditional heuristic algorithms. For example, in instance 4, TGA-BB consumed only 33.66 s, whereas TGA-ACO, TGA-GA, TGA-PSO, and TGA-SA required 173.15, 456.43, 495.77, and 1113.35 s, respectively. As the problem scale increased, TGA-BB maintained superior performance. Particularly in large-scale instances (e.g., instance 7 and instance 8), TGA-BB exhibited a relatively slow increase in runtime, while maintaining a high solution accuracy, demonstrating strong scalability.

Solution Quality. As shown in Table 7 and Figure 6, TGA-BB achieved the shortest delivery time in most test instances, indicating its superiority in solution quality. For instance, in instance 7, TGA-BB required only 527.99 h, outperforming TGA-ACO (663.43 h), TGA-GA (1046.91 h), TGA-PSO (1108.44 h), and TGA-SA (535.03 h). This advantage became even more pronounced in larger-scale problems.

Stability of Solutions. From the distribution of results across 30 independent runs for each algorithm, as illustrated in Figure 7, TGA-BB not only achieved a better average performance across all problem scales but also produced more concentrated and less volatile results, demonstrating a higher stability and consistency in solution quality. Although TGA-SA also performed well across the different scenarios, its significantly higher computational cost limits its practical applicability.

Compared with various heuristic algorithms, the proposed approach that incorporates BB for local search after stage adjustment demonstrated significantly better performance in both computational efficiency and solution quality. The underlying reason for this lies in the fact that, in real-world scenarios, once the set of disaster areas to be served in each stage has been determined, the EMS problem becomes a small-scale optimization problem under complex constraints. In such cases, the BB approach exhibits strong capabilities in delivering fast and accurate solutions. Therefore, BB is particularly well suited to the multi-stage EMS optimization model developed in this study. In summary, the hybrid TGA-BB algorithm designed in this paper effectively enhances both the quality and efficiency of scheduling solutions, providing strong support for priority-based, multi-stage EMS. Regarding the implications and future research directions, it is recommended to explore the integration of different methodologies based on problem characteristics, leveraging the respective strengths of each approach to address various types of challenges. This will help in developing more practical and effective solution methods that better align with real-world emergency logistics scenarios.

5.3. Analysis of Results

In summary, the TGA-BB algorithm proposed in this paper demonstrated excellent performance in solving multi-stage EMS problems. By incorporating the single-point stage-adjustment operator and the Tabu dictionary, the algorithm achieved superior results in terms of computational efficiency, solution quality, and stability compared to traditional heuristic methods.

Experimental results showed that TGA-BB is applicable to scheduling problems of varying scales, significantly improves solution speed, and effectively avoids becoming trapped in local optima. The algorithm exhibits strong scalability and practical applicability. Overall, TGA-BB provides an efficient and reliable optimization solution for EMS, offering strong support for rapid response and resource allocation in emergency situations.

However, the experimental data in this study were generated randomly. This is because applying a real-world case would require systematic collection and validation of detailed disaster information, such as road damage, material demand, and drone deployment constraints. Given that the primary focus of this research lay in constructing a priority-oriented, multi-stage scheduling model and algorithmic framework, the integration of specific case studies has not yet been undertaken.

In our future work, we plan to incorporate publicly available data from actual disasters, such as the 2025 Tibet earthquake, to further validate the applicability of the proposed model in real-world scenarios. Specifically,

(1)

We will integrate actual geographic coordinates and post-disaster road conditions into the three-tier network modeling to optimize the path planning for trains and drones;

(2)

The priority evaluation index system will be adjusted based on real disaster data, with increased weight given to indicators such as infrastructure damage, to ensure a more realistic and needs-driven classification of priority levels;

(3)

By comparing the model outputs with actual dispatch plans, we aim to extract actionable optimization recommendations.

6. Conclusions and Future Work

In this paper, a multi-stage EMS optimization method based on the priority of drones in a disaster area was proposed, aiming to realize the rapid response and on-demand distribution of emergency materials, relying on the limited EMS resources after a disaster. Firstly, considering the limited road resources and harsh environment after a disaster, drones were introduced for EMS, and a three-level EMS network of “storage warehouse–transit center–disaster area” was constructed. Secondly, the storage capacity and transfer capacity of each node and the limited transport and distance capacity of drones were fully considered. With the minimum response time as the optimization goal, a multi-stage EMS model was established, and a priority determination method of the disaster area based on fuzzy comprehensive evaluation was proposed, which provides a theoretical basis for EMS based on priority. In terms of algorithm design, the stage-adjustment operator and Tabu dictionary mechanism were introduced under the framework of GA, and a hybrid optimization algorithm TGA-BB, which integrates GA and BB, was constructed, which effectively improved the performance and solution stability of the algorithm. Finally, a series of simulation experiments were conducted. By comparing experiments with and without the stage-adjustment operator and the TS mechanism, we confirmed that the algorithm performed best when both components were included. Based on this finding, we further compared TGA-BB with several classical heuristic algorithms. The results showed that across eight test instances, the average response time of TGA-BB was never worse than that of the other four algorithms. Notably, in Instance 7, TGA-BB achieved an average response time of 527.99 h, significantly shorter than the 1108.44 h of TGA-PSO, representing a reduction of approximately 52.37%. In terms of average computation time, TGA-BB outperformed all other algorithms across all eight instances. In particular, in Instance 2, TGA-BB required only 10.31 s, far less than the 502.71 s of TGA-SA, a reduction of about 97.95%. These results fully validate the effectiveness and superiority of the TGA-BB algorithm in solving the problem at hand.

Considering the limitations of the current study, future research will proceed along the following directions: From the modeling perspective: Conduct research on real-time data-driven optimization for EMS, where real-time data include updates on priority, material demands, and transportation capacities. Introduce a multi-source collaborative scheduling mechanism, allowing multiple transit centers to jointly deliver supplies to the same disaster area; Consider heterogeneous material distribution by taking into account differences in demand and priority levels between categories such as medical supplies and food; Incorporate multimodal transportation mechanisms, including trucks and helicopters as alternative transport options. Elastic variables and constraints will be embedded into the model to provide interfaces for integrating various transportation modes, facilitating future extensions. From the algorithmic perspective: Explore the introduction of an adaptive mechanism to dynamically select the stage-adjustment operator, aiming to further enhance the algorithm’s computational efficiency and robustness. Investigate the use of advanced artificial intelligence methods, such as deep reinforcement learning, to address EMS problems. This could provide more intelligent and real-time optimization strategies for complex disaster environments.