Differential Flatness-Based Singularity-Free Control of a Class of 5-DOF Aerial Platforms with Applications to Passively Articulated Dual-UAV Systems
Abstract
1. Introduction
- We propose a singularity-free control strategy for a class of 5-DOF aerial platforms. The control allocation for position tracking is designed based on the system’s differential flatness, ensuring the avoidance of singularities. We show that this approach enables the platform to achieve almost global stability in arbitrary configurations.
- We develop an integrated control framework for the PADUAV platform by combining the proposed 5-DOF controller with a singularity-free attitude control allocation scheme. This enables the PADUAV system to maintain stability across all configurations.
- We validate the effectiveness of the proposed approach through numerical simulations, demonstrating its ability to ensure stable and reliable performance of the PADUAV platform under various configurations.
2. Modeling of a Class of 5-DOF Aerial Platform
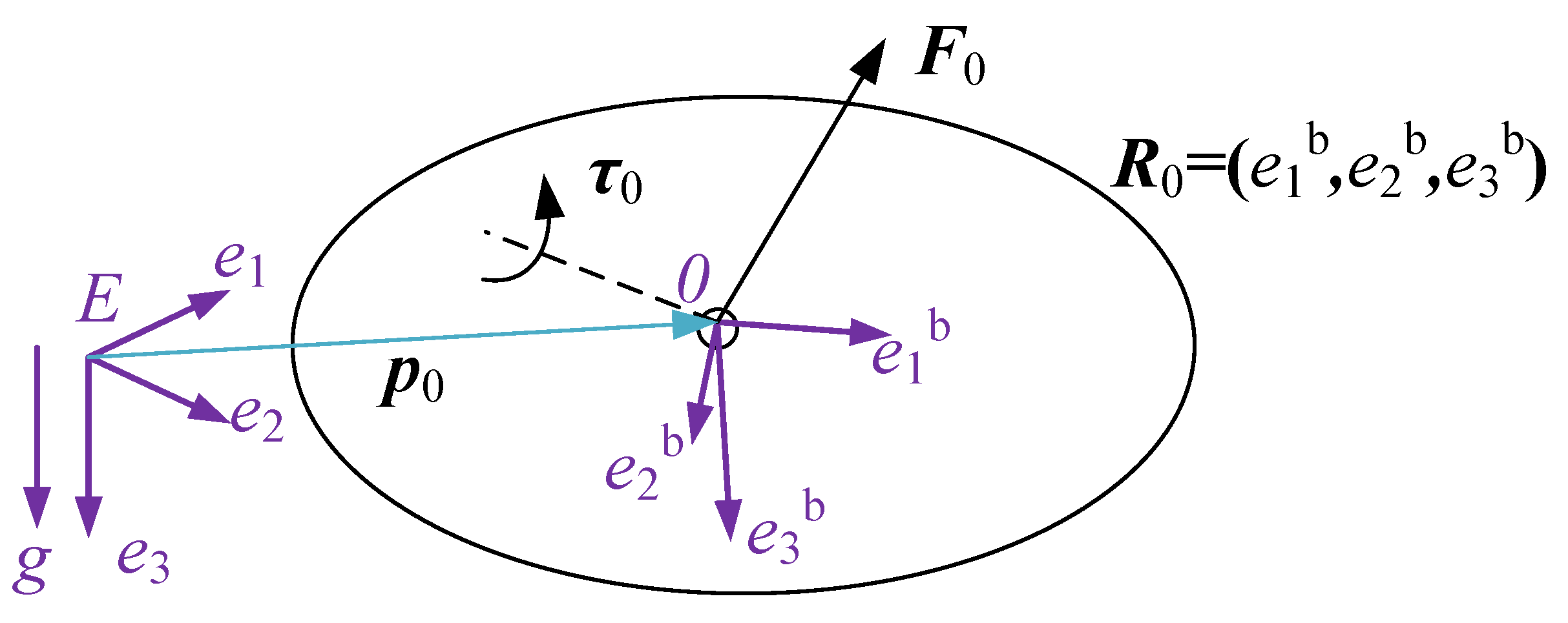
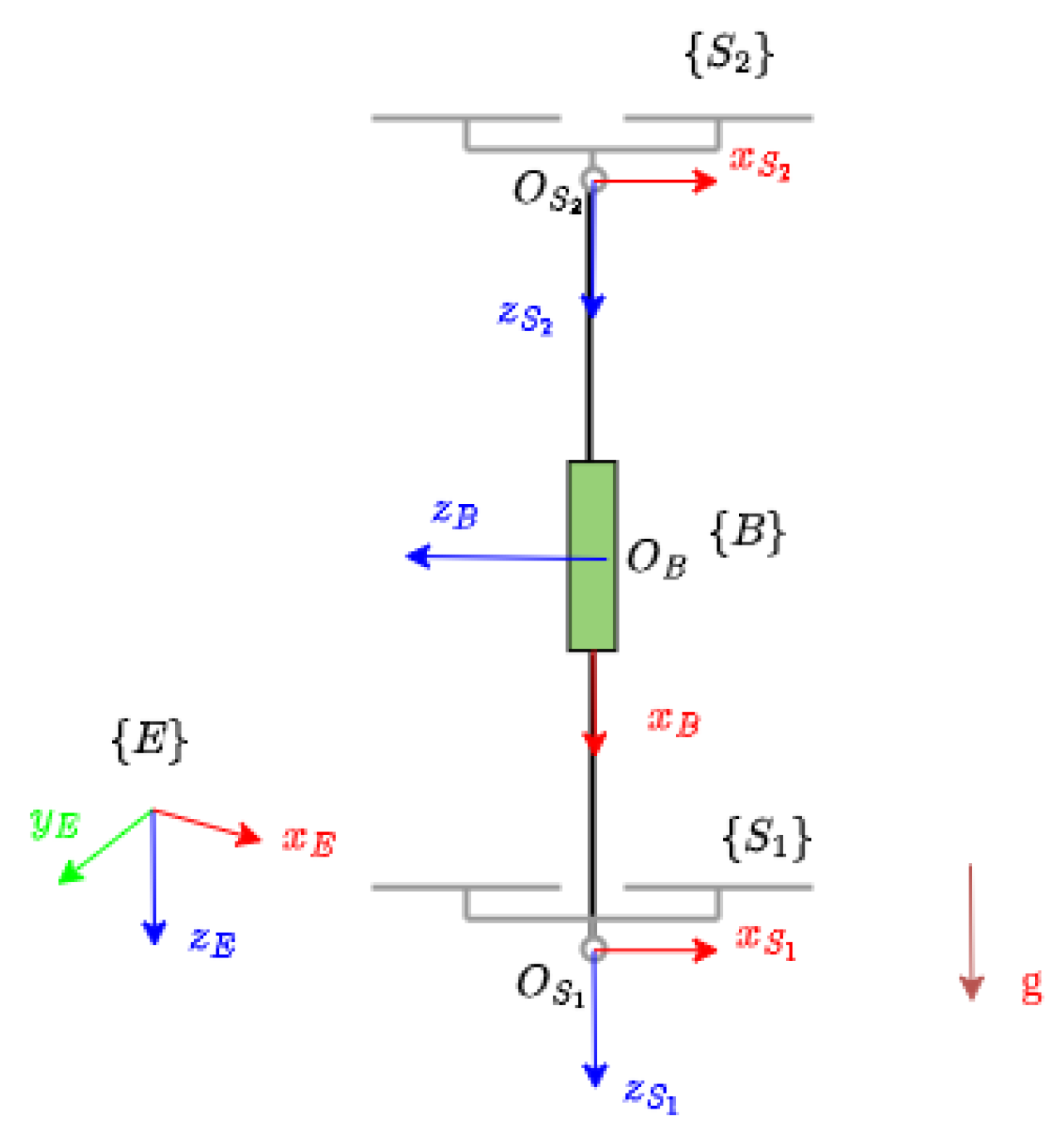
2.1. System Description and Modeling
Modeling Assumptions
- The aerial platform is treated as a rigid body with known mass and inertia;
- Aerodynamic effects such as drag and wind disturbances are neglected in the model.
2.2. Flat Output Definition
- According to Lemma 1, we can express the rotation matrix corresponding to attitude asWe express ; then, we haveFrom , one can obtain a unit vector in the plane such that . It is evident that lies within the span of and . If we assume that is not bounded, then based on the flat outputs , the input force can always be determined along the directions and as follows:We introduce a rotation matrix . Since , we haveThen, the force allocation in Equation (5) can be reformulated aswhere . Then, the components can be computed asand . Therefore, the attitude matrix of the vehicle base is obtained byThen, the input can be further derived using the following equation:However, it should be noted that if , a singularity in (9) occurs, and cannot be solved. To avoid this singularity, we propose an algorithm to modify , i.e., to let point in the direction that maximizes . As maximizing implies minimizing , the solution of can be expressed asTo obtain from (12), we first construct a local frame by rotating the inertial frame using . We then project the vector onto the plane of the local frame , and we define to be perpendicular to this projected vector within the plane. To compute the desired direction in the local plane, we proceed as follows.Let be the force vector with the gravitational component removed. Note that it is expressed in the inertial frame. We project onto the plane of by removing its component along the local y axis:The components of along the x- and z-axes of are computed asWe then construct a vector normal to in the planewhich is expressed in the inertial frame.
- This vector is normalized to obtain a unit direction:We then express this unit vector in the local coordinate frame :This local vector is then used as the solution toEquations (13)–(18) together define a consistent method to extract and reorient the direction of interest in the local plane. It is seen that this is the solution of (12).The angular velocity can be expressed in terms of the rotation matrix asSince is a function of and a finite number of its derivatives, it follows that can also be expressed as a function of and a finite number of its derivatives.
- Moreover, because , the rotational system is fully actuated, and it is seen that . Therefore, can also be derived as the function of and a finite number of its derivatives. For brevity, the detailed derivation is omitted here, as it does not affect the validity of the proof.
- By now, it is seen that all the states and inputs of the system can be expressed as functions of and the finite number of its derivatives. The proof that is the flat output is, thus, complete. Furthermore, by designing in this proof, the input and state can always be derived from finite-order derivatives of the flat output. □
3. Global Control Design and Stability Analysis
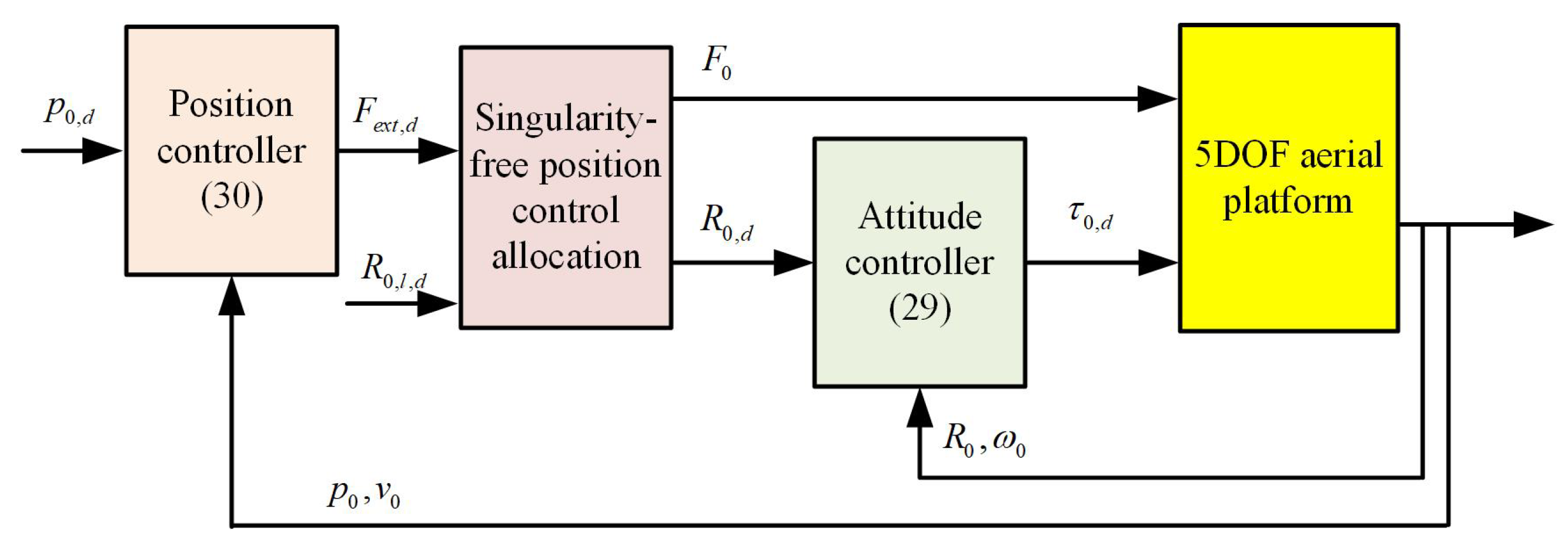
3.1. Control Strategy
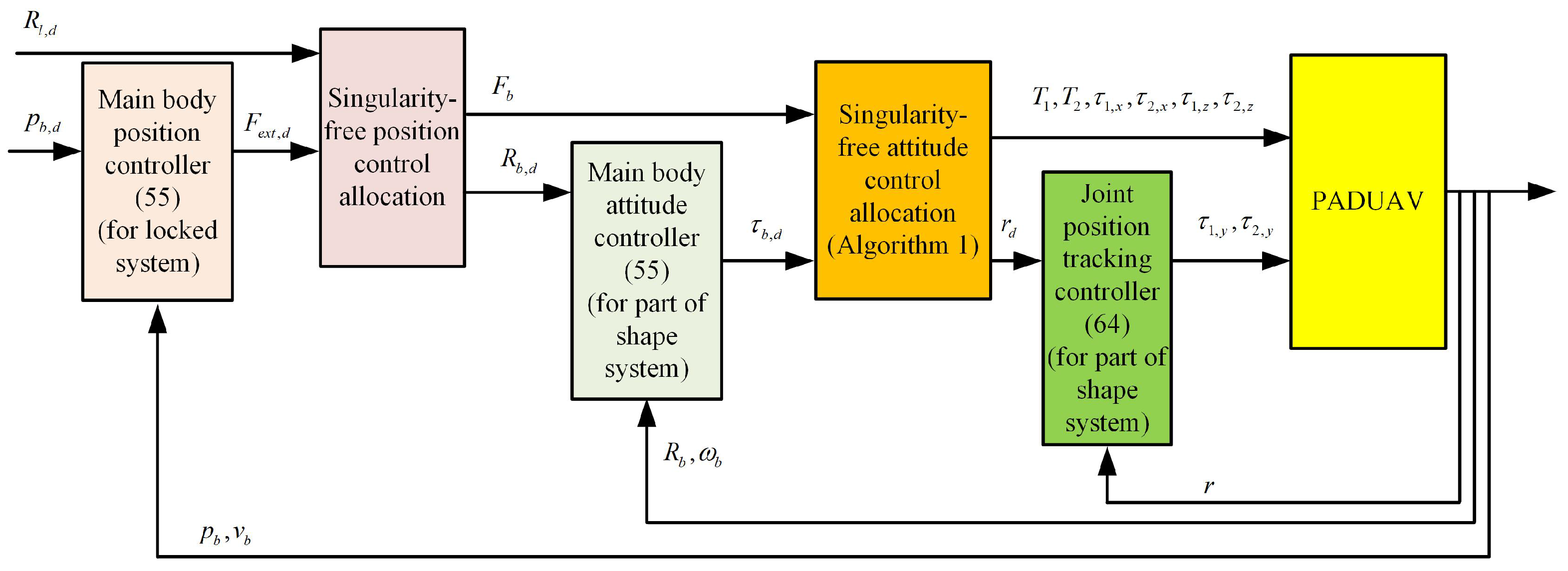
Overall Control Architecture
3.2. Attitude Tracking Controller
3.3. Position Controller
3.4. Position Control Allocation
3.5. Stability Analysis
- For the coupling term, we haveTo finish the proof, we first prove the boundedness of and , which is given in [43]where and d are positive constants.
- We now aim to establish that the term remains bounded. Specifically, we show that there exists a constant such thatSince the 2-norm is submultiplicative and consistent with the vector norm, we can writeTo bound , we expand using Rodrigues’ formula:We now estimate the second term on the right-hand side:Using the identity , it follows thatMoreover, we note thatfor some constant . Substituting into (40), we obtainThis proved the inequality result of (38).
- Consequently, according to Lemma 2, the system described by (36) is stable at the equilibrium point . Applying the stability results for cascade systems, it then follows thathold asymptotically for the entire system. □
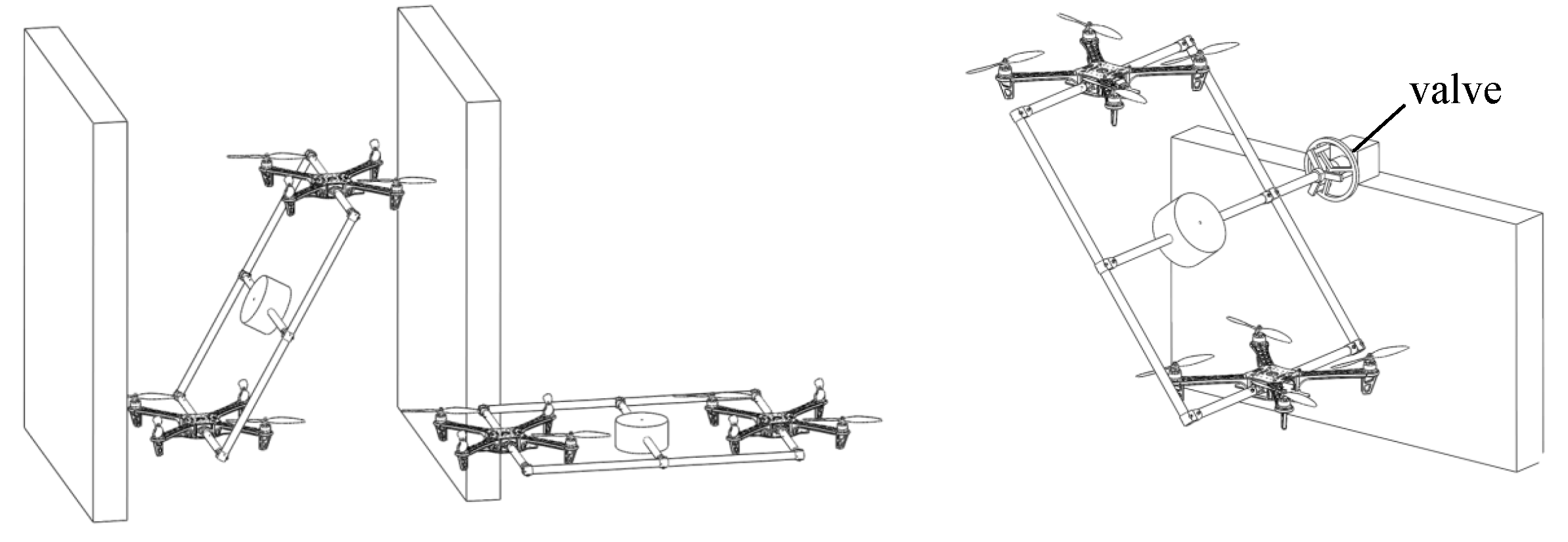
4. Applications on the PADUAV Platform
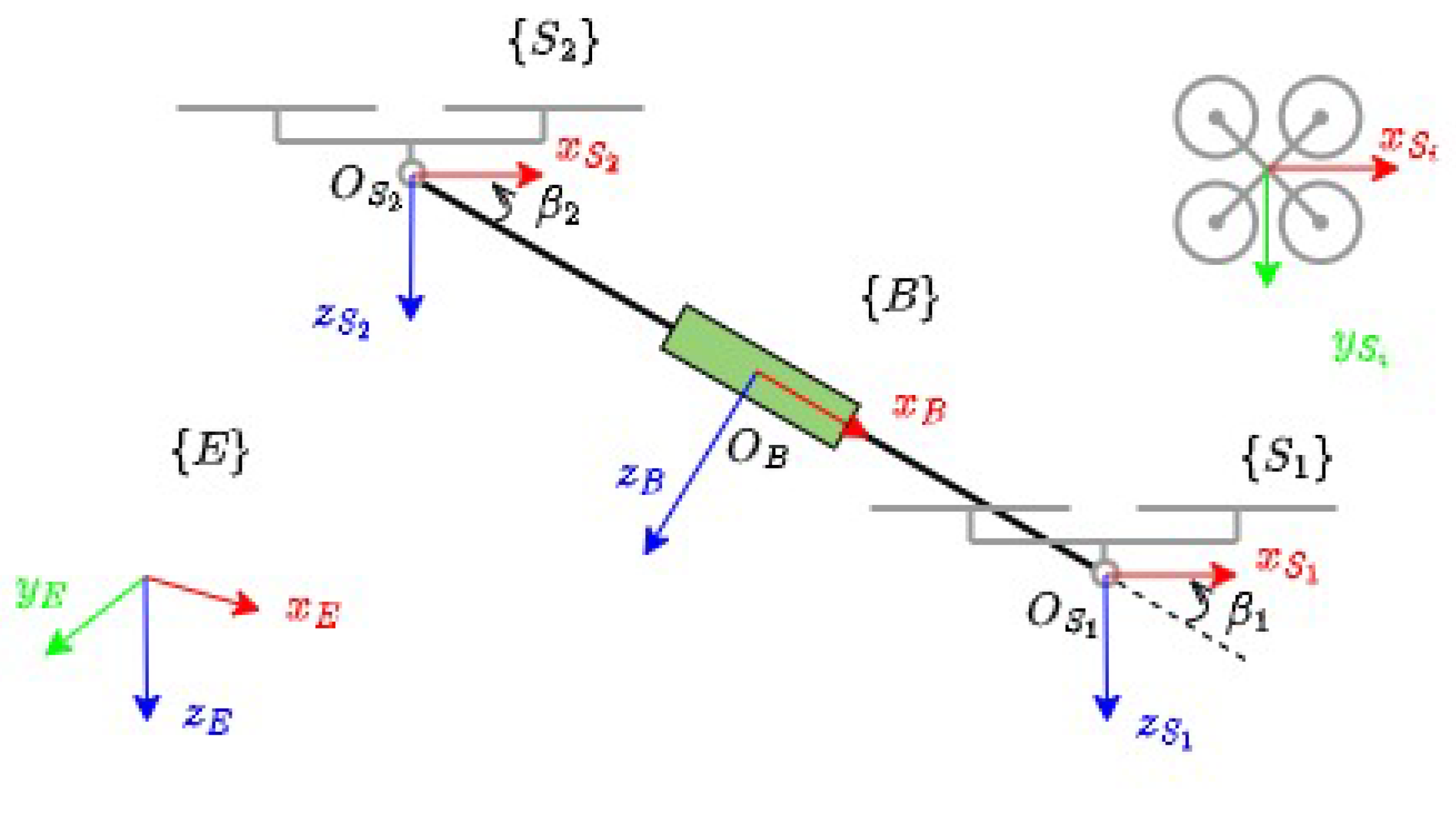
4.1. Configuration of the PADUAV Platform
4.2. Dynamics Modeling
4.3. Dynamics Analysis and Decoupling
4.3.1. Decouple the Translation Motion from General Rotations
4.3.2. Decoupling Main Body Rotation from Position and Joint Rotation
4.4. Controller Design
4.4.1. Position and Attitude Control of the Main Frame
4.4.2. Singularity-Free Attitude Control Allocation
| Algorithm 1 Singularity-Free Thrust Allocation for Two Sub-Aircraft |
|
4.4.3. Joint Position Tracking
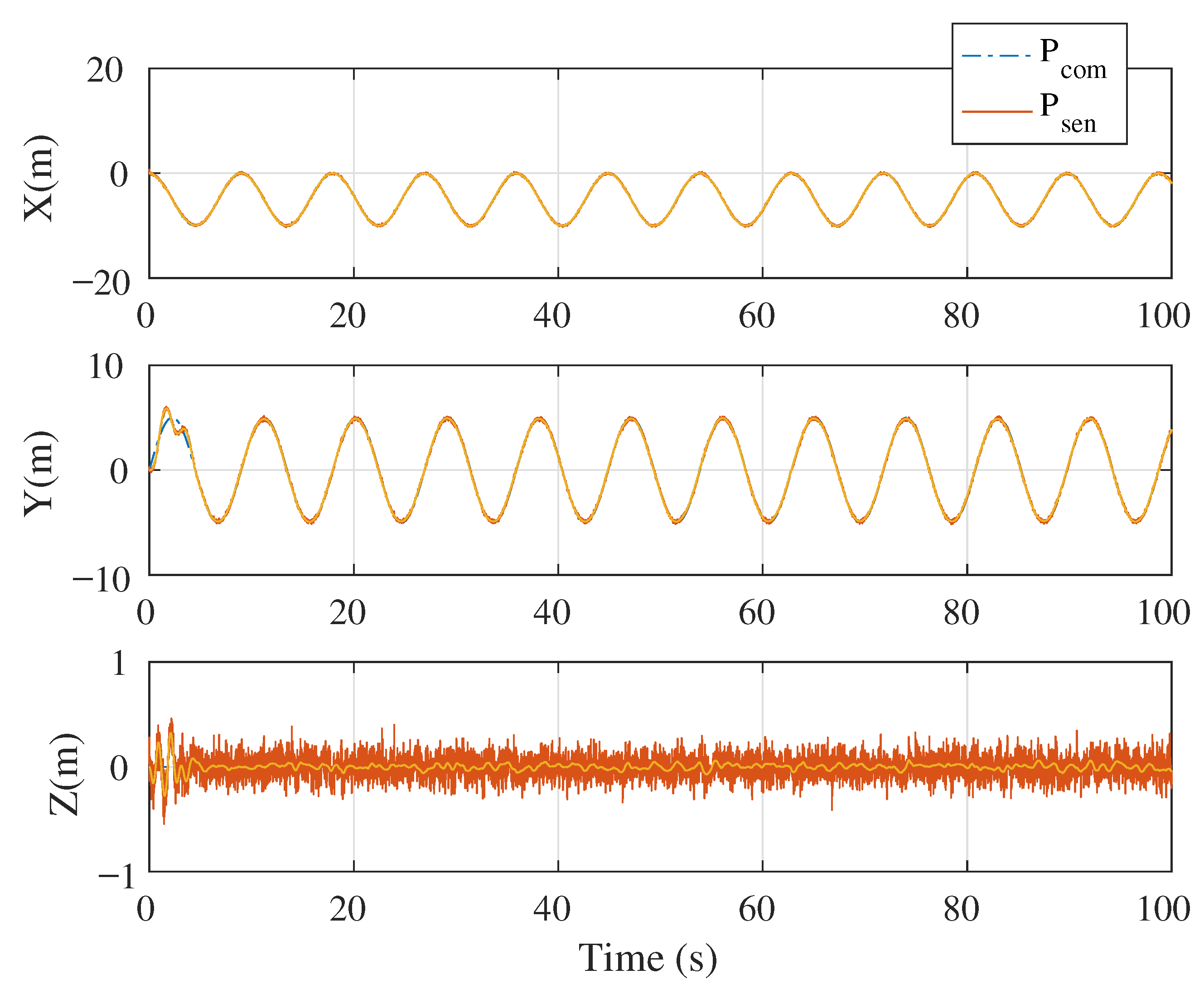
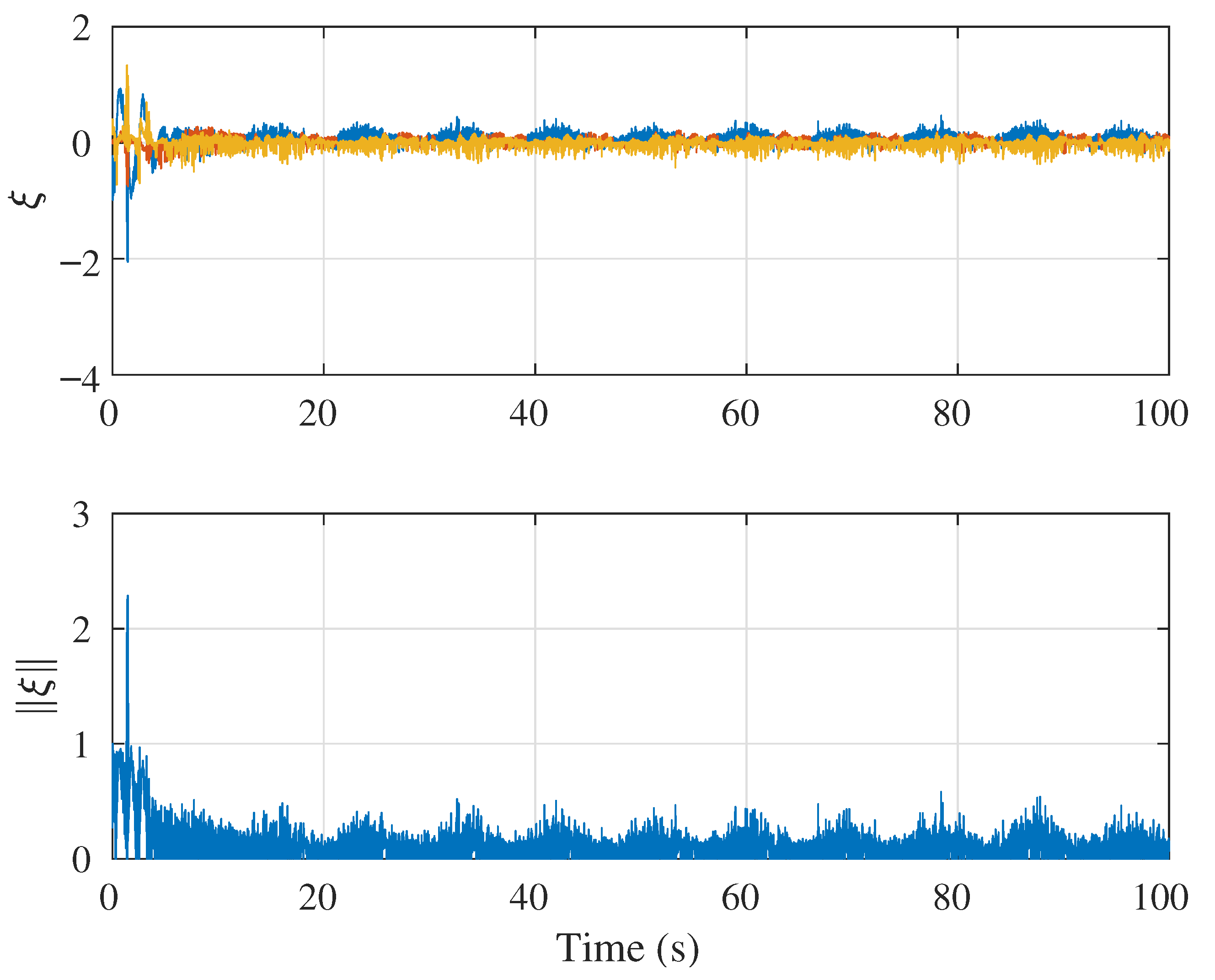
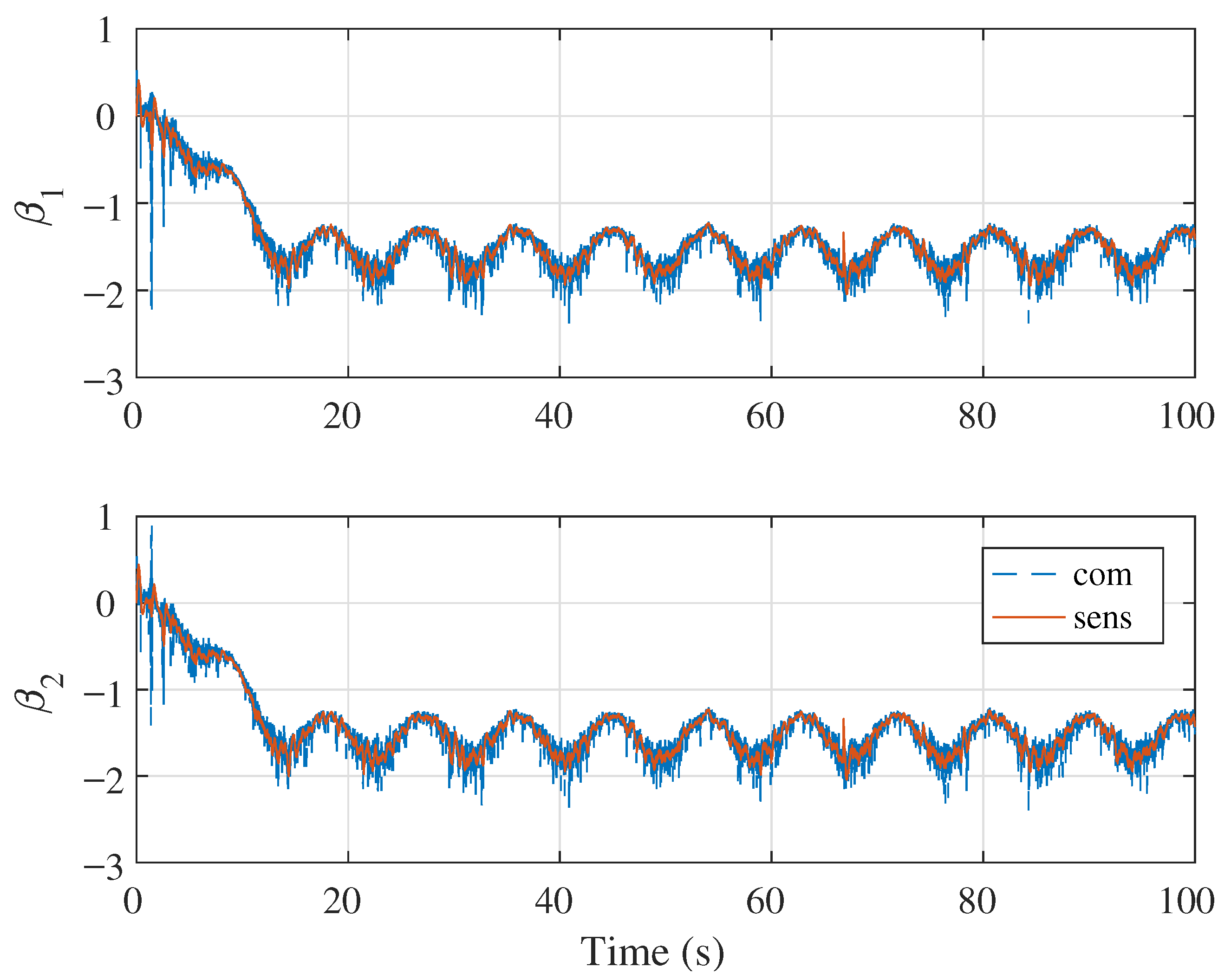
5. Numerical Simulation
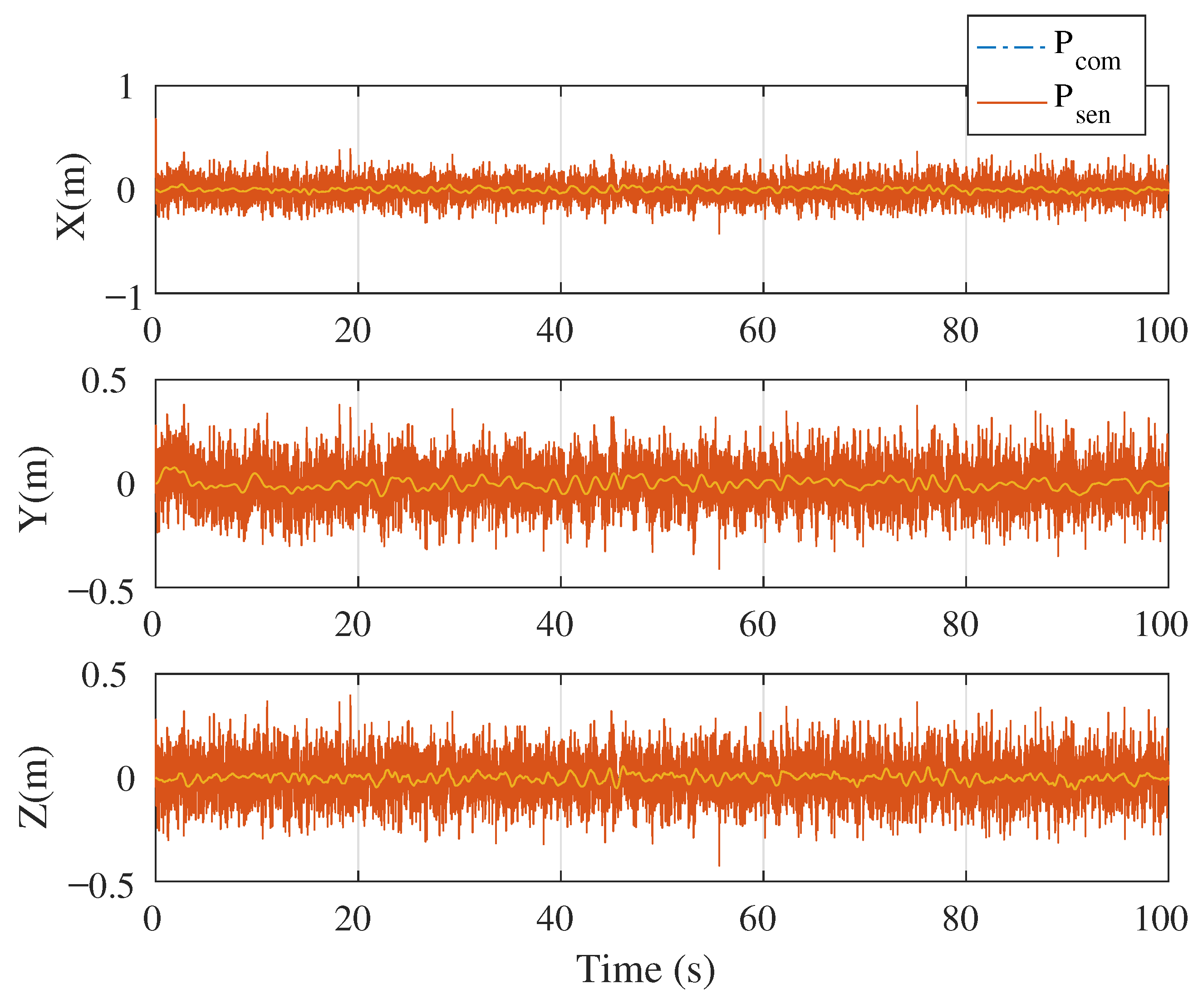
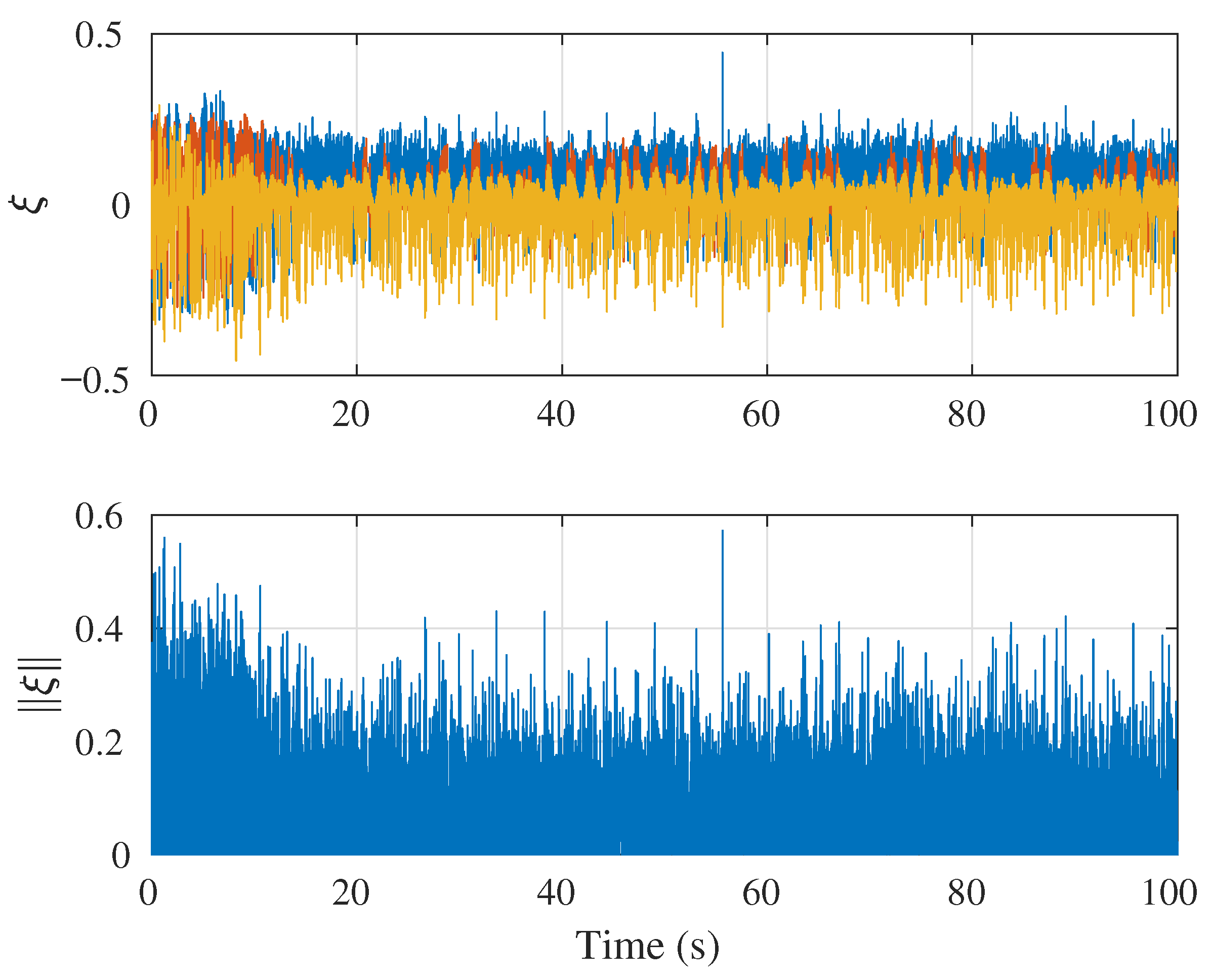
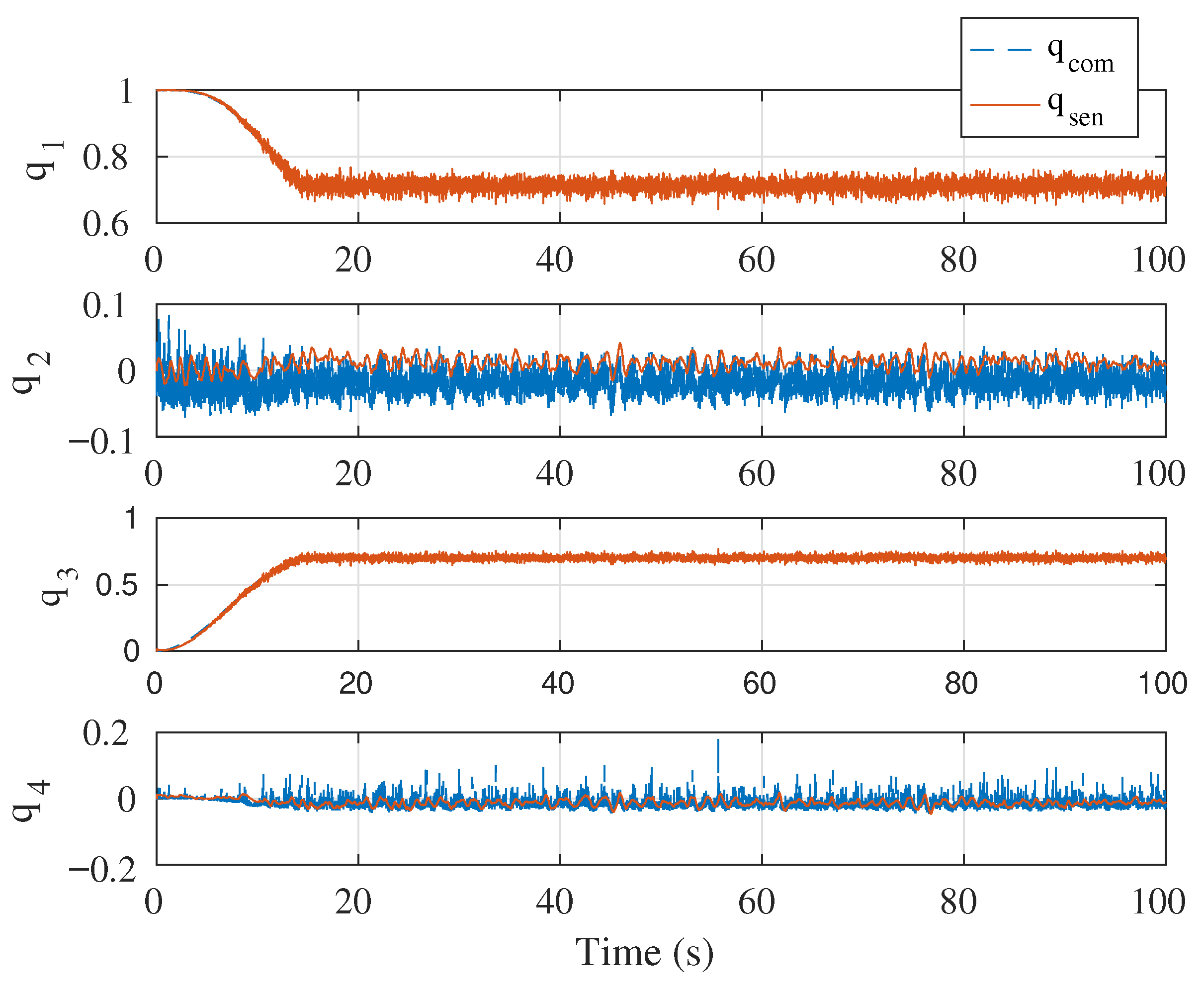
5.1. Simulation Case 1: Demonstration of Singularity-Free Capability

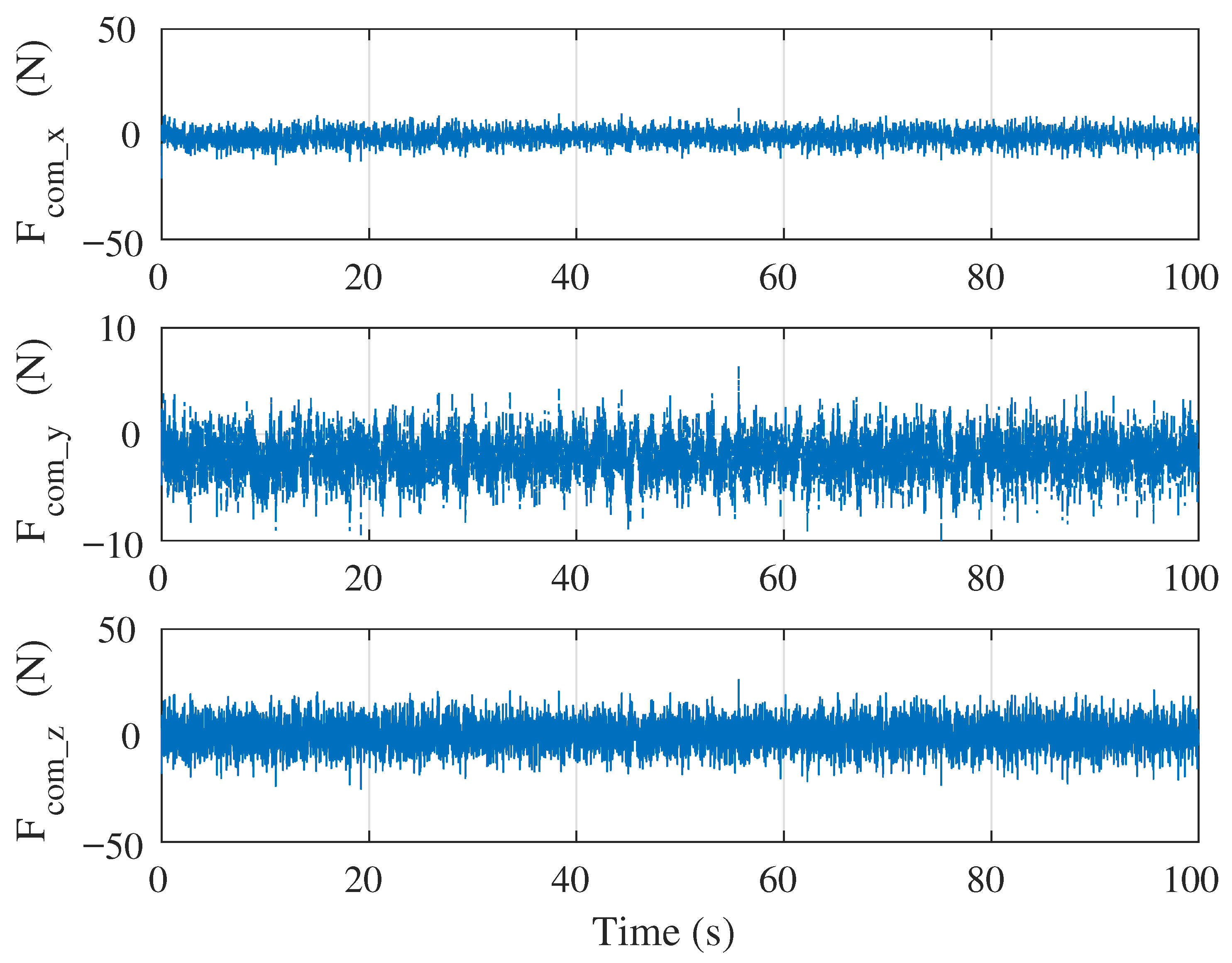
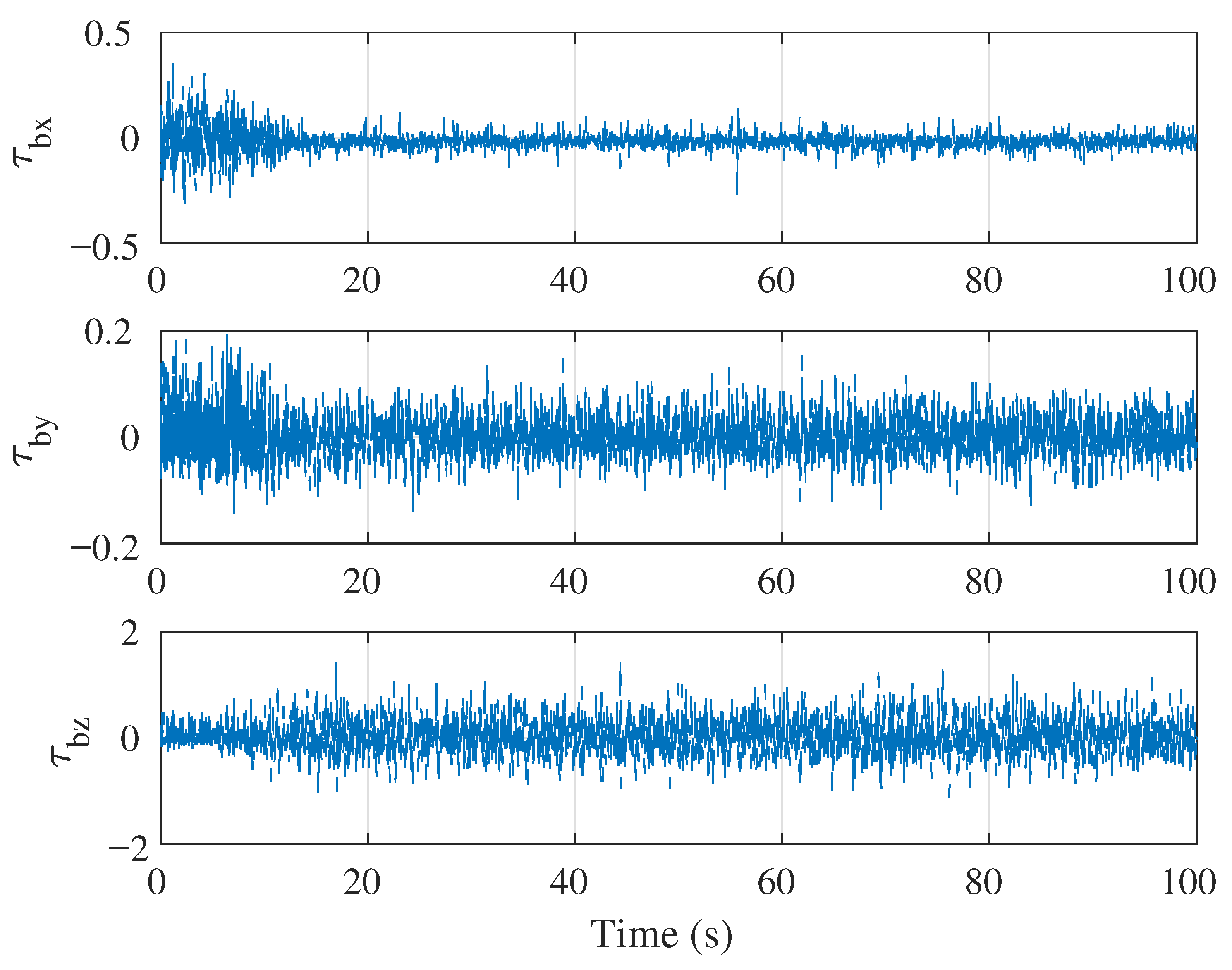
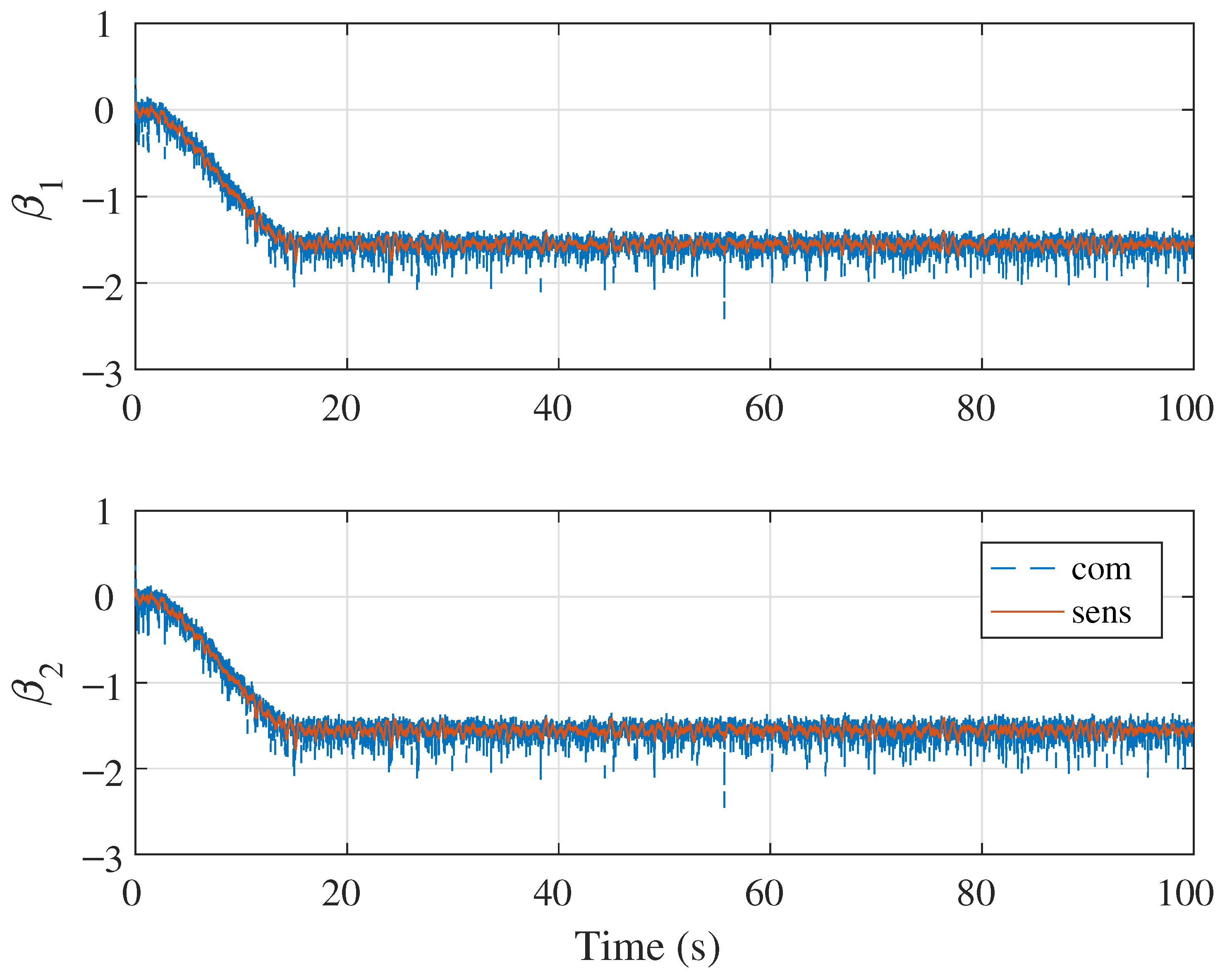
5.2. Simulation Case 2: Circular Position Tracking
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ding, X.; Guo, P.; Xu, K.; Yu, Y. A review of aerial manipulation of small-scale rotorcraft unmanned robotic systems. Chin. J. Aeronaut. 2019, 32, 200–214. [Google Scholar] [CrossRef]
- Lippiello, V.; Fontanelli, G.A.; Ruggiero, F. Image-based visual-impedance control of a dual-arm aerial manipulator. IEEE Robot. Autom. Lett. 2018, 3, 1856–1863. [Google Scholar] [CrossRef]
- Wang, M.; Chen, Z.; Guo, K.; Yu, X.; Zhang, Y.; Guo, L.; Wang, W. Millimeter-Level Pick and Peg-in-Hole Task Achieved by Aerial Manipulator. IEEE Trans. Robot. 2024, 40, 1242–1260. [Google Scholar] [CrossRef]
- Yu, Y.; Ding, X. A Global Tracking Controller for Underactuated Aerial Vehicles: Design, Analysis, and Experimental Tests on Quadrotor. IEEE/ASME Trans. Mechatronics 2016, 21, 2499–2511. [Google Scholar] [CrossRef]
- Ollero, A.; Tognon, M.; Suarez, A.; Lee, D.; Franchi, A. Past, Present, and Future of Aerial Robotic Manipulators. IEEE Trans. Robot. 2022, 38, 626–645. [Google Scholar] [CrossRef]
- Kim, S.J.; Lee, D.Y.; Jung, G.P.; Cho, K.J. An origami-inspired, self-locking robotic arm that can be folded flat. Sci. Robot. 2018, 3, eaar2915. [Google Scholar] [CrossRef] [PubMed]
- Estrada, M.A.; Mintchev, S.; Christensen, D.L.; Cutkosky, M.R.; Floreano, D. Forceful manipulation with micro air vehicles. Sci. Robot. 2018, 3, eaau6903. [Google Scholar] [CrossRef] [PubMed]
- Ruggiero, F.; Lippiello, V.; Ollero, A. Aerial manipulation: A literature review. IEEE Robot. Autom. Lett. 2018, 3, 1957–1964. [Google Scholar] [CrossRef]
- Meng, X.; He, Y.; Han, J. Survey on aerial manipulator: System, modeling, and control. Robotica 2020, 38, 1288–1317. [Google Scholar] [CrossRef]
- Ryll, M.; Muscio, G.; Pierri, F.; Cataldi, E.; Antonelli, G.; Caccavale, F.; Bicego, D.; Franchi, A. 6D interaction control with aerial robots: The flying end-effector paradigm. Int. J. Robot. Res. 2019, 38, 1045–1062. [Google Scholar] [CrossRef]
- Rajappa, S.; Ryll, M.; Bülthoff, H.H.; Franchi, A. Modeling, control and design optimization for a fully-actuated hexarotor aerial vehicle with tilted propellers. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4006–4013. [Google Scholar] [CrossRef]
- Brunner, M.; Rizzi, G.; Studiger, M.; Siegwart, R.; Tognon, M. A planning-and-control framework for aerial manipulation of articulated objects. IEEE Robot. Autom. Lett. 2022, 7, 10689–10696. [Google Scholar] [CrossRef]
- Bodie, K.; Brunner, M.; Pantic, M.; Walser, S.; Pfändler, P.; Angst, U.; Siegwart, R.; Nieto, J. Active Interaction Force Control for Contact-Based Inspection With a Fully Actuated Aerial Vehicle. IEEE Trans. Robot. 2021, 37, 709–722. [Google Scholar] [CrossRef]
- Park, S.; Lee, J.; Ahn, J.; Kim, M.; Her, J.; Yang, G.H.; Lee, D. ODAR: Aerial Manipulation Platform Enabling Omnidirectional Wrench Generation. IEEE/ASME Trans. Mechatronics 2018, 23, 1907–1918. [Google Scholar] [CrossRef]
- Zheng, P.; Tan, X.; Kocer, B.B.; Yang, E.; Kovac, M. TiltDrone: A fully-actuated tilting quadrotor platform. IEEE Robot. Autom. Lett. 2020, 5, 6845–6852. [Google Scholar] [CrossRef]
- Yiğit, A.; Perozo, M.A.; Cuvillon, L.; Durand, S.; Gangloff, J. Novel omnidirectional aerial manipulator with elastic suspension: Dynamic control and experimental performance assessment. IEEE Robot. Autom. Lett. 2021, 6, 612–619. [Google Scholar] [CrossRef]
- Jiao, R.; Rong, Y.; Dong, M.; Li, J. Hybrid-disturbance-observer-based interaction control for a fully actuated UAV with tether-based positioning system. Ind. Robot. Int. J. Robot. Res. Appl. 2023, 50, 740–752. [Google Scholar] [CrossRef]
- Shi, C.; Wang, K.; Yu, Y. Expandable Fully Actuated Aerial Vehicle Assembly: Geometric Control Adapted from an Existing Flight Controller and Real-World Prototype Implementation. Drones 2022, 6, 272. [Google Scholar] [CrossRef]
- Du, J.; Wang, K.; Fan, Y.; Lai, G.; Yu, Y. High-Fidelity Integrated Aerial Platform Simulation for Control, Perception, and Learning. IEEE Trans. Autom. Sci. Eng. 2025, 22, 13662–13683. [Google Scholar] [CrossRef]
- Lee, T. Geometric Control of Quadrotor UAVs Transporting a Cable-Suspended Rigid Body. IEEE Trans. Control Syst. Technol. 2018, 26, 255–264. [Google Scholar] [CrossRef]
- Six, D.; Briot, S.; Chriette, A.; Martinet, P. The Kinematics, Dynamics and Control of a Flying Parallel Robot With Three Quadrotors. IEEE Robot. Autom. Lett. 2018, 3, 559–566. [Google Scholar] [CrossRef]
- Cardona, G.; Tellez-Castro, D.; Mojica-Nava, E. Cooperative Transportation of a Cable-Suspended Load by Multiple Quadrotors. IFAC-PapersOnLine 2019, 52, 145–150. [Google Scholar] [CrossRef]
- Nguyen, H.; Dang, T.; Alexis, K. The Reconfigurable Aerial Robotic Chain: Modeling and Control. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 5328–5334. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Park, S.; Park, J.; Lee, D. A Novel Robotic Platform for Aerial Manipulation Using Quadrotors as Rotating Thrust Generators. IEEE Trans. Robot. 2018, 34, 353–369. [Google Scholar] [CrossRef]
- Su, Y.; Jiao, Z.; Zhang, Z.; Zhang, J.; Li, H.; Wang, M.; Liu, H. Flight Structure Optimization of Modular Reconfigurable UAVs. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14–18 October 2024; pp. 4556–4562. [Google Scholar] [CrossRef]
- Su, Y.; Yu, P.; Gerber, M.J.; Ruan, L.; Tsao, T.C. Fault-Tolerant Control of an Overactuated UAV Platform Built on Quadcopters and Passive Hinges. IEEE/ASME Trans. Mechatronics 2024, 29, 602–613. [Google Scholar] [CrossRef]
- Su, Y.; Zhang, J.; Jiao, Z.; Li, H.; Wang, M.; Liu, H. Real-time Dynamic-consistent Motion Planning for Over-actuated UAVs. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 11789–11795. [Google Scholar] [CrossRef]
- Ruan, L.; Pi, C.H.; Su, Y.; Yu, P.; Cheng, S.; Tsao, T.C. Control and experiments of a novel tiltable-rotor aerial platform comprising quadcopters and passive hinges. Mechatronics 2023, 89, 102927. [Google Scholar] [CrossRef]
- Pereira, P.O.; Dimarogonas, D.V. Collaborative transportation of a bar by two aerial vehicles with attitude inner loop and experimental validation. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, VIC, Australia, 12–15 December 2017; pp. 1815–1820. [Google Scholar]
- Bosio, C.; Mueller, M.W. Automated Layout and Control Co-Design of Robust Multi-UAV Transportation Systems. IEEE Robot. Autom. Lett. 2025, 10, 3956–3963. [Google Scholar] [CrossRef]
- Li, J.; Sugihara, J.; Zhao, M. Servo Integrated Nonlinear Model Predictive Control for Overactuated Tiltable-Quadrotors. IEEE Robot. Autom. Lett. 2024, 9, 8770–8777. [Google Scholar] [CrossRef]
- Nishio, T.; Zhao, M. Singularity-Free Flight using Rotor-Distributed Aerial Manipulator. IEEE Robot. Autom. Lett. 2024, 9, 1460–1467. [Google Scholar] [CrossRef]
- Nishio, T.; Zhao, M.; Okada, K.; Inaba, M. Design, Control, and Motion-Planning for a Root-Perching Rotor-Distributed Manipulator. IEEE Trans. Robot. 2023, 40, 660–676. [Google Scholar] [CrossRef]
- Ding, C.; Lu, L. A Tilting-Rotor Unmanned Aerial Vehicle for Enhanced Aerial Locomotion and Manipulation Capabilities: Design, Control, and Applications. IEEE/ASME Trans. Mechatronics 2021, 26, 2237–2248. [Google Scholar] [CrossRef]
- Ding, C.; Lu, L.; Wang, C.; Ding, C. Design, Sensing, and Control of a Novel UAV Platform for Aerial Drilling and Screwing. IEEE Robot. Autom. Lett. 2021, 6, 3176–3183. [Google Scholar] [CrossRef]
- Qin, Z.; Wei, J.; Cao, M.; Chen, B.; Li, K.; Liu, K. Design and Flight Control of a Novel Tilt-Rotor Octocopter Using Passive Hinges. IEEE Robot. Autom. Lett. 2024, 9, 199–206. [Google Scholar] [CrossRef]
- Yu, Y.; Lippiello, V. 6D Pose Task Trajectory Tracking for a Class of 3D Aerial Manipulator From Differential Flatness. IEEE Access 2019, 7, 52257–52265. [Google Scholar] [CrossRef]
- Welde, J.; Kumar, V. Coordinate-free dynamics and differential flatness of a class of 6DOF aerial manipulators. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 4307–4313. [Google Scholar]
- Sun, J.; Wang, K.; Shi, C.; Li, X.; Yi, X.; Yu, Y.; Sun, F.; Dong, Y. Modeling and Control of PADUAV: A Passively Articulated Dual UAVs Platform for Aerial Manipulation*. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 6159–6165. [Google Scholar] [CrossRef]
- Van Nieuwstadt, M.J.; Murray, R.M. Real-time trajectory generation for differentially flat systems. Int. J. Robust Nonlinear Control 1998, 8, 995–1020. [Google Scholar] [CrossRef]
- Iserles, A.; Munthe-Kaas, H.Z.; Norsett, S.P.; Zanna, A. Lie-group methods. Acta Numer. 2000, 9, 215–365. [Google Scholar] [CrossRef]
- Murray, R.M.; Li, Z.; Sastry, S.S. A Mathematical Introduction to Robotic Manipulation; CRC Press, Inc.: Boca Raton, FL, USA, 1994. [Google Scholar]
- Kendoul, F. Nonlinear Hierarchical Flight Controller for Unmanned Rotorcraft: Design, Stability, and Experiments. J. Guigance, Control. Dyn. 2009, 32, 1954–1958. [Google Scholar] [CrossRef]
- Khalil, H.K.; Grizzle, J.W. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002; Volume 3. [Google Scholar]
- Wang, K.; Lai, G.; Yu, Y.; Du, J.; Sun, J.; Xu, B.; Franchi, A.; Sun, F. Versatile Tasks on Integrated Aerial Platforms Using Only Onboard Sensors: Control, Estimation, and Validation. IEEE Trans. Robot. 2025, 41, 3518–3538. [Google Scholar] [CrossRef]
- Lee, D. Passive Decomposition and Control of Nonholonomic Mechanical Systems. IEEE Trans. Robot. 2010, 26, 978–992. [Google Scholar] [CrossRef]
- Yang, H.; Lee, D. Dynamics and Control of Quadrotor with Robotic Manipulator. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 5544–5549. [Google Scholar]




| Definition | Symbol | Value in Sim. |
|---|---|---|
| Mass of sub-quadrotor | 1.251 kg | |
| Inertia tensor of sub-quadrotor | 0.0167 0.021 0.0167 kg · | |
| Inertia tensor of the main body | 0.019 0.021 0.039 kg · | |
| distance of the center of the two sub-quadrotors | 0.4 m | |
| Mass of the center stack | 1.251 kg | |
| Maximum thrust of each quadrotor | 40 N |
| Gain | Value |
|---|---|
| 1.2 | |
| 1.2 | |
| 2.0 | |
| 5.0 | |
| 2.0 | |
| 5.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Yu, Y.; Chen, Z.; Jiang, M.; Meng, X. Differential Flatness-Based Singularity-Free Control of a Class of 5-DOF Aerial Platforms with Applications to Passively Articulated Dual-UAV Systems. Drones 2025, 9, 503. https://doi.org/10.3390/drones9070503
Sun J, Yu Y, Chen Z, Jiang M, Meng X. Differential Flatness-Based Singularity-Free Control of a Class of 5-DOF Aerial Platforms with Applications to Passively Articulated Dual-UAV Systems. Drones. 2025; 9(7):503. https://doi.org/10.3390/drones9070503
Chicago/Turabian StyleSun, Jiali, Yushu Yu, Zhe Chen, Meichen Jiang, and Xin Meng. 2025. "Differential Flatness-Based Singularity-Free Control of a Class of 5-DOF Aerial Platforms with Applications to Passively Articulated Dual-UAV Systems" Drones 9, no. 7: 503. https://doi.org/10.3390/drones9070503
APA StyleSun, J., Yu, Y., Chen, Z., Jiang, M., & Meng, X. (2025). Differential Flatness-Based Singularity-Free Control of a Class of 5-DOF Aerial Platforms with Applications to Passively Articulated Dual-UAV Systems. Drones, 9(7), 503. https://doi.org/10.3390/drones9070503







