Cooperative Jamming for RIS-Assisted UAV-WSN Against Aerial Malicious Eavesdropping
Abstract
1. Introduction
- A UAV-WSN system assisted by an RIS is under the threat of a UAV-E, and a cooperative jammer is deployed to counter unauthorized information interception. To maximize secure communication bits, the MDOP is formulated by collaboratively optimizing the TP of SNs, the PSM of the RIS, the FL of time slots, and the FT of the UAV-L.
- The specific MDOP being considered is inherently challenging due to its non-convex structure. To address this complexity, we decompose the original MDOP into a series of interrelated and easily solvable sub-problems and design an iterative algorithm to improve the convergence speed and solution accuracy.
- The numerical results demonstrate that the developed algorithm outperforms various benchmark algorithms with significant improvements, providing important methodological support and a practical basis for subsequent theoretical research and technological innovation in related fields.
2. System Model and Methods
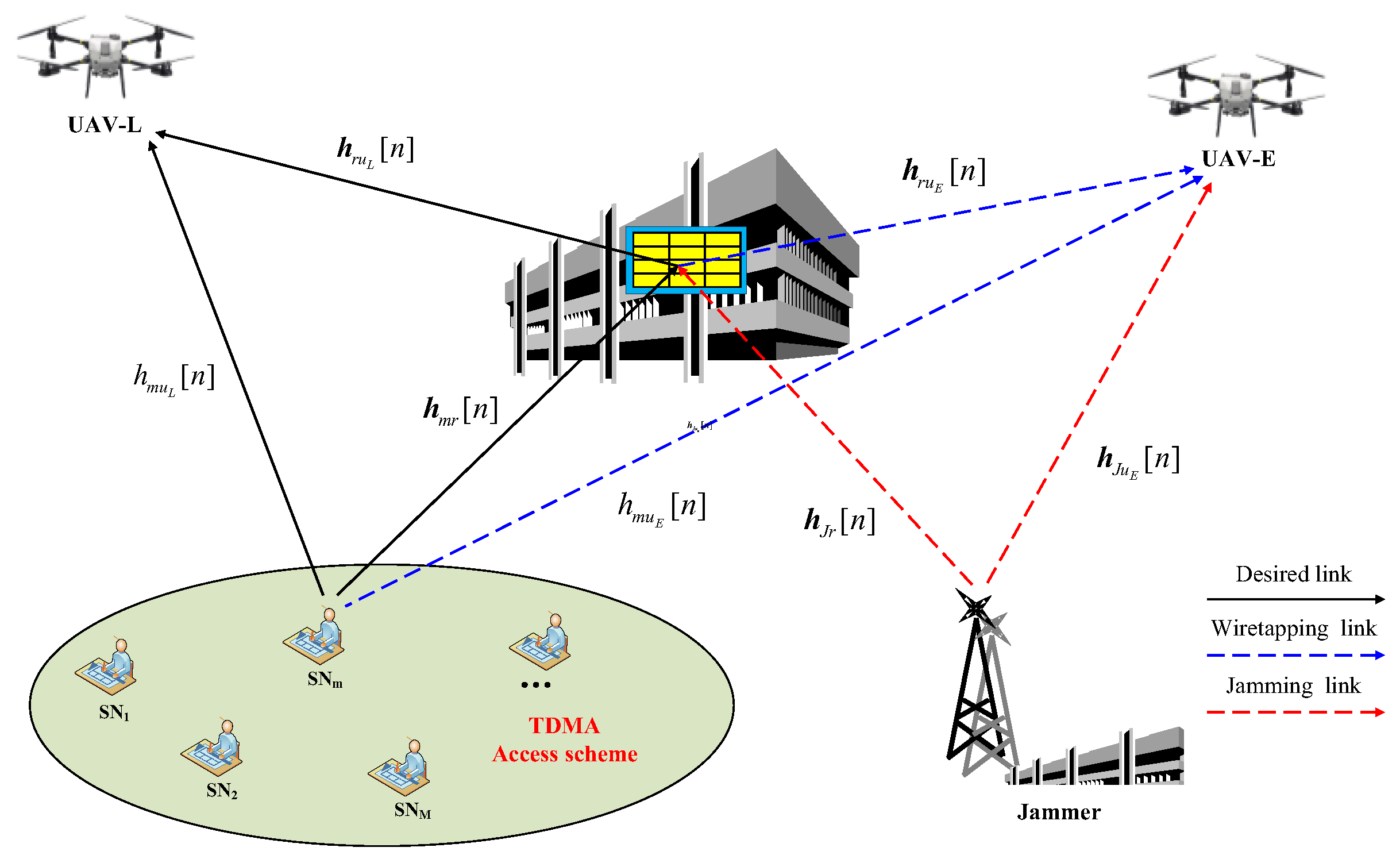
2.1. System Model
2.2. Methods
3. Proposed Algorithm
3.1. Phase Shift Matrix Optimization
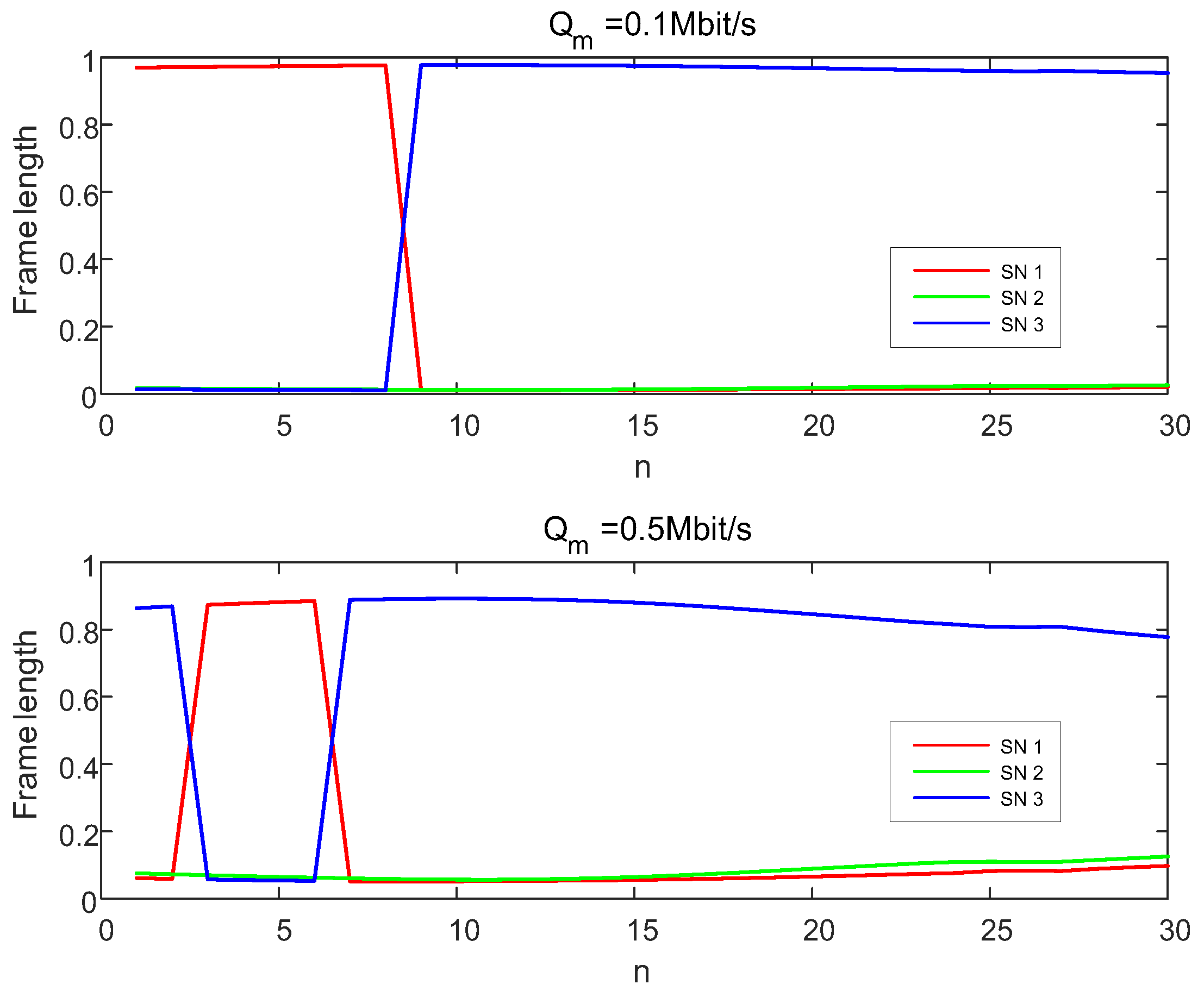
3.2. Frame Length Optimization
3.3. Transmit Power of SNm Optimization
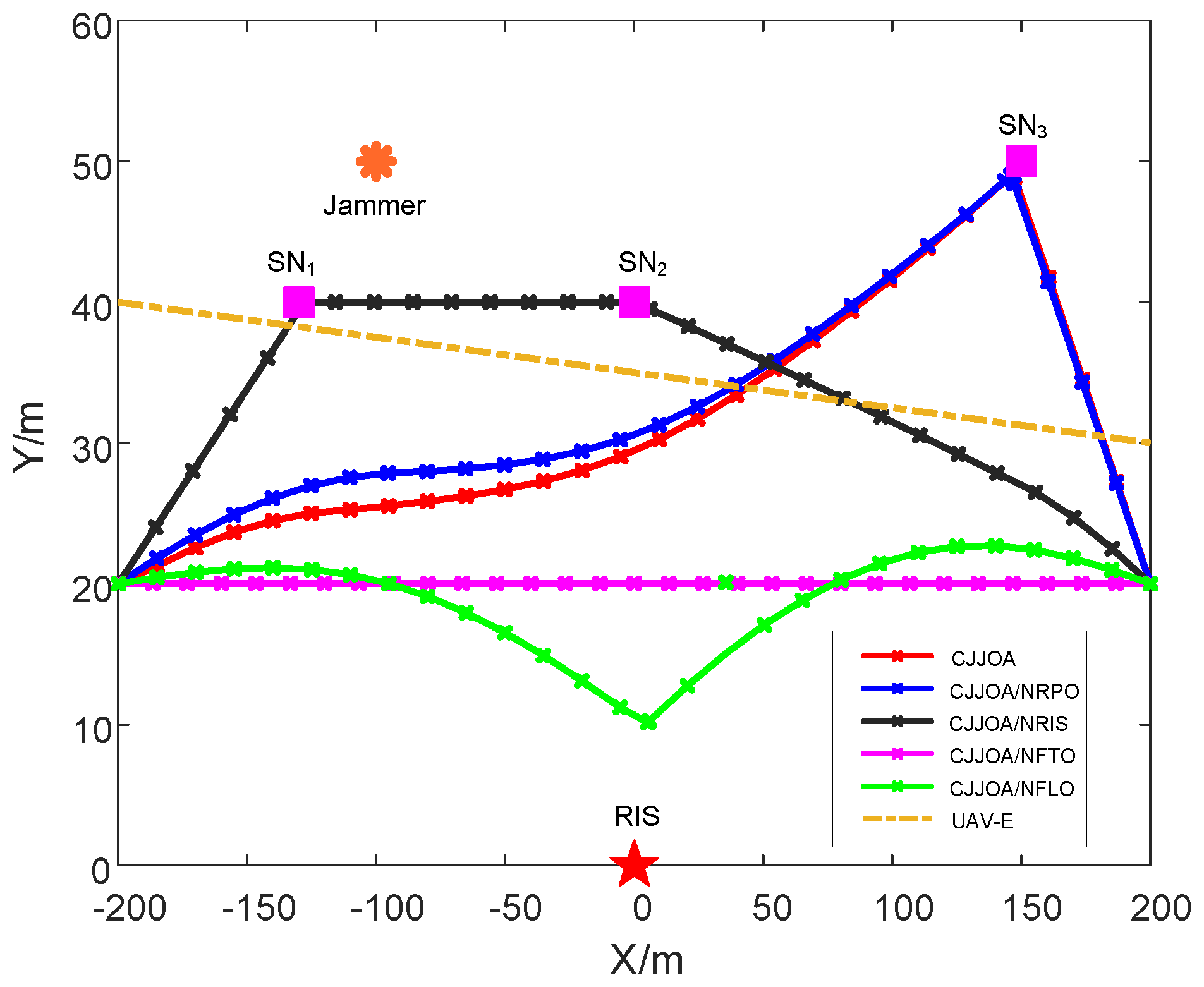
3.4. Trajectory Optimization
| Algorithm 1. Cooperative Jamming Joint Optimization Algorithm (CJJOA). |
| 1: Input: Let is the iteration index, and initialize variables along with the precision 2: Iterative Loop Repeat:
The objective value of Equation (31) tends to approach convergence. |
| 4: Output Final variables |
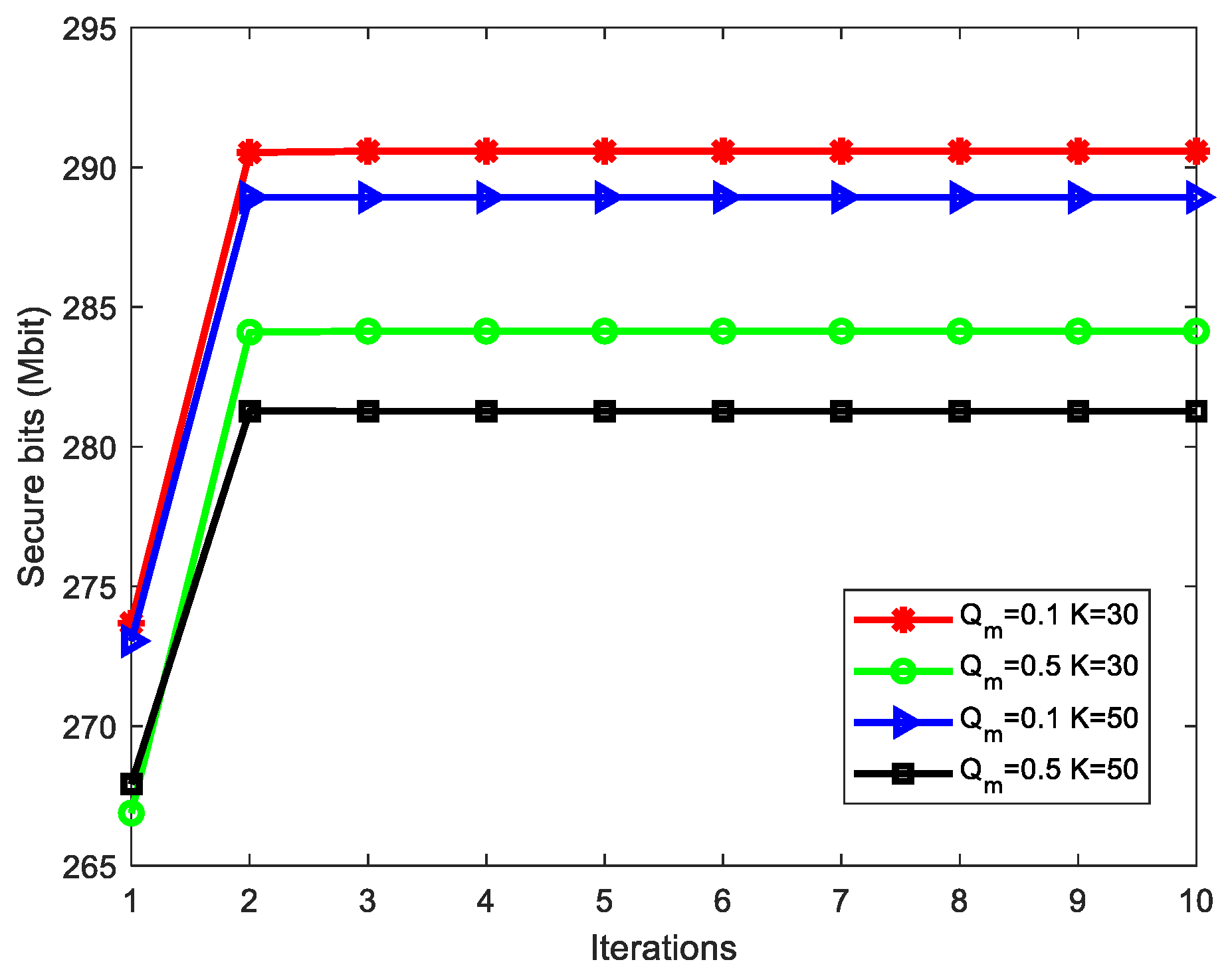
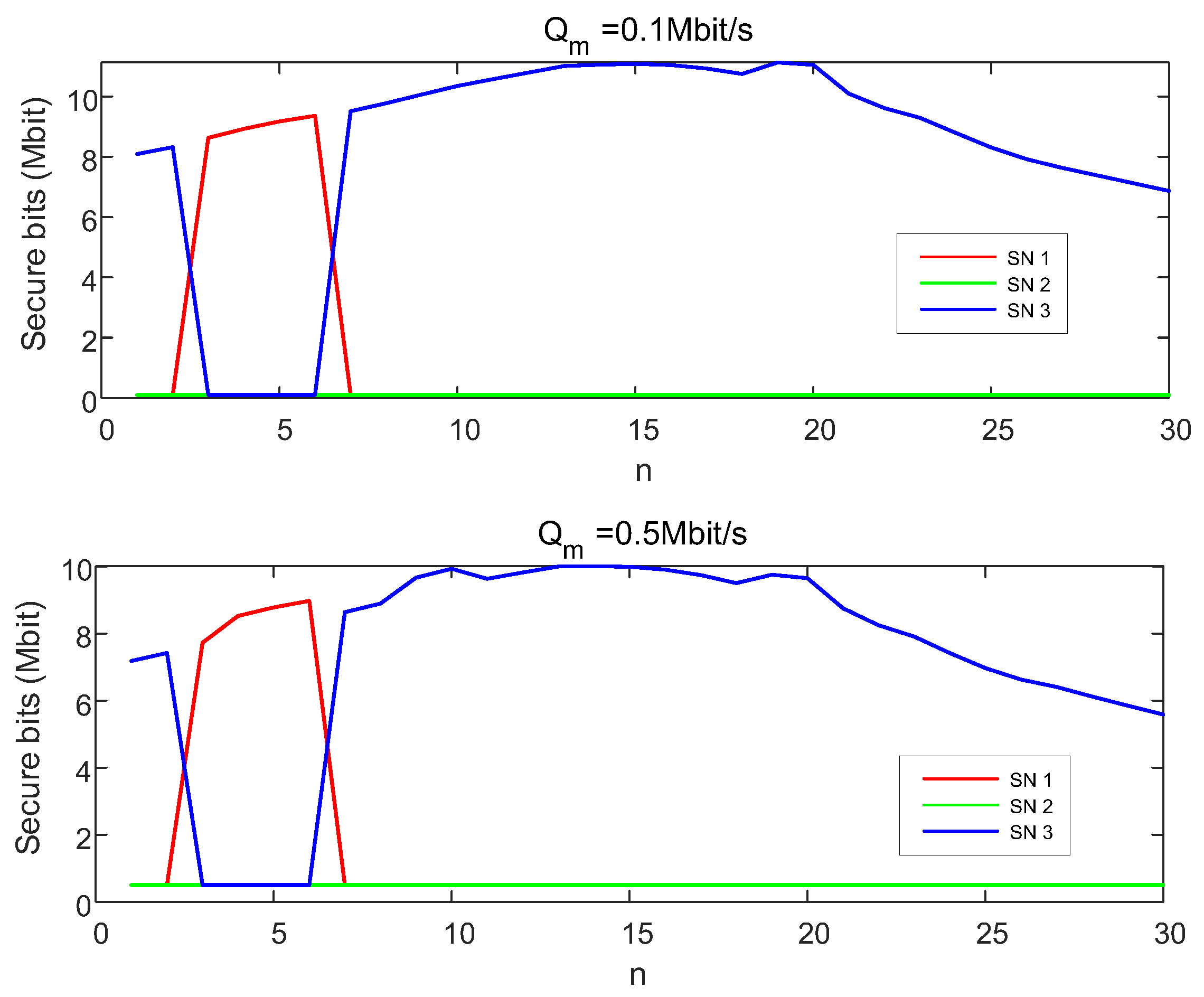
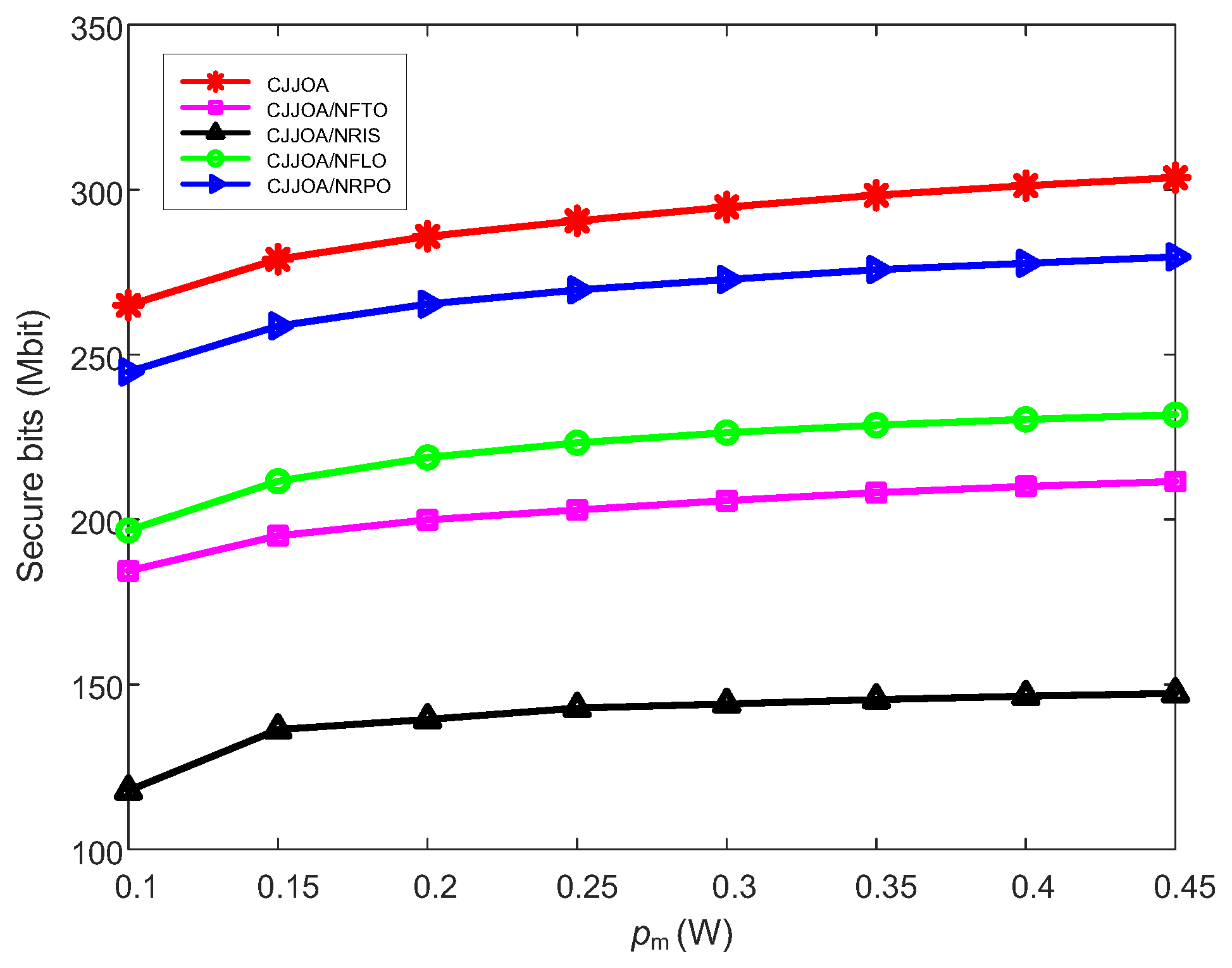
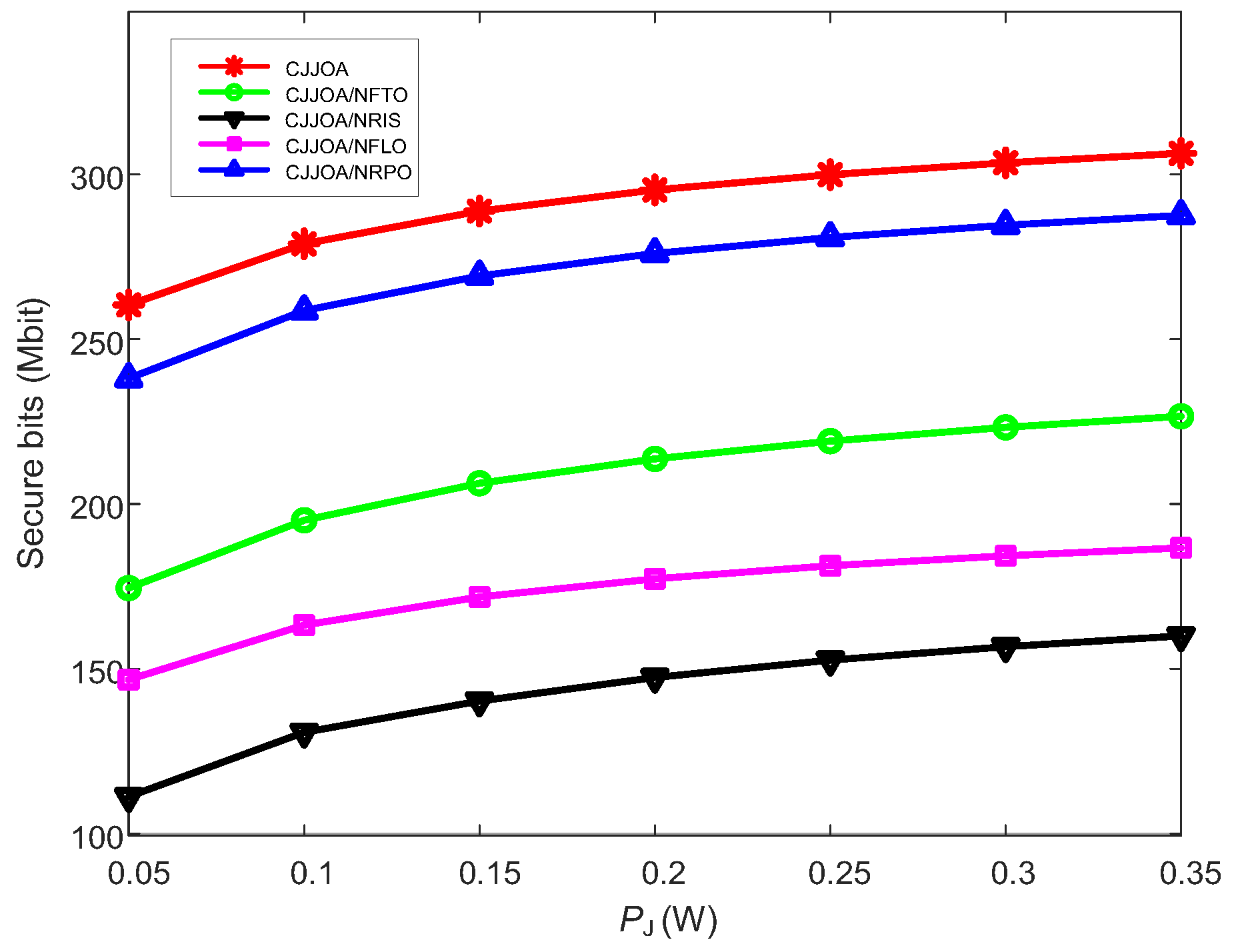
4. Numerical Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, X.; Zhu, X.; Zhai, L. AoI-sensitive data collection in multi-UAV-assisted wireless sensor networks. IEEE Trans. Wirel. Commun. 2023, 22, 5185–5197. [Google Scholar] [CrossRef]
- Yuan, X.; Hu, Y.; Zhang, J.; Schmeink, A. Joint user scheduling and UAV trajectory design on completion time minimization for UAV-aided data collection. IEEE Trans. Wirel. Commun. 2022, 22, 3884–3898. [Google Scholar] [CrossRef]
- Nguyen, K.K.; Duong, T.Q.; Do-Duy, T.; Claussen, H.; Hanzo, L. 3D UAV trajectory and data collection optimisation via deep reinforcement learning. IEEE Trans. Commun. 2022, 70, 2358–2371. [Google Scholar] [CrossRef]
- Zhai, D.; Wang, C.; Zhang, R.; Cao, H.; Yu, F.R. Energy-saving deployment optimization and resource management for UAV-assisted wireless sensor networks with NOMA. IEEE Trans. Veh. Technol. 2022, 71, 6609–6623. [Google Scholar] [CrossRef]
- Li, S.; Wu, F.; Luo, S.; Fan, Z.; Chen, J.; Fu, S. Dynamic online trajectory planning for a UAV-enabled data collection system. IEEE Trans. Veh. Technol. 2022, 71, 13332–13343. [Google Scholar] [CrossRef]
- Saxena, K.; Gupta, N.; Gupta, J.; Sharma, D.K.; Dev, K. Trajectory optimization for the UAV assisted data collection in wireless sensor networks. Wirel. Netw. 2022, 28, 1785–1796. [Google Scholar] [CrossRef]
- Zhang, R.; Pang, X.; Lu, W.; Zhao, N.; Chen, Y.; Niyato, D. Dual-UAV enabled secure data collection with propulsion limitation. IEEE Trans. Wirel. Commun. 2021, 20, 7445–7459. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, N.; Chang, Z.; Hämäläinen, T.; Wang, X. UAV-aided secure short-packet data collection and transmission. IEEE Trans. Commun. 2023, 71, 2475–2486. [Google Scholar] [CrossRef]
- Xiong, X.; Sun, C.; Ni, W.; Wang, X. Three-dimensional trajectory design for unmanned aerial vehicle-based secure and energy-efficient data collection. IEEE Trans. Veh. Technol. 2022, 72, 664–678. [Google Scholar] [CrossRef]
- Wang, Y.; Su, Z.; Xu, Q.; Li, R.; Luan, T.H.; Wang, P. A secure and intelligent data sharing scheme for UAV-assisted disaster rescue. IEEE/ACM Trans. Netw. 2023, 31, 2422–2438. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, J.; Lu, Y.; Cao, R.; Yao, L.; Xia, Y.; Han, D. Lightweight blockchain-enabled secure data sharing in dynamic and resource-limited UAV networks. IEEE Netw. 2024, 38, 25–31. [Google Scholar] [CrossRef]
- Wang, Z.; Tao, J.; Gao, Y.; Xu, Y.; Sun, W.; Gao, Y.; Li, W. Joint flight scheduling and task allocation for secure data collection in UAV-aided IoTs. Comput. Netw. 2022, 207, 108849. [Google Scholar] [CrossRef]
- Deng, Q.; Huang, S.; Li, Z.; Guo, B.; Xiang, L.; Ran, R. A secure data collection strategy using mobile vehicles joint UAVs in smart city. Comput. Netw. 2021, 199, 108440. [Google Scholar] [CrossRef]
- Wang, D.; Yang, Y.; Li, X.; Wang, C.; Liu, F.; Hu, Y. Energy-efficient and secure power allocation and trajectory optimization for UAV-enabled data collection in wireless sensor networks. J. Commun. Inf. Netw. 2022, 7, 333–348. [Google Scholar] [CrossRef]
- Lei, H.; Ran, H.; Ansari, I.S.; Park, K.H.; Pan, G.; Alouini, M.S. DDPG-based aerial secure data collection. IEEE Trans. Commun. 2024, 72, 5179–5193. [Google Scholar] [CrossRef]
- Fu, R.; Ren, X.; Li, Y.; Wu, Y.; Sun, H.; Al-Absi, M.A. Machine-learning-based UAV-assisted agricultural information security architecture and intrusion detection. IEEE Internet Things J. 2023, 10, 18589–18598. [Google Scholar] [CrossRef]
- Dang-Ngoc, H.; Nguyen, D.N.; Ho-Van, K.; Hoang, D.T.; Dutkiewicz, E.; Pham, Q.V.; Hwang, W.J. Secure swarm UAV-assisted communications with cooperative friendly jamming. IEEE Internet Things J. 2022, 9, 25596–25611. [Google Scholar] [CrossRef]
- Wang, W.; Li, X.; Zhang, M.; Cumanan, K.; Ng, D.W.K.; Zhang, G.; Tang, J.; Dobre, O.A. Energy-constrained UAV-assisted secure communications with position optimization and cooperative jamming. IEEE Trans. Commun. 2020, 68, 4476–4489. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, J.; Chen, Z.; Yu, L.; Wang, Y.; Rao, H. Robust secure UAV relay-assisted cognitive communications with resource allocation and cooperative jamming. J. Commun. Netw. 2022, 24, 139–153. [Google Scholar] [CrossRef]
- Yin, Z.; Lin, Y.; Zhang, Y.; Qian, Y.; Shu, F.; Li, J. Collaborative multiagent reinforcement learning aided resource allocation for UAV anti-jamming communication. IEEE Internet Things J. 2022, 9, 23995–24008. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, W.; Hong, X.; Zhang, C. Multi-UAV cooperative anti-jamming for GNSS signals based on frequency-domain power inversion. IEEE Sens. J. 2024, 24, 30778–30791. [Google Scholar] [CrossRef]
- Fang, C.; Feng, Y.; Li, X.; Yang, Y. Multi-UAV Energy-Efficient Detection Coverage Under Jamming Environment: A Hierarchical Collaborative Learning Approach. IEEE Trans. Veh. Technol. 2025, 74, 7351–7363. [Google Scholar] [CrossRef]
- Yin, Z.; Li, J.; Wang, Z.; Qian, Y.; Lin, Y.; Shu, F.; Chen, W. UAV communication against intelligent jamming: A Stackelberg game approach with federated reinforcement learning. IEEE Trans. Green Commun. Netw. 2024, 8, 1796–1808. [Google Scholar] [CrossRef]
- Hu, G.; Li, Z.; Si, J.; Xu, K.; Xu, D.; Cai, Y.; Al-Dhahir, N. Maxmin fairness for UAV-enabled proactive eavesdropping with jamming over distributed transmit beamforming-based suspicious communications. IEEE Trans. Commun. 2023, 71, 1595–1614. [Google Scholar] [CrossRef]
- Rahmatov, N.; Baek, H. RIS-carried UAV communication: Current research, challenges, and future trends. ICT Express 2023, 9, 961–973. [Google Scholar] [CrossRef]
- Guo, J.; Yu, L.; Chen, Z.; Yao, Y.; Wang, Z.; Wang, Z.; Zhao, Q. RIS-assisted secure UAV communications with resource allocation and cooperative jamming. IET Commun. 2022, 16, 1582–1592. [Google Scholar] [CrossRef]
- Shang, Y.; Peng, Y.; Ye, R.; Lee, J. RIS-assisted secure UAV communication scheme against active jamming and passive eavesdropping. IEEE Trans. Intell. Transp. Syst. 2024, 25, 16953–16963. [Google Scholar] [CrossRef]
- Ye, R.; Peng, Y.; Al-Hazemi, F.; Boutaba, R. A robust cooperative jamming scheme for secure UAV communication via intelligent reflecting surface. IEEE Trans. Commun. 2023, 72, 1005–1019. [Google Scholar] [CrossRef]
- Zou, C.; Li, C.; Li, Y.; Yan, X. RIS-assisted robust beamforming for UAV anti-jamming and eavesdropping communications: A deep reinforcement learning approach. Electronics 2023, 12, 4490. [Google Scholar] [CrossRef]
- Mughal, U.A.; Alkhrijah, Y.; Almadhor, A.; Yuen, C. Deep learning for secure UAV-assisted RIS communication networks. IEEE Internet Things Mag. 2024, 7, 38–44. [Google Scholar] [CrossRef]
- Gu, X.; Duan, W.; Zhang, G.; Sun, Q.; Wen, M.; Ho, P.H. Physical layer security for RIS-aided wireless communications with uncertain eavesdropper distributions. IEEE Syst. J. 2022, 17, 848–859. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, Y.; Wu, Q.; Shi, Q.; Zhao, Y. Enhanced secure communication via novel double-faced active RIS. IEEE Trans. Commun. 2023, 71, 3497–3512. [Google Scholar] [CrossRef]
- Chen, Y.; Hao, C.; Feng, J.; Chen, G. Optimization of multi-user fairness in RIS-enhanced UAV secure transmission systems. Phys. Commun. 2024, 66, 102431. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Hoang, T.M.; Tran, P.T. Secrecy performance optimization for UAV-based relay NOMA systems with friendly jamming. Comput. Commun. 2025, 235, 108086. [Google Scholar] [CrossRef]
- Liu, L.; Yao, R.; Xie, Y.; Fan, Y.; Zuo, X.; Xu, J.; Zhong, R.; Zheng, S.; Li, X. Joint Optimization of User Scheduling, Flight Path and Power Allocation in a UAV Secure Communication System. Electronics 2024, 13, 2443. [Google Scholar] [CrossRef]
- Lai, H.; Li, D.; Xu, F.; Wang, X.; Ning, J.; Hu, Y.; Duo, B. Optimization of full-duplex UAV secure communication with the aid of RIS. Drones 2023, 7, 591. [Google Scholar] [CrossRef]
- Zhao, H.; Xu, Z.; Ni, Y.; Sun, W.; Zhu, H.; Liu, Y.; Mo, Z. Optimization strategy of UAV-ARIS assisted vehicular communication system. IET Commun. 2024, 18, 1179–1190. [Google Scholar] [CrossRef]
- Dong, R.; Wang, B.; Cao, K.; Tian, J.; Cheng, T. Secure transmission design of RIS enabled UAV communication networks exploiting deep reinforcement learning. IEEE Trans. Veh. Technol. 2024, 73, 8404–8419. [Google Scholar] [CrossRef]


| Task | Complexity |
|---|---|
| Subtask 1 | |
| Subtask 2 | |
| Subtask 3 | |
| Subtask 4 | |
| The whole task |
| Attack Scenario | Single UAV Advantages | Technical Bottleneck |
|---|---|---|
| Urban canyon environment | Using high-rise building reflections to form multipath eavesdropping | Channel estimation error due to multipath ambiguity |
| Open field scenario | The line-of-sight (LoS) link improves the eavesdropping SNR | Easy to be detected by radar |
| Mountainous undulating terrain | Using terrain shadows to implement covert eavesdropping | The change in communication elevation angle leads to Doppler frequency shift |
| Multi-objective collaborative scenario | Dynamically selecting high-value targets for eavesdropping | The data shunting processing capability is limited by the onboard CPU |
| Notation and Assigned Value | Physical Interpretation |
|---|---|
| RIS horizontal position coordinate | |
| RIS vertical elevation | |
| Altitudes for UAV-L and UAV-E | |
| Total flight time span | |
| Time slot duration | |
| Quantity of reflecting components | |
| Power spectral density of AWGN | |
| Path loss attenuation exponent | |
| Factor characterizing Rician fading |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wang, G.; Wu, W.; Zhou, J.; Liu, Y.; Wei, Y.; Li, W. Cooperative Jamming for RIS-Assisted UAV-WSN Against Aerial Malicious Eavesdropping. Drones 2025, 9, 431. https://doi.org/10.3390/drones9060431
Li J, Wang G, Wu W, Zhou J, Liu Y, Wei Y, Li W. Cooperative Jamming for RIS-Assisted UAV-WSN Against Aerial Malicious Eavesdropping. Drones. 2025; 9(6):431. https://doi.org/10.3390/drones9060431
Chicago/Turabian StyleLi, Juan, Gang Wang, Weijia Wu, Jing Zhou, Yingkun Liu, Yangqin Wei, and Wei Li. 2025. "Cooperative Jamming for RIS-Assisted UAV-WSN Against Aerial Malicious Eavesdropping" Drones 9, no. 6: 431. https://doi.org/10.3390/drones9060431
APA StyleLi, J., Wang, G., Wu, W., Zhou, J., Liu, Y., Wei, Y., & Li, W. (2025). Cooperative Jamming for RIS-Assisted UAV-WSN Against Aerial Malicious Eavesdropping. Drones, 9(6), 431. https://doi.org/10.3390/drones9060431




