DDPG-Based UAV-RIS Framework for Optimizing Mobility in Future Wireless Communication Networks
Abstract
1. Introduction
1.1. Related Work
1.2. Motivations and Contributions
- A novel UAV-RIS framework is proposed to enhance signal strength and improve LoS connectivity between UAVs and GUs in dense urban environments by addressing communication disruptions caused by ground obstacles.
- A modified K-means clustering algorithm is introduced for efficient user partitioning, alongside a DDPG algorithm to intelligently optimize UAV trajectories and RIS configurations simultaneously in a continuous action space for managing GUs mobility.
- The proposed framework, utilizing the DDPG algorithm, significantly improves key network performance metrics, including HOF, OP, EE, throughput, and LoS probability, compared to state-of-the-art schemes.
2. System Model
3. Problem Formulation
3.1. User Partitioning
| Algorithm 1: Proposed SINR/Distance-based User Partitioning Scheme |
|
Input: Number of GUs, SINR threshold, sum rate threshold Initialization: Randomly generate each user’s locations and initial data rates. 1: for every user do 2: Calculate Euclidean distance between the user and neighboring users. 3: Randomly assign data rate to each user using random distribution techniques. 4: Assign the user to the group with the highest SINR, minimum distance, and maximum data rate. 5: Repeat steps 2–4 for all users in the network until convergence. 6: end for Until Groups achieve minimal inter-user distances, highest SINR, and maximum data rates. Output: Optimal User Groups |
3.2. Joint Optimization of UAV Location and RIS Phase Shifts
- State Space: The set of spaces, including the UAV’s optimal location and RIS phase shifts, at time is described as
- Action Space: The action space includes a UAV movement and RIS phase shifts when transitioning from the current to the next state. The suggested approach enables the agent to continuously determine the optimal movement while considering the long-term reward and identify the optimal phase shift for each time instance. The agent (UAV-RIS) inputs the state at time step t to determine the appropriate action based on the current environment, resulting in the optimal UAV horizontal location and updated RIS phase shift to improve connectivity and mobility issues in urban environments. The action space is expressed as
- Reward: After performing action in state at time t, the agent obtains a reward . Based on the objective of the paper, the sum rate per user group describes the reward and can be written as
| Algorithm 2: Proposed DDPG Algorithm for Joint Optimization of UAV Location and RIS Phase Shifts |
Initialization:
|
4. Numerical Results and Analysis
4.1. Scenario Setup
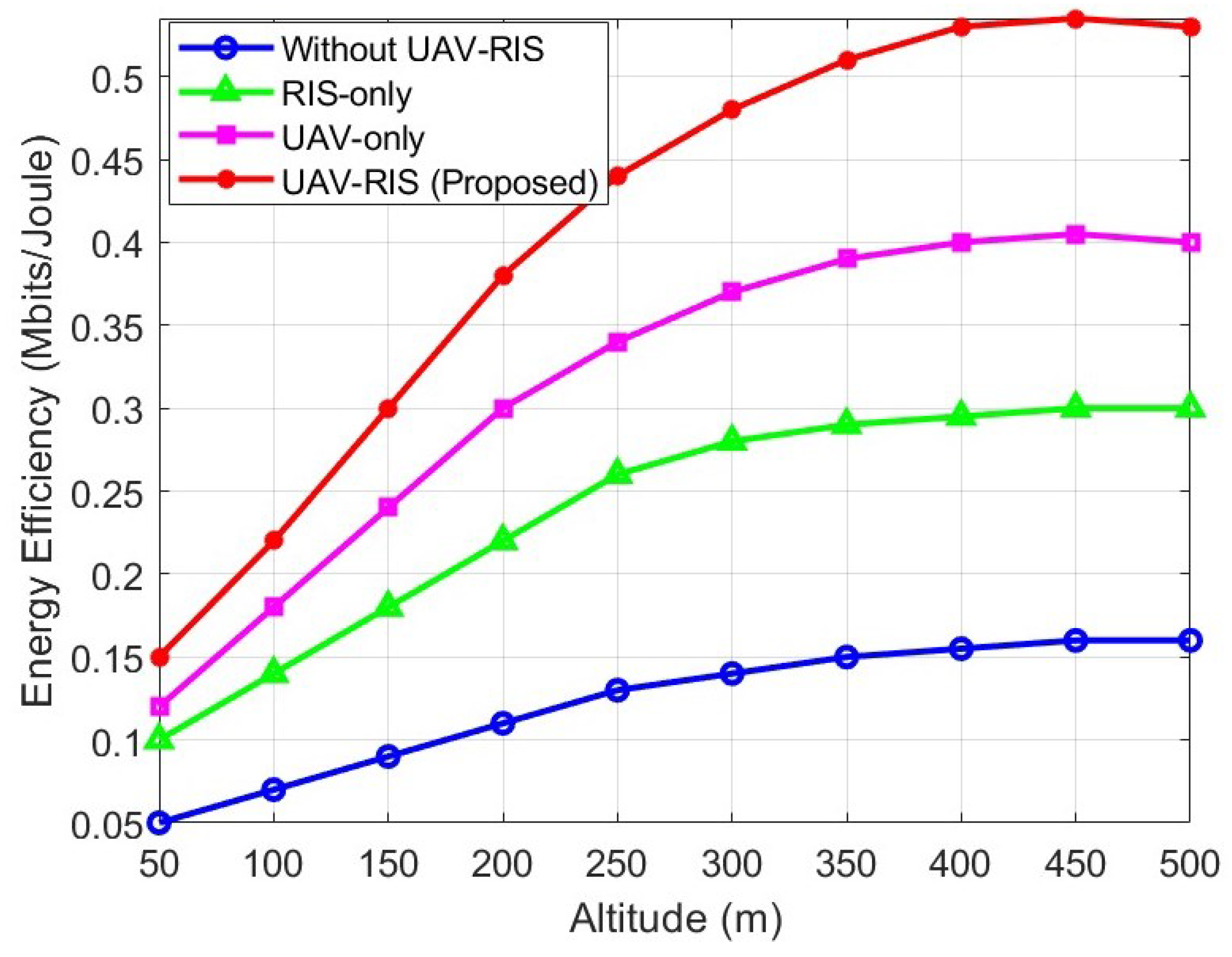
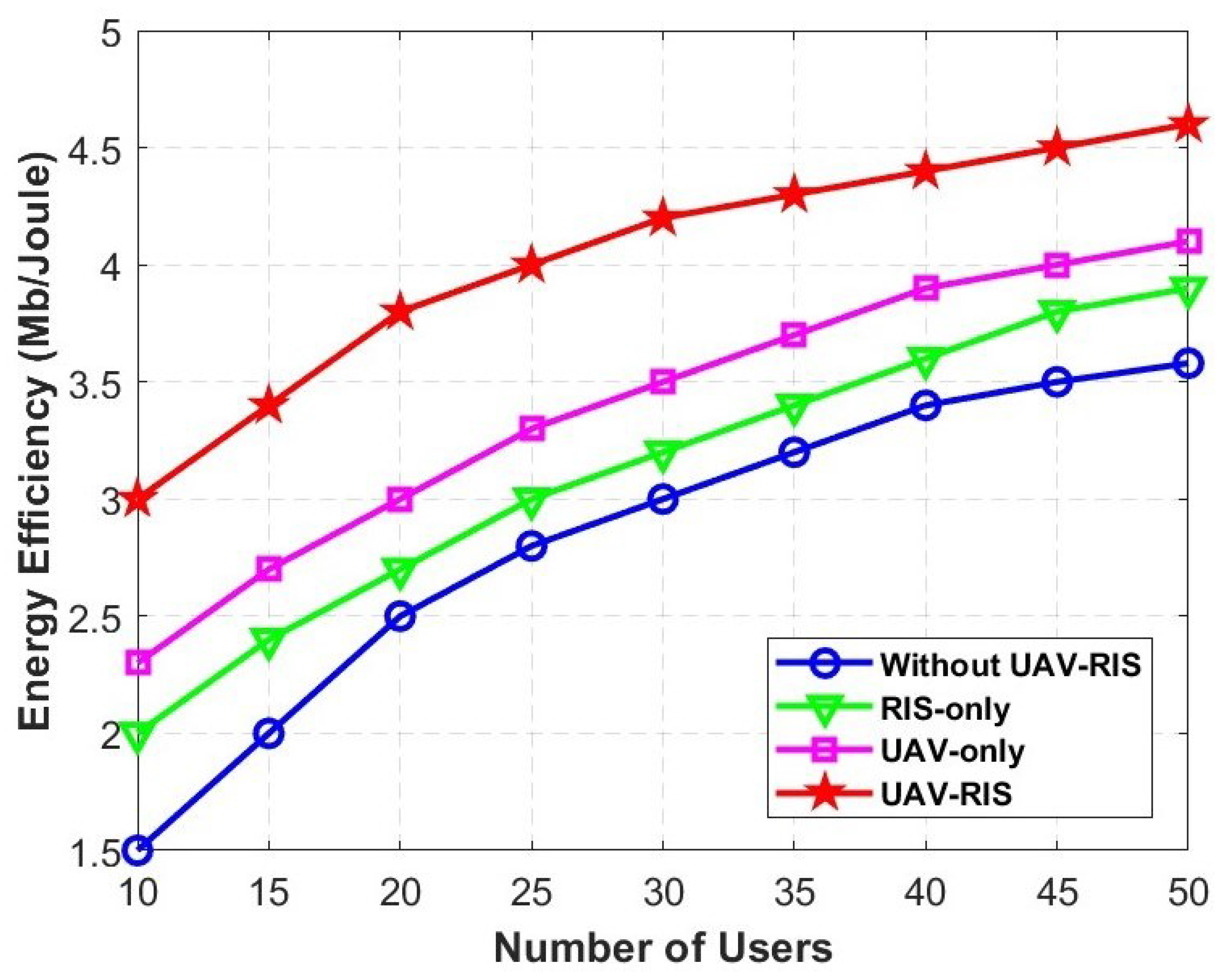
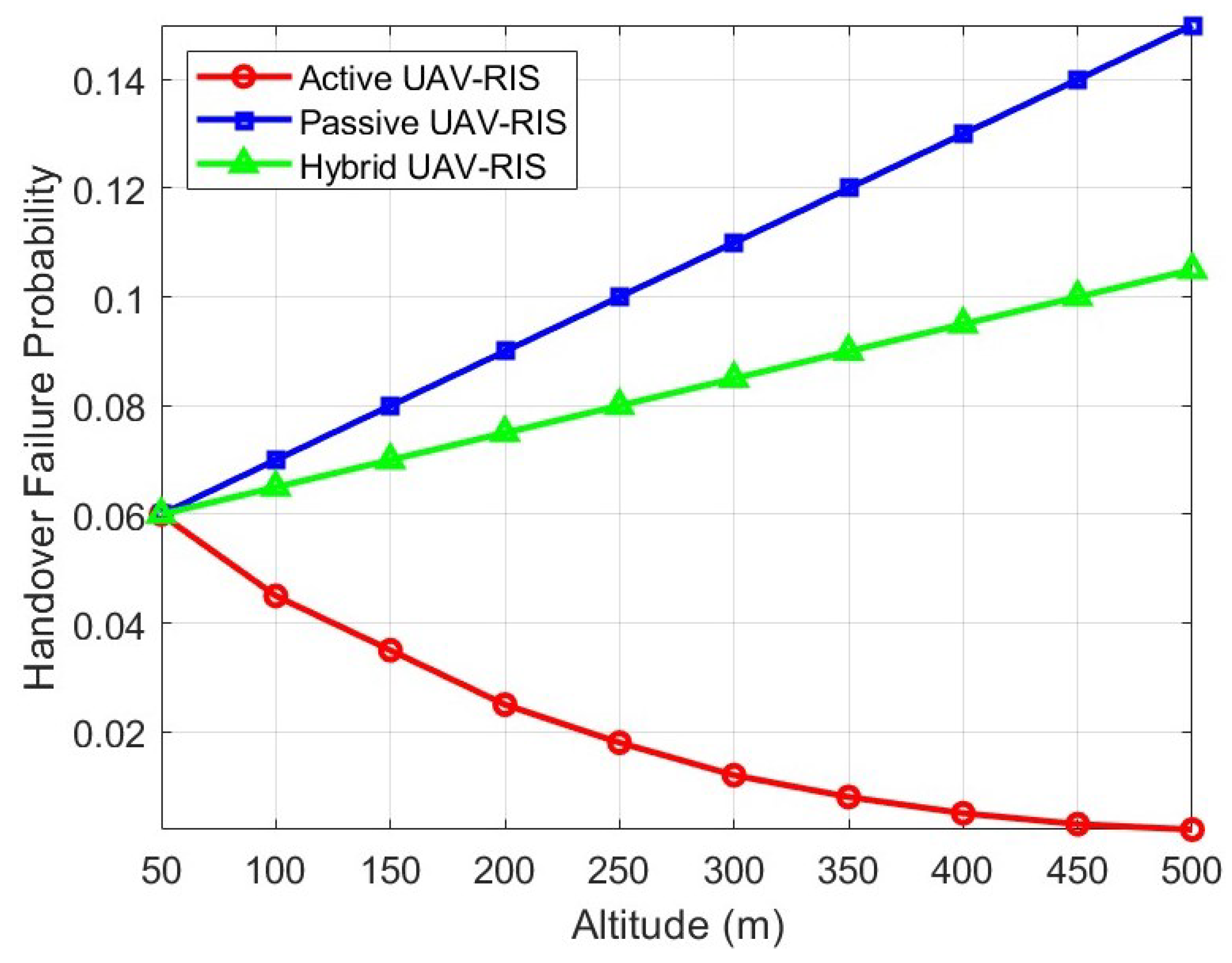
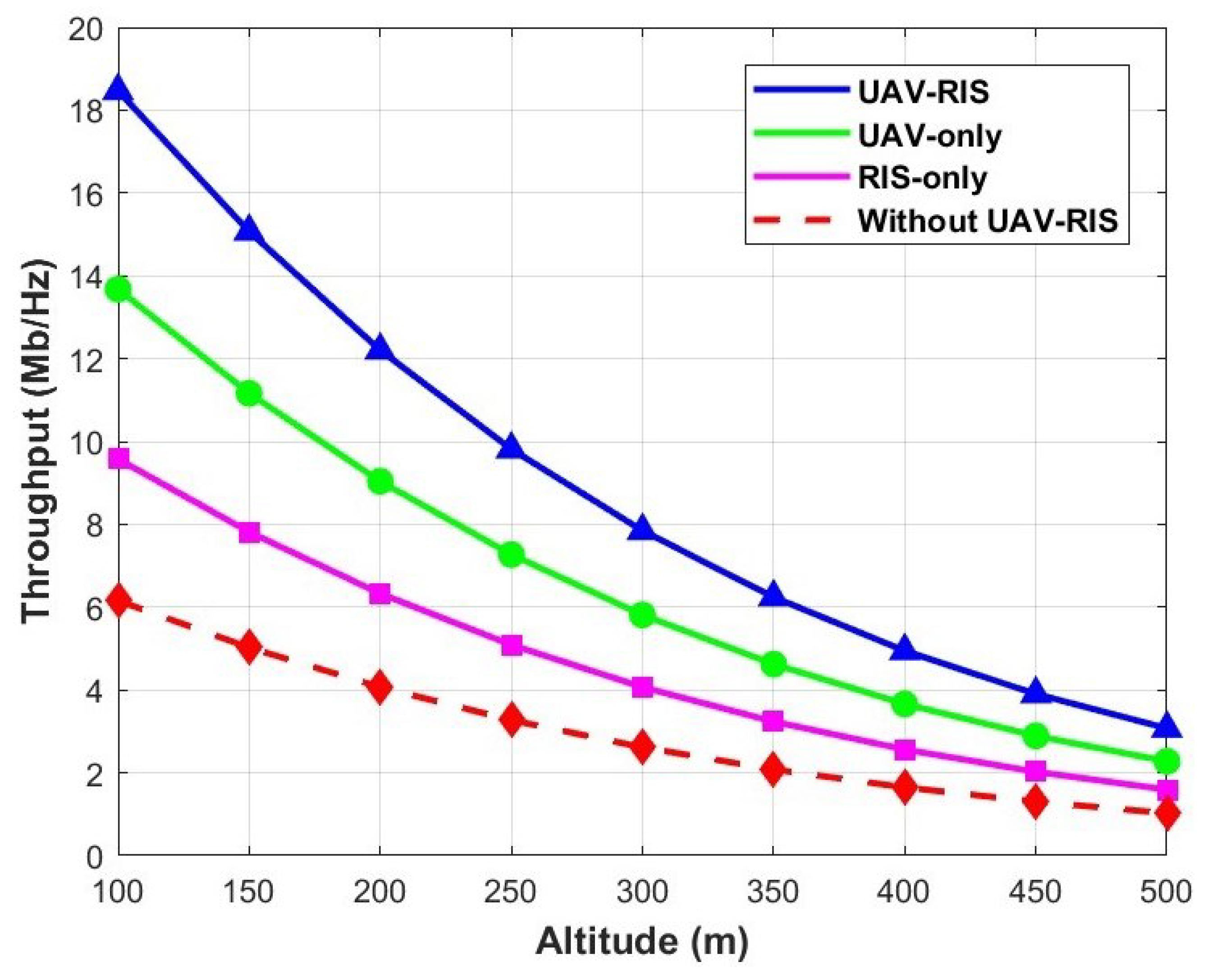
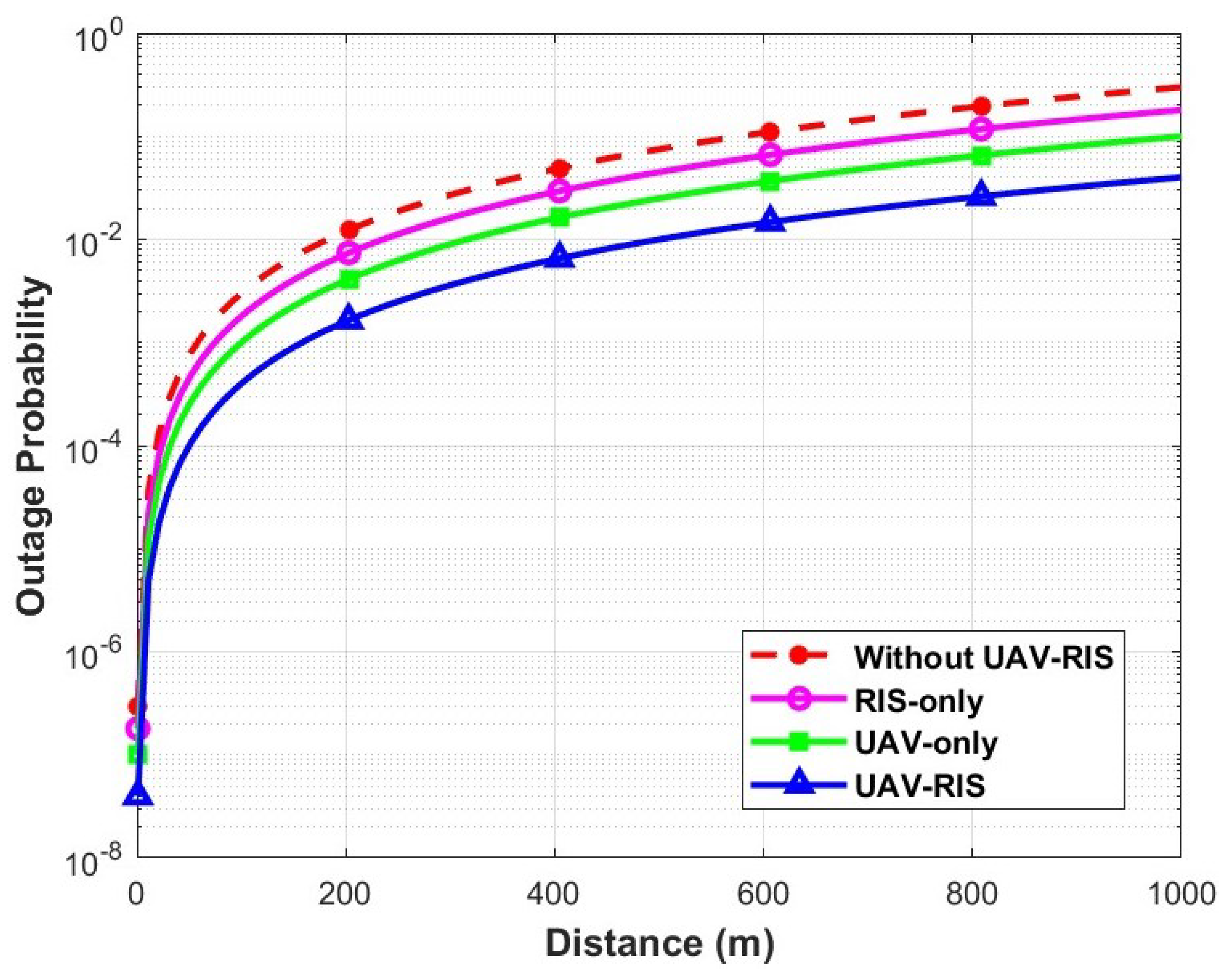
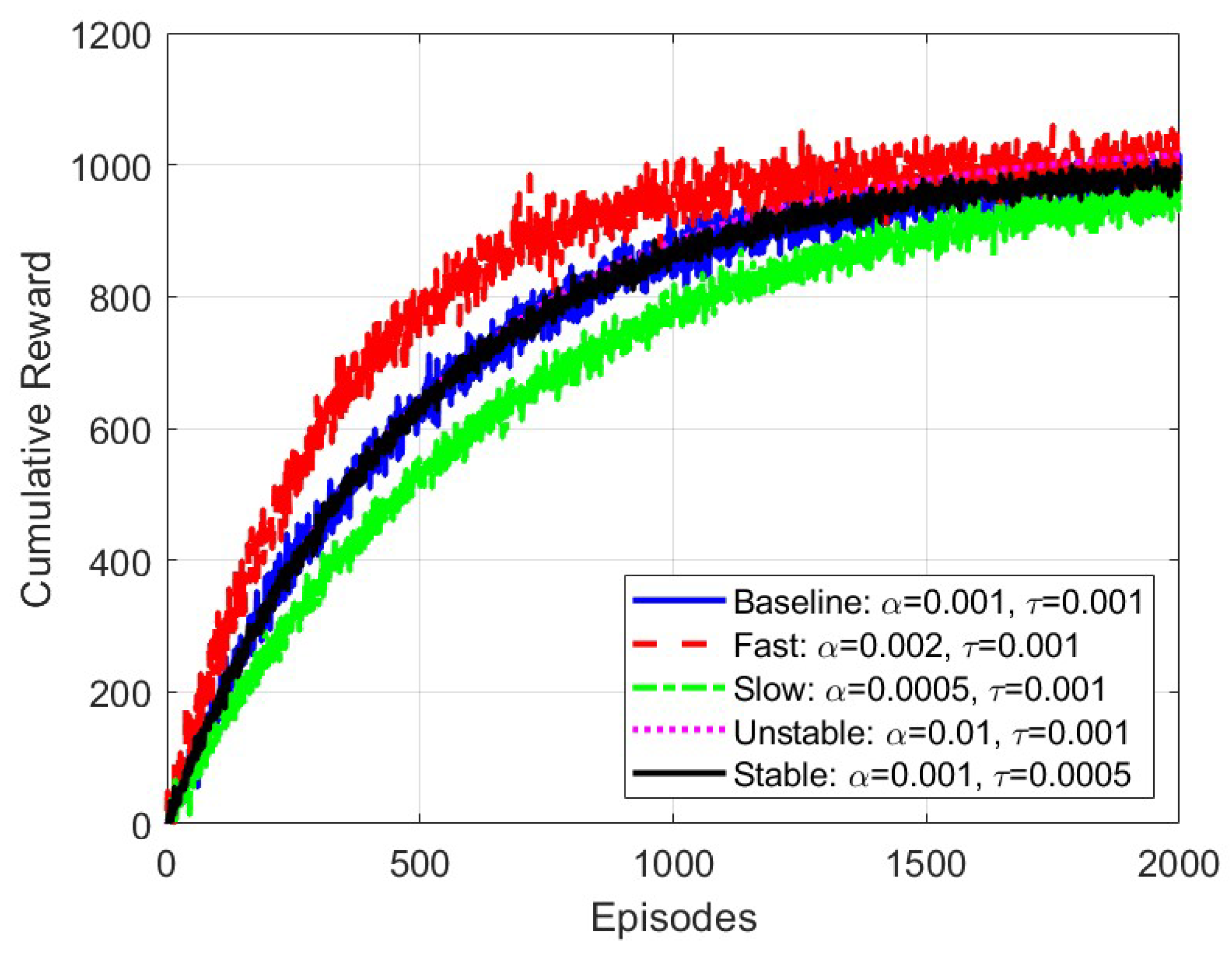
4.2. Simulation Discussion and Comparison
5. Conclusions and Future Work
Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Redondi, A.E.; Innamorati, C.; Gallucci, S.; Fiocchi, S.; Matera, F. A Survey on Future Millimeter-Wave Communication Applications. IEEE Access 2024, 12, 133165–133182. [Google Scholar] [CrossRef]
- Roy, S.; Tiang, J.J.; Roslee, M.B.; Ahmed, M.T.; Mahmud, M.A.P. A Quad-Band Stacked Hybrid Ambient RF-Solar Energy Harvester with Higher RF-to-DC Rectification Efficiency. IEEE Access 2021, 9, 39303–39321. [Google Scholar] [CrossRef]
- Roslee, M.B.; Abdullah, R.S.A.R.; Shafr, H.Z. Road pavement density analysis using a new non-destructive ground penetrating radar system. Prog. Electromagn. Res. B 2010, 21, 399–417. [Google Scholar] [CrossRef]
- Banafaa, M.; Shayea, I.; Din, J.; Azmi, M.H.; Alashbi, A.; Daradkeh, Y.I.; Alhammadi, A. 6G mobile communication technology: Requirements, targets, applications, challenges, advantages, and opportunities. Alex. Eng. J. 2023, 64, 245–274. [Google Scholar] [CrossRef]
- Khan, S.A.; Shayea, I.; Ergen, M.; El-Saleh, A.A.; Roslee, M. An Improved Handover Decision Algorithm for 5G Heterogeneous Networks. In Proceedings of the 2021 IEEE 15th Malaysia International Conference on Communication (MICC), Kuala Lumpur, Malaysia, 1–2 December 2021; pp. 25–30. [Google Scholar]
- Li, B.; Fei, Z.; Zhang, Y. UAV communications for 5G and beyond: Recent advances and future trends. IEEE Internet Things J. 2018, 6, 2241–2263. [Google Scholar] [CrossRef]
- Ullah, Y.; Roslee, M.B.; Mitani, S.M.; Khan, S.A.; Jusoh, M.H. A survey on handover and mobility management in 5G HetNets: Current state, challenges, and future directions. Sensors 2023, 23, 5081. [Google Scholar] [CrossRef]
- Chen, P.; Luo, L.; Guo, D.; Tang, G.; Zhao, B.; Li, Y.; Luo, X. Why and How Lasagna Works: A New Design of Air-Ground Integrated Infrastructure. IEEE Netw. 2024, 38, 132–140. [Google Scholar] [CrossRef]
- Elnabty, I.A.; Fahmy, Y.; Kafafy, M. A survey on UAV placement optimization for UAV-assisted communication in 5G and beyond networks. Phys. Commun. 2022, 51, 101564. [Google Scholar] [CrossRef]
- Dai, M.; Sun, G.; Yu, H.; Wang, S.; Niyato, D. User Association and Channel Allocation in 5G Mobile Asymmetric Multi-Band Heterogeneous Networks. IEEE Trans. Mob. Comput. 2025, 24, 3092–3109. [Google Scholar] [CrossRef]
- Ullah, Y.; Roslee, M.; Mitani, S.M.; Sheraz, M.; Ali, F.; Aurangzeb, K.; Osman, A.F.; Ali, F.Z. A survey on AI-enabled mobility and handover management in future wireless networks: Key technologies, use cases, and challenges. J. King Saud Univ. Comput. Inf. Sci. 2025, 37, 1–37. [Google Scholar] [CrossRef]
- Chu, H.; Pan, X.; Jiang, J.; Li, X.; Zheng, L. Adaptive and Robust Channel Estimation for IRS-Aided Millimeter-Wave Communications. IEEE Trans. Veh. Technol. 2024, 73, 9411–9423. [Google Scholar] [CrossRef]
- Renzo, M.D.; Debbah, M.; Phan-Huy, D.T.; Zappone, A.; Alouini, M.S.; Yuen, C.; Sciancalepore, V.; Alexandropoulos, G.C.; Hoydis, J.; Gacanin, H.; et al. Smart radio environments empowered by reconfigurable AI meta-surfaces: An idea whose time has come. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 1–20. [Google Scholar] [CrossRef]
- Huang, S.; Sun, C.; Pompili, D. Meta-ETI: Meta-Reinforcement Learning with Explicit Task Inference for UAV-IoT Coverage. IEEE Internet Things J. 2025. [Google Scholar] [CrossRef]
- Di Renzo, M.; Zappone, A.; Debbah, M.; Alouini, M.S.; Yuen, C.; De Rosny, J.; Tretyakov, S. Smart radio environments empowered by reconfigurable intelligent surfaces: How it works, state of research, and the road ahead. IEEE J. Sel. Areas Commun. 2020, 38, 2450–2525. [Google Scholar] [CrossRef]
- Chen, J.; Cao, K.; Ding, H.; Lv, L.; Ye, Y.; Chi, H.; Yang, L. Double-RIS Enabled Physical Layer Security for Wireless-Powered Communication Systems Over Rayleigh Fading Channels. IEEE Trans. Commun. 2025. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Chen, Y. Machine learning empowered trajectory and passive beamforming design in UAV-RIS wireless networks. IEEE J. Sel. Areas Commun. 2020, 39, 2042–2055. [Google Scholar] [CrossRef]
- Ullah, Y.; Roslee, M.; Mitani, S.M.; Sheraz, M.; Ali, F.; Osman, A.F.; Jusoh, M.H.; Sudhamani, C. Reinforcement learning-based unmanned aerial vehicle trajectory planning for ground users’ mobility management in heterogeneous networks. J. King Saud Univ.-Comput. Inf. Sci. 2024, 36, 102052. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, K.; Han, J.; Zhu, L.; Xiao, Z.; Xia, X.G. Resource allocation and 3-D placement for UAV-enabled energy-efficient IoT communications. IEEE Internet Things J. 2020, 8, 1322–1333. [Google Scholar] [CrossRef]
- Azari, A.; Ghavimi, F.; Ozger, M.; Jantti, R.; Cavdar, C. Machine learning assisted handover and resource management for cellular connected drones. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; IEEE: New York, NY, USA, 2020; pp. 1–7. [Google Scholar]
- Jiao, L.; Wang, P.; Alipour-Fanid, A.; Zeng, H.; Zeng, K. Enabling efficient blockage-aware handover in RIS-assisted mmWave cellular networks. IEEE Trans. Wirel. Commun. 2021, 21, 2243–2257. [Google Scholar] [CrossRef]
- Li, S.; Duo, B.; Yuan, X.; Liang, Y.C.; Di Renzo, M. Reconfigurable intelligent surface assisted UAV communication: Joint trajectory design and passive beamforming. IEEE Wirel. Commun. Lett. 2020, 9, 716–720. [Google Scholar] [CrossRef]
- Ma, D.; Ding, M.; Hassan, M. Enhancing cellular communications for UAVs via intelligent reflective surface. In Proceedings of the 2020 IEEE Wireless Communications and Networking Conference (WCNC), Seoul, Republic of Korea, 25–28 May 2020; IEEE: New York, NY, USA, 2020; pp. 1–6. [Google Scholar]
- Joshi, N.; Budhiraja, I.; Garg, D.; Garg, S.; Choi, B.J.; Alrashoud, M. Deep reinforcement learning based rate enhancement scheme for RIS assisted mobile users underlaying UAV. Alex. Eng. J. 2024, 91, 1–11. [Google Scholar] [CrossRef]
- Wei, Z.; Cai, Y.; Sun, Z.; Ng, D.W.K.; Yuan, J.; Zhou, M.; Sun, L. Sum-rate maximization for IRS-assisted UAV OFDMA communication systems. IEEE Trans. Wirel. Commun. 2020, 20, 2530–2550. [Google Scholar] [CrossRef]
- Yao, Y.; Lv, K.; Huang, S.; Li, X.; Xiang, W. UAV Trajectory and Energy Efficiency Optimization in RIS-Assisted Multi-User Air-to-Ground Communications Networks. Drones 2023, 7, 272. [Google Scholar] [CrossRef]
- Saif, M.; Valaee, S. Improving Connectivity of RIS-Assisted UAV Networks using RIS Partitioning and Deployment. In Proceedings of the 2024 IEEE 100th Vehicular Technology Conference (VTC2024-Fall), Washington, DC, USA, 7–10 October 2024; IEEE: New York, NY, USA, 2024; pp. 1–6. [Google Scholar]
- Zhao, H.; Sun, W.; Ni, Y.; Xia, W.; Gui, G.; Zhu, C. Deep Deterministic Policy Gradient-Based Rate Maximization for RIS-UAV-Assisted Vehicular Communication Networks. IEEE Trans. Intell. Transp. Syst. 2024, 25, 15732–15744. [Google Scholar] [CrossRef]
- Jiao, S.; Xie, X.; Ding, Z. Deep reinforcement learning based optimization for IRS based UAV-NOMA downlink networks. arXiv 2021, arXiv:2106.09616. [Google Scholar]
- Peng, H.; Wang, L.C.; Li, G.Y.; Tsai, A.H. Long-lasting UAV-aided RIS communications based on SWIPT. In Proceedings of the 2022 IEEE Wireless Communications and Networking Conference (WCNC), Austin, TX, USA, 10–13 April 2022; IEEE: New York, NY, USA, 2022; pp. 1844–1849. [Google Scholar]
- Liu, X.; Yu, Y.; Peng, B.; Zhai, X.B.; Zhu, Q.; Leung, V.C.M. RIS-UAV Enabled Worst-Case Downlink Secrecy Rate Maximization for Mobile Vehicles. IEEE Trans. Veh. Technol. 2023, 72, 6129–6141. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.; Liu, L.; Han, Z.; Poor, H.V.; Di, B. Target Detection and Positioning Aided by Reconfigurable Surfaces: Reflective or Holographic? IEEE Trans. Wirel. Commun. 2024, 23, 19215–19230. [Google Scholar] [CrossRef]
- Jiang, F.; Li, T.; Lv, X.; Rui, H.; Jin, D. Physics-Informed Neural Networks for Path Loss Estimation by Solving Electromagnetic Integral Equations. IEEE Trans. Wirel. Commun. 2024, 23, 15380–15393. [Google Scholar] [CrossRef]
- Xu, F.; Duo, B.; Xie, Y.; Pan, G.; Yang, Y.; Zhang, L.; Wang, Y. Multi-UAV Assisted Mixed FSO/RF Communication Network for Urgent Tasks: Fairness Oriented Design With DRL. IEEE Trans. Veh. Technol. 2025, 74, 1736–1741. [Google Scholar] [CrossRef]
- Abbas, Y.; Alarfaj, A.A.; Alabdulqader, E.A.; Algarni, A.; Jalal, A.; Liu, H. Drone-Based Public Surveillance Using 3D Point Clouds and Neuro-Fuzzy Classifier. Comput. Mater. Contin. 2025, 82, 4759–4776. [Google Scholar] [CrossRef]
- Alshehri, M.; Zahoor, L.; AlQahtani, Y.; Alshahrani, A.; AlHammadi, D.; Jalal, A.; Liu, H. Unmanned aerial vehicle based multi-person detection via deep neural network models. Front. Neurorobot. 2025, 19, 1582995. [Google Scholar] [CrossRef] [PubMed]
- Xu, K.; Wei, A.; Zhang, C.; Chen, Z.; Lu, K.; Hu, W.; Lu, F. HiFusion: An Unsupervised Infrared and Visible Image Fusion Framework With a Hierarchical Loss Function. IEEE Trans. Instrum. Meas. 2025, 74, 5015616. [Google Scholar] [CrossRef]




| Ref. | System Configuration | Optimization Technique | Mobility Consideration | Remarks |
|---|---|---|---|---|
| [23] | RIS-assisted UAV | RIS location optimization for gain maximization | UAV users | Does not consider GU mobility; focuses only on RIS deployment in buildings. |
| [24] | RIS-assisted UAV | DRL-based rate enhancement | Mobile GUs | Limited joint design for RIS and UAV trajectories. |
| [29] | IRS-based UAV-NOMA | DRL-based beamforming and UAV optimization | Mobility clustering not considered | Lacks user mobility clustering despite IRS integration. |
| [30] | UAV-RIS-SWIPT | SWIPT-based energy optimization | Static users | Does not considered mobile users, focus on static users with energy-harvesting RIS. |
| [31] | RIS-UAV Mobile Vehicle | Successive convex approximation-based secrecy rate maximization | UAV is assumed to be static | No dynamic UAV mobility; RIS for secrecy enhancement. |
| This Work | UAV-RIS with user clustering | DDPG-based joint UAV trajectory and RIS phase optimization | Dynamic mobility management of mobile GUs | Fully dynamic, adaptive UAV-RIS integration with user clustering. |
| Parameter | Value |
|---|---|
| Maximum UAV-RIS speed | 72 km/h |
| Maximum UAV-RIS height | 500 m |
| Carrier frequency | 100 GHz |
| Bandwidth | 10 GHz |
| No. of randomly distributed GUs | 50 |
| GUs speed | 3 km/h |
| GBS to GU transmit power | 40 dBm |
| UAV-RIS to GU transmit power | 30 dBm |
| PL exponent for LoS and NLoS links | 2, 3 |
| GBS antenna spacing | |
| Rician factor (R) | 2 |
| Discount factor | 0.9 |
| Hidden layers | 2 |
| Training networks’ learning rate | 0.001 |
| Target networks’ learning rate | 0.001 |
| Number of RIS elements | 100, 200, 300 |
| RIS elements spacing (vertical and horizontal) | = mm |
| Number of episodes | 6000 |
| Number of steps per episode | 2000 |
| Experience replay buffer size | 150,000 |
| Mini-batch size | 128 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, Y.; Adeoye, I.O.; Roslee, M.; Ismail, M.A.; Ali, F.; Ahmad, S.; Osman, A.F.; Ali, F.Z. DDPG-Based UAV-RIS Framework for Optimizing Mobility in Future Wireless Communication Networks. Drones 2025, 9, 437. https://doi.org/10.3390/drones9060437
Ullah Y, Adeoye IO, Roslee M, Ismail MA, Ali F, Ahmad S, Osman AF, Ali FZ. DDPG-Based UAV-RIS Framework for Optimizing Mobility in Future Wireless Communication Networks. Drones. 2025; 9(6):437. https://doi.org/10.3390/drones9060437
Chicago/Turabian StyleUllah, Yasir, Idris Olalekan Adeoye, Mardeni Roslee, Mohd Azmi Ismail, Farman Ali, Shabeer Ahmad, Anwar Faizd Osman, and Fatimah Zaharah Ali. 2025. "DDPG-Based UAV-RIS Framework for Optimizing Mobility in Future Wireless Communication Networks" Drones 9, no. 6: 437. https://doi.org/10.3390/drones9060437
APA StyleUllah, Y., Adeoye, I. O., Roslee, M., Ismail, M. A., Ali, F., Ahmad, S., Osman, A. F., & Ali, F. Z. (2025). DDPG-Based UAV-RIS Framework for Optimizing Mobility in Future Wireless Communication Networks. Drones, 9(6), 437. https://doi.org/10.3390/drones9060437






