High-Precision Trajectory-Tracking Control of Quadrotor UAVs Based on an Improved Crested Porcupine Optimiser Algorithm and Preset Performance Self-Disturbance Control
Abstract
1. Introduction
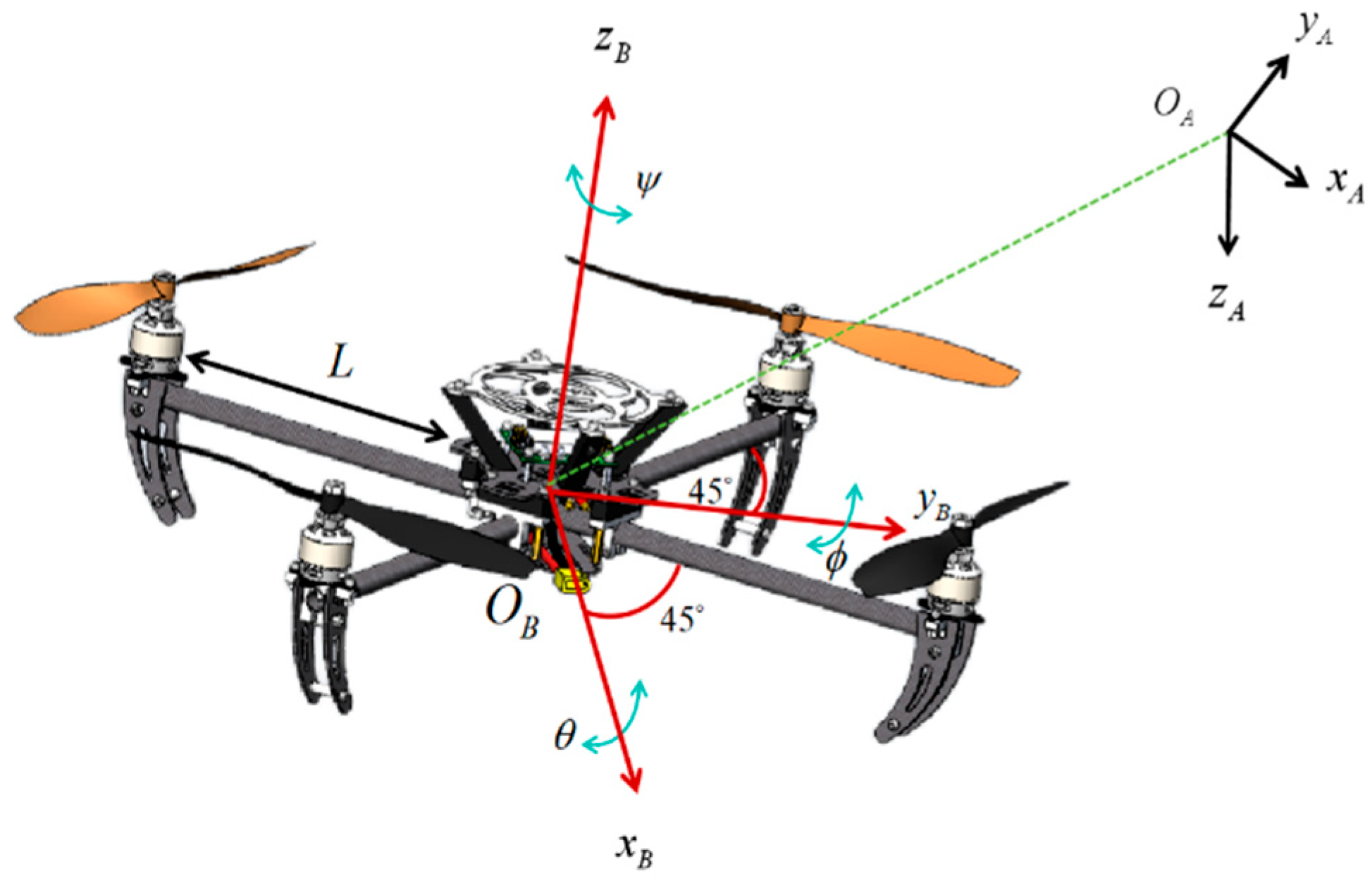
2. Modelling of Four-Rotor UAVs
2.1. Mathematical Modelling of Quadcopter UAVs
- (1)
- the aircraft is a rigid body with complete geometric and structural symmetry;
- (2)
- the mass characteristics and rotational moment of inertia of the system are kept constant;
- (3)
- the geometrical centre of symmetry and the spatial position of the centre of mass coincide.
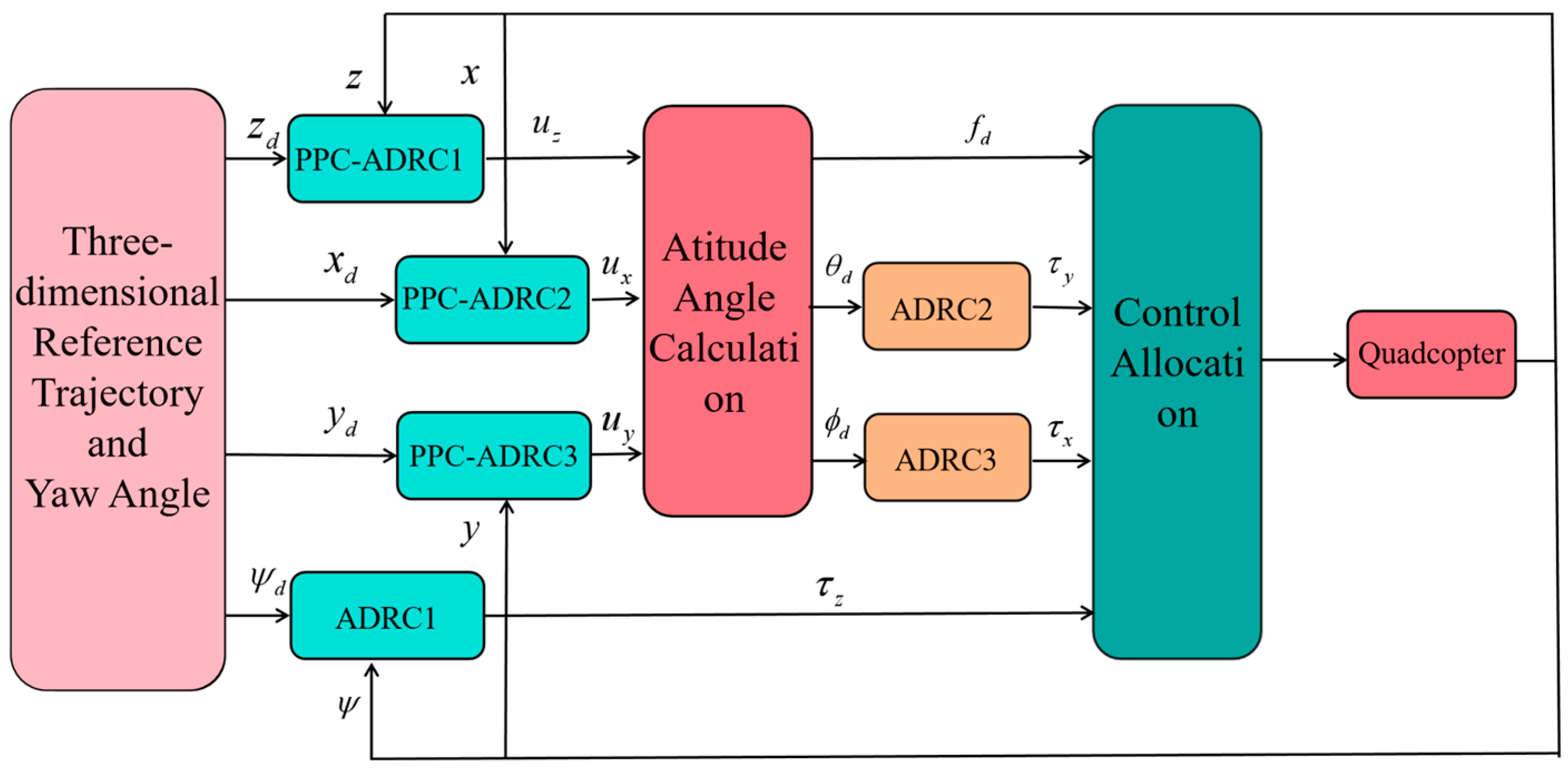
2.2. Quadcopter UAV Control System Design
- (1)
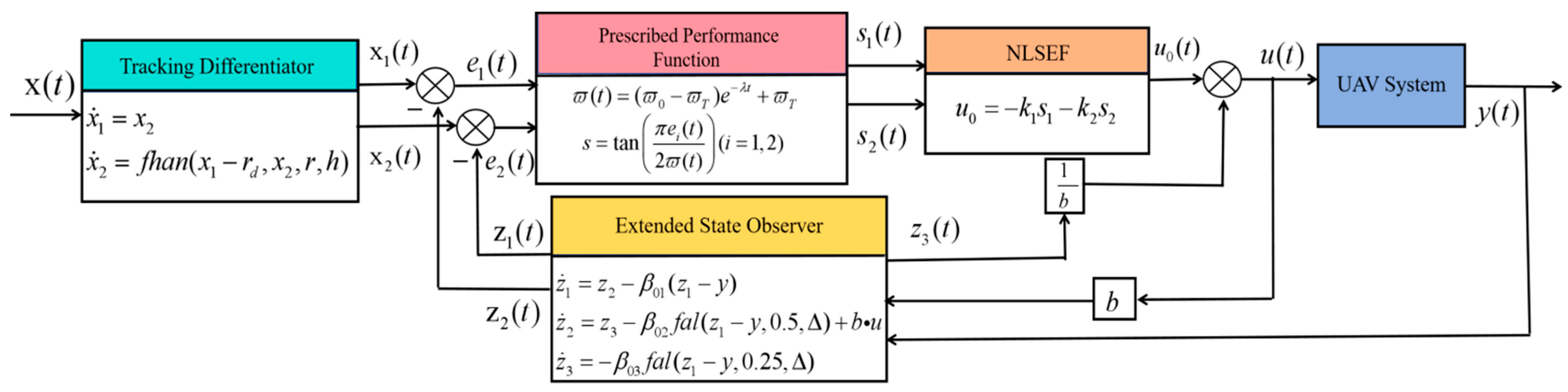
- ADRC design with preset performance for the outer loop
- (2)
- Quadrotor kinematic decoupling and dynamic command mapping
- (3)
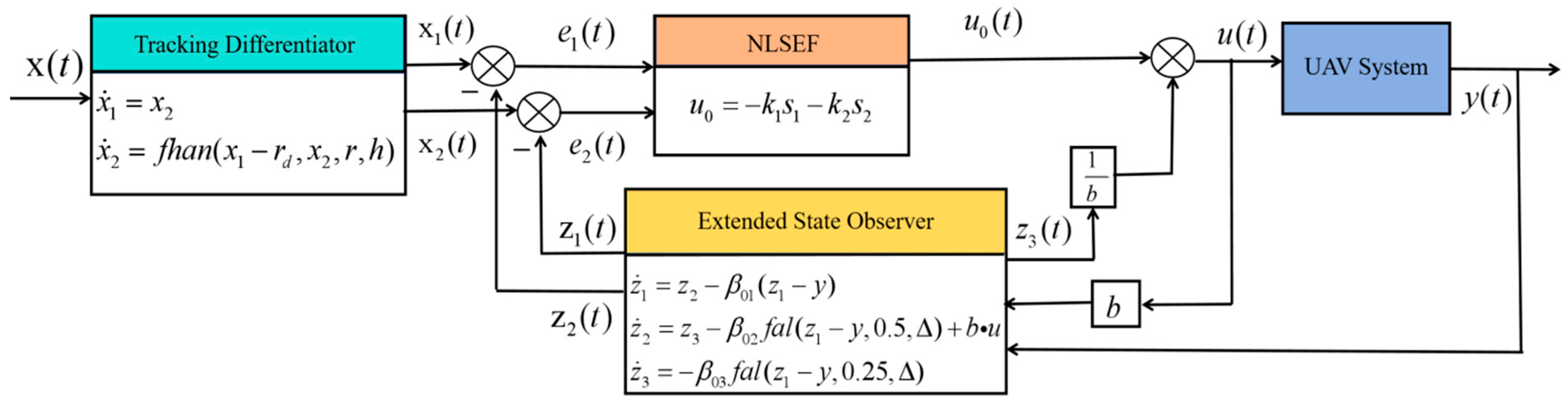
- Inner-loop ADRC controller design
3. Crested Porcupine Optimiser (CPO) Principle and Improvements: Integration with ADRC
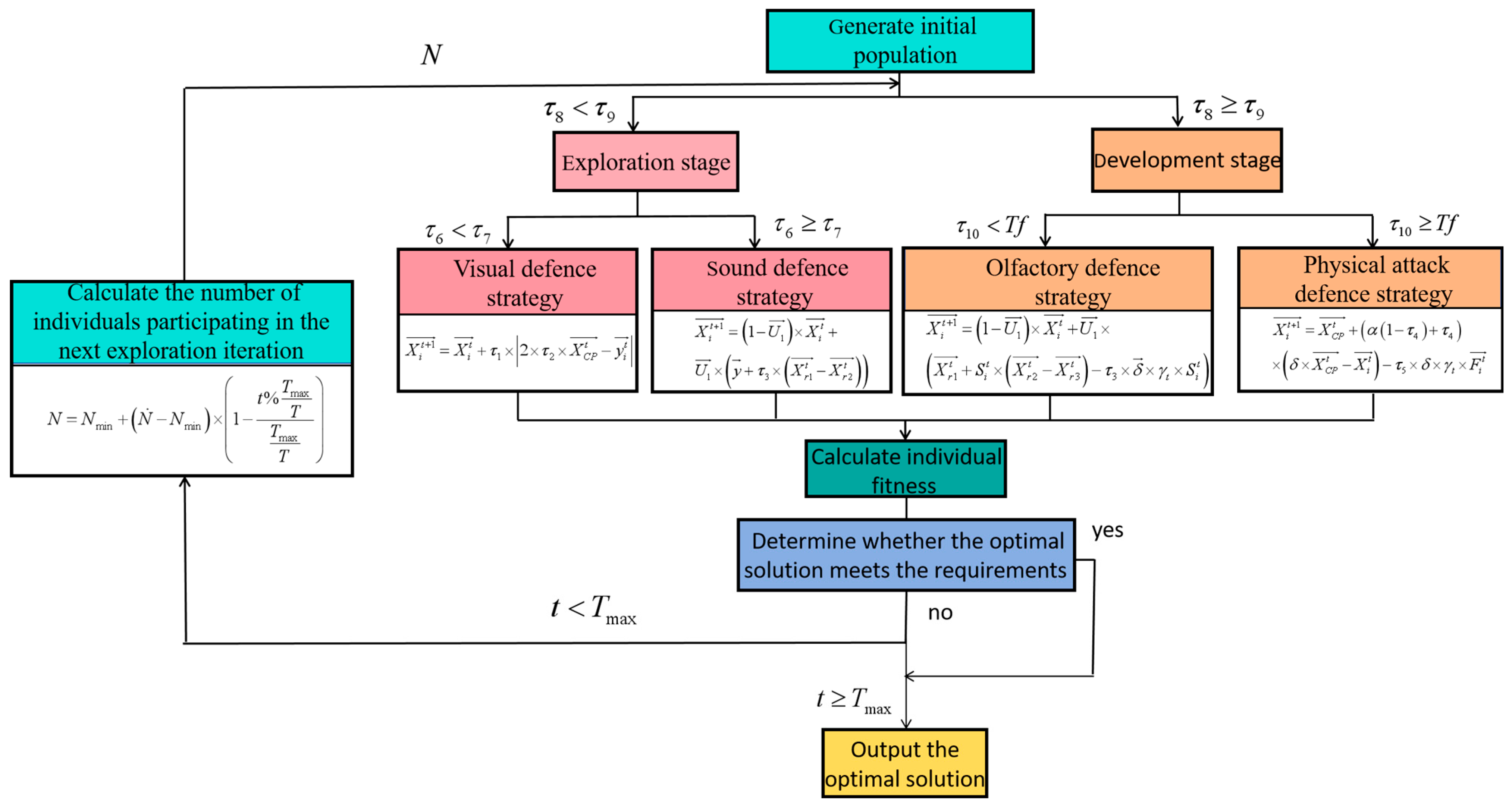
3.1. Crested Porcupine Optimiser (CPO) Principle
- (1)
- Population initialisation
- (2)
- Division of the exploration phase
3.2. Optimisation Algorithm Design
- (1)
- Defects of classical crown porcupine optimisation
- (2)
- Improvement method
- (a)
- fitness-based individual ranking operator is constructed to reorder individuals based on their fitness values , and the individuals are sorted in ascending order to ensure that low-fitness individuals are prioritised for elimination when adjusting the number of individuals in the population in each round of the cycle, thus enhancing the selection pressure.
- (b)
- The generation of random numbers in the original algorithm is changed to a time-varying deterministic threshold :where is the current number of iterations of the algorithm, and is the maximum number of iterations. The design follows the principle of the “exploration–exploitation trade-off”: at the beginning, the high value promotes a global search to break through the local optimum; in the middle, the equilibrium state maintains the diversity of the population; and at the end, the low value accelerates the local convergence, which is in line with the demand for dynamic adjustment of the algorithm optimisation process.
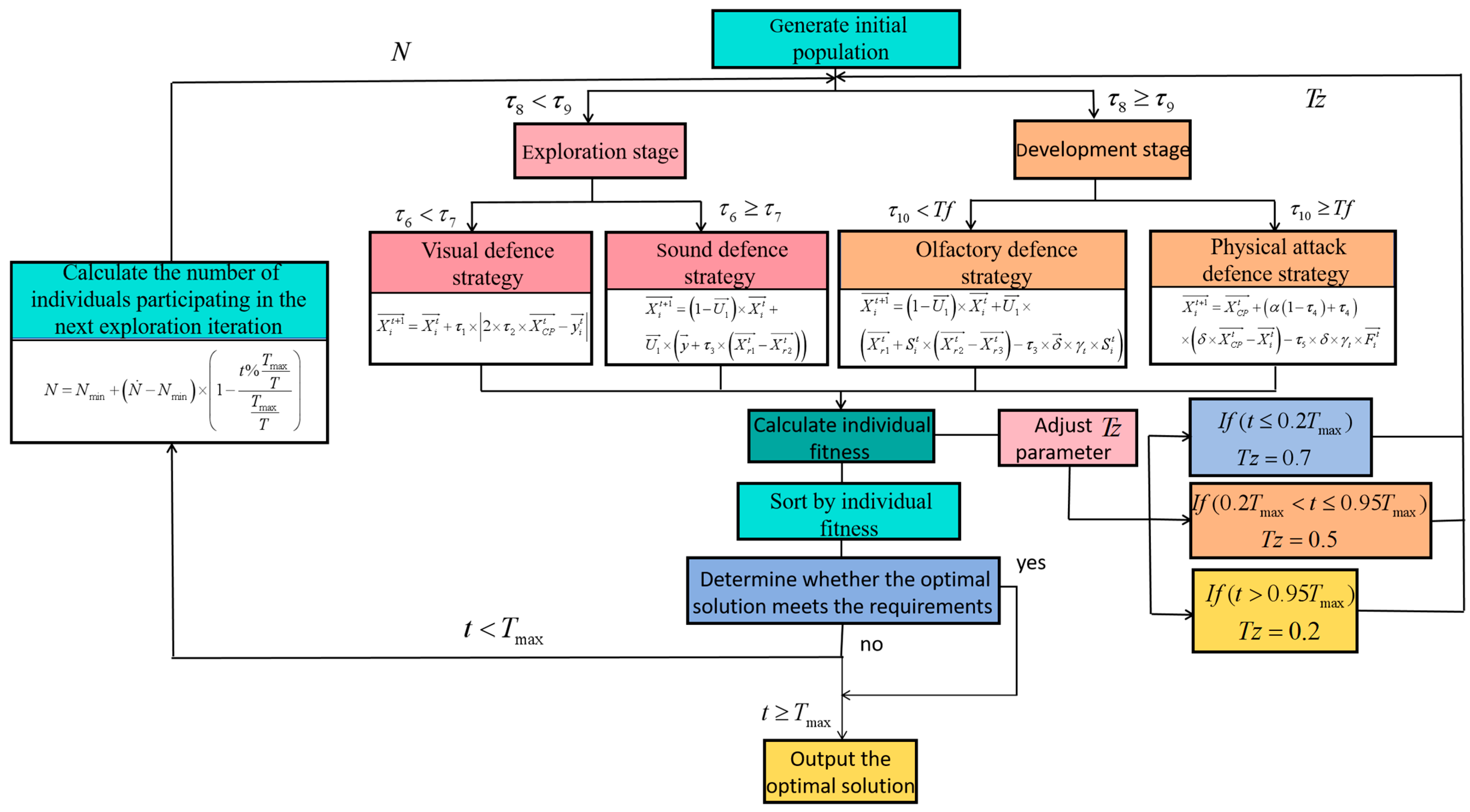
3.3. Integration of Active Disturbance Rejection Control (ADRC) and Crested Porcupine Optimiser Algorithm (CPO)
- (1)
- Combination of ADRC and ICPO
| Pseudocode for a quadrotor PPC-ADRC + ADRC control system with CPO parameter tuning Input: reference trajectory instruction , desired yaw angle Output: angle of attitude , control input BEGIN 1. Initialise system parameters: , , , inertia matrix , quality , arm length , thrust coefficient , drag coefficient 2. ICPO parameter tuning process Define the vector of optimisation parameters: define upper and lower bounds: Define CPO optimisation parameters: population size:, maximum number of iterations , dimension . Define fitness function: CPO algorithm: Initialise population , Evaluate initial population fitness: Update global best solution and global best fitness For to For to If : Exploration stage: If : visual defence strategy: If : sound defence strategy: If : development stage: If : olfactory defence strategy: If : Physical attack defence strategy: Boundary handling evaluate the fitness of the new solution update the individual best solution and the global best solution End For Update population size : End For optimal parameter set 3. Initialise the controller using the optimal parameters position control parameter: posture control parameter: Initialise the preset performance function parameters: initial state: 4. Definition of a non-linear function Predefined performance functions: Error conversion function definition: 5. Start quadcopter tracking control loop For to Obtain the desired states Obtain the current states For to 3: //location tracking control Corresponds to the x-, y-, and z-axes—Update the state of the tracking differentiator: Update the expansion status observer (ESO) status: Apply preset performance function transformation: computational control law: End For Calculate desired roll and pitch angles: For to 3: //Posture control cycle calculation Update the pose tracker differentiator state: Update the posture expansion state observer: calculate posture control: (Note: The PPC-ADRC + ADRC is not required for the yaw angle’s control input . As it is only a first-order system, the yaw angle can be directly controlled by the inner-loop ADRC controller, which outputs .) End For //Final control input calculation Calculation of the motor speed from thrust and torque: Real-time assessment of the quadrotor response Apply control inputs to the motors Measure and record state variables, errors and performance indicators End For END |
- (2)
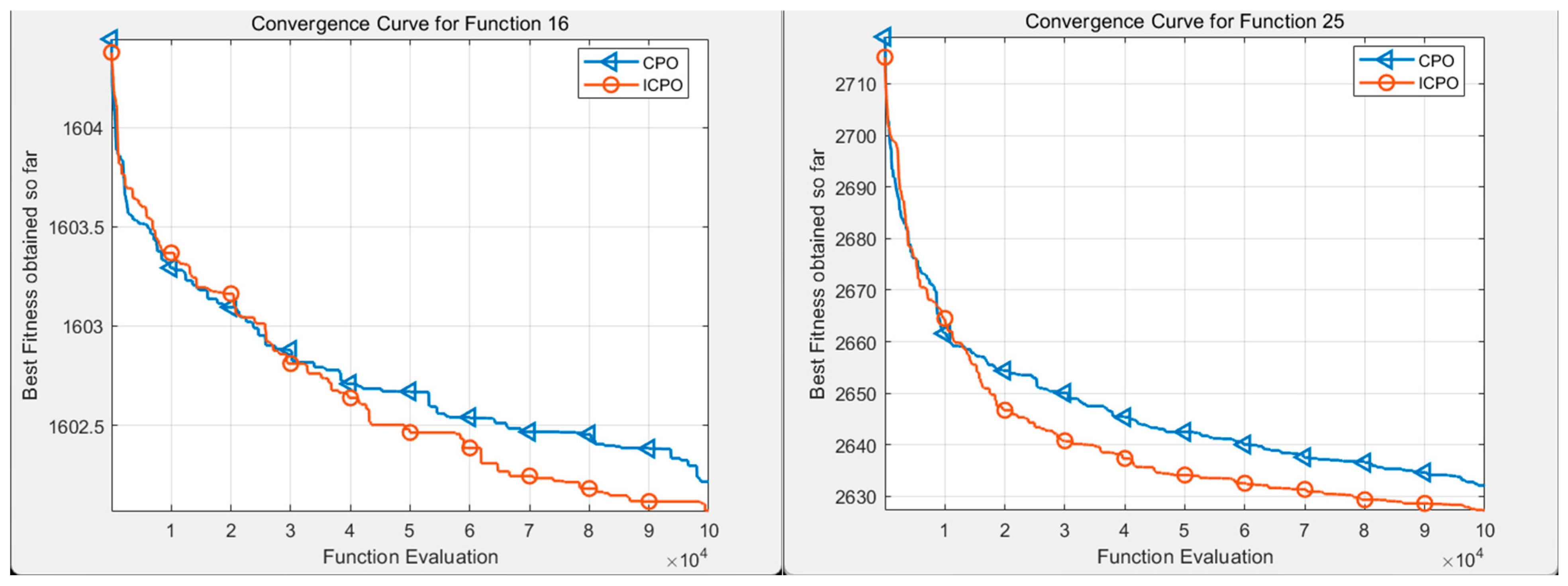
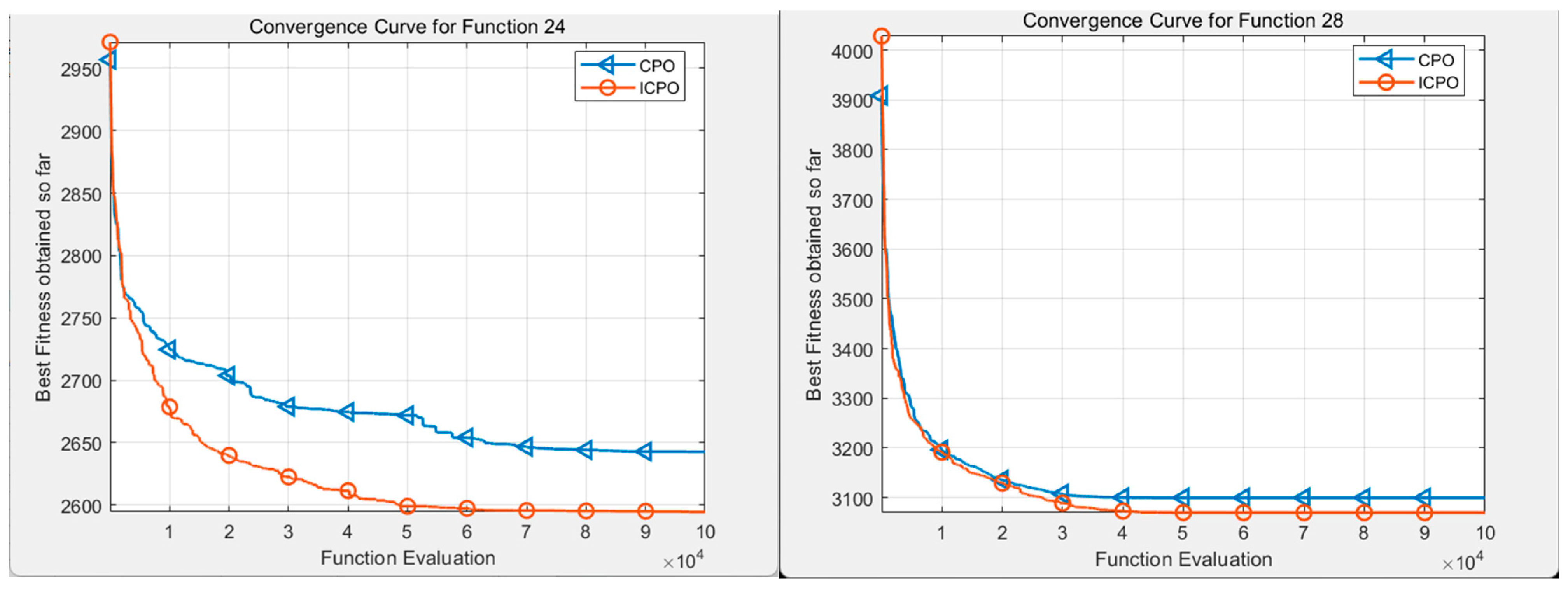
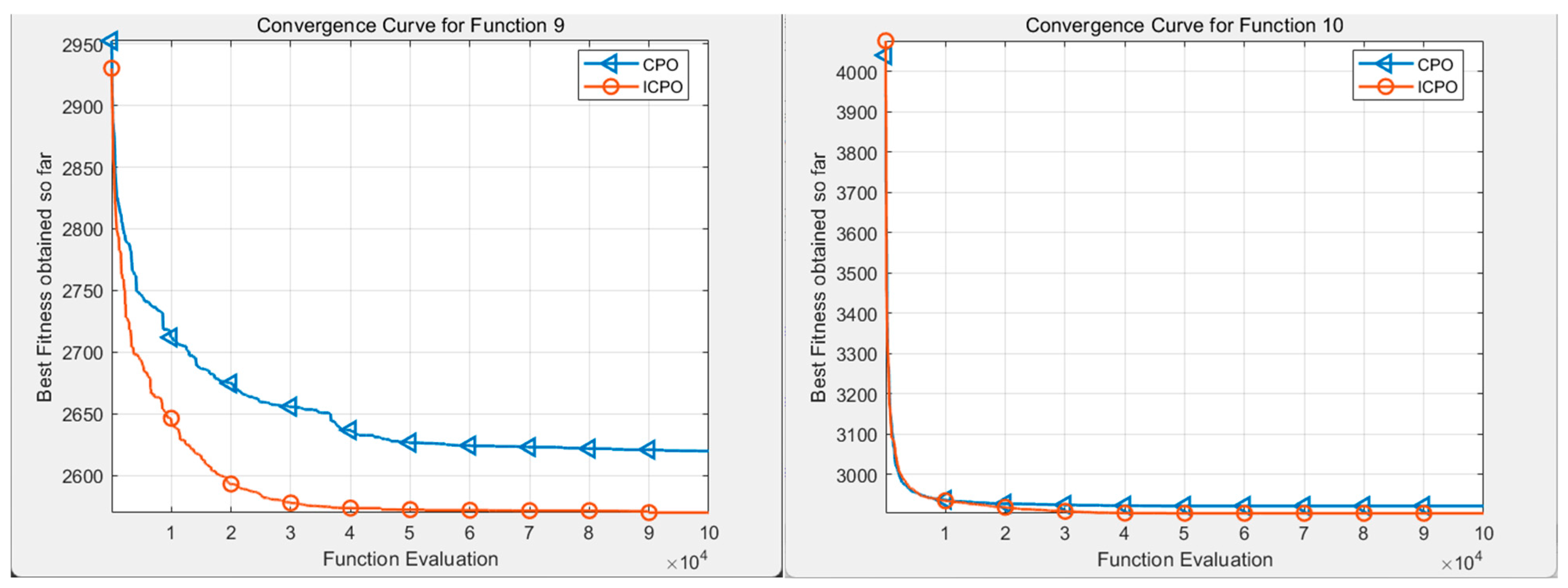
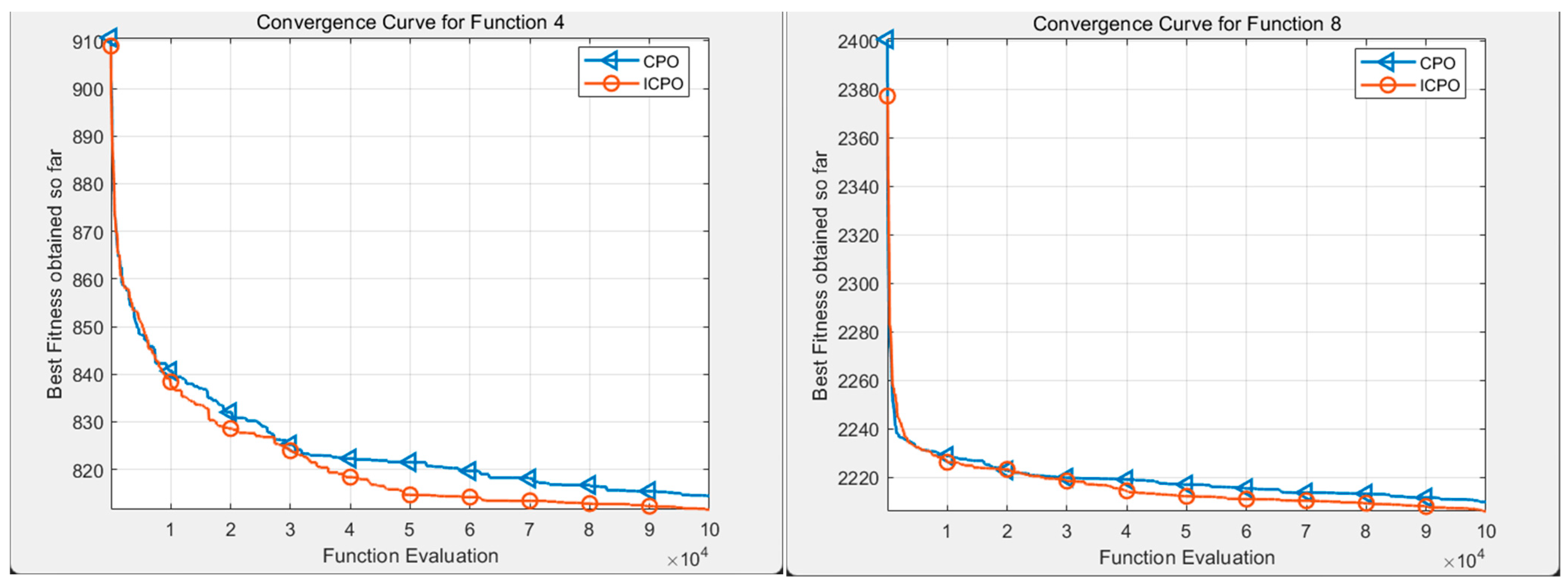
- Improved CPO(ICPO) vs. classical CPO algorithms on CEC benchmarks
- (a)
- Comparative analysis of the CEC2014 benchmark test
- (b)
- Comparative analysis of the CEC2017 benchmark test
- (c)
- Comparative Analysis of CEC2020 Benchmarks
- (d)
- Comparative Analysis of CEC2022 Benchmark
- (3)
- Optimised Crowned Porcupine Optimisation of ADRC Parameters
4. Stability Analysis
4.1. Preliminary Preparations for Stability Proofs
4.2. Finite-Time Convergence Proof of the Extended State Observer (ESO)
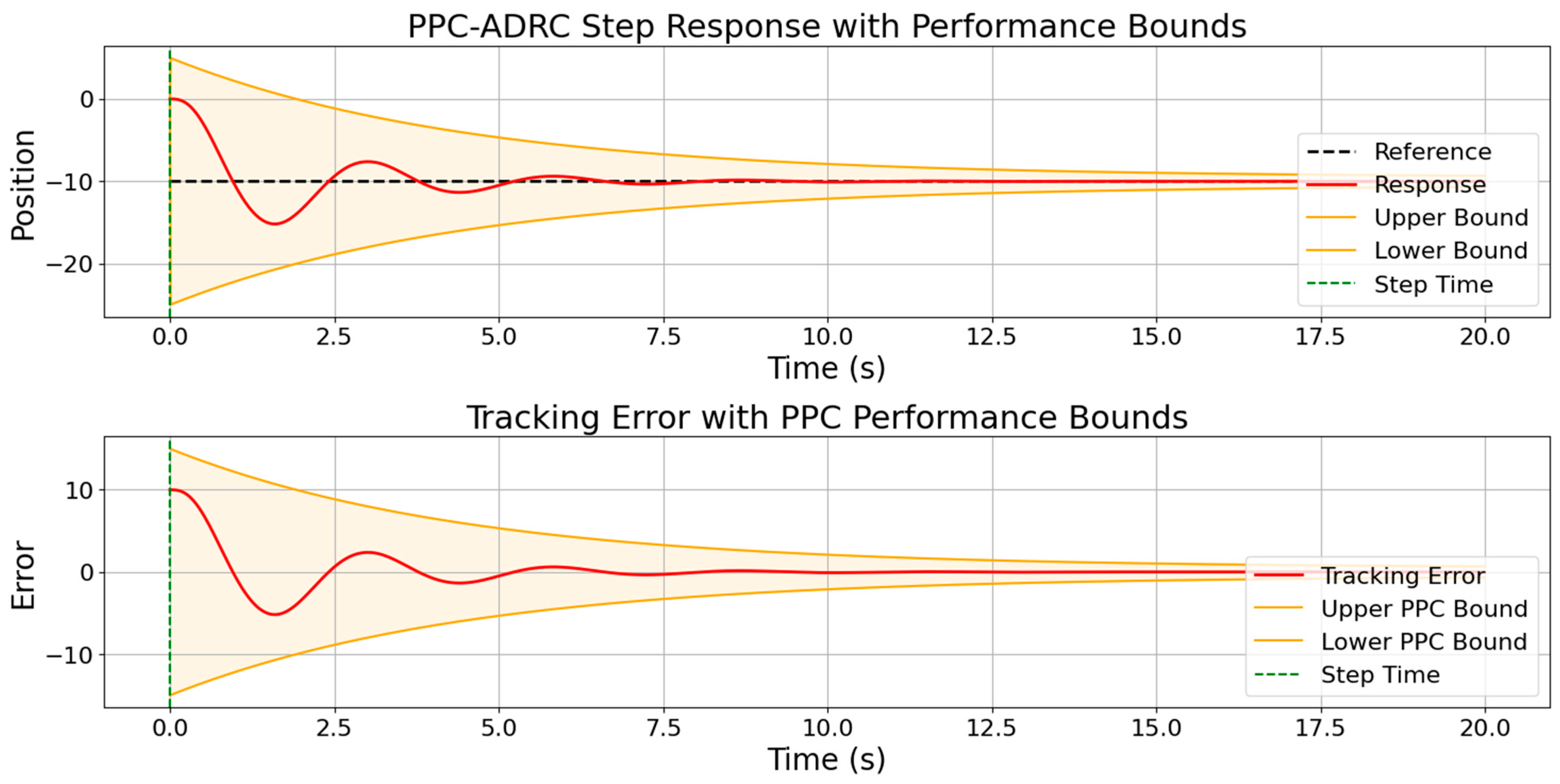
4.3. Stability Analysis of the PPC-ADRC Controller System
- (1)
- Boundedness of the system state when the ESO does not converge
- (2)
- Convergence of the ESO-convergent system state of convergence proof
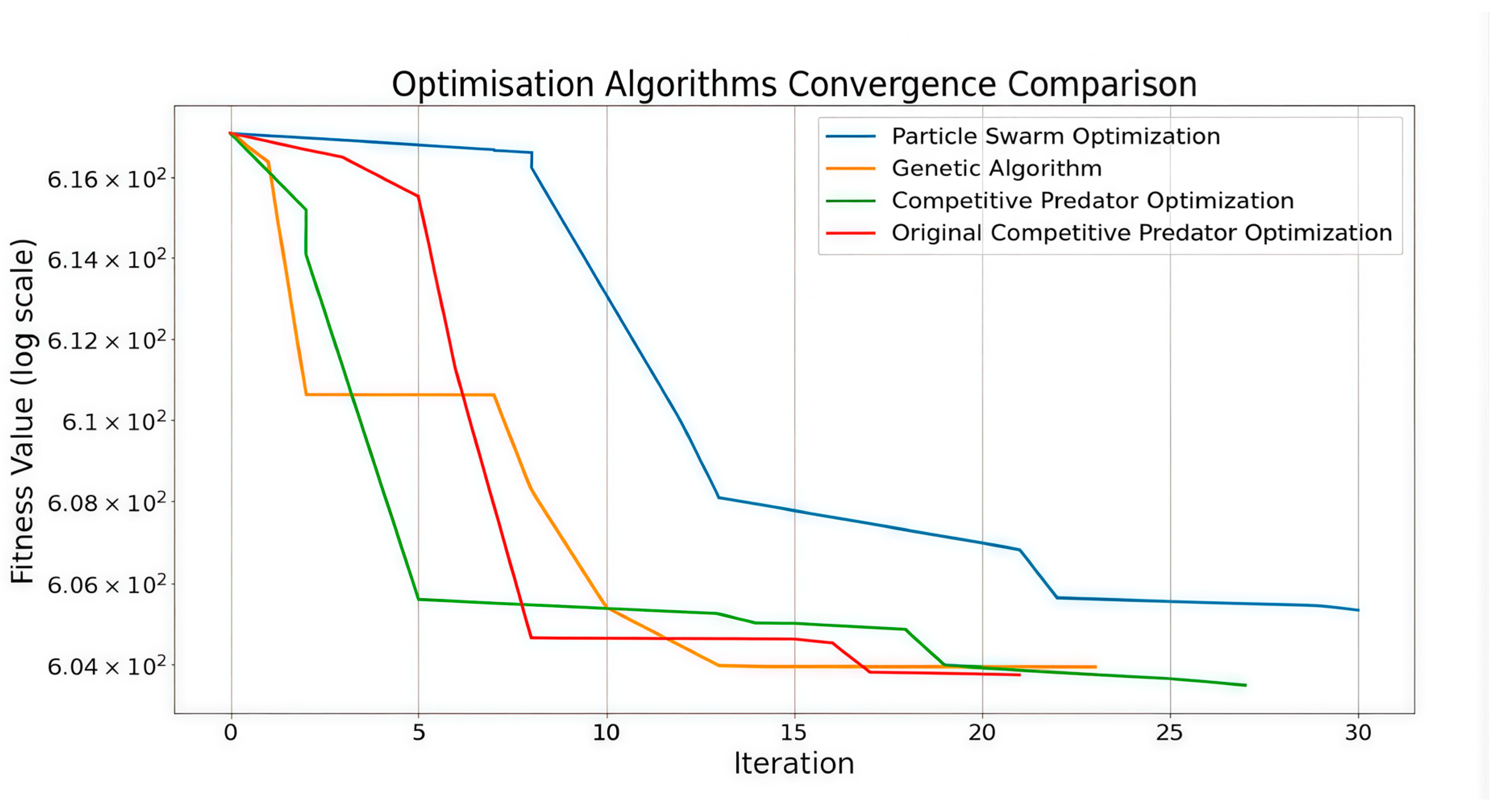
5. Results and Discussion
5.1. Simulation Parameter Settings
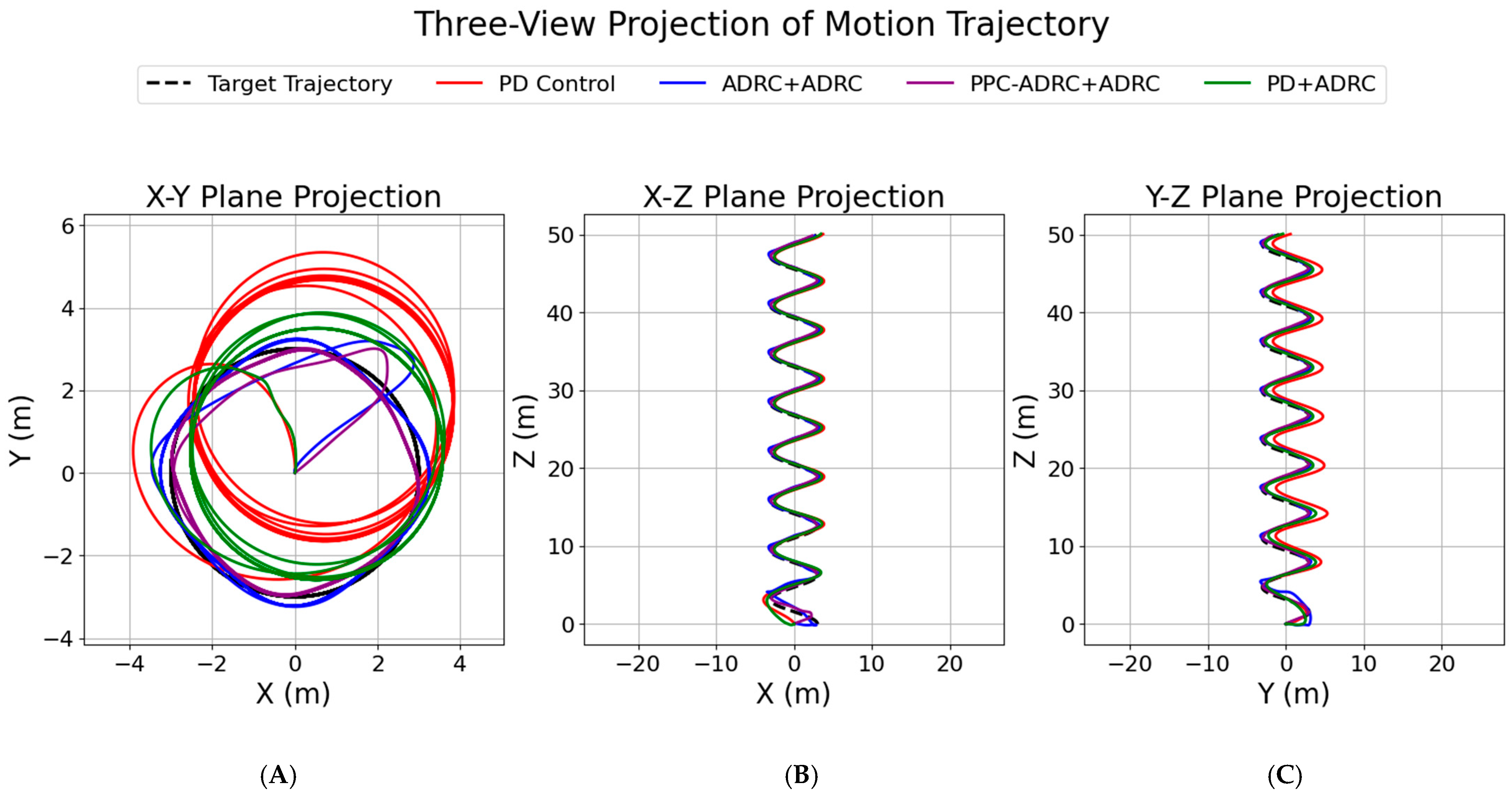
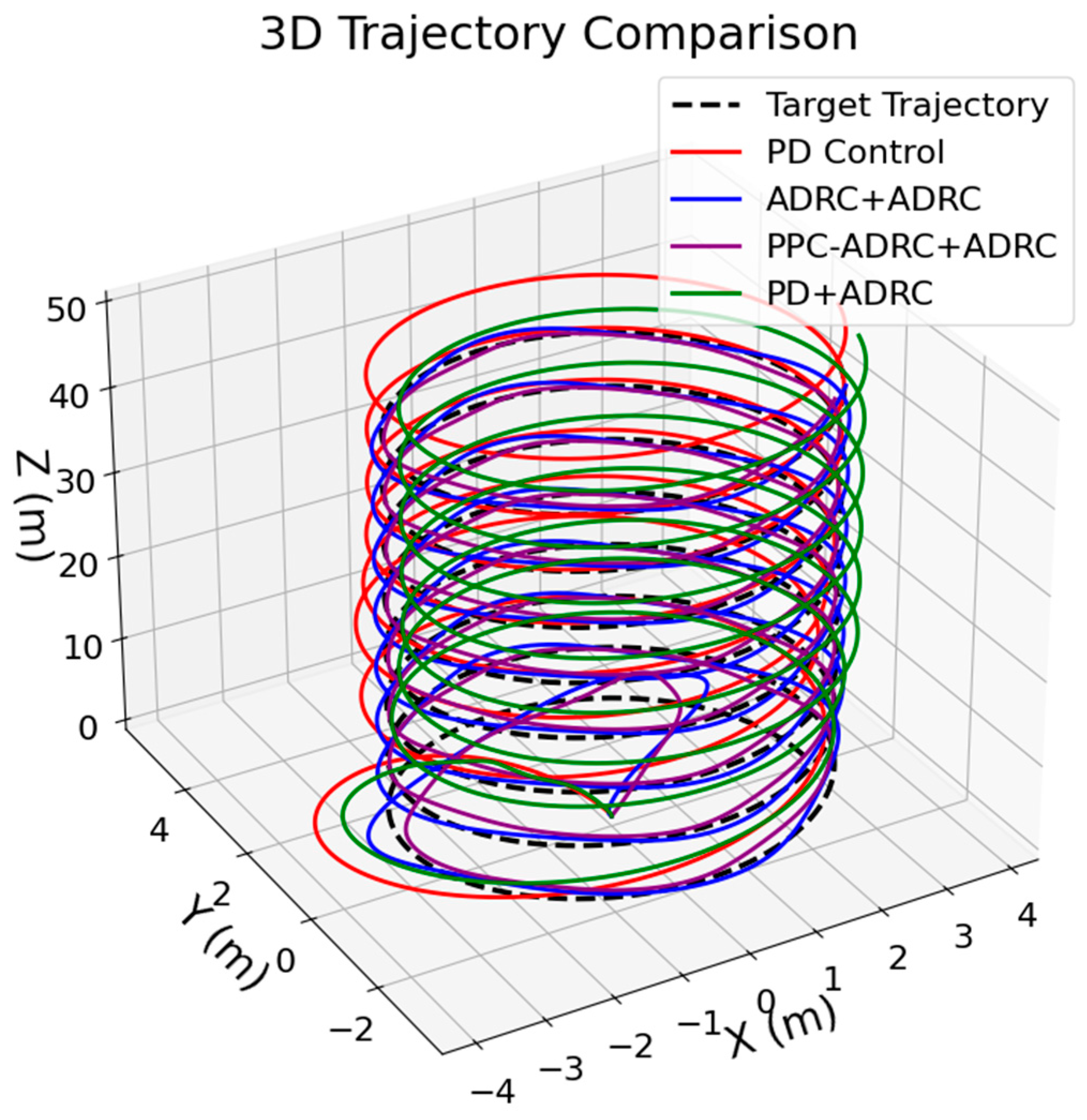
5.2. Analysis of Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Comparative Analysis of CPO Algorithm and CPO Improved Algorithm on Various CEC Benchmark Test Functions
| Function_ID | Avg Fitness Rank (CPO) | Avg Fitness Rank (ICPO) | SD Fitness Rank (CPO) | SD Fitness Rank (ICPO) |
|---|---|---|---|---|
| 1 | 2 | 1 | 2 | 1 |
| 2 | 2 | 1 | 1 | 2 |
| 3 | 2 | 1 | 2 | 1 |
| 4 | 2 | 1 | 1 | 2 |
| 5 | 1 | 2 | 1 | 2 |
| 6 | 2 | 1 | 2 | 1 |
| 7 | 2 | 1 | 2 | 1 |
| 8 | 2 | 1 | 2 | 1 |
| 9 | 2 | 1 | 2 | 1 |
| 10 | 2 | 1 | 1 | 2 |
| 11 | 1 | 2 | 2 | 1 |
| 12 | 2 | 1 | 1 | 2 |
| 13 | 2 | 1 | 1 | 2 |
| 14 | 2 | 1 | 2 | 1 |
| 15 | 2 | 1 | 1 | 2 |
| 16 | 2 | 1 | 1 | 2 |
| 17 | 2 | 1 | 1 | 2 |
| 18 | 2 | 1 | 1 | 2 |
| 19 | 2 | 1 | 2 | 1 |
| 20 | 2 | 1 | 2 | 1 |
| 21 | 2 | 1 | 2 | 1 |
| 22 | 2 | 1 | 2 | 1 |
| 23 | 1.5 | 1.5 | 1.5 | 1.5 |
| 24 | 2 | 1 | 1 | 2 |
| 25 | 2 | 1 | 1 | 2 |
| 26 | 2 | 1 | 1 | 2 |
| 27 | 1 | 2 | 1 | 2 |
| 28 | 1 | 2 | 2 | 1 |
| 29 | 2 | 1 | 1 | 2 |
| Function_ID | Avg Fitness Rank (CPO) | Avg Fitness Rank (ICPO) | SD Fitness Rank (CPO) | SD Fitness Rank (ICPO) |
|---|---|---|---|---|
| 1 | 2 | 1 | 2 | 1 |
| 2 | 2 | 1 | 1 | 2 |
| 3 | 1 | 2 | 1 | 2 |
| 4 | 2 | 1 | 1 | 2 |
| 5 | 2 | 1 | 1 | 2 |
| 6 | 2 | 1 | 2 | 1 |
| 7 | 2 | 1 | 2 | 1 |
| 8 | 1 | 2 | 2 | 1 |
| 9 | 1.5 | 1.5 | 1.5 | 1.5 |
| 10 | 2 | 1 | 2 | 1 |
| 11 | 2 | 1 | 2 | 1 |
| 12 | 2 | 1 | 1 | 2 |
| 13 | 2 | 1 | 1 | 2 |
| 14 | 2 | 1 | 2 | 1 |
| 15 | 2 | 1 | 1 | 2 |
| 16 | 2 | 1 | 1 | 2 |
| 17 | 2 | 1 | 1 | 2 |
| 18 | 2 | 1 | 1 | 2 |
| 19 | 2 | 1 | 2 | 1 |
| 20 | 1 | 2 | 1 | 2 |
| 21 | 2 | 1 | 2 | 1 |
| 22 | 2 | 1 | 2 | 1 |
| 23 | 1.5 | 1.5 | 1.5 | 1.5 |
| 24 | 1 | 2 | 1 | 2 |
| 25 | 1 | 2 | 1 | 2 |
| 26 | 1 | 2 | 1 | 2 |
| 27 | 2 | 1 | 1 | 2 |
| 28 | 1 | 2 | 2 | 1 |
| 29 | 2 | 1 | 1 | 2 |
| Function_ID | Avg Fitness Rank (CPO) | Avg Fitness Rank (ICPO) | SD Fitness Rank (CPO) | SD Fitness Rank (ICPO) |
|---|---|---|---|---|
| 1 | 1 | 2 | 1 | 2 |
| 3 | 2 | 1 | 1 | 2 |
| 4 | 2 | 1 | 2 | 1 |
| 5 | 2 | 1 | 1 | 2 |
| 6 | 2 | 1 | 1 | 2 |
| 7 | 1 | 2 | 2 | 1 |
| 8 | 2 | 1 | 2 | 1 |
| 9 | 1 | 2 | 2 | 1 |
| 10 | 2 | 1 | 2 | 1 |
| Function_ID | Avg Fitness Rank (CPO) | Avg Fitness Rank (ICPO) | SD Fitness Rank (CPO) | SD Fitness Rank (ICPO) |
|---|---|---|---|---|
| 1 | 2 | 1 | 2 | 1 |
| 3 | 2 | 1 | 2 | 1 |
| 4 | 2 | 1 | 2 | 1 |
| 5 | 2 | 1 | 2 | 1 |
| 6 | 2 | 1 | 2 | 1 |
| 7 | 2 | 1 | 1 | 2 |
| 8 | 2 | 1 | 1 | 2 |
| 9 | 2 | 1 | 2 | 1 |
| 10 | 2 | 1 | 2 | 1 |
| 11 | 1 | 2 | 2 | 1 |
| 12 | 1 | 2 | 1 | 2 |
Appendix B. Model Parameters of the Quadrotor UAV
| Parameter Name | Parameter Symbol | Value | Unit | Description |
|---|---|---|---|---|
| Mass | 0.600 | Total mass of the quadrotor UAV | ||
| Moment of Inertia about x-axis | 0.002107 | Moment of inertia about the x-axis | ||
| Moment of Inertia about y-axis | 0.002107 | Moment of inertia about the y-axis | ||
| Moment of Inertia about z-axis | 0.004259 | Moment of inertia about the z-axis | ||
| Arm Length | 0.125 | Distance from the centre to the motor | ||
| Minimum Motor Speed | 0 | Minimum rotational speed of the motor | ||
| Maximum Motor Speed | 3600 | Maximum rotational speed of the motor | ||
| Thrust Coefficient | 0.00000018 | Coefficient to convert motor speed to thrust | ||
| Drag Coefficient | 0.0000000008475 | Coefficient to convert motor speed to torque | ||
| Acceleration due to Gravity | 9.81 | Gravitational acceleration | ||
| Simulation Time Step | 0.01 | Time step for simulation | ||
| Simulation Frequency | 100 | Update frequency for simulation | ||
| Control Frequency | 50 | Update frequency for the controller | ||
| Maximum Motor Speed | 2500 | Maximum rotational speed of the motor | ||
| Thrust Coefficient | Coefficient to convert motor speed to thrust | |||
| Drag Coefficient | Coefficient to convert motor speed to torque |
References
- Hui, X.; Bian, J.; Zhao, X.; Tan, M. Vision-based autonomous navigation approach for unmanned aerial vehicle transmission-line inspection. Int. J. Adv. Robot. Syst. 2018, 15, 1729881417752821. [Google Scholar] [CrossRef]
- Lemardelé, C.; Estrada, M.; Pagès, L.; Bachofner, M. Potentialities of drones and ground autonomous delivery devices for last-mile logistics. Transp. Res. Part E Logist. Transp. Rev. 2021, 149, 102325. [Google Scholar] [CrossRef]
- Lyu, M.; Zhao, Y.; Huang, C.; Huang, H. Unmanned Aerial Vehicles for Search and Rescue: A Survey. Remote Sens. 2023, 15, 3266. [Google Scholar] [CrossRef]
- Bouabdallah, S.; Siegwart, R. Backstepping and sliding-mode techniques applied to an indoor micro quadrotor. IEEE Trans. Robot. 2005, 21, 665–680. [Google Scholar]
- Åström, K.J.; Hägglund, T. PID Controllers: Theory, Design, and Tuning, 2nd ed.; Instrument Society of America: Research Triangle Park, NC, USA, 1995. [Google Scholar]
- Han, J.Q. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and bandwidth-parameterisation based controller tuning. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003; Volume 6, pp. 4989–4996. [Google Scholar]
- Chen, Z.; Li, Y.; Zhang, Y. Optimization of ADRC Parameters Based on Particle Swarm Optimization Algorithm. In Proceedings of the 2021 IEEE 4th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 18–20 June 2021; pp. 1956–1959. [Google Scholar] [CrossRef]
- Hu, W.H.; Cao, R.Y. Quadrotor ADRC attitude control based on improved particle swarm optimisation algorithm. Electron. Opt. Control 2019, 26, 12–16+27. [Google Scholar] [CrossRef]
- Li, X.; Gu, C.; Chen, C. Parameters Optimization of ADRC Based on DBO Algorithm. In Proceedings of the 2023 6th International Conference on Computer Network, Electronic and Automation (ICCNEA), Xi’an, China, 22–24 September 2023; pp. 354–358. [Google Scholar] [CrossRef]
- Gu, M.K.; Zhong, X.Y. Optimisation parameters of quadrotor ADRC based on improved artificial bee colony algorithm. Sci. Technol. Eng. 2022, 22, 5693–5699. [Google Scholar]
- Huang, W.J. Research and Development of Servo Control Technology Based on Optimised ADRC. Master’s Thesis. Jiangnan University, Wuxi, China, 2025. [Google Scholar]
- Li, W.; Yang, F.; Zhong, L.; Wu, H.; Jiang, X.; Chukalin, A.V. Attitude Control of UAVs with Search Optimization and Disturbance Rejection Strategies. Mathematics 2023, 11, 3794. [Google Scholar] [CrossRef]
- Kang, C.; Wang, S.; Ren, W.; Lu, Y.; Wang, B. Optimisation Design and Application of Active Disturbance Rejection Controller Based on Intelligent Algorithm. IEEE Access 2019, 7, 59862–59870. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M. Crested Porcupine Optimizer: A new nature-inspired metaheuristic. Knowl.-Based Syst. 2024, 284, 111257. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, T.; Cao, D. Trajectory Tracking Control for Quadrotor UAVs based on Composite Nonsingular Terminal Sliding Mode method. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 5110–5115. [Google Scholar] [CrossRef]
- Anwaar, A.; Ashraf, A.; Bangyal, W.H.K.; Iqbal, M. Genetic Algorithms: Brief review on Genetic Algorithms for Global Optimization Problems. In Proceedings of the 2022 Human-Centered Cognitive Systems (HCCS), Shanghai, China, 17–18 December 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Sienz, J.; Innocente, M.S. Particle Swarm Optimisation: Fundamental Study and its Application to Optimisation and to Jetty Scheduling Problems. In Trends in Engineering Computational Technology; Saxe-Coburg Publications: Stirlingshire, UK, 2008; pp. 103–126. [Google Scholar]
- Zhao, K.; Song, J.; Hu, Y.; Xu, X.; Liu, Y. Deep Deterministic Policy Gradient-Based Active Disturbance Rejection Controller for Quad-Rotor UAVs. Mathematics 2022, 10, 2686. [Google Scholar] [CrossRef]
- Wang, S.; Chen, J.; He, X. An adaptive composite disturbance rejection for attitude control of the agricultural quadrotor UAV. ISA Trans. 2022, 129 Pt A, 564–579. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, X.; Zhang, H. Disturbance observer-based elegant anti-disturbance control for stochastic systems with multiple disturbances. Asian J. Control 2017, 19, 1966–1976. [Google Scholar] [CrossRef]
- Song, J.; Zhao, M.; Gao, K.; Su, J. Error Analysis of ADRC Linear Extended State Observer for the System with Measurement Noise. IFAC-Pap. 2020, 53, 1306–1312. [Google Scholar] [CrossRef]
- Song, M.; Huang, P. Dynamics and anti-disturbance control for tethered aircraft system. Non-Linear Dyn. 2022, 110, 2383–2399. [Google Scholar] [CrossRef]
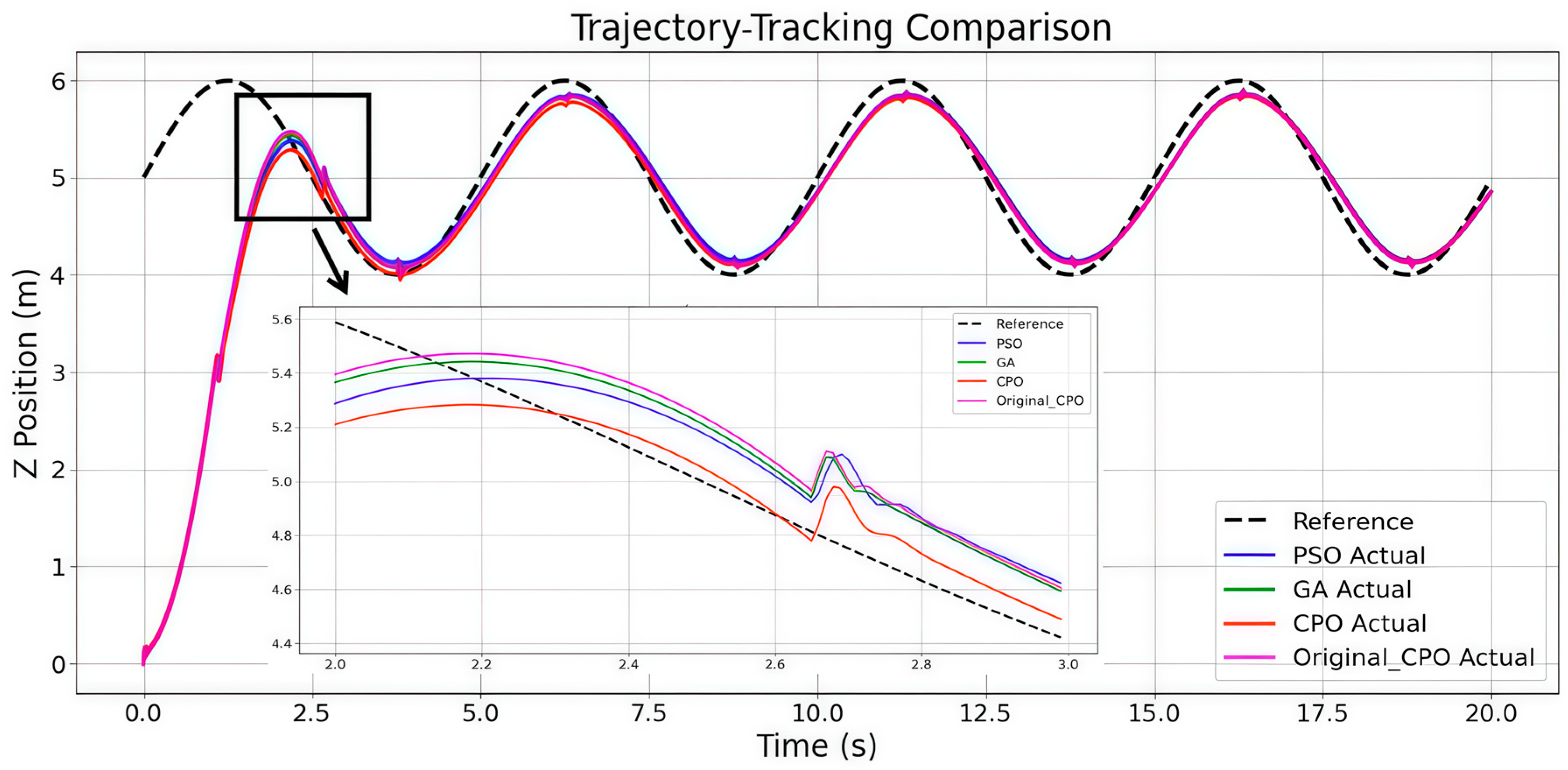
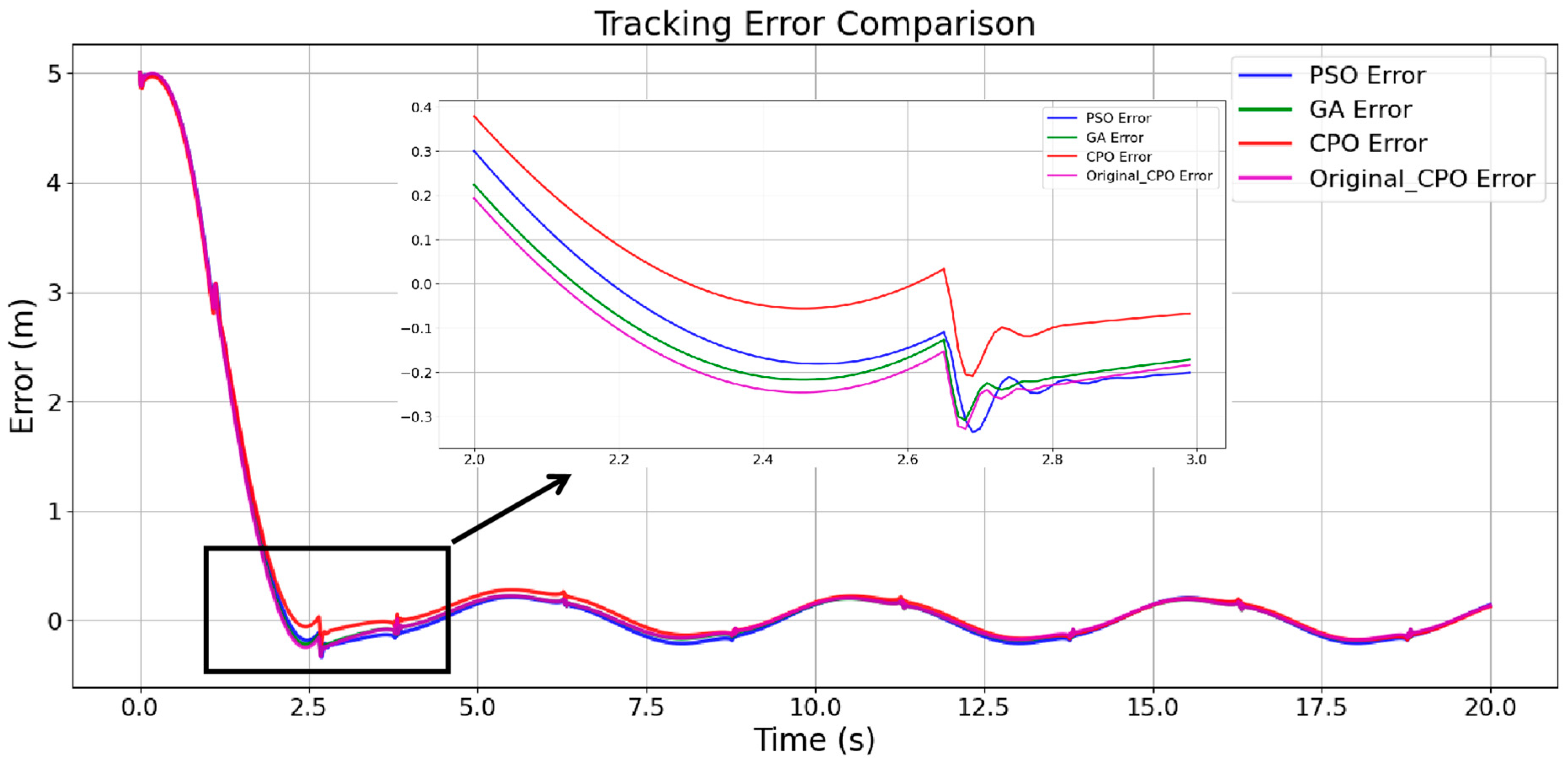
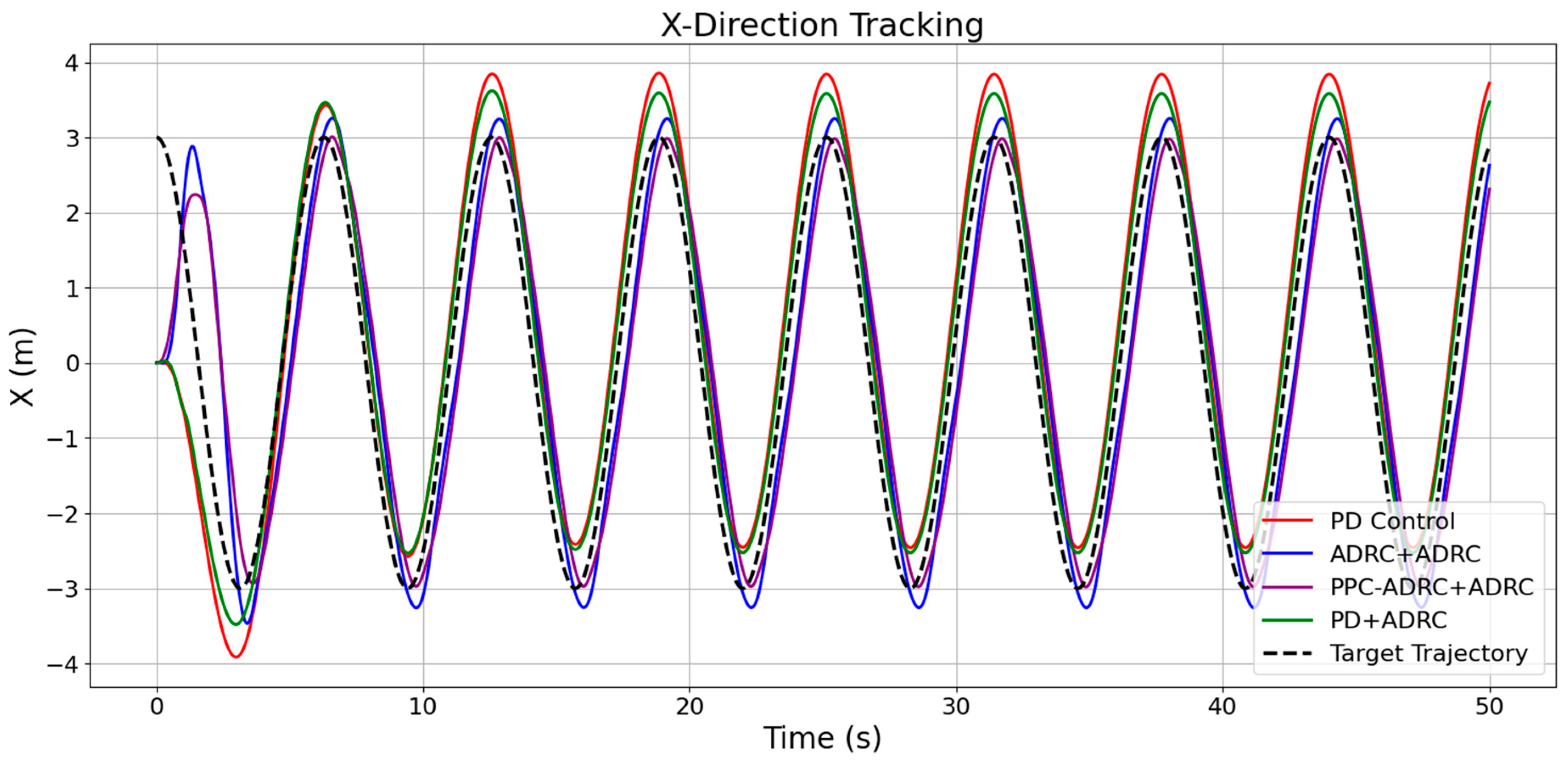

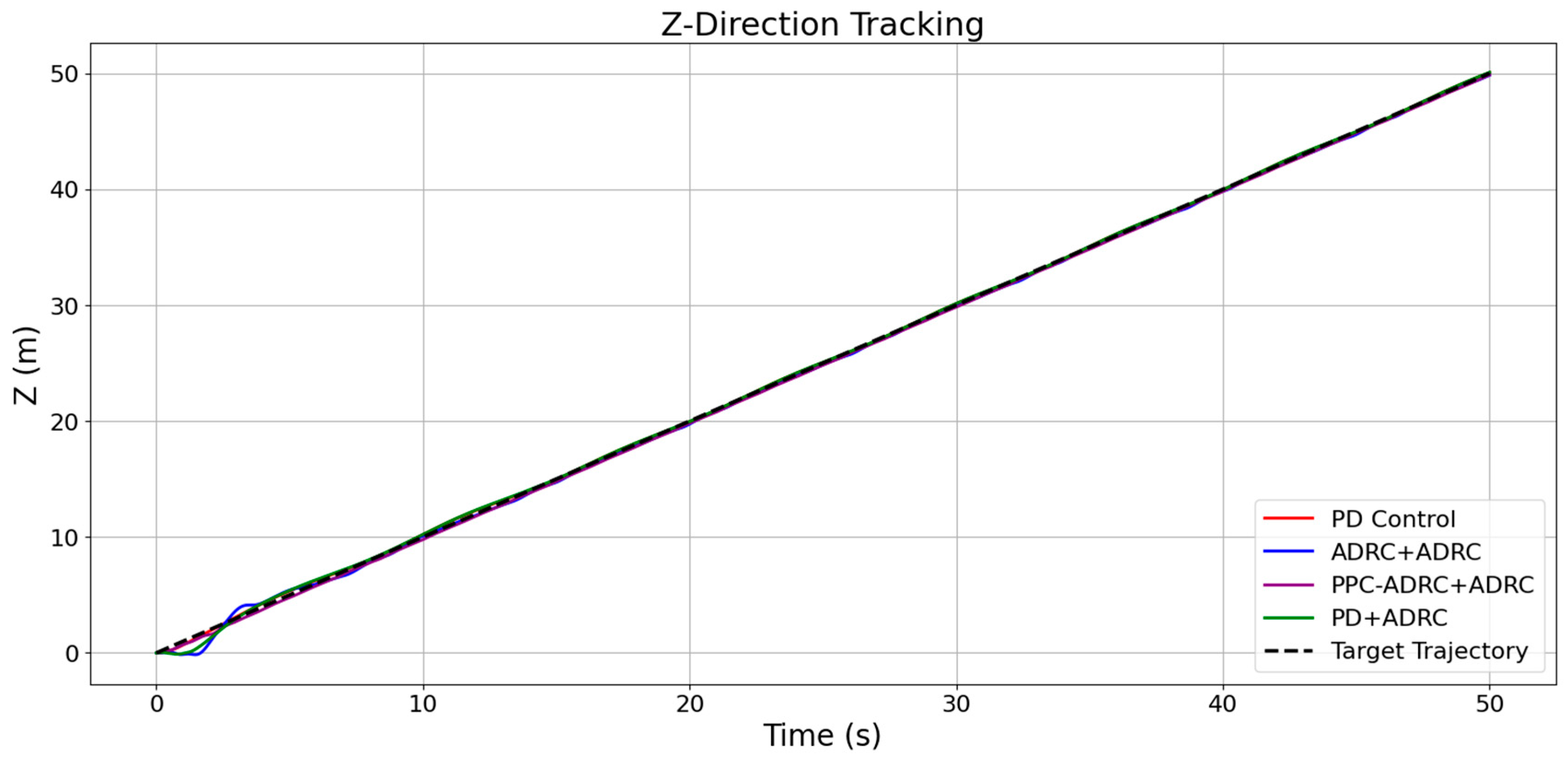
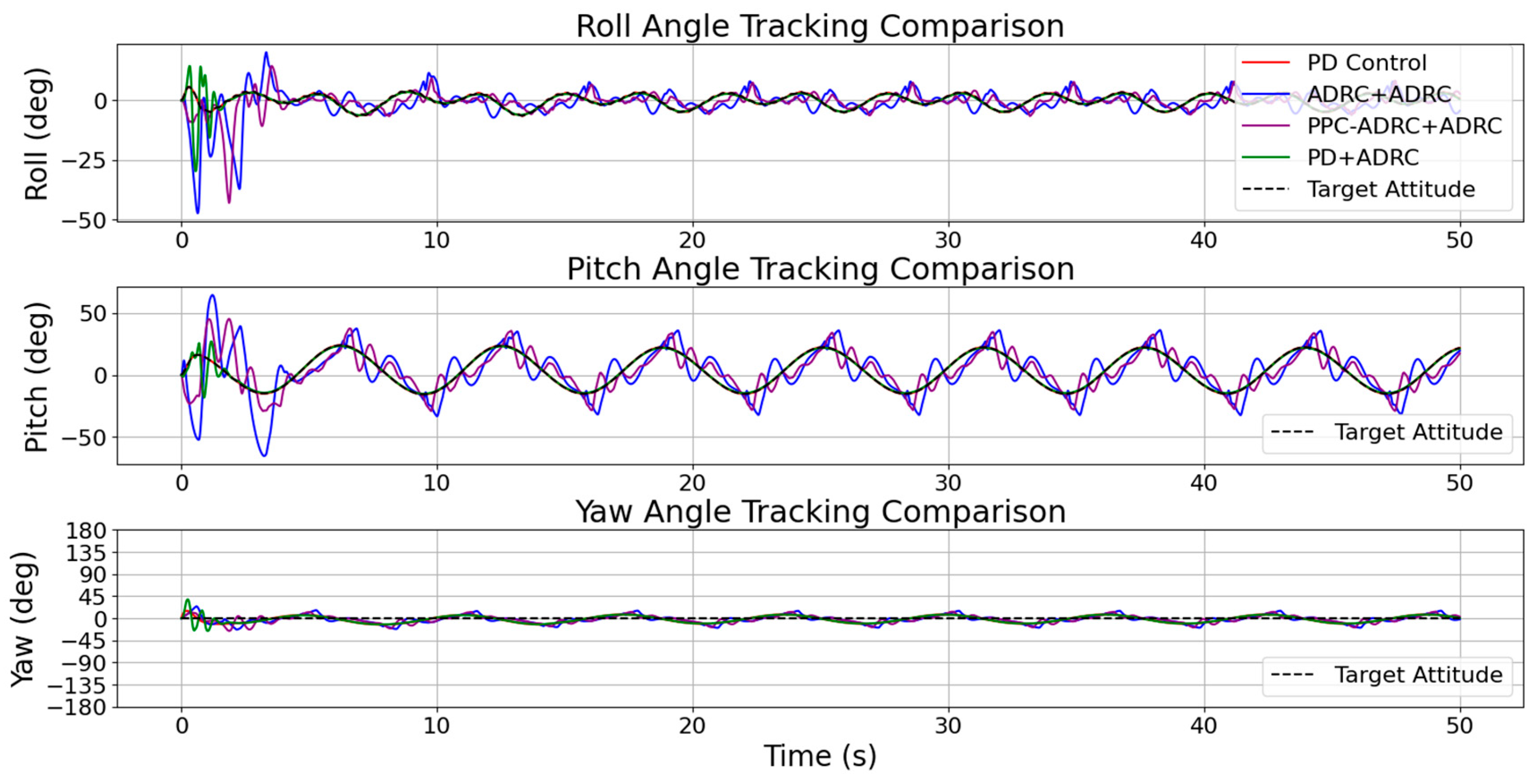
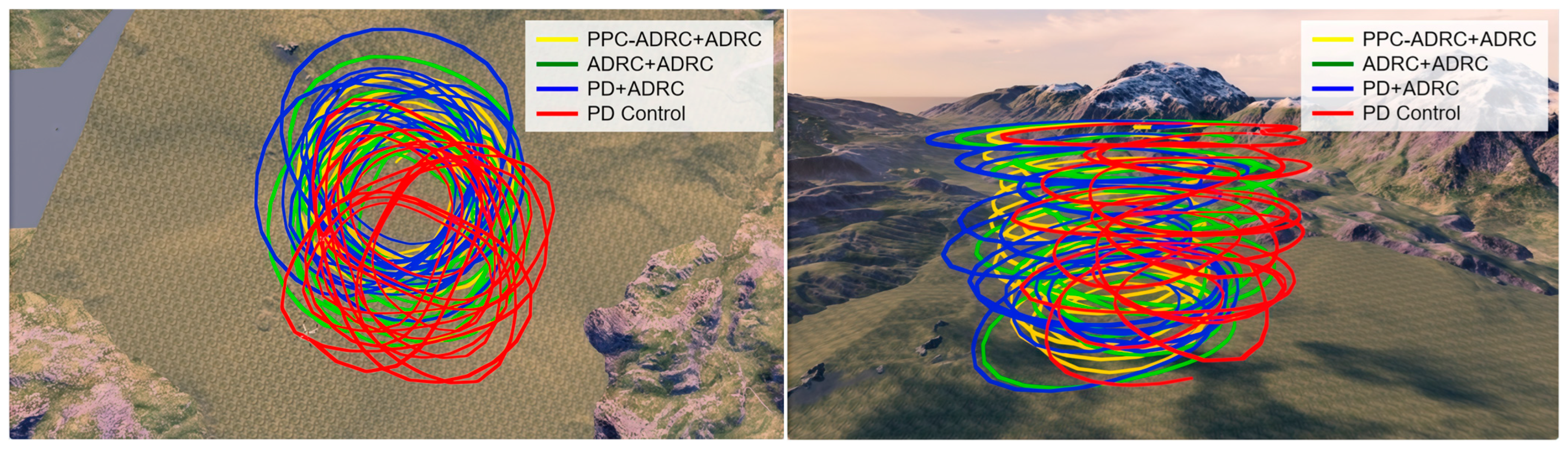
| PSO | 8.5282 | 0.0048 | 5.0000 | 0.0669 |
| GA | 8.3502 | 0.0048 | 5.0000 | 0.0624 |
| ICPO | 8.4632 | 0.0045 | 5.0000 | 0.0656 |
| CPO | 8.3901 | 0.0040 | 5.0000 | 0.0631 |
| Outer-Loop PP_ADRC Parameters | Inner-Loop ADRC Parameters | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PP_ADRC + ADRC | X-Pitch Channel | 10.27 | 8.74 | 10.62 | 2.5 | 0.5 | 0.01 | 15 | 330.46 | 20.82 | 7.55 | 1.21 |
| Y-Roll Channel | 20.34 | 6.27 | 9.12 | 1.68 | 0.5 | 0.01 | 15 | 262.66 | 14.19 | 15 | 0.81 | |
| Z-Altitude Channel | 12.07 | 6.01 | 12.1 | 2.64 | 0.5 | 0.01 | 15 | |||||
| Heading Channel | 116.63 | 18.17 | 11.2 | 0.74 | ||||||||
| Outer-Loop ADRC Parameters | Inner-Loop ADRC Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ADRC + ADRC | X-Pitch Channel | 1.66 | 20.7 | 12.13 | 2.31 | 400.22 | 60.13 | 13.14 | 0.72 |
| Y-Roll Channel | 2.13 | 18.69 | 8.11 | 0.93 | 380.62 | 59.55 | 16.22 | 1.21 | |
| Z-Altitude Channel | 1.06 | 21.23 | 9.32 | 2.65 | 360.79 | 72.16 | 11.87 | 2.11 | |
| Heading Channel | 310.23 | 50.16 | 15.11 | 1.24 | |||||
| Outer-Loop PID Parameters | Inner-Loop ADRC Parameters | ||||||
|---|---|---|---|---|---|---|---|
| PID + ADRC | X-Pitch Channel | 1.28 | 1.75 | 247.38 | 6.62 | 18.61 | 0.5665 |
| Y-Roll Channel | 1.62 | 1.58 | 230.85 | 3.15 | 20.84 | 0.81 | |
| Z-Altitude Channel | 2.35 | 0.46 | |||||
| Heading Channel | 233.03 | 5.36 | 24.11 | 0.60 | |||
| Outer-Loop PID Parameters | Inner-Loop PID Parameters | ||||
|---|---|---|---|---|---|
| PID + PID | X-Pitch Channel | 5.89 | 2.12 | 551.82 | 90.58 |
| Y-Roll Channel | 4.39 | 2.28 | 689.09 | 80.01 | |
| Z-Altitude | 13.67 | 1.12 | |||
| Heading Channel | 270.95 | 2.69 | |||
| Variable | PID-PID | ADRC + ADRC | PID + ADRC | This Method |
|---|---|---|---|---|
| X | 5752.135 | 101.23 | 960.092 | 48.3689 |
| Y | 8024.14 | 150.7155 | 1130.8809 | 82.3208 |
| Z | 10.21 | 13.41 | 8.05 | 6.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Bai, J.; Wang, J. High-Precision Trajectory-Tracking Control of Quadrotor UAVs Based on an Improved Crested Porcupine Optimiser Algorithm and Preset Performance Self-Disturbance Control. Drones 2025, 9, 420. https://doi.org/10.3390/drones9060420
Li J, Bai J, Wang J. High-Precision Trajectory-Tracking Control of Quadrotor UAVs Based on an Improved Crested Porcupine Optimiser Algorithm and Preset Performance Self-Disturbance Control. Drones. 2025; 9(6):420. https://doi.org/10.3390/drones9060420
Chicago/Turabian StyleLi, Junhao, Junchi Bai, and Jihong Wang. 2025. "High-Precision Trajectory-Tracking Control of Quadrotor UAVs Based on an Improved Crested Porcupine Optimiser Algorithm and Preset Performance Self-Disturbance Control" Drones 9, no. 6: 420. https://doi.org/10.3390/drones9060420
APA StyleLi, J., Bai, J., & Wang, J. (2025). High-Precision Trajectory-Tracking Control of Quadrotor UAVs Based on an Improved Crested Porcupine Optimiser Algorithm and Preset Performance Self-Disturbance Control. Drones, 9(6), 420. https://doi.org/10.3390/drones9060420





