Abstract
This paper presents a neural network-based path planning method for fixed-wing UAVs under terminal roll-angle constraints. The nonlinear optimal path planning problem is first formulated as an optimal control problem. The necessary conditions derived from Pontryagin’s Maximum Principle are then established to convert extremal trajectories as the solutions of a parameterized system. Additionally, a sufficient condition is presented to guarantee that the obtained solution is at least locally optimal. By simply propagating the parameterized system, a training dataset comprising at least locally optimal trajectories can be constructed. A neural network is then trained to generate the nonlinear optimal control command in real time. Finally, numerical examples demonstrate that the proposed method robustly ensures the generation of optimal trajectories in real time while satisfying the prescribed terminal roll-angle constraint.
1. Introduction
Fixed-Wing Unmanned Aerial Vehicles (UAVs) are now playing a vital role in complex scenarios such as intelligence [1], surveillance [2], and reconnaissance [3]. To effectively perform these tasks, a UAV must have the ability of autonomously navigating itself to a desired target while satisfying various constraints. Path planning is a key aspect for a UAV to achieve such autonomy, which involves generating feasible paths from an initial position to an expected target position. Current UAV path planning methods can generally be classified into four categories: path-following methods [4,5,6,7,8,9,10], waypoint-based methods [11,12,13,14,15,16], optimization-based methods [17,18,19,20,21,22,23], and neural network-based methods [24,25,26,27,28,29,30,31].
Path-following methods rely on designing tracking control laws so that a UAV can be guided to accurately track a predefined path [4,5]. In [6,7,8], by considering a virtual target moving along the predefined path, some Light-of-Sight (LOS)-based methods have been developed to control the UAV to continuously move around the predefined path. Furthermore, a nonlinear adaptive LOS path-following controller was proposed by Cui et al. [7] via integrating an adaptive control scheme and sideslip compensation into the traditional LOS guidance law. Nelson et al. [9] proposed a vector-field-based path following method, whose main idea is to construct a vector field in the vicinity of the desired path. A natural extension was presented in [10] by proposing a Gradient Vector Field (GVF) which involves tuning some parameters according to the dynamics of the UAV to achieve better performance. Although path-following methods are easy to implement, the UAV may not complete its missions if the external environment changes.
Waypoint-based methods involve defining a sequence of points (waypoints) and guiding a UAV to navigate between waypoints so that it can reach the target location. In the framework of waypoint-based methods, algorithms such as Dijkstra’s algorithm [11], roadmaps [12], Rapidly-exploring Random Trees (RRT) [13,14] have been extensively studied to find feasible paths. Specifically, Wang et al. [11] introduced an Elevation-based Dijkstra Algorithm (EDA) that leverages terrain elevation information to discretize the trajectory from the starting point to the target point into a series of straight-line segments. Compared with the traditional Dijkstra algorithm, the EDA exhibits superior computational efficiency. Xu et al. [15] introduced a Dubins-A* algorithm, which integrates Dubins path properties into the well-known A* algorithm to ensure both optimality and adherence to turning constraints, thereby demonstrating improved performance in environments with irregular obstacles. However, waypoint-based methods often neglect the dynamics of UAVs, which may lead to infeasible trajectories or necessitate subsequent curvature adjustments and smoothing processes to ensure physical feasibility [16].
Optimization-based methods cast path planning as an Optimal Control Problem (OCP). By using Pontryagin’s Maximum Principle (PMP), a criterion (e.g., time or energy) is optimized while satisfying the dynamics of the UAVs [17,18]. De Marinis et al. [19] developed a minimum-time path planning method capable of avoiding obstacles by combining classical optimal control theory with continuation methods. Forkan et al. [20] presented an approach for computing the shortest path to visit multiple target points while maintaining a minimum turning radius constraint, which employs the PMP to establish necessary optimality conditions and uses an arc parameterization technique to determine the ideal sequence of turns and straight segments. Additionally, Na et al. [21] introduced a path planning approach utilizing an enhanced Particle Swarm Optimization (PSO) algorithm, with the goal of optimizing the energy efficiency of fixed-wing UAVs when flying over mountainous regions. These methods can guarantee the generation of optimal paths while accommodating complex constraints. However, they often require solving two-point boundary value problems [22] or performing exhaustive searches over trajectory families [23], leading to a significant computational burden for onboard computers [32].
Path planning methods based on neural networks can be categorized into supervised learning and Deep Reinforcement Learning (DRL). Supervised learning involves offline generation of a large amount of optimal trajectories and training neural networks to approximate the mapping from state to control commands. Horn et al. [24] introduced a neural-network-based trajectory optimization approach that approximates both the objective function and vehicle dynamics, eliminating collocation points and thus improving computational efficiency and flexibility. However, despite employing the Sparse Nonlinear OPTimizer (SNOPT) [25] to efficiently generate training data, this approach cannot guarantee the solutions to be at least locally optimal, potentially affecting the learning performance of the neural network. Phillips et al. [26] presented an approach that utilizes a lightweight Multi-Layer Perceptron (MLP) to estimate the cost of the neighbor path, facilitating real-time prediction of the optimal path length for fixed-wing UAVs under wind disturbances. Since supervised learning requires only a single forward computation of the neural network, it is ideal for scenarios with stringent real-time demands. However, supervised learning strongly relies on the quality and diversity of the training data [27].
DRL enables UAVs to autonomously learn optimal or near-optimal flight path through trial-and-error and reward mechanisms [28]. For instance, Li et al. [29] proposed an algorithm that integrates DRL with adaptive control strategies. Babel [30] employs Deep Q-Networks (DQNs) for online decision making of fixed-wing UAVs in dynamic environments, enabling adaptive avoidance of sudden obstacles. Compared with traditional re-planning algorithms, its average computational cost is substantially reduced. Ji and Wang [31] incorporated energy consumption into the reward function of DRL, and through extensive simulation training, proposed a strategy that comprehensively optimizes speed, heading, and roll angle. Although DRL exhibits remarkable adaptability in complex environments and uncertain conditions, it demands a large amount of interactive data for training. Additionally, its convergence speed and stability are greatly influenced by the choice of algorithm and hyperparameter settings [5].
To ensure that a UAV moves optimally while satisfying mission constraints, it is necessary to design optimal path-planning methods that can meet multiple terminal constraints and the nonlinear kinematics while optimizing a specific performance index. Consequently, the OCP with nonlinear kinematics has become an active research area over the past decades. Typically, a real-time method is required to solve the associated OCP. However, standard numerical methods often exhibit slow convergence or fail to converge, which limits their applicability in real-time scenarios [24,33]. To overcome these limitations, analytical or semi-analytical approaches have been explored. The first attempt to obtain a closed-form solution for OCP was made in [34], where a set of nonlinear equations was solved numerically. However, numerical solvers may fail to find all roots of multiple nonlinear equations, potentially resulting in local optima rather than the desired global optimum. A parameterization method was proposed by Chen and Shima in [35] to generate semi-analytical solutions for the OCP in [34]. As a natural extension of [35], Wang et al. developed a parameterized approach for the OCP with a fixed impact time [36], which was extended in [37] to the OCP with constraints on both impact time and impact angle.
Besides the constraints on impact time and impact angle, it is challenging, but necessary, to consider the constraint of terminal roll angle, i.e., to ensure that the roll angle equals a prescribed value [38] at the end of the mission. In various missions, such as reconnaissance and formation flight, meeting this constraint is crucial for aligning onboard sensors accurately toward the target location (the desired destination point) upon arrival. To address this challenge, we employ the PMP to derive necessary optimality conditions and obtain a parameterized system whose solutions correspond precisely to optimal UAV trajectories. Essentially, these conditions are embedded within a set of differential equations (state and costate equations) parameterized by specific initial values. By propagating this parameterized system, feasible optimal trajectories can be generated without iterative optimization.
The feasible optimal trajectories generated by the proposed method can be used to train a neural network, so that a neural-network-based path planning method is presented to generate the optimal feedback control with the final constraint on roll angle being satisfied. The key contributions of our work include:
- Neural Network Planner for Fixed-Wing UAVs: We develop a neural-network-based path planner capable of generating feasible flight trajectories in real time. The neural network is trained offline and rapidly predicts trajectories, thus eliminating the need for iterative online optimization.
- Incorporation of Terminal Roll-Angle Constraints: Our approach explicitly incorporates terminal roll-angle constraints into the path-planning process. Unlike previous approaches that may overlook terminal attitude constraints, our method ensures that UAVs reliably attain the desired roll angle upon arrival at the target location.
- Robust Performance Validation: The proposed method has been validated through extensive Monte Carlo simulations involving thousands of randomized initial conditions. Simulation results demonstrate that the neural network-based planner consistently produces feasible and accurate trajectories, satisfying terminal roll constraints in all tested scenarios. The results demonstrate the robustness and reliability of the proposed framework for real-time fixed-wing UAV path planning.
2. Problem Formulation
In this section, the kinematics for a fixed-wing UAV will first be described, and then the nonlinear optimal path planning problem will be formulated as an OCP.
2.1. Kinematics
Throughout this work, the fixed-wing UAV is assumed to cruise in altitude-hold mode, i.e., its true air speed V and geometric altitude h remain constant. Under this condition, the motion is confined to the horizontal coordinate frame , as shown in Figure 1, where the Ox axis points north and the Oy axis points east. The state is therefore fully described by the planar position and the heading angle , with the normal acceleration u as control input. The kinematic equations can be written as
where represents roll angle, and g denotes the Earth’s gravitational acceleration. Note that the roll angle is not an additional differential state; it is obtained algebraically from the control u via . Hence, the planar model in Equation (1) uniquely determines the attitude of the UAV without increasing the system order.
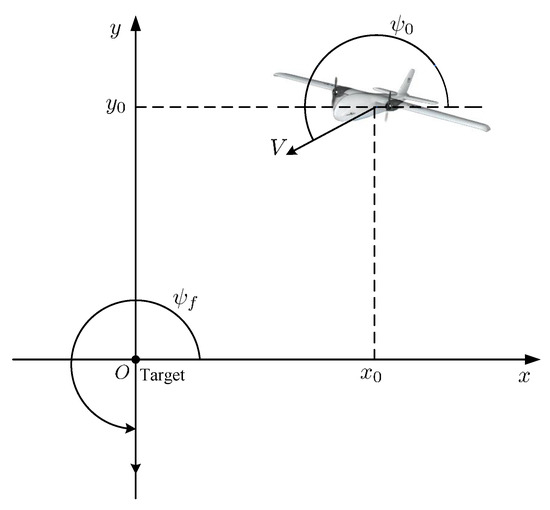
Figure 1.
Horizontal coordinate frame .
2.2. Optimal Control Problem
The OCP consists of steering the UAV, or the kinematics in Equation (1), from an initial state at to a final state at so that the control effort is minimized. Because the objective and constraints depend only on relative distances and heading differences, rotating the entire coordinate frame leaves the problem unchanged; hence, the terminal heading angle can be treated as a free optimization variable; see, e.g., [37].
In order to make the final roll angle equal to the desired roll angle , we consider the following control constraint:
Combined with the algebraic relation in Equation (1), Equation (2) guarantees without introducing an additional state.
To minimize the control effort, one needs to use
as the criterion to optimize [37]. However, addressing the above OCP with the criterion in Equation (3) cannot guarantee that the final roll angle of the UAV will be equal to a desired value. To make sure that the final normal acceleration will be equal to a desired value, we propose augmenting the criterion in Equation (3) as
where is the expected value of the final control and is an infinitesimal positive number. Notice that the term in Equation (4) is a penalty function, which restricts the final control to be close to , with . According to the above analysis, it amounts to addressing the OCP with the criterion in Equation (4) to obtain the optimal path with a desired final roll angle. In the next section, the solution of the OCP will be characterized for developing numerical methods.
3. Characterization of Optimal Solutions
In this section, the necessary conditions will first be presented by applying PMP. Using these necessary conditions, a parameterized system will then be established. In addition, a sufficient condition will be presented to ensure that the solution trajectory obtained by this parameterized system is at least locally optimal.
3.1. Necessary Conditions for Optimality
The Hamiltonian of the OCP is expressed as
where , and denote the co-state variables of x, y, and , respectively. The co-state variables are governed by
It is apparent from Equations (6) and (7) that the co-state variables and are constant. Thus, by integrating Equation (8), we have
where is a constant. According to stationarity condition (PMP), we have
Rewriting Equation (10) eventually leads to
Substituting Equation (9) into Equation (11), we have that the optimal control u is determined by , , and , i.e.,
The differential equations in Equations (6)–(8) as well as the maximum principle in Equation (10) constitute the necessary conditions for the OCP. Hereafter, any trajectory of the kinematics in Equation (1) that satisfies the above necessary conditions will be referred to as an extremal trajectory, and the corresponding control along the extremal trajectory will be termed as extremal control.
3.2. Parameterization of Extremal Trajectories
Let take values in and let take values in . Then, define an initial value problem as below:
where . Then, it is apparent that the solution of the initial value problem in Equation (13) is totally determined by , , and . For notational simplicity, set . Then, we say that the system in Equation (13) is a -parameterized system, and we denote by
the solution of the -parameterized system. By comparing the form of the system in Equation (13) with the necessary conditions presented in Section 3.1, it is evident that, for any , the solution trajectory is an extremal trajectory of the OCP. In other words, for any extremal trajectory for , of the OCP, there exists a so that
We denote by the right side of the third equation in Equation (13), i.e.,
Similarly, we have that is the extremal control along the extremal trajectory . It is worth noting that the extremal trajectory cannot be guaranteed to be at least locally optimal unless sufficient conditions for optimality are met. In the following paragraph, we shall present a sufficient condition for optimality.
Before proceeding, we first set
as the Jacobian of vector function with respect to the parameter vector .
Lemma 1
(Chen et al. [39]). Let T be a positive number in . Given any , the extremal trajectory for is a local optimum if for . Otherwise, the extremal trajectory for loses its local optimum if there exists a time so the changes its sign at .
Lemma 1 is a direct result of Theorem 2 in [39], and it presents a sufficient condition for local optimality. Combining the sufficient condition in Lemma 1 and the parameterized system in Equation (13), we shall present an approach for real-time generation of optimal control command via neural networks in the next section.
4. Real-Time Solutions via Neural Networks
4.1. Scheme for Real-Time Solution via Neural Network
Let be the current time, and let be the current state at . Then, the time-to-go is given by
A pair will be said to be feasible if there exists a feasible trajectory of the kinematics in Equation (1) so that and , where . Furthermore, let be the optimal feedback control at .
According to the above definitions and notations, if one is able to obtain the value of optimal control command for any feasible within [40,41], one can generate the solution of the OCP in real time. However, as stated in the Introduction, existing numerical methods, including indirect methods and direct methods, cannot guarantee the generation of the optimal control command within .
To obtain the value of optimal control command for any feasible in real time, an alternative approach is to use a simple neural network, trained by the dataset of mapping from to , to approximate the value of . The scheme for using the trained neural network to generate the control command is shown in Figure 2. In the following subsection, we shall present how the developments in Section 3 allow us to generate the dataset of the mapping for training a neural network.
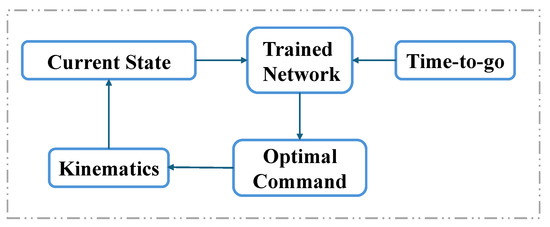
Figure 2.
Diagram for real-time solution via neural network.
4.2. Dataset Generation for Training Neural Network
The process for generating the dataset is presented by the pseudo-code in Algorithm 1.
| Algorithm 1 Dataset Generation Procedure |
Input: Positive values , T, and step size Output: Dataset for
to step do for to step do for to step do Set Integrate the system using Equation (13) with the parameter Extract the trajectory and control for if for then Add to dataset end if end for end for end for Return
|
It should be noted that, for the mapping contained in the dataset generated by Algorithm 1, we have . By the following lemma, we shall show that even if , a neural network trained by the dataset in Algorithm 1 can be adjusted to approximate .
Lemma 2
(Wang et al. [36]). Given a feasible pair , for any , we have
Readers interested in the proof of this lemma are referred to [36]. Let us denote by the neural network trained by the dataset in Algorithm 1. This is to say that for any feasible pair with , we can use to approximate , i.e.,
As a consequence of Lemma 2, given any feasible pair , if , one can use to approximate .
In Algorithm 1, , T, and are set as 20, 1 and 0.02, respectively. The resulting dataset contains approximately elements. These data are randomly divided into training, validation and test subsets in an 8:1:1 ratio and used to train an MLP that has three hidden layers, each with 30 tanh-activated neurons and a single output. The MLP is implemented in TensorFlow 2.1 (Google LLC, Mountain View, CA, USA) and trained for 10 epochs with a batch size of 1024, using the Levenberg-Marquardt optimizer to minimize the mean-squared-error loss; an early-stopping criterion terminates training once the loss drops below . For any given as input, the trained neural network takes around to generate the output on a desktop PC equipped with an AMD Ryzen 5 3600 6-Core Processor at 3.60 GHz (AMD Inc., Santa Clara, CA, USA), 16 GB RAM, and Windows 10 Pro 64-bit (Microsoft Corp., Redmond, WA, USA). This indicates the trained neural network can generate the optimal control command within a small period of time, which is enough for onboard applications.
In the following section, we shall demonstrate how the trained neural network allows us to guide the UAV to the target with the final desired roll angle being met.
5. Numerical Simulations
5.1. Comparisons with Optimization Methods
In this section, we conduct comparative simulations between the proposed approach, the direct transcription solver SNOPT, and an Indirect Shooting Method (ISM). Trajectories generated by SNOPT were obtained using GPOPS-II v2.3 (gpops2 Software, Gainesville, FL, USA), which employs SNOPT 7.6 (Stanford Business Software Inc., Palo Alto, CA, USA) to solve the resulting NLP. All simulations were executed using MATLAB R2024a (MathWorks, Natick, MA, USA). The SNOPT is configured with the following parameters. Major Feasibility Tolerance (Major-FeasTol) and Major Optimization Tolerance (Major-OptTol) are set to , allowing for a maximum of 100 major iterations. Derivatives are supplied using sparse second-order central finite differences. The hp-pseudospectral mesh is initialized with 10 segments, each containing 4 to 6 collocation points. The mesh tolerance is also set to , and there can be a maximum of 20 adaptive refinements.
Consider a scenario in which three UAVs are required to be guided to a desired position simultaneously. Without loss of generality, the target is considered to be located at m. Note that the position of the target can be arbitrarily chosen through coordinate translation. For notational simplicity, let us use UAV to denote the ith UAV among the three UAVs, and let be the expected final control for UAV . The values of , , are set as m/s2, 5 m/s2, and 0 m/s2, respectively. All three UAVs are required to reach the common target at s with the final heading angle being . The initial conditions for the three UAVs are summarized in Table 1.

Table 1.
Initial conditions and control effort cost for the three UAVs.
The trajectories generated by the proposed method are illustrated as solid green curves. The trajectories produced by SNOPT are shown as red dashed lines, while those generated by ISM are represented by blue dashed lines. These trajectories can be found in Figure 3. The time histories of the corresponding controls are presented in Figure 4. Let , and denote the control effort required by SNOPT, ISM and the proposed method, respectively. Then, the values of , and for the three UAVs are presented in Table 1.
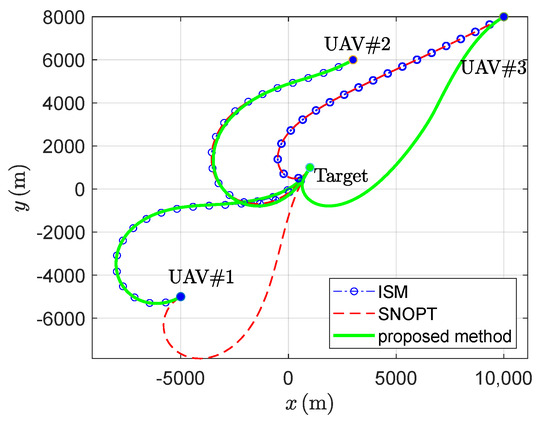
Figure 3.
Trajectories generated by three different methods for three UAVs.
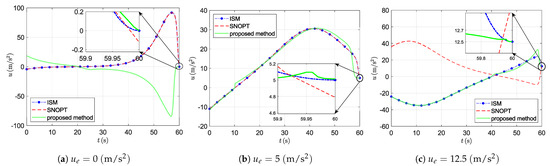
Figure 4.
Control profiles of different methods under different control constraints.
It is seen from Figure 3 that the SNOPT, ISM and the proposed method can be used to generate paths for the three UAVs to the same target. However, we can see from Figure 3 and Figure 4 that the trajectories generated by the proposed method may be different from those generated by optimization methods SNOPT and ISM (UAV and UAV ). As illustrated in Table 1, a comparison of the control effort required for the two UAVs reveals that the proposed method performed better than the SNOPT and ISM. Note that the SNOPT has fallen into a local optimum. For UAV , although the control performances of the proposed methods and SNOPT are similar, the expected control at the final time cannot be precisely met by the SNOPT, as shown by Figure 4. It is worth noting that although the ISM can meet the terminal-control constraint when the initial guess is well chosen, it is highly sensitive to that guess; a poor initial value often falls into a local optimum, preventing the UAV from reaching the target. In addition, for UAV #1 and UAV #3, our proposed method achieves substantially lower control-effort costs than both SNOPT and ISM, as reported in Table 1. Comparisons across all three sets of experiments reveal that our method significantly reduces control energy consumption under most initial conditions, while strictly satisfying the terminal roll angle requirement. Across 100 independent trials, the command-generation time for the proposed method is only , whereas the corresponding averages for ISM and SNOPT are and , respectively; therefore, the proposed method is three to four orders of magnitude faster than the indirect and direct optimization methods. By combining offline training with a parameterized system, the proposed method exhibits remarkable real-time performance during online execution, whereas traditional numerical optimizations (SNOPT and ISM) require multi-step solving.
5.2. Monte Carlo Simulations
To demonstrate the robustness of the proposed method, a Monte Carlo test is implemented by disturbing the initial conditions. In this Monte Carlo test, 1000 initial conditions are randomly selected. To be more specific, the initial values , , and are randomly selected within the intervals km, km, and , respectively. The speed of the UAV is 250 m/s. The target is located at km. The terminal control command and the desired impact time are set as 5 m/s2 and 60 s, respectively. The terminal heading angle is randomly selected within the interval .
The trajectories generated by Monte Carlo test are shown in Figure 5, and the distributions of the terminal errors are presented in Figure 6. We can see from Figure 6 that the maximum error of position is around , that the maximum error of expected flight time is less than , and that the maximum error of the terminal control command is . Overall, the Monte Carlo test results demonstrate that the proposed method not only achieves high accuracy but also ensures stable and robust performance under uncertainty.
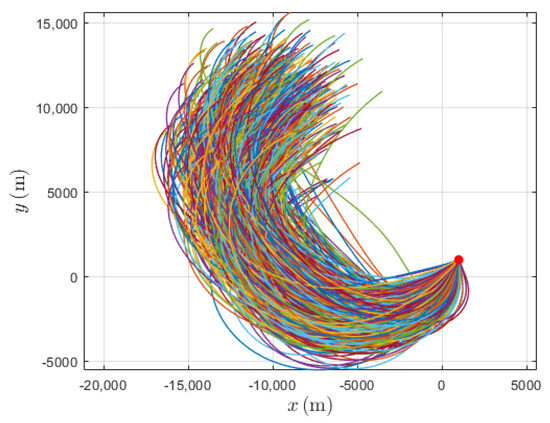
Figure 5.
Trajectories generated by Monte Carlo test.
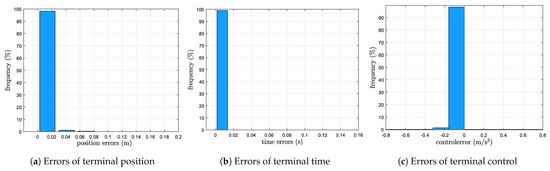
Figure 6.
Histograms for errors of Monte Carlo test.
To demonstrate that the proposed guidance law remains effective over the entire heading spectrum, we conducted the Monte Carlo test with the desired terminal heading uniformly sampled from to . The initial state was fixed at ), the air speed and flight time are and , respectively, and the target is located at . The desired terminal roll angle is set to zero. Figure 7 illustrates trajectories generated under fixed initial conditions with the final heading angle varying from to . Figure 8 displays histograms of the terminal position, arrival time and control command errors obtained from 200 randomly selected terminal heading commands. The largest miss distance is , the greatest arrival time error is , and the peak deviation of the terminal control command is . In comparison with the above Monte Carlo test, which restricted the terminal heading to the interval , position and time errors increase, whereas the control accuracy changes only marginally.
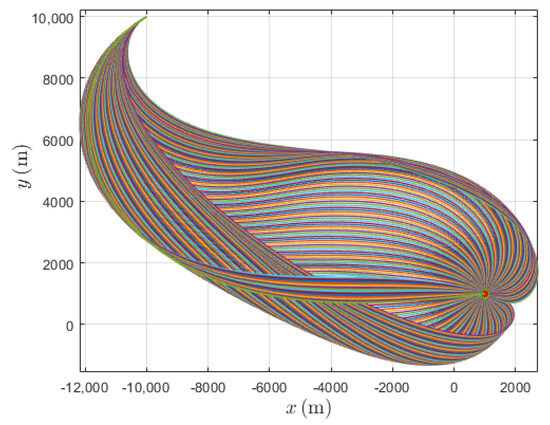
Figure 7.
Monte Carlo trajectories under the constraint of final heading angles ranging from to .
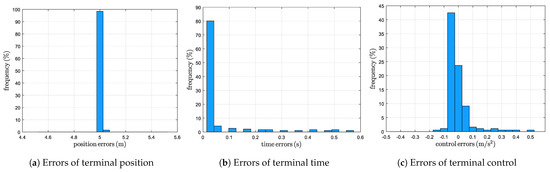
Figure 8.
Histograms for errors of Monte Carlo test.
The larger errors are primarily due to limitations in the training data. Although the set comprises samples, the terminal roll-angle constraint now ranges from to ; maintaining the previous level of accuracy over this enlarged range would require a much denser sampling of training data. Generating and handling such an enlarged data set would require prohibitive computational resources, and so the present work adopts the existing database as a practical compromise. Nevertheless, for the intended reconnaissance application, a miss distance below and a timing error within remain comfortably within sensor’s field-of-view and mission scheduling margins. The current performance is therefore operationally acceptable, and future work will focus on rebalancing the data set or adopting active-learning strategies to achieve sub-meter accuracy across the full heading spectrum.
6. Conclusions
This paper proposed a neural network-based path-planning method for fixed-wing UAVs under terminal roll-angle constraints. By formulating the path planning as a nonlinear optimal control problem and applying PMP, we introduced a parameterized system to generate optimal training data with a sufficient condition being embedded to ensure local optimality. A lightweight MLP was trained by the dataset so that we can generate the guidance command within a millisecond while satisfying the prescribed terminal roll-angle constraint. We achieve sub-millisecond command generation while still satisfying the prescribed terminal roll-angle constraints. Extensive comparisons with SNOPT and ISM, together with two Monte Carlo tests, demonstrate that the proposed method reduces control effort consumption by up to , maintains a worst-case miss distance below , and is three to four orders of magnitude faster than the SNOPT and ISM. Despite these promising results, our study has three main limitations: (1) the method currently relies on a constant-altitude flight model; (2) the training dataset is sparse, particularly for extreme terminal-heading cases; and (3) the proposed approach has not yet been validated through real-world flight tests. In future work, we plan to extend the parameterized method to three-dimensional flight dynamics incorporating wind disturbances, generate a larger and denser training dataset, and implement the proposed method on embedded hardware for validation in actual flight conditions.
Author Contributions
Q.X. developed the main conceptual framework and path planning method, implemented the proposed method, and drafted the manuscript. F.W. contributed to manuscript review and editing. Z.C. provided theoretical guidance and revision suggestions. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Malamiri, H.R.G.; Aliabad, F.A.; Shojaei, S.; Morad, M.; Band, S.S. A study on the use of UAV images to improve the separation accuracy of agricultural land areas. Comput. Electron. Agric. 2021, 184, 106079. [Google Scholar] [CrossRef]
- Darbari, V.; Gupta, S.; Verma, O.P. Dynamic motion planning for aerial surveillance on a fixed-wing UAV. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 488–497. [Google Scholar]
- Anand, T.P.; Abishek, K.; Kailash, R.K.; Nithiyanantham, K. Development and automation of fixed wing UAV for reconnaissance mission with FPV capability. INCAS Bull. 2022, 14, 111–118. [Google Scholar] [CrossRef]
- Sujit, P.; Saripalli, S.; Sousa, J.B. Unmanned aerial vehicle path following: A survey and analysis of algorithms for fixed-wing unmanned aerial vehicless. IEEE Control Syst. Mag. 2014, 34, 42–59. [Google Scholar]
- Ghambari, S.; Golabi, M.; Jourdan, L.; Lepagnot, J.; Idoumghar, L. UAV path planning techniques: A survey. RAIRO-Oper. Res. 2024, 58, 2951–2989. [Google Scholar] [CrossRef]
- Chen, P.; Zhang, G.; Li, J.; Chang, Z.; Yan, Q. Path-following control of small fixed-wing UAVs under wind disturbance. Drones 2023, 7, 253. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, Y. Nonlinear adaptive line-of-sight path following control of unmanned aerial vehicles considering sideslip amendment and system constraints. Math. Probl. Eng. 2020, 2020, 4535698. [Google Scholar] [CrossRef]
- Qi, W.; Tong, M.; Wang, Q.; Song, W.; Ying, H. Curved-line path-following control of fixed-wing unmanned aerial vehicles using a robust disturbance-estimator-based predictive control approach. Appl. Sci. 2023, 13, 11577. [Google Scholar] [CrossRef]
- Nelson, D.R.; Barber, D.B.; McLain, T.W.; Beard, R.W. Vector field path following for miniature air vehicles. IEEE Trans. Robot. 2007, 23, 519–529. [Google Scholar] [CrossRef]
- Wilhelm, J.P.; Clem, G. Vector field UAV guidance for path following and obstacle avoidance with minimal deviation. J. Guid. Control Dyn. 2019, 42, 1848–1856. [Google Scholar] [CrossRef]
- Medeiros, F.L.L.; Da Silva, J.D.S. A Dijkstra algorithm for fixed-wing UAV motion planning based on terrain elevation. In Proceedings of the Advances in Artificial Intelligence–SBIA 2010: 20th Brazilian Symposium on Artificial Intelligence, São Bernardo do Campo, Brazil, October 23–28, 2010; Proceedings 20; Springer: Berlin/Heidelberg, Germany, 2010; pp. 213–222. [Google Scholar]
- Babel, L. Curvature-constrained traveling salesman tours for aerial surveillance in scenarios with obstacles. Eur. J. Oper. Res. 2017, 262, 335–346. [Google Scholar] [CrossRef]
- Yang, K.; Sukkarieh, S. Real-time continuous curvature path planning of UAVs in cluttered environments. In Proceedings of the 2008 5th International Symposium on Mechatronics and Its Applications, Amman, Jordan, 27–29 May 2008; pp. 1–6. [Google Scholar]
- Lee, D.; Shim, D.H. RRT-based path planning for fixed-wing UAVs with arrival time and approach direction constraints. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 317–328. [Google Scholar]
- Xu, J.; Shi, M.; Tang, F.; Sun, X.; Yue, J.; Lin, B.; Qin, K. Dubins-A*: A new global path planning scheme for fixed-wing UAV with irregular obstacles avoidance. In Proceedings of the 2024 7th International Conference on Electronics Technology (ICET), Chengdu, China, 17–20 May 2024; pp. 636–641. [Google Scholar]
- Airlangga, G. Advancing UAV path planning system: A software pattern language for dynamic environments. Bul. Ilm. Sarj. Tek. Elektro 2023, 5, 475–497. [Google Scholar] [CrossRef]
- Arifianto, O.; Farhood, M. Optimal control of fixed-wing uavs along real-time trajectories. In Proceedings of the Dynamic Systems and Control Conference; American Society of Mechanical Engineers: New York, NY, USA, 2012; Volume 45295, pp. 205–214. [Google Scholar]
- Din, A.F.U.; Mir, I.; Gul, F.; Mir, S.; Alhady, S.S.N.; Al Nasar, M.R.; Alkhazaleh, H.A.; Abualigah, L. Robust flight control system design of a fixed wing UAV using optimal dynamic programming. Soft Comput. 2023, 27, 3053–3064. [Google Scholar] [CrossRef]
- De Marinis, A.; Iavernaro, F.; Mazzia, F. A minimum-time obstacle-avoidance path planning algorithm for unmanned aerial vehicles. Numer. Alg. 2022, 89, 1639–1661. [Google Scholar] [CrossRef]
- Forkan, M.; Rizvi, M.M.; Chowdhury, M.A.M. Optimal path planning of Unmanned Aerial Vehicles (UAVs) for targets touring: Geometric and arc parameterization approaches. PLoS ONE 2022, 17, e0276105. [Google Scholar] [CrossRef]
- Na, Y.; Li, Y.; Chen, D.; Yao, Y.; Li, T.; Liu, H.; Wang, K. Optimal energy consumption path planning for unmanned aerial vehicles based on improved particle swarm optimization. Sustainability 2023, 15, 12101. [Google Scholar] [CrossRef]
- Ryu, S.K.; Moncton, M.; Choi, H.L.; Frew, E. Path planning in 3D with motion primitives for wind energy-harvesting fixed-wing aircraft. arXiv 2023, arXiv:2311.10915. [Google Scholar]
- Techy, L.; Woolsey, C.A. Minimum-time path planning for unmanned aerial vehicles in steady uniform winds. J. Guid. Control Dyn. 2009, 32, 1736–1746. [Google Scholar] [CrossRef]
- Horn, J.F.; Schmidt, E.M.; Geiger, B.R.; DeAngelo, M.P. Neural network-based trajectory optimization for unmanned aerial vehicles. J. Guid. Control Dyn. 2012, 35, 548–562. [Google Scholar] [CrossRef]
- Gill, P.E.; Murray, W.; Saunders, M.A. SNOPT: An SQP algorithm for large-scale constrained optimization. SIAM Rev. 2005, 47, 99–131. [Google Scholar] [CrossRef]
- Phillips, T.; Stölzle, M.; Turricelli, E.; Achermann, F.; Lawrance, N.; Siegwart, R.; Chung, J.J. Learn to path: Using neural networks to predict Dubins path characteristics for aerial vehicles in wind. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 1073–1079. [Google Scholar]
- Airlangga, G.; Bata, J.; Nugroho, O.I.A.; Sugianto, L.F. Neural network architectures for UAV path planning: A comparative study with A* algorithm as benchmark. Int. J. Robot. Control Syst. 2025, 5, 625–639. [Google Scholar] [CrossRef]
- Dong, R.; Pan, X.; Wang, T.; Chen, G. UAV path planning based on deep reinforcement learning. In Artificial Intelligence for Robotics and Autonomous Systems Applications; Springer: Berlin/Heidelberg, Germany, 2023; pp. 27–65. [Google Scholar]
- Li, J.; Liu, Y. Deep reinforcement learning based adaptive real-time path planning for UAV. In Proceedings of the 2021 8th International Conference on Dependable Systems and Their Applications (DSA), Yinchuan, China, 11–12 September 2021; pp. 522–530. [Google Scholar]
- Babel, L. Online flight path planning with flight time constraints for fixed-wing UAVs in dynamic environments. Int. J. Intell. Unmanned Syst. 2022, 10, 416–443. [Google Scholar] [CrossRef]
- Ji, X.; Wang, T. Energy minimization for fixed-wing UAV assisted full-duplex relaying with bank angle constraint. IEEE Wirel. Commun. Lett. 2023, 12, 1199–1203. [Google Scholar] [CrossRef]
- Betts, J.T. Survey of numerical methods for trajectory optimization. J. Guid. Control Dyn. 1998, 21, 193–207. [Google Scholar] [CrossRef]
- Roberts, S.; Shipman, J. Continuation in shooting methods for two-point boundary value problems. J. Math. Anal. Appl. 1967, 18, 45–58. [Google Scholar] [CrossRef]
- Guelman, M.; Shinar, J. Optimal guidance law in the plane. J. Guid. Control Dyn. 1984, 7, 471–476. [Google Scholar] [CrossRef]
- Chen, Z.; Shima, T. Nonlinear optimal guidance for intercepting a stationary target. J. Guid. Control Dyn. 2019, 42, 2418–2431. [Google Scholar] [CrossRef]
- Wang, K.; Chen, Z.; Wang, H.; Li, J.; Shao, X. Nonlinear optimal guidance for intercepting stationary targets with impact-time constraints. J. Guid. Control Dyn. 2022, 45, 1614–1626. [Google Scholar] [CrossRef]
- Wu, F.; Chen, Z.; Shao, X.; Wang, K. Nonlinear optimal guidance with constraints on impact time and impact angle. arXiv 2024, arXiv:2406.04707. [Google Scholar]
- Zou, F.; Li, J.; Niu, Y. Time-coordinated path following for multiple agile fixed-wing UAVs with end-roll expectations. Guid. Navig. Control 2023, 3, 2350020. [Google Scholar] [CrossRef]
- Chen, Z.; Caillau, J.B.; Chitour, Y. L1-minimization for mechanical systems. SIAM J. Control Optim. 2016, 54, 1245–1265. [Google Scholar] [CrossRef]
- Meier, L.; Tanskanen, P.; Heng, L.; Lee, G.H.; Fraundorfer, F.; Pollefeys, M. PIXHAWK: A micro aerial vehicle design for autonomous flight using onboard computer vision. Auton. Robot. 2012, 33, 21–39. [Google Scholar] [CrossRef]
- Meier, L.; Honegger, D.; Pollefeys, M. PX4: A node-based multithreaded open source robotics framework for deeply embedded platforms. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 6235–6240. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).