Model-Based RL Decision-Making for UAVs Operating in GNSS-Denied, Degraded Visibility Conditions with Limited Sensor Capabilities
Abstract
1. Introduction
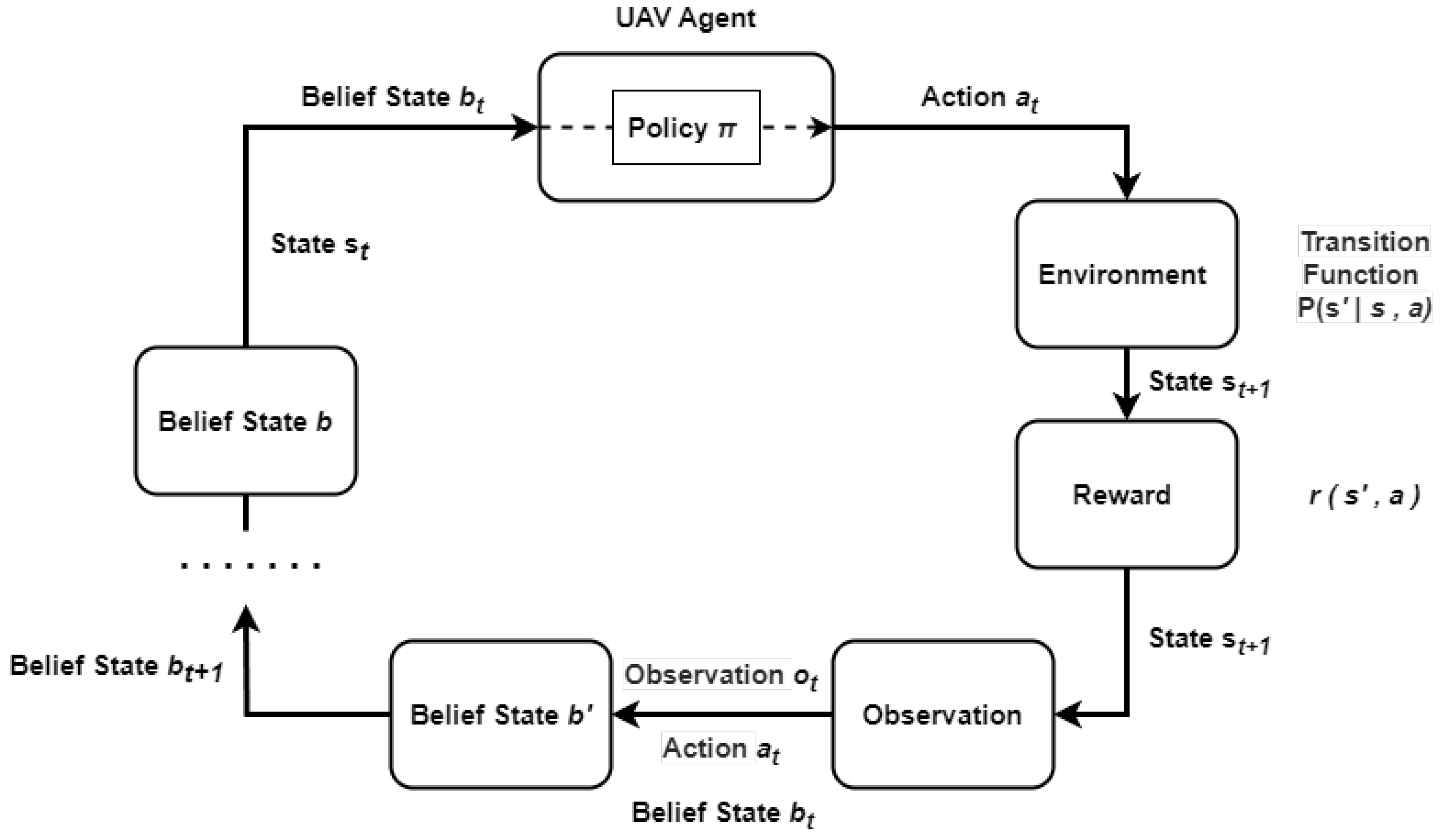
2. Problem Definition and POMDP Framework
- Limited and noisy observations: Constrained UAV platforms often rely on limited onboard sensors such as thermal cameras, LIDARs, and IMUs, which provide incomplete and uncertain information about the environment.
- Dynamic and cluttered environments: UAVs must operate in spaces where obstacles limit freedom of movement and visibility conditions constantly change.
- Computational constraints: UAVs must process real-time sensor data and execute decision-making algorithms efficiently on embedded hardware.
- Decision-making: UAVs need to plan sequences of actions that maximize mission success while handling uncertainty in perception and state estimation.
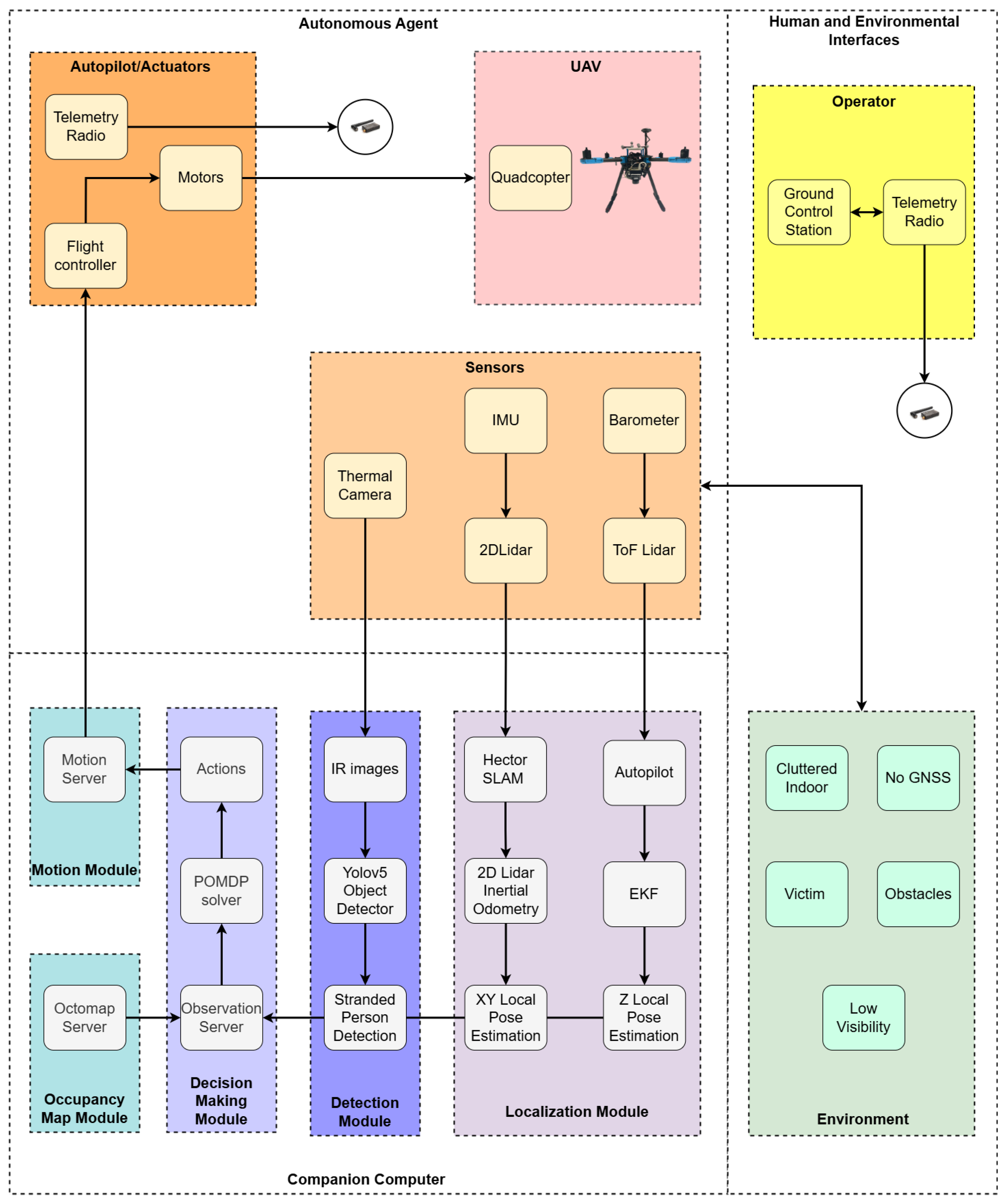
3. System Design
4. POMDP Formulation
- The POMDP algorithm starts outputting actions when the agent reaches a predefined initial waypoint.
- Observations consist of thermal imagery from the thermal camera and local pose estimation from the LIDARs, IMU, and barometer.
- The POMDP problem is formulated to find and detect a single target.
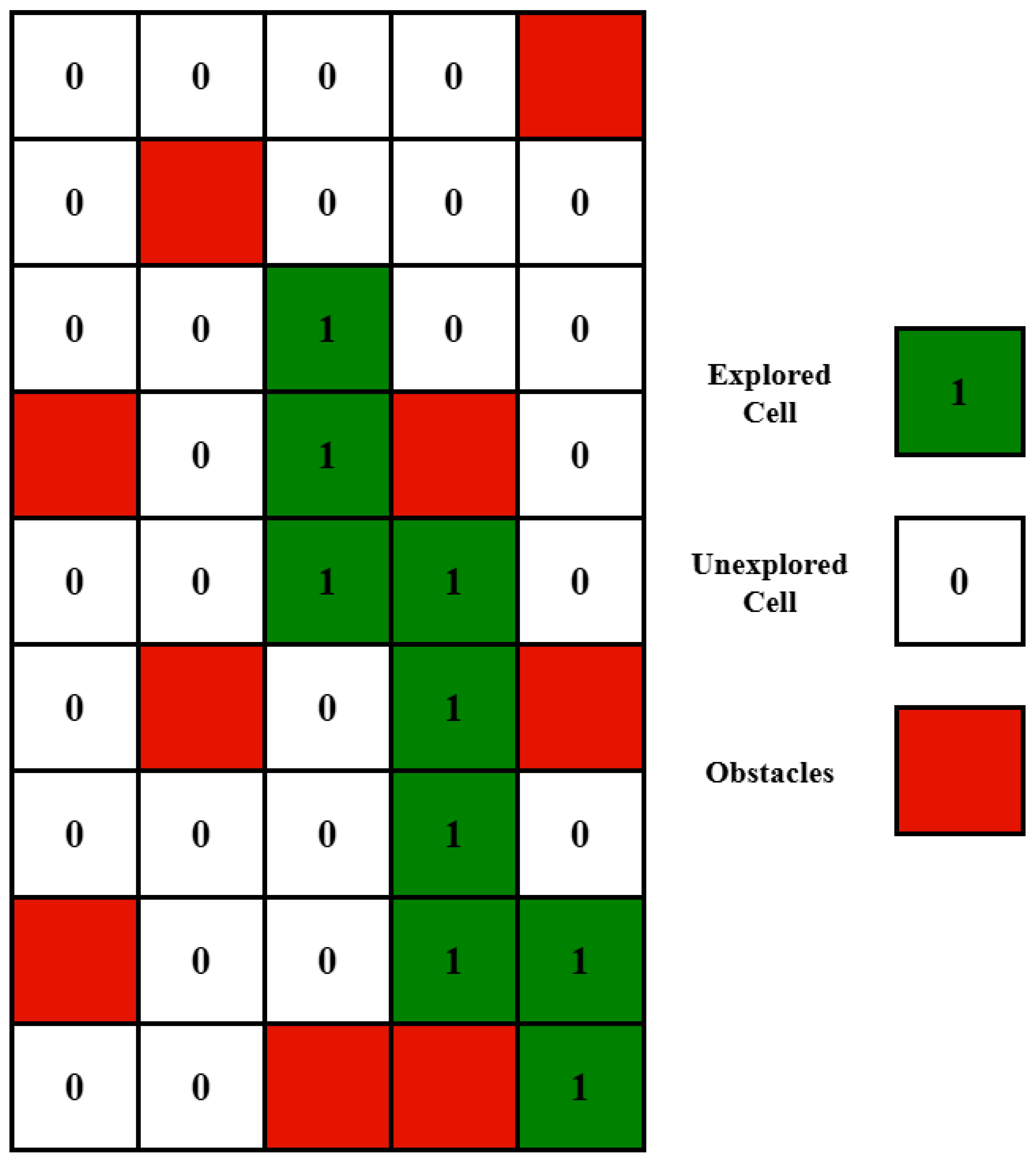
- The map of the environment is assumed to be known to the agent, with a 3D occupancy map being preloaded and used in the decision-making process.
- The detection of the target or the maximum flight time concludes the mission.
- Obstacles and the victim are not dynamic and do not change position during the mission.
- The drone’s set of actions is limited to translations with no rotations.
- The thermal camera is assumed to be mounted facing downward.
- The altitude of the UAV is assumed to be known with little to no uncertainty.
4.1. POMDP Solver
4.2. State–Action Transition Model
4.3. Reward Function
| Algorithm 1 Reward function algorithm |
|
5. Observation Function
5.1. Agent: Localization, Observations, and Belief State
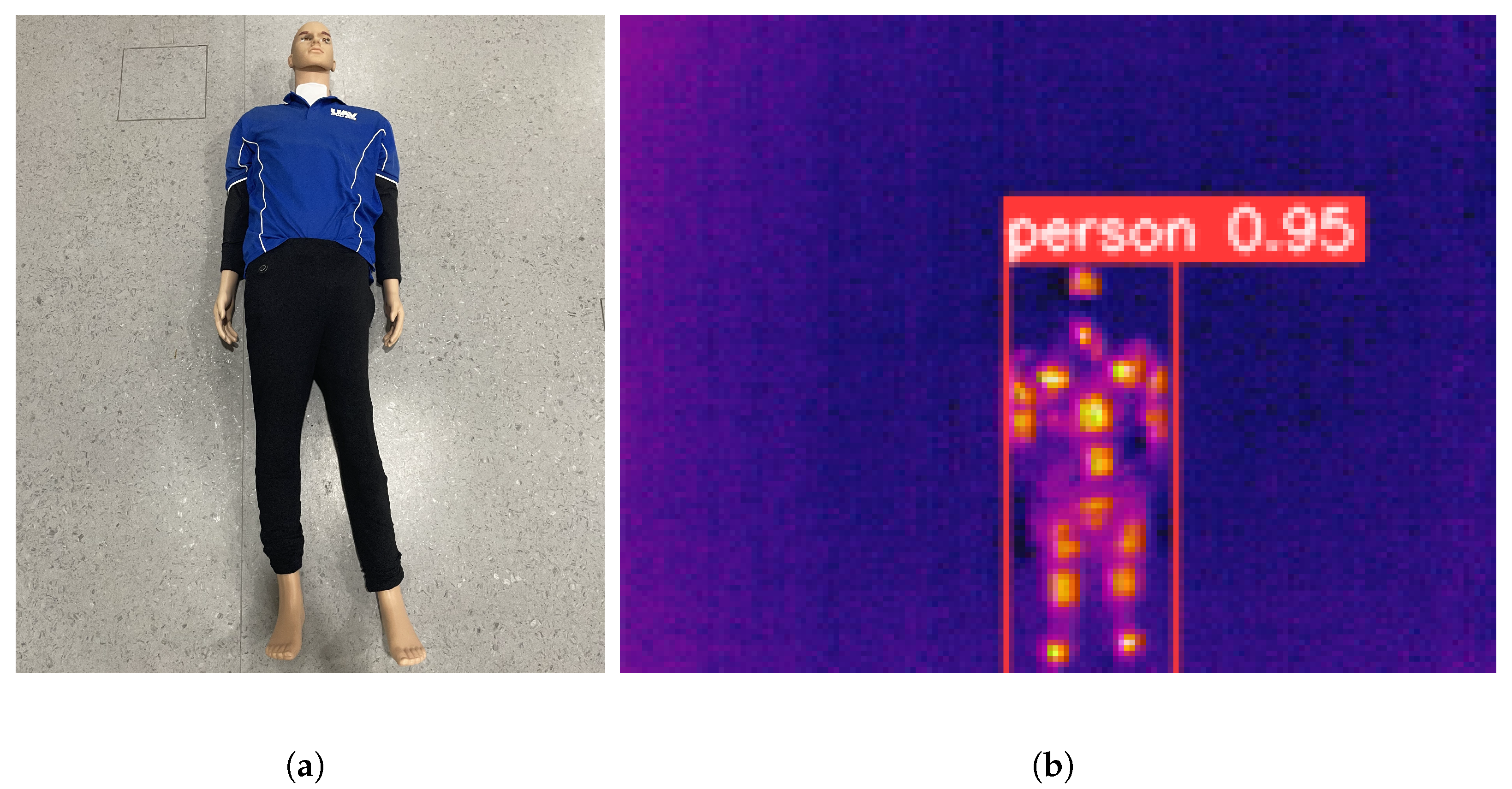
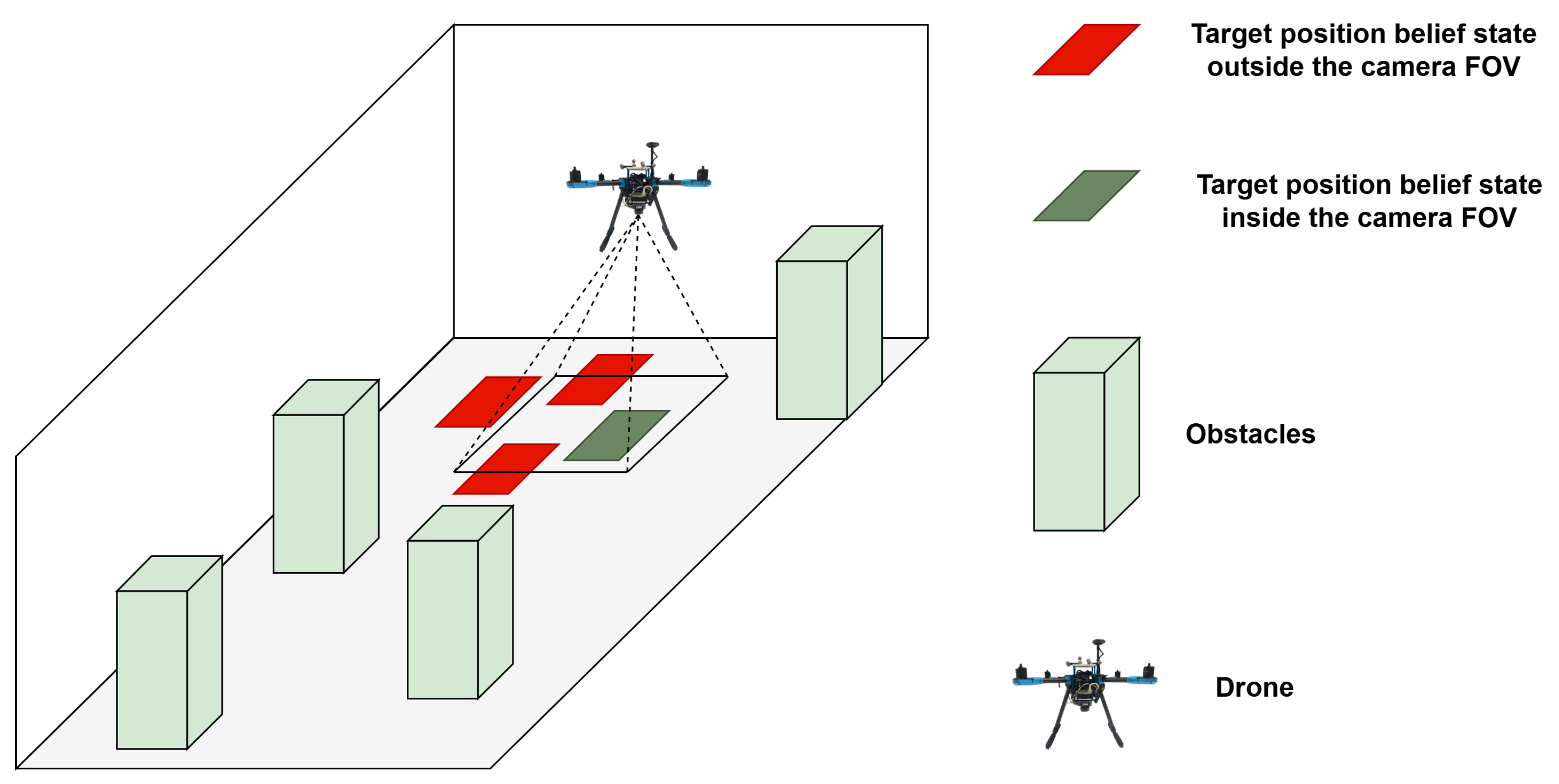
5.2. Target: Detection, Observation Model, and Belief Update
6. Experiments
6.1. Baseline Algorithm
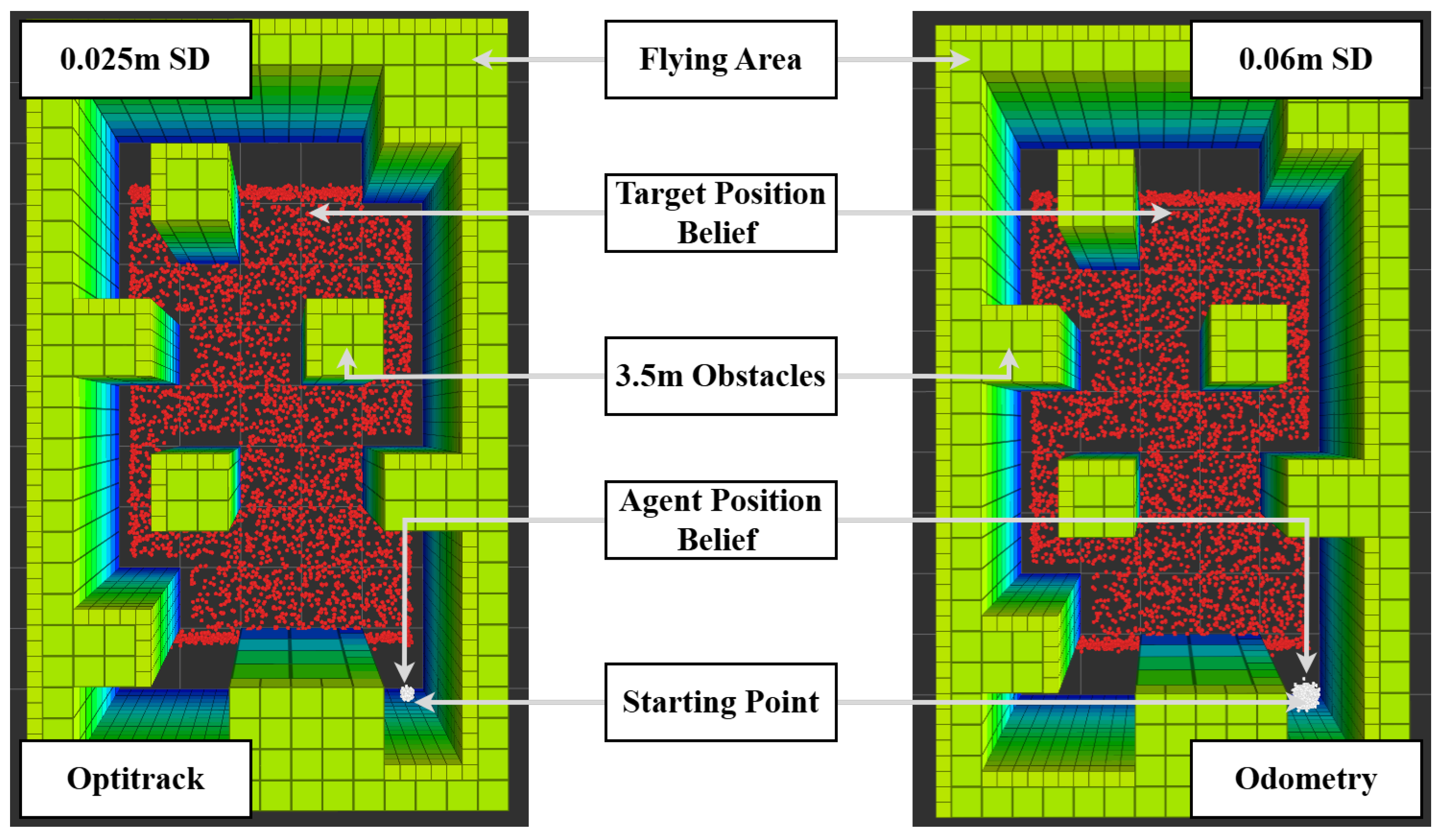
6.2. Experiment Setup
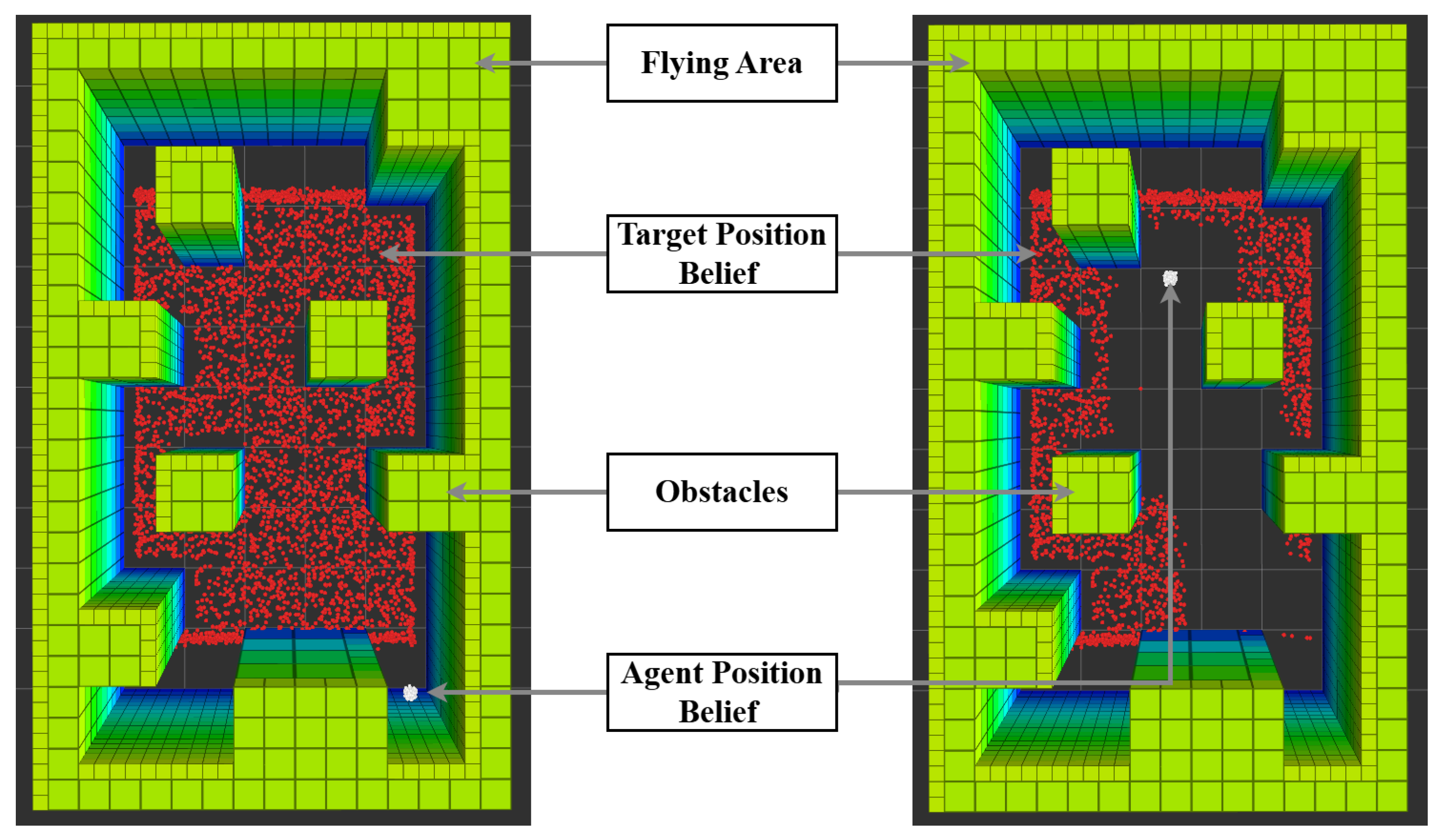
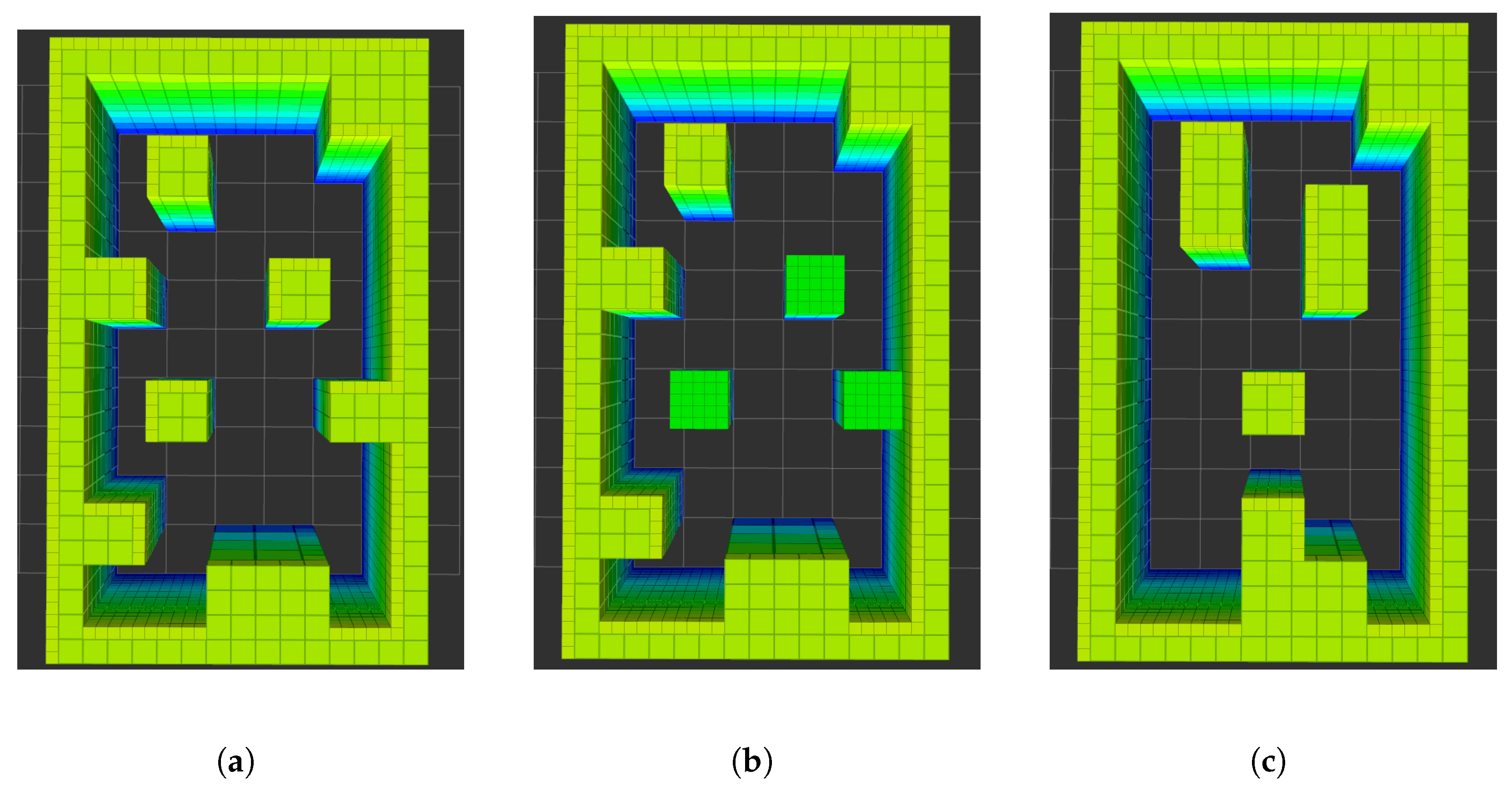
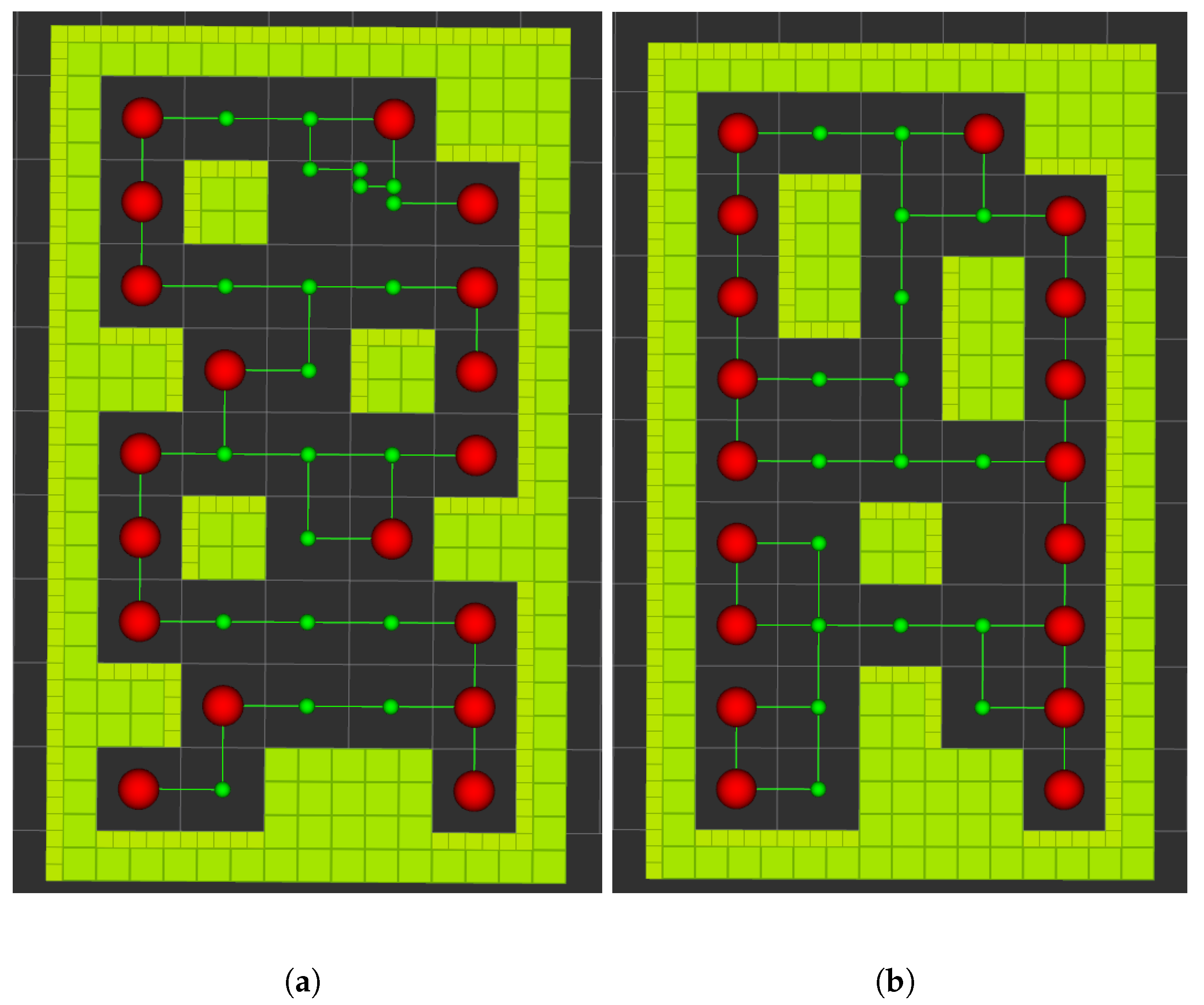
6.3. Flying Area and Maps
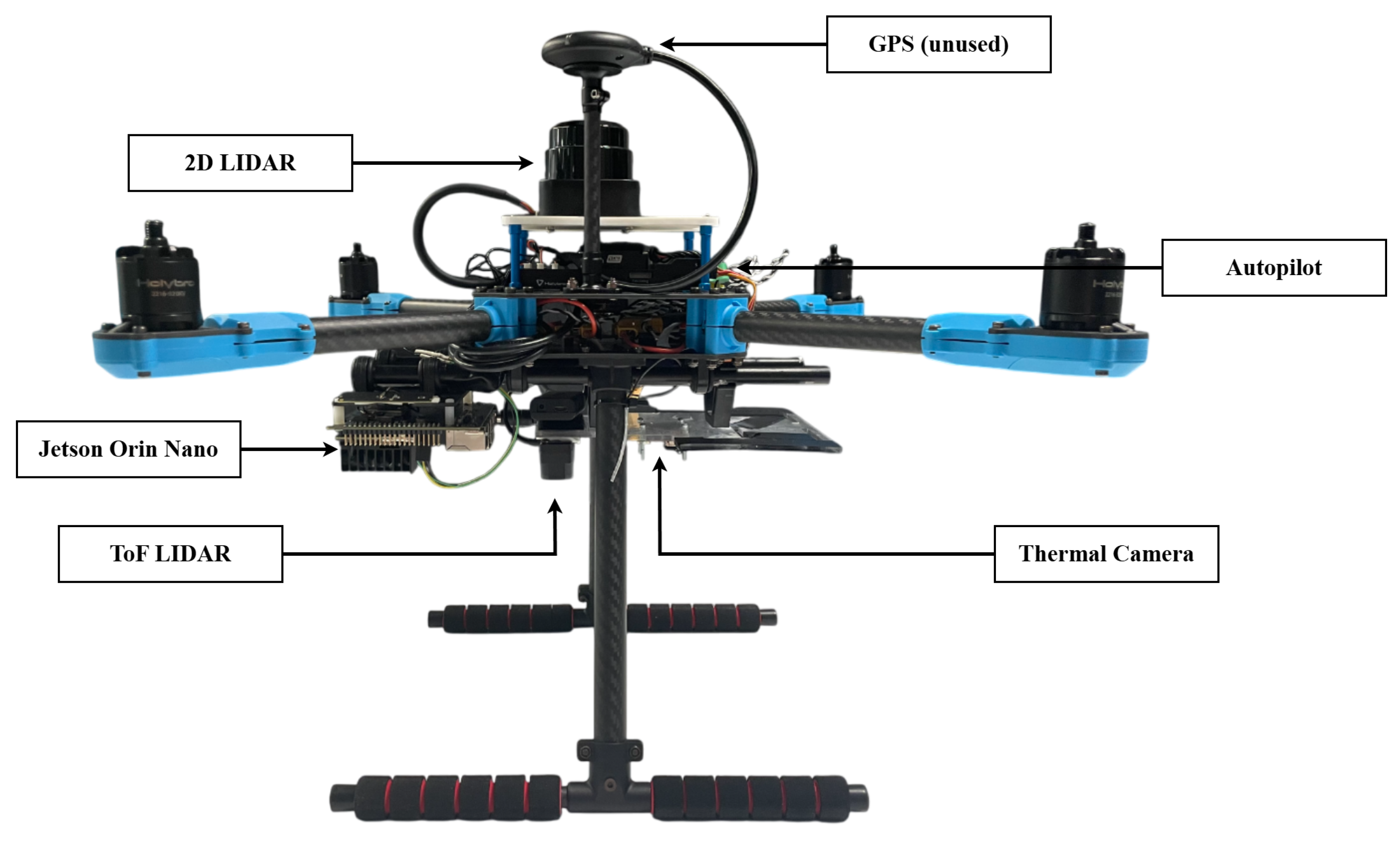
6.4. Hardware and Software for Real-World Experiments
6.5. POMDP Parameters
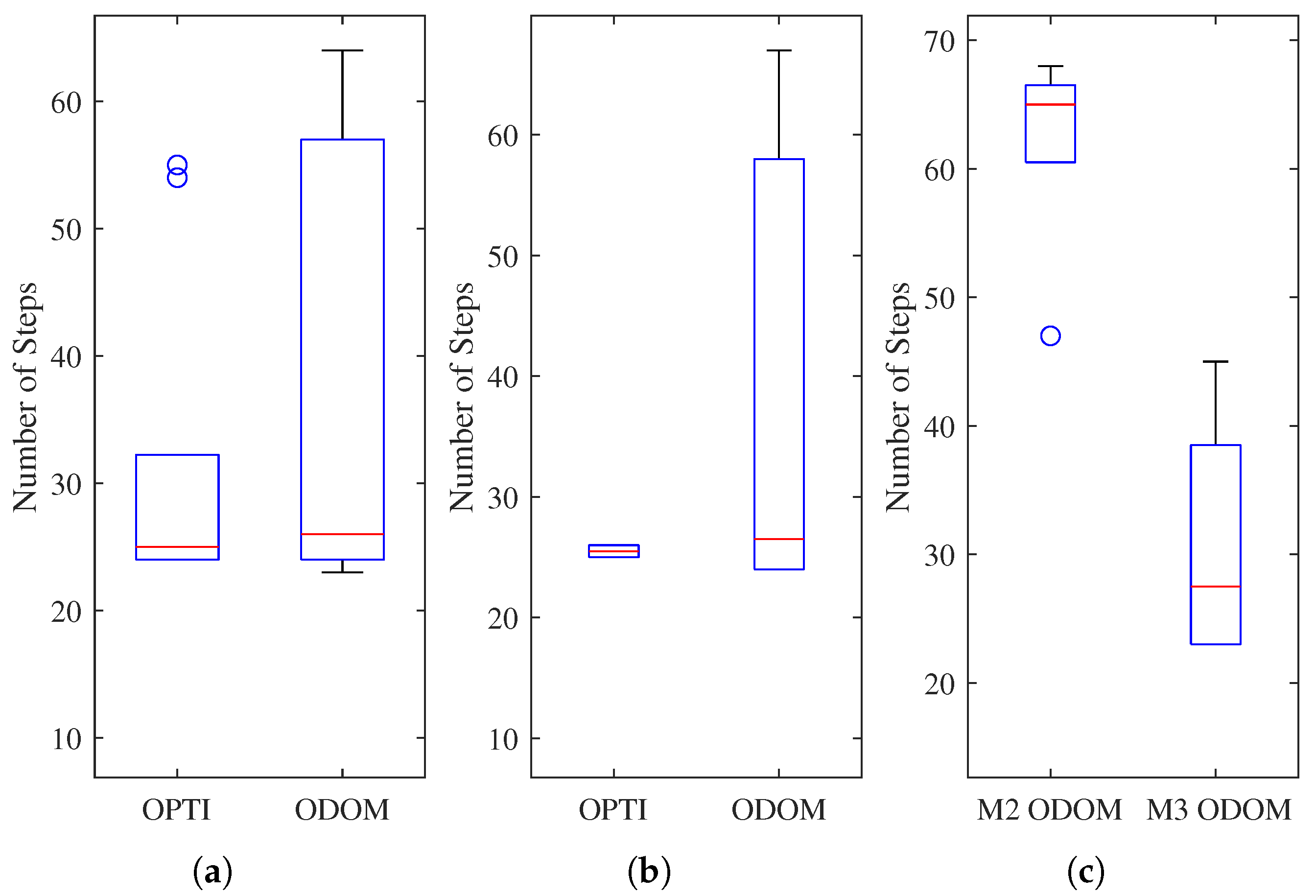
7. Results
7.1. Simulation Results: POMDP vs. Baseline
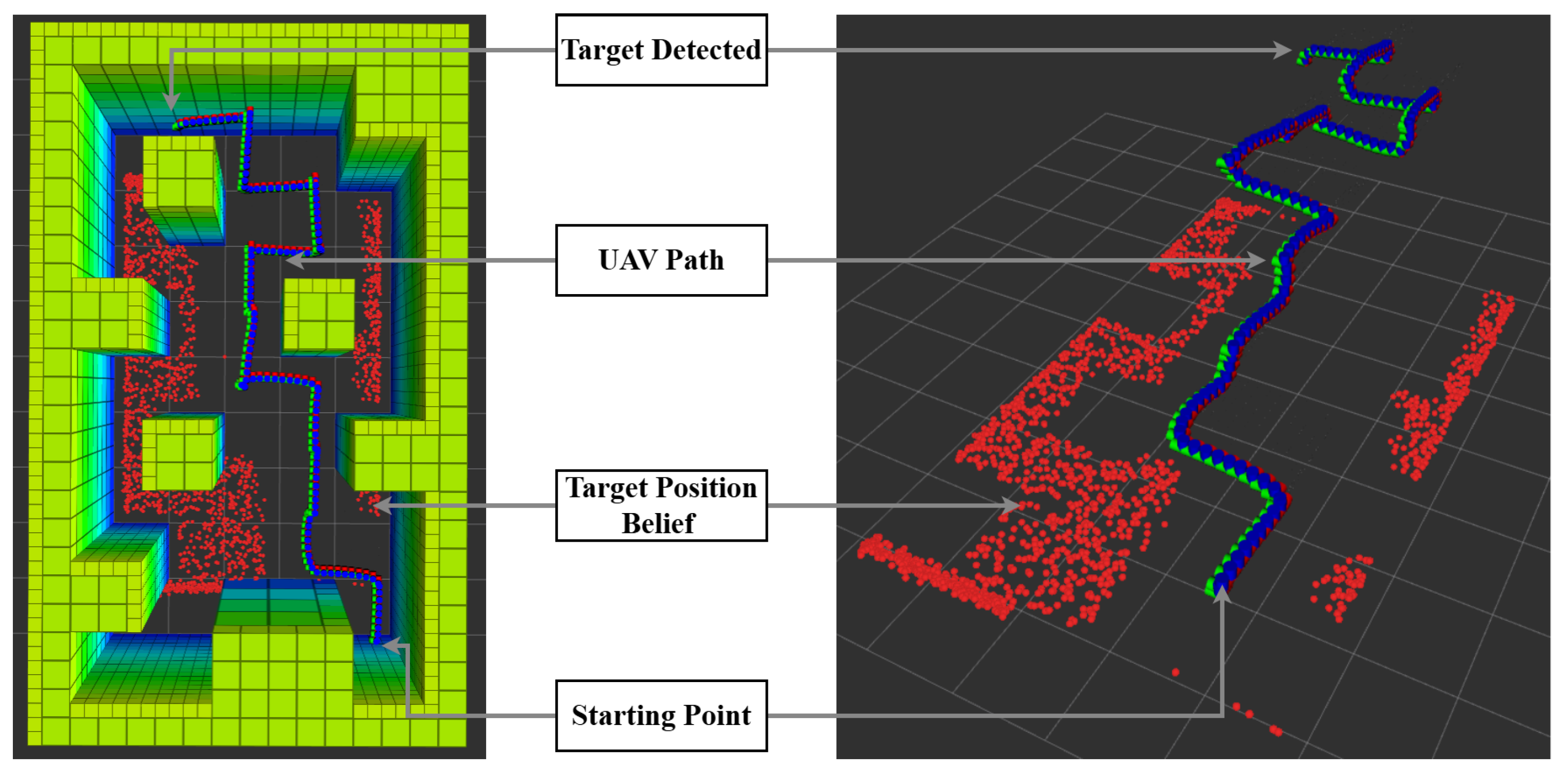
7.2. Real-World Results: POMDP
8. Discussion
9. Conclusions and Future Work
- This paper validates the feasibility of deploying a POMDP-based reinforcement learning framework for autonomous UAV navigation and target detection in visually degraded, cluttered, and GNSS-denied environments. The complete framework was implemented and tested on a fully integrated UAV system that relies entirely on onboard sensing and computation, demonstrating its real-world applicability for critical missions such as search and rescue.
- A realistic observation model was developed by integrating a modern onboard object detection system into the POMDP formulation. The target detection is modeled as a probabilistic observation aligned with the camera’s field of view and bounding box detection’s output, allowing the belief over the target’s location to be updated effectively during flight.
- The framework explicitly incorporates sensor uncertainty into the belief space of the UAV’s pose, enabling robust navigation in GNSS-denied environments. Two levels of uncertainty are compared: low uncertainty using OptiTrack and high uncertainty using Hector SLAM, both represented within the POMDP formulation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | Two-dimensional; |
| 3D | Three-dimensional; |
| ABT | Augmented Belief Tree; |
| FOV | Field of View; |
| GNSS | Global Navigation Satellite System; |
| GPS | Global Positioning System; |
| HIL | Hardware in the Loop; |
| IoU | Intersection over Union; |
| IR | Infrared; |
| LiDAR | Light Detection and Ranging; |
| mAP | Mean Average Precision; |
| MDP | Markov Decision Process; |
| ODOM | Odometry; |
| OPTI | Optitrack System; |
| OS | Operating System; |
| POMDP | Partially Observable Markov Decision Process; |
| RGB | Red, Green, Blue; |
| RL | Reinforcement Learning; |
| RLT | Real-Life Testing; |
| RMSE | Root Mean Square Deviation; |
| ROI | Region of Interest; |
| ROS | Robot Operating System; |
| SDP | Sequential Decision Process; |
| SITL | Software in the Loop; |
| SLAM | Simultaneous Localization and Mapping; |
| ToF | Time of Flight; |
| UAS | Unmanned Aircraft System; |
| UAV | Unmanned Aerial Vehicle. |
References
- Zimroz, P.; Trybala, P.; Wroblewski, A.; Goralczyk, M.; Szrek, J.; Wojcik, A.; Zimroz, R. Application of UAV in search and rescue actions in underground mine a specific sound detection in noisy acoustic signal. Energies 2021, 14, 3725. [Google Scholar] [CrossRef]
- Zhou, D.; Qi, L.; Zhang, D.; Zhou, B.; Guo, L. Unmanned aerial Vehicle (UaV) Photogrammetry Technology for Dynamic Mining Subsidence Monitoring and Parameter Inversion: A Case Study in China. IEEE Access 2020, 8, 16372–16386. [Google Scholar]
- Ebadi, K.; Bernreiter, L.; Biggie, H.; Catt, G.; Chang, Y.; Chatterjee, A.; Denniston, C.E.; Deschênes, S.P.; Harlow, K.; Khattak, S.; et al. Present and Future of SLAM in Extreme Environments: The DARPA SubT Challenge. IEEE Trans. Robot. 2024, 40, 936–959. [Google Scholar] [CrossRef]
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics; The MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Kochenderfer, M.J. Decision Making Under Uncertainty: Theory and Application; Lincoln Laboratory Series; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Russell, S.J.S.J. Artificial Intelligence: A Modern Approach, 4th ed.; Pearson: London, UK, 2021. [Google Scholar]
- Deshpande, S.V.; R, H.; Walambe, R. POMDP-based probabilistic decision making for path planning in wheeled mobile robot. Cogn. Robot. 2024, 4, 104–115. [Google Scholar] [CrossRef]
- Martins, G.S.; Al Tair, H.; Santos, L.; Dias, J. POMDP-based user-adaptive decision-making for social robots. Pattern Recognit. Lett. 2019, 118, 94–103. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Kailas, S.; Badyal, S.; Gil, S.; Bertsekas, D. Multiagent Reinforcement Learning: Rollout and Policy Iteration for POMDP with Application to Multirobot Problems. IEEE Trans. Robot. 2024, 40, 2003–2023. [Google Scholar] [CrossRef]
- Sharma, P.; Kraske, B.; Kim, J.; Laouar, Z.; Sunberg, Z.; Atkins, E. Investigation of risk-aware MDP and POMDP contingency management autonomy for UAS. arXiv 2023, arXiv:2304.01052. [Google Scholar]
- Yang, Q.; Zhang, J.; Shi, G. Modeling of UAV path planning based on IMM under POMDP framework. J. Syst. Eng. Electron. 2019, 30, 545–554. [Google Scholar] [CrossRef]
- dos Santos, M.A.A.; Vivaldini, K.C.T. A Modeling Strategy Using Bayesian Optimization with POMDP for Exploration and Informative Path Planning of UAVs in Monitoring of Forest. In Proceedings of the 2022 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 14–16 December 2022; pp. 451–456. [Google Scholar] [CrossRef]
- Ragi, S.; Chong, E.K.P. UAV Path Planning in a Dynamic Environment via Partially Observable Markov Decision Process. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 2397–2412. [Google Scholar] [CrossRef]
- Eaton, C.M.; Chong, E.K.; Maciejewski, A.A. Robust UAV path planning using POMDP with limited FOV sensor. In Proceedings of the 2017 IEEE Conference on Control Technology and Applications (CCTA), Maui, HI, USA, 27–30 August 2017; pp. 1530–1535. [Google Scholar] [CrossRef]
- Trotti, F.; Farinelli, A.; Muradore, R. An online path planner based on POMDP for UAVs. In Proceedings of the 2023 European Control Conference (ECC), Bucharest, Romania, 13–16 June 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Jiang, W.; Lyu, Y.; Li, Y.; Guo, Y.; Zhang, W. UAV path planning and collision avoidance in 3D environments based on POMPD and improved grey wolf optimizer. Aerosp. Sci. Technol. 2022, 121, 107314. [Google Scholar] [CrossRef]
- Zaninotti, M.; Lesire, C.; Watanabe, Y.; Chanel, C.P.C. Learning Path Constraints for UAV Autonomous Navigation under Uncertain GNSS Availability. In Proceedings of the Frontiers in Artificial Intelligence and Applications, Hangzhou, China, 29–30 October 2022; Volume 351, pp. 59–71. [Google Scholar]
- Guan, X.; Lu, Y.; Ruan, L. Joint Optimization Control Algorithm for Passive Multi-Sensors on Drones for Multi-Target Tracking. Drones 2024, 8, 627. [Google Scholar] [CrossRef]
- Zhang, B.; Jing, T.; Lin, X.; Cui, Y.; Zhu, Y.; Zhu, Z. Deep Reinforcement Learning-based Collaborative Multi-UAV Coverage Path Planning. J. Phys. Conf. Ser. 2024, 2833, 012017. [Google Scholar] [CrossRef]
- Wang, Y.; Zeng, W.; Li, G.; Xiong, C.; Wang, Z.; Mao, Y. An Energy-Aware UAVs Path Coverage for Critical Infrastructure Inspections. In Proceedings of the 2024 Twelfth International Conference on Advanced Cloud and Big Data (CBD), Brisbane, Australia, 28 November–2 December 2024; pp. 222–227. [Google Scholar] [CrossRef]
- Floriano, B.; Borges, G.A.; Ferreira, H. Planning for Decentralized Formation Flight of UAV fleets in Uncertain Environments with Dec-POMDP. In Proceedings of the 2019 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019; pp. 563–568. [Google Scholar] [CrossRef]
- Sandino, J.; Vanegas, F.; Maire, F.; Caccetta, P.; Sanderson, C.; Gonzalez, F. UAV Framework for Autonomous Onboard Navigation and People/Object Detection in Cluttered Indoor Environments. Remote Sens. 2020, 12, 3386. [Google Scholar] [CrossRef]
- Sandino, J.; Caccetta, P.A.; Sanderson, C.; Maire, F.; Gonzalez, F. Reducing Object Detection Uncertainty from RGB and Thermal Data for UAV Outdoor Surveillance. In Proceedings of the IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 5–12 March 2022. [Google Scholar]
- Systems, V.M. Vicon: Award Winning Motion Capture Systems. Available online: https://www.vicon.com/ (accessed on 21 January 2025).
- Vanegas, F.; Gonzalez, F. Enabling UAV navigation with sensor and environmental uncertainty in cluttered and GPS-denied environments. Sensors 2016, 16, 666. [Google Scholar] [CrossRef] [PubMed]
- Vanegas, F.; Gaston, K.J.; Roberts, J.; Gonzalez, F. A Framework for UAV Navigation and Exploration in GPS-Denied Environments. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; pp. 1–6. [Google Scholar]
- Khattak, S.; Nguyen, H.; Mascarich, F.; Dang, T.; Alexis, K. Complementary Multi–Modal Sensor Fusion for Resilient Robot Pose Estimation in Subterranean Environments. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; pp. 1024–1029. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in real-time. Robot. Sci. Syst. Conf. 2014, 2, 109–111. [Google Scholar]
- Khattak, S.; Papachristos, C.; Alexis, K. Keyframe-based Direct Thermal—Inertial Odometry. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 3563–3569. [Google Scholar] [CrossRef]
- Bloesch, M.; Omari, S.; Hutter, M.; Siegwart, R. Robust visual inertial odometry using a direct EKF-based approach. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 298–304. [Google Scholar] [CrossRef]
- Lynen, S.; Achtelik, M.W.; Weiss, S.; Chli, M.; Siegwart, R. A robust and modular multi-sensor fusion approach applied to MAV navigation. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 3923–3929. [Google Scholar] [CrossRef]
- Dang, T.; Mascarich, F.; Khattak, S.; Papachristos, C.; Alexis, K. Graph-based Path Planning for Autonomous Robotic Exploration in Subterranean Environments. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 3105–3112. [Google Scholar] [CrossRef]
- Tsiourva, M.; Papachristos, C. Multi-modal Visual-Thermal Saliency-based Object Detection in Visually-degraded Environments. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–9. [Google Scholar] [CrossRef]
- Boiteau, S.; Vanegas, F.; Sandino, J.; Gonzalez, F.; Galvez-Serna, J. Autonomous UAV Navigation for Target Detection in Visually Degraded and GPS Denied Environments. In Proceedings of the 2023 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2023; pp. 1–10. [Google Scholar] [CrossRef]
- Boiteau, S.; Vanegas, F.; Gonzalez, F. A Comprehensive Framework for UAV-Based Autonomous Target Finding in Environments with Limited Global Navigation Satellite Systems and Reduced Visibility. In Proceedings of the 2024 International Conference on Unmanned Aircraft Systems (ICUAS), Chania-Crete, Greece, 4–7 June 2024; pp. 160–167. [Google Scholar] [CrossRef]
- Boiteau, S.; Vanegas, F.; Gonzalez, F. Framework for Autonomous UAV Navigation and Target Detection in Global-Navigation-Satellite-System-Denied and Visually Degraded Environments. Remote Sens. 2024, 16, 471. [Google Scholar] [CrossRef]
- Optitrack. OptiTrack for Robotics. Available online: https://optitrack.com/applications/robotics/ (accessed on 5 May 2023).
- Klimenko, D.; Song, J.; Kurniawati, H. TAPIR: A Software Toolkit for Approximating and Adapting POMDP Solutions Online. In Proceedings of the Proc. Australasian Conference on Robotics and Automation, Melbourne, Australia, 2–4 December 2014. [Google Scholar]
- Kurniawati, H.; Yadav, V. An Online POMDP Solver for Uncertainty Planning in Dynamic Environment; Springer International Publishing: Cham, Switzerland, 2016; pp. 611–629. [Google Scholar] [CrossRef]
- Chovancová, A.; Fico, T.; Chovanec, Ľ.; Hubinsk, P. Mathematical Modelling and Parameter Identification of Quadrotor (a survey). Modelling of Mechanical and Mechatronic Systems. Procedia Eng. 2014, 96, 172–181. [Google Scholar] [CrossRef]
- Kohlbrecher, S.; von Stryk, O.; Meyer, J.; Klingauf, U. A flexible and scalable SLAM system with full 3D motion estimation. In Proceedings of the 2011 IEEE International Symposium on Safety, Security, and Rescue Robotics, Kyoto, Japan, 1–5 November 2011; pp. 155–160. [Google Scholar] [CrossRef]
- Ultralytics. yolov5. Available online: https://github.com/ultralytics/yolov5 (accessed on 15 May 2023).
- Jiang, C.; Ren, H.; Ye, X.; Zhu, J.; Zeng, H.; Nan, Y.; Sun, M.; Ren, X.; Huo, H. Object detection from UAV thermal infrared images and videos using YOLO models. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102912. [Google Scholar] [CrossRef]
- Qutas. Breadcrumb (baselineTest Branch). 2025. Available online: https://github.com/qutas/breadcrumb/tree/baselineTest (accessed on 24 March 2025).
- Qutas. Spar (breadcrumbTest Branch). 2025. Available online: https://github.com/qutas/spar/tree/breadcrumbTest (accessed on 24 March 2025).
- Meier, L.; Honegger, D.; Pollefeys, M. PX4: A node-based multithreaded open source robotics framework for deeply embedded platforms. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 6235–6240. [Google Scholar] [CrossRef]
- Open Robotics. Rescue Randy—Gazebo Model. 2025. Available online: https://app.gazebosim.org/OpenRobotics/fuel/models/Rescue%20Randy (accessed on 24 March 2025).
- Foundation, O.S.R. Robot Operating System. Available online: https://www.ros.org/ (accessed on 5 May 2023).
- Ermakov, V. Mavros. Available online: http://wiki.ros.org/mavros (accessed on 5 May 2023).
- Koubâa, A.; Allouch, A.; Alajlan, M.; Javed, Y.; Belghith, A.; Khalgui, M. Micro Air Vehicle Link (MAVlink) in a Nutshell: A Survey. IEEE Access 2019, 7, 87658–87680. [Google Scholar] [CrossRef]







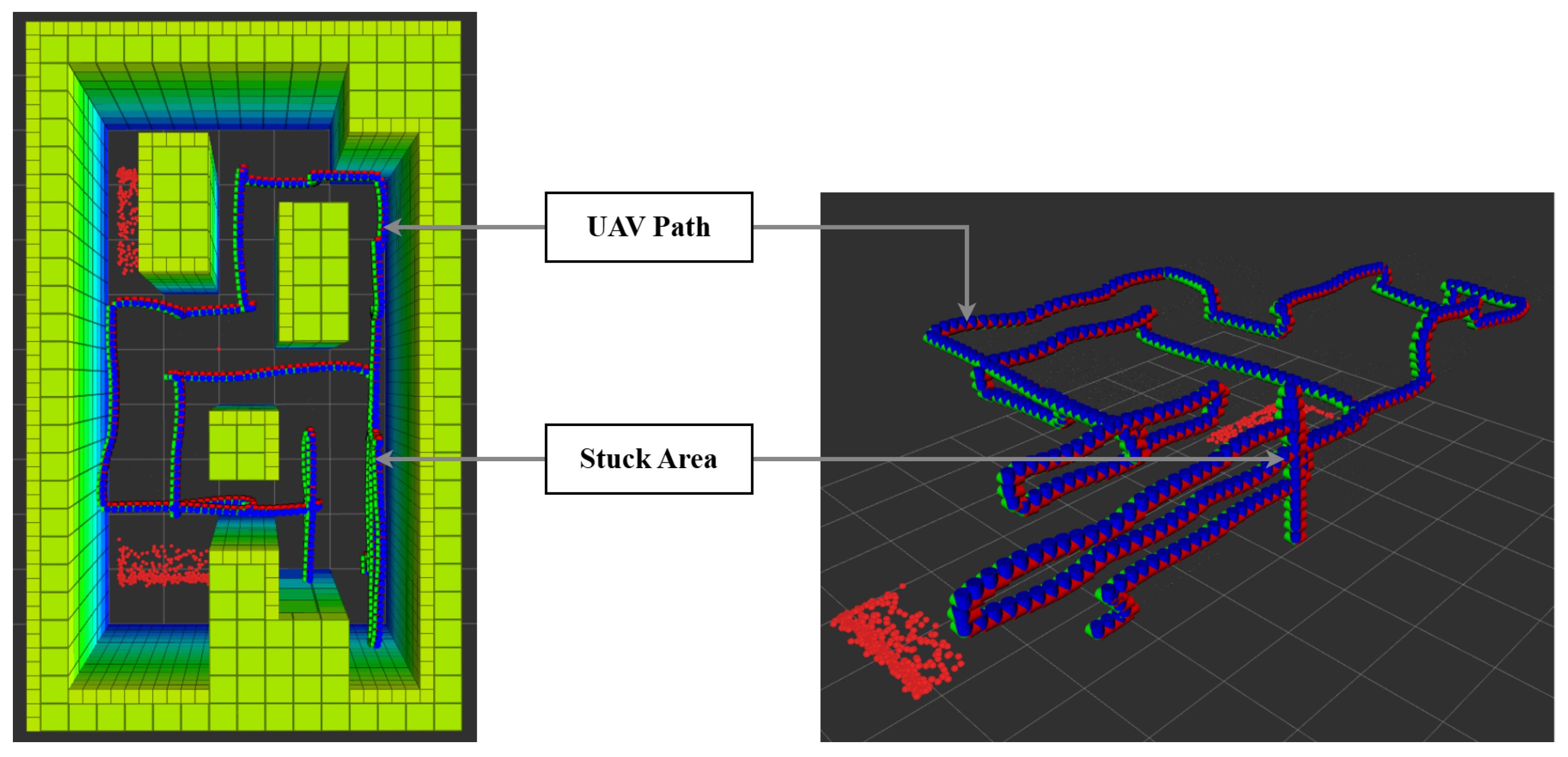
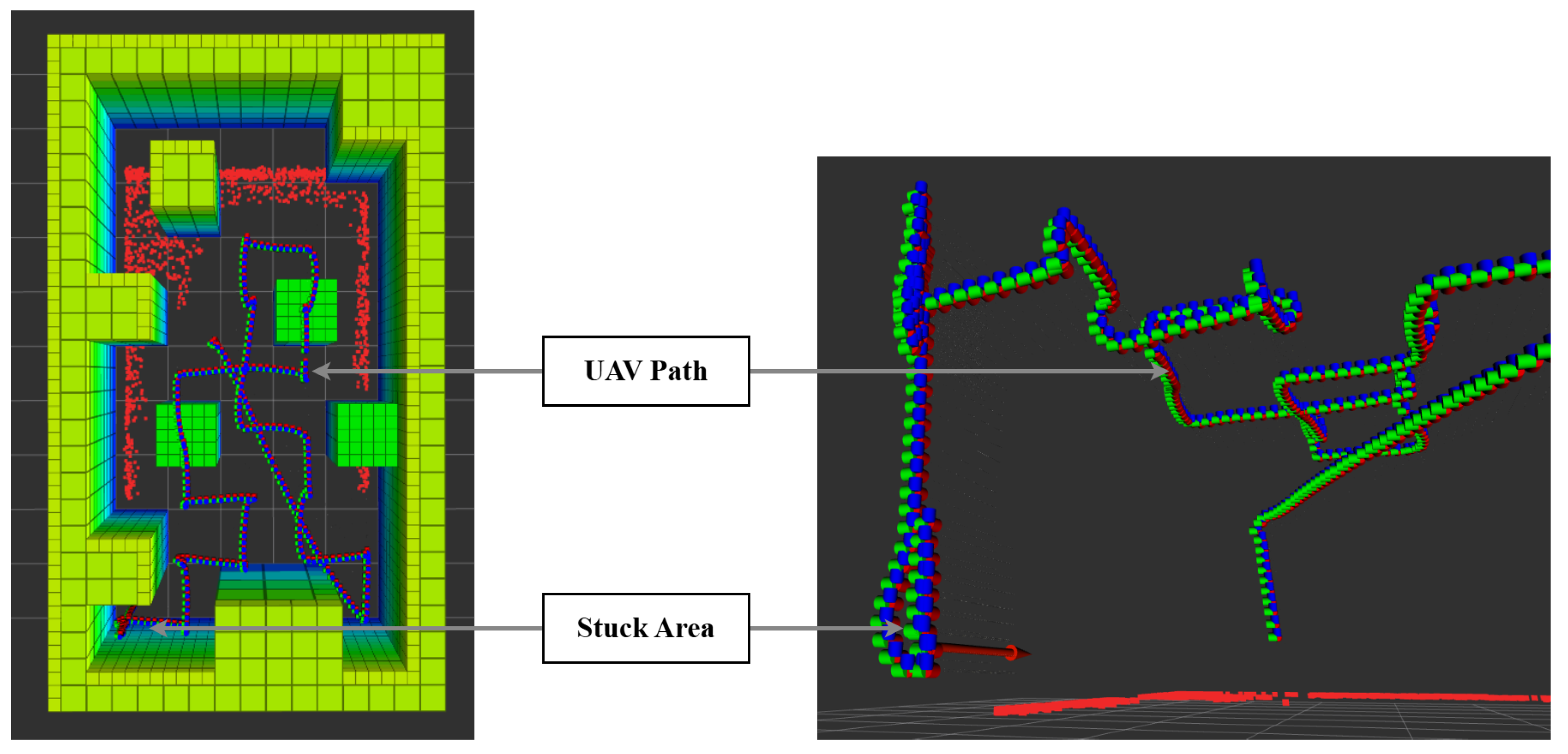
| Action | xa(t + 1) | ya(t + 1) | za(t + 1) |
|---|---|---|---|
| Forward | |||
| Backward | |||
| Left | |||
| Right | |||
| Up | |||
| Down | |||
| Hover |
| Reward | Value | Description |
|---|---|---|
| rcrash | −110 | Crashing |
| rout | −110 | Out of ROI |
| rf | 200 | Victim located |
| rexp | −5 | Explored area |
| rnew | 20 | Explore new area |
| ralt | −75 | Leaving altitude range |
| Equipment | Origin | Description |
|---|---|---|
| X500 V2 multirotor kit | Shenzhen City, China | Quadcopter |
| Pixhawk 6X | Shenzhen City, China | Autopilot |
| FLIR Lepton FS | Wilsonville, U.S. | Thermal camera |
| PureThermal 3 Lepton Board | Wilsonville, U.S. | Thermal camera board |
| Jetson Orin Nano | Santa Clara, U.S. | Onboard computer |
| RPI S1 2D LiDAR | Shanghai, China | 2D LiDAR |
| TFMini Plus Micro LiDAR | Beijing, China | ToF LiDAR |
| Variable | Value | Description |
|---|---|---|
| 0.93 | Discount factor | |
| 2.0 m | Minimum altitude | |
| 3.5 m | Maximum altitude | |
| 1 m | x displacement | |
| 1 m | y displacement | |
| 0.3 m | z displacement | |
| (−4.5; −2.5; 2.0) | Intial agent position | |
| 100 | Number of time steps | |
| 2 s | Time step | |
| v | 0.5 m/s | Velocity |
| 1 rad | Angle uncertainty |
| Experiment | Environment | Altitude | Algorithm |
|---|---|---|---|
| Baseline-1 | Map 1 | Fixed: 3 m | Lawn mower A* |
| Baseline-2 | Map 1 | Fixed: 2 m | Lawn mower A* |
| Baseline-3 | Map 3 | Fixed: 3 m | Lawn mower A* |
| Baseline-4 | Map 3 | Fixed: 2 m | Lawn mower A* |
| POMDP-1 | Map 1 | Dynamic | POMDP |
| POMDP-2 | Map 2 | Dynamic | POMDP |
| POMDP-3 | Map 3 | Dynamic | POMDP |
| Setup | Iterations | Success | Average Time (s) | Average Time Steps |
|---|---|---|---|---|
| Baseline-1 | 10 | 100% | 88 | 44 |
| Baseline-2 | 10 | 0% | N/A | N/A |
| Baseline-3 | 10 | 100% | 106 | 53 |
| Baseline-4 | 10 | 0% | N/A | N/A |
| POMDP-1 | 10 | 100% | 87.1 | 41.1 |
| POMDP-2 | 10 | 80% | 70.1 | 33 |
| POMDP-2 | 10 | 100% | 109.5 | 52.2 |
| Baseline | 40 | 50% | 97 | 70.5 |
| POMDP | 30 | 93.3% | 88.9 | 42.1 |
| Category | Baseline Algorithm | POMDP Framework |
|---|---|---|
| Algorithm Type | Lawn-mower + A* | Decision-making under uncertainty |
| Altitude Control | Fixed (2D navigation) | Adaptive (3D navigation) |
| Uncertainty Handling | None | Probabilistic modeling |
| Obstacle Avoidance | A* (2D) | Adaptive 3D path planning |
| Target Detection Rate | 50% (FOV limitation) | 93.3% (altitude adjustment) |
| Environmental Adaptability | Follows set paths | Adjusts to observations |
| Performance on Terrain | No adaptation to obstacle height | Adjusts path based on terrain |
| Experiment | Environment | Visibility Conditions | Localization |
|---|---|---|---|
| Exp-1 | Map 1 | Normal | Optitrack |
| Exp-2 | Map 1 | Normal | Odometry |
| Exp-3 | Map 1 | Low visibilty | Optitrack |
| Exp-4 | Map 1 | Low visibilty | Odometry |
| Exp-5 | Map 2 | Normal | Odometry |
| Exp-6 | Map 3 | Normal | Odometry |
| Setup | Iterations | Target Found | Crash Rate | ROI Out | Max Altitude | Timeout Rate |
|---|---|---|---|---|---|---|
| Exp-1 | 10 | 100% | 0% | 0% | 0% | 0% |
| Exp-2 | 10 | 100% | 0% | 0% | 20% | 0% |
| Exp-3 | 10 | 100% | 0% | 0% | 0% | 0% |
| Exp-4 | 10 | 100% | 0% | 0% | 20% | 0% |
| Exp-5 | 5 | 80% | 0% | 0% | 0% | 20% |
| Exp-6 | 6 | 83.3% | 0% | 0% | 0% | 16.7% |
| Total | 51 | 96.08% | 0% | 0% | 7.84% | 3.92% |
| Test Case | RMSE x (m) | RMSE y (m) | SD x (m) | SD y (m) |
|---|---|---|---|---|
| Exp-2 | 0.0400 | 0.0509 | 0.0254 | 0.0254 |
| Exp-4 | 0.0440 | 0.0585 | 0.0276 | 0.0276 |
| Exp-5 | 0.0476 | 0.0627 | 0.0308 | 0.0308 |
| Exp-6 | 0.0536 | 0.0546 | 0.0265 | 0.0265 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boiteau, S.; Vanegas, F.; Galvez-Serna, J.; Gonzalez, F. Model-Based RL Decision-Making for UAVs Operating in GNSS-Denied, Degraded Visibility Conditions with Limited Sensor Capabilities. Drones 2025, 9, 410. https://doi.org/10.3390/drones9060410
Boiteau S, Vanegas F, Galvez-Serna J, Gonzalez F. Model-Based RL Decision-Making for UAVs Operating in GNSS-Denied, Degraded Visibility Conditions with Limited Sensor Capabilities. Drones. 2025; 9(6):410. https://doi.org/10.3390/drones9060410
Chicago/Turabian StyleBoiteau, Sebastien, Fernando Vanegas, Julian Galvez-Serna, and Felipe Gonzalez. 2025. "Model-Based RL Decision-Making for UAVs Operating in GNSS-Denied, Degraded Visibility Conditions with Limited Sensor Capabilities" Drones 9, no. 6: 410. https://doi.org/10.3390/drones9060410
APA StyleBoiteau, S., Vanegas, F., Galvez-Serna, J., & Gonzalez, F. (2025). Model-Based RL Decision-Making for UAVs Operating in GNSS-Denied, Degraded Visibility Conditions with Limited Sensor Capabilities. Drones, 9(6), 410. https://doi.org/10.3390/drones9060410








