Bridging ACO-Based Drone Logistics and Computing Continuum for Enhanced Smart City Applications
Abstract
1. Introduction
1.1. Background
1.2. Problem Statement
- Path Planning: Design path planning algorithms to find the optimal path in terms of fuel consumption to guide UAVs to targets.
- Dynamic Resource Allocation: Develop algorithms that enable the cloud to dynamically allocate computing resources, storage capacity, and communication bandwidth to UAVs based on their current needs and mission requirements.
- Scalable Fleet Management: Design a scalable cloud architecture that can efficiently manage hundreds or even thousands of UAVs, ensuring consistent performance and reliability as the fleet size grows.
- Collaborative Decision-Making: The exploitation of CC facilities enables collaborative decision-making among multiple UAVs, enabling them to coordinate their actions effectively and achieve common goals.
- Data Analytics and Insights: Leverage cloud-based data analytics tools to extract valuable insights from the vast amount of data collected by UAVs. This can include identifying patterns, predicting future trends, and optimizing operational strategies.
- Data Integration and Interoperability: Mutual data exchange among UAVs, applications, and Smart Cities is a key element involving multiple stakeholders who share technologies and data.
2. Mission Planning: Path Optimization and Target Assignment
2.1. Problem Definition and Inputs
- A single starting depot for all UAVs, denoted by .
- A known number, m, of UAVs, each with a specific payload capacity Q.
- A set of mission targets, denoted by , with , each with a specific demand for goods .
- A static environment where obstacles are known a priori.
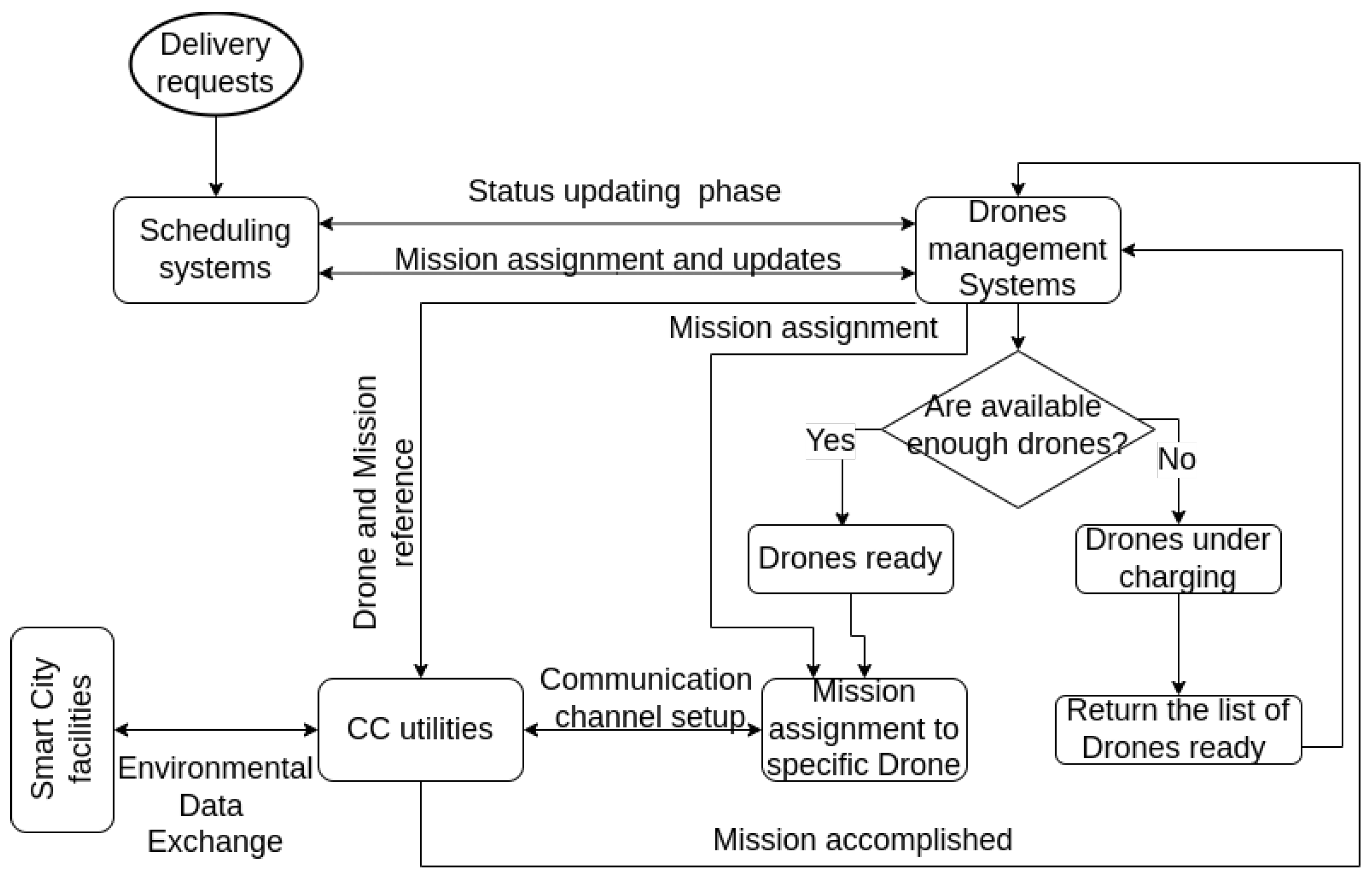
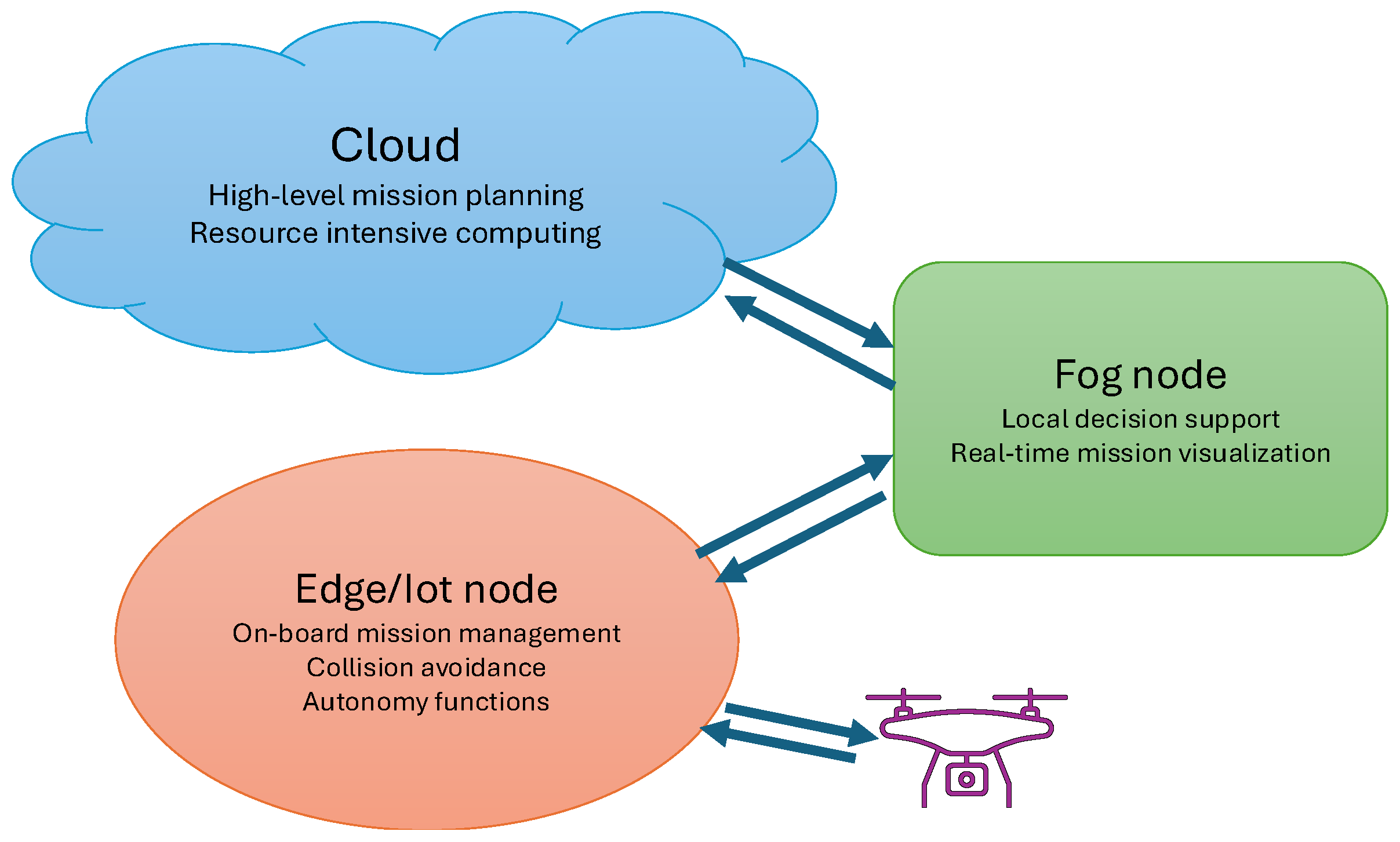
2.2. Command and Control Infrastructure Overview
- Cloud: It is responsible for high-level mission planning, resource allocation, and overall network orchestration. It hosts the service logic, network control agents, and communication middleware.
- Fog Node: Located closer to the UAVs, this layer provides real-time mission visualization and local decision support, integrating optimization procedures (e.g., through a Ground Control Station such as QGroundControl).
- Edge/IoT Node: Onboard nodes to manage sensor data, basic autonomy functions, and communication with upper layers.
2.3. Preparatory Phase for Drones Coordination Process
| Listing 1. Prototype of the points collection. |
| { "_id":ObjectId, // MongoDB auto-generated unique ID "uuid":String, // Unique identifier for the point "lat":Number, // Latitude of the point "long":Number, // Longitude of the point "height":Number, // Height of the point "id_building":String } |
| Listing 2. Prototype of the buildings collection. |
| { "_id":ObjectId, // MongoDB auto-generated unique ID "uuid":String, // Unique identifier for the building "heights":[{"height":Number,"points":[String]}, ...// Array of UUIDs referencing points at the same quota ]// Array of height levels with points } |
2.4. Trajectory Precomputation Using VG
- Obstacles are approximated with polygons.
- The minimum turn radius is shorter than any obstacle edge and the distance between the points A/B and any obstacle vertex.
- The starting and target heading and are locally obtained using a smoothing procedure with a negligible increase in the total path length.
2.5. Ant Colony Optimization for CVRP
- The total demand served in each route must not exceed the UAV capacity Q:
- Each target must be visited exactly once.
| Algorithm 1: Ant Colony Optimization for CVRP. |
 |
2.6. Model Predictive Control for UAV Trajectory Tracking
- is the state vector, including position and velocity ,
- is the control input vector representing the accelerations,
- and are the system matrices:
3. Results
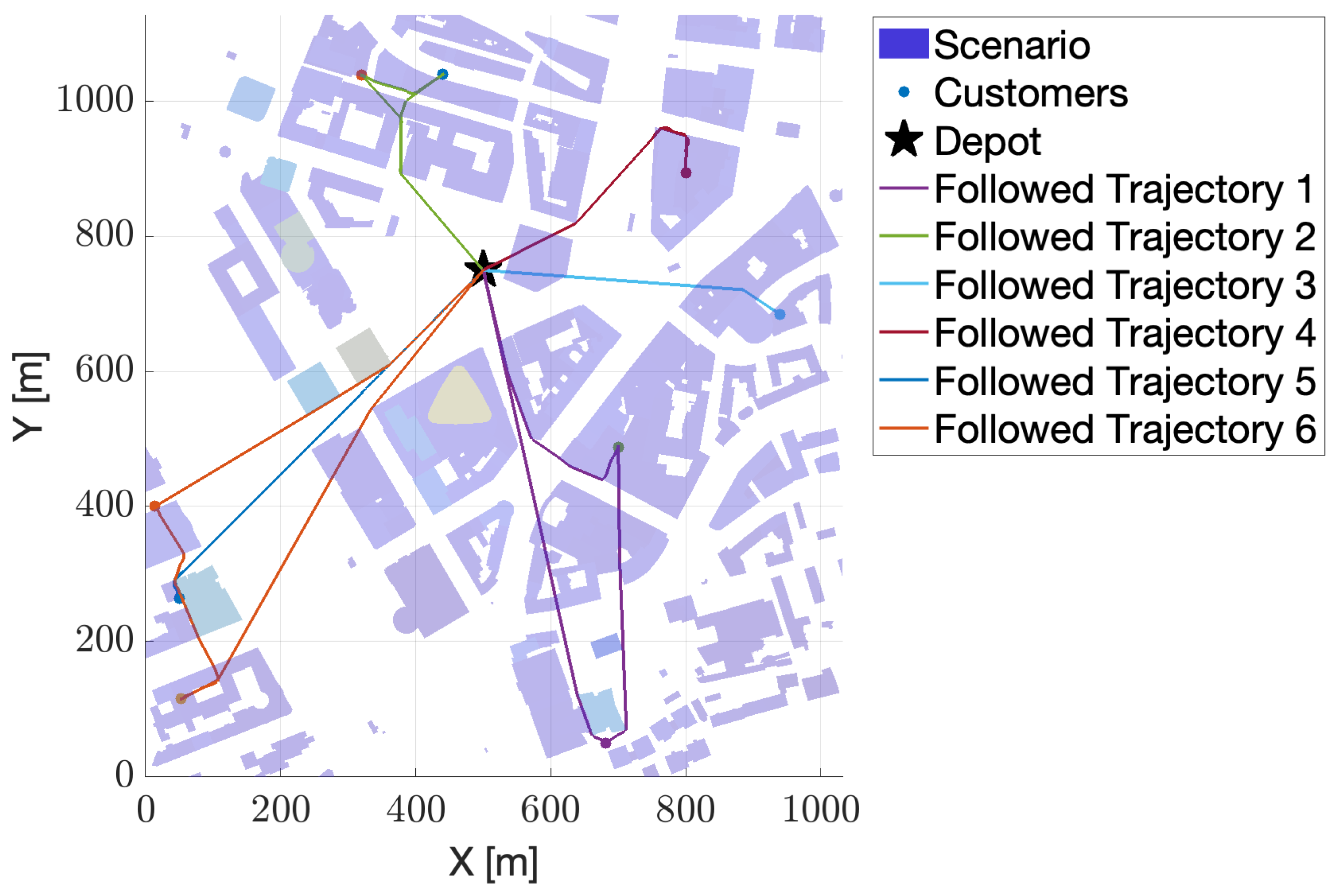
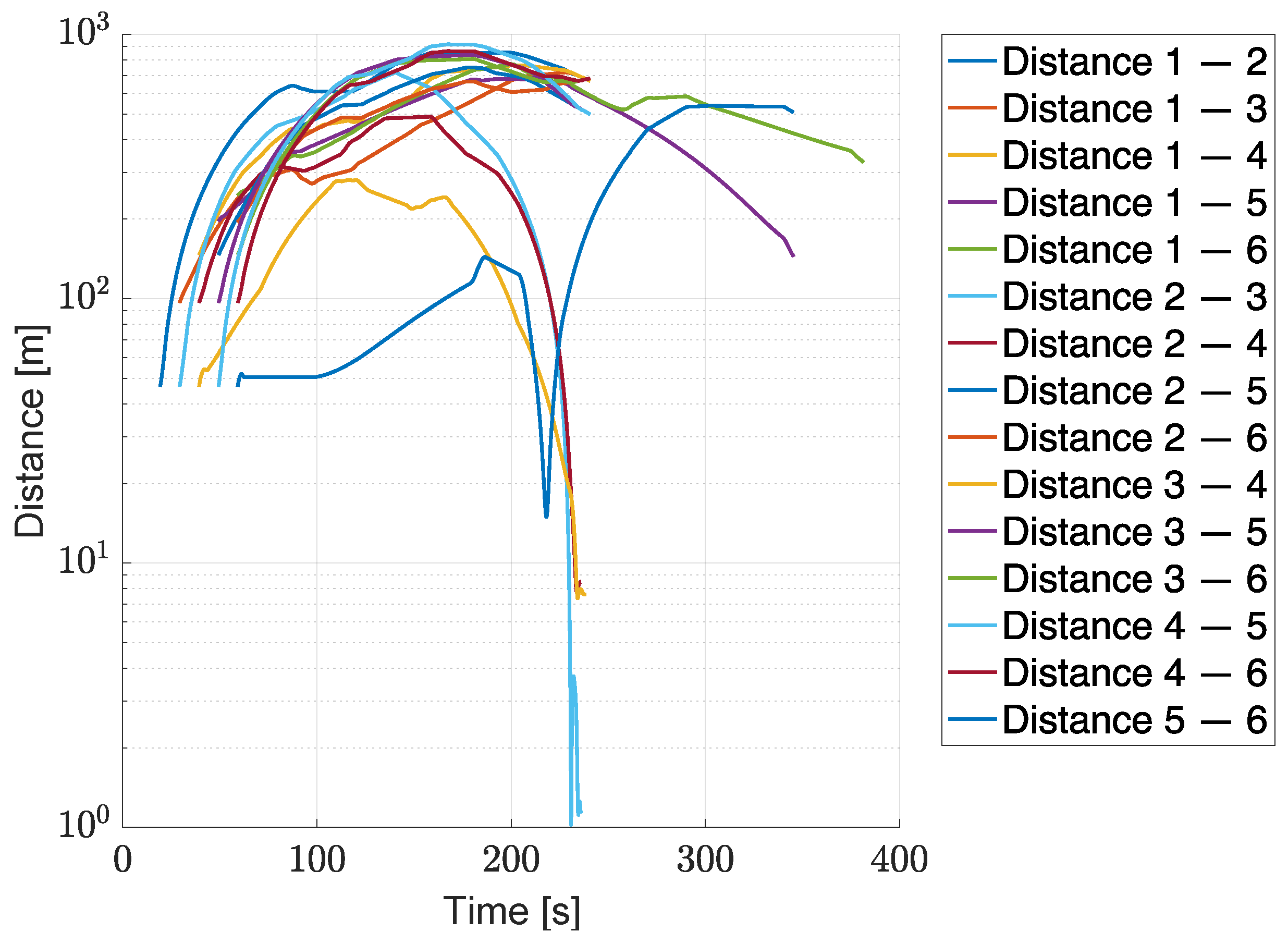
3.1. Test Case #1
3.2. Test Case #2
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Identification of Connected Points
| Algorithm A1: Retrieve Points and Connected Buildings |
 |
Appendix B. RVG Algorithm
| Algorithm A2: Pseudo-code for the RVG graph generation |
 |
References
- Kamienski, C.; Zyrianoff, I.; Bittencourt, L.F.; Di Felice, M. IoTinuum: The IoT Computing Continuum. In Proceedings of the 2024 20th International Conference on Distributed Computing in Smart Systems and the Internet of Things (DCOSS-IoT), Abu Dhabi, United Arab Emirates, 29 April–1 May 2024; IEEE: New York, NY, USA, 2024; pp. 732–739. [Google Scholar]
- Milojicic, D. The edge-to-cloud continuum. Computer 2020, 53, 16–25. [Google Scholar] [CrossRef]
- Qubaa, A.R.; Hamdon, A.N. Smart Cities and The UAVs Applications. A Review Of The Ongoing Research in The UAVs Unit. J. Port Sci. Res. 2023, 6, 136–147. [Google Scholar] [CrossRef]
- Huang, F.; Zhang, X.; Su, X. Optimization of Drone Delivery Routes for E-commerce in Urban Areas. J. Eng. Sci. Technol. Rev. 2024, 17, 165–174. [Google Scholar] [CrossRef]
- Deng, M.; Yang, Q.; Peng, Y. A real-time path planning method for urban low-altitude logistics UAVs. Sensors 2023, 23, 7472. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, S.; Hu, X. Cooperative path planning of UAVs & UGVs for a persistent surveillance task in urban environments. IEEE Internet Things J. 2020, 8, 4906–4919. [Google Scholar]
- Ferraro, A.; Scordamaglia, V. Coordinated trajectory planning for ground-based multi-robot systems in exploration and surveillance missions. In Proceedings of the 2023 IEEE International Workshop on Technologies for Defense and Security (TechDefense), Rome, Italy, 20–22 November 2023; IEEE: New York, NY, USA, 2023; pp. 131–136. [Google Scholar]
- Bu, Y.; Yan, Y.; Yang, Y. Advancement challenges in UAV swarm formation control: A comprehensive review. Drones 2024, 8, 320. [Google Scholar] [CrossRef]
- Musliman, I.A.; Rahman, A.A.; Coors, V. Implementing 3D network analysis in 3D GIS. Int. Arch. ISPRS 2008, 913–918. [Google Scholar]
- De Filippis, L.; Guglieri, G.; Quagliotti, F. Path planning strategies for UAVS in 3D environments. J. Intell. Robot. Syst. 2012, 65, 247–264. [Google Scholar] [CrossRef]
- Chang, B.R.; Tsai, H.F.; Lyu, J.L. Drone-Aided Path Planning for Unmanned Ground Vehicle Rapid Traversing Obstacle Area. Electronics 2022, 11, 1228. [Google Scholar] [CrossRef]
- Lin, Y.; Saripalli, S. Path planning using 3D dubins curve for unmanned aerial vehicles. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; IEEE: New York, NY, USA, 2014; pp. 296–304. [Google Scholar]
- Véras, L.G.; Medeiros, F.L.; Guimarães, L.N. Rapidly exploring Random Tree* with a sampling method based on Sukharev grids and convex vertices of safety hulls of obstacles. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419825941. [Google Scholar] [CrossRef]
- Eun, Y.; Bang, H. Cooperative control of multiple unmanned aerial vehicles using the potential field theory. J. Aircr. 2006, 43, 1805–1814. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, J. The three-dimension path planning of UAV based on improved artificial potential field in dynamic environment. In Proceedings of the 2013 5th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), Washington, DC, USA, 26–27 August 2013; IEEE: New York, NY, USA, 2013; Volume 2, pp. 144–147. [Google Scholar]
- Kitamura, Y.; Tanaka, T.; Kishino, F.; Yachida, M. 3-D path planning in a dynamic environment using an octree and an artificial potential field. In Proceedings of the 1995 IEEE/RSJ International Conference on Intelligent Robots and Systems. Human Robot Interaction and Cooperative Robots, Pittsburgh, PA, USA, 5–9 August 2024; IEEE: New York, NY, USA, 1995; Volume 2, pp. 474–481. [Google Scholar]
- Roberge, V.; Tarbouchi, M.; Labonté, G. Fast Genetic Algorithm Path Planner for Fixed-Wing Military UAV Using GPU. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2105–2117. [Google Scholar] [CrossRef]
- Chai, R.; Tsourdos, A.; Savvaris, A.; Chai, S.; Xia, Y. Solving Constrained Trajectory Planning Problems Using Biased Particle Swarm Optimization. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1685–1701. [Google Scholar] [CrossRef]
- Belge, E.; Altan, A.; Hacıoğlu, R. Metaheuristic optimization-based path planning and tracking of quadcopter for payload hold-release mission. Electronics 2022, 11, 1208. [Google Scholar] [CrossRef]
- Jia, Y.; Zhou, S.; Zeng, Q.; Li, C.; Chen, D.; Zhang, K.; Liu, L.; Chen, Z. The UAV Path Coverage Algorithm Based on the Greedy Strategy and Ant Colony Optimization. Electronics 2022, 11, 2667. [Google Scholar] [CrossRef]
- Mazzeo, S.; Loiseau, I. An ant colony algorithm for the capacitated vehicle routing. Electron. Notes Discret. Math. 2004, 18, 181–186. [Google Scholar] [CrossRef]
- Fuellerer, G.; Doerner, K.F.; Hartl, R.F.; Iori, M. Ant colony optimization for the two-dimensional loading vehicle routing problem. Comput. Oper. Res. 2009, 36, 655–673. [Google Scholar] [CrossRef]
- Huang, S.H.; Huang, Y.H.; Blazquez, C.A.; Chen, C.Y. Solving the vehicle routing problem with drone for delivery services using an ant colony optimization algorithm. Adv. Eng. Inform. 2022, 51, 101536. [Google Scholar] [CrossRef]
- Gu, Q.; Fan, T.; Pan, F.; Zhang, C. A vehicle-UAV operation scheme for instant delivery. Comput. Ind. Eng. 2020, 149, 106809. [Google Scholar] [CrossRef]
- Kuriki, Y.; Namerikawa, T. Consensus-based cooperative formation control with collision avoidance for a multi-UAV system. In Proceedings of the 2014 American Control Conference (ACC), Portland, OR, USA, 4–6 June 2014; IEEE: New York, NY, USA, 2014; pp. 2077–2082. [Google Scholar]
- Ren, W.; Beard, R.W. Distributed Consensus in Multi-Vehicle Cooperative Control; Springer: London, UK, 2008; Volume 27. [Google Scholar]
- Ariola, M.; Mattei, M.; D’Amato, E.; Notaro, I.; Tartaglione, G. Model predictive control for a swarm of fixed wing uavs. In Proceedings of the 30th Congress of the International Council of the Aeronautical Sciences, ICAS, 2016, Daejeon, Republic of Korea, 25–30 September 2016. [Google Scholar]
- Franze, G.; Mattei, M.; Ollio, L.; Scordamaglia, V. A robust constrained model predictive control scheme for norm-bounded uncertain systems with partial state measurements. Int. J. Robust Nonlinear Control 2019, 29, 6105–6125. [Google Scholar] [CrossRef]
- Franzè, G.; Mattei, M.; Ollio, L.; Scordamaglia, V. A Norm-Bounded based MPC strategy for uncertain systems under partial state availability. arXiv 2018, arXiv:1807.07819. [Google Scholar]
- Zhang, H.; Xin, B.; Dou, L.H.; Chen, J.; Hirota, K. A review of cooperative path planning of an unmanned aerial vehicle group. Front. Inf. Technol. Electron. Eng. 2020, 21, 1671–1694. [Google Scholar] [CrossRef]
- Beard, R.W.; McLain, T.W.; Goodrich, M.A.; Anderson, E.P. Coordinated target assignment and intercept for unmanned air vehicles. IEEE Trans. Robot. Autom. 2002, 18, 911–922. [Google Scholar] [CrossRef]
- Qie, H.; Shi, D.; Shen, T.; Xu, X.; Li, Y.; Wang, L. Joint optimization of multi-UAV target assignment and path planning based on multi-agent reinforcement learning. IEEE Access 2019, 7, 146264–146272. [Google Scholar] [CrossRef]
- Chen, X.; Lao, S.; Zhu, X.; Pan, Q.; Tang, J.; Zhang, P. Research on multi-UAV dynamic mission assignment method based on clustering algorithm. In Proceedings of the 2020 6th International Conference on Big Data and Information Analytics (BigDIA), Shenzhen, China, 4–6 December 2020; IEEE: New York, NY, USA, 2020; pp. 301–307. [Google Scholar]
- Balanji, H.M.; Yanmaz, E. Priority-Based Dynamic Multi-UAV Positioning for Multi-Target Search and Connectivity. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024; IEEE: New York, NY, USA, 2024; pp. 1–6. [Google Scholar]
- Güven, I.; Yanmaz, E. Maintaining connectivity for multi-UAV multi-target search using reinforcement learning. In Proceedings of the Int’l ACM Symposium on Design and Analysis of Intelligent Vehicular Networks and Applications, New York, NY, USA, 30 October–3 November 2023; pp. 109–114. [Google Scholar]
- Westheider, J.; Rückin, J.; Popović, M. Multi-uav adaptive path planning using deep reinforcement learning. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023; IEEE: New York, NY, USA, 2023; pp. 649–656. [Google Scholar]
- Poudel, S.; Moh, S. Priority-aware task assignment and path planning for efficient and load-balanced multi-UAV operation. Veh. Commun. 2023, 42, 100633. [Google Scholar] [CrossRef]
- Liang, Z.; Li, Q.; Fu, G. Multi-UAV collaborative search and attack mission decision-making in unknown environments. Sensors 2023, 23, 7398. [Google Scholar] [CrossRef]
- Li, K.; Yan, X.; Han, Y. Multi-mechanism swarm optimization for multi-UAV task assignment and path planning in transmission line inspection under multi-wind field. Appl. Soft Comput. 2024, 150, 111033. [Google Scholar] [CrossRef]
- Kuru, K. Planning the future of smart cities with swarms of fully autonomous unmanned aerial vehicles using a novel framework. IEEE Access 2021, 9, 6571–6595. [Google Scholar] [CrossRef]
- Fernando, N.; Shrestha, S.; Loke, S.W.; Lee, K. On Edge-Fog-Cloud Collaboration and Reaping Its Benefits: A Heterogeneous Multi-Tier Edge Computing Architecture. Future Internet 2025, 17, 22. [Google Scholar] [CrossRef]
- Yazid, Y.; Ez-Zazi, I.; Guerrero-González, A.; El Oualkadi, A.; Arioua, M. UAV-enabled mobile edge-computing for IoT based on AI: A comprehensive review. Drones 2021, 5, 148. [Google Scholar] [CrossRef]
- McEnroe, P.; Wang, S.; Liyanage, M. A survey on the convergence of edge computing and AI for UAVs: Opportunities and challenges. IEEE Internet Things J. 2022, 9, 15435–15459. [Google Scholar] [CrossRef]
- Alharbi, H.A.; Yosuf, B.A.; Aldossary, M.; Almutairi, J.; Elmirghani, J.M. Energy efficient UAV-based service offloading over cloud-fog architectures. IEEE Access 2022, 10, 89598–89613. [Google Scholar] [CrossRef]
- Aldossary, M. Optimizing Task Offloading for Collaborative Unmanned Aerial Vehicles (UAVs) in Fog—Cloud Computing Environments. IEEE Access 2024, 12, 74698–74710. [Google Scholar] [CrossRef]
- Rezaee, M.R.; Hamid, N.A.W.A.; Hussin, M.; Zukarnain, Z.A. Fog Offloading and Task Management in IoT-Fog-Cloud Environment: Review of Algorithms, Networks and SDN Application. IEEE Access 2024, 12, 39058–39080. [Google Scholar] [CrossRef]
- Merlino, G.; Tricomi, G.; D’agati, L.; Benomar, Z.; Longo, F.; Puliafito, A. FaaS for IoT: Evolving Serverless towards Deviceless in I/Oclouds. Future Gener. Comput. Syst. 2024, 154, 189–205. [Google Scholar] [CrossRef]
- Tricomi, G.; Giacobbe, M.; Ficili, I.; Peditto, N.; Puliafito, A. Smart City as Cooperating Smart Areas: On the Way of Symbiotic Cyber–Physical Systems Environment. Sensors 2024, 24, 3108. [Google Scholar] [CrossRef]
- Pujol, V.C.; Raith, P.; Dustdar, S. Towards a new paradigm for managing computing continuum applications. In Proceedings of the 2021 IEEE Third International Conference on Cognitive Machine Intelligence (CogMI), Virtual Conference, 13–15 December 2021; IEEE: New York, NY, USA, 2021; pp. 180–188. [Google Scholar]
- D’Agati, L.; Longo, F.; Merlino, G.; Puliafito, A.; Tricomi, G. Enhancing UAV Operational Efficiency through Cloud Computing and Autopilot System Integration. In Proceedings of the 2024 IEEE International Conference on Smart Computing (SMARTCOMP), Osaka, Japan, 29 June–2 July; IEEE: New York, NY, USA, 2024; pp. 85–92. [Google Scholar]
- Tricomi, G.; D’Agati, L.; Arena, M.; Longo, F.; Merlino, G.; Puliafito, A.; Silvestri, S. On the way to distribute Compute Continuum Urban applications by deploying Clusters of Drones. In Proceedings of the 2024 34rd International Telecommunication Networks and Applications Conference, Sidney, Australia, 27–29 November 2024. [Google Scholar]
- Luo, C.; Nightingale, J.; Asemota, E.; Grecos, C. A UAV-cloud system for disaster sensing applications. In Proceedings of the 2015 IEEE 81st Vehicular Technology Conference (VTC Spring), Glasgow, UK, 11–14 May 2015; IEEE: New York, NY, USA, 2015; pp. 1–5. [Google Scholar]
- Mahmoud, S.Y.M.; Mohamed, N. Toward a cloud platform for UAV resources and services. In Proceedings of the 2015 IEEE Fourth Symposium on Network Cloud Computing and Applications (NCCA), Munich, Germany, 11–12 June 2015; IEEE: New York, NY, USA, 2015; pp. 23–30. [Google Scholar]
- Itkin, M.; Kim, M.; Park, Y. Development of cloud-based UAV monitoring and management system. Sensors 2016, 16, 1913. [Google Scholar] [CrossRef]
- Cheng, Z.; Gao, Z.; Liwang, M.; Huang, L.; Du, X.; Guizani, M. Intelligent task offloading and energy allocation in the UAV-aided mobile edge-cloud continuum. IEEE Netw. 2021, 35, 42–49. [Google Scholar] [CrossRef]
- Militano, L.; Arteaga, A.; Toffetti, G.; Mitton, N. The cloud-to-edge-to-IoT continuum as an enabler for search and rescue operations. Future Internet 2023, 15, 55. [Google Scholar] [CrossRef]
- Zeng, D.; Ansari, N.; Montpetit, M.J.; Schooler, E.M.; Tarchi, D. Guest editorial: In-network computing: Emerging trends for the edge-cloud continuum. IEEE Netw. 2021, 35, 12–13. [Google Scholar] [CrossRef]
- Salhaoui, M.; Guerrero-González, A.; Arioua, M.; Ortiz, F.J.; El Oualkadi, A.; Torregrosa, C.L. Smart industrial iot monitoring and control system based on UAV and cloud computing applied to a concrete plant. Sensors 2019, 19, 3316. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Li, X.; Wang, J.; Wei, F.; Yang, J. Reinforcement-Learning-Based Multi-UAV Cooperative Search for Moving Targets in 3D Scenarios. Drones 2024, 8, 378. [Google Scholar] [CrossRef]
- Su, K.; Qian, F. Multi-UAV cooperative searching and tracking for moving targets based on multi-agent reinforcement learning. Appl. Sci. 2023, 13, 11905. [Google Scholar] [CrossRef]
- Latombe, J.C. Robot Motion Planning; Springer Science & Business Media: New York, NY, USA, 2012; Volume 124. [Google Scholar]
- D’Amato, E.; Notaro, I.; Mattei, M. Optimal flight paths over essential visibility graphs. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018; IEEE: New York, NY, USA, 2018; pp. 708–714. [Google Scholar]
- Dubins, L.E. On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents. Am. J. Math. 1957, 79, 497–516. [Google Scholar] [CrossRef]
- Bassolillo, S.R.; D’amato, E.; Notaro, I.; Blasi, L.; Mattei, M. Decentralized mesh-based model predictive control for swarms of UAVs. Sensors 2020, 20, 4324. [Google Scholar] [CrossRef]
- Narasimha, K.V.; Kivelevitch, E.; Sharma, B.; Kumar, M. An ant colony optimization technique for solving min–max multi-depot vehicle routing problem. Swarm Evol. Comput. 2013, 13, 63–73. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| Number of Ants | 200 |
| Maximum number of epochs | 300 |
| Safety distance (m) | 1.00 |
| Maximum speed norm (m/s) | 15.00 |
| Minimum speed norm (m/s) | 0.00 |
| Maximum acceleration | |
| Cruise speed (m/s) | 5.00 |
| Vertical speed (for take-off and landing) (m/s) | 2.00 |
| Cruise altitude (m) | 20.00 |
| Simulation sampling time (s) | 0.10 |
| MPC prediction horizon | 10 |
| ID | x (m) | y (m) | Demand (kg) |
|---|---|---|---|
| (Depot) | 500 | 750 | 0 |
| 50 | 264 | 4 | |
| 14 | 400 | 3 | |
| 53 | 115 | 2 | |
| 682 | 50 | 1 | |
| 700 | 488 | 2 | |
| 940 | 684 | 3 | |
| 800 | 894 | 4 | |
| 440 | 1040 | 1 | |
| 320 | 1039 | 2 |
| 0.0 | 675.6 | 603.0 | 786.2 | 731.8 | 434.9 | 452.4 | 436.2 | 364.0 | 356.3 | |
| 675.6 | 0.0 | 151.7 | 195.5 | 687.7 | 739.8 | 1051.5 | 1105.5 | 900.3 | 891.7 | |
| 603.0 | 151.7 | 0.0 | 347.0 | 756.4 | 734.8 | 1005.8 | 1036.2 | 801.9 | 767.2 | |
| 786.2 | 195.5 | 347.0 | 0.0 | 632.3 | 765.2 | 1073.9 | 1213.8 | 1039.9 | 1032.7 | |
| 731.8 | 687.7 | 756.4 | 632.3 | 0.0 | 454.3 | 691.0 | 1008.7 | 1090.0 | 1075.2 | |
| 434.9 | 739.8 | 734.8 | 765.2 | 454.3 | 0.0 | 313.6 | 583.3 | 718.4 | 780.7 | |
| 452.4 | 1051.5 | 1005.8 | 1073.9 | 691.0 | 313.6 | 0.0 | 348.9 | 654.3 | 758.7 | |
| 436.2 | 1105.5 | 1036.2 | 1213.8 | 1008.7 | 583.3 | 348.9 | 0.0 | 426.9 | 554.9 | |
| 364.0 | 900.3 | 801.9 | 1039.9 | 1090.0 | 718.4 | 654.3 | 426.9 | 0.0 | 133.4 | |
| 356.3 | 891.7 | 767.2 | 1032.7 | 1075.2 | 780.7 | 758.7 | 554.9 | 133.4 | 0.0 |
| UAV | Assigned Targets Number | Route Length (m) |
|---|---|---|
| UAV 1 | 1621 | |
| UAV 2 | 854 | |
| UAV 3 | 905 | |
| UAV 4 | 872 | |
| UAV 5 | 1351 | |
| UAV 6 | 1736 |
| Parameter | Value |
|---|---|
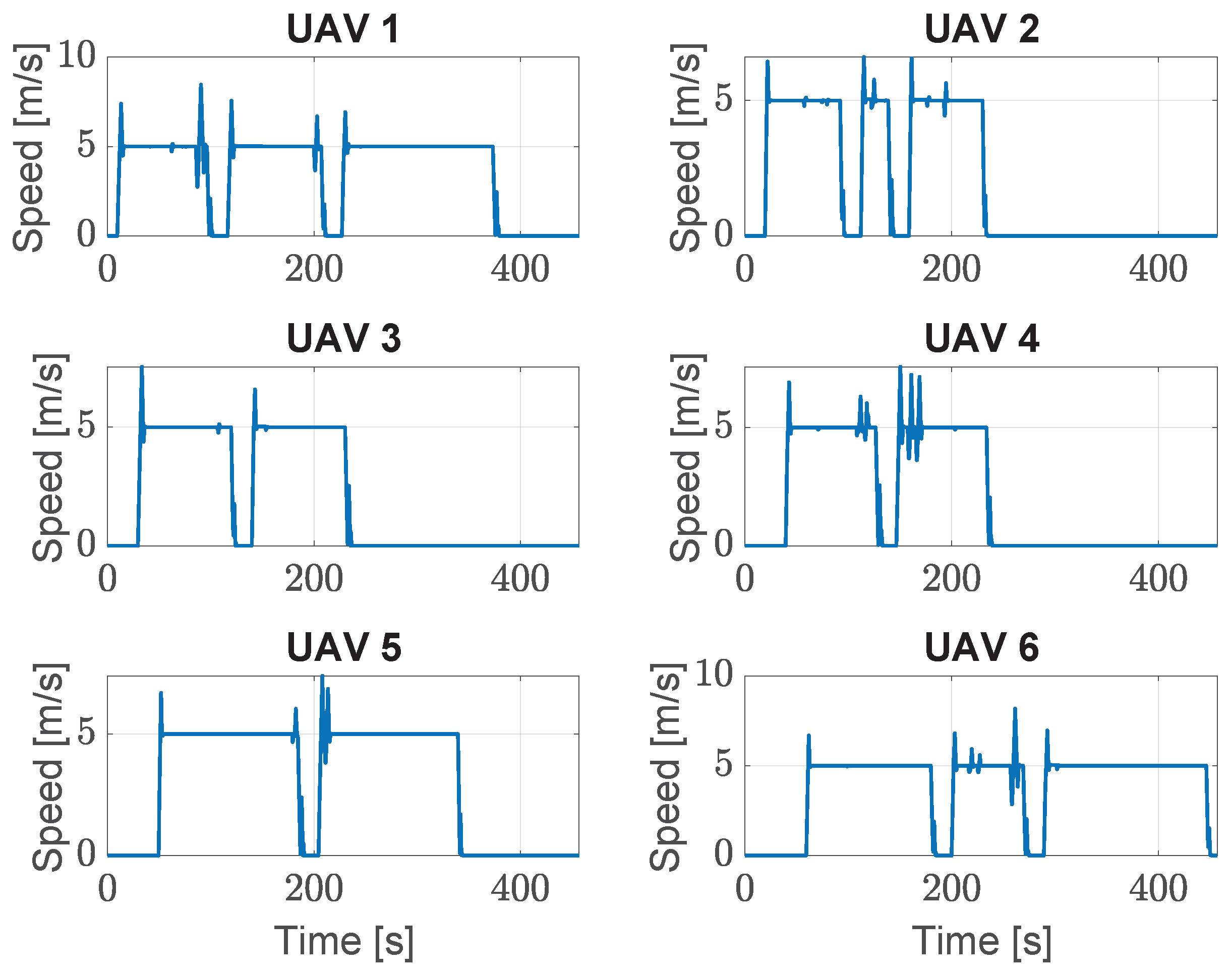
| Maximum tracking error (m) | 5.36 |
| Average tracking error (m) | 0.09 |
| Maximum horizontal speed (m/s) | 8.45 |
| Average horizontal speed (m/s) | 4.71 |
| Minimum mutual distance (m) | 1.02 |
| Minimum planned mutual distance (m) | 0.59 |
| Minimum flight time (s) | 221 |
| Average flight time (s) | 301 |
| Maximum flight time (s) | 413 |
| Planning Phase | Time to Complete (s) |
|---|---|
| RVG Graph | 261 |
| CVRP Graph | 0.15 |
| ACO Solution | 0.92 |
| Parameter | Value |
|---|---|
| Maximum Length (m) | 1435 |
| Minimum Length (m) | 4.639 |
| Maximum n. of edges | 13 |
| Minimum n. of edges | 2 |
| Average n. of edges | 4.68 |
| Parameter | Value |
|---|---|
| N. of needed UAVs | 27 |
| Overall Length (m) | 36,019 |
| Max route length (m) | 2108 |
| Min route length (m) | 143 |
| Average route length (m) | 1334 |
| Planning Phase | Time to Plan (s) |
|---|---|
| RVG Graph | 549 |
| CVRP Graph | 35 |
| ACO Solution | 104 |
| Parameter | Value |
|---|---|
| Maximum tracking error (m) | 21.37 |
| Average tracking error (m) | 0.11 |
| Maximum horizontal speed (m/s) | 11.08 |
| Average horizontal speed (m/s) | 4.52 |
| Minimum mutual distance (m) | 1.05 |
| Minimum planned mutual distance (m) | 0.01 |
| Minimum flight time (s) | 137 |
| Average flight time (s) | 367 |
| Maximum flight time (s) | 529 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bassolillo, S.R.; D’Amato, E.; Notaro, I.; D’Agati, L.; Merlino, G.; Tricomi, G. Bridging ACO-Based Drone Logistics and Computing Continuum for Enhanced Smart City Applications. Drones 2025, 9, 368. https://doi.org/10.3390/drones9050368
Bassolillo SR, D’Amato E, Notaro I, D’Agati L, Merlino G, Tricomi G. Bridging ACO-Based Drone Logistics and Computing Continuum for Enhanced Smart City Applications. Drones. 2025; 9(5):368. https://doi.org/10.3390/drones9050368
Chicago/Turabian StyleBassolillo, Salvatore Rosario, Egidio D’Amato, Immacolata Notaro, Luca D’Agati, Giovanni Merlino, and Giuseppe Tricomi. 2025. "Bridging ACO-Based Drone Logistics and Computing Continuum for Enhanced Smart City Applications" Drones 9, no. 5: 368. https://doi.org/10.3390/drones9050368
APA StyleBassolillo, S. R., D’Amato, E., Notaro, I., D’Agati, L., Merlino, G., & Tricomi, G. (2025). Bridging ACO-Based Drone Logistics and Computing Continuum for Enhanced Smart City Applications. Drones, 9(5), 368. https://doi.org/10.3390/drones9050368












