Pigeon-Inspired UAV Swarm Control and Planning Within a Virtual Tube
Abstract
1. Introduction
- Curved virtual tube planning based on pigeon-inspired optimization (PIO): A novel virtual tube planning method is proposed using PIO, ensuring obstacle-free paths for UAV swarms. This approach adapts better to narrow or obstacle-dense environments than traditional methods, avoiding excessively narrow tubes.
- Distributed swarm controller inspired by pigeon flocking: A distributed controller based on pigeon flocking hierarchical behavior is designed to guide UAVs within the virtual tube. It guarantees collision avoidance, safe passage, and adherence to the tube, addressing scalability and deadlock issues in complex scenarios.
- Integrated framework combining pigeon flocking behaviors and virtual tube methods: This work integrates pigeons’ flocking properties with virtual tube techniques, offering a unified framework for both planning and control. It enhances navigation efficiency and safety for large-scale UAV swarms in cluttered environments.
2. Preliminaries and Problem Formulation
2.1. UAV Modeling
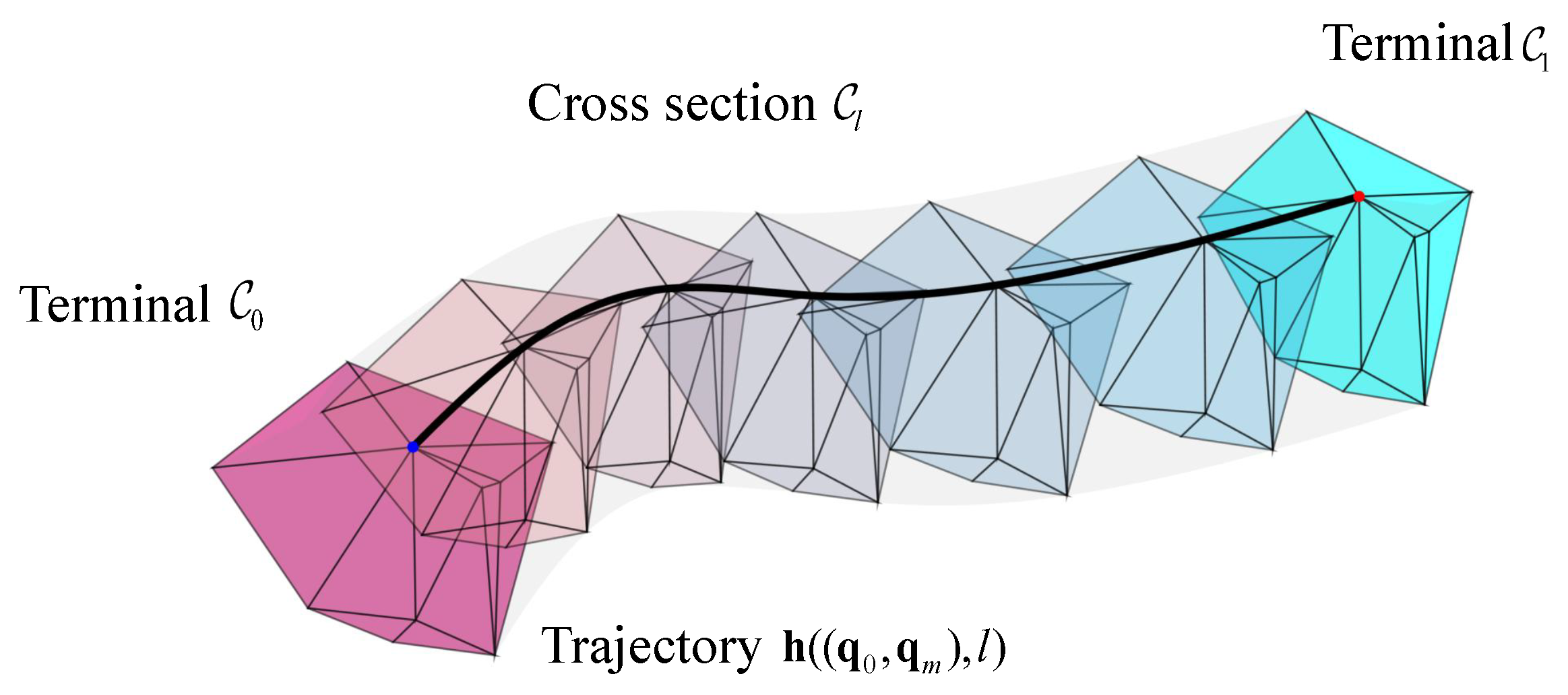
2.2. Virtual Tube Model
2.3. Problem Formulation
- Virtual tube planning: Denote as free space, where is the configuration space and is the obstacle space. The virtual tube planning method aims to find the center path (generating curve) in free space, and the radius of the virtual tube is determined, satisfying the requirement of smoothness and width.
- Velocity command design: Based on the assumption above, design the velocity command based on the pigeons flocking behaviors. During the passing-through process, all UAVs should avoid collisions with each other and stay within the curved virtual tube.
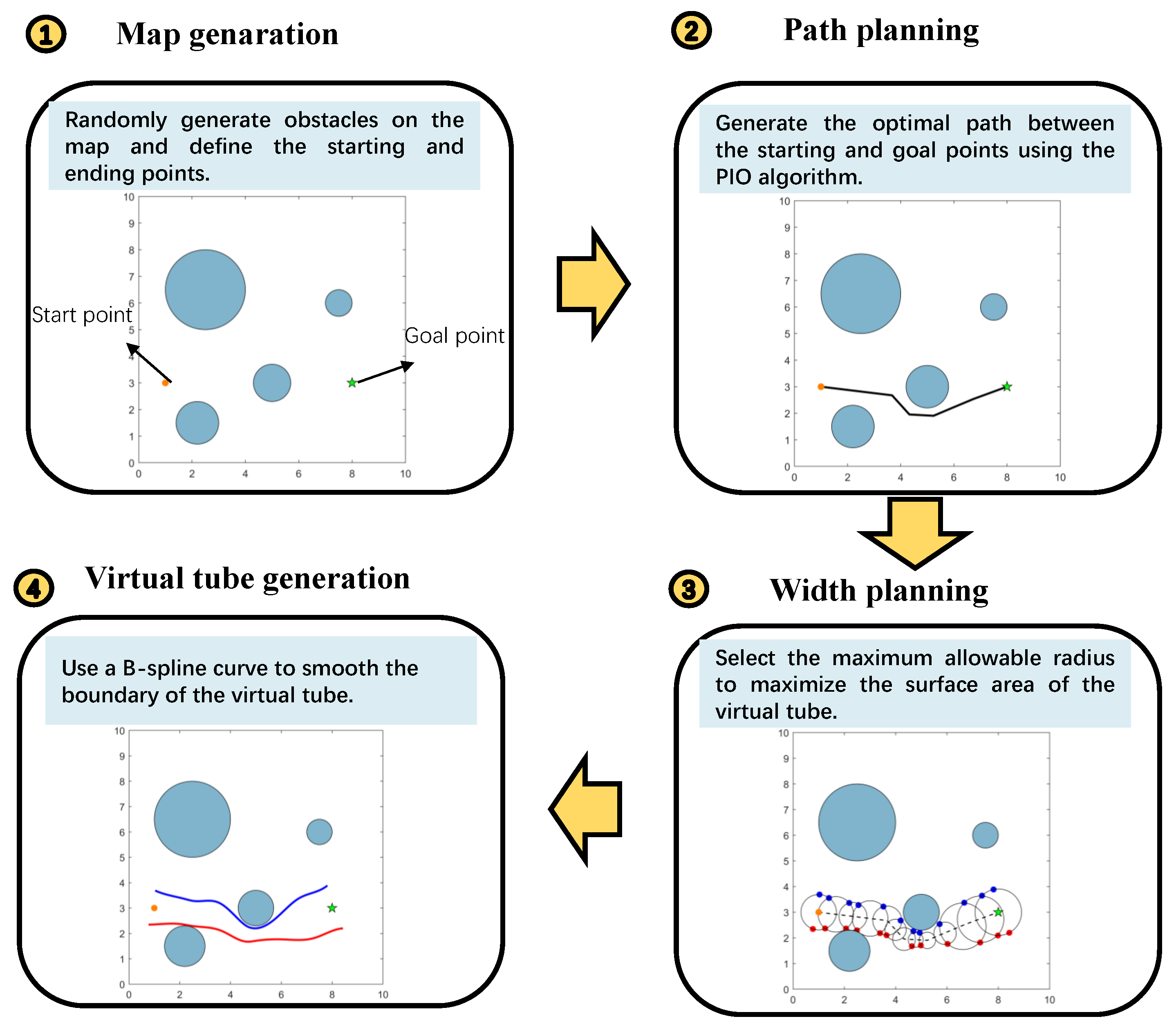
3. Virtual Tube Planning Based on Pigeon-Inspired Optimization
4. Pigeon-Inspired Velocity Command Design for UAV Swarm
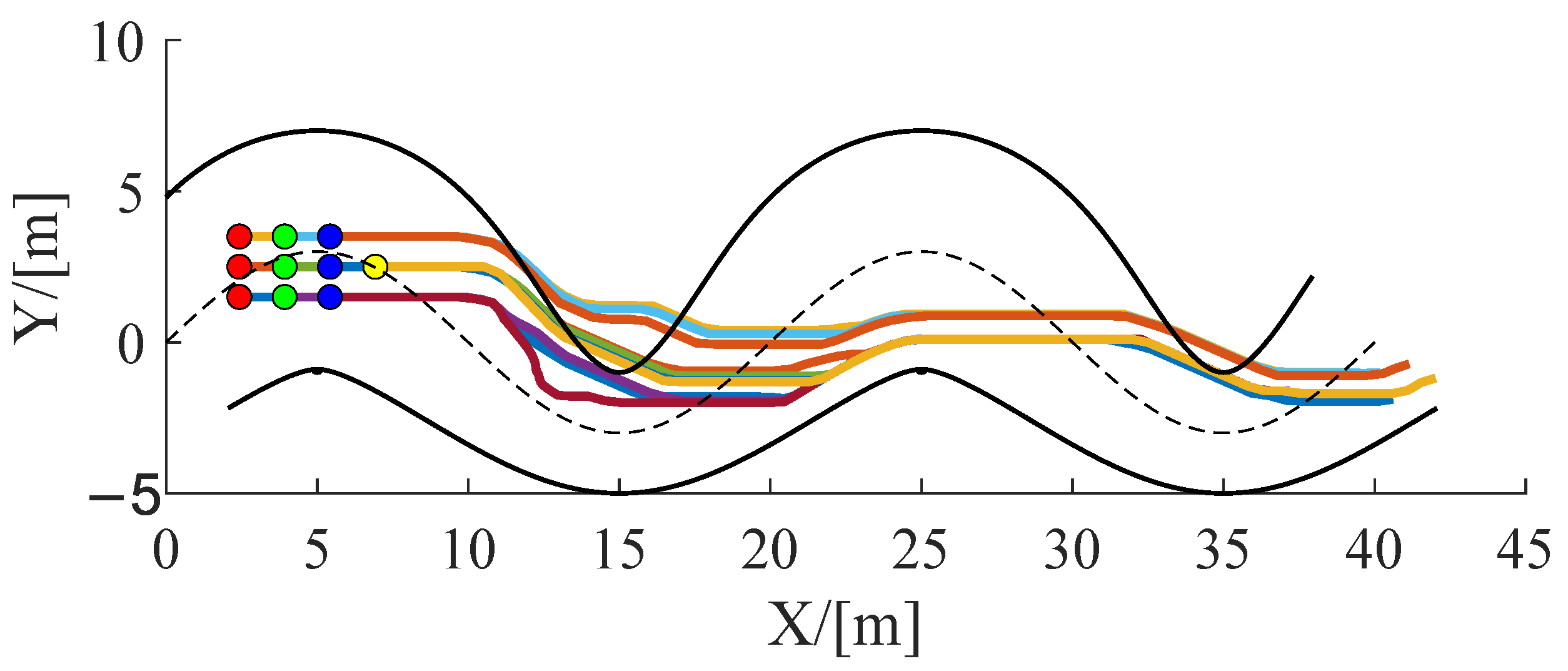
4.1. Pigeon Flocking Hierarchical Strategies
4.2. Controller Design
5. Simulation Results
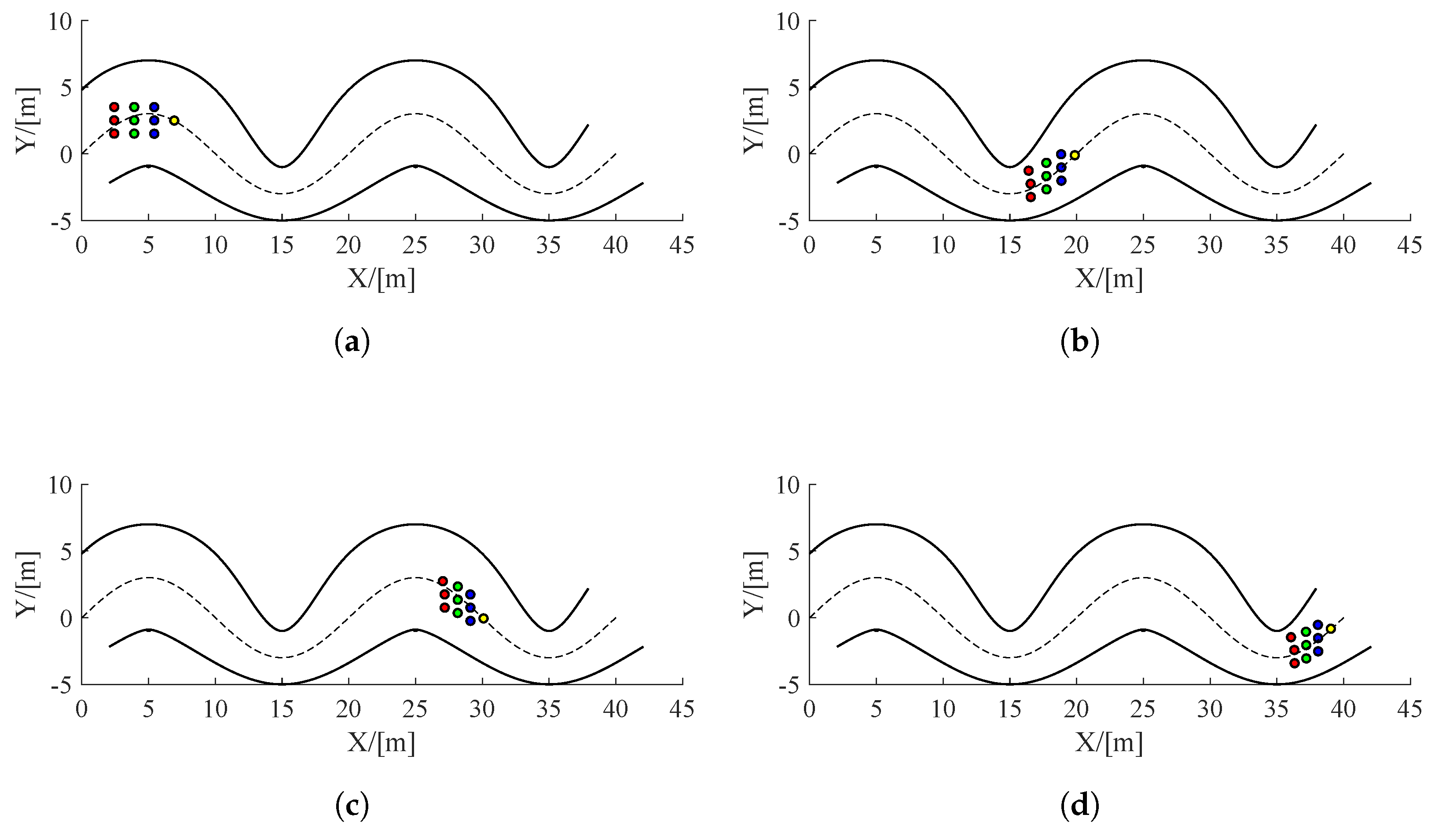
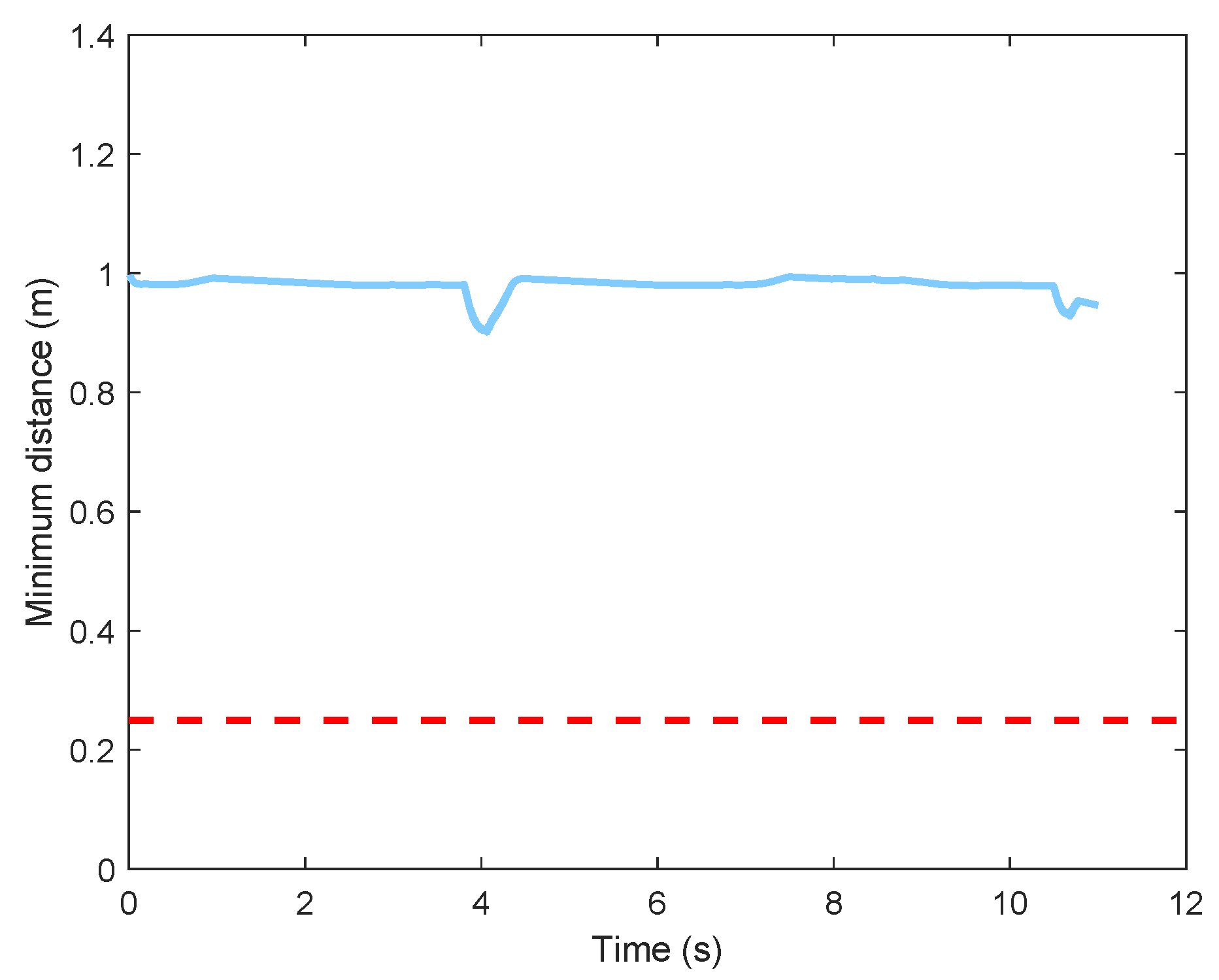
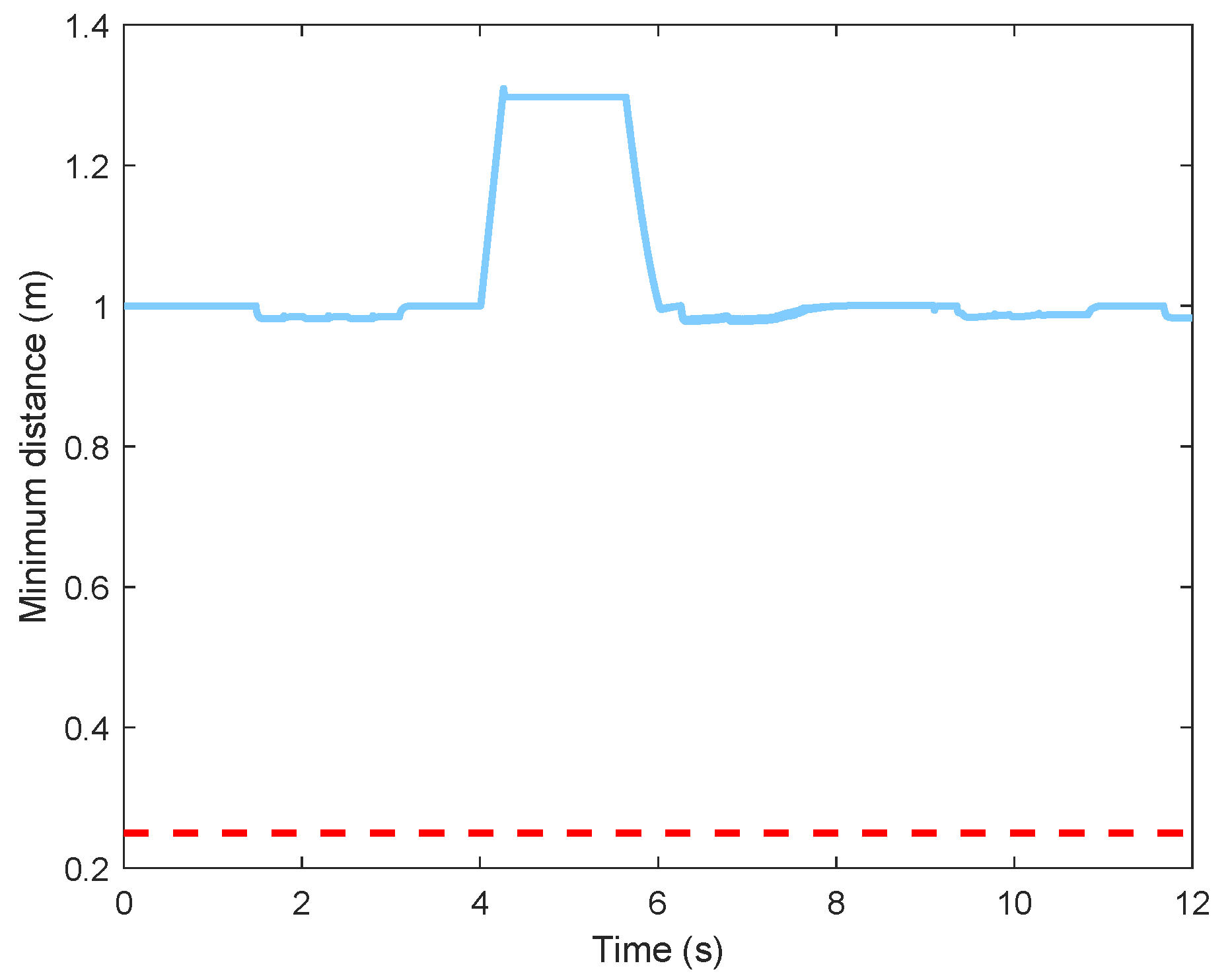
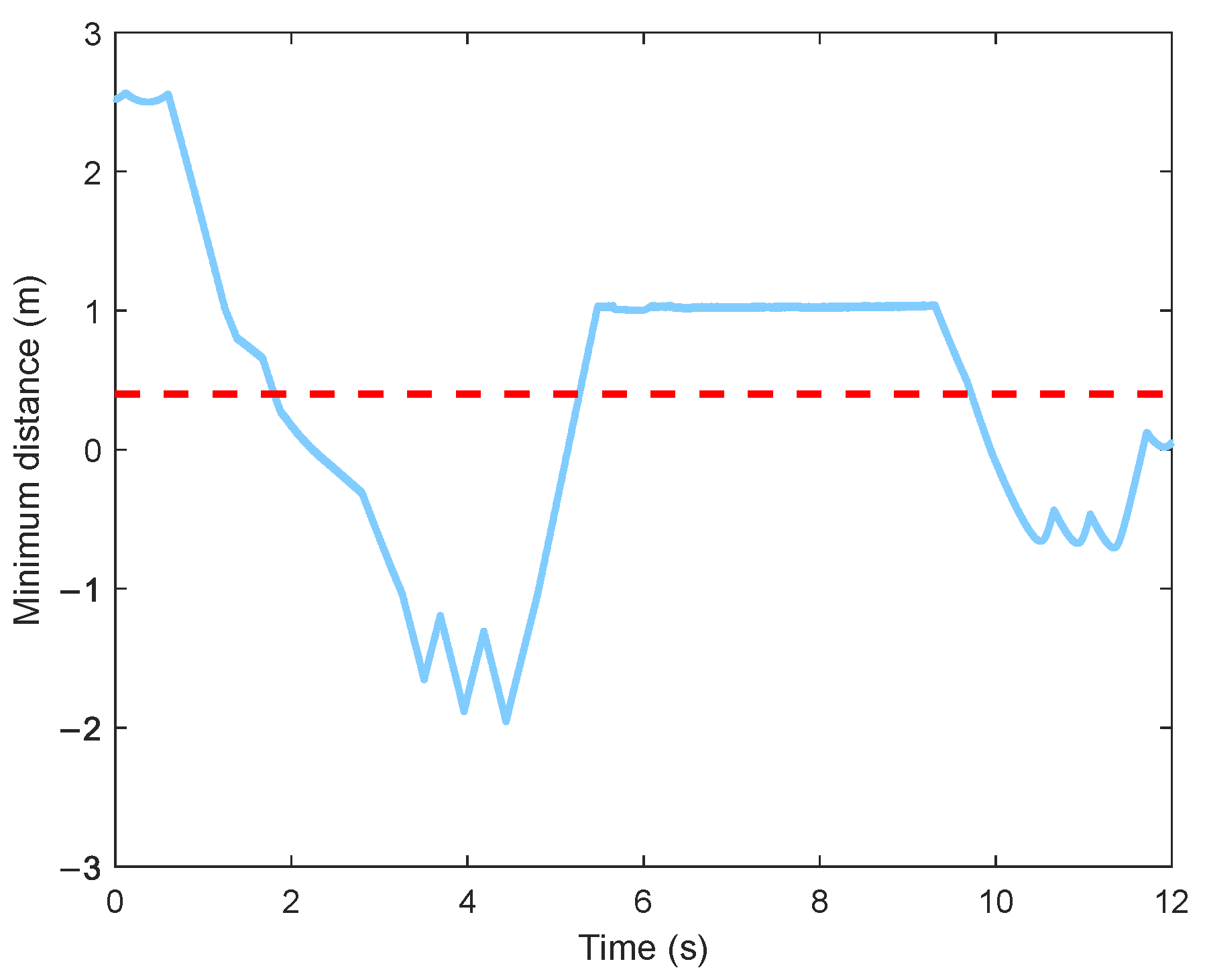
5.1. UAV Swarm Control
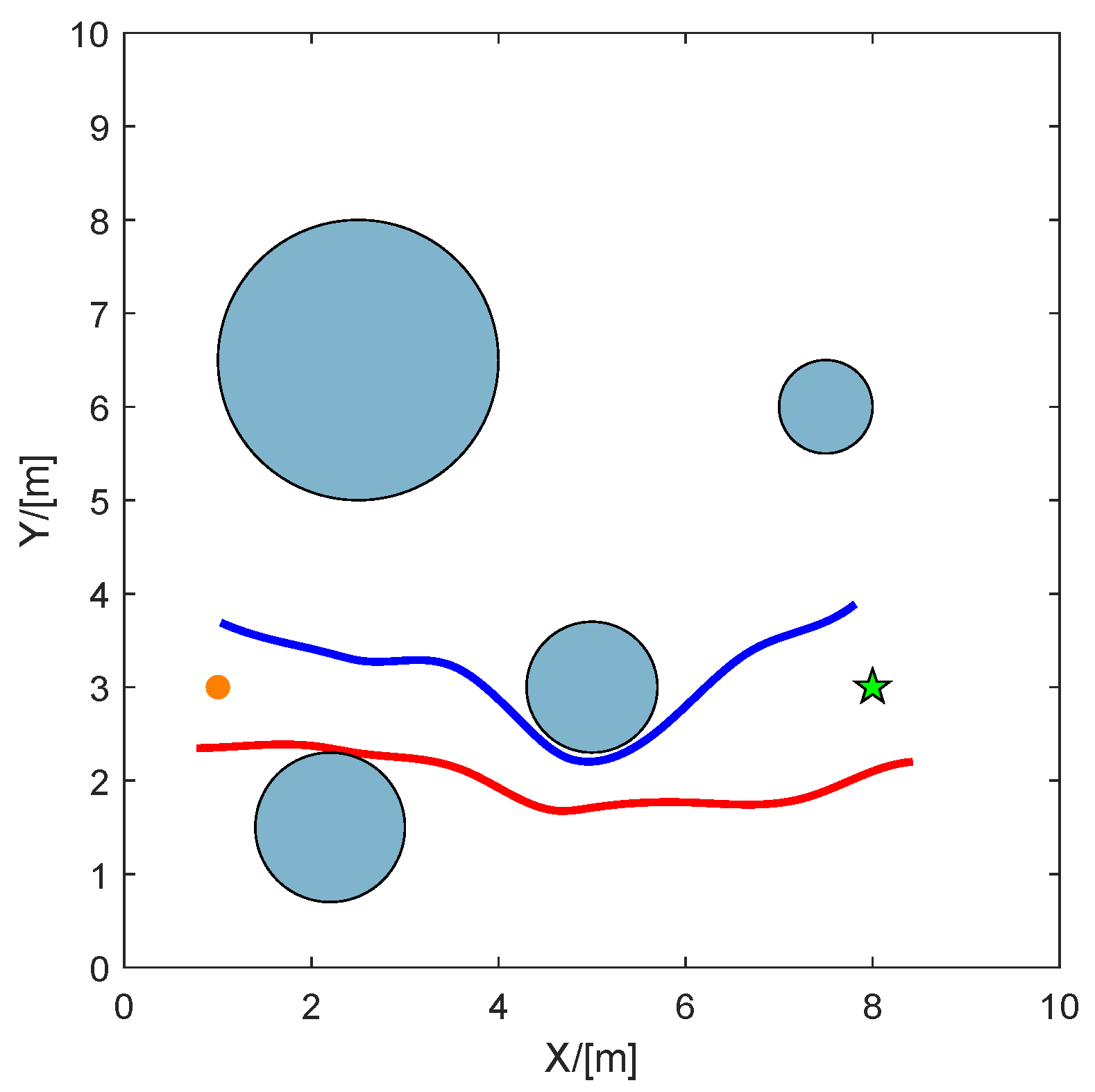
5.2. Virtual Tube Planning
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chung, S.; Paranjape, A.A.; Dames, P.; Shen, S.; Kumar, V. A survey on aerial swarm robotics. IEEE Trans. Robot. 2018, 34, 837–855. [Google Scholar] [CrossRef]
- Qi, J.; Guo, J.; Wang, M.; Wu, C.; Ma, Z. Formation tracking and obstacle avoidance for multiple quadrotors with static and dynamic obstacles. IEEE Robot. Autom. Lett. 2022, 7, 1713–1720. [Google Scholar] [CrossRef]
- Luis, C.; Schoellig, A. Trajectory generation for multiagent point-to-point transitions via distributed model predictive control. IEEE Robot. Autom. Lett. 2019, 4, 375–382. [Google Scholar] [CrossRef]
- Rezende, A.; Goncalves, V.; Pimenta, L. Constructive time-varying vector fields for robot navigation. IEEE Trans. Robot. 2021, 38, 852–867. [Google Scholar] [CrossRef]
- Quan, Q.; Fu, R.; Li, M.; Wei, D.; Gao, Y.; Cai, K.-Y. Practical distributed control for VTOL UAVs to pass a virtual tube. IEEE Trans. Intell. Veh. 2022, 7, 342–353. [Google Scholar] [CrossRef]
- Wang, L.; Ames, A.; Egerstedt, M. Safety barrier certificates for collisions-free multirobot systems. IEEE Trans. Robot. 2017, 33, 661–674. [Google Scholar] [CrossRef]
- Vásárhelyi, G.; Virágh, C.; Somorjai, G.; Nepusz, T.; Eiben, A.; Vicsek, T. Optimized flocking of autonomous drones in confined environments. Sci. Robot. 2018, 3, eaat3536. [Google Scholar] [CrossRef]
- Quan, Q.; Gao, Y.; Bai, C. Distributed control for a robotic swarm to pass through a curve virtual tube. Robot. Auton. Syst. 2023, 162, 104368. [Google Scholar] [CrossRef]
- Mao, P.; Quan, Q. Making robotics swarm flow more smoothly: A regular virtual tube model. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 4498–4504. [Google Scholar]
- Mao, P.; Fu, R.; Quan, Q. Optimal virtual tube planning and control for swarm robotics. Int. J. Robot. Res. 2024, 43, 602–627. [Google Scholar] [CrossRef]
- Qiu, H.; Duan, H. Pigeon interaction mode switch-based UAV distributed flocking control under obstacle environments. ISA Trans. 2017, 71, 93–102. [Google Scholar] [CrossRef]
- Lin, Z.; Wu, K.; Shen, R.; Yu, X.; Huang, S. An efficient and accurate A-star algorithm for autonomous vehicle path planning. IEEE Trans. Veh. Technol. 2024, 73, 9003–9008. [Google Scholar] [CrossRef]
- Prasad, N.; Ramkumar, B. 3-D deployment and trajectory planning for relay based UAV assisted cooperative communication for emergency scenarios using Dijkstra’s algorithm. IEEE Trans. Veh. Technol. 2023, 72, 5049–5063. [Google Scholar] [CrossRef]
- Wang, J.; Chi, W.; Li, C.; Wang, C.; Meng, M. Neural RRT*: Learning-based optimal path planning. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1748–1758. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, J.; Ling, K.; Zhang, W. Real-Time Path Planning for Autonomous UAVs: An Event-Triggered Multimodal Adaptive Pigeon-Inspired Optimization Approach. IEEE Trans. Aerosp. Electron. Syst. 2025. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, L.; Cai, B.; Liang, Y. Unified path planning for composite UAVs via Fermat point-based grouping particle swarm optimization. Aerosp. Sci. Technol. 2024, 148, 109088. [Google Scholar] [CrossRef]
- Wu, L.; Huang, X.; Cui, J.; Liu, C.; Xiao, W. Modified adaptive ant colony optimization algorithm and its application for solving path planning of mobile robot. Expert Syst. Appl. 2023, 215, 119410. [Google Scholar] [CrossRef]
- Zheng, J.; Ding, M.; Sun, L.; Liu, H. Distributed stochastic algorithm based on enhanced genetic algorithm for path planning of multi-UAV cooperative area search. IEEE Trans. Intell. Transp. Syst. 2023, 24, 8290–8303. [Google Scholar] [CrossRef]
- Duan, H.; Qiao, P. Pigeon-inspired optimization: A new swarm intelligence optimizer for air robot path planning. Int. J. Intell. Comput. Cybern. 2014, 7, 24–37. [Google Scholar] [CrossRef]
- Zhang, D.; Duan, H. Social-class pigeon-inspired optimization and time stamp segmentation for multi-UAV cooperative path planning. Neurocomputing 2018, 313, 229–246. [Google Scholar] [CrossRef]
- Duan, H.; Zhao, J.; Deng, Y.; Shi, Y.; Ding, X. Dynamic discrete pigeon-inspired optimization for multi-UAV cooperative search-attack mission planning. IEEE Trans. Aerosp. Electron. Syst. 2020, 57, 706–720. [Google Scholar] [CrossRef]
- Song, W.; Gao, Y.; Quan, Q. Speed and density planning for a speed-constrained robot swarm through a virtual tube. IEEE Robot. Autom. Lett. 2024, 9, 10628–10635. [Google Scholar] [CrossRef]
- Zhao, J.; Duan, H.; Chen, L.; Huo, M. Leadership hierarchy-based formation control via adaptive chaotic pigeon-inspired optimization. IFAC-PapersOnLine 2020, 53, 9348–9353. [Google Scholar] [CrossRef]

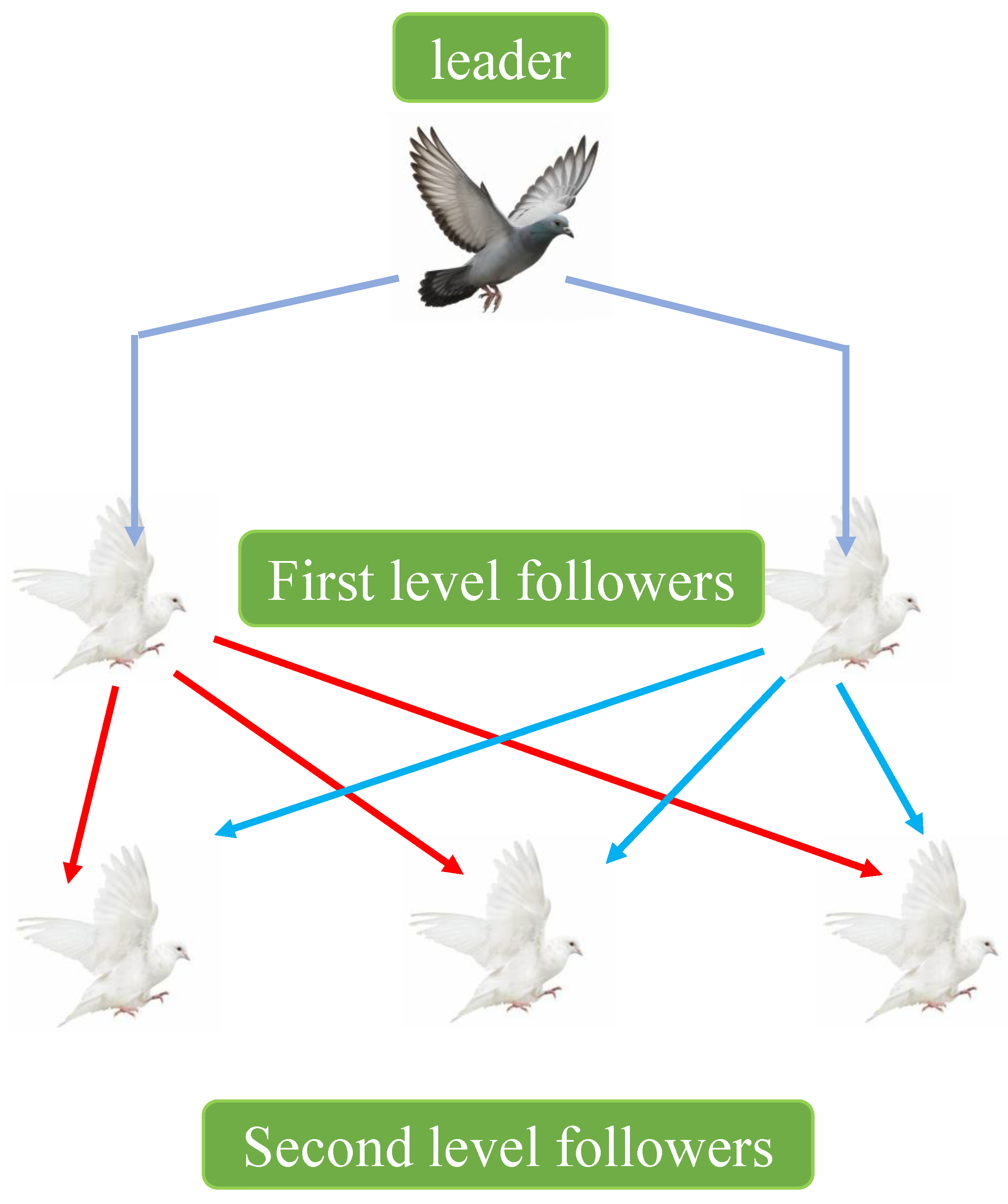



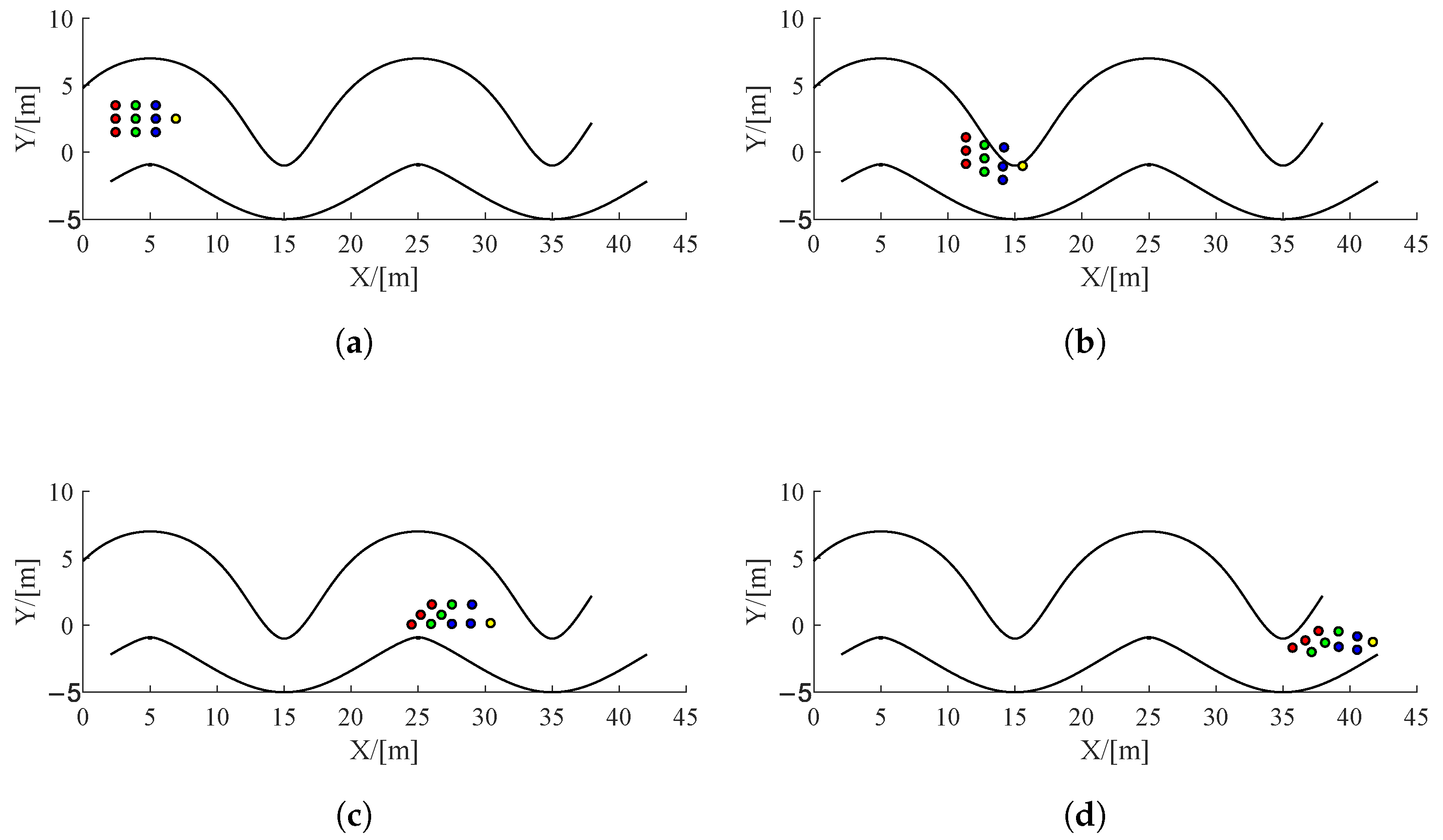

| Type | Level | Number | Set of Leaders Number |
|---|---|---|---|
| Leader | ∖ | 1 | ∖ |
| Followers | first-level | 2, 3, 4 | 1 |
| second-level | 5 | 1, 2 | |
| 6 | 1, 3 | ||
| 7 | 1, 4 | ||
| third-level | 8 | 1, 2, 5 | |
| 9 | 1, 3, 6 | ||
| 10 | 1, 4, 7 |
| Starting Point | Endpoint | Obstacle 1 | Obstacle 2 | Obstacle 3 | Obstacle 4 | |
|---|---|---|---|---|---|---|
| Position | 1 | 8 | 2.5 | 5 | 2.2 | 7.5 |
| 3 | 3 | 6.5 | 3 | 1.5 | 6 | |
| Radius | ∖ | ∖ | 1.5 | 0.8 | 0.8 | 0.5 |
| PSO | PIO | PPPIO | GA | |
|---|---|---|---|---|
| Path length (m) | 8.037 | 7.117 | 7.013 | 9.282 |
| Running time (s) | 1.216 | 1.536 | 1.704 | 1.449 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, Y.; She, Z.; Quan, Q. Pigeon-Inspired UAV Swarm Control and Planning Within a Virtual Tube. Drones 2025, 9, 333. https://doi.org/10.3390/drones9050333
Lei Y, She Z, Quan Q. Pigeon-Inspired UAV Swarm Control and Planning Within a Virtual Tube. Drones. 2025; 9(5):333. https://doi.org/10.3390/drones9050333
Chicago/Turabian StyleLei, Yangqi, Zhikun She, and Quan Quan. 2025. "Pigeon-Inspired UAV Swarm Control and Planning Within a Virtual Tube" Drones 9, no. 5: 333. https://doi.org/10.3390/drones9050333
APA StyleLei, Y., She, Z., & Quan, Q. (2025). Pigeon-Inspired UAV Swarm Control and Planning Within a Virtual Tube. Drones, 9(5), 333. https://doi.org/10.3390/drones9050333






