Modeling Non-Equilibrium Rarefied Gas Flows Past a Cross-Domain Reentry Unmanned Flight Vehicle Using a Hybrid Macro-/Mesoscopic Scheme
Abstract
1. Introduction
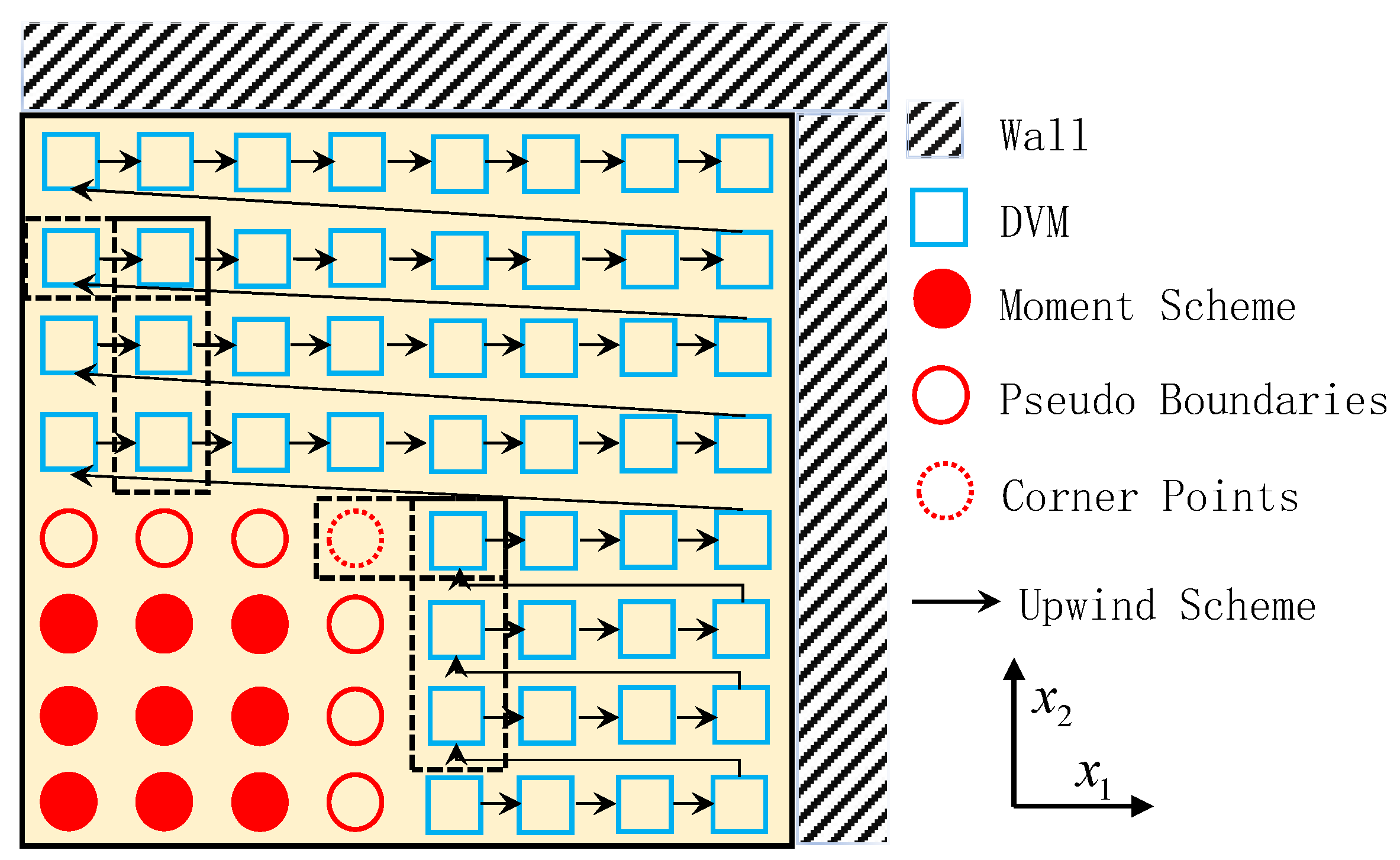
2. The R26 Moment Method
3. Shakhov Model Equation and the WBCs
4. Results and Discussion
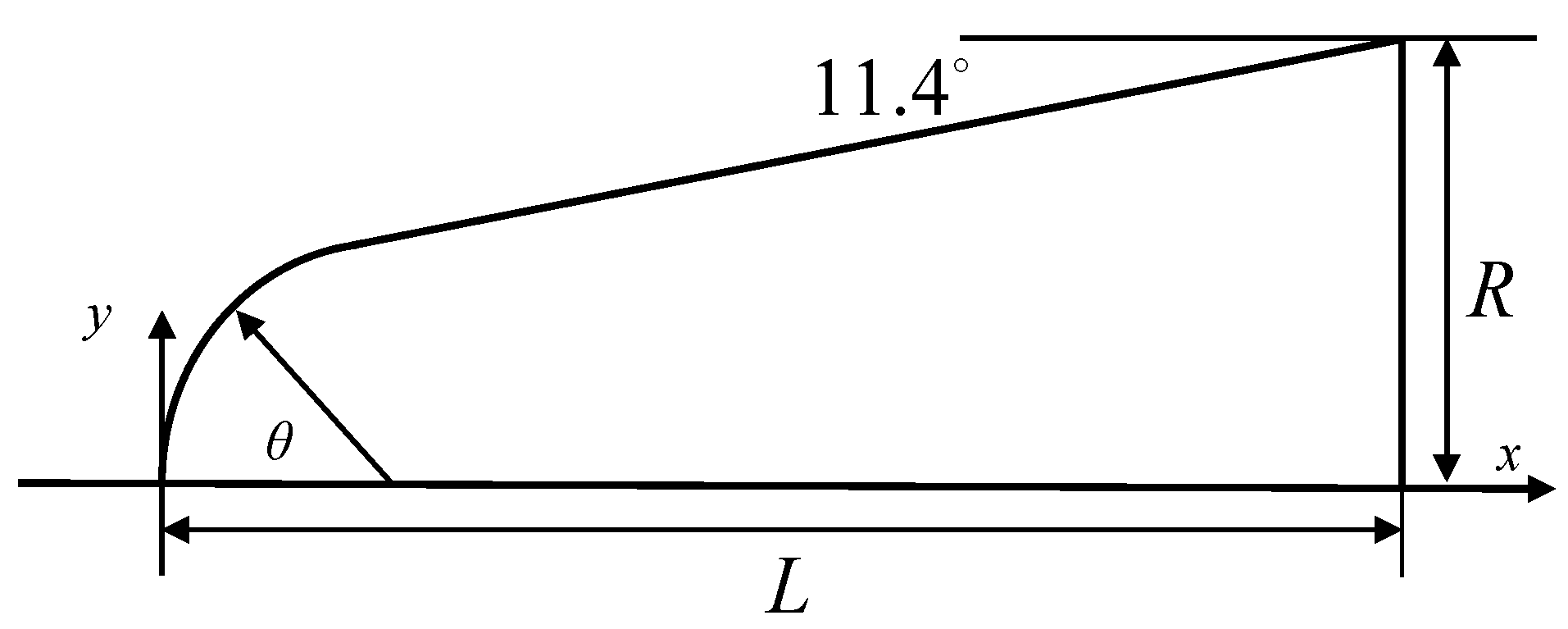
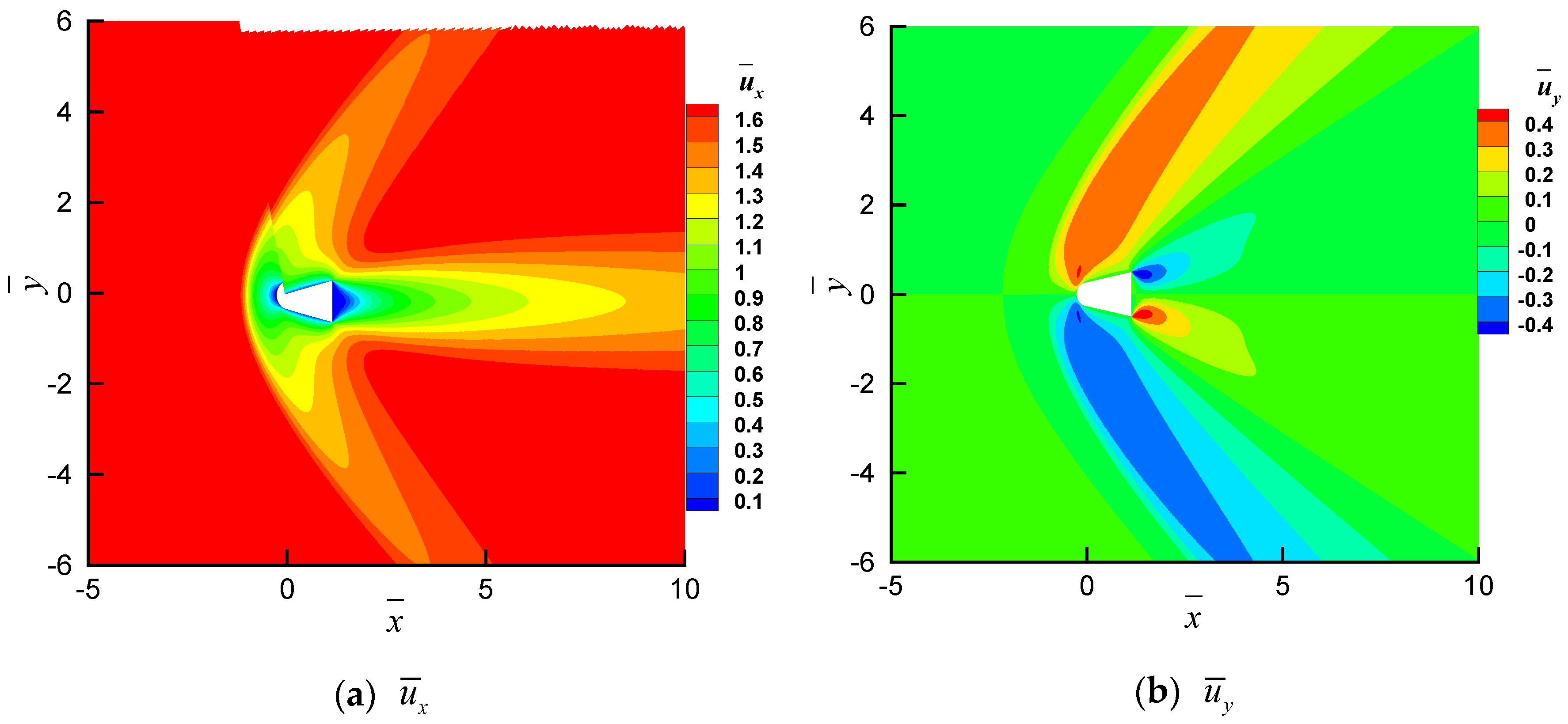
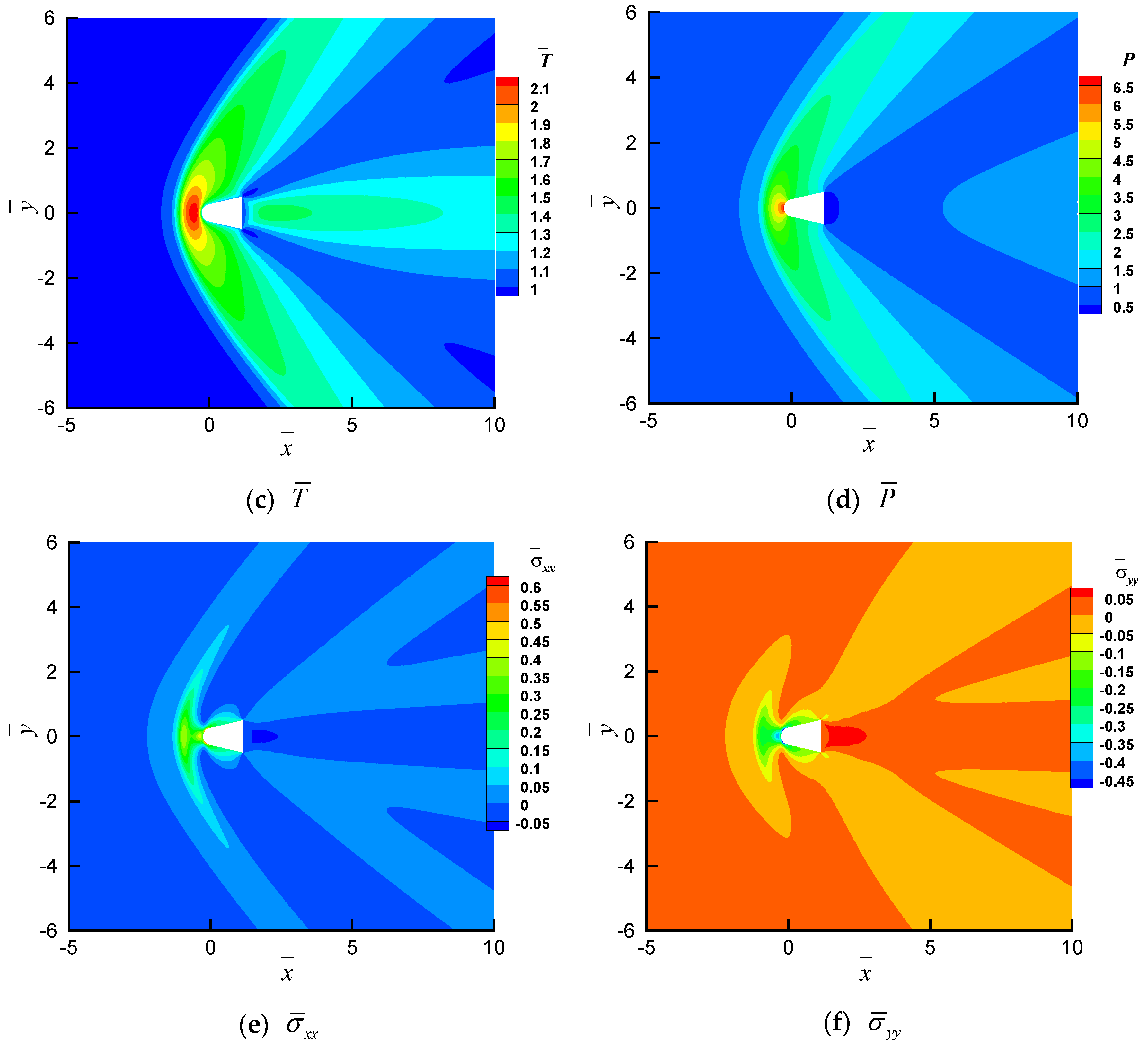
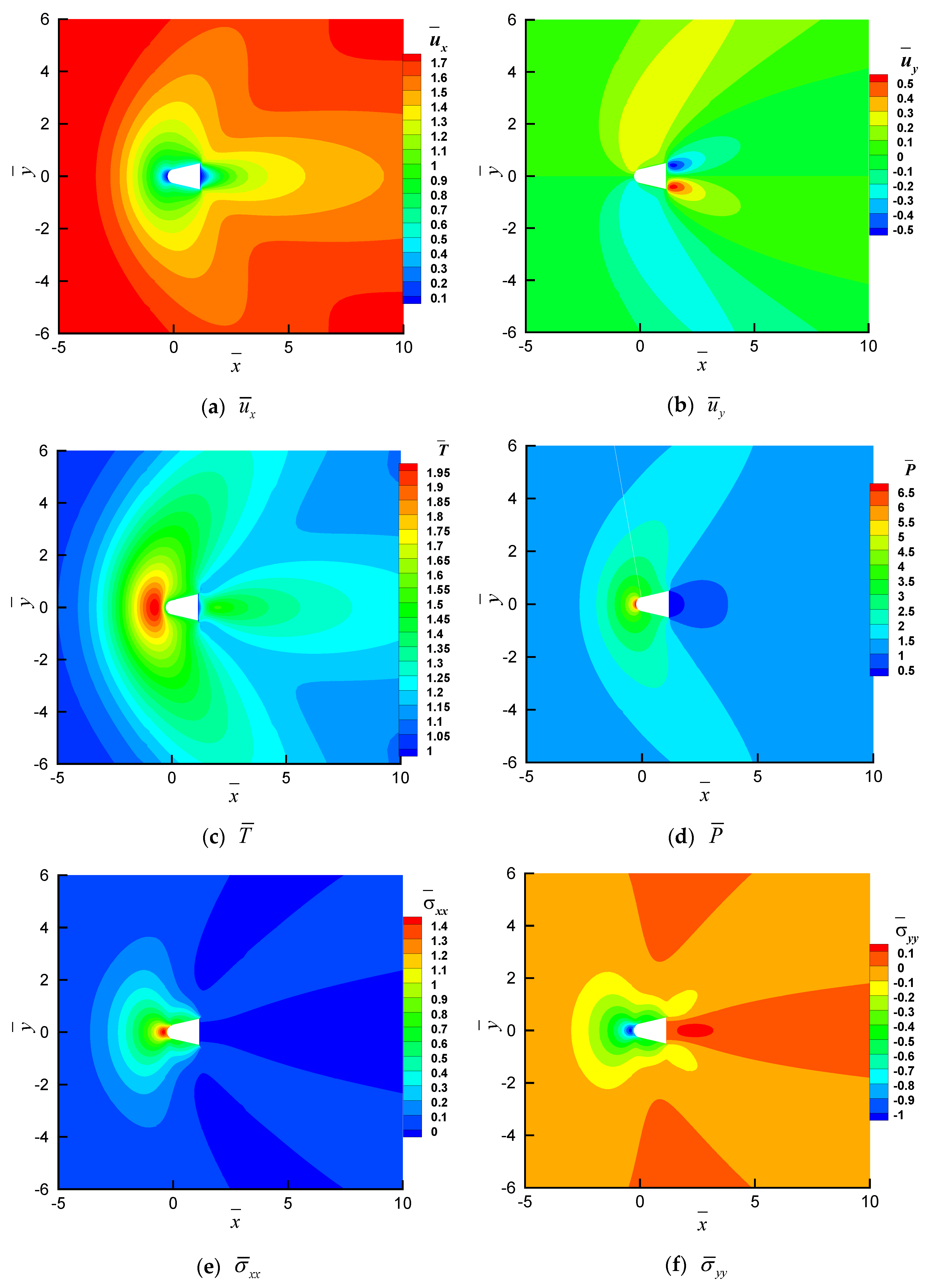
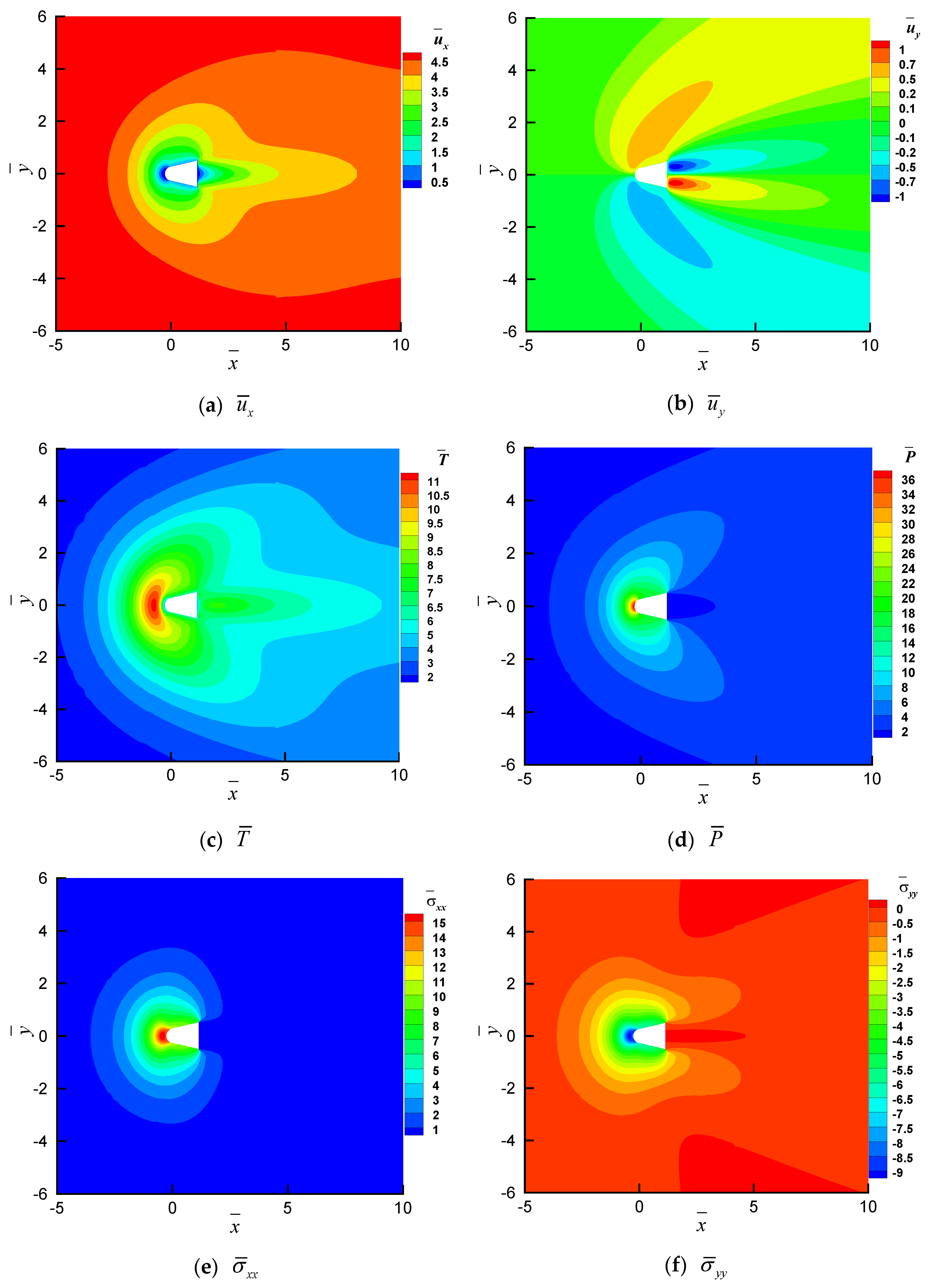
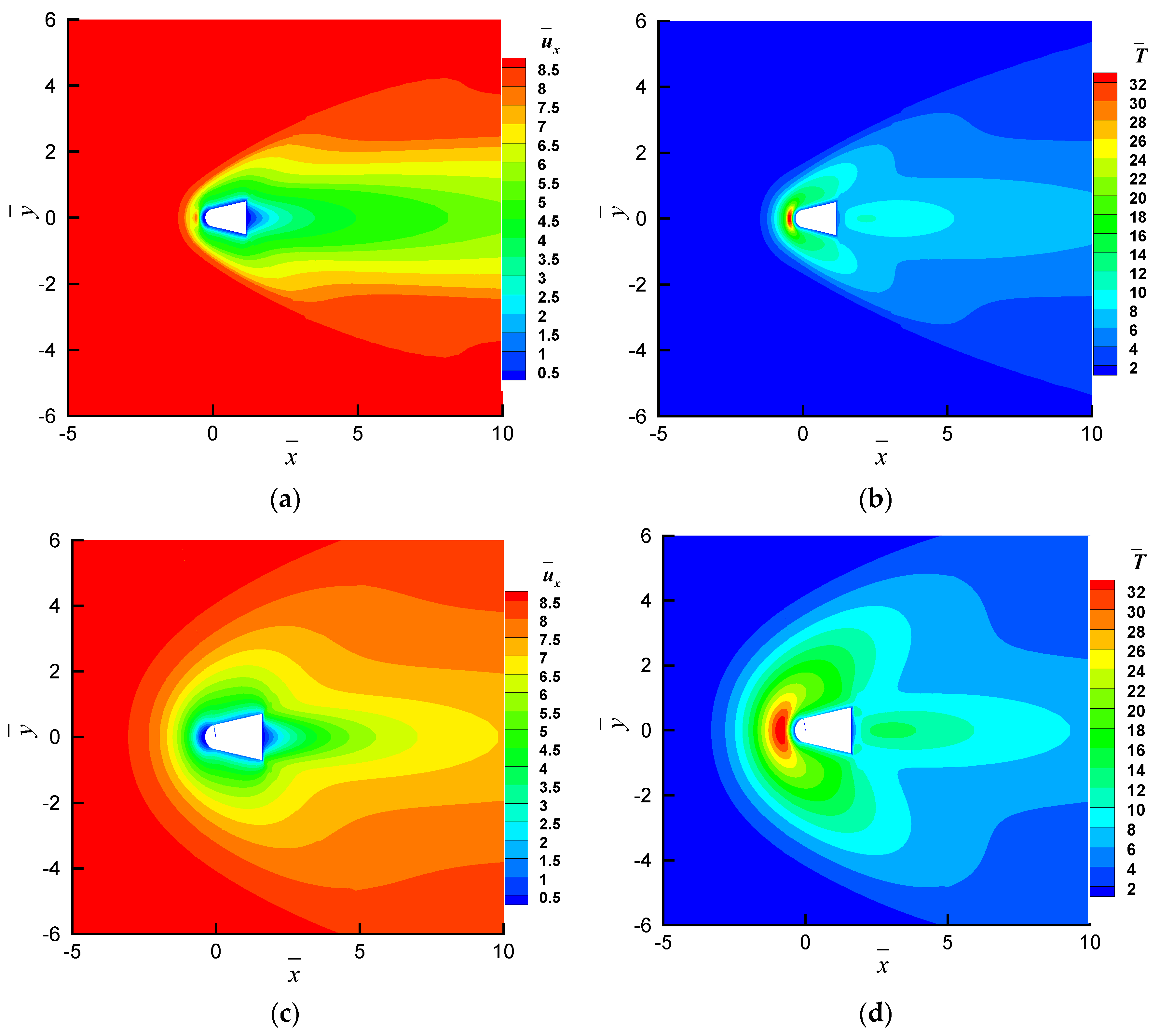
4.1. Gas Dynamics of a Cross-Domain Reentry Spheroid–Cone Unmanned Flight Vehicle
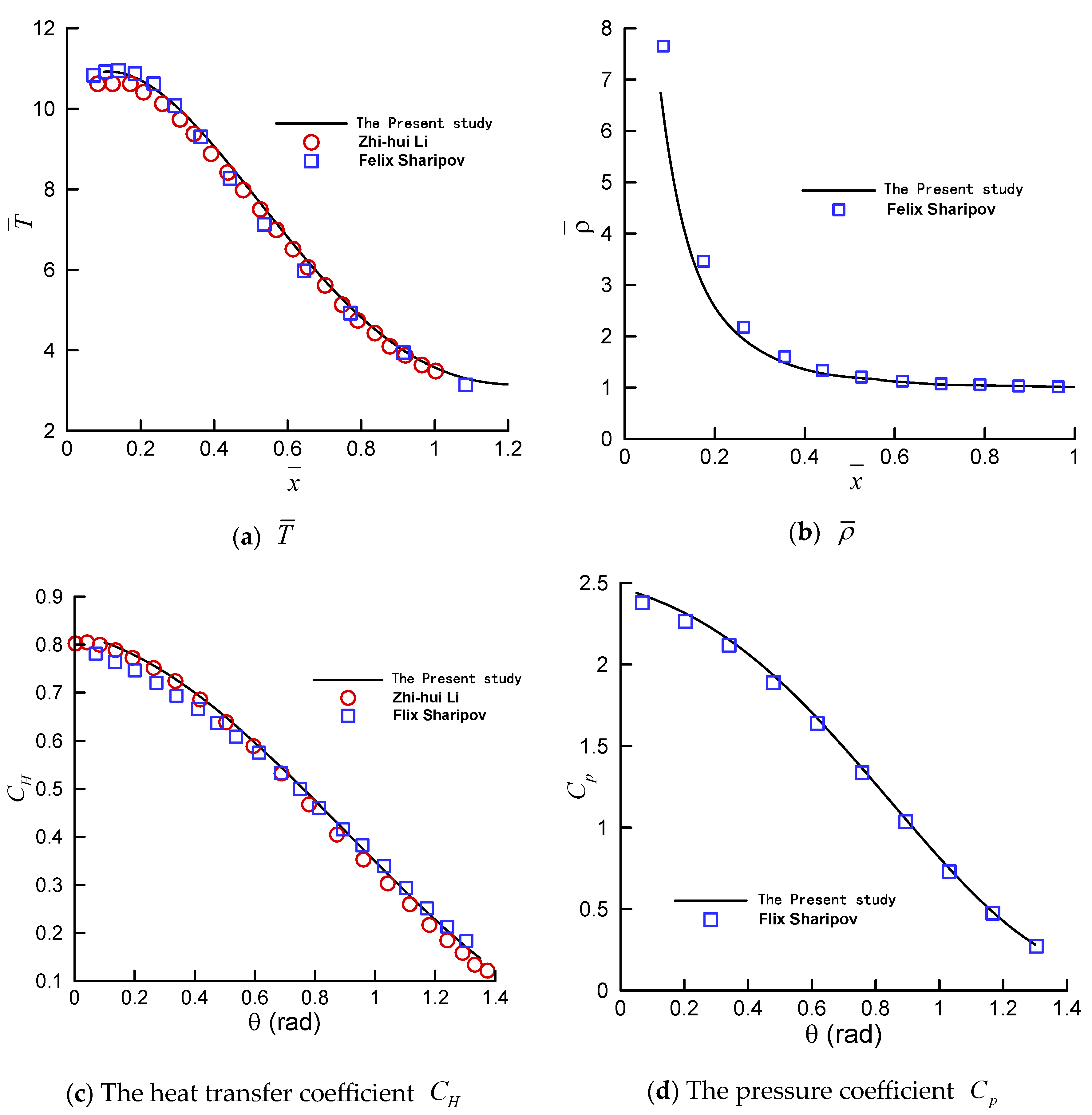
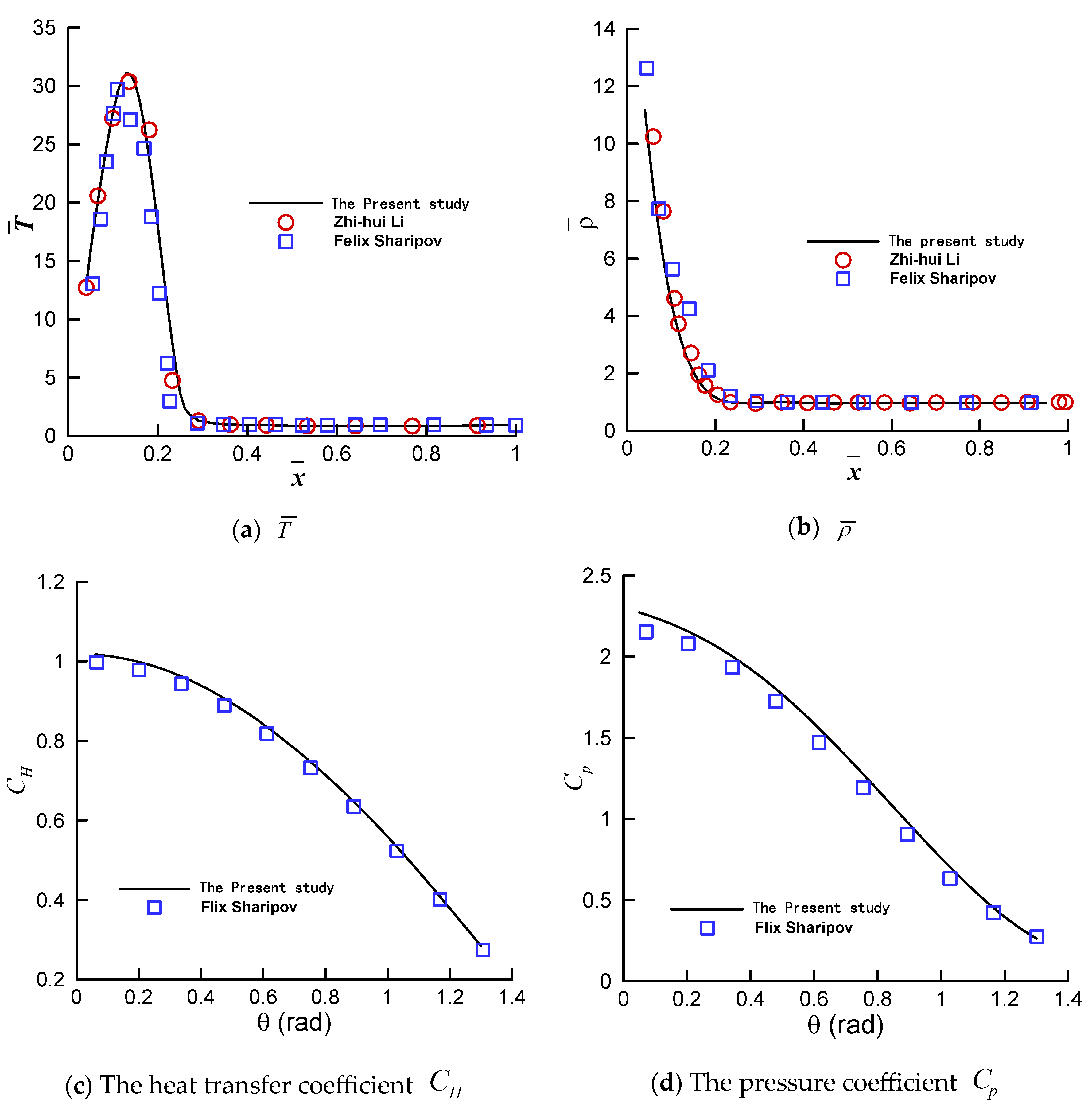
4.2. Comparison of the Computational Accuracy
- (i)
- The Ma number is defined asin which represents the speed of sound, which can be calculated as follows:in which k, m, and are the Boltzmann constant, molecular mass, and specific heat ratio, respectively.
- (ii)
- Re and Kn are defined as follows:in which R and represent the radius of the bottom and the viscosity of the gas, respectively.
- (iii)
- The relationship between Re, Kn, and Ma is
- (iv)
- The pressure coefficient is expressed as follows:in which P and represent the pressure of the aircraft and the pressure of the free flow, which follows the ideal gas law .
- (v)
- The heat transfer coefficient is expressed as follows:where represents the heat flux perpendicular to the wall.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liang, Y.; Li, Z.; Jiang, X. The influence of reflected gas molecules state on flow characteristics at reentry condition. Flow Turbul. Combust. 2025. [Google Scholar] [CrossRef]
- Sun, J.; Zhu, H.; Han, H.; Xu, D.; Cai, G. Optimization of mechanical deployable reentry vehicle based on multi-fidelity aerodynamic-trajectory coupling model. Aerosp. Sci. Technol. 2025, 157, 109777. [Google Scholar]
- Yang, W.; Yang, H.; Tang, S. Optimization and control application of sensor placement in aeroservoelastic of UAV. Aerosp. Sci. Technol. 2019, 85, 61–74. [Google Scholar]
- Yang, W.; Gu, X.J.; Emerson, D.R.; Wu, L.; Zhang, Y.; Tang, S. A Hybrid Approach to Couple the Discrete Velocity Method and Method of Moments for Rarefied Gas Flows. J. Comput. Phys. 2020, 410, 109397. [Google Scholar]
- Yang, W.; Tang, S.; Yang, H. Analysis of the Moment method and the Discrete Velocity Method in Modeling Non-equilibrium Rarefied Gas Flows: A Comparative Study. Appl. Sci. 2019, 9, 2733. [Google Scholar] [CrossRef]
- Bird, G.A. Molecular Gas Dynamics and the Direct Simulation of Gas Flows; Clarendon Press: Oxford, UK, 1994; pp. 46–98. [Google Scholar]
- Goldstein, D.; Sturtevant, B.; Broadwell, J.E. Investigations of the motion of discrete-velocity gases. Prog. Astronaut. Aeronaut. 1989, 118, 100–117. [Google Scholar]
- Fang, M.; Li, Z.; Li, Z.; Liang, J.; Zhang, Y. DSMC modeling of rarefied ionization reactions and applications to hypervelocity spacecraft reentry flows. Adv. Aerodyn. 2020, 2, 7. [Google Scholar]
- Fang, M.; Li, Z.; Li, Z.; Li, C. DSMC Approach for Rarefied Air Ionization during Spacecraft Reentry. Commun. Comput. Phys. 2018, 23, 4. [Google Scholar]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar]
- Holway, L.H., Jr. New statistical models for kinetic theory: Methods of construction. Phys. Fluids 1966, 9, 1658–1673. [Google Scholar]
- Shakhov, E. Generalization of the Krook kinetic relaxation equation. Fluid Dyn. 1968, 3, 95–96. [Google Scholar]
- Wu, L.; White, C.; Scanlon, T.J.; Reese, J.M.; Zhang, Y. Deterministic numerical solutions of the Boltzmann equation using the fast-spectral method. J. Comput. Phys. 2013, 250, 27–52. [Google Scholar]
- Li, Z.; Zhang, H. Gas-kinetic numerical studies of three-dimensional complex flows on spacecraft re-entry. J. Comput. Phys. 2009, 228, 1116–1138. [Google Scholar]
- Li, Z.; Liang, Y.; Peng, A.; Wu, J.; Wei, H. Gas-kinetic unified algorithm for aerodynamics covering various flow regimes by computable modeling of Boltzmann equation. Comput. Fluids 2025, 287, 106472. [Google Scholar]
- Li, F.; Li, Z.; Hu, J.; Hu, W. Application of gas-kinetic unified algorithm for solving Boltzmann model equation with vibrational energy excitation. Commun. Comput. Phys. 2025, 37, 250–288. [Google Scholar]
- Sone, Y. Flows induced by temperature fields in a rarefied gas and their ghost effect on the behavior of a gas in the continuum limit. Annu. Rev. Fluid Mech. 2000, 32, 779–811. [Google Scholar]
- Grad, H. On the kinetic theory of rarefied gases. Commun. Pure Appl. Math. 1949, 2, 331–407. [Google Scholar]
- Struchtrup, H.; Torrilhon, M. Regularization of Grad’s 13 moment equations: Derivation and linear analysis. Phys. Fluids 2003, 15, 2668–2680. [Google Scholar]
- Gu, X.-J.; Emerson, D.R. A computational strategy for the regularized 13 moment equations with enhanced wall-boundary conditions. J. Comput. Phys. 2007, 225, 263–283. [Google Scholar]
- Struchtrup, H.; Torrilhon, M. H Theorem, regularization and boundary conditions for linearized 13 moment equations. Phys. Rev. Lett. 2007, 99, 014502. [Google Scholar]
- Maxwell, J.C. On stresses in rarified gases arising from inequalities of temperature. Philos. Trans. R. Soc. Lond. A 1879, 170, 231–256. [Google Scholar]
- Gu, X.-J.; Emerson, D.R. A high-order moment approach for capturing non-equilibrium phenomena in the transition regime. J. Fluid Mech. 2009, 636, 177–216. [Google Scholar]
- Gu, X.-J.; Barber, R.W.; John, B.; Emerson, D.R. Non-equilibrium effects on flow past a circular cylinder in the slip and early transition regime. J. Fluid Mech. 2019, 860, 654–681. [Google Scholar]
- Gu, X.-J.; Emerson, D.R.; Tang, G.-H. Analysis of the slip coefficient and defect velocity in the Knudsen layer of a rarefied gas using the linearized moment equations. Phys. Rev. E 2010, 81, 016313. [Google Scholar]
- Yang, W.; Xu, B.; Niu, Y.; Zhou, Y. Thermally induced oscillatory rarefied gas flow inside a rectangular cavity. Phys. Fluids 2024, 36, 092033. [Google Scholar]
- Yang, W.; Gu, X.J.; Emerson, D.R.; Zhang, Y.; Tang, S. Modelling thermally induced non-equilibrium gas flows by coupling kinetic and extended thermodynamic methods. Entropy 2019, 21, 816. [Google Scholar] [CrossRef]
- Yang, W.; Gu, X.J.; Emerson, D.R.; Zhang, Y.; Tang, S. Comparative study of the discrete velocity and the moment method for rarefied gas flows. In Proceedings of the 31st International Symposium on Rarefied Gas Dynamics, Glasgow, UK, 23–28 July 2018; Volume 2132, p. 120006. [Google Scholar]
- Yang, W. Kinetic Theory and Applications of Rarefied Gas Flows Based on the Hybrid Discrete Velocity Method and Moment Method. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2019. (In Chinese). [Google Scholar]
- Li, Z.; Peng, A.; Zhang, H.; Yang, J. Rarefied gas flow simulations using high-order gas-kinetic unified algorithms for Boltzmann model equations. Prog. Aerosp. Sci. 2015, 74, 81–113. [Google Scholar]
- Sharipov, F. Hypersonic flow of rarefied gas near the Brazilian satellite during its reentry into atmosphere. Braz. J. Phys. 2003, 2, 398–405. [Google Scholar]


| Notation | ||||||||
|---|---|---|---|---|---|---|---|---|
| Shakhov | 1 | Pr | 1 | 1,0 | 1,0 | 1,0 | 1,0,0 | 1,0,0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Men, J.; Xu, B.; Ding, H.; Li, J. Modeling Non-Equilibrium Rarefied Gas Flows Past a Cross-Domain Reentry Unmanned Flight Vehicle Using a Hybrid Macro-/Mesoscopic Scheme. Drones 2025, 9, 239. https://doi.org/10.3390/drones9040239
Yang W, Men J, Xu B, Ding H, Li J. Modeling Non-Equilibrium Rarefied Gas Flows Past a Cross-Domain Reentry Unmanned Flight Vehicle Using a Hybrid Macro-/Mesoscopic Scheme. Drones. 2025; 9(4):239. https://doi.org/10.3390/drones9040239
Chicago/Turabian StyleYang, Weiqi, Jing Men, Bowen Xu, Haixia Ding, and Jie Li. 2025. "Modeling Non-Equilibrium Rarefied Gas Flows Past a Cross-Domain Reentry Unmanned Flight Vehicle Using a Hybrid Macro-/Mesoscopic Scheme" Drones 9, no. 4: 239. https://doi.org/10.3390/drones9040239
APA StyleYang, W., Men, J., Xu, B., Ding, H., & Li, J. (2025). Modeling Non-Equilibrium Rarefied Gas Flows Past a Cross-Domain Reentry Unmanned Flight Vehicle Using a Hybrid Macro-/Mesoscopic Scheme. Drones, 9(4), 239. https://doi.org/10.3390/drones9040239






