Fast Entry Trajectory Planning Method for Wide-Speed Range UASs
Abstract
1. Introduction
- (1)
- In terms of environmental adaptability, in order to solve the problem of the sensitivity of the initial value of convex programming in complex environments, this paper improves the traditional linear initial value generation method and proposes an adaptive initial value generation strategy to improve its solution ability.
- (2)
- In terms of the convergence of the algorithm, which is different from the fixed trust region strategy of traditional algorithms, this paper proposes a variable trust region strategy that significantly improves the convergence speed of the algorithm and meets the needs of online applications.
2. Formulation of the Entry Trajectory Planning Problem
2.1. UAS Motion Model
2.2. Constraints
- (1)
- Equation of motion constraints
- (2)
- Entry path constraints
- (3)
- Control constraints
- (4)
- Initial constraints
- (5)
- Terminal constraints
- (6)
- NFZ constraints
2.3. Performance Index
3. Convexification and Discretization of the Original Optimal Control Problem
3.1. Convexification of Constraints
3.1.1. Equivalent Transformations of Entry Path Constraints
3.1.2. Slack Method for Control Constraints
3.1.3. Linearization of the Performance Index
3.1.4. Convexification of Terminal Constraints
3.1.5. Linearization of the Equation of Motion
3.1.6. Conversion of NFZ Constraints
3.2. Discretization
4. Convex Programming Combined with a Variable Trust Region and Adaptive Initial Value Generation Strategies
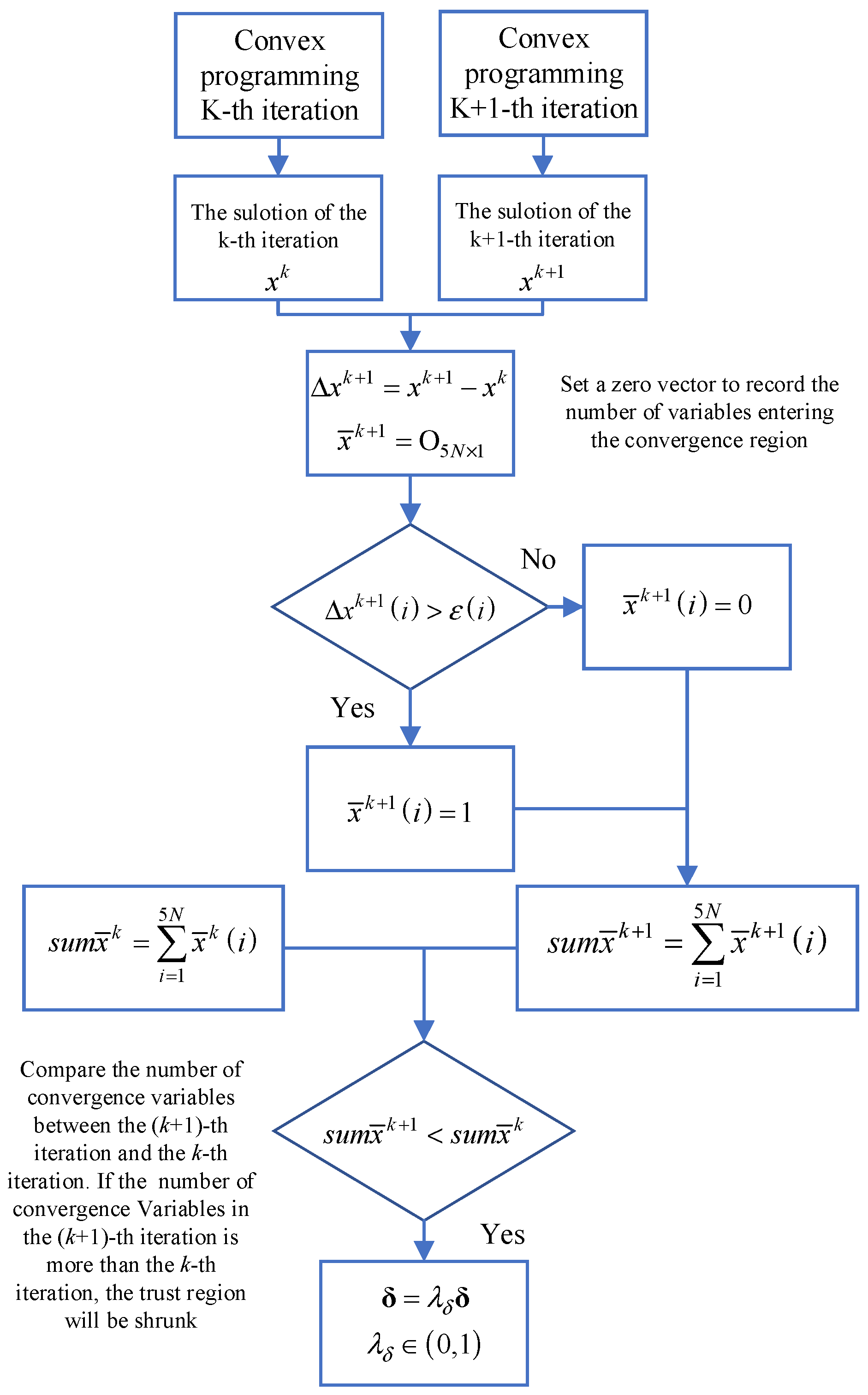
4.1. Variable Trust Region Strategy
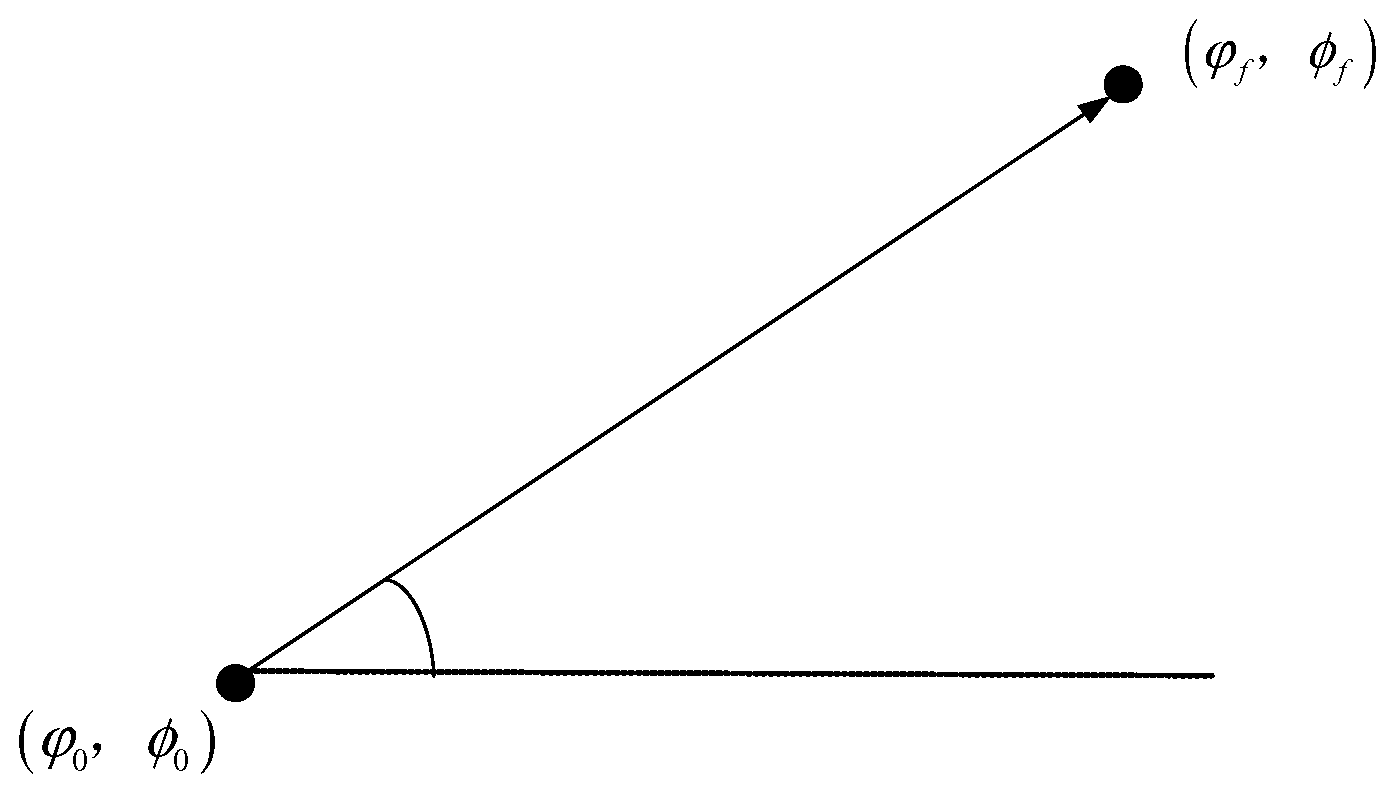
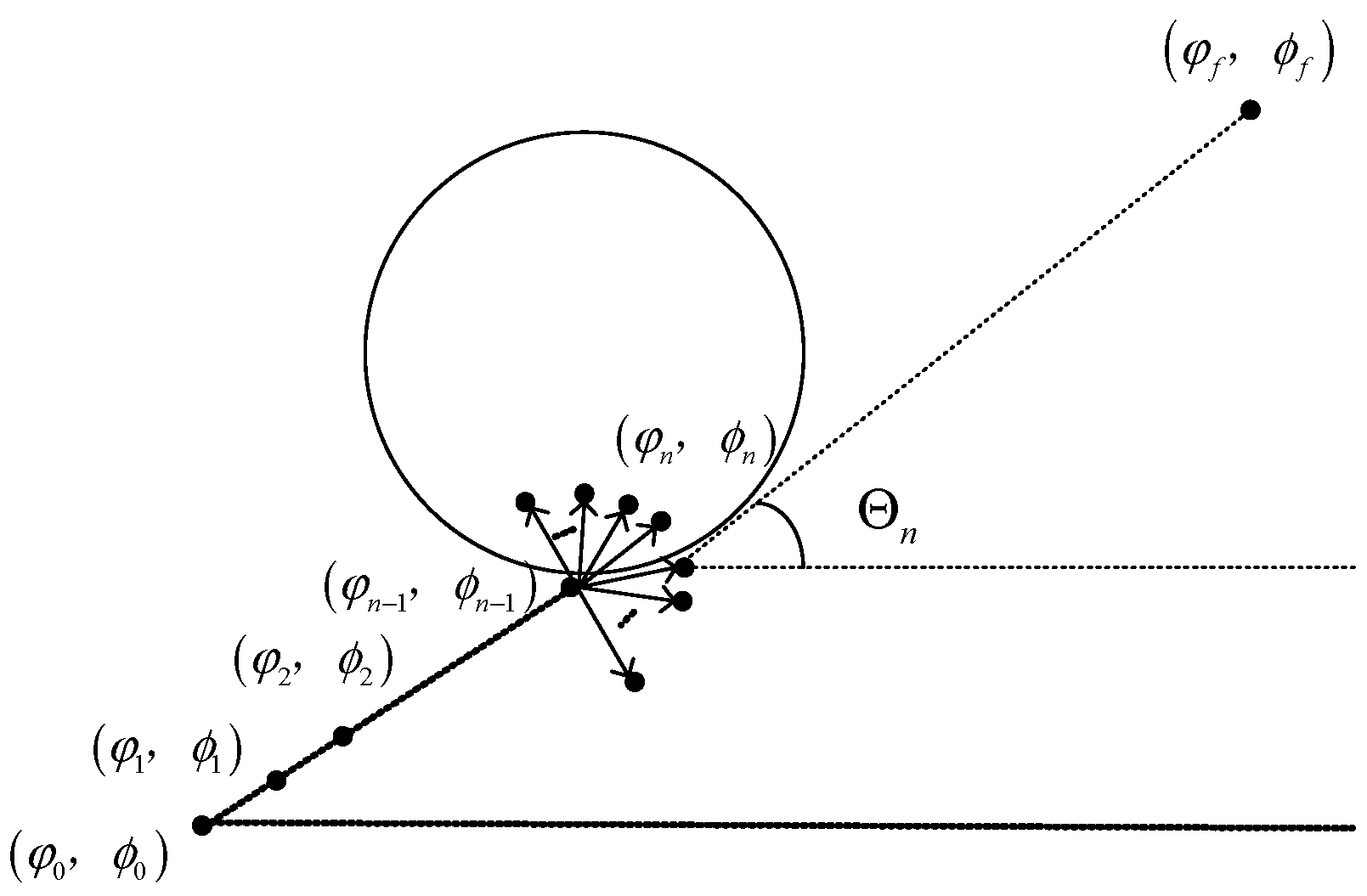
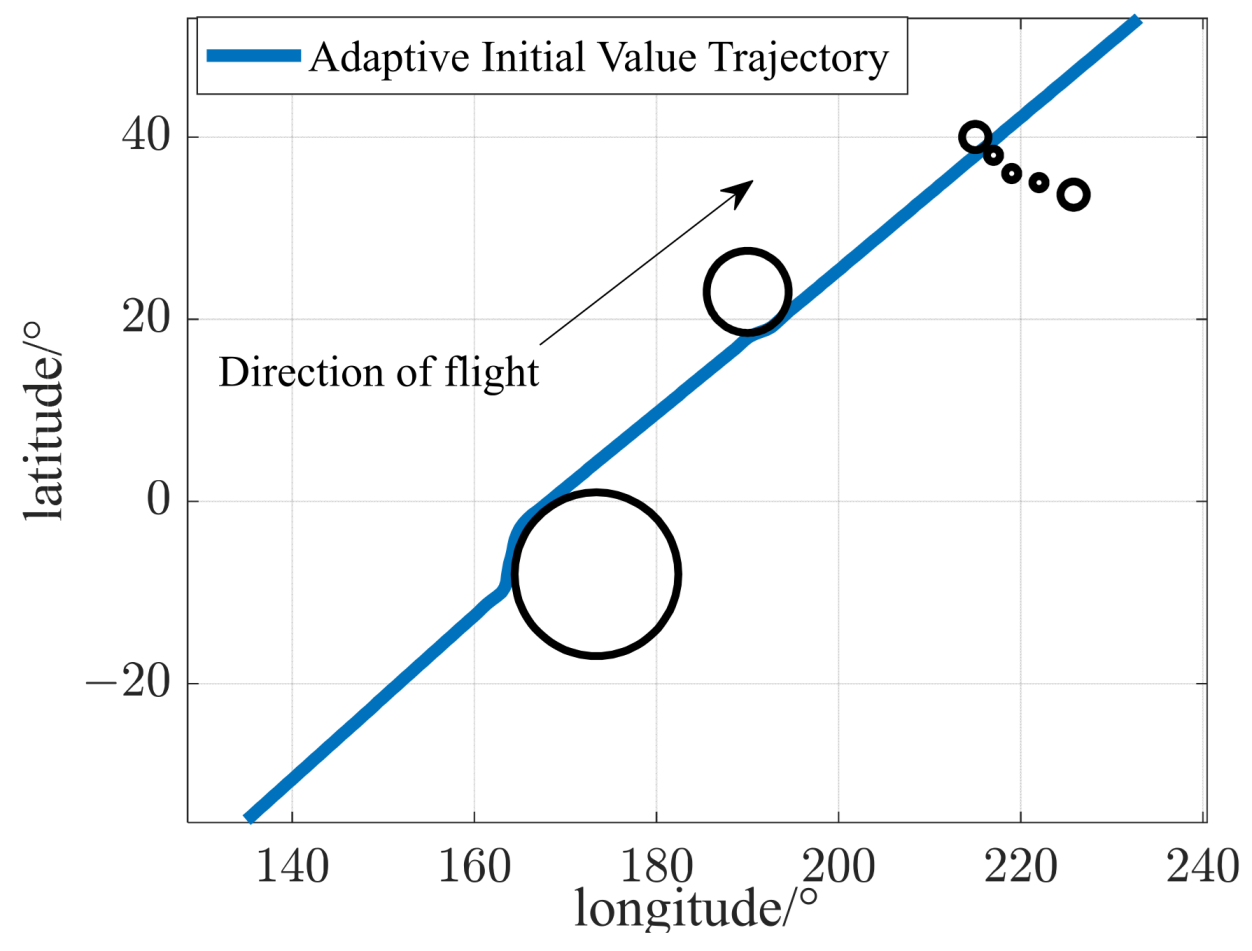
4.2. Adaptive Initial Value Generation Strategy
- (1)
- Generation of initial height values during entry.
- (2)
- Generation of initial longitude and latitude values
- (3)
- Flight path angle
- (4)
- Flight heading angle
4.3. Summary
5. Results and Analysis
5.1. Algorithm Flow and Simulation Conditions
- (1)
- Algorithm flow
| Algorithm 1 adaptive initial value and variable trust region convex programming method |
| Convert the original optimal problem P0 to the convex optimal control problem P1 by convex processing and discretize P1 to get the convex programming problem P2. Initialize the initial state variables according to the adaptive initial value strategy. Set the scaling factor of the trust region, which is 0.9 in this example. for k = 0: 1: MaxInteration_Num: Solve P2, get If : break else: continue end if end for |
- (2)
- Simulation conditions
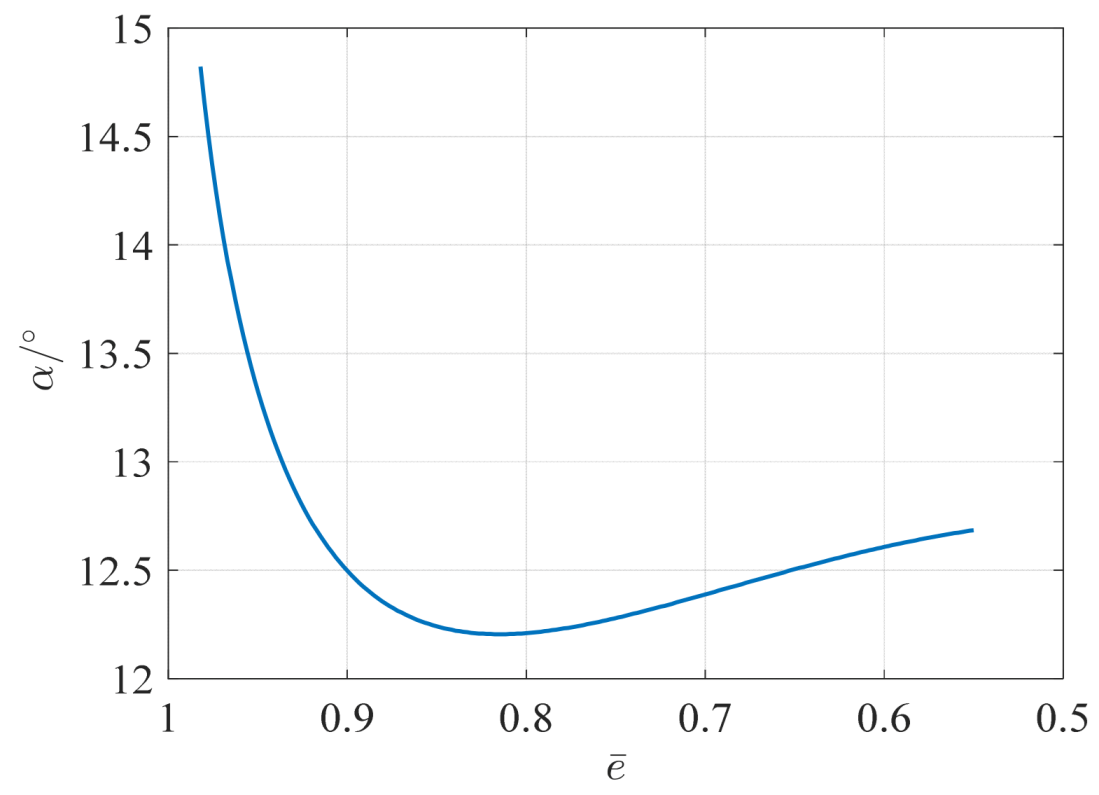
- (3)
- Profile of the angle of attack
- (4)
- Parameter setting
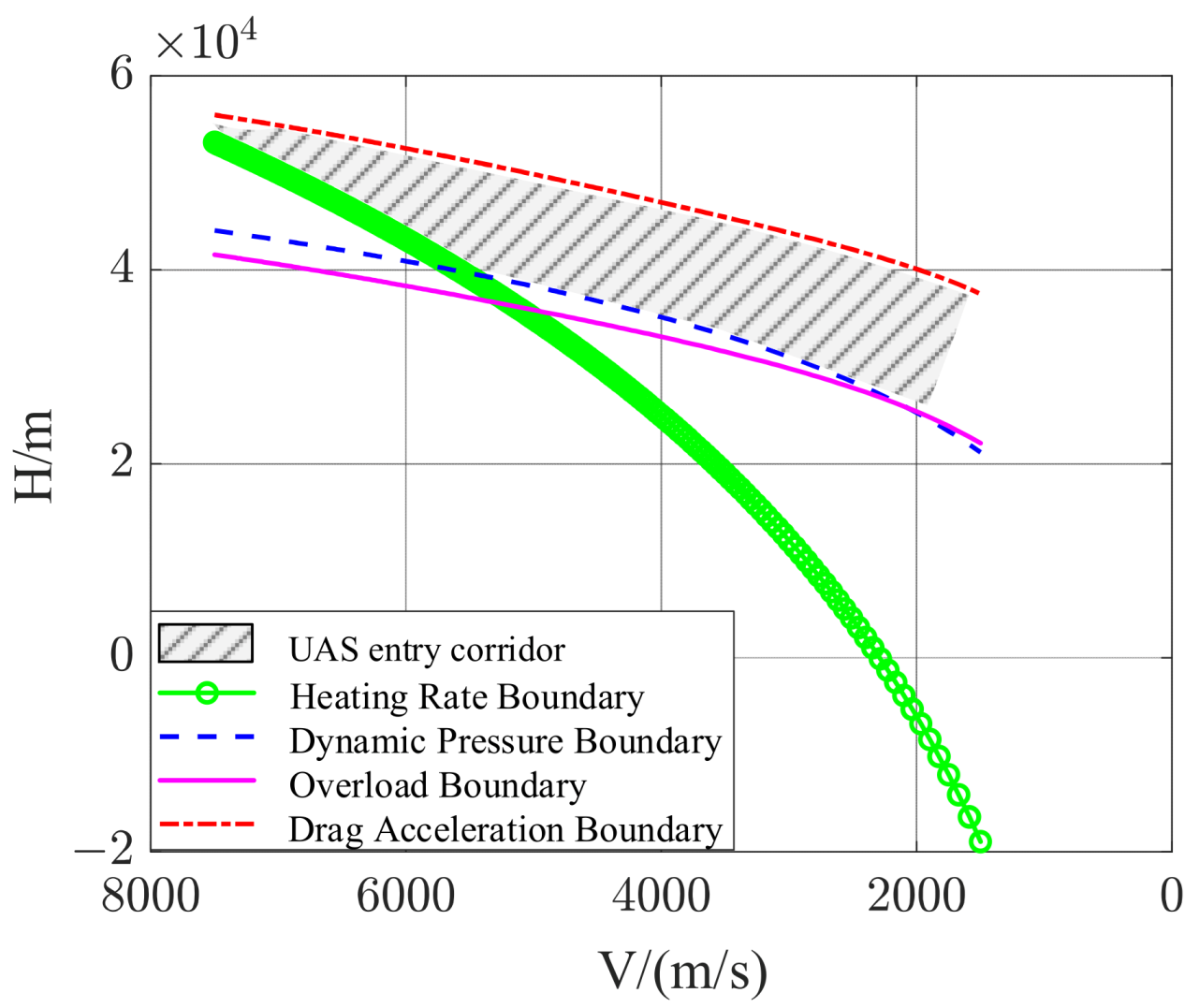
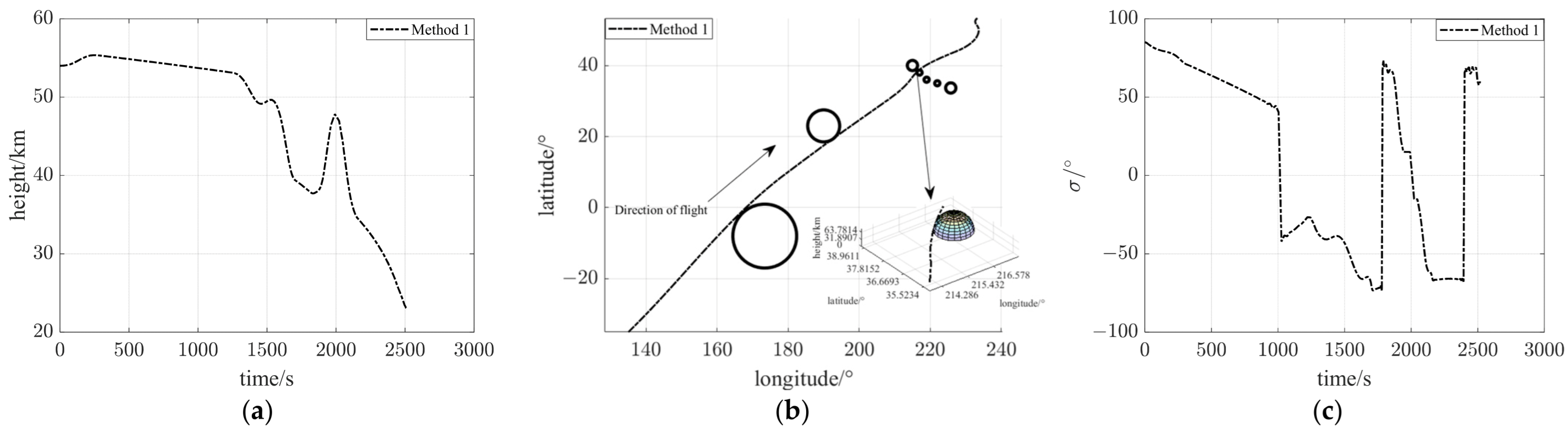
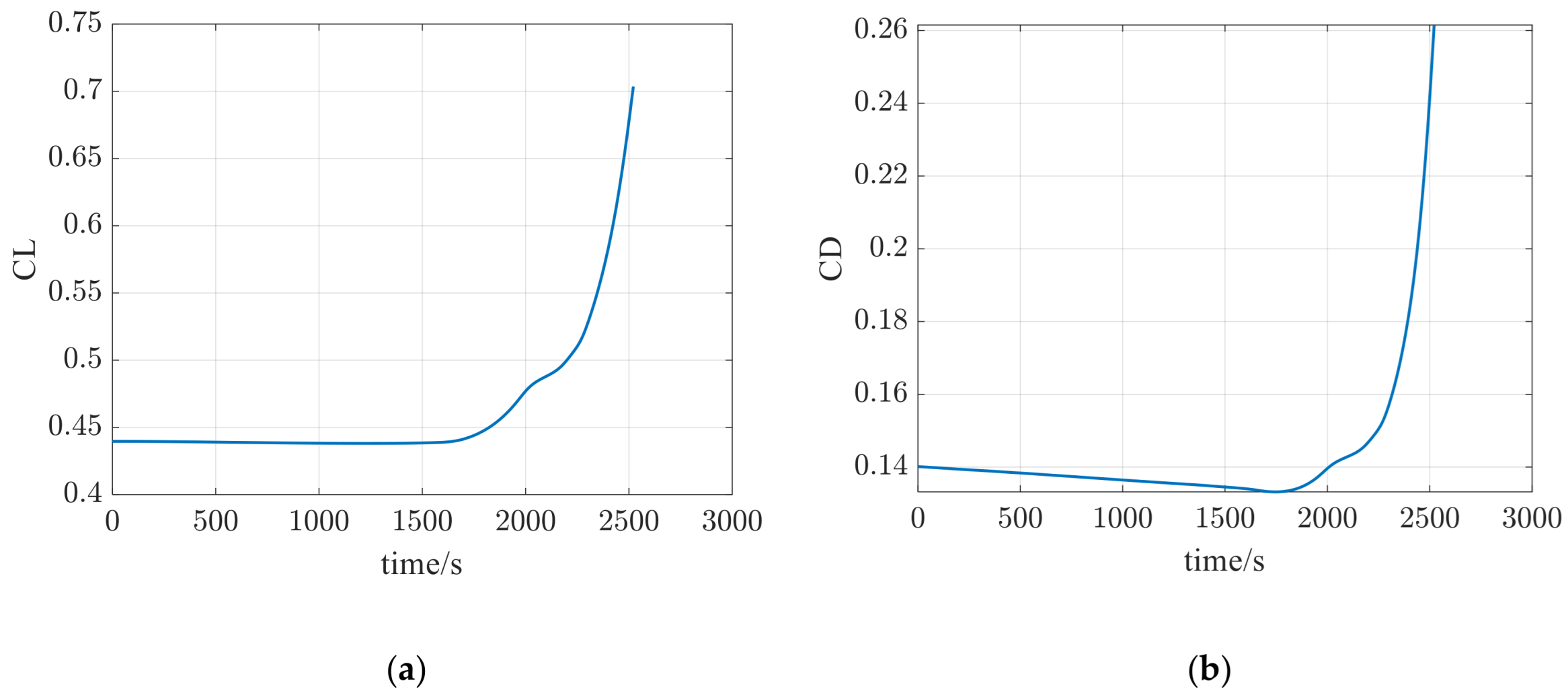
5.2. Analysis of Simulation Results for Method 1
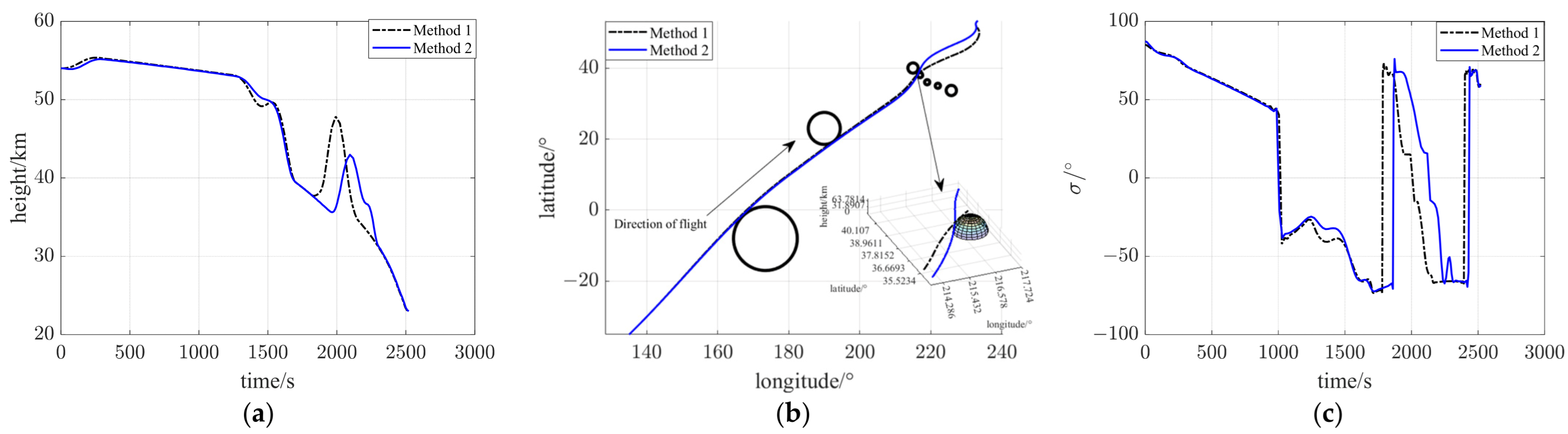
5.3. Analysis of Simulation Results for Method 2
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, S.; Yan, B.; Huang, W.; Zhang, X.; Yan, J. Current status and prospects of terminal guidance laws for intercepting hypersonic vehicles in near space: A review. J. Zhejiang Univ.-Sci. A 2023, 24, 387–403. [Google Scholar] [CrossRef]
- Liu, S.; Lin, Z.; Wang, Y.; Huang, W.; Yan, B.; Li, Y. Three-body cooperative active defense guidance law with overload constraints: A small speed ratio perspective. Chin. J. Aeronaut. 2025, 38, 103171. [Google Scholar] [CrossRef]
- Williams, P. Hermite-legendre-gauss-lobatto direct transcription in trajectory optimization. J. Guid. Control Dyn. 2009, 32, 1392–1395. [Google Scholar] [CrossRef]
- Darby, C.L.; Hager, W.W.; Rao, A.V. An hp-adaptive pseudospectral method for solving optimal control problems. Optim. Control Appl. Methods 2011, 32, 476–502. [Google Scholar] [CrossRef]
- Song, X.; Yao, X.; Ye, S. Trajectory Optimization of Small Supersonic UAV Based on Pseudospectral Method. J. ZheJiang Univ. (Eng. Sci.) 2022, 56, 193–201. (In Chinese) [Google Scholar] [CrossRef]
- Cai, G.; Liu, Z.; Luo, K.; Guan, F. Trajectory Optimization of Near-Space Variable-Wing Aircraft Based on Improved Pseudospectral Method. Aerosp. Technol. 2022, 5, 45–57. (In Chinese) [Google Scholar] [CrossRef]
- Mu, L.; Cao, S.; Wang, B.; Zhang, Y.; Feng, N.; Li, X. Pseudospectral-Based Rapid Trajectory Planning and Feedforward Linearization Guidance. Drones 2024, 8, 371. [Google Scholar] [CrossRef]
- Benedikter, B.; Zavoli, A.; Colasurdo, G. A Convex Optimization Approach for Finite-Thrust Time-Constrained Cooperative Rendezvous. Astrodyn. Spec. Conf. 2019, 171, 1483–1498. [Google Scholar] [CrossRef]
- Lu, P.; Liu, X. Autonomous Trajectory Planning for Rendezvous and Proximity Operations by Conic Optimization. J. Guid. Control Dyn. 2013, 36, 375–389. [Google Scholar] [CrossRef]
- Morgan, D.; Chung, S.; Hadaegh, F. Model Predictive Control of Swarms of Spacecraft Using Sequential Convex Programming. J. Guid. Control Dyn. 2014, 37, 1725–1740. [Google Scholar] [CrossRef]
- Foust, R.; Chung, S.; Hadaegh, F. Optimal Guidance and Control with Nonlinear Dynamics Using Sequential Convex Programming. J. Guid. Control Dyn. 2019, 43, 633–644. [Google Scholar] [CrossRef]
- Szmuk, M.; Acikmese, B.; Berning, A. Successive Convexification for Fuel-Optimal Powered Landing with Aerodynamic Drag and Non-Convex Constraints. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, San Diego, CA, USA, 4–8 January 2016. [Google Scholar] [CrossRef]
- Liu, X. Fuel-Optimal Rocket Landing with Aerodynamic Controls. J. Guid. Control Dyn. 2019, 42, 65–77. [Google Scholar] [CrossRef]
- Pinson, R.; Lu, P. Rapid Generation of Optimal Asteroid Powered Descent Trajectories via Convex Optimization. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Vail, CO, USA, 10–13 August 2015. [Google Scholar] [CrossRef]
- Liu, X.; Shen, Z.; Lu, P. Solving the maximum-crossrange problem via successive second-order cone programming with a line search. Aerosp. Sci. Technol. 2015, 47, 10–20. [Google Scholar] [CrossRef]
- Liu, X.; Shen, Z.; Lu, P. Entry Trajectory Optimization by Second-Order Cone Programming. J. Guid. Control Dyn. 2016, 39, 227–241. [Google Scholar] [CrossRef]
- Zhao, D.; Song, Z. Reentry trajectory optimization with waypoint and no-fly zone constraints using multiphase convex programming. Acta Astronaut. 2017, 137, 60–69. [Google Scholar] [CrossRef]
- Song, R.; Zhu, Y.; Xu, G.; Sun, J.; Long, T. Cooperative Reentry Trajectory Planning for Hypersonic Vehicles Based on Sequential Convex Optimization. Tactical Missile Technol. 2020, 6, 7–16. (In Chinese) [Google Scholar] [CrossRef]
- Sagliano, M.; Mooij, E. Optimal drag-energy entry guidance via pseudospectral convex optimization. Aerosp. Sci. Technol. 2021, 117, 106946. [Google Scholar] [CrossRef]
- Sun, Y. Trajectory Optimization and Guidance of Hypersonic Vehicle Based on Improved Gauss Pseudospectral Method. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2012. (In Chinese). [Google Scholar]
- Yang, F.; Gong, Z.; Wei, Q.; Lei, Y. Secure Containment Control for Multi-UAV Systems by Fixed-Time Convergent Reinforcement Learning. IEEE Trans. Cybern. 2025, 1–14. [Google Scholar] [CrossRef]
- Gong, Z.; Yang, F. Secure tracking control via fixed-time convergent reinforcement learning for a UAV CPS. IEEE/CAA J. Autom. Sin. 2024, 11, 1699–1701. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, J.; Jiang, J.; Liang, H. Reentry trajectory planning for hypersonic vehicles via an improved sequential convex programming method. Aerosp. Sci. Technol. 2024, 149, 109130. [Google Scholar] [CrossRef]
- Dai, P.; Feng, D.; Feng, W.; Cui, J.; Zhang, L. Entry trajectory optimization for hypersonic vehicles based on convex programming and neural network. Aerosp. Sci. Technol. 2023, 137, 108259. [Google Scholar] [CrossRef]
- Zong, Q.; Li, Z.; Ye, L.; Tian, B. Online reconstruction of RLV reentry trajectory with variable trust domain sequence convex programming. J. Harbin Inst. Technol. 2020, 52, 147–155. (In Chinese) [Google Scholar]
- Phillips, T. A Common Aero Vehicle (CAV) Model, Description, and Employment Guide; Schafer Corp. for Air Force Research Lab and Air Force Space Command: Greene County, OH, USA, 2003. [Google Scholar]
| State Variables | Initial Condition | Terminal Condition |
|---|---|---|
| height/m | 54,000 | 23,000 |
| longitude/° | 130 | 233.3 |
| latitude/° | −35 | 53.3 |
| velocity/(m·s−1) | 7500 | 1500 |
| flight path angle/° | 0 | 0 |
| flight heading angle/° | 45.12 | 50 |
| Longitude/° | Latitude/° | Radius/km |
|---|---|---|
| 173 | −8 | 1000.5 |
| 210 | 8 | 501 |
| Longitude/° | Latitude/° | Radius/km |
|---|---|---|
| 219 | 36 | 80 |
| 217 | 38 | 80 |
| 222 | 35 | 80 |
| 215 | 40 | 160 |
| 226 | 33.7 | 160 |
| Solution | Total Entry Time/s | Solving Time/s | Iteration Number |
|---|---|---|---|
| Normal convex programming | not feasible | not feasible | not feasible |
| Method 1 | 2518.6796 | 40.17 | 50 |
| Method 2 | 2521.4330 | 18.37 | 21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, W.; Feng, D.; Dai, P.; Li, S.; Zhang, C.; Ma, J. Fast Entry Trajectory Planning Method for Wide-Speed Range UASs. Drones 2025, 9, 210. https://doi.org/10.3390/drones9030210
Feng W, Feng D, Dai P, Li S, Zhang C, Ma J. Fast Entry Trajectory Planning Method for Wide-Speed Range UASs. Drones. 2025; 9(3):210. https://doi.org/10.3390/drones9030210
Chicago/Turabian StyleFeng, Weihao, Dongzhu Feng, Pei Dai, Shaopeng Li, Chenkai Zhang, and Jiadi Ma. 2025. "Fast Entry Trajectory Planning Method for Wide-Speed Range UASs" Drones 9, no. 3: 210. https://doi.org/10.3390/drones9030210
APA StyleFeng, W., Feng, D., Dai, P., Li, S., Zhang, C., & Ma, J. (2025). Fast Entry Trajectory Planning Method for Wide-Speed Range UASs. Drones, 9(3), 210. https://doi.org/10.3390/drones9030210






