Modeling, Control, and Validation of an Unmanned Gyroplane Based on Aerodynamic Identification

Highlights

What are the main findings?

• A modified aerodynamic identification structure for gyroplanes was proposed based on prior knowledge and coherence analysis to enhance modeling accuracy.
• An autonomous flight control system for unmanned gyroplanes was designed to mitigate control coupling, delayed pitch response, and throttle-airspeed nonlinearities.

What are the implications of the main findings?

• The proposed identification framework enabled a high-fidelity aerodynamic model for gyroplanes with coefficients of determination above 0.92 between identified and measured responses.
• Flight tests were conducted on an unmanned gyroplane, achieving reliable autonomous flight and verifying the engineering feasibility of the proposed methods.

Abstract

The autonomous operation of unmanned gyroplanes is constrained by the limited fidelity of aerodynamic models and control challenges posed by unique flight characteristics. To address these issues, a comprehensive methodology for unmanned gyroplane modeling and autonomous flight control is proposed. High-fidelity aerodynamic models were developed through a modified parameter identification structure, and the longitudinal and lateral modal characteristics of the prototype gyroplane were subsequently analyzed. Targeting the control coupling, delayed pitch response, and throttle-airspeed nonlinearities, a novel autonomous flight control strategy is proposed for unmanned gyroplanes. Precise energy management and longitudinal-lateral decoupling were achieved through feedforward trim compensation, pitch-damping augmentation, and coordinated allocation of throttle and rotor tilt. Comparative analysis verified the high accuracy of the identified aerodynamic models, with the coefficient of determination between measured and simulated attitude responses exceeding 0.92. Furthermore, flight tests were conducted on an unmanned gyroplane prototype, including climb and descent maneuvers, climb to level flight transitions, and turning trajectory tracking. The results show that the proposed autonomous control strategy achieves precise tracking of altitude, airspeed, and trajectory, with airspeed errors remaining within 1.5 m/s.

1. Introduction

The gyroplane is similar to a helicopter in having a large rotor on top to generate lift. Unlike helicopters, however, its rotor is driven by the incoming airflow rather than by engine power [1], which leads to minimal counter-torque and thus does not require an associated torque-balance mechanism. In addition, the large rotor diameter and high-speed rotation provide strong damping and gyroscopic effects, significantly enhancing flight stability [2]. The development of gyroplanes can be traced back to the pioneering work of Spanish engineer Cierva in the 1920s [3]. Due to the limitations of the rotor connection structure, which restricted high-speed flight capability, gyroplanes were gradually replaced by helicopters after the 1940s. Nevertheless, because of their mechanical simplicity, excellent low-speed performance, and cost-effectiveness, light gyroplanes once again attracted attention from 1955, marked by the introduction of the Bensen-8M “Gyrocopter” [4]. Since then, NASA and other institutions [5] have gradually resumed research on unmanned gyroplane design, modeling, and control.

Dynamic modeling is the foundation of flight control design and simulation. The modeling methods for unmanned gyroplanes have evolved from theoretical aerodynamic analyses to high-fidelity numerical simulations. McCormick’s theory established the basis for gyroplane performance studies [6] and was later extended to high Reynolds number conditions to capture the transient aerodynamic effects [7]. Subsequent studies have gradually focused on component-level modeling and flow interactions between the rotor and fuselage [8,9]. However, despite the maturity of traditional aerodynamic theories, their limited accuracy and computational complexity have restricted practical applications [10]. In recent years, geometric mechanics approaches have been proposed to model the nonlinear dynamics of complex rotating systems [11], which enable structure-preserving numerical simulations. The strong nonlinearity in unmanned gyroplane aerodynamics remains a major challenge to capturing overall aerodynamic dynamics accurately.

Effective dynamic modeling for helicopters typically relies on professional simulation platforms, which are supported by extensive flight test databases. However, due to the slow development of gyroplanes, comparable mature tools are still lacking. To address this limitation, system identification has been recognized as a practical approach for unmanned gyroplane modeling, and the University of Glasgow has achieved significant progress in modeling, flight dynamics, and flight quality analysis [12,13,14]. Thomson and Houston revealed the nonlinear characteristics underlying unmanned gyroplane flight dynamics and improved model accuracy through experimental measurements [15]. Meanwhile, based on these results, flight quality has been further analyzed [16,17], and these analyses provide a foundation for control system design [18]. Nevertheless, compared with fixed-wing aircraft and helicopters, unmanned gyroplane modeling methods remain of limited reliability and present significant challenges for flight control design.

With the development of unmanned aerial vehicles, the autonomous control of unmanned gyroplanes has gradually become a central topic [4]. Based on linearized models and simulation environments, traditional proportional-integral-derivative (PID) and nonlinear PID methods have been implemented to improve the stability and safety of unmanned gyroplanes under various flight conditions [19,20,21]. Subsequently, the dynamic behavior of compound gyroplanes has been explored [22,23], and a precise altitude control strategy was proposed [24]. Nevertheless, since the unmanned gyroplane relies on passively driven rotors to generate lift, its dynamics exhibit strong nonlinearity and coupling, which continue to hinder the development of effective control designs [19,22,25]. Firstly, the lack of high-fidelity dynamic models introduces uncertainties into the control system. Furthermore, the three-axis attitude and velocity of the unmanned gyroplane are governed by the rotor disk, resulting in strong coupling among the channels. Finally, the flexible connection between the rotor and the fuselage generates a pendulum effect, leading to a noticeable lag in attitude response.

To address these challenges, this paper developed a high-fidelity aerodynamic model based on system identification, analyzed the unique flight characteristics of unmanned gyroplanes, and subsequently proposed an autonomous flight control system for unmanned gyroplane platforms. The main motivation of this study is to overcome the control coupling, delayed pitch response, and nonlinear throttle-airspeed dynamics, thereby enabling autonomous and precise control of unmanned gyroplane systems. The key contributions are fourfold:

(1)

A modified identification model structure is developed, which eliminates terms with low coherence or frequency mismatch, thereby improving the accuracy of the identified aerodynamic model.

(2)

A trim-decoupling feedforward control strategy is proposed, which mitigates the control interference between the longitudinal and lateral channels under a single-actuator configuration.

(3)

A pitch-damping augmentation control combined with rotor-tilt-based allocation is proposed to achieve efficient and precise airspeed tracking, overcoming the performance degradation of conventional flight control frameworks when applied to unmanned gyroplanes.

(4)

The proposed control strategy is implemented on an unmanned gyroplane prototype converted from a manned vehicle, enabling fully autonomous flight.

The remainder of this paper is organized as follows. Section 2 introduces the unmanned prototype gyroplane platform and the modified aerodynamic identification model. Section 3 presents the evaluation of the identified model and the corresponding modal analysis. In Section 4, control challenges of unmanned gyroplanes are described, followed by the development of the autonomous flight control system. Section 5 provides the experimental validation, where the flight data and control performance are analyzed. Finally, Section 6 summarizes the main conclusions.

2. Configuration for Parameter Identification

Following the objectives described in Section 1, this section introduces the configuration and methodology used for aerodynamic parameter identification of the unmanned prototype gyroplane. First, the flight test platform and onboard data acquisition system are described. Then, the excitation input design for system identification is presented. Finally, a modified aerodynamic model structure is proposed to enhance model accuracy.

2.1. Flight Test Platform

The unmanned prototype gyroplane used for validation in this study is the Spanish ELA-07 autogyro, manufactured by ELA Aviación of Fuente Obejuna, Córdoba, Spain, with its main parameters listed in Table 1. The aircraft features a semirigid rotor with fixed pitch blades, a tricycle landing gear, three vertical tails, and a horizontal stabilizer. It is operated via four actuators: a longitudinal rotor tilt stick, a lateral rotor tilt stick, the engine throttle, and the rudder. The empty weight is 258 kg, allowing for a payload of 192 kg, and is powered by a ROTAX 912 engine, manufactured by BRP-Rotax GmbH & Co KG of Gunskirchen, Austria. The actual aircraft is shown in Figure 1.

Table 1. Main parameters of the ELA-07 autogyro.

Parameters	Value
Fuselage length (m)	5.0
Height (m)	2.8
Rotor diameter (m)	8.25
Empty weight (kg)	258
Max takeoff weight (kg)	450
Takeoff/Landing distance (m)	100/0–30

Figure 1. Picture of the validation prototype ELA-07.

A reliable hardware system for synchronous data acquisition is essential for accurate identification, as delays and sampling frequencies of input/output data directly affect the convergence of the identification process. According to engineering practice, the sampling frequency should be at least 25 times the maximum target frequency [26]. In this study, flight data were recorded at 100 Hz. The data logger, MPC5674 flight control computer, global positioning system (GPS), and attitude sensors were installed near the center of gravity. Considering the actuation mechanisms of the joystick and the rudder, displacement sensors were used to measure the relative deflections of the rotor tilt angles and the rudder surface.

2.2. Input Signal for Parameter Excitation

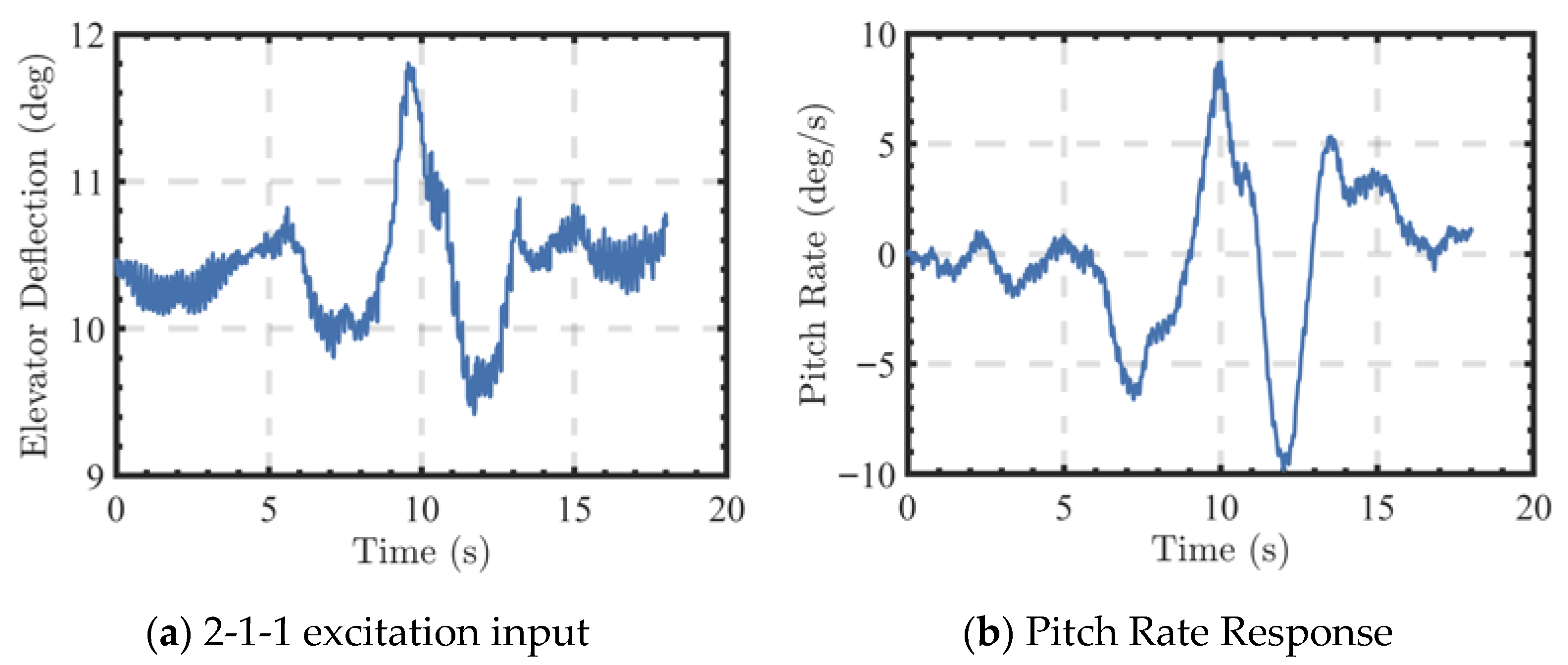
The typical 2-1-1 square wave, characterized by alternating positive and negative pulses in a 2:1:1 width ratio, was selected as the experimental excitation signal. Its frequency spectrum is broad, allowing sufficient excitation energy within the target modal range by adjusting the pulse width. Two parameters, amplitude and frequency, must be specified.

The amplitude was determined such that the response of the angular rate reached about ±10°/s. The frequency of the 2-1-1 square wave $f_r$ was designed to be close to the natural frequency $f_n$ of the aircraft dynamics to adequately excite the motion modes. The following relation is commonly used in engineering practice [27]

$$f_r={\displaystyle \frac{0.7}{2f_n}}.$$

(1)

The typical attitude frequency of the unmanned gyroplane is approximately 0.25 Hz [14]; therefore, the unit pulse width of the 2-1-1 input was set to 1.5 s.

Figure 2 shows the actual rotor longitudinal tilt input and the corresponding pitch rate response during a 2-1-1 excitation test. Each test started and ended in a steady state, and a steady flight of at least 3 s was maintained before and after the excitation.

Figure 2. Longitudinal 2-1-1 excitation input and pitch rate response during flight test.

2.3. Identification Model Structure and Modification

Based on the gyroplane aerodynamic identification model developed in Ref. [14], a modified model structure is proposed in this section. Flight data were analyzed using coherence functions [28], and the model formulation is further guided by prior knowledge of the prototype gyroplane.

Considering the six-degree-of-freedom linear aerodynamic model of aircraft, a decoupled model for longitudinal and lateral dynamics is proposed. The state space equation can be described as

$$\dot{\mathit{x}}=\mathit{A}\mathit{x}+\mathit{B}\mathit{u}.$$

(2)

where A is the state transition matrix, B is the input matrix, u is the control vector, and x is the state variables.

For the longitudinal model, the state variables ${\mathit{x}}_a\triangleq {[\begin{array}{ccc}\begin{array}{cc}\begin{array}{cc}u& w\end{array}& q\end{array}& \theta & \Omega \end{array}]}^{\mathrm{T}}$ consist of the body-axis forward velocity u, vertical velocity w, pitch angle q, pitch angle rate q, and rotor speed W; and the control variable $u_a\triangleq {\delta }_e$ is the longitudinal deflection of the rotor. For the lateral model, the state variables ${\mathit{x}}_L\triangleq {[\begin{array}{cccc}\beta & p& r& \phi \end{array}]}^{\mathrm{T}}$ consist of the sideslip angle b, roll rate p, yaw rate r, and roll angle j; and the control variables ${\mathit{u}}_L\triangleq {[\begin{array}{cc}{\delta }_a& {\delta }_r\end{array}]}^{\mathrm{T}}$ are the lateral deflection of the rotor ${\delta }_a$ and rudder deflection ${\delta }_r$.

According to the Nyquist criterion and identification practice, a common requirement for ensuring sufficient amplitude and phase resolution is that the identifiable bandwidth should be no less than one-fifth of the sampling frequency [29]. Given the 100 Hz data-logging rate in our flight tests, the effective update rate of the rotor speed W (below 5 Hz) falls far short of the 20 Hz minimum required for reliable identification. Therefore, with the rotor speed excluded from the state variables, the modified longitudinal aerodynamic model is established as

$$\begin{array}{cc}{\dot{\stackrel{⌢}{\mathit{x}}}}_a\hfill & ={\mathit{A}}_a{\stackrel{⌢}{\mathit{x}}}_a+{\mathit{B}}_a{u}_a\hfill \\ & \triangleq \left[\begin{array}{cccc}{X}_u& X_w& X_q& X_{\theta }\\ Z_u& Z_w& Z_q& Z_{\theta }\\ M_u& M_w& M_q& M_{\theta }\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}u\\ w\\ q\\ \theta \end{array}\right]+\left[\begin{array}{c}{X}_{{\delta }_e}\\ Z_{{\delta }_e}\\ M_{{\delta }_e}\\ 0\end{array}\right]{\delta }_e\hfill \end{array},$$

(3)

where X_∗, Z_∗, and M_∗ represent the derivatives of the longitudinal force, vertical force, and pitching moment with respect to the corresponding variable “*”, respectively.

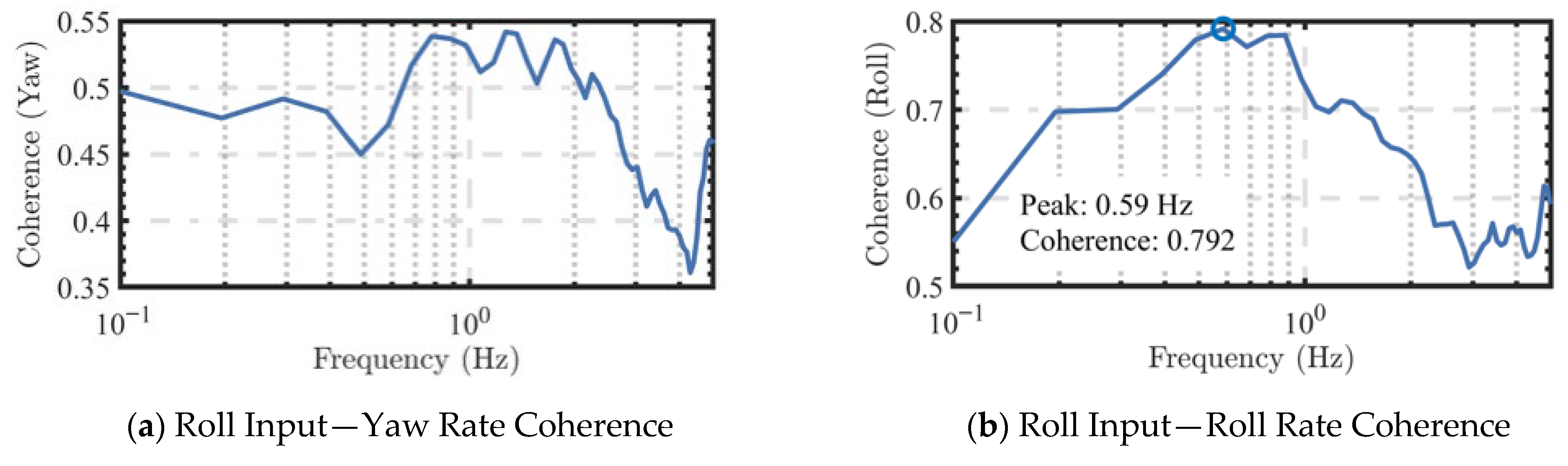
Coherence analysis was conducted to simplify the lateral aerodynamic model. Figure 3a presents the coherence function between roll excitation and the corresponding yaw rate, while Figure 3b shows the between roll excitation and roll rate.

Figure 3. Coherence analysis of lateral excitations. The blue circle in subfigure (b) indicates the peak coherence point.

Within the frequency range of interest 0.2~2 Hz, the coherence function between roll excitation and yaw rate remained below 0.6, indicating weak correlation. In contrast, the coherence between roll and roll rate exceeded 0.6 and showed no oscillations at low frequencies. Since a coherence level above 0.6 is generally regarded as acceptable for system identification [30,31], these results confirm good coherence quality. Therefore, it is suggested that lateral rotor deflection primarily excites roll responses while inducing weak yaw coupling. Similarly, in rudder excitation tests, rudder inputs primarily affect yaw motion and show a slight influence on roll responses.

Thus, the modified lateral aerodynamic model is given as

$$\begin{array}{cc}{\dot{\mathit{x}}}_L\hfill & ={\mathit{A}}_L{\mathit{x}}_L+{\mathit{B}}_L{\mathit{u}}_L\hfill \\ & \triangleq \left[\begin{array}{cccc}{Y}_{\beta }& 0& Y_r& Y_{\phi }\\ L_{\beta }& L_p& 0& 0\\ N_{\beta }& 0& N_r& 0\\ 0& 1& 0& 0\end{array}\right]\left[\begin{array}{c}\beta \\ p\\ r\\ \phi \end{array}\right]+\left[\begin{array}{cc}\begin{array}{c}0\\ L_{{\delta }_a}\\ 0\\ 0\end{array}& \begin{array}{c}{Y}_{{\delta }_r}\\ 0\\ N_{{\delta }_r}\\ 0\end{array}\end{array}\right]\left[\begin{array}{c}{\delta }_a\\ {\delta }_r\end{array}\right]\hfill \end{array},$$

(4)

where Y_∗, L_∗, and N_∗ represent the derivatives of the lateral force, rolling moment, and yawing moment with respect to the corresponding variable “*”, respectively.

3. Evaluation of Aerodynamic Model and Modal Characteristics

According to the model structure defined in Section 2, the aerodynamic model is decoupled into individual channels and identified using a combined method to ensure both efficiency and accuracy. The equation error method solved via linear regression provided an initial estimate, which was optimized by the maximum likelihood method to minimize the output error [32]. Based on the identified results, a six-degree-of-freedom model for the unmanned gyroplane was constructed, and its validity and modal characteristics were analyzed, which serves as a basis for flight control law design.

3.1. Time and Frequency Domain Validation

Flight tests were conducted at an airspeed of 31.5 m/s and an altitude of 200 m, with multiple longitudinal and lateral excitations. The aerodynamic force and moment derivatives obtained for each group exhibited an approximately normal distribution with low dispersion. By taking the expected values, the state and input matrices of the state-space functions in Equations (3) and (4) were derived. For the longitudinal model, there is

$${\mathit{A}}_a=\left[\begin{array}{cccc}-0.147& -0.198& 1.339& -9.286\\ -0.393& -0.588& 31.020& -5.686\\ 0.011& -0.071& -0.691& -0.408\\ 0& 0& 1& 0\end{array}\right], \mathrm{and} {\mathit{B}}_a=\left[\begin{array}{l}-10.142\\ 21.385\\ -5.059\\ 0\end{array}\right],$$

(5)

and for the lateral-directional model, there is

$${\mathit{A}}_L=\left[\begin{array}{cccc}0.271& 0& -0.215& 0.066\\ -5.836& -2.045& 0& 0\\ 15.249& 0& -1.264& 0\\ 0& 1& 0& 0\end{array}\right], \mathrm{and} {\mathit{B}}_L=\left[\begin{array}{cc}0& -0.130\\ -18.722& 0\\ 0& -4.045\\ 0& 0\end{array}\right],$$

(6)

The identified aerodynamic derivatives exhibited physically stable dynamics.

Remark 1. 

The Dutch-roll mode is typically unstable. However, in Equation (6), the Dutch-roll damping N_r is relatively large, and specifically, N_b > 0, leading to a stable Dutch-roll mode. This stability is attributed to the tail flow generated by the propeller, which increases the rudder damping.

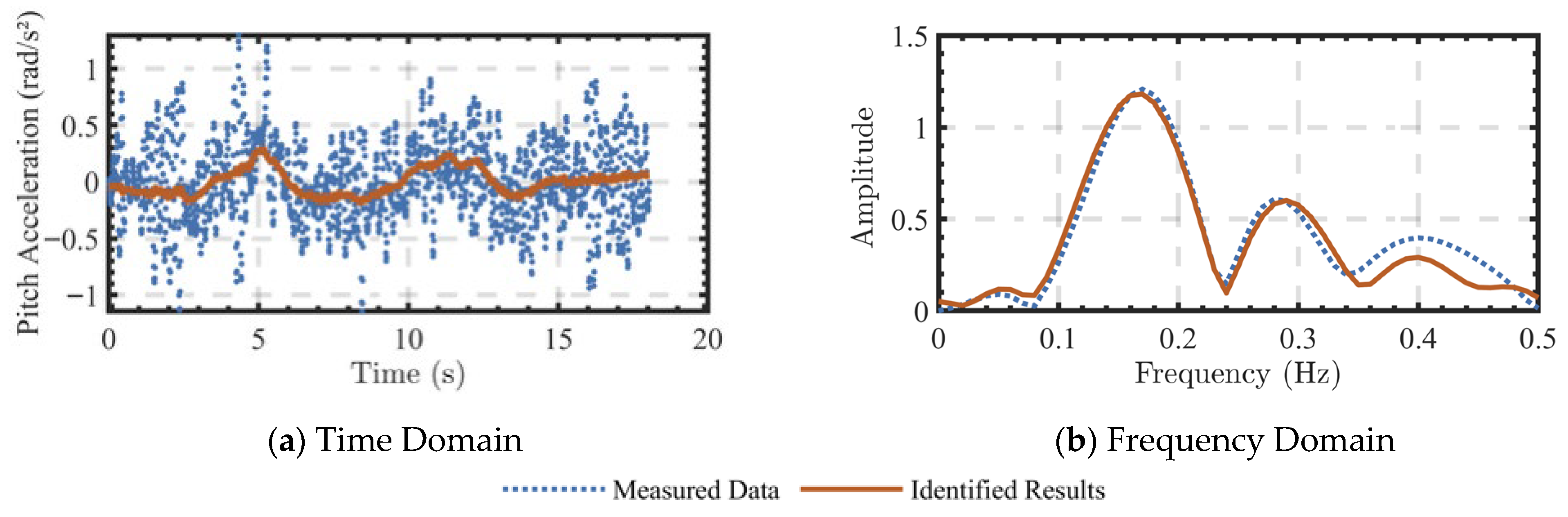
To assess the model’s credibility [33], simulations were conducted in both the time and frequency domains. Flight data not used for identification were applied as inputs to the identified model given by Equations (5) and (6), and the attitude responses of the model were compared with the actual flight data. The coefficient fitting results for derivatives of the pitch, roll, and yaw moments are presented in Figure 4, Figure 5 and Figure 6, respectively. Each figure shows the total response of the linearized system, resulting from the combined contributions of the state-feedback and control input terms. The corresponding attitude responses are shown in Figure 7. The mean absolute error (MAE), standard deviation (SD), and coefficient of determination between the measured and identified attitude responses are summarized in Table 2. A positive phase delay indicates that the simulation leads the flight data, whereas a negative phase delay indicates a lag.

Figure 4. Time- and frequency-domain fitting of the pitch moment derivatives.

Figure 5. Time- and frequency-domain fitting of the roll moment derivatives.

Figure 6. Time- and frequency-domain fitting of the yaw moment derivatives.

Figure 7. Time-domain comparison of measured and identified attitude responses.

Table 2. Comparison Analysis of Measured and Identified Attitude Responses.

Attitude	MAE (deg/s)	SD (deg/s)	R2	Phase Delay (s)
Pitch Rate	1.31	1.62	0.934	−0.07
Roll Rate	1.64	2.03	0.926	0.08
Yaw Rate	0.86	1.06	0.925	−0.06

As shown in Figure 4, Figure 5, Figure 6 and Figure 7, the responses of the identified model and the measured flight data exhibited high consistency under identical excitation. In the time-domain results of Figure 4a, Figure 5a and Figure 6a, the measured and estimated coefficients shared a consistent tendency, although considerable noise was observed in the measurements. To further evaluate the accuracy of parameter identification, frequency-domain fitting was employed, as illustrated in Figure 4b, Figure 5b and Figure 6b, where the spectral characteristics of the measured and estimated parameters showed a high degree of consistency. Figure 7 demonstrates that the time-domain attitude responses of the pitch, roll, and yaw rates matched well with the measured data. Quantitatively, as shown in Table 2, all channels achieved low MAE values (within 2 deg/s) and high coefficients of determination (above 0.92), confirming the reliability of the identified aerodynamic model. In particular, compared with the results reported in [33], where the roll rate exhibited a noticeable phase lag between simulation and measurement, the present model achieved a marked improvement, with the phase delay reduced to 0.08 s.

Overall, the modifications to the aerodynamic model presented in Section 2.3 were demonstrated to be effective, and the accuracy of the unmanned prototype gyroplane model was confirmed.

3.2. Modal Characteristics Analysis

Based on the identified longitudinal and lateral-directional linear models, the modal characteristics of the unmanned prototype gyroplane were obtained, as shown in Table 3 and Table 4. The eigenvalues in Table 3 and Table 4 (e.g., −0.040 ± 0.290 i) are complex numbers, where “i” denotes the imaginary unit.

Table 3. Longitudinal Modal Characteristics.

Modal	Eigenvalue	Damping	Period (s)
Phugoid mode	−0.040 ± 0.290 i	0.139	21.444
Short-period mode	−0.673 ± 1.570 i	0.395	3.696

Table 4. Lateral-Directional Modal Characteristics.

Spiral Time Constant (s)	Roll Time Constant (s)	Dutch-Roll Mode
		Eigenvalue	Damping	Period (s)
78.994	3.340	−0.381 ± 1.670 i	0.222	3.673

For the longitudinal dynamics, the unmanned prototype gyroplane exhibited both short-period and phugoid modes, similar to those for fixed-wing aircraft [34]. As shown in Table 3, the short-period mode had a period of 3.696 s, which was slightly slower than that of fixed-wing aircraft (2–3 s), and a damping ratio of 0.395, indicating good pitch stability. The phugoid period had a period of 21.444 s with a low damping ratio; therefore, additional damping through altitude control is required to satisfy flight quality requirements.

In terms of lateral-directional dynamics, the unmanned prototype gyroplane exhibited typical roll, Dutch-roll, and spiral modes. As shown in Table 4, the Dutch-roll mode had a pair of negative roots with a period of 3.673 s and a damping ratio of 0.222. This oscillatory mode arises from a coupling between roll, sideslip, and yaw motions when a sideslip disturbance occurs. Its frequency is primarily governed by L_b and N_b, while its damping is significantly influenced by yaw damping N_r and roll damping L_p. The roll mode had a time constant of 3.34 s, indicating fast convergence due to the large roll damping derivative L_p. The spiral mode had a long-time constant of 78.994 s, determined by the small roll static stability and large yaw static stability derivatives. Since the spiral mode converged slowly, its impact on short-term flight dynamics was relatively small.

The spiral mode time constant can be calculated analytically [30]. From Equation (4), by assuming that the L_r and N_p terms of the unmanned prototype gyroplane are zero, a simplified expression is obtained

$${\lambda }_s={\displaystyle \frac{g\left(L_{\beta }{N}_r\right)}{u\left(L_p{N}_{\beta }+g{L}_{\beta }/u\right)},}$$

(7)

where g is the gravitational acceleration, and l_s is the eigenvalue of the spiral mode.

This analytical approximation is highly effective for estimating the spiral mode eigenvalue. From Equation (7), the spiral eigenvalue l_s is influenced by both L_p, L_b, N_b, and N_r. Specifically, the large value of yaw damping N_r and the positive dihedral effect L_b both contribute to the negative eigenvalue, thereby ensuring a stable spiral mode.

In conclusion, the identified aerodynamic parameters accurately reproduce the flight dynamics of the unmanned prototype gyroplane, demonstrating high fidelity across three-axis attitude maneuvers. The modal analysis clarifies the dynamic characteristics of both longitudinal- and lateral-directional modes, thereby establishing a reliable basis for the design of control systems.

4. Autonomous Flight Control System Design

The main control actuators of the unmanned gyroplane include the rotor tilt angles, rudder, and throttle. The actions of these actuators result in pronounced coupling between longitudinal and lateral motions, as well as between airspeed and altitude. In addition, the response delays and trim requirements of each control channel pose significant challenges. Based on the aerodynamic model established in Section 3, this section presents an autonomous flight control architecture for the unmanned prototype gyroplane, and control laws are developed for each channel.

4.1. Flight Control Architecture

Unlike fixed-wing aircraft, the unmanned gyroplane adjusts the thrust vector through the tilt angles of the rotor in both the longitudinal and lateral directions. The throttle governs attitude and airspeed, while the rudder is responsible for heading control. To achieve stable and autonomous flight of the unmanned gyroplane, the main control challenges were analyzed.

(1)

The rotor disk serves as the primary actuator for both longitudinal and lateral control, meaning that any input in one channel affects the other. Achieving effective decoupling between the two channels remains a major challenge.

(2)

A particular challenge in pitch control arises from the fact that the fuselage itself does not generate lift, making conventional attitude-based feedback control unsuitable. In addition, the flexible structure connecting the control surfaces to the fuselage reduces the effectiveness of such schemes.

(3)

Control allocation between altitude and airspeed also poses a challenge. Thrust is typically used to control airspeed while pitch controls altitude, whereas the unmanned gyroplane exhibits nonlinear throttle-to-airspeed dynamics. Thus, the throttle is inadequate for precise airspeed control; instead, the rotor tilt angle proved to be more effective.

To address these challenges, an autonomous flight control architecture for the unmanned prototype gyroplane is proposed, as shown in Figure 8. It consists of four components: trim-decoupling feedforward control, airspeed control with pitch-damping augmentation, altitude and airspeed control allocation, and trajectory control based on roll attitude.

Figure 8. Autonomous flight control architecture for the unmanned prototype gyroplane.

As shown in Figure 8, trim-decoupling feedforward control is proposed to compensate for the coupling between the longitudinal and lateral channels. In this scheme, the control input and the corresponding attitude trim value of one channel (longitudinal or lateral) serve as feedforward signals to the other channel. For the specific pitch dynamics, pitch feedback is used to enhance longitudinal damping, serving as a stability augmentation of the airspeed control. The control allocation strategy assigns the throttle to manage altitude, while the longitudinal rotor tilt controls airspeed, enabling faster response and higher accuracy in airspeed control. Lateral-directional control follows a typical scheme: the outer-loop trajectory controller generates roll command, the inner-loop roll controller achieves stable tracking, and the rudder is used for trim and decoupling.

4.2. Control Law Design

4.2.1. Longitudinal Control System

The main challenge for longitudinal control is the management of altitude and airspeed, with the available actuators being the rotor longitudinal tilt and the engine throttle [35]. This problem is fundamentally different from that in fixed-wing aircraft, where lift is generated by the wings and correlates strongly with airspeed, making the traditional allocation of pitch for altitude and throttle for speed physically intuitive. For a gyroplane, in contrast, rotor thrust depends on both rotor speed and rotor tilt angle, leading to a strongly coupled dynamic between altitude and airspeed.

To clarify the physical rationale behind the longitudinal control design, the dynamic effects of the individual actuators on longitudinal channels were analyzed.

(1)

Isolated longitudinal rotor tilt input. A longitudinal rotor tilt generates an immediate horizontal force that directly affects airspeed. Meanwhile, the associated increase in angle of attack and rotor inflow leads to a rise in rotor thrust, compensating for the loss in vertical lift due to the tilt. Consequently, longitudinal rotor tilt has a dominant effect on airspeed while it has only a minor effect on altitude.

(2)

Isolated throttle input. Increasing the throttle produces an immediate forward acceleration, raising airspeed. The increased airspeed subsequently alters rotor inflow, which in turn raises the vertical lift component and induces a noticeable climb rate. Thus, the throttle input has a strong and rapid effect on altitude.

Moreover, the throttle–airspeed relationship is inherently nonlinear due to the unpowered rotor aerodynamics. Unlike in fixed-wing aircraft, where thrust often translates nearly linearly into acceleration, in a gyroplane, increasing throttle produces forward thrust and increases airspeed, while the higher airspeed modifies the rotor inflow and leads to a nonlinear rise in rotor RPM and its associated drag. Consequently, this nonlinearity between throttle and airspeed makes altitude regulation challenging when using throttle for speed control.

Therefore, the allocation strategy that assigns the longitudinal rotor tilt to airspeed and the throttle to altitude is proposed in Section 4.1. This scheme leverages the natural actuation characteristics of the gyroplane, where each control input is assigned to the variable it influences most directly and effectively. By aligning the control architecture with the vehicle’s unique physical dynamics, the coupling between altitude and airspeed is mitigated. This represents a fundamental architectural innovation, distinctly departing from conventional fixed-wing control systems.

Accordingly, the longitudinal control law of the unmanned gyroplane consists of two loops: the airspeed control loop and the altitude control loop. Altitude holding is achieved by a PID controller based on the trim throttle, where the throttle adjusts forward thrust and thus indirectly manages lift. The altitude control law is given as

$${\delta }_T={\overline{\delta }}_T+K_P^H(H-H_c)+K_I^H{\displaystyle \int (H-H_c)dt}+K_D^H\dot{H},$$

(8)

where ${\overline{\delta }}_T$ is the trim throttle; $K_P^H$, $K_I^H$, and $K_D^H$ denote the proportional, integral, and derivative gains for altitude control, respectively; $H$ is the altitude measurement; $H_c$ is the altitude command; and ${\delta }_T$ is the engine throttle.

Due to the delayed pitch response caused by rotor inflow dynamics, the conventional fixed-wing scheme, which uses pitch attitude as an inner loop for altitude tracking, is unsuitable for gyroplanes and would result in poor performance. Consequently, the pitch feedback control is redesigned as a stability augmentation system. Its primary objective is to enhance the longitudinal damping and thereby provide a stable platform for accurate airspeed tracking, rather than to track commands directly.

Accordingly, the airspeed control system adopts a parallel augmentation structure, where pitch state feedback control and an airspeed PI controller feed into the longitudinal rotor tilt, ensuring accurate airspeed tracking and stable dynamics. The longitudinal control law is designed as

$${\delta }_e={\overline{\delta }}_e+K_D^{\theta }q+K_P^{\theta }\theta +K_P^V(V_t-V_c)+K_I^V{\displaystyle \int (V_t-V_c)dt},$$

(9)

where ${\overline{\delta }}_e$ is the trim longitudinal rotor tilt; $K_P^{\theta }$ and $K_D^{\theta }$ denote the proportional and derivative gains for pitch control, respectively; $V_t$ is the airspeed measurement; $V_c$ is the airspeed command; $K_P^V$ and $K_I^V$ denote the proportional and integral gains for airspeed control, respectively; and ${\delta }_e$ is the longitudinal rotor tilt.

Remark 2. 

In Equation (9), the state feedback control of the pitch loop primarily provides sufficient damping for the airspeed control system, in which accurate tracking is not required. The airspeed integral term automatically trims pitch and enhances disturbance rejection.

4.2.2. Lateral-Directional Control System

The lateral-directional control of the unmanned gyroplane is designed to achieve trajectory tracking. As shown in Table 4, its lateral-directional characteristics are similar to those of fixed-wing unmanned aerial vehicles (UAVs). Accordingly, the inner loop is a roll attitude controller, and the outer loop generates roll commands based on trajectory errors. Note that the identified Dutch-roll mode is stable, and thus, yaw-rate feedback for stabilization is unnecessary, with the rudder employed only for decoupling.

Trajectory control is achieved through the lateral tilt of the rotor, where the roll command is generated by the heading error and the cross-track error, that is

$${\phi }_c=K_P^{\psi }(\psi -{\psi }_c)+K_P^Z(Z-Z_c)+K_I^Z{\displaystyle \int (Z-Z_c)dt},$$

(10)

where $\psi$ is the heading angle; ${\psi }_c$ is the heading angle command; $K_P^{\psi }$ is the proportional gain for heading control; $K_P^Z$ and $K_I^Z$ denote the proportional and integral gains for cross-track control, respectively; $Z$ is the cross-track distance; $Z_c$ is the cross-track command; and ${\phi }_c$ is the roll angle command.

The roll angle control loop is a PID controller, with its control input applied to the lateral tilt of the rotor. The control law is given as

$${\delta }_a={\overline{\delta }}_a+K_P^{\phi }(\phi -{\phi }_c)+K_I^{\phi }{\displaystyle \int (\phi -{\phi }_c)dt}+K_D^{\phi }p,$$

(11)

where ${\overline{\delta }}_a$ is the trim lateral rotor tilt; $K_P^{\phi }$, $K_I^{\phi }$, and $K_D^{\phi }$ denote the proportional, integral, and derivative gains for roll control, respectively; and ${\delta }_a$ is the lateral rotor tilt.

Finally, the rudder control law is given by

$${\delta }_r={\overline{\delta }}_r,$$

(12)

where ${\overline{\delta }}_r$ is the trim rudder for decoupling, and ${\delta }_r$ is the rudder deflection.

4.3. Simulation Verification

Based on the linear model at the cruise condition of 31.5 m/s illustrated in Section 3.1, control gains were designed using the root locus method [36] and simulated in the MATLAB/Simulink platform (R2023b).

For the longitudinal control system, the short-period damping ratio was set to 0.76, with stability margins of 24.9 dB and 67.6°. The designed altitude control gains were $K_P^H=0.4$, $K_I^H=0.05$, and $K_D^H=0.1$; the airspeed gains were $K_P^V=0.2$ and $K_I^V=0.1$; and the pitch gains were $K_P^{\theta }=0.4$ and $K_D^{\theta }=0.5$. The corresponding step responses are shown in Figure 9 and Figure 10. As shown in Figure 9, the rise time of the airspeed was approximately 8.5 s, with an overshoot of less than 10%, and the pitch angle converged to its trim value.

Figure 9. Response of the unmanned gyroplane to a step command in airspeed.

Figure 10. Step response of the altitude.

For lateral control, the heading gain was tuned as $K_P^{\psi }=0.5$; cross-track gains as $K_P^Z=0.12$ and $K_I^Z=0.05$; and the roll control gains as $K_P^{\phi }=0.5$, $K_I^{\phi }=0.05$, and $K_D^{\phi }=0.1$. The corresponding step responses are shown in Figure 11. The cross-track response had a rise time of 16 s with a maximum overshoot of 12%, while the roll response rose in less than 1 s with a maximum overshoot of 5%.

Figure 11. Step responses of the lateral-directional control system.

The simulation results demonstrate that the proposed control architecture effectively decouples the longitudinal and lateral channels and ensures accurate tracking of airspeed, altitude, and trajectory commands. Both transient and steady-state performance meet the requirements for autonomous flight of the unmanned prototype gyroplane.

5. Experimental Validation

Based on the unmanned gyroplane aerodynamic model and autonomous flight control strategies proposed in Section 3 and Section 4, this section conducts the actual flight tests to assess the engineering practicality. The control performance is separately evaluated in terms of altitude, airspeed, and trajectory tracking.

5.1. Experimental Setup for Flight Test

A photograph of the flight is presented in Figure 12. The flight route consists of two 5.5 km straight segments and two semicircular turns with a radius of 1 km. During the straight segments, altitude commands were applied, while lateral-directional tracking was tested during the semicircular turns. The flight began with a takeoff, followed by a climb to 300 m, after which the aircraft switched to autonomous flight and tracked the designated trajectory. Details of the controller design are provided in Appendix A.

Figure 12. On-site test photo of the unmanned gyroplane.

5.2. Results and Analysis

5.2.1. Airspeed Control Performance

To evaluate the longitudinal energy management of the unmanned gyroplane, the altitude command consisted of a descent from 300 m to 100 m, followed by a climb back to 320 m. The corresponding airspeed and pitch angle tracking results are shown in Figure 13.

Figure 13. Airspeed control results during descent and climb.

As illustrated in Figure 13a, the airspeed control maintained precise tracking even during large-altitude variations. The tracking errors were constrained within ±1.5 m/s, with an MAE of 0.57 m/s. This validates the altitude and airspeed allocation strategy presented in Section 4.1. Figure 13b shows that the pitch angle tracking achieved an MAE of 3.49°, which, as anticipated, did not compromise the accurate airspeed control. The pitch control primarily provided damping for flight stability rather than command tracking. Overall, the utilization of rotor tilt as the control input for airspeed regulation proved effective.

Remark 3. 

The airspeed and pitch commands shown in Figure 13 are determined by the trim values obtained from prior pilot flight data. When the flight mode transitions from descent to climb, these trim values change, resulting in a step in the command.

5.2.2. Altitude Control Performance

To verify the performance of the altitude control, a flight test was performed where the unmanned gyroplane transitioned from a climb to level flight. The flight data are shown in Figure 14.

Figure 14. Altitude and airspeed tracking during climb and level flight with trim correction.

As shown in Figure 14a, when the unmanned gyroplane transitioned from climb to level flight, the throttle dropped abruptly from 85% to 30%, leading to a descent with a vertical speed of −5 m/s, as observed in Figure 14d. The preset trim throttle of 30% was obtained at low altitude, whereas at higher flight altitudes, the reduced air density requires a higher throttle setting to maintain level flight. Consequently, the integral action of the altitude controller actively compensated for this discrepancy, adjusting the throttle until it converged to a stable value of 57%. This converged value was thus identified as the necessary trim setting for level flight at that altitude and was used as the corrected throttle trim command for the subsequent flight test.

Consequently, a second flight test was conducted with the corrected throttle trim command. The altitude tracking is shown in Figure 14c, and Figure 14d illustrates the comparison of vertical speed before and after trim correction. The MAE and SD of tracking errors are summarized in Table 5.

Table 5. Tracking Error Indices of Altitude Control Before and After Trim Correction.

Indicators	Before Trim Correction		After Trim Correction		Improvement
	MAE	SD	MAE	SD
Airspeed Error (m/s)	0.89	1.10	0.57	0.70	35.94% (of MAE)
Altitude Error (m)	46.79	52.36	38.48	50.69	15.97% (of MAE)
Vertical Speed (m/s)	1.13	2.38	1.41	1.42	40.45% (of SD)

From Figure 14c,d, it can be seen that the corrected trim led to smoother altitude tracking and vertical speed response, and the throttle no longer experienced excessive drops. The distribution of vertical speed in the 1.5~5 m/s range became more concentrated, and its peak value decreased from 3.8 m/s to 3 m/s. Table 5 shows that airspeed tracking was consistently accurate, with mean errors below 1 m/s. Meanwhile, the MAE of altitude error and the SD of vertical speed were improved by 16% and 40%, respectively. These results confirm that the proposed altitude control strategy exhibits sufficient robustness.

5.2.3. Trajectory Tracking Performance

Finally, the trajectory tracking performance was evaluated through turning maneuvers. The flight results are shown in Figure 15 and Table 6.

Figure 15. Flight test results of the unmanned gyroplane during a left-turn maneuver.

Table 6. Tracking Error Analysis of the Unmanned Gyroplane During the Left-Turn Maneuver.

Indicators	Roll Angle (°)	Speed (m/s)	Altitude (m)	Cross-Track Distance (m)
MAE	0.75	1.00	27.07	8.54
SD	1.02	1.17	33.85	11.66

As shown in Figure 15a and Table 6, during the left-turn maneuver, the maximum roll command reached 10°, with an MAE of 0.75°. This indicates that the roll tracking performance is satisfactory. For trajectory control, Figure 15b shows that the cross-track deviation increased up to 30 m during the turn but gradually converged to zero, with an MAE of 8.54 m. Figure 15c presents the altitude and airspeed tracking results, which are consistent with those presented in Section 5.2.1 and Section 5.2.2. It was observed that the airspeed tracking error increased during the period when the corresponding lateral rotor tilt was non-zero. This behavior is attributed to the additional aerodynamic drag and transient coupling induced by the turning maneuver. Since the trim-decoupling feedforward control is designed based on a model identified under single-axis excitation, it cannot fully compensate for these transient effects, resulting in a temporary drop in airspeed. Notably, Dutch-roll oscillations were not observed, confirming that the rudder is mainly used for trim.

In conclusion, the autonomous flight experiments demonstrate that the proposed control architecture can effectively manage the longitudinal energy and achieve lateral trajectory tracking under dynamic flight conditions. Moreover, the applicability of the trim-based decoupling strategy is confirmed, which performs reliably in the steady-state condition.

6. Conclusions

To address the key issues in aerodynamic modeling and control design of unmanned gyroplanes, a targeted methodology is proposed in this paper.

For aerodynamic modeling, a modified parameter identification structure was developed based on coherence analysis, which effectively improved the modeling accuracy. Both time-domain and frequency-domain validations demonstrated that the identified model reproduces the longitudinal and lateral dynamics with high fidelity. In particular, the coefficients of determination exceeding 0.92 and the small phase delays within ±0.1 s indicate high consistency between the identified model and flight responses, thereby providing a solid foundation for subsequent control design.

To address the unique flight characteristics of unmanned gyroplanes, a novel autonomous flight control system is proposed. The proposed control strategy achieves longitudinal-lateral decoupling under a single actuator, compensates for throttle-airspeed nonlinearities, and enhances airspeed control performance under delayed pitch dynamics through pitch-damping augmentation. This approach overcomes the limitations of conventional flight control frameworks when applied to unmanned gyroplane platforms and provides theoretical support for achieving efficient control of unmanned gyroplanes.

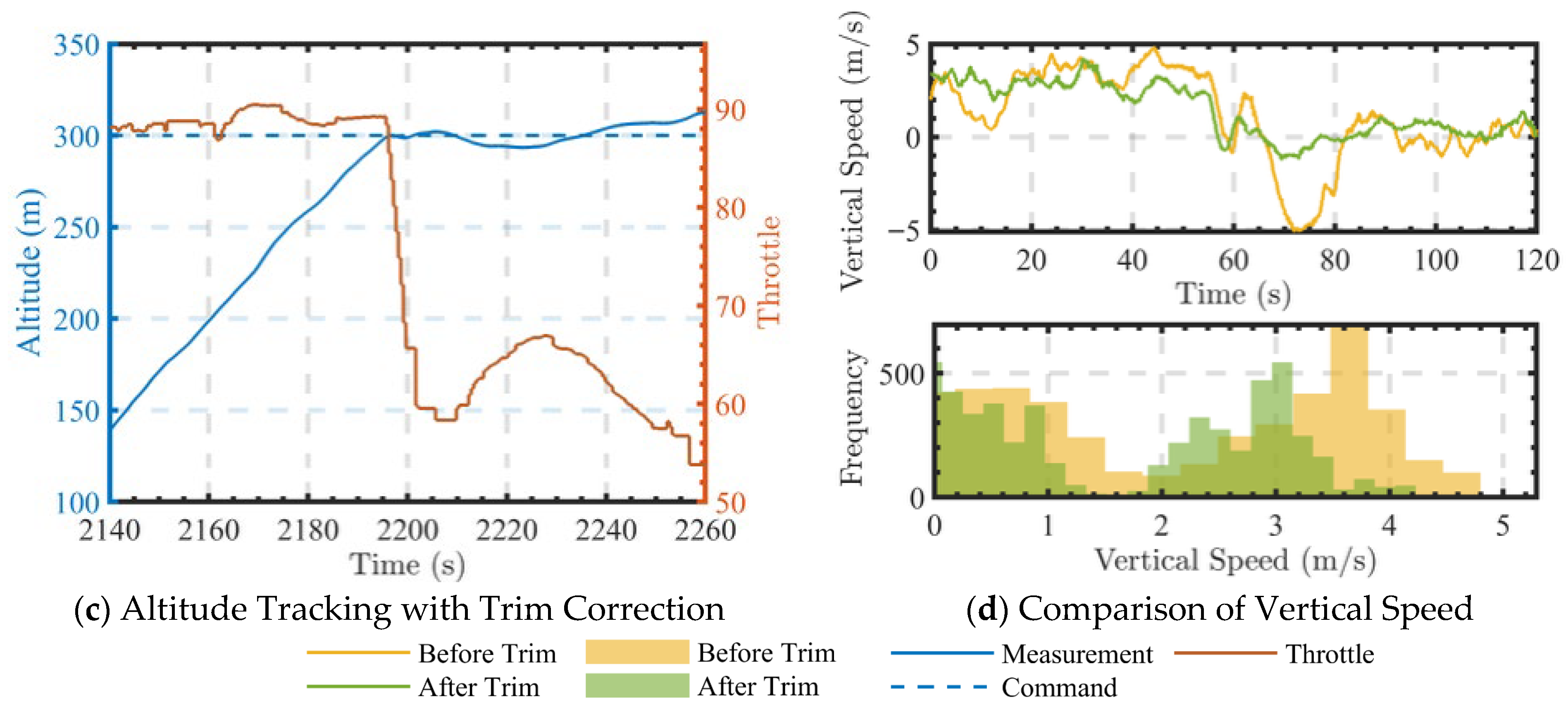
In terms of the practical aspect, the proposed autonomous flight control system was implemented on an unmanned gyroplane prototype converted from a manned platform. Flight tests showed a 40% improvement in climb rate stability with corrected throttle trim, and the airspeed tracking error remained within 1.5 m/s under dynamic conditions, demonstrating the effectiveness and practical applicability of the proposed control strategy. Notably, the high-precision airspeed control effectively prevents unmanned gyroplane stall, ensuring flight safety.

Overall, a comprehensive methodology for high-fidelity aerodynamic modeling and autonomous control of unmanned gyroplanes was established. Both theoretical and experimental results verified its effectiveness, providing a basis for future flight envelope expansion and performance improvements. Future work will focus on extending its applicability by incorporating transient coupling effects into the control framework and investigating the applicability of the total energy control system to the unique rotorcraft dynamics.