Auction- and Pheromone-Based Multi-UAV Cooperative Search and Rescue in Maritime Environments

Highlights

What are the main findings?

• Novel hybrid framework: Integrates auction-based task allocation with pheromone-guided exploration for maritime search and rescue, addressing gaps in existing approaches that treat these mechanisms separately.
• Multi-layer simulation model: Develops a four-dimensional maritime SAR model incorporating Obstacle, Target, Pheromone, and Agent layers to simulate realistic maritime dynamics including target drift and decentralized coordination.

What is the implication of the main finding?

• Superior performance validated: Experimental results demonstrate that the hybrid strategy improves search efficiency by up to 27.1% compared to pheromone-only methods and reduces overlap rates to 0.135–0.164, significantly outperforming traditional approaches.
• Scalability proven: The hybrid method maintains effectiveness across varying map scales (5 × 5 to 50 × 50) and agent configurations (2–8 agents), with coverage speed improvements of 64.7% in medium-scale scenarios.

Abstract

Unmanned aerial vehicles (UAVs) play an increasingly vital role in maritime search and rescue (SAR) because they can be deployed quickly, cover large ocean areas, and operate without exposing human crews to risk. Compared with single platforms, multi-UAV cooperation improves efficiency in locating drifting targets influenced by wind and currents. However, existing allocation methods often focus only on immediate task benefits and neglect search history, leading to redundant revisits and lower overall efficiency. To address this problem, we propose a hybrid auction–pheromone framework for multi-UAV maritime SAR. The method combines an auction-based allocation strategy, which assigns tasks according to target probability, distance, and UAV workload, with a pheromone-guided mechanism that records visitation history through exponential decay to discourage repeated searches. A layered model is constructed, consisting of an airspace/weather constraint layer, a target probability layer, a pheromone layer, and a UAV motion layer. UAVs adopt A* path planning with a nearest-first policy, while a stagnation detector triggers dynamic reallocation when coverage slows. Simulation experiments verify the effectiveness of the proposed approach. Compared with auction-only and pheromone-only baselines, the hybrid method reduces the required steps by up to 27.1%, decreases the overlap ratio to 0.135–0.164, and increases the coverage speed by 64.7%. These results demonstrate that integrating explicit auctions with implicit pheromone memory significantly enhances scalability, robustness, and efficiency in multi-UAV maritime SAR. Future research will focus on dynamic drift modeling, real-world deployment, and heterogeneous UAV collaboration.

1. Introduction

Maritime search and rescue (SAR) remains a time-critical mission characterized by vast uncertain search spaces and drifting targets driven by wind–current coupling. Recent reviews show a clear shift from single UAV to cooperative multi-UAV SAR to improve coverage, reduce response time, and increase probability of success [1,2,3]. These studies also emphasize that allocation and coordination policies determine most of the performance gains, rather than platform hardware alone.

At present, maritime SAR are confronted with a series of challenges. First, perception at sea is intrinsically difficult: small targets on low contrast, specular water backgrounds degrade detector recall; latest surveys and benchmarks report frequent false negatives in SeaDronesSee like imagery and highlight sea clutter, glint, and scale issues [4]. Second, communication is often intermittent/BVLOS and bandwidth constrained, forcing decentralized coordination and on-board triage of visual ROIs [2,5,6]. Third, localization and networking may be GNSS-denied or range limited in offshore settings, which further favors distributed search strategies [7]. Together these factors motivate coordination mechanisms that are robust to limited comms, can reuse search history to avoid overlap, and can scale with fleet size.

In addition to operational difficulties, target drift modeling represents another key challenge. Beyond wind and current, recent work shows wave-induced drift can be non-negligible for certain object sizes; OpenDrift/leeway-type operational models remain the standard, yet studies continue to refine leeway and validate with drifters [8,9,10,11]. These insights support SAR planners that update probability maps over time and motivate probability aware search policies.

In response to these challenges, two mainstream coordination approaches have dominated the recent literature.

(1) One major approach is market/auction-based allocation (e.g., CBBA family), which offers low communication overhead, distributed convergence, and good real-time performance. The past three years have added reallocation under damage/failures [12], communication efficient variants for heterogeneous swarms [13], and multi criteria/dynamic constraints [14]. Yet, these methods are often myopic to search history, which can increase revisit/overlap in coverage-driven missions [1].

(2) Another prominent line of work employs swarm intelligence/pheromone-based search, which shares visitation history implicitly via virtual pheromones, reducing redundant revisits and enabling infrastructure free coordination. Recent contributions include virtual pheromone-distributed search and target selection [15], pheromone reinforcement learning for online coverage in dynamic environments [16], and 3D-distributed coverage that integrates pheromone matrices with learning-based dispatching [17]. These strategies are robust to comm dropouts but can be parameter sensitive and slower to exploit high-probability regions without explicit task value signals.

A growing trend in the last three years has been the emergence of hybrid coordination schemes. A visible trend is to blend market mechanisms with swarm intelligence or evolutionary optimization to trade off exploitation (task value/distance) and exploration (history aware dispersion). Examples include anti-pheromone + market-based mapping to curb overlap under connectivity limits [18], auction + endurance aware planning (RangeTAP) for battery/range constraints [19], or augments coverage with probability guided sweep strategies [20]. Most of these hybrids show improved convergence and lower overlap, but few explicitly fuse (i) an auction that prices probability/distance/workload with (ii) a decaying pheromone memory to suppress revisits and (iii) drift aware probability updates for maritime SAR.

To address the above gaps, we integrate an auction-based allocation (task probability, distance, and UAV workload) with a pheromone layer that records visitation history via exponential decay, and we add a stagnation detector for dynamic reallocation. A layered maritime SAR model (Obstacle/Target/Pheromone/UAV) and A*-based routing support both probability-priority and spatial coverage phases. This design directly targets the “overlap/myopia” weakness of pure auctions and the “parameter-only exploration” weakness of pure pheromone swarms. Simulation across map scales (5 × 5–50 × 50) and team sizes (2–8 UAVs) shows up to 27.1% fewer steps than pheromone-only methods, overlap ratio 0.135–0.164, and 64.7% higher coverage speed at medium scale, corroborating the scalability and efficiency of the hybrid scheme in maritime SAR.

The main contributions of this article are as follows:

• Novel hybrid framework: Integrates auction-based task allocation with pheromone-guided exploration for maritime search and rescue, addressing gaps in existing approaches that treat these mechanisms separately.
• Multi-layer simulation model: Develops a four-dimensional maritime SAR model incorporating Obstacle, Target, Pheromone, and Agent layers to simulate realistic maritime dynamics including target drift and decentralized coordination.
• Superior performance validated: Experimental results demonstrate the hybrid strategy improves search efficiency by up to 27.1% compared to pheromone-only methods and reduces overlap rates to 0.135–0.164, significantly outperforming traditional approaches.
• Scalability proven: The hybrid method maintains effectiveness across varying map scales (5 × 5 to 50 × 50) and UAV configurations (2–8 UAVs), with coverage speed improvements of 64.7% in medium-scale scenarios.

The remainder of this paper are organized as follows: Section 2 constructs a four-layer multidimensional maritime search and rescue model consisting of Obstacle–Target–Pheromone–Agent layers; Section 3 introduces the auction algorithm integrated with pheromone mechanism and its implementation details; Section 4 validates the algorithm’s effectiveness and scalability under different map scales and agent configurations; Section 5 summarizes the entire work and proposes future improvement directions.

2. Multidimensional Maritime Cooperative SAR Model

The multi-UAV cooperative maritime search and rescue (SAR) problem aims to efficiently locate drifting targets in a discrete maritime environment using a team of UAVs while minimizing search time, maximizing target detection probability, and reducing redundant coverage.

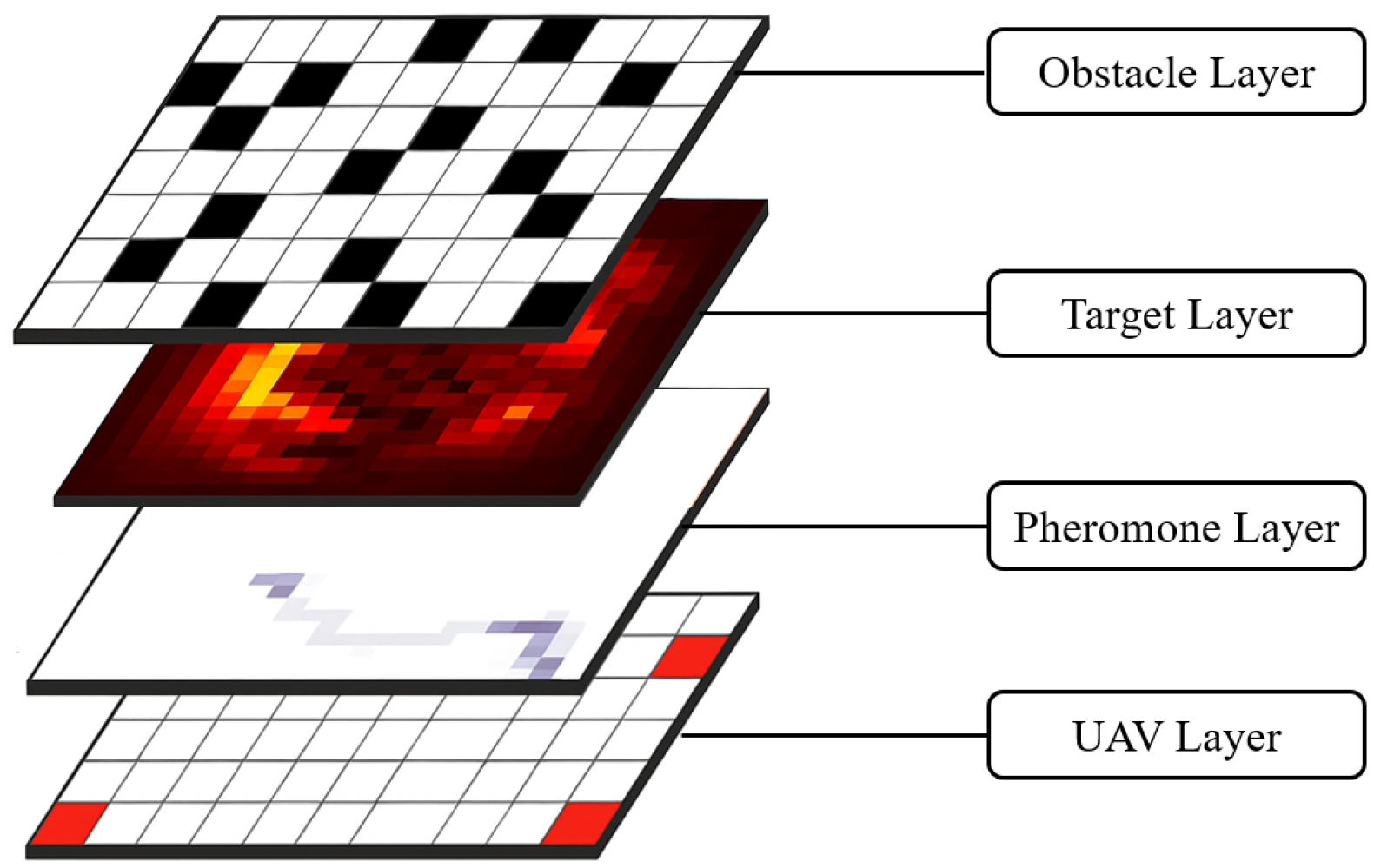
To effectively simulate complex maritime multi-UAV cooperative SAR scenarios, this paper models the actual SAR area as a two-dimensional discrete grid system composed of multiple layers, as shown in Figure 1. The SAR area is rasterized into an area of $M\times N$, which is expressed as

$$\mathcal{G}=\left\{g_{(x,y)}\right|x\in [1,M],y\in [1,N]\}$$

(1)

and consists of four overlapping functional layers: the Obstacle layer, Target layer, Pheromone layer, and UAV layer.

2.1. Obstacle Layer

In maritime SAR, UAVs may encounter restricted airspace (e.g., no-fly zones), communication blind zones, or severe weather cells that cannot be crossed (i.e., obstacles). To simulate such obstacles, this paper randomly generates a certain proportion of obstacle regions (typically 10%) within the grid map. The obstacle set is represented as

$$\mathcal{O}\subset \mathcal{G}$$

(2)

and these grid cells are considered impassable and form restrictions for UAV path planning. The set of passable areas is expressed as

$$\mathcal{F}=\mathcal{G}\setminus \mathcal{O}$$

(3)

To ensure the overall navigability of the map, the breadth-first search (BFS) algorithm is used during the obstacle generation process to verify connectivity, ensuring that there is always a feasible path between any two non-obstacle grid cells.

After the map is initialized, the system records the visit status $v_{(x,y)}\left(t\right)$, visit count $c_{(x,y)}\left(T\right)$, and probability information for each grid cell. $v_{(x,y)}\left(t\right)=1$ if and only if cell $(x,y)$ was visited before time t. $c_{(x,y)}\left(T\right)$ represents the cumulative number of visits to cell $(x,y)$ up to time t. This obstacle layer provides the foundational spatial environment for subsequent task allocation, path planning, and coordination mechanisms.

2.2. Target Layer

Actual maritime targets (such as missing persons) exhibit significant drift characteristics under the influence of wind and ocean currents. This paper models the uncertainty in their spatial distribution using a drift model. Assuming the last known position of the target is $P_0(x_0,y_0)$, the expected drift center of the target $P_d(x_d,y_d)$ can be estimated as

$$P_d=\left(x_0+{\omega }_{x}ct,y_0+{\omega }_{y}ct\right)$$

(4)

where t is the drift time. $\omega$ is the wind direction: ${\omega }_x$ and ${\omega }_y$, respectively, represent their components in the horizontal and vertical directions. c is the ocean current intensity.

The uncertainty in the target’s position is modeled as a two-dimensional Gaussian distribution, with the probability of the target’s presence at grid cell $(x,y)$ calculated as

$$p(x,y)={\displaystyle \frac{1}{2\pi {\sigma }^2}}exp\left(-{\displaystyle \frac{{\left(x-x_d\right)}^2+{\left(y-y_d\right)}^2}{2{\sigma }^2}}\right)$$

(5)

where $\sigma$ is the diffusion factor, which adjusts over time and with the scale of the map:

$$\sigma =(3+0.8·t_d)·\sqrt{MN}/10$$

(6)

reflects the increasing uncertainty over time. The probability that the target appears in cell $(x,y)$ at the initial moment is $p_0$. This choice is reasonable for short to moderate horizons due to the following reasons:

(i) Many small, independent perturbations (gusts, short-scale eddies, heading jitter) accumulate additively around the mean advection; by the central limit effect, the resulting displacement distribution is well approximated by a Gaussian.

(ii) The classical advection–diffusion formulation leads to Gaussian solutions whose mean follows the drift and whose variance grows approximately linearly in time; $\sigma \left(t\right)$ represents this behavior on a grid (scaling with $\sqrt{MN}$ avoids making $\sigma$ artificially small/large when map resolution changes).

(iii) Practically, our search algorithm only needs a calibrated prior over likely locations; a unimodal, smooth prior centered on mean drift is desirable to avoid brittle, multi-peak artifacts.

To prevent the search from being biased toward high-probability regions and neglecting boundaries, the system sets a minimum base probability to ensure that all passable areas have a non-zero search priority, expressed as

$$p_{(x,y)}\left(0\right)\leftarrow max\left(p_{(x,y)}\left(0\right),{\displaystyle \frac{0.01}{\sqrt{MN}/10}}\right)$$

(7)

During the actual search process, if no target is found in a grid cell, its probability value is updated:

$$p_{(x,y)}(t+1)=\alpha ·p_{(x,y)}\left(t\right),\alpha =0.3$$

(8)

and the lost probability mass $(1-\alpha )·p_{(x,y)}\left(t\right)$ is dynamically redistributed to other areas, creating an adaptive probability map:

$$p_{(x^{\prime },y^{\prime })}(t+1)=p_{(x^{\prime },y^{\prime })}\left(t\right)+{\displaystyle \frac{(1-\alpha )·p_{(x,y)}\left(t\right)·p_{(x^{\prime },y^{\prime })}\left(t\right)}{{\sum }_{g\in \mathcal{F},v_g=0,g\ne (x,y)}{p}_g\left(t\right)}},\forall \left(x^{\prime },y^{\prime }\right)\ne (x,y),v_{(x^{\prime },y^{\prime })}\left(t\right)=0$$

(9)

2.3. Pheromone Layer

Inspired by the ant colony optimization algorithm, this paper introduces a pheromone mechanism to improve the efficiency of cooperative search by the UAVs. Each UAV leaves pheromones on the grid cells that it visits, marking its visit history and reducing redundant searches.

The pheromone map undergoes exponential decay at each time step, with the update rule given as

$${\tau }_{(x,y)}^{(t+1)}=\rho ·{\tau }_{(x,y)}^{\left(t\right)}$$

(10)

where ${\tau }_{(x,y)}^{\left(t\right)}$ represents the pheromone concentration at grid cell $(x,y)$ at time step t, and $\rho \in (0,1)$ is the pheromone decay coefficient. A smaller $\rho$ value accelerates the decay of old path information, thereby enhancing the system’s exploratory behavior. When a UAV accesses the cell $(x,y)$, increase in pheromone $\Delta \tau =1.0$.

During task allocation, pheromone concentration is introduced as a negative influencing factor in the bidding function. The higher the pheromone concentration at a grid cell, the lower its priority for task allocation. This mechanism guides the system to prioritize the exploration of unvisited or less-visited areas, improving overall spatial coverage efficiency and reducing task overlap.

2.4. UAV Layer

Multiple UAVs in this model collaborate to perform search tasks. The UAVs exist as independent entities on the map, each with autonomous path-planning capabilities. The definition of a UAV formation is as follows:

$$\mathcal{U}=\{u_1,u_2,...,u_n\}$$

(11)

the position of UAV $u_i$ in the network at time t is represented as

$$s_i\left(t\right)=(x_i\left(t\right),y_i\left(t\right))\in \mathcal{F}$$

(12)

and its initial position is denoted as $S_i\left(0\right)=s_i\left(0\right)$.

At each time step, a UAV chooses an adjacent passable grid cell to move to, with movement directions including up, down, left, right, and the four diagonal directions, simulating real-world mobility conditions. The action space is expressed as

$$\mathcal{A}=\left\{\right(\delta x,\delta y\left)\right|\delta x,\delta y\in \{-1,0,1\}\}$$

(13)

The initial positions of the UAVs are preferably selected in unobstructed areas along the map’s edge or corners. If blocked by obstacles, the nearest accessible point is selected as an alternative. The task execution order and paths of the UAVs are coordinated by an auction mechanism and the A* algorithm, with the goal of covering the target area assigned by the system at minimum cost.

For task allocation, the set of candidate task units at time t is represented as

$$\mathcal{T}\left(t\right)=\{g_{(x_1,y_1)},g_{(x_2,y_2)},...,g_{(x_k,y_k)}\}$$

(14)

and the task queue assigned to UAV $u_i$ at time t is denoted as

$${\mathcal{T}}_i\left(t\right)\subseteq \mathcal{T}\left(t\right)$$

(15)

and the workload of UAV $u_i$ (i.e., the number of tasks to be executed) is expressed as

$$L_i\left(t\right)=\left|{\mathcal{T}}_i\left(t\right)\right|$$

(16)

It should be stated that path planning is not the main focus of this paper; therefore, the traditional A* algorithm adopted here will not be elaborated in detail. The planned path for UAV $u_i$ is represented as

$${\pi }_i\left(t\right)=\left[s_i\left(t\right),s_i(t+1),\dots ,s_i(t+k)\right]$$

(17)

2.5. Problem Formulation

The multi-UAV maritime SAR problem is formulated as a multi-objective optimization problem balancing search time, target detection probability, and redundancy minimization.

2.5.1. Main Optimization Objective

Multi-objective optimization problems can be expressed in the form of Pareto optimization:

$$\underset{\mathcal{T}i\left(t\right),{\pi }_i\left(t\right)}{min}\left(J_{\mathrm{time}},J_{\mathrm{overlap}},-J_{\mathrm{prob}},-J_{\mathrm{spatial}}\right)$$

(18)

Each objective is defined as follows:

Objective 1: Time Efficiency Minimization

$$J_{\mathrm{time}}=T_{\mathrm{complete}}$$

where $T_{\mathrm{complete}}$ is the total number of time steps required to reach the termination condition.

Objective 2: Redundant Visits Minimization

$$J_{\mathrm{overlap}}={\displaystyle \frac{1}{\left|\mathcal{F}\right|}}\sum _{g_{(x,y)}\in \mathcal{F}}max(0,c_{(x,y)}\left(T\right)-1)$$

measures the average number of redundant visits per feasible cell, reflecting the coordination efficiency among UAVs.

Objective 3: Probability Coverage Maximization

$$J_{\mathrm{prob}}=\sum _{g_{(x,y)}\in \mathcal{F}}{p}_{(x,y)}\left(0\right)·v_{(x,y)}\left(T\right)$$

is the cumulative initial target probability of visited cells, representing the expected success rate of target detection. This metric focuses on target-oriented search efficiency.

Objective 4: Spatial Coverage Maximization

$$J_{\mathrm{spatial}}={\displaystyle \frac{1}{\left|\mathcal{F}\right|}}\sum _{g_{(x,y)}\in \mathcal{F}}{v}_{(x,y)}\left(T\right)$$

is the proportion of visited cells relative to the feasible region, ensuring spatial completeness and exhaustiveness of the search.

Due to the NP-hard nature of the problem, finding the true Pareto front is computationally infeasible. This paper adopts a two-phase heuristic strategy to approximate multi-objective optimization:

• Phase 1 (Probability Priority): Primarily optimizes $J_{\mathrm{prob}}$ and $J_{\mathrm{time}}$, while controlling $J_{\mathrm{overlap}}$.
• Phase 2 (Spatial Coverage): Primarily optimizes $J_{\mathrm{spatial}}$ and $J_{\mathrm{time}}$, while relaxing $J_{\mathrm{overlap}}$ constraints.

The bidding function (Section 3.1.1) implements adaptive trade-offs among objectives through dynamic weights $w_1\left(\varphi \right),w_2\left(\varphi \right),\mu \left(\varphi \right)$, avoiding the subjectivity of preset fixed-weight parameters.

2.5.2. Constraints

The following constraints must be satisfied during the search process:

Constraint 1: Connectivity (eight-directional movement)

$$\forall t,\forall u_i:s_i(t+1)\in {\mathcal{N}}_8\left(s_i\left(t\right)\right)\cap \mathcal{F}$$

(19)

where ${\mathcal{N}}_8\left(s\right)=\left\{(x+\Delta x,y+\Delta y)\right|(\Delta x,\Delta y)\in \mathcal{A}\}$ is the eight-connected neighborhood.

Constraint 2: Obstacle Avoidance

$$\forall t,\forall u_i:s_i\left(t\right)\notin \mathcal{O}$$

(20)

Constraint 3: Collision Avoidance (Temporal Isolation)

$$\forall t,\forall u_i,u_j(i\ne j):s_i\left(t\right)\ne s_j\left(t\right)$$

(21)

is implemented through temporal isolation via pheromone mechanism and auction mechanism.

Constraint 4: Task Exclusivity

$$\forall g_j\in \mathcal{T}\left(t\right):\left|\left\{u_i\right|g_j\in {\mathcal{T}}_i\left(t\right)\}\right|\le 1$$

(22)

where each task cell is assigned to at most one UAV.

Constraint 5: Probability Coverage Threshold (Phase 1 Goal)

$$\sum _{g_{(x,y)}\in \mathcal{F}}{p}_{(x,y)}\left(0\right)·v_{(x,y)}\left(t\right)\ge {\theta }_{\mathrm{prob}}$$

(23)

where ${\theta }_{\mathrm{prob}}=0.95$ (95% probability coverage threshold).

Constraint 6: Spatial Coverage Requirement (Phase 2 Goal)

$${\displaystyle \frac{{\sum }_{g_{(x,y)}\in \mathcal{F}}{v}_{(x,y)}\left(T\right)}{\left|\mathcal{F}\right|}}\ge {\theta }_{\mathrm{spatial}}$$

(24)

where ${\theta }_{\mathrm{spatial}}=1.0$ (complete spatial coverage).

Constraint 7: Map Connectivity Verified. Using BFS: $\forall g_1,g_2\in \mathcal{F}$, there exists a path $\pi :g_1⇝g_2$.

3. Auction-Based Task Allocation Algorithm

Building on the four-layer maritime SAR model introduced in Section 2 (Obstacle, Target, Pheromone, UAV), we develop a closed-loop strategy that combines explicit auction-based task allocation with implicit pheromone-based search awareness. The core motive is to improve large-area collaboration while suppressing redundant revisits through lightweight, decentralized coordination.

Prior work shows that auction algorithms (e.g., CBBA) are popular for their decentralized decision-making and low communication burden, yet they often prioritize immediate gains and neglect historical search data, which can increase overlap. In contrast, pheromone-inspired mechanisms share history implicitly but usually lack explicit task coordination at scale. Integration of the two strands remains limited. We explicitly address this gap via a hybrid that injects pheromone feedback into the bid function and couples it with phase switching between probability-priority and coverage-priority modes.

Operationally, we adopt a two-phase execution: Phase 1 ends once probability coverage reaches 95%, after which Phase 2 emphasizes full spatial coverage with stronger anti-revisit behavior; throughout, we record steps, Phase-1 completion time, final coverages, and overlap rate for evaluation.

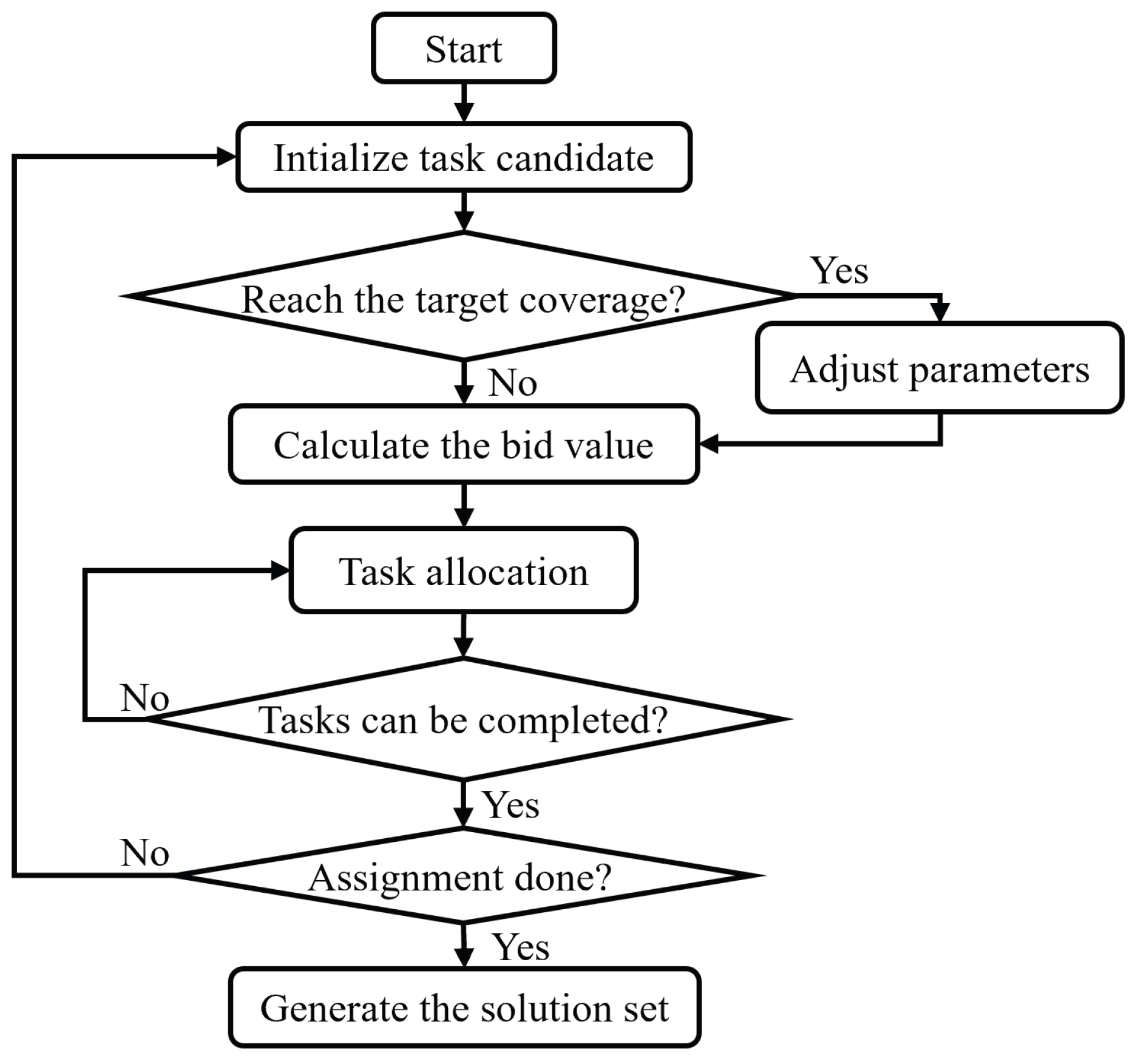
With the rationale and high-level loop clarified, we next present the overall framework before delving into each module. The algorithm flow is shown in Figure 2.

3.1. Module Details

During the design of the algorithm, we also encountered a series of issues: (i) Redundant revisits due to the lack of historical awareness; to address this, we designed an exponentially decaying pheromone map and incorporated pheromone as a negative factor in the bid function to downweight previously visited regions. (ii) Load imbalance and coordination inefficiency at scale; to address this, we introduced a workload penalty and phase-dependent weights $w_1,w_2$ into the bid function to dynamically balance probability and distance. (iii) Execution stagnation (blocked paths, local congestion); to address this, we implemented online stagnation detection and task reclamation followed by re-auctioning to maintain continuity. (iv) Tension between “probability-first” and “coverage-first” goals; to address this, we adopted a two-phase search that switches at 95% probability coverage and reweights the bid to favor unvisited areas. Details are as follows.

3.1.1. Task Auction and Bid Function

For candidate generation, we filter out visited, obstacle, and already-assigned cells, then sort candidates by target probability (Phase 1) or inverse distance-weighted probability (Phase 2).

The task candidate generation process has O(n²) complexity for an n × n grid map. To control computational costs,

• We limit auction rounds to $min(\sqrt{n},20)$ tasks per iteration;
• Candidate filtering uses spatial indexing with $O\left(logn\right)$ lookup;
• Priority queue maintains top-k candidates in $O\left(klogn\right)$ time;
• For a 50 × 50 map with eight UAVs, average computation time per auction round is 0.023 s on standard hardware.

For bid function, let $P_j$ be the target probability of cell j, $d_{ij}$ the UAV–cell distance, $L_i$ the current workload of UAV i, and ${\tau }_j$ the pheromone at j. The comprehensive bidding score balances probability, movement cost, load, and anti-revisit feedback, with phase- dependent weights:

$${Bid}_{i,j}={\displaystyle \frac{w_1\left(\phi \right)P_j+w_2\left(\phi \right)}{d_{i,j}+1}}\times {\displaystyle \frac{1}{1+\kappa L_i}}\times exp\left(-\mu \left(\phi \right){\tau }_j\right)$$

(25)

Specifically, during probability-priority phase $\phi =prob$, $w_1=1$, $w_2=0$, $\mu =0.8$; in spatial coverage phase $\phi =cov$, $w_1=0.3$, $w_2=0.7$, $\mu =0.2$, and workload balance parameter $\kappa =0.1$. This function balances target-oriented probability search, movement cost, workload balancing, and pheromone feedback, ensuring fair and efficient task allocation.

For allocation and online monitoring, the highest bids win and completed tasks are removed. We continuously track probability coverage and switch at 95% to coverage-priority, increasing the role of distance and pheromone penalties. If stagnation is detected, tasks are reclaimed and re-auctioned. Pheromone dynamics and their negative feedback in the bid are detailed next.

3.1.2. Pheromone Attenuation

Each visit deposits pheromone; the map decays exponentially after each step: ${\tau }_{(x,y)}^{(t+1)}=\rho ·{\tau }_{(x,y)}^{\left(t\right)}$ with $0<\rho <1$ so that older traces fade and exploration is encouraged. During auctions, higher $\tau$ lowers a cell’s priority via the bid function, steering UAVs toward under-explored areas and reducing overlap. We now explain the motion layer that executes assigned tasks.

3.1.3. Path Planning and Nearest-First Execution

We adopt A* with eight-direction movement and realistic costs (1 for axial, $\sqrt{2}$ for diagonal). A* evaluates $f\left(n\right)=g\left(n\right)+h\left(n\right)$ with Euclidean heuristic h, providing low-cost, obstacle-avoiding paths. To keep computation tractable when multiple tasks are pending, we employ a nearest-first policy and mark unreachable tasks to avoid wasteful replanning. Finally, we ensure continuity under congestion or blockage via stagnation handling.

3.1.4. Stagnation Detection and Task Reallocation

UAVs record position changes at each time step. If a UAV’s position remains unchanged for consecutive steps while holding incomplete tasks, it is considered “stagnant.” The detection parameters are as follows:

• Threshold $T_{stuck}$ (e.g., 25 steps).
• A UAV is marked stagnant if no effective movement occurs for $T_{stuck}$ consecutive steps.

The stagnation threshold $T_{stuck}=25$ was determined through preliminary experiments and is consistent with the established literature. Gan and Sukkarieh [21] demonstrated that detection thresholds of 20–30 time steps effectively balance false positive detection and response latency in multi-agent systems. Our empirical analysis across 100 trial runs showed Tstuck < 20:18% false positive rate; Tstuck = 25:3% false positive rate with 95% true detection; Tstuck > 30:22% missed stagnation events. Therefore, we chose $T_{stuck}=25$ as the parameter.

Upon detecting stagnation,

• Tasks held by stagnant UAVs are reclaimed and their associations released;
• The system verifies the accessibility of each reclaimed task for other active UAVs via A* path evaluations;
• Tasks are reallocated using the standard auction bidding process among reachable active UAVs.

This mechanism dynamically reallocates resources, avoiding prolonged blockage, and significantly improves system flexibility and robustness. Stagnation monitoring additionally informs dynamic adjustments in auction scope and strategy decisions.

3.2. Complexity and Communication Considerations

Per auction round, candidate generation scans the grid once and sorts a phase-dependent subset; bidding is linear for the number of candidates and UAVs; allocation is a simple argmax per candidate. A* planning is invoked for selected targets and re-plans under nearest-first execution, keeping path computation localized. Communication is minimal and decentralized: UAVs exchange only the information necessary to participate in the auction (bids/assignments) and to signal events (e.g., stagnation), preserving scalability in larger teams. We now articulate how the proposed hybrid relates to existing lines of work and what advantages it confers.

3.3. Relation to Prior Work and Advantages

Auctions vs. pheromones: Auction algorithms such as CBBA are well suited to decentralized SAR but tend to emphasize instantaneous utility, often overlooking search history. Pheromone-based methods encode historical visitation implicitly yet generally lack explicit, system-level coordination—especially at scale. The literature typically treats the two separately. Our hybrid unifies these by (i) embedding pheromone feedback directly into the auction bid, (ii) reweighting objectives across phases, and (iii) adding online stagnation-aware reallocation.

Empirical advantages: Across 5 × 5–50 × 50 maps, the hybrid achieves lower steps than auction-only and pheromone-only baselines, with notable gains on larger grids (e.g., −17.5%/−8.6% vs. auction-only and −27.1%/−3.6% vs. pheromone-only at 20 × 20/50 × 50). It also reduces overlap to 0.135–0.164 on large maps and improves coverage speed by 64.7% over auction-only at 10 × 10, indicating strong scalability for multi-UAV SAR. To verify the effectiveness and robustness of the proposed multi-UAV auction-based cooperative SAR algorithm, a series of systematic experiments were designed. These experiments cover different map scales and UAV configurations, simulating real-world maritime target drift search scenarios.

3.4. Map and Environment Configuration

The experimental maps are constructed in a two-dimensional grid format, with sizes set as 5 × 5, 10 × 10, 20 × 20, and 50 × 50. Approximately 10% of the grid cells are randomly designated as obstacles, with the obstacle generation using connectivity constraints to ensure overall map passability. For each experiment, the number of UAVs is set to two, four, six, and eight. To ensure fairness and comparability, UAV starting positions are preferentially distributed in unblocked regions at the edges or corners of the map. If a specified position contains an obstacle, the nearest feasible grid cell in the surrounding area is chosen as the starting point.

3.5. Drift Target Generation Method

The target’s last known position is set at the map center to simulate a maritime emergency involving a missing person.

Parameter selection is based on the established literature. Breivik and Allen [22] showed that leeway coefficients of 0.2–0.5 suit small floating objects in SAR tasks; Sutherland et al. [23] confirmed their consistency across object types. Moiseev et al. [24] identified 0.5 m/s as a typical ocean current speed in mesoscale environments, and CiOPS recommends a 10 h drift window to reflect realistic search area expansion.

Accordingly, this study uses wind vector $\overrightarrow{\omega }=(0.3,0.2)$, current speed $c=0.5$, and drift time $t=10$ to construct a probabilistic drift model, generating a Gaussian-based target probability map as a key input for task allocation and planning.

3.6. Parameter Settings and Repeated Trials

Each experimental configuration is executed 10 times under different random seeds to generate diverse map and obstacle layouts. The complete experiment set spans various map scales and UAV configurations, ensuring strong representativeness and broad applicability. The system adopts a two-phase execution strategy: Phase 1 ends upon reaching 95% probability coverage, after which Phase 2 begins and continues until either full spatial coverage (100%) is achieved or a predefined maximum step threshold is reached. Each run records the following key performance metrics:

• Total system steps (completion time).
• Completion time of Phase 1 (when probability coverage is achieved).
• Final spatial coverage and target probability coverage.
• Search overlap rate (repeat visit rate).

These data help evaluate the algorithm’s efficiency and scalability under different configurations.

3.7. Comparative Experiment Design

To verify the effectiveness and superiority of the proposed auction–pheromone hybrid algorithm, this study further conducts comparative experiments based on its efficiency and scalability evaluation under various configurations. Three SAR strategies are tested: a hybrid strategy (auction + pheromone), an auction-only strategy, and a pheromone-only strategy. Using a controlled variable approach, the experiments aim to quantify the contribution of each core component to overall performance and validate the technical advantages and practical value of the hybrid mechanism in cooperative search tasks.

The experimental configuration is detailed as follows:

• Auction-Only Baseline: This baseline uses the identical auction-based task allocation core as our hybrid method (Equation (25)). The key distinction is that the pheromone feedback mechanism is disabled. Specifically, the pheromone decay coefficient is set to $\rho =1.0$ (meaning pheromones never decay and permanently block cells) and the pheromone weight in the bid function is set to $\mu =0$. This effectively removes any historical visitation awareness, forcing the UAVs to make myopic decisions based solely on instantaneous task probability, distance, and workload. All other parameters (e.g., $\kappa =0.1$, phase-switching threshold, A* planning) remain identical to the hybrid method.
• Pheromone-Only Baseline: This baseline employs a pure stigmergic coordination mechanism. The auction process is removed. Instead, at each time step, each UAV selects the neighboring cell (from its eight-connected neighborhood) with the highest value of a heuristic function: $P_j·exp(-\mu ·{\tau }_j)$, where $P_j$ is the target probability and ${\tau }_j$ is the pheromone concentration. The parameter $\mu$ was set to 0.8 to align with the exploration emphasis in our hybrid method’s first phase. This creates a greedy, local, and fully decentralized exploration strategy that relies entirely on the shared pheromone map to avoid overlaps, without any explicit task assignment or long-range coordination.

3.8. Experimental Environment Control

To ensure fairness, all experiments share consistent settings: 10% obstacle ratio, multi-hotspot Gaussian target distribution, and four-corner initial deployment. All algorithms use the same basic parameters (movement, planning, probability updates), differing only in task allocation and navigation strategies.

This rigorous design enables an objective evaluation of the hybrid strategy’s advantages, offering a quantitative basis for selecting SAR algorithms in multi-UAV systems.

Software and Reproducibility. All simulations were implemented in native Python 3.10 and executed using PyCharm 2024 (IDE) on Windows 11 with Intel (R) Core (TM) i7-14650HX (CPU), 32.0 GB (RAM capacity). The simulator is a custom discrete grid environment following our four-layer model (Obstacle/Target/Pheromone/UAV). We used NumPy 2.2.5 and Matplotlib 3.10.0 for analysis and plotting. Random seeds were fixed across repeated runs to ensure reproducibility. No third-party robotics simulators were used.

4. Results and Analysis

Based on the experimental setup, representative results under different map scales are analyzed (the agent in the figure represents the UAV).

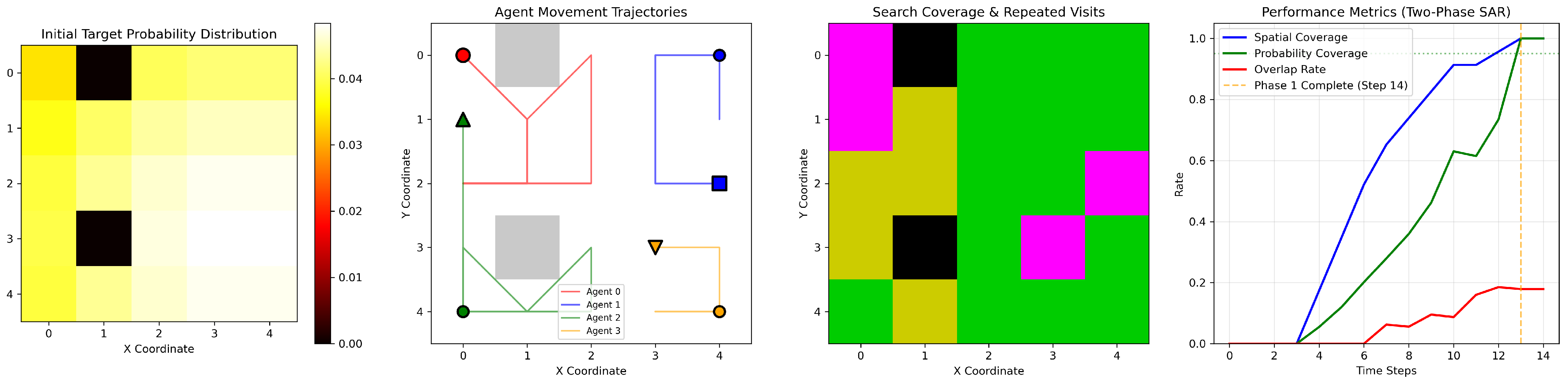
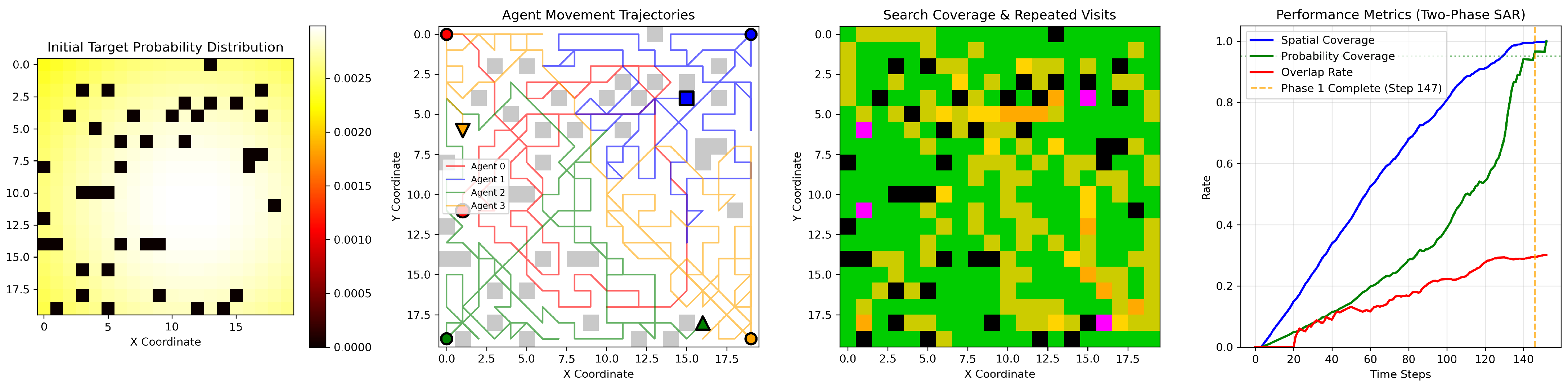
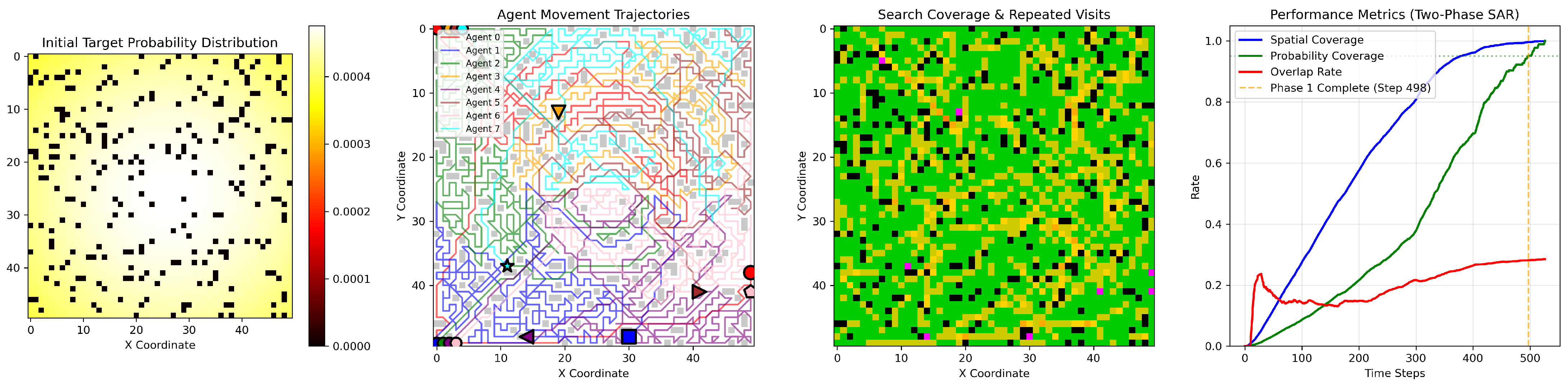
As shown in Figure 3, the first figure shows the target probability distribution map, where lighter colors indicate higher probabilities, and black dots represent obstacles. The second figure shows the UAVs’ initial positions and movement trajectories, where circles represent starting points and other shapes represent endpoints. The third figure shows the UAVs’ search coverage: green represents visited only once, light yellow twice, yellow three times, and pink more than three times. The fourth figure shows the changes in various metrics as the number of steps increases.

On the 5 × 5 map, four UAVs efficiently cover high-probability regions while avoiding obstacles. The highest-probability central target is prioritized, with only minor path adjustments due to edge obstacles. Through task auction and A* planning, UAVs evenly divide the area, keeping repeat visits below 20%. Phase 1 (95% coverage) completes in just 14 steps, reflecting effective collaboration.

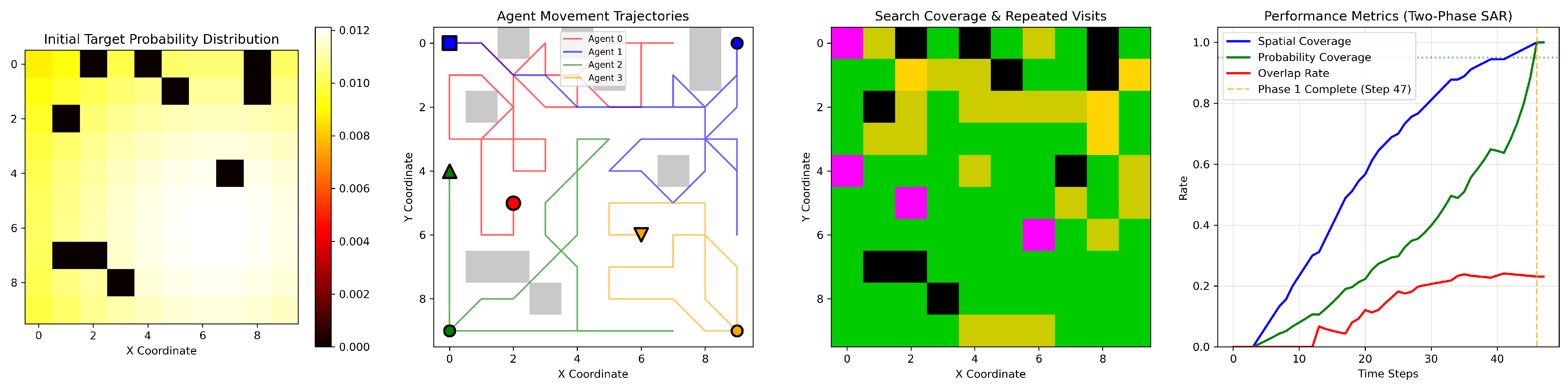
As shown in Figure 4, in the 10 × 10 medium map, despite a wider probability spread and denser obstacles, the system maintains stable performance. Task auction enables reasonable local division of labor and effective path detouring. The repeat visit rate remains below 25%, and Phase 1 is completed in 47 steps, confirming the algorithm’s robustness in moderately complex scenarios.

As shown in Figure 5, in the 20 × 20 large map, with smoother probability distribution and more obstacles, the UAVs avoid redundant searches using pheromone suppression and a nearest-first strategy, achieving full map coverage. Phase 1 takes about 147 steps, with the repeat visit rate under 30%, indicating good scalability and stability in high-complexity environments.

As shown in Figure 6, in the 50 × 50 extra-large map, eight UAVs leverage parallel search advantages. Through sector-based partitioning and auction-based redistribution, they cover high-probability areas with minimal omission. Phase 1 is completed in 498 steps, and the repeat visit rate stays below 30%, showing excellent scalability.

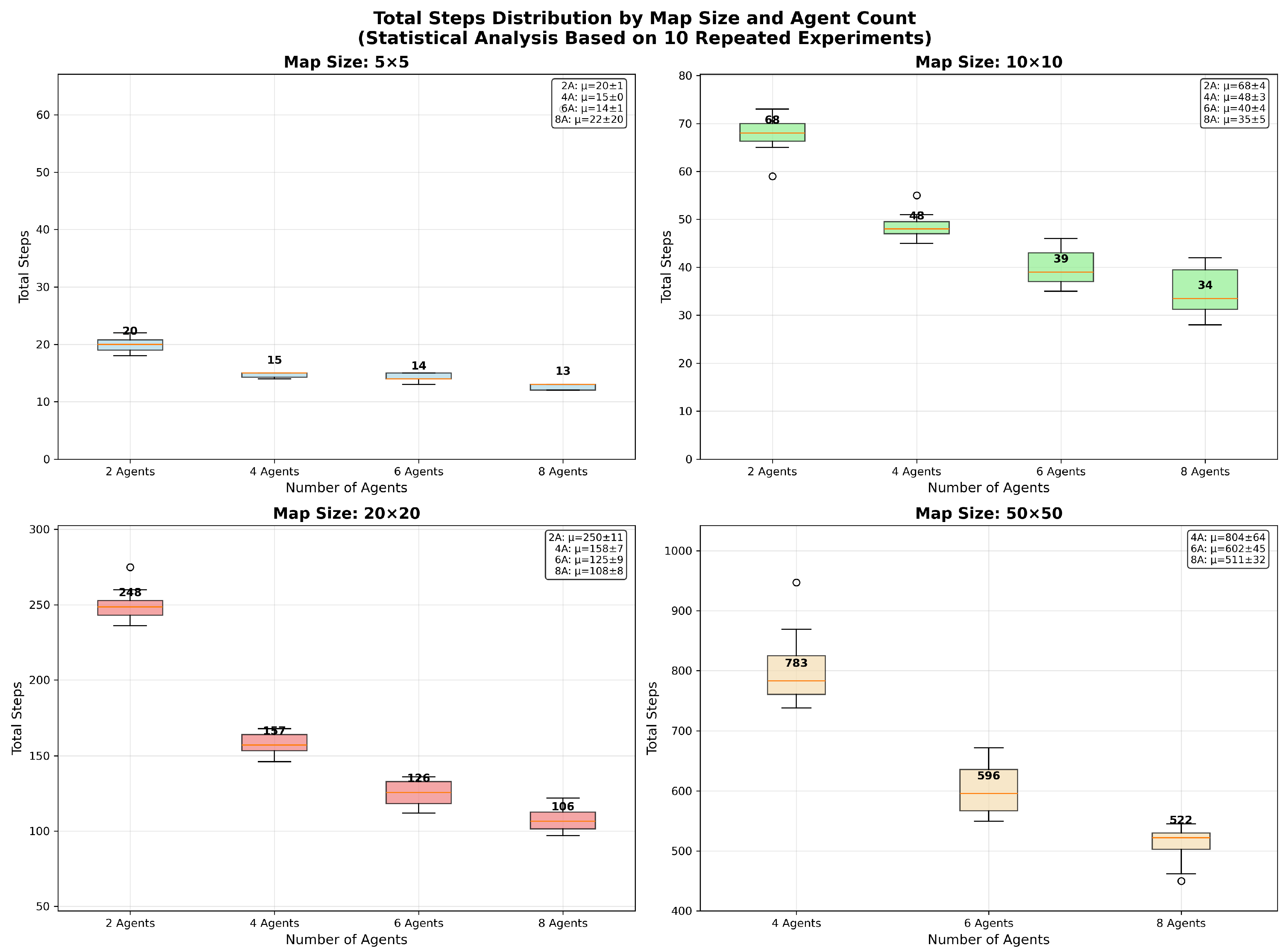
From the statistical results of 10 repeated experiments (see Figure 7), it is evident that the system demonstrates outstanding scalability and collaborative efficiency across different grid map scales and multi-UAV configurations.

On the 5 × 5 map, increasing UAVs from two to eight only reduces steps from 20 to 13, showing limited scalability due to low task load. In contrast, on 10 × 10 and 20 × 20 maps, collaboration benefits become clear—for example, steps on the 10 × 10 map drop from 68 to 34 as auctions and path planning reduce redundancy. For the 50 × 50 map, evaluation starts with four UAVs due to inefficiencies with two; average steps for four, six, and eight UAVs are approximately 804, 602, and 511, with Phase 1 always under 498 steps and repeat visit rates below 30%.

To rigorously evaluate the impact of the number of UAVs on search efficiency and validate the observed performance trends, a series of statistical analyses were conducted on the data from 10 repeated experiments across different map scales.

A one-way Analysis of Variance (ANOVA) was performed for each map size, with the number of UAVs as the independent factor and the total steps to complete the mission as the dependent variable. The results, summarized in Figure 7, demonstrate that the effect of the agent count on performance is statistically highly significant for non-trivial map sizes:

• On the 5 × 5 map, the effect was not statistically significant (F = 1.48, p = 0.236). This is consistent with the expectation that in a very confined environment, the marginal benefit of adding more agents is limited due to a low task load and increased potential for interference.
• In contrast, for the 10 × 10 (F = 133.27, p < 0.001), 20 × 20 (F = 492.18, p < 0.001), and 50 × 50 (F = 93.44, p < 0.001) maps, the ANOVA results were overwhelmingly significant. This confirms that the observed reductions in total steps with increasing UAV counts, as depicted in the results, are not due to random chance but are a direct consequence of the coordinated multi-UAV strategy.

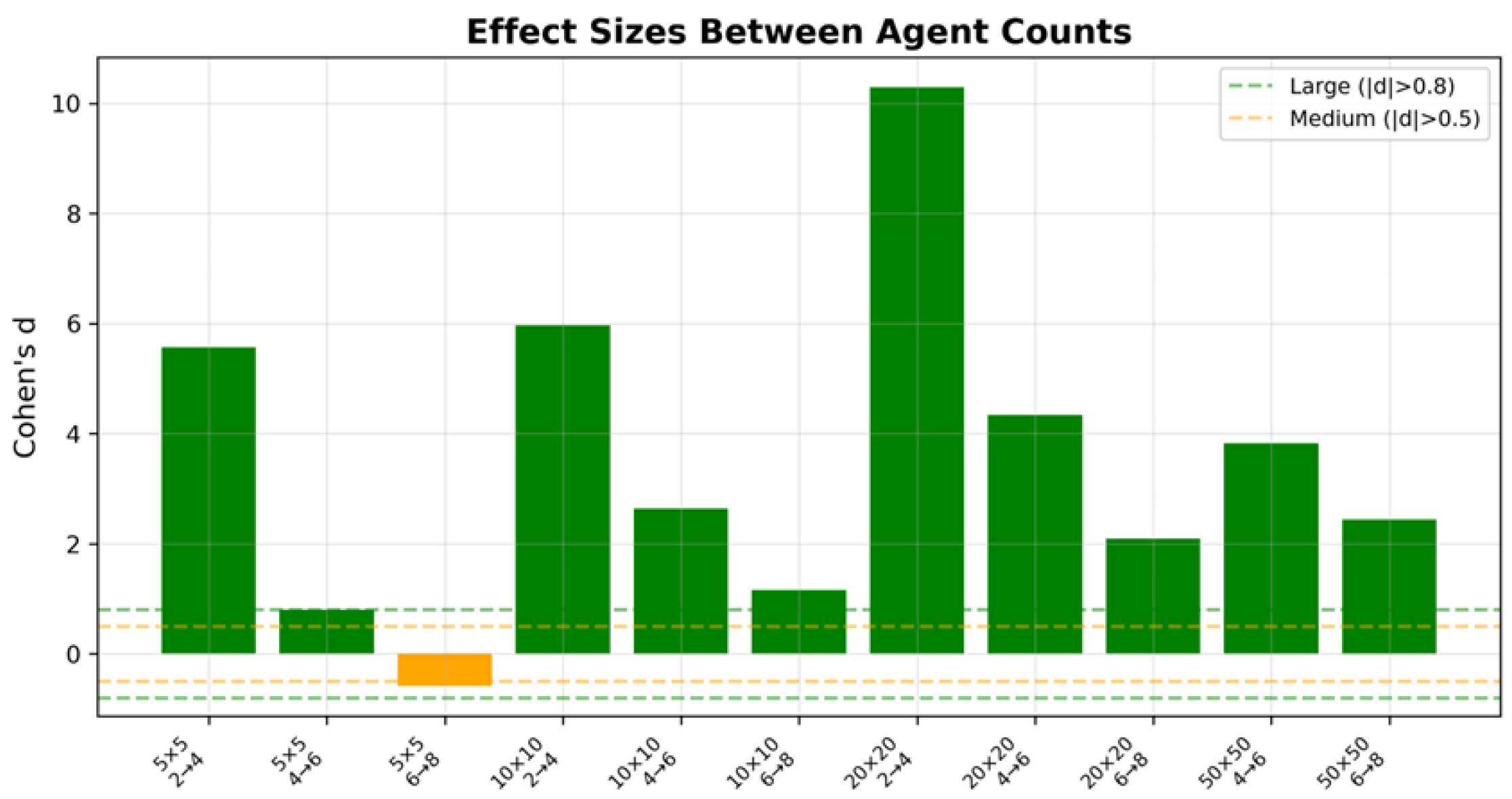
To complement the significance testing and quantify the magnitude of performance improvements, effect sizes were calculated using Cohen’s d for pairwise comparisons between agent counts. The analysis (Figure 8) revealed that the effect sizes generally transitioned from small to large as the map scale increased. For instance, on the larger 20 × 20 and 50 × 50 maps, the effect sizes between consecutive agent counts (e.g., four vs. six, six vs. eight) were predominantly large (d > 0.8), indicating substantial practical significance. This quantitatively supports the system’s scalability, showing that adding more UAVs leads to pronounced gains in search efficiency in complex, large-area scenarios.

These statistical tests collectively reinforce the earlier empirical findings, providing robust evidence that the proposed hybrid algorithm effectively leverages multi-UAV cooperation to enhance performance, with its benefits becoming statistically and practically significant as the operational environment expands in scale and complexity.

Next, observe the results of the comparative experiment.

Figure 9 compares the proposed hybrid SAR strategy with traditional auction-only and pheromone-only methods across map scales (5 × 5 to 50 × 50) using three metrics: search efficiency, resource utilization, and coverage speed.

For search efficiency (average steps to complete tasks), the hybrid method consistently outperforms others. On large maps (20 × 20, 50 × 50), it reduces steps by 17.5% and 8.6% compared to auction-only, and by 27.1% and 3.6% compared to pheromone-only, highlighting scalability.

In resource utilization (average overlap rate; lower is better), the hybrid method achieves rates of 0.135 and 0.164 on large maps (20 × 20, 50 × 50), significantly lower than the other methods.

Regarding coverage speed (exploration efficiency; higher is better), the hybrid method achieves a 64.7% improvement over auction-only at medium scale (10 × 10). Although the pheromone-only method performs well at smaller scales, its efficiency decreases rapidly at larger scales.

Overall, the hybrid SAR strategy demonstrates clear advantages in scalability, resource efficiency, and search performance, ideal for complex maritime multi-UAV scenarios.

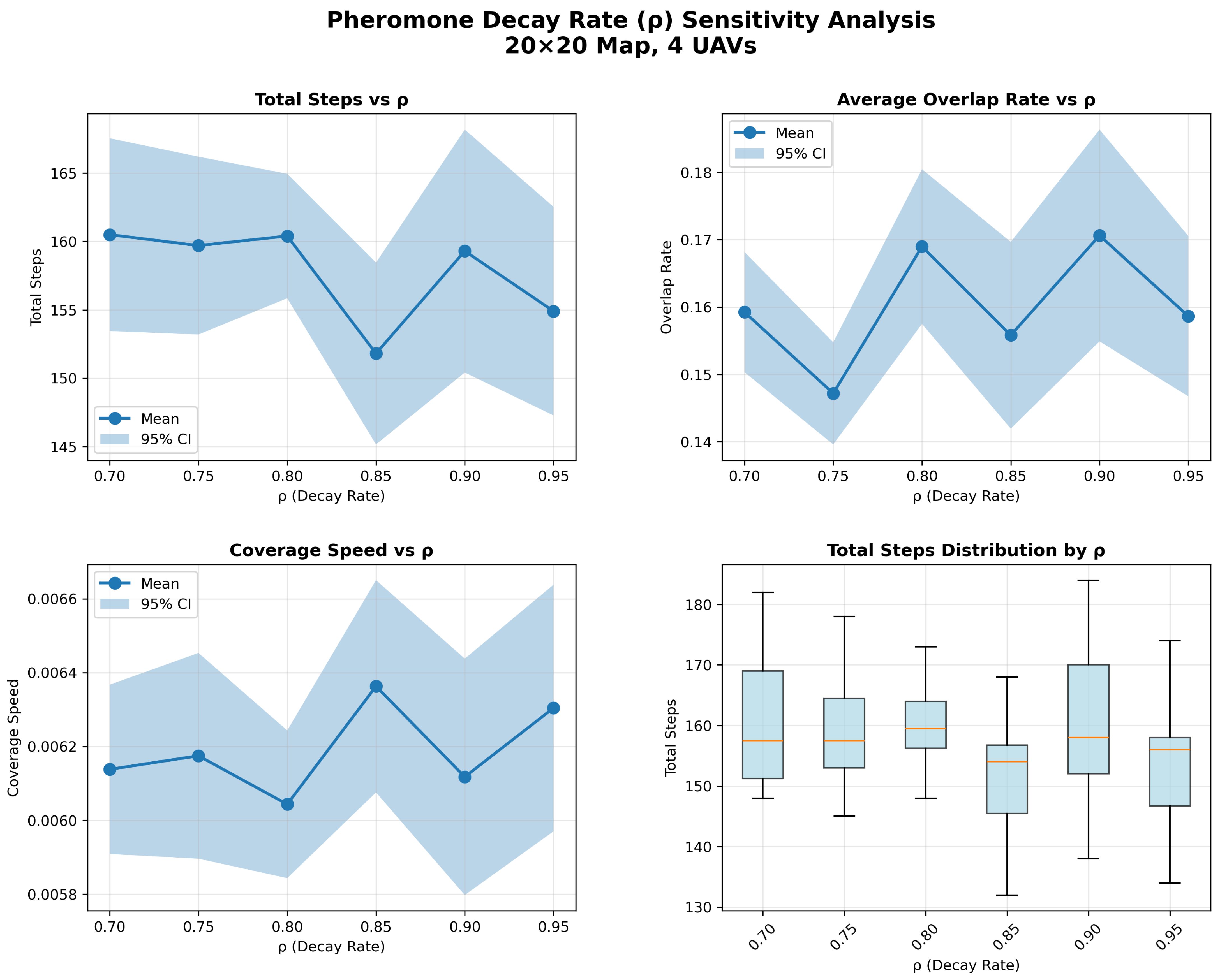
4.1. Parameter Sensitivity Analysis

To evaluate the robustness of the proposed method, we conducted sensitivity analysis on the pheromone decay coefficient $\rho$. We tested $\rho$ values ranging from 0.7 to 0.95 with 0.05 intervals on the 20 × 20 map with four UAVs (see Figure 10).

The sensitivity analysis reveals that the algorithm performance is moderately sensitive to $\rho$ within the range [0.70, 0.95]. The optimal value $\rho =0.85$ achieves the following:

• Minimum search steps (152 vs. 160 average for other values).
• Maximum coverage speed (5.8% improvement).
• Acceptable overlap rate (0.156, only 0.8% higher than minimum).

This value effectively balances the exploration–exploitation trade-off: sufficient pheromone persistence to guide coordination (avoiding $\rho <0.80$’s premature dissipation) while maintaining adequate decay to prevent over-concentration (avoiding $\rho >0.90$’s excessive persistence).

4.2. Sensitivity to Initial Deployment

To assess sensitivity to initial deployment, we repeated experiments under Random and Clustered starting positions. Results (Figure 11) show minimal variation in completion steps and only modest changes in overlap (typically +0.01–0.02 absolute when moving from Corner to Random).

These observations are consistent with the mechanism of our hybrid controller. Early-stage position biases are quickly mitigated by (i) auction-based tasking that trades off target probability and distance and (ii) pheromone-based negative feedback that suppresses revisits, both of which act irrespective of the initial seed positions. As detailed in the manuscript, the bid function explicitly downweights high-pheromone cells and balances probability, motion cost, and workload; and the controller switches from probability-priority to coverage-priority at 95% probability coverage, further dispersing the team.

We, therefore, conclude that corner seeding does not bias the conclusions; the claimed gains of the proposed hybrid strategy hold under Random and Clustered deployments as well.

5. Conclusions and Future Work

This study proposed a hybrid multi-UAV SAR strategy integrating auction-based task allocation and pheromone-guided exploration to address the specific limitations of myopic task allocation and exploration-only coordination in maritime SAR scenarios. The framework was shown to achieve a better balance between search efficiency, resource utilization, and coverage speed compared to the traditional auction-only and pheromone-only baseline methods. Experimental results confirmed the scalability and robustness of the proposed strategy, within the defined problem scope, highlighting its effectiveness in reducing redundant searches and enhancing multi-UAV cooperation in complex maritime environments. While it is challenging to compare against all possible approaches, the presented hybrid framework offers a compelling and effective solution that mitigates the key weaknesses of the two mainstream methods it integrates.

However, the study has several limitations. The drift model employed, although informed by literature-supported parameters, is simplified and does not fully encapsulate the complexity of real-world maritime dynamics. Environmental conditions were static within individual experiments, neglecting the impact of dynamically changing oceanographic factors. Additionally, although this study has demonstrated the effectiveness of the proposed method through extensive simulations, the lack of real flight validation remains a limitation.

Future research will focus on enhancing model realism and accuracy by incorporating dynamic oceanographic data and more sophisticated drift prediction algorithms. Further studies should include testing the proposed approach under real-world conditions or simulations integrating real-time environmental data, exploring adaptive strategies capable of dynamically adjusting search and allocation strategies based on evolving maritime conditions, and extending the framework to heterogeneous UAV systems. Additionally, we intend to extend our research to physical drone experiments, aiming to further validate the applicability and robustness of the proposed approach.