Operational Performance of a 3D Urban Aerial Network and Agent-Distributed Architecture for Freight Delivery by Drones

Highlights

What are the main findings?

• 3D-UAN and agent-based framework supported well the simulation of scenarios for freight delivery by aerial drones.
• As the fleet size increases, travel time increases, while the use of the link dynamic property reduces and layer changes increase.

What is the implication of the main finding?

• Structuring airspace by a 3D-UAN with dynamic links could support effective freight distribution by aerial drones in urban and peri-urban areas.
• A cooperative architecture for exchanging data among aerial drones, hubs (vertiports, Urban Consolidation Centres), and an Airspace Management Authority would improve safety by containing delays.

Abstract

The growing demand for fast and sustainable urban deliveries has accelerated exploration of the use of Unmanned Aerial Vehicles as viable logistics solutions for the last mile. This study investigates the integration of a distributed multi-agent system with a structured three-dimensional Urban Aerial Network (3D-UAN) for drone delivery operations. The proposed architecture models each drone as an autonomous agent operating within predefined air corridors and communication protocols. Unlike traditional approaches, which rely on simplified 2D models or centralized control systems, this research exploits a multi-layered 3D network structure combined with decentralized decision-making for improving scalability, safety, and responsiveness in complex environments. Through agent-based simulations, this study evaluates the operational performance of the proposed system under varying fleet size conditions, focusing on travel times and system scalability. Preliminary results demonstrate that the potential of this approach in supporting efficient, adaptive, resilient logistics within Urban Air Mobility frameworks depends on both the size of the fleet operating in the 3D-UAN and constraints linked to the current regulations and technological properties, such as the maximum allowed operational height. These findings contribute to ongoing efforts to define robust operational architectures and simulation methodologies for next-generation urban freight transport systems.

1. Introduction

Freight delivery systems via Unmanned Aerial Vehicles (UAVs) are emerging as one of the most promising solutions in the field of urban and peri-urban logistics. With the increasing demand for fast deliveries, especially for e-commerce and essential goods, UAVs are emerging as a scalable, efficient, and sustainable solution [1]. The main probable benefits include the fact that UAVs are expected to significantly reduce delivery times, especially in congested urban areas, due to their ability to directly and quickly connect two origin/destination points by avoiding ground traffic. Some studies have shown that delivering goods by UAV, or combined truck–drone modes, may significantly reduce Greenhouse Gases (GHGs) [2,3], particularly by considering factors such as cruise speed and payload mass [4]. Optimal routing aspects are also relevant for obtaining important reductions in CO₂ emissions [5], although such reductions depend on drone size and the recharging system, particularly with respect to low-emission energy sources [6]. Furthermore, drones are particularly useful for reaching rural, mountainous, or disaster-stricken areas where traditional delivery methods are limited or expensive and can ensure a quick delivery of essential goods, such as medical supplies [7,8].

The opportunities offered by drones for last-mile deliveries are not limited to the reduction of delivery times but also extend to the transformation of airspace into an intelligent logistics infrastructure, thanks to the development of 3D aerial networks. These aerial networks represent a new paradigm for organizing UAV urban traffic. Compared to traditional 2D models, 3D networks make it possible to exploit vertical urban space by defining 3D aerial “corridors” that can be traversed by autonomous fleets of drones. Research by Chowdhury et al. (2023) [9] and Li et al. (2025) [10] highlights how optimized trajectory planning in 3D environments can drastically reduce the risk of collisions, improve energy efficiency, and enable higher operational density in high-demand urban areas. From an operational perspective, these networks enable the creation of “air hubs” and exchange stations at altitude, from which drones can depart and land safely. This opens up new scenarios for managing deliveries in congested environments, making it possible to decentralize distribution centers and create vertical micro-depots integrated with urban buildings. Furthermore, thanks to the use of air traffic control algorithms based on artificial intelligence and V2V (Vehicle-to-Vehicle) or V2I (Vehicle-to-Infrastructure) communications [11,12], it is possible to coordinate the movements of many drones in real time, by reducing the risk of congestion and ensuring greater safety.

In this context, using intelligent agent approaches (intelligent agents or multi-agent systems, MASs) combined with 3D networks to simulate a UAV last-mile delivery system may offer several advantages. Each agent may represent a drone, a depot, a customer, or a vehicle and can act autonomously by making local decisions based on its own state and the given environment. Particularly, dynamic environments with changing conditions (e.g., air traffic, weather conditions, new delivery requests) may benefit from the flexibility provided by intelligent agents [13,14]. Furthermore, multi-agent systems can handle an increasing number of actors (drones, clients, or hubs) while maintaining high performances, even in complex scenarios, because the distribution of the decision load allows for reducing the computation burden. In distributed multi-agent architectures, agents collaborate and coordinate with each other in a distributed manner and there is no need for a single central control entity, although it can be introduced for increased safety. This feature makes the system more resilient to failures [15].

In the above perspective, the aim of this paper is to provide further insights into the use of UAVs for last-mile delivery by combining a multi-agent approach with a recent 3D Urban Air Network model, which explicitly sets the lower space aerial graph and the related cost functions for finding optimal paths between points of interest (POIs). This approach has the advantage of providing a simulation tool for exploring operational solutions in real urban environments, so that stakeholders may identify suitable scenarios based on selected criteria. Particularly, this study aims to evaluate the scalability and effectiveness of the proposed architecture by examining how its performance is affected by an increasing number of drones as freight traffic increases. The advantage of the proposed integrated approach, which combines a rigorous 3D network model with the operational flexibility of the agent-based approach, lies in the ability to test different scenarios by simulating their effects, regardless of the specific context. Specifically, the highly general 3D network model can be tailored to the needs of different stakeholders, while also considering both environmental (such as physical obstacles or non-flyable areas) and operational constraints, the latter modeled using the agent-based framework. After discussing the framework and the operational structure, the paper provides an example of a simulated system by using travel time as target criterion. The results—although still preliminary due to the prototype features of the main elements, i.e., UAV and 3D networks—are encouraging and show some potential for the use of drones for goods delivery.

The rest of the paper is organized as follows. Section 2 describes the related literature and identifies the main gaps that this research aims to fill. Section 3 provides the relevant features of the agent-distributed architecture and the 3D network model used in this study. Section 4 introduces the tested scenarios and the main results. Finally, Section 5 discusses the main implications of the obtained results and provides lines for future research.

2. Related Works

As UAVs become increasingly viable for last-mile delivery and other urban services, a significant body of work is emerging around simulation frameworks, conflict resolution strategies, and system-level optimization.

This research study proposes the use of 3D aerial networks and distributed multi-agent frameworks to analyze the impact of using drones for goods delivery in a peri-urban environment, which could replace or supplement the current ground-based system. Therefore, the following analysis of the main literature is structured with respect to three main aspects: (1) impacts of drones for goods delivery; (2) multi-agent architectures for the considered problem; (3) aerial networks supporting UAV operations.

2.1. Impacts of Drones for Goods Delivery

Many studies in the literature refer to the expected environmental impacts of last-mile delivery by drones, mainly by combining drones with ground modes to optimize the whole journey. For example, a truck equipped to function as a mobile depot transports one or more UAVs, and both the truck and the UAVs are employed to perform deliveries [16]. As found by some studies [3,6,17,18], compared to conventional road distribution models, truck–drone delivery systems may substantially reduce GHG emissions, particularly for short distances and small numbers of recipients, while the economic viability is strongly influenced by the degree of drone automation. Both of them, however, depend on the optimization of delivery routes. As for noise, which is another important transport-related impact, some results have been found by setting a simulation platform, acting as a supporting tool for analyzing the trade-offs affecting drone noise [19]. The study concludes that higher speeds and heavier payloads generally produce increased noise levels.

Although predominant in the literature, environmental aspects are not the only ones to be explored in drone delivery systems. Travel times, mainly compared with equivalent ground systems, are another important element when comparing drone-based delivering models with ground-based ones. Some studies have found that mixed, particularly synchronized, truck-and-drone systems perform well in terms of waiting times, depending on the level of synchronization and the number of drones, and could lead to significant time saving and reductions in customer waiting times [20]. Other research has found that the optimal number of drones exhibits a diminishing trend with an increasing marginal rate as the waiting time threshold increases from 0.3 to 0.7 h, suggesting that delivery time windows are the prevailing factor influencing the determination of the necessary drone fleet size [21]. A mathematical model that allows a truck and a drone to perform deliveries and pick-ups in a single mission, optimizing total service time, has been developed by [22]. In this approach, the drone can carry more parcels, allowing for more stops per mission, increasing the operational use and responsiveness to customer expectations regarding returns. Depending on the return rate and the drone load capacity, the numerical experiments show significant time savings; particularly, they show up to 36.2% improvement over traditional truck-only deliveries.

2.2. Multi-Agent Architectures for the Considered Problem

Conventional vehicle routing approaches often struggle to accommodate real-world complexities such as traffic congestion, energy limitations, and dynamically evolving delivery demands. In response to these challenges, Multi-Agent Reinforcement Learning is a promising approach for enhancing truck–drone collaborative logistics, offering decentralized decision-making, real-time re-routing capabilities, and intelligent resource allocation [23]. In fact, simulation techniques are useful particularly when one or more elements of the considered system are not yet operational yet or are still at a prototype level, as is the case of most UAVs. In this perspective, multi-agent simulation models have been used in several contexts to model, simulate, and analyze complex, adaptive systems thanks to their ability to represent distributed interactions, individual behaviors, and emerging dynamics.

The literature dealing with good delivery by drones proposes several studies dealing with simulations based on multi-agent-based system (MABS) models to explore one or more aspects of the problem. For example, the environmental and economic impacts of drone-based and e-bike-based takeaway delivery systems have been compared with a MABS model by providing findings on GHG emission and revenues for the real case of Qixia District, Nanjing, in China [24]. A cooperative asynchronous multi-agent system has been used to solve the Truck-multi-Drone Team Logistics Problem, where a truck and multiple drones collaborate to visit a set of locations in minimum amount of time [25]. In this approach, a central manager agent has the role of mediator, while the remaining agents represent individual locations to be visited, including both the origin and destination points, which offers a novel perspective on agent representation of the delivery problem. Generally, agents represent vehicles or orders. Such an approach has proved to be more efficient than alternative metaheuristic methods, particularly for large problems with up to 500 locations and six drones.

An important line of research concerns the implementation of agent-based simulation platforms to model hybrid air–ground mobility systems. Based on the use of the open source multi-agent transport simulation framework MATSim, a dedicated UAV module has been developed to incorporate urban air mobility (UAM) scenarios into traditional ground-based transport networks [26], to enable comprehensive analyses of multimodal transport systems by capturing the interactions between air and ground mobility components. In this respect, the study presented in [27] introduces some scheduling capabilities solvers into Multi-Agent Path Finding (MAPF) in order to enhance the resolution of conflicts among UAVs operating in densely populated urban airspace. Their proposed framework introduces two primary strategies: takeoff scheduling, which postpones UAV departures to prevent potential collisions, and speed adjustment, which dynamically changes UAV speeds along suitable segments of their flight paths. These mechanisms enable real-time responsiveness to evolving airspace conditions. The approach has been applied to the real case of the city of Tokyo. The recent work [28] addresses safe and scalable airspace management to enable high density operations using Agent-Based Modeling simulations. Several operational contexts are considered as terminal areas (e.g., vertiports) and airspace management, including offer, demand, and costs for both passengers and operators. The study emphasizes the importance of modeling realistic constraints, including infrastructure limitations and regulatory considerations, in the evaluation of UAV system performance.

2.3. Aerial Networks Supporting UAV Operations

Most of the literature on good delivery by drones does not refer to a structured air network but to case studies or, at most, to the positioning of vertiports or warehouses to represent the origin/destination points, loading/unloading operations, and battery recharging. The structure of the airspace actually plays an important role in the development of a UAM system. Establishing a functional UAM ecosystem requires a comprehensive technical and organizational framework that ensures operational safety, efficient airspace utilization, and seamless integration with existing aviation systems [29,30,31,32]. While much of the current literature focuses on the characteristics and constraints of low-altitude airspace, there is a relative lack of research addressing the formal modeling of Urban Air Networks (UANs). One significant contribution in this area is the modeling of uncontrolled urban airspace (Class G) as a multi-layer network, where aerial corridors serve as links between nodes and vertical transitions occur at specific locations [33,34]. These corridors are governed by speed limits, capacity constraints, and V2V communication, allowing for decentralized navigation [12]. Corridor geometry depends on vehicle type, distribution of points of interest, and fixed obstacles. The Metropolis project [35] proposes four structured urban airspace models: (a) Full Mix—unstructured airspace relying on onboard equipment for navigation; (b) Layered Structure—horizontal layers with regulated transitions; (c) Zonal Structure—circular and radial zones guiding traffic similar to ground roundabouts; (d) Tube Network—predefined, conflict-free 3D routes with vertical separation for varying flight ranges. In a similar effort, AirMatrix [36] structures urban airspace into standardized, multi-layered air blocks with predefined way-points and corridors. Trajectories are planned according to navigational constraints to facilitate scalable UAM service deployment, avoiding potential conflicts. However, simulation results indicate the need for further refinement to accommodate increasing traffic volumes. The Dynamic Delegated Corridors model [37] introduces flexible airspace structuring through dynamically managed corridor volumes. Drones equipped with autonomous navigation, collision avoidance, and V2V communication manage separation locally. Corridor status is dynamically adjusted based on weather and traffic density, supported by an Automated Decision Support system to optimize airspace utilization. Further, a graph-based air traffic planning framework [38] models airspace as volume segments (edges) and nodes (droneports and delivery points), including vertical connections and node complexity. It employs an objective function that accounts for congestion and operational efficiency and a two-phase algorithm to balance path complexity and manage traffic flow. Recent research explores the integration of digital twin technologies with UANs [39,40], leveraging real-time data to identify critical parameters—such as obstacle heights, access points, and optimal routing—thereby improving situational awareness and enabling adaptive UAM operations.

A structured aerial network model was recently proposed by [41]. It introduces a three-dimensional Urban Air Network (3D-UAN) that explicitly incorporates vertical links. This model enables the representation of UAV trips as sequences of dynamic aerial links connecting origin and destination points, guided by a defined cost function. It differs from other UAN approaches in the literature in several aspects. It is a three-dimensional layered network, composed of a series of 2D graphs superimposed on different altitude levels, thus allowing for vertical movements between layers. The aim is to create safe and separate air routes between different origin–destination pairs. It has been designed for future multimodal urban air mobility to serve passenger, freight, and emergency trips. Finally, it is a dynamic network, since links can be enabled/disabled depending on traffic capacity or operating conditions. Compared to the AirMatrix model, the 3D-UAN model does not include air blocks, but it introduces the concept of link capacity, which enables the safe management of air traffic flow along different links as it moves between origin/destination pairs. Compared to the Dynamic Delegated Corridors model, in which aerospace volumes are activated, deactivated, or modified over time based on traffic, environmental conditions, or other operational factors, the 3D-UAN model is a complete three-dimensional air network structure (nodes, horizontal and vertical links, multiple levels) that represents the entire urban air mobility system, including both traffic and the air network.

2.4. Main Contributions of This Study

Building upon the framework of the 3D-UAN [41], this study investigates its application to freight distribution among designated Urban Consolidation Centers located near urban areas. The proposed architecture includes a distributed multi-agent model, where each drone (identified also as an Aerial Freight Vehicle, AFV, in the following) represents an agent. Flight safety is delegated to individual AFVs, which are assumed to be fully autonomous and equipped with advanced onboard systems, but a control center is also introduced to strengthen safety and coordination. Drones are constrained to operate within predefined air corridors, maintain specific altitudes and speeds, and adhere to pre-approved flight plans authorized by the air traffic control center. An experimental analysis was conducted using an agent-based simulation environment and a representative 3D-UAN model. The goal was to explore a range of operational scenarios, with a particular focus on comparing the performance of drone-based freight distribution as the number of drones increased.

Compared to the existing body of literature on drone-based urban delivery systems, this research addresses two critical and largely under-explored gaps. First, it introduces a rigorously defined three-dimensional aerial network structure for urban freight logistics. While much of the current research either assumes simplified 2D routing frameworks [42,43] or models drone paths as point-to-point trajectories in unconstrained airspace [44], this study adopts a network-based approach that explicitly incorporates the vertical dimension. This layered 3D network—comprising fixed nodes (e.g., vertiports), transition nodes (enabling inter-layer movement), and dynamic links (aerial corridors)—reflects recent conceptual developments in UAM and Unmanned Traffic Management (UTM), where structured, rule-based airspace segmentation is crucial for safety, scalability, and integration with existing aviation systems [45]. Second, building upon this structured 3D network, the study proposes an agent-based, distributed, and cooperative control architecture for managing drone operations in urban freight delivery. While centralized planning models dominate much of the optimization literature (e.g., [23,46]), such systems often face limitations in scalability and responsiveness, particularly in dynamic urban environments with high vehicle density and real-time constraints. In contrast, this research leverages multi-agent system (MAS) principles, where autonomous freight drones (agents) operate under decentralized decision-making protocols, yet coordinate with each other via V2V and V2X communication. This distributed architecture enables real-time adaptive scheduling, conflict resolution, and collaborative resource allocation, reflecting the direction of recent work in autonomous multi-UAV systems and cooperative robotics [47,48,49].

It is important to emphasize that the technological ecosystem underpinning drone logistics—encompassing both the aerial vehicles and the supporting communication infrastructure, as well as regulatory frameworks and operational procedures—remains in an evolving state of development. Accordingly, the findings of this study should be interpreted as part of an exploratory investigation, aimed at providing preliminary insights into the feasibility, efficiency, and structural requirements of urban freight delivery within UAM frameworks. The results contribute to the ongoing discussion on defining suitable operational architectures and simulation-based validation methods for next-generation urban logistics networks. In summary, the main contributions of this study with respect to the current literature are as follows:

• definition of a 3D-UAN for the delivery of goods by drones, which represents an advance over the 2D networks used to date to address similar problems;
• definition of a structured agent-based architecture that leverages the characteristics of the 3D-UAN to analyze scenarios exploring the potential benefits and the limits of a drone-based goods delivery system.

3. Freight Distribution Problem Using 3D Urban Air Network Model and Agent-Distributed Architecture

The problem addressed in this research focuses on freight transport among Urban Consolidation Centers (UCCs). UCCs are strategically located logistics hubs situated near city boundaries, designed to aggregate freight from long-haul carriers and facilitate efficient last-mile delivery operations within urban areas [50,51]. Within the proposed framework, vertiports—designated for vertical take-off and landing actions—are assumed to be co-located with or integrated into UCC facilities.

The previously cited 3D-UAN model is employed in this study to address the challenges associated with freight distribution between UCCs, together with a distributed agent-based architecture where each AFV is modeled as an autonomous agents cooperating with other nearby agents. In addition, a control center is considered, whose aim is to coordinate the whole network.

The following sub-sections will describe in detail the 3D-UAN model and the distributed agent-based architecture.

3.1. The 3D-UAN Model to Support Freight Distribution by Drones

The 3D-UAN model, initially proposed in [34,41], was originally conceptualized to support a wide range of aerial services operating in Very Low-Level (VLL) and uncontrolled airspace—defined as airspace typically below 500 feet Above Ground Level (AGL) and not subject to active air traffic control—in accordance with regulatory frameworks like those outlined by the FAA and EASA [52,53,54].

In this study, the 3D-UAN is adapted and extended to address freight distribution operations in urban settings. In detail, the 3D-UAN model is a multi-layered airspace structure, where the vertical dimension is discretized into a finite number of flight levels (or layers) separated by fixed vertical distances, a concept aligned with proposals for structured airspace segmentation in urban air mobility systems [36,55]. The 3D graph representing the 3D-UAN includes the following nodes and links:

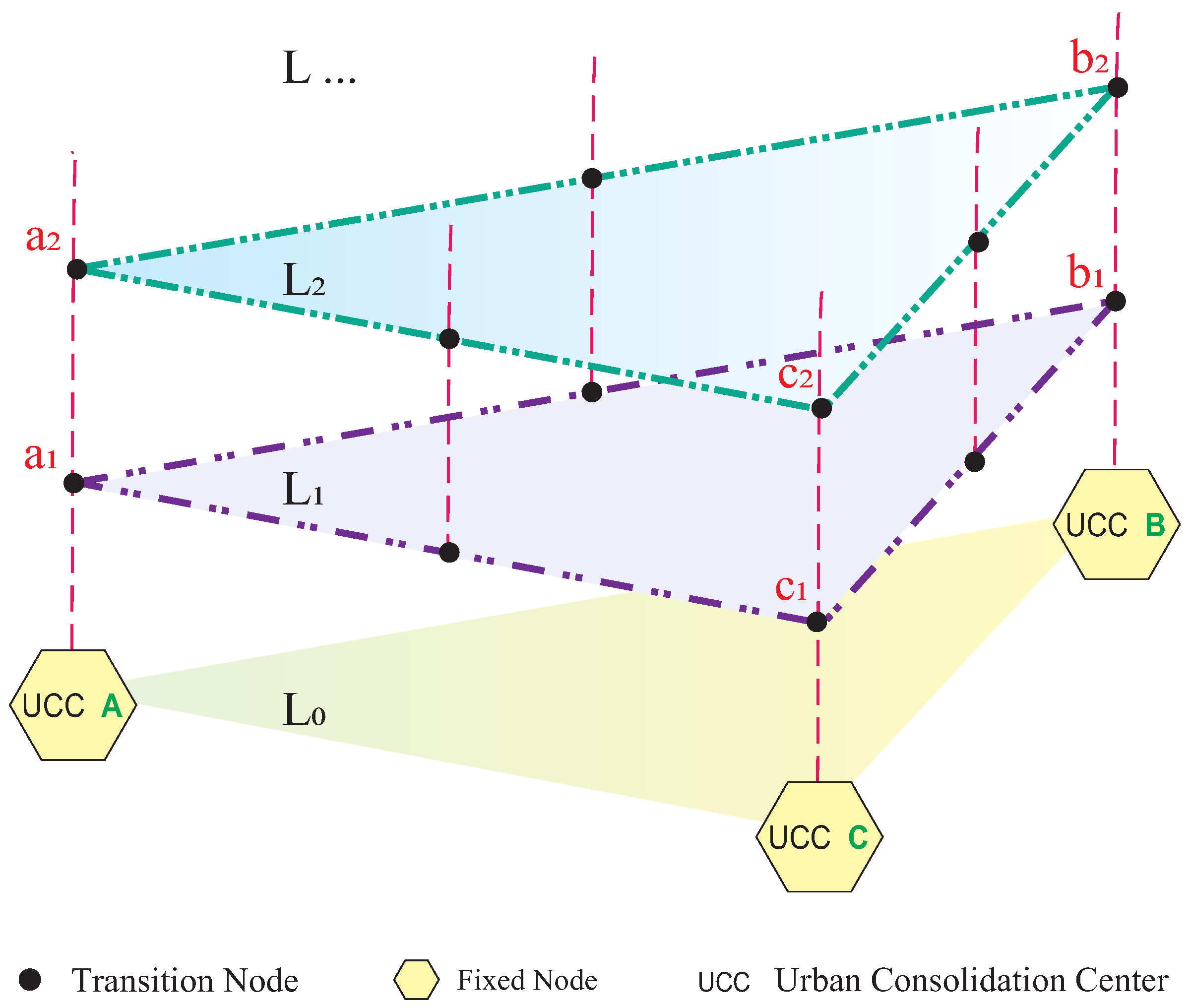
• Fixed nodes: They denote entry and exit points within the network (such as vertiports, logistics hubs, or recharging stations). The set of fixed nodes, $N_F=\left\{q_L\right\}$, $q_L=1,\cdots ,Q_L$, is defined only at the first layer ($L=0$), and the nodes correspond to the physical infrastructures;
• Transition nodes: They represent points where horizontal routing, as well as vertical transitions between adjacent layers, occur. The set of transition nodes for each layer is $N_{T,L}=\left\{p_L\right\}$, $p_L=1,\cdots ,P_L$, where $P_L$ is the number of transition nodes at layer L. It is worthwhile to note that some transition nodes share the same $x-y$ coordinates as fixed nodes but differ in their vertical (z) coordinate. In other words, some fixed nodes represent vertical projections of physical infrastructure onto the corresponding layer, for $L>0$;
• Dynamic links: They are directional, aerial corridors that connect two nodes, either within the same layer (horizontal links) or across different layers (vertical links), enabling flexible routing depending on operational constraints and prevailing environmental conditions. The existence of a link between two nodes depends on the feasibility of the connection, e.g., absence of obstacles or of no-fly zones. The complete set of dynamic links is D.

Each dynamic link $d\in D$, both horizontal and vertical, is characterized by its activation status, i.e., the link may be activated or deactivated depending on factors such as airspace capacity, conflict resolution requirements, and meteorological conditions. Furthermore, link geometry—including width, curvature, and allowable altitude ranges—may be adapted based on the physical and operational characteristics of the AFVs. For instance, minimum separation distances between vehicles (as required by detect-and-avoid protocols) influence corridor width, while energy constraints between recharging-enabled nodes (e.g., between two vertiports) impose restrictions on maximum allowable link lengths. Additionally, AFV physical dimensions directly impact the required vertical separation between adjacent layers. Larger AFVs with increased wingspans or rotor diameters necessitate greater protection volumes, thereby increasing the inter-layer spacing to maintain airspace deconfliction and operational safety margins [56]. This scalable design allows the 3D-UAN to accommodate a heterogeneous fleet of aerial freight vehicles, each operating within its designated layer and corridor parameters.

To enhance the description of the 3D-UAN model, two dynamic link subsets within the set D are considered:

$$\begin{array}{c}{D}_{h,L}=\{h\in D|h=1,2,\dots ,M_{h,L}\}\hfill \\ D_{v,L,L+1}=\{v\in D|v=1,2,\dots ,M_{v,L,L+1}\},\hfill \end{array}$$

where h and v are, respectively, the generic horizontal link for a given layer L and the generic vertical link connecting two adjacent layers L and $L+1$; $M_{h,L}$ and $M_{v,L,L+1}$ are, respectively, the number of horizontal links at layer L and the number of vertical links connecting two adjacent layers (L and $L+1$). Note that when the last layer is reached, $M_{v,L,L+1}$ is set equal to $M_{v,L-1,L}$.

For each layer L, a 2D graph $G_L$ is defined, comprising the set of nodes (fixed and transitions) and the set of horizontal links $D_{h,L}$: $G_L=\left\{N_{F,L},N_{T,L},D_{h,L}\right\}$. Finally, the 3D graph $\Gamma$ representing the topological structure of the 3D-UAN includes the horizontal graphs for each layer L and the subset $D_{v,L,L+1}$: $\Gamma ={\bigcup }_{L=1}^n\left(G_L\cup D_{v,L,L+1}\right)$.

To complete the 3D-UAN model, a cost function—corresponding to travel time—is associated with the links belonging to G. (Note that the following cost functions, from (1) to (2b), refer to the 3D-UAN model proposed in [34] and are here summarized for clarity.):

$$c(T_t,T_g)=\left\{\begin{array}{cc}{T}_{t_i}\hfill & \mathrm{for}i=1\hfill \\ T_{t_i}+T_{g,(i,i-1)}\hfill & \forall i>1\hfill \end{array}\right.$$

(1)

where i is the i-th AFV using the dynamic link d (horizontal or vertical) at a given time period; $T_{t_i}$ is the travel time of i on d; and $T_{g,(i,i-1)}$ is the time gap between i and $i-1$. It should be noted that the horizontal and vertical operating characteristics are different; therefore, two suitable specifications, which describe Equation (1) in detail, are adopted for horizontal (Equation (2a)) and vertical (Equation (2b)) links, respectively:

$$\begin{array}{cc}\hfill c_h& =c\left(T_{t_i}\right)=\left\{\begin{array}{cc}{T}_{r_i}\hfill & i=1\hfill \\ T_{r_i}+T_{g,(i,i-1),h}\hfill & \forall i>1\hfill \end{array}\right.\hfill \end{array}$$

(2a)

$$\begin{array}{cc}\hfill c_v& =c\left(T_{t_i}\right)=\left\{\begin{array}{cc}{T}_{a_i,v}\hfill & \mathrm{upper}\mathrm{layer},i=1\hfill \\ T_{a_i,v}+T_{g,(i,i-1),v}\hfill & \mathrm{upper}\mathrm{layer},i>1\hfill \\ T_{f_i,v}\hfill & \mathrm{lower}\mathrm{layer},i=1\hfill \\ T_{f_i,v}+T_{g,(i,i-1),v}\hfill & \mathrm{lower}\mathrm{layer},i>1\hfill \end{array}\right.\hfill \end{array}$$

(2b)

In (2a), the total travel time $T_{t_i}$ is equal to the running time $T_{r_i}$ if only one AFV is traveling along the link h, while, if more than one AFV are running on the same link ($i>1$), an additional time $T_{g,(i,i-1)}$ is considered, which ensures a suitable separation between next two AFVs and therefore safe travel conditions among AFVs operating along the same trajectory. The running time depends on AFV characteristics and any applicable airspace regulations.

To guarantee the time gap across each link d within the network and prevent collisions among AFVs traversing the network, AFV take-off from fixed nodes is allowed only when the preceding vehicle is far away from the departing AFV. More formally, a headway time $h\left(I_{N_{F,0}}\right)$ for any two AFVs, i and $i-1$, is considered at each node belonging to the set $N_{F,0}$. In detail, let i be the i-th AFV departing from the generic fixed node $q_0$ and flying towards the generic transition node $p_L$. The headway time $h_i^{q_0}$ assigned to i at the departing fixed node $q_0$ is defined as:

$$h_i^{q_0}=I_i+\sum _{j=1}^{n-i}{I}_{i-j}$$

(3)

with

$$I_i=\left\{\begin{array}{cc}{T}_{a_i,v}+T_{g_{(i,i-1)},v}+\left[T_{r_i}+T_{g_{(i,i-1)},h}\right]\hfill & \mathrm{if}i-1\mathrm{is}\mathrm{ahead}\mathrm{of}\mathrm{the}\mathrm{transition}\mathrm{node}{N}_{T,L}\hfill \\ T_{r_{i-1}}+\left[T_{g_{(i,i-1)},h}+T_{a_i,v}\right]\hfill & \mathrm{if}i-1\mathrm{is}\mathrm{over}\mathrm{the}\mathrm{transition}\mathrm{node}{N}_{T,L}\hfill \end{array}\right.$$

(4)

In the 3D-UAN, paths between relevant pairs of nodes (e.g., fixed nodes) includes both horizontal and vertical links. In other words, based on suitable algorithms (for example, the well-know Dijkstra or A+), 3D paths between pairs of nodes may be generated within the 3D-UAN as sequences of horizontal and vertical links, by minimizing factors such as travel time, energy consumption, airspace congestion, or a combination of these. If travel time is considered, the combination of both node and link cost functions—respectively $h_i^{q_0}$ and $c(T_t,T_g)$—has to be considered for identifying suitable 3D paths.

3.2. The Distributed, Cooperative Agent-Based Architecture for the Freight Distribution Problem

In the freight distribution problem considered in this study, AFVs are assumed to realize the transportation of goods between UCCs, where goods are aggregated and subsequently redistributed for last-mile delivery (see Figure 1). Vertiports designated for take-off and landing are assumed to be located either within or in close proximity to UCCs. Consequently, the terms vertiport and UCC are used interchangeably in the context of the 3D-UAN operational framework, unless otherwise specified.

In this context, the utility of the 3D-UAN model—particularly the multi-layered aerial corridors—is fundamental for ensuring safe and conflict-free navigation in urban and peri-urban environments where UCCs are located. Unlike traditional two-dimensional routing schemes, the 3D-UAN layered design described in the previous section supports vertical separation of traffic and structured flight paths by reducing the risk of mid-air collisions and improving throughput in high-density scenarios. Furthermore, although UCCs are generally located in urban peripheral areas, these areas often contain various man-made and natural vertical obstacles, such as high-rise buildings, communication towers, and high-voltage pylons, which pose significant safety risks. Thus, the adoption of a fixed yet flexible network infrastructure is fundamental to ensure safe, efficient freight transport operations.

In the distributed, cooperative agent-based architecture based on the 3D-UAN model here proposed, there are three classes of software agents, each one with specific roles and functions (see also Figure 2):

• The freight drone agents ($AF{V}_A$);
• The airspace management authority ($AA{M}_A$);
• The fixed node agents ($F{N}_A$).

As described in Figure 2, each $AF{V}_A$, representing an autonomous aerial cargo drone, must submit to $AA{M}_A$ a detailed flight plan when traveling from an origin (O) to a destination (D), which corresponds to fixed node agents $F{N}_A$ (i.e., $UC{C}_s$, vertiports, or any infrastructure equipped for cargo loading, unloading, and, potentially, recharging operations).

The submitted flight plan must include specifications regarding the requested air corridors (i.e., links in the 3D-UAN) for moving between two $F{N}_A$ and nominal cruise speeds. In addition, to ensure safe travel conditions, layer transitions and landing and take-off operations are admissible only on links belonging to $D_{v,L}$. Therefore, both horizontal and vertical links may belong to the path from O to D, which means that, in general, 3D paths will link two $F{N}_A$.

Authorization for the flight plan is granted by a designated software agent representing the airspace management authority ($AA{M}_A$), which checks for conflicts with existing or concurrent flight plans, in alignment with both UTM protocols [54,57]—or U-Space—and the HyperTwin platform created as part of the project “Digital Twin for Innovative Air Services— DT4IAS” (https://hypertwin.enac.gov.it/). If necessary, the flight plan is changed and sent to $AF{V}_A$ for approval and adoption.

Once authorized and in flight, each $AF{V}_A$ is assumed to operate autonomously, relying entirely on navigation, obstacle avoidance, and decision-making systems onboard. The $AF{V}_A$ maintains real-time situational awareness through Vehicle-to-Vehicle (V2V) and Vehicle-to-Infrastructure/Everything (V2I/V2X) communication protocols. Therefore, the system architecture incorporates a level of operational autonomy, enabling each agent $AF{V}_A$ to dynamically adjust certain flight parameters in response to real-time contingencies, which may include interactions with other agents, adverse weather conditions, or unexpected obstacles, and reflecting the necessity of reactive flight path adaptation within urban and peri-urban airspace, as also suggested in [46,58].

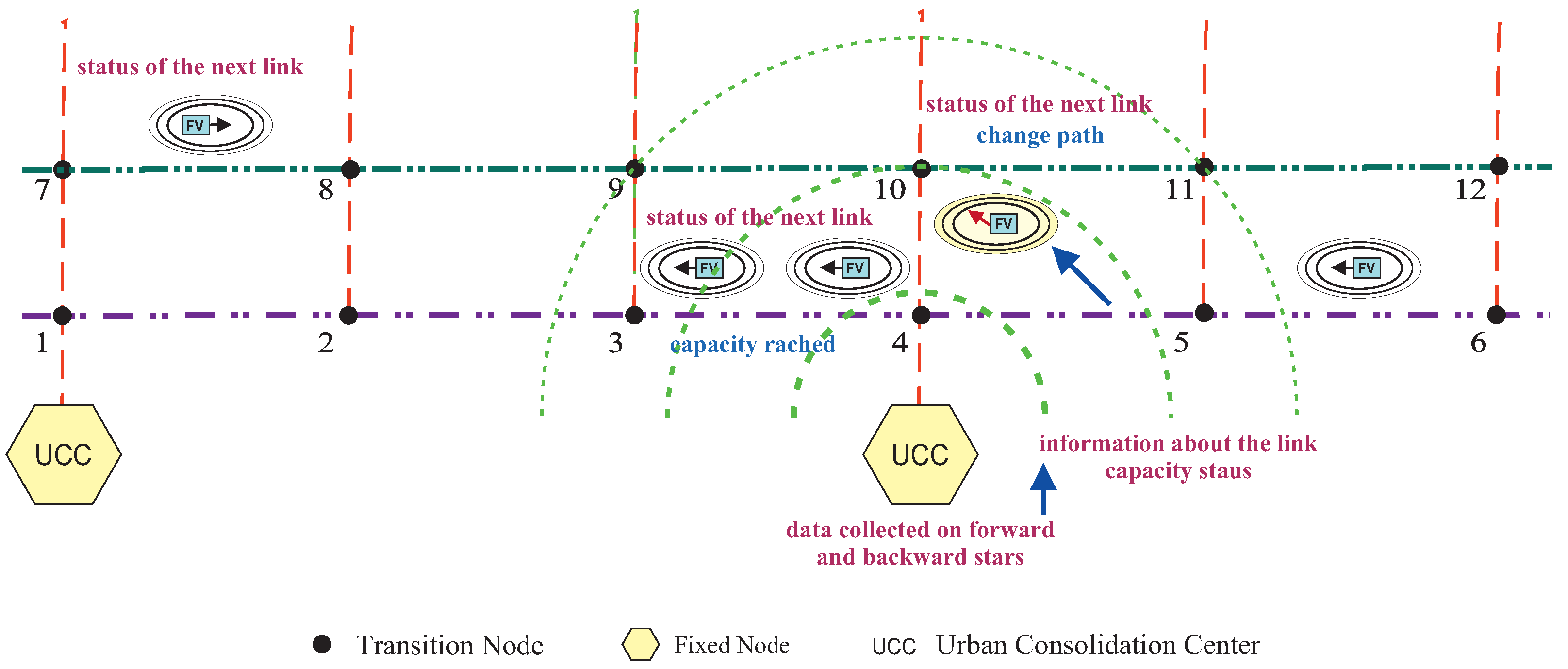
Adjustment of flight parameters may result in a new path generated within the 3D-UAN, based on the information exchanged among AFVs and between AFVs and fixed node agents. In detail, upon receiving approval for its flight plan, the generic $AF{V}_A$ departs from the designated $F{N}_A$ and proceeds within the 3D-UAN in accordance with the authorized path. Throughout its journey, $AF{V}_A$ exchanges data with other $AF{V}_A$ within an effective communication range and transmits to/receives from $F{N}_A$ information concerning the state of the 3D-UAN. This communication occurs over a spatial extent equivalent to at least twice the average link length. Specifically, the information refers to the occupancy status of the upcoming links $AF{V}_A$ is expected to traverse. Based on the data received from both $AF{V}_A$s and the neighboring $F{N}_A$, $AF{V}_A$ determines whether to continue along its originally planned path or to initiate a route modification. A deviation from the initial path becomes necessary if the $AF{V}_A$ is informed—relative to its current position—that the next link in its planned route has reached its occupancy threshold. To uphold system safety, let d denote the link currently occupied by $AF{V}_A$, and let $d+1$ and $d+2$ represent the subsequent links along its intended path. $AF{V}_A$ makes routing decisions based on occupancy information pertaining to both $d+1$ and $d+2$. The cooperative, distributed framework in the 3D-UAN environment described above is shown in Figure 3.

Finally, it is important to note that the headway time allocated to each $AF{V}_A$ at take-off ensures sufficient spatial and temporal separation between agents. This separation enables $AF{V}_A$ to safely reconfigure its path in the event that a link reaches its capacity, by utilizing the first available vertical link to switch to an alternative flight level.

The algorithm searching itineraries between origin/destination points, or between the current position of AFV and its final destination, is a customization of the conventional Alpha–Beta algorithm [59]—named Alpha–Beta Pruning ($\alpha$–$\beta$ P)—enhanced with some specific heuristics for optimizing the cut-off mechanism in the depth-first search process.

The main characteristics of this algorithm are as follows: (i) A defined positive function depending on a “cost function” (like time, monetary cost, power consumption, and so on) is optimized at each visited node of the search-tree; (ii) The optimal solution is returned if it lies into the imposed in-depth search horizon; otherwise, when the solution search ends in advance, due to the horizon depth or other constraints, the best solution found at the boundary nodes will be always returned; (iii) Each time that the boundary conditions change, the optimal route is recalculated; (iv) The partial solutions estimation, the Branch and Bound activities, and the in-depth search are guided by heuristic functions; (v) Any temporary lists of expanded nodes are stored.

Without loss of generality, the adopted approach consists of considering any route problem as a sequence of best path search problems between two consecutive nodes, and each partial solution is assumed to be independent from all the other paths linking the other nodes belonging to the route. However, for each AFV request for a flight plan, the $\alpha$–$\beta$ P algorithm will exclude all those paths that do not match with the AFV start and maximum arrival times, safety, and power autonomy constraints. In the worst case, it exhibits a time complexity of $b^m$, denoting with b the branching factor and with m the maximum search depth set. A comparison among $\alpha$–$\beta$ P with other algorithms is provided in

Table 1. Algorithm comparison: Brute Force (BF), Depth-First Search Branch and Bound (DFS), Minimum Cost Path (M), $\alpha$Pruning ($\alpha$P), $A^{+}$, Alpha–Beta Pruning ($\alpha$–$\beta$ P); with b—branching factor, m—maximum search depth, d—solution depth.

		BF	DFS	M	$\mathit{\alpha }$P	${\mathit{A}}^{+}$	$\mathit{\alpha }$−$\mathit{\beta }\mathit{P}$
Complexity	in time	$b^d$	$b^d$	$b^d$	$b^d$	$b^m$	$b^m$
	in space	$b^d$	$bd$	$b^m$	$bd$	$bm$	$bm$
Heuristic	search			✓	✓		✓
	Branch and Bound						✓
	boundary nodes					✓	✓
Solution	optimal	✓	✓		✓		✓
	complete	✓	✓		✓		✓
	partial					✓	✓
Pruning	global				✓		✓
	tree cuts		✓			✓	✓

.

The $\alpha$–$\beta$ P algorithm has been implemented in a proprietary code written in C++ in numeric form without a graphic user interface [60].

To conclude this section, it is important to note that the legal and regulatory aspects, which are currently under development or, in some cases, yet to be defined, have been intentionally excluded from the scope of this study. Although regulatory aspects are not within the scope of this study, it is worthwhile to note that the regulation of UAV (or AFV in this study) operations is one of the main enabling—or limiting—factors for their large-scale implementation. Currently, national and international regulatory frameworks are heterogeneous and under development, with significant differences in certification requirements, flight limitations, airspace management, and legal liability in the event of accidents or malfunctions. This regulatory uncertainty is a key challenge for the transition from controlled trials to stable and safe commercial use. Elements such as the integration of drones into urban airspace, privacy protection, data management, and communications security require a clear and shared regulatory framework to outline the operational conditions under which a drone delivery system within a framework such as the one proposed here may be implemented in the future. Looking ahead, the convergence between technological research and regulatory development—for example through the establishment of common standards and recognized safety protocols—will be instrumental in fostering the uptake of reliable UAV systems that comply with emerging regulations.

4. Results

To test the agent-based approach in a 3D-UAN context, according to the aerial net-work model introduced in Section 3.1, a test network was considered, consisting of three fixed nodes (UCCs) and three levels, with a variable number of drones in a reference period (assumed to be two hours of operation). The objective of the experiments conducted is twofold: (1) check if and to what extent the combined agent-based/3D-UAN structure supports drone delivery operations; (2) check the scalability of the proposed architecture as the number of operational drones changes.

To carry out the experiment, some key elements related to the characteristics of the drones (

Table 2. Main features of the VTOL drones adopted in the experiments for operating in urban centers.

Real operating range	15–50 km
Cruising speed	80–120 km/h
Take-off/landing speed	45 km/h
Useful payload	320 kg (typical urban use)
Energy autonomy	≥30 min for intermediate missions

) have been set, as well as the main features of the communication system (

Table 3. Communication range features assumed in the experiments.

Communication range between drones	up to 5000 m
Communication range between drones and UCCs	up to 10,000 m

), which is crucial for the exchange of information in the proposed distributed system. The characteristics of the AFVs have been identified by considering the average features of drones on the basis of what is currently proposed by the involved industries. Similarly, the characteristics of the communication system between the various agents (drones, fixed nodes, and control center) have been identified, in particular, the range. Specifically, an average speed of each $AF{V}_A$ equal to 100 km/h has been assumed and a communication range of up to 5000 m between $AF{V}_A$s and up to 10,000 m between UCC and $AF{V}_A$s. Finally, the range of $AA{M}_A$ is still 10,000 m, but it was considered that in each fixed node, there is a duplicate of $AA{M}_A$. In other words, $AA{M}_A$ is still one, but to ensure the continuous exchange of information, each fixed node also hosts a copy of $AA{M}_A$ that receives and transmits the same information from each fixed node.

As for the links of the test network, it has been assumed that the horizontal lengths are the same, as well as the vertical link lengths. This assumption does not limit the generality of the experiment. In detail, the network consists of three fixed nodes. The distance between two fixed nodes is 8 km, which corresponds to the average distance observed between UCCs in real cases. The lengths of the horizontal links have been assumed to be 2000 m, while the lengths of the vertical links have been fixed to 30 m, which corresponds to a suitable safety distance between two successive layers. The length of 2000 m is compatible with the assumption made in Section 3 that the range of communication between drones for the exchange of information must be at least twice the average length of the link. In fact, this communication range, together with the headway time associated with the generic $AF{V}_A$, allows for obtaining information on the occupancy level of the links—both horizontal and vertical—before arriving at the transition node (or fixed node) where the level change is allowed, in such a way as to always guarantee the safety distance between the drones and therefore the safety conditions on the network. The main characteristics of the 3D-UAN used in the experiments are summarized in

Table 4. Main characteristics of the 3D-UAN used in the experiments.

Number of fixed nodes (UCC)	3
Number of transition nodes	36
Number of vertical links	24
Number of horizontal links	36
UCC separation distance	8000 m
Length of horizontal links	2000 m
Length of vertical links	30 m

.

The recommended minimum horizontal distance between two drones flying at 100 km/h is at least 100–150 m, to ensure that they can maneuver safely and avoid collisions, especially in scenarios with heavy air traffic or unforeseen conditions. This is based on international regulations such as those of the EASA [61] and the FAA [62]. By considering the maximum speed at which drones can travel (assumed to be 120 km/h for horizontal links) and the safety distance that must be maintained between them to ensure safe running, the maximum number of drones that can occupy a link at the same time has been considered equal to six for horizontal links and one for vertical links. The minimum distance between two drones on horizontal links has been calculated as $D_{min}=s·t+s^2/(2·a)$, where s is the speed, a is the deceleration in case of slowdown due to the need to adapt the kinetics for the presence of obstacles (including the presence of other drones), and t is the latency time, which includes the transmission of information from other agents, onboard processing, and physical reaction (e.g., deceleration, turn, and so on).

Finally, the maximum altitude permitted for drones used to transport goods varies according to the regulations in force in each country, the technologies used, and any environmental conditions or obstacles present. In general, however, international recommendations indicate that the operating height of cargo drones is normally kept below 120 m. In the case under consideration, a vertical distance of 30 m between the various levels has been assumed, which together with the height above ground of the vertiport results in a total height consistent with the maximum suggested value of 120 m.

It should be noted that operational drone systems for delivery goods by using 3D structured networks do not yet exist (drones are still prototypes, as is the space organization for supporting 3D-UAN models). Therefore, the data used in the simulated test case is based on available information regarding the current characteristics of aerial drones and communication capabilities, as shown in Table 2 and Table 3, while the assumptions regarding UCCs are consistent with the real case. Consequently, although simulated, the test case is realistic, since all data used is consistent with the representative characteristics of the various elements. Therefore, findings and discussion are in line with possible future scenarios in the real world.

As regards the total number of drones operating on the network, three scenarios have been considered, with 20 drones (SC1), 30 drones (SC2), and 40 drones (SC3), respectively. By taking into account the network structure and the assumption about the headway time, it has been assumed that each drone exchanges information with a number of nearby drones that is constant in the three scenarios. This assumption is consistent with the assumption of the link occupancy limit value, which is constant in the different scenarios, and the headway time, which ensures both separation between drones and compliance with the link occupancy limit.

To verify how this system may operate, the average travel time on the network (in minutes) between two pairs of fixed nodes for the three scenarios considered has been computed. In addition, further simulations have been carried out by considering simulated disturbances that generate delays in the planned flight plans, thus requiring adjustments to the flight plans during the trip. In the simulation, disturbances, which have been here considered depending on environmental and technological issues, generate delays at the take-off from the vertiport, speed variations during the trip, and increased requests of level switches.

It is worthwhile to note that experimental validation using real data is generally the most robust approach to confirm the conclusions of a study. However, the use of simulated data is a justifiable choice at this stage as physical experimentation in this context entails high costs and is subject to regulatory constraints that currently limit the use of drones. In the case under consideration, the simulations have made it possible to systematically analyze different scenarios and operating conditions that are currently difficult to reproduce in a real environment for what is said above, while ensuring the control of variables and the repeatability of experiments. The use of simulated but realistic data is an essential preliminary tool for exploring the feasibility of the system, optimizing design parameters, and identifying the most promising configurations for subsequent experimental testing and should therefore be considered as a preliminary step towards validation with real data. From this perspective, results with simulated data provide consistent and useful quantitative evidence to guide future experimental activities in a more efficient and targeted manner.

The simulations were carried out on a workstation equipped with a Windows 24H2 system, featuring a 10th Gen Intel Core i7-10850H processor, 128 GB of RAM, and a base clock speed of 2.70 GHz up to 5.10 GHz. The $\alpha$–$\beta$ P algorithm was implemented without parallelization, i.e., performing a purely sequential execution on a unique thread, obtaining computation time suitable for real-time operations.

The results of the different tests are shown in

Table 5. Comparison of the results for the three scenarios, with and without disturbances.

	SC1	SC2	SC3
Without disturbances *	5.2	7.8	12.7
With disturbances *	8.4	15.1	21.6

* time in minutes.

.

In SC1, the average travel time between pairs of fixed nodes corresponds to standard conditions under the considered hypotheses (i.e., the 3D-UAN structure, the fleet size, and the parameters assumed for the AFVs). In other words, SC1 can be considered the baseline scenario where drones move according to their planned flight. When the fleet size increases, in SC2 and SC3, the number of switches for the changing layer increases with respect to the baseline scenario (see

Table 6. Average percentage of layer switches with respect to SC1 as the fleet size increases.

	SC1	SC2	SC3
Without disturbances *	-	+8%	+12%
With disturbances *	-	+15%	+21%

* time in minutes.

).

Finally, the adoption of dynamic links allows the effective use of the network, because the same link can be used in two directions, according to its status. However, as the fleet size increases, links are more likely to reach their limit, which has been assumed equal to six in the experiment, coherently with the drone kinematics and safety recommendations from the stakeholders involved. To explore the effect of fleet size on the link dynamic property, the percentage of links that can be used in both directions during the simulation time (i.e., two hours) has also been computed and reported in

Table 7. Percentage of links that can be used bidirectionally as the fleet size increases.

	SC1	SC2	SC3
Without disturbances *	25%	19%	13%
With disturbances *	18%	14%	9%

* values rounded to the nearest whole number.

. As can be seen, the number reduces as the fleet size increases.

Finally, the role of the AAM is to keep consistency among the path changes, when required, by allowing drones autonomy for improving their journeys in cases of deviation from the scheduled flight plan. Although the AAM may introduce some additional constraints, if it is removed from the simulation, the system easily reaches a congested status as the fleet increases and disturbances are introduced. As a result, only a few drones can complete their journey in the simulation period.

5. Discussion and Conclusions

The results in Table 5 provide some interesting food for thought to contribute to the discussion on the use of aerial drones for cargo delivery. In particular, the hypothesized 3D-UAN structure has allowed for the exploration of possible operational scenarios by considering an increasing number of drones.

Before discussing the results, it is useful to start with some general considerations. In a distributed agent system, each drone is an autonomous agent that communicates with other agents to make decisions by continuously exchanging information. In general, as the number of agents increases, interactions and network usage density increase, and this potentially poses scalability problems by reducing the system’s ability to maintain acceptable performance (e.g., in terms of communication, response time, use of resources). Moreover, as the number of drones increases, it can become difficult to ensure appropriate vertical and horizontal separations, which is important for safety purposes. In particular, vertical operations (climbing/descending for a level change) can become critical points, as queues, conflicts, and slowdowns can form because, often, vertical maneuvers are limited (e.g., only one drone at a time on a segment).

In the proposed network model, two elements make it possible to manage the increase in the average travel time generated as the number of drones on the network increases, while ensuring safe conditions: (1) dynamic links; (2) headway time.

In fact, the structure of the network with dynamic links makes it possible to make more intensive use of the overall capacity of the network by exploiting the link in both directions. The headway time, on the one hand, introduces a time separation at departure to prevent the increase in the number of drones from leading to poor safety conditions during the journey. On the other hand, this delay at departure may result in an increase in the average travel time, which is more significant the greater the number of drones involved.

By considering the experiments conducted on the test network, when the system works optimally (i.e., without disturbances), each drone-agent follows the route planned and approved by the AAM. As the number of drones increases, it may be necessary to activate the headway time to ensure safety conditions on the network and at the same time comply with the initial flight plan as much as possible. As can be seen from Table 5, the average travel time between two fixed nodes tends to increase as the number of drones increases, as is to be expected. In the three disturbance-free scenarios, the increase in average travel time is linked to the increase in headway time.

The presence of disturbances represents a more realistic operating condition, as it takes into account any changes compared to what was initially planned, which may be due to delays in loading/unloading of drones, unforeseen weather conditions, or other factors that can change the initial scheduling. The opportunity, however, of using dynamic links and modifying the planned route in real time, while introducing an additional complexity linked precisely to this modification, nevertheless makes it possible to limit the delays that are generated as the number of drones increases.

As it can be seen from Table 5, the presence of disturbances further increases the travel time compared to the basic condition in which optimal system operations are assumed. Note that for both conditions—with and without disturbances—travel time increases more than linearly as the number of drones increases.

The increase in travel times as the fleet size increases is also linked to the maximum number of layers assumed, in this case three, in line with current regulations on the maximum operating height allowed for drone deliveries. Introducing additional levels can reduce travel times. In fact, although changing the layer involves additional time to move along the vertical link (compare results in Table 5 and Table 6), this increase is less than the delay associated with each drone when it has to wait for take-off because one or more links have reached the maximum number of drones allowed. It is worthwhile to note that the increase in travel times as the fleet size increases and disturbances are also considered (see Table 5) is the combination of both changing levels and delay at take-off, which is introduced by the headway time.

Finally, the 3D-UAN with dynamic links offers the opportunity to use effectively the residual capacity (here considered in terms of the number of AFVs on the link). However, as reported in Table 7, the greater the fleet size and the presence of disturbances, the less the link dynamic property can be used, because of the several constraints that take place (i.e., number of AFVs on the link, safety restrictions, allowable paths).

To conclude, the 3D-UAN network makes it possible to manage an increasing number of drones effectively, thanks to the defined architecture that introduces distributed rules, vertical stratification, and strategic planning together with autonomous and distributed operational control. By combining a 3D-UAN with a scalable agent-based control system, this research provides a fundamental framework for exploring complex urban logistics scenarios. It supports both simulation-based performance assessment and policy-driven scenario testing, facilitating the identification of operationally feasible solutions.

In the context of UAM development, the operational and strategic implications of the above findings for the involved stakeholders are particularly relevant for the efficient and sustainable management of urban airspace.

For UAM operators, the need to plan multi-level and dynamic flights to reduce congestion and waiting times at key network nodes emerges. This requires the adoption of take-off schedule optimization strategies and flexible trajectory management to ensure maximum operational efficiency.

From the perspective of airspace managers (UTM/U-Space), the implementation of predictive capacity and traffic management systems capable of anticipating changes in demand and potential operational disruptions is expected. These systems should enable the dynamic adaptation of flight corridors based on environmental conditions and the evolution of urban air traffic.

Regulatory authorities (such as the EASA and the FAA) are called upon to reassess current altitude indications and introduce flexible regulatory frameworks that allow for the creation of multiple operational levels within urban airspace. This approach would allow for greater operational density without compromising safety or minimal separation between different flight levels. Ultimately, network designers and urban planners should integrate the spatial and operational dimensions of urban air mobility to ensure interoperability, accessibility, and long-term sustainability.

Although the results of combining 3D-UANs with an agent-distributed architecture are encouraging, several developments can be expected, which are discussed below.

The proposed model considered the use of drones within the operational range of energy consumption. Further developments are to be expected by explicitly considering the constraint on energy consumption, which is an important element to ensure both service continuity and system safety. In addition, drones have always been considered “reliable”, meaning that disruptions or failures in information communication systems have not been considered. Also on this aspect, further developments are to be expected by modeling potential failures in communication systems and identifying the most appropriate strategies to continue to ensure safety on the network.

In detail, an important aspect in the design and analysis of drone cargo delivery systems concerns the management of the energy available on board, which is a limited resource and directly determines both the continuity of the service and the overall safety of the system. In this study, explicit energy constraints within the model were not considered, although, in the simulations carried out, the energy constraint was implicitly taken into account by considering a maximum time to achieve the mission compatible with the operational energy range. However, the explicit introduction of energy constraints would make it possible to represent in detail aspects such as the possible interruption of the service to allow the recharging of drones (which was implicitly considered here through the introduction of disturbances) and the definition of management policies that guarantee adequate safety margins, especially in complex or densely populated urban environments. From a service continuity perspective, power consumption modeling makes it possible to analyze in detail whether the set of planned missions can actually be completed with the remaining battery capacity. In terms of safety, monitoring of energy status can predict critical situations such as battery depletion during flight or inability to reach a safe landing point. In addition, the energy consumption, but also the flight stability and overall reliability of the mission, depend on atmospheric factors such as wind intensity, precipitation, and temperature. In the simulations considered, the variability of weather conditions was considered, again, in terms of disturbances, which take into account the deviation between ideal and real conditions, in particular with regard to environmental and technological factors. Explicit energy models will have to introduce the relationship between the operational parameters of the drone (such as mass, speed, altitude, weather conditions) and energy consumption. These energy models can be integrated into the overall framework through a modification of cost functions to penalize energy-inefficient solutions. In addition, stochastic or probabilistic approaches (e.g., Monte Carlo simulations) can be used to capture the variability of weather conditions in the simulation phase, while real-time weather data and weather forecasting services can be part of the information exchanged between drones, fixed nodes, and AAMs in the proposed framework.

As regards communication systems, continuity and quality of communications are key elements in the proposed framework to ensure coordination, air traffic control, and safety of operations. Failure or interruptions in communication systems were not introduced, because the system was considered in “ideal” conditions. However, factors such as electromagnetic interference, signal loss, network congestion, or sensor malfunction can compromise the transmission of critical data, negatively affecting system performances. The assumption made in this study of the complete reliability of drones and the absence of failures or interruptions is, again, an ideal limit condition compared to real operational scenarios, which can obviously lead to an overestimation of the reliability and efficiency of the system. Including communication failure models in future developments—for example, by introducing probability of error, delay, or loss of information packages—would allow for analyzing the resilience of the system and developing mitigation strategies such as redundancy protocols, multi-channel communications, or autonomous emergency procedures. In this way, the model would be more in line with real operating conditions for a better assessment of the overall safety and reliability of the system. Moreover, the modeling of potential failures in communication systems would allow for the identification and implementation of strategies that ensure the maintenance of the operational security, in order to preserve service continuity even in the presence of anomalies or interruptions in information flows. Fault tolerance strategies may include the adoption of redundant communication architectures and automatic data-recovery protocols, while distributed control systems and autonomous decision-making mechanisms on board the drone, which are already present in the proposed framework, may be specified in more detail to explicitly include the case of loss of connection to the core network. Integrating these strategies into the model would allow for the analysis of the overall resilience of the system, and the likelihood of failure cascading, while ensuring safety even under adverse operating conditions. Looking ahead, a fault tolerance approach is a key step towards developing reliable, safe, and sustainable autonomous delivery infrastructures.

In conclusion, although several advances have been made and many studies are now present in the literature to analyze the various aspects of the problem, several challenges still remain. The implementation of UAV-based logistics, in reality, has to deal with airspace congestion, regulatory uncertainty, environmental variability (e.g., weather conditions), and infrastructure dependencies. At the same time, integration with U-Space infrastructures, promoted at the European level, or with UTM systems at the international level, is an essential element for the coordinated and safe management of drone air traffic, as these systems allow monitoring and information-sharing among operators, improving the safety and overall efficiency of delivery operations. Furthermore, ensuring the scalability, safety, and sustainability of such systems requires continuous innovation in both algorithm design and system architecture, while the management of data generated and exchanged during UAV missions raises important privacy and IT security issues, particularly in relation to the collection of sensitive data (e.g., images, locations, or user data) and their transmission via potentially vulnerable networks. These gaps suggest developing delivery models with more adaptable, intelligent, and fault-resistant UAVs that can operate effectively in dynamic urban environments.