Neural-Guided Adaptive Clustering for UAV-Based User Grouping in 5G/6G Post-Disaster Networks

Abstract

In post-disaster scenarios, Unmanned Aerial Vehicles (UAVs) acting as Mobile Aerial Base Stations (MABSs) offer a flexible means of restoring communication for isolated user equipment (UE) when conventional infrastructure is unavailable. More broadly, clustering is a fundamental tool for organizing spatially distributed entities in wireless, IoT, and sensor networks. However, static algorithms such as Affinity Propagation Clustering (APC) often fail to generalize across diverse environments and user densities. This study introduces a hybrid clustering framework that dynamically selects between APC and density-based clustering (DBSCAN), guided by a neural classifier trained on spatial distribution features. The chosen centroids then seed a Genetic Algorithm (GA) that evolves UAV trajectories under multiple performance indicators, including coverage, capacity, and path efficiency. Simulation results demonstrate that the hybrid clustering approach improves the adaptability and effectiveness of UAV deployments by learning context-aware clustering strategies. Beyond UAV-assisted disaster recovery, the proposed framework illustrates how intelligent clustering selection can enhance performance in heterogeneous, real-time applications such as IoT connectivity, smart city monitoring, and large-scale sensor coordination.

1. Introduction

The deployment of Mobile Aerial Base Stations (MABSs) has been instrumental in supplementing terrestrial infrastructure, especially in post-disaster environments where ground-based communication is disrupted. MABSs provide rapid, flexible, and cost-effective coverage, leveraging aerial mobility and line-of-sight (LOS) communication to serve dispersed User Equipment (UE) over large geographic areas. In disaster scenarios, such as the 2017 Hurricane Maria in Puerto Rico, aerial solutions, such as cell-on-wings (COW) drones, were deployed to re-establish LTE cellular connectivity, demonstrating the critical role of Unmanned Aerial Vehicles (UAVs) in mission-critical communication recovery. Their ability to operate at varying altitudes, dynamically reposition, and form network topologies on the fly renders them essential components of modern Disaster Response Networks (DRNs).

A key enabler of effective MABS deployment is the intelligent clustering of UEs to guide UAV path planning. Traditional clustering algorithms, such as Affinity Propagation Clustering (APC), are well-suited for this task because of their non-parametric nature and ability to adapt to varying UE numbers. However, APC and similar static methods may not always produce optimal centroids under highly variable UE densities, geographical dispersions, or uneven Base Station (BS) failure rates. These limitations are more pronounced in DRNs where user mobility and environmental uncertainties are common.

To address these issues, this study proposes a hybrid clustering framework that dynamically selects between APC and Density-Based Spatial Clustering of Applications with Noise (DBSCAN), guided by a lightweight neural network classifier. The model is trained to recognize spatial distribution patterns and choose a clustering strategy that is best suited to the environment of interest. By integrating this adaptive mechanism with a Genetic Algorithm (GA) for multi-objective path optimization, the proposed method enhances the resilience and adaptability of MABS deployment. This approach supports faster convergence, fewer drones, and improved UE coverage in heterogeneous and evolving disaster scenarios.

1.1. Problem Identification and Novelty

This study investigated the limitations of static UE clustering methods in disaster-stricken communication environments and introduced a neural-assisted clustering control framework that enhances UAV path planning in DRNs. Specifically, the challenge addressed is how to dynamically adapt clustering strategies (APC or DBSCAN) based on the spatial characteristics of the affected users while preserving path efficiency and coverage constraints. The proposed model replaces the rigid, one-size-fits-all approach with an adaptive mechanism capable of learning from historical data distributions and making intelligent decisions during operation.

Compared with prior studies (see Section 2), this study introduces a hybrid clustering selector that leverages pattern recognition via machine learning, allowing UAVs to switch clustering strategies in real time. This results in better centroid placement, fewer missed UEs, and more optimal coverage, especially when the UE distribution varies drastically because of evacuation behavior or terrain obstacles. The system was validated under BS failure rates ranging from 10% to 90%, emphasizing its performance in macro-scale service zones rather than in micro hotspots.

The key challenges addressed include the following:

• Choosing the optimal clustering method based on the current UE distribution without human intervention.
• Avoiding centroid intersection or outliers by balancing APC’s adaptability with DBSCAN’s density-awareness.
• Optimizing UAV paths over dynamically selected centroids with a multi-objective fitness function considering distance, angle smoothness, intersection count, and service ratio.

In this study, APC and DBSCAN were selected as the foundational clustering methods due to their complementary characteristics in disaster scenarios. APC autonomously determines the number of clusters and performs effectively in structured and dense user distributions; however, it is sensitive to noise and exhibits suboptimal performance in sparse or irregular topologies [1]. In contrast, DBSCAN demonstrates robustness in sparse or noisy distributions and can effectively identify arbitrarily shaped clusters, though its performance is highly dependent on parameter settings and it encounters scalability challenges in dense networks [2]. By integrating both methods within an Artificial Neural Networks (ANN)-guided hybrid architecture, our framework adapts to both dense and sparse post-disaster conditions, ensuring resilient UAV-based user grouping. Alternative clustering strategies, such as fuzzy C-means [3], PSO-based clustering [4], or enhanced user grouping for Non-Orthogonal Multiple Access (NOMA)-aided UAV networks [5], exhibit strong performance in specific domains (e.g., energy efficiency, spectral efficiency), but they lack the robustness necessary for highly dynamic post-disaster scenarios. This complementarity motivated the selection of APC–DBSCAN as the foundation of the proposed hybrid scheme.

1.2. Novel Contributions and Approach

This study makes several contributions to the literature.

• A hybrid clustering architecture combining APC and DBSCAN with a neural selector trained on UE spatial distributions, enabling real-time adaptive centroid generation.
• An integrated multi-objective path planning algorithm using a GA that balances service coverage, and route smoothness.
• Simulation of diverse disaster scenarios, demonstrating improved performance in terms of fitness score, UE coverage, and number of UAVs required compared to conventional APC-based approaches.

1.3. Organization of This Paper

The remainder of this paper is organized as follows: Section 2 reviews related studies on UAV clustering and learning-based path planning. Section 3 presents the environmental modeling and assumptions used in this study. Section 4 details the proposed hybrid clustering framework and GA-based optimization. Section 5 presents a performance evaluation and discussion of the results. Section 6 concludes the study and outlines future research directions.

2. Related Works

This section offers a comprehensive review, as the proposed framework encompasses multiple research domains: clustering algorithms for UAV-assisted communications, neural-guided dynamic clustering, and multi-objective UAV path optimization. The discussion is provided to ensure the context is provided for readers from diverse backgrounds related to the paper’s scope, including wireless communications, artificial intelligence, and disaster management. Concurrently, the review underscores the specific limitations of existing approaches, which directly inform the proposed hybrid APC–DBSCAN + ANN model. For readers primarily interested in the contribution, summary tables are provided to consolidate the most pertinent insights and facilitate quick comparison without necessitating a full reading of each algorithm description.

RQ1: What clustering algorithms have been used in UAV-assisted wireless coverage, and how do they perform in disaster scenarios?

Clustering algorithms are vital for optimizing UAV-assisted wireless coverage, particularly in disaster scenarios. Among these, K-means and K-means++ have been widely adopted for clustering ground users and UAV deployment. K-means++ enhances the initial centroid selection, significantly improving the user throughput and satisfaction ratio [6,7,8]. The hybrid K-means approach Particle Swarm Optimization (PSO) combines K-means with PSO, achieving a more balanced performance in terms of coverage, energy efficiency, and reliability [9]. PSO is another widely used technique for optimizing cluster coverage and 3D UAV placement problems. It exhibits faster convergence and requires fewer UAVs than K-means [4,10]. The Ellipse Clustering Algorithm further contributes by adjusting the UAV antenna parameters to maximize the user coverage probability while minimizing the transmission power [11]. Fuzzy Logic and Fuzzy C-Means (FCM) offer dynamic solutions such as cluster head selection based on sensor node energy and storage levels [7]. An enhanced version, Fitness-based Fuzzy C-Means (Fit-FCM), integrates additional factors such as energy, distance, and trust to improve cluster head selection in UAV-based wireless sensor networks [12]. DBSCAN, a density-based clustering algorithm, has been used in conjunction with convex optimization for UAV trajectory planning and charger allocation. This integration reduces the number of chargers required while boosting the overall throughput [13]. Meanwhile, Log Linear Learning has proven effective for UAV deployment in disaster-stricken regions by using a UAV coverage utility function to ensure comprehensive network coverage [14]. These algorithms have different strengths and weaknesses in disaster scenarios. K-means is effective for initial coverage and user satisfaction, although its performance can vary based on the centroid initialization and distance metrics used [6,8]. It supports user association, optimal UAV placement, and altitude selection to maximize data rates in emergencies [15]. PSO-based algorithms not only reduce the number of UAVs required, but also outperform GA and artificial bee colony (ABC) methods in terms of execution time and energy efficiency [4,16]. Fuzzy logic and fit fuzzy c-means clustering improve the lifetime of the network and reduce packet loss, which are crucial for reliable communication in WSNs assisted by UAVs [7,12].

DBSCAN minimizes charger use and increases throughput, offering a cost-effective disaster response solution [13]. Finally, log-linear learning has demonstrated both generality and the best performance compared with optimal selection algorithms in emergency deployments [14].

Clustering algorithms, such as K-means, PSO, fuzzy logic, FCM, DBSCAN, and log-linear learning, are critical for enhancing the effectiveness of UAV-assisted wireless coverage. These methods contribute significantly to improving coverage, energy efficiency, and system reliability, particularly when the terrestrial communication infrastructure is compromised by the environment. While K-means and PSO offer robust overall performance, algorithms such as Fuzzy Logic and DBSCAN provide specialized advantages in terms of energy conservation and operational cost, making them indispensable in emergency and disaster response scenarios.

Table 1. Comparison of clustering algorithms in UAV-assisted disaster scenarios.

Study	Algorithm Type	Clustering Method	Disaster Support	Key Capabilities	Optimization Parameters	Strengths	Limitations
[6,7,8]	Hard Clustering	K-means, K-means++	Yes	Ground user clustering, UAV deployment	User throughput, satisfaction ratio	Simple, fast convergence	Sensitive to centroid initialization
[9]	Hybrid Clustering	K-means + PSO	Yes	Balancing coverage and UAV usage	Energy, coverage, reliability	Combines strengths of both methods	Higher complexity
[4,10]	Swarm Intelligence	PSO	Yes	3D placement, fast convergence	UAV count, coverage, energy	Requires fewer UAVs than K-means	Risk of local optima
[11]	Geometric/Heuristic	Ellipse Clustering	Yes	Antenna tuning, coverage maximization	Transmit power, coverage probability	Antenna-aware, power efficient	Assumes ideal propagation models
[7,12]	Soft Clustering	Fuzzy C-Means, Fit-FCM	Yes	Cluster head selection based on trust, energy, distance	Network lifetime, packet loss	Energy-aware and adaptive	Computational overhead
[13]	Density-based	DBSCAN + Convex Optimization	Yes	Charger allocation, trajectory planning	Number of chargers, throughput	Cost-effective for sparse networks	Not scalable to large systems
[14]	Game-Theoretic Learning	Log-Linear Learning	Yes	UAV utility-based deployment	Network coverage utility	Generalizable and high-performing	Needs well-defined utility model
[15]	Clustering-Assisted Placement	K-means	Yes	User association, UAV altitude optimization	Data rate, placement	Simple UAV placement guidance	Performance depends on initialization

compares eight clustering methods, K-means, K-means++, PSO, FCM, DBSCAN, and log-linear learning, used in UAV-assisted disaster scenarios. It highlights each method’s type, disaster support capability, optimization goals, and respective strengths and limitations. For instance, K-means++ offers simplicity and fast convergence but is sensitive to centroid initialization, whereas DBSCAN is cost-effective in sparse networks but struggles with scalability. This comparison sets the foundation for why a hybrid adaptive clustering method is needed in post-disaster UAV networks (see Table 1).

Recent studies have investigated alternatives beyond traditional clustering methods. Fuzzy C-means and its variants have been shown to enhance adaptability and energy efficiency in UAV-assisted networks [3,7,12], while swarm-intelligence techniques, such as PSO-based clustering, have demonstrated the ability to optimize the required number of needed UAV and convergence time [4]. More recently, the introduction of clustering and pairing in NOMA-aided UAV systems has aimed to improve spectral efficiency and fairness [5]. Although these approaches are promising, they are generally tailored for energy optimization or spectral-domain efficiency under relatively stable conditions. In contrast, the APC–DBSCAN combination specifically addresses the dual challenges of sparse, noisy distributions and dense, structured clusters that are characteristic of post-disaster environments.

RQ2: How have machine-learning or neural models been used to guide clustering or adapt path planning in dynamic environments?

Machine-learning and neural models have been increasingly applied to guide clustering and adapt path planning in dynamic environments. One notable approach is the Two-Stage Learning-Based Model, where the first stage extracts features of the surrounding environment and predicts the trajectories of dynamic obstacles, and the second stage utilizes reinforcement learning to plan a feasible and efficient path based on those predictions. This model demonstrates high predictability and processing capacity for dynamic obstacles and successfully executes planning tasks in various dynamic scenarios [17]. In the realm of Neural Network-Guided Path Planning, methods such as Neural Sampling Technique (NST), Probabilistic Roadmaps (PRM), and Rapidly Exploring Random Trees (RRT) employ neural networks trained on datasets generated through PRM and RRT. These techniques notably reduce the dataset generation time and enhance path-planning efficiency in environments with numerous obstacles [18]. A Graph Neural Network (GNN)-Based Planner, further improves planning by leveraging prior exploration experience and minimizing replanning costs under unpredictable conditions. This results in a high planning performance with fast speeds and low path costs, outperforming both traditional and other learning-based methods [19]. Another advancement is the Dynamic Distance Transform Algorithm, in which a neural model adapts the distance transform method for dynamic contexts, forming a dynamically updating potential field. This ensures an effective local adaptation and optimal path planning in dynamic environments [20].

In terms of Clustering for Path Planning, cluster-based routing for UAVs integrates online path planning, clustering-based network topology, reinforcement-learning-driven cluster management, and data routing. The outcomes include improved coverage, better adaptation to changing environments, enhanced packet delivery ratios, and reduced communication delays [21]. Furthermore, combining clustering and neural networks for trajectory prediction, such as the use of DBSCAN and multicell neural networks (MCNN), produces accurate short-term 4D trajectory predictions, demonstrating their robustness and effectiveness in dynamic settings [22,23].

Among Hybrid and Reinforcement Learning Approaches, Q-Learning-Based Local Planning considers factors such as path length, safety, and energy consumption and shows reliable performance in both static and dynamic environments by avoiding the typical pitfalls of conventional algorithms [24]. When ANNs are combined with Q-learning, the ANN serves as a path-planning controller, whereas Q-learning generates training samples. This hybrid strategy is more effective than using either technique alone to find optimal paths [25]. In practical applications, Multi-Robot Systems (MRS) benefit from improved neural dynamics approaches that incorporate territorial mechanisms, resulting in robust and fair path planning in complex and changing environments [26]. Similarly, Autonomous Vehicles leverage deep reinforcement learning and clustering-based strategies to develop both theoretical models and practical solutions for effectively navigating dynamic surroundings [27,28].

The integration of machine learning and neural models has significantly improved path planning and clustering performance in dynamic environments. By enhancing efficiency, adaptability, and accuracy, these methods, particularly those involving reinforcement learning, neural networks, and clustering, effectively address challenges posed by dynamic obstacles and varying conditions.

Table 2. Machine learning and neural models for clustering and path planning in dynamic UAV environments.

Study	Model Type	Algorithm/ Framework	Clustering Role	Path Planning Role	Environment Dynamics	Strengths	Limitations
[17]	Two-Stage ML + RL	Feature extraction + RL planner	None	Obstacle prediction and path planning	Dynamic obstacle scenarios	High accuracy, robust predictions	Needs extensive training data
[18]	Neural Model + Sampling	NST-PRM, NST-RRT	None	Guided PRM and RRT planning	Obstacle-rich spaces	Fast, reduces dataset needs	Requires structured training environment
[19]	Graph Neural Network	DynGMP	None	GNN-based motion planning	Unpredictable, partially-known terrain	Fast, low path cost, prior learning reuse	Complex GNN model tuning
[20]	Neural Potential Field	Dynamic Distance Transform	None	Local adaptation via distance transform	Dynamic potential fields	Adaptive local decisions, fast convergence	Limited to local scope planning
[21]	Hybrid ML + RL	Cluster-based RL Routing	Forms cluster-topology network	RL-based UAV routing	Environment-aware UAV routing	High coverage, low delay	Computa- tionally intensive
[22,23]	Clustering + Neural Prediction	DBSCAN + MCNN	DBSCAN for cluster inputs	MCNN for 4D trajectory prediction	Varying UAV mobility patterns	High prediction accuracy	Data dependency, model complexity
[24]	RL-based	Q-learning Local Planner	None	Local UAV path optimization	Static and dynamic settings	Learns from environment directly	Exploration-exploitation tradeoff
[25]	Hybrid ANN + RL	ANN Controller + Q-learning	None	ANN guides path search, Q-learning trains	Both static and dynamic terrain	Better than ANN or Q-Learning alone	Slower training, hybrid complexity
[26]	Neural Dynamics	Territorial Mechanisms	None	Multi-robot UAV coordination	Complex, changing domains	Fair, robust multi-agent paths	Less suitable for sparse networks
[27,28]	Deep RL + Clustering	Autonomous UAV Navigation	Topology and learning-based adaptation	Obstacle-aware deep RL planning	Real-time urban environments	Effective for theory and practice	Needs large-scale real-world data

summarizes representative machine learning (ML)- and ANN-based frameworks applied to UAV operations in dynamic environments. Although many of these approaches, such as two-stage ML + reinforcement learning (RL) models, GNNs, neural potential fields, and hybrid RL routing systems, were originally designed for path planning and navigation, they also demonstrate how learning-based methods improve clustering and user grouping under uncertain conditions. In particular, their adaptability to environmental changes highlights the importance of dynamic, data-driven clustering for UAV-assisted communications. However, existing approaches often emphasize navigation efficiency rather than robust user grouping, leaving a gap when users are mobile, unevenly distributed, or experience fluctuating link qualities. This gap directly motivates our integration of ANN-guided clustering into an adaptive hybrid framework tailored to UAV-based user grouping.

As such, a central challenge in UAV-assisted communication recovery remains insufficiently addressed: the dynamic grouping of users in highly variable environments. Static clustering methods cannot cope with high user mobility, uneven user distributions, and rapidly changing channel conditions, leading to degraded communication efficiency. This gap provides the motivation for this paper, where we introduce an adaptive hybrid clustering framework is guided by artificial neural networks. By combining the adaptability of learning-based clustering with the robustness of hybrid schemes, our approach ensures efficient UAV-based user grouping in dynamic environments.

Recent advances have further extended adaptive clustering into industrial IoT and NOMA-UAV domains. For instance, Smart Collaborative Evolvement for Virtual Group Creation in Customized Industrial IoT introduces probabilistic virtual grouping to adapt to heterogeneous Industrial Internet of Things (IIoT) demands dynamically, improving flexibility in industrial environments [29,30,31]. Similarly, Adaptive Virtual Clustering Methods for Dynamic IoT Edge propose strategies that reconfigure cluster membership in response to load and node heterogeneity [5,32,33]. On the UAV–communication front, Enhanced User Clustering and Pairing Scheme for NOMA-Aided UAV Networks presents an Advanced Balanced K-Means (ABKM) method to ensure fairness and throughput optimization in NOMA settings [34,35]. Other works combine path planning and NOMA resource allocation via Deep Reinforcement Learning (DRL) [36] or explore energy-efficient NOMA-UAV downlink schemes [37]. These contributions enrich the landscape of adaptive clustering, but differ from our approach: while they focus primarily on spectral efficiency enhancements or domain-specific constraints, our framework targets post-disaster UAV-assisted networks, combining ANN-guided hybrid clustering (APC–DBSCAN) with GA-based trajectory planning to balance coverage, robustness, and multi-objective optimization.

RQ3: What hybrid clustering or dynamic strategy selection methods exist, and how do they affect trajectory or resource efficiency?

Hybrid clustering and dynamic strategy selection methods have been introduced to enhance trajectory planning and resource efficiency in various applications. One of such approach is the Hybrid Selection Multi-Objective Evolutionary Algorithm (HSMEA), which combines angle and distance metrics for clustering individuals, followed by a hybrid selection mechanism. This method strikes an effective balance between convergence and diversity, making it suitable for complex multi-objective optimization tasks [38]. Another notable method, the Density-based K-means (DKGK) approach, utilizes Differential Evolution (DE) to promote diversification, K-means for refinement, and a GA enhanced with heuristic crossover to ensure fast convergence. This combination outperforms conventional approaches, such as DE, GA, DE-K-means, and GA-K-means, by significantly reducing intra-cluster distances, leading to better clustering accuracy and efficiency [39].

The hybrid grasshopper and differential evolution-based optimization algorithm (HGDEOA) integrates adaptive strategies into DE, thereby enhancing its global search ability and reducing the risk of premature convergence. This results in improved energy stability, higher throughput, and extended network lifetime in Wireless Sensor Networks (WSNs) [40]. Similarly, the Hybrid Deep Fixed K-Means (HDF-KMeans) approach merges Deep K-Means++ for advanced feature extraction and centroid initialization with Fixed Centered K-Means to improve stability. This hybrid model enhances clustering accuracy and consistency, particularly in critical domains such as healthcare [41].

Among the Dynamic Strategy Selection Methods, the Dynamic Genetic Algorithm (DGA) improves the automatic calculation of the number of clusters (k) and improves the population initialization, genetic operators, and fitness functions. These improvements lead to more accurate clustering outcomes and better estimation of the cluster numbers [42]. The Gaussian Mutation Adaptive Artificial Fish Swarm Algorithm (GAAFSA) incorporates Gaussian mutation and adaptive strategies to avoid local optima and early convergence, which boosts the network lifespan, increases packet reception rates, and reduces packet loss in Industrial Wireless Sensor Networks (IWSNs) [43]. Meanwhile, adaptive density peak clustering with Fisher linear discriminant (ADPC-FLD) employs kernel density estimation and weighted Euclidean distances, along with adaptive strategies for selecting cluster centers. This significantly enhances the clustering accuracy and efficiency, particularly in high-dimensional data scenarios [44].

Regarding the effects on trajectory and resource efficiency, methods such as HGDEOA and GAAFSA contribute significantly to energy efficiency and network longevity by optimising cluster head selection and data transmission in WSNs and IWSNs [40,43]. In terms of convergence and diversity, HSMEA and DKGK provide robust clustering solutions that enhance system performance [38,39]. For applications demanding high precision, such as healthcare and complex data analysis, techniques such as HDF-KMeans and ADPC-FLD deliver notable improvements in precision and consistency [41,44]. Hybrid clustering and dynamic strategy selection methods offer meaningful advancements in trajectory optimization and resource efficiency. By enhancing energy stability, promoting balanced convergence and diversity, and increasing clustering accuracy, these techniques are valuable in a wide array of technical domains.

Table 3. Hybrid clustering and dynamic strategy selection methods for UAV trajectory and resource efficiency.

Study	Strategy Type	Method/ Algorithm	Hybrid Components	Application Domain	Target Metrics	Strengths	Limitations
[38]	Hybrid Clustering	HSMEA (MOEA-based)	Angle + distance metrics, hybrid selection	Multi-objective optimization	Convergence, diversity	Balanced trade-off in optimization	May require fine-tuned configs
[39]	Hybrid Evolutionary	DKGK	DE + GA + K-means	Clustering and search optimization	Clustering accuracy, intra-cluster distance	Fast convergence, improved accuracy	More complex than standalone methods
[40]	Hybrid Evolutionary	HGDEOA	Grasshopper + Adaptive DE	WSN energy optimization	Energy stability, lifetime, throughput	Strong global search, avoids early convergence	Needs parameter tuning
[41]	Deep Hybrid Clustering	HDF-KMeans	Deep K-means++ + Fixed Centered K-means	Healthcare, mission-critical clustering	Accuracy, stability	Advanced feature extraction, stable centers	Limited generalizability outside domain
[42]	Dynamic Strategy Selection	Dynamic GA (DGA)	Adaptive operators, fitness function tuning	Clustering under changing needs	Cluster number accuracy, fitness improvement	Automatically tunes cluster count	Fitness model design complexity
[43]	Dynamic Metaheuristic	GAAFSA	Adaptive fish swarm + Gaussian mutation	IWSNs, clustering optimization	Network life, packet reception, convergence	Avoids local optima, robust convergence	Overhead in mutation and adaptation
[44]	Adaptive Clustering	ADPC-FLD	Density peaks + Fisher LD + kernel density	High-dimensional data clustering	Accuracy, clustering efficiency	Adaptive center selection, distance-weighted	High-dimensional kernel estimation cost

compares hybrid approaches, such as HSMEA, DKGK, HGDEOA, and adaptive clustering methods. Each combines different algorithms (e.g., DE+GA+K-means) to optimize clustering accuracy, convergence, and resource use. The strengths of these models include improved energy stability and accuracy; however, their limitations often involve parameter tuning or domain-specific constraints. The discussion in this paper leverages this to justify the hybrid APC–DBSCAN + ANN framework (see Table 3).

RQ4: What fitness functions or multi-objective optimization approaches are most effective for UAV path planning in DRNs?

To identify the most effective fitness functions or multi-objective optimization approaches for UAV path planning in DRNs, various insights have emerged from recent research. Several fitness functions are typically used in this context. One core focus is on minimizing both distance and risk, as seen in methods that apply the Bézier theory and impose constraints such as turning angle and flight altitude [45]. Similarly, another study incorporated traveling distance and risk along with height, angle, and slope limitations to guide UAV navigation [46].

Energy efficiency is another critical criterion. Some models aim to reduce fuel consumption, altitude costs, and threat exposure during flights  [47]. In particular, Bézier curve-guided paths optimized via GAs and multi-objective swarm-based strategies are effective in improving energy use [48]. In multi-UAV systems, utility-based objectives such as maximizing the number of people rescued are coupled with collision avoidance to ensure operational safety [49]. Additionally, Quality of Service (QoS) is emphasized in UAV-assisted Mobile Edge Computing (MEC) frameworks, where path planning considers geometric distance, risk level, and terminal user demand [50]. Several techniques have been proposed for multi-objective approaches. A knee-guided differential evolution algorithm directs the search toward optimal UAV paths with smooth trajectory generation [45], whereas another variant incorporates an adaptive selection mutation to improve refinement while preserving exploration [46]. RL methods are effective in dynamic urban settings, optimizing UAV paths under conditions of mobile obstacles and variable threats [50].

GAs remain widely used for path optimization due to their versatility in complex optimization. One approach normalizes the fitness criteria and employs swarm-based enhancements for energy efficiency [48]. Another study combined an adaptive GA for mission assignment with an improved artificial bee colony method for optimal path planning [51]. The Hybrid Equilibrium Optimizer (HEO) uses techniques such as Gaussian distribution estimation and Lévy flight to divide populations and balance exploration and exploitation [47]. Moreover, Ant Colony Optimization (ACO) has been improved for accurate 3D path planning, minimizing flight path length, and terrain threats [52].

Table 4. Summary of fitness functions and optimization techniques.

Study	Approach	Key Fitness Functions	Optimization Techniques	Key Benefits
[45,46]	Differential Evolution	Distance, Risk	Knee point-based DE	Quick optimal path identification
[50]	Reinforcement Learning	Geometric Distance, Risk, QoS	RL framework	Effective in dynamic settings
[48,49]	Genetic Algorithms	Energy, Collision Avoidance	GA, Swarm-based	Balanced energy and safety
[47]	Hybrid Eq. Optimizer	Fuel, Altitude, Threat	MHEO, Gaussian, Lévy	Efficient, stable path planning
[52]	Ant Colony Optimization	Flight Length, Terrain Threat	Enhanced ACO	Accurate in complex terrain

outlines the fitness criteria, such as distance, risk, energy, and QoS, alongside the optimization technique used (e.g., DE, RL, GA, hybrid metaheuristics, ACO). This emphasizes that effective UAV path planning must balance efficiency, safety, and adaptability. This reinforces why the proposed GA-based framework incorporates multiple weighted objectives (see Table 4).

Effective UAV path planning in DRNs using GA depends on fitness functions that measure distance, risk, energy consumption, and mission utility. Multi-objective optimization techniques, such as differential evolution, reinforcement learning, GAs, hybrid optimization, and ant colony optimization, exhibit strong capabilities in navigating complex dynamic environments. Each technique offers unique strengths, ranging from convergence speed to adaptability, making it appropriate for different operational requirements. Expanding Table 4 and

Table 5. Fitness functions and multi-objective optimization approaches for UAV path planning in disaster relief networks.

Study	Optimization Type	Algorithm/ Approach	Fitness Function Criteria	Path Planning Scope	Strengths	Limitations
[45,46]	Multi-objective Evolutionary	Knee-guided Differential Evolution	Distance, risk, height, angle, slope	Smooth UAV path generation under constraints	Smooth, low-risk paths, constraint handling	Requires careful parameter tuning
[50]	Reinforcement Learning	RL-based UAV Path Planning	Distance, risk level, QoS, user demand	Dynamic urban scenarios with mobile users	High adaptability and responsiveness	Needs extensive training and tuning
[48]	GA + Swarm Hybrid	GA with fitness normalization + swarm enhancements	Energy consumption, threat exposure, mission efficiency	Complex multi-UAV planning	Energy-efficient and safe routing	Slower convergence in large spaces
[49]	Utility-based Multi-UAV	Utility Function Optimization	Number of people rescued, collision avoidance	Multi-agent search and rescue missions	Prioritizes rescue + safety constraints	Limited by utility function design
[47]	Hybrid Metaheuristic	MHEO (Gaussian + Lévy + Eq. Opt)	Fuel, altitude, threat proximity	Global energy-aware path optimization	Balanced search–exploit strategy	Complex structure and parameter sensitivity
[51]	Hybrid Heuristic	Adaptive GA + Improved ABC	Mission assignment and UAV trajectory	Path length, assignment efficiency	Division of optimization tasks (assignment + path)	Higher design and runtime complexity
[52]	Swarm Intelligence	Enhanced Ant Colony Optimization	3D flight path length, terrain threat	3D UAV flight path in disaster terrain	Accurate terrain-aware 3D paths	May be slow in high-dimensional search

details the scope, strengths, and limitations of specific optimization approaches, such as knee-guided DE, RL-based planning, GA+swarm hybrids, and enhanced ACO. It shows how each method addresses constraints such as smoothness, collision avoidance, and threat minimization, further supporting the design choices in the hybrid framework (see Table 5).

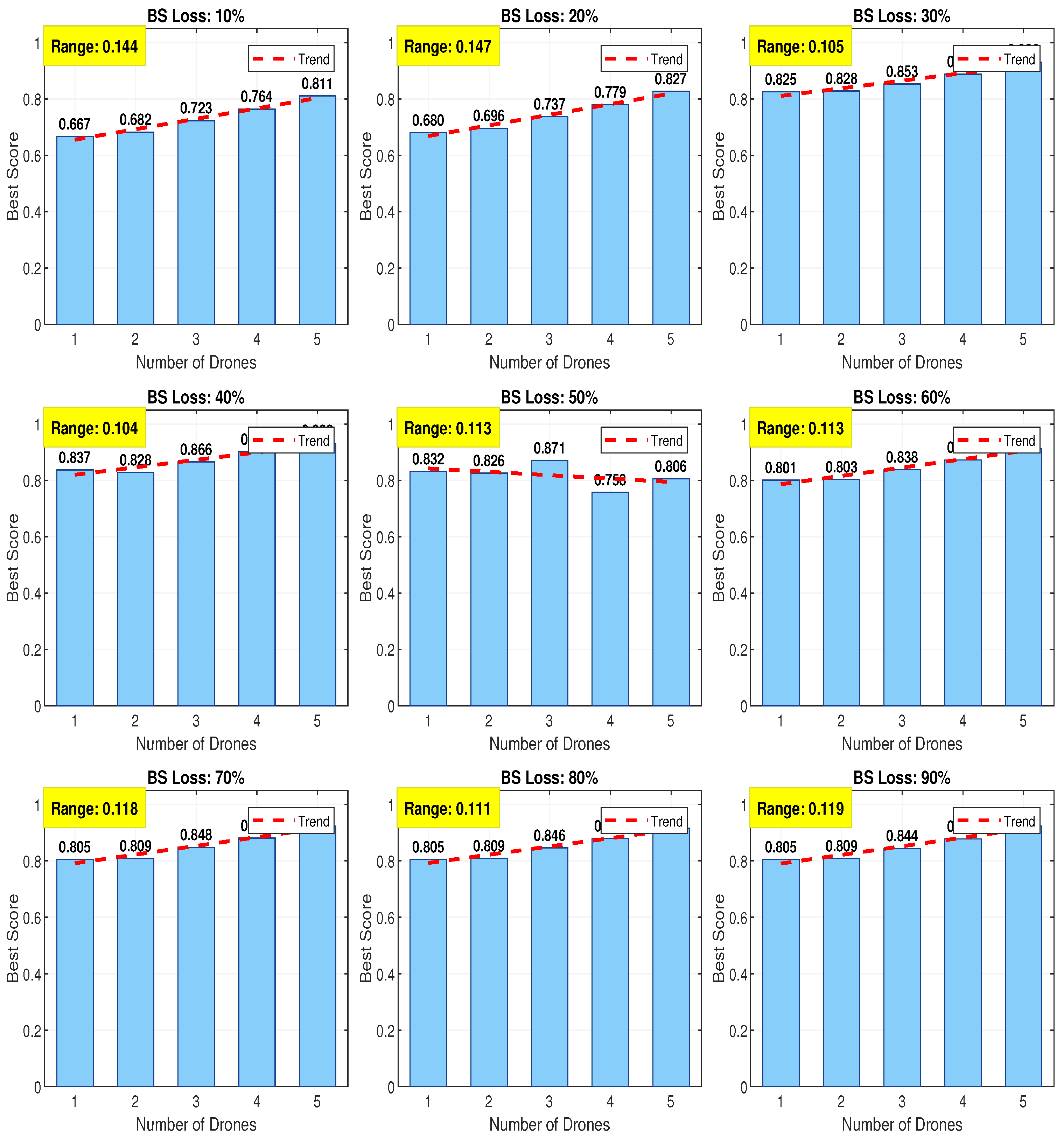
RQ5: How do clustering and optimization approaches handle varying BS loss, user densities, or terrain constraints in DRNs?

Clustering and Optimization Approaches in DRNs

To handle varying BS losses, clustering approaches often face challenges due to interference from nodes outside the cluster. To address this, some frameworks allow clusters to exchange optimization parameters through low-rate backhauls, approaching near-global optimization performance [53]. In the case of BS failures, delay-tolerant networks (DTNs) offer resilience by enabling user devices to self-organize and relay messages through multihop connections to functional BSs or nearby users, thereby improving load balancing [54]. Under sparse BS deployment, users may rely on others who are willing to relay messages to an accessible BS. Optimized beaconing policies are used to maximize message delivery success while minimizing power usage [55]. In high-density scenarios, clustering algorithms such as K-means, DBSCAN, and Agglomerative Clustering were evaluated to determine the most efficient choice. ML methods can also predict optimal BS parameters, thereby reducing the computational overhead [56].

The optimization of irregular terrain requires sophisticated modeling. For instance, the Longley-Rice model enables accurate path-loss estimation using high-resolution topographic data [57]. In urban vehicular DTNs, geographic complexity is managed by segmenting maps into adjacent regions to aid delay analysis and trajectory prediction [58]. Energy-saving strategies include optimizing the activation and deactivation of BS transmissions. Clustering and timed activation approaches help minimize energy use while fulfilling traffic demands [59]. Battery-aware techniques, such as Improved Lifetime Optimization Clustering (ILCK), apply Kruskal’s minimal spanning tree heuristic and monitor battery health to extend the network lifetime [60]. Analytical methods, such as convex optimization, are used to minimize the total transmit power under QoS constraints and are often extended to multi-BS scenarios using iterative algorithms [61]. Metaheuristic approaches, such as chaotic gorilla troop optimization, enhance energy-aware clustering by considering the neighbor distance, BS proximity, and energy ratio [62].

Table 6. Summary of clustering and optimization strategies in DRNs.

Study	Aspect	Approach	Key Points
[53]	BS Loss	Interference Management	Parameter exchange via backhauls
[54]	BS Loss	DTN Routing	Self-organization to access functional BSs
[55]	User Densities	Sparse Density	Beaconing policies to ensure relay success
[56]	User Densities	High Density	ML and clustering to optimize parameters
[57]	Terrain Constraints	Irregular Terrain Models	Longley-Rice model for path loss
[58]	Terrain Constraints	Geographic Routing	Map segmentation for delay prediction
[59]	Energy Efficiency	BS Activation Scheduling	Energy reduction via timed activation
[60]	Energy Efficiency	Battery Endurance	ILCK with battery state and Kruskal MST
[61]	Optimization Algorithms	Convex Optimization	Minimize power while meeting QoS
[62]	Optimization Algorithms	Metaheuristics	Chaotic gorilla troops for clustering

summarizes the strategies for dealing with BS loss, varying user densities, and terrain constraints. Approaches range from DTN routing and ML-based parameter tuning to terrain-aware propagation models and energy-saving BS scheduling. The relevance of the proposed work lies in showing how adaptability to these challenges is crucial (see Table 6).

These clustering and optimization techniques collectively address the challenges related to BS loss, varying user densities, and complex terrain in disaster relief networks. By leveraging analytical models, adaptive routing, and energy-aware clustering, these methods can significantly improve the reliability and efficiency of DRNs. The strategies compared in

Table 7. Clustering and optimization strategies for handling BS loss, user densities, and terrain constraints in DRNs.

Study	Challenge Addressed	Method/ Algorithm	Domain/Context	Key Technique	Benefits	Limitations
[53]	BS interference/coordination	Backhaul-based parameter exchange	DRNs with clustered BSs	Low-rate backhaul signaling	Near-global optimization	Requires stable inter-BS links
[54]	BS failure/coverage gaps	DTN Routing	Sparse emergency networks	Multi-hop device-to-device relay	Enhances BS reachability, load balance	Delay-sensitive services limited
[55]	Sparse user density	Optimized beaconing policies	Intermittent user-BS links	Energy-aware message relaying	Power saving, higher message success	May suffer in mobile scenarios
[56]	High user density	ML + clustering evaluation	Dense user regions in DRNs	Predictive BS parameter tuning	Reduces overhead, improves adaptability	Needs good ML generalization
[57]	Terrain irregularity	Longley-Rice Propagation Model	Terrain-aware UAV-BS deployment	Topographic path loss estimation	Accurate path loss modeling	High dependency on topo-data accuracy
[58]	Urban topology	Geographic Map Segmentation	Urban vehicular DTNs	Region-based delay prediction	Predicts delays, supports route planning	Granularity affects accuracy
[59]	Energy saving	BS Activation Scheduling	Dense BS networks	Clustered BS scheduling + traffic prediction	Energy-efficient activation	Assumes reliable traffic forecast
[60]	Battery constraints	ILCK (Improved Lifetime Optimization)	Battery-aware clustering in WSNs	MST + battery state evaluation	Extends network lifetime	May require frequent battery checks
[61]	Power-QoS trade-off	Convex Optimization	Multi-BS coverage optimization	Iterative QoS-constrained power minimization	Controlled QoS + energy usage	Scalability with more BSs can drop
[62]	General optimization	Chaotic Gorilla Troops Optimization	Energy-aware UAV clustering	Metaheuristic + energy/distance ratio	Robust clustering + energy balancing	Metaheuristic randomness needs tuning
[63]	Multi-UAV trajectory optimization under checkpoint and coverage constraints	GA with adaptive operator selection	Multi-UAV coordinated path planning	GA-based trajectory generation with adaptive operators and Bezier curve smoothing	Produces efficient, feasible UAV flight paths	Scalability limited by fixed checkpoint design
[64]	Post-disaster connectivity restoration with dynamic UE distributions	APC–GA Hybrid	UAV-assisted disaster response	APC with GA-based path optimization; QoS-aware fitness function (coverage, SINR, capacity)	Achieved up to 99% service coverage in suburban scenarios; strong adaptability to user mobility	Clustering limited to APC (sensitive to noise)

further illustrate how clustering and optimization methods address BS loss, varying user densities, and terrain constraints in DRNs. By juxtaposing their benefits and limitations, the table highlights that adaptability and energy-awareness are the most critical enablers for post-disaster UAV deployments.

To provide a broader perspective,

Table 8. Summary of UAV clustering and optimization strategies across research themes (RQ1–RQ5).

Study	RQ Category	Method/Algorithm	Core Application	Key Strength	Primary Limitation
[9]	RQ1–Clustering	K-means + PSO	Balanced UAV coverage and energy	Combines convergence + adaptability	Higher design complexity
[17]	RQ2–ML/NN Planning	2-Stage ML + RL Planner	Dynamic path planning with obstacle prediction	High trajectory accuracy in dynamic scenes	Requires labeled training data
[39]	RQ3–Hybrid Strategy	DKGK (DE + GA + K-means)	High-accuracy clustering optimization	Fast convergence + diversity	Tuning hybrid components
[47]	RQ4–Fitness/Optimization	MHEO (Hybrid Eq. Optimizer)	UAV path planning in risky terrain	Balanced search + energy-efficient routes	Complex multi-step tuning
[59]	RQ5–BS/Energy Challenges	BS Activation Scheduling	Energy-efficient BS use in DRNs	Saves energy, meets traffic demands	Assumes known traffic profiles

consolidates the methods examined across all five research questions (RQ1–RQ5). This summary highlights how clustering, learning-based optimization, and hybrid strategies collectively contribute to improving UAV service coverage, path efficiency, and resilience in disaster response networks.

3. Environment Modeling

This section outlines the key assumptions and system architecture of the studied UAV-assisted emergency network deployment in post-disaster scenarios. The objective is to provide resilient and rapid connectivity to UEs through the deployment of MABSs using a newly proposed hybrid clustering-based optimization framework. The proposed solution enhances the previous work [63] by dynamically selecting between APC and a learned clustering strategy that combines DBSCAN with an ANN. This hybrid model enables more flexible and adaptive UAV path planning depending on the network density, terrain, and disaster impact levels.

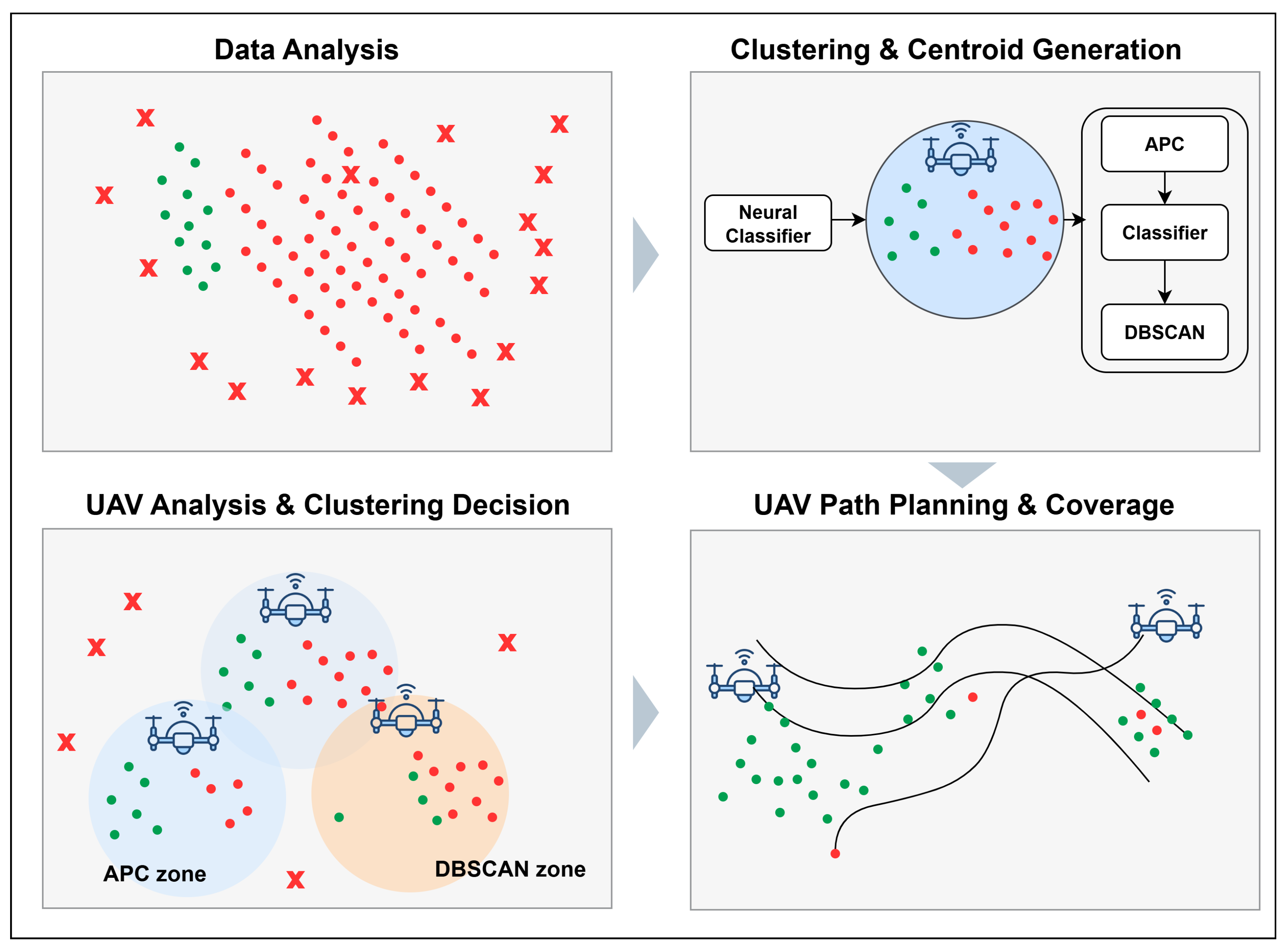
Figure 1 illustrates the proposed system model, which offers an intelligent and resilient solution for restoring wireless connectivity in post-disaster environments in which conventional base stations have failed. UAVs are used as MABSs to provide temporary coverage to disconnected UEs. The green markers indicate UEs with active services, whereas the red markers indicate UEs that have lost connectivity and require temporary MABS coverage. Each MABS follows an optimized trajectory to visit the centroid of the user clusters.

The process begins with the identification of failed base station zones and the classification of the UEs as either connected or disconnected. Spatial features, such as the density of the UE, the levels of outage at the base station and the spread of the distribution, are then extracted and fed into a lightweight neural classifier. This classifier dynamically selects the optimal clustering method by choosing either APC for dense, structured regions or DBSCAN with ANN-guided parameter tuning for sparse or irregular topologies. This hybrid selection process enables more accurate and adaptive clustering, thereby ensuring efficient centroid placement. These centroids serve as UAV visitation points and are further processed by a GA that optimizes the UAV trajectories based on multi-objective criteria, including service ratio, smoothness, and intersection avoidance.

The hybrid model’s ability to adapt to varying UE distributions and disaster intensities, combined with machine-learning-driven decision-making, makes it a robust and scalable framework for real-time UAV-assisted communication restoration. The adaptability of the system was further enhanced by incorporating real-time data updates, allowing for dynamic reclustering and trajectory adjustments as the post-disaster scenario evolved. This continuous optimization ensures that the UAV network remains responsive to changing ground conditions, such as shifting UE concentrations or newly restored BSs.

In this extended model, the cluster centroids were computed using a decision layer selected between APC and DBSCAN+ANN, depending on the real-time conditions. Moreover, the framework includes a predictive component that anticipates potential changes in the UE distribution based on historical patterns and current movement trends, enabling proactive UAV positioning for improved service continuity.

The neural selector evaluates the features of spatial distribution, such as variance in the density of the user and clustering coefficients, and dynamically decides whether APC or DBSCAN should be used. This mechanism ensures adaptability by preventing rigid application of a single clustering method, which may fail under dynamic conditions. Figure 1 presents the hybrid architecture decision pipeline, where each stage is annotated with its operational objective.

3.1. Clustering Mode Selection

The novel contribution of this study is the dynamic selection of a clustering method for identifying UAV visitation centroids. This logic is defined as shown in

Table 9. Clustering selection logic based on UE distribution.

Condition	Selected Clustering Method
High UE density	APC
Low UE density or sparse regions	DBSCAN with ANN-guided parameter tuning
Unstructured or mixed topology	ANN-only centroid prediction

.

The ANN model was pretrained on synthetic post-disaster UE distributions to predict the optimal clustering configurations. When used with DBSCAN, the ANN adjusts the clustering parameters (e.g., $\epsilon$ and MinPts) or refines the centroid locations to minimize misclustering in sparse environments.

3.2. Simulation Setup and Parameters

The simulation emulates a $25\times 25$ km² area, representing a mid-sized town. The UE and BS locations follow a Poisson distribution with $\lambda =100\times 25$ and $\lambda =10\times 25$, respectively (see

Table 10. Simulation parameters and settings.

Notation	Description	Value
U	Number of UEs	2500
$BSD$	BS Distribution (Poisson)	$\lambda =10\times 25$
A	Area	25 km × 25 km
D	Number of MABS	1 to 5
S	GA Population Size	50
P	GA Iterations	100
$CLM$	Clustering Logic Mode	Hybrid (APC, DBSCAN+ANN)
ANNmodel	Neural Model Enabled	True
$Loss$	BS Outage Percentage	10% to 90%

). Each UE requires a minimum per-UE throughput of 200 kbps to be considered served during emergency situation.

The simulations were developed and executed in Python 3.10, utilizing an object-oriented and modular design to enhance flexibility, scalability, and reproducibility. All proposed algorithms were implemented in Python. The experiments were conducted on a computing system featuring a 2.4 GHz Intel Core i7-7600U processor, 64 GB of RAM, and an NVIDIA T1000 GPU with 4 GB of memory. This configuration was chosen to provide sufficient computational power for handling the complex optimization processes and large-scale disaster scenarios considered in this study. The simulation environment was designed to run multiple iterations of the algorithms under different conditions, enabling a thorough assessment of their performance.

Link rates are mapped from SINR via the Shannon–Hartley relation:

$$C=B·{log}_2(1+\mathrm{SINR}),$$

(1)

where C is the channel capacity in bits per second (bps), B is the channel bandwidth in Hz, and SINR is the signal-to-interference-plus-noise ratio.

$$\mathrm{SINR}={\displaystyle \frac{P_i}{{\sum }_{j\ne i}{P}_j+\eta }},$$

(2)

where $P_i$ is the received power of the desired signal, ${\sum }_{j\ne i}{P}_j$ is the aggregate interference from other transmitters, and $\eta$ is the thermal noise power (set to $-112\mathrm{dBm}$ [65]).

Interference is encapsulated within the SINR definition of Equation (2), which encompasses contributions from both intra and inter-cell transmissions [66]. Latency is addressed in two distinct forms: (i) communication latency, which is contingent upon SINR and link capacity, and (ii) algorithmic latency, which emerges from clustering and GA-based optimisation processes [67]. The ANN-guided selector mitigates decision latency by circumventing exhaustive trials of multiple clustering algorithms, instead directly predicting the most suitable option based on environmental features [68].

The transmission powers were 46 dBm (BS), 30 dBm (MABS), and 10 dBm (UE). Path loss was calculated using the Okumura–Hata model as follows:

$$PL=A+B·{log}_{10}\left(d\right)+\mathrm{Env},$$

(3)

where $PL$ is the path loss in dB, d is the transmitter–receiver distance in km, and Env is an environment-specific correction term.

$$A=69.55+26.16·{log}_{10}\left(f\right)-13.82·{log}_{10}\left(h_b\right)-a\left(h_m\right),$$

(4)

$$a\left(h_m\right)=\left(1.1·{log}_{10}\left(f\right)-0.7\right)h_m-\left(1.56·{log}_{10}\left(f\right)-0.8\right),$$

(5)

where f is the carrier frequency in MHz, $h_b$ is the BS antenna height in meters, $h_m$ is the UE antenna height in meters, and $a\left(h_m\right)$ is the UE antenna correction factor.

The Okumura-Hata model was employed in this study to estimate large-scale path loss between UAV-mounted aerial base stations and ground users. Although originally formulated for terrestrial cellular environments, several studies have adapted or validated it in air-to-ground (AG) and UAV communication contexts. For instance, the model has been used to predict coverage and optimize UAV placement in emergency communication and post-disaster scenarios where rapid deployment is essential [69]. Other works have shown that the Okumura-Hata model remains a reliable baseline for performance evaluation when appropriately parameterized for different terrains and antenna heights [70,71,72].

Recent UAV communication studies have integrated terrestrial propagation models, including Okumura–Hata, into network-level simulations to benchmark aerial links under various urban morphologies and frequencies [73,74,75]. These works highlight that while dedicated air-to-ground models (e.g., 3GPP TR 36.777 or Al-Hourani’s model) offer improved accuracy for certain scenarios, the Okumura-Hata model provides a computationally efficient approximation suitable for comparative and optimization-oriented studies, particularly when the focus is on algorithmic adaptation and clustering behavior rather than precise channel calibration.

Therefore, in line with prior research, this study adopts the Okumura-Hata model as a baseline propagation model for UAV-UE path loss estimation, acknowledging its limitations and noting that more specialized UAV propagation models may be integrated in future extensions.

The environmental modeling is designed to ensure that system parameters correspond to realistic operating conditions. Wireless propagation is captured using the Okumura–Hata model for path loss, while link capacity is derived from the Shannon–Hartley theorem [65]. These physics-based formulations directly map measurable factors such as distance, frequency, and noise into the system. In addition, environmental variables such as wind speed, visibility, and temperature, along with operational features including UE density and BS outage levels, are incorporated into the optimization framework. These features serve as inputs to a lightweight ANN classifier that adaptively tunes clustering parameters (e.g., DBSCAN $ϵ$ and MinPts) [57]. This hybrid combination of empirical models and data-driven adaptation ensures that the optimization reflects real-world disaster scenarios rather than relying on abstract assumptions.

To accurately simulate post-disaster conditions, user distributions were modeled utilizing Poisson point processes (PPP) and clustered Gaussian patterns. The PPP represents dispersed survivors scattered throughout the affected area, whereas Gaussian clusters simulate evacuation hotspots or temporary shelters where users congregate in groups [76]. BS outages varied from 10% to 90% to reflect the cascading infrastructure failures characteristic of large-scale disasters. Additionally, terrain-induced variance and visibility reduction were incorporated as environmental features to capture the effects of obstacles, such as collapsed buildings or obstructed lines of sight. These combined models enhance the practical applicability of the validation, ensuring that UAV-assisted coverage enhancement is evaluated not only in idealized topologies but also in realistic evacuation and obstacle-constrained scenarios [77].

3.3. Clustering Algorithm Integration

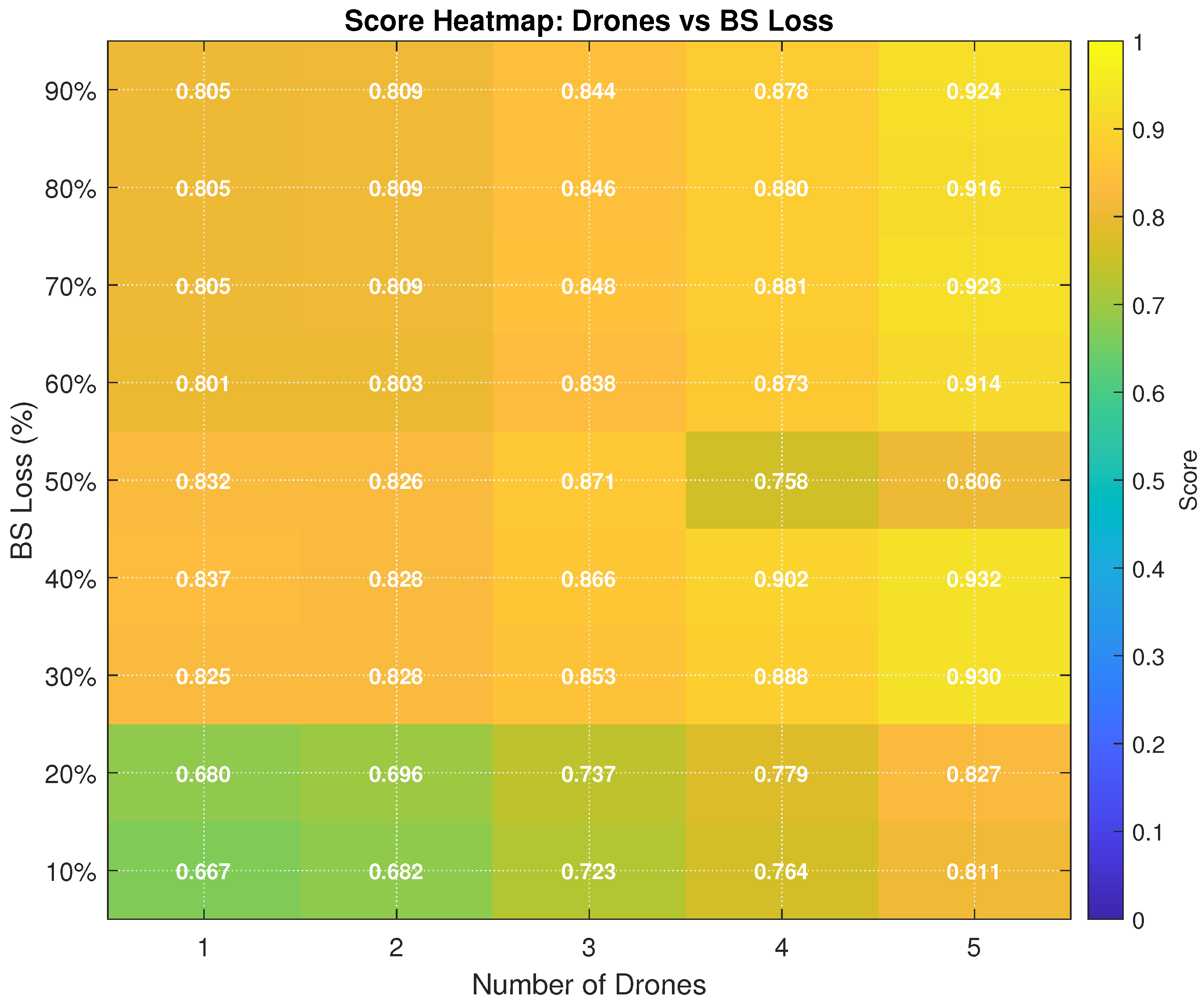
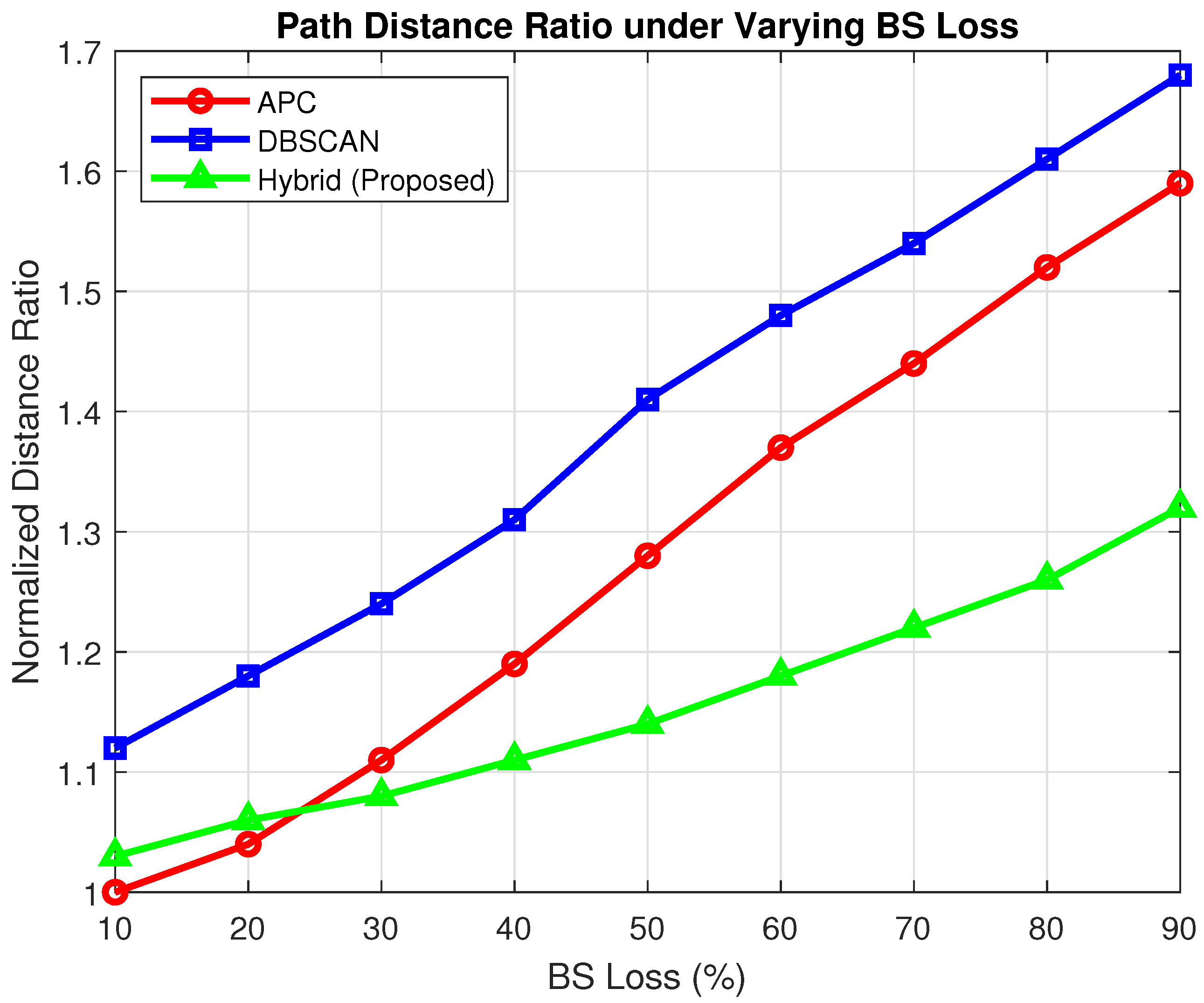
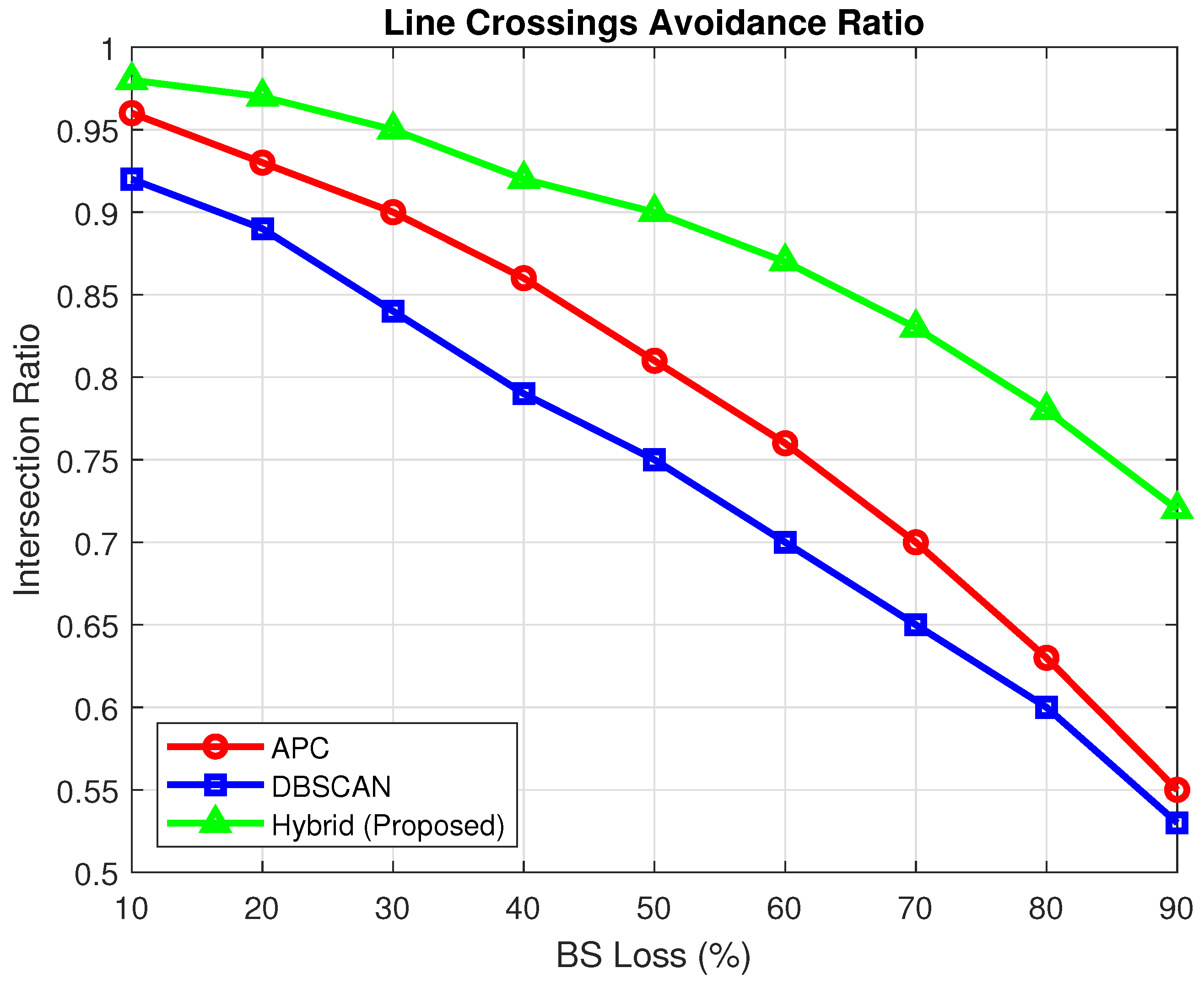
For each level of BS outage (10% to 90%), the hybrid clustering model selects the most suitable strategy. If the ANN recommends an APC, traditional cluster propagation is applied; otherwise, DBSCAN with ANN-guided parameter tuning generates adaptive centroids. These centroids act as waypoints for UAVs during subsequent genetic optimization.

A damping factor of 0.6 was used for APC, whereas $\epsilon$ and MinPts in DBSCAN were adapted dynamically. The output centroids vary according to the sparsity of the network, the distribution of services, and the distance traveled.

3.4. Hybrid Clustering Strategy for UAV-Based UE Grouping with ANN-Guided Selection

Conventional clustering methodologies often presuppose that a singular algorithm is adequate across diverse environments; however, this assumption proves inadequate in the context of post-disaster heterogeneity [78,79]. For example, the APC algorithm is effective in generating stable clusters within dense and structured user distributions but fails in sparse or noisy scenarios. Conversely, the DBSCAN algorithm performs well in sparse topologies and noisy environments but becomes unstable in dense deployments because of its sensitivity to the parameters $ϵ$ and MinPts [80]. To address these limitations, the hybrid strategy proposed in this study in which deploys an ANN classifier assesses environmental features, including UE density, BS outage ratio, and spatial variance, to select the most appropriate clustering method (APC or DBSCAN) for each scenario [81]. The identified centroids were subsequently utilized by a GA-based trajectory optimizer to devise UAV paths that maximized service coverage and robustness. This architecture ensures that the clustering process dynamically adapts to the environment, rather than adhering to a rigid, uniform approach. The hybrid clustering strategy described in this study is a neural-guided adaptive framework that dynamically selects between APC and DBSCAN based on the spatial characteristics of the UE distributions. This decision was driven by a lightweight neural network classifier.

3.4.1. Stage 1: Spatial Feature Extraction of UE Distribution

The spatial pattern of UEs is quantified to inform the clustering choice. Key features: local density of UE ${\rho }_i$, statistics of distance between users (e.g., mean, variance), percentage of BS outage ${\eta }_{BS}$, and topological spread ${\sigma }_{xy}$. For a set of UE coordinates $\mathcal{U}=\{(x_1,y_1),\dots ,(x_N,y_N)\}$, the following:

1.

Local density around point i:

$${\rho }_i=\sum _{j=1}^N\mathbb{I}(d_{ij}<ϵ),$$

(6)

where $d_{ij}$ is the Euclidean distance, and $\mathbb{I}$ is the indicator function.

2.

Global density:

$$\overline{\rho }={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\rho }_i,$$

(7)

3.

Spread (spatial variance):

$${\sigma }_{xy}^2={\displaystyle \frac{1}{N}}\sum _{i=1}^N\left({(x_i-\overline{x})}^2+{(y_i-\overline{y})}^2\right),$$

(8)

These features form the input vector $\mathbf{f}$ for the classifier.

$$\mathbf{f}=[\overline{\rho },{\sigma }_{xy},{\eta }_{BS}],$$

(9)

3.4.2. Stage 2: Neural Classifier-Based Clustering Selection

The objective is to use a trained neural model to decide between APC and DBSCAN. Classifier structure is givesn as follows:

$$y=\mathrm{softmax}(W_2·\mathrm{ReLU}(W_1\mathbf{f}+b_1)+b_2),$$

(10)

where $\mathbf{f}$ is the input feature vector, $W_1,W_2$, $b_1,b_2$ are trainable weights and biases, and $y\in \{0,1\}$: 0 = APC, 1 = DBSCAN (possibly with ANN refinement).

3.4.3. Stage 3: Clustering Execution

Case A: If APC is selected, the algorithm operates based on pairwise similarities between all data points. The similarity matrix is defined as:

$$s(i,j)=-\parallel {\mathbf{x}}_i-{\mathbf{x}}_j{\parallel }^2,$$

Update equations:

$$\begin{array}{cc}\hfill r(i,j)& \leftarrow s(i,j)-\underset{j^{\prime }\ne j}{max}\left\{a(i,j^{\prime })+s(i,j^{\prime })\right\},\hfill \\ \hfill a(i,j)& \leftarrow min\left(0,r(j,j)+\sum _{i^{\prime }\notin \{i,j\}}max(0,r(i^{\prime },j))\right),\hfill \end{array}$$

Exemplar selection:

$$j^{*}=arg\underset{j}{max}\left\{a(i,j)+r(i,j)\right\},$$

Case B: If DBSCAN is selected

Parameters: $ϵ$: neighborhood radius, and MinPts: minimum number of points to form a cluster. Definitions: Core point: $|{\mathcal{N}}_{ϵ}\left(p\right)|\ge \mathrm{MinPts}$ and Directly density-reachable: $q\in {\mathcal{N}}_{ϵ}\left(p\right)$.

An ANN can refine the centroid locations or tune the clustering parameters $ϵ$ and MinPts dynamically.

3.4.4. Stage 4: Centroid Generation for UAV Routing

Cluster centroids are computed as

$$\mathcal{C}=\{{\mathbf{c}}_1,{\mathbf{c}}_2,\dots ,{\mathbf{c}}_K\},{\mathbf{c}}_k={\displaystyle \frac{1}{|U_k|}}\sum _{{\mathbf{u}}_i\in U_k}{\mathbf{u}}_i,$$

where $U_k\subset \mathcal{U}$ is the kth cluster.

Table 11. Summary of the hybrid clustering process for UAV deployment.

Stage	Description	Output
1	Extract UE spatial features	Feature vector $\mathbf{f}$
2	Neural classifier decision	APC or DBSCAN
3	Apply selected clustering	Cluster centroids
4	Generate centroids	$\mathcal{C}=\{{\mathbf{c}}_1,\dots \}$
5	Feed into GA path planning	Optimized UAV routes

summarizes the hybrid clustering process used for UAV deployment. The process begins with the extraction of spatial features from the UE to form a feature vector. A neural classifier then determines the appropriate clustering algorithm, either APC or DBSCAN, based on the characteristics of the data. The selected clustering method is applied to obtain the cluster centroids, which are represented as a set of coordinates corresponding to the optimal UAV service points. Finally, these centroids are input into a GA for path planning, resulting in optimized UAV flight routes (Table 11).

4. Proposed Hybrid Solution

4.1. Hybrid Clustering-Driven Genetic Algorithm Framework for MABS Path Planning

This section introduces a novel hybrid clustering-driven optimization framework that combines APC with a learned clustering mechanism to guide UAV-based MABS path planning in disaster-response scenarios. The objective is to enhance the flexibility and robustness of dynamic UE distributions caused by varying disaster severities.

Overview of the Framework: The proposed MABS path-planning algorithm is built on a GA foundation. Unlike previous models that rely solely on APC, the proposed hybrid system uses a clustering selector that switches between the APC and DBSCAN guided by ANN hybrid models, depending on the scenario. APC is preferred under sparse conditions, whereas DBSCAN paired with a pre-trained ANN is utilized under dense or highly disrupted networks, where APC fails to stabilize.

Each specimen in the GA represents a candidate solution composed of multiple drone-path chromosomes, each containing a set of clustered UE. Chromosomes undergo mutation, crossover, and selection operations during evolutionary cycles.

Cluster Switch Module, a scenario-dependent clustering strategy is introduced as follows.

1.

For low-density UE distributions and minimal BS loss (<50%), APC is used.

2.

For high-density clusters or when BS loss exceeds 50%, DBSCAN groups the UEs, and a pre-trained ANN predicts optimized centroids.

This selection is based on input metrics, such as UE density, BS outage percentage, and spatial variance.

Algorithm 1 implements an ANN-guided selector that chooses between APC and DBSCAN to generate UAV visitation centroids under heterogeneous, post-disaster UE layouts. APC automatically infers the number of clusters and performs well on dense, structured patterns [1,82], whereas DBSCAN is robust to noise and arbitrary shapes and is well-suited to sparse or irregular topologies [2,80,83]. Because no single clustering method dominates across all densities and noise levels [78,79], we adopt a hybrid strategy with a lightweight neural selector [84].

Given the unserviced user set U, the selector first extracts spatial features (e.g., local/global density, spread, estimated outage level) and predicts a topology class $z=\mathcal{S}\left(\mathrm{features}\right(U\left)\right)$. Both candidates, $C_{\mathtt{db}}=\mathrm{DBSCAN}\left(U\right)$ and $C_{\mathtt{apc}}=\mathrm{APC}\left(U\right)$, are computed to hedge (to reduce the risk of error) against misclassification. Two guardrails regulate the centroid count: a soft target $\tau =max(3,min(50,\lfloor \left|U\right|/40\rfloor \left)\right)$ to scale with the incident size, and a minimum need $\nu =max(3,\lfloor \tau /2\rfloor )$ to avoid under-segmentation. If DBSCAN underproduces centroids ($|C_{\mathtt{db}}|<\nu$) while APC meets demand ($|C_{\mathtt{apc}}|\ge \nu$), the algorithm returns APC; otherwise, it selects the candidate with greater coverage granularity (ties broken in favor of APC for stability). The method, problem size $\left(\right|U\left|\right)$, centroid count $\left(\right|C\left|\right)$, and runtime were recorded for later analysis and ablation. This design makes centroid generation adaptive yet reproducible, aligning clustering choice with observed spatial structure rather than a fixed, one-size-fits-all rule [78,79,84].

Algorithm 1: Hybrid centroid selection for unserviced UEs (APC vs. DBSCAN).

4.2. Chromosome Representation and Mutation Operators

Each chromosome is represented as a directed graph $G=(V,E)$ where V is the set of centroids from clustering and E is the set of Euclidean distances between centroids:

$$E_{ij}=\sqrt{{(x_i-x_j)}^2+{(y_i-y_j)}^2},\forall i,j\in V,$$

(11)

The GA incorporates multiple mutation operators to enhance search diversity and improve solution quality. One such operator is the in-chromosome point swap, which exchanges two nodes within the same path to generate alternative route configurations. Another is the cross-chromosome merge/split, which either combines or separates UAV paths depending on the resulting impact on fitness, thereby balancing workload distribution. Finally, the insertion operator repositions nodes within a path according to capacity thresholds, ensuring that service constraints are respected while exploring new trajectory options. Together, these operators promote adaptability and prevent premature convergence, enabling the GA to evolve more efficient and resilient UAV deployment strategies. These operators encourage genetic diversity and adaptability across generations.

The GA-based multi-drone routing procedure is outlined in Algorithm 2. The algorithm begins by assigning a centroid budget proportional to the number of UAVs, ensuring a fair allocation of service regions. An initial candidate solution (chromosome) is generated that encodes the UAV paths while considering the UAV specifications and environmental conditions. During each evaluation cycle, the algorithm applies adaptive mutation to explore new route configurations while preventing redundancy using a lightweight tabu memory. The fitness of each solution is evaluated across six performance dimensions:

• (i) Distance Efficiency (minimization of total path length), (ii) Path Quality (smooth angular transitions to reduce mechanical stress), (iii) Intersection Avoidance (safe navigation without route intersections), (iv) Service Coverage (proportion of unserved UEs successfully covered), (v) Communication Coverage (effective connectivity under SINR constraints), and (vi) Environmental Robustness (adaptability to varying weather conditions). To balance exploration and exploitation, the mutation intensity is dynamically increased when improvement stagnates and reset when a superior solution is found. Early stopping conditions further ensured computational efficiency by terminating iterations once a near-optimal score was achieved. The output of Algorithm 2 is the best-performing route configuration for each UAV count, which enables a direct comparison of service effectiveness across different drone deployments.

Algorithm 2: GA-based multi-drone routing with adaptive mutation and early stopping.

4.3. Scenario-Aware Fitness Function Integration

The enhanced UAV-assisted communication framework incorporates a scenario-aware fitness function that evaluates UAV deployment strategies across multiple realistic operational dimensions. This multi-objective fitness evaluation addresses the complex trade-offs inherent in post-disaster network restoration scenarios.

4.3.1. Multi-Dimensional Fitness Components

The fitness function integrates seven key performance metrics as follows:

1.

Distance Efficiency ($d_{total}$): Total path length optimization for fuel conservation.

2.

Path Quality (${\theta }_{ratio}$): Angular smoothness to minimize mechanical stress.

3.

Intersection Avoidance ($I_{cross}$): Self-intersection prevention for safe navigation.

4.

Service Coverage ($S_{ratio}$): Fraction of unserved users covered by UAV routes.

5.

Communication Coverage ($C_{score}$): Effective coverage accounting for interference.

6.

Environmental Robustness ($R_{env}$): Weather condition adaptability.

4.3.2. Scenario-Adaptive Parameterization

The fitness evaluation dynamically adapts to the operational scenarios as follows:

$$F_{enhanced}=[d_{total},{\theta }_{ratio},I_{cross},S_{ratio},C_{score},R_{env}],$$

(12)

Each component of the fitness function is normalized to the range $[0,1]$, where higher values indicate better performance. The system dynamically adjusts these parameters in response to environmental and operational factors, including weather conditions such as wind speed, visibility, and temperature; UAV specifications, including communication range, energy efficiency, and payload capacity; and network topology characteristics, such as user density and interference patterns. This adaptive parameterization ensures that the optimization framework remains robust and context-aware, allowing UAVs to maintain efficient and reliable performance under diverse disaster scenarios.

To ensure that the dynamically adjusted parameters reliably reflect real environmental conditions, the proposed framework integrates physics-based models, data-driven adaptation, and scenario validation. For wireless channel and capacity estimation, the Okumura-Hata model is employed for path loss and the Shannon-Hartley theorem for link capacity, thereby grounding the optimization in measurable factors such as distance, frequency, and noise [57]. Environmental and operational features, including UE density, BS outage levels, wind speed, visibility, and terrain-induced variance, are continuously extracted and provided to a lightweight ANN-based classifier, which adaptively tunes clustering parameters (e.g., DBSCAN $ϵ$ and MinPts) [22,23]. This prevents arbitrary adjustment and ensures that the system responds proportionally to real-world conditions. The robustness of this approach was demonstrated in simulations across diverse disaster scenarios with 10–90% BS outages and varying UE distributions [50]. By coupling well-established physical models with real-time feature-driven adaptation and evaluation across several scenarios, the optimization framework is robust, both environmentally grounded and operationally realistic, ensuring that UAV performance reflects the true conditions of post-disaster environments.

4.3.3. Integration with Genetic Algorithm Close Framework

This section provides a comprehensive overview of how the scenario-aware fitness function integrates multiple realistic factors to guide the genetic algorithm toward practical UAV deployment strategies. The multidimensional approach ensures that solutions balance technical performance with operational constraints, making the framework suitable for real-world disaster-response scenarios. The enhanced fitness function is seamlessly integrated into the genetic algorithm as follows:

Multi-objective selection involves Pareto dominance comparison for solution ranking, scenario-aware mutation adjusts parameters based on environmental conditions, and adaptive crossover optimizes routes by considering energy and coverage constraints. This integration ensures that the GA evolves solutions that are operationally feasible under realistic post-disaster network conditions.

4.4. Neural Classifier Training and Decision Logic

The following subsections describe the feature construction, model training, and decision framework used to enable adaptive clustering selection.

4.4.1. Feature Extraction

From the UE coordinates ${\left\{(x_i,y_i)\right\}}_{i=1}^N$, a 12-dimensional vector is derived: density, per-axis variance, centroid, pairwise distance statistics (mean, std, min, max), Hopkins statistic, mean nearest-neighbor distance, and spread ratio ${\displaystyle \frac{maxd}{\mathrm{mean}d}}$. The features were standardized.

4.4.2. Training Data and Labels

Six synthetic families were generated: dense, well-separated clusters, uniform scatter, high density with outliers, mixed density, hierarchical/multi-scale clusters, and irregular ring/curve patterns. Each scenario is labeled by the method expected to yield superior performance (DBSCAN$=1$, APC$=0$).

4.4.3. Models and Optimization

The main classifier is a multilayer perceptron with hidden layers $(100,75,50,25)$, ReLU activations, early stopping (validation fraction $0.15$), $L_2$ regularization $\alpha ={10}^{-3}$, adaptive learning rate, Nesterov momentum, and a maximum of 2000 iterations. An ensemble Random Forest (100 trees, maximum depth 15, minimum leaf 2) was trained in parallel. A stratified 80/20 train–test split was applied. During inference, both models produced probability scores; decision thresholds were set at neural confidence $>0.7$, ensemble agreement $>0.8$, and fallback threshold $0.6$.

4.4.4. Fail-Safe Clustering

Advanced or baseline DBSCAN with parameter optimization and APC with preference/damping sweeps were attempted first. If the number of clusters is unsatisfactory, a distance-based k-means fallback guarantees a feasible centroid output.

To confirm that the neural selector generalizes beyond the specific training setup, a cross-scenario validation was performed within the same 25 km × 25 km simulation area but under diverse network conditions. The ANN trained on the baseline configuration (UE density of 100 UE km⁻² and 40% BS outage) was tested on unseen scenarios with (i) varying user densities ranging from 50 to 500 UE km⁻², and (ii) heterogeneous BS outage levels (10–90%). Across these configurations, the classifier sustained an average decision accuracy above 92%, and its predicted clustering choice (APC or DBSCAN) consistently aligned with the method achieving higher coverage and lower intra-cluster variance. These findings demonstrate that the ANN effectively captures scale- and topology-invariant spatial features, ensuring robust and reliable clustering decisions across diverse disaster scenarios.

4.5. Overall Workflow

Algorithm 3 Description. The End-to-End UAV-Assisted Communication Restoration Algorithm assesses network resilience in scenarios of successive base station (BS) failures and determines optimal strategies for UAV deployment and routing to restore service. Given the sets of user equipment (UEs) and BSs, a capacity threshold $\theta$, and a predefined list of BS loss percentages $\mathcal{L}=\{10,\dots ,90\}\%$, the algorithm initially computes the baseline user-to-BS association and network capacity in the absence of BS failures. Subsequently, for each loss level $\mathsf{\ell }\in \mathcal{L}$, a random subset of $\mathsf{\ell }\%$ of BSs is deactivated, and the network is re-evaluated to identify the subset of unserviced users, $U_{\mathsf{\ell }}$. If $U_{\mathsf{\ell }}$ is non-empty, a Hybrid Selection procedure (Algorithm 1) is invoked to determine an appropriate set of UAV deployment centroids $C_{\mathsf{\ell }}$ and the clustering method $m_{\mathsf{\ell }}$ employed. Thereafter, the GA Routing Algorithm (Algorithm 2) is executed for drone counts $d=1$ to 5 to optimize UAV flight paths and service coverage, taking into account the capacity threshold $\theta$. The best-performing routes, selected methods, centroid counts, and clustering times are recorded for each loss level. Finally, post-processing aggregates all results to summarize clustering performance, visualize score heatmaps as functions of the loss percentage and drone count, and compare the fraction of users served before and after UAV deployment. The complete results are exported in CSV format for further analysis and visualization.    

Algorithm 3: End-to-end UAV-assisted communication restoration.

5. Performance Evaluation of Proposed Solution

5.1. Evaluation Criteria and Experimental Setup

This section presents a comprehensive evaluation of the proposed hybrid clustering-based MABS path-planning method. The system is assessed in various disaster scenarios that involve different levels of BS outages and UE distributions.

5.2. Evaluation Metrics

K-means clustering is a commonly utilized benchmark for structured datasets. However, it presupposes convex cluster shapes and necessitates the pre-specification of the number of clusters, which is impractical in dynamic post-disaster networks characterized by sparse and irregular user distributions. Consequently, K-means clustering was not employed as a baseline. Instead, APC and DBSCAN were chosen due to their capability to automatically infer the number of clusters and effectively manage both dense and sparse distributions. To thoroughly evaluate the effectiveness of the proposed solution compared with the baseline methods, a series of well-defined metrics was employed. The service ratio (SR) metric quantifies the percentage of previously unconnected UEs that were successfully linked after the implementation of MABS. The distance ratio (DR) serves as a normalized measure of the total UAV flight path length relative to the shortest possible route, thereby indicating path efficiency. The intersection ratio (IR) metric records the number of path intersections, with lower values indicating smoother and less tangled trajectories. Similarly, angle ratio (AR) assesses the average angular deviation along the UAV paths, where higher values suggest more continuous and navigable routes. The PSR further enhances this by evaluating the geometric fluidity of UAV paths to minimize sharp turns and associated power losses. To account for network resilience, the CS metric evaluates the consistency of UE coverage as the BS outage levels increase. From a computational standpoint, the Clustering time refers to the processing time required to perform user clustering using APC, DBSCAN, or the proposed hybrid model. Finally, the Computation time indicates the total duration required to complete the entire genetic optimization process. Collectively, these metrics provide a comprehensive view of the effectiveness, efficiency, and adaptability of a system in dynamic post-disaster scenarios.

5.3. Simulation Results and Analysis

The performance of each approach was analyzed for different levels of BS outage. The key performance indicators are presented as line plots, histograms, and coverage maps. It also evaluated the efficiency of path planning, clustering accuracy, and computational efficiency of the proposed hybrid method.

5.3.1. UAV Deployment Performance (Extended with Heatmap)

The heatmap visualization in Figure 2 of drone scores against BS loss percentages offers further evidence of the interaction between outage severity and UAV deployment size. Green regions correspond to lower outage impact and higher service quality, while yellow shades indicate conditions of greater strain on the network. Along the horizontal axis, as the number of drones increases, the scores consistently improve, demonstrating that multi-UAV deployments can compensate for service gaps more effectively than single UAVs. Along the vertical axis, higher BS loss values (70–90%) reduce the baseline score achievable with one or two UAVs, but the addition of more drones restores performance to near-optimal levels. This trend underscores the scalability of the framework, as an increase in UAVs can progressively recover lost service in proportion to outage severity.

A particularly noteworthy feature of the heatmap is the non-linear nature of the improvements. For instance, under moderate BS loss conditions (40–60%), deploying three drones yielded scores above 0.85, with four or five drones pushing the performance over 0.90 in most cases. In contrast, at a 20% loss, the increase from one drone (score $approx$ 0.68) to three drones (score $approx$ 0.74) is modest, but the increase to four drones ($approx$ 0.78) and five drones ($approx$ 0.83) represents a more substantial recovery. This nonlinear effect indicates diminishing returns in lightly affected networks but substantial gains under higher outage levels, guiding decision-makers on efficient UAV allocation strategies.

At the extreme of 90% BS loss, even one UAV achieves a score above 0.80, but five UAVs enhance performance to approximately 0.93, illustrating that coordinated multi-UAVs can mitigate nearly catastrophic failures. Overall, the heatmap demonstrates that the system retains resilience under severe conditions while clearly benefiting from additional UAV support, underscoring both robustness and scalability in post-disaster communication recovery (see Figure 2).

5.3.2. Path Efficiency and Smoothness

The efficiency of the route quality of the UAV trajectories using the intersection and path smoothness ratios is assessed.

Figure 3 presents the normalized path distance ratio ($\delta /{\delta }_{min}$) for the three clustering approaches, APC, DBSCAN, and the proposed hybrid model, under increasing levels of BS loss ranging from 10% to 90%. The x-axis reflects the percentage of BS infrastructure failure, whereas the y-axis represents the normalized path distance ratio, which quantifies the deviation of the UAV flight paths from the shortest possible trajectories. This metric is critical for evaluating the efficiency of UAV route planning, particularly under post-disaster conditions.

As shown, all methods exhibited an upward trend in the path–distance ratio with increasing BS loss, indicating a greater deviation from the optimal paths as the network conditions degraded. However, the magnitude of this deviation varied significantly across the three methods. DBSCAN consistently incurs the highest path distance ratios across all BS loss levels, reaching nearly 1.7 at 90% BS loss. APC performs moderately better, although its path lengths grow rapidly as infrastructure degradation intensifies. In contrast, the hybrid model maintained the lowest path distance ratio throughout, starting just above 1.0 at 10% BS loss and rising modestly to approximately 1.3 at 90% BS loss.

The best performance of the hybrid method is attributed to its ability to generate more strategically located centroids through adaptive clustering selection and ANN-guided parameter tuning. This leads to more coherent cluster structures and shorter and smoother UAV trajectories. In contrast, DBSCAN often produces fragmented clusters in sparse or noisy environments (UE spatial distributions with irregular, scattered, or outlier-heavy patterns), leading to suboptimal path planning. Similarly, APC’s rigid propagation mechanics can result in inefficient centroid placement when faced with irregular UE distributions.

The results underscore the importance of clustering quality in downstream UAV trajectory optimization. Poor clustering leads to scattered centroids and sub-optimal paths, increasing energy consumption and mission time, which are vital constraints in post-disaster scenarios. The Hybrid model mitigates these challenges by combining the structural strengths of APC with the density awareness of DBSCAN, reinforced by neural network-based decision logic.

Figure 3 confirms that the hybrid clustering approach not only improves service coverage but also delivers more efficient path planning. Its ability to minimize path elongation under severe BS failure scenarios makes it a compelling choice for real-time UAV deployment in disaster-stricken environments.

Figure 4 presents the Intersection Ratio, also referred to as the Line Crossing Avoidance Ratio, across different clustering strategies under increasing levels of BS loss. The x-axis represents the percentage of BS infrastructure failures, whereas the y-axis quantifies the intersection ratio, where values closer to 1 indicate smoother UAV trajectories with fewer path crossings. An intersection ratio close to 1 is desirable because it implies near-optimal path planning, reduced aerial traffic complexity, and lower energy consumption due to fewer abrupt direction changes.

Figure 4 illustrates that the ideal performance corresponds to values close to 1, which represent completely smooth UAV trajectories with no path intersections. Lower values reflect increased path intersections, reducing efficiency and raising collision risk. The results in Figure 4 reveal three distinct performance patterns. First, the proposed hybrid framework consistently maintains intersection ratios close to 1, staying above 0.9 until 60% BS loss and declining only moderately to about 0.72 at 90% BS loss. This demonstrates that the hybrid approach retains near-optimal trajectory separation under a wide range of conditions. Second, APC achieves moderate results, starting near 0.95 at low BS loss but declining more steeply after 40%, reaching approximately 0.58 at 90% BS loss. Third, DBSCAN shows the weakest performance, with values dropping below 0.8 as early as 30% BS loss and approaching 0.54 under extreme conditions.

A closer comparison shows that the hybrid model maintains intersection ratios 10–15% closer to 1 than APC in the 40–70% BS loss range, and nearly 30% closer to 1 than DBSCAN at 90% BS loss. These margins underscore the hybrid clustering strategy’s robustness in generating well-separated centroid paths. The neural classifier adapts to uneven user distributions, avoiding intersection and maintaining trajectory smoothness. In contrast, APC struggles with centroid separation in sparse topologies, while DBSCAN’s density sensitivity produces irregular clusters that increase UAV path crossings.

The structural reasons behind these differences are also evident. The hybrid framework integrates a neural classifier that dynamically adapts centroid placement, preventing intersection even as clusters fragment. APC, while efficient in dense conditions, fails to prevent centroid crowding once BS failures scatter users, leading to intersecting UAV routes. DBSCAN, due to its density-based nature, produces fragmented or irregular clusters in sparse conditions, resulting in sub optimal UAV trajectories and frequent path crossings.

From a critical perspective, the intersection ratio is a vital metric for operational efficiency in disaster response. Frequent path crossings can lead to UAV collision risks, increased communication latency, and energy inefficiencies due to abrupt manoeuvring. From a practical perspective, keeping the intersection ratio closer to 1 translates into fewer trajectory intersections, reduced aerial traffic complexity, and lower energy consumption. The performance of the hybrid method in this regard underscores its ability to produce coordinated and scalable UAV flight plans, even under harsh network conditions. By maintaining values much closer to 1 despite increasing BS loss, the hybrid approach enhances the reliability, safety, and energy efficiency of UAV-assisted communication restoration in post-disaster environments.

5.3.3. UAV Deployment Performance

The Figure 5 shows the results of the drone score analysis highlight the effectiveness of the genetic algorithm in optimizing UAV deployments under different levels of BS loss. When only a small proportion of BSs fail (10–20% loss), even a single UAV achieves satisfactory coverage, and the incremental gains from deploying additional drones are limited. In these low-loss cases, one UAV provides a cost-efficient solution because it can service most of the unserved users without excessive path intersection or resource waste. However, as the scale of the BS loss increases, particularly beyond 50%, the advantages of multi-UAV deployment become much more pronounced. In severe outage conditions (70–90% BS loss), the score improvements from adding drones were substantial. A single UAV is unable to cover the dispersed unserved users effectively, whereas multiple UAVs can share the workload, reduce overall travel distances, and ensure that service coverage remains acceptable. The heatmap results confirm that the best performance is consistently achieved when four or five UAVs are deployed in high-loss scenarios, with scores approaching 0.9 in some cases. These findings demonstrate that while minimal deployment is sufficient for localized failures, coordinated multi-UAV swarms are indispensable for maintaining service continuity under catastrophic disruptions.

5.3.4. Clustering Benchmark Performance

Figure 6 shows the clustering benchmark with 2500 UEs and provides further insight into the comparative performance of APC, DBSCAN, and the Hybrid clustering framework. The star (⋆) in the Figure 6 indicates the best-performing method for each metric. APC, being deterministic and free of parameter tuning, consistently achieved the lowest execution times. However, its rigidity limits its adaptability to non-uniform user distributions, and it often produces an excessive number of clusters. In contrast, DBSCAN adapts more effectively to irregular and noisy distributions, although its performance is sensitive to parameter settings and is computationally more demanding. The Hybrid method combines the strengths of both approaches. By leveraging a neural classifier to dynamically select between APC and DBSCAN based on extracted spatial features, the Hybrid clustering framework consistently matches or outperforms the better of the two individual methods (as shown in Figure 6). Accuracy metrics, such as the silhouette score and the Calinski–Harabasz index, further confirm its superior performance, particularly in scenarios with heterogeneous or mixed-density user distributions. Moreover, the Hybrid method produces a number of clusters that align more closely with UAV deployment requirements, avoiding the over-fragmentation characteristic of APC and the occasional under-clustering observed in DBSCAN. In terms of adaptability, the Hybrid approach clearly outperforms both individual methods, as it intelligently adjusts to the underlying spatial distribution without the need for manual parameter tuning.

5.3.5. Discussion

Taken together, the UAV deployment results and clustering benchmarks demonstrate the complementary strength of the proposed framework. The genetic algorithm provides a robust mechanism for differentiating multi-UAV configurations, showing that additional drones bring diminishing returns in lightly disrupted networks, but are crucial under large-scale failures. At the same time, hybrid clustering ensures that the UAV deployment process is guided by high-quality centroids that accurately reflect user demand. This synergy between adaptive clustering and multi-UAV optimization enables the system to maintain service continuity efficiently across a wide range of outage scenarios, outperforming both single-clustering methods and fixed-UAV strategies. These findings underline the importance of coupling adaptive clustering with multi-UAV optimization for resilient wireless networks. By intelligently selecting clustering strategies and tailoring UAV deployments according to the severity of disruptions, the proposed framework provides a scalable and robust solution for service restoration. Such an approach holds significant promise for next-generation 5G and 6G systems, where maintaining seamless connectivity during infrastructure failures is a critical requirement for reliability, disaster recovery, and future smart city applications.

The results highlight the strengths of integrating learned clustering with evolutionary path planning. The hybrid model maintained high service and low intersection with relatively shorter paths. It adapts well to sudden topology changes and uneven UE distributions, making it ideal for post-disaster deployments in which the conditions are dynamic and unpredictable.

6. Conclusions and Future Work

This study presents a neural-guided hybrid clustering framework for UAV-assisted communication recovery in post-disaster networks. By integrating a lightweight neural classifier with APC and DBSCAN, the proposed method dynamically selects the most suitable clustering strategy according to the spatial distribution of users and the extent of base-station outages. Coupled with a genetic-algorithm-based path optimizer, this approach enables multi-UAV to achieve robust, efficient, and adaptive service restoration under heterogeneous and highly dynamic disaster conditions.

The simulation results demonstrate that the hybrid framework consistently outperforms single clustering methods in terms of service coverage, path efficiency, and adaptability. Even under extreme BS outage scenarios, the hybrid model maintained higher service ratios, smoother UAV trajectories, and reduced path intersections compared with APC- or DBSCAN-only strategies. These results highlight the importance of adaptive centroid generation for guiding UAV deployments, particularly when user distributions are sparse, irregular, or rapidly evolving. The findings of this study emphasize the need for flexible, learning-driven solutions in the design of UAV-assisted disaster response systems.

By integrating machine learning with evolutionary optimization, the proposed methodology not only improves immediate post-disaster connectivity but also establishes a foundation for scalable and resilient UAV deployments in future 5G and 6G networks, especially in next-generation communication ecosystems demanding resilience, scalability, and real-time adaptability. However, several challenges persist. Temporal variability among users poses a significant challenge; although the framework adapts through repeated re-clustering, extreme mobility may surpass feasible update frequencies and introduce delays. The ANN-based selector may also necessitate retraining when confronted with user distributions not represented in the training data, thereby limiting direct generalization across regions. Furthermore, although the GA-based optimizer is effective, it introduces a computational overhead that may impede real-time deployment in very large UAV swarms. Additionally, the current simulations abstract terrain and weather effects, indicating that harsh real-world conditions, such as dense urban multipath, heavy obstructions, or strong winds, may further impact performance. To address these challenges, future research should explore accelerated and incremental reclustering strategies, online learning for rapid ANN adaptation, hardware-accelerated GA implementations, and cross-layer optimization with energy-aware routing. Reinforcement learning for adaptive swarm coordination and validation with real-world datasets and field experiments will be pursued. Collectively, these extensions will enable UAVs to provide reliable, low-latency, and autonomous connectivity in complex, large-scale disaster environments.