Highlights
What are the main findings?
- A novel reinforcement learning-based Grey Wolf Optimizer (RL-GWO) is proposed, which adaptively selects search strategies to balance exploration and exploitation.
- Experimental results show the proposed RL-GWO significantly outperforms standard GWO and DE in both convergence speed and final solution quality for cooperative path planning.
What is the implication of the main finding?
- The proposed method provides a more efficient and robust solution for achieving high-precision time synchronization among heterogeneous UAVs in complex environments.
- The developed dual-layer dynamic planning framework demonstrates high practical value, enabling rapid and effective online replanning to ensure safety against sudden threats.
Abstract
Addressing the challenge of high-precision time-coordinated path planning for manned and unmanned aerial vehicle (UAV) clusters operating in complex dynamic environments during missions like high-level autonomous coordination, this paper proposes a reinforcement learning-based Adaptive Grey Wolf Optimizer (RL-GWO) method. We formulate a comprehensive multi-objective cost function integrating total flight distance, mission time, time synchronization error, and collision penalties. To solve this model, we design multiple improved GWO strategies and employ a Q-Learning framework for adaptive strategy selection. The RL-GWO algorithm is embedded within a dual-layer “global planning + dynamic replanning” framework. Simulation results demonstrate excellent convergence and robustness, achieving second-level time synchronization accuracy while satisfying complex constraints. In dynamic scenarios, the method rapidly generates safe evasion paths while maintaining cluster coordination, validating its practical value for heterogeneous UAV operations.
1. Introduction
1.1. Research Background and Significance
With the rapid advancement of unmanned systems technology, heterogeneous UAV clusters composed of different types of aircraft demonstrate immense application potential in critical infrastructure monitoring, civilian logistics, and emergency search and rescue [1,2,3]. A typical coordinated surveillance and task-execution mission formation often involves fixed-wing UAVs for high-altitude reconnaissance and helicopters for low-altitude precision operations [4,5]. This combination leverages the unique advantages of distinct platforms. However, translating this potential into reliable mission capability necessitates solving the core challenge of cooperative trajectory planning for heterogeneous clusters in complex dynamic environments [6]. Specifically, this problem involves challenges at three levels:
- Heterogeneity Coordination: Significant differences exist between fixed-wing UAVs and helicopters regarding flight speed envelopes, maneuverability, and operating altitudes. Planning spatiotemporally coupled trajectories that satisfy their respective physical constraints is the primary objective for achieving efficient coordination [7].
- Dynamic Environment: The mission airspace is volatile, potentially harboring unforeseen dynamic threats [8]. This demands that the planning system possesses rapid online response and replanning capabilities to perceive environmental changes in real-time during mission execution and quickly generate new safe paths for the cluster.
- Time Synchronization: The success of many missions relies on precise temporal coordination between vehicles. For instance, the strike helicopter must arrive precisely at the target within the brief “window” created by the illuminating UAV [9]. This stringent requirement for “simultaneous arrival” capability across the entire cluster elevates path planning from a traditional three-dimensional (3D) spatial problem to a four-dimensional (4D) spatiotemporal problem, imposing extremely high demands on the algorithm’s optimization capability and precision.
Therefore, researching trajectory planning methods capable of holistically addressing the aforementioned challenges holds significant theoretical value and practical importance for enhancing the mission success rate, operational efficiency, and autonomous survivability of heterogeneous UAV clusters.
1.2. Literature Review
Path planning is a key technology for autonomous vehicle navigation [10,11]. Researchers have proposed various flight path planning methods tailored to different application scenarios and environmental complexities. Existing research can be categorized into three classes: Graph search-based algorithms, such as A* and its variants, can find optimal paths in discrete spaces, but computational cost increases drastically with dimensionality, making them difficult to apply directly to complex 3D continuous spaces [12]. Sampling-based algorithms, such as Rapidly exploring Random Trees (RRT) and its improved versions (RRT*), exhibit advantages in handling high-dimensional spaces and complex constraints; however, solution sub-optimality and convergence speed remain challenges [13]. Intelligent optimization-based algorithms, such as metaheuristics including Genetic Algorithms (GA), Particle Swarm Optimization (PSO), and Grey Wolf Optimization (GWO), have gained widespread attention for handling multi-objective, nonlinear UAV path planning problems due to their global search capability and flexibility [14,15].
However, standard versions of these algorithms often suffer from inherent drawbacks [16]. For instance, the standard GWO is frequently criticized for its tendency toward premature convergence and its susceptibility to local optima when applied to high-dimensional, highly constrained problems like multi-UAV path planning. To mitigate these issues, numerous studies have proposed hybrid metaheuristics. While these hybrid methods have shown improved performance, many rely on fixed rules or simple adaptive mechanisms to switch between their integrated strategies. The selection of operators is often not fully responsive to the algorithm’s real-time search state, leaving a performance gap. This points to the need for a more intelligent, online adaptive framework. Recently, integrating reinforcement learning (RL) to dynamically manage search operators has emerged as a promising frontier to fill this gap [17]. An RL agent can learn an optimal policy for strategy selection based on the feedback from the optimization process, rather than depending on predefined rules.
In the field of multi-vehicle coordination, research focuses on spatial and temporal coordination. Spatial coordination constraints aim to ensure flight safety and avoid collisions. Temporal coordination constraints ensure vehicles arrive at targets simultaneously or in sequence according to mission requirements, often necessitating time synchronization [18,19,20]. For temporal coordination, existing works frequently employ adding time window constraints or treating time as an optimization objective. However, current research has limitations: On one hand, most studies focus on homogeneous UAV clusters, inadequately addressing the deep coordination challenges arising from physical performance disparities among heterogeneous platforms [21,22,23]. On the other hand, many methods treat path planning and obstacle avoidance separately, or struggle to balance global optimality with online real-time performance. Particularly, while metaheuristic algorithms like GWO show promise, standard versions suffer from inherent drawbacks such as slow convergence and susceptibility to local optima when dealing with high-dimensional, highly constrained path planning problems, limiting their effectiveness in complex scenarios [24,25,26]. In summary, research that holistically addresses the three major challenges of heterogeneity, dynamic environments, and precise time coordination within a unified framework remains insufficient.
1.3. Main Contributions
Addressing the aforementioned issues, this paper proposes a reinforcement learning-based Adaptive Grey Wolf Optimizer (RL-GWO) and constructs a dual-layer “global planning–local replanning” framework to solve the cooperative trajectory planning problem for heterogeneous UAV clusters in dynamic environments. The main contributions are as follows:
- (1)
- A Novel Hybrid Intelligent Optimization Algorithm (RL-GWO): To overcome the standard GWO’s tendency to converge to local optima and its slow convergence speed when solving complex path planning problems, a reinforcement learning mechanism is introduced. The core idea of RL-GWO is to utilize a Q-Learning model to adaptively adjust optimization strategies, effectively balancing the algorithm’s global exploration and local exploitation capabilities, significantly improving solution quality and convergence efficiency.
- (2)
- An Integrated Optimization Scheme for Heterogeneous Clusters: A comprehensive multi-objective fitness function is designed, unifying total flight distance, mission time, time coordination error, and collision risks with static/dynamic obstacles. This transforms the complex 4D cooperative path planning problem into a clear minimization problem, achieving holistic, end-to-end optimization for the entire heterogeneous cluster.
- (3)
- Construction and Validation of a Dual-Layer Dynamic Planning Framework: A practical “offline global planning + online dynamic replanning” framework is proposed. This framework first utilizes the RL-GWO algorithm for global cooperative path planning to obtain an initial optimal solution. During mission execution, an efficient collision prediction mechanism triggers local replanning, invoking RL-GWO again to rapidly generate new safe paths. Simulation experiments prove that this framework effectively balances global planning quality with online dynamic response capability.
2. Problem Formulation and Mathematical Modeling
This section formally describes the cooperative path planning problem for heterogeneous UAV clusters, establishing the corresponding environmental model, vehicle model, path model, and multi-objective optimization function, laying the mathematical foundation for subsequent algorithm design and solution.
2.1. Environment Modeling
Mission Space:The airspace for mission execution is defined as a bounded 3D cubic space, delimited by minimum coordinates and maximum coordinates . All vehicle paths must lie within this space.The mission space is denoted by .
Static Terrain Model: The ground environment within the mission space is described using a Digital Elevation Model (DEM). The terrain surface is modeled as a height function . For any given planar coordinate , represents the ground elevation at that point. In this study, complex terrain is generated by superimposing multiple Gaussian functions to simulate natural landforms like mountains:
Here, denotes the center coordinates of the k-th peak; is the terrain parameter controlling height; and control the decay rate along the x-axis and y-axis for the k-th peak, respectively, determining the slope; and n is the total number of peaks in the environment. The environment model constructed according to Equation (1) is illustrated in Figure 1.
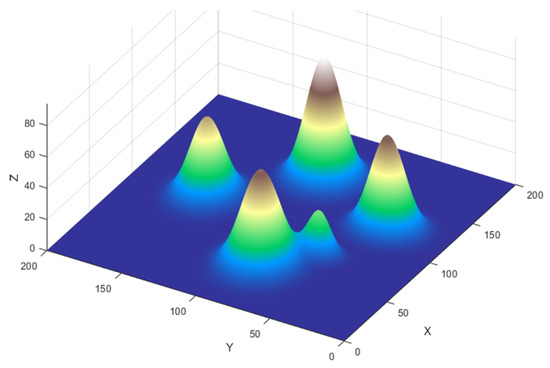
Figure 1.
Schematic diagram of a mountainous terrain.
Dynamic Threat Model: Mobile threats present in the mission airspace (e.g., enemy patrol units) are modeled as a set of spheres moving at constant velocities. The state of the j-th dynamic threat at time t is described by its center position and radius . Its position updates over time as follows:
where and are its initial position and velocity vector, respectively. The dynamic threats in this study are modeled as non-adversarial, physical obstacles (e.g., other non-cooperative aircraft or patrol units) with predictable, constant-velocity trajectories.
2.2. Heterogeneous Vehicle Model
The heterogeneous UAV cluster is defined as a set , where N is the total number of vehicles in the cluster. The heterogeneous cluster in this study consists of two primary vehicle types: fixed-wing UAVs for high-altitude reconnaissance and helicopters for low-altitude precision operations. For the purpose of high-level trajectory planning, all vehicles are represented by a point-mass kinematic model. For any vehicle , its key attributes are modeled as follows:
- Start and Target Positions: and represent its start point and target point, respectively;
- Velocity Constraints: is the cruise speed of , constrained by its physical performance, i.e., . Different vehicle types (e.g., helicopters vs. fixed-wing UAVs) have distinct speed constraint ranges, which is a core manifestation of “heterogeneity”;
- Safety Radius: is the safety radius assigned to the vehicle for collision detection.
2.3. Path Representation
The flight path for vehicle is defined as a polyline connecting its start and end points, composed of m intermediate waypoints. The path can be represented as a sequence of waypoints:
where , , and the set comprises the intermediate waypoints to be optimized by the path planning algorithm. The total length of the path is the sum of all segment lengths:
Here, denotes the Euclidean distance. The time for vehicle to complete the entire path at speed is .
2.4. Optimization Objective Function
The path planning problem in this study is formulated as a multi-objective optimization problem, aiming to find an optimal set of waypoints and speeds that minimizes a comprehensive cost function J. This function is a weighted sum of four core sub-objectives:
where are the weighting coefficients for each term. The weighting coefficients are crucial parameters that balance the trade-offs between the different objectives, and they are set based on mission priorities through empirical tuning. A significantly large value is assigned to to enforce the hard constraints of flight safety, ensuring that collision avoidance is prioritized above all other objectives. Among the optimization goals, time synchronization () and mission time () are considered critical for tactical success and are thus given higher importance. The total distance () is weighted lower to reflect that mission speed and coordination are prioritized over path economy. This hierarchy ensures that the algorithm aggressively seeks safe and temporally coordinated solutions before optimizing for the shortest possible path length.
The sub-objectives are defined as follows:
(1) Total Flight Distance Cost: Due to limited vehicle fuel, shorter paths reduce fuel consumption and lower the risk of encountering unexpected threats. This cost measures the cluster’s energy efficiency, defined as the sum of all vehicle path lengths:
(2) Mission Time Cost: This cost measures the rapidity of mission completion, defined as the maximum flight time among all vehicles in the cluster:
(3) Time Coordination Cost: This is key to achieving the tactical goal of “simultaneous arrival,” defined as the difference between the maximum and minimum flight times in the cluster:
(4) Comprehensive Penalty Term: This term ensures path feasibility and safety, comprising terrain collision penalty, inter-vehicle separation penalty, and dynamic threat collision penalty. Costs increase drastically if paths intersect or approach obstacles too closely:
- Terrain Penalty: For any point q on the path, compute its vertical clearance height above the underlying terrain . If , apply a large penalty proportional to the intrusion depth.
- Inter-Vehicle Separation Penalty: This penalty ensures that the flight paths of any two vehicles and in the cluster maintain a minimum safe distance , mitigating potential collision risks. This is a strong constraint guaranteeing physical separation in space, independent of the vehicles’ temporal synchronization. For any two distinct paths and , the penalty is calculated as follows:where p and q are discretized sampling points along paths and , respectively, and is a penalty constant. This formula counts and accumulates penalties for all point pairs violating the safety distance, driving the optimization algorithm to find spatially separated paths.
- Dynamic Threat Penalty: This is the core for handling dynamic environments. For any point q on path , first, compute the time at which vehicle reaches that point. Subsequently, predict the position of dynamic threat j at that time. If the spatiotemporal distance , apply a large penalty.
By minimizing the comprehensive cost function J, we can simultaneously achieve path efficiency, safety, and time coordination within a unified optimization framework.
3. Reinforcement Learning-Based Adaptive Grey Wolf Optimization Method
To effectively solve the complex multi-objective optimization problem formulated in Section 2, this paper proposes a novel hybrid intelligent optimization algorithm: the reinforcement learning-based Adaptive Grey Wolf Optimizer (RL-GWO). The core idea is to, first, design multiple improved GWO update strategies with different search characteristics and, then, utilize a reinforcement learning framework to dynamically and intelligently select the currently most suitable strategy based on the optimization progress. This effectively overcomes the standard GWO’s tendency to get trapped in local optima and significantly enhances solution performance.
3.1. Overall Algorithm Framework
This study adopts a dual-layer planning framework of “offline global planning + online dynamic replanning,” both driven by the proposed RL-GWO algorithm. The framework flowchart is shown in Figure 2.
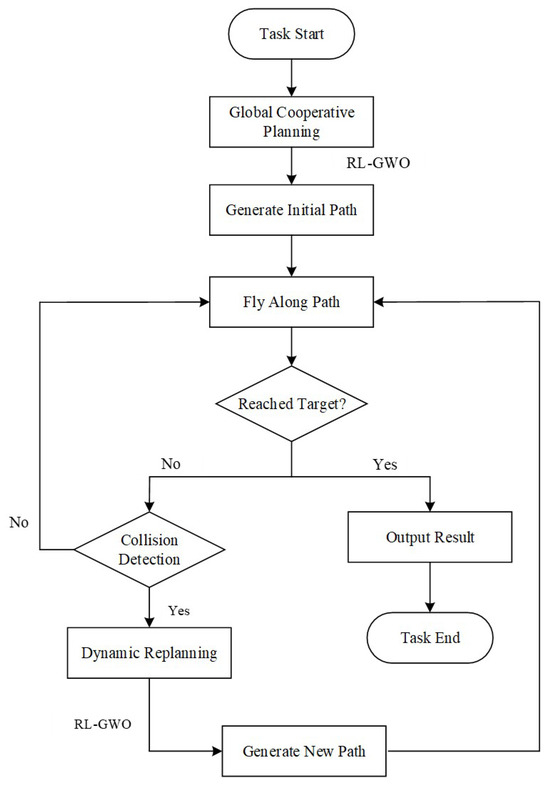
Figure 2.
Flowchart of the dual-layer “Global Planning + Dynamic Replanning” framework.
- Global Planning Stage: Before the mission starts, the system takes predefined start/target points and static environment information as input. It invokes the RL-GWO algorithm for sufficient iterations to solve an initial cooperative path plan satisfying all constraints and achieving global optimality.
- Dynamic Replanning Stage: During mission execution, the system continuously performs collision prediction. Upon predicting a potential collision with a dynamic threat, it immediately triggers the replanning module, using the current positions of all vehicles as new starting points. The RL-GWO algorithm is invoked again to rapidly solve a new locally optimal path that avoids the dynamic threat within fewer iterations. The vehicles seamlessly switch to the new path to continue the mission.
3.2. Standard Grey Wolf Optimization Algorithm
The Grey Wolf Optimization (GWO) algorithm is a metaheuristic algorithm simulating the social hierarchy and hunting behavior of grey wolves. The wolf pack is divided into four hierarchical levels: Alpha (), Beta (), Delta (), and Omega (). The , , and wolves are considered leaders, guiding the entire pack (composed of wolves) to search towards the prey’s position (the optimal solution).
The core operations of GWO encompass two phases: encircling the prey and attacking the prey. In the first phase, the encircling behavior is described as follows:
where t is the current iteration number, X represents the wolf’s position, and represents the prey’s position. Parameters A and C are
where and are random numbers in the range , parameter a decreases linearly from 2 to 0, and is the maximum number of iterations.
In the subsequent attacking phase, guided by , , and , the pack updates positions to hunt the prey:
Here, , , and represent the positions of the leading wolves in the search space. In Equations (17)–(19), , , and denote the distance between the current solution’s position and the , , and wolves, respectively. Although standard GWO is structurally simple, it suffers from inherent drawbacks when dealing with high-dimensional, multi-modal complex problems: slow convergence and susceptibility to local optima due to reduced population diversity.
3.3. Proposed RL-GWO Algorithm
To address the shortcomings of standard GWO, improvements are made at two levels: First, two different hybrid update operators are designed to enhance exploration and exploitation capabilities. Second, a Q-Learning framework is introduced to dynamically and intelligently select between these two operators.
3.3.1. Improved GWO Search Strategies
Two search strategies with different biases are designed, focusing on global exploration and local exploitation, respectively. These constitute the “action space” or “operator library” for the RL agent.
(1) Elite-Guided Exploration Strategy. This strategy aims to enhance global exploration capability. Building upon the standard GWO position update formula, it introduces random guidance from the entire population’s elite group (e.g., top 10% individuals by fitness), not just the , , and wolves. The position update no longer simply moves towards the average position of the three leaders but incorporates an additional guiding direction by randomly selecting an elite wolf with a certain probability:
where is the updated position from standard GWO, is the position of an individual randomly selected from the elite group, and is a dynamically changing inertia weight. A linearly decreasing strategy is used to update this weight:
where t is the current iteration number and is the maximum iteration number. In early iterations (t small), is large (e.g., ), meaning the algorithm relies more on the convergence direction of standard GWO ( dominates), ensuring rapid convergence towards the current best solution. As iterations progress, decreases linearly, gradually increasing the weight of the elite guidance term, thereby introducing more population diversity to help explore broader regions and avoid premature convergence to local optima.
(2) Differential Evolution-based Hybrid Exploitation Strategy. This strategy aims to combine the strong local exploitation capability of GWO with the excellent population perturbation capability of Differential Evolution (DE) to balance convergence and diversity. In each iteration, this strategy generates two candidate solutions in parallel: one () is calculated via the standard GWO formula, tending towards the current optimal region; the other () is generated through DE’s mutation and crossover operations, possessing stronger randomness:
Here, , , and are three distinct individuals randomly selected from the population, and is a scaling factor. Subsequently, this mutation vector undergoes a crossover operation with the original individual with a crossover probability to generate the final candidate solution . This candidate generation process does not rely on information about the current best solution but utilizes the distribution information of the entire population, giving it stronger randomness and global exploration capability, representing the algorithm’s effort to maintain population diversity.
After generating the two candidate solutions, a greedy selection is employed. These two candidates, and , represent a strategic choice between an exploitation step and an exploration step. The greedy selection mechanism then chooses the candidate with the superior fitness for the next generation. This elitist approach ensures the solution does not degrade in a given iteration and effectively balances the two search behaviors to enhance the algorithm’s ability to escape local optima.
3.3.2. Reinforcement Learning-Based Adaptive Strategy Selection
Balancing global exploration and local exploitation is crucial for multi-UAV cooperative path planning in complex mountainous environments. Relying solely on a single search strategy, whether biased towards broad exploration or fine exploitation, may be insufficient for efficiently navigating the complex search space and finding the optimal or near-optimal solution.
Intelligently selecting the most suitable update operator at different optimization stages is key to improving algorithm performance. This paper models this selection as a Q-Learning task. Reinforcement learning is one of the most prominent methods in machine learning. In this technique, an agent learns to take actions in a specific environment through interactions, aiming to maximize cumulative reward.
- State: The optimization process is discretized into K stages (e.g., ). The current iteration stage is the state s of the RL agent:where denotes the ceiling operator.
- Action: The agent’s action space A is the set containing the two hybrid update operators described above—A = {, execute the the elite-guided strategy, and , execute the hybrid DE strategy}. The Q-table structure is shown in Table 1.
 Table 1. Q-table framework.Table 1. Q-table framework.
Table 1. Q-table framework.Table 1. Q-table framework.State/Action ⋮ ⋮ ⋮ - Reward: The reward mechanism is designed to directly reflect the contribution of the selected action to the optimization progress. It primarily consists of the improvement in the global best fitness. If there is no improvement, the reward is 0 or a small negative value. This mechanism directly encourages actions that effectively enhance solution quality:
- Policy and Q-table Update: For action selection, the -greedy policy is used to balance exploitation and exploration. Specifically, at each decision point, the agent chooses the action with the highest current Q-value with a high probability of . Conversely, with a small probability of , it ignores the Q-values and selects a random action from the action space. This simple yet effective mechanism ensures that while the agent predominantly leverages its learned knowledge, it also continually dedicates a fraction of its trials to discovering potentially superior strategies, which is crucial for escaping suboptimal policies. After obtaining the reward in each iteration, the Q-table is updated according to the standard Q-Learning formula:where is the learning rate and is the discount factor.
At each decision point, the agent selects an action (update strategy) based on the Q-table and the -greedy policy to update the entire population. After execution, the corresponding Q-value in the Q-table is updated based on the environmental feedback (reward) and the next state. Through this mechanism, the Q-table gradually learns and records which update strategy (action) yields higher long-term rewards at different optimization stages (states). For instance, the elite-guided strategy might receive higher rewards early in optimization, while the fine-search GWO-DE operator might be more advantageous later. Ultimately, the RL-GWO algorithm forms a data-driven, adaptive, dynamic search strategy. The flowchart of the RL-GWO algorithm is shown in Figure 3.
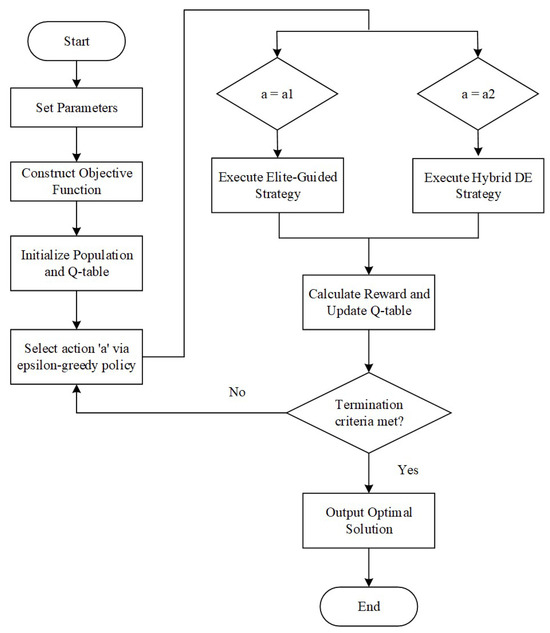
Figure 3.
Flowchart of the RL-GWO algorithm.
3.4. Application of RL-GWO to Multi-Vehicle Path Planning
This subsection details the application of the aforementioned RL-GWO algorithm to solve the cooperative path planning problem for heterogeneous UAV clusters. The process follows clear, standardized steps:
- (1)
- Define Cooperative Task Scenario and Encoding Scheme: Load all mission-related parameters within the 3D mission space. This includes the start position, target position, and speed constraints for each vehicle (helicopters and UAVs) in the cluster, as well as environmental information on static terrain and dynamic threats. Determine the dimension of each solution (i.e., grey wolf individual), defined by the total number of 3D waypoints for all UAVs plus the speed variables.
- (2)
- Initialize Population and Fitness Evaluation: Generate initial waypoints between the start and end points of each vehicle using linear interpolation with added random perturbations. Concatenate the coordinates of all waypoints, and randomly generated speed values for all vehicles to form the initial position vector of each grey wolf individual. Subsequently, use the comprehensive cost function J defined in Section 2.4 as the fitness function to compute the fitness value of each initial individual. Sort the population based on fitness to determine the initial , , and wolves, and initialize the RL Q-table.
- (3)
- Iterative Optimization Solution: Enter the main loop of the algorithm. Use the proposed RL-GWO algorithm to optimize the model. In each iteration, the RL module selects an update strategy based on the current iteration stage. Then, update the path based on a fitness evaluation, and compute the reward value to update the Q-table.
- (4)
- Output Optimal Cooperative Solution: When the algorithm reaches the maximum iteration count or satisfies a stopping condition, terminate the search process, and output the individual with the highest fitness (lowest comprehensive cost) found in the population. Decoding this individual yields the optimal multi-vehicle cooperative path plan. If the stopping conditions are not met, return to Step 3 to continue iteration.
The four steps above detail the process for generating the initial, globally optimized path plan. This plan is augmented during mission execution by the online dynamic replanning capability, for which the collision prediction mechanism is central. This mechanism operates as follows: At each time step, the system discretizes each UAV’s currently planned future path into a sequence of time-stamped waypoints. Simultaneously, it predicts the future position of all dynamic threats based on their known velocity vectors. A conflict is detected if, at any future time step, the predicted Euclidean distance between a UAV’s waypoint and a threat’s center is less than the sum of their respective safety radii . The first such detected violation triggers the online replanning module, which uses the vehicles’ current positions as new starting points and re-invokes the RL-GWO algorithm (as described in Step 3) to rapidly find a new, locally optimal safe path.
4. Simulation Experiments and Analysis
To systematically evaluate the performance of the proposed RL-GWO algorithm in solving the heterogeneous UAV cluster cooperative path planning problem, this section designs and conducts two simulation experiments. Experiment 1 aims to systematically analyze the comprehensive performance of RL-GWO in a static environment. Experiment 2 validates the proposed dual-layer framework’s dynamic replanning and coordination maintenance capabilities when responding to sudden threats in a dynamic environment.
4.1. Experimental Setup
Simulation Platform and Environment: All experiments were conducted on the MATLAB R2021b platform, with a computer configuration of Intel Core i7-9700 CPU@3.00 GHz, 16 GB RAM. The mission airspace was set as a 100 km × 100 km × 50 km 3D space, containing simulated mountainous terrain with complex undulations generated by multiple Gaussian functions.
Heterogeneous Cluster Configuration: The overall evaluation is conducted through two main experiments. Experiment 1 focuses on the algorithm’s performance and scalability in a static environment and is divided into two tasks. Task 1 is designed for a comprehensive performance comparison against benchmark algorithms, utilizing a three-vehicle cluster. Task 2 is designed to verify the algorithm’s scalability with an expanded six-vehicle cluster. Experiment 2 evaluates the system’s online replanning capabilities in a dynamic environment using the three-vehicle cluster. The specific parameter settings for all experiments and tasks are consolidated in Table 2 and Table 3.

Table 2.
Heterogeneous cluster parameter settings in Experiment 1.

Table 3.
Heterogeneous cluster parameter settings in Experiment 2.
Algorithm Parameters: Population size , maximum iterations , number of intermediate waypoints per path = 8. RL learning rate , discount factor , exploration rate .
4.2. Simulation Results in Experiment 1
4.2.1. Performance Comparison with Three-UAV Cluster
This experiment is designed to systematically evaluate the comprehensive performance of the proposed RL-GWO algorithm in a static scenario without dynamic threats. To validate its effectiveness, we compare it against three carefully selected benchmarks: the standard GWO, the DE algorithm, and the state-of-the-art SDPSO algorithm [20]. Standard GWO serves as the essential baseline to verify the efficacy of our proposed RL mechanism. DE is chosen as a representative of powerful, classic metaheuristics, while SDPSO provides a direct comparison against a recent, high-performance method in the field of UAV path planning. The analysis proceeds from three dimensions: convergence, coordination accuracy, and path quality, with the results presented in Table 4 and Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8.

Table 4.
Performance metrics (Scenario 1).
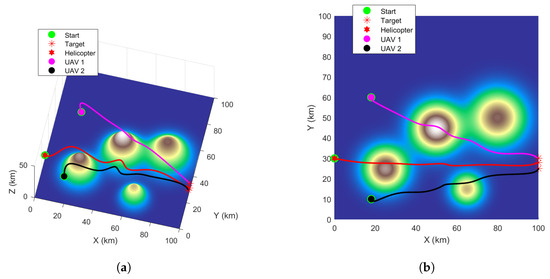
Figure 4.
GWO algorithm path planning. (a) The path planning results in 3D view. (b) The path planning results in top view.
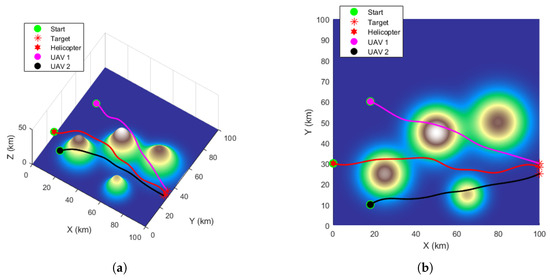
Figure 5.
DE algorithm path planning. (a) The path planning results in 3D view. (b) The path planning results in top view.
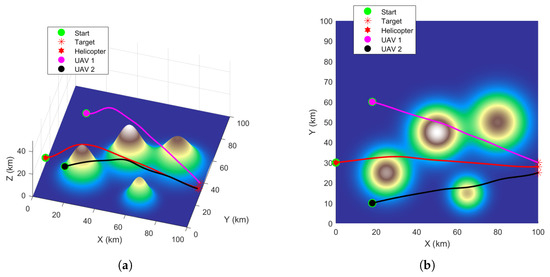
Figure 6.
SDPSO algorithm path planning. (a) The path planning results in 3D view. (b) The path planning results in top view.
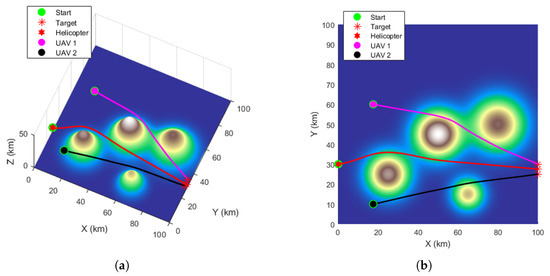
Figure 7.
RL-GWO algorithm path planning. (a) The path planning results in 3D view. (b) The path planning results in top view.
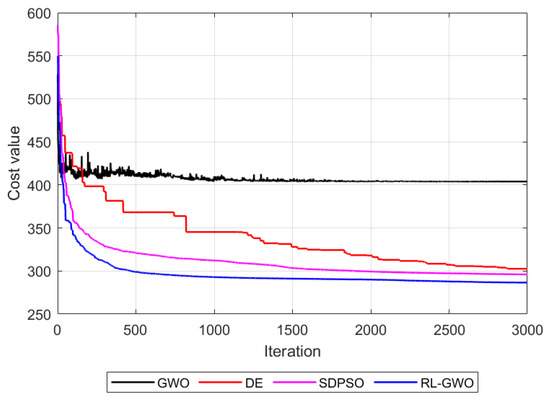
Figure 8.
Fitness function convergence curves.
A detailed analysis of the results in Table 4 reveals a clear performance hierarchy across all four algorithms. In terms of mission time, a key indicator of operational efficiency, the proposed RL-GWO is the most effective, planning a mission completion time of only 0.59 h. This represents a notable improvement over the SDPSO (0.63 h), the DE (0.66 h), and the GWO (0.94 h). The DE algorithm’s intermediate performance can be attributed to its effective mutation strategy, which maintains population diversity to avoid the severe premature convergence seen in GWO, though its convergence speed is ultimately slower than the more specialized hybrid approaches. Regarding path economy, RL-GWO also demonstrates significant superiority. It planned a total cooperative path length of only 279.39 km, a substantial reduction compared to SDPSO (293.91 km), DE (296.83 km), and especially the standard GWO (366.97 km). In terms of computational cost, the proposed RL-GWO (6.13 s) is marginally slower than the simpler baseline algorithms, GWO (5.26 s) and DE (5.58 s). However, this minor time increase is a justifiable trade-off for the significant gains in solution quality.
Beyond these quantitative metrics, a qualitative assessment of the planned trajectories in Figure 4, Figure 5, Figure 6 and Figure 7 shows distinct differences in path quality. The paths generated by RL-GWO are visibly smoother with more gradual turns, which is more conducive to the tracking control of physical UAVs.
Figure 8 shows the fitness change curves of the four algorithms. The RL-GWO curve exhibits both the fastest convergence rate and converges to the lowest final cost value (approximately 280), significantly outperforming SDPSO (approx. 295), DE (approx. 300), and GWO (approx. 405). This superior performance can be attributed to the reinforcement learning mechanism, which adaptively selects the optimal search strategy. It allows RL-GWO to effectively balance global exploration in the early stages to quickly locate promising regions and local exploitation in the later stages to refine the solution, thus avoiding the premature convergence seen in GWO and achieving a higher quality solution than the other metaheuristics.
The experimental results convincingly demonstrate the effectiveness and efficiency of the proposed RL-GWO algorithm. Furthermore, while satisfying the fundamental “simultaneous arrival” goal achievable by all algorithms, RL-GWO demonstrates superior performance in three key dimensions, time efficiency, path economy, and path quality, highlighting its advantage as an advanced hybrid intelligent optimization method for complex multi-objective problems.
4.2.2. Scalability Verification with Six-UAV Cluster
To further evaluate the performance and effectiveness of the proposed RL-GWO algorithm in more complex, larger-scale scenarios, we designed a task with a six-UAV heterogeneous cluster (defined as Task 2 in Table 2). This task doubled the cluster size, significantly increasing the problem’s dimensionality and coordination complexity.
The path planning results are visualized in Figure 9, which clearly shows that RL-GWO generated a set of smooth and collision-free trajectories for all six vehicles. The corresponding quantitative metrics, detailed in Table 5, confirm this success. The algorithm enabled all six vehicles to arrive at their respective targets with a precise, synchronized flight time of 0.74 h, validating its high-precision coordination capability in a more crowded environment. In summary, this successful validation demonstrates the strong scalability of our proposed method for moderately sized UAV clusters and lays the groundwork for the subsequent discussion on its limitations.
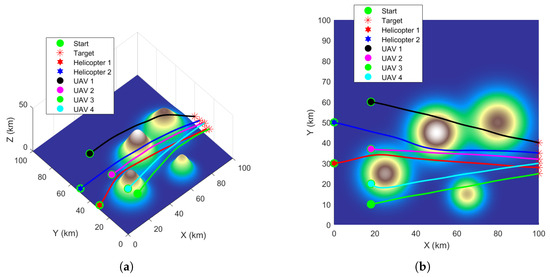
Figure 9.
RL-GWO path planning results for the 6-UAV scalability task. (a) The path planning results in 3D view. (b) The path planning results in top view.

Table 5.
Performance metrics for the 6-UAV scalability task using RL-GWO.
4.3. Experiment 2: Dynamic Environment Replanning Capability Verification
This experiment aims to simulate a scenario closer to real missions, testing the effectiveness of the “dual-layer planning framework” in responding to sudden dynamic threats. Building upon the static optimal path generated in Experiment 1, a dynamic obstacle moving at constant velocity is introduced. This threat is modeled as a sphere with parameters listed in Table 6. Simulation results are shown in Figure 10 and Table 7 and Table 8.

Table 6.
Dynamic threat parameter settings (Scenario 2).
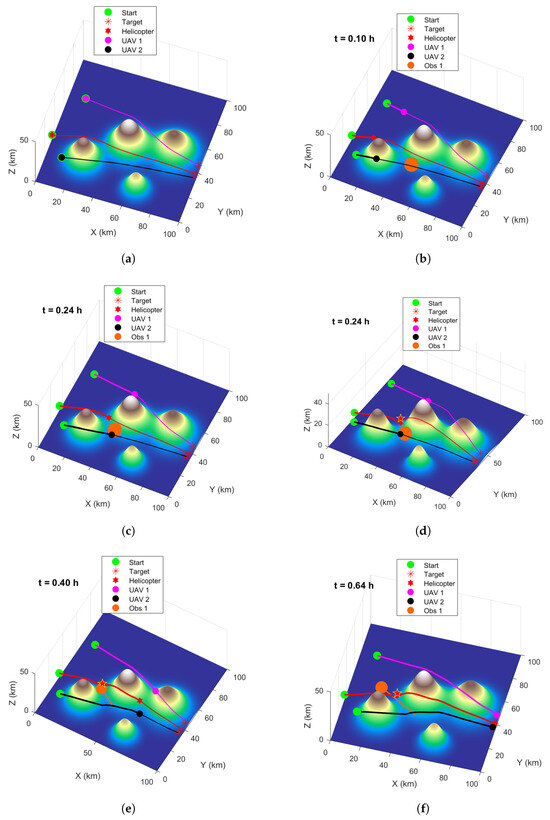
Figure 10.
Replanning process under dynamic threat. (a) Initial path. (b) Dynamic threat appears ( h). (c) Replanning triggered ( h). (d) New safe path generated. (e) Executing replanned trajectory ( h). (f) Simultaneous arrival at targets ( h).

Table 7.
Initial planned path metrics.

Table 8.
Replanned path metrics (triggered at h).
From Figure 10a and Table 7, it can be seen that the initial flight paths planned by the system for the multiple vehicles not only perfectly avoid mountainous terrain but also meet the simultaneous arrival requirement. At h, the dynamic threat appears. When the system predicts a collision at time 0.24 h, it immediately triggers the online replanning module before the collision occurs (Figure 10c). This replanning trigger is marked by a red star, which represents the predicted future location where a vehicle’s path would first violate the safety margin with the threat. It is important to note that although the threat appears spatially closer to UAV-2 at this instant, the spatiotemporal prediction correctly identifies the helicopter’s trajectory as the one with the earliest predicted conflict. The system invokes the RL-GWO algorithm, using the current positions of all three vehicles as new start points, to quickly generate a new set of cooperative paths. Observing Figure 10d and Table 8, it is evident that the replanned paths successfully avoid the dynamic threat, ensuring flight safety, while the entire cluster still achieves simultaneous arrival with minimal time error.
This experiment fully validates the effectiveness and robustness of the proposed “global planning + dynamic replanning” dual-layer framework. This framework not only generates globally optimal cooperative paths but also endows the heterogeneous cluster with advanced autonomous capability to cope with environmental uncertainty. However, it is crucial to discuss the limitations of this real-time capability, particularly concerning scalability.
The primary challenge is computational complexity. While the replanning time was minimal in the three-UAV test, the computation time is expected to grow non-linearly with the number of vehicles. For very large-scale swarms (e.g., dozens of UAVs), this could become a significant constraint on the system’s ability to guarantee a timely response to sudden threats.
5. Conclusions
This paper conducted in-depth research on the challenging path planning problem for heterogeneous clusters composed of helicopters and fixed-wing UAVs executing highly coordinated missions in complex dynamic environments. The main work and contributions are summarized as follows:
- (1)
- A Novel RL-GWO Hybrid Intelligent Optimization Algorithm: Addressing the tendency of standard metaheuristics to converge to local optima when solving complex multi-objective problems, multiple improved Grey Wolf Optimization (GWO) strategies with distinct search characteristics were designed. A reinforcement learning (RL) framework was innovatively introduced to dynamically and adaptively select among these strategies. This method intelligently balances global exploration and local exploitation based on optimization progress, significantly enhancing solution quality and efficiency.
- (2)
- A Complete Dual-Layer Dynamic Planning Framework: This framework combines “offline global planning” with “online dynamic replanning.” The global planning stage utilizes RL-GWO for thorough optimization to generate an initial optimal path satisfying high-precision time coordination. The online replanning stage enables rapid response to sudden dynamic threats, maximally preserving cluster coordination while ensuring safety.
- (3)
- Systematic Validation via Simulation Experiments: Experimental results demonstrate that the proposed RL-GWO algorithm exhibits good convergence and robustness. It achieves time synchronization accuracy at the second level while satisfying multiple complex constraints like terrain avoidance and inter-vehicle safety separation, and ensures path smoothness and economy. In dynamic scenarios, the constructed dual-layer framework enables fast and effective online replanning, proving the method’s practical value in handling environmental uncertainty.
In addition to the extensive simulation results presented, the practical feasibility of the proposed cooperative framework has been preliminarily validated. Initial hardware-in-the-loop simulations and functional field tests were conducted using an AC332 helicopter platform and ASN-209 fixed-wing UAVs (Xi’an ASN Technology Group, Xi’an, China). While not as exhaustive as the simulations, these tests successfully demonstrated the core functionalities of the RL-GWO planner in generating and executing coordinated trajectories for heterogeneous vehicles, confirming the significant practical potential of our proposed method.
Although the proposed method achieves promising results, there remains room for extension. Future work will focus on the following:
- (1)
- Introducing more refined vehicle dynamic models;
- (2)
- Investigating the impact of communication delays and uncertainties on cooperative planning;
- (3)
- Further validating its feasibility in real-world systems.
Author Contributions
Conceptualization, W.J. and L.L.; methodology, W.J. and W.S.; software, L.L. and T.S.; validation, L.L. and T.S.; formal analysis, T.S.; investigation, L.L.; resources, W.J. and W.S.; data curation, R.D. and W.S.; writing—original draft preparation, W.J.; writing—review and editing, L.L., R.D. and W.S.; visualization, W.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 62173330, No. 62371375); the Shaanxi Key R&D Plan Key Industry Innovation Chain Project (No. 2022ZDLGY03-01); the China College Innovation Fund of Production, Education and Research (No. 2021ZYAO8004); and the Xi’an Science and Technology Plan Project (No. 2022JH-RGZN-0039).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors upon request.
DURC Statement
Current research is limited to the academic field of cooperative trajectory planning for unmanned aerial vehicles, which is beneficial for enhancing autonomous coordination and operational efficiency in complex environments and does not pose a threat to public health or national security. The authors acknowledge the dual-use potential of the research involving multi-agent mission planning and control and confirm that all necessary precautions have been taken to prevent potential misuse. As an ethical responsibility, the authors strictly adhere to relevant national and international laws about DURC. The authors advocate for responsible deployment, ethical considerations, regulatory compliance, and transparent reporting to mitigate misuse risks and foster beneficial outcomes.
Conflicts of Interest
Author Wei Jia was employed by the company Xi’an ASN Technology Group Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Yu, X.; Jiang, N.; Wang, X.; Li, M. A Hybrid Algorithm Based on Grey Wolf Optimizer and Differential Evolution for UAV Path Planning. Expert Syst. Appl. 2022, 215, 119327. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Jia, W.; He, R.F.; Sun, W. High-Precision localization tracking and motion state estimation of ground-based moving target utilizing unmanned aerial vehicle high-altitude reconnaissance. Remote Sens. 2025, 17, 735. [Google Scholar] [CrossRef]
- Skorobogatov, G.; Barrado, C.; Salamí, E. Multiple UAV systems: A survey. Unmanned Syst. 2020, 8, 149–169. [Google Scholar] [CrossRef]
- Han, Z.; Feng, X.; Lv, Z.; Yang, L. An Improved Environment Modeling Method for UAV Path Planning. Inf. Control 2018, 47, 371–378. (In Chinese) [Google Scholar]
- Zhang, H.; Li, W.; Zheng, J.; Liu, H.; Zhang, P.; Gao, P.; Gan, X. Manned/Unmanned Aerial Vehicle Cooperative Operations: Concepts, Technologies and Challenges. Acta Aeronaut. Astronaut. Sin. 2024, 45, 029653. (In Chinese) [Google Scholar]
- Zhen, Z.Y.; Xing, D.J.; Gao, C. Cooperative search-attack mission planning for multi-UAV based on intelligent self-organized algorithm. Aerosp. Sci. Technol. 2018, 76, 402–411. [Google Scholar] [CrossRef]
- Erdelj, M.; Natalizio, E.; Chowdhury, K.R.; Akyildiz, I.F. Help from the sky: Leveraging UAVs for disaster management. IEEE Pervasive Comput. 2017, 16, 24–32. [Google Scholar] [CrossRef]
- Xu, L.; Cao, X.B.; Du, W.B.; Li, Y.M. Cooperative path planning optimization for multiple UAVs with communication constraints. Knowl.-Based Syst. 2023, 110164, 260. [Google Scholar] [CrossRef]
- Ayawli, B.; Mei, X.; Shen, M.; Appiah, A.Y.; Kyeremeh, F. Mobile Robot Path Planning in Dynamic Environment Using Voronoi Diagram and Computation Geometry Technique. IEEE Access 2019, 7, 86026–86040. [Google Scholar] [CrossRef]
- Zhan, W.; Wang, W.; Chen, N.; Wang, C. Efficient UAV Path Planning with Multiconstraints in a 3D Large Battlefield Environment. Math. Probl. Eng. 2014, 2014, 597092. [Google Scholar] [CrossRef]
- Qadir, Z.; Zafar, M.H.; Moosavi, S.K.R.; Le, K.N.; Mahmud, M.A.P. Autonomous UAV path-planning optimization using metaheuristic approach for predisaster assessment. IEEE Internet Things 2021, 9, 12505–12514. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, D.; Zhang, T.; Cui, Y.; Chen, L.; Liu, S. Novel Best Path Selection Approach Based on Hybrid Improved A* Algorithm and Reinforcement Learning. Appl. Intell. 2021, 51, 9015–9029. [Google Scholar] [CrossRef]
- Beak, J.; Han, S.I.; Han, Y. Energy-efficient UAV Routing for Wireless Sensor Networks. IEEE Trans. Veh. Technol. 2019, 69, 1741–1750. [Google Scholar] [CrossRef]
- Dewangan, R.K.; Shukla, A.; Godfrey, W.W. Three dimensional path planning using Grey wolf optimizer for UAVs. Appl. Intell. 2019, 49, 2201–2217. [Google Scholar] [CrossRef]
- Lu, L.; Dai, Y.; Ying, J.; Zhao, Y. UAV Path Planning Based on APSODE-MS Algorithm. Control Decis. 2022, 37, 1695–1704. (In Chinese) [Google Scholar]
- Lv, L.; Liu, H.; He, R.; Jia, W.; Sun, W. A novel HGW optimizer with enhanced differential perturbation for efficient 3D UAV path planning. Drones 2025, 9, 212. [Google Scholar] [CrossRef]
- Wang, F.; Wang, X.; Sun, S. A reinforcement learning level-based particle swarm optimization algorithm for large-scale optimization. Inf. Sci. 2022, 602, 298–312. [Google Scholar] [CrossRef]
- Meng, Q.; Chen, K.; Qu, Q. PPSwarm: Multi-UAV Path Planning Based on Hybrid PSO in Complex Scenarios. Drones 2024, 8, 192. [Google Scholar] [CrossRef]
- Gupta, H.; Verma, O.P. A novel hybrid Coyote-Particle Swarm Optimization Algorithm for three-dimensional constrained trajectory planning of Unmanned Aerial Vehicle. Appl. Soft. Comput. 2023, 110776, 147. [Google Scholar] [CrossRef]
- Yu, Z.H.; Si, Z.J.; Li, X.B.; Wang, D.; Song, H.B. A novel hybrid particle swarm optimization algorithm for path planning of UAVs. IEEE Internet Things 2022, 9, 22547–22558. [Google Scholar] [CrossRef]
- Yu, X.; Luo, W. Reinforcement Learning-based Multi-strategy Cuckoo Search Algorithm for 3D UAV Path Planning. Expert Syst. Appl. 2022, 223, 119910. [Google Scholar]
- Du, Y.; Peng, Y.; Shao, S.; Liu, B. Multi-UAV Cooperative Path Planning Based on Improved Particle Swarm Optimization. Sci. Technol. Eng. 2020, 20, 13258–13264. (In Chinese) [Google Scholar]
- Pan, Z.; Zhang, C.; Xia, Y.; Xiong, H.; Shao, X. An Improved Artificial Potential Field Method for Path Planning and Formation Control of the Multi-UAV Systems. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 1129–1133. [Google Scholar]
- Niu, Y.; Yan, X.; Wang, Y.; Niu, Y. Three-dimensional Collaborative Path Planning for Multiple UCAVs Based on Improved Artificial Ecosystem Optimizer and Reinforcement Learning. Knowl.-Based Syst. 2022, 276, 110782. [Google Scholar]
- He, W.; Qi, X.; Liu, L. A Novel Hybrid Particle Swarm Optimization for Multi-UAV Cooperate Path Planning. Appl. Intell. 2021, 51, 7350–7364. [Google Scholar] [CrossRef]
- Jiang, W.; Lyu, Y.X.; Li, Y.F.; Guo, Y.C.; Zhang, W.G. UAV path planning and collision avoidance in 3D environments based on POMPD and improved grey wolf optimizer. Aerosp. Sci. Technol. 2022, 107314, 121. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).