Abstract
Target assignment for UAV swarms represents a pivotal and formidable endeavor, characterized by intricate combinatorial optimization and complex constraints. This study introduces an innovative and sophisticated constraint-handling method that adeptly tackles the inherent challenges of this problem. By meticulously partitioning the intricate constraints into distinct soft constraints and hard constraints, we then employ an adaptive penalty function to gracefully manage the former, while leveraging a dedicated repair heuristic to effectively address the latter. This strategy effectively surmounts the daunting hurdle of managing a substantial number of infeasible individuals that resist conventional repair techniques. Through a comprehensive series of comparative experiments, we meticulously evaluate the validity and efficacy of our proposed method, juxtaposing it against conventional penalty-based and repair-based approaches. The results unequivocally underscore the superior performance of our approach, yielding extraordinary allocation outcomes by deftly managing both soft and hard constraints. Furthermore, the versatility and applicability of our methodology transcend the confines of the target assignment problem, offering promising avenues for resolving allocation problems in diverse domains such as transportation systems, distributed computing, and construction management.
1. Introduction
As the real-world battlefield becomes more complex and defense systems are further enhanced, the cooperative operations of UAV swarms will emerge as a crucial combat paradigm in the future. Compared to an individual UAV, UAV swarms are capable of executing more intricate combat missions, such as multi-target engagements and multi-task coordination [1]. It is acknowledged that the operational effectiveness of collaborative modes surpasses traditional individual operations by a significant margin [2,3]. However, the success of such operations relies on effective mission-planning methods. One key problem in mission planning is target assignment (TA), on which this paper is focused.
As a critical component of mission planning, TA involves the allocation of appropriate UAVs to each identified enemy target for engagement [4]. During this process, an allocation algorithm should undertake a comprehensive analysis of battlefield information in order to ensure operational efficacy [5]. For each UAV and target, it is typically necessary to consider the level of danger along the trajectory and the range of the trajectory. Additionally, it should take into account the potential gains that can be achieved by executing the mission. In theory, all of these factors should be optimized during the process of TA. In addition, to ensure the rationality of the allocation results, the decision variables in TA should satisfy specific constraints. In summary, it can be concluded that the target assignment problem of UAV swarms is essentially a combinatorial optimization problem (COP) with binary decision variables.
From the perspective of optimization, the TA problem in this paper is similar to the well-known knapsack problem, which has been proven to be an NP-complete COP. In the literature, several exact and heuristic methods for binary COPs have been proposed. Initially, exact methods, such as linear programming, branch and bound, and dynamic programming, were applied to address binary COPs. However, although they could achieve exact optimal solutions in small-scale situations, they become impractical for large-scale instances due to an exponentially increasing computational time. On the other hand, several heuristic algorithms, which are viewed as advanced optimization methodologies for solving large-scale optimization problems with various complex situations, have been introduced in the literature. Evolutionary computation-based algorithms are the most popular examples of heuristic techniques, several versions of which exist for solving binary COPs, such as the genetic algorithm (GA), differential evolution (DE), particle swarm intelligence (PSO) [6,7].
Among these heuristic algorithms, the GA has a natural advantage in handling discrete optimization problems due to its unique encoding method [8,9]. However, it is well known that pure GAs do not perform well in difficult problems with complex combinational spaces or a high number of constraints. Constrained problems have traditionally been challenging problems for GAs [10,11,12]. Thus, the management of constraints is a key point for obtaining good-quality solutions to these problems. In the literature, several constraint-handling techniques have been developed for Gas: penalty terms in the objective function, special representations and operators, separation of objectives and constraints, and repair heuristics [13,14]. The rationale of repair techniques is to reduce the search space to feasible solutions so that no special operators or modifications of the fitness function need to be considered. It has been reported that the hybridization of GAs with repair heuristics obtains better results than other constraint-handling techniques [15,16,17]. In light of this, a GA with a repair mechanism dedicated to target assignment in UAV swarms may be an applicable solution.
Repairing infeasible candidates requires a repair procedure that modifies a given chromosome such that it will not violate constraints. This technique is thus problem-dependent. For example, ref. [18] proposes a specific repair method for evolutionary approaches in order to address the terminal-assignment problem in communication networks. After crossover, some terminals may be either present in duplicate or completely missing, and hence, cause infeasible individuals. Stochastic repair is then used to make these individuals feasible by deleting duplicated terminals or adding missing terminals. However, constraints in the optimization problem of target assignment are more complex since both UAVs and targets need to meet certain requirements. Specifically, the number of targets assigned to each UAV should not exceed one, and each target should be assigned to at least one UAV. The difficulty of repairing infeasible candidates under two (or more) types of constraints is much greater than that under only one type of constraint. Assuming an individual violates only one constraint, the repair method should not solely focus on that specific constraint. Instead, it should consider all constraints simultaneously, since repairing based solely on one constraint may lead to a result that violates other constraints. Meanwhile, as the number of constraints increases, the occurrence of situations where repair becomes infeasible also increases. In such cases, modifying an individual according to partial constraints will result in the violation of other constraints. Furthermore, with an increasing number of constraints, the sparsity of feasible solutions and the complexity of the feasible region will make the search more challenging.
For GAs with repair techniques, a feasibility check should be conducted on all individuals in the population before the operations of repair. Infeasible individuals will be identified and repaired before the evolutionary operations. However, due to the complexity of constraints in target assignment of UAV swarms and the blind nature of genetic operators (crossover and mutation) in GAs, many individuals that cannot be repaired will be generated in each evolution. How to handle these unrepaired infeasible individuals poses a new challenge. From our point of view, a simple approach is to replace them with certain feasible candidates. One possible option is to use the best feasible individual from the current population. However, if the number of unrepaired individuals is large, such a method will force the search to converge on that best individual, which may be a low-quality solution. Another possible option is to use a random feasible individual sampled from the current population. Although this method can alleviate the problem of premature convergence, excessive randomness will slow the convergence when the number of unrepaired individuals is large. In summary, we can conclude that designing a single repair heuristic to handle constraints in the target assignment of UAV swarms is extremely difficult.
To address the challenges posed by complex constraints, this paper proposes a GA with hybrid constraint-handling techniques. Specifically, we regard one type of constraint as soft constraints and put them into the fitness function as a penalty term. The significance of such a transformation is threefold. Firstly, as the number of constraints decreases, the number of infeasible individuals is expected to decrease as well. Consequently, the computational effort required for repair will also decrease. Secondly, since there is only one type of constraint remaining, there will be no occurrence of unrepaired individuals during the evolutionary process. This will effectively mitigate issues such as premature and slow convergence caused by unrepaired individuals. Finally, the difficulty of repair will be significantly reduced since we only need to consider the satisfaction of one type of constraint. In the literature regarding constraint handling, penalty-based methods are categorized into the indirect group, and repair heuristic-based methods are categorized into the direct group. Therefore, the proposed hybrid constraint-handling method, which combines one indirect method and one direct method, is expected to inherit the advantages of both methods. To this end, two key issues should be fully considered. One is how to devise the penalty term; the other is how to repair infeasible individuals. To address the first problem, we use an adaptive penalty function where information gathered from the search process can be used to control the amount of penalty added to infeasible individuals. Adaptive penalty functions are easy to implement, and they do not require users to define parameters. With respect to the second problem, we propose a repair method called semi-greedy repair (SGR). By incorporating the information of soft constraints into the greedy algorithm, SGR is expected to yield more feasible individuals for subsequent evolution, which can accelerate the convergence of the GA.
The remainder of this paper is organized as follows. Section 2 presents some related works on constraint-handling methods for GAs. Section 3 presents the methodology, including presentation of the problem of target assignment of UAV swarms, the framework of a hybrid GA with a repair technique, and the details of the proposed method. The results and comparative discussions are presented in Section 4. Section 5 concludes the paper.
2. Related Works
As previously analyzed, target assignment of UAV swarms is a constrained combinatorial optimization problem (COP) with binary decision variables. Considering the superiority of the GA in solving COPs, this paper focuses on utilizing the GA to address the target-assignment problem. Effectively handling constraints becomes the key to achieving optimal solutions with a GA. In the literature, constraint-handling techniques developed for GAs can be categorized into four groups: penalty functions, special representations and operators, repair heuristics, and multi-objective optimization [19]. Here we pay more attention to methods based on penalty functions and repair heuristics since both types of method are related to our proposed method.
Using penalty functions to transform a constrained COP into an unconstrained one is the most common approach to handle constraints used by a GA. As analyzed in [20], the primary objective of a penalty method is to strike a proper balance between the objective function and the penalty function, aiming to guide the search towards the optimal solutions within the feasible space. When the penalty is excessively high and the optimal solution resides at the boundary of the feasible region, the GA will rapidly converge inside the feasible region, making it difficult to explore towards the boundary of the infeasible region. Conversely, when the penalty is too low, a significant portion of the search process will be dedicated to exploring the infeasible region since the penalty becomes negligible in comparison to the objective function.
Based on the calculation of penalty factors, existing methods based on penalty functions can be broadly categorized into three types, namely static penalty, dynamic penalty, and adaptive penalty [21]. Static methods have penalty factors that are independent of the current generation number, resulting in constant values that remain unchanged throughout the entire evolutionary process. The interaction between an infeasible individual and the feasible region of the search space is recognized as a crucial factor in penalizing the infeasible individual. The most common measure of penalty is the amount of constraint violation, which can be used for both discrete and continuous constrained optimization. Such a measure has been used in several methods to develop diverse penalty functions [22]. Unlike static penalties, dynamic methods utilize the current generation number to dynamically determine and adjust the penalty factors. The fundamental idea of dynamic methods is to enforce an increase in penalty factors as the number of generations increases during the evolution process [23]. The underlying principle is to allow some infeasible solutions to participate in the early stages of evolution, where solution diversity is more crucial. As the population approaches convergence in later stages, the feasibility of solutions becomes more important. Some researchers have advocated for the effectiveness of dynamic penalties compared to static penalties [24]. Nevertheless, deriving suitable dynamic penalty functions in practical scenarios is still challenging.
Despite the progress achieved by dynamic methods, the challenges associated with static methods still exist. If an inappropriate penalty factor is chosen, the evolutionary algorithm may converge on suboptimal feasible solutions (if the penalty is too high) or infeasible solutions (if the penalty is too low). In this situation, the notion of adaptive penalty is proposed and used to alleviate the problem of determining penalty factors. In adaptive methods, the penalty factors are usually determined by the information derived from the search process. For example, ref. [25] uses the performance of the best individual in the last k generations to determine the magnitude of the penalty. If all the best individuals in the last k generations are feasible (infeasible), the penalty for infeasible individuals will become decreased (increased) in the current generation. Otherwise, the penalty does not change. Similarly, the fitness of the best individual so far has also been used by other research but in different applications [26,27].
The representation of potential solutions to the problem and the evolutionary operators that alter the composition of offspring are the basic components to implement a GA. It is thus straightforward to propose the idea of developing special representations and genetic operators to handle constraints for a GA [12]. The motivation may be that traditional binary representation is not appropriate to tackle a certain problem. Then, the design of new genetic operators becomes natural since they must be synchronized with the new representation. In this type of constraint-handling method, the purpose of changing the representation is to simplify the shape of the search space, while special operators are typically employed to ensure the feasibility throughout the evolutionary process. Undoubtedly, the utilization of specific representations and operators is highly beneficial for the intended application they are designed for. However, their applicability and effectiveness in other (even similar) problems are not necessarily straightforward or guaranteed. Furthermore, generating a feasible initial population can sometimes be a challenge for this type of method.
Repairing infeasible candidates such that they will not violate any constraint before the calculation of fitness is also a straightforward strategy. The repair heuristics can be categorized as Lamarckian or Baldwinian approaches based on whether the repaired individuals replace the original ones [28]. If the infeasible candidates are substituted by their repaired ones, we obtain a Lamarckian algorithm. Conversely, in Baldwinian algorithms, the population remains unchanged after the repair heuristic is applied, and only the fitness function is modified. The question of which type of repair method performs better remains an open issue, as the answer largely depends on the specific application under consideration. However, regardless of the type of repair method used, there are currently no standard guidelines or heuristics available for the design of such methods. In general, utilizing the greedy strategy to construct repair methods is a simple and practical choice [29]. The rationale behind the greedy strategy is to make locally optimal choices at each step, aiming to achieve the best immediate outcome without considering the long-term consequences. While the greedy strategy may not always lead to the globally optimal solution, it is often efficient and straightforward to implement, making it a popular choice in many optimization problems. Hopfield networks can also be used as repair heuristics in COPs where binary encoding is used for the representation of potential solutions [18,19]. Hopfield networks are recurrent neural networks that can store and retrieve patterns, making them suitable for finding solutions that violate constraints. By utilizing the energy-based dynamics of Hopfield networks, the repair process can be formulated as an optimization problem. The network’s dynamics strive to converge to a stable state that represents a feasible solution by minimizing the energy function associated with the constraints. This approach allows the Hopfield network to iteratively modify the solution until it satisfies the imposed constraints. However, due to the sequential- updating rule of neurons, Hopfield networks usually take time to converge on a feasible solution. In large-scale applications, the efficiency of such repair heuristics may be challenging.
When regarding constraints as one or more objectives, then the original constrained optimization problem with a single objective will be transformed into an unconstrained multi-objective optimization problem [30]. In this way, any existing algorithm designed for multi-objective optimization may have potential for addressing the constrained optimization problem. Such a type of method seems to create a new direction for solving constrained optimization problems. In spite of this, several issues still need to be considered carefully. First, we should note that some solutions of multi-objective optimization problems may be infeasible since the primary objective of multi-objective optimization algorithms is to find a set of balanced optimal solutions among different objectives. Second, an extra procedure for determining the optimal feasible solution is necessary since the solution set from multi-objective optimization can be large and complex. Lastly, the computational cost of multi-objective optimization algorithms can be higher compared to those of single-objective optimization methods. The need to maintain and update the Pareto front and handle the constraints increases the computational burden.
3. Methodology
3.1. Problem Representation
This paper focuses on the scenario of offline target assignment, where all information about the battlefield is assumed to be known. Assume that the situation awareness module has detected M targets and K threat sources. Let the number of available UAVs be N. This paper assumes that the number of UAVs (N) is greater than the number of targets (M) to ensure that each target can be assigned to at least one UAV. Given all this information as inputs, it is expected that the TA algorithm will derive an assignment result that could achieve the best operational effectiveness. It is straightforward to use a certain number of binary decision variables to represent the assignment result. If the jth target is assigned to the ith UAV, the value of binary decision is set to 1; otherwise, it equals 0. In our assumed scenario, the assignment result can be represented by a matrix X, which is referred to as a decision matrix.
In this paper, we use three ingredients to represent the operational effectiveness of UAV swarms. The first one is the total trajectory length of all UAVs, which should be as small as possible. The second one is the total threat exposure of all trajectories, which should also be as small as possible. The last one is the total profit of all UAVs, which should be as large as possible. In addition, to ensure the rationality of the allocation results, the decision variables need to satisfy certain constraints. The first one is that each UAV can only be assigned a maximum of one target. This will yield N constraints for N UAVs. Second, due to the omission of a damage assessment in this paper and the assumption that all UAVs could complete their assigned missions, it is required that each target be assigned to at least one UAV. This will produce M constraints for M targets. In summary, target assignment of UAV swarms is essentially a constrained multi-objective optimization problem, which can be formulated as follows:
where denote the trajectory length, threat exposure, and UAV profit, respectively. Note that as we assume all UAVs could complete their mission, can then be simply replaced by the target value.
Note that the calculation of both trajectory length and threat exposure depends on the specific trajectory from the ith UAV to the jth target. Therefore, prior to performing target assignment, it is essential to acquire the trajectory from each UAV to each target. In this paper, we derive all trajectories through a path-planning algorithm called A* [31]. More information about A* will not be introduced here. One interesting result of using A* is that the objective function in (2) can be omitted since all trajectories found by A* can avoid all threats. Actually, once we obtain the assignment result, the corresponding trajectories will be available simultaneously.
In practical applications, multi-objective optimization problems are often transformed into single-objective optimization problems. Then, the optimization problem of interest can be formulated as follows:
where denotes the target value, and indicates the parameter controlling the balance between trajectory length and UAV profit.
3.2. Framework of the Repair-Based GA
The primary goal of this paper is to use a repair-based GA to address the constrained binary COP extracted from the target assignment of UAV swarms. We show the framework of a repair-based GA in Figure 1. At each iteration, we will first check the feasibility of all individuals in the population so that infeasible ones can be identified. In this paper, the repair algorithm uses a Lamarckian approach, implying that infeasible individuals are substituted by their repaired ones. The repaired feasible population then undergoes the selection, crossover, and mutation in the GA to obtain the offspring population, along with the feasible ones. Because the crossover and mutation operators are blind to the constraints, it is inevitable that infeasible individuals will be produced during the evolution. As a result, it is necessary to execute a feasibility check for each population, unless the evolution has converged.
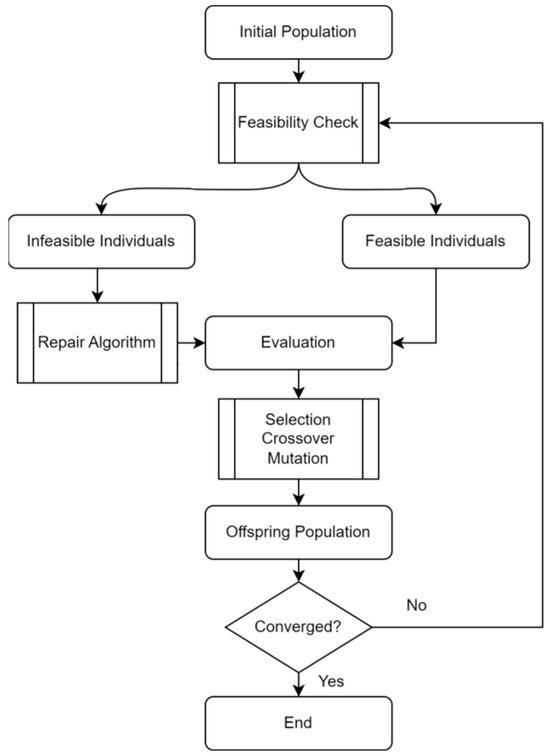
Figure 1.
General framework of repair-based GA.
3.3. Dedicated Repaired GA
In this section, we will present the proposed GA dedicated to target assignment of UAV swarms. The problem representation will first be modified by transforming one type of constraint into the objective function, so that the problem triggered by unrepaired individuals can be conquered. Under this premise, we will present the dedicated penalty function and repair heuristic.
3.3.1. Modification of Problem Representation
Problem representation introduced in Section 3.1 shows that our optimization problem has two groups of constraints. In general, a GA is likely to yield more infeasible individuals with an increase in the number of constraints. The repaired GA presented in Section 3.2 may be an effective approach to handling constraints, as long as we can design a repair heuristic that can easily transform infeasible individuals into feasible ones. According to (4), the violation of this set of constraints implies that more than one target has been assigned to the same UAV. It is natural to repair such individuals by removing the redundant assignments. According to (5), the violation of this set of constraints implies that certain targets have been omitted. The repair of such individuals is equivalent to searching for available UAVs. We refer to the above two repair methods as basic repair heuristics. Based on this analysis, it seems that we have found a simple repair procedure with basic repair heuristics. Even if there are individuals who violate both sets of constraints simultaneously, it is still possible to repair them in a specific order.
In practice, however, the combination of these two sets of constraints presents significant challenges for the repair algorithm. The primary difficulty is rooted in the presence of unrepaired individuals, which denote infeasible individuals that cannot be repaired by basic repair heuristics. Without loss of generality, assume that a particular infeasible individual violates the constraints in (4). After applying the basic repair heuristic, the result is that this individual satisfies the constraints in (4), but it violates the constraints in (5). Some examples of unrepaired individuals can be as follows:
The individual shown by (7) implies that the first target has been omitted. So, the basic repair heuristic needs to search for one or more idle UAVs. However, each UAV has been assigned one target in this case, resulting in an unrepaired infeasible individual. At the same time, the individual shown by (8) implies that the first UAV has been assigned two targets (first and second). So, the basic repair heuristic needs to remove one or both assignments. However, both targets have only been assigned to the first UAV, resulting in an unrepaired infeasible individual. Note that the number of unrepaired individuals will increase with an increase in combat scale. Unfortunately, the difficulty of repairs will indeed increase as the number of unrepaired individuals increases.
Clearly, two basic repair heuristics are unable to process unrepaired individuals. To ensure the effectiveness of the proposed hybrid constraint-handling method, there are three key issues that need to be addressed: determining the transformed constraints, designing the penalty function, and designing the repair heuristic. Here we refer to the transformed constraints as soft constraints since they may be violated if the penalty is too small. By observing the constraints in (4) and (5), it can be deduced that violating the constraint in (4) is not permissible because it is impossible for one UAV to visit two targets in one mission. Conversely, the violation of the constraints in (5) indicates that a few targets are missed. Therefore, it is more reasonable to regard all the constraints in (5) as soft constraints. Then, the formulation of the optimization problem of interest can be formulated as follows:
where X denotes the decision matrix and is the value of the objective function shown in (6). indicates the penalty of the jth constraint , and implies the penalty factor. The determination of the penalty factor, namely the second issue, will be presented in the subsequent subsection, followed by the approach to the third issue.
3.3.2. Adaptive Penalty Function
In Section 2, we discussed the properties of the static penalty, the dynamic penalty, and the adaptive penalty. Compared to the former two methods, the adaptive penalty has clear advantages. Therefore, in response to the second question raised earlier, the decision was made to utilize the adaptive penalty in this paper.
As acknowledged in [32], the fundamental goal of a penalty function is to find an appropriate trade-off between the objective function and the constraint violations when calculating values of the objective function. For any evolution, the population will inevitably be in one of the following three states: ① only containing infeasible individuals; ② containing both feasible and infeasible individuals; ③ only containing feasible individuals. We must note that the notion of feasibility here is specific to soft constraints rather than all constraints. In the first state, it is more significant to guide individuals towards the feasible region. Therefore, we can disregard the objective function and only consider the constraint violations. In the third state, as all individuals are feasible, it is more significant to find feasible individuals with better objective values. Hence, individual comparisons rely solely on their objective function values.
In contrast to the first and third states, individuals in the second state are a combination of feasible and infeasible ones. In this paper, the information concerning the last population is used. Specifically, if the proportion of feasible individuals in the last population was relatively high, more outstanding infeasible individuals are allowed to be selected in the current population. On the contrary, if the proportion of infeasible individuals in the last population was relatively high, it is advisable to reduce their probability of being selected. In order to reflect such a heuristic, the objective function of infeasible individuals is designed as follows:
where indicates the fraction of feasible individuals in the last population. and are the minimum and maximum objective values, respectively, of feasible individuals in the current population. We can observe that when the value of is large, the objective values of the infeasible individuals in the current population tend to be low, leading to a high probability of their selection. However, when the value of is too large, the objective values of the infeasible individuals may surpass those of most feasible individuals, resulting in an excessive selection of infeasible individuals. This situation is not conducive to the evolutionary process. Therefore, we modify (8) as follows:
Finally, it is necessary to normalize both the terms of the objective function and the terms of the constraint violations prior to adding them together. Specifically, we scale the values of the objective function into by
where and denote the minimum and maximum objective values, respectively, of all individuals in the current population. The values of the constraint violations are scaled into by
where denotes the total constraint violations. denotes the maximum constraint violations. Note that we define according to (5) as follows:
It can be easily found that the penalty for any constraint violation equals 1. Therefore, the total penalty of any infeasible individual equals the number of constraint violations. The final fitness value of one individual is derived by adding the objective function value and the constraint violation value.
3.3.3. Semi-Greedy Repair Heuristic
After transforming the constraints in (5) into the objective function, the repair of infeasible individuals violating the remaining constraints becomes much easier. Note that the feasibility here is completely different from that in Section 3.3.2. Specifically, infeasible individuals here violate the hard constraints shown in (4), and infeasible individuals in Section 3.3.2 violate the soft constraints shown in (5). The violation of constraints in (4) implies that certain UAVs have been assigned more than one target. By checking if the sum of all elements from each row in the decision matrix exceeds 1, the feasibility of an individual can be determined. For rows with a sum greater than 1, we can first identify all elements in those rows where the decision variables are equal to 1. Then, by examining the cost matrix, we can utilize a greedy approach to sequentially repair the infeasible individuals on a per-row basis. We refer to such a repair method as greedy repair, which can be illustrated by the pseudocode in Algorithm 1.
| Algorithm 1. Greedy Repair |
Inputs: cost matrix C, decision matrix D
|
| Output: repaired decision matrix D_new. |
As discussed in Section 3.2, once the infeasible individuals have been repaired, they can be included as part of the parent population and participate in the evolution of the GA. In Section 3.3.2, we introduced three states that the population may encounter. From a convergence perspective, these three states exhibit a progressive relationship. In other words, the more feasible individuals there are in the population, the more favorable it is for convergence. However, the greedy repair method, which is blind to the soft constraints in (5), may produce repaired individuals that are still infeasible with respect to those soft constraints. This can indeed hinder the convergence of a GA. In order to alleviate this problem of greedy repair, we propose a modified heuristic called semi-greedy repair. In this repair method, the satisfaction of soft constraints is taken into account by the greedy repair. If the removal of a certain assignment increases the number of violations of soft constraints, that removal will be canceled, regardless of its cost. However, in the event of an unrepairable situation similar to (8), the semi-greedy repair will have no choice but to prioritize the hard constraints, even if it means violating the soft constraints. We use pseudocode in Algorithm 2 to illustrate the proposed semi-greedy repair.
| Algorithm 2. Semi-greedy Repair |
Inputs: cost matrix C, decision matrix D
|
| Output: repaired decision matrix D_repair. |
Now, we employ an example to illustrate the difference between greedy repair and semi-greedy repair. Consider the following decision matrix of one infeasible individual:
Suppose that the cost values of three assignments in the first row to be 0.5, 1, and 2, respectively. For this infeasible individual, greedy repair will delete the second and third assignments due to their high-cost values. This will result in the violation of soft constraints as the third target is omitted. Conversely, the semi-greedy repair will delete the first and second assignments so as to ensure satisfaction of the soft constraints.
Then, consider the following decision matrix of another assumed-infeasible individual:
Let the cost values of three assignments in the first row still be 0.5, 1, and 2. For this individual, as the removal of any two assignments will not result in the violation of soft constraints, both greedy repair and semi-greedy repair will delete the second and third assignments.
Then, consider the third case, where the decision matrix is
The cost values of three assignments in the first row remain unchanged. For this individual, greedy repair will still delete the second and third assignments only, due to their high-cost values, while semi-greedy repair will delete the first and third assignments. Deleting the first assignment instead of the second one demonstrates the importance that semi-greedy repair places on the hard constraints.
4. Experimental Results and Analysis
4.1. Comparative Experiments
In order to validate the performance of our method, we tackle a set of target assignment problems of UAV swarms of varying sizes. The main characteristics of the experimental problems are reported in Table 1, which includes three small-size scenarios (S.1, S.2, and S.3), three middle-size scenarios (M.1, M.2, and M.3), and three large-size scenarios (L.1, L.2, and L.3). The network size is indicated by , where N and M denote the number of UAVs and the number of targets, respectively. In each scenario, we configured 10 threat sources, with their positions and threat radii generated randomly. In general, as the problem size increases, the size of the search space, the number of constraints (denoted by C), and the number of decision variables also tend to increase, resulting in an increase in the difficulty of the optimization problem. In addition, for constrained optimization problems, the ratio between the size of the feasible search space and that of the entire search space can also be considered as an indicator of the difficulty of the optimization problem. In our experiment, such a ratio is approximated by , where is the number of randomly generated individuals, and is the number of feasible individuals out of these random ones. In this experiment, we set to be 10,000. Table 1, displaying a feasibility ratio of 0 across all instances, implies the inherent difficulty in solving the optimization problem under investigation.

Table 1.
Summary of experimental problems. O, C, R denote the number of threat sources, constraints, and the ratio between the size of the feasible search space and that of the entire search space, respectively.
In each experimental instance, a specified number of UAVs and targets are randomly generated in the virtual battlefield represented by a grid map. Additionally, a certain number of threat sources (including their positions and threat radii) are also randomly generated. Algorithm A* is employed to yield the trajectory from each UAV to each target, so that we can obtain the length of each trajectory. To encourage a more balanced assignment and prevent certain targets from being favored by a majority of UAVs, the setting of target values follows the following principle: the value of each target is directly proportional to its average distance to all UAVs. Values of both trajectory length and target value are normalized by the corresponding maximum and minimum. Unless otherwise specified, the weight in (6) is assumed to be 0.5 by default.
In this experiment, we will refer to the proposed method as GA_Hybrid, since both a penalty function and a repair heuristic are used to handle the constraints. We compare GA_hybrid with the following four competitors:
- ➢
- GA_SP: GA where a static penalty function is used to handle constraints.
- ➢
- GA_AP: GA where an adaptive penalty function is used to handle constraints.
- ➢
- GA_Re I: GA where greedy repair is used to handle constraints; when encountering an unrepairable individual, replacing it with the best feasible individual.
- ➢
- GA_Re II: GA where greedy repair is used to handle constraints; when encountering an unrepairable individual, replacing it with a random feasible individual.
To ensure fairness, the parameter settings of GAs in all compared methods remain identical. Specifically, we set the following: population size , roulette wheel selection, one-point crossover operator with a probability , probability of mutation , and the maximum number of generations to 500. Every algorithm is run 30 times, and the best results are recorded. Note that the impact of these parameters will not be further investigated in this paper.
Table 2 shows the results of all of the compared methods. A notable result is that the proposed GA_hybrid achieved the best result in all simulated instances. The GA with a static penalty could not obtain feasible solutions on the four largest-size instances, whereas an adaptive penalty improved the results of GA_SP in the M.3 instance. Although two repair heuristics could obtain feasible solutions in all instances, the quality of their solutions was poor, especially that of GA_Re II.

Table 2.
Comparative results of all five PSO. Symbol NA implies that a feasible solution has not been achieved. The best results are presented in bold.
Hybrid vs. Pure penalty: By comparing GA_Hybrid with GA_SP and GA_AP, we find that the advantages of our method become increasingly prominent as the problem size increases. For three small-size instances, the results of these three methods are consistent. With an increase in the problem size, it becomes more difficult for GAs with penalty functions to find feasible solutions. However, we should note that the adaptive penalty may be an effective way of alleviating such a problem. The fundamental reason for the issue with penalty functions is an excessive number of constraints. In the proposed GA_Hybrid, we transform the constraints on targets into the objective function to play the role of soft constraints, which are handled by the penalty function. The remaining hard constraints (i.e., constraints on UAVs) are handled by the proposed repair heuristic. Such a combination can effectively address the aforementioned problem because the number of constraints assigned to the penalty function significantly decreases. Actually, the penalty function in either GA_SP or GA_AP needs to handle N + M constraints, whereas that in GA_Hybrid only needs to handle M constraints. It is noteworthy that the value of N is usually larger than M. Based on this comparison, it is apparent that employing solely a penalty function could be a viable option for instances with modest dimensions. However, its efficacy diminishes with an escalating number of constraints. In contrast, the proposed hybrid constraint-handling method, amalgamating the penalty function with the repair heuristics, is more inclined to unearth superlative feasible solutions of exceptional quality.
Hybrid vs. Pure repair: By observing the results of GA_Re I, GA_Re II, and GA_Hybrid, we find that the proposed hybrid constraint-handling method is more effective than that using solely a repair heuristic, especially in instances of larger sizes. For two small-size instances (S.1 and S.2), these three methods obtain the same solution. This outcome indicates that when the constraints are relatively simple, employing only the repair heuristic can yield satisfactory results. With the increasing complexity of constraints, there is a rising proliferation of unrepaired individuals, rendering it arduous to attain favorable outcomes, regardless of whether random or optimal feasible individuals are employed for replacement. However, the proposed hybrid method effectively avoids such occurrences. By separating the original optimization problem’s constraints into two sets, namely hard constraints and soft constraints, the repair heuristic only needs to handle the hard constraints. Compared to the original problem, this significantly reduces the complexity of repair as there is no need to consider the coupling relationship between the two sets of constraints. By comparing GA_Re I with GA_Re II, an intriguing finding emerges: replacing unrepaired individuals with random feasible individuals often leads to the discovery of superior solutions, as opposed to replacing them with the best individuals. The reason for this is that when a significant portion of the population consists of unrepaired individuals, replacing them with the best individuals often leads to getting trapped in local optima. Additionally, we have also observed that one advantage of using the repair heuristic to handle constraints is that it always manages to find feasible solutions, regardless of their quality. This attribute holds significant relevance and value in real-world applications.
Next, we use datasets S.1 and M.2 to demonstrate the convergence speed of the different methods. The results are shown in Figure 2, from which it can be observed that the algorithms exhibit different convergence speeds across scenarios of varying scales. Specifically, in small-scale scenarios, the convergence speed of repair-based methods is generally slower than that of penalty-based methods. As the scale increases, the convergence speed of repair-based methods changes significantly; the convergence speed of GA_Re 1 accelerates noticeably. This is because with the increase in scale, the proportion of unrepaired individuals rises, and replacing these individuals with the current optimal solution causes the algorithm to fall into a local optimum prematurely. In contrast, the convergence speed of GA_Re 2 slows down. The reason for this is that replacing unrepaired individuals with random individuals introduces excessive random factors, leading to a decrease in the convergence speed. Considering all methods collectively, our constraint-handling method maintains a relatively stable convergence speed across scenarios of different scales, demonstrating good robustness.
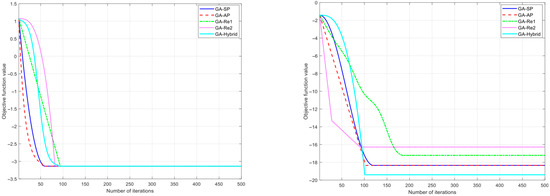
Figure 2.
Demonstration of convergence speed across scenarios of different scales (left for S.1 and right for M.2).
In terms of computational complexity, we must acknowledge that the pure penalty function method has a distinct advantage over the pure repair method and the proposed hybrid method. We show this comparison in Figure 3. In constraint-handling methods that utilize a repair heuristic, within each evolutionary step of the GA, the initial focus lies on repairing the infeasible individuals present in the current population, followed by the evolutionary operations. By comparing the proposed hybrid method with the pure repair method, it can be observed that our hybrid method requires less repair time. Due to the inherent blindness of the evolutionary operators towards the constraints, each generation of the population may contain infeasible individuals. However, our hybrid method focuses only on repairing the hard constraints, while the pure repair method addresses all constraints. As a result, the pure repair method needs to repair a significantly higher number of individuals compared to the hybrid method, leading to a longer repair time requirement.
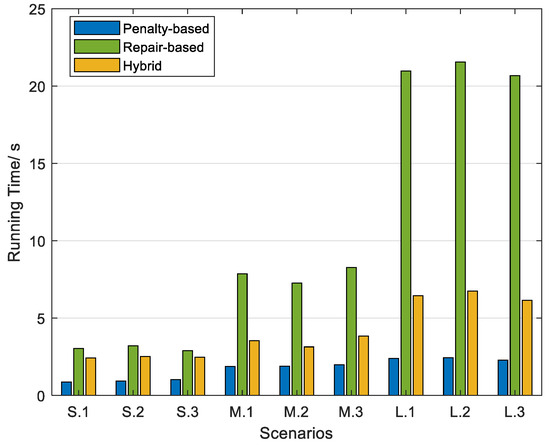
Figure 3.
Comparative results of running time in three instances.
In large-scale UAV swarm missions, the number of UAVs and targets increase significantly, leading to a rise in the constraints within the target assignment problem and posing substantial challenges to constraint handling. A pure inverse function-based method struggles to yield feasible solutions, primarily due to the extremely low proportion of feasible solutions in the solution space. While forcibly increasing the weight of constraints in the objective function can alleviate this issue, it severely compromises the optimality of the resulting solutions. On the other hand, a repair-based constraint handling method incurs a substantial increase in computational load, as the proportion of infeasible solutions grows; more infeasible solutions mean more resources are consumed to modify and validate the solutions until they meet all constraints. The hybrid method we proposed combines the advantages of penalty function and repair heuristics; it leverages the penalty mechanism to guide the algorithm toward feasible solution regions (avoiding the inefficiency of blind repair) and uses targeted repair to rectify critical infeasible solutions (preventing excessive penalty-induced loss of optimality). This enables a better balance between solution optimality and solving efficiency, endowing it with strong applicability in large-scale UAV swarm missions.
Finally, to verify the applicability of the proposed constraint-handling method, we combined it with the particle swarm optimization (PSO) algorithm and conducted verification using the aforementioned scenarios. The experimental results are shown in Table 3. It can be observed from the table that our method still outperforms its competitors under the PSO framework, which proves its effectiveness. In addition, through comparison with a GA series, it is found that under the premise of the same constraint-handling method, the assignment results obtained by the GA are generally better than those by the PSO. However, further comparison between GA and PSO is beyond the scope of this paper.

Table 3.
Comparative results of all five GAs. Symbol NA implies that a feasible solution has not been achieved. The best results are presented in bold.
4.2. Further Investigation
Repair and penalty are the two core ideas of our proposed hybrid method. With the aim of maximizing the efficacy of the hybrid approach, we have introduced two additional constituents, namely an adaptive penalty and semi-greedy repair. Despite the confirmation of our method’s efficacy through the aforementioned comparative experiments, we deem it imperative to conduct further investigation regarding the contributions of these two constituents. To this end, we have carefully devised three methods and meticulously conducted a comparative evaluation thereof. We refer to the first method as Hybrid I, which does not use the information from the last population to modify the objective values of infeasible individuals. The second method is referred to as Hybrid II, which uses the pure-greedy repair, rather than the proposed semi-greedy repair. The third method is referred to as Hybrid_None, which uses the pure-greedy repair and is non-adaptive. For ease of reference, we will refer to the proposed methods as Hybrid_All in this experiment. The comparative results in terms of the best solution are listed in Table 4.

Table 4.
Results of the investigation experiment in terms of the best solution among 30 trials. The best results are presented in bold.
The comparative results indicate that the performance of these four methods is highly similar in all instances. Only methods Hybrid II and Hybrid_None exhibit slightly inferior results in the three large-size instances. This observation suggests that the advantages of our method may be more pronounced and evident in large-scale problem scenarios. Furthermore, exclusively using the best solution from 10 trials might not provide a comprehensive means to effectively differentiate the superiority of these four methods. To address this, we have devised new problem instances and adopted new evaluation metrics. Table 4 shows the results on large-size instances in terms of the best solution. Table 5 shows the results in terms of the feasibility ratio, which implies the proportion of feasible solutions obtained in 30 experimental runs. Note that in this experiment, we maintain a constant size of 100 UAVs while augmenting the number of targets from 30 to 100.

Table 5.
Comparative results on large-size instances in terms of the best solution. The best results are presented in bold. N and M denote the number of UAVs and targets, respectively.
From Table 5, we can observe that in terms of the best solution, Hybrid_All outperforms all of the other methods in all seven large-scale instances. Furthermore, the results in Table 6 indicate that Hybrid_All consistently discovers feasible solutions in all 30 experimental runs, while none of the other methods are able to achieve this. These sets of experimental results unequivocally validate the significant merit of our proposed adaptive penalty function and semi-greedy repair heuristic in augmenting the performance of the hybrid method.

Table 6.
Comparative results on large-size instances in terms of feasibility ratio. N and M denote the number of UAVs and targets, respectively.
By observing the experimental results of Hybrid I, it becomes apparent that while this method exhibits a performance similar to Hybrid_All in terms of the best solution, it also has a relatively higher probability of generating infeasible solutions. The inadequacy of Hybrid I in searching for feasible solutions can be attributed to its penalty function lack of adaptive adjustment of the objective function for infeasible individuals, thereby failing to leverage historical evolutionary information. This drawback becomes magnified with an increase in the number of soft constraints, as the prevalence of infeasible individuals in the population rises proportionally. Without the real-time reduction in the objective function for infeasible individuals, they may predominate over the feasible ones. This issue leads to the failure of discovering excellent, feasible solutions. In the proposed Hybrid_All, when a substantial number of infeasible individuals is prevalent in the preceding generation, the objective function weights are dynamically adjusted in the current generation to promptly mitigate the abundance of infeasible solutions within the population.
By observing the experimental results of Hybrid II, it becomes evident that this method outperforms Hybrid I in searching for feasible solutions and is comparable to Hybrid_All. It is worth noting that in this particular experiment, we exclusively augmented the number of objectives, representing an increase in the quantity of soft constraints, while keeping the number of hard constraints constant. Consequently, in terms of the feasibility ratio, Hybrid II exhibits a performance level that is on par with Hybrid_All. However, according to the results in both Table 3 and Table 5, we can see that in terms of the best solution, Hybrid II is inferior to Hybrid I and Hybrid_All. This result suggests that as the number of hard constraints increases, the advantages of the proposed semi-greedy repair become more pronounced. The underlying reason lies in that as the number of hard constraints increases, the pure-greedy repair heuristic yields more infeasible solutions (with respect to the soft constraints). Although the adaptive penalty function endeavors to promptly regulate the proportion of feasible individuals, its influence on the pursuit of optimal solutions remains adverse.
5. Conclusions
This paper proposes a hybrid constraint-handling method, which, when combined with a genetic algorithm (GA), addresses the challenges posed by complex constraints in a UAV swarm target assignment. Through a series of simulation experiments, we verified the advantages of the proposed method over penalty-based and repair heuristic-based methods. Specifically, compared with pure penalty-based methods, our method consistently yields feasible solutions in large-scale scenarios. On the other hand, compared with pure repair-based methods, it can find better solutions while achieving a faster convergence rate. However, in large-scale scenarios, due to the excessively high proportion of infeasible solutions, our repair mechanism exhibits high computational complexity, which limits its applicability in online applications, namely, it is difficult to apply in scenarios with strong dynamic characteristics. In the future, we intend to research more efficient repair mechanisms to alleviate this issue.
Author Contributions
Conceptualization, T.L. and J.A.; methodology, T.L. and B.W.; software Z.S.; writing—review and editing, T.L. and B.W.; project administration, J.A.; funding acquisition, B.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been funded by the Aeronautica Science Foundation of China (grant: No 20230048054001).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Johnson, J. Artificial intelligence, drone swarming and escalation risks in future warfare. RUSI J. 2020, 165, 26–36. [Google Scholar] [CrossRef]
- Materak, W. The evolution of air threats in future conflicts. Saf. Def. 2023, 9, 24–30. [Google Scholar]
- Yang, Y.; Li, J.; Liu, C.; Yang, Y.; Li, J.; Wang, Z.; Wu, X.; Fu, L.; Xu, X. Automatic terminal guidance for small fixed-wing unmanned aerial vehicles. J. Field Robot. 2023, 40, 3–29. [Google Scholar] [CrossRef]
- Cui, J.; Liu, Y.; Nallanathan, A. Multi-Agent Reinforcement Learning-Based Resource Allocation for UAV Networks. IEEE Trans. Wirel. Commun. 2020, 19, 729–743. [Google Scholar]
- Zhan, C.; Zeng, Y.; Zhang, R. Energy-Efficient Data Collection in UAV Enabled Wireless Sensor Network. IEEE Wirel. Commun. Lett. 2018, 7, 328–331. [Google Scholar]
- Radhakrishnan, A.; Jeyakumar, G. Evolutionary algorithm for solving combinatorial optimization—A review. In Innovations in Computer Science and Engineering: Proceedings of 8th ICICSE; Springer: Singapore, 2021; pp. 539–545. [Google Scholar]
- Santucci, V.; Baioletti, M.; Milani, A. An algebraic framework for swarm and evolutionary algorithms in combinatorial optimization. Swarm Evol. Comput. 2020, 55, 100673. [Google Scholar] [CrossRef]
- Wei, H.; Tang, X.-S.; Liu, H. A genetic algorithm (GA)-based method for the combinatorial optimization in contour formation. Appl. Intell. 2015, 43, 112–131. [Google Scholar]
- Basmassi, M.; Benameur, L.; Chentoufi, J.A. A novel greedy genetic algorithm to solve combinatorial optimization problem. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 44, 117–120. [Google Scholar]
- Wang, H.; Jin, Y. A random forest-assisted evolutionary algorithm for data-driven constrained multiobjective combinatorial optimization of trauma systems. IEEE Trans. Cybern. 2018, 50, 536–549. [Google Scholar] [CrossRef]
- Gu, Q.; Wang, Q.; Li, X.; Li, X. A surrogate-assisted multi-objective particle swarm optimization of expensive constrained combinatorial optimization problems. Knowl. Based Syst. 2021, 223, 107049. [Google Scholar]
- Venkatraman, S.; Yen, G.G. A generic framework for constrained optimization using genetic algorithms. IEEE Trans. Evol. Comput. 2005, 9, 424–435. [Google Scholar] [CrossRef]
- Coello, C.A.C. Theoretical and numerical constraint-handling techniques used with evolutionary algorithms: A survey of the state of the art. Comput. Methods Appl. Mech. Eng. 2002, 191, 1245–1287. [Google Scholar] [CrossRef]
- Mallipeddi, R.; Suganthan, P.N. Ensemble of constraint handling techniques. IEEE Trans. Evol. Comput. 2010, 14, 561–579. [Google Scholar] [CrossRef]
- Samanipour, F.; Jelovica, J. Adaptive repair method for constraint handling in multi-objective genetic algorithm based on relationship between constraints and variables. Appl. Soft Comput. 2020, 90, 106143. [Google Scholar] [CrossRef]
- Chootinan, P.; Chen, A. Constraint handling in genetic algorithms using a gradient-based repair method. Comput. Oper. Res. 2006, 33, 2263–2281. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S. A survey of repair methods used as constraint handling techniques in evolutionary algorithms. Comput. Sci. Rev. 2009, 3, 175–192. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Yao, X. Assignment of cells to switches in a cellular mobile network using a hybrid Hopfield network-genetic algorithm approach. Appl. Soft Comput. 2008, 8, 216–224. [Google Scholar] [CrossRef]
- Pan, Y.A.; Li, F.; Li, A.; Niu, Z.; Liu, Z. Urban intersection traffic flow prediction: A physics-guided stepwise framework utilizing spatio-temporal graph neural network algorithms. Multimodal Transp. 2025, 4, 100207. [Google Scholar]
- Tessema, B.; Yen, G.G. An adaptive penalty formulation for constrained evolutionary optimization. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2009, 39, 565–578. [Google Scholar]
- Barbosa, H.J.; Lemonge, A.C.; Bernardino, H.S. A critical review of adaptive penalty techniques in evolutionary computation. In Evolutionary Constrained Optimization; Springer: New Delhi, India, 2015; pp. 1–27. [Google Scholar]
- Yeniay, Ö. Penalty function methods for constrained optimization with genetic algorithms. Math. Comput. Appl. 2005, 10, 45–56. [Google Scholar] [CrossRef]
- Paszkowicz, W. Properties of a genetic algorithm equipped with a dynamic penalty function. Comput. Mater. Sci. 2009, 45, 77–83. [Google Scholar] [CrossRef]
- Dadios, E.P.; Ashraf, J. Genetic algorithm with adaptive and dynamic penalty functions for the selection of cleaner production measures: A constrained optimization problem. Clean Technol. Environ. Policy 2006, 8, 85–95. [Google Scholar] [CrossRef]
- Elsayed, S.M.; Sarker, R.A.; Mezura-Montes, E. Self-adaptive mix of particle swarm methodologies for constrained optimization. Inf. Sci. 2014, 277, 216–233. [Google Scholar] [CrossRef]
- Elsayed, S.M.; Sarker, R.A.; Essam, D.L. Training and testing a self-adaptive multi-operator evolutionary algorithm for constrained optimization. Appl. Soft Comput. 2015, 26, 515–522. [Google Scholar] [CrossRef]
- Qiao, K.; Liang, J.; Yu, K.; Wang, M.; Qu, B.; Yue, C.; Guo, Y. A Self-Adaptive Evolutionary Multi-Task Based Constrained Multi-Objective Evolutionary Algorithm. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 7, 1098–1112. [Google Scholar] [CrossRef]
- Ali, I.M.; Essam, D.; Kasmarik, K. Novel binary differential evolution algorithm for knapsack problems. Inf. Sci. 2021, 542, 177–194. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Ruiz, R.; Sui, S. An iterated greedy heuristic for mixed no-wait flowshop problems. IEEE Trans. Cybern. 2017, 48, 1553–1566. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, Z.; Guo, G.; Zhou, Y. Multiobjective optimization and hybrid evolutionary algorithm to solve constrained optimization problems. IEEE Trans. Syst. Man Cybern. Part B 2007, 37, 560–575. [Google Scholar] [CrossRef] [PubMed]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Runarsson, T.P.; Yao, X. Stochastic ranking for constrained evolutionary optimization. IEEE Trans. Evol. Comput. 2000, 4, 284–294. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).