Dual-Objective Model Predictive Control for Longitudinal Tracking and Connectivity-Aware Trajectory Optimization of Fixed-Wing UAVs

Highlights

What are the main findings?

• A dual-objective MPC framework is developed for fixed-wing UAVs, simultaneously addressing longitudinal tracking and connectivity-aware trajectory optimization.
• The proposed MPC outperforms the benchmark LQR in both disturbance rejection and constraint handling under realistic flight conditions.

What is the implication of the main finding?

• The framework enables UAVs to balance flight-time efficiency with reliable cellular connectivity, supporting communication-critical missions.
• The approach provides a foundation for real-time predictive control integration in 5G-assisted UAV systems.

Abstract

This paper presents a dual-objective Model Predictive Control (MPC) framework for fixed-wing unmanned aerial vehicles (UAVs). The framework was designed with two goals in mind: improving longitudinal motion control and optimizing the flight trajectory when connectivity and no-fly zone constraints are present. A multi-input–multi-output model derived from NASA’s Generic Transport Model (T-2) was used and linearized for controller design. We compared the MPC controller with a Linear Quadratic Regulator (LQR) in MATLAB simulations. The results showed that MPC reached the reference values faster, with less overshoot and phase error, particularly under sinusoidal reference inputs. These differences became even more evident when the UAV had to fly in windy conditions. Trajectory optimization was carried out using the CasADi framework, which allowed us to evaluate paths that balance two competing requirements: reaching the target quickly and maintaining cellular connectivity. We observed that changing the weights of the cost function had a strong influence on the trade-off between direct flight and reliable communication, especially when multiple base stations and no-fly zones were included. Although the study was limited to simulations at constant altitude, the results suggest that MPC can serve as a practical tool for UAV missions that demand both accurate flight control and robust connectivity. Future work will extend the framework to more complete models and experimental validation.

1. Introduction

Unmanned aerial vehicles (UAVs) have rapidly evolved from experimental tools into reliable platforms for real-world missions. Fixed-wing UAVs, in particular, are valued for their ability to fly long distances efficiently, which makes them well suited for applications such as environmental monitoring, mapping, logistics, and disaster response. Their low energy consumption and wide coverage area have turned them into indispensable assets in many domains.

With this growth comes a demand for increasingly robust control systems. Early studies relied heavily on classical methods such as Proportional–Integral–Derivative (PID) and Linear Quadratic Regulator (LQR) controllers [1,2,3,4]. These controllers are simple and intuitive, which explains their popularity. However, experience has shown that PID controllers often require constant retuning when operating in variable environments, and their performance in multi-input–multi-output settings is limited [5,6]. Similarly, LQR has been widely applied for both longitudinal and lateral flight [7,8], including applications in MIMO decoupling control [9], and extended through multi-model approaches to cope with different regimes [10]. Still, these methods are not designed to handle constraints directly, and their effectiveness declines in highly dynamic conditions.

To overcome these limitations, researchers began exploring more advanced approaches. Adaptive and sliding mode controllers, for example, have been used to improve robustness when the model is uncertain or external disturbances are present [11,12,13]. Composite MRAC-style adaptations have also been proposed for fixed-wing platforms to enhance tracking under uncertainty [14]. Backstepping and dynamic inversion have been tested for agile maneuvers [15]. Beyond control laws, attention has also turned toward planning safe and efficient trajectories. Some studies considered complete terrain coverage [16] or evolutionary algorithms for 3D navigation [17], while others investigated cooperative surveillance and large-scale search-and-rescue planning with distributed charging logistics [18,19]. GPU-based fast path planning methods have also been proposed to enable real-time route generation [20]. In addition to these approaches, adaptive optimal control and reinforcement learning (RL)-based methods have recently gained attention for UAV applications. For example, fixed-time concurrent learning-based robust optimal control has been proposed to achieve convergence without requiring complete system knowledge, while fixed-time convergent RL strategies have been applied for secure containment control in multi-UAV systems [21,22].

As operations expanded, coordinating multiple UAVs became a central challenge. Formation flight strategies based on artificial potential fields and sliding mode control [23], as well as distributed architectures for cooperative tracking [24], have been proposed. Optimization-based methods have also gained ground: the virtual target vehicle method [25] and predictive control approaches for quadrotors with payloads [26] show how constraints and mission goals can be balanced more effectively.

This progression of research naturally led to increasing interest in Model Predictive Control (MPC). Unlike classical controllers, MPC can predict system behavior over a horizon and directly include state and input constraints. Several works have already applied MPC to UAV path planning with encouraging results [27,28,29]. Yet, most of these studies separate flight control from communication requirements. In practice, UAVs increasingly rely on stable links to ground networks, both for mission data and for regulatory compliance. For cellular-connected UAVs, maintaining communication reliability is as critical as satisfying kinematic and safety constraints [30]. Previous works have considered connectivity using signal strength and angle-of-arrival information [31] as well as genetic algorithms and fast path planning techniques for large-scale missions [19,20], but these remain largely disconnected from the control design itself.

Recent studies have explored MPC-driven trajectory generation for agile UAV landings [32], sensor-aware trajectory optimization that combines perception and motion constraints [33], and distributed MPC schemes for cooperative UAV formations [34]. Our work complements these by focusing specifically on connectivity-aware MPC in constrained, multi-objective path planning, which extends the applicability of predictive control to communication-critical UAV missions.

In recent years, communication-aware UAV control has gained increasing attention, particularly with the rise of 5G-enabled aerial networks. Several studies have investigated connectivity maintenance and power-efficient path planning for cellular-connected UAVs, highlighting the importance of reliable communication links in mission planning [35,36]. These findings emphasize that robust connectivity is as critical as dynamic feasibility, which motivates the connectivity-aware MPC framework proposed in this study.

The aim of this paper is to integrate both aspects into a unified predictive framework. Specifically, we contribute in three ways:

• We propose a dual-objective MPC approach that simultaneously addresses longitudinal motion control and connectivity-aware trajectory optimization for fixed-wing UAVs.
• We compare the proposed MPC framework with the LQR benchmark to demonstrate the advantages of predictive control under realistic disturbance conditions. In contrast to prior LQR and sliding mode control (SMC) schemes in literature, the MPC formulation explicitly incorporates system constraints and enables multi-objective optimization, providing improved flexibility and performance for UAV applications.
• We implement the trajectory optimization using the CasADi framework, which enables real-time nonlinear optimization suitable for onboard deployment.

By combining flight dynamics with connectivity constraints, this work takes a step toward UAV systems that are not only stable and efficient but also communication-aware—an increasingly critical requirement for autonomous aerial operations.

The remainder of this paper is organized as follows. Section 2 presents the UAV mathematical model and control design. Section 3 introduces the trajectory optimization framework. Simulation environment and case studies on trajectory optimization are discussed in Section 4, results and discussion are given in Section 5 and conclusions with directions for future work are provided in Section 6.

2. UAV Dynamics and Control Framework

In this part of the paper, we explain how the UAV was modeled and how the controllers were designed. The starting point is a simplified version of NASA’s Generic Transport Model, which provides the basic longitudinal dynamics of a fixed-wing aircraft. On top of this model, two control approaches are considered. The first is the well-known LQR, included here mainly as a benchmark. The second is MPC, which has the advantage of taking constraints into account while predicting the system’s future behavior. These two designs form the basis for the trajectory optimization studies that follow.

2.1. Mathematical Model of UAV

In this study, the Generic Transport Model (GTM), developed under NASA’s technology transfer program, is used as the basis for the dynamics of UAVs. The GTM represents a 5.5% scale replica of a typical passenger aircraft, designed as an unmanned fixed-wing platform. NASA conducted validation flight tests to ensure the reliability of the model.

The dynamics of a fixed-wing UAV can be described by six degrees of freedom (6-DOF), which are generally divided into lateral and longitudinal motion. Since the primary focus of this study is longitudinal motion, only the corresponding equations are considered. The longitudinal dynamics are expressed as follows:

$$\dot{V}={\displaystyle \frac{Tcos\left(\alpha \right)-D-mgsin\left(\gamma \right)}{m}}$$

(1)

$$\dot{\alpha }=q-{\displaystyle \frac{L+Tsin\left(\alpha \right)-mgcos\left(\gamma \right)}{mV}}$$

(2)

$$\dot{q}={\displaystyle \frac{M}{I_{yy}}}$$

(3)

$$\dot{\theta }=q$$

(4)

where V is the airspeed (m/s), m is the aircraft mass (kg), q is the pitch rate (rad/s), $\theta$ is the pitch angle (rad), $\alpha$ is the angle of attack (rad), $\gamma$ is the flight path angle (rad), M is the pitching moment (Nm), $I_{yy}$ is the pitch-axis moment of inertia (kg·m²), T, D, L are the thrust, drag, and lift forces (N), respectively.

The aerodynamic forces are defined as

$$M={\displaystyle \frac{1}{2}}\rho V^{2}Sc{C}_M$$

(5)

$$L={\displaystyle \frac{1}{2}}\rho V^{2}S{C}_L$$

(6)

$$D={\displaystyle \frac{1}{2}}\rho V^{2}S{C}_D$$

(7)

$$\dot{T}={\tau }_t\left({\delta }_t{T}_{max}-T\right)$$

(8)

with $\rho$ the air density, S the wing area, c the mean aerodynamic chord, ${\delta }_t$ the throttle input, and $T_{max}$ the maximum thrust. The aerodynamic coefficients are expressed as

$$C_L=C_{L0}+C_{L\alpha }\alpha$$

(9)

$$C_D=C_{D0}+k{C}_L^2$$

(10)

$$C_M=C_{M0}+C_{M\alpha }\alpha +C_{M{\delta }_e}{\delta }_e+C_{Mq}{\displaystyle \frac{qc}{V}}$$

(11)

where ${\delta }_e$ is the elevator deflection angle.

In order to simplify controller design, the nonlinear equations are linearized at the trim condition corresponding to straight and level flight ($\gamma =0^{°}$) at an airspeed of 80 knots and altitude of 800 ft. The linearized continuous-time state-space model can be expressed as

$$\dot{x}=Ax+Bu$$

(12)

where the state vector is $x={\left[V\alpha q\theta \right]}^T$ and the control inputs are $u={\left[{\delta }_e{\delta }_t\right]}^T$. The output vector is $y={\left[V\theta \right]}^T$. The discrete-time representation is given by

$$x_{k+1}=A_d{x}_k+B_d{u}_k$$

(13)

with $A_d$ and $B_d$ the discrete-time system matrices obtained from the continuous model.

2.2. Controller Design

In this section, two control strategies are introduced for the longitudinal dynamics of the UAV: (i) the Linear Quadratic Regulator (LQR), which serves as a classical benchmark controller, and (ii) the Model Predictive Control (MPC), which allows explicit handling of system constraints and prediction over a finite horizon.

2.2.1. Linear Quadratic Regulator (LQR)

The LQR is widely applied in linear systems due to its simplicity and analytical tractability. It aims to stabilize the system while minimizing a quadratic cost function over an infinite horizon:

$$J={\int }_0^{\infty }\left(x^{T}Qx+u^{T}Ru\right)dt$$

(14)

where x is the state vector, u is the control input, $Q⪰0$ is the state-weighting matrix, and $R\succ 0$ is the input-weighting matrix. The optimal feedback gain K is obtained as [37]

$$K=R^{-1}{B}^{T}P$$

(15)

where P is the positive semi-definite solution of the continuous-time Algebraic Riccati Equation (ARE):

$$A^{T}P+PA-PB{R}^{-1}{B}^{T}P+Q=0.$$

(16)

The control law is then expressed as

$$u\left(t\right)=-Kx\left(t\right).$$

(17)

Although computationally efficient, LQR cannot explicitly handle state or input constraints, and its performance may degrade under strongly nonlinear or constrained scenarios.

2.2.2. Model Predictive Control (MPC)

MPC is a modern control method that predicts the future evolution of the system over a finite horizon and optimizes the control sequence at each sampling instant. At each step, an optimization problem is solved:

$$J=\sum _{k=0}^{N_p}\left[{(y_k-y_{ref})}^T{Q}_y(y_k-y_{ref})+\Delta u_k^{T}R\Delta u_k\right]$$

(18)

subject to the UAV’s discrete-time dynamics

$$x_{k+1}=A_d{x}_k+B_d{u}_k,$$

(19)

and the following constraints

$$\begin{array}{c}\hfill u_{min}\le u_k\le u_{max},\end{array}$$

(20)

$$\begin{array}{c}\hfill \Delta u_{min}\le \Delta u_k\le \Delta u_{max},\end{array}$$

(21)

$$\begin{array}{c}\hfill y_{min}\le y_k\le y_{max}.\end{array}$$

(22)

Here, $N_p$ denotes the prediction horizon, $\Delta u_k=u_k-u_{k-1}$ is the input increment, and $Q_y$, R are weighting matrices. Only the first control action is applied, and the procedure is repeated at the next time step in a receding horizon fashion.

In this study, the MPC problem is formulated and solved using the CasADi framework, which enables real-time nonlinear optimization. This allows constraints on the inputs (elevator deflection ${\delta }_e$, throttle ${\delta }_t$), states, and outputs to be explicitly enforced during the control process.

3. Connectivity-Aware Trajectory Optimization with MPC

In this section, a trajectory planning strategy is introduced which employs Model Predictive Control (MPC) for fixed-wing UAVs operating in environments where both communication requirements and environmental restrictions must be considered. Rather than focusing solely on flight dynamics, the approach is designed to address two practical objectives at the same time. The first is to ensure that the UAV reaches its target in the shortest possible time, which is critical for mission efficiency. The second is to guarantee continuous connectivity with cellular base stations while simultaneously avoiding no-fly zones, thereby maintaining both communication reliability and operational safety. By integrating these objectives within a single predictive framework, the proposed method reflects the realities of modern UAV missions, where efficiency, safety, and connectivity cannot be treated independently.

In order to formulate the problem in a manageable way and emphasize the optimization of trajectories, the UAV dynamics are represented in a simplified manner. Specifically, the aircraft is assumed to maintain constant altitude and constant speed during the mission. Under these conditions, its motion can be modeled on a two-dimensional $(x,y)$ plane. This abstraction does not capture the full complexity of UAV flight, but it provides a balance between computational efficiency and practical insight, allowing us to focus on the interplay between flight time, connectivity, and environmental constraints.

3.1. UAV Kinematics and Dynamics

In this study, UAV motion is analyzed in the longitudinal plane under the assumption of constant altitude and constant airspeed. This simplification, widely used for fixed-wing UAVs during the cruise phase, allows focusing on horizontal motion where vertical dynamics are negligible. Representing the motion on a two-dimensional $(x,y)$ plane provides a good balance between computational efficiency and physical realism, making it suitable for real-time predictive trajectory planning. Under these assumptions, the UAV position is described by the ground coordinates $(x,y)$ and the heading angle $\psi$, which defines its orientation. These kinematic relations form the basis of the MPC-based trajectory optimization framework developed in the following sections.

The translational dynamics of the UAV in the x- and y-directions are therefore expressed as

$$\begin{array}{c}\hfill \dot{x}=vcos\left(\psi \right)\\ \hfill \dot{y}=vsin\left(\psi \right)\end{array}$$

(23)

where x and y denote the UAV position in the ground plane (m), v represents the constant forward velocity (m/s), and $\psi$ is the heading angle (rad).

To enable UAV maneuvering, the characteristic roll–yaw coupling observed in fixed-wing aerial platforms is taken into account. In this context, the heading rate $\dot{\psi }$ is not directly commanded but instead is governed indirectly through the roll dynamics:

$$\begin{array}{c}\hfill \dot{\psi }={\displaystyle \frac{gtan\left(\varphi \right)}{v}}\\ \hfill \dot{\varphi }={\displaystyle \frac{{\varphi }_{\mathrm{cmd}}-\varphi }{\tau }}\end{array}$$

(24)

where $\varphi$ is the roll angle (rad), ${\varphi }_{\mathrm{cmd}}$ is the commanded roll angle (rad), $\tau$ denotes the time constant of roll dynamics (s), and g is the gravitational acceleration (9.81 m/s²).

The control inputs of the aircraft are expressed as

$$u=\left[\begin{array}{c}v\\ {\psi }_{\mathrm{cmd}}\end{array}\right]$$

(25)

where v denotes the constant airspeed of the UAV, and ${\psi }_{\mathrm{cmd}}$ is the commanded heading angle. There exists a coupling between the commanded roll angle ${\varphi }_{\mathrm{cmd}}$ in the aircraft dynamics and the heading angle control input ${\psi }_{\mathrm{cmd}}$. Through this relationship, the roll dynamics of the fixed-wing UAV is incorporated into the trajectory optimization framework.

$$\begin{array}{c}\hfill {\dot{\psi }}_{\mathrm{cmd}}=K\left({\psi }_{\mathrm{cmd}}-\psi \right)\\ \hfill {\dot{\varphi }}_{\mathrm{cmd}}={tan}^{-1}\left(v{\displaystyle \frac{{\dot{\psi }}_{\mathrm{cmd}}}{g}}\right)\end{array}$$

(26)

Here, the roll dynamics are represented as a first-order linear system using the gain $K=1$ and the time constant $\tau =0.76$. By balancing computing efficiency and fidelity, this modeling choice enables the system to capture the fundamental roll behavior without adding needless complexity. This low-order dynamic model balances control fidelity and computational efficiency, making it suitable for real-time embedded MPC implementations.

3.2. Wind-Extended Motion Model

Although the basic kinematic model assumes ideal flight in still air, actual operating environments are rarely so simple. In practice, UAVs are frequently exposed to steady winds or variable gusts that can noticeably alter their trajectories. To capture this effect in the modeling stage, wind components are introduced as external disturbances acting in the global x- and y-directions. Specifically, the wind speed W and its direction $\omega$ are incorporated into the translational dynamics as additive terms. In this way, the equations of motion describe the ground-relative velocity of the UAV, reflecting both its commanded forward motion and the influence of ambient wind.

In the absence of commanded motion, the UAV’s ground-relative velocity due to wind alone can be expressed as

$$\begin{array}{cc}\hfill \dot{x}& =Wcos\left(\omega \right),\hfill \\ \hfill \dot{y}& =Wsin\left(\omega \right).\hfill \end{array}$$

(27)

When the commanded forward motion of the UAV is included, the kinematic model becomes

$$\begin{array}{cc}\hfill \dot{x}& =vcos\left(\psi \right)+Wcos\left(\omega \right),\hfill \\ \hfill \dot{y}& =vsin\left(\psi \right)+Wsin\left(\omega \right).\hfill \end{array}$$

(28)

These equations represent the UAV’s velocity relative to the ground under the combined effect of its commanded velocity and the ambient wind. Throughout the mission horizon, the wind is assumed to be steady and spatially uniform, which keeps the model computationally efficient while still capturing the main environmental influence.

It is worth noting that incorporating wind into the dynamics provides a more realistic description of UAV behavior, particularly in missions where external disturbances cannot be ignored. In this study, the wind parameters W and $\omega$ are treated as known quantities, either assumed constant or obtained from onboard measurements and meteorological data. A natural extension of this work would be to relax this assumption and model wind uncertainty explicitly, for example by treating it as a stochastic disturbance or by bounding it within an uncertainty set.

The overall system dynamics used in this study are therefore obtained by combining the previously derived equations of motion with the wind-augmented terms. This formulation serves as the foundation for the state–space model developed in the next section.

$$\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\psi }\\ \dot{\varphi }\end{array}\right]=\left[\begin{array}{c}vcos\psi +Wcos\omega \\ vsin\psi +Wsin\omega \\ {\displaystyle \frac{gtan\varphi }{v}}\\ {\displaystyle \frac{{\varphi }_{\mathrm{cmd}}-\varphi }{\tau }}\end{array}\right]\left[\begin{array}{c}x\\ y\\ \psi \\ \varphi \end{array}\right]$$

(29)

3.3. State-Space Formulation for CasADi Optimization

While the state-space model in Equation (29) captures the essential kinematics of the UAV, two additional states were introduced to extend the formulation. The motivation for this extension is twofold. First, it allows us to represent variables that directly influence system behavior, such as communication-related measures. Second, it ensures full compatibility with the symbolic computation and optimization framework provided by CasADi [38]. The augmented state-space model is shown in Equation (30).

$$\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\psi }\\ \dot{\varphi }\\ \dot{J}\\ \dot{time}\end{array}\right]=\left[\begin{array}{c}vcos\psi +Wcos\omega \\ vsin\psi +Wsin\omega \\ {\displaystyle \frac{gtan\varphi }{v}}\\ {\displaystyle \frac{{\varphi }_{\mathrm{cmd}}-\varphi }{\tau }}\\ \eta \\ t\end{array}\right]\left[\begin{array}{c}x\\ y\\ \psi \\ \varphi \\ J\\ time\end{array}\right]$$

(30)

Here, the additional state variable J represents the received signal strength. It is defined in Equation (31) and takes its maximum value at the center of a base station’s coverage area. When J exceeds 67%, the objective function related to connectivity is activated, as expressed in Equation (31).

The second additional state, $time$, simply tracks mission time. This inclusion makes it possible to evaluate objectives and constraints that depend explicitly on elapsed time within the prediction horizon.

To ensure consistency across the optimization framework, all objective functions in this study are normalized to the range $[0,1]$. For this reason, the formulation of J is written in the form $(1-\cdots )$, so that it follows the same normalized structure. In this formulation, the variable $\chi$, expresses the distance between the UAV and the base stations, while $r_{BS}$ denotes the radius of the base station coverage area.

$$\eta =\sum (1-e^{-{\displaystyle \frac{{\chi }^2}{r_{BS}^2}}})$$

(31)

The time state variable added in Equation (30) is expressed in Equation (32).

$$t=\sum \left(t+(1-t)\left(heaviside(r_{BS}-\chi )\right)\right)$$

(32)

Equation (33) defines the calculation of the distance variable ($\chi$) based on the position of the unmanned aerial vehicle, $(x_{\mathrm{UAV}},y_{\mathrm{UAV}})$, and the coordinates of the base stations, $(x_{\mathrm{BS}},y_{\mathrm{BS}})$.

$$\chi =\sqrt{{(x_{UAV}-x_{BS})}^2+{(y_{UAV}-y_{BS})}^2}$$

(33)

While the Heaviside function used in Equation (32) is specific to MATLAB R2025b, the corresponding values it takes under different conditions are explicitly illustrated in the expression given in Equation (34).

$$heaviside\left(x\right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}x<0\hfill \\ 0.5,\hfill & \mathrm{if}x=0\hfill \\ 1,\hfill & \mathrm{if}x>0\hfill \end{array}\right.$$

(34)

The Q weight matrix determines how much emphasis is placed on each state variable during optimization. In this study, the values shown in Equation (35) were selected after considering both results reported in the literature and our own practical observations. The last state variable, which represents time, was assigned a weight of zero. This choice was deliberate, as the time state was introduced only to keep track of mission progress and does not directly influence performance. The effect of disconnection duration is instead captured through the signal-strength objective, which provides a more meaningful way of penalizing poor connectivity.

$$Q=\left[\begin{array}{cccccc}4& 0& 0& 0& 0& 0\\ 0& 5& 0& 0& 0& 0\\ 0& 0& 0.05& 0& 0& 0\\ 0& 0& 0& 0.1& 0& 0\\ 0& 0& 0& 0& 11& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right]$$

(35)

The weighting values in Q were chosen following standard MPC design guidelines [39,40], combined with iterative simulation-based tuning to balance tracking accuracy, overshoot, and constraint activity. The preliminary tuning was conducted through a coarse-to-fine parameter sweep in the range ${10}^{-2}$–${10}^1$ (after state scaling), ensuring well-conditioned optimization and stable closed-loop responses.

The R weight matrix, which reflects the weighting of the control inputs, was determined as presented in Equation (36).

$$R=\left[\begin{array}{cc}0.5& 0\\ 0& 0.05\end{array}\right]$$

(36)

The weighting values in R were determined through parametric tuning to achieve a balance between control smoothness and responsiveness. Larger weighting values were found to slow down the system response, while smaller values increased actuator activity and overshoot. The chosen values provided the best compromise between performance and control effort in our simulations.

3.3.1. Objective Function Design

Trajectory optimization for cellular-connected UAVs is essentially about handling a trade-off between two goals that are not always easy to satisfy at the same time. On one hand, the UAV should minimize the time spent outside the coverage of cellular base stations, since losing the link can quickly compromise mission reliability. On the other hand, the trajectory should be as accurate and efficient as possible, reducing flight time and conserving energy. In our tests, it became clear that these two goals often pull in opposite directions, especially when obstacles or restricted zones were added to the scenario.

Within the MPC framework, both objectives are written as quadratic cost terms and evaluated over the prediction horizon. Their balance can be shifted through weighting coefficients, which gave us the flexibility to emphasize one goal over the other depending on the situation. For instance, in dense urban environments where buildings frequently interrupt the signal, it makes more sense to prioritize connectivity. In contrast, for time-critical missions such as rapid inspections, minimizing travel time naturally becomes the dominant objective. This ability to adjust the trade-off is, in our view, one of the main strengths of the proposed approach.

In the following formulation, $W_{o1}$ corresponds to the priority given to reaching the final target efficiently, whereas $W_{o2}$ accounts for the importance of maintaining uninterrupted cellular connectivity during the mission.

$$W_{o1}+W_{o2}=1$$

(37)

where $W_{o1}$ denotes the weight of objective 1 and $W_{o2}$ denotes the weight of objective 2.

Objective 1: Target-Oriented Progress

The first objective is determined by guiding the UAV all the way to its designated target. Since every mission ultimately requires the vehicle to reach its destination, we formulate this objective by tracking the difference between the current position of the UAV and the desired target location. This difference, expressed as a position error vector, provides a direct measure of progress. The associated velocities $v_{xy}$ are obtained from the derivatives of the position states in the system dynamics, which keeps the objective function consistent with the underlying kinematic model. The evaluation is performed over the prediction horizon so that progress is assessed at every step. Within the cost function, this tracking term is labeled as $\mathrm{objective}1$, and its relative importance is controlled by the weight $WO1$.

$$objectiv{e}_1={\displaystyle \frac{1}{2N}}\sum _{k=0}^{N-1}\left(1-{\displaystyle \frac{{\delta }_{xy,k}^{\top }{v}_{xy,k}}{\parallel {\delta }_{xy,k}\parallel \parallel v_{xy,k}\parallel +\epsilon }}\right),\epsilon >0.$$

(38)

Here, ${\delta }_{xy}$ represents the 2D vector extending from the UAV’s current position to the target. That is, it is the vectorial difference, or distance, between the target and the UAV.

$${\delta }_{xy}=\left[\begin{array}{c}{x}_{target}-x_{UAV},y_{target}-y_{UAV}\end{array}\right]$$

(39)

The objective is normalized with respect to the prediction horizon N, ensuring that the resulting cost remains consistent and comparable regardless of the horizon length, as shown in the equation below.

$$objectiv{e}_1=\left({\displaystyle \frac{1+objectiv{e}_1}{N}}\right)\ast 0.5$$

(40)

Objective 2: Connectivity Preservation

The base station coverage objective function is formulated based on the signal strength received from the base stations. Specifically, the total signal power is normalized by the number of base stations, the length of the prediction horizon, and the sampling time, since the evaluation is carried out in continuous time.

Let $BS$ denote the total number of base stations, N the prediction horizon, and T the sampling time. Then, the base station coverage objective function is expressed as

$$objectiv{e}_2={\displaystyle \frac{J}{BS\ast N\ast T}}$$

(41)

where the cumulative strength of the received signal throughout the planning horizon is denoted by J. Regardless of the length of the planning process or the number of base stations taken into account, this normalization guarantees that the signal strength contribution stays constant.

It is assumed that the signal strength ratios are equivalent and that each base station has the same height and transmit power. The overall cost function can use $objectiv{e}_2$ directly under these assumptions. This objective is given a weight, $W_{O2}$, in order to integrate it with others. Allowing for adjustable trade-offs between various mission objectives then yields the final overall goal.

$$objectiv{e}_g={\displaystyle \frac{W_{o1}\ast objectiv{e}_1+W_{o2}\ast objectiv{e}_2}{W_{o1}+W_{o2}}}$$

(42)

Here, $objectiv{e}_g$ represents the overall cost function that balances multiple objectives through a weighted combination. While the weighting factors $W_{o1}$ and $W_{o2}$ were manually selected to illustrate the trade-off between flight-time minimization and connectivity preservation, their optimal values could be adaptively tuned or optimized using higher-level search or learning-based strategies. Such adaptive weight tuning could automatically balance the objectives according to mission type and environmental conditions, and is therefore identified as a promising direction for future work.

Weighted Multi-Objective Cost Function

In this study, two criteria were used to evaluate alternative routes. The first criterion, denoted as DH, measures how directly the UAV reaches the target. The second, BSH, reflects the ability of the route to reach the target while minimizing the time spent disconnected from base stations. The relative importance of the directness criterion (DH) is expressed on a scale from 1 to 10, where higher values correspond to assigning less priority to route directness [41].

To make the two criteria comparable, a normalization step was applied using the maximum score method. In this approach, each raw criterion value x is divided by the maximum observed value $x_{max}$, yielding the normalized score $x_i^{\prime }$. This procedure ensures that all normalized values fall within the $[0,1]$ range, which allows the criteria to be evaluated on an equal basis [42].

$$x_i^{\prime }={\displaystyle \frac{x_i}{x_{max}}}$$

(43)

The parameters utilized in this study were normalized in accordance with the equations presented below.

$$\begin{array}{c}\hfill D{H}_i^{\prime }={\displaystyle \frac{D{H}_i}{D{H}_{\max }}}\\ \hfill BS{H}_i^{\prime }={\displaystyle \frac{BS{H}_i}{BS{H}_{\max }}}\end{array}$$

(44)

The

Table 1. Weight Selection Chart.

	DH	BSH
DH	1	9
BSH	1/9	1

below provides an example of the weight assignments for a scenario in which minimizing disconnection time is considered significantly more important than directly reaching the target.

In order to obtain the relative weights, the table is arranged as in the matrix given in the below equation.

$$\left[\begin{array}{cc}{\displaystyle \frac{1}{1+0.11}}& {\displaystyle \frac{9}{9+1}}\\ {\displaystyle \frac{0.11}{1+0.11}}& {\displaystyle \frac{1}{9+1}}\end{array}\right]=\left[\begin{array}{cc}0.9& 0.9\\ 0.1& 0.1\end{array}\right]$$

(45)

After this normalization step, each element of the matrix is divided by the sum of the elements in its respective column. This process ensures that the resulting values represent relative proportions within each decision criterion.

Subsequently, the relative weights for two distinct objectives are determined:

• Reaching the target directly ($W_{o1}$)
• Reaching the target while minimizing the disconnection time ($W_{o2}$)

The weights are determined according to the equations presented in the following.

$$\begin{array}{c}\hfill W_{o1}={\displaystyle \frac{0.9+0.9}{2}}=0.9\\ \hfill W_{o2}={\displaystyle \frac{0.1+0.1}{2}}=0.1\end{array}$$

(46)

3.3.2. Constraint Formulation

Objective functions are formulated to ensure that the unmanned aerial vehicle reaches the target in an optimal time while avoiding no-fly zones, maintaining operations within the base station coverage area for the minimum required duration, and satisfying specified constraints. These constraints are explained in detail under the following four headings. Since the speed is assumed constant, the velocity limits are defined as

$$v_{min}=v_{max}=23.15\mathrm{m}/\mathrm{s}$$

AeroVironment, 2017 [43] for the selected fixed-wing unmanned aerial vehicle. Head or yaw angle limits are applied to the $\psi$ commands and are bounded by 0–2$\pi$:

$$\begin{array}{c}\hfill v_{min}<u\left(1\right)<v_{max}\\ \hfill {\psi }_{{\mathrm{cmd}}_{\mathrm{m}}\mathrm{in}}<u\left(2\right)<{\psi }_{{\mathrm{cmd}}_{\mathrm{m}}\mathrm{ax}}\end{array}$$

(47)

Constraint 1: Input (Control) Constraints

The UAV control input is the commanded roll angle $\left({\varphi }_{cmd}\right)$, which is restricted by the boundaries of the flight envelope.

$$-{30}^{°}⩽{\varphi }_{cmd}⩽{30}^{°}$$

(48)

Constraint 2: State Constraints

The X and Y axes along which the unmanned aerial vehicle (UAV) moves (in meters) must be constrained to ensure that the resulting solutions remain within the defined area.

$$\begin{array}{c}\hfill x_{min}=-1000,x_{max}=1000\\ \hfill y_{min}=-1000,y_{max}=1000\end{array}$$

(49)

Constraint 3: Connectivity Zone and No-Fly Zone Constraint

No-fly zones are incorporated as constraint within the MPC to prevent the UAV from entering restricted areas. If Equation (50) is satisfied, that is, when it is greater than zero, the condition of being outside or not in the no-fly zone is added as a constraint. The position of the unmanned aircraft in the coordinate plane $(x_{UAV},y_{UAV})$, the positions of the no-fly zones $(x_{area},y_{area})$, $r_{UAV}$ imaginary drawn around the UAV. The radius and $r_{area}$ represent the radius of the no-fly zone.

$$\left(\sqrt{{(x_{\mathrm{UAV}}-x_{\mathrm{area}})}^2+{(y_{\mathrm{UAV}}-y_{\mathrm{area}})}^2}\right)-(r_{\mathrm{UAV}}+r_{\mathrm{area}})>0$$

(50)

Constraint 4: Dynamics as Equality Constraints

The UAV’s nonlinear dynamics are enforced within the MPC framework as equality constraints, using Euler integration. The g function in the equation numbered 45 is given an equality constraint to express the prediction state equation depending on the states ($X_N$) and inputs ($u_N$). $X_{N+1}$ includes the states in the next step.

$$X_{N+1}-g(X_N,u_N)=0$$

(51)

This constraint ensures the optimizer respects system dynamics while planning over the prediction horizon.

4. Simulation Setup and Case Studies

To evaluate the proposed trajectory optimization method, we designed six different simulation scenarios, each reflecting a distinct combination of environmental conditions and weight settings. All simulations were carried out in MATLAB, where the optimization routines were implemented using CasADi. In all simulations, the prediction horizon and sampling time were set to $N_p=120$ and $T_s=0.05\mathrm{s}$, respectively. This setup allowed us to test the method in a flexible yet computationally efficient environment.

In every scenario, the UAV starts from the same fixed launch point and aims to reach a specified target location. Along the way, it must maintain reliable communication with cellular base stations spread across the environment. The UAV is assumed to fly at constant altitude and airspeed, which keeps the focus on the path planning aspect of the problem. Its trajectory is determined by solving a constrained optimal control problem over a finite horizon, ensuring that both mission objectives and environmental limitations are considered at each step.

Each scenario introduces a specific challenge, such as the presence of wind, limited coverage, or no-fly zones. The performance of the proposed method is evaluated with respect to two main criteria: the continuity of communication and the UAV’s ability to adapt to environmental disturbances. To study the effect of weight selection, simulations were repeated using three different sets of objective function weights, as summarized in

Table 2. Simulation Steps.

Step	${\mathit{W}}_{\mathit{o}1}$	${\mathit{W}}_{\mathit{o}2}$	Line Type
1	0.1	0.9	Blue, Dash-Dot
2	0.3	0.7	Pink, Dashed
3	0.99	0.01	Black, Solid

. The line types and colors in the scenario result graphs correspond to the steps indicated in the table.

The impact of weight selection in both windy and no wind conditions is analyzed using three weight sets.

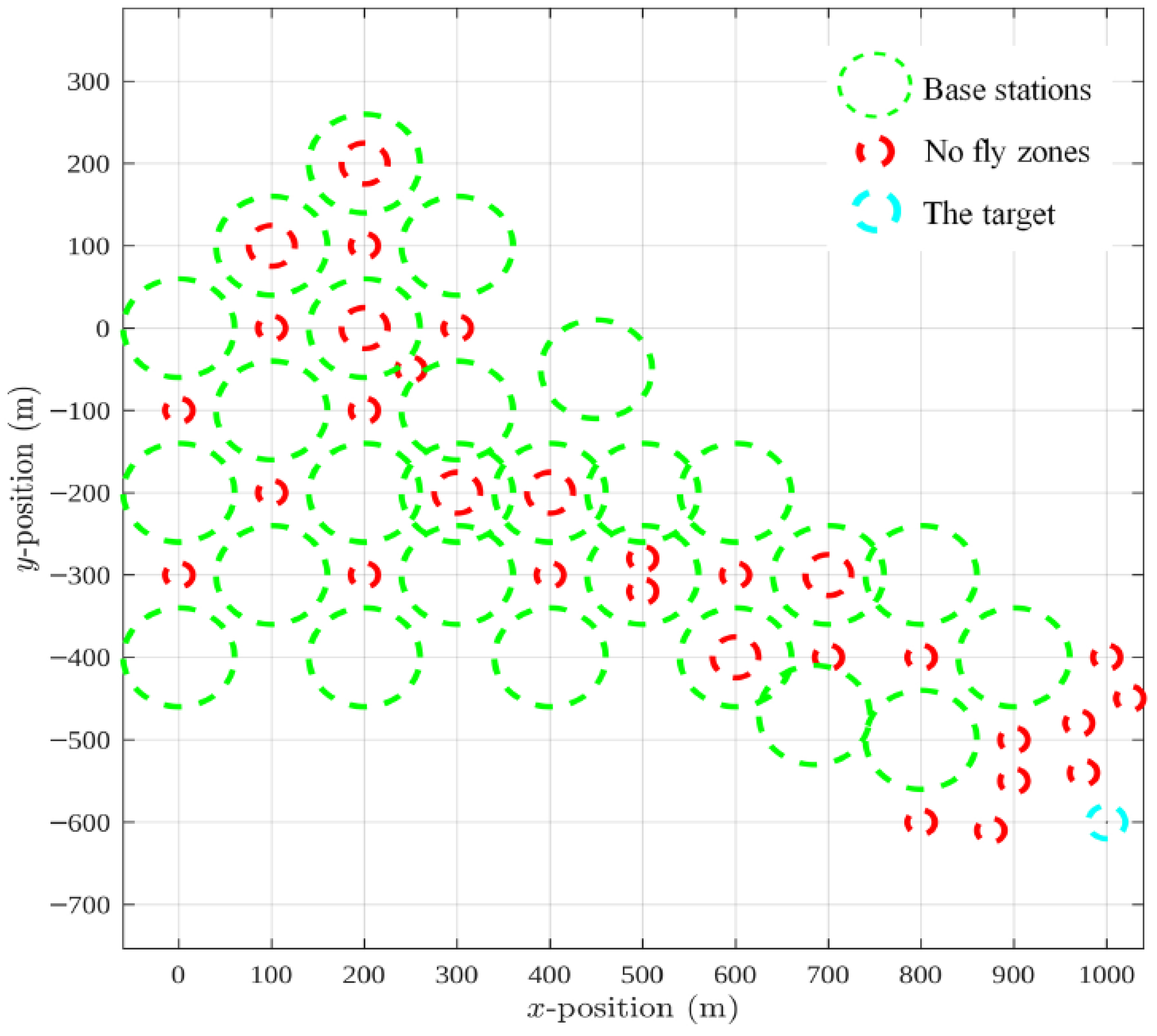
The two-dimensional simulation environment covers an area extending from 0 to 1000 m along the x-axis and from −700 to 300 m along the y-axis. Within this space, 26 base stations (green circles) and 30 no-fly zones (red circles) are distributed. Each base station provides coverage over a circular region with a diameter of 120 m, located at a common altitude and offering identical signal strength. No-fly zones are modeled as circular regions with a diameter of 30 m. To reflect stricter safety regulations, the diameter of a no-fly zone is increased to 50 m if it falls within the coverage area of a base station. The overall simulation environment is illustrated in Figure 1.

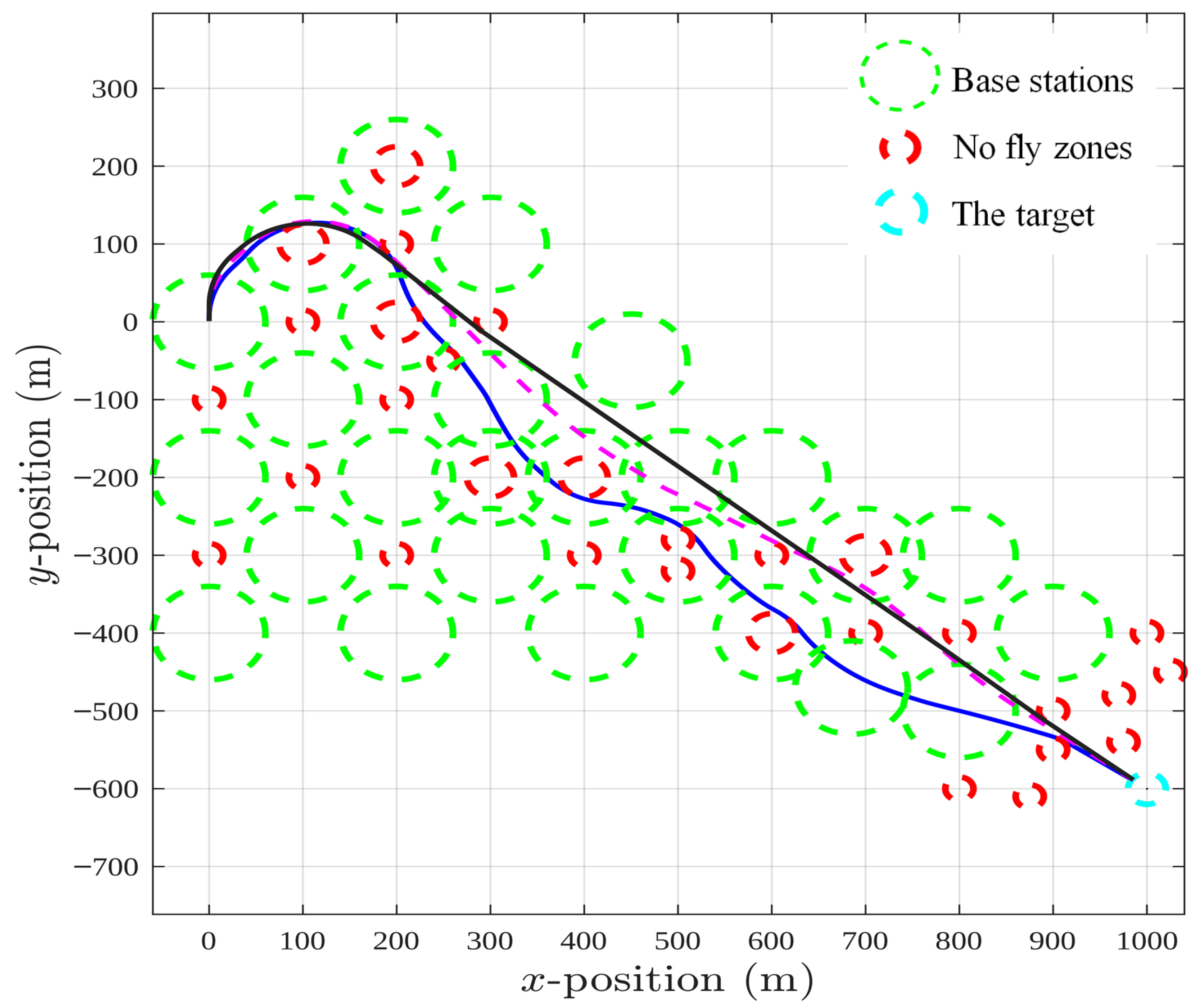
4.1. Scenario 1: No Wind

Figure 2 shows how the UAV chooses its path when there is no wind, and it makes very clear how sensitive the results are to the choice of weights. Three routes are plotted, and although they start from the same point and aim for the same target, their shapes look noticeably different once the objective priorities are changed.

The blue dash-dotted trajectory belongs to the case $W_{o1}=0.1$ and $W_{o2}=0.9$. Here the optimization strongly favors the second objective, so the UAV deliberately takes detours to remain in coverage rather than rushing straight to the goal. The pink dashed trajectory, obtained with $W_{o1}=0.3$ and $W_{o2}=0.7$, is more balanced. It reflects a compromise: the UAV still makes an effort to stay connected, but it also tries not to stray too far from a direct route. Finally, the black solid trajectory corresponds to $W_{o1}=0.99$ and $W_{o2}=0.01$. In this case, the UAV clearly “ignores” the communication aspect and heads almost straight toward the target, even if that means spending time outside base station coverage.

A small adjustment in the weight coefficients $W_{o1}$ and $W_{o2}$ leads to visibly different UAV behaviors, reflecting the trade-off between minimizing mission time and maximizing connectivity. Increasing $W_{o2}$ consistently improves the connectivity metric while slightly increasing total flight time, whereas larger $W_{o1}$ values produce shorter but less connected trajectories. These results confirm the expected trend and demonstrate that the proposed MPC framework can smoothly adjust mission priorities through continuous weight tuning rather than discrete controller changes.

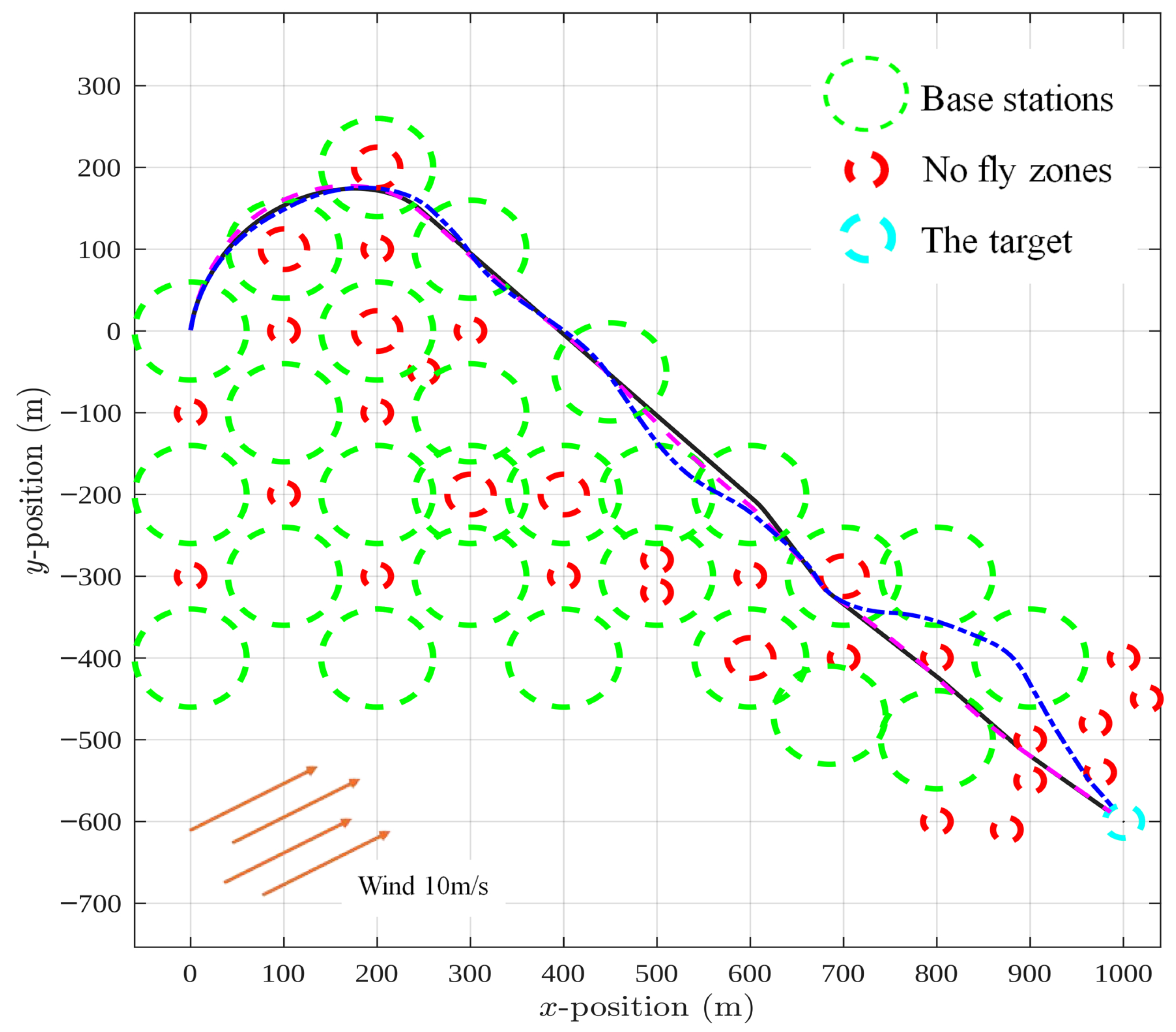
4.2. Scenario 2: Constant Wind

Figure 3 shows the UAV trajectories when a steady wind of 10 m/s is applied at an angle of 60°. Compared with the no-wind scenario, the overall pattern is similar—three routes are produced depending on how the objectives are weighted—but the wind clearly shifts and bends the paths, making the trade-offs easier to see.

The blue dash-dotted trajectory corresponds to the case $W_{o1}=0.1$ and $W_{o2}=0.9$. Here, as in the no-wind scenario, the UAV strongly favors the second objective and adjusts its route to stay connected, but the presence of wind forces additional deviations from a straight line. The pink dashed trajectory, obtained with $W_{o1}=0.3$ and $W_{o2}=0.7$, again represents a compromise. The UAV tries to balance directness with connectivity, but wind drift makes this balance more challenging, resulting in a route that is less smooth than in still-air conditions. Finally, the black solid trajectory with $W_{o1}=0.99$ and $W_{o2}=0.01$ reflects a near-exclusive focus on reaching the target quickly. The UAV essentially flies straight toward the goal, but the wind pushes it sideways, producing noticeable offsets along the way.

What stands out in this figure is how the same weighting strategy that worked in calm conditions leads to quite different behavior once wind is introduced. Even when the optimization “wants” the UAV to fly a direct path, the environment forces compromises. This illustrates that the weighting factors not only define the relative importance of objectives but also determine how resilient the chosen strategy will be under external disturbances.

5. Results and Discussion

In this section, we share and reflect on the results obtained with both the MPC and LQR controllers. Running the same tests with the two methods made their differences quite visible. While LQR provided acceptable performance, it struggled with overshoot and constraint handling. MPC, on the other hand, offered smoother responses and better adaptability, which gave us more confidence in its suitability. Based on these observations, we decided to use MPC as the main strategy for trajectory optimization.

We then moved on to trajectory optimization under two types of environmental conditions: one with no wind and one with a steady wind applied. For each case, we varied the weight settings to see how changing the balance between the objectives would affect the UAV’s path. This gave us the chance to evaluate not only how quickly the UAV reached its target, but also how well it maintained communication and avoided no-fly zones along the way.

Figure 2 and Figure 3 illustrate the resulting trajectories in the two scenarios. In each figure, three different paths are shown, each reflecting a different choice of weighting between $W_{o1}$ and $W_{o2}$. What stands out is that, regardless of the chosen weights or the presence of wind, the UAV consistently managed to avoid restricted areas. This confirms that the MPC framework not only generates feasible paths but also respects safety constraints even under changing conditions.

MPC versus LQR

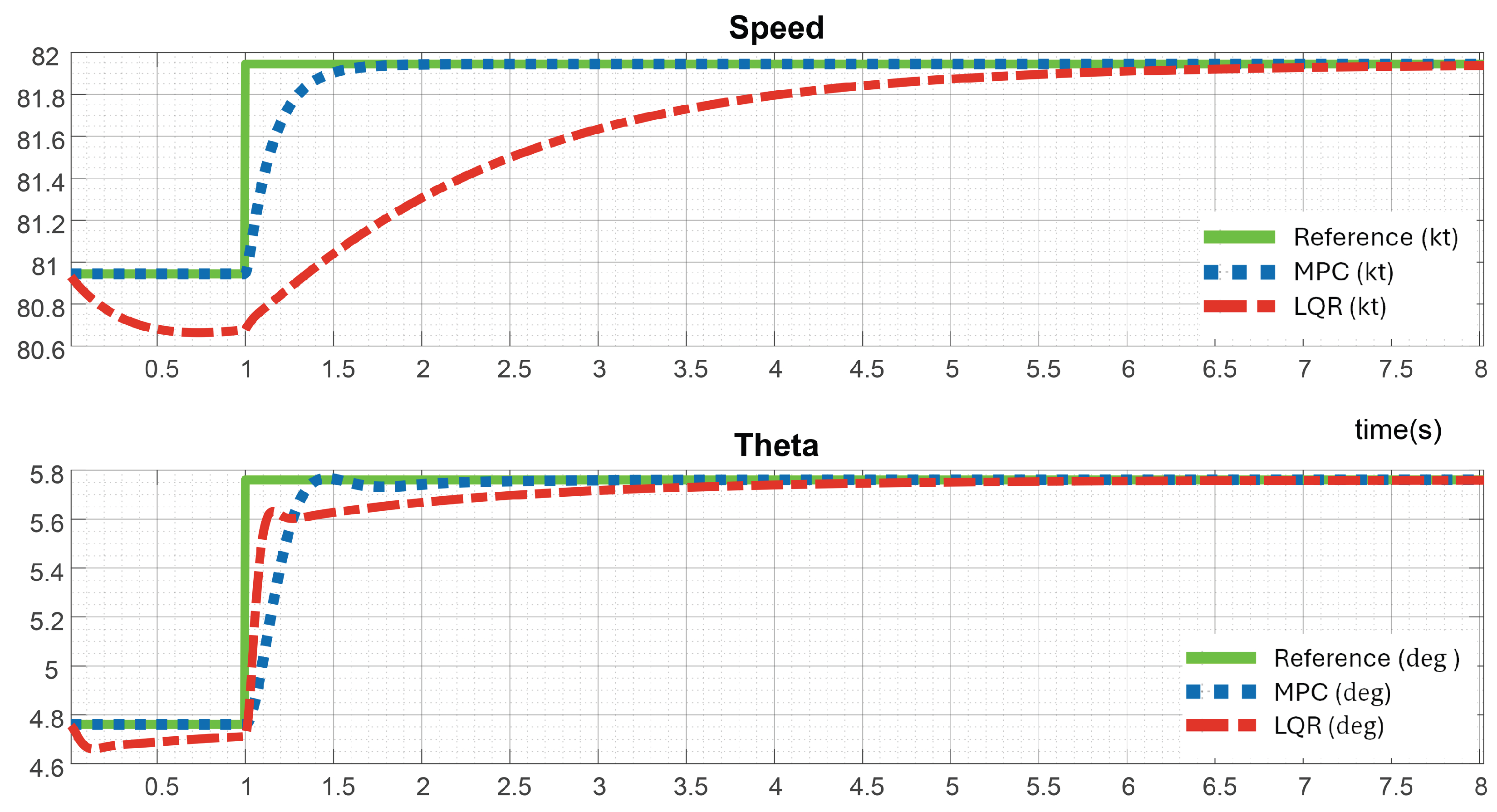
As shown in Figure 4, the difference between the MPC and LQR controllers becomes evident when a step reference is applied to both channels at the first second of the simulation. In the velocity channel, the MPC controller tracks the reference smoothly, reaching the target in only $1.75\mathrm{s}$ without overshoot or spurious peaks. The LQR controller, on the other hand, exhibits an initial reverse peak before the reference step and requires $7.852\mathrm{s}$ to settle.

A similar pattern can be observed in the $\theta$ channel. MPC shows a very small overshoot of about $1.04\%$, with a peak response time of $1.465\mathrm{s}$, and reaches the desired value in $4.274\mathrm{s}$. LQR again produces a reverse peak before following the reference and takes much longer—$10.519\mathrm{s}$—to converge.

These results highlight that MPC not only converges faster but also produces more reliable and stable responses compared to LQR. In practical terms, this suggests that MPC-based control can ensure quicker adaptation and smoother tracking under similar conditions.

The MPC controller naturally requires higher computational effort than LQR due to the online optimization performed at each sampling step. In our MATLAB/CasADi implementation, each optimization cycle (with a prediction horizon of $N_p=10$) required approximately 3–5 ms on a standard Intel i7 processor, which is well within real-time feasibility for embedded ARM-based UAV platforms. By contrast, the LQR gain is computed offline and thus imposes negligible online cost. Although MPC demands slightly more processing power, its ability to explicitly handle constraints and to integrate multiple objectives justifies its use in autonomous UAV missions, where adaptability and safety outweigh minimal computational overhead.

No Wind Scenario

As presented in

Table 3. No-wind condition results.

	Step 1	Step 2	Step 3
Disconnection Time	13.9 s	27.25 s	32.6 s
Total Flight Time	59.1 s	57.6 s	57.2 s

, the impact of weight selection under calm conditions can be clearly seen. The main goal in this set of tests was to reduce disconnection time while still completing the mission efficiently. Three different weight settings were evaluated, and the resulting disconnection and flight times are listed in the table.

The results reveal a very clear trade-off. In Step 1, where the optimization gave more weight to maintaining connectivity, the UAV kept its disconnection time to just 13.9 s. The cost of this choice was a slightly longer flight, with the mission taking 59.1 s in total. In Steps 2 and 3, as the priority shifted toward reaching the target more directly, the flight became a little shorter—57.6 and 57.2 s, respectively—but this came at a high price. The disconnection periods more than doubled, climbing to 27.25 and 32.6 s.

Put simply, the UAV saved only a couple of seconds by flying more directly, but it lost continuous contact with the network for much longer. This underlines how strongly the weighting factors shape the outcome, and it suggests that in practice the “right” balance depends less on raw travel time and more on how critical communication is for the mission at hand.

In other words, prioritizing direct target achievement shortened the overall mission by just a couple of seconds, but it more than doubled the time spent outside base station coverage. This illustrates how sensitive the optimization is to the chosen weights, and it highlights the importance of balancing connectivity against efficiency depending on the mission requirements.

Constant Wind Scenario

As summarized in

Table 4. Results under constant wind of 10 m/s at 60°.

	Step 1	Step 2	Step 3
Disconnection Time	23.9 s	30.5 s	31.25 s
Total Flight Time	70.6 s	69.0 s	68.7 s

, the influence of weight selection under constant wind conditions follows the same trend as in the no-wind case, but with more pronounced effects. Here, the UAV faced a steady wind of 10 m/s at a 60° angle, which naturally extended the overall flight duration.

In Step 1, where the weight favored connectivity, the UAV completed the mission in 70.6 s with a disconnection time of 23.9 s. When more weight was placed on reaching the target directly (Steps 2 and 3), the total flight time dropped slightly to 69.0 and 68.7 s. However, this small improvement came at a cost: the disconnection time rose to 30.5 and 31.25 s, respectively.

In simple terms, prioritizing speed in the presence of wind saved the UAV only a couple of seconds overall, but significantly increased the time spent outside base station coverage. This once again highlights the trade-off between efficiency and communication integrity, and shows that in windy environments the impact of weight selection becomes even more critical for mission planning.

6. Conclusions and Future Work

In this work, we designed and tested a dual-objective Model Predictive Control (MPC) framework for fixed-wing UAVs. The study combined two aspects that are often treated separately: longitudinal control and connectivity-aware trajectory planning. By integrating both into a single predictive framework, we were able to evaluate not only stability and tracking but also communication performance during missions.

The simulation results gave us several clear observations. First, the MPC controller responded faster and with less overshoot than the benchmark LQR, especially in step-reference tests. We also noticed that the MPC handled sinusoidal references with much smaller phase error, which is important for reliable tracking in dynamic conditions. Second, when trajectory optimization was included, the UAV could adapt its route to minimize disconnection time while still reaching the target. The trade-off between direct path and persistent connectivity became very visible in windy scenarios, which confirms the value of using tunable weights in the cost function.

One limitation of our current approach is that the model assumes constant altitude and simplified roll dynamics. While this keeps the optimization problem tractable, it also means that effects such as altitude change or lateral–yaw coupling were not considered. Another limitation is that the validation was restricted to MATLAB/CasADi simulations. Although these simulations are informative, they do not fully reflect the uncertainties of real flight.

For future work, we plan to extend the framework to six-degree-of-freedom models and to validate it on hardware-in-the-loop test benches. We are also preparing for small-scale flight experiments to see how the method performs with real communication delays and wind disturbances. In addition, adaptive elements such as online parameter estimation or reinforcement learning will be investigated, since they could help the controller maintain performance under conditions that are difficult to predict in advance.

Taken together, these findings suggest that MPC is not only a strong alternative to classical controllers like LQR but also a practical tool for UAV missions that depend on both stable flight and reliable connectivity. Our results show that predictive control can be used as a bridge between vehicle-level control and mission-level planning, making it a promising direction for future UAV operations. Although the current results are based on simulations, future work will focus on experimental validation. The proposed MPC framework will be implemented on a real UAV platform and tested under realistic wind conditions and communication delays using hardware-in-the-loop (HIL) and outdoor flight experiments. Future research will extend the current framework by considering non-uniform and time-varying wind profiles, irregular obstacle geometries, and more complex communication environments to increase the realism and robustness of the proposed approach. These improvements will enable a more accurate representation of real-world operating conditions for connectivity-aware UAV missions.