1. Introduction
Drone fleets have emerged as promising candidates for aerial base stations in future wireless networks, leveraging their flexible deployment and collaborative communication capabilities [
1]. With advancements in 5G and 6G technologies, drones can achieve higher data rates and lower latency, significantly enhancing their operational efficiency [
2]. This advantage becomes particularly critical in scenarios where traditional terrestrial base stations face network congestion or high traffic demands. However, as drone swarm size increases, conventional radio frequency (RF) communication technologies encounter two major challenges: susceptibility to interference from other devices and vulnerability to signal interception or eavesdropping.
VLC presents a promising solution to address these issues, enabling high-speed data transmission through the high-frequency flickering of LEDs [
3]. Drones equipped with VLC technology exhibit lower sensitivity to RF interference, and their communication is primarily affected by line-of-sight (LoS) fading. In outdoor environments, the impact of non-line-of-sight (NLoS) VLC-channels is largely negligible, thereby minimizing the scattering or reflection through unintended and non-visible routes [
4]. Furthermore, VLC-enabled drones can flexibly adjust the coverage of communication cells, thereby delivering secure services to specific groups of UEs [
5]. However, if a ground-based eavesdropper infiltrates the user equipments’ group, the LoS properties of air-to-ground channel links improves the quality of interception, posing a security threat to VLC-enabled drones.
In recent years, physical layer security (PLS) has emerged as a promising technique to protect drone-aided communications from malicious eavesdroppers [
6]. Unlike traditional encryption methods that rely on cryptographic keys, PLS leverages the inherent characteristics of wireless channels to enhance security [
7]. Existing PLS strategies primarily utilize friendly jamming [
8], UE–drone association [
9], trajectory optimization [
10], and power allocation [
11] to safeguard drone fleets. Specifically, Ref. [
8] proposed a deep reinforcement learning-based friendly jammer, which employs deep convolutional neural networks to degrade the interception capability of eavesdroppers. An efficient cooperative data dissemination algorithm was developed in [
9] to maximize the minimum amount of data received by all drones through optimizing multi-UE scheduling, association, bandwidth allocation, and drone mobility. Ref. [
10] employed a multi-agent deep deterministic policy gradient algorithm to maximize secure capacity by jointly optimizing drone trajectories, transmit power, and jamming power. A suboptimal power strategy for jammers was designed by using successive convex approximation, aiming to maximize the minimum average secrecy rate [
11].
Researches on VLC-enabled drones have recently attracted significant attention. Ref. [
12] proposed a multi-objective optimization problem that jointly maximizes the sum-rate and rate fairness of UEs using particle swarm optimization algorithm. In [
1], an algorithm that combines a machine learning algorithm of gated recurrent units with convolution neural networks was proposed to jointly optimize drone deployment, user association, and power efficiency while meeting the illumination and communication requirements. In [
13], a Harris Hawks optimization-based algorithm was proposed to maximize the sum rate of a VLC-enabled drone system using non-orthogonal multiple-access. Ref. [
14] jointly optimized the drone’s height and peak optical intensity for a weather-dependent covert VLC system. However, there are two key limitations in the aforementioned literature: First, most studies investigate simplified yet impractical models, such as single-drone systems, single-eavesdropper (Eve) systems, or scenarios with a limited number of UEs. Second, few works have explored the security of VLC-enabled drone systems.
To the best of our knowledge, this work is the first attempt to study the joint optimization of drone position and user association against eavesdropping in a VLC-enabled drone systems. In this work, we consider a multi-UE VLC-enabled multi-drone systems, where UEs are overheard by multiple ground eavesdroppers, and downlink transmissions between the drone and UEs follow the TDMA principle. Contributions offered by our work can be summarized as follows:
- 1.
We formulate an optimization problem to maximize the sum of the worst-case secrecy rates of UEs, subject to a UE–drone association constraint. This maximization problem consists of two core subproblems: drone position adjustment and UE–drone association.
- 2.
To address this problem, we first propose a Tabu Search (TS)-based grouping algorithm (TS-GA) to solve the UE–drone association subproblem, and then propose a Q-learning-based position decision algorithm (Q-PDA) to solve the drone position adjustment subproblem. TS-GA first guides the training process of Q-PDA by calculating initial rewards for drones in each state, and then associates UEs once the drone positions are determined.
- 3.
We evaluate the probability that Q-PDA and TS-GA find the optimal solution for their respective subproblems, respectively.
- 4.
Simulation results demonstrate that the performance of the proposed Q-PDA and Q-PDA-lite exceeds those of Random-PDA and K-means-PDA. Similarly, the proposed TS-GA outperforms random grouping, UE-channel-gain-based grouping, and channel-gain-based grouping. Finally, the proposed hybrid approach achieves near-global optimality compared with other combinations of position decision algorithms and association strategies.
The remainder of this paper is structured as follows:
Section 2 presents the system model and problem formulation,
Section 3 describes the proposed algorithms,
Section 4 discusses the simulation results, and
Section 5 concludes the study.
2. System Model
Consider a wireless network consisting of a set
with
D LED-equipped drones. These drones serve a set
of
U UEs that are randomly distributed across a geographical area
. As illustrated in
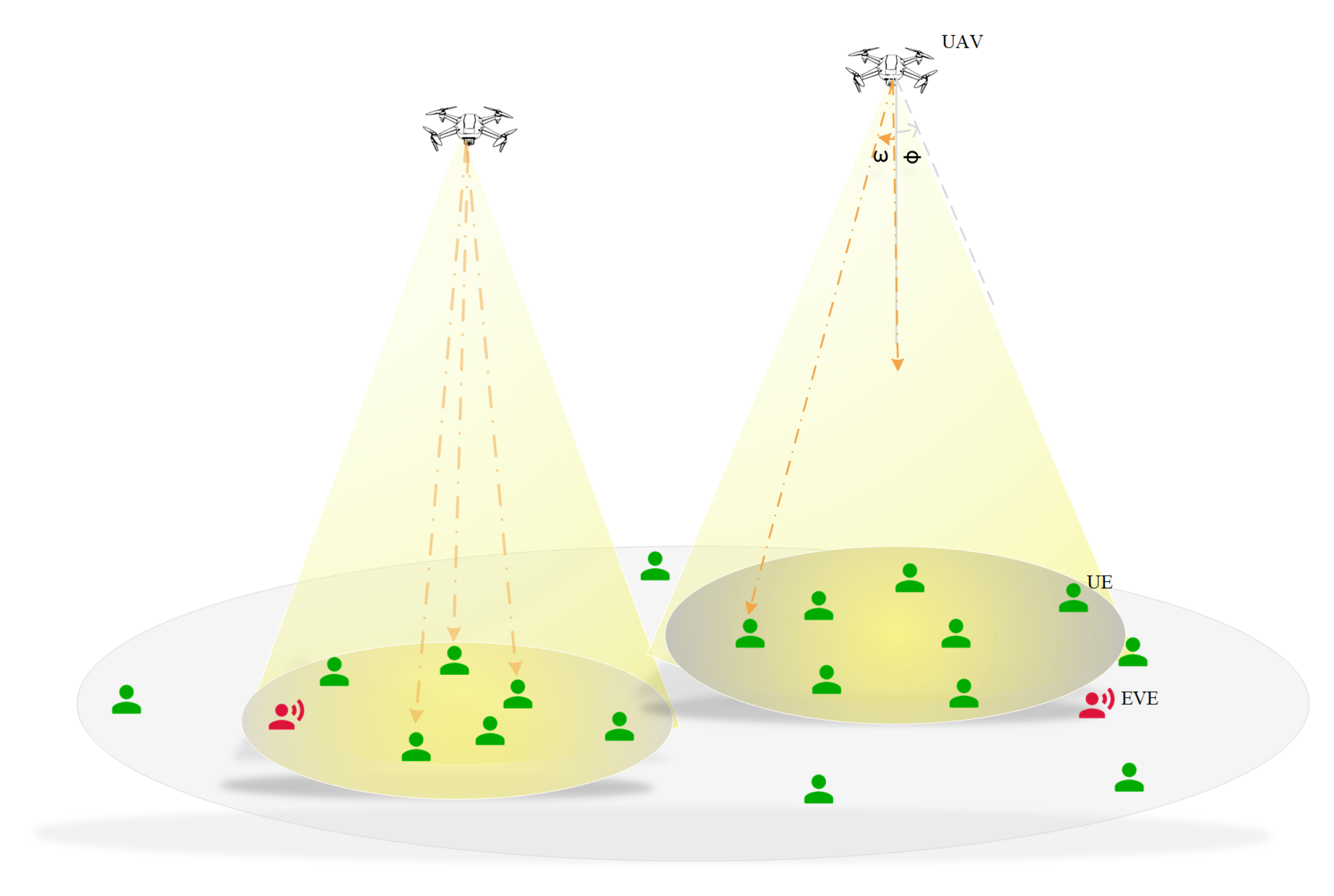
Figure 1, the drones are designed to simultaneously provide downlink communication services and illumination using VLC technique to the ground area. Within this area, multiple eavesdroppers (Eves) attempt to eavesdrop on user equipments (UEs) and intercept confidential data transmitted from drones that associated with the UEs.
In this model, we assume that as long as a UE’s position lies within the illumination coverage of the drones, the drones are capable of obtaining the spatial location information of these ground UEs. Moreover, this location information can be shared among the drones through an internal communication mechanism.
When the drones transmit confidential information, a one-to-many relationship exists between the drones and the associated UEs. Specifically, a single drone adopts an equal time allocation to send signals to the associated UEs. Conversely, each UE is restricted to associate only one drone from which to receive confidential information.
We assume that each drone does not commence serving the ground users until it has maneuvered to its optimal position. During the process of wireless transmission, for the purpose of analysis, the drones can be regarded as stationary aerial base stations, simplifying the consideration of communication interactions within the network.
2.1. Transmission Model
Given a drone located at and a ground UE located at , the probabilistic LoS and NLoS channel model is used to model the VLC link between the drone and the ground UE. A malicious e-th Eve intends to overhear the confidential information of u-th UE, which is located at .
For simplicity, we do not consider the diffusion of visible light in outdoor environments. Therefore the LoS and NLoS channel gain of the VLC link between the
d-th drone to the
u-th UE can be expressed as [
15]
where
denotes the Lambertian emission order, and
and
are the half-intensity radiation angle and the area of drone’s photodiode (PD), respectively.
is the Euclidean distance from the
d-th drone to
u-th UE, and
and
are the irradiance angle and incidence angle, respectively. These two angles are equal if both the transmitter and receiver are horizontal.
is the gain of the optical filter, and
denotes the gain of the optical concentrator which is given by [
16]
with
w and
as the refractive index and the field-of-view (FoV) of the PD used at the
u-th UE’s side, respectively. According to [
1], the probability of the LoS link is
, where
X and
Y are environmental parameters and
is the elevation angle. The average channel gain from the
d-th drone to the
u-th UE can be given by
where
.
Define the binary association matrix
between drones and UEs. Its element
indicates the association status, where
signifies that the
d-th drone is paired with the
u-th UE, and
otherwise. In our system model, not all UEs will establish connections with drones. This is because providing service to UEs close to Eve or at geographical corners can significantly compromise the system’s security. The subset of UEs that are successfully associated with drones is denoted by
, where
. Moreover, each UE within
is restricted to be associated with exactly one drone
, so we have the following constraint:
On the contrary, a drone is allowed to associate with multiple UEs, and the drone employs a uniform time allocation for associated UEs in turn, so that each UE receives its signal during an equal time resource. The number of UEs connected to a drone is not limited. The channel capacity of the
u-th UE can be reformulated by
where
is the transmit power of each drone. The noise source inside the receiver’s circuit is mainly dominated by thermal noise and shot noise. These are modeled as additive zero-mean Gaussian noise with the derivation of
.
indicates the interference over the VLC link between the
d-th drone and the
u-th UE, which is defined as follows:
When the j-th drone is also inside u-th UE’s reception range but not associated with the u-th UE, the signal transmitted from the j-th drone mixes up with the one from the d-th drone and causes interference to the u-th UE. When the j-th drone is outside the u-th UE’s reception range, the channel gain between the j-th drone and the u-th UE is equal to zero, that is, .
For a static Eve
overhearing the
u-th UE, the channel capacity of the
e-th Eve can be given by
where
denotes the channel gain of the VLC link between the
d-th drone and the
e-th Eve,
denotes the zero-mean Gaussian noise, and
indicates the interference over the VLC link between the
d-th drone and the
e-th Eve, which is defined as follows:
When a UE can be overheard by multiple Eves, the Eve with the strongest signal quality should be considered to calculate the worst-case secrecy rate of the UE, while the Eve with less signal quality can be ignored. The worst-case secrecy rate of the
u-th UE is given by substituting (
6) and (
8) as follows:
2.2. Problem Formulation
Under the proposed system model, our objective is to identify an optimal strategy that maximizes the sum worst-case secrecy rate across all UEs. This strategy involves two intertwined aspects: drone position adjustment and UE–drone association. Drone position adjustment aims to maximize coverage while minimizing the risk of eavesdropping. Meanwhile, UE–drone association is designed to group drones with UEs while considering the existence of eavesdroppers and the bandwidth utilization. This problem can be formulated as follows:
The constraint implies that each UE is limited to being associated with exactly one drone. The aforementioned problem constitutes an integer programming problem, presenting two key challenges: its non-convex nature and a large discrete solution space.
3. Methodology
To address this problem, we first propose a Tabu Search (TS)-based grouping algorithm (TS-GA) to solve the UE–drone association subproblem, and then propose a Q-learning-based position decision algorithm (Q-PDA) to solve the drone position adjustment subproblem. Together, the hybrid algorithm TS-GA+Q-PDA solves the problem (
11). In this section, we first introduce the proposed TS-GA, followed by the procedure of the Q-PDA and a simplified version of this algorithm.
Q-learning can directly navigate non-convex and discrete solution spaces through iterative learning of optimal policies via state–action value estimation. However, when directly applying Q-learning to scenarios where multiple drones serve a relatively large number of UEs, the UE–drone association subproblem significantly expands the Q-table size and increases training time—making it impractical for high-mobility scenarios. Thus, we first employed TS to solve the UE–drone association subproblem and also provide the UE–drone association results for the training process of Q-learning.
3.1. TS-Based Grouping Algorithm (TS-GA)
In the UE–drone association process, a TS-based grouping algorithm (TS-GA) is proposed to associate UEs and drones from the perspective of the UE. Denote the set of drones within the received signal range of the u-th UE as , where . For example, means that within the received signal range of 1-th UE, there are only two drones indexed 1 and 3, and it can only associate with either the 1-th or 3-th drones. Based on the set of drones, a near-optimal solution can be obtained by applying TS-GA. The basic idea of TS-GA is to use a tabu list to record the solutions that have been searched recently, preventing the algorithm from cycling back to these solutions and thus avoiding getting trapped in local optima. The generation rules of the initial solution, candidate solutions, tabu rules, and aspiration principles are designed as follows:
A. Initial Solution: The initial solution determines the starting point of the search. If the quality of the initial solution is high, the algorithm can conduct in-depth exploration near the high-quality solution from the beginning, accelerating the convergence of the algorithm.
A channel-gain grouping algorithm, which will be introduced in
Section 4, is applied to match drones for all UEs according to
to generate a set of solutions. This set of solutions is used as the initial solution
.
represents the index of the drone connected to
u-th UE. If
, it means that the
u-th UE is not connected to any drone.
B. Candidate Solution Specification: The candidate solutions are a set of new solutions obtained by making small adjustments and transformations to a known basic solution according to specified rules, and are used to select a solution in a new round of iteration. This scheme inherits the local search ability of the Tabu Search, which is more conducive to in-depth exploration of potential high-quality solutions near the current high-quality solution.
During the
l-th iteration, we assume that the grouping solution obtained in this iteration is denoted as
. We take
as the basic solution for generating candidate solutions in the
-th iteration. The number of candidate solutions is set in each iteration to be the same as the number of UEs
U. The rule of candidate solution generation is designed as follows: switch a different drone for the
u -th UE in the solution
to form the
u-th candidate solution. Specifically, for the
u-th candidate solution, we replace the drone connected to the
u-th UE in the solution
with a drone randomly selected from the set
, as follows:
where
means randomly selecting a connectable drone from the set
for the
u-th UE. The matrix of the candidate solutions in the
-th iteration is
.
C. Tabu Rules: To prevent the algorithm from repeatedly choosing near the local optimum and falling into an infinite loop, we have set up a tabu list in the algorithm. The tabu list is used to record and store the solutions visited recently. When a set of solutions is visited, all the associations between UEs and drones are put into the tabu list for restriction to prevent from being selected again in the near future. A tabu period in this algorithm is set as , and the tabu period defines the number of iterations during which the solutions in the tabu list are restricted. When the times for a solution to be banned reaches the tabu period, it will be released and can be selected again.
The tabu list and the tabu period interact with each other, which can effectively guide the search process and are important tools for achieving the global optimization of the tabu algorithm. represents whether the association between the i-th UE and the j-th drone is tabued. When initialized, is a matrix of all 0s. In the process of algorithm, if , it means that this UE–drone association is not tabued. If , it means that this connection has been tabued and has not been released temporarily. A tabu times matrix is also set to record the number of times that each UE–drone connection is tabued. When a group of connections is tabued too many times, the algorithm stops iterating.
(1) Tabu Condition: If the drone and user are repeatedly connected within the tabu period, that connection becomes tabu. Any candidate solution with a tabu connection is prohibited from being selected, unless the Aspiration Criterion is satisfied. This prevents the algorithm from revisiting recently searched areas in the short term (tabu period ).
(2) Aspiration Criterion: The Aspiration Criterion serves as an override mechanism to the Tabu Condition. If a candidate solution includes tabu connections and yields a sum worst-case secrecy rate superior to the global best solution, the tabu status of these connections will be disregarded. In such cases, amnesty is granted to these connections, and the resulting candidate solution is selected as the new current solution, thus preventing the algorithm from missing potential improvements solely due to rigid tabu restrictions.
(3) Tabu Operation: In each iteration, when the algorithm selects a candidate solution
as the solution, we record the connections in this solution by updating the tabu list
and set its value as the tabu period. The equation is as follows:
(4) Release Operation: After each iteration, all the banned associations in the tabu list
need to release one time, that is, decreased by 1. At this time, update the
matrix operation. The equation is as follows:
The procedure of the proposed algorithm is described in Algorithm 1.
| Algorithm 1: TS-GA. |
| Input: d-th drone’s position qd, ∀d = 1, …, D |
| Output: The grouping solution with the best secrecy performance xmax |
| Initialize x(0) |
| 2: for each iteration index l ∈ [1, max-time] do |
| Generate the Matrix of candidate solutions (l) according to x(l−1) |
| 4: for each candidate solution index u ∈ [1, U] do |
| if (l)u does not meet the Tabu condition then |
| 6: Execute Release Operation by using Equation (19) |
| Execute Tabu Operation by using Equation (18) |
| 8: x(l) = (l)u |
| break |
| 10: else |
| if (l)u meets the Aspiration Criterion then |
| 12: Execute Release Operation by using Equation (19) |
| Execute Tabu Operation by using Equation (18) |
| 14: x(l) = (l)u |
| xmax = (l)u |
| 16: break |
| else |
| 18: Execute Release Operation by using Equation (19) |
| end if |
| 20: end if |
| end for |
| 22: if any element in Ttime(u, du) > Threshold then |
| break |
| 24: end if |
| end for |
| 26: return xmax |
3.2. Theoretical Analysis
To quantify the probability of TS-GA finding the optimal solution for the UE–drone association subproblem, we first introduce a realistic assumption: high-quality solutions are locally connected, including the optimal solution. TS-GA search for the optimal solution proceeds in two sequential phases:
(1) Exploration phase: Assuming each iteration has an independent probability
of transitioning into the high-quality solution set
, the probability of not entering
in
iteration is
. Thus, the probability of entering
within
iterations is
where
T is the total number of iterations.
(2) Stability phase: Each iteration in this phase has a probability
of remaining in
and an average probability
of transitioning into the optimal solution from any high-quality solution in
. Overall, the probability of finding the optimal solution in
for all
iterations is
where
.
In conclusion, combining the two phases, the total probability of finding the optimal solution for the UE–drone association subproblem until iteration
T is
By setting the tabu period and the maximum iteration number in the TS-GA, we can have and . In this case, even if and , we still obtain .
3.3. Benchmark Algorithms
The benchmark algorithms for evaluating the performance of TS-GA are defined as follows:
Random grouping: Under random grouping, each UE randomly chooses one drone from those within its signal reception range. The probability of finding the optimal solution for the UE–drone association subproblem is
where
is the probability of finding the best association for the
u-th UE, and
is the set that includes the drones within the reception range of the
u-th UE.
UE-channel-gain grouping: Each UE selects the drone with the highest received channel gain as its fixed signal source. The probability of finding the optimal solution for the UE–drone association subproblem is given by
In practice, the optimal solution rarely requires all UEs to choose the drone with the highest channel gain, since the strongest channel gain does not equate to the highest security. For instance, if an Eve is located near a drone, the Eve may also intercept the strongest signal, leading to a significant drop in the overall system security performance.
Channel-gain grouping: Channel-gain grouping is similar to the UE-channel-gain strategy, but only choose a drone for which the UE’s received channel gain is greater than Eve’s intercepted channel gain. The probability of finding the optimal solution for the UE–drone association subproblem is
where
is the probability that the
u-th UE selects the optimal drone. Here,
denotes the set of drones that can make the associated
u-th UE’s received channel gain higher than that of any Eve. The optimal association is contained in
, since associating with drones in
typically satisfies the security constraint.
In conclusion, the probability of finding the optimal solution using channel-gain grouping is higher than that using random grouping, i.e., . For UE-channel-gain grouping, the probability of finding the optimal solution is in most cases.
Compared to these three benchmark algorithms, by properly setting the parameters in TS-GA, the probability of finding the optimal solution is nearly 1, i.e., .
3.4. A Q-Learning-Based Position Decision Algorithm (Q-PDA)
This algorithm determines the optimal drone position by identifying the state that occurs most frequently among the end states reached by paths originating from multiple states. In a complex operational environment with numerous possible states for the drone, the most frequently occurring end state among those reached from multiple starting states is likely to represent a stable and efficient position. This approach allows Q-learning to quickly converge to a near-optimal position, especially in scenarios without specifying the target state in advance. The procedure of the proposed algorithm is described in Algorithm 2. The variables for the subsequent operations in the proposed algorithm are described as follows:
A. State: In this algorithm, we consider the candidate position of a drone as state, , and the total number of states is , where , , where and are the edges of the map, respectively. A minimum separation distance v is maintained to prevent potential collisions among drones. We use v as the degree of discretizations, which determines the size of the divided grid in the predefined service area.
B. Action: We define the movement action space of the drone as
When the drone is in state , it takes an action , where .
C. Q-table: Similarly as traditional Q-learning, we use Q values to represent the expected cumulative rewards obtained after taking a certain action in a certain state and storing the values of each state–action pair in a matrix.
(1) Initialize Q-table using vector: vector provides initial values to matrix. The worst-case secrecy rate is calculated for each candidate position and recorded in the corresponding vector. By sequentially assuming a drone is positioned at each candidate location, we systematically obtain the worst-case secrecy rate varying with location. when calculating it, the proposed TS-GA (or other grouping algorithms) is needed to associate drones at position with nearby UEs. Furthermore, if , the previously trained drones participate in the grouping process, and the worst-case secrecy rates of the previously deployed positions and their adjacent positions are set to 0 in the matrix to prevent collisions.
Before training the
i-th drone,
i-th Q matrix
is initialized using the
at the beginning, that is
(2) Update Q-table: Drones approach the optimal position by continuously choosing the actions and updating the Q values. Through continuous Q-value updates, the optimal strategy is learned, with the aim of finding the most secure positions. At time step
t, after performing the action
in state
, we update the Q-value table
following the Bellman optimality equation [
17]:
where
is the current Q-value when taking action
in state
, and
is the maximum Q-value when choosing the best action
in the next state
.
is the learning rate
, which controls the influence of new experience on the Q-value update,
is the immediate reward obtained after performing action
at time step
t, and
is the discount factor
, which controls the influence of future rewards on the current decision.
D. Suboptimal position decision: The suboptimal position of a drone is determined by the end state toward which most starting points eventually converge. In each episode, the i-th drone is placed at a random initial position; after training its Q-table (), the drone executes actions yielding the highest reward in each step until it reaches a terminal state . We then record the frequency of each terminal state across all episodes, with the most frequently encountered terminal state selected as the suboptimal position. This approach leverages the inherent stability of the Q-learning policy, where high-frequency terminal states emerge as “attractors” that balance exploration and exploitation—reflecting positions robust to variations in initial conditions and thus suitable for practical deployment.
| Algorithm 2: Q-PDA.
|
| Input: input state set , action set
|
| 1: Training process: |
| 2: Initialize ri (Initialize ri as defined in Section 3.2),
∀st = (xt, yt) ∈ S,
∀at ∈
, Flag = 1 |
| 3: for Each drone i ∈ [1, D] do |
| 4: Generate Qi, Initialize send(st) |
| 5: for Each episode t ∈ [1, 2000] do |
| 6: if Flag = 1 then |
| 7: random initial state s0 ∈ S, select a random action a0 from this state s0, Flag = 0. |
| 8: end if |
| 9: Generate random number β ∈ [1, 100] |
| 10: if β < 80 − t/25 then |
| 11: Random choose an action at = random() |
| 12: else |
| 13: Choose the action with best reward at = argmaxa Qit(st, a) |
| 14: end if |
| 15: Calculate the reward value by using Equation (32) and update Qit. |
| 16: if st = st+1 or st = 0 then |
| 17: send(st) = send(st) + 1; Flag = 1; |
| 18: continue; |
| 19: else |
| 20: st ← st+1; |
| 21: Place i-th drone in st; |
| 22: end if |
| 23: if count(||Qit − Qit−1|| ≤ 0.0001) = 1000 then |
| 24: Break; |
| 25: end if |
| 26: end for |
| 27: Determine i-th drone’s location by using the most frequently occurred end state, that is qi = argmaxst(send(st)), |
| if the drone’s position has already been selected, choose the suboptimal solution. |
| 28: return qi |
| 29: end for |
3.5. A Simplified Q-Learning-Based Position Decision Algorithm (Q-PDA-Lite)
Building upon the previous algorithm, we introduce a simplified version, Q-PDA-Lite, that relies on the to streamline the training process without grouping UEs with the previously trained drones. By eliminating the need to compute additional matrices, this approach significantly reduces computational overhead. During the training for i-th drone, when initializing the i-th Q matrix, the is preprocessed by setting the values corresponding to previously deployed drones’ positions and their adjacent postions to zero.
3.6. Theoretical Analysis
To quantify the probability of Q-PDA finding the optimal solution for the drone position adjustment subproblem, we first introduce two realistic assumptions: Under the -greedy policy, every state–action pair is visited with positive probability. When Q-values converge to stable values, the greedy policy selects actions corresponding to the optimal policy. Q-PDA searches for the optimal solution proceed in two sequential phases:
(1) Exploration phase: Suppose that starting from any non-optimal state, the probability of jumping directly to the optimal state within one step is
where
is the action space. The probability of visiting the optimal solution within
iterations is
(2) Convergence and Lock-in phase:
After Q-values converge to a stable value, Q-PDA will stably take optimal actions, thereby stably outputting the optimal solution. By setting learning rate and ergodicity conditions, Q-PDA converges with probability 1, that is
In conclusion, combining the properties of the two phases, the probability that Q-PDA finds the optimal solution for the drone position adjustment subproblem within
steps can be expressed as
When T is sufficiently large, .
3.7. Convergence and Complexity Analysis
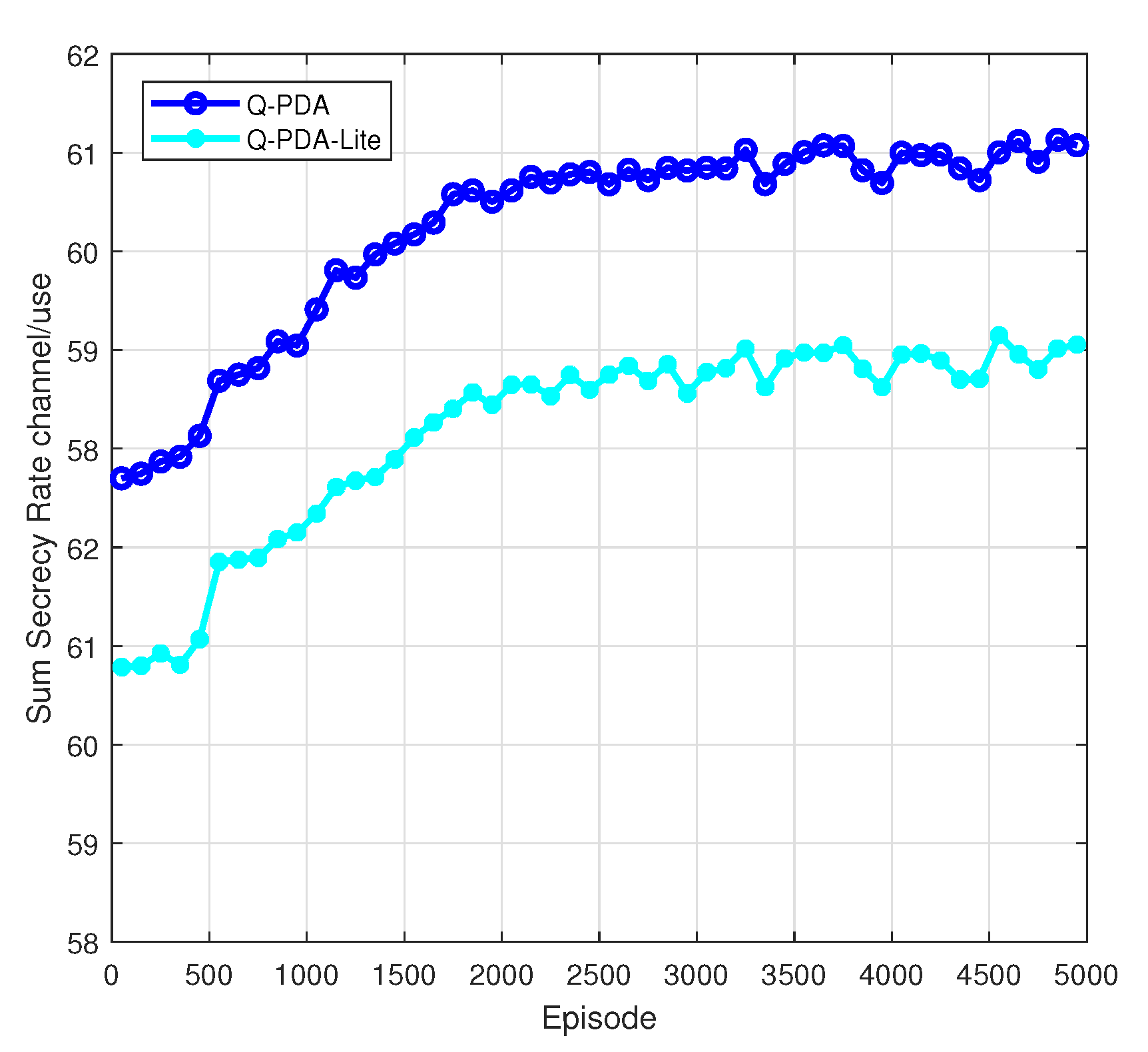
As shown in
Figure 2, the secrecy performance of Q-PDA and Q-PDA-Lite tends to stabilize in the episode of 2000. Therefore, the number of learning episodes is set to 2000 in the following simulations.
The time complexity of TS-GA depends on three steps: candidate solution generation, candidate solution analysis, and tabu-list management. The time cost of the above three steps are , , and , respectively. The total worst-complexity of TS-GA is , where T represents the maximum number of iterations.
The time complexity of Q-learning needs to be analyzed from two aspects: single update and convergence iteration. The time complexity of a single update is mainly due to the traversal during action selection, that is .The time complexity of convergence iteration is , where represents the maximum number of episode, and Avgstep is the average number of steps in each episode. In conclusion, the time complexity of Q-PDA and Q-PDA-Lite are and , respectively.
3.8. Benchmark Algorithms
The benchmark algorithms for evaluating the performance of Q-PDA and Q-PDA-Lite are defined as follows.
Random-PDA: Within the deployment area, a random two-dimensional coordinate is generated for each drone to be deployed. The drones are directed to these positions, which form the deployment solution of the Random-PDA algorithm. The probability of finding the optimal solution for the drone position adjustment subproblem is
where
S is the total number of states.
K-means-PDA: Assuming the system has knowledge of all user locations within the area, the standard K-means algorithm is used to partition the users into a number of clusters equal to the number of drones. The drones are then guided to the centroids of these clusters, which constitute the deployment solution of the K-means-PDA algorithm. This method aims to maximize the channel quality of UEs. The probability of finding the optimal solution for the drone position adjustment subproblem is
In practice, the optimal solution rarely requires drones to select positions based on UE density. Although being surrounded by a large number of UEs (and associating with them) improves UE channel quality, the highest UE channel quality does not equate to the highest system security. For instance, if a drone is deployed near an Eve in a UE-dense cluster, Eve can easily intercept the strong signals intended for UEs—leading to a significant drop in overall security performance.
The probability of Q-PDA finding the optimal solution is approximately 1. For the benchmark algorithms, their probabilities of finding the optimal solution are usually or even . This is because the benchmark algorithms only rely on a single selection, making it difficult to hit the optimal solution.
4. Simulation Results
In
Section 4.1, we examine the hybrid algorithm TS-GA+Q-PDA by comparing it with other hybrid algorithms. Then, an ablation study is conducted to investigate the impact of each modular algorithm on the hybrid algorithm TS-GA+Q-PDA. In
Section 4.2, we examine the Q-PDA module within the hybrid algorithm TS-GA+Q-PDA. In
Section 4.3, we investigate the TS-GA module from the hybrid algorithm TS-GA+Q-PDA. In
Section 4.4, the security performance of the hybrid algorithms TS-GA+Q-PDA and TS-GA+Q-PDA-Lite is compared with that of exhaustive search.
All simulations were implemented using MATLAB (version 2016). software. In the simulations, we configured 20 UEs to be distributed within a specified spatial area, all at a uniform height of 0.8 m. To mimic real-world application scenarios more accurately, the UEs’ positions were randomly assigned within this area. In the same model, we assumed the presence of four drones, also distributed within the area but at a unified height of 10 m. Since all drones maintain a fixed altitude, our analysis focuses on the two-dimensional plane at that altitude. The parameters used in the following simulations are shown in
Table 1.
4.1. Comparison of TS-GA+Q-PDA Versus Other 15 Hybrid Algorithms
Based on
Section 3.3 and
Section 3.8, there are four position decision algorithms (including the proposed Q-PDA and Q-PDA-Lite) and four grouping algorithms (including the proposed TS-GA). This yields a total of 16 possible hybrid combinations of position decision and grouping algorithms. In this subsection, we compare the proposed TS-GA+Q-PDA with the other 15 hybrid algorithms.
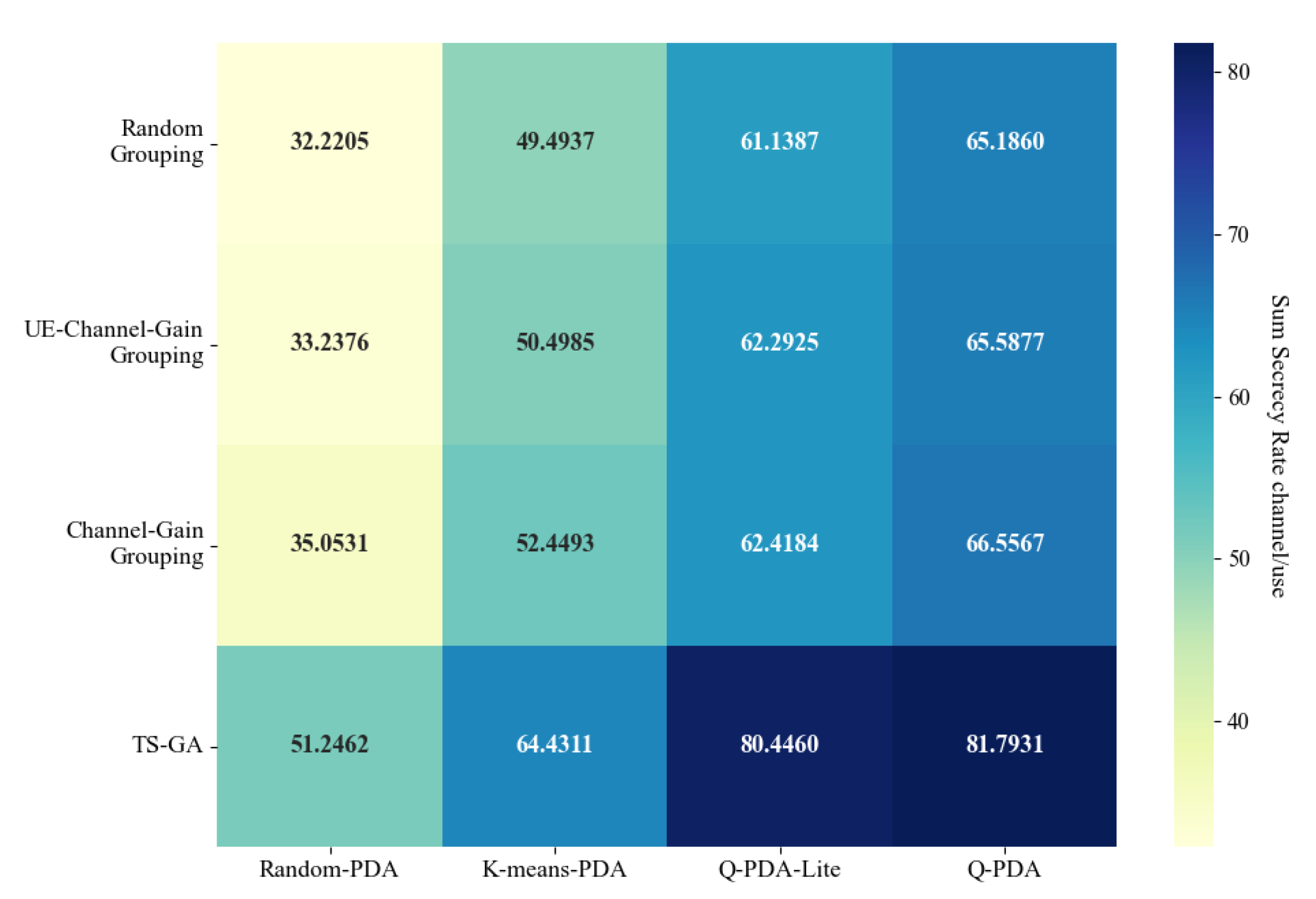
In
Figure 3, the security performance of TS-GA+Q-PDA is presented and compared with other hybrid algorithms at the drone’s transmit power of 50 W. Among all the hybrid algorithms, TS-GA+Q-PDA achieves the highest worst-case sum secrecy rate, reaching approximately 81 channel/use.
Additionally, among TS-GA and the benchmark grouping algorithms, all the position decision algorithms have higher performance with the combination of TS-GA. This is because TS-GA focuses its search directly on finding solutions with the best security performance, rather than (like the benchmark algorithms) only identifying solutions that exhibit the characteristics of the optimal solution.
Among Q-PDA and the benchmark position decision algorithms, all the grouping algorithms have higher performance with the combination of Q-PDA. This is because Q-PDA arranges drones in areas with dense UEs while keeping them far from Eves. This deployment enhances the received SINR of UEs and reduces the probability of signal interception by Eves, thereby improving the overall system security performance.
4.2. Comparison of Q-PDA and Q-PDA-Lite Versus Other Benchmark Algorithms
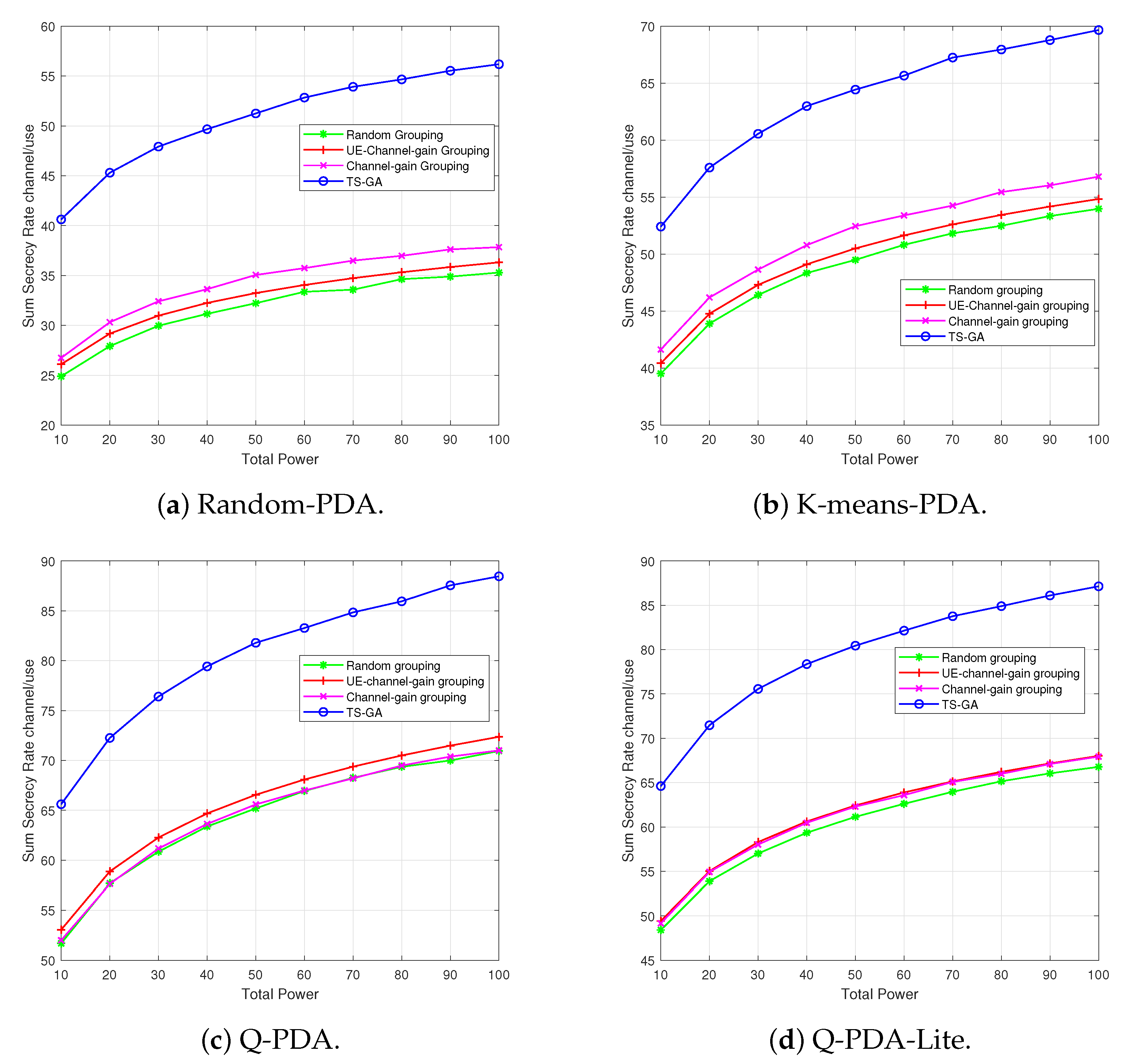
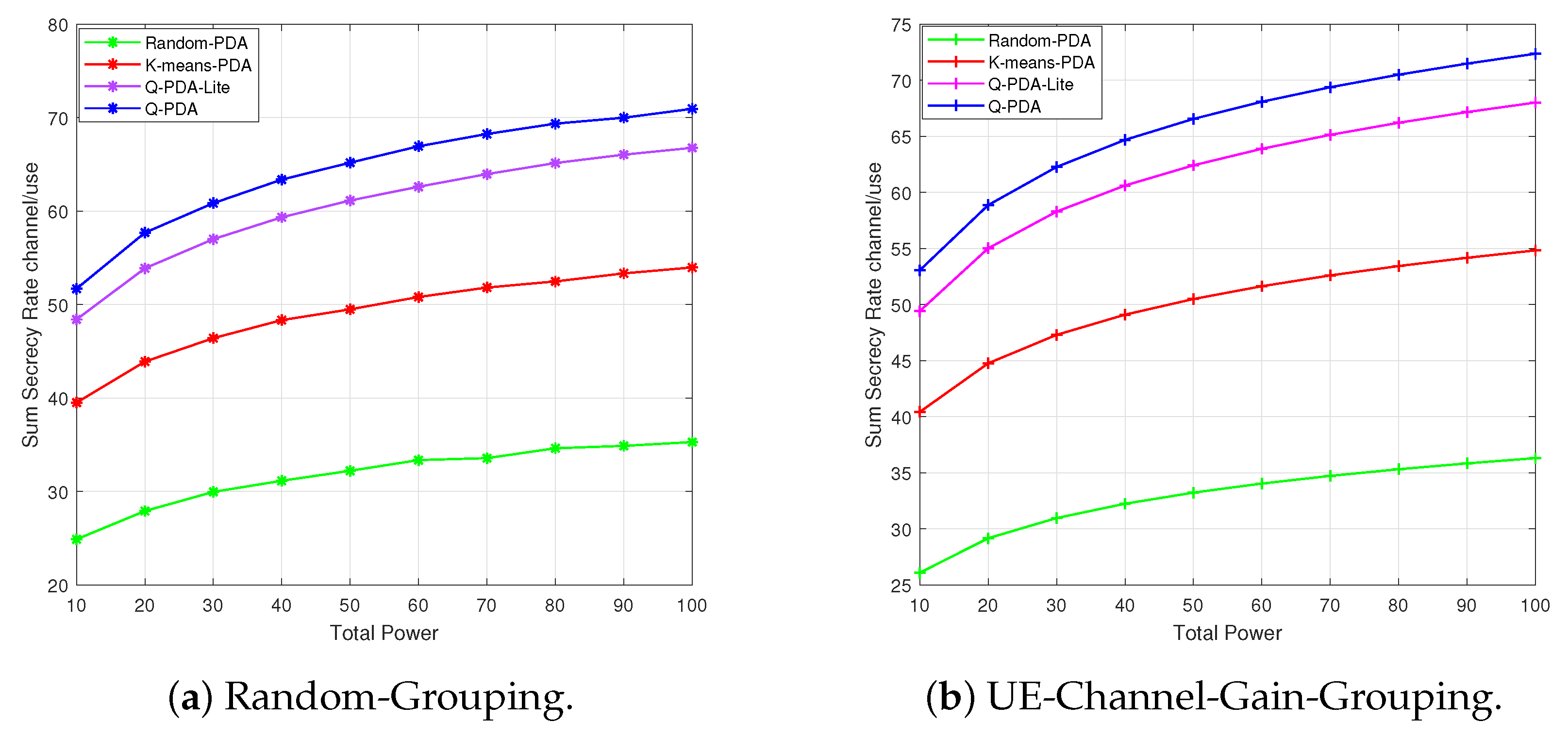
In
Figure 4, the security performance of Q-PDA and Q-PDA-Lite variation with the transmit power is presented and compared with random-PDA and K-means-PDA. With an increase in the drones’ transmit power, the received SINR of the associated UEs rises, thus improving the system’s secrecy performance of Q-PDA, Q-PDA-Lite, and benchmark algorithms.
By conducting a horizontal comparison of different subfigures, both Q-PDA and Q-PDA-Lite outperform Random-PDA and K-means-PDA. This is because Q-PDA and Q-PDA-Lite consider both the positions of UEs and Eves. By using Q-PDA and Q-PDA-Lite, drones are arranged in a dense UE area and are far from Eves. In Q-PDA-Lite, we do not implement the grouping of UEs with pre-trained drones in the training, which leads to relatively lower performance compared to Q-PDA. In
Figure 4a, when the Random-PDA is employed instead of Q-PDA, drones may end up in sparse regions with a small number of UEs. Moreover, since Eve’s presence is disregarded, drones can get close to Eve. This proximity increases the risk of signal interception and decreases the secrecy rate. In
Figure 4b, when the K-means-PDA is employed instead of Q-PDA, the K-means-PDA selects centroid positions to maximize user coverage by taking into account the UE distribution. Nevertheless, it still overlooks Eve’s positions, and drones may occasionally be deployed in closer proximity to eavesdroppers, which results in degradation of the secrecy rate.
4.3. Comparison of TS-GA Versus Other Benchmark Algorithms
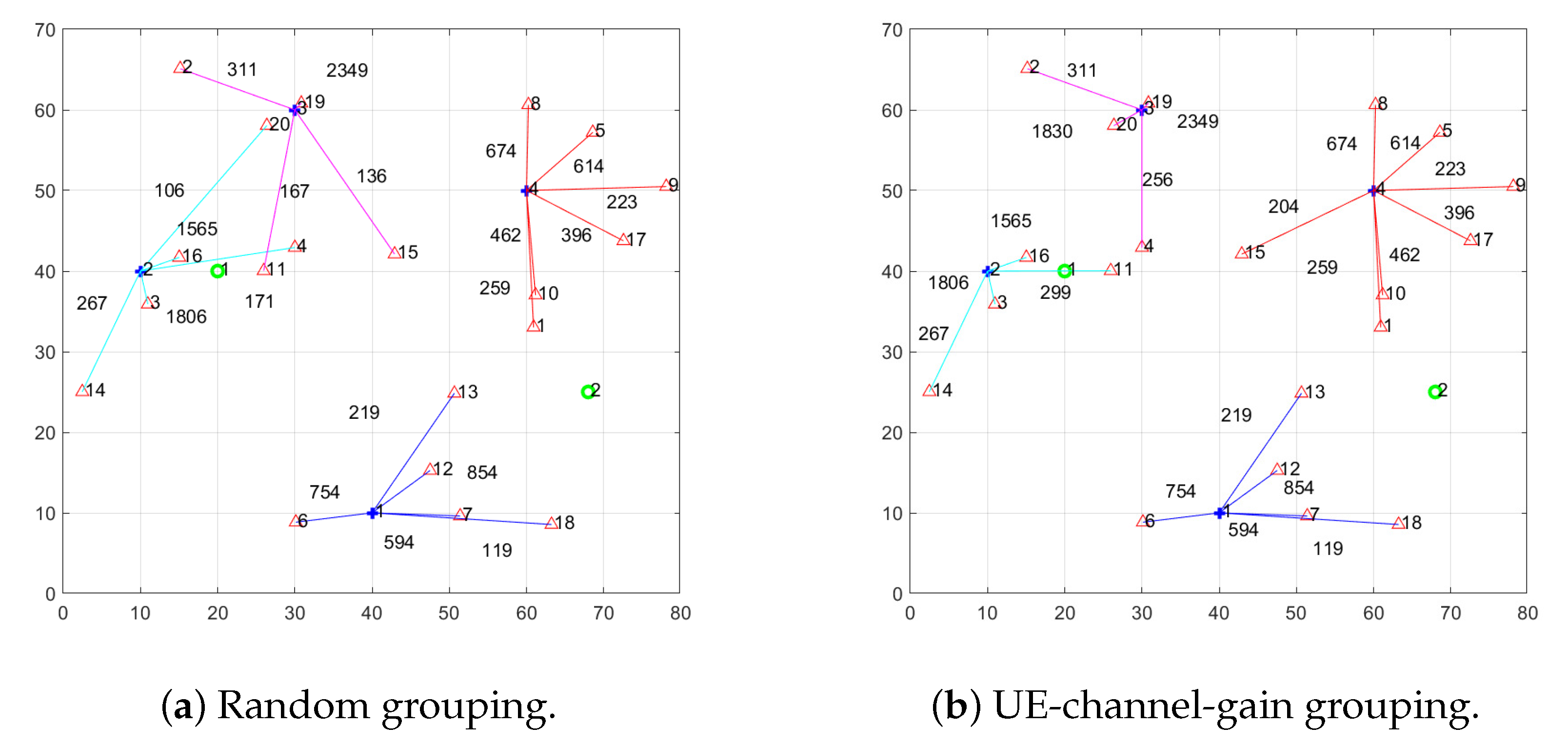
In this subsection, we first compare the performance of TS-GA and its benchmark grouping algorithms, while using Q-PDA as the position decision algorithm. Compared with the benchmark grouping algorithms, TS-GA has fewer associations, yet each association is effective. In the time-sharing system, the reduced number of associations allows UEs with better positions (which are close to drone and far away from Eve) to receive signals for a longer duration, consequently increasing the overall system secrecy rate.
In
Figure 5a, the channel gain of most UEs associated to drones is 0, which leads to a zero secrecy rate. This is because random-grouping does not consider the signal strength of the UE or the Eve and randomly selects a drone from those within the UE’s signal reception range. Unlike the random-grouping, as shown in
Figure 5b, the UE-channel-gain-grouping has each UE selects the drones with the highest channel gain as the association target. However, the secrecy performance of the system may degrade to zero if Eves have better channel gains from the drone than the associated UEs.
The channel-gain-grouping differs from the above two methods by taking the positions of the Eves into account. As shown in
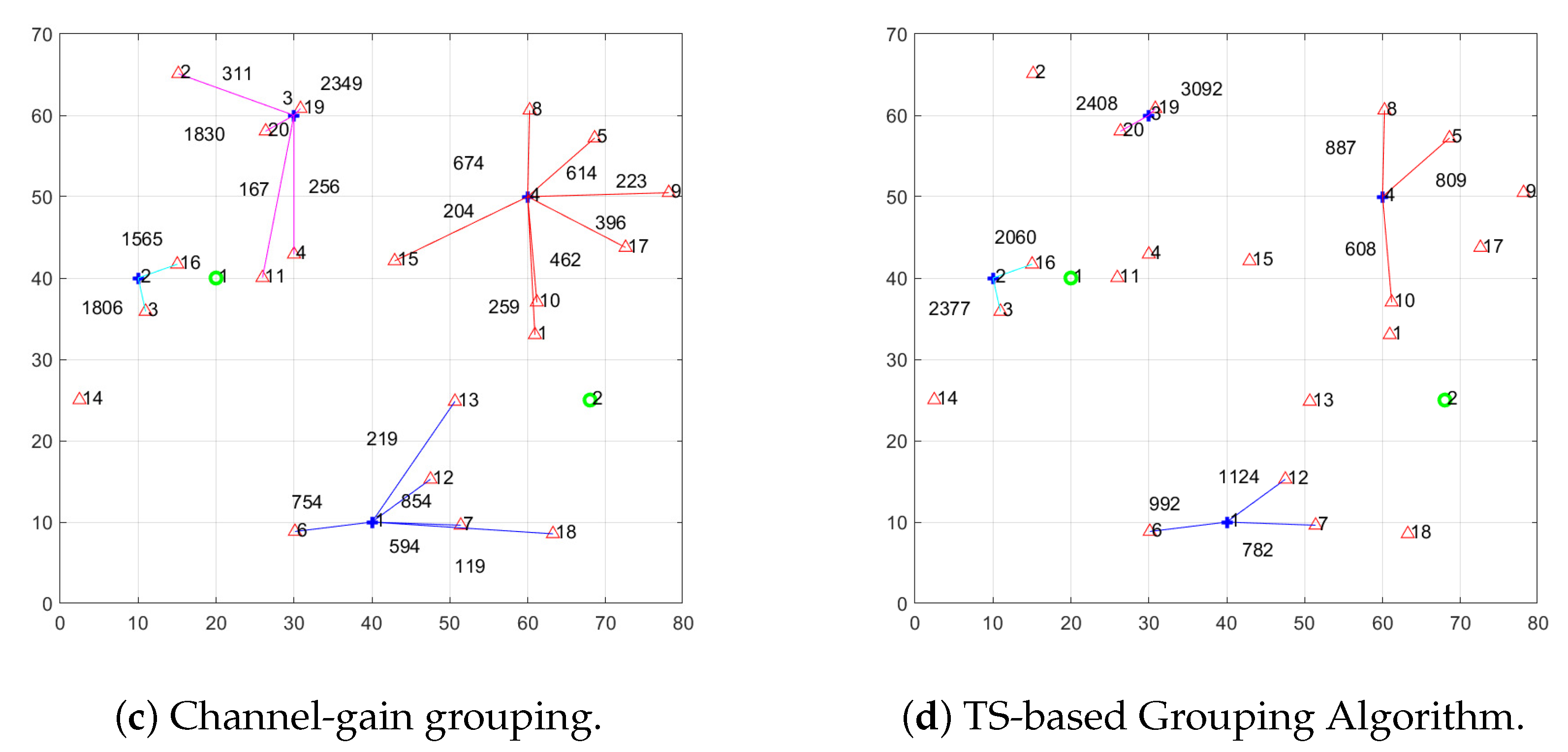
Figure 5c, drones can only associate to UEs that are closer to it than Eve. By selecting a drone with a channel gain greater than the intercepted channel gain for each UE, the number of effective associations increases, thereby better than random-grouping and UE-channel-gain-grouping.
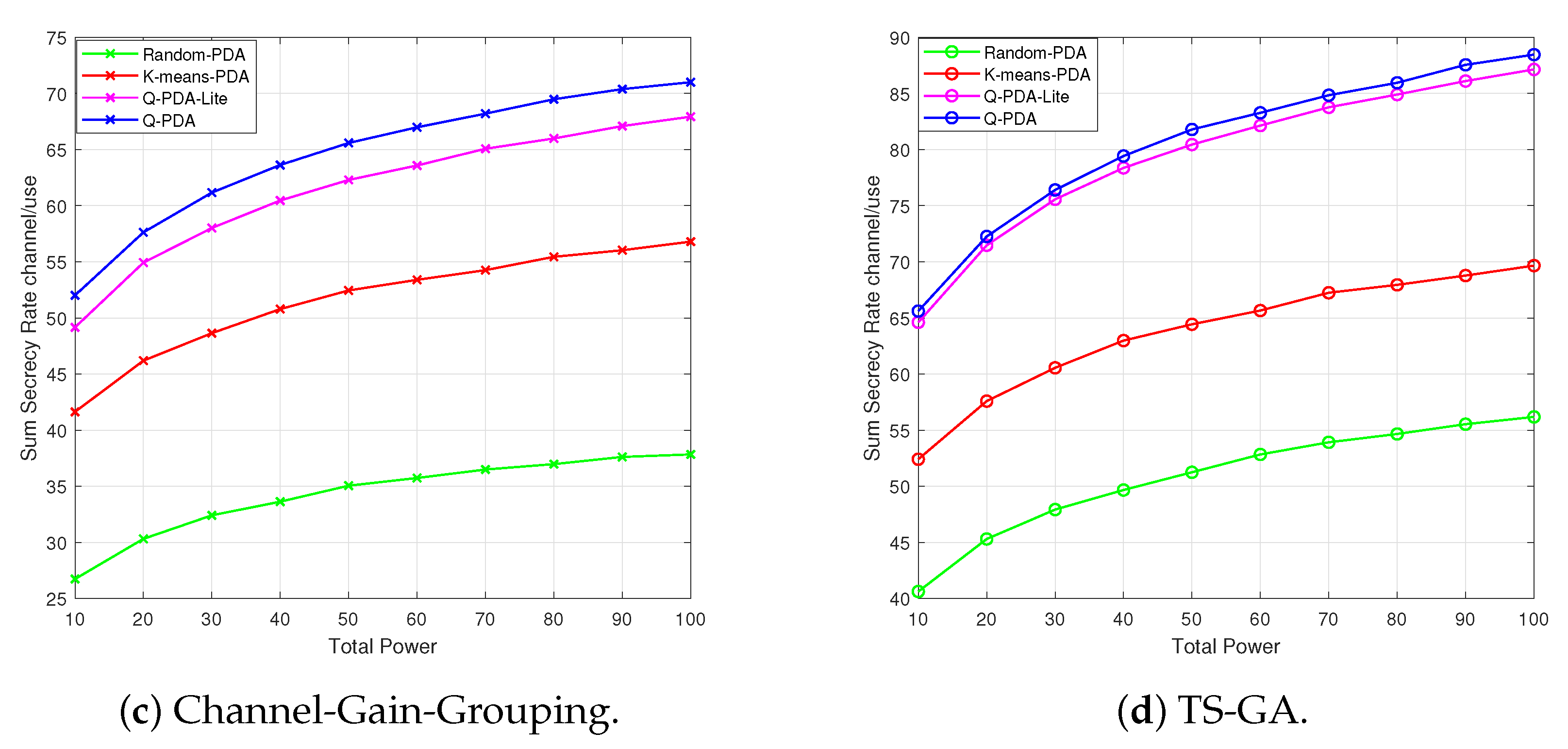
Then, in
Figure 6, the security performance of TS-GA varying with the transmit power is presented and compared with random-grouping, UE-channel-gain-grouping, and channel-gain-grouping. With an increase in the drones’ transmit power, the received SINR of the associated UEs rises, thus improving the system’s secrecy performance of TS-GA and benchmark algorithms.
By conducting a horizontal comparison of different subfigures, TS-GA outperforms random-grouping, UE-channel-gain-grouping, and channel-gain-grouping, reaching up to approximately 88 channel/use. This is because TS-GA focuses its search within the neighborhood of good-quality solutions to explore better candidates, thereby increasing the probability of finding the optimal solution. In
Figure 6c, when the channel-gain-grouping is employed instead of TS-GA, the performance improves slightly relative to random-grouping and UE-channel-gain-grouping but still cannot match TS-GA. This is because the channel-gain-grouping only prioritizes the “UE–drone–Eve distance” metric, while TS-GA explores multiple dimensions to generate more optimal groupings.
In
Figure 6a, when the random-grouping is employed instead of TS-GA, it merely selects a drone randomly from those within the UE’s signal reception range, leading to numerous invalid associations that fail to contribute to the security of the system. In
Figure 6b, when the UE-channel-gain-grouping is employed instead of TS-GA, it overlooks the threat of Eves. If an Eve has a better channel gain from the associated drone than the UE itself, the system’s security is severely compromised.
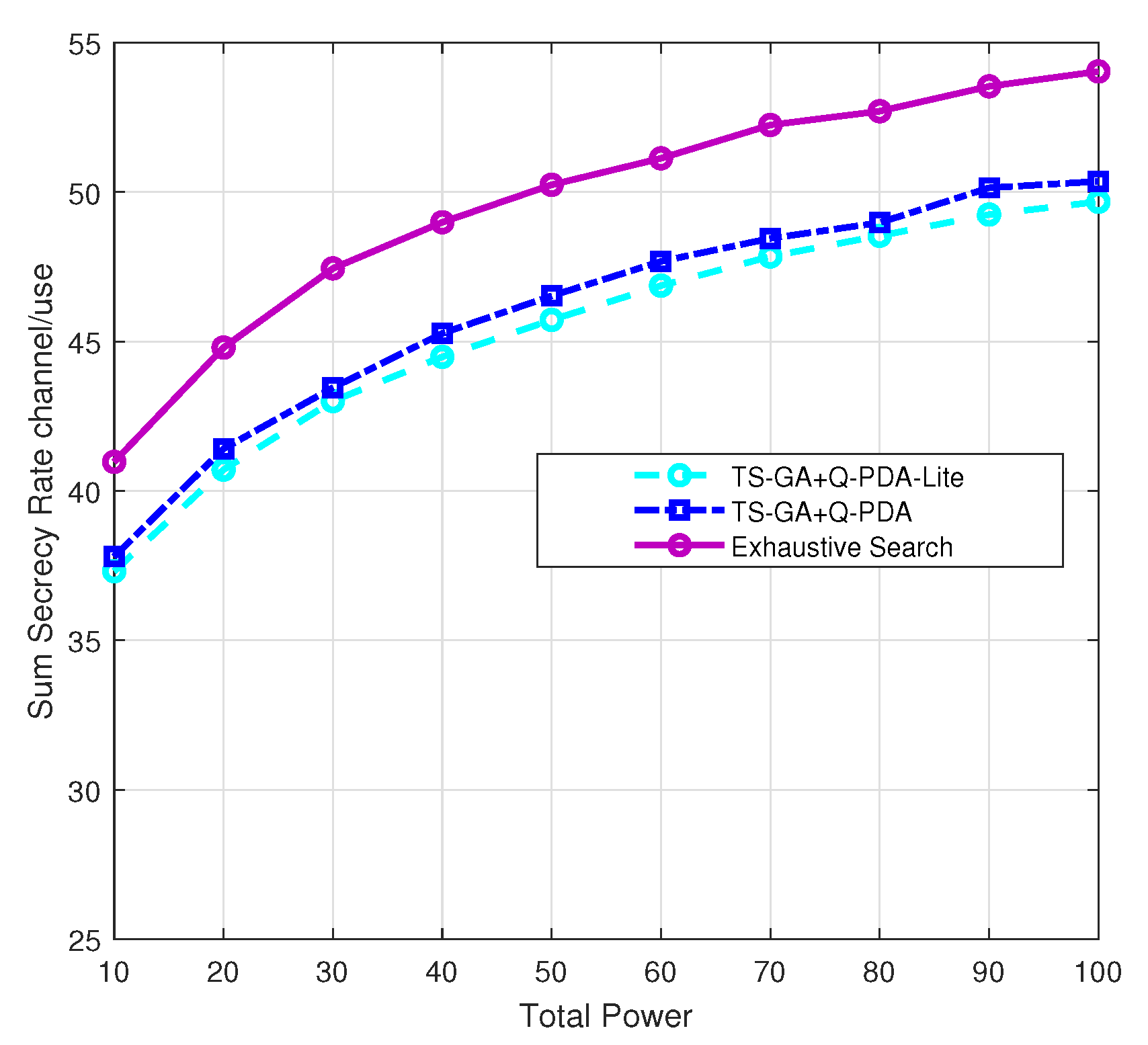
4.4. Compared with Exhaustive Search
As shown in
Figure 7, our simulation results show that the performance gap between our proposed algorithms and the global optimum is about 10%. In practical applications, this minor performance gap is often acceptable to gain orders of magnitude in speed and reduce energy consumption, which is critical for extending drone flight times. Q-PDA-Lite combined with TS-GA exhibits performance comparable to Q-PDA paired with TS-GA, while boasting lower complexity—making it well-suited for drone deployment. In this simulation, we employed 2 drones to serve 20 UEs, aiming to reduce the time required for the exhaustive search.