UAV Equipped with SDR-Based Doppler Localization Sensor for Positioning Tactical Radios †
Abstract
Highlights
- A novel UAV-mounted Doppler-based SDR sensor system was developed and validated for localizing realistic tactical radio emitters.
- The system achieves accurate localization (average error below 50 m) in real-world conditions without relying on multiple UAVs or external infrastructure.
- The proposed method enables flexible, cost-effective RF emitter localization suitable for critical infrastructure protection, public safety, and spectrum management.
- The research confirms the safe and responsible use of dual-use technology, adhering to ethical and regulatory standards, with no threat to public health or national security.
Abstract
1. Introduction
- We propose a novel RF emitter localization method based solely on Doppler frequency measurements from a single UAV-mounted SDR sensor, eliminating the need for multi-UAV synchronization or fixed ground-based infrastructure.
- We develop and validate a custom-designed localization system capable of detecting and tracking modern tactical radios characterized by limited frequency stability, such as the L3Harris AN/PRC-152A.
- We demonstrate the effectiveness of the proposed system through a combination of emulation studies and real-world field experiments, showing that meter-scale accuracy can be achieved under realistic conditions.
- We provide a critical analysis of system performance across carrier frequencies and acquisition times, identifying practical limitations as well as application domains such as spectrum monitoring, infrastructure protection, and search and rescue (SAR) missions.
2. Doppler-Based Location System
2.1. Brief Overview of Location Methods Based on Doppler Effect
2.2. Signal Doppler Frequency Location Method
2.3. UAV Reconnaissance System
2.4. Practical Implementation of Doppler Localization Sensor
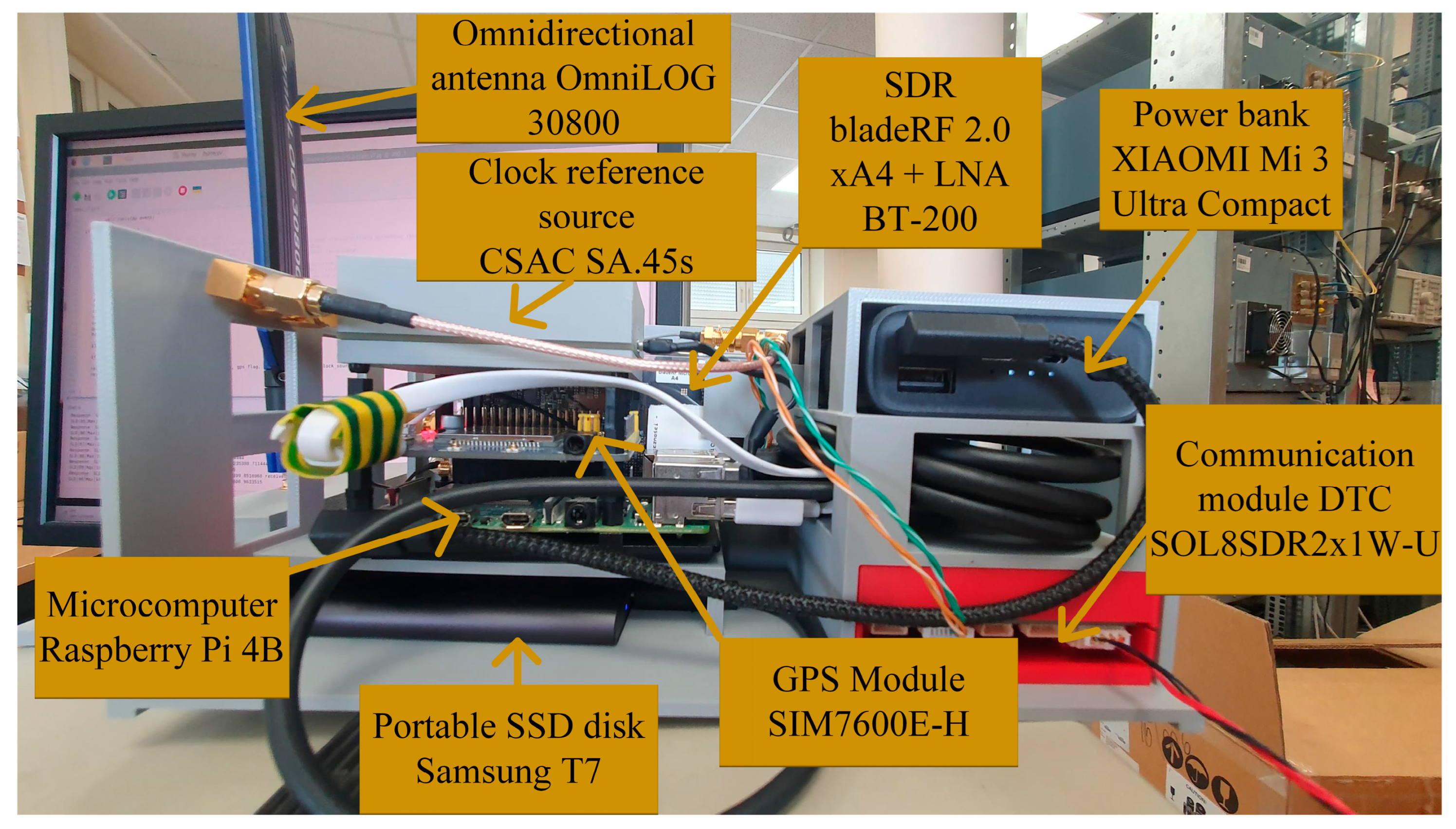
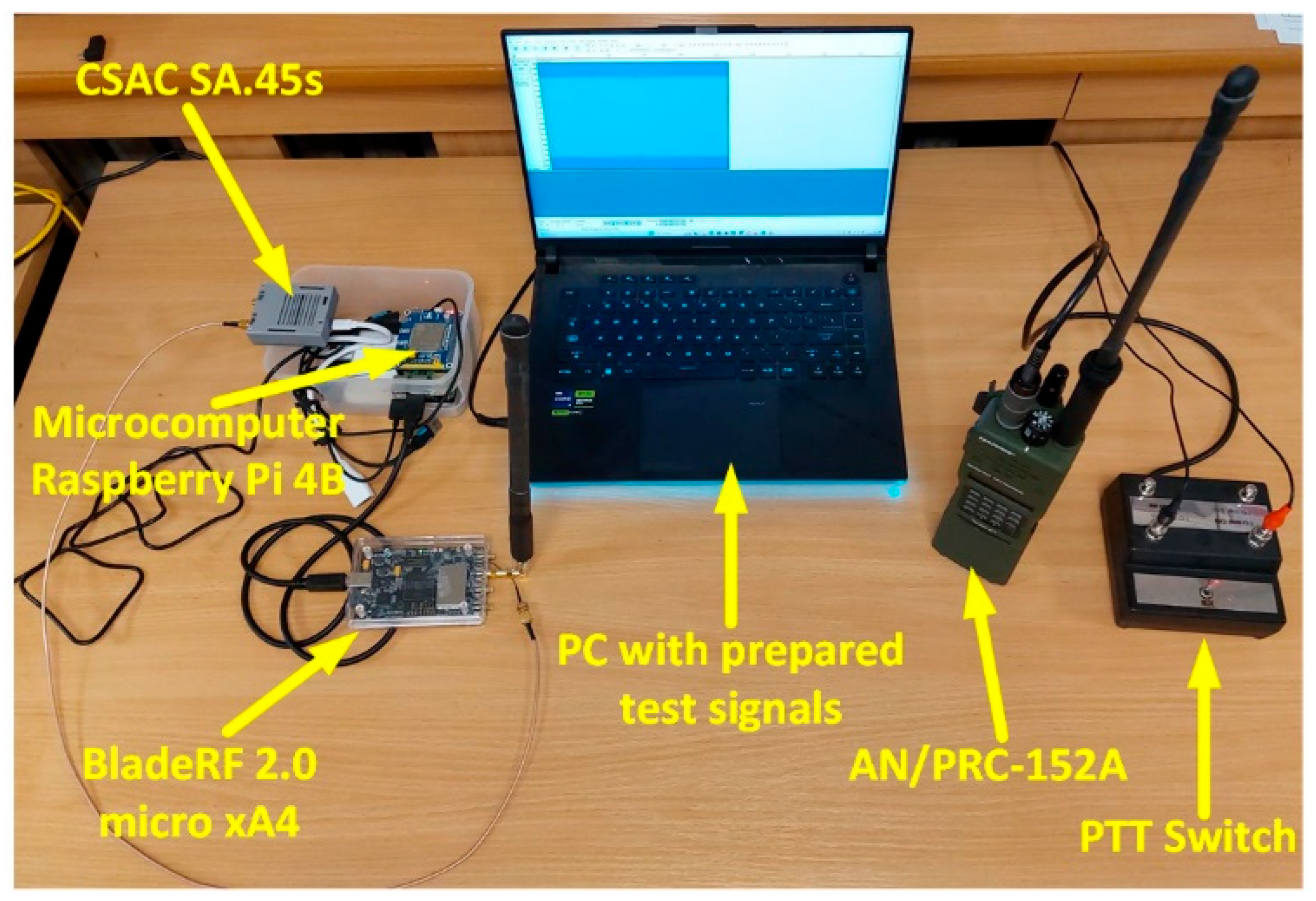
- Raspberry Pi 4B [23]—a microcomputer used to control the sensor and signal processing; the device consists of a single printed circuit board, Broadcom BCM2711 quad-core Cortex-A72 (ARM v8) 64-bit system on a chip (SoC) @ 1.8 GHz processor, 8 GB read access memory (RAM), two Universal Serial Bus (USB) 2.0 ports, two USB 3.0 ports, a Gigabit Ethernet interface, two Micro-High-Definition Multimedia Interface (Micro-HDMI) ports, a USB-C power connector, and General-Purpose Input/Output (GPIO) ports; the selected model has 8 GB RAM, which allows for dynamic allocation of the received signal and then saving it to static memory on a micro secure digital (microSD) card or external drive;
- bladeRF 2.0 xA4 [24,25]—an SDR used to receive radio signals from localized emitters and transmit them to a microcomputer; bladeRF is a modern generation of SDR, offering a frequency range of 47 MHz to 6 GHz or 70 MHz to 6 GHz for transmitting and receiving, respectively; the maximum bandwidth is 56 MHz; housed in a small form factor, the bladeRF 2.0 micro is designed for high performance and mobile applications; the SDR can be used optional with low noise amplifier (LNA) BT-200 [26] allows for a significantly lower noise figure and increased dynamic range in most applications;
- SA.45s [27]—a chip-scale atomic clock (CSAC) used to increase the stability and accuracy of frequency recovering; SA.45s is the specific CSAC solution available on the market; its small size, light weight, and energy efficiency make it perfect for designs, where minimizing size and power consumption are crucial; it is the only atomic clock that does not use the thermal stabilization technique;
- XIAOMI MI 3 Ultra Compact [28]—a power bank used to power DLS components during testing; ultimately, the systems will be powered from the UAV’s onboard power supply; the used model is an extremely compact and efficient solution with a capacity of 10 Ah, which allows for powering the sensor systems for about 300 min;
- SIM7600E-H [29]—a global navigation satellite system (GNSS) module used to determine a current DLS position during testing independently from the UAV platform; this module is dedicated for use with Raspberry Pi 4B and supports different GNSSs, i.e., GPS, GLONASS, BeiDou Navigation Satellite System (BDS), and location-based service (LBS); finally, the actual DLS coordinates will be provided by UAV telemetry;
- Samsung T7 [30]—a portable solid-state drive (SSD) used to fast record in-phase and quadrature (IQ) components of complex samples and store the history of calculation results; its capacity is 2 TB, and the recording speed is up to 1000 MB/s; additionally, it is extremely compact and durable, which is important when used on a UAV;
- OmniLOG 30800 [31]—wideband (i.e., operating in the range from 300 MHz to 8 GHz) omnidirectional antenna of small dimensions (173 mm × 63 mm × 9 mm) and weight (54 g); it has a standard SubMiniature version A (SMA) connector, is characterized by an impedance of 50 Ω and a gain of −3 dBi;
- DTC SOL8SDR2x1W-U [32]—communication module used to control DLS elements in real time and send results to the C2S; it is an advanced solution, designed specifically for integration in unmanned systems; the device, depending on the version, can operate in the frequency sub-ranges of 1.2–1.7 GHz, 1.78–2.29 GHz, 1.98–2.7 GHz, or 4.4–5 GHz with a bandwidth of 1.25–20 MHz; the module supports various types of phase-shift keying (PSK) and quadrature amplitude modulation (QAM), such as binary PSK (BPSK), quadrature PSK (QPSK), 16-QAM, or 64-QAM; the device offers an output power of 2 W (i.e., up to 1 W for each channel); the manufacturer declares the Rx sensitivity at −110 dBm; it is characterized by high flexibility thanks to the number of connectors: Ethernet, USB-C, Recommended Standard 232 (RS232) [33], and low power consumption (7 W in Internet Protocol (IP) mesh mode); the transmission can be secured using Advanced Encryption Standard (AES)128/256; at this stage, the module has not been fully integrated with the rest of the DLS—we plan to do it only on the target UAV platform.
3. Laboratory Tests of Doppler Localization Sensor
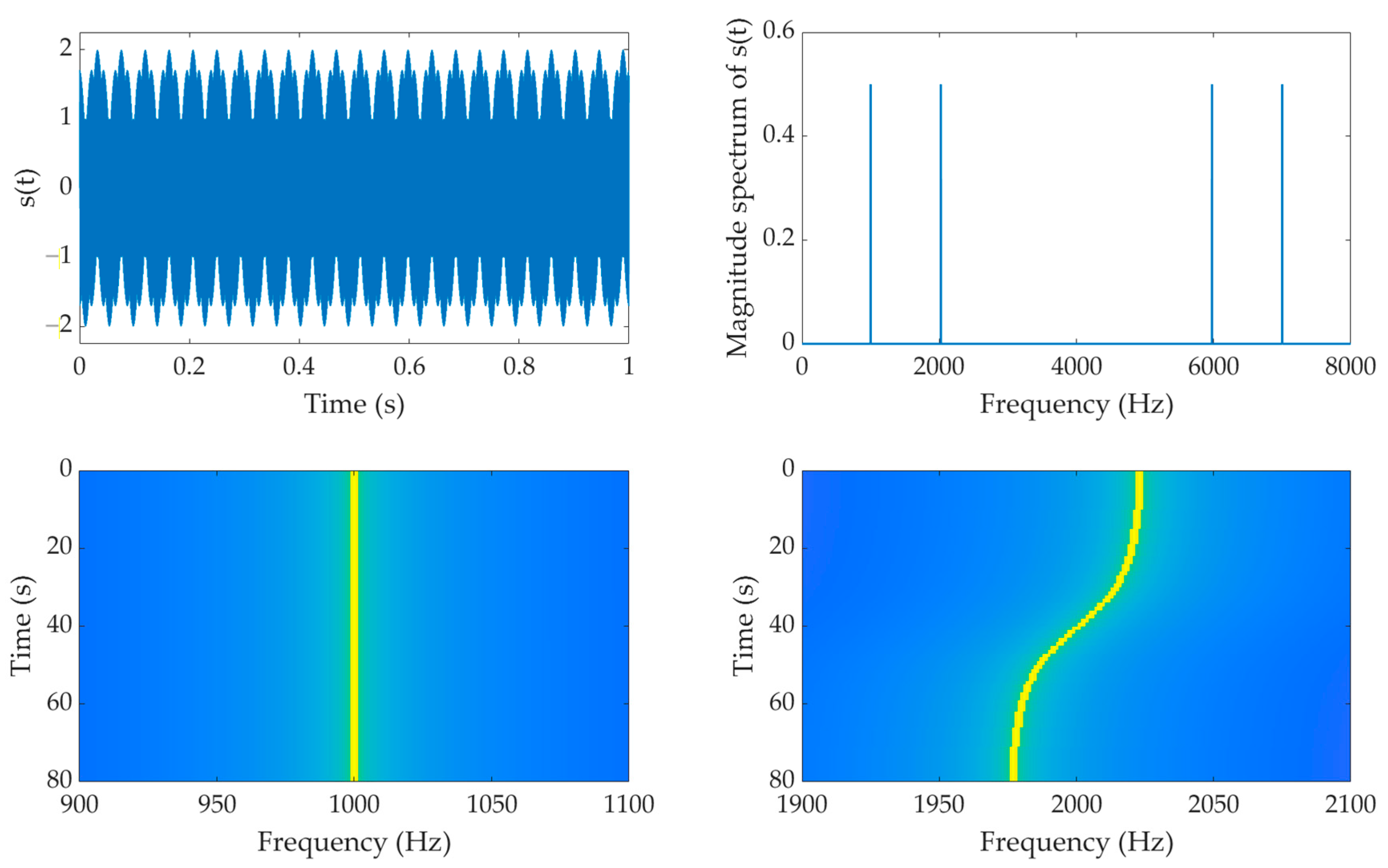
3.1. Idea of Doppler Effect Emulation by Acoustic Signal
3.2. Emulation Test-Bed
- bladeRF 2.0 micro xA4 as an SDR platform with an antenna designed for the required frequency range, responsible for receiving the signal;
- Raspberry Pi 4B microcomputer connected to the SDR platform, responsible for its control, as well as acquisition and processing of the received signal;
- CSAC SA.45s atomic clock, whose 10 MHz reference signal is fed to the SDR;
- power supply—in laboratory conditions, the microcomputer is supplied via a dedicated Raspberry Pi power supply, and the CSAC is powered by an independent battery.
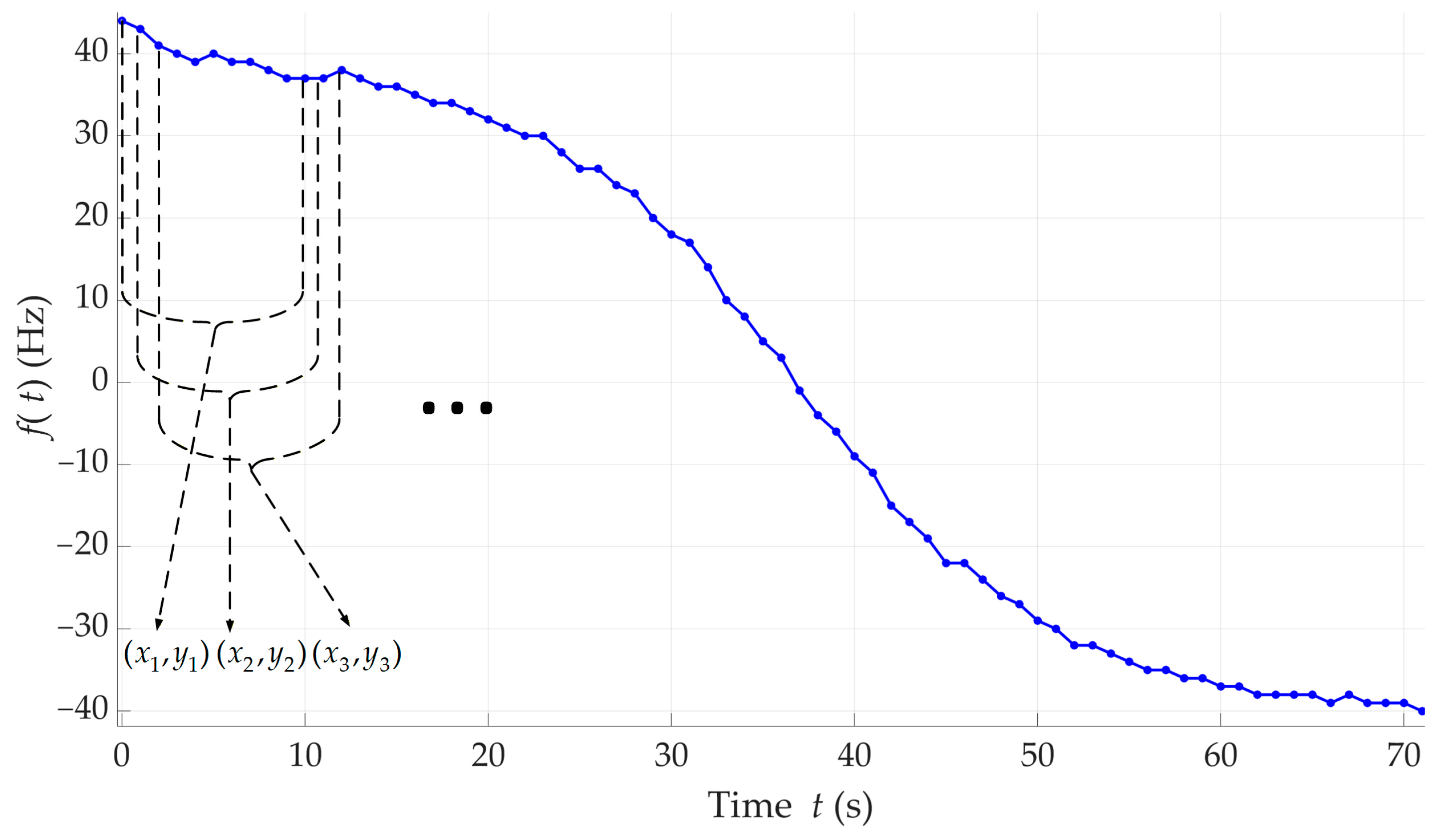
3.3. Emulation Scenario
- sensor (i.e., DLS/Rx) moves on a UAV with constant speed at a constant altitude above the flat land, along a straight trajectory with a length of
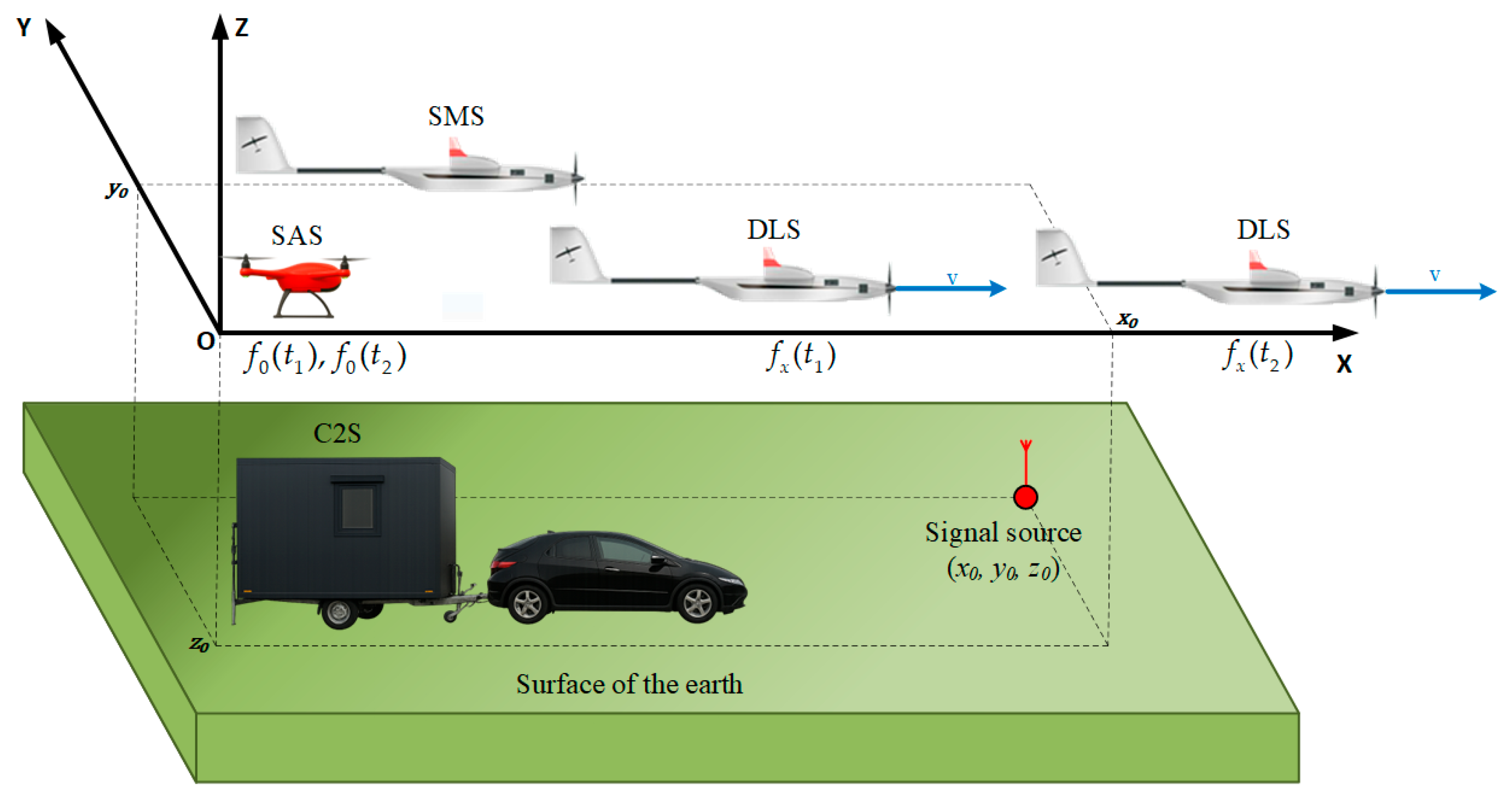
- origin of the local coordinate system OXYZ is located at point A (i.e., the beginning of the Rx path), and the OX axis is oriented along the AB segment (i.e., related to the direction of the Rx movement);
- emitter (i.e., Tx) position relative to the local coordinate system OXYZ is ;
- sensor performs 2D localization in the OXY plane (i.e., the Rx flight at a constant altitude and the coordinate is known, );
- location sensor estimates the instantaneous frequency every 1 s;
- acquisition time of the received signal is equal to 30 s, which means the coordinates of the AN/PRC-152A are estimated every 1 s based on 30 DSFs;
- tactical radio AN/PRC-152A conducts a continuous radio transmission lasting approximately 70 s;
- test signals are prepared according to the procedure presented in Section 3.1.
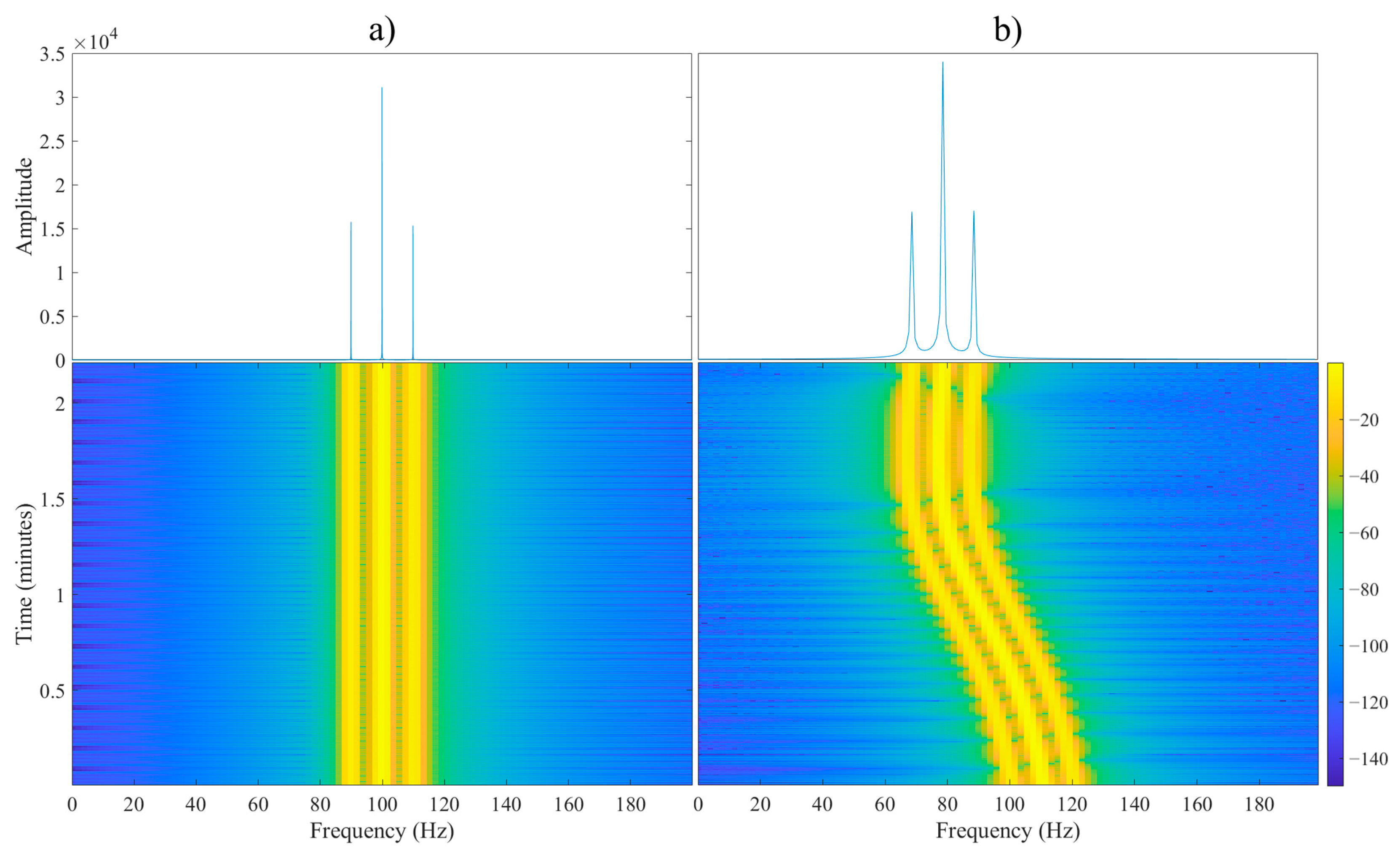
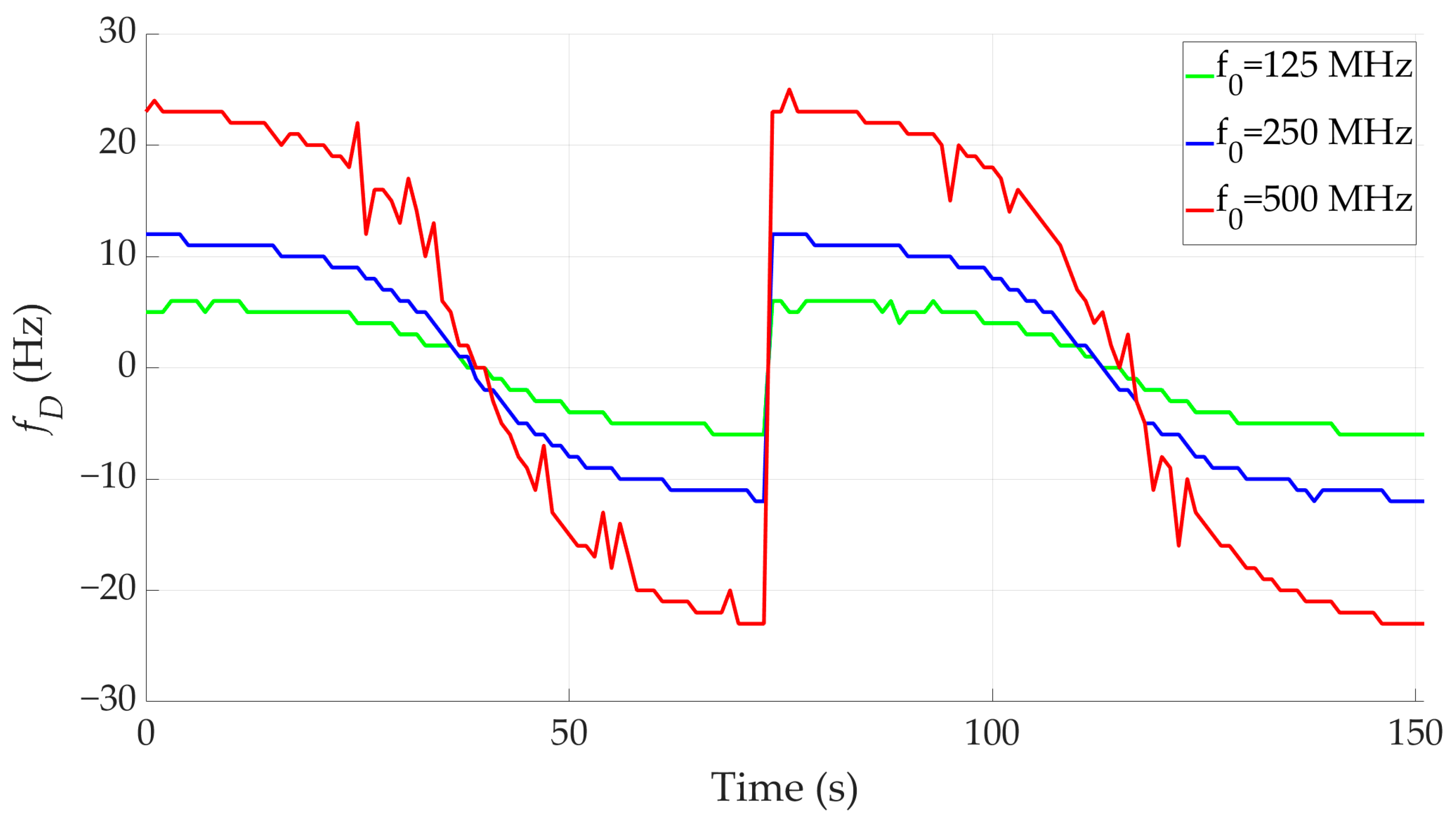
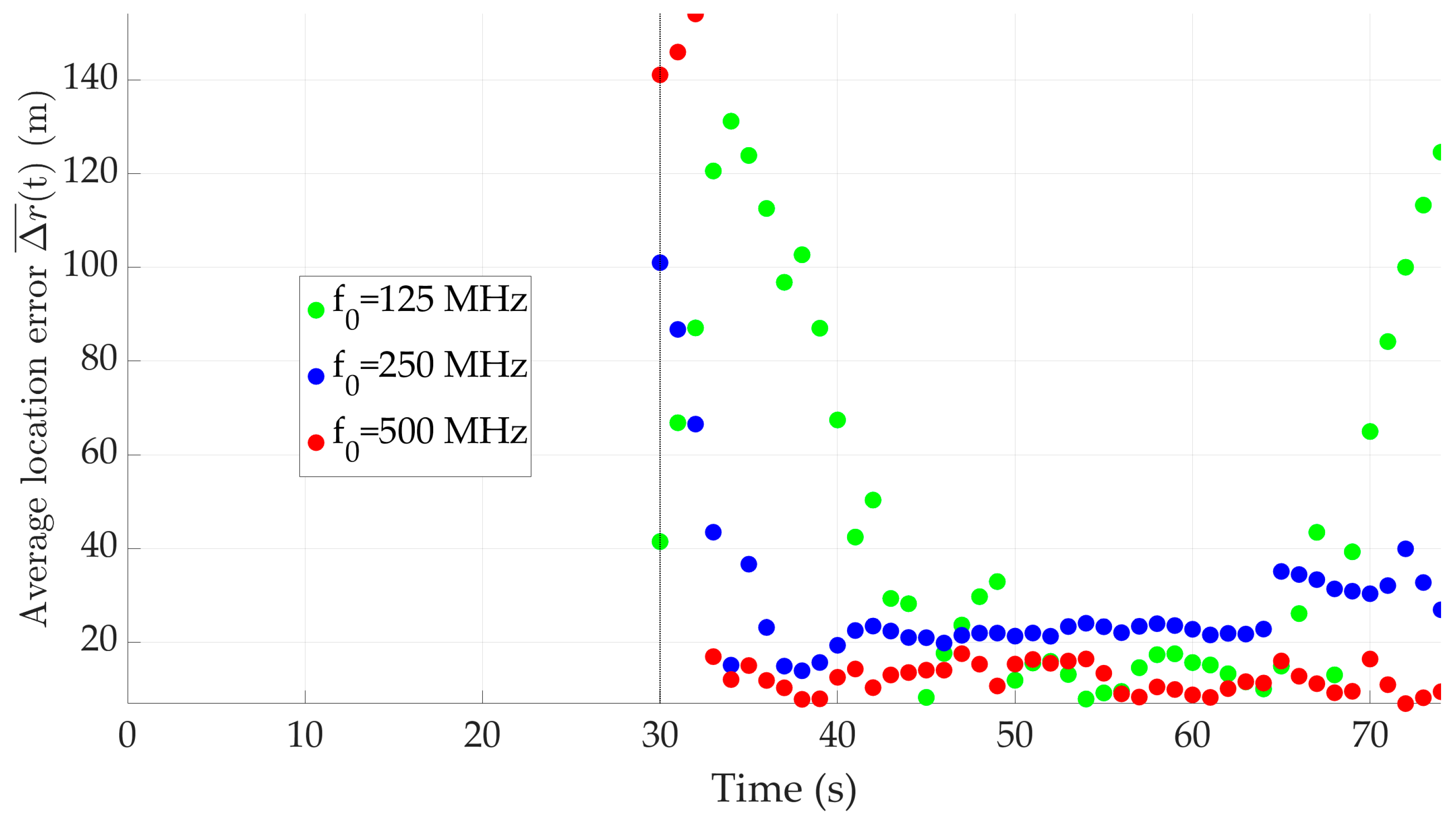
3.4. Emulation Result Analysis
4. Empirical Studies of Doppler Localization Sensor
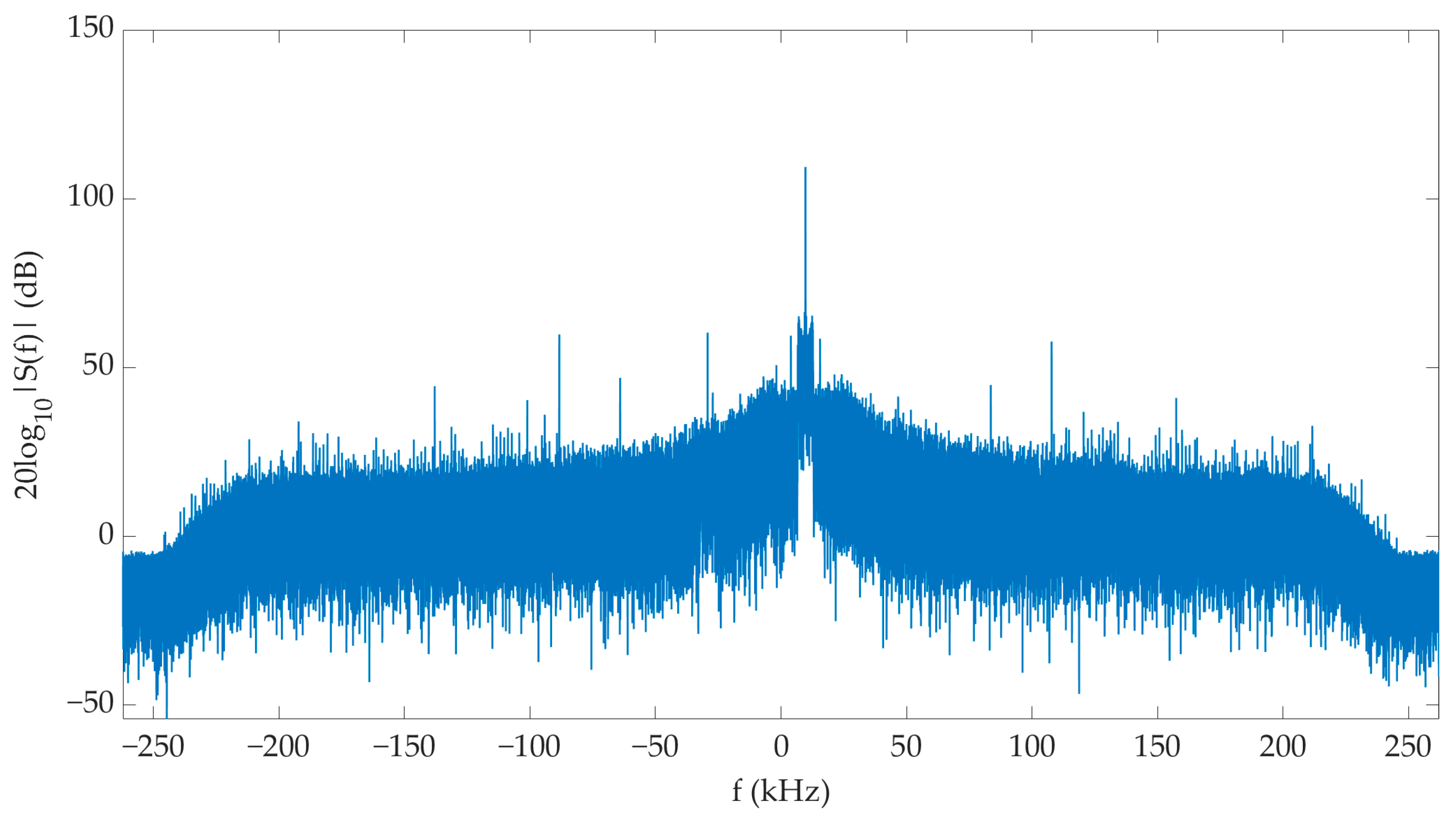
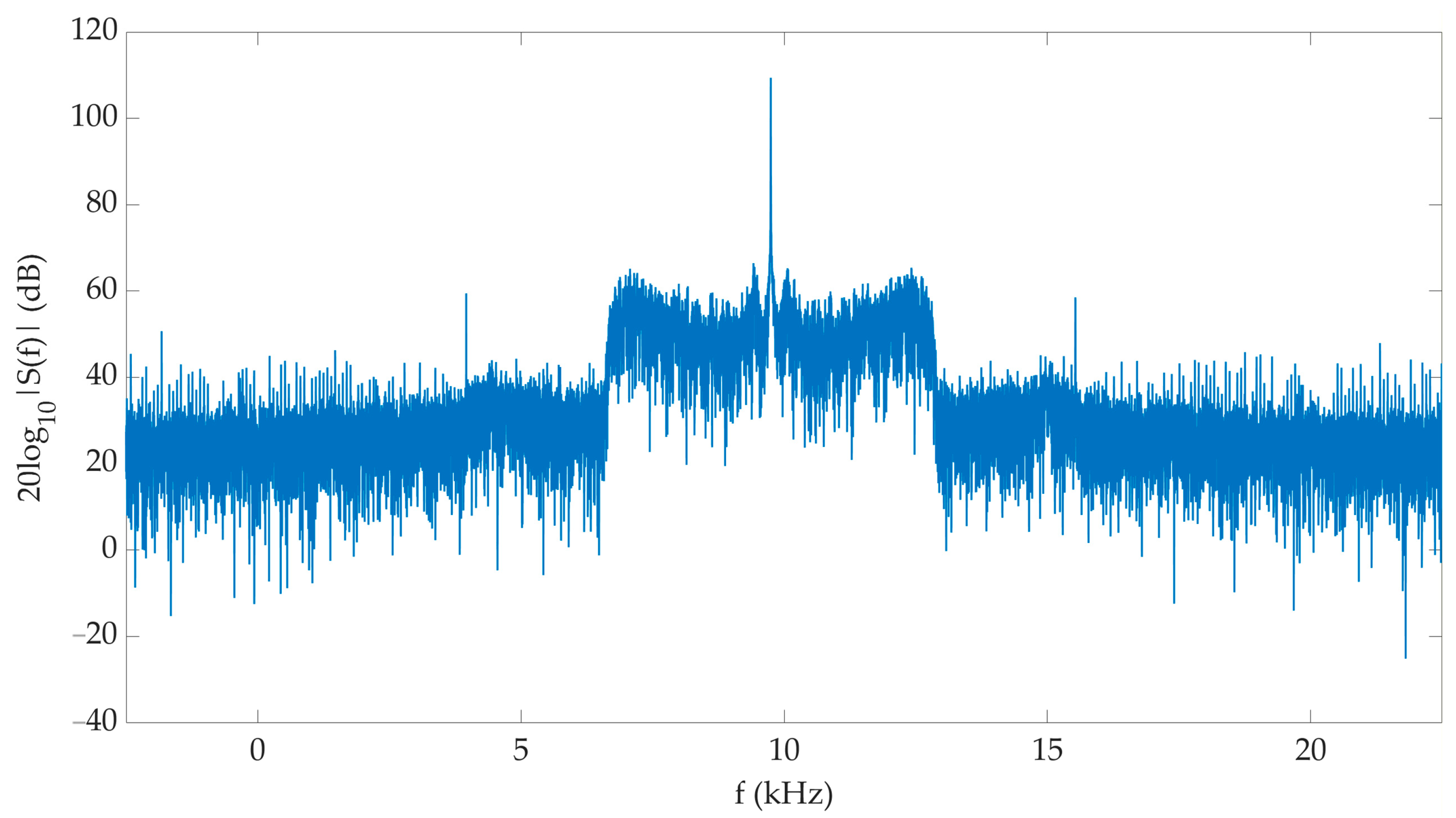
4.1. Measurement Test-Bed
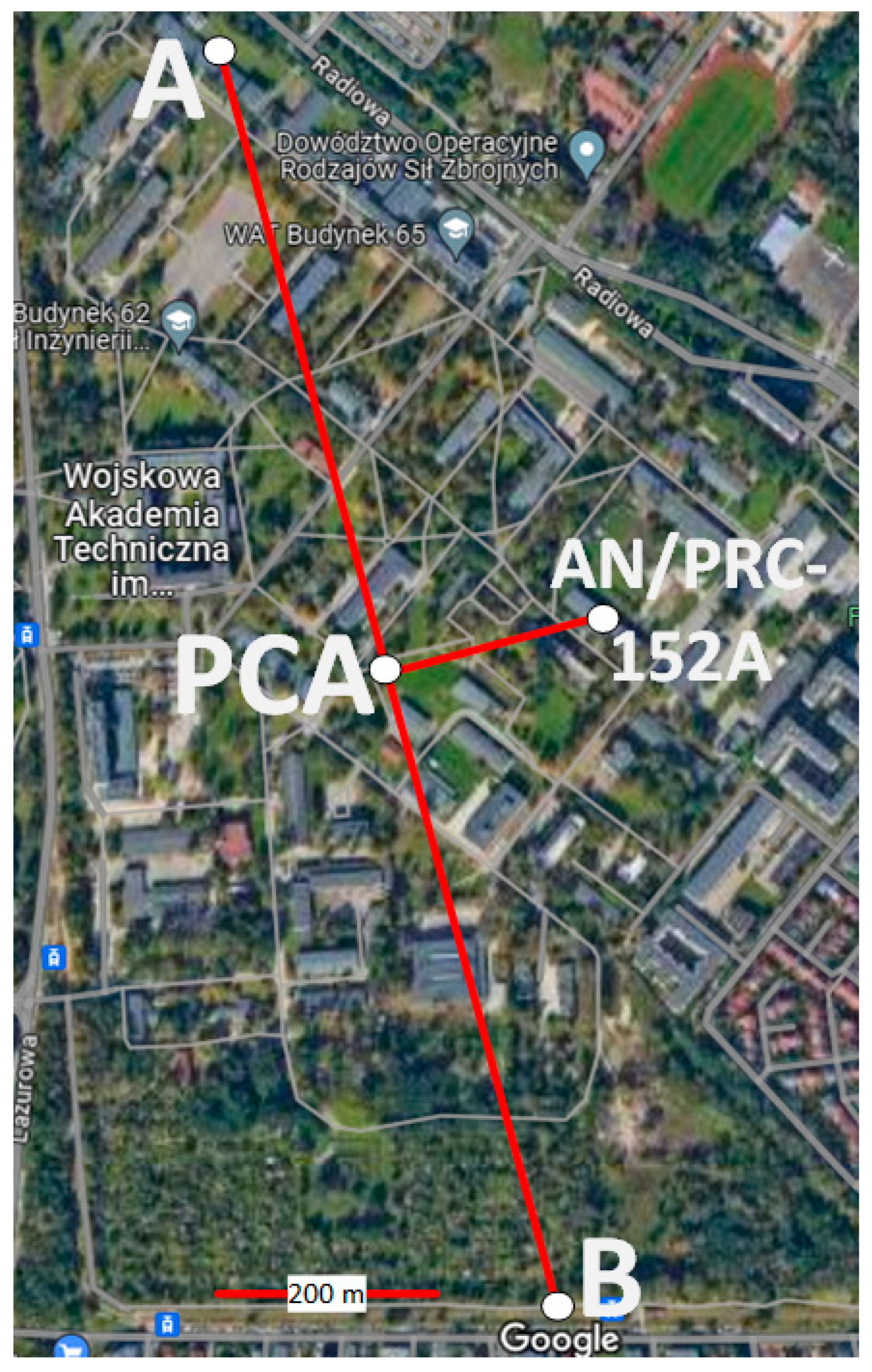
4.2. Measurement Scenario
- UAV with the DLS flight velocity is set to ;
- AN/PRC-152A conducts a continuous radio transmission with the signal modulated AM on the tested carrier frequency ;
- mounting height of the transmitting antenna (tactical radio) is equal to ;
- test is performed for two carrier frequencies set on the tactical radio;
- receiving frequency set on DLS/SAS is equal ;
- radio output power was 1W;
- five copies of the AN/PRC-152A radios were used for the study;
- for each radio and each carrier frequency , four passes were made along the route shown in Figure 7, which gives forty results (i.e., the Doppler curves);
- the analyzed signal bandwidth is set to ;
- every 1 s, DLS and SAS estimate the instantaneous frequency or carrier frequency , respectively;
- acquisition time of the received signal is equal to 10 s that means the emitter (i.e., AN/PRC-152A) coordinates are estimated every 1 s based on 10 DFSs.
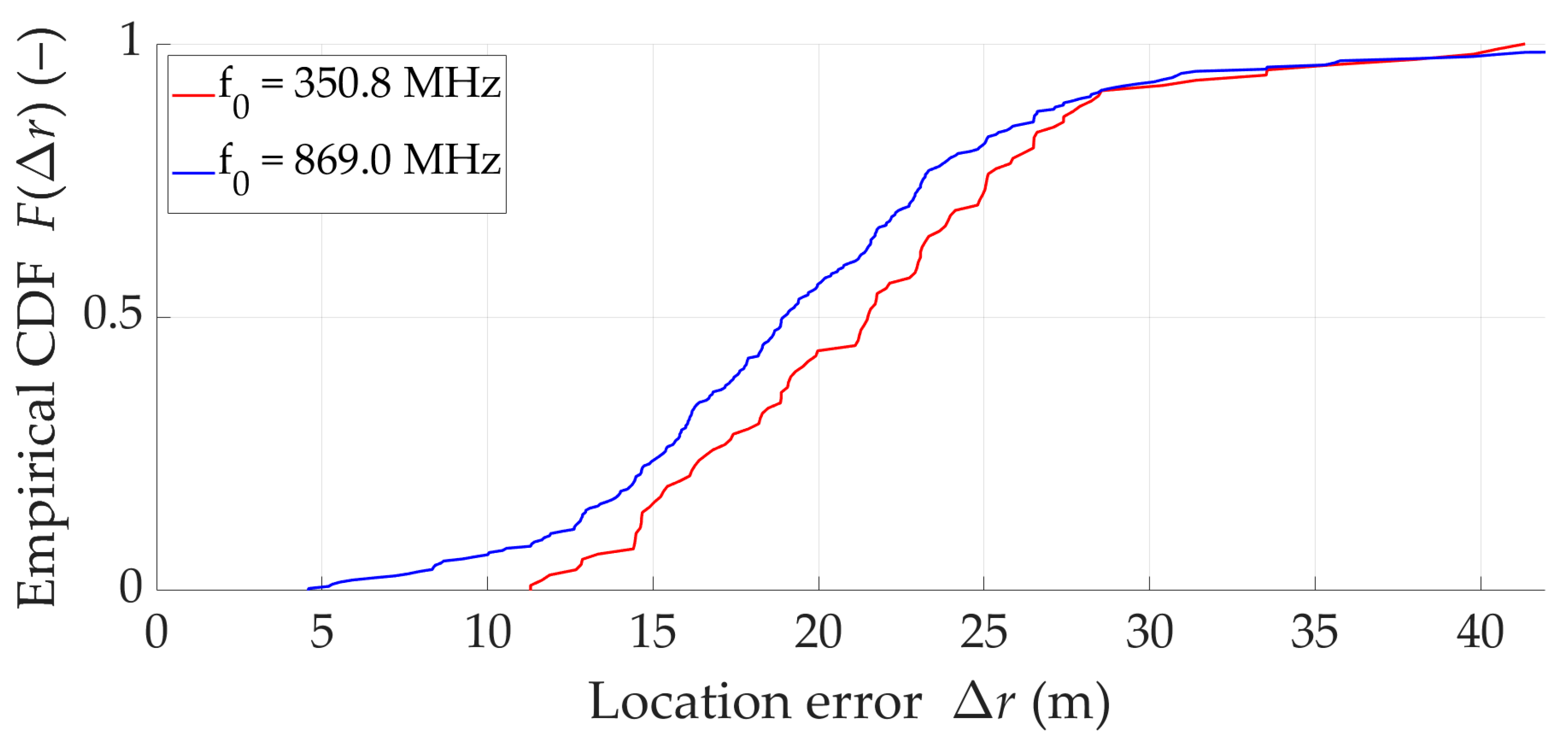
4.3. Result Analysis
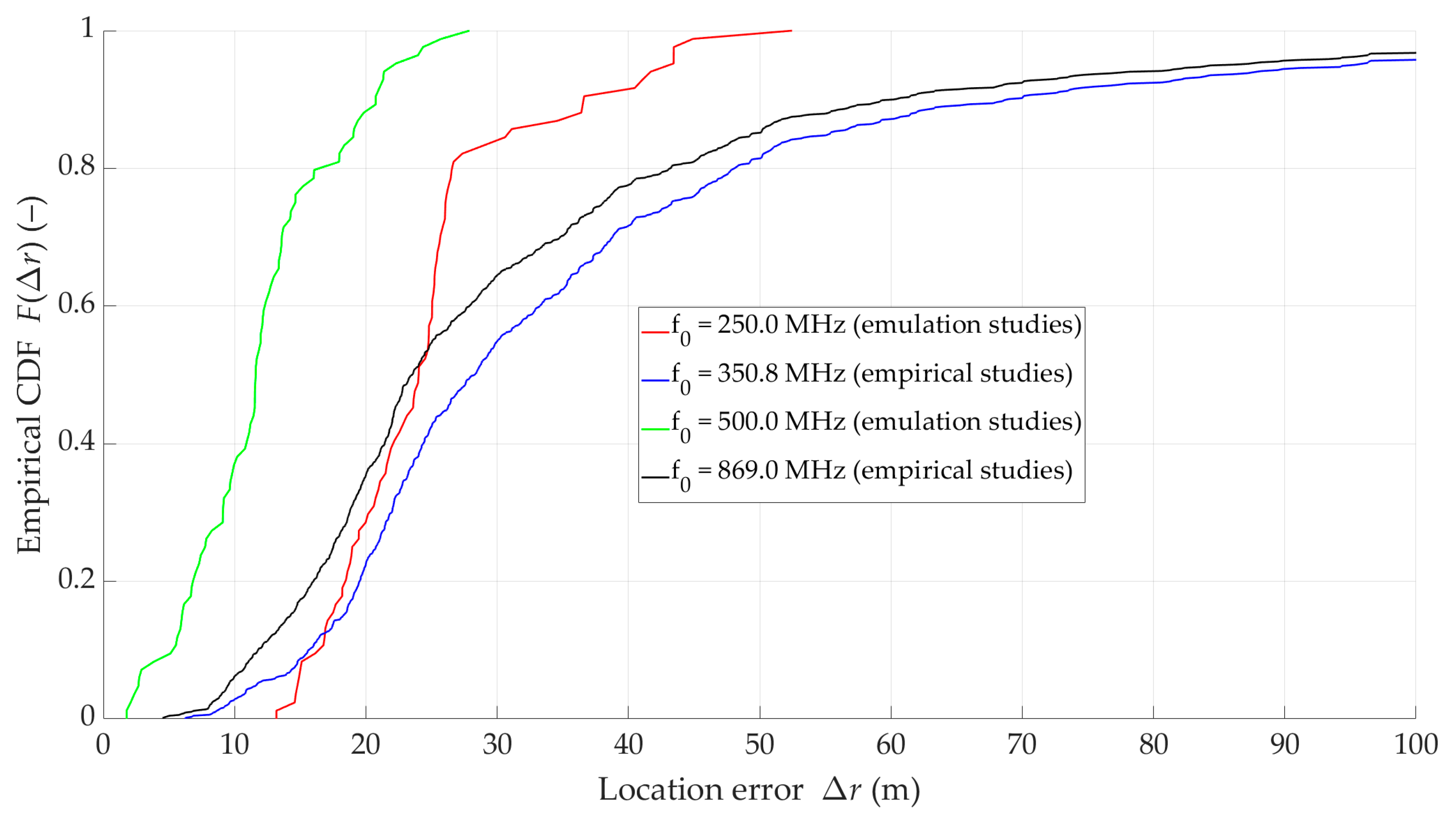
5. Synthesis of Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
DURC Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | Two-Dimensional |
| 3D | Three-Dimensional |
| AES | Advanced Encryption Standard |
| AI | Artificial Intelligence |
| AM | Amplitude Modulation |
| AOA | Angle Of Arrival |
| BDS | BeiDou Navigation Satellite System |
| BPSK | Binary Phase-Shift Keying |
| C2S | Command and Control Station |
| CDF | Cumulative Distribution Function |
| CSAC | Chip Scale Atomic Clock |
| DFS | Doppler Frequency Shift |
| DJI | Da-Jiang Innovations |
| DLS | Doppler Localization Sensor |
| DPD | Direct Position Determination |
| DURC | Dual-Use Research of Concern |
| FDOA | Frequency Difference Of Arrival |
| FEMA | Federal Emergency Management Agency |
| FOA | Frequency Of Arrival |
| GLOM | Generalized Local Orientation Matrix |
| f | Global Navigation Satellite System |
| GPIO | General-Purpose Input/Output |
| GPS | Global Positioning System |
| GUI | Graphical User Interface |
| HDMI | High-Definition Multimedia Interface |
| INS | Inertial Navigation System |
| IP | Internet Protocol |
| IQ | In-phase and Quadrature |
| LBS | Location-Based Service |
| LIDAR | Light Detection and Ranging |
| LLS | Linear Least Squares |
| LNA | Low Noise Amplifier |
| LOS | Line-Of-Sight |
| microSD | micro Secure Digital |
| MLE | Maximum Likelihood Estimation |
| NATO | North Atlantic Treaty Organization |
| NLOS | Non-Line-Of-Sight |
| OLOS | Obscured Line-Of-Sight |
| PCA | Point of Closest Approach |
| PSK | Phase-Shift Keying |
| PTT | Push-To-Talk |
| QAM | Quadrature Amplitude Modulation |
| QPSK | Quadrature Phase-Shift Keying |
| RAM | Read Access Memory |
| RF | Radio Frequency |
| RS232 | Recommended Standard 232 |
| RTK | Real-Time Kinematic |
| Rx | Receiver |
| SAR | Search And Rescue |
| SAS | reference Signal Acquisition Sensor |
| SDF | Signal Doppler Frequency |
| SDR | Software-Defined Radio |
| SMA | SubMiniature version A |
| SMS | Spectrum Monitoring Sensor |
| SNR | Signal-to-Noise Ratio |
| SoC | System on a Chip |
| SSD | Solid-State Drive |
| SWAT | Special Weapons and Tactics |
| Tx | Transmitter |
| UAS | Unmanned Aerial System |
| UAV | Unmanned Aerial Vehicle |
| UHF | Ultra-High Frequency |
| US | United States |
| USB | Universal Serial Bus |
| UWB | Ultra-WideBand |
| WLS | Weighted Least Squares |
| VHF | Very High Frequency |
| VTOL | Vertical Take-Off and Landing |
| VULOS | VHF/UHF Line-Of-Sight |
References
- Yang, B.; Yang, E. A Survey on Radio Frequency Based Precise Localisation Technology for UAV in GPS-Denied Environment. J. Intell. Robot. Syst. 2021, 103, 38. [Google Scholar] [CrossRef]
- Du, M.; Zou, H.; Wang, T.; Zhu, K. A Cooperative Target Localization Method Based on UAV Aerial Images. Aerospace 2023, 10, 943. [Google Scholar] [CrossRef]
- Kwon, H.; Guvenc, I. RF Signal Source Search and Localization Using an Autonomous UAV with Predefined Way-points. In Proceedings of the 2023 IEEE 97th Vehicular Technology Conference (VTC2023-Spring), Florence, Italy, 20–23 June 2023; pp. 1–6. [Google Scholar]
- Yang, X.; Lin, D.; Zhang, F.; Song, T.; Jiang, T. High Accuracy Active Stand-off Target Geolocation Using UAV Platform. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (IC-SIDP), Chongqing, China, 11–13 December 2019; pp. 1–4. [Google Scholar]
- Li, M.; Lang, J.; Liu, M. Ground Targets Passive Location by Multiple UAVs. In Proceedings of the 2023 IEEE 23rd International Conference on Communication Technology (ICCT), Wuxi, China, 20–22 October 2023; pp. 272–275. [Google Scholar]
- Shuangping, D.; Li, C.; Ying, X.; Liu, K. Study on Cross Location by EW UAVs. In Proceedings of the 2023 9th International Conference on Big Data and Information Analytics (BigDIA), Haikou, China, 15–17 December 2023; pp. 90–94. [Google Scholar]
- Shao, H.; Lee, M.; Liu, D.; Cao, J.; He, Q.; Liu, W. Situation Awareness Method and Simulation Test of UAVs and Observer Wards Air-Ground Cooperation. In Proceedings of the 2022 8th International Conference on Big Data and Information Analytics (BigDIA), Guiyang, China, 24–25 August 2022; pp. 518–526. [Google Scholar]
- Kramarić, L.; Jelušić, N.; Radišić, T.; Muštra, M. A Comprehensive Survey on Short-Distance Localization of UAVs. Drones 2025, 9, 188. [Google Scholar] [CrossRef]
- Couturier, A.; Akhloufi, M.A. A Review on Deep Learning for UAV Absolute Visual Localization. Drones 2024, 8, 622. [Google Scholar] [CrossRef]
- Szczepanik, R.; Kelner, J.M. Filtering and Overlapping Data for Accuracy Enhancement of Doppler-Based Location Method. Sensors 2025, 25, 1465. [Google Scholar] [CrossRef] [PubMed]
- Kelner, J.M.; Ziółkowski, C. Effectiveness of Mobile Emitter Location by Cooperative Swarm of Unmanned Aerial Vehicles in Various Environmental Conditions. Sensors 2020, 20, 2575. [Google Scholar] [CrossRef] [PubMed]
- Bednarz, K.; Wojtuń, J.; Szczepanik, R. Localization Accuracy Assessment of Tactical Radio Based on Acoustic Doppler Effect in Laboratory Conditions. In Proceedings of the 2024 International Radar Symposium (IRS), Wroclaw, Poland, 2–4 July 2024; pp. 162–166. [Google Scholar]
- Bednarz, K.; Wojtuń, J.; Kelner, J.M.; Różyc, K. Frequency Instability Impact of Low-Cost SDRs on Doppler-Based Localization Accuracy. Sensors 2024, 24, 1053. [Google Scholar] [CrossRef] [PubMed]
- Engel, U. A Geolocation Method Using ToA and FoA Measurements. In Proceedings of the 2009 6th Workshop on Positioning, Navigation and Communication (WPNC), Hannover, Germany, 19 March 2009; pp. 77–82. [Google Scholar]
- Chestnut, P.C. Emitter Location Accuracy Using TDOA and Differential Doppler. IEEE Trans. Aerosp. Electron. Syst. 1982, AES-18, 214–218. [Google Scholar] [CrossRef]
- Schultheiss, P.M.; Weinstein, E. Estimation of Differential Doppler Shifts. J. Acoust. Soc. Am. 1979, 66, 1412–1419. [Google Scholar] [CrossRef]
- Amar, A.; Weiss, A.J. Analysis of the Direct Position Determination Approach in the Presence of Model Errors. In Proceedings of the 2004 23rd IEEE Convention of Electrical and Electronics Engineers in Israel, Tel-Aviv, Israel, 6–7 September 2004; pp. 408–411. [Google Scholar]
- Witzgall, H. Ground Vehicle Doppler Geolocation. In Proceedings of the 2014 IEEE Aerospace Conference (AERO), Big Sky, MT, USA, 1–8 March 2014; pp. 1–8. [Google Scholar]
- Yang, X. Enhanced Moving Source Localization with Time and Frequency Difference of Arrival: Motion-Assisted Method for Sub-Dimensional Sensor Networks. Appl. Sci. 2024, 14, 3909. [Google Scholar] [CrossRef]
- Pei, Y.; Li, X.; Guo, F.; Zhang, M. Moving Source Localization Using Frequency Difference of Arrival Measurements Only. IEEE Trans. Veh. Technol. 2025, 74, 1052–1063. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, Y.; Xie, L.; Liu, N.; Wan, Q. An Iterative Direct Position Determination Approach Based on Doppler Frequency Shifts. IEEE Trans. Veh. Technol. 2024, 73, 2431–2443. [Google Scholar] [CrossRef]
- Rafa, J.; Ziółkowski, C. Influence of Transmitter Motion on Received Signal Parameters—Analysis of the Doppler Effect. Wave Motion 2008, 45, 178–190. [Google Scholar] [CrossRef]
- Raspberry Pi 4 Model B. Available online: https://www.raspberrypi.com/products/raspberry-pi-4-model-b/ (accessed on 7 February 2025).
- bladeRF 2.0 Micro xA4. Available online: https://www.nuand.com/product/bladerf-xa4/ (accessed on 7 February 2025).
- BladeRF in Python|PySDR: A Guide to SDR and DSP Using Python. Available online: https://pysdr.org/content/bladerf.html (accessed on 8 September 2025).
- BT-200 Bias-Tee Low Noise Amplifier. Available online: https://www.nuand.com/product/bt-200/ (accessed on 7 February 2025).
- CSAC-SA45S. Available online: https://www.microchip.com/en-us/product/csac-sa45s (accessed on 7 February 2025).
- Powerbank Mi Power Bank Ultra Compact 10000mAh | Mi-Home.pl. Available online: https://mi-home.pl/products/mi-power-bank-3-ultra-compact-10000mah (accessed on 7 February 2025).
- SIM7600E-H 4G HAT—Waveshare Wiki. Available online: https://www.waveshare.com/wiki/SIM7600E-H_4G_HAT (accessed on 7 February 2025).
- SSD T7 USB 3.2 1TB | MU-PC1T0H/WW|Samsung. Available online: https://www.samsung.com/pl/memory-storage/portable-ssd/portable-ssd-mu-t7-1tb-blue-mu-pc1t0h-ww/ (accessed on 7 February 2025).
- OmniLOG® 30800. Available online: https://aaronia.com/en/ultra-broadband-antenna-omnilog-30800 (accessed on 7 February 2025).
- SDR-UC Single Board UxV Transceiver. Available online: https://www.domotactical.com/products/sol8sdr-u-single-board-uxv-transceiver (accessed on 7 February 2025).
- TIA-232-F, Interface Between Data Terminal Equipment and Data Circuit-Terminating Equipment Employing Serial Binary Data Interchange. Telecommunications Industry Association (TIA), Arlington, USA. 1997. Available online: https://d1.amobbs.com/bbs_upload782111/files_35/ourdev_608717A327FT.pdf (accessed on 7 February 2025).
- Tretter, S.A. (Ed.) Amplitude Modulation. In Communication System Design Using DSP Algorithms with Laboratory Experiments for the TMS320C6713TM DSK; Springer: Boston, MA, USA, 2008; pp. 121–132. ISBN 978-0-387-74886-3. [Google Scholar]
- Google Maps—Military University of Technology. Available online: https://maps.app.goo.gl/4k5yapvKMAzSBhUJ9 (accessed on 8 October 2025).
- Szczepanik, R.; Kelner, J.M. Two-Stage Overlapping Algorithm for Signal Doppler Frequency Location Method. In Proceedings of the 2023 Signal Processing Symposium (SPSympo), Karpacz, Poland, 26–28 September 2023; pp. 184–188. [Google Scholar]



| Method | Type | Min. sensors (UAVs) Required | Sensor motion Required | Time Synchronization Required | Known Transmit Frequency Required | Computational Complexity | Localization Accuracy | Key Advantages | Main Limitations |
|---|---|---|---|---|---|---|---|---|---|
| FOA | Two-step | 1 | Yes | No | Yes | Low | Moderate | Simple, requires only one UAV | Requires known frequency, sensitive to drift |
| SDF | Two-step | 1 | Yes | No | No | Low | Moderate | Low-cost, single UAV, unsynchronized | Requires motion and accurate trajectory |
| FDOA | Two-step | 2 | No (relative motion) | Yes | No | Medium | High | Good accuracy, robust to noise | Sensitive to synchronization and clock drift |
| DPD | One-step | 3–4 | No | Yes | No | High | Very high | Highest accuracy, robust in low SNR | High complexity, needs synchronization and computing |
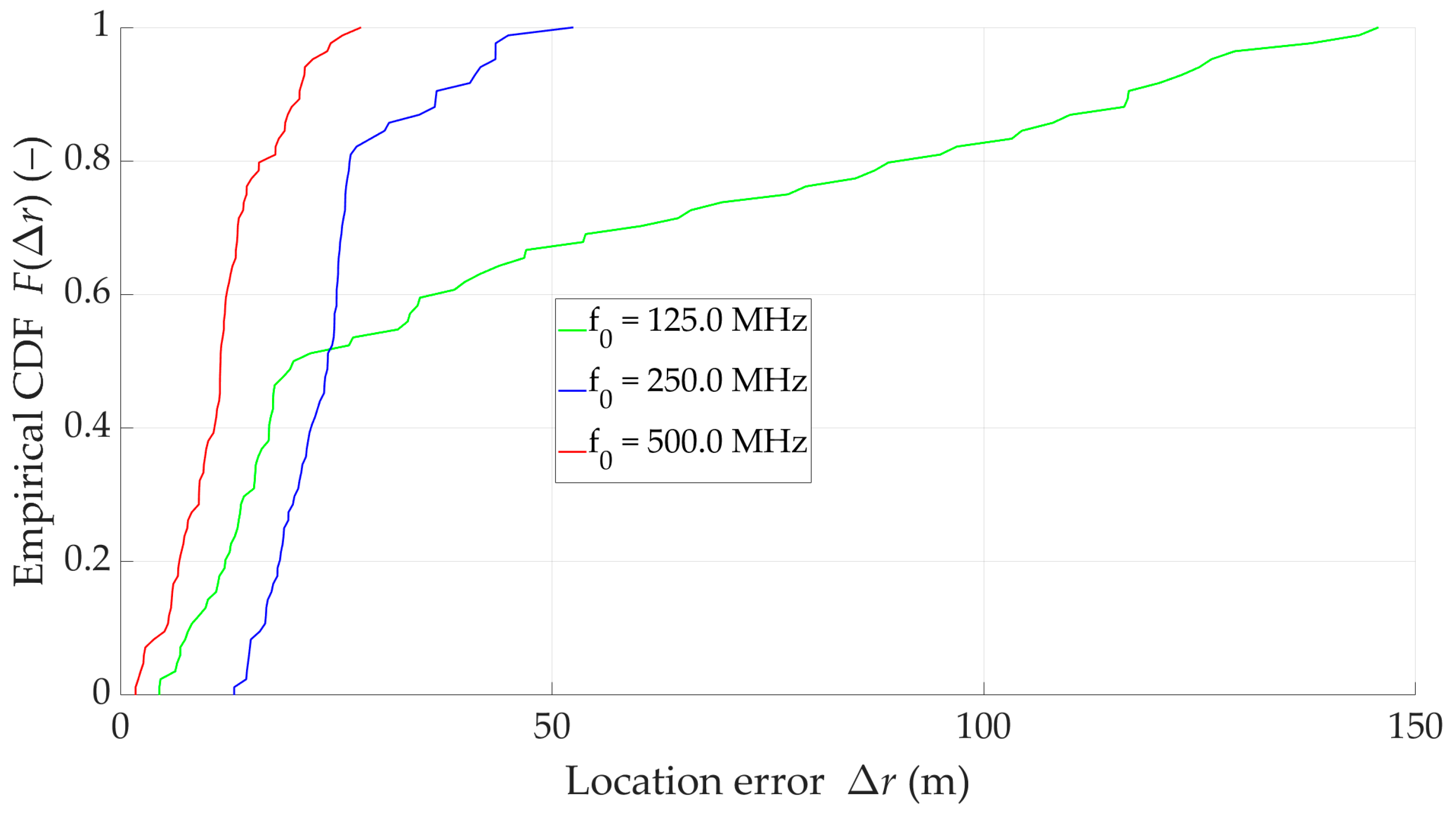
| Tested Carrier Frequency (MHz) | Location Error (m) | |||
|---|---|---|---|---|
| 125 | 7.9 | 131.2 | 47.2 | 40.3 |
| 250 | 13.9 | 101.0 | 28.8 | 16.8 |
| 500 | 6.9 | 154.1 | 21.1 | 34.2 |
| Tested Carrier Frequency (MHz) | Location Error (m) | |||
|---|---|---|---|---|
| 125 | 7.9 | 131.2 | 45.9 | 41.1 |
| 250 | 13.9 | 43.5 | 24.8 | 6.7 |
| 500 | 6.9 | 17.5 | 12.1 | 3.0 |
| Tested Radio | Tested Carrier Frequency (MHz) | Location Error (m) | |||
|---|---|---|---|---|---|
| 1 | 350.8 | 11.88 | 26.50 | 20.49 | 5.29 |
| 869.0 | 4.59 | 30.83 | 15.75 | 7.54 | |
| 2 | 350.8 | 14.61 | 38.01 | 20.18 | 5.09 |
| 869.0 | 11.41 | 38.01 | 18.44 | 4.45 | |
| 3 | 350.8 | 12.67 | 39.77 | 22.86 | 8.26 |
| 869.0 | 5.92 | 89.44 | 20.57 | 13.54 | |
| 4 | 350.8 | 14.41 | 31.40 | 21.12 | 4.83 |
| 869.0 | 14.41 | 52.10 | 21.67 | 8.02 | |
| 5 | 350.8 | 11.30 | 41.35 | 23.74 | 7.48 |
| 869.0 | 11.30 | 41.35 | 22.96 | 5.40 | |
| Acquisition Time (s) | Tested Carrier Frequency (MHz) | Location Error (m) | |||
|---|---|---|---|---|---|
| 10 | 350.8 | 11.30 | 41.35 | 21.78 | 6.34 |
| 869.0 | 4.59 | 89.44 | 20.07 | 8.53 | |
| 20 | 350.8 | 4.20 | 89.76 | 28.29 | 14.72 |
| 869.0 | 3.34 | 179.24 | 26.02 | 17.54 | |
| 30 | 350.8 | 6.24 | 235.86 | 37.11 | 28.21 |
| 869.0 | 4.52 | 235.86 | 32.37 | 26.52 | |
| (MHz) | Location Error (m) | |||
|---|---|---|---|---|
| 250.0 | 13.9 | 101.0 | 28.8 | 16.8 |
| 350.8 | 6.24 | 235.86 | 37.11 | 28.21 |
| 500.0 | 6.9 | 154.1 | 21.1 | 34.2 |
| 869.0 | 4.52 | 235.86 | 32.37 | 26.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bednarz, K.; Wojtuń, J.; Szczepanik, R.; Kelner, J.M. UAV Equipped with SDR-Based Doppler Localization Sensor for Positioning Tactical Radios. Drones 2025, 9, 698. https://doi.org/10.3390/drones9100698
Bednarz K, Wojtuń J, Szczepanik R, Kelner JM. UAV Equipped with SDR-Based Doppler Localization Sensor for Positioning Tactical Radios. Drones. 2025; 9(10):698. https://doi.org/10.3390/drones9100698
Chicago/Turabian StyleBednarz, Kacper, Jarosław Wojtuń, Rafał Szczepanik, and Jan M. Kelner. 2025. "UAV Equipped with SDR-Based Doppler Localization Sensor for Positioning Tactical Radios" Drones 9, no. 10: 698. https://doi.org/10.3390/drones9100698
APA StyleBednarz, K., Wojtuń, J., Szczepanik, R., & Kelner, J. M. (2025). UAV Equipped with SDR-Based Doppler Localization Sensor for Positioning Tactical Radios. Drones, 9(10), 698. https://doi.org/10.3390/drones9100698








