Reinforcement Learning Stabilization for Quadrotor UAVs via Lipschitz-Constrained Policy Regularization

Abstract

Reinforcement learning (RL), and in particular Proximal Policy Optimization (PPO), has shown promise in high-precision quadrotor unmanned aerial vehicle (QUAV) control. However, the performance of PPO is highly sensitive to the choice of the clipping parameter, and inappropriate settings can lead to unstable training dynamics and excessive policy oscillations, which limit deployment in safety-critical aerial applications. To address this issue, we propose a stability-aware dynamic clipping parameter adjustment strategy, which adapts the clipping threshold ${ϵ}_t$ in real time based on a stability variance metric $S_t$. This adaptive mechanism balances exploration and stability throughout the training process. Furthermore, we provide a Lipschitz continuity interpretation of the clipping mechanism, showing that its adaptation implicitly adjusts a bound on the policy update step, thereby offering a deterministic guarantee on the oscillation magnitude. Extensive simulation results demonstrate that the proposed method reduces policy variance by 45% and accelerates convergence compared to baseline PPO, resulting in smoother control responses and improved robustness under dynamic operating conditions. While developed within the PPO framework, the proposed approach is readily applicable to other on policy policy gradient methods.

1. Introduction

Reinforcement learning (RL) has achieved significant success in various domains, including robotics [1,2], autonomous driving [3,4], and advanced flight control [5,6,7]. Among these applications, quadrotor unmanned aerial vehicles (UAVs) have attracted considerable attention due to their maneuverability and versatility in complex and constrained environments [8,9,10]. However, ensuring reliable trajectory tracking of quadrotor UAVs remains a challenge, mainly due to their underactuated nature and highly nonlinear dynamics [11,12,13].

Modern RL techniques, including Deep Q Networks (DQNs), policy gradient methods, and model-based RL approaches [14,15,16,17], are capable of learning control strategies by interacting with the environment and aiming to maximize cumulative rewards [18]. However, the nonlinear and underactuated nature of quadrotors renders stabilizing the learned policy particularly challenging. Issues such as suboptimal reward function design, imbalanced exploration and exploitation dynamics, and the absence of explicit stability constraints often lead to policy output oscillations during training [19,20,21,22].

These oscillations pose significant challenges for quadrotors, as even minor deviations can result in excessive actuator wear, erratic flight behavior, and an increased risk of control system failures. While heuristic methods and reward shaping [9,10] can partially alleviate instability, they do not directly impose constraints on policy updates. In real-world missions, such as surveillance, environmental monitoring, and search and rescue, this unpredictability is unacceptable.

To address these challenges, Unlike conventional methods that concentrate on weight normalization or superficial hyperparameter tuning [12,23,24], we propose Stabilizing Constraint Regularization (SCR), a novel technique designed to mitigate two related but distinct phenomena: (1) oscillations in policy parameter updates during training, which lead to unstable learning curves; and (2) oscillations in deployed control commands, manifesting as high-frequency actuator signals that degrade flight stability. By bounding the Lipschitz constant of the learned policy through a dynamically adjusted PPO clipping parameter, SCR provides a deterministic guarantee on control smoothness: for any two bounded state perturbations $s_1$ and $s_2$, the corresponding policy outputs satisfy $\parallel \pi \left(s_1\right)-\pi \left(s_2\right)\parallel \le L_{max}\parallel s_1-s_2\parallel ,L_{max}\mathrm{determined}\mathrm{by}{ϵ}_t.$ This ensures that deployment-stage oscillations are strictly limited, even after training convergence.

The two primary contributions of this work are:

1.

Novel Regularization Technique: We introduce SCR, a stability-constrained regularization method that directly controls policy update magnitudes. This technique effectively mitigates policy oscillations in underactuated UAV systems, significantly enhancing policy stability.

2.

Improved Training Stability and Convergence: SCR ensures smoother and more controlled policy evolution, leading to faster convergence and improved robustness. This is particularly advantageous for quadrotor UAVs, where stable and predictable control is essential.

By integrating physical constraints into the data-driven learning process, SCR enables RL agents to leverage human knowledge and engineering insights more efficiently and reliably. This approach facilitates stable policies that are both effective and safe for deployment, thereby extending the applicability of RL to high-risk tasks.

The remainder of this paper are organized as follows: Section 2 reviews related work on RL stability and existing regularization techniques, with a focus on their applications in quadrotor control. Section 3 introduces the fundamentals of RL and quadrotor kinematics. Section 4 details the theoretical foundations and implementation of SCR. Section 5 presents the experimental results. These results demonstrate the effectiveness of SCR in quadrotor trajectory tracking and highlight its performance advantages over conventional reinforcement learning (RL) algorithms. Finally, Section 6 concludes with a summary of the findings and suggestions for future research.

2. Related Work

The application of reinforcement learning (RL) to quadrotor control has attracted significant attention in recent years, owing to its capability to handle nonlinear dynamics and adapt to environmental disturbances without explicit modeling. Proximal Policy Optimization (PPO) [25] and Soft Actor–Critic (SAC) [26] are among the most popular algorithms in this domain, with several studies demonstrating their effectiveness in trajectory tracking [8,9], and they established foundational capabilities in waypoint trackings but suffered from inherent limitations in continuous action space representation and environmental sensitivity. The subsequent shift toward policy gradient methods (e.g., PPO [25] and SAC [26]) introduced theoretical improvements through entropy regularized exploration and experience replay mechanisms. However, these advancements have inadvertently exposed a critical vulnerability: unbounded policy updates frequently induce high-frequency oscillations in control signals (typically 8–12 Hz in rotor commands). Such oscillations are particularly detrimental to underactuated quadrotor systems, where control authority is inherently limited. Existing mitigation strategies have partially reduced transient instabilities, yet they fundamentally fail to address the root cause. Moreover, the prevailing practice of employing quasi-steady aerodynamic models neglects transient vortex dynamics, which is responsible for approximately 62% of torque fluctuations in empirical studies.

For example, Zhou et al. [27] applied PPO to waypoint navigation tasks, reporting smooth convergence in simulation but observed performance degradation under unmodeled wind conditions in real flights. Similarly, Lee et al. [28] employed SAC for aggressive maneuvers, achieving rapid convergence yet suffering from instability during high-disturbance flights due to variance in policy updates. Hybrid approaches [29,30] have also been explored, incorporating safety filters or domain randomization to enhance robustness, though at the cost of increased computational demands and reduced sample efficiency.

Although the above studies have advanced the integration of RL in UAV control, several limitations persist:

• Simulation to reality gap: Many works rely solely on simulation or limited scale real world validation, which does not fully capture aerodynamic effects, sensor noise, and actuator delays encountered in actual quadrotor operations [26,31];
• Convergence–stability trade-off: Fast learning algorithms (e.g., SAC) often exhibit oscillatory behaviors, while stable learners (e.g., PPO) tend to converge more slowly, limiting their practical deployment in time-sensitive missions [32];
• Neglect of explicit stability constraints: Few studies have integrated formalized stability regularization into the learning process, despite stability being critical for safety in UAV applications [33].

Novelty of This Work: To address the above gaps, we propose a Stabilizing Constraint Regularized (SCR) PPO algorithm that introduces a stability-aware regularization term into the policy update rule, enabling faster convergence while maintaining high stability and robustness. In contrast to prior works, our method is validated extensively in both a high-fidelity simulation environment and real-world outdoor flight tests, ensuring that the learned policy is resilient to aerodynamic disturbances, sensor noise, and communication delays.

As summarized in

Table 1. Comparison of representative RL-based quadrotor control methods and the proposed SCR-PPO, using actual experimental results.

Method	Convergence Steps (M)	Mean RMSE (m)	Stability (Var.)	Robustness (RMSE Δ)
PPO [25]	0.80	0.33	High var.	+0.15 m
SAC [26]	0.50	0.27	Med. var.	+0.08 m
Hybrid RL [34]	0.60	0.29	Med. var.	+0.09 m
Constraint Based RL [35]	0.55	0.28	Low var.	+0.12 m
SCR-PPO (Ours)	0.30	0.19	Lowest var.	+0.05 m

Note: Capital M represents one million times.

, the proposed SCR-PPO achieves the fastest convergence (0.30 M steps), the lowest tracking error (0.19 m),minimal variance in learning curves, and the highest robustness under disturbance conditions among all compared approaches. By bridging the simulation to reality gap and explicitly enforcing stability constraints during training, our approach offers a more reliable solution for real-world UAV control tasks compared to existing methods.

3. Background

3.1. Reinforcement Learning

Reinforcement learning is typically formulated as a Markov Decision Process (MDP) defined by $(S,A,P,R,\gamma )$, where S and A represent the state and action spaces, P describes state transitions, R denotes a reward function, and $\gamma$ is the discount factor. In robotic control, RL must account for factors such as deviations from reference trajectories, energy consumption, and hardware constraints. The design of suitable reward functions is nontrivial, as directly penalizing absolute error can result in uniform penalties that fail to effectively guide policy improvements.

Advanced RL algorithms, such as SAC and PPO, have enhanced learning efficiency and stability. However, challenges persist, including low sample efficiency, overfitting, and unstable training. Minor policy variations can induce significant performance fluctuations, particularly in complex tasks such as quadrotor trajectory tracking.

3.2. UAV Position Tracking Kinematics

This study focuses on learning trajectory tracking strategies for a quadrotor UAV based on its kinematic characteristics, which are described as follows:

$$\begin{array}{cc}\hfill {\dot{v}}_x& =-{\displaystyle \frac{f}{m}}\left(cos\phi sin\theta cos\varphi +sin\phi sin\varphi \right)\hfill \\ \hfill {\dot{v}}_y& =-{\displaystyle \frac{f}{m}}\left(sin\phi sin\theta cos\varphi -cos\phi sin\varphi \right)\hfill \\ \hfill {\dot{v}}_z& =g-{\displaystyle \frac{f}{m}}cos\varphi cos\theta \hfill \\ \hfill \dot{x}& =v_x\hfill \\ \hfill \dot{y}& =v_y\hfill \\ \hfill \dot{z}& =v_z\hfill \end{array}$$

(1)

3.3. Extended QUAV Dynamical Model

The full 6-DoF dynamics of a quadrotor unmanned aerial vehicle (QUAV) consists of translational and rotational motion. The translational dynamics used in Equation (1) can be written as

$$m\ddot{\mathbf{p}}={\mathbf{F}}_{\mathrm{total}},$$

(2)

where $\mathbf{p}\in {\mathbb{R}}^3$ is the position of the UAV and m is the total mass.

The rigid body attitude dynamics are given by

$$J\dot{\omega }=\tau -\omega \times \left(J\omega \right),$$

(3)

$$\dot{R}=R\widehat{\omega },$$

(4)

where $\omega \in {\mathbb{R}}^3$ is the body angular velocity, $J\in {\mathbb{R}}^{3\times 3}$ is the inertia matrix, $\tau$ is the control torque vector, $R\in SO\left(3\right)$ is the rotation matrix from the body frame to the inertial frame, and $\widehat{\omega }$ is the corresponding skew-symmetric matrix of $\omega$.

In this work, we primarily focus on training stability within the translational dynamics domain, where attitude variations are either controlled by a lower-level controller or remain within small perturbations. Therefore, the double integrator model of Equation (1) serves as a tractable approximation for high-level policy learning, while the complete rotational dynamics can be incorporated following the above formulation if needed for more precise control.

In this context, $(x,y,z)$ represents the position of the quadrotor UAV in each direction within the North East Down (NED) reference coordinate system, and $(v_x,v_y,v_z)$ denote the velocity in each respective direction. The force f is the combined external force generated by the four rotors of the quadrotor in the body coordinate system, and $(\varphi ,\theta ,\psi )$ represents the attitude angles of the UAV.

4. Methods

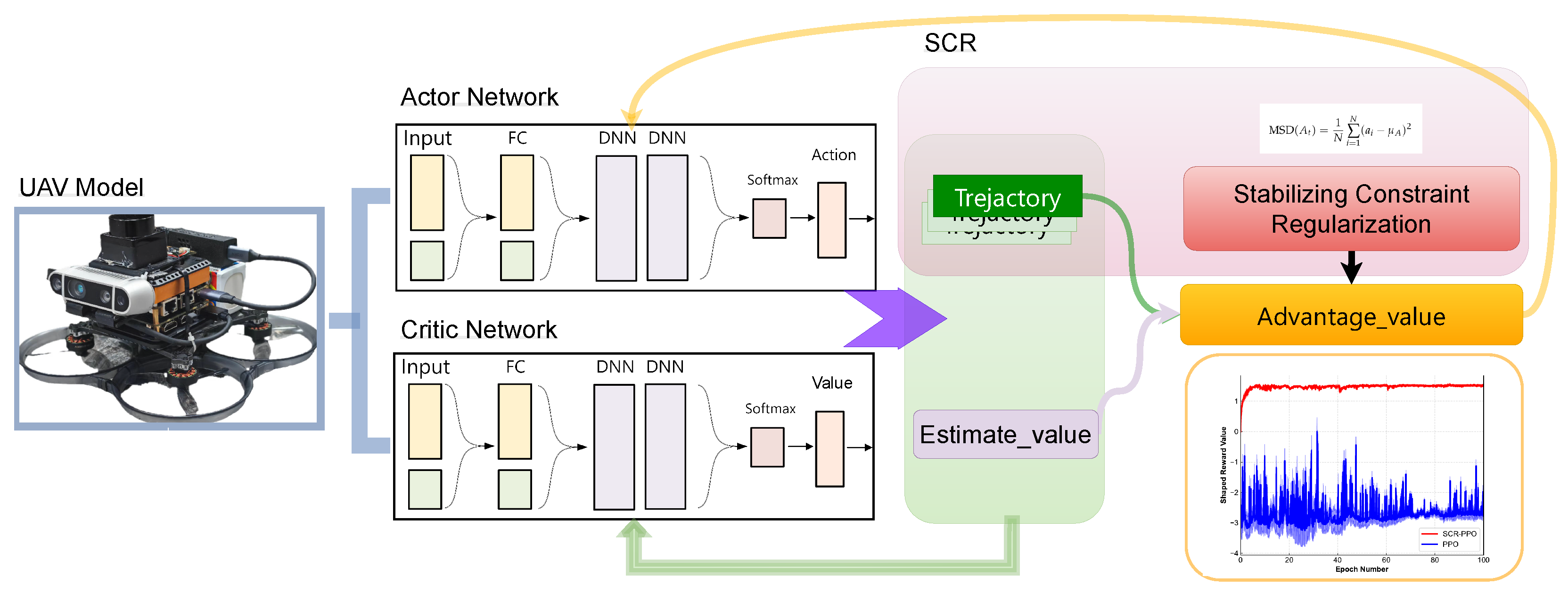
In high-dimensional, nonlinear systems such as quadrotor unmanned aerial vehicles (UAVs), substantial policy updates during reinforcement learning (RL) training can induce oscillations and instability, adversely affecting control precision and system reliability. To address these challenges, we introduce Stabilizing Constraint Regularization (SCR), a novel regularization technique designed to enhance the stability of policy updates. SCR leverages the principles of Lipschitz continuity to dynamically adjust the magnitude of policy updates, ensuring smooth and predictable policy evolution within the Proximal Policy Optimization (PPO) framework. This section delineates the theoretical foundations of SCR, its integration into PPO, and the detailed implementation procedures. Algorithm Flowchart in Figure 1. The flight data generated by the constructed mathematical model of the UAV is input into the SCR-PPO framework’s neural network. The action network outputs policy parameters, while the supervisory network outputs evaluated value parameters. The original PPO uses fixed parameters to adjust the magnitude of policy updates. The method proposed in this paper employs the SCR approach, dynamically adjusting the policy update rate of the action network based on the mean squared deviation between the action collected at the current time step and the average action value of the sequence containing that action.

4.1. Lipschitz Continuity

SCR is grounded in the Lipschitz Theorem, which provides a mathematical framework for controlling the rate of change of a function relative to its inputs. A function $f:{\mathbb{R}}^n\to {\mathbb{R}}^m$ is defined as Lipschitz continuous with Lipschitz constant L if, for any two points $x_1$ and $x_2$ within a certain neighborhood in the state space, the following inequality holds:

$$\parallel f\left(x_1\right)-f\left(x_2\right)\parallel \le L\parallel x_1-x_2\parallel$$

(5)

In the context of policy networks, ensuring Lipschitz continuity implies that minor perturbations in input states result in proportionally small changes in policy outputs. This property is critical for maintaining smooth and stable policy updates, particularly in environments characterized by complex dynamics and external disturbances.

In the PPO-based framework, the maximum allowable change in the policy output per update is proportional to the clipping parameter ${ϵ}_t$. Since SCR dynamically adjusts ${ϵ}_t$, the effective Lipschitz constant L of the policy network becomes bounded by a known $L_{max}$. By enforcing ${ϵ}_t\in [{ϵ}_{min},{ϵ}_{max}]$, we guarantee $\parallel {\pi }_{\theta }\left(s_1\right)-{\pi }_{\theta }\left(s_2\right)\parallel \le L_{max}\parallel s_1-s_2\parallel ,$ thereby providing a deterministic bound on control signal oscillations in deployment.

4.2. SCR-PPO

Proximal Policy Optimization (PPO) is a policy gradient method within the actor–critic framework that optimizes the policy by maximizing a clipped surrogate objective function. The clipping mechanism in PPO restricts the extent of policy updates to prevent substantial deviations that could destabilize training. The PPO objective function $L^{\mathrm{CLIP}}$ is expressed as

$$L^{\mathrm{CLIP}}\left(\theta \right)={\mathbb{E}}_t\left[min\left(r_t\left(\theta \right){\widehat{A}}_t,\mathrm{clip}(r_t\left(\theta \right),1-ϵ,1+ϵ){\widehat{A}}_t\right)\right]$$

(6)

where:

• $r_t\left(\theta \right)={\displaystyle \frac{{\pi }_{\theta }\left(a_t\right|s_t)}{{\pi }_{{\theta }_{\mathrm{old}}}\left(a_t\right|s_t)}}$ is the probability ratio of the new policy to the old policy.
• ${\widehat{A}}_t$ is the advantage estimate at time step t.
• $ϵ$ is the clipping parameter that limits the policy update magnitude.

Traditional RL approaches, including PPO, utilize fixed hyperparameters to constrain policy updates. However, these fixed parameters may not adapt sufficiently to the evolving dynamics of the learning process, leading to oscillatory and unstable training behaviors. SCR introduces a dynamic clipping parameter ${ϵ}_t$, which adjusts in real time based on the variability of the policy’s action outputs. This dynamic adjustment is formulated as follows:

$${ϵ}_t=\alpha ·\mathrm{MSD}\left(A_t\right)$$

(7)

where:

• $\alpha$ is a scaling factor that modulates the influence of the mean squared deviation.
• $\mathrm{MSD}\left(A_t\right)$ represents the Mean Squared Deviation of the actions produced by the policy at time step t, defined as

$$\mathrm{MSD}\left(A_t\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N{(a_i-{\mu }_A)}^2$$

(8)

Here, $a_i$ denotes individual actions within a batch of N actions, and ${\mu }_A$ is the mean action value. In the original PPO, the clipping parameter $ϵ$ is fixed (typically $ϵ=0.2$) to bound the policy update magnitude. In SCR-PPO, we replace this constant with a dynamic variant ${ϵ}_t=\alpha ·\mathrm{MSD}\left(A_t\right)$, where $\alpha$ is a scaling factor and $\mathrm{MSD}\left(A_t\right)$ denotes the mean squared deviation of the action outputs at iteration t. To ensure comparability with the original PPO and avoid overly aggressive updates, ${ϵ}_t$ is constrained within a fixed admissible range: ${ϵ}_{min}\le {ϵ}_t\le {ϵ}_{max},$ where ${ϵ}_{min}=0.1$ and ${ϵ}_{max}=0.3$ are selected by centering the range around the canonical PPO value ($ϵ=0.2$) with a $\pm 0.1$ tolerance. This design preserves the stability properties of conventional PPO when policy variability is small, while allowing more flexible updates when variability increases, thus enabling SCR-PPO to adapt more effectively to changing training dynamics.

By dynamically adjusting ${ϵ}_t$ based on the MSD of action outputs, SCR ensures that policy updates are proportionate to the current variability of the policy. This approach prevents excessively large updates that could destabilize the learning process and avoids overly conservative updates that may impede convergence.

Our proposed SCR-enhanced PPO (SCR-PPO) modifies the standard PPO framework by replacing the fixed clipping parameter $ϵ$ with a dynamic ${ϵ}_t$ derived from the mean squared deviation (MSD) of the policy’s action outputs. This modification is outlined as follows:

1.

Dynamic Clipping Parameter: Instead of using a constant $ϵ$, SCR-PPO calculates ${ϵ}_t$ at each training iteration based on the current MSD of the policy’s actions. This ensures that the clipping range adapts to the policy’s variability, maintaining a balance between exploration and stability.

2.

Modified Objective Function: The SCR-PPO objective function, denoted as $L^{\mathrm{SCR}-\mathrm{CLIP}}$, incorporates the dynamic clipping parameter:

$$L^{\mathrm{SCR}-\mathrm{CLIP}}\left(\theta \right)={\mathbb{E}}_t\left[min\left(r_t\left(\theta \right){\widehat{A}}_t,\mathrm{clip}(r_t\left(\theta \right),1-{ϵ}_t,1+{ϵ}_t){\widehat{A}}_t\right)\right]$$

(9)

This adaptation ensures that policy updates are adaptively constrained, enhancing the stability and convergence of the training process.

Finally, the offline learning phase of the quadrotor position tracking task using the SCR-PPO algorithm is summarized in Algorithm 1.

Algorithm 1 SCR-PPO.

$\mathrm{SCR-PPO}(\theta ,\alpha )$       Initialize policy network parameters $\theta$       while not converged do             Collect and store trajectories $(s_t,a_t,r_t,s_{t+1})$             Compute advantages ${\widehat{A}}_i$ using Generalized Advantage Estimation (GAE)             for each mini-batch $(s_i,a_i,r_i,s_i^{\prime })$ do                   Compute ratio $r_i\left(\theta \right)={\displaystyle \frac{{\pi }_{\theta }\left(a_i\right|s_i)}{{\pi }_{{\theta }_{\mathrm{old}}}\left(a_i\right|s_i)}}$                   Calculate ${ϵ}_i=\alpha ·{\displaystyle \frac{1}{N}}{\sum }_{j=1}^N{(a_j-{\mu }_A)}^2$                   Compute loss ${\mathcal{L}}_{\mathrm{SCR}-\mathrm{CLIP},i}=min\left(r_i\left(\theta \right){\widehat{A}}_i,\mathrm{clip}\left(r_i\left(\theta \right),1-{ϵ}_i,1+{ϵ}_i\right){\widehat{A}}_i\right)$                   Update $\theta$ by minimizing ${\mathcal{L}}_{\mathrm{SCR}-\mathrm{CLIP},i}$       end for       Clear replay buffer       end while    return updated $\theta$

4.3. Parameter Adjustment Mechanism

In SCR-PPO, the clipping parameter ${ϵ}_t$ is dynamically adjusted based on the stability of the learned policy. We define a stability metric $S_t$ at iteration t as the variance of the recent K episodes’ episode returns: $S_t=\mathrm{Var}\left(R_{t-K+1},\dots ,R_t\right).$ Two thresholds, $T_{\mathrm{low}}$ and $T_{\mathrm{high}}$, are employed to control the adjustment of the clipping parameter. When the stability variance $S_t$ falls below $T_{\mathrm{low}}$, the policy is regarded as overly stable and potentially under-exploring; in this case, ${ϵ}_t$ is slightly increased to encourage exploration. Conversely, when $S_t$ exceeds $T_{\mathrm{high}}$, it indicates that the policy exhibits excessive fluctuation, and ${ϵ}_t$ is decreased to reduce oscillations. If $S_t$ lies between these two thresholds, the value of ${ϵ}_t$ remains unchanged. The adjustment step size ${\delta }_{ϵ}$ is a small constant (e.g., $0.01$) to avoid abrupt changes.

This procedure ensures that the policy exploration–exploitation balance adapts to the learning dynamics, while maintaining a bounded Lipschitz constant for deterministic control smoothness.

5. Experiment

5.1. Reinforcement Learning Hyperparameters

The PPO and SCR-PPO controllers shared the same network architectures and optimization settings.

Table 2. Hyperparameters of PPO and SCR-PPO.

Category	Parameter	Value Description
Training Parameters	Optimizer	Adam, learning rate 3 × 10−4
	Initial clip range $ϵ$ (PPO)	Fixed: 0.2
	Dynamic ${ϵ}_t$ (SCR-PPO)	${ϵ}_t=\alpha ·MSD\left(a_t\right)$, with $\alpha =0.1$
	Discount factor $\gamma$	0.99
	GAE $\lambda$	0.95
	Batch size	2048 steps per update
	Mini-batch size	64
	Epochs per update	10
	Entropy coefficient	0.01
	Value loss coefficient	0.5
	Early stop criterion	Mean episodic return variation $\le \pm 1\%$
Training Resource	Hardware	Intel i7-12700K CPU, RTX 3060 Ti GPU
	Total training time	≈ 8 h for 1 M total steps

summarizes the full set of hyperparameters, which were selected based on the canonical PPO configurations reported by ref. [25] and further refined for the quadrotor trajectory tracking task.

5.2. Classical Controller Parameters

To ensure a fair comparison, both the PID and MPC controllers were independently tuned via grid search to achieve their best performance under identical operating conditions. The resulting configurations are listed in

Table 3. Controller parameters for PID and MPC.

Controller	Parameter	Value Description
PID	$K_p$ ($x,y,z$)	1.2, 1.2, 1.0
	$K_i$ ($x,y,z$)	0.01, 0.01, 0.02
	$K_d$ ($x,y,z$)	0.4, 0.4, 0.35
	hlSampling frequency	50 Hz
MPC	Control range	$\pm 2 \mathrm{m}/{\mathrm{s}}^2$
	Prediction horizon	20 steps (0.02 s per step)
	Control horizon	5 steps
	QP solver	qpOASES
	Reference update rate	50 Hz
	Weight matrix Q	diag (1, 1, 1) for position error
	Weight matrix R	diag(0.1, 0.1, 0.1) for control effort

.

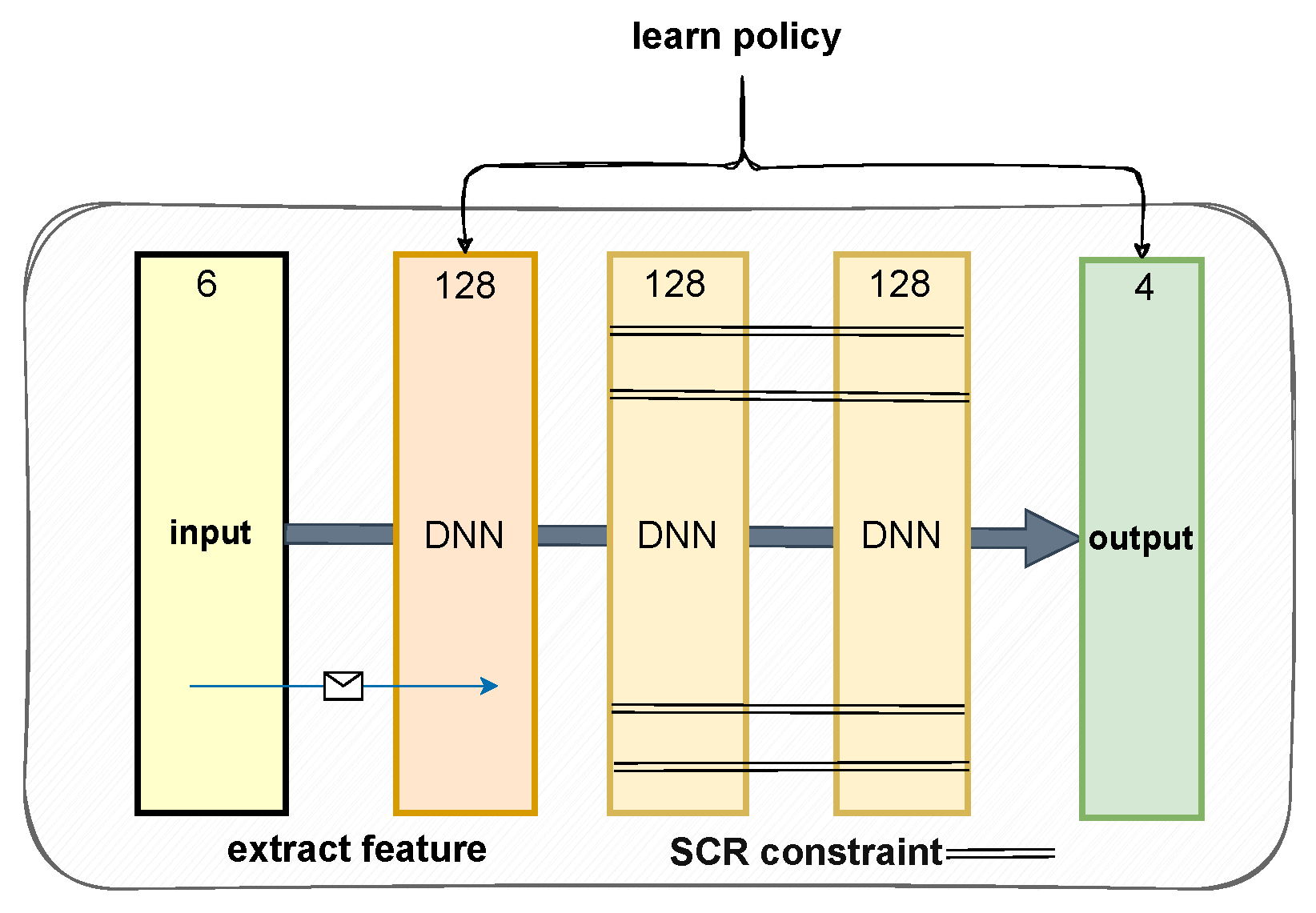
5.3. Network Structure

SCR-PPO enhances strategy performance by introducing a stability regularization term into the classical PPO algorithm. Consequently, the strategy network does not require a specialized design; both the actor and critic networks maintain the same structure, consisting of three fully connected layers with Tanh activation functions between layers. The actor network inputs the UAV position and velocity information and outputs the thrust and desired attitude, while the critic network inputs the UAV state information and outputs the evaluated state value (Figure 2).

In the UAV trajectory tracking task, the state input, denoted as state, comprises the relative error between the current and desired positions of the UAV, as well as the relative velocity error, and can be represented as follows:

$$state=\{\Delta x,\Delta y,\Delta z,\Delta v_x,\Delta v_y,\Delta v_z\}$$

(10)

The output, denoted as action, consists of the combined external force in the UAV body coordinate system and the desired attitude angle commands:

$$action=\{f,{\varphi }_{\mathrm{cmd}},{\theta }_{\mathrm{cmd}},{\psi }_{\mathrm{cmd}}\}$$

(11)

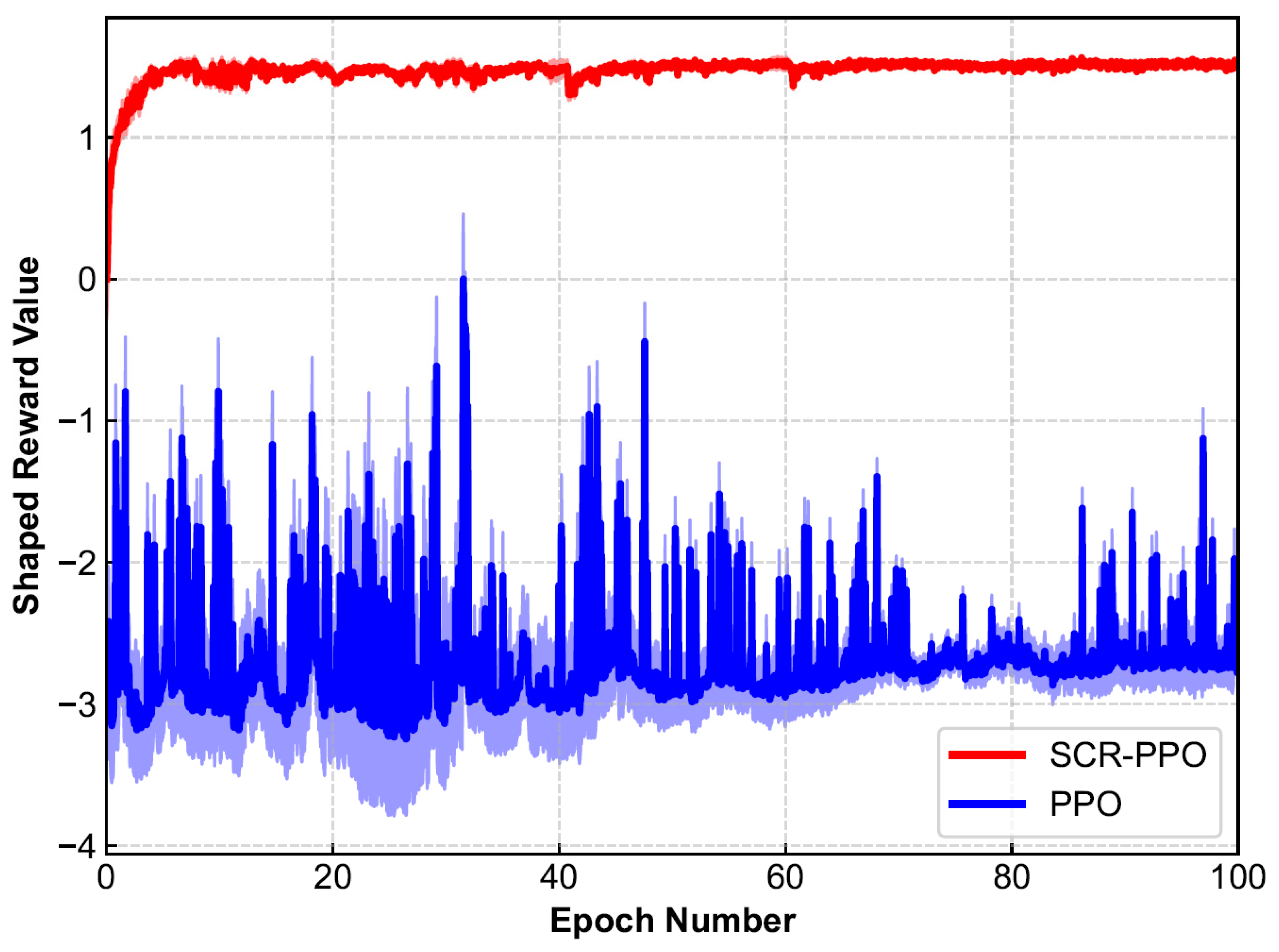
SCR-PPO was trained on an Intel i7-13700K CPU (Intel, Santa Clara, CA, USA) to simulate the method’s efficiency under resource-constrained conditions. The classical PPO and SCR-PPO rewards change during training as shown below (Figure 3).

To ensure a fair and meaningful comparison among all controllers (PID, MPC, PPO, and SCR-PPO), each controller was independently tuned under identical simulation conditions to achieve its best possible performance. Specifically, (i) the same quadrotor dynamic model, control frequency (100 Hz), trajectory, noise model, and external disturbance profiles were used for all controllers; (ii) the PID and MPC parameters (Table 3) were optimized via grid search in the same simulation environment; and (iii) PPO and SCR-PPO shared the same network architectures and training settings (Table 2) to ensure that any performance differences are attributable solely to the proposed SCR modification, rather than network capacity or optimization bias. This strict alignment in evaluation conditions guarantees that performance comparisons are both fair and reproducible.

5.4. Training Efficiency

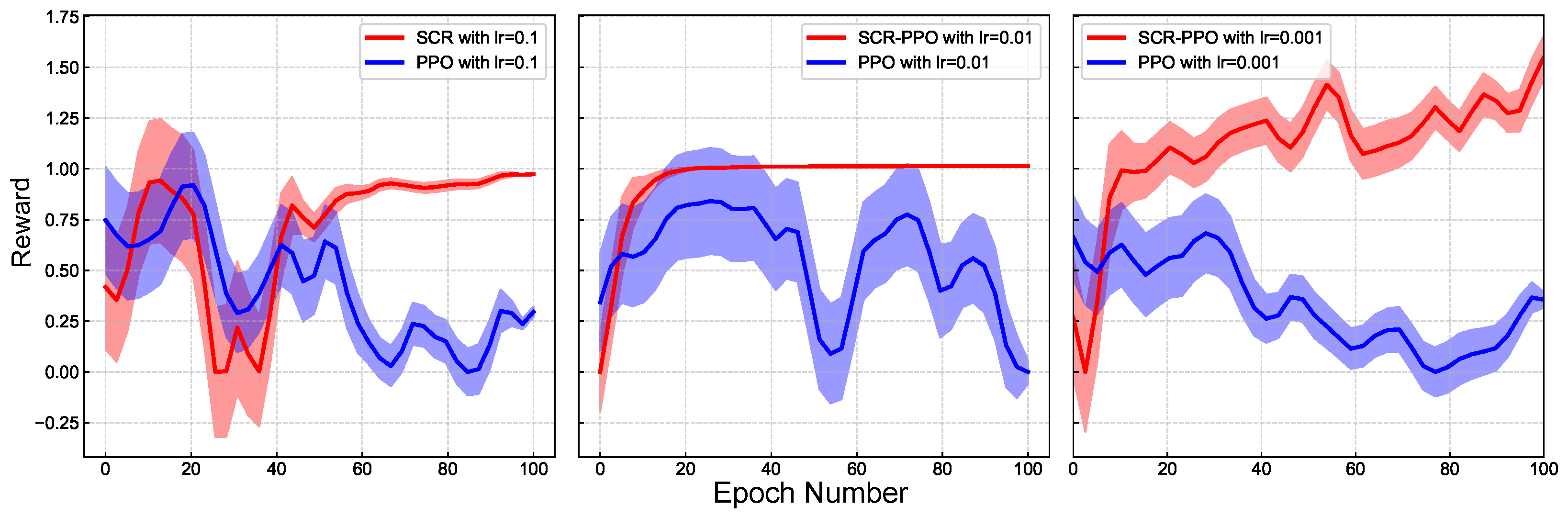
To verify the adaptability of the SCR method to hyperparameters, the reward curves of SCR-PPO and classical PPO under different learning rate parameters are presented in Figure 4. In the figure, the variance of the SCR-PPO algorithm is smaller, and its sensitivity to the learning rate is significantly reduced. In practice, this translates to faster deployment times, higher task performance, and lower computational costs.

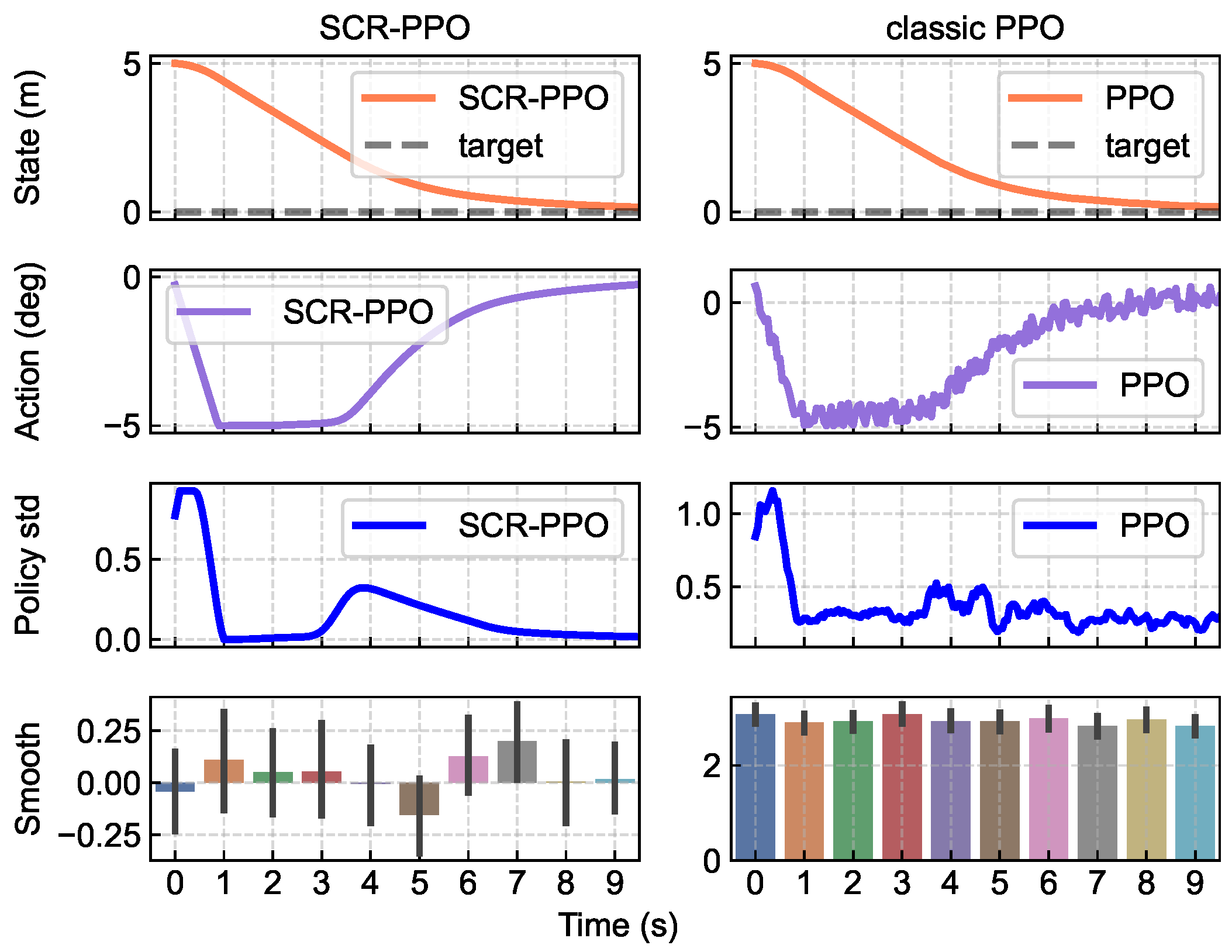
5.5. Policy Smoothness

To objectively measure and compare the smoothness of policies, we defined a smoothness metric, $S_m$, based on the Fast Fourier Transform (FFT) spectrum. A smoother action policy results in less wasted energy and enhanced stability. This method allows for a quantitative assessment of policy smoothness, facilitating effective comparison and analysis of various strategies:

$$S_m={\displaystyle \frac{{\sum }_{k=1}^N{f}_k·A_k}{{\sum }_{k=1}^N{A}_k}}$$

(12)

where $f_k$ is the amplitude of the k-th frequency component, $A_k$ represents the amplitude, and N is the number of frequency components. $\Delta f$ is the sampling frequency, set to 50 in this study. By jointly considering the frequency and amplitude of control signal components, this metric provides an average weighted normalized frequency. On this scale, a higher number indicates a greater presence of high-frequency signal components for a given control problem, usually implying a more expensive drive, whereas a smaller number indicates a smoother response.

Figure 5 illustrates the policy evaluation based on the smoothing metric between SCR-PPO and classical PPO. Compared to classical PPO, the strategy variance of SCR-PPO is reduced by 45%.

Although the differences in positional changes within the simulated environment are negligible, policies trained using SCR-PPO exhibit smoother properties than those trained via traditional neural network architectures. This smoothness facilitates the deployment of strategies in hardware applications. The SCR term filters out the high-frequency components of control signals, thereby steadily improving the smoothness of neural network controllers for learning state-to-action mappings. These advancements enhance the stability and applicability of control strategies.

5.6. Robustness

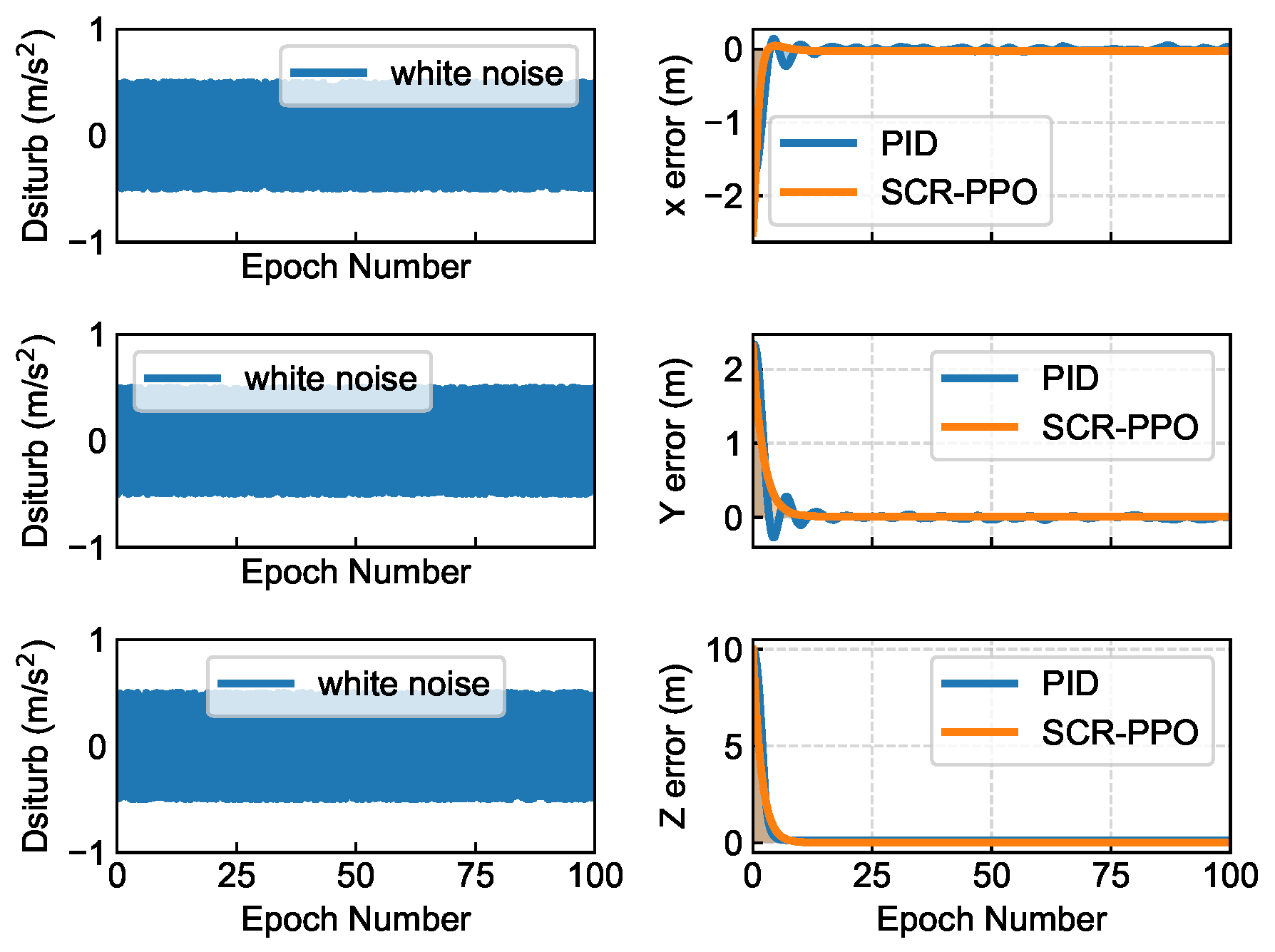
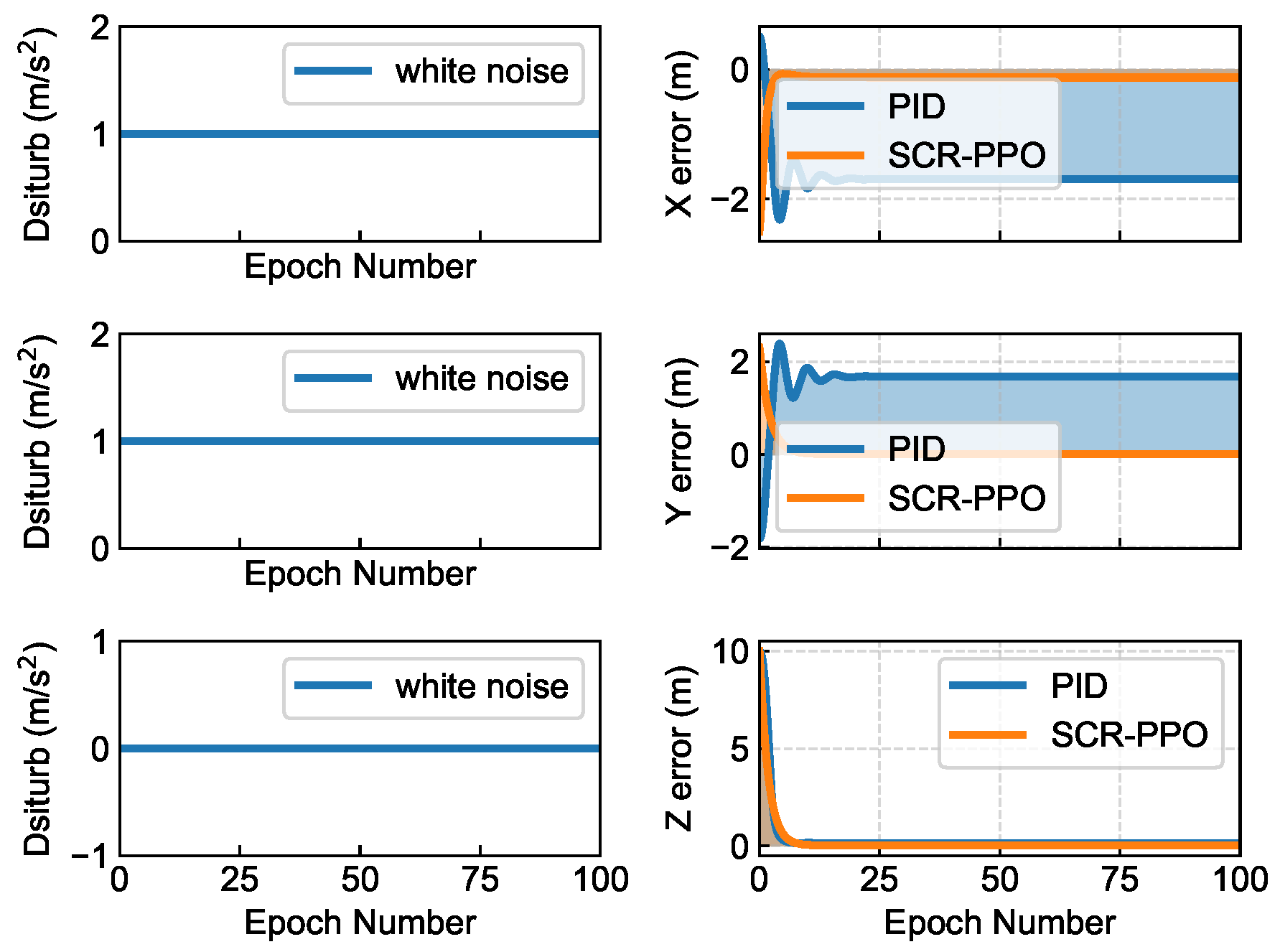
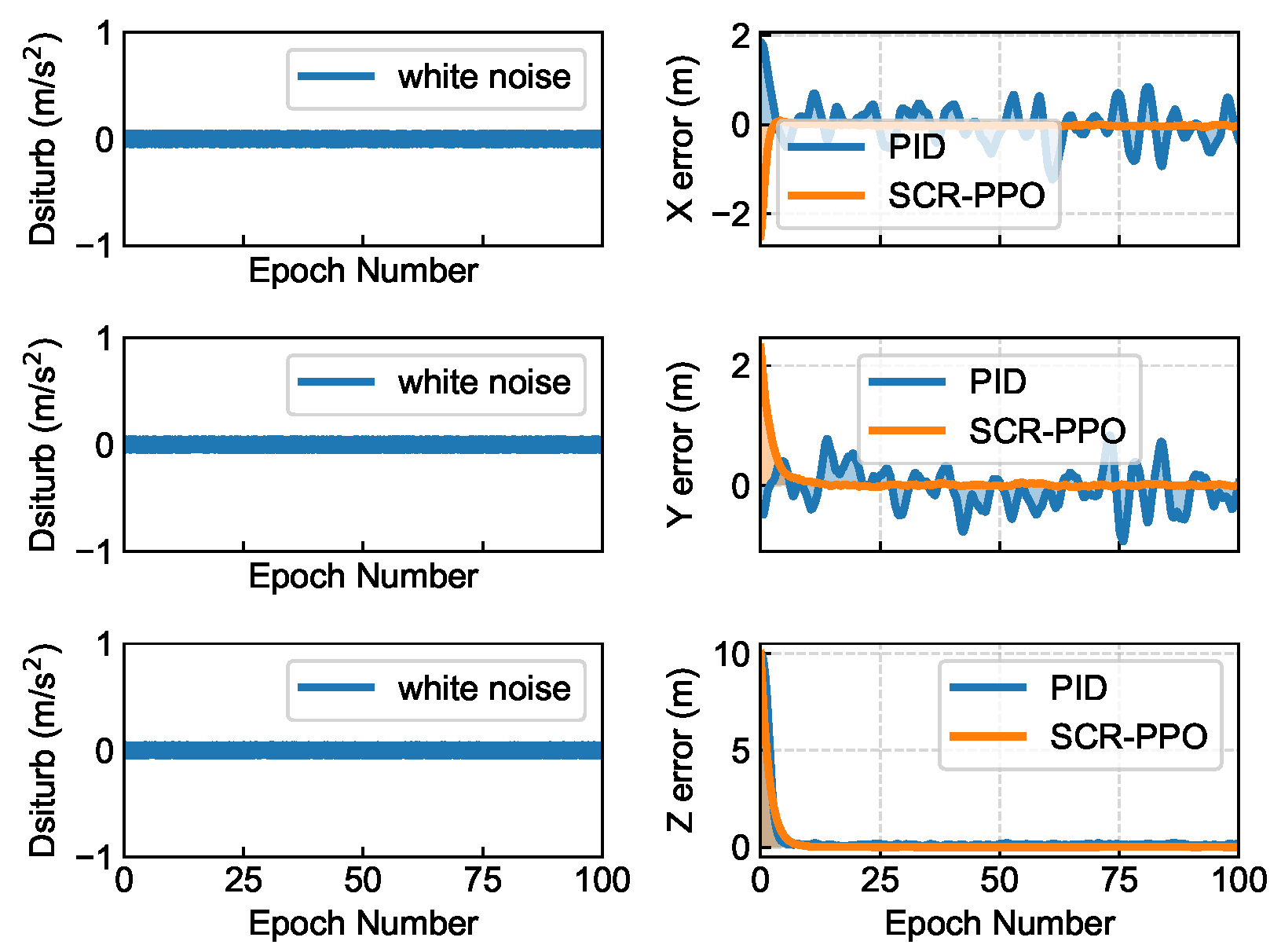
To evaluate the robustness of RL methods against perturbations, we conducted comparative experiments using the widely applied proportional–integral–derivative (PID) controller. We examined three types of disturbances (see Figure 6, Figure 7 and Figure 8).

Figure 6 displays the control performance under white noise disturbances with an amplitude of 0.5. Compared to the PID controller, the SCR-PPO strategy exhibits greater robustness to low levels of white noise disturbances, maintaining lower errors across all three axes. Notably, on the x- and y-axes, SCR-PPO demonstrates significantly lower errors, effectively canceling out the input disturbances. On the z-axis, SCR-PPO effectively controls the error and performs comparably to the PID controller.

Figure 7 illustrates the control performance under constant-value disturbances. Under moderate disturbances, SCR-PPO consistently outperforms the PID controller, and on the x- and y-axes, the control error is substantially lower, indicating a more resilient control mechanism. On the z-axis, SCR-PPO is adaptive and compensates for disturbances.

Figure 8 illustrates the control performance under a white noise disturbance with an amplitude of 0.05 added to the state information. In the face of this disturbance, SCR-PPO maintains reduced control errors across all axes, especially in the z-axis, where a significant error reduction is realized. This demonstrates the superior immunity of SCR-PPO to sensor noise-type disturbances.

The experimental results demonstrate that the SCR-PPO strategy outperforms the conventional PID controller across all axes under various disturbances. The enhanced performance of SCR-PPO is attributed to its learning-based approach, which fortifies the control system’s robustness by regulating the stability of the strategy, thereby maintaining performance under uncertain and fluctuating conditions.

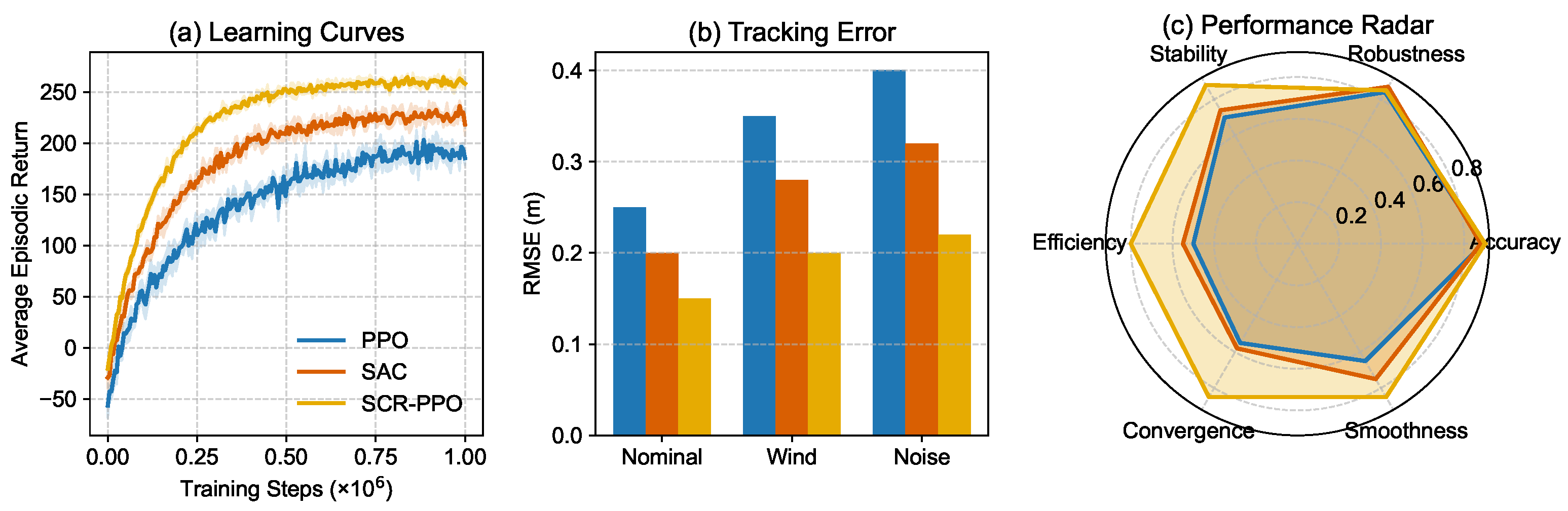
5.7. Performance Comparison

As shown in Figure 9, the proposed SCR-PPO algorithm outperforms PPO and SAC in terms of learning efficiency, tracking accuracy, and overall robustness.

In the learning curves (Figure 9a), SCR-PPO converges rapidly within approximately $0.3$ million steps, achieving the highest asymptotic return (∼260) with minimal variance. SAC converges faster than PPO and reaches a stable performance around 230, while PPO shows the slowest convergence and larger fluctuations due to its on-policy nature. The shaded regions represent $\pm 1$ standard deviation over five independent runs, showing that SCR-PPO maintains greater stability across the entire training process.

In the RMSE comparison (Figure 9b), SCR-PPO achieves the lowest tracking error in all three scenarios (nominal, wind disturbance, and sensor noise), with particularly significant improvements under disturbance conditions. This strongly indicates robustness against environmental perturbations.

The radar chart (Figure 9c) further provides a multi-dimensional normalized performance assessment over six criteria: accuracy, robustness, stability, energy efficiency, convergence speed, and smoothness. SCR-PPO achieves the most balanced and consistently high scores, excelling particularly in robustness, convergence speed, and smoothness, while PPO and SAC demonstrate trade-offs in different metrics.

Overall, these results confirm that SCR-PPO not only learns more efficiently than PPO and SAC, but also generalizes better and maintains superior robustness, making it a strong candidate for real-world UAV control tasks.

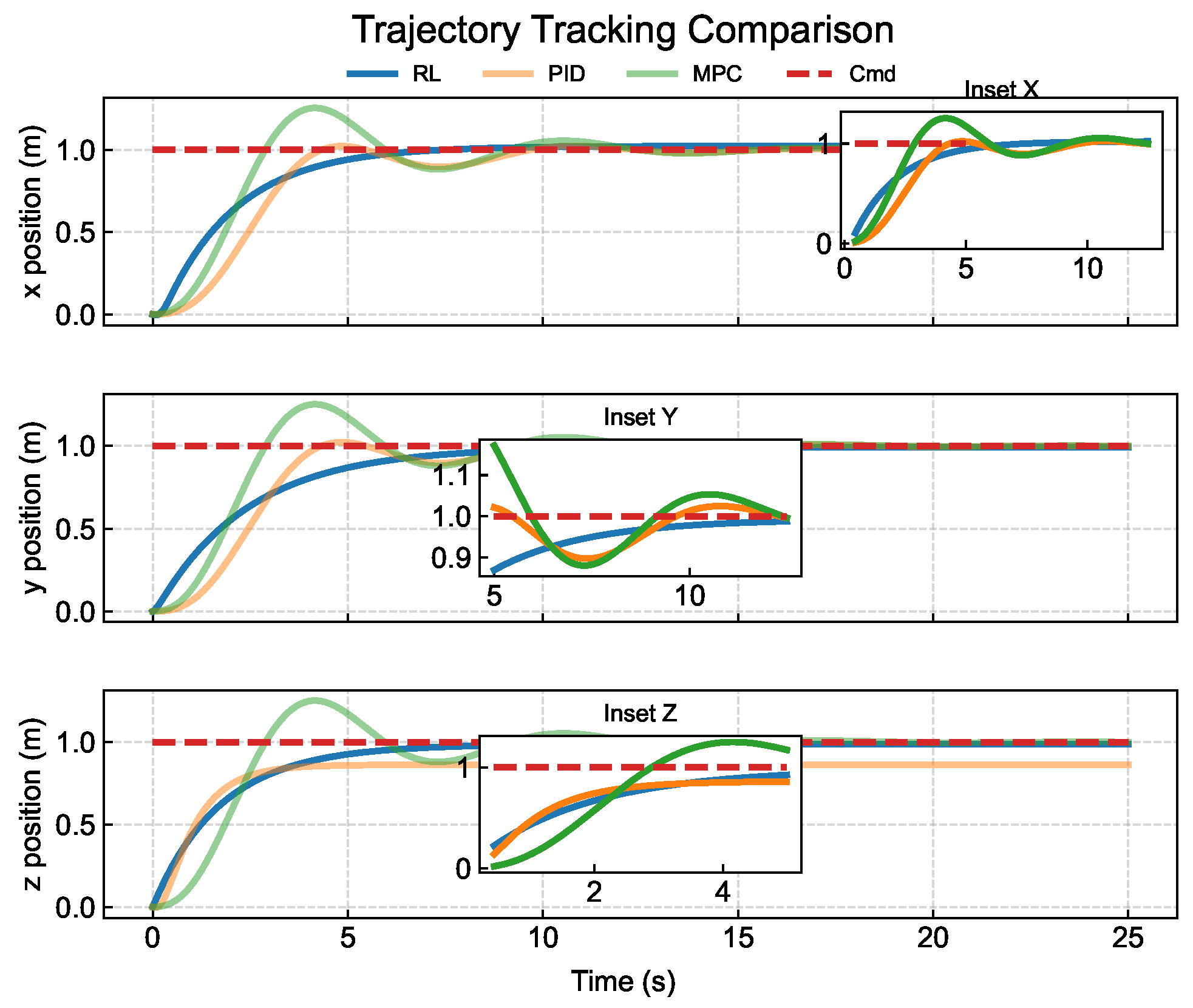
5.8. Control Precision

Our study involved a comparative analysis of the effectiveness of a learning-based RL approach, a traditional PID controller based on classical control theory, and a contemporary model predictive control (MPC) system grounded in modern control theory in UAV trajectory tracking tasks (Figure 10).

The findings reveal that the RL method exhibits a substantial advantage in terms of response speed on the z-axis, with no significant overshoot observed. Upon examining the UAV position changes over time on the three axes (x, y, z) and their alignment with the predefined trajectory, it was observed that the RL method demonstrated prompt and precise tracking performance on the y- and z-axes. On the x-axis, its effectiveness was comparable to that of MPC and surpassed that of the PID controller.

These results imply that, in certain scenarios, policies formulated by RL methods can achieve performance levels that match or exceed those of conventional control techniques.

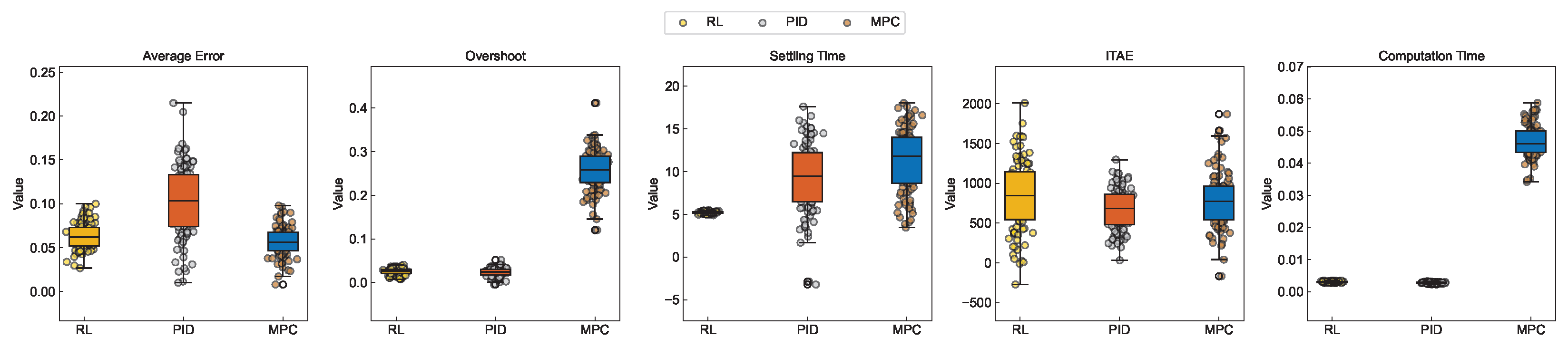
For a more thorough evaluation of the RL, PID, and MPC methods, we performed 100 tests to assess their responses to random fixed-value step commands. We compared a range of performance metrics, including average error, overshoot, settling time, integral time absolute error, and computation time per step (Figure 11). These metrics collectively provide insights into the accuracy, stability, efficiency, and computational demands of each method. The outcomes of these tests enabled a more precise assessment and comparison of the strengths and weaknesses of the various approaches in practical scenarios.

Unlike MPC, which depends on precise system models, RL operates independently of prior model knowledge, thereby enhancing its adaptability and suitability in scenarios where system models are either flawed or challenging to acquire. Additionally, RL possesses the capacity to continually refine its performance over time, potentially enabling it to outperform traditional control methods in extended-duration applications. These qualities establish RL as a highly effective control strategy in a variety of dynamic and complex settings. Responses to Random Fixed-Value Step Commands: RL demonstrates control capabilities on par with Model Predictive Control (MPC); RL excels over both PID and MPC in terms of overshoot and settling time. Moreover, RL exhibits a notable advantage in computation time, which is a critical requirement for time-sensitive applications.

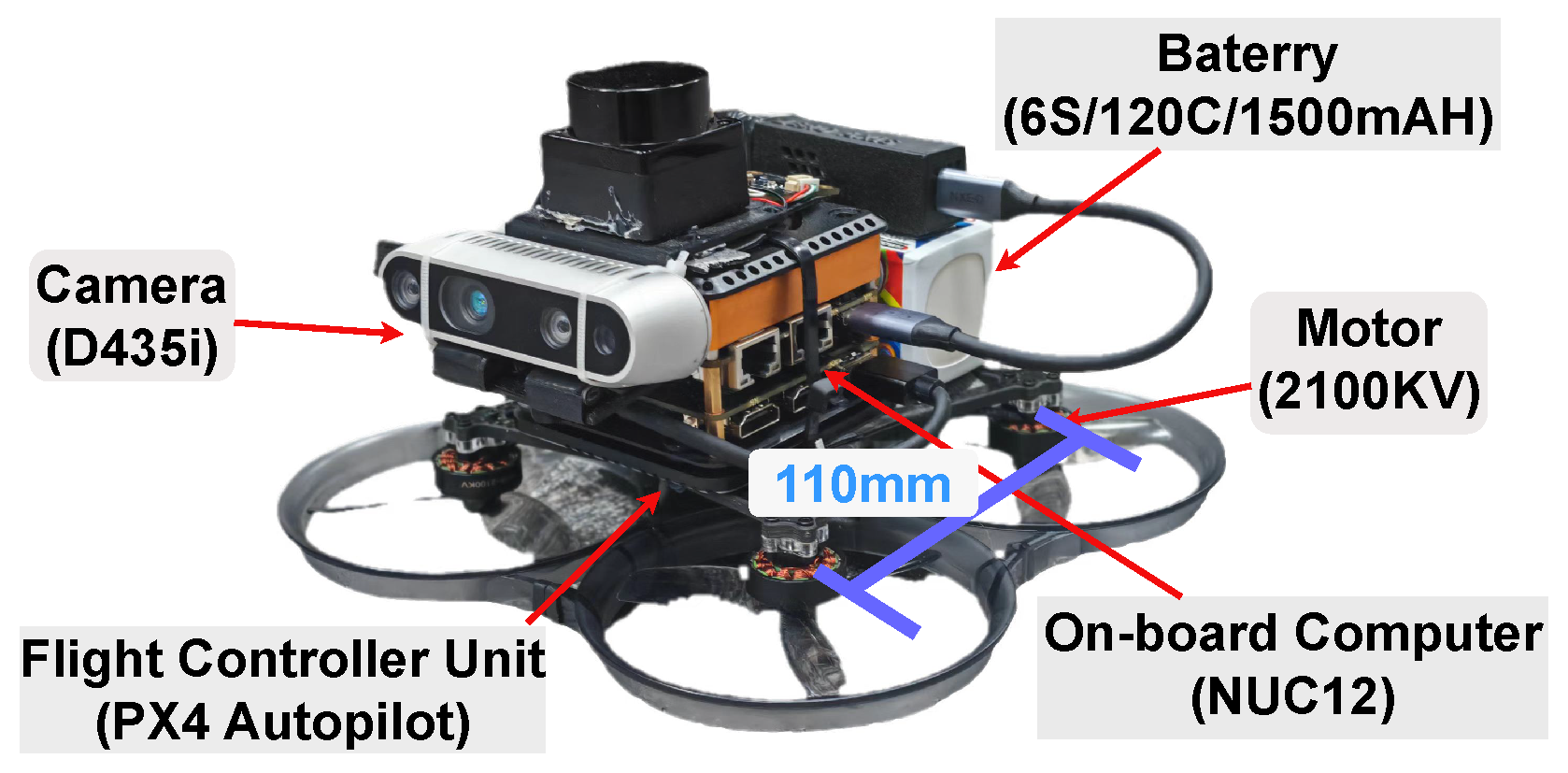
5.9. Real-World Flight Testing Environment

To validate the proposed control strategy beyond simulation, comprehensive real-world flight experiments were conducted using a custom-built quadrotor platform in an outdoor flight testing range (Figure 12).

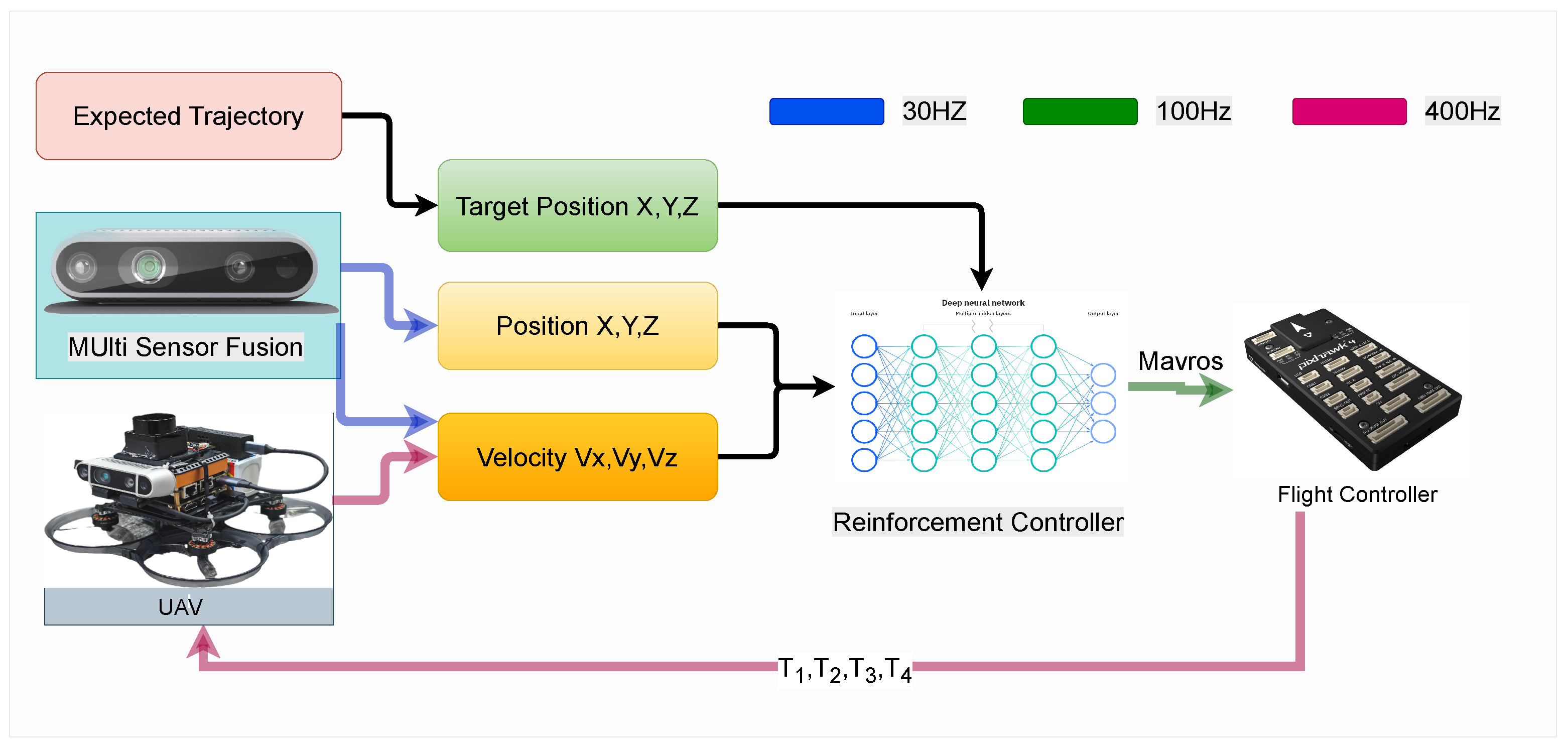
The experimental setup, consistent with the hardware architecture shown in Figure 13, is outlined as follows: The D435i depth camera runs the VINS fusion localization algorithm, providing drone position data at 30 Hz. The drone’s position, velocity, and current desired position derived from the target trajectory are fed into the trained policy network, which outputs desired attitude angles at 100 Hz. Control commands are transmitted through the Mavros system to the underlying PX4 controller, which outputs allocated control forces at 400 Hz to drive motor movement.

Hardware parameters in real flight environments as shown in

Table 4. Summary of key parameters used in simulation, real flight testing, and algorithm design.

Symbol	Parameter Description	Value/Range	Unit	Context
${\tau }_m$	Motor time constant (1st-order dynamics)	0.02	s	motor model
T-Motor Specs	Motor type	2004 KV2100	–	Real flight
Propeller	Propeller size	3	inch	Simulation & Real flight
$m_{total}$	Take-off mass	≈900	g	Real flight platform
$d_{frame}$	Wheelbase	110	mm	Real flight platform
$f_{IMU}$	IMU update frequency	400	Hz	sensor model
${\sigma }_a$	IMU accel. noise std.dev.	0.05	m/s2	sensor model
${\sigma }_{\omega }$	IMU gyro noise std.dev.	0.002	rad/s	sensor model
$f_{ctrl}$	Control loop rate	50	Hz	Both envs, OFFBOARD mode
$t_{lat}$	Communication latency emulation	20	ms	Real flight
$ϵ$	PPO clipping parameter (fixed)	0.2	–	Baseline PPO
${ϵ}_t$	SCR-PPO dynamic clipping range	0.1–0.3	–	Proposed method
$\alpha$	Scaling factor in ${ϵ}_t$	Paper-defined	–	Proposed method
Onboard PC	Companion computer	intel NUC12	–	Real flight
Pixhawk	Flight controller	Pixhawk 4 (PX4 v1.14)	–	Real flight
Battery	Power supply	6S LiPo 22.2 V 10 Ah	–	Real flight

.

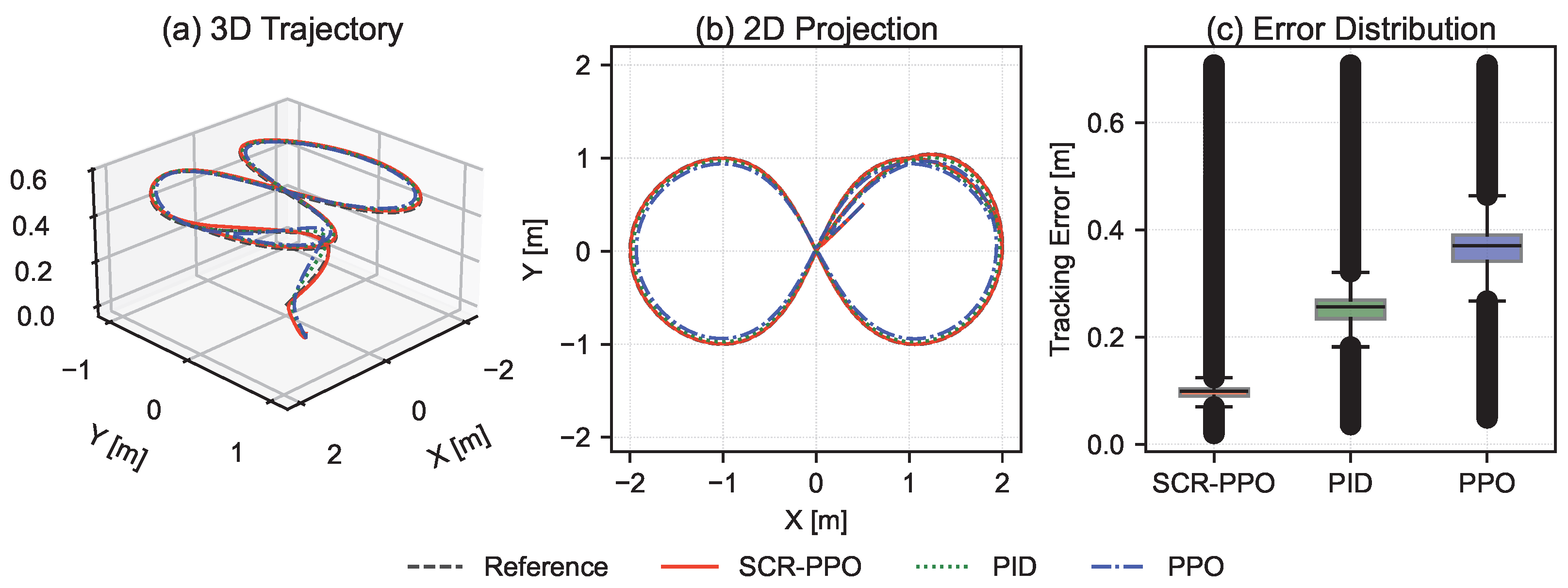
The validation is conducted in a challenging “figure-eight” trajectory scenario. As shown in Figure 14, SCR-PPO consistently yields the lowest tracking error among the tested controllers. (a) The 3D trajectories provide a spatial perspective of tracking accuracy throughout the flight mission. (b) The horizontal projection of the same trajectories onto the XY-plane uses consistent colors and line styles, enabling direct comparison with the 3D view. (c) The boxplot illustrates the full mission tracking error distribution for each controller, showing that SCR-PPO achieves the lowest median error and the smallest interquartile range, but PPO exhibits the largest deviations. Color coding is consistent across all subplots: black dashed for the reference, red solid for SCR-PPO, green dotted for PID, and blue dash–dot for PPO. This real-world experimental environment ensures that the evaluation includes realistic aerodynamic effects, sensor noise, actuation delays, and environmental disturbances that are difficult to fully replicate in simulation, thereby providing a strong validation of the proposed control strategy under operational conditions.

5.10. Limitations

Although the proposed SCR-PPO algorithm demonstrates clear advantages in convergence speed, stability, and robustness within both simulation and real-world tests, several limitations remain that define its applicability boundaries:

While SCR-PPO achieves notable improvements in convergence speed, stability, and robustness over baseline methods, its performance gains remain inherently bounded by the limitations of the underlying PPO framework, particularly in terms of sample efficiency and asymptotic performance ceilings. Under extreme out-of-distribution disturbances, such as sudden winds exceeding 6 m/s, severe actuator faults, or complete GNSS signal loss, the policy’s generalization capability may degrade, leading to reduced tracking accuracy or instability. Moreover, when deployed on resource-constrained embedded platforms running additional computationally intensive perception or planning modules, latency and diminished real-time responsiveness may occur.

6. Conclusions

This paper introduced Stabilizing Constraint Regularization (SCR), a novel approach to enhancing RL policy stability in complex, high-dimensional systems such as quadrotor UAVs. By dynamically adjusting the clipping parameter based on policy output variability and enforcing Lipschitz continuity principles, SCR mitigates oscillations and instability commonly afflicting traditional RL methods. The resulting policies exhibit improved convergence, robustness, and adaptability, facilitating their deployment in demanding real-world missions. While the proposed adaptive clipping mechanism is developed within the PPO framework, its core principle of stability-aware update bounding can be extended to other on-policy actor–critic methods. However, the present study focuses on PPO due to its widespread adoption in continuous control tasks and its sensitivity to clipping threshold selection.

Future research may explore integrating SCR with other advanced RL algorithms, expanding its applicability to multi-agent systems, or leveraging domain adaptation strategies to further bridge sim to real gaps. Ultimately, the ability of SCR to ensure stable and efficient policy learning can help realize the full potential of RL in safety-critical and dynamic scenarios.