Novel Twist Morphing Aileron and Winglet Design for UAS Control and Performance
Abstract
:1. Introduction
2. Asymmetric Analysis-Twist Morphing Ailerons
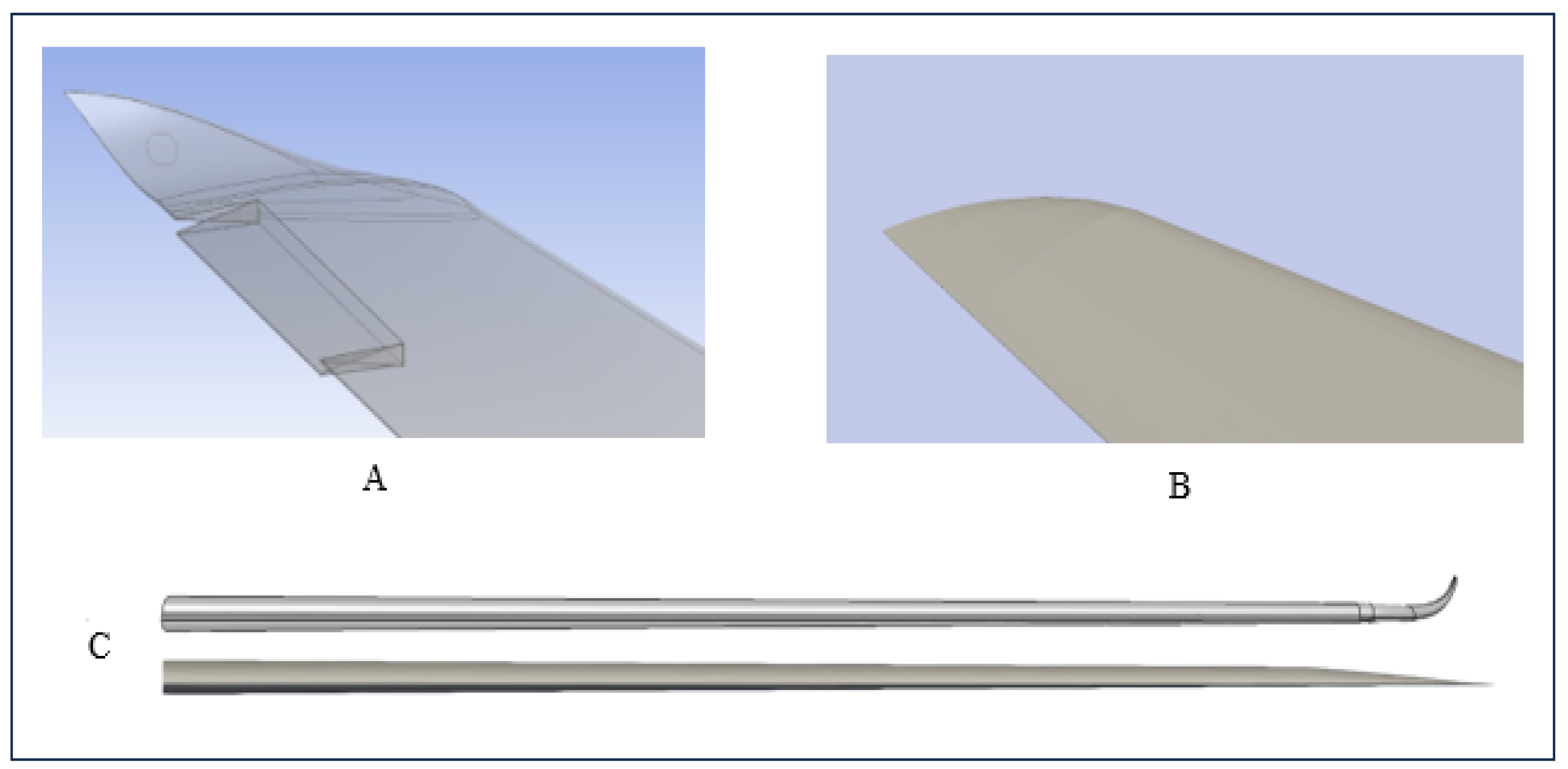
2.1. Implementation of a UAS-S45 Wing for Twist Morphing
2.2. Methodology Used for Asymmetric Twist Analysis (Twist Morphing Ailerons)
2.2.1. Roll Motion
2.2.2. Optimization of Asymmetric Morphing Ailerons for Rolling Maneuver
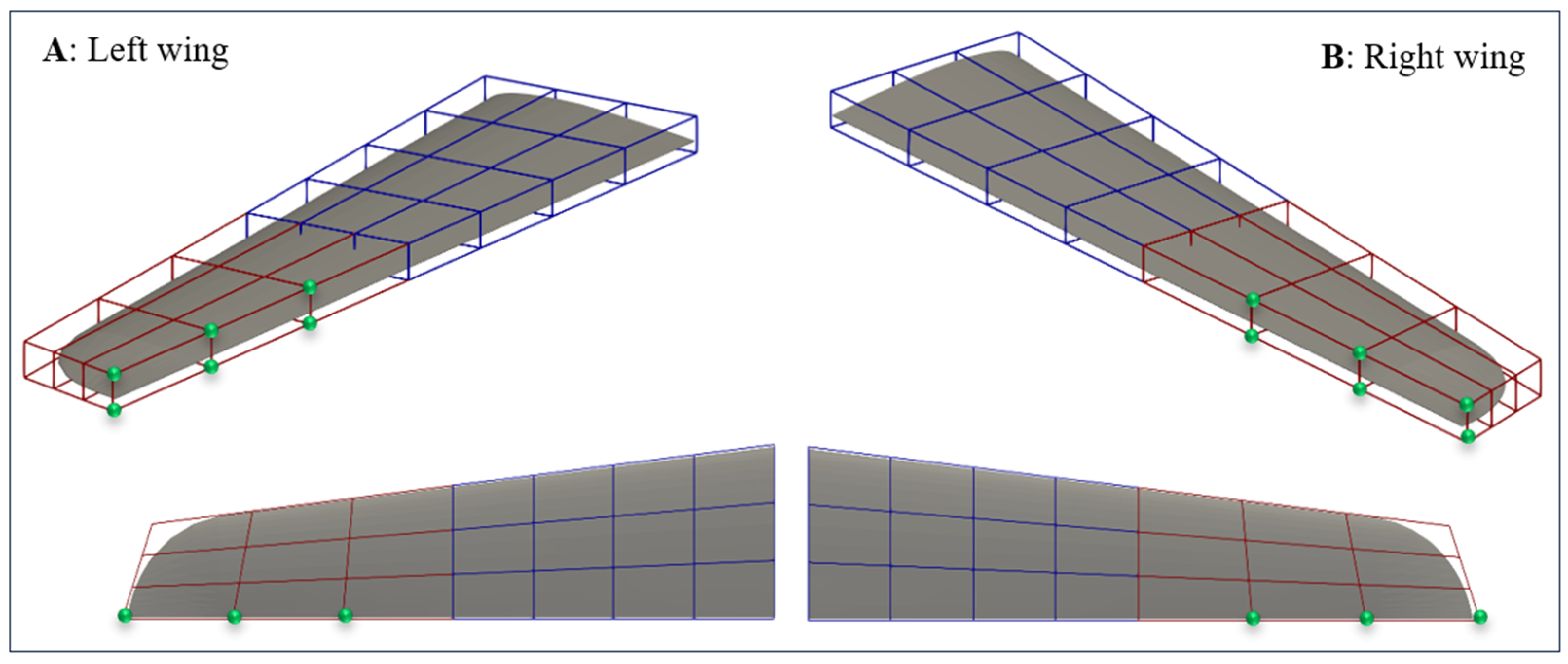
2.2.3. Wing Parametrization
2.2.4. Optimization Setup
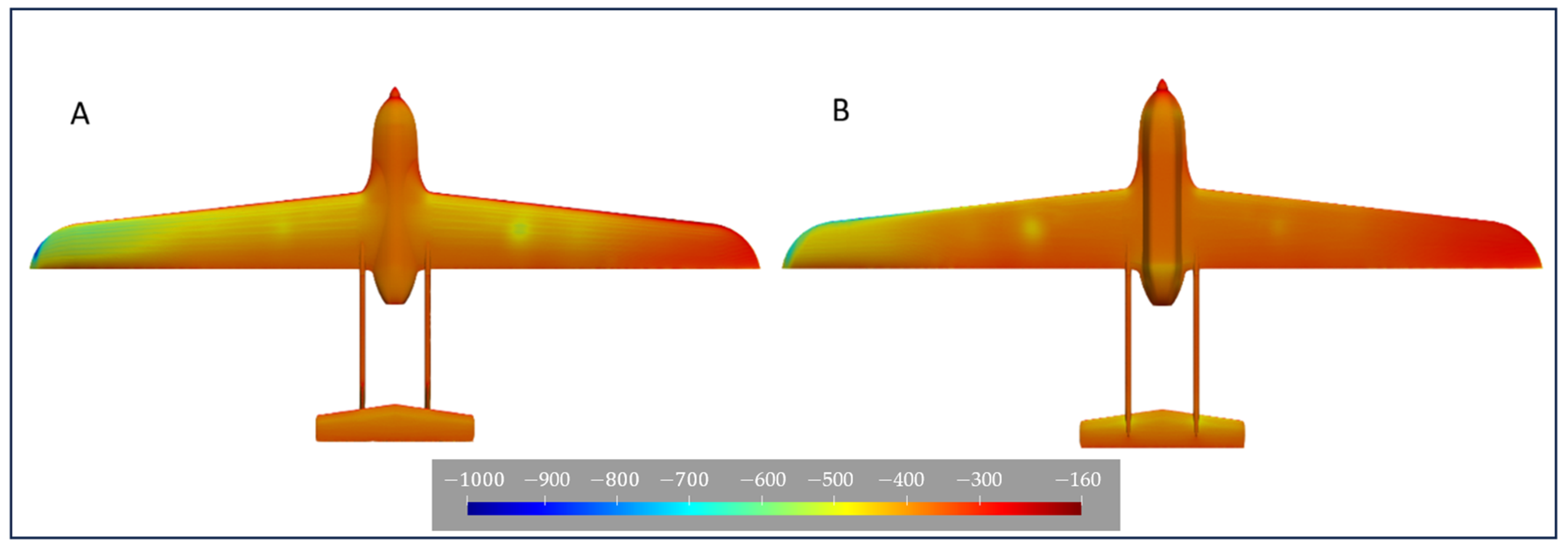
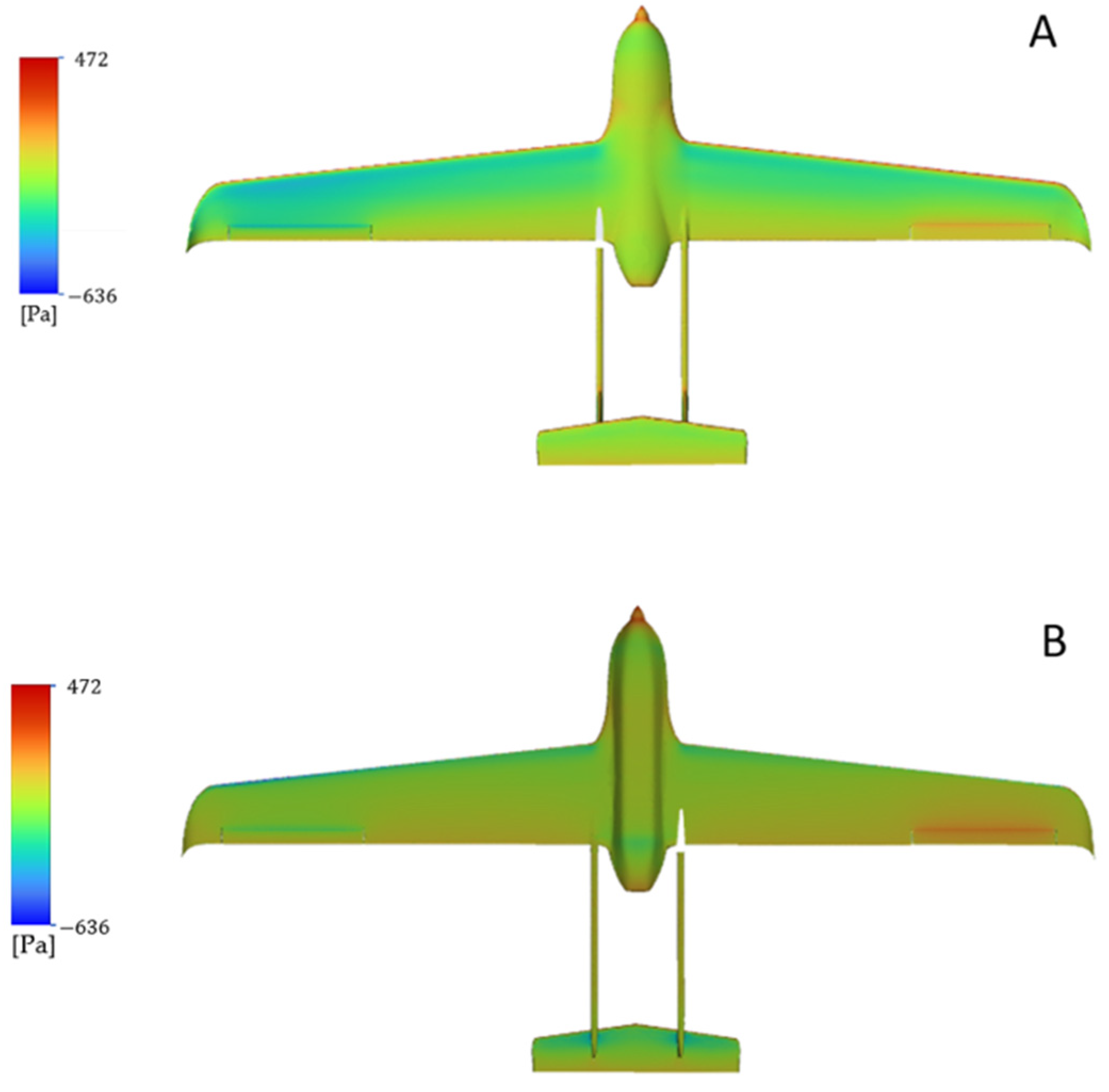
2.3. Results and Discussions for Asymmetric Twist Analysis
2.3.1. Morphing Ailerons
2.3.2. Hinged Ailerons
2.3.3. Comparison of Hinged and Morphing Ailerons
3. Symmetric Twist Analysis (Twist Morphing Wingtips)
3.1. Twist Morphing Wingtips
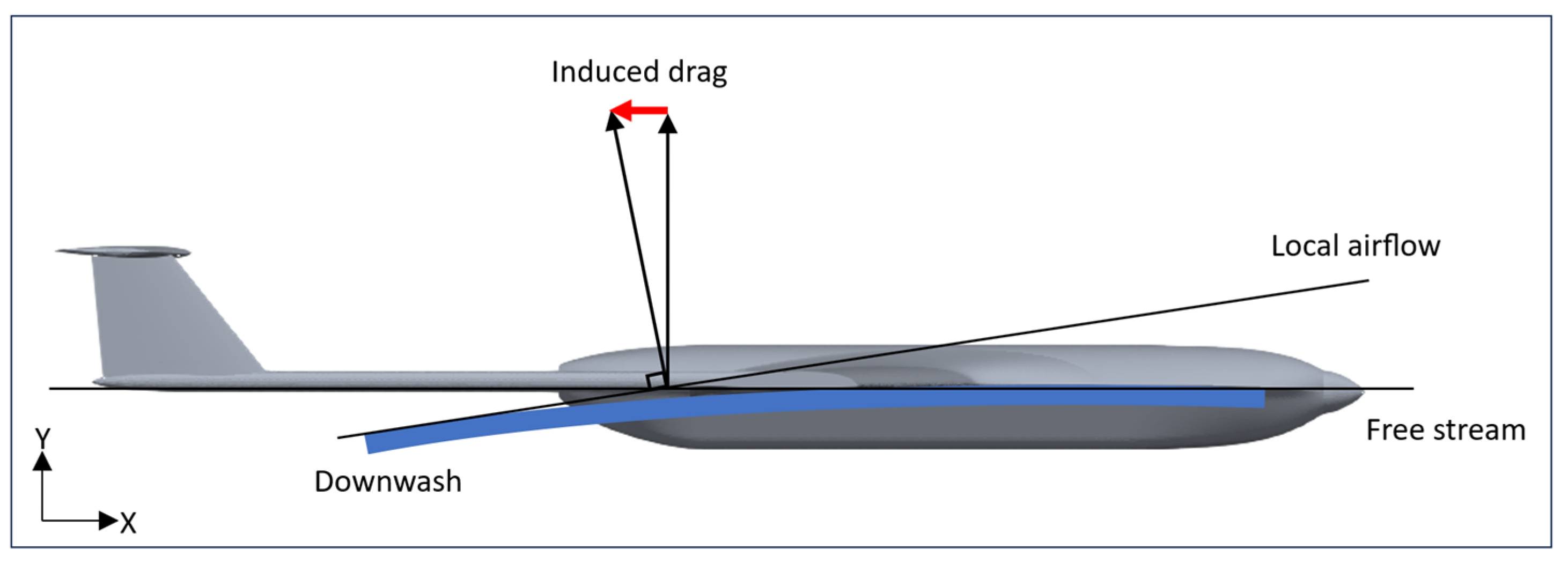
3.2. Induced Drag
3.3. Methodology Used for the Symmetric Twist (Twist Morphing Wingtips)
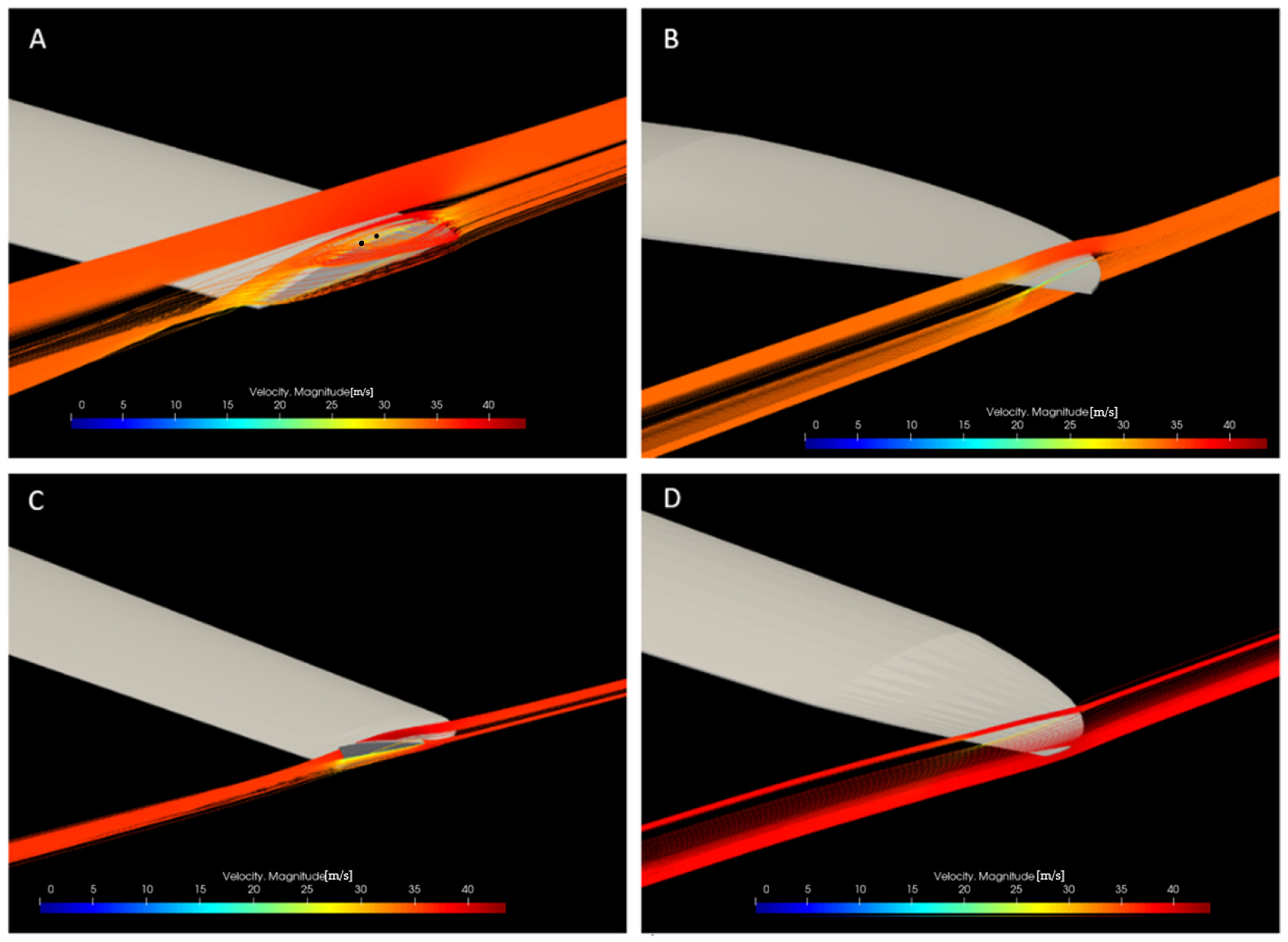
3.4. Results and Discussion for Symmetric Analysis (Twist Morphing Wingtip)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dimino, I.; Lecce, L.; Pecora, R. Morphing Wing Technologies: Large Commercial Aircraft and Civil Helicopters; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Ameduri, S.; Concilio, A. Morphing wings review: Aims, challenges, and current open issues of a technology. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 237, 4112–4130. [Google Scholar] [CrossRef]
- Pecora, R. Morphing wing flaps for large civil aircraft: Evolution of a smart technology across the Clean Sky program. Chin. J. Aeronaut. 2021, 34, 13–28. [Google Scholar] [CrossRef]
- Kota, S.; Osborn, R.; Ervin, G.; Maric, D.; Flick, P.; Paul, D. Mission adaptive compliant wing–design, fabrication and flight test. In Proceedings of the RTO Applied Vehicle Technology Panel (AVT) Symposium, Evora, Portugal, 20–24 May 2009; pp. 1–18. [Google Scholar]
- Samuel, J.B.; Pines, D. Design and testing of a pneumatic telescopic wing for unmanned aerial vehicles. J. Aircr. 2007, 44, 1088–1099. [Google Scholar] [CrossRef]
- Elelwi, M.; Botez, R.M.; Dao, T.-M. Structural sizing and topology optimization based on weight minimization of a variable tapered span-morphing wing for aerodynamic performance improvements. Biomimetics 2021, 6, 55. [Google Scholar] [CrossRef]
- Elelwi, M.; Pinto, F.S.; Botez, R.M.; Dao, T.-M. Multidisciplinary optimization for weight saving in a variable tapered span-morphing wing using composite materials—Application to the UAS-S4. Actuators 2022, 11, 121. [Google Scholar] [CrossRef]
- Bashir, M.; Negahban, M.H.; Botez, R.M.; Wong, T. Numerical Simulation of the Transient Flow around the Combined Morphing Leading-Edge and Trailing-Edge Airfoil. Biomimetics 2024, 9, 109. [Google Scholar] [CrossRef] [PubMed]
- Bashir, M.; Longtin-Martel, S.; Botez, R.M.; Wong, T. Optimization and design of a flexible droop-nose leading-edge morphing wing based on a novel black widow optimization algorithm—Part I. Designs 2022, 6, 10. [Google Scholar] [CrossRef]
- Bashir, M.; Botez, R.M.; Wong, T. Design and Optimization of Droop Nose Leading Edge (DNLE) Morphing Wing Skin for the UAS-S45. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024; Volume 2150. [Google Scholar]
- An, J.; Yan, M.; Zhou, W.; Sun, X.; Yan, Z.; Qiu, C. Aircraft dynamic response to variable wing sweep geometry. J. Aircr. 1988, 25, 216–221. [Google Scholar] [CrossRef]
- Koreanschi, A.; Gabor, O.S.; Acotto, J.; Brianchon, G.; Portier, G.; Botez, R.M.; Mamou, M.; Mebark, Y. Optimization and Design of a Morphing Aircraft Wing Tip Demonstrator at Low Speed for Drag Reduction, Part I–Aerodynamic Optimizations Using 3 Algorithms: Genetic, Bee Colony and Gradient Descent algorithms. Chin. J. Aeronaut. 2017, 30, 149–163. [Google Scholar] [CrossRef]
- Botez, R.M.; Koreanschi, A.; Gabor, O.S.; Tondji, Y.; Guezguez, M.; Kammegne, J.; Grigorie, L.; Sandu, D.; Mebarki, Y.; Mamou, M.; et al. Numerical and experimental transition results evaluation for a morphing wing and aileron system. Aeronaut. J. 2018, 122, 747–784. [Google Scholar] [CrossRef]
- Popov, A.V.; Botez, R.M.; Labib, M. Transition point detection from the surface pressure distribution for controller design. J. Aircr. 2008, 45, 23–28. [Google Scholar] [CrossRef]
- Botez, R.M.; Molaret, P.; Laurendeau, E. Laminar flow control on a research wing project presentation covering a three year period. In Proceedings of the Canadian Aeronautics and Space Institute Annual General Meeting, Toronto, ON, Canada, 25–26 April 2007. [Google Scholar]
- Liu, Z.; Dai, N.; Wang, H.; Wu, L. Design of Variable Thickness Wing Based on Two-way Shape Memory Alloy Drive. In Proceedings of the 2021 2nd International Conference on Intelligent Design (ICID), Xi’an, China, 19 October 2021; pp. 88–92. [Google Scholar]
- Xiasheng, S.; Jingfeng, X.; Jin, Z.; Zhigang, W.; Wenjuan, W.; Zhang, M. Design and validation of a variable camber wing structure. Chin. J. Aeronaut. 2024, 37, 1–11. [Google Scholar]
- Negahban, M.H.; Botez, R.M.; Razavi, S.E. New method for the flow modeling around chord-wise morphing airfoil. In Proceedings of the AIAA SciTech 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 2574. [Google Scholar]
- Pecora, R.; Magnifico, M.; Amoroso, F.; Monaco, E. Multi-parametric flutter analysis of a morphing wing trailing edge. Aeronaut. J. 2014, 118, 1063–1078. [Google Scholar] [CrossRef]
- Pecora, R.; Dimino, I.; Amoroso, F.; Ciminello, M. Structural design of an adaptive wing trailing edge for enhanced cruise performance. In Proceedings of the 24th AIAA/AHS Adaptive Structures Conference, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Concilio, A.; Dimino, I.; Pecora, R. SARISTU: Adaptive trailing edge device (ATED) design process review. Chin. J. Aeronaut. 2021, 34, 187–210. [Google Scholar] [CrossRef]
- Barbarino, S.; Bilgen, O.; Ajaj, R.M.; Friswell, M.I.; Inman, D.J. A review of morphing aircraft. J. Intell. Mater. Syst. Struct. 2011, 22, 823–877. [Google Scholar] [CrossRef]
- Negahban, M.H.; Bashir, M.; Traisnel, V.; Botez, R.M. Seamless morphing trailing edge flaps for UAS-S45 using high-fidelity aerodynamic optimization. Chin. J. Aeronaut. 2024, 37, 12–29. [Google Scholar] [CrossRef]
- Amendola, G.; Dimino, I.; Concilio, A.; Pecora, R.; Amoroso, F. Actuation system design for a morphing aileron. Appl. Mech. Mater. 2015, 798, 582–588. [Google Scholar] [CrossRef]
- Ameduri, S.; Dimino, I.; Concilio, A.; Mercurio, U.; Pellone, L. Specific Modeling Issues on an Adaptive Winglet Skeleton. Appl. Sci. 2021, 11, 3565. [Google Scholar] [CrossRef]
- Majji, M.; Rediniotis, O.; Junkins, J. Design of a morphing wing: Modeling and experiments. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Hilton Head, SC, USA, 20–23 August 2007; Volume 6310. [Google Scholar]
- Garcia, H.; Abdulrahim, M.; Lind, R. Roll control for a micro air vehicle using active wing morphing. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Austin, TX, USA, 11–14 August 2003; Volume 5347. [Google Scholar]
- Phillips, W.; Alley, N.; Goodrich, W. Lifting-line analysis of roll control and variable twist. J. Aircr. 2004, 41, 1169–1176. [Google Scholar] [CrossRef]
- Abdulrahim, M. Flight performance characteristics of a biologically-inspired morphing aircraft. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005; Volume 345. [Google Scholar]
- KAYGANE; Ulusoy, C. Effectiveness of twist morphing wing on aerodynamic performance and control of an aircraft. J. Aviat. 2018, 2, 77–86. [Google Scholar]
- Pecora, R.; Amoroso, F.; Lecce, L. Effectiveness of wing twist morphing in roll control. J. Aircr. 2012, 49, 1666–1674. [Google Scholar] [CrossRef]
- Rodrigue, H.; Cho, S.; Han, M.-W.; Bhandari, B.; Shim, J.-E.; Ahn, S.-H. Effect of twist morphing wing segment on aerodynamic performance of UAV. J. Mech. Sci. Technol. 2016, 30, 229–236. [Google Scholar] [CrossRef]
- Ahmed, M.; Abdelrahman, M.; ElBayoumi, G.; ElNomrossy, M. Optimal wing twist distribution for roll control of MAVs. Aeronaut. J. 2011, 115, 641–649. [Google Scholar] [CrossRef]
- Stanford, B.; Abdulrahim, M.; Lind, R.; Ifju, P. Investigation of membrane actuation for roll control of a micro air vehicle. J. Aircr. 2007, 44, 741–749. [Google Scholar] [CrossRef]
- Vos, R.; Gürdal, Z.; Abdalla, M. Mechanism for warp-controlled twist of a morphing wing. J. Aircr. 2010, 47, 450–457. [Google Scholar] [CrossRef]
- Rodrigue, H.; Wang, W.; Bhandari, B.; Han, M.-W.; Ahn, S.-H. Cross-shaped twisting structure using SMA-based smart soft composite. Int. J. Precis. Eng. Manuf. Green Technol. 2014, 1, 153–156. [Google Scholar] [CrossRef]
- Nelson, R.C. Flight Stability and Automatic Control; WCB/McGraw Hill: New York, NY, USA, 1998. [Google Scholar]
- He, P.; Mader, C.A.; Martins, J.R.; Maki, K.J. Dafoam: An open-source adjoint framework for multidisciplinary design optimization with openfoam. AIAA J. 2020, 58, 1304–1319. [Google Scholar] [CrossRef]
- He, P.; Mader, C.A.; Martins, J.R.; Maki, K. An object-oriented framework for rapid discrete adjoint development using OpenFOAM. In Proceedings of the AIAA SciTech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; Volume 1210. [Google Scholar]
- Sripawadkul, V.; Padulo, M.; Guenov, M. A comparison of airfoil shape parameterization techniques for early design optimization. In Proceedings of the 13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference, Fort Worth, TX, USA, 13–15 September 2010; Volume 9050. [Google Scholar]
- Sederberg, T.W.; Parry, S.R. Free-form deformation of solid geometric models. In Proceedings of the 13th Annual Conference on Computer Graphics and Interactive Techniques, Dallas, TX, USA, 18–22 August 1986; pp. 151–160. [Google Scholar]
- Samareh, J. Aerodynamic shape optimization based on free-form deformation. In Proceedings of the 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Albany, NY, USA, 30 August–1 September 2004; Volume 4630. [Google Scholar]
- Ronzheimer, A. Shape Parameterisation Based on Freeform Deformation in Aerodynamic Design Optimization. In Proceedings of the ERCOFTAC Design Optimization: Methods & Applications, Athen, Greece, 31 March–2 April 2004. [Google Scholar]
- Negahban, M.H.; Bashir, M.; Botez, R.M. Free-form deformation parameterization on the aerodynamic optimization of morphing trailing edge. Appl. Mech. 2023, 4, 304–316. [Google Scholar] [CrossRef]
- Negahban, M.H.; Bashir, M.; Botez, R.M. Impact of Free-Form Deformation Control Points on the Optimization of the UAS-S45. In Proceedings of the International Symposium on Unmanned Systems and the Defense Industry, Madrid, Spain, 30 May–1 June 2022; pp. 21–27. [Google Scholar]
- Caughey, D.A. Introduction to Aircraft Stability and Control Course Notes for M&AE 5070; Sibley School of Mechanical & Aerospace Engineering Cornell University: Ithaca, NY, USA, 2011; Volume 15. [Google Scholar]















| Function/Variable | Description | Total Number |
|---|---|---|
| (A) | ||
| Objective function | ||
| min | objective function for right wing | 1 |
| w.r.t: | ||
| Y T | FFD control points Twist | 64 1 |
| Subject to: | ||
| AOA initial = AOA final | Constant angle of attack | 1 |
| Volume constraint | 64 | |
| Design variable bounds | 6 | |
| Twist deformation bounds | 24 | |
| (B) | ||
| Objective function | ||
| max | objective function for left wing | 1 |
| w.r.t: | ||
| Y T | FFD control points Twist | 64 1 |
| Subject to: | ||
| AOA initial = AOA final | Constant angle of attack | 1 |
| Volume constraint | 64 | |
| Design variable bounds | 6 | |
| Twist deformation bounds | 24 | |
| Far-Field (m) | Density Box (m) | Total Number () | |
|---|---|---|---|
| Mesh 1 | 1.75 | 0.045 | 10.52 |
| Mesh 2 | 1.75 | 0.05 | 8.845 |
| Mesh 3 | 2 | 0.075 | 4.16 |
| Cl | Relative Error (%) | Cd | Relative Error (%) | |
|---|---|---|---|---|
| Mesh 1 | 0.1930 | - | 0.03 | - |
| Mesh 2 | 0.1930 | 0 | 0.0288 | 4 |
| Mesh 3 | 0.1930 | 0 | 0.0285 | 5 |
| Ailerons | Roll Moment Coefficient () | Induced Drag | () Variations (%) | |||
|---|---|---|---|---|---|---|
| Hinged ailerons | 0 | 0.289 | 0.0427 | 0.463 | 0.00296 | - |
| Twist morphing ailerons | 0 | 0.188 | 0.0395 | 0.701 | 0.00115 | +34 |
| Function/Variable | Description | Total Number |
|---|---|---|
| Objective function | ||
| min | objective function | 1 |
| w.r.t: | ||
| Y T | FFD control points Twist | 52 1 |
| Subject to: | ||
| Constant drag | ||
| AOA initial = AOA final | Constant angle of attack | 1 |
| Volume constraint | 52 | |
| Design variable bounds | 2 | |
| Twist deformation bounds | 12 |
| Wingtip | Variation % | ||||
|---|---|---|---|---|---|
| A | 11.55 | 0.1788 | 0.0170 | 0.0012591 | 0.00 |
| B | 13.90 | 0.1894 | 0.0167 | 0.0011736 | −7.28 |
| C | 12.83 | 0.1937 | 0.0169 | 0.0013303 | +5.35 |
| D | 13.90 | 0.1749 | 0.0170 | 0.0010016 | −25.70 |
| Flight Condition | Angle of Attack/Climb () | Airspeed | Altitude | Air Density |
|---|---|---|---|---|
| Cruise | 0 | 28.3 | 15,000 | 0.771 |
| Climb | 5, 8, 10 | 33.44 | 0 | 1.225 |
| Wingtip | Reduction (%) | |
|---|---|---|
| 5 | −8.66 | |
| B | 8 | −10.44 |
| 10 | −12.04 | |
| 5 | −1.99 | |
| C | 8 | −3.28 |
| 10 | −3.92 | |
| 5 | −7.90 | |
| D | 8 | −15.10 |
| 10 | −16.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Negahban, M.H.; Bashir, M.; Priolet, C.; Botez, R.M. Novel Twist Morphing Aileron and Winglet Design for UAS Control and Performance. Drones 2024, 8, 392. https://doi.org/10.3390/drones8080392
Negahban MH, Bashir M, Priolet C, Botez RM. Novel Twist Morphing Aileron and Winglet Design for UAS Control and Performance. Drones. 2024; 8(8):392. https://doi.org/10.3390/drones8080392
Chicago/Turabian StyleNegahban, Mir Hossein, Musavir Bashir, Clovis Priolet, and Ruxandra Mihaela Botez. 2024. "Novel Twist Morphing Aileron and Winglet Design for UAS Control and Performance" Drones 8, no. 8: 392. https://doi.org/10.3390/drones8080392
APA StyleNegahban, M. H., Bashir, M., Priolet, C., & Botez, R. M. (2024). Novel Twist Morphing Aileron and Winglet Design for UAS Control and Performance. Drones, 8(8), 392. https://doi.org/10.3390/drones8080392








