Application of Deep Reinforcement Learning to Defense and Intrusion Strategies Using Unmanned Aerial Vehicles in a Versus Game
Abstract
1. Introduction
2. Preliminary
2.1. Reinforcement Learning
2.2. Deep Q-Learning
2.3. Soft Actor–Critic
- Soft value function.represents the replay buffer of previously explored information. This function is used for stable training and assists in calculating the target Q function. Its gradient can be computed as shown in Equation (15). Actions must be selected according to the current policy, not from the replay buffer.
- Soft Q function.
- Policy update target.Adopting the reparameterization trick for action selection means that . Actions are sampled from a distribution, typically Gaussian, where outputs the mean and standard deviation, and is the noise. This allows for forming a distribution for sampling, enabling the gradient to be backpropagated through actions. The policy update objective function is shown in Equation (20).The problem with random sampling is that the action space is unbounded, while actions are usually a bounded number. To solve this, we use an invertible squashing function () to restrict actions to the range. The probability density function must also be corrected. Let be a random variable, then is its density, and the action is . The density becomes as shown in Equation (21).Equation (22) shows the correction needed for the action’s .Thus, the updated gradient is given by Equation (23).
3. Counteraction Simulation
3.1. Software Environments
3.2. Mission Scenario
3.3. Network
4. Reward Function Optimization
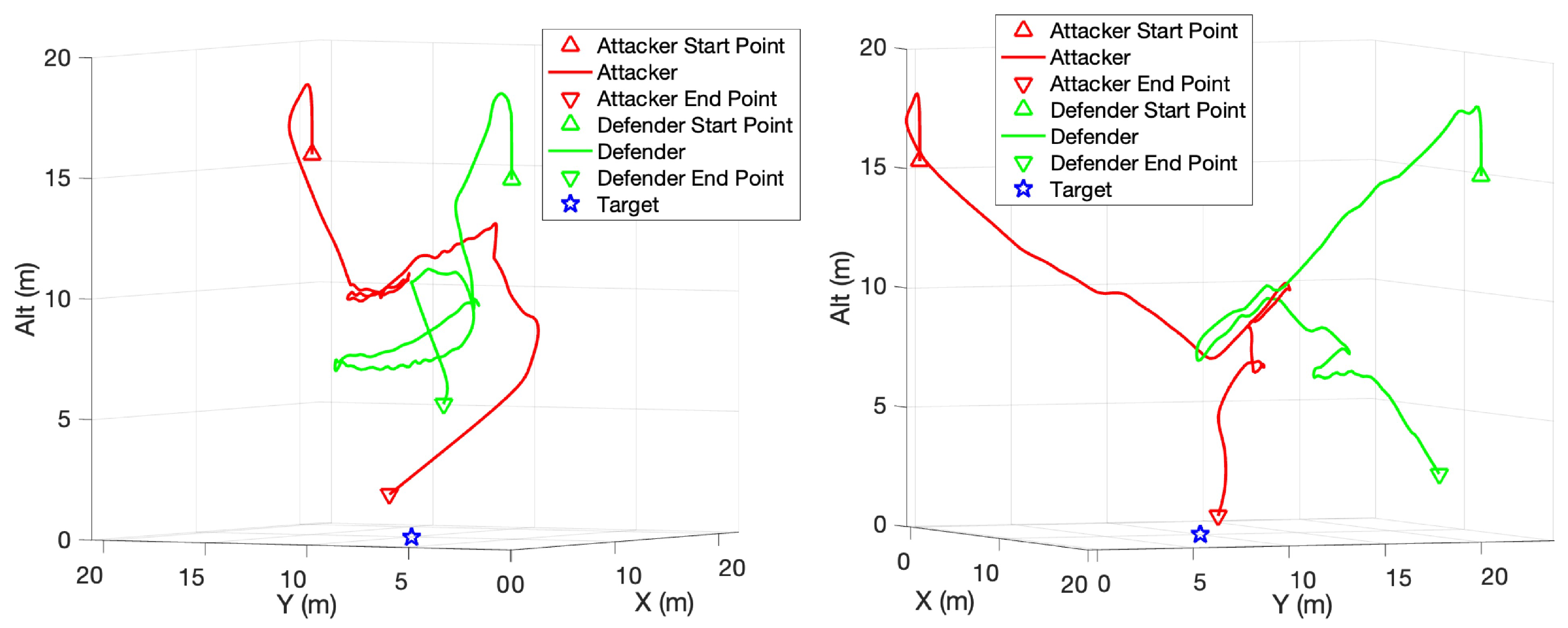
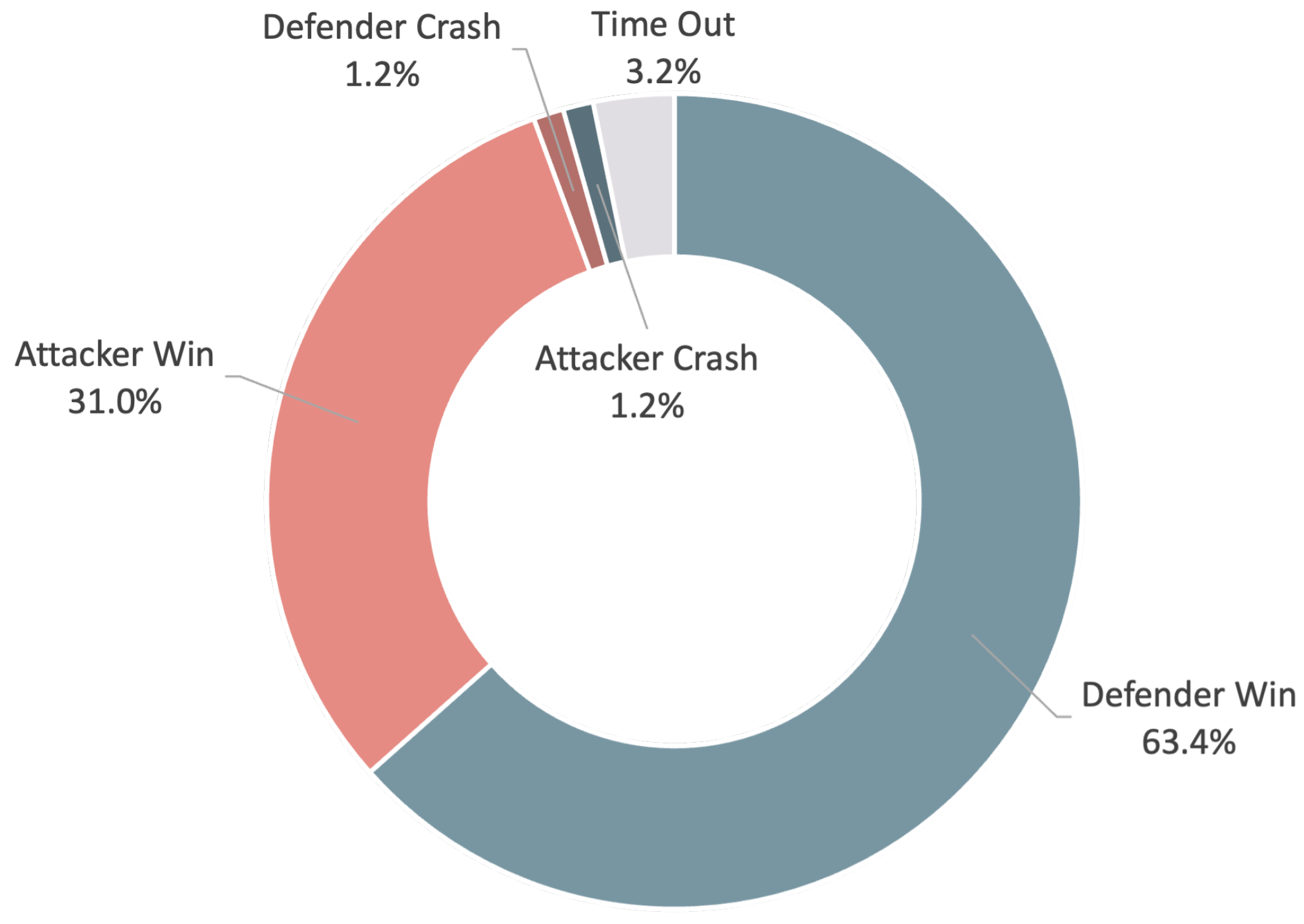
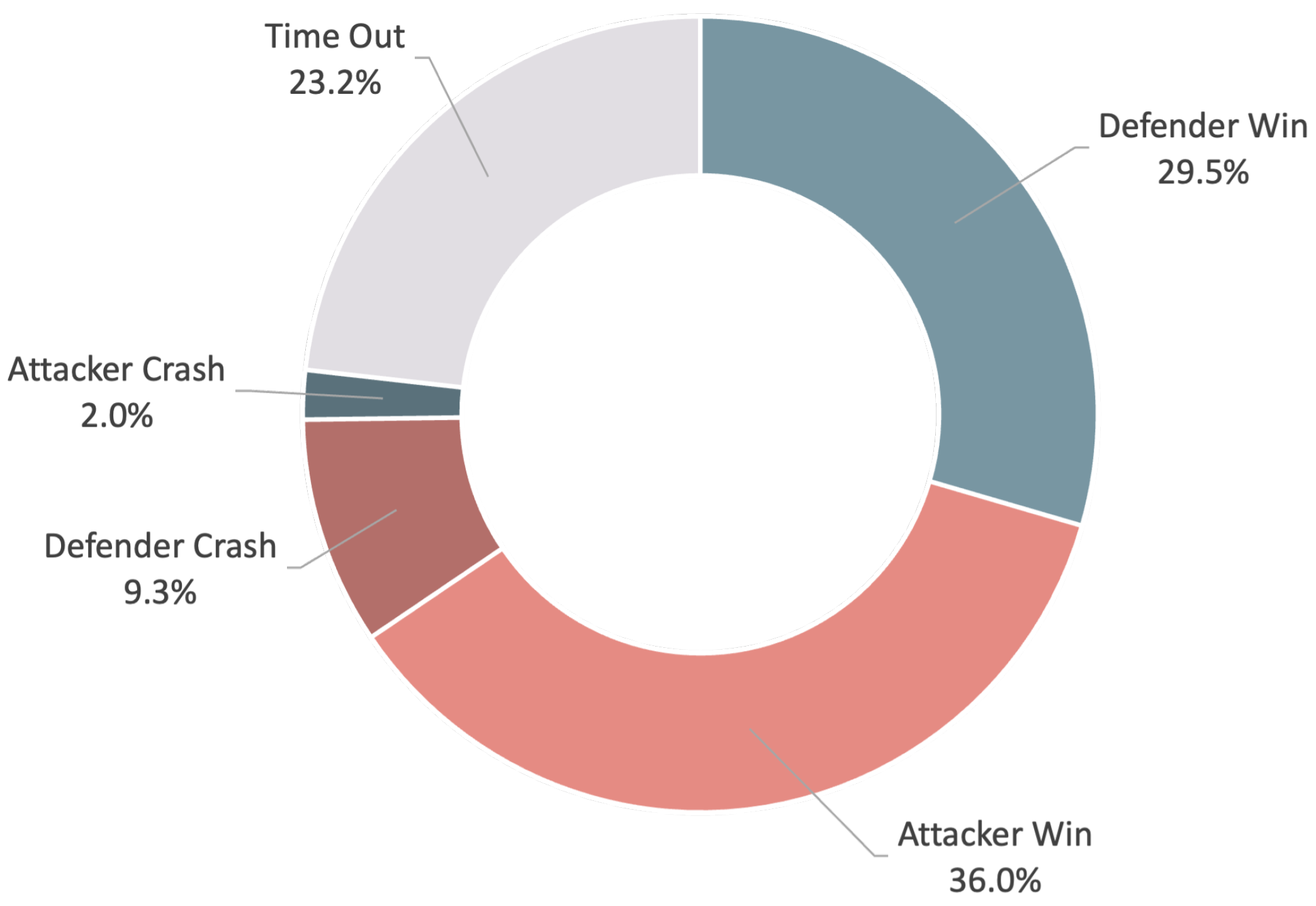
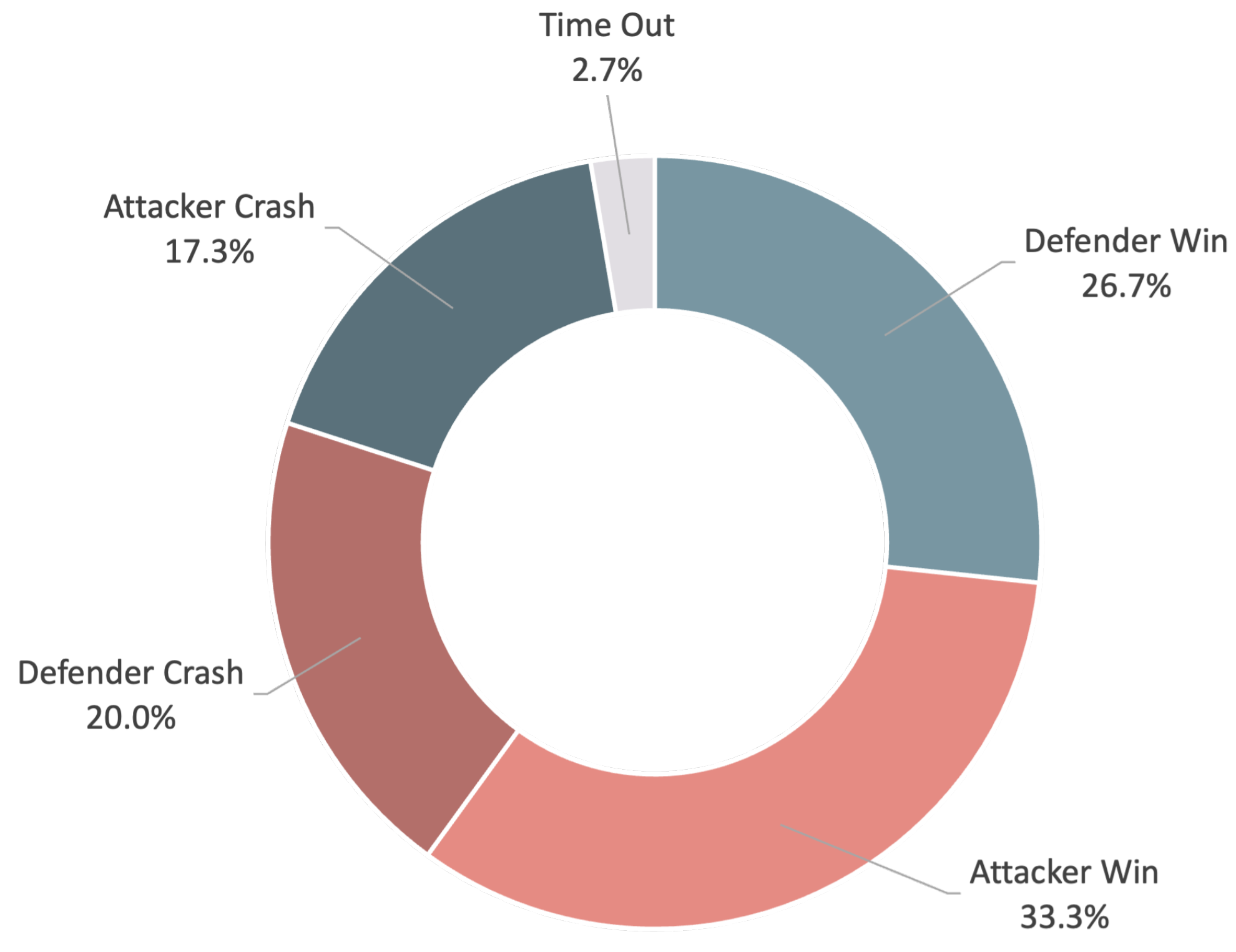
5. Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Hosu, I.A.; Rebedea, T. Playing atari games with deep reinforcement learning and human checkpoint replay. arXiv 2016, arXiv:1607.05077. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Gu, S.; Lillicrap, T.; Sutskever, I.; Levine, S. Continuous deep q-learning with model-based acceleration. In Proceedings of the International Conference on Machine Learning, PMLR, New York, NY, USA, 20–22 June 2016; pp. 2829–2838. [Google Scholar]
- Gu, S.; Holly, E.; Lillicrap, T.P.; Levine, S. Deep reinforcement learning for robotic manipulation. arXiv 2016, arXiv:1610.00633. [Google Scholar]
- Wang, Y.; Huang, C.; Tang, C. Research on unmanned combat aerial vehicle robust maneuvering decision under incomplete target information. Adv. Mech. Eng. 2016, 8, 1687814016674384. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P.; et al. Soft actor-critic algorithms and applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Kurniawan, B.; Vamplew, P.; Papasimeon, M.; Dazeley, R.; Foale, C. An empirical study of reward structures for actor-critic reinforcement learning in air combat manoeuvring simulation. In Proceedings of the Australasian Joint Conference on Artificial Intelligence, Adelaide, Australia, 2–5 December 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 54–65. [Google Scholar]
- Yang, Q.; Zhu, Y.; Zhang, J.; Qiao, S.; Liu, J. UAV air combat autonomous maneuver decision based on DDPG algorithm. In Proceedings of the 2019 IEEE 15th International Conference on Control and Automation (ICCA), Edinburgh, Scotland, 16–19 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 37–42. [Google Scholar]
- Lei, X.; Dali, D.; Zhenglei, W.; Zhifei, X.; Andi, T. Moving time UCAV maneuver decision based on the dynamic relational weight algorithm and trajectory prediction. Math. Probl. Eng. 2021, 2021, 1–19. [Google Scholar] [CrossRef]
- Pope, A.P.; Ide, J.S.; Mićović, D.; Diaz, H.; Rosenbluth, D.; Ritholtz, L.; Twedt, J.C.; Walker, T.T.; Alcedo, K.; Javorsek, D. Hierarchical reinforcement learning for air-to-air combat. In Proceedings of the 2021 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 275–284. [Google Scholar]
- Pope, A.P.; Ide, J.S.; Mićović, D.; Diaz, H.; Twedt, J.C.; Alcedo, K.; Walker, T.T.; Rosenbluth, D.; Ritholtz, L.; Javorsek, D. Hierarchical Reinforcement Learning for Air Combat At DARPA’s AlphaDogfight Trials. IEEE Trans. Artif. Intell. 2022, 4, 1371–1385. [Google Scholar] [CrossRef]
- Zheng, J.; Ma, Q.; Yang, S.; Wang, S.; Liang, Y.; Ma, J. Research on cooperative operation of air combat based on multi-agent. In Proceedings of the International Conference on Human Interaction and Emerging Technologies, Virtual, 27–29 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 175–179. [Google Scholar]
- Zhou, K.; Wei, R.; Xu, Z.; Zhang, Q. A brain like air combat learning system inspired by human learning mechanism. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 10–12 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Zhou, K.; Wei, R.; Xu, Z.; Zhang, Q.; Lu, H.; Zhang, G. An air combat decision learning system based on a brain-like cognitive mechanism. Cogn. Comput. 2020, 12, 128–139. [Google Scholar] [CrossRef]
- Zhou, K.; Wei, R.; Zhang, Q.; Xu, Z. Learning System for air combat decision inspired by cognitive mechanisms of the brain. IEEE Access 2020, 8, 8129–8144. [Google Scholar] [CrossRef]
- Kong, W.; Zhou, D.; Yang, Z.; Zhao, Y.; Zhang, K. UAV autonomous aerial combat maneuver strategy generation with observation error based on state-adversarial deep deterministic policy gradient and inverse reinforcement learning. Electronics 2020, 9, 1121. [Google Scholar] [CrossRef]
- Sun, Z.; Piao, H.; Yang, Z.; Zhao, Y.; Zhan, G.; Zhou, D.; Meng, G.; Chen, H.; Chen, X.; Qu, B.; et al. Multi-agent hierarchical policy gradient for air combat tactics emergence via self-play. Eng. Appl. Artif. Intell. 2021, 98, 104112. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Shah, S.; Dey, D.; Lovett, C.; Kapoor, A. AirSim: High-Fidelity Visual and Physical Simulation for Autonomous Vehicles. In Proceedings of the Field and Service Robotics, Zurich, Switzerland, 12–15 September 2017; Available online: http://xxx.lanl.gov/abs/arXiv:1705.05065 (accessed on 15 December 2022).


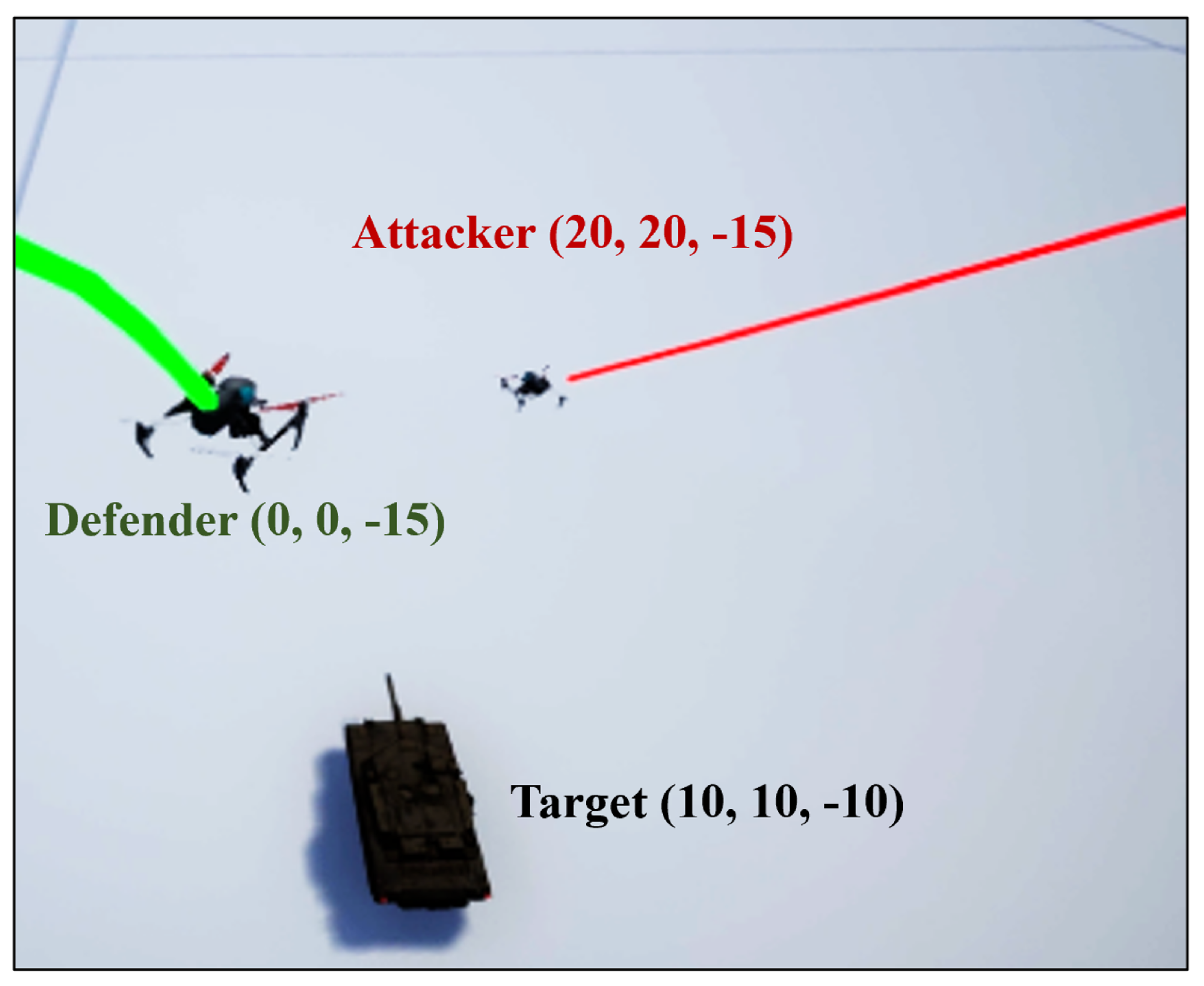


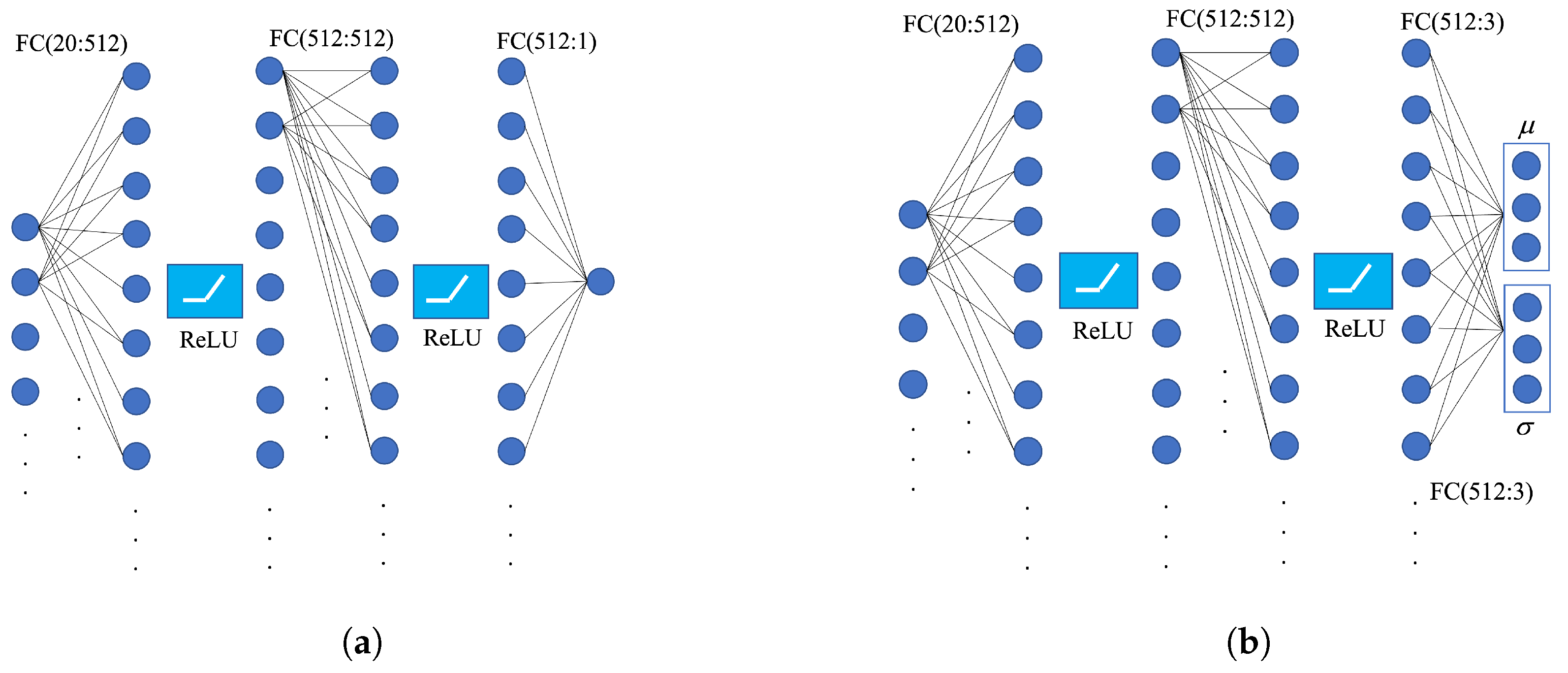
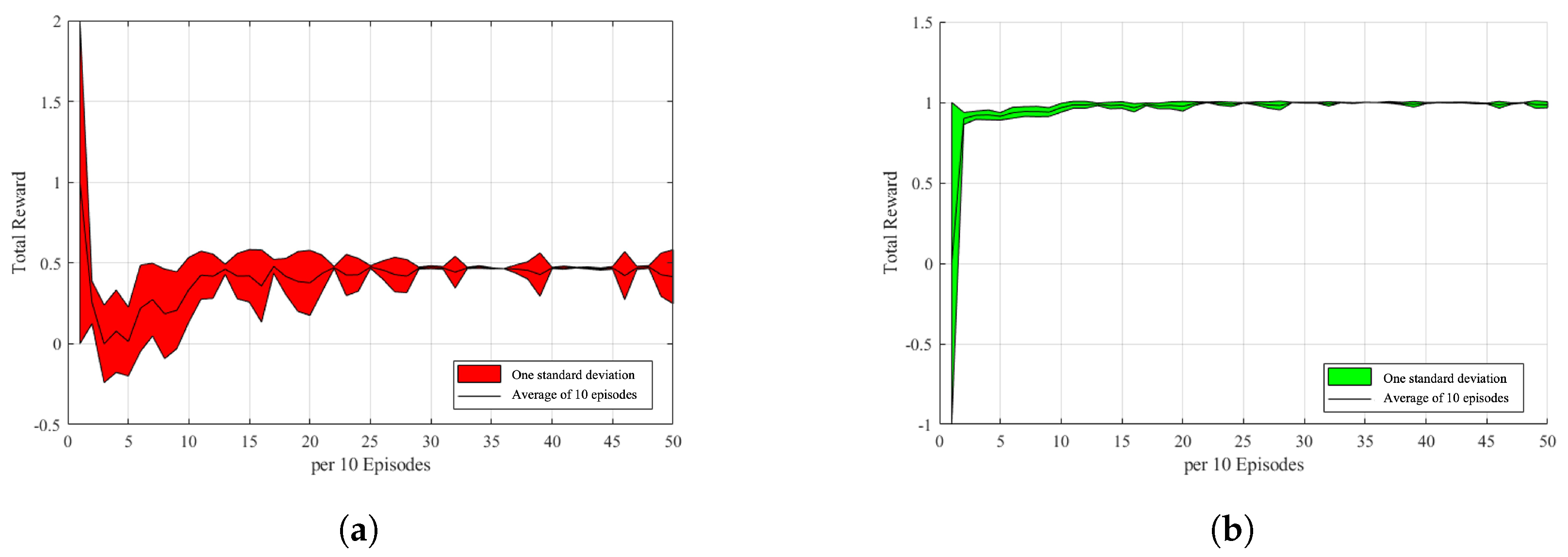
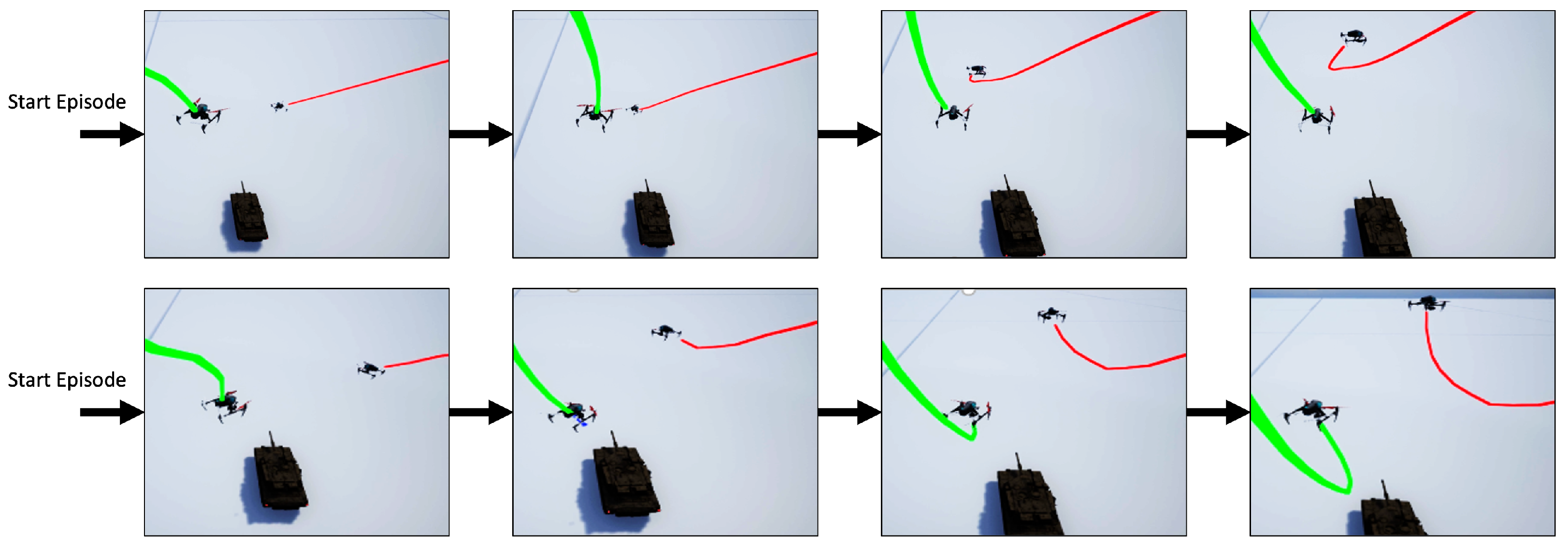




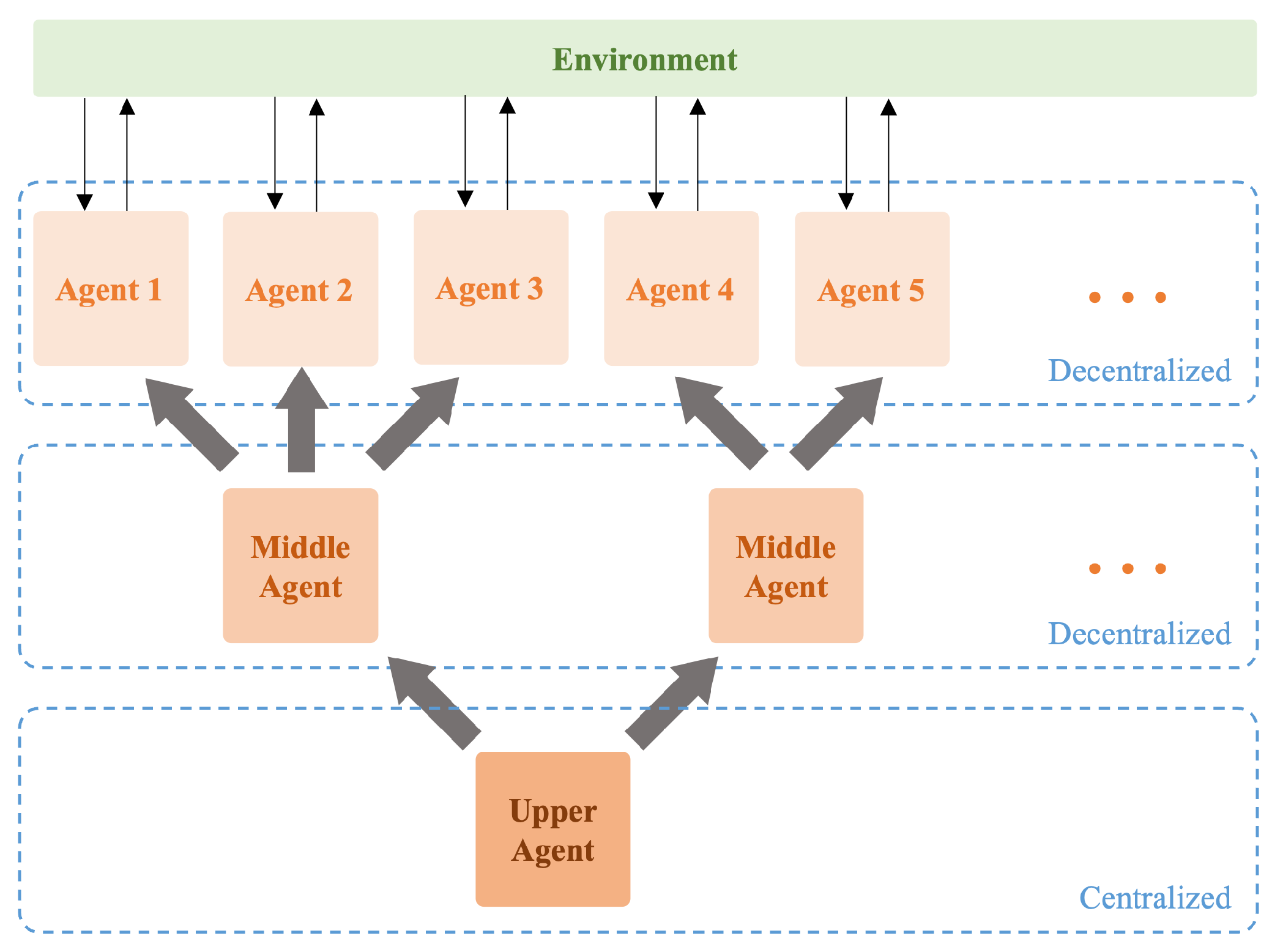
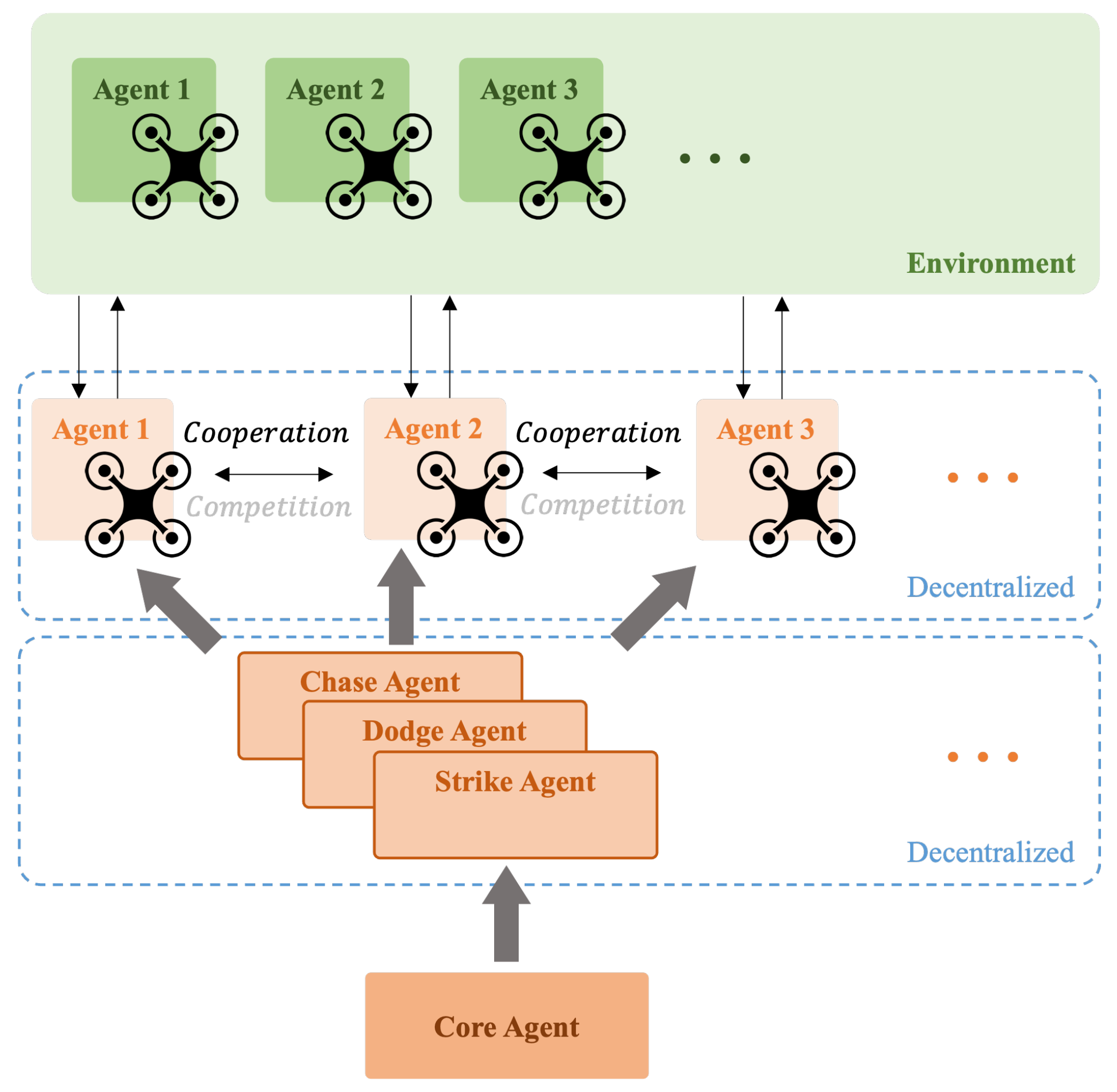
| Scenario | Defender | Attacker |
|---|---|---|
| 1 | X distance from the attacker < 0.5 m Y distance from the attacker < 0.5 m Z distance from the attacker < 0.5 m | X distance from target < 0.5 m Y distance from target < 0.5 m Z distance from target < 0.5 m |
| 2 | Distance of attacker and target > 40 m | - |
| 3 | Attacker land 1 | Defender land 1 |
| No. | States | Value | Symbol | Unit |
|---|---|---|---|---|
| 1 | Position of the defender relative to the attacker (X) | - | m | |
| 2 | Position of the defender relative to the attacker (Y) | - | m | |
| 3 | Position of the defender relative to the attacker (Z) | - | m | |
| 4 | Velocity of the defender relative to the attacker (X) | [−1.0, +1.0] | m/s | |
| 5 | Velocity of the defender relative to the attacker (Y) | [−1.0, +1.0] | m/s | |
| 6 | Velocity of the defender relative to the attacker (Z) | [−1.0, +1.0] | m/s | |
| 7 | Position of the attacker relative to the target (X) | - | m | |
| 8 | Position of the attacker relative to the target (Y) | - | m | |
| 9 | Position of the attacker relative to the target (Z) | - | m | |
| 10 | Velocity of the attacker relative to the target (X) | [−1.0, +1.0] | m/s | |
| 11 | Velocity of the attacker relative to the target (Y) | [−1.0, +1.0] | m/s | |
| 12 | Velocity of the attacker relative to the target (Z) | [−1.0, +1.0] | m/s | |
| 13 | Battle Results | 1, 2, 3, 4 | ||
| 14 | Time Elapsed | [0, 50] | s | |
| 15 | Acceleration of defender/attacker (X direction) | - | m/s2 | |
| 16 | Acceleration of defender/attacker (Y direction) | - | m/s2 | |
| 17 | Acceleration of defender/attacker (Z direction) | - | m/s2 |
| No. | Action | Value | Unit |
|---|---|---|---|
| 1 | Velocity of defender/attacker (X) | [−1.0, +1.0] | m/s |
| 2 | Velocity of defender/attacker (Y) | [−1.0, +1.0] | m/s |
| 3 | Velocity of defender/attacker (Z) | [−1.0, +1.0] | m/s |
| Parameter | Value | |
|---|---|---|
| 1 | Actor Network Learning Rate | 0.0005 |
| 2 | Critic Network Learning Rate | 0.0005 |
| 3 | Value Network Learning Rate | 0.0005 |
| 4 | Reward Discount Rate | 0.9 |
| 5 | Batch Size | 10,000 |
| 6 | Reward Multiplier | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.-L.; Huang, Y.-W.; Shen, T.-J. Application of Deep Reinforcement Learning to Defense and Intrusion Strategies Using Unmanned Aerial Vehicles in a Versus Game. Drones 2024, 8, 365. https://doi.org/10.3390/drones8080365
Chen C-L, Huang Y-W, Shen T-J. Application of Deep Reinforcement Learning to Defense and Intrusion Strategies Using Unmanned Aerial Vehicles in a Versus Game. Drones. 2024; 8(8):365. https://doi.org/10.3390/drones8080365
Chicago/Turabian StyleChen, Chieh-Li, Yu-Wen Huang, and Ting-Ju Shen. 2024. "Application of Deep Reinforcement Learning to Defense and Intrusion Strategies Using Unmanned Aerial Vehicles in a Versus Game" Drones 8, no. 8: 365. https://doi.org/10.3390/drones8080365
APA StyleChen, C.-L., Huang, Y.-W., & Shen, T.-J. (2024). Application of Deep Reinforcement Learning to Defense and Intrusion Strategies Using Unmanned Aerial Vehicles in a Versus Game. Drones, 8(8), 365. https://doi.org/10.3390/drones8080365






