Intelligent Decision-Making Algorithm for UAV Swarm Confrontation Jamming: An M2AC-Based Approach
Abstract
1. Introduction
- We established a mathematical model for UAVs-CJ based on MGs, which comprehensively captures the interactivity and dynamics of UAVs-CJ, enabling the description of the adversarial process between two opposing UAV swarms continuously adjusting their strategies.
- We designed an indicator function that combines the AC algorithm with MGs, incorporating NE into the policy network evaluation metrics, guiding the convergence of the policy network toward the MPE strategy.
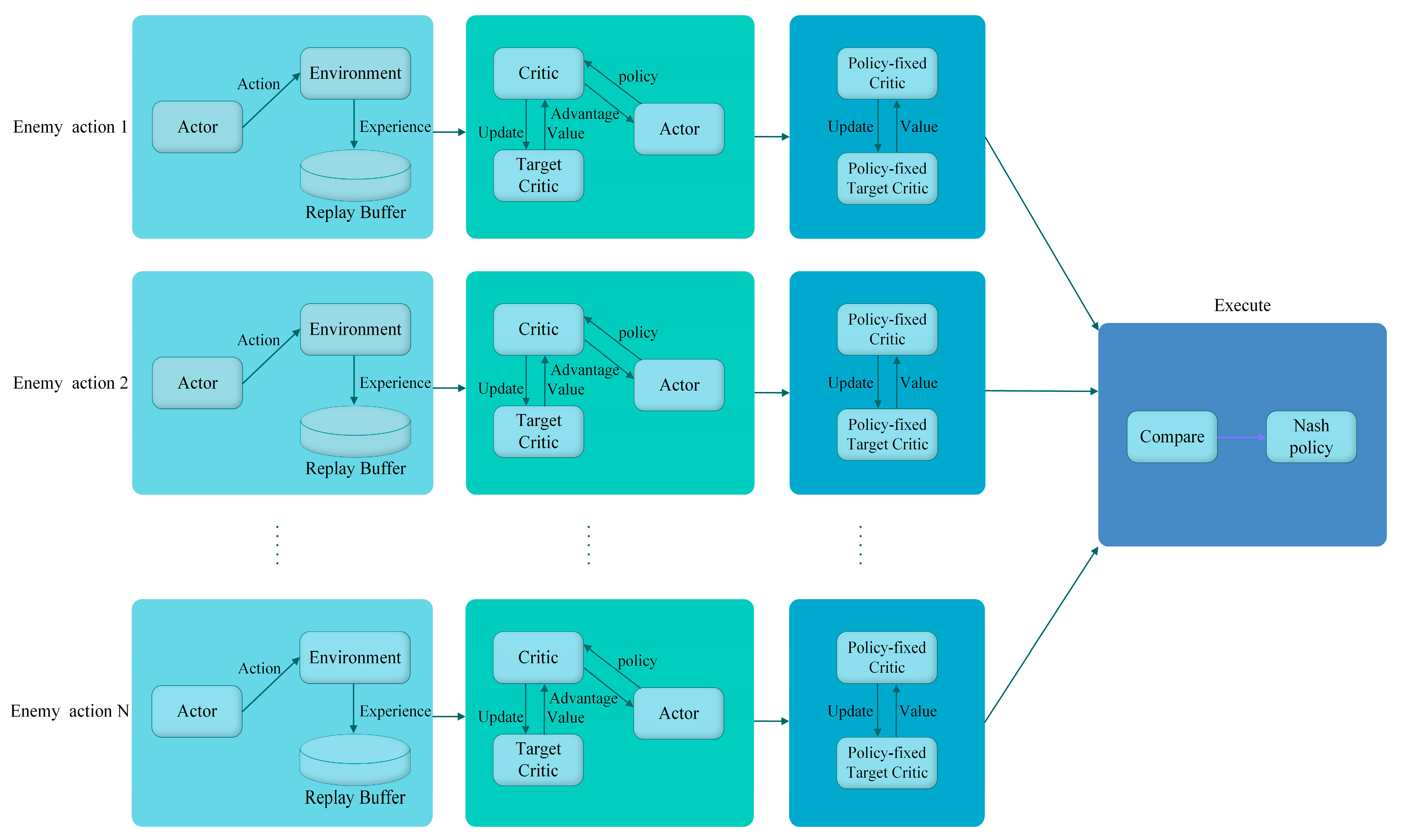
- We constructed a model-solving algorithm using multithreaded parallel training–contrastive execution, avoiding linear programming operations during the process, thereby enhancing the timeliness of the UAVs-CJ intelligent decision-making algorithm.
2. Problem Description and Mathematical Model
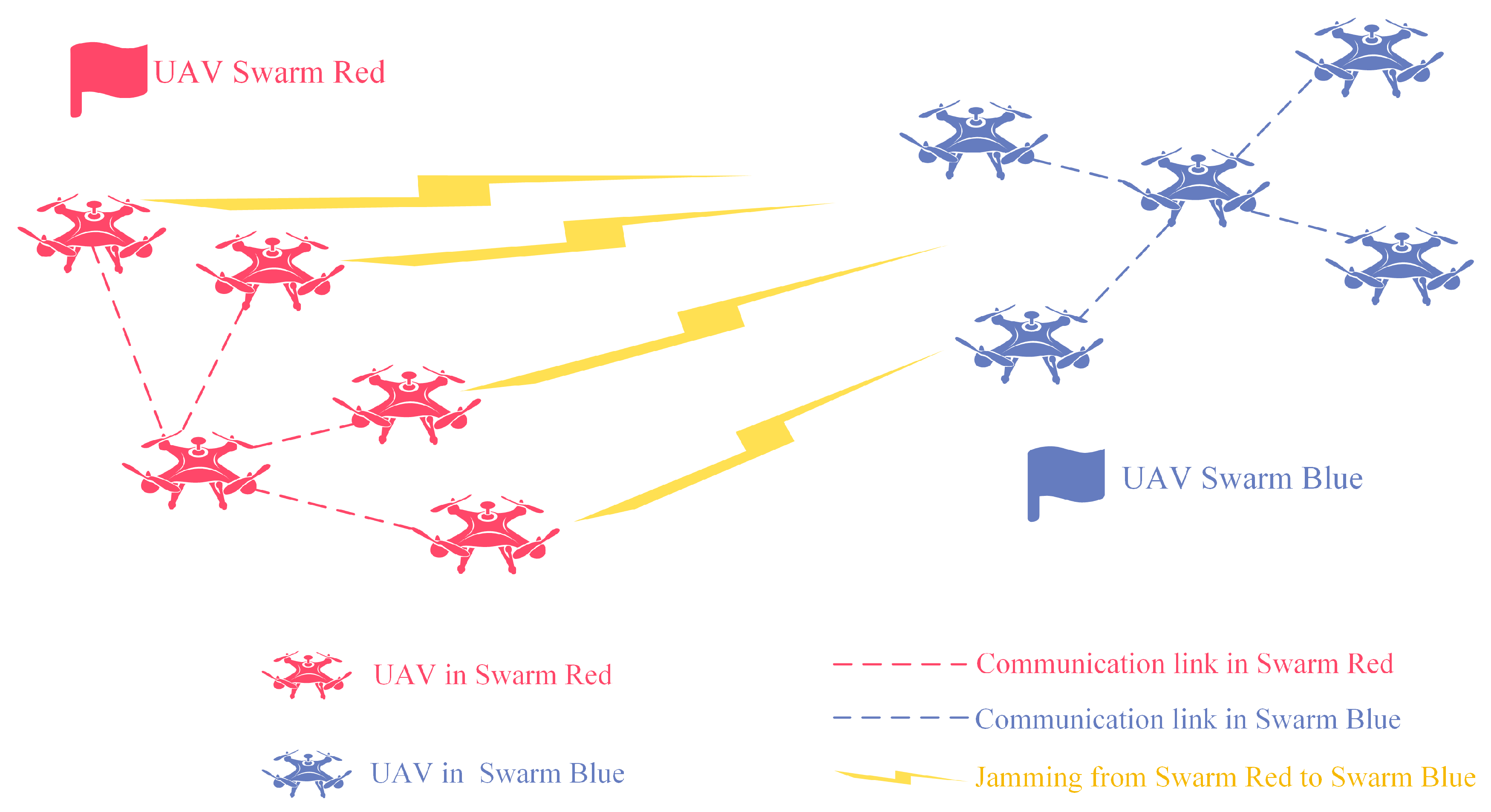
2.1. UAVs-CJ Scenario and Decision-Making Process
2.2. Intelligent Mathematical Decision-Making Model Based on MGs
3. Intelligent Decision-Making Algorithm for UAVs-CJ Based on M2AC
3.1. M2DQN Algorithm
| Algorithm 1: M2DQN Learning Algorithm |
| 1: Initialization neural network parameter |
| 2: For = 0, 1, … do |
| 3: Choose action according to policy like this: |
| 4: Choose opponent action |
| 5: , |
| 6: , |
| 7: end for |
| Output: minimax police |
3.2. M2AC Algorithm
- Indicator function of the M2AC algorithm
- 2.
- M2AC model-solving algorithm
| Algorithm 2: M2AC Learning Algorithm |
| Input: Behavior policy , discount factor , exploration factor , sample number , target update steps and learning rate , soft update parameter |
| 1: Initialization: neural actor network parameter under N enemy action , neural critic network parameter under N enemy action and , experience memory , and get initial state |
| 2: For = 0, 1, … do |
| 3: For = 0, 1, … do |
| 4: Build thread |
| 5: Choose action according to behavior policy |
| 6: Choose opponent action (which are fixed in each thread) |
| 7: Execute and and get and and store in |
| 8: Sample batches from |
| 9: |
| 10: |
| 11: |
| 12: |
| 13: end for |
| 14: end for |
| 15: Train Critic Network |
| Output: minimax police |
4. Simulation and Analysis
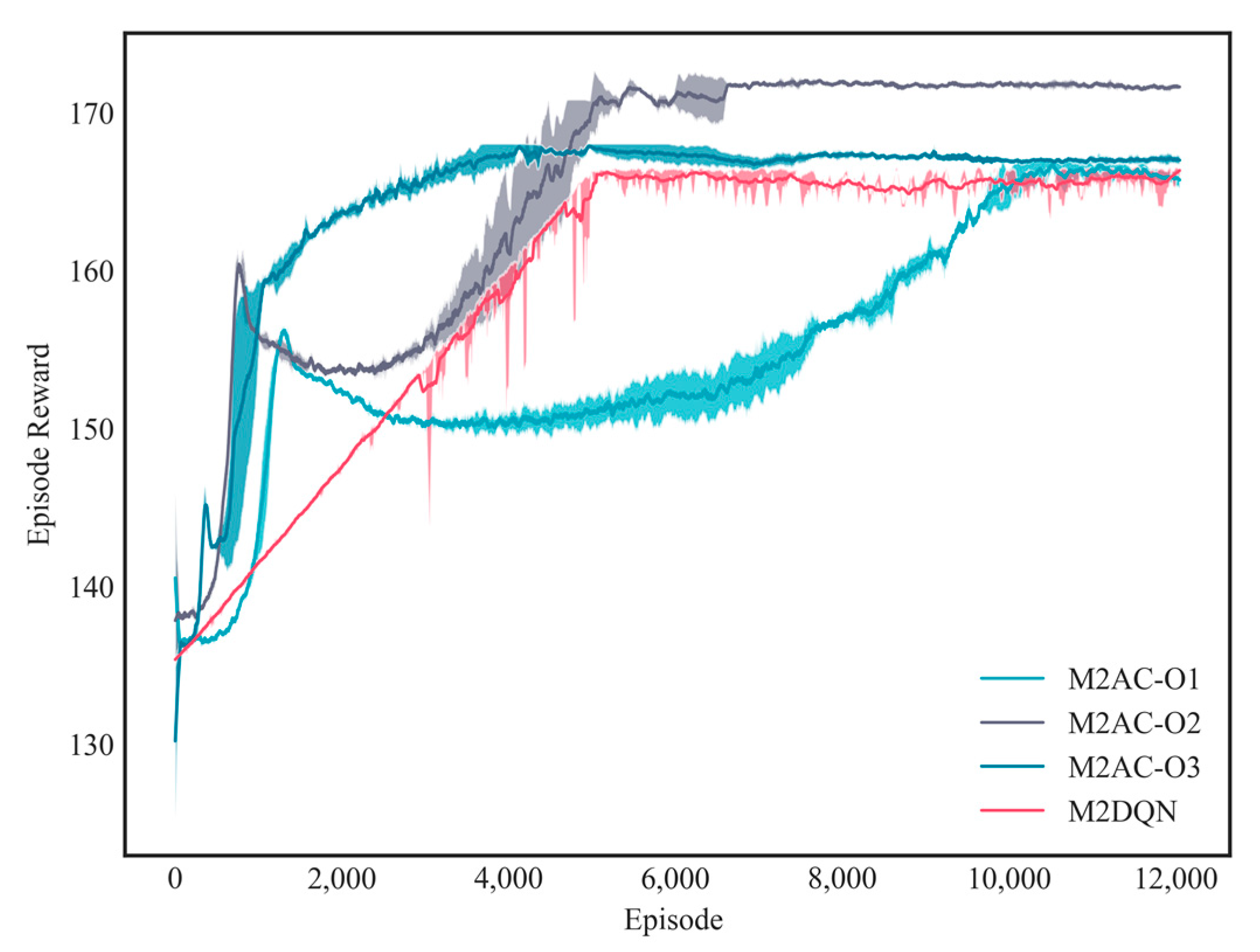
4.1. Analysis of Algorithm Effectiveness
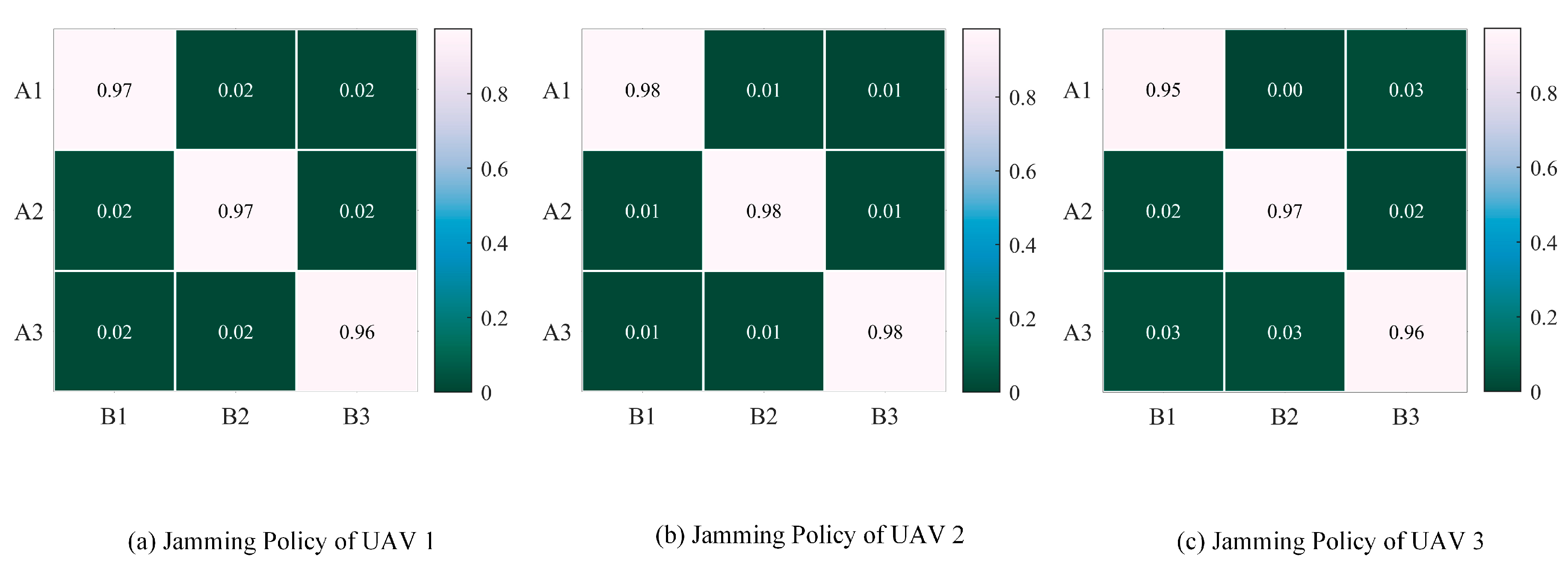
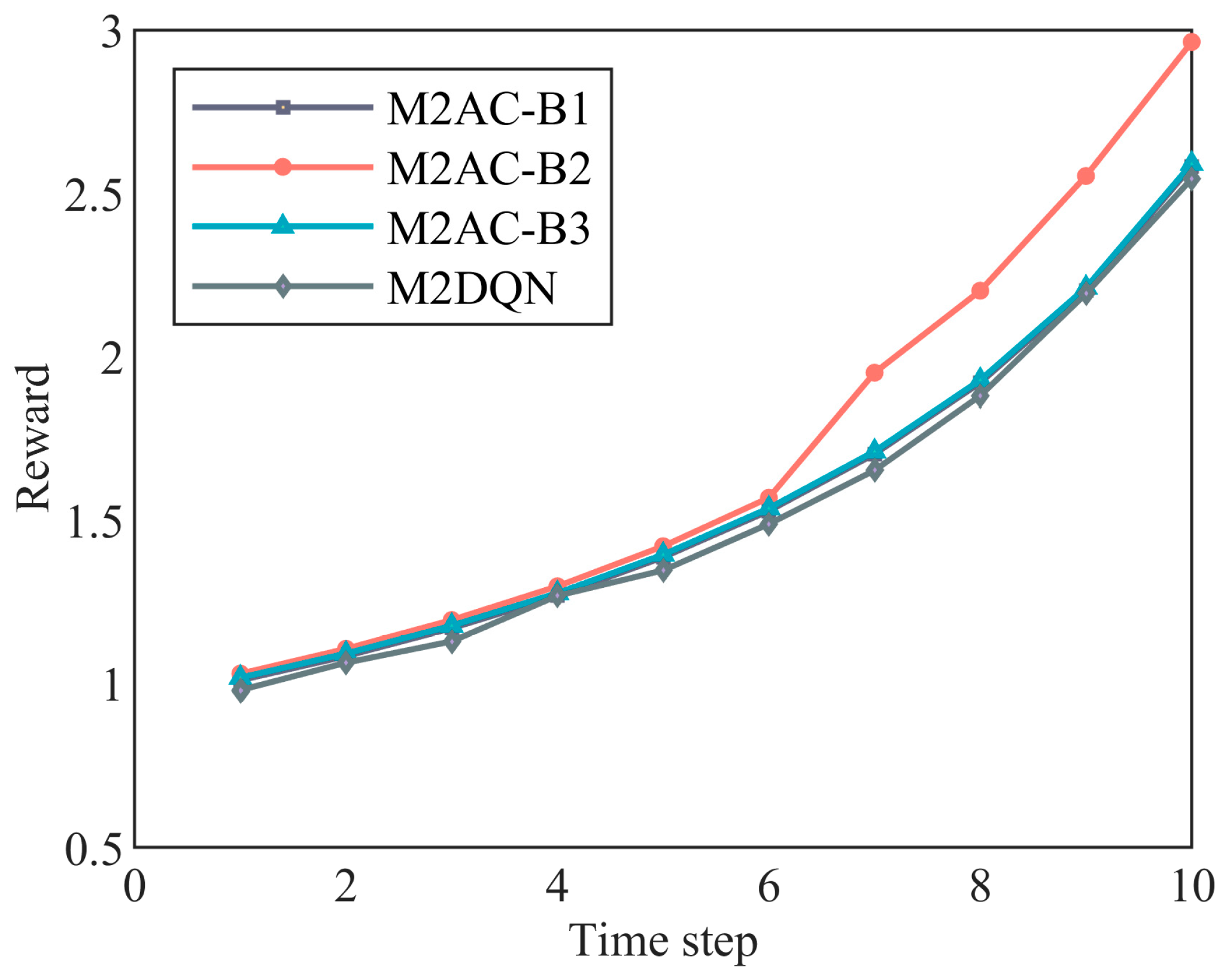
4.2. Effectiveness of Jamming Strategies
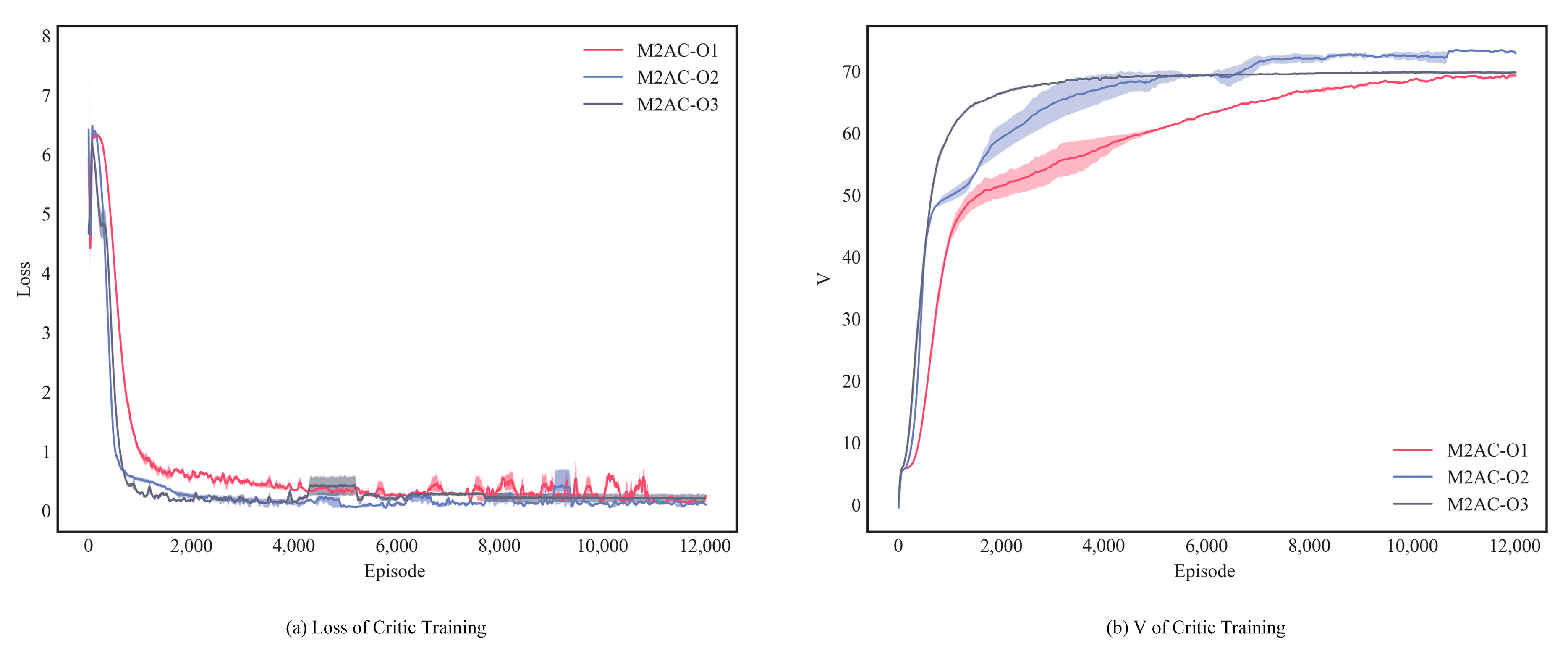
4.3. Effectiveness of Value Function Prediction
4.4. Effectiveness of the Decision Results
4.5. Decision-Making Effectiveness in Scenarios Involving UAV Swarms of Different Scales
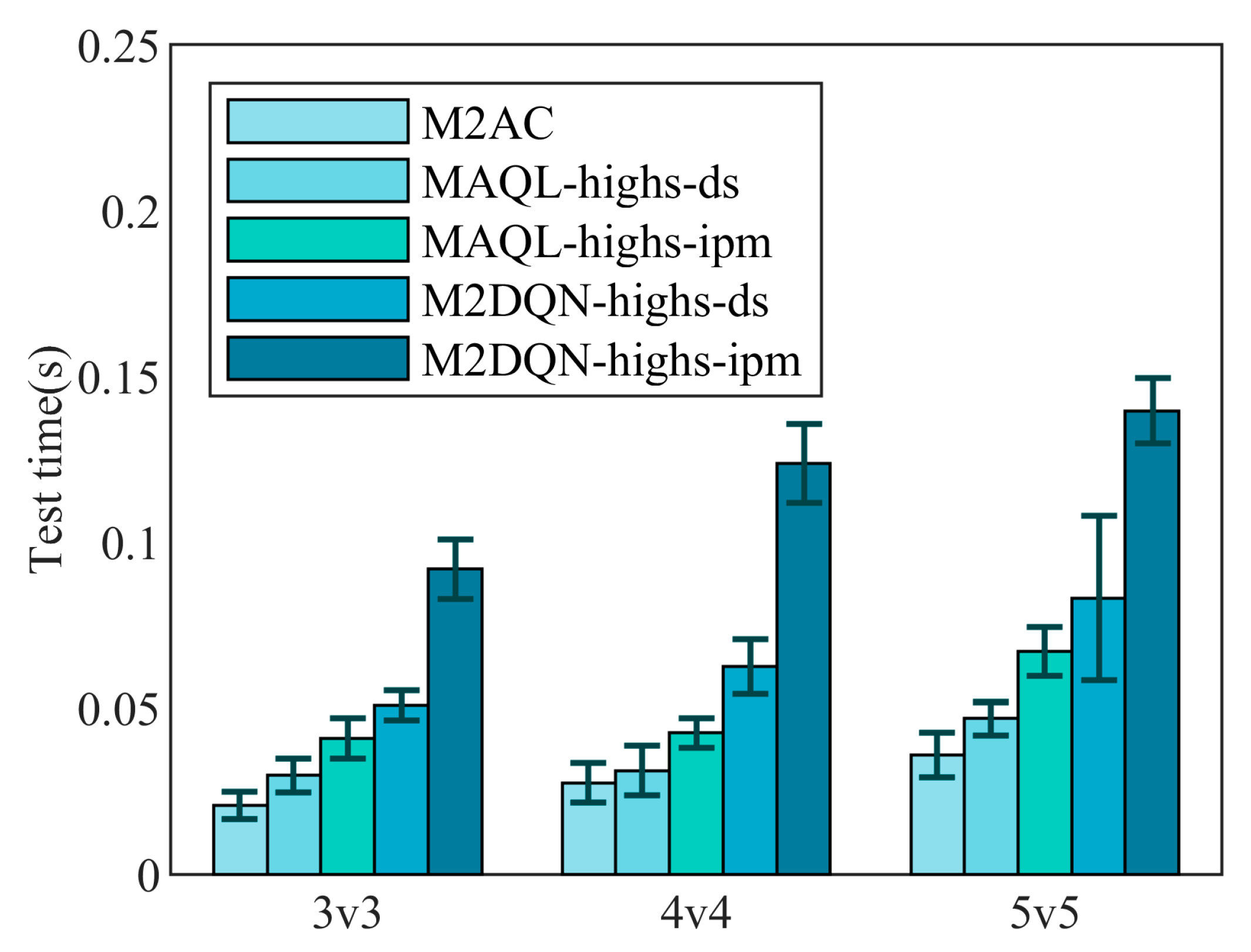
4.6. Analysis of Algorithm Timeliness
5. Future Research Directions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
DURC Statement
Conflicts of Interest
Appendix A
References
- Wang, B.; Li, S.; Gao, X.; Xie, T. UAV swarm confrontation using hierarchical multiagent reinforcement learning. Int. J. Aerosp. Eng. 2021, 2021, 360116. [Google Scholar] [CrossRef]
- Ji, X.; Zhang, W.; Xiang, F.; Yuan, W.; Chen, J. A swarm confrontation method based on Lanchester law and Nash equilibrium. Electronics 2022, 11, 896. [Google Scholar] [CrossRef]
- Mo, Z.; Sun, H.-w.; Wang, L.; Yu, S.-z.; Meng, X.-y.; Li, D. Research on foreign anti-UAV swarm warfare. Command Control Simul./Zhihui Kongzhi Yu Fangzhen 2023, 45, 24–30. [Google Scholar] [CrossRef]
- Williams, H.P. Model Building in Mathematical Programming; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Xing, D.X.; Zhen, Z.; Gong, H. Offense–defense confrontation decision making for dynamic UAV swarm versus UAV swarm. Proc. Inst. Mech. Eng. G 2019, 233, 5689–5702. [Google Scholar] [CrossRef]
- Jones, A.J. Game Theory: Mathematical Models of Conflict; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Li, S.-Y.; Chen, M.; Wang, Y.; Wu, Q. Air combat decision-making of multiple UCAVs based on constraint strategy games. Def. Technol. 2022, 18, 368–383. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, G.; Hu, X.; Luo, H.; Lei, X. Cooperative occupancy decision making of Multi-UAV in Beyond-Visual-Range air combat: A game theory approach. IEEE Access 2019, 8, 11624–11634. [Google Scholar] [CrossRef]
- Puterman, M.L. Markov decision processes. Handb. Oper. Res. Manag. Sci. 1990, 2, 331–434. [Google Scholar]
- Wang, B.; Li, S.; Gao, X.; Xie, T. Weighted mean field reinforcement learning for large-scale UAV swarm confrontation. Appl. Intell. 2023, 53, 5274–5289. [Google Scholar] [CrossRef]
- Fernando, X.; Gupta, A. Analysis of unmanned aerial vehicle-assisted cellular vehicle-to-everything communication using markovian game in a federated learning environment. Drones 2024, 8, 238. [Google Scholar] [CrossRef]
- Papoudakis, G.; Christianos, F.; Rahman, A.; Albrecht, S.V. Dealing with non-stationarity in multi-agent deep reinforcement learning. arXiv 2019, arXiv:1906.04737v1. [Google Scholar]
- Littman, M.L. Markov games as a framework for multi-agent reinforcement learning. In Machine Learning Proceedings 1994; Morgan Kaufmann: Burlington, MA, USA, 1994; pp. 157–163. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Zhao, D. Online minimax Q network learning for two-player zero-sum Markov games. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 1228–1241. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Li, G.; Chen, Y.; Fan, J. Model-based reinforcement learning for offline zero-sum markov games. Oper. Res. 2024, 1–16. [Google Scholar] [CrossRef]
- Zhong, H.; Xiong, W.; Tan, J.; Wang, L.; Zhang, T.; Wang, Z.; Yang, Z. Pessimistic minimax value iteration: Provably efficient equilibrium learning from offline datasets. In Proceedings of the 39th International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022. [Google Scholar]
- Nika, A.; Mandal, D.; Singla, A.; Radanovic, G. Corruption-robust offline two-player zero-sum markov games. In Proceedings of the 27th International Conference on Artificial Intelligence and Statistics, Valencia, Spain, 2–4 May 2024. [Google Scholar]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep reinforcement learning: A brief survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Grondman, I.; Busoniu, L.; Lopes, G.A.D.; Babuska, R. A survey of actor-critic reinforcement learning: Standard and natural policy gradients. IEEE Trans. Syst. Man. Cybern. C (Appl. Rev.) 2012, 42, 1291–1307. [Google Scholar] [CrossRef]
- Vakin, S.A.; Shustov, L.N. Principles of Jamming and Electronic Reconnaissance-Volume I; Tech. Rep. FTD-MT-24-115-69; US Air Force: Washington, DC, USA, 1969; Volume AD692642.
- Paine, S.; O’Hagan, D.W.; Inggs, M.; Schupbach, C.; Boniger, U. Evaluating the performance of FM-based PCL radar in the presence of jamming. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 631–643. [Google Scholar] [CrossRef]
- Li, Y. Deep reinforcement learning: An overview. arXiv 2017, arXiv:1701.07274. [Google Scholar]
- Patek, S.D. Stochastic and Shortest Path Games: Theory and Algorithms. Ph.D. Thesis, Laboratory for Information and Decision Systems, Massachusetts Institute of Technology, Cambridge, MA, USA, 1997. [Google Scholar]
- Sutton, R.S.; McAllester, D.; Singh, S.; Mansour, Y. Policy Gradient Methods for Reinforcement Learning with Function Approximation. In Proceedings of the 12th International Conference on Neural Information Processing Systems, Denver, CO, USA, 29 November–4 December 1999; pp. 1057–1063. [Google Scholar]
- Amari, S.I. Backpropagation and stochastic gradient descent method. Neurocomputing 1993, 5, 185–196. [Google Scholar] [CrossRef]
- Ruppert, D. Efficient Estimations from a Slowly Convergent Robbins-Monro process; Cornell University Operations Research and Industrial Engineering: Ithaca, NY, USA, 1988. [Google Scholar]
- Arena, P.; Fortuna, L.; Occhipinti, L.; Xibilia, M.G. Neural Networks for Quaternion-Valued Function Approximation. In Proceedings of the IEEE International Symposium on Circuits and Systems—ISCAS ’94, London, UK, 30 May–2 June 1994. [Google Scholar] [CrossRef]
- Van Seijen, H.; Mahmood, A.R.; Pilarski, P.M.; Machado, M.C.; Sutton, R.S. True online temporal-difference learning. J. Mach. Learn. Res. 2015, 17, 5057–5096. [Google Scholar]
- Babaeizadeh, M.; Frosio, I.; Tyree, S.; Clemons, J.; Kautz, J. Reinforcement Learning Through Asynchronous Advantage Actor-Critic on a GPU. arXiv 2016, arXiv:1611.06256. [Google Scholar]
- Degris, T.; White, M.; Sutton, R.S. Off-policy actor-critic. arXiv 2012, arXiv:1205.4839. [Google Scholar]
- Sayin, M.; Zhang, K.; Leslie, D.; Basar, T.; Ozdaglar, A. Decentralized Q-learning in zero-sum Markov games. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–14 December 2021; Volume 34, pp. 18320–18334. [Google Scholar]
- Phadke, A.; Medrano, F.A.; Sekharan, C.N.; Chu, T. An analysis of trends in UAV swarm implementations in current research: Simulation versus hardware. Drone Syst. Appl. 2024, 12, 1–10. [Google Scholar] [CrossRef]
- Calderón-Arce, C.; Brenes-Torres, J.C.; Solis-Ortega, R. Swarm robotics: Simulators, platforms and applications review. Computation 2022, 10, 80. [Google Scholar] [CrossRef]


| Initial position of Red (/km) | (0.0, 1.0), (0.3, 0.5), (0.0, 0.0) |
| Initial position of Blue (/km) | (15.0, 1.0), (14.7, 0.5), (15.0, 0.0) |
| Termination position of Red (/km) | (5.0, 1.0), (5.3, 0.5), (5.0, 0.0) |
| Termination position of Blue (/km) | (10.0, 1.0), (9.7, 0.5), (10.0, 0.0) |
| Movement speed of UAV (m/s) | 5 |
| Initial position of Red | (0.0, 1.0), (0.3, 0.7), (0.3, 0.3), (0.0, 0.0) |
| Initial position of Blue | (15.0, 1.0), (14.7, 0.7), (14.7, 0.3), (15.0, 0.0) |
| Termination position of Red | (5.0, 1.0), (5.3, 0.7), (5.3, 0.3), (5.0, 0.0) |
| Termination position of Blue | (10.0, 1.0), (9.7, 0.7), (9.7, 0.3), (10.0, 0.0) |
| Initial position of Red | (0.0, 1.0), (0.3, 0.7), (0.3, 0.5), (0.3, 0.3), (0.0, 0.0) |
| Initial position of Blue | (15.0, 1.0), (14.7, 0.7), (14.7, 0.5), (14.7, 0.3), (15.0, 0.0) |
| Termination position of Red | (5.0, 1.0), (5.3, 0.7), (5.3, 0.5), (5.3, 0.3), (5.0, 0.0) |
| Termination position of Blue | (10.0, 1.0), (9.7, 0.7), (9.7, 0.5), (9.7, 0.3), (10.0, 0.0) |
| M2AC | M2DQN-Highs-ds | M2DQN-Highs-ipm | MAQL-Highs-ds | MAQL-Highs-ipm | |
|---|---|---|---|---|---|
| 3v3 | 1 h 50 min | 16 h 12 min | 25 h 23 min | 4 h 25 m | 6 h 4 m |
| 4v4 | 2 h 17 min | 22 h 1 min | 34 h 53 min | 6 h 51 m | 8 h 57 m |
| 5v5 | 2 h 55 min | 27 h | 44 h 15 min | 7 h 22 m | 10 h 5 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, R.; Wu, D.; Hu, T.; Tian, Z.; Yang, S.; Xu, Z. Intelligent Decision-Making Algorithm for UAV Swarm Confrontation Jamming: An M2AC-Based Approach. Drones 2024, 8, 338. https://doi.org/10.3390/drones8070338
He R, Wu D, Hu T, Tian Z, Yang S, Xu Z. Intelligent Decision-Making Algorithm for UAV Swarm Confrontation Jamming: An M2AC-Based Approach. Drones. 2024; 8(7):338. https://doi.org/10.3390/drones8070338
Chicago/Turabian StyleHe, Runze, Di Wu, Tao Hu, Zhifu Tian, Siwei Yang, and Ziliang Xu. 2024. "Intelligent Decision-Making Algorithm for UAV Swarm Confrontation Jamming: An M2AC-Based Approach" Drones 8, no. 7: 338. https://doi.org/10.3390/drones8070338
APA StyleHe, R., Wu, D., Hu, T., Tian, Z., Yang, S., & Xu, Z. (2024). Intelligent Decision-Making Algorithm for UAV Swarm Confrontation Jamming: An M2AC-Based Approach. Drones, 8(7), 338. https://doi.org/10.3390/drones8070338





