Addressing Launch and Deployment Uncertainties in UAVs with ESO-Based Attitude Control
Abstract
1. Introduction
- We develop a comprehensive numerical simulation model for UAVs with rocket-assisted tube launch and wing deployment after launch. The model accounts for lumped disturbances, including model uncertainties and external disturbances. The accuracy of the model is thoroughly validated using data from an initial test flight.
- An autopilot is designed for the UAVs based on the ESO disturbance observer. We prove the boundedness of the control error using Lyapunov stability theory and provide an upper bound estimate for the error.
- Successful engineering implementation is demonstrated through comparative experiments and experimental data analysis, highlighting the strong robustness and anti-disturbance capabilities of the controller under high-disturbance launch conditions. This provides a widely applicable approach for implementing such UAVs with rocket-assisted tube launch and wing deployment after launch.
2. Problem Formulation
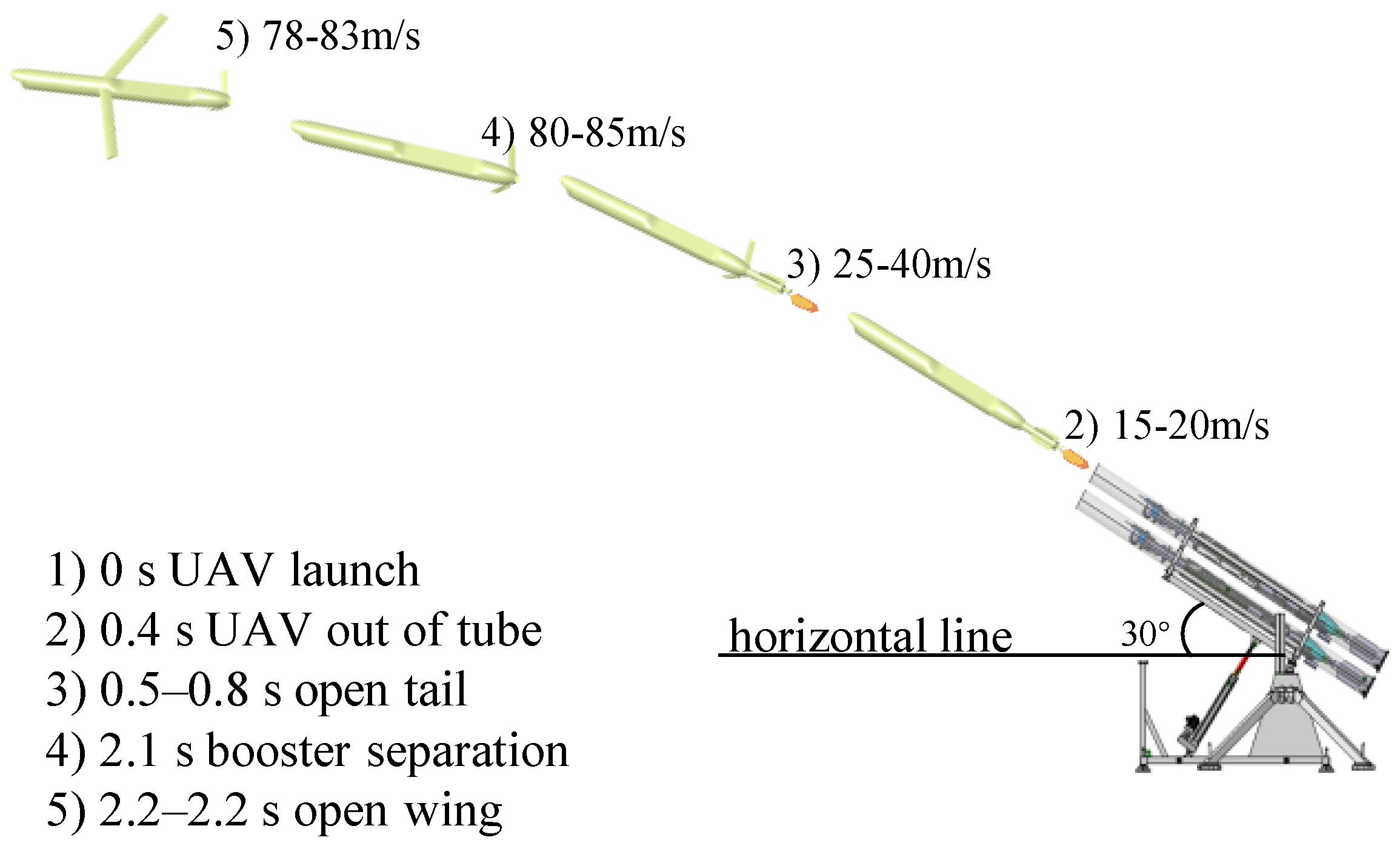
- The short ejection time results in an insufficient initial velocity, causing the relatively heavy UAV to immediately enter the programmed turn after ejection. This reduces the aerodynamic stabilization effect and exacerbates the adverse influence of gravity on the pitch channel.
- Disturbances from installation errors and thrust deviations in the booster rocket can lead to side and normal forces, resulting in force and torque disturbances.
- Asynchronous tail fin deployment at high speeds (over 50 m/s) can induce additional aerodynamic moments, further deteriorating the roll rate.
- Abrupt changes in the center of gravity during wing deployment and booster separation cause variations in the aerodynamic forces, control forces, and stability.
3. Materials and Methods
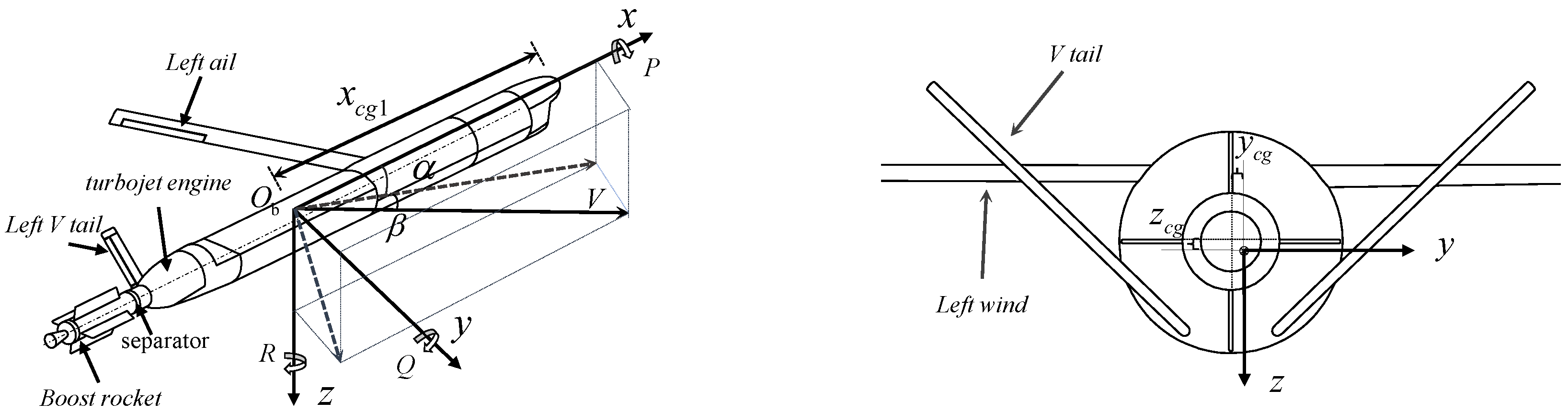
3.1. Reliable Mathematical Model
3.2. Model Reliability Verification
4. Robust Observer and Controller Design
4.1. Scheme Iteration
4.2. Disturbance Models
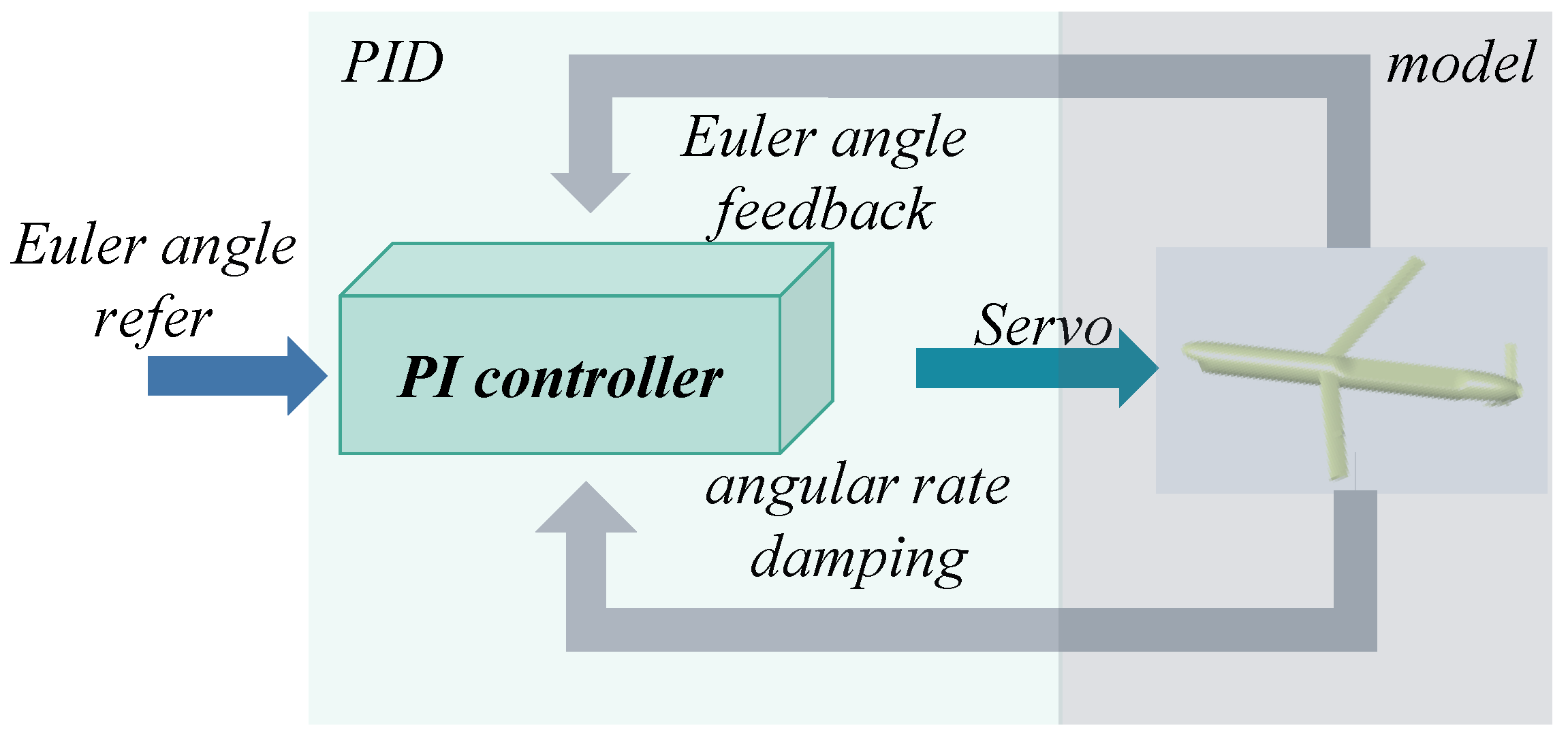
4.3. ESO-Based Controller Design
4.4. Closed-Loop Stability Analysis
- The result from Theorem 4.14: Let be a local Lipschitz function defined over a domain if the origin is an exponentially stable of . Then, there is a function, , that satisfies the following inequalities:where are positive constants.
- The result from Theorem 4.18: Let be a domain and be a function such thatand , where are class functions and is a continuous positives definite function. Take such that and suppose that ; then, there exists a class function , and for any initial state, , satisfying , there exists a time, , such that the solution of the system satisfies
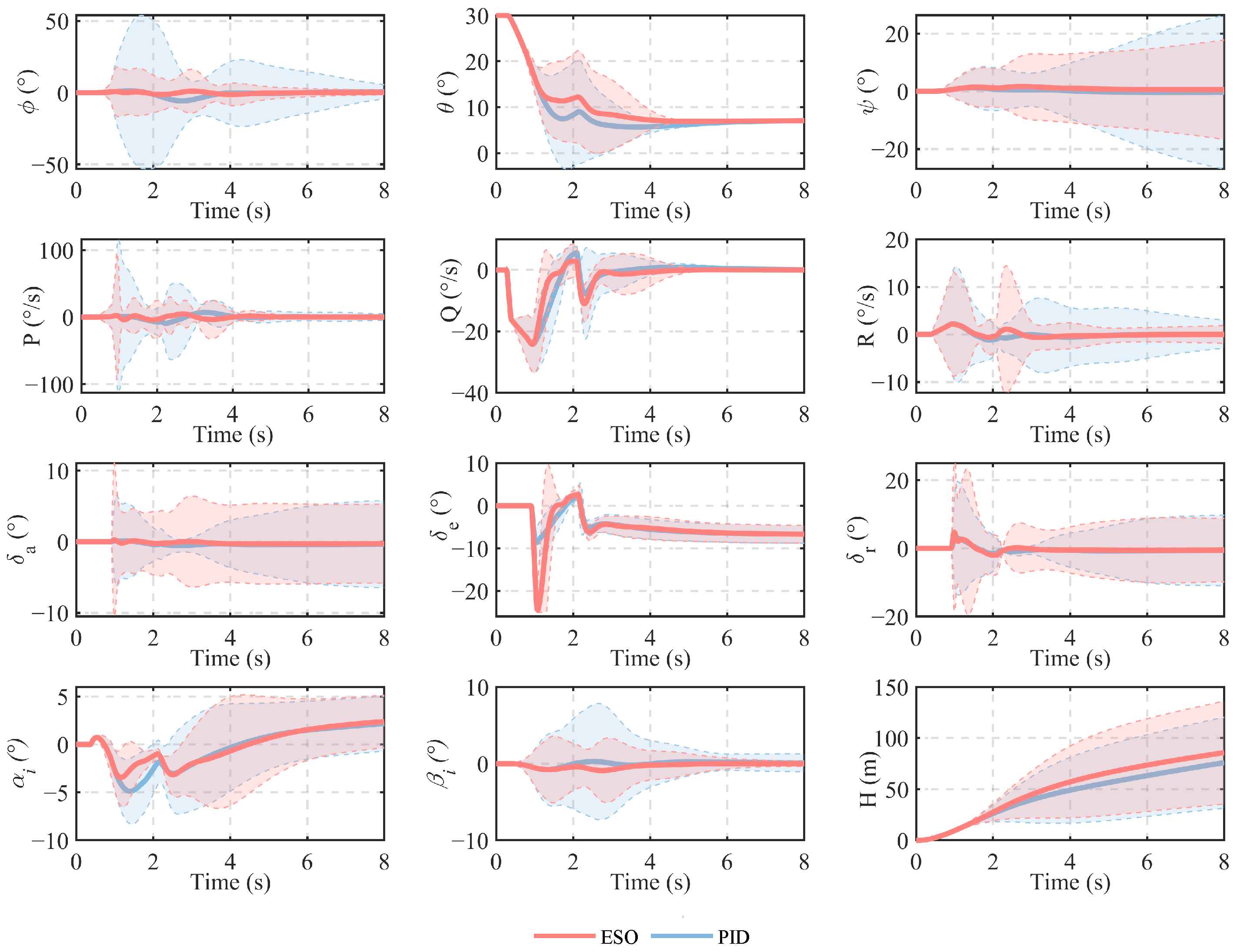
5. Simulation Results
5.1. The Case of Fixed Operating Points
5.2. Monte Carlo Analysis
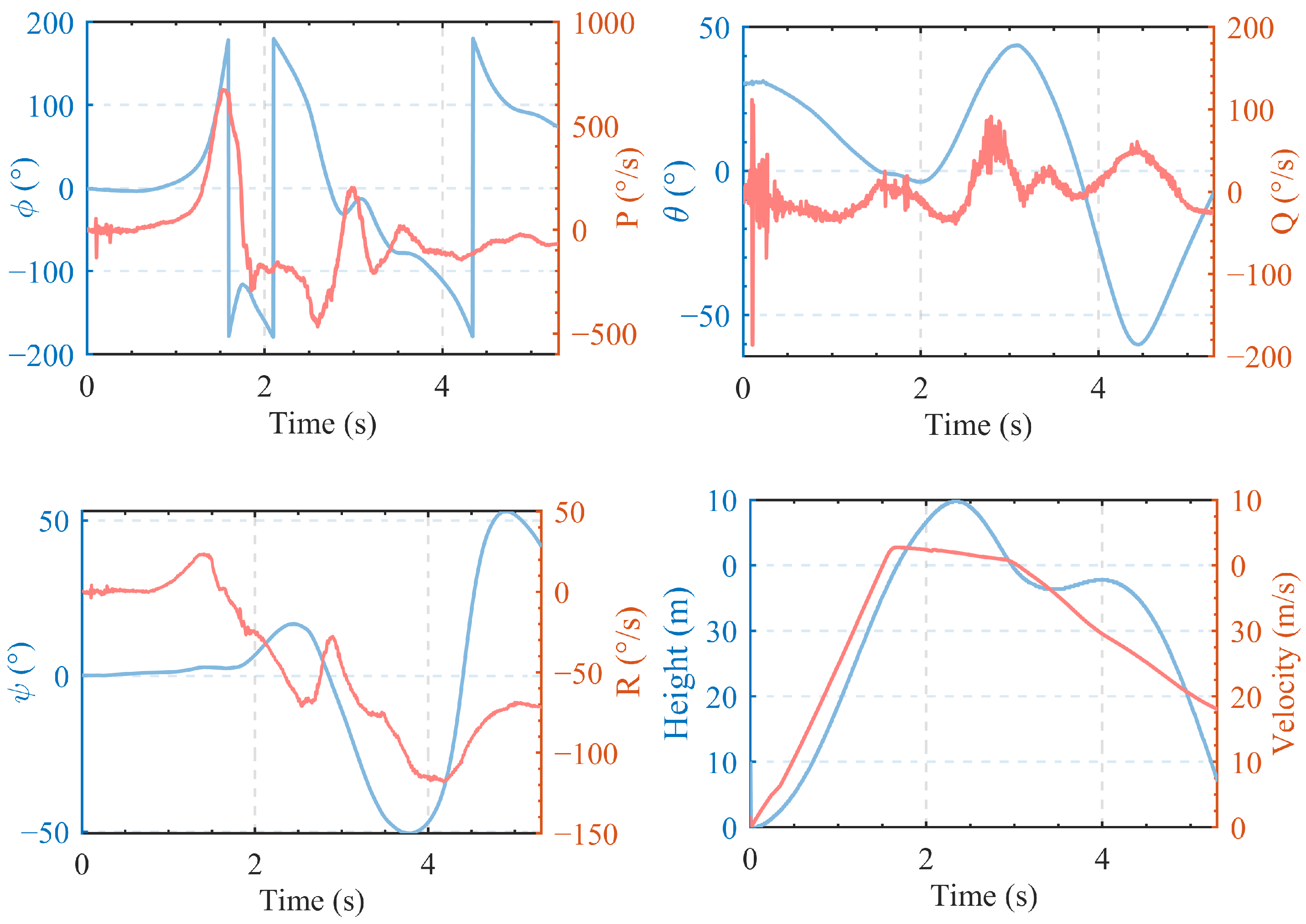
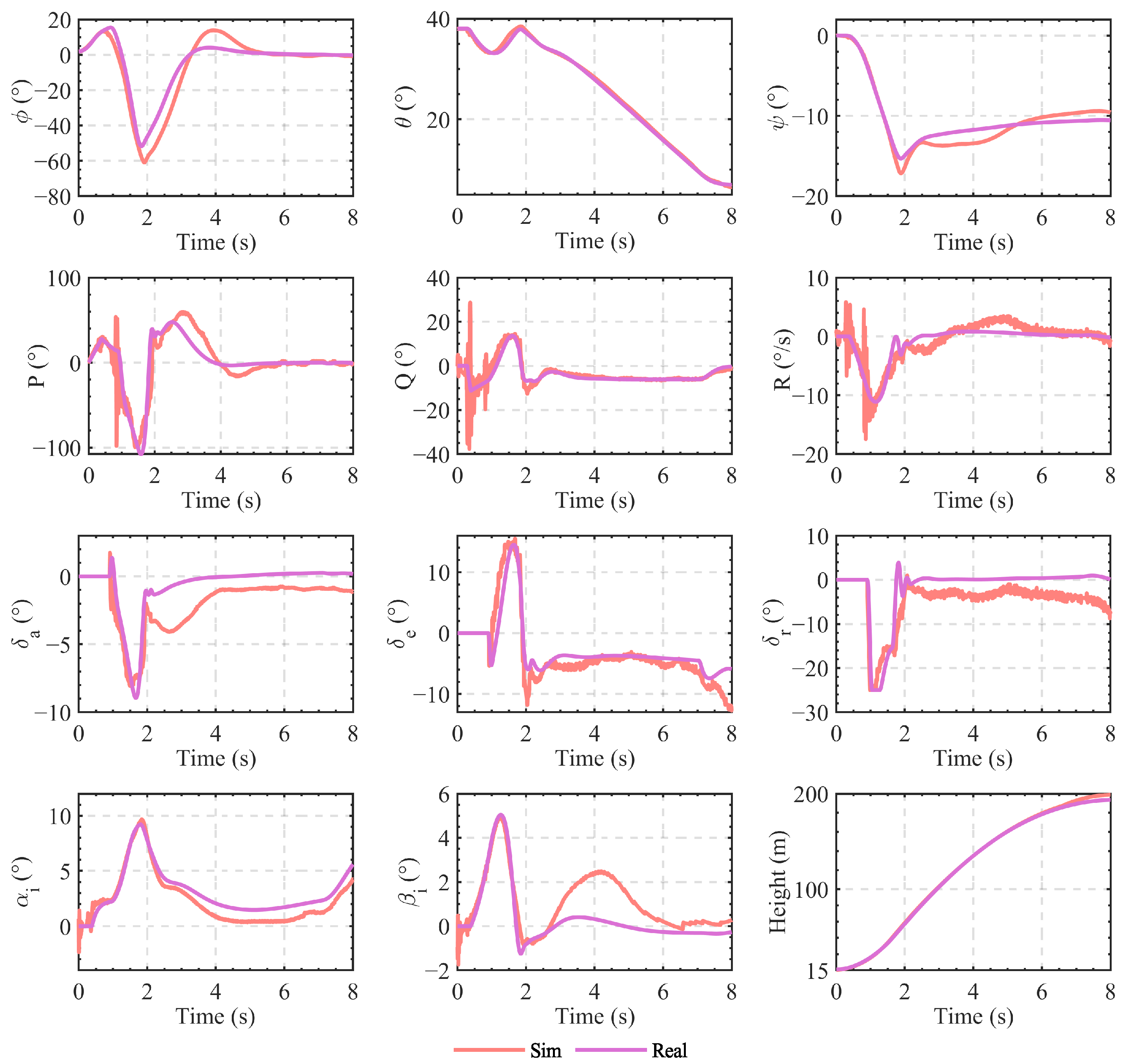
6. Flight Tests
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Z.; Li, J.; Yang, Y.; Yang, C.; Mao, R. Research on Speed Scheme for Precise Attack of Miniature Loitering Munition. Math. Probl. Eng. 2020, 2020, 4963738. [Google Scholar] [CrossRef]
- Yang, X.; Wang, T.; Liang, J.; Yao, G.; Liu, M. Survey on the Novel Hybrid Aquatic–Aerial Amphibious Aircraft: Aquatic Unmanned Aerial Vehicle (AquaUAV). Prog. Aerosp. Sci. 2015, 74, 131–151. [Google Scholar] [CrossRef]
- Gao, L.; Zhu, Y.; Zang, X.; Zhang, J.; Chen, B.; Li, L.; Zhao, J. Dynamic Analysis and Experiment of Multiple Variable Sweep Wings on a Tandem-Wing MAV. Drones 2023, 7, 552. [Google Scholar] [CrossRef]
- Chakravarthy, A.; Grant, D.T.; Lind, R. Time-Varying Dynamics of a Micro Air Vehicle with Variable-Sweep Morphing. J. Guid. Control. Dyn. 2012, 35, 890–903. [Google Scholar] [CrossRef]
- Grant, D.T.; Abdulrahim, M.; Lind, R. Flight Dynamics of a Morphing Aircraft Utilizing Independent Multiple-Joint Wing Sweep. Int. J. Micro Air Veh. 2010, 2, 91–106. [Google Scholar] [CrossRef]
- Seigler, T.M.; Neal, D.A.; Bae, J.S.; Inman, D.J. Modeling and Flight Control of Large-Scale Morphing Aircraft. J. Aircr. 2007, 44, 1077–1087. [Google Scholar] [CrossRef]
- Liu, B.; Fang, Z.; Li, P.; Hao, C.C. Takeoff Analysis and Simulation of a Small Scaled UAV with a Rocket Booster. Adv. Mater. Res. 2011, 267, 674–682. [Google Scholar] [CrossRef]
- Eymann, T.; Martel, J. Numerical investigation of launch dynamics for subscale aerial drone with Rocket Assisted Take-Off (RATO). In 2008 US Air Force T&E Days; American Institute of Aeronautics and Astronautics: Los Angeles, CA, USA, 2008; p. 1622. [Google Scholar] [CrossRef]
- Martel, J.; Eymann, T. Numerical Investigation of Rail Influence on Initial Forces and Moments for Subscale Aerial Drone with Rocket Assisted Take-Off (RATO). In Proceedings of the 26th AIAA Applied Aerodynamics Conference, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar] [CrossRef]
- Martel, J.; Dudley, J. External Pitching Moment (EPM) Due to Turbine Engine Exhaust Impingement on Rocket Assisted Take Off (RATO) Bottle. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. [Google Scholar] [CrossRef]
- Voskuijl, M. Performance Analysis and Design of Loitering Munitions: A Comprehensive Technical Survey of Recent Developments. Def. Technol. 2022, 18, 325–343. [Google Scholar] [CrossRef]
- Sayıl, A.; Erden, F.; Tüzün, A.; Baykara, B.; Aydemir, M. A Folding Wing System for Guided Ammunitions: Mechanism Design, Manufacturing and Real-Time Results with LQR, LQI, SMC and SOSMC. Aeronaut. J. 2024, 128, 788–811. [Google Scholar] [CrossRef]
- Cheng, H.; Shi, Q.; Wang, H.; Shan, W.; Zeng, T. Flight Dynamics Modeling and Stability Analysis of a Tube-Launched Tandem Wing Aerial Vehicle during the Deploying Process. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2022, 236, 262–280. [Google Scholar] [CrossRef]
- Finigian, M.; Kavounas, P.A.; Ho, I.; Smith, C.C.; Witusik, A.; Hopwood, A.; Avent, C.; Ragasa, B.; Roth, B. Design and Flight Test of a Tube-Launched Unmanned Aerial Vehicle. Aerospace 2024, 11, 133. [Google Scholar] [CrossRef]
- Li, C.Y.; Jing, W.X.; Gao, C.S. Adaptive Backstepping-Based Flight Control System Using Integral Filters. Aerosp. Sci. Technol. 2009, 13, 105–113. [Google Scholar] [CrossRef]
- Lungu, R.; Lungu, M. Application of H 2 /H ∞ and Dynamic Inversion Techniques to Aircraft Landing Control. Aerosp. Sci. Technol. 2015, 46, 146–158. [Google Scholar] [CrossRef]
- Doyle, J.; Glover, K.; Khargonekar, P.; Francis, B. State-Space Solutions to Standard H/Sub 2/ and H/Sub Infinity/Control Problems. IEEE Trans. Autom. Control 1989, 34, 831–847. [Google Scholar] [CrossRef]
- Carter, L.H.; Shamma, J.S. Gain-Scheduled Bank-to-Turn Autopilot Design Using Linear Parameter Varying Transformations. J. Guid. Control. Dyn. 1996, 19, 1056–1063. [Google Scholar] [CrossRef]
- Utkin, V. Variable Structure Systems with Sliding Modes. IEEE Trans. Autom. Control 1977, 22, 212–222. [Google Scholar] [CrossRef]
- Moore, B. Principal Component Analysis in Linear Systems: Controllability, Observability, and Model Reduction. IEEE Trans. Autom. Control 1981, 26, 17–32. [Google Scholar] [CrossRef]
- Altan, A.; Hacıoğlu, R. Model Predictive Control of Three-Axis Gimbal System Mounted on UAV for Real-Time Target Tracking under External Disturbances. Mech. Syst. Signal Process. 2020, 138, 106548. [Google Scholar] [CrossRef]
- Chang, X.H.; Xiong, J.; Park, J.H. Fuzzy Robust Dynamic Output Feedback Control of Nonlinear Systems with Linear Fractional Parametric Uncertainties. Appl. Math. Comput. 2016, 291, 213–225. [Google Scholar] [CrossRef]
- Jiang, B.; Li, B.; Zhou, W.; Lo, L.Y.; Chen, C.K.; Wen, C.Y. Neural Network Based Model Predictive Control for a Quadrotor UAV. Aerospace 2022, 9, 460. [Google Scholar] [CrossRef]
- Altan, A.; Aslan, O.; Hacioglu, R. Real-Time Control Based on NARX Neural Network of Hexarotor UAV with Load Transporting System for Path Tracking. In Proceedings of the 2018 6th International Conference on Control Engineering & Information Technology (CEIT), Istanbul, Turkey, 25–27 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Altan, A.; Aslan, O.; Hacioglu, R. Model Reference Adaptive Control of Load Transporting System on Unmanned Aerial Vehicle. In Proceedings of the 2018 6th International Conference on Control Engineering & Information Technology (CEIT), Istanbul, Turkey, 25–27 October 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Shen, S.; Xu, J.; Xia, Q. A Fuzzy Backstepping Attitude Control Based on an Extended State Observer for a Tilt-Rotor UAV. Aerospace 2022, 9, 724. [Google Scholar] [CrossRef]
- Shen, S.; Xu, J. Adaptive Neural Network-Based Active Disturbance Rejection Flight Control of an Unmanned Helicopter. Aerosp. Sci. Technol. 2021, 119, 107062. [Google Scholar] [CrossRef]
- Talole, S.E.; Godbole, A.A.; Kolhe, J.P.; Phadke, S.B. Robust Roll Autopilot Design for Tactical Missiles. J. Guid. Control. Dyn. 2011, 34, 107–117. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, H.; Li, N.; Su, Z.; Wu, J. Automatic Carrier Landing System Based on Active Disturbance Rejection Control with a Novel Parameters Optimizer. Aerosp. Sci. Technol. 2017, 69, 149–160. [Google Scholar] [CrossRef]
- Hu, Y.; Wu, M.; Zhao, K.; Song, J.; He, B. ADRC-Based Compound Control Strategy for Spacecraft Multi-Body Separation. Aerosp. Sci. Technol. 2023, 143, 108686. [Google Scholar] [CrossRef]
- Ai, S.; Song, J.; Cai, G.; Zhao, K. Active Fault-Tolerant Control for Quadrotor UAV against Sensor Fault Diagnosed by the Auto Sequential Random Forest. Aerospace 2022, 9, 518. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, L.; Ren, Y.; Li, Y. Trajectory Tracking of UAVs Using Sigmoid Tracking Differentiator and Variable Gain Finite-Time Extended State Observer. Drones 2022, 6, 350. [Google Scholar] [CrossRef]
- Åström, K.; Hägglund, T.; Hang, C.; Ho, W. Automatic Tuning and Adaptation for PID Controllers—A Survey. IFAC Proc. Vol. 1992, 25, 371–376. [Google Scholar] [CrossRef]
- Głębocki, R.; Jacewicz, M. Sensitivity Analysis and Flight Tests Results for a Vertical Cold Launch Missile System. Aerospace 2020, 7, 168. [Google Scholar] [CrossRef]
- Devaud, E.; Harcaut, J.P.; Siguerdidjane, H. Three-Axes Missile Autopilot Design: From Linear to Nonlinear Control Strategies. J. Guid. Control. Dyn. 2001, 24, 64–71. [Google Scholar] [CrossRef]
- Lee, Y.; Kim, Y.; Moon, G.; Jun, B.E. Sliding-Mode-Based Missile-Integrated Attitude Control Schemes Considering Velocity Change. J. Guid. Control. Dyn. 2016, 39, 423–436. [Google Scholar] [CrossRef]
- Lee, S.; Kim, Y.; Lee, Y.; Moon, G.; Jeon, B.E. Robust-Backstepping Missile Autopilot Design Considering Time-Varying Parameters and Uncertainty. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4269–4287. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and Bandwidth-Parameterization Based Controller Tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; Volume 6, pp. 4989–4996. [Google Scholar] [CrossRef]
- Chien, M.T.; Fang, S.T.; Su, Y.X. A Generalization of Gershorin Circles. Appl. Comput. Math. 2016, 15, 106–111. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]

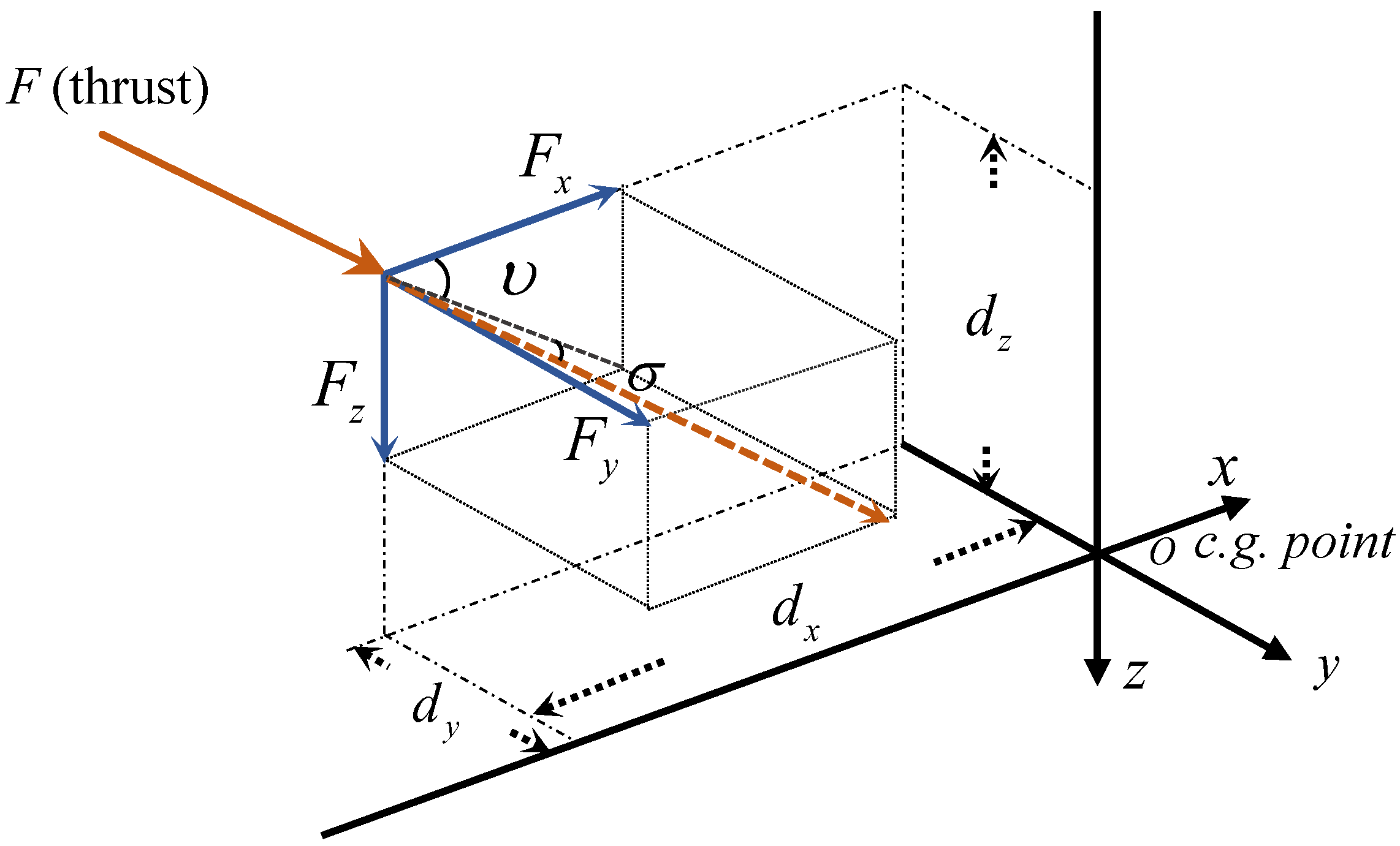


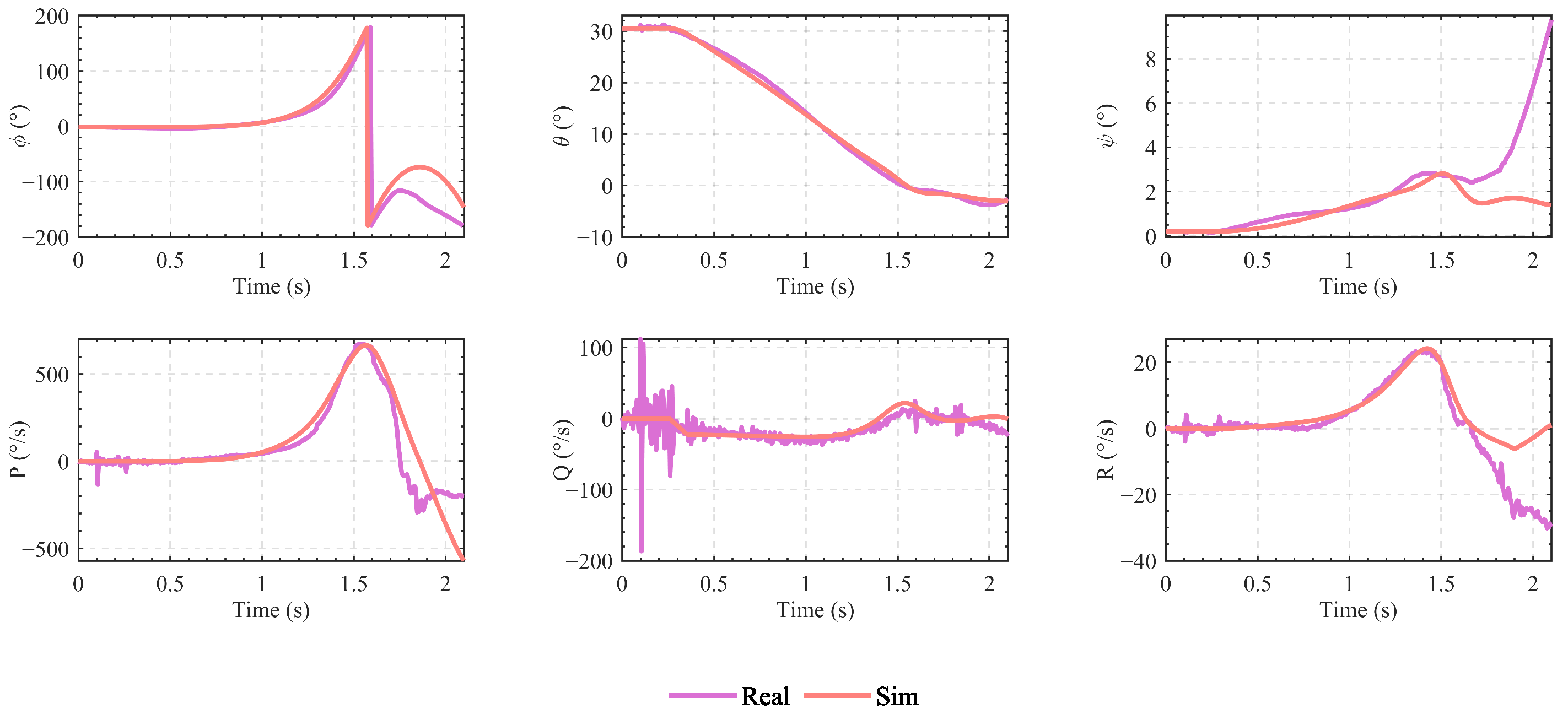

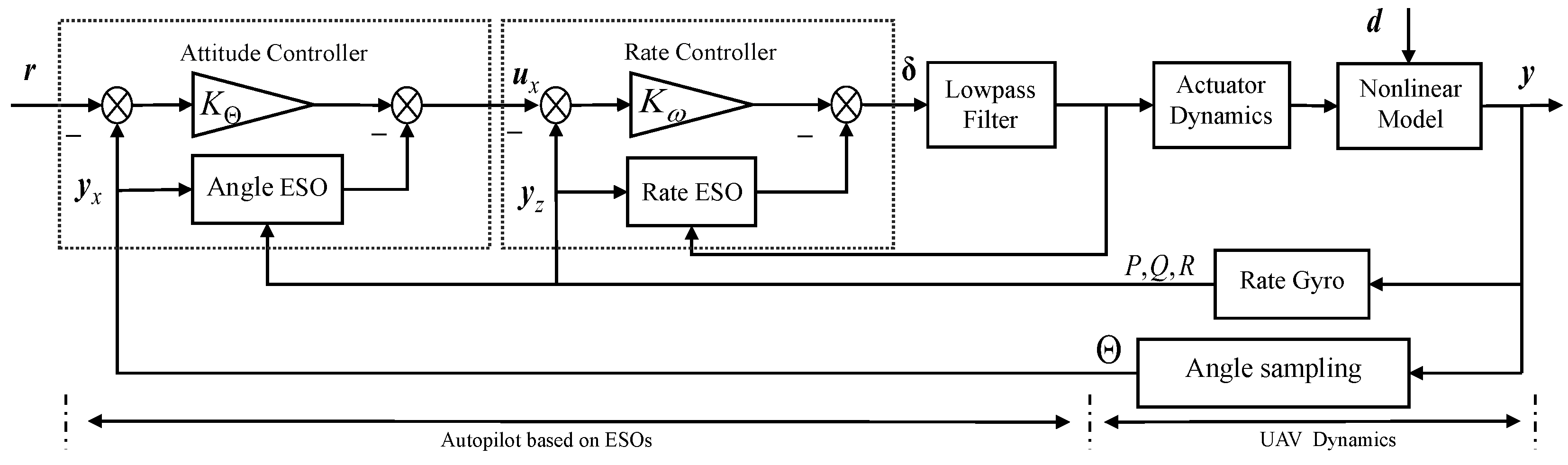
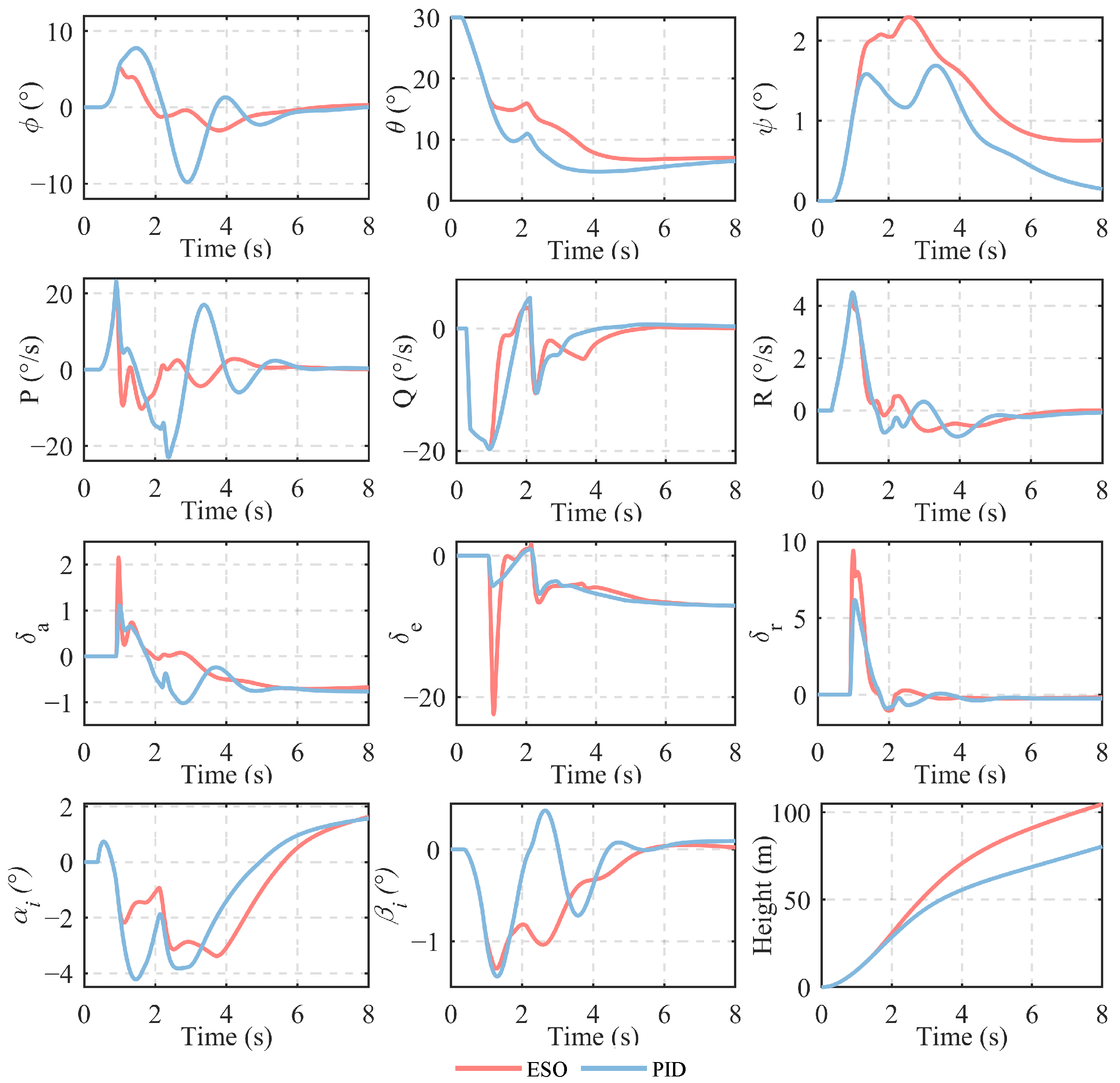

| Notation | Definition | Value |
|---|---|---|
| m | UAV mass | |
| Reference area | ||
| Mean aerodynamic chord | ||
| Y axis moment of inertia | ||
| X axis moment of inertia (fold closed) | ||
| X axis moment of inertia (fold open) | ||
| X axis c.g. with rocket | ||
| X axis c.g. without rocket | ||
| V | Cruise speed |
| Notation | / | |||||
|---|---|---|---|---|---|---|
| ESO | 22.1120 | 47.0476 | 15.6231 | 132.4590 | 110.3229 | 25.8892 |
| PID | 45.4432 | 104.3141 | 12.8780 | / | / | / |
| Notation | Wind | ||||
|---|---|---|---|---|---|
| Bias | m/s | 0.1 m | 4 mm | 5 mm | 2’ |
| Notation | |||||
| Bias | 3’ | 50% | 70% | 60% | 35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Cai, X.; Wu, L.; Guo, Z. Addressing Launch and Deployment Uncertainties in UAVs with ESO-Based Attitude Control. Drones 2024, 8, 363. https://doi.org/10.3390/drones8080363
Yang C, Cai X, Wu L, Guo Z. Addressing Launch and Deployment Uncertainties in UAVs with ESO-Based Attitude Control. Drones. 2024; 8(8):363. https://doi.org/10.3390/drones8080363
Chicago/Turabian StyleYang, Chao, Xiaoru Cai, Liaoni Wu, and Zhiming Guo. 2024. "Addressing Launch and Deployment Uncertainties in UAVs with ESO-Based Attitude Control" Drones 8, no. 8: 363. https://doi.org/10.3390/drones8080363
APA StyleYang, C., Cai, X., Wu, L., & Guo, Z. (2024). Addressing Launch and Deployment Uncertainties in UAVs with ESO-Based Attitude Control. Drones, 8(8), 363. https://doi.org/10.3390/drones8080363






