Abstract
Uncrewed Aerial Vehicles (UAVs) are increasingly deployed across various domains due to their versatility in navigating three-dimensional spaces. The utilization of UAV swarms further enhances the efficiency of mission execution through collaborative operation and shared intelligence. This paper introduces a novel decentralized swarm control strategy for multi-UAV systems engaged in intercepting multiple dynamic targets. The proposed control framework leverages the advantages of both learning-based intelligent algorithms and rule-based control methods, facilitating complex task control in unknown environments while enabling adaptive and resilient coordination among UAV swarms. Moreover, dual flight modes are introduced to enhance mission robustness and fault tolerance, allowing UAVs to autonomously return to base in case of emergencies or upon task completion. Comprehensive simulation scenarios are designed to validate the effectiveness and scalability of the proposed control system under various conditions. Additionally, a feasibility analysis is conducted to guarantee real-world UAV implementation. The results demonstrate significant improvements in tracking performance, scheduling efficiency, and overall success rates compared to traditional methods. This research contributes to the advancement of autonomous UAV swarm coordination and specific applications in complex environments.
1. Introduction
Uncrewed Aerial Vehicles (UAVs), renowned for their flexibility, swift deployment, and advanced surveying capabilities, significantly augment the Internet of Things (IoT) ecosystem [1,2]. Various examples can be found in agricultural monitoring [3], unidentified aircraft engagement [4,5], and post-disaster search and rescue operations [6,7]. As aerial mobile nodes, UAVs bridge the gap between physical devices and digital systems by facilitating efficient data collection, transmission, and processing [8,9]. However, given a single UAV’s limited coverage for large-scale and complex missions, the coordination of multiple UAVs–or a UAV swarm–can significantly amplify their collective strengths [10]. Compared to single-unit setups, swarms provide greater coverage, sensing, computing, and processing power while also improving overall efficiency through information sharing [11] and dynamic task allocation [12]. Beyond that, it enhances the system’s robustness and fault tolerance, ensuring mission continuity and completion even when a few individual units fail [13]. A swarm architecture not only simplifies the complexity of tasks assigned to each UAV, thereby boosting energy efficiency, but also lowers the environmental adaptation requirements [14], enabling new possibilities for a broader spectrum of UAV applications.
With population growth and technological progression, the scale and complexity of UAV-involved tasks are continuously increasing. Breakthroughs in swarm control technology are necessary. Beni and Wang [15] developed a behavior-based UAV swarm control architecture that defines a set of basic actions (e.g., obstacle avoidance, aggregation, dispersion) to achieve coordination under simple conditions. Although straightforward and intuitive, this approach lacks flexibility and adaptability. To overcome computational bottlenecks and communication overhead of centralized control methods, Kada et al. [16] introduced a distributed control framework utilizing consensus algorithms that enable each UAV to update control inputs independently based on local state and neighbor data while achieving global coordination and simultaneously enhancing robustness and scalability. Similarly, drawing inspiration from natural foraging behaviors, the authors of [17] proposed an ant colony optimization (ACO)-based strategy for UAV swarms in which the UAVs release and detect pheromones to coordinate their search in unknown environments, facilitating efficient and distributed cooperative exploration.
Despite progress in traditional (or code-based) methods, significant challenges are still encountered in dynamic environments with uncertainties. Predefined control rules struggle to cover all possible scenarios and cannot adapt to changes. Moreover, these methods often require extensive manual tuning of parameters, complicating the achievement of optimal swarm performance [18,19]. To further enhance the autonomy and intelligence of UAV swarms, it is crucial to integrate advanced artificial intelligence (AI) techniques, such as machine learning [20] and reinforcement learning, enabling UAV swarms to learn and optimize from experience [21].
In [22], Weng et al. borrowed concepts from artificial immune systems to design an adaptive UAV swarm control strategy mimicking the recognition, learning, and memory functions of immune cells to dynamically respond to environmental changes and quickly generate countermeasures. Among supervised learning approaches, Tang et al. [23] employed convolutional neural networks (CNNs) [24] to enable UAV swarm navigation and obstacle avoidance in complex environments. By collecting a vast dataset of aerial images and corresponding control commands, the CNN model learns a mapping function from visual inputs to navigation decisions, eliminating the need for handcrafted features and control rules.
On the other hand, researchers have explored multi-agent reinforcement learning (MARL) for swarm control. Chen et al. [25] developed a centralized-critic MARL framework for surveillance and monitoring, which employs centralized value function estimation alongside decentralized policy optimization, enabling efficient coverage of large areas with minimal overlap by a swarm of UAVs. Building upon this, Qie et al. [26] introduced an actor–critic-based multi-agent deep deterministic policy gradient (MADDPG) algorithm in a fully cooperative scenario. This algorithm enhances the stability and convergence of MARL, making it capable of handling nonstationary environments and learning robust swarm coordination policies.
However, MARL systems face inherent challenges. As the complexity of the environment grows, standard policy gradient methods suffer from high variance estimates, leading to suboptimal or unstable learning [27]. Furthermore, policy changes in one agent can alter the environment’s dynamics perceived by others, further destabilizing the learning process. Additionally, the curse of dimensionality [28] presents significant obstacles in MARL; as the number of agents increases, the state–action space grows exponentially, demanding substantial computational resources to learn effective policies.
To address these challenges, researchers have developed various approaches. Lowe et al. [29] introduced a "centralized training and decentralized execution" paradigm to tackle the nonstationarity issue in MARL. During the centralized training phase, all agents’ observation and action information is collected in a central critic network that learns to estimate the value function of each agent’s decisions. In the decentralized execution phase, each agent uses only its own observational data, which maintains autonomy while leveraging additional information gathered during training to stabilize the learning process. Besides, Li et al. [30] enhanced the MADDPG algorithm with transfer learning techniques to improve generalization capabilities across different tasks. Specifically, they first trained the MADDPG agents on a set of source tasks, covering various environmental settings and objectives. Then, meta-learning techniques were used to embed this acquired knowledge into a meta-policy network, allowing quick adaptation to new tasks with minimal tuning, significantly speeding up the learning process and boosting adaptability in new environments.
Based on the above discussion, although significant advancements in UAV swarm control methods have been made, limitations persist when facing increasingly complex mission requirements and unpredictable environmental conditions. To clarify, traditional code-based methods lack flexibility and adaptability, struggling to cope with dynamic and uncertain environments [31]. Supervised learning methods, although possessing learning capabilities, have limited effectiveness in handling dynamic constraints and with insufficient pre-provided training data [32,33]. While reinforcement learning methods demonstrate powerful real-time decision-making intelligence through interaction with the environment, they still encounter issues in multi-objective and large-scale swarm cases, including safety concerns, energy consumption, and practical deployment [34]. This paper develops a multilayered UAV swarm control approach that addresses these problems for multiple dynamic intruder aircraft interception. It utilizes a modular control system design that combines reinforcement learning capabilities to handle uncertainties with the determinacy brought by code-based algorithms. From low-level operational controls to high-level strategic decisions, the system enables the generation of real-time states for each ownship, supports various flight modes and their autonomous transitions, and implements a coordination mechanism for information sharing within multi-ownship systems.
The remainder of this paper is organized as follows: Section 2 formulates the problem, reviews related previous works, and highlights the main contributions. Section 3 elaborates the proposed distributed swarm control framework and associated algorithms involved in the system. Section 4 presents numerical and simulation results showcasing the effectiveness and robustness of the proposed method. An analysis of the feasibility of applying the control system to real-world UAV swarms is provided as well. Finally, Section 5 summarizes this work and outlines future research directions.
2. Related Work and Problem Definition
In order to develop an efficient swarm control strategy suitable for complex tasks, we took cues from our earlier work. In [35], we proposed a hybrid control framework that combines the Soft Actor–Critic method with a Fuzzy Inference System (SAC-FIS) for single UAV dynamic multi-target interception. This framework boosts training efficiency and ensures robust generalization by integrating universal expert experience through the FIS, effectively tackling prevalent reinforcement learning challenges in dynamic and multi-target environments. The framework’s modular design enhances its scalability to a variety of problems, allowing for straightforward modifications or upgrades to specific modules. Additionally, we developed a UAV autonomous navigation and collision avoidance system using two deep reinforcement learning (DRL) methods in [36,37], which was evaluated in multi-agent scenarios including two independent ownships and three cooperative UAVs (one leader and two followers). In [38], we introduced an integrated UAV emergency landing system designed for GPS-denied environments, ensuring safe mission aborts and landings under emergency conditions.
This paper extends the SAC-FIS controller to multi-UAV systems. The ownships employ a decentralized target selection algorithm to identify unauthorized UAVs as targets. Upon successful interception of a current target, an ownship may either proceed to another intruder or transition to the safe returning mode, landing in a designated area. The environment situations between each ownship and its target are entirely unknown and unpredictable. For any given ownship, other ownships and unselected intruder aircraft are treated as mobile obstacles. This setup demands dynamic real-time response to evolving threats, ensuring mission safety and success.
In summary, this study synthesizes previous works and introduces significant innovations with the aim of developing a hybrid approach that combines code-based and neural network-based methods. This integration seeks to enhance scheduling efficiency within the swarm and improve the resilience of various objectives. By dynamically and flexibly distributing tasks within the swarm, the proposed approach not only simplifies the assignments for each UAV but also ensures that the mission can proceed without disruption even if one or more ownships fail. However, managing the inherent complexity of this swarm problem involves addressing multiple facets: ensuring safety by preventing unintended collisions, enhancing mission efficiency by guaranteeing that ownships complete all interception tasks asynchronously, and managing contingencies to ensure the overall mission’s success despite potential individual failures.
Contributions
Table 1 displays the improvements and innovations made in this paper based on our previous work. The main contributions of this paper are also outlined below.

Table 1.
Comparative overview of key differences between previous work and the current study.
- A new hybrid layered control architecture for intercepting swarms: A three-layer control system is developed to address advanced swarm control problems. This architecture establishes a highly flexible and scalable framework for swarm activities across different scales, ensuring robust control in dynamic and unpredictable environments.
- A new decentralized target allocation algorithm: A dynamic target selection algorithm is designed to enable distributed target allocation for each ownship with capabilities for prompt responses in emergency situations.
- An integrated method for enhancing safe flight operations: A strategy for random waypoint generation is created for adaptable return mode processes, and a control signal optimizer is employed to enhance the security of physical UAV applications.
3. Methodology
As depicted in Figure 1, the use cases involve a swarm of n ownships (blue quadrotors) and m intruder aircraft (in other colors). A rectangular drone hub acts as both a home base and a safe landing site. The ownships are initially stationed at the hub and will intercept all intruder aircraft if they enter a specified airspace. Successfully intercepted intruders will hover at their capture points. After successfully intercepting all intruders or in emergencies, ownships automatically revert to safe returning mode, landing and disarming at the drone hub. Additionally, each ownship is equipped with a 3D LiDAR sensor, which has azimuth () and elevation () limits defined by and , respectively, and a maximum range of 20 m.
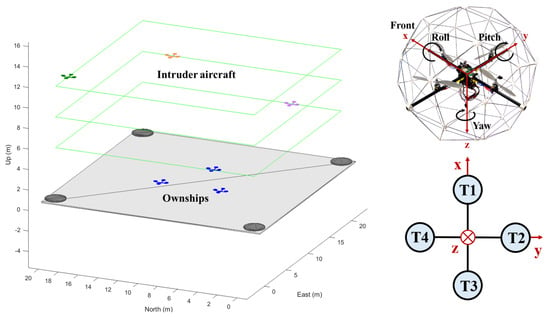
Figure 1.
Illustration of the simulation environment, featuring the drone hub, ownships (blue quadrotors), and intruder aircraft at varied altitudes. The right panel shows a “+” type quadrotor model [39], detailing axes (x, y, z), rotational conventions (roll, pitch, yaw), and rotor thrust numbering (T1–T4).
Figure 2 details the architecture of the proposed hybrid swarm control system. This system integrates SAC-FIS and PID controllers to manage distinct flight modes, processing environment feedback at each time step; concurrently, intruder UAVs follow particular and predefined trajectories, providing continuous position and velocity data.
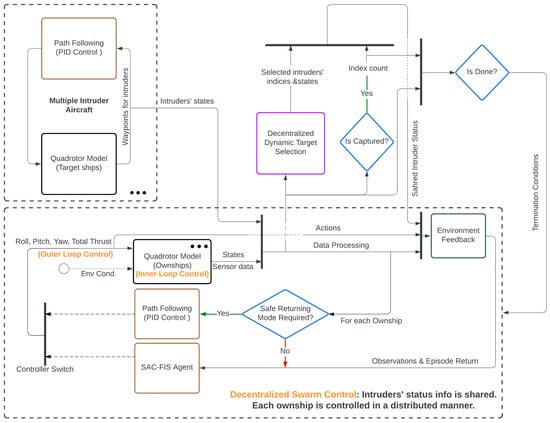
Figure 2.
Architecture diagram of the multilayered swarm control system.
To address the challenges posed by the defined swarm control problem, the framework includes several strategies and algorithms. These encompass an inner loop controller that converts underactuated inputs (roll, pitch, yaw, thrust) into UAV states, outer loop controllers that generate desired real-time model inputs, and a decentralized swarm control protocol. This protocol features a host of capabilities: a dynamic target selection algorithm, methods for assessing target capture success, emergency response strategies, flight mode transition criteria, and test termination conditions. The rest of this section provides a comprehensive breakdown of each component within this system.
3.1. Inner Loop Control
In this study, we employed the North–East–Downward (NED) coordinate system for both the earth coordinate system (), which is also regarded as the inertial reference frame, and the body coordinate system () of the UAV.
We derived the equations of motion for the ‘+’ type quadrotor using the Newton–Euler formulation. Although the fourth-order Runge–Kutta method (RK4) [40,41] is more accurate, it requires more complex computations and is less intuitive. It is important to note that the Newton–Euler equations of motion are usually derived in the inertial reference frame, whereas describing the motion of the object is more convenient in the body coordinate system. For example, the UAV’s position and attitude are variables in the earth coordinate system, whereas the translational velocity and rotational velocity are defined in the body frame. In addition, the data collected by onboard sensors is also relative to the body-fixed frame. Therefore, a transform matrix from the body-fixed frame to the inertial reference frame is necessary.
The rotation matrix, defined as , follows the ZYX rotation sequence (yaw –pitch –roll ), and is provided by
The angular velocity transformation matrix can be derived according to Equation (2) as follows:
Therefore, the transformation matrix is
During the inner loop control process, the inputs are Roll (), Pitch (), Yaw (), and Total Thrust (T), representing the desired values. The outputs are the states, including the position, attitude, and velocities. Initially, as presented in Equation (4), the required torques , , are calculated using PID controllers based on the difference between the current and desired attitude angles:
where
For the tuning process (gain parameters , , ) of all PID controllers designed in this paper, the pidTuner tool from MATLAB was utilized. The primary objectives are to ensure the stability of the closed-loop system at all predetermined operating points, minimize the response time, reduce overshoot, and maintain smooth system output. For specific PID controllers (e.g., Section 3.2.2), appropriate integral action was employed to reduce or eliminate steady-state errors.
Simultaneously, the torques from Equation (4) can also be expressed using thrusts, as shown below.
Because all of the thrust–torque relationships can be directly represented as the product of a unit matrix, the form of the thrust distribution matrix (Equation (6)) becomes more concise when assuming that both the arm length and torque coefficient are equal to 1:
At this point, the linear velocity, position, angular velocity, and attitude can be updated over time accordingly.
3.1.1. Linear Velocity and Position Update
Assuming that the mass of the UAV is m, the acceleration is , and the total force is , according to Newton’s second law we have:
For the quadcopter, the total force can be decomposed into thrust and gravity:
Therefore,
and
The updated linear velocities () can be obtained by integrating the corresponding linear accelerations (). Assuming that the velocities at the previous time step are given by with a time step of , the velocities for the current time step can be computed as follows:
Similarly, the position is updated through numerical integration of the linear velocity:
3.1.2. Angular Velocity and Attitude Update
The relationship between angular velocity and angular acceleration can also be described by the Newton–Euler equation:
where , is the inertia matrix, is the angular acceleration, and is the angular velocity.
The angular acceleration is calculated using
The updated angular velocities are obtained by integrating the angular accelerations. Assuming that the initial angular velocities from the last time step are and the angular accelerations are provided by with a time increment of , the new angular velocities can be computed as follows:
The attitude is then updated:
where the attitude rates in the earth coordinate system are obtained through the angular velocity transformation matrix:
3.2. Outer Loop Control
As the inner loop control manages the transformation of desired inputs into updated UAV states, the outer loop control’s role is to determine these desired inputs at each time step.
In this study, two outer loop controllers are utilized. During the intruder chasing phase, each ownship employs a DRL-based intelligent SAC-FIS agent. Additionally, PID controllers are applied to regulate the safe returning mode.
3.2.1. SAC-FIS Controller for Mobile Intruder Interception
In our previous work [35], we detailed the design and validation of the SAC-FIS controller for single-ownship operations. Specifically, the FIS processes readings from onboard 3D LiDAR to perform object detection and real-time obstacle avoidance by controlling yaw. The SAC model, which controls roll, pitch, and total thrust, serves as the core of the algorithm. It progressively understands the UAV dynamic model and the logic provided by the FIS via its neural networks. Through training, it continuously strengthens cooperation with the FIS, allowing this approach to achieve efficient control and dynamic tracking in unpredictable environments without compromising the UAV’s maneuverability. This paper will not revisit the specific design process explained in that work, and will instead focus on new enhancements for swarm control settings.
The SAC-FIS agent relies on environmental information and feedback to determine actions, which are the inputs to the quadrotor model.
For each individual ownship, the observation space (S) is constructed as follows:
which includes:
- : The Euclidean distance between the ownship and selected target ship.
- : The ownship’s Euler angles in ZYX order, represented as .
- : The ownship’s linear velocities; .
- : The ownship’s angular velocities, represented as p, q, r.
- : The coordinate differences between the ownship and selected target ship in the XYZ directions, represented as , , and .
- : The selected target ship’s linear velocities.
- : The ownship’s angular velocities about the earth coordinate system’s X and Y axes, represented by and .
- : The roll (), pitch (), yaw (), and thrust () actions.
- : Inputs of the FIS, consisting of the ownship–target angle () and sampled readings from the 3D LiDAR, including the front distance () and lateral distance error ().
- : The speed vector’s projection onto the direction (vector) formed between the ownship and the selected target ship.
- : The component of the speed vector that is perpendicular to the vector formed between the ownship and the selected target ship.
- : The number of successfully intercepted intruders.
In addition, to maintain high sensitivity to slight state changes within complex and dynamic environments, exponential terms are utilized to formulate an effective reward function for each ownship in the swarm. This design ensures that each component possesses bounded outputs, typically ranging from −1 to 0 or from 0 to 1, which facilitates the fine-tuning of weights for each component according to the importance of different objectives:
where to and are weight coefficients. For this study, these coefficients were tuned as follows:
and
This reward function comprises multiple elements. The primary element employs the ownship’s distance to the designated target, encouraging the minimization of this difference, while the second and third components guide the agent to advance directly toward the chosen target by imposing penalties for deviations in alternative directions. Additionally, penalties are applied to the control inputs ( and ) and angular velocities ( and ) to mitigate oscillations and excessive fluctuations, thereby enhancing safety and conserving energy. The term with is included to reward the agent for each successfully intercepted intruder UAV.
Furthermore, the reset function utilized for the agent training process, originally described in [35], has been improved to accommodate swarm systems and ensure adaptive generalization. At the start of each episode, the initial orientation (yaw angle) of each ownship is randomized, and their initial positions on the drone hub are also randomly generated. This step guarantees that each ownship maintains a minimum distance of one meter from the drone hub boundary and at least two meters from one another. Additionally, the initial positions of each intruder aircraft are randomly assigned along their predefined paths.
3.2.2. PID Control for Safe Returning
When an ownship has successfully captured all its allocated targets and no unassigned intruders remain, it automatically switches to return mode. This also occurs if it encounters an emergency, such as impending battery depletion, prompting a return to the drone hub. The specific conditions for triggering the flight modes are detailed in Section 3.3.2.
Upon returning, the system generates a random landing point on the drone hub for the ownship, defined as . Similar to the mechanism for generating the initial positions of ownships, this point must be at least one meter from the drone hub’s edge and two meters from any previously assigned landing points of other ownships, unless it is the first ownship to return.
Given a specified three-dimensional coordinate and the current UAV position, the waypoint-following control that guides the quadrotor to the specified location can be designed using the PID controllers based on the quadrotor model described in Section 3.1. The same control principle is applicable to the predefined path following of intruder aircraft. Specifically, if the desired landing point or waypoint is and the current position is , then the desired velocities can be calculated as follows:
and
Given the desired accelerations, according to Equation (10), the desired inputs at each time step are as follows:
Because the quadrotor’s yaw angle does not affect its velocity in any direction [42], the desired yaw can be simply calculated by
To ensure the flight stability and control response of the quadrotor, the roll and pitch control should be bounded:
3.3. Decentralized Swarm Control
At this stage, it is crucial to develop an efficient and decentralized swarm control strategy that can coordinate all ownships. This strategy encompasses a dynamic target selection algorithm, conditions that direct individual ownships to transition to landing mode, and criteria for concluding a test.
3.3.1. Dynamic Target Selection Algorithm
Developing a target selection algorithm for single-ownship scenarios is straightforward. However, the challenges escalate in swarm scenarios involving n ownships and m intruder aircraft. When , the situation is similar to as only m ownships are needed, with each assigned an intruder based on proximity. Conversely, when , some ownships must intercept more than one intruder UAV to complete the mission.
At the mission’s outset, each ownship can be uniformly assigned an intruder aircraft according to a sequence (Initial Allocation Phase). Yet, the completion times for the first interception will vary among ownships, necessitating a distributed dynamic target selection mechanism in which the ownship that completes its task first is promptly reassigned a new target (Dynamic Reallocation Phase). This cycle continues until an ownship completes its current target’s interception and no unassigned intruder aircraft remain in the environment.
To implement such a strategy, ownships in the swarm must share their intruder status information, indicating whether each intruder UAV has been assigned (represented by 1 or 0); for instance, if an ownship encounters an emergency, it will abandon its assigned intruder, whose status then reverts to ’unassigned’. Due to the information-sharing mechanism, one of the other ownships will intercept this intruder after completing its current task, ensuring the overall mission’s success.
A flowchart of the distributed swarm control strategy is illustrated in Figure 3, and the detailed pseudocode of the dynamic target selection algorithm is provided in Algorithm 1.
3.3.2. Conditions for Triggering Safe Return Mode
For each individual ownship, the return mode is triggered under two specific conditions:
- The ownship successfully neutralizes its current target and no unassigned intruder aircraft remain in the environment.
- The ownship encounters an emergency situation, e.g., a collision or .
In testing, we simulated low battery conditions by adjusting the ‘distance traveled’ threshold of the corresponding ownship, thereby further validating the effectiveness of the information-sharing and reallocation mechanism. The traveled distance can be calculated by:
The distance change at each time step is
where N is the number of time steps.
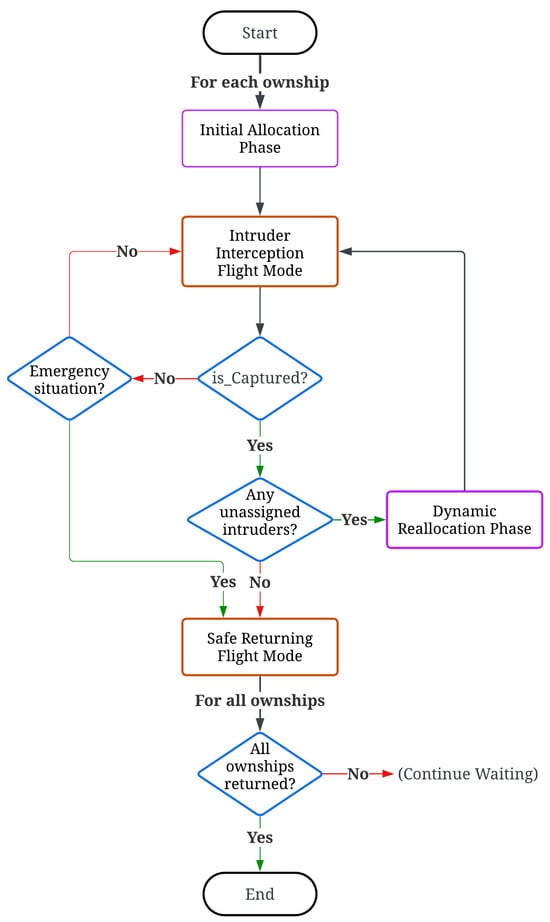
Figure 3.
Flowchart of the distributed swarm control strategy.
| Algorithm 1: Dynamic Target Selection Algorithm for Multiple Ownships and Intruders |
|
3.3.3. Termination Conditions
Compared to single-ownship tasks, utilizing a swarm not only significantly enhances the mission’s fault tolerance but also markedly improves its time efficiency. A test concludes under one of the following conditions:
- Each ownship is positioned more than 30 m away from its assigned target ship:
- The duration surpasses the predefined maximum time threshold:
- All intruders have been successfully intercepted and all ownships have been safely disarmed on the drone hub (note that if any ownship lands outside the drone hub, it is considered a failed mission):
- Each individual ownship has collided with an obstacle, identified by a minimal LiDAR reading (from the 3D point cloud) dropping below 0.75 m (note: in this study, the distance from the center of an ownship to its edge should not exceed 0.4 m):
To summarize, this section has first offered a detailed overview of the UAV model applicable to each quadrotor, including ownships and intruder aircraft. Next, we have covered the inner loop controller (Section 3.1) and the various outer loop control strategies suitable for different flight modes (Section 3.2). Finally, we have introduced a decentralized control algorithm for the swarm featuring a dynamic target selection algorithm, intruder information sharing mechanism, and methods to ensure ownship safety in emergency situations and mission completion (Section 3.3). In the subsequent Section 4, we validate this control system through simulation results.
4. Results
In this chapter, we demonstrate and analyze the effectiveness and flexibility of the proposed control system across various scenarios, employing the MATLAB UAV Toolbox (2023b) for incorporation of realistic UAV dynamics and consideration of environmental factors. As established in Section 3, scenarios with more ownships (n) than intruder aircraft (m) are treated as if . Therefore, we do not further discuss the case, instead focusing on the and scenarios, including situations where ownships face emergencies during interception. Additionally, the smoothing of control signals and the feasibility of the control system for use with physical drones are analyzed.
The tuning and training process of the RL agent for intruder interception is detailed in [35], and will not be reiterated here. This paper applies well-trained SAC-FIS agents, known for their strong generalization efficacy in managing intruder interception and collision avoidance tasks across various configurations. Additionally, as this study uses the NED coordinate system, all z-axis values above ground are represented as negative. The drone hub is defined by coordinates , with ownships depicted as blue quadrotors and intruder aircraft in other colors. Each intruder’s motion pattern exhibits different speeds: the purple intruder moves at approximately 0.8 m/s, the orange one at 1 m/s, and the green one at 1.2 m/s. Meanwhile, since the magnitudes of the control inputs for each ownship are bounded, the speed of each individual ownship can be up to 10 m/s.
4.1. Equal Number of Ownships and Intruder Aircraft ()
In this scenario, as illustrated in Figure 4, three ownships () are stationed at the drone hub, with three intruders breaching the airspace. The initial positions of the ownships are , , and . The intruders’ initial positions are , , and , with their flight paths delineated by the waypoints , , and , respectively.
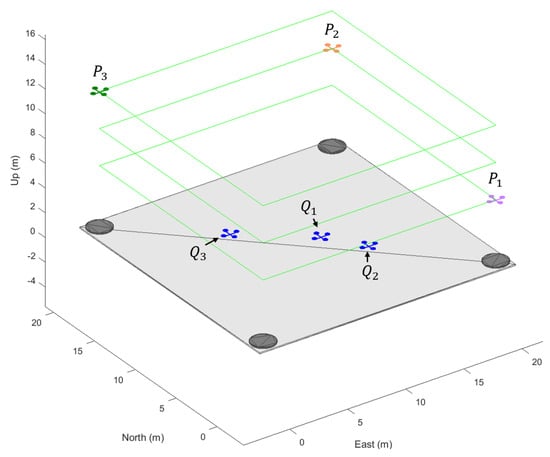
Figure 4.
Initial configurations of swarm control scenario with three ownships and three intruder aircraft.
At the beginning of the test, based on the target selection algorithm and the ownships’ sequence, first selected the nearest intruder as its target ship. Subsequently, locked on to , leaving to be automatically assigned to . Figure 5 shows the complete simulation results, including both the flight modes of the ownships and their trajectories during this task. The figure also indicates the takeoff and landing points for each ownship (e.g., and represent the off-ground and landing points of ). The results show that each ownship successfully completed the task and safely returned to the drone hub.
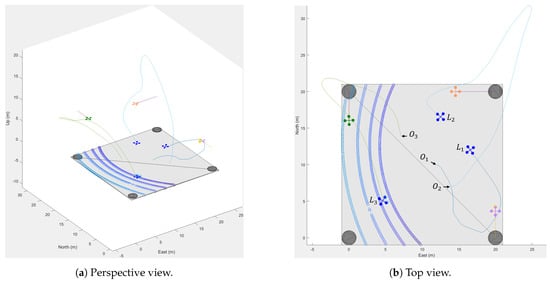
Figure 5.
Simulation results with trajectories in different views.
Figure 6, Figure 7 and Figure 8 detail each ownship’s performance via time-based metrics. Specifically, the test duration was 15.4 s, well below the 30-second limitation. Figure 6 depicts the distance from each ownship to its target ship. Ownship 1 () intercepted its target in 6.2 s and subsequently initiated a return, disarming at 13.8 s and waiting for the others to return. Similarly, Ownship 3 took 7.1 s to intercept its assigned intruder, while Ownship 2 took 9.3 s. Upon successful completion, each intruder hovered in place. The trial concluded after returned to the hub.
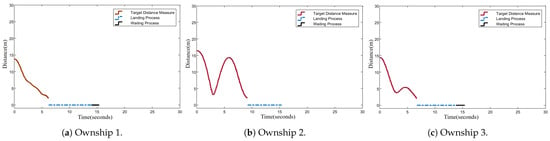
Figure 6.
Euclidean distance from each ownship to its target ship.
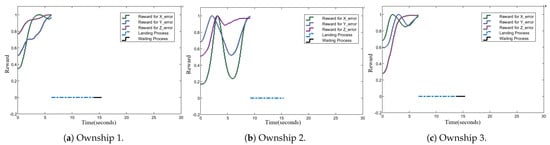
Figure 7.
Rewards for individual ownship coordinate errors in the X, Y, and Z directions.
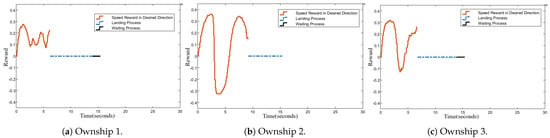
Figure 8.
Rewards for speed vector’s projection on the ownship–target direction.
Figure 7 and Figure 8 quantify the reward values from the reward function’s first and second terms. The first term calculates the coordinate errors between an ownship and its target across the X, Y, and Z axes, with each component constrained between 0 and 1. Smaller differences result in higher rewards. The second term evaluates the alignment of the speed vector’s projection with the ownship–target vector, within bounds of to , rewarding positive alignments and penalizing negative ones.
4.2. Fewer Ownships than Intruder Aircraft ()
Next, as depicted in Figure 9, we created a scenario with fewer ownships compared to intruders.
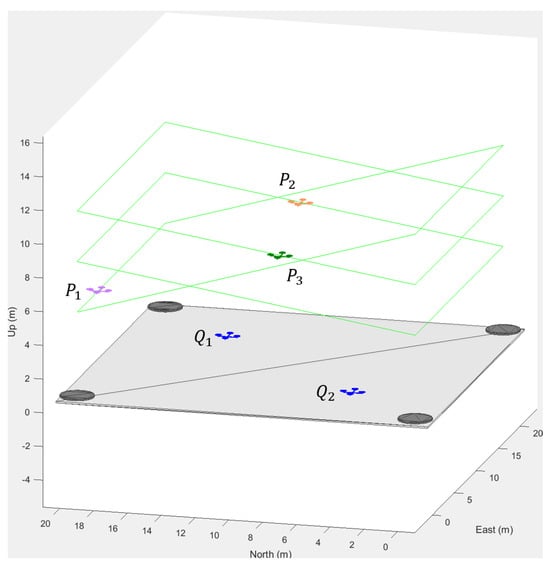
Figure 9.
Initial configuration of swarm control scenario with two ownships and three intruder aircraft.
In this case, the initial positions of the ownships are and . To increase the complexity of the mission, the intruders’ predefined trajectories are diversified, and each displays a distinct movement pattern. The intruders’ paths are as follows: adheres to , follows , and traces .
At mission onset, Ownship 1 targeted the nearest intruder, , and Ownship 2 pursued , while was initially unassigned, pending the completion of the first interception.
The resulting dynamic is detailed in Figure 10, Figure 11, Figure 12 and Figure 13, where Figure 11 records Ownship 1 rapidly engaging in 5.5 s. This was faster than Ownship 2, which took 6.9 s. Consequently, according to the dynamic reallocation phase of the target selection algorithm, was automatically assigned to Ownship 1, serving as its second target. Ultimately, Ownship 1 required 14.2 s to intercept two intruder UAVs, including the landing process, with the total mission duration amounting to 18.8 s.
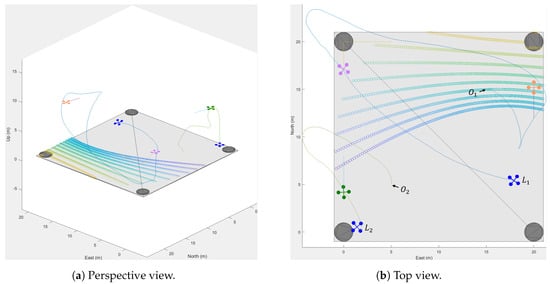
Figure 10.
Simulation results with trajectories in different views.
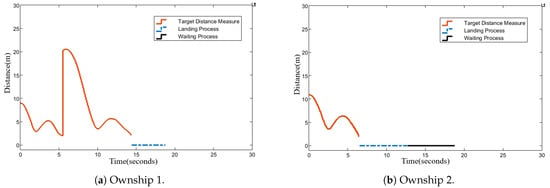
Figure 11.
Euclidean distance from each ownship to its target ship.
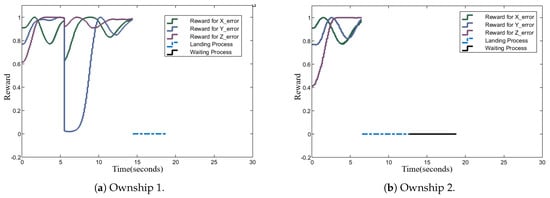
Figure 12.
Rewards for individual ownship coordinate errors in the X, Y, and Z directions.
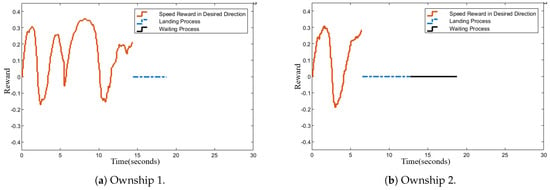
Figure 13.
Rewards for speed vector’s projection on the ownship–target direction.
4.3. Equal Number of Ownships and Intruder Aircraft ( with Emergency Situations)
To further verify the effectiveness of the proposed control system, an emergency scenario simulation was conducted. This test aimed to assess whether other ownships could successfully intercept the intruder initially assigned to the failed ownship. The scenario utilized the mission layout from Section 4.1 (Figure 4).
For Ownship 2, was set to 2 m, meaning that this ownship would enter an emergency state when its flight distance reached two meters. The originally assigned would then become unallocated and be reassigned to either Ownship 1 or Ownship 3 depending on the timing of their initial interceptions. Figure 14, Figure 15, Figure 16 and Figure 17 show the detailed simulation results for each ownship.
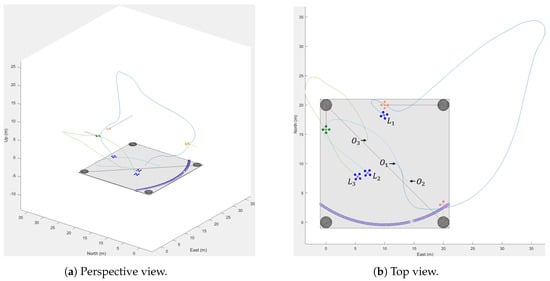
Figure 14.
Simulation results with trajectories in different views.
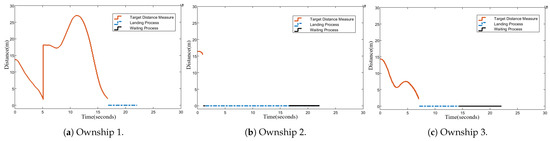
Figure 15.
Euclidean distance from each ownship to its target ship.
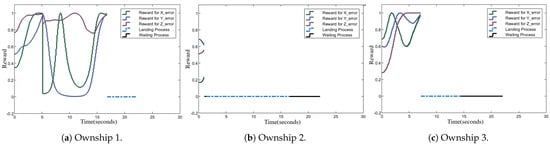
Figure 16.
Rewards for individual ownship coordinate errors in the X, Y, and Z directions.

Figure 17.
Rewards for speed vector’s projection on the ownship–target direction.
From these figures, it is evident that Ownship 2 encountered an emergency situation in less than two seconds of flight. During landing, it significantly reduced its speed to minimize further risk. Meanwhile, thanks to the dynamic reallocation mechanism and information-sharing with regard to the intruders’ status, Ownship 1 was assigned the remaining intruder UAV after completing the first target interception. It took 12 s to successfully intercept the second intruder. Together with the landing process, the total duration of this mission was 22.1 s.
These findings confirm the resilience and efficacy of the swarm control protocol, demonstrating that the mission objectives can be achieved even with limited ownship availability or in emergency situations.
4.4. Control System Feasibility Analysis
The preceding subsections have validated the control system’s performance across various scenarios; however, determining the practical applicability of these control signals on physical UAVs remains a critical step.
In this study, the mass of each quadrotor UAV is set to and the gravity is set to . The UAV’s weight is adjustable; however, this requires retraining the SAC-FIS agent. Taking Ownship 1 () from Section 4.3 as an example, its original control signals throughout the mission are displayed in Figure 18. It was propelled by the SAC-FIS controller during the initial 17.2 s, then subsequently by the PID controller. Clearly, the control variables (roll, pitch, yaw, thrust) exhibit significant fluctuations which, while effective in simulations, could lead to mechanical wear and safety hazards when applied to physical drones [43].
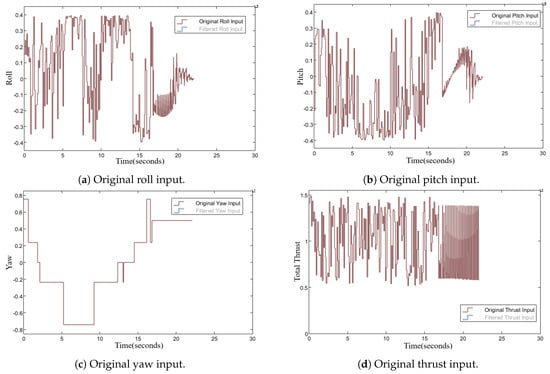
Figure 18.
Temporal dynamics of Ownship 1’s original control variables from Section 4.3.
Therefore, such control signals must be further smoothed to meet both the maneuverability requirements for successfully completing the mission and the safety constraints of physical UAV motors. We tested and compared various filters to identify the best method for smoothing the control signals. Traditional low-pass filters [44] can delay signals and reduce amplitude by filtering out high frequencies. The performance of the Kalman filter [45,46] would significantly decrease if the system’s dynamic model and noise statistical characteristics were inaccurate, making it unsuitable for this study’s model-free context. After testing, we finally opted for a moving average filter. A window size of 10 was used for the SAC-FIS controller (intruder interception phase), and a window size of 400 was applied to the PID controller (landing process), based on their different noise frequencies. The final results are shown in Figure 19.
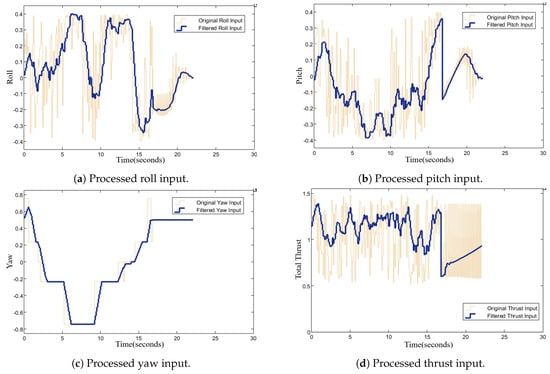
Figure 19.
Temporal dynamics of Ownship 1’s filtered control variables from Section 4.3.
The simulations presented in Section 4 applied the filtered signals, further confirming that this control signal processing method successfully achieves a balance between performance and applicability.
5. Conclusions
This research presents a novel multilayered control architecture that integrates intelligent and rule-driven methods for multi-UAV systems. This integration enables real-time path planning and execution of complex tasks, which are difficult with a single method alone. It also provides a safe and efficient solution to the swarm control problem. Specifically, the proposed framework encompasses an inner-loop controller, two outer-loop controllers, and a decentralized swarm control strategy. The main strengths of this system can be summarized as follows: first, the introduction of dual flight modes enhances performance by not only enabling autonomous decision-making in unpredictable environments but also ensuring higher reliability under controllable conditions, thereby improving overall system safety and efficiency; second, the dynamic target selection algorithm can perform distributed target allocation for each ownship through information sharing and accommodate diverse challenges, thus efficiently coordinating ownships, saving time, and enhancing system fault tolerance and mission success rates; finally, the entire system is designed with a modular architecture, facilitating the replacement and upgrading of components to adapt to different problems. However, the proposed framework still exhibits certain limitations, such as the use of PID controllers at certain points. While straightforward to deploy, these controllers introduce steady-state errors and potential for integral windup, making them suboptimal for control scenarios that demand high precision.
In the future, we will continue to explore various combinations of neural network-based and code-based algorithms for more complex problems, such as leader–follower structures and environments with dense and randomly localized obstacles. By defining and adjusting the control scope of AI methods, we aim to unlock new possibilities for UAV applications.
Author Contributions
Conceptualization, B.X.; methodology, B.X.; software, B.X.; validation, B.X.; formal analysis, B.X., I.M. and W.X.; investigation, B.X.; resources, B.X., I.M. and W.X.; data curation, B.X.; writing—original draft preparation, B.X.; writing—review and editing, B.X., I.M. and W.X.; visualization, B.X.; supervision, I.M. and W.X.; project administration, I.M. and W.X.; funding acquisition, I.M. and W.X. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to acknowledge financial support from the National Research Council of Canada (Integrated Autonomous Mobility Program) and NSERC (Grant No. 400003917) for the work reported in this paper.
Data Availability Statement
All data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Xu, X.; Zhao, H.; Yao, H.; Wang, S. A blockchain-enabled energy-efficient data collection system for UAV-assisted IoT. IEEE Internet Things J. 2020, 8, 2431–2443. [Google Scholar] [CrossRef]
- Feng, W.; Wang, J.; Chen, Y.; Wang, X.; Ge, N.; Lu, J. UAV-aided MIMO communications for 5G Internet of Things. IEEE Internet Things J. 2018, 6, 1731–1740. [Google Scholar] [CrossRef]
- Phang, S.K.; Chiang, T.H.A.; Happonen, A.; Chang, M.M.L. From Satellite to UAV-based Remote Sensing: A Review on Precision Agriculture. IEEE Access 2023, 11, 127057–127076. [Google Scholar] [CrossRef]
- Song, X.; Yang, R.; Yin, C.; Tang, B. A cooperative aerial interception model based on multi-agent system for uavs. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021; pp. 873–882. [Google Scholar]
- Evdokimenkov, V.N.; Kozorez, D.A.; Rabinskiy, L.N. Unmanned aerial vehicle evasion manoeuvres from enemy aircraft attack. J. Mech. Behav. Mater. 2021, 30, 87–94. [Google Scholar] [CrossRef]
- Wu, J.; Li, D.; Shi, J.; Li, X.; Gao, L.; Yu, L.; Han, G.; Wu, J. An Adaptive Conversion Speed Q-Learning Algorithm for Search and Rescue UAV Path Planning in Unknown Environments. IEEE Trans. Veh. Technol. 2023, 72, 15391–15404. [Google Scholar] [CrossRef]
- Dong, J.; Ota, K.; Dong, M. UAV-based real-time survivor detection system in post-disaster search and rescue operations. IEEE J. Miniaturization Air Space Syst. 2021, 2, 209–219. [Google Scholar] [CrossRef]
- Campion, M.; Ranganathan, P.; Faruque, S. UAV swarm communication and control architectures: A review. J. Unmanned Veh. Syst. 2018, 7, 93–106. [Google Scholar] [CrossRef]
- Khalil, H.; Rahman, S.U.; Ullah, I.; Khan, I.; Alghadhban, A.J.; Al-Adhaileh, M.H.; Ali, G.; ElAffendi, M. A UAV-Swarm-Communication Model Using a Machine-Learning Approach for Search-and-Rescue Applications. Drones 2022, 6, 372. [Google Scholar] [CrossRef]
- Shrit, O.; Martin, S.; Alagha, K.; Pujolle, G. A new approach to realize drone swarm using ad-hoc network. In Proceedings of the 2017 16th Annual Mediterranean Ad Hoc Networking Workshop (Med-Hoc-Net), Budva, Montenegro, 28–30 June 2017; pp. 1–5. [Google Scholar]
- Khalil, H.; Ali, G.; Rahman, S.U.; Asim, M.; El Affendi, M. Outage Prediction and Improvement in 6G for UAV Swarm Relays Using Machine Learning. Prog. Electromagn. Res. 2024, 107, 33–45. [Google Scholar] [CrossRef]
- Li, H.; Sun, Q.; Wang, M.; Liu, C.; Xie, Y.; Zhang, Y. A baseline-resilience assessment method for UAV swarms under heterogeneous communication networks. IEEE Syst. J. 2022, 16, 6107–6118. [Google Scholar] [CrossRef]
- Qin, B.; Zhang, D.; Tang, S.; Xu, Y. Two-layer formation-containment fault-tolerant control of fixed-wing UAV swarm for dynamic target tracking. J. Syst. Eng. Electron. 2023, 34, 1375–1396. [Google Scholar] [CrossRef]
- Altshuler, Y.; Yanovski, V.; Wagner, I.A.; Bruckstein, A.M. Multi-agent cooperative cleaning of expanding domains. Int. J. Robot. Res. 2011, 30, 1037–1071. [Google Scholar] [CrossRef]
- Beni, G.; Wang, J. Swarm intelligence in cellular robotic systems. In Robots and Biological Systems: Towards a New Bionics? Springer: Berlin/Heidelberg, Germany, 1993; pp. 703–712. [Google Scholar]
- Kada, B.; Khalid, M.; Shaikh, M.S. Distributed cooperative control of autonomous multi-agent UAV systems using smooth control. J. Syst. Eng. Electron. 2020, 31, 1297–1307. [Google Scholar] [CrossRef]
- Perez-Carabaza, S.; Besada-Portas, E.; Lopez-Orozco, J.A.; de la Cruz, J.M. Ant colony optimization for multi-UAV minimum time search in uncertain domains. Appl. Soft Comput. 2018, 62, 789–806. [Google Scholar] [CrossRef]
- Tong, P.; Yang, X.; Yang, Y.; Liu, W.; Wu, P. Multi-UAV Collaborative Absolute Vision Positioning and Navigation: A Survey and Discussion. Drones 2023, 7, 261. [Google Scholar] [CrossRef]
- Maddula, T.; Minai, A.A.; Polycarpou, M.M. Multi-target assignment and path planning for groups of UAVs. In Recent Developments in Cooperative Control and Optimization; Springer: Boston, MA, USA, 2004; pp. 261–272. [Google Scholar]
- Arafat, M.Y.; Moh, S. Localization and clustering based on swarm intelligence in UAV networks for emergency communications. IEEE Internet Things J. 2019, 6, 8958–8976. [Google Scholar] [CrossRef]
- Venturini, F.; Mason, F.; Pase, F.; Chiariotti, F.; Testolin, A.; Zanella, A.; Zorzi, M. Distributed reinforcement learning for flexible and efficient uav swarm control. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 955–969. [Google Scholar] [CrossRef]
- Weng, L.; Liu, Q.; Xia, M.; Song, Y.D. Immune network-based swarm intelligence and its application to unmanned aerial vehicle (UAV) swarm coordination. Neurocomputing 2014, 125, 134–141. [Google Scholar] [CrossRef]
- Tang, D.; Shen, L.; Hu, T. Online camera-gimbal-odometry system extrinsic calibration for fixed-wing UAV swarms. IEEE Access 2019, 7, 146903–146913. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Chen, Y.J.; Chang, D.K.; Zhang, C. Autonomous tracking using a swarm of UAVs: A constrained multi-agent reinforcement learning approach. IEEE Trans. Veh. Technol. 2020, 69, 13702–13717. [Google Scholar] [CrossRef]
- Qie, H.; Shi, D.; Shen, T.; Xu, X.; Li, Y.; Wang, L. Joint optimization of multi-UAV target assignment and path planning based on multi-agent reinforcement learning. IEEE Access 2019, 7, 146264–146272. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, Z.; Başar, T. Multi-agent reinforcement learning: A selective overview of theories and algorithms. In Handbook of Reinforcement Learning and Control; Springer: Cham, Switzerland, 2021; pp. 321–384. [Google Scholar]
- Williams, R.J. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach. Learn. 1992, 8, 229–256. [Google Scholar] [CrossRef]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Pieter, A.O.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Li, B.; Liang, S.; Gan, Z.; Chen, D.; Gao, P. Research on multi-UAV task decision-making based on improved MADDPG algorithm and transfer learning. Int. J. -Bio-Inspired Comput. 2021, 18, 82–91. [Google Scholar] [CrossRef]
- Rizk, Y.; Awad, M.; Tunstel, E.W. Decision making in multiagent systems: A survey. IEEE Trans. Cogn. Dev. Syst. 2018, 10, 514–529. [Google Scholar] [CrossRef]
- Amorim, W.P.; Tetila, E.C.; Pistori, H.; Papa, J.P. Semi-supervised learning with convolutional neural networks for UAV images automatic recognition. Comput. Electron. Agric. 2019, 164, 104932. [Google Scholar] [CrossRef]
- Yuan, F.; Liu, Y.J.; Liu, L.; Lan, J. Adaptive neural network control of non-affine multi-agent systems with actuator fault and input saturation. Int. J. Robust Nonlinear Control 2024, 34, 3761–3780. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Wu, Z.; Xu, J. Deep reinforcement learning for UAV swarm rendezvous behavior. J. Syst. Eng. Electron. 2023, 34, 360–373. [Google Scholar] [CrossRef]
- Xia, B.; Mantegh, I.; Xie, W. UAV Multi-Dynamic Target Interception: A Hybrid Intelligent Method Using Deep Reinforcement Learning and Fuzzy Logic. Drones 2024, 8, 226. [Google Scholar] [CrossRef]
- Xia, B.; Mantegh, I.; Xie, W.F. Intelligent Method for UAV Navigation and De-confliction–Powered by Multi-Agent Reinforcement Learning. In Proceedings of the 2023 International Conference on Unmanned Aircraft Systems (ICUAS), Warsaw, Poland, 6–9 June 2023; pp. 713–722. [Google Scholar]
- Xia, B.; He, T.; Mantegh, I.; Xie, W. AI-Based De-confliction and Emergency Landing Algorithm for UAS. Proceedings of the STO-MP-AVT-353 Meeting; NATO Science & Technology Organization: Brussels, Belgium, 2022; p. 12. Available online: https://www.sto.nato.int/publications/pages/results.aspx?k=bingze&s=Search%20All%20STO%20Reports (accessed on 1 January 2020).
- Xia, B.; Mantegh, I.; Xie, W. Integrated emergency self-landing method for autonomous uas in urban aerial mobility. In Proceedings of the 2021 21st International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 12–15 October 2021; pp. 275–282. [Google Scholar]
- Quanser Qball-X4 User Manual. Available online: https://users.encs.concordia.ca/~realtime/coen421/doc/Quanser%20QBall-X4%20-%20User%20Manual.pdf (accessed on 1 January 2020).
- Cui, J.S.; Zhang, F.R.; Feng, D.Z.; Li, C.; Li, F.; Tian, Q.C. An improved SLAM based on RK-VIF: Vision and inertial information fusion via Runge-Kutta method. Def. Technol. 2023, 21, 133–146. [Google Scholar] [CrossRef]
- Runge-Kutta 4th Order Method (RK4). Available online: https://primer-computational-mathematics.github.io/book/c_mathematics/numerical_methods/5_Runge_Kutta_method.html (accessed on 1 January 2020).
- Talaeizadeh, A.; Pishkenari, H.N.; Alasty, A. Quadcopter fast pure descent maneuver avoiding vortex ring state using yaw-rate control scheme. IEEE Robot. Autom. Lett. 2021, 6, 927–934. [Google Scholar] [CrossRef]
- Di Rito, G.; Galatolo, R.; Schettini, F. Self-monitoring electro-mechanical actuator for medium altitude long endurance unmanned aerial vehicle flight controls. Adv. Mech. Eng. 2016, 8, 1687814016644576. [Google Scholar] [CrossRef]
- Cordeiro, T.F.K.; Ishihara, J.Y.; Ferreira, H.C. A Decentralized Low-Chattering Sliding Mode Formation Flight Controller for a Swarm of UAVs. Sensors 2020, 20, 3094. [Google Scholar] [CrossRef] [PubMed]
- Bauer, P.; Bokor, J. LQ Servo control design with Kalman filter for a quadrotor UAV. Period. Polytech. Transp. Eng. 2008, 36, 9–14. [Google Scholar] [CrossRef]
- Liu, Y.; Duan, C.; Liu, L.; Cao, L. Discrete-Time Incremental Backstepping Control with Extended Kalman Filter for UAVs. Electronics 2023, 12, 3079. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).