Federated Reinforcement Learning for Collaborative Intelligence in UAV-Assisted C-V2X Communications
Abstract
1. Introduction
1.1. Contributions
- Enhance throughput and reduce the number of communication rounds between the vehicles and the UAV.
- Develop effective model learning and sharing strategies between the vehicles and the UAV to minimize the required number of communication rounds [14].
- Examine the impact of transmitting model parameter updates between the vehicles and UAVs on data traffic, number of hyper-parameters, and the overall decision making in UAV-assisted C-V2X communications [15].
- Implement DQN and duellingDQN for collaborative data sharing to minimize processing and queuing delay, as well as to optimize the convergence time of FRL models.
- We plot the FRL model convergence characteristics for UAV-assisted C-V2X communications where each agent is trained using a random 10% slice of the V2X-Sim dataset.
- We evaluate the proposed FRL algorithm based on the number of communication rounds () between the vehicles and the UAVs in a single sub frame of C-V2X mode 4 communications [16].
- We study the variation in average throughput vs. the number of communication rounds () for a varying number of vehicles. To monitor the model convergence characteristics with an increasing number of vehicles, we plot the variation in the mean square error against a varying number of vehicles.
- We plot the variation in optimal FRL model training time and convergence time for FedAvg and FedSGD with a varying discount factor (). Then, we identify some optimal values of () to analyze the losses. We also vary the learning rate () with respect to the number of global aggregations, as well as the number of training episodes.
1.2. Organization
2. Related Works
2.1. Reinforcement Learning Applications in C-V2X
2.2. Applications of Federated Learning in Vehicular Communications
2.3. Challenges in Applying FRL to C-V2X Communication
2.3.1. Vehicle Selection
- (i)
- Communication overhead: The UAVs may experience an increase in traffic due to model updates. Moreover, a vehicle’s communication may be several orders of magnitude slower than the local computation speed [42]. Even if a subset of randomly selected vehicles transmit the local model, the statistical heterogeneity is not addressed [42].
- (ii)
- Communication rounds: Reducing the number of iterations is another approach to minimize the number of communication rounds. Rather than updating the UAVs with each batch of local updates, more iterations of local updates can be performed at the vehicle edge network, as depicted in Figure 2. The local updates are facilitated by iterations involving multiple mini-batches, which result in fewer communication rounds [43]. A trade-off may arise, with local updates deviating significantly from global updates that impact meaningful driving decisions [43].
- (iii)
- Statistical heterogeneity: The training data in conventional machine learning are assumed to be i.i.d., whereas model updates are typically biased or non-i.i.d. due to multiple sensors [44].

2.3.2. Vehicle Selection and Local Model Averaging
2.3.3. System Heterogeneity and Statistical Heterogeneity
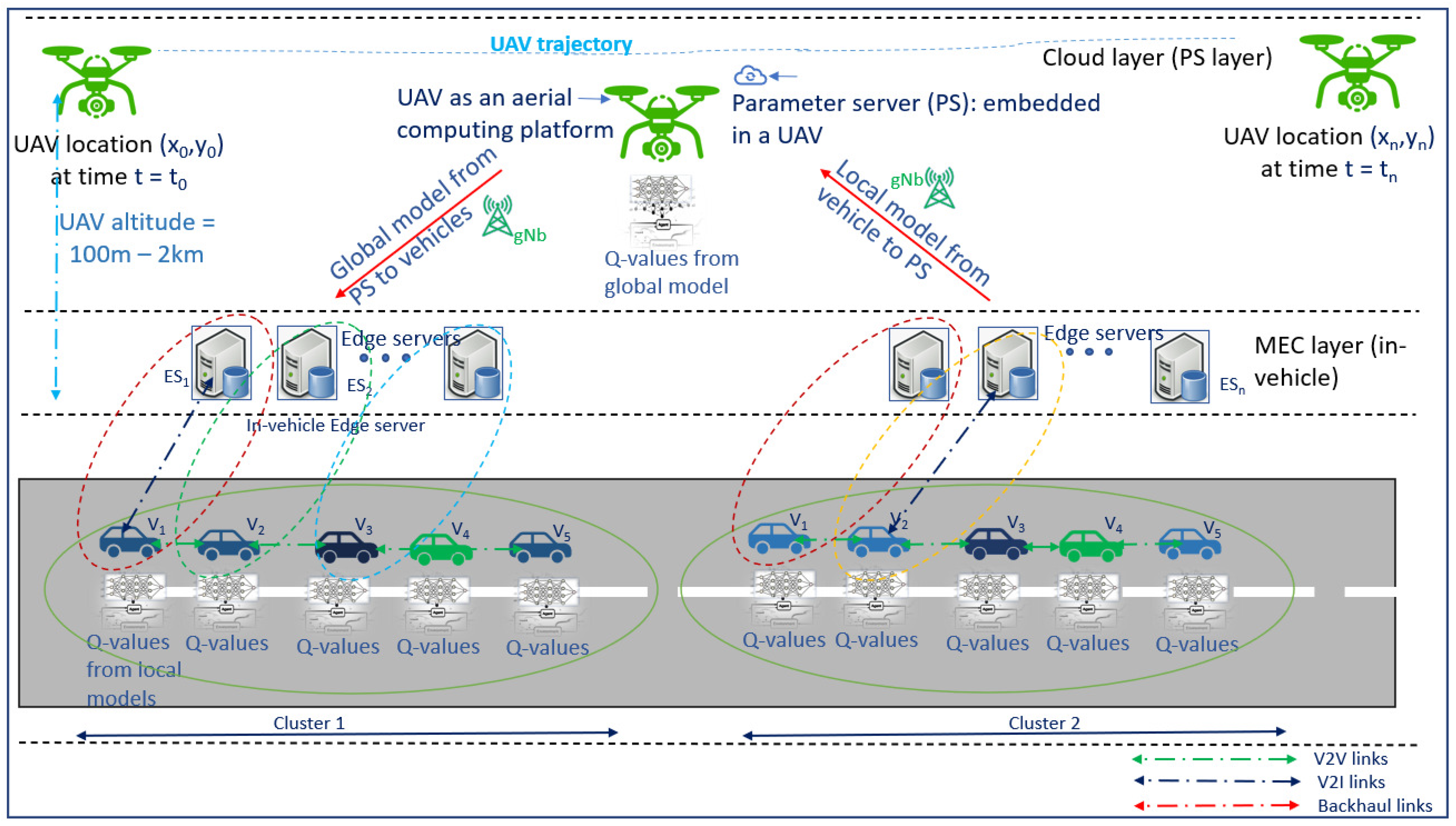
3. System Model
4. Problem Formulation
Dataset Description
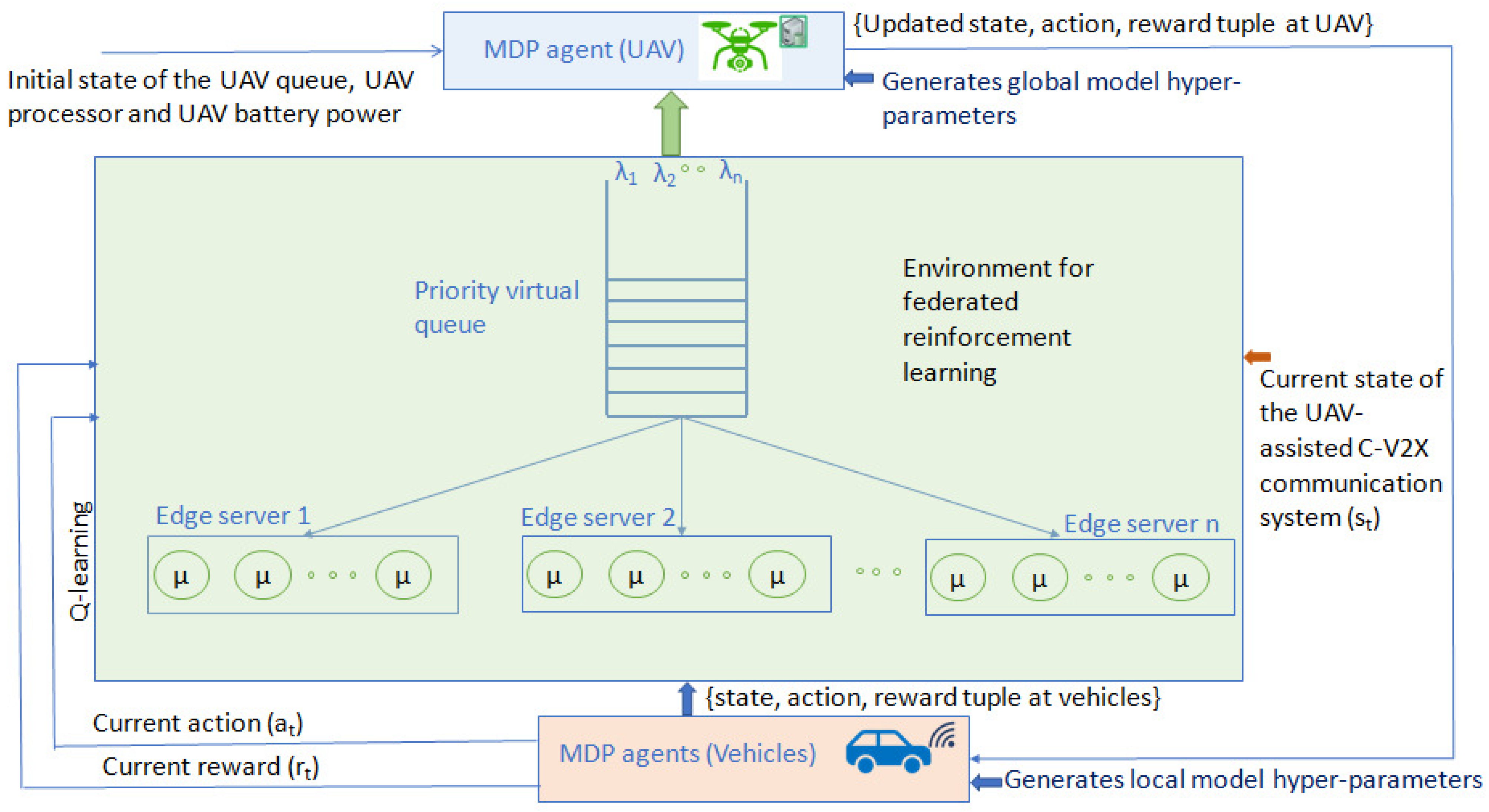
5. Proposed FRL Solution
5.1. Federated Reinforcement Learning for Minimizing Communication Rounds () between Vehicles (V) and UAVs
5.2. Q-Value Accumulation and Reward Function in FRL
5.3. -Greedy Approach for Vehicle Selection by the UAVs
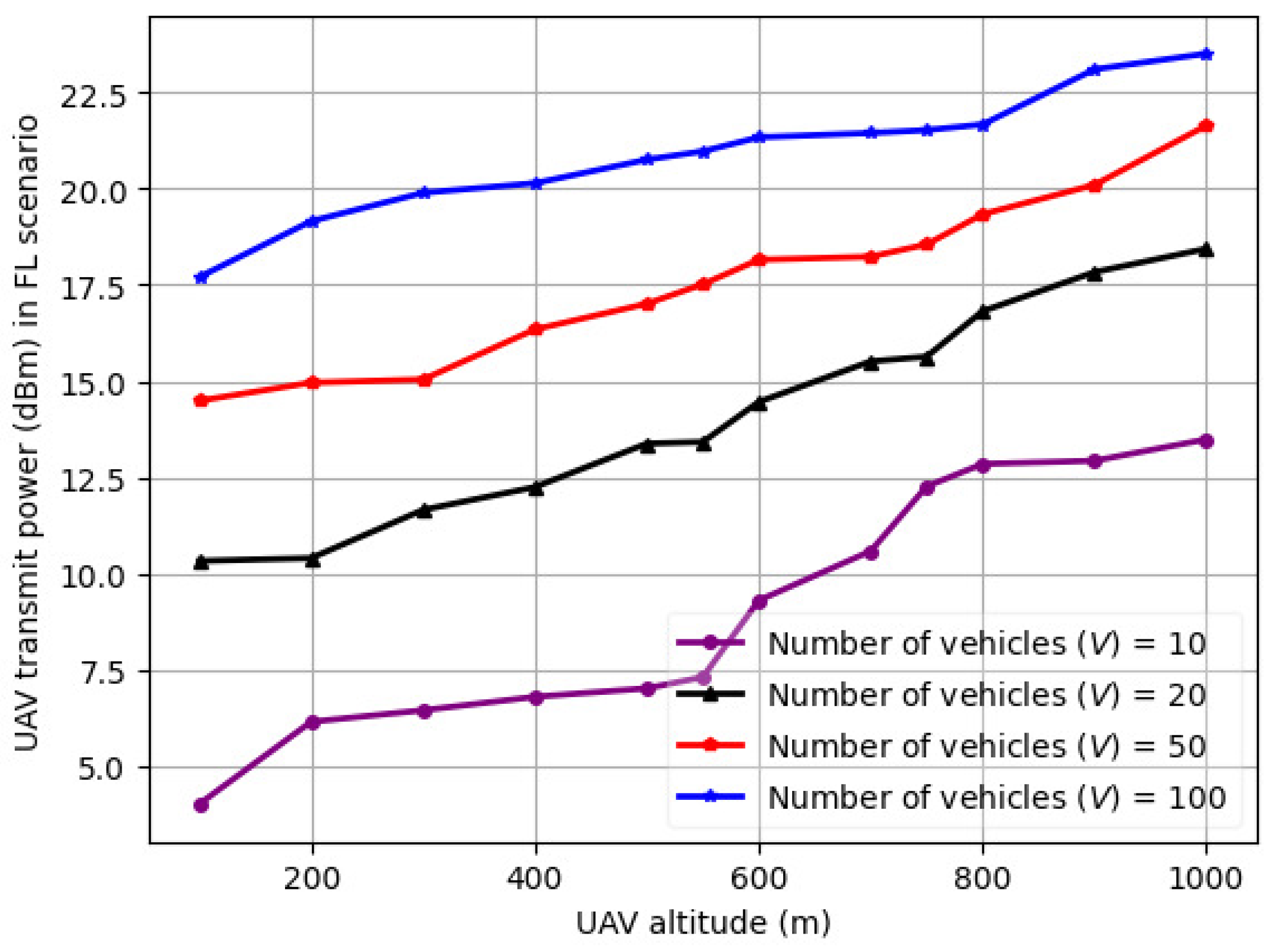
6. Simulation Results and Discussion
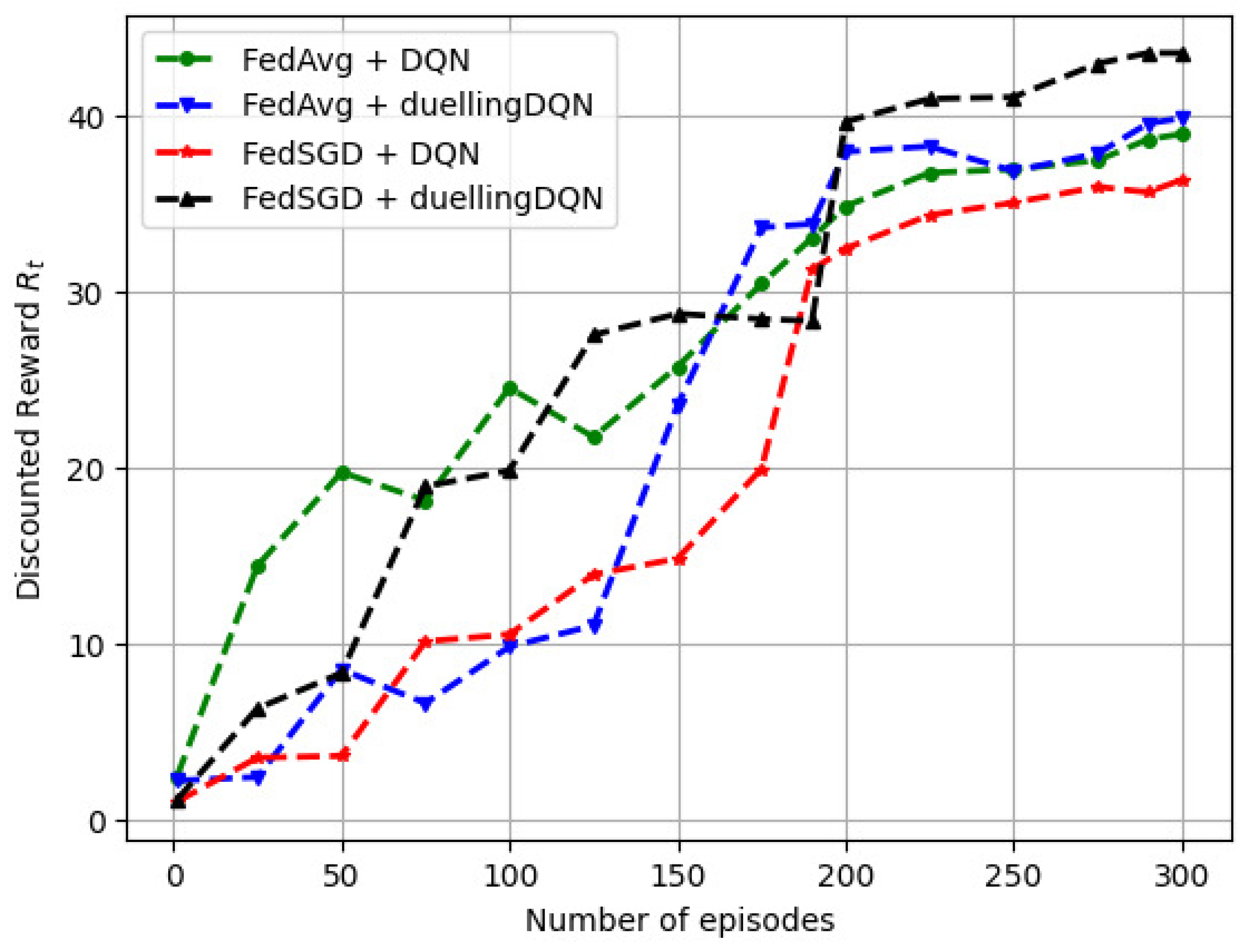
6.1. Federated Model Training
6.2. Model Convergence Characteristics
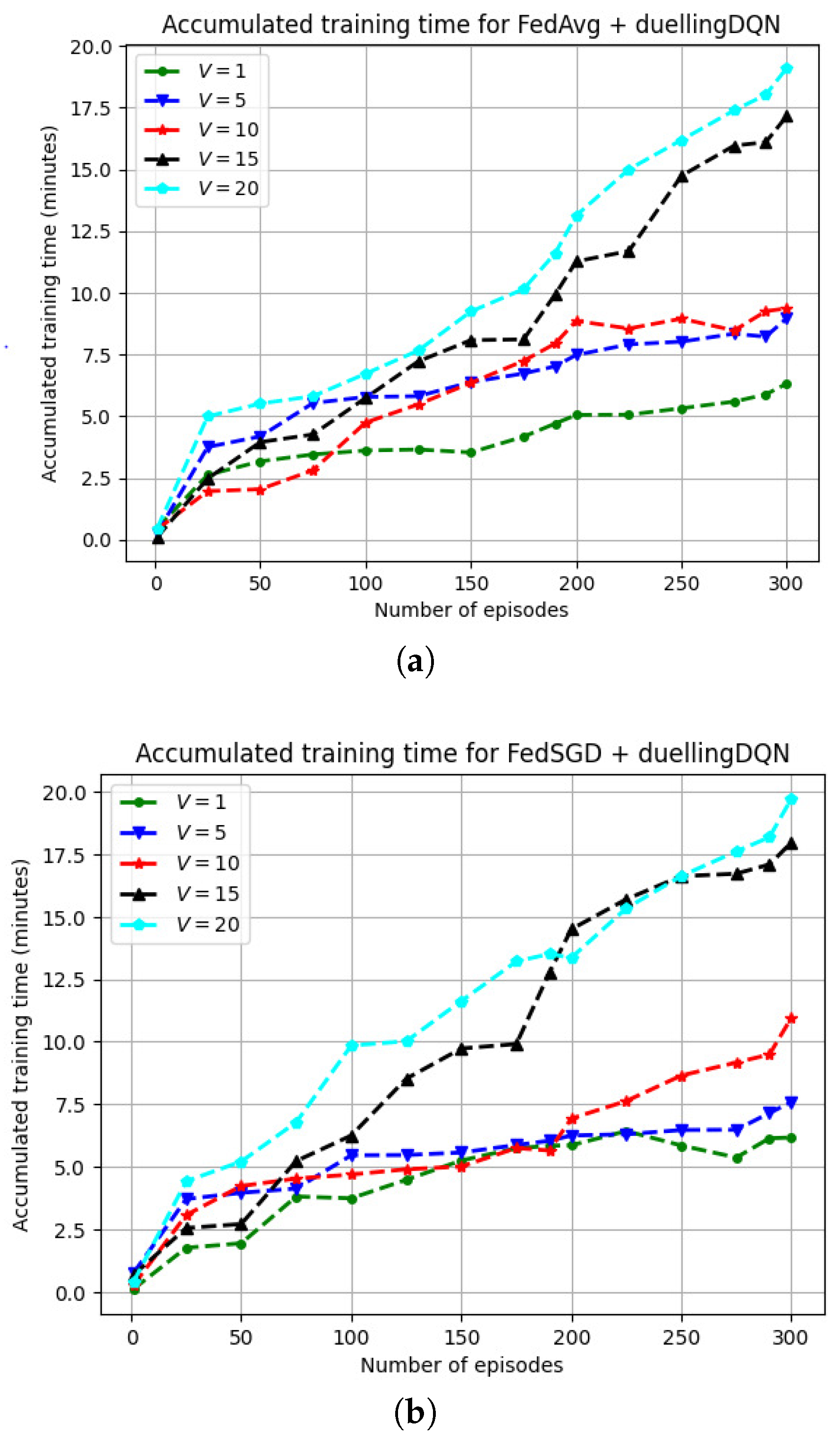
6.2.1. Variation in the Discounted Reward () with the Number of Training Episodes
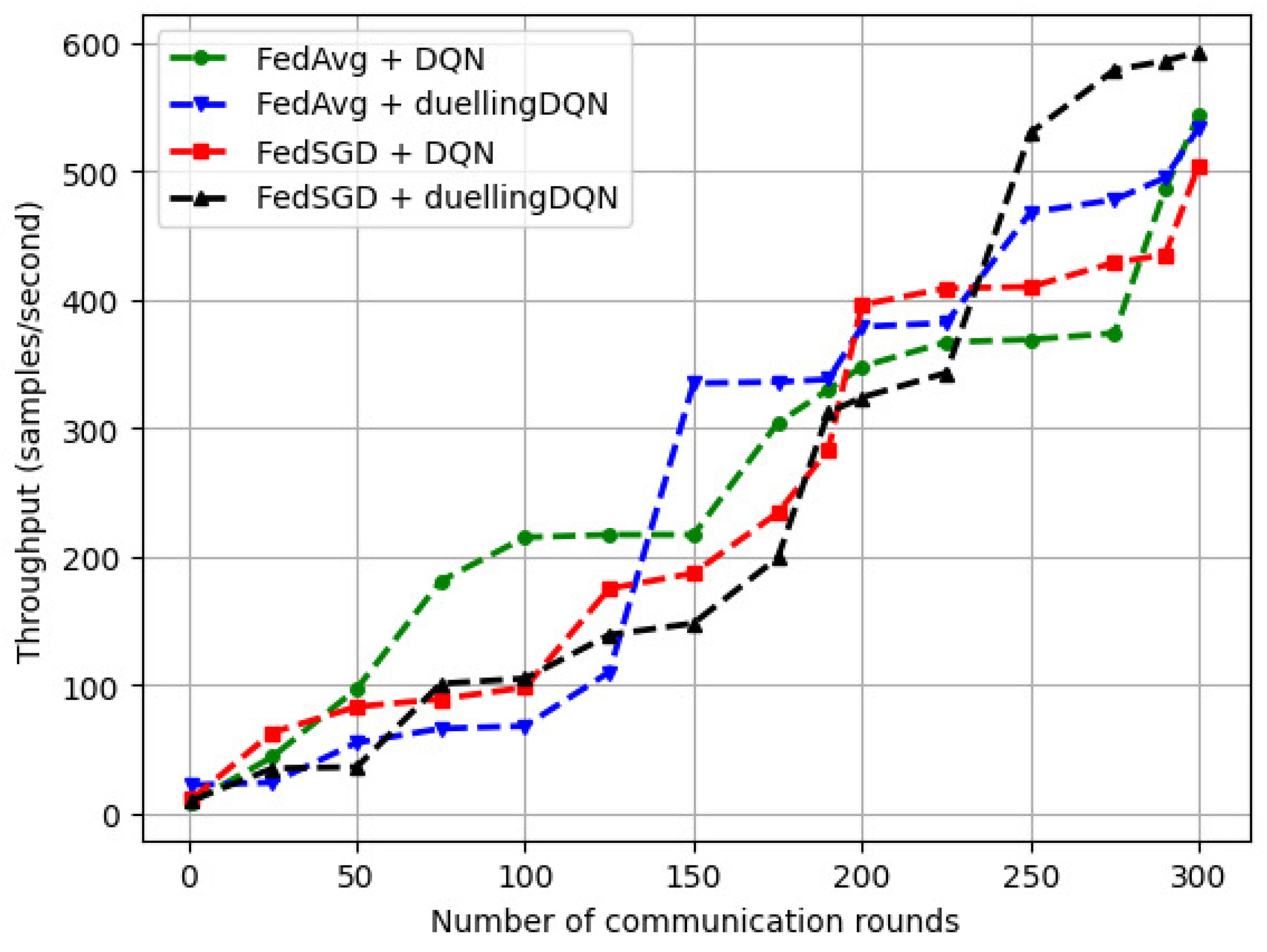
6.2.2. Variation in the System Throughput with the Number of Communication Rounds ()
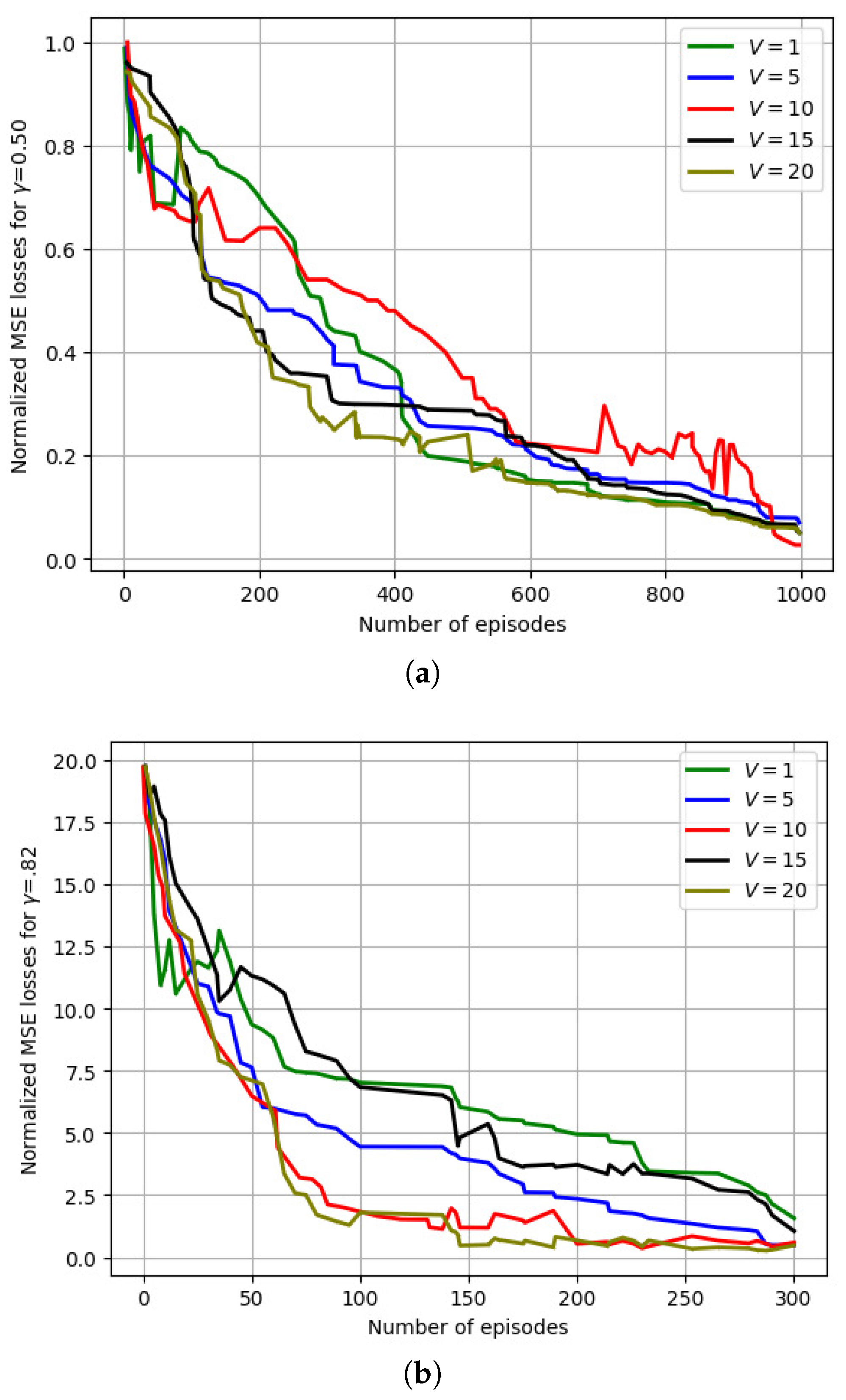
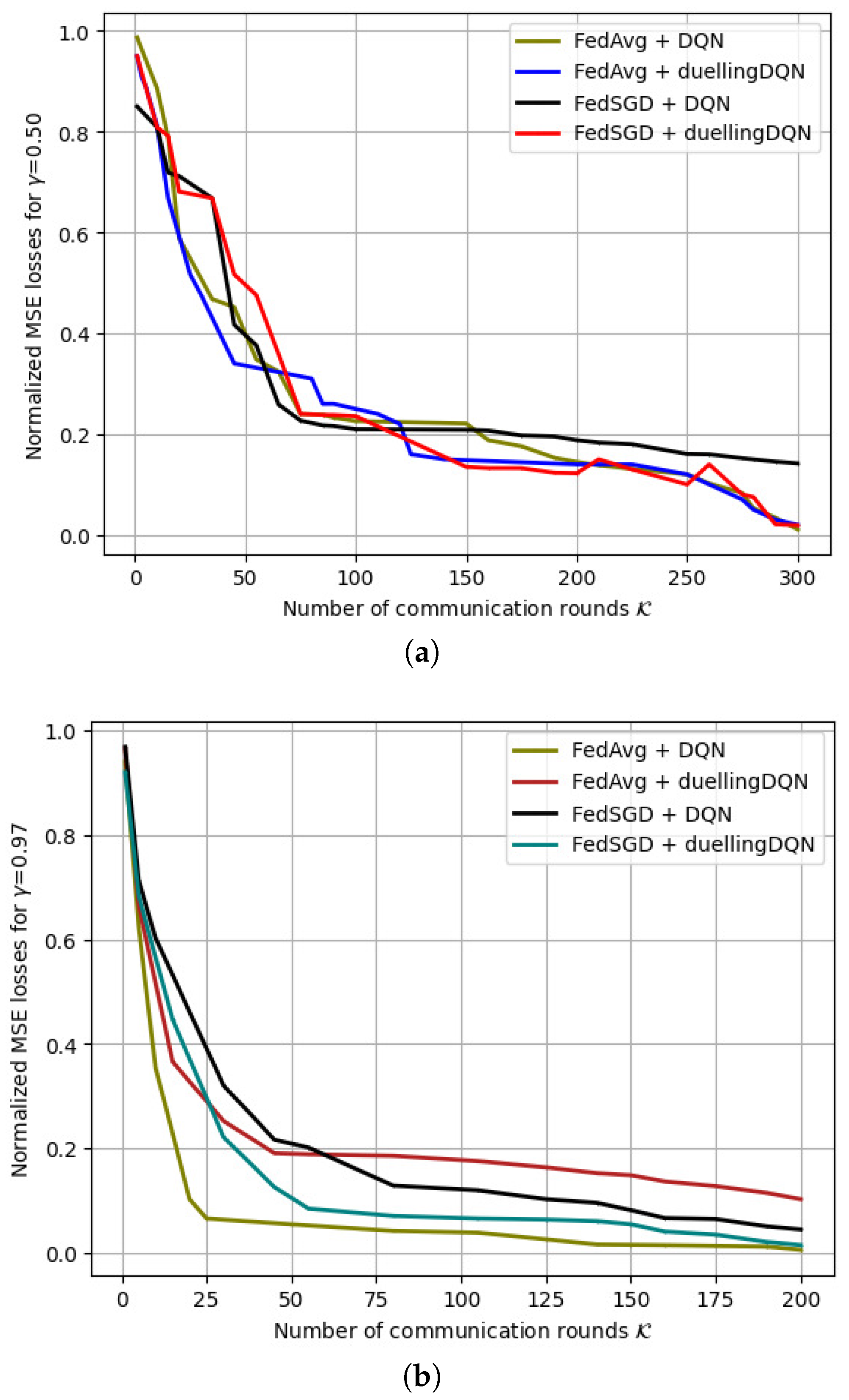
6.2.3. Variation in the MSE Losses with Discount Factor ()
6.3. Discussion and Comparison with Existing Works
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3GPP | Third-generation partnership project |
| 5GAA | Fifth-generation automotive association |
| 6G | Sixth generation (communication networks) |
| A2C | Advantage actor critic |
| AWGN | Additive white Gaussian noise |
| BS | Base station |
| C-ITS | Cooperative intelligent transport systems |
| C-V2X | Cellular vehicle-to-everything |
| DEM | Distributed expectation maximization |
| DNN | Deep neural network |
| DQN | Deep Q-network |
| DRL | Deep reinforcement learning |
| E2E | End-to-end |
| ES | Edge server |
| FAP | Fog access point |
| FD-SPS | Full duplex semi-persistent scheduling |
| FDRL | Federated deep reinforcement learning |
| FedAvg | Federated averaging |
| FedSGD | Federated stochastic gradient descent |
| FL | Federated learning |
| FL-DDPG | FL-based dual deterministic policy gradient |
| FRL | Federated reinforcement learning |
| GMM | Gaussian mixture model |
| HAP | High-altitude platform |
| i.i.d. | Independent-and-identically-distributed |
| IMU | Inertial measurement unit |
| LAP | Low-altitude platform |
| LiDAR | Light detection and ranging |
| LoS | Line of sight |
| MAB | Multi-armed bandit |
| MAC | Medium access control |
| MADRL | Multi-agent deep reinforcement learning |
| MEC | Mobile edge computing |
| ML | Machine learning |
| MSE | Mean square error |
| NOMA | Non-orthogonal multiple access |
| NLoS | Non line of sight |
| NR-V2X | New-radio vehicle-to-everything |
| OTFS | Orthogonal time frequency space |
| PCC | Partially collaborative caching |
| PDR | Packet delivery ratio |
| QoS | Quality of service |
| RL | Reinforcement learning |
| RSU | Road side unit |
| RTT | Round trip time |
| SAE | Society of Automotive Engineers |
| SINR | Signal-to-interference-plus-noise ratio |
| SB-SPS | Sensing-based semi persistent scheduling |
| TTI | Transmission time interval |
| UAV | Unmanned aerial vehicle |
| VEC | Vehicular edge computing |
References
- Shah, G.; Saifuddin, M.; Fallah, Y.P.; Gupta, S.D. RVE-CV2X: A Scalable Emulation Framework for Real-Time Evaluation of C-V2X based Connected Vehicle Applications. In Proceedings of the 2020 IEEE Vehicular Networking Conference (VNC), New York, NY, USA, 16–18 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–8. [Google Scholar]
- Amadeo, M.; Campolo, C.; Molinaro, A.; Harri, J.; Rothenberg, C.E.; Vinel, A. Enhancing the 3GPP V2X Architecture with Information-Centric Networking. Future Internet 2019, 11, 199. [Google Scholar] [CrossRef]
- Park, H.; Lim, Y. Deep Reinforcement Learning Based Resource Allocation with Radio Remote Head Grouping and Vehicle Clustering in 5G Vehicular Networks. Electronics 2021, 10, 3015. [Google Scholar] [CrossRef]
- Manias, D.M.; Shami, A. Making a Case for Federated Learning in the Internet of Vehicles and Intelligent Transportation Systems. IEEE Netw. 2021, 35, 88–94. [Google Scholar] [CrossRef]
- Zang, J.; Shikh-Bahaei, M. Full Duplex-Based Scheduling Protocol for Latency Enhancement in 5G C-V2X VANETs. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, 29 March–1 April 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Farokhi, F.; Wu, N.; Smith, D.; Kaafar, M.A. The Cost of Privacy in Asynchronous Differentially-Private Machine Learning. IEEE Trans. Inf. Forensics Secur. 2021, 16, 2118–2129. [Google Scholar] [CrossRef]
- Javed, M.A.; Zeadally, S. AI-Empowered Content Caching in Vehicular Edge Computing: Opportunities and Challenges. IEEE Netw. 2021, 35, 109–115. [Google Scholar] [CrossRef]
- Sabeeh, S.; Wesołowski, K.; Sroka, P. C-V2X Centralized Resource Allocation with Spectrum Re-Partitioning in Highway Scenario. Electronics 2022, 11, 279. [Google Scholar] [CrossRef]
- Li, X.; Cheng, L.; Sun, C.; Lam, K.Y.; Wang, X.; Li, F. Federated Learning Empowered Collaborative Data Sharing for Vehicular Edge Networks. IEEE Netw. 2021, 35, 116–124. [Google Scholar] [CrossRef]
- Nie, L.; Wang, X.; Sun, W.; Li, Y.; Li, S.; Zhang, P. Imitation-Learning-Enabled Vehicular Edge Computing: Toward Online Task Scheduling. IEEE Netw. 2021, 35, 102–108. [Google Scholar] [CrossRef]
- Gupta, A.; Fernando, X. Co-operative Edge Intelligence for C-V2X Communication using Federated Reinforcement Learning. In Proceedings of the 2023 IEEE 34th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Toronto, ON, Canada, 5–8 September 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Wei, W.; Gu, H.; Li, B. Congestion Control: A Renaissance with Machine Learning. IEEE Netw. 2021, 35, 262–269. [Google Scholar] [CrossRef]
- Li, J.; Ryzhov, I.O. Convergence Rates of Epsilon-Greedy Global Optimization Under Radial Basis Function Interpolation. Stoch. Syst. 2022, 13, 1–180. [Google Scholar] [CrossRef]
- Zhao, L.; Xu, H.; Wang, Z.; Chen, X.; Zhou, A. Joint Channel Estimation and Feedback for mm-Wave System Using Federated Learning. IEEE Commun. Lett. 2022, 26, 1819–1823. [Google Scholar] [CrossRef]
- Amiri, M.M.; Gunduz, D. Federated Learning Over Wireless Fading Channels. IEEE Trans. Wirel. Commun. 2020, 19, 3546–3557. [Google Scholar] [CrossRef]
- Sempere-García, D.; Sepulcre, M.; Gozalvez, J. LTE-V2X Mode 3 scheduling based on adaptive spatial reuse of radio resources. Ad Hoc Netw. 2021, 113, 102351. [Google Scholar] [CrossRef]
- Gupta, A.; Fernando, X. Analysis of Unmanned Aerial Vehicle-Assisted Cellular Vehicle-to-Everything Communication Using Markovian Game in a Federated Learning Environment. Drones 2024, 8, 238. [Google Scholar] [CrossRef]
- Qiao, D.; Liu, G.; Guo, S.; He, J. Adaptive Federated Learning for Non-Convex Optimization Problems in Edge Computing Environment. IEEE Trans. Netw. Sci. Eng. 2022, 9, 3478–3491. [Google Scholar] [CrossRef]
- Roshdi, M.; Bhadauria, S.; Hassan, K.; Fischer, G. Deep Reinforcement Learning based Congestion Control for V2X Communication. In Proceedings of the 2021 IEEE 32nd Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Helsinki, Finland, 13–16 September 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Kang, B.; Yang, J.; Paek, J.; Bahk, S. ATOMIC: Adaptive Transmission Power and Message Interval Control for C-V2X Mode 4. IEEE Access 2021, 9, 12309–12321. [Google Scholar] [CrossRef]
- Ali, Z.; Lagen, S.; Giupponi, L.; Rouil, R. 3GPP NR-V2X Mode 2: Overview, Models and System-Level Evaluation. IEEE Access 2021, 9, 89554–89579. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Yin, H.; Wei, R.; Zhang, L. Optimize Semi-Persistent Scheduling in NR-V2X: An Age-of-Information Perspective. In Proceedings of the 2022 IEEE Wireless Communications and Networking Conference (WCNC), Austin, TX, USA, 10–13 April 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 2053–2058. [Google Scholar]
- Dogahe, B.M.; Murthi, M.N.; Fan, X.; Premaratne, K. A distributed congestion and power control algorithm to achieve bounded average queuing delay in wireless networks. Telecommun. Syst. 2010, 44, 307–320. [Google Scholar] [CrossRef]
- Gemici, O.F.; Hokelek, I.; Crpan, H.A. Modeling Queuing Delay of 5G NR with NOMA Under SINR Outage Constraint. IEEE Trans. Veh. Technol. 2021, 70, 2389–2403. [Google Scholar] [CrossRef]
- Kumar, A.S.; Zhao, L.; Fernando, X. Multi-Agent Deep Reinforcement Learning-Empowered Channel Allocation in Vehicular Networks. IEEE Trans. Veh. Technol. 2022, 71, 1726–1736. [Google Scholar] [CrossRef]
- Kumar, A.S.; Zhao, L.; Fernando, X. Task Offloading and Resource Allocation in Vehicular Networks: A Lyapunov-based Deep Reinforcement Learning Approach. IEEE Trans. Veh. Technol. 2023, 72, 13360–13373. [Google Scholar] [CrossRef]
- Kumar, A.S.; Zhao, L.; Fernando, X. Mobility Aware Channel Allocation for 5G Vehicular Networks using Multi-Agent Reinforcement Learning. In Proceedings of the ICC 2021—IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Ibrahim, A.M.; Yau, K.L.A.; Chong, Y.W.; Wu, C. Applications of Multi-Agent Deep Reinforcement Learning: Models and Algorithms. Appl. Sci. 2021, 11, 10870. [Google Scholar] [CrossRef]
- Raff, E. Inside Deep Learning: Math, Algorithms, Models; Manning Publications: New York, NY, USA, 2022. [Google Scholar]
- Fan, B.; He, Z.; Wu, Y.; He, J.; Chen, Y.; Jiang, L. Deep Learning Empowered Traffic Offloading in Intelligent Software Defined Cellular V2X Networks. IEEE Trans. Veh. Technol. 2020, 69, 13328–13340. [Google Scholar] [CrossRef]
- Chen, M.; Poor, H.V.; Saad, W.; Cui, S. Convergence Time Optimization for Federated Learning Over Wireless Networks. IEEE Trans. Wirel. Commun. 2021, 20, 2457–2471. [Google Scholar] [CrossRef]
- Samarakoon, S.; Bennis, M.; Saad, W.; Debbah, M. Distributed Federated Learning for Ultra-Reliable Low-Latency Vehicular Communications. IEEE Trans. Commun. 2020, 68, 1146–1159. [Google Scholar] [CrossRef]
- Jayanetti, A.; Halgamuge, S.; Buyya, R. Deep reinforcement learning for energy and time optimized scheduling of precedence-constrained tasks in edge–cloud computing environments. Future Gener. Comput. Syst. 2022, 137, 14–30. [Google Scholar] [CrossRef]
- Gyawali, S.; Qian, Y.; Hu, R. Deep Reinforcement Learning Based Dynamic Reputation Policy in 5G Based Vehicular Communication Networks. IEEE Trans. Veh. Technol. 2021, 70, 6136–6146. [Google Scholar] [CrossRef]
- Sial, M.N.; Deng, Y.; Ahmed, J.; Nallanathan, A.; Dohler, M. Stochastic Geometry Modeling of Cellular V2X Communication Over Shared Channels. IEEE Trans. Veh. Technol. 2019, 68, 11873–11887. [Google Scholar] [CrossRef]
- Li, Y. Model Training Method and Device Based on FedMGDA + and Federated Learning. CN202211060911.4, 31 August 2022. [Google Scholar]
- Zhan, Y.; Li, P.; Guo, S.; Qu, Z. Incentive Mechanism Design for Federated Learning: Challenges and Opportunities. IEEE Netw. 2021, 35, 310–317. [Google Scholar] [CrossRef]
- Liu, S.; Yu, J.; Deng, X.; Wan, S. FedCPF: An Efficient Communication Federated Learning Approach for Vehicular Edge Computing in 6G Communication Networks. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1616–1629. [Google Scholar] [CrossRef]
- Xu, C.; Liu, S.; Yang, Z.; Huang, Y.; Wong, K.K. Learning Rate Optimization for Federated Learning Exploiting Over-the-Air Computation. IEEE J. Sel. Areas Commun. 2021, 39, 3742–3756. [Google Scholar] [CrossRef]
- He, J.; Yang, K.; Chen, H.H. 6G Cellular Networks and Connected Autonomous Vehicles. IEEE Netw. 2021, 35, 255–261. [Google Scholar] [CrossRef]
- Xia, Q.; Ye, W.; Tao, Z.; Wu, J.; Li, Q. A survey of federated learning for edge computing: Research problems and solutions. High-Confid. Comput. 2021, 1, 100008. [Google Scholar] [CrossRef]
- Abreha, H.G.; Hayajneh, M.; Serhani, M.A. Federated Learning in Edge Computing: A Systematic Survey. Sensors 2022, 22, 450. [Google Scholar] [CrossRef] [PubMed]
- Brecko, A.; Kajati, E.; Koziorek, J.; Zolotova, I. Federated Learning for Edge Computing: A Survey. Appl. Sci. 2022, 12, 9124. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhai, R.; Wang, Y.; Wang, X. Survey on challenges of federated learning in edge computing scenarios. In Proceedings of the International Conference on Internet of Things and Machine Learning (IOTML 2021), Shanghai, China, 17–19 December 2021; SPIE: Bellingham, WA, USA, 2022; Volume 12174, p. 121740C. [Google Scholar]
- Moon, S.; Lim, Y. Federated Deep Reinforcement Learning Based Task Offloading with Power Control in Vehicular Edge Computing. Sensors 2022, 22, 9595. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.T.; Sehwag, V.; Hosseinalipour, S.; Brinton, C.G.; Chiang, M.; Vincent Poor, H. Fast-Convergent Federated Learning. IEEE J. Sel. Areas Commun. 2021, 39, 201–218. [Google Scholar] [CrossRef]
- Ma, Z.; Chen, X.; Ma, T.; Chen, Y. Deep Deterministic Policy Gradient Based Resource Allocation in Internet of Vehicles. In Parallel Architectures, Algorithmsand Programming, Proceedings of the 11th International Symposium, PAAP 2020, Shenzhen, China, 28–30 December 2020; Springer: Singapore, 2021; pp. 295–306. [Google Scholar]
- Zhu, Q.; Liu, R.; Wang, Z.; Liu, Q.; Chen, C. Sensing-Communication Co-Design for UAV Swarm-Assisted Vehicular Network in Perspective of Doppler. IEEE Trans. Veh. Technol. 2023, 73, 2578–2592. [Google Scholar] [CrossRef]
- Qu, G.; Xie, A.; Liu, S.; Zhou, J.; Sheng, Z. Reliable Data Transmission Scheduling for UAV-Assisted Air-to-Ground Communications. IEEE Trans. Veh. Technol. 2023, 72, 13787–13792. [Google Scholar] [CrossRef]
- Li, Y.; Ma, D.; An, Z.; Wang, Z.; Zhong, Y.; Chen, S.; Feng, C. V2X-Sim: Multi-Agent Collaborative Perception Dataset and Benchmark for Autonomous Driving. IEEE Robot. Autom. Lett. 2022, 7, 10914–10921. [Google Scholar] [CrossRef]
- Sun, G.; Boateng, G.O.; Ayepah-Mensah, D.; Liu, G.; Wei, J. Autonomous Resource Slicing for Virtualized Vehicular Networks With D2D Communications Based on Deep Reinforcement Learning. IEEE Syst. J. 2020, 14, 4694–4705. [Google Scholar] [CrossRef]
- Morales, E.F.; Murrieta-Cid, R.; Becerra, I.; Esquivel-Basaldua, M.A. A survey on deep learning and deep reinforcement learning in robotics with a tutorial on deep reinforcement learning. Intell. Serv. Robot. 2021, 14, 773–805. [Google Scholar] [CrossRef]
- Ali, R.; Zikria, Y.B.; Garg, S.; Bashir, A.K.; Obaidat, M.S.; Kim, H.S. A Federated Reinforcement Learning Framework for Incumbent Technologies in Beyond 5G Networks. IEEE Netw. 2021, 35, 152–159. [Google Scholar] [CrossRef]
- Arani, A.H.; Hu, P.; Zhu, Y. Re-envisioning Space-Air-Ground Integrated Networks: Reinforcement Learning for Link Optimization. In Proceedings of the ICC 2021—IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–7. [Google Scholar]



| Symbol | Definition |
|---|---|
| Local update of ith agent’s Q values | |
| Reward of ith agent | |
| Delay at kth communication round | |
| Likelihood of a state-action-reward tuple leading to vector | |
| Q-value of state-action pair | |
| Q-value vector of K vehicles | |
| FRL objective function | |
| Number of model hyper-parameters implying an upper bound on Q-functions | |
| kth agent’s hyperparameter weights | |
| Optimal action-value or Q-value | |
| Optimal Q-value for agent’s policy | |
| Agent’s optimal policy | |
| Set of policies | |
| Discount factor for future rewards | |
| Discounted reward function | |
| =s | Agent’s state at given time t |
| =a | Action taken by agent at time t |
| Learning rate | |
| Packet arrival rate | |
| Packet service rate | |
| Utilization of processing | |
| Set of Gaussian distributed random variables for | |
| A random variable representing an arbitrary sequence of packets | |
| Time window when a packet is transmitted or queued | |
| Transmission window duration in seconds | |
| kth vehicle’s initial model parameter weights |
| Parameter | Value |
|---|---|
| Vehicle mobility model | Manhattan mobility |
| Number of vehicles (V) | 1–100 |
| Number of UAVs | 1 |
| UAV deployment altitude | 100 m–2 km |
| Edge server location | In-vehicle |
| Distance between vehicles | 10–100 m |
| Communication frequency | 5.9 GHz |
| Modulation technique | 16-QAM |
| Optimizer | Adam and SGD |
| Road length | 1–5 km |
| Payload size of FL models | 1 byte–10 Megabytes |
| 1000–2000 packets/s | |
| 500–2500 packets/s | |
| Tunable parameters | , , , , , |
| Neural network | DQN, duellingDQN |
| Dataset used | V2X-Sim |
| UAV transmission power | 20 dBm (100 mW) |
| UAV receiving threshold | −80 dBm |
| Vehicle transmission power | 25 dBm (316.2 mW) |
| Speed of vehicles | 50–80 km/h |
| Speed of UAV | 25–40 km/h |
| No. of Agents | Algorithm Used | Accumulated Q-Values | Training Episodes |
|---|---|---|---|
| V = 1 | DQN | 156.78 | 250 |
| V = 2 | duellingDQN | 150 | 340 |
| V = 5 | duellingDQN | 150 | 340 |
| V = 10 | DQN | 180 | 220 |
| V = 20 | duellingDQN | 200 | 500 |
| UAV | DQN | 214.71 | 200 |
| UAV | duellingDQN | 522.71 | 200 |
| Local updates | DQN | 400 | 150 |
| Global updates | duellingDQN | 500 | 150 |
| References | Proposed Method | Objectives | Cost Function | Reported Results |
|---|---|---|---|---|
| [19] |
|
|
|
|
| [25,26] |
|
|
|
|
| [31] |
|
|
|
|
| [32] |
|
|
|
|
| [33] |
|
|
|
|
| [34,35] |
|
|
|
|
| [54] |
|
|
|
|
| Our Work |
|
|
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, A.; Fernando, X. Federated Reinforcement Learning for Collaborative Intelligence in UAV-Assisted C-V2X Communications. Drones 2024, 8, 321. https://doi.org/10.3390/drones8070321
Gupta A, Fernando X. Federated Reinforcement Learning for Collaborative Intelligence in UAV-Assisted C-V2X Communications. Drones. 2024; 8(7):321. https://doi.org/10.3390/drones8070321
Chicago/Turabian StyleGupta, Abhishek, and Xavier Fernando. 2024. "Federated Reinforcement Learning for Collaborative Intelligence in UAV-Assisted C-V2X Communications" Drones 8, no. 7: 321. https://doi.org/10.3390/drones8070321
APA StyleGupta, A., & Fernando, X. (2024). Federated Reinforcement Learning for Collaborative Intelligence in UAV-Assisted C-V2X Communications. Drones, 8(7), 321. https://doi.org/10.3390/drones8070321







