Abstract
This paper provides an in-depth analysis of the current research landscape in the field of UAV (Unmanned Aerial Vehicle) swarm formation control. This review examines both conventional control methods, including leader–follower, virtual structure, behavior-based, consensus-based, and artificial potential field, and advanced AI-based (Artificial Intelligence) methods, such as artificial neural networks and deep reinforcement learning. It highlights the distinct advantages and limitations of each approach, showcasing how conventional methods offer reliability and simplicity, while AI-based strategies provide adaptability and sophisticated optimization capabilities. This review underscores the critical need for innovative solutions and interdisciplinary approaches combining conventional and AI methods to overcome existing challenges and fully exploit the potential of UAV swarms in various applications.
1. Introduction
Drones, also known as unmanned aerial vehicles (UAVs), have found their way into wide-ranging applications across various fields, showcasing their flexibility and effectiveness, such as military affairs [1], agriculture [2], search and rescue operations [3], environmental monitoring [4], and delivery services [5]. However, operating a single UAV has several limitations, such as limited area coverage, reduced reliability, and scalability challenges. The UAV swarm brings some advantages over operating single or isolated UAVs, particularly in terms of efficiency, resilience, scalability, and cost [6,7].
UAV or aerial swarm has become an area of intense research within the robotics and control community [8]. This field draws inspiration from natural swarm behaviors observed in birds, fish, and insects [9], applying these principles to enhance the capabilities of UAV swarms through technology. The main objective is to enable these swarms to autonomously navigate, adapt to dynamic environments, and complete complex missions with higher efficiency and resilience than single UAVs. As a kind of swarm operation, flying formation (e.g., line-formation, V-formation, diamond-formation, grid-formation) can offer numerous advantages for tasks requiring coordinated effort, efficiency, and precision. UAV formation control refers to the coordinated management and guidance of UAVs flying in a precise geometric arrangement or pattern. The formation control ensures that each UAV maintains its position relative to the others in the formation, adapting to changes in speed, direction, and external conditions.
The formation control problem has been well studied in the context of UAV swarms, as well as multi-agent systems (MAS), in which UAVs are viewed as agents. Do et al. [10] conducted a comprehensive survey on formation control algorithms for UAVs from the perspectives of leader–follower methods, virtual structure methods, behavior-based methods, artificial potential field (APF) methods, consensus methods, and intelligent methods. Moreover, Ouyang et al. [11] compared the existing formation control strategies of the UAV swarm and highlighted that decentralization and intelligence are the future development trends. Based on the sensing capability and the interaction topology of agents, Oh et al. [12] categorized formation control methods into position-, displacement-, and distance-based control. Differently, Liu et al. [13] discussed four types of distributed formation control methods based on position and displacement in the global coordinate system, as well as distance and bearing in the non-global coordinate system. For the way information flows between agents, Chen et al. [14] divided the available methods into communication-based control as well as vision-based control. The literature [10,11,12,13,14] shows significant advancements in UAV swarm formation control in the past few decades. Despite these progresses, UAV swarm formation control still faces significant challenges, particularly in terms of scalability, robustness, and environmental adaptability [15].
Recently, there have been notable advancements in artificial intelligence (AI) algorithms, such as artificial neural network (ANN) [16] and deep reinforcement learning (DRL) [17]. Unlike conventional approaches (e.g., leader–follower and virtual structure), which are based on specific prior models, modern AI algorithms represent a data-driven paradigm and offer a more general approach to the formation control problems. Applying these AI algorithms in UAV swarm formation control has the potential to bring several substantial advantages, such as autonomous decision-making, efficient coordination, and robustness to failures, which enhance their effectiveness, flexibility, and scalability. Nevertheless, the application of these AI algorithms also brings some challenges, including computational complexity and the need for extensive training data.
By examining the current literature and recent studies, this review offers insights into the state of the art in UAV swarm formation control methods. Unlike existing work [10,11,12,13,14], current strategies are classified into model-based conventional strategy and model-free data-driven AI strategy. Conventional methods such as leader–follower methods, virtual structure methods, behavior-based methods, consensus-based methods, and APF methods are reviewed and discussed. Furthermore, AI methods such as ANN-based methods and DRL-based methods are investigated. This work aims to reveal technological breakthroughs and pave the way for future directions to overcome existing limitations. The rest of this article is organized as follows. Section 2 discusses the definition of formation control problems in the context of UAV swarm. Section 3 analyzes three formation control schemes: centralized, decentralized, and distributed. The research literature on conventional strategy and AI strategy are summarized in Section 4 and Section 5, respectively. The discussion about challenges and future directions is conducted in Section 6. The conclusion is drawn in Section 7.
2. Formation Control Problem
The UAV swarm formation control problem involves the development and implementation of strategies, algorithms, and systems designed to manage and coordinate the movement and behavior of a group of UAVs flying in a specified formation. This involves ensuring that each UAV maintains its relative position, speed, and orientation within the group, despite external influences such as wind or obstacles, and internal factors like UAV failures or communication disruptions. The key sub-problems include formation representation, trajectory tracking, formation generation, formation keeping or maintenance, formation switching, collision and obstacle avoidance, and formation dissolution.
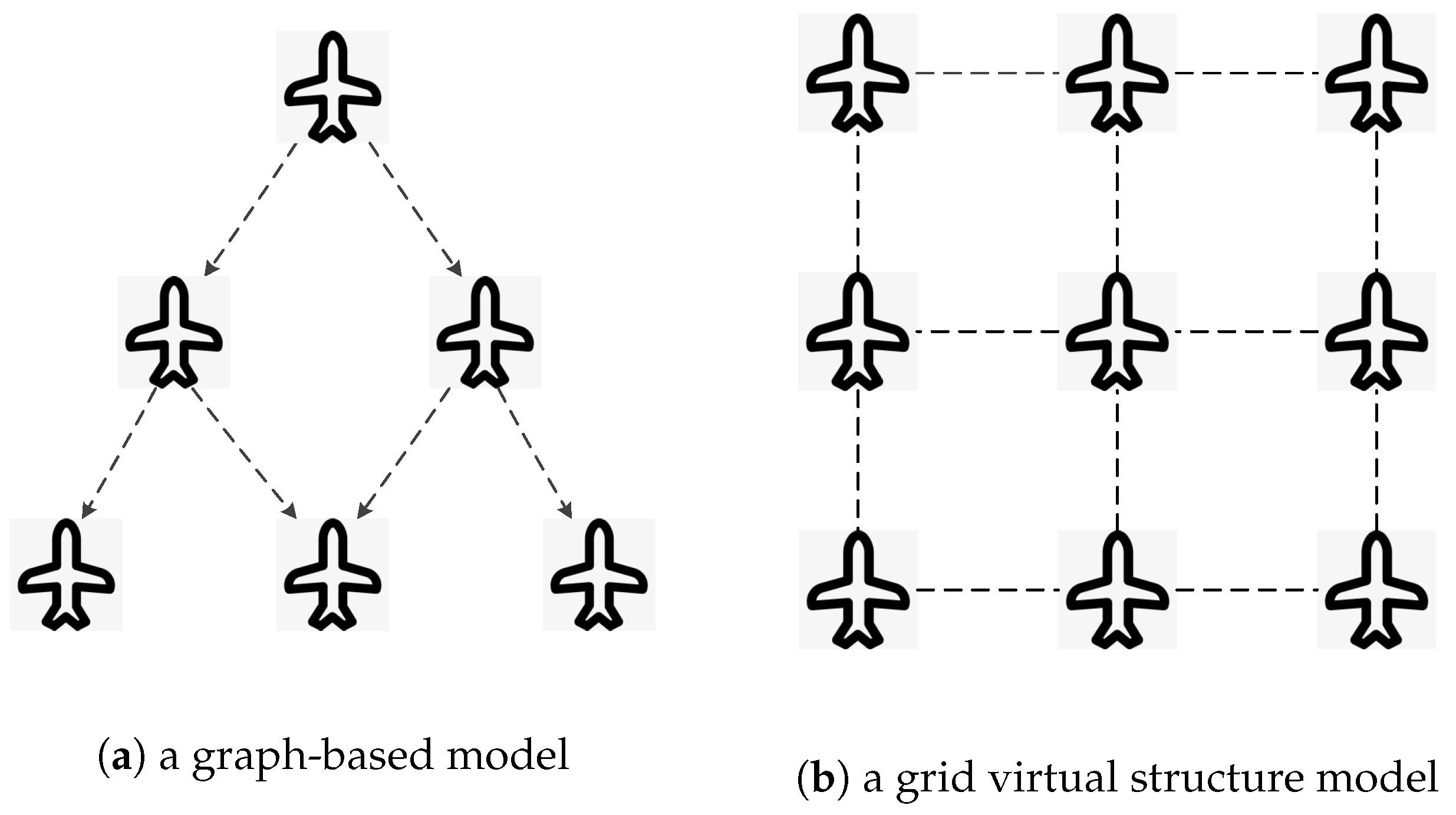
Formation representation is the method used to define the spatial arrangement of UAVs in a swarm. There are various models for formation representation, such as graph-based models [18] and virtual structure models [19]. In graph-based models, UAVs are vertices connected by edges representing communication or control links. In virtual leader or virtual structure models, virtual leaders or reference points in the virtual structure are employed to guide the formation. UAVs maintain their positions relative to these virtual entities. Figure 1 shows a graph-based model and a virtual structure model, respectively. In the graph-based model, UAVs are viewed as vertexes and control links are viewed as edges in the graph as shown in Figure 1a. In the grid virtual structure model, UAVs are viewed as vertexes of the grid structure as shown in Figure 1b. The choice of formation representation directly influences the swarm’s efficiency and stability. Several typical formations include line-formation, column-formation, V-formation, diamond-formation, grid-formation, and echelon-formation.
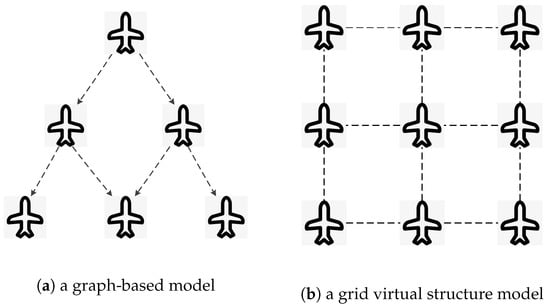
Figure 1.
Examples of UAV (Unmanned Aerial Vehicle) swarm formation representation: (a) a graph-based model with UAVs as vertexes and control links as edges; (b) a grid virtual structure model with UAVs as vertexes of the grid.
Trajectory tracking is the capability of UAV swarms to follow a predefined or dynamically generated path while maintaining formation. Formation generation refers to the process through which UAVs in a swarm form a predefined pattern. Formation keeping or maintenance is a critical aspect of UAV swarm operations, focusing on maintaining the predefined spatial arrangement of UAVs within a formation as they fly to the destination. Formation switching refers to the process through which a UAV swarm transitions from one geometric configuration to another while maintaining coherence and minimizing disruptions to the ongoing mission. Collision and obstacle avoidance is a critical area of research that focuses on ensuring that UAVs within a swarm do not collide with obstacles or collide with each other while maintaining a desired formation. Formation dissolution refers to the process of disbanding a structured formation into a more dispersed arrangement or completely individual behaviors. The strategies for maintaining formation integrity (e.g., formation keeping, formation switching, collision and obstacle avoidance) must be aligned with trajectory tracking efforts to ensure that the entire swarm moves in the right direction and adapts seamlessly to changes in the trajectory.
In summary, in the context of UAV swarm formation control, formation representation is the foundation; trajectory tracking, formation generation, and formation dissolution are for dynamic operations; formation keeping and switching are for adaptability; and collision and obstacle avoidance are for safety and continuity [20,21]. Each aspect’s effectiveness relies on the support and proper functioning of the others. Together, they enable UAV swarms flying in formation to perform complex tasks with high efficiency, adaptability, and safety. Different research focuses on different aspects of the formation control problem of the UAV swarm. Jaydev et al. [18,22] discussed formation representation, keeping and switching, as well as obstacle avoidance. In contrast, Tan et al. [19,23] mainly focused on formation keeping. In addition, Matthew et al. [24] proposed methods for trajectory tracking and formation keeping.
3. Formation Control Scheme
The control scheme of UAV swarm formation can be divided into the centralized scheme, decentralized scheme, and distributed scheme.
3.1. Centralized
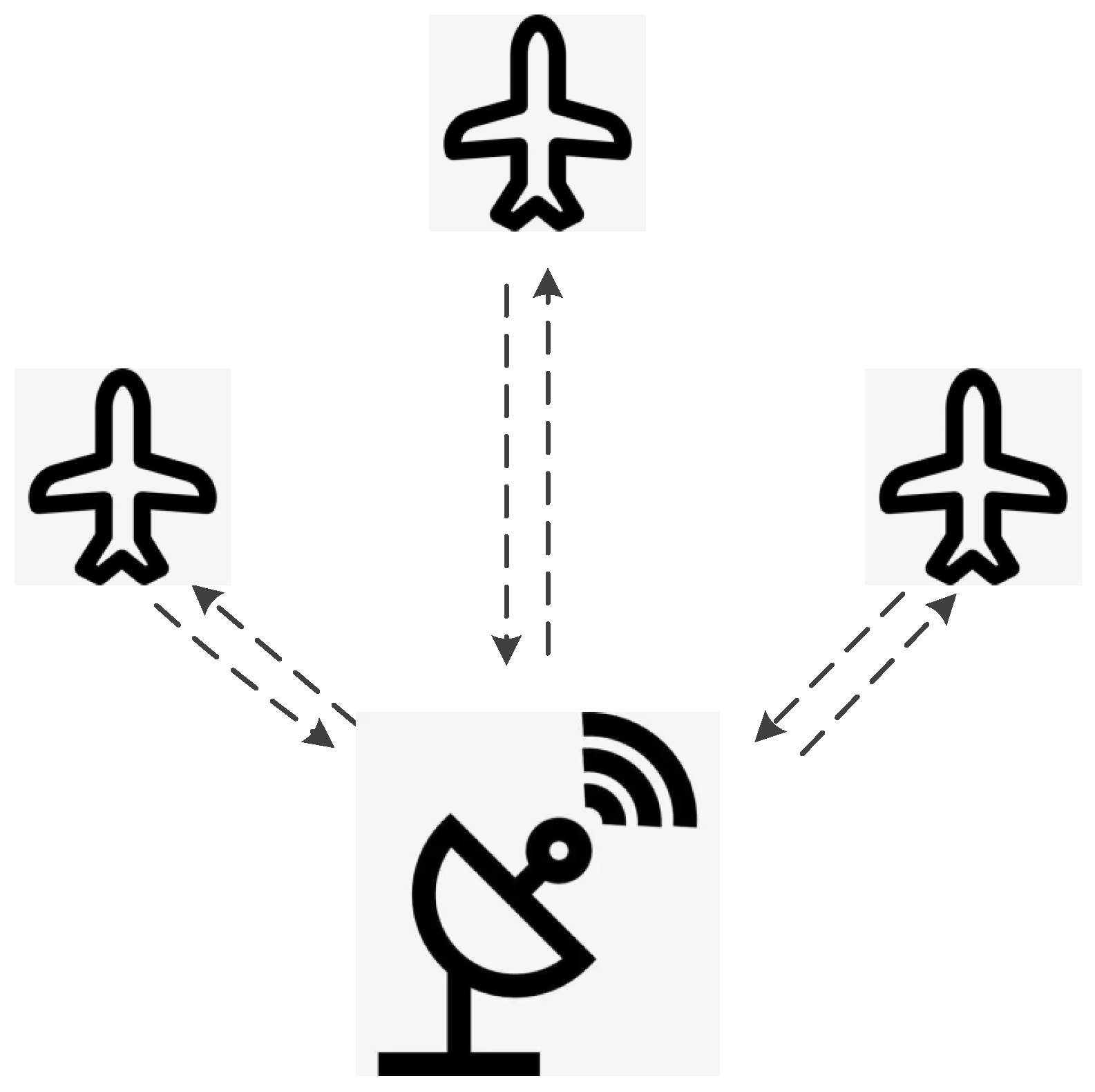
The centralized control scheme for UAV swarms involves a single control point (e.g., a ground control station) that processes all relevant information, makes decisions, and issues commands to individual UAVs. Figure 2 shows an example of a centralized control scheme of a UAV swarm with a centralized ground control station. Advantages of centralized control include simplicity in decision-making, consistency in actions, and ease of implementation. Despite its advantages, the centralized control scheme faces several challenges, such as scalability issues, single point of failure, and communication overheads. The control of leaders in leader–follower methods [18,22] and the control of virtual structure [19,23] in virtual structure methods can use the centralized control scheme.
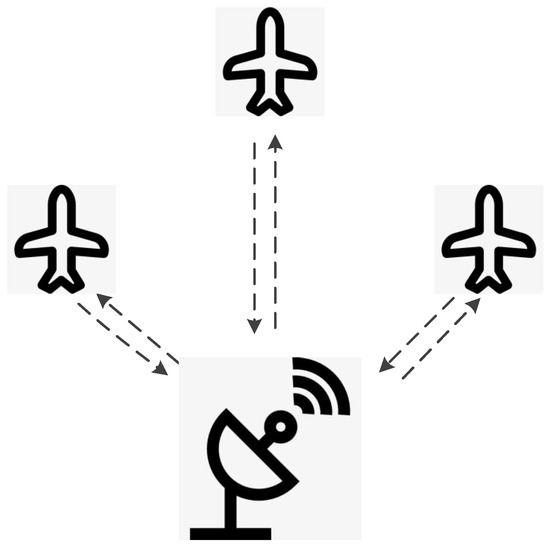
Figure 2.
An example of a centralized control scheme is a UAV swarm with a centralized ground control station.
3.2. Decentralized
The decentralized control scheme allows UAV swarms to manage themselves through distributed decision-making processes. Each UAV in the swarm acts based on information and predefined rules, coordinating with its immediate neighbors by communication-based, sensor-based, or vision-based methods to maintain formation. Figure 3 illustrates an example of a decentralized control scheme, in which a UAV swarm flies in formation based on its sensors without explicit communication. Advantages of decentralized control include scalability, flexibility, and adaptability. Despite its advantages, decentralized control presents several challenges, including coordination, design, and testing complexity. Behavior-based formation control methods [25] and APF methods [26] often use the decentralized control scheme.

Figure 3.
An example of a decentralized control scheme is a UAV swarm flying in formation based on its sensors without explicit communication.
3.3. Distributed
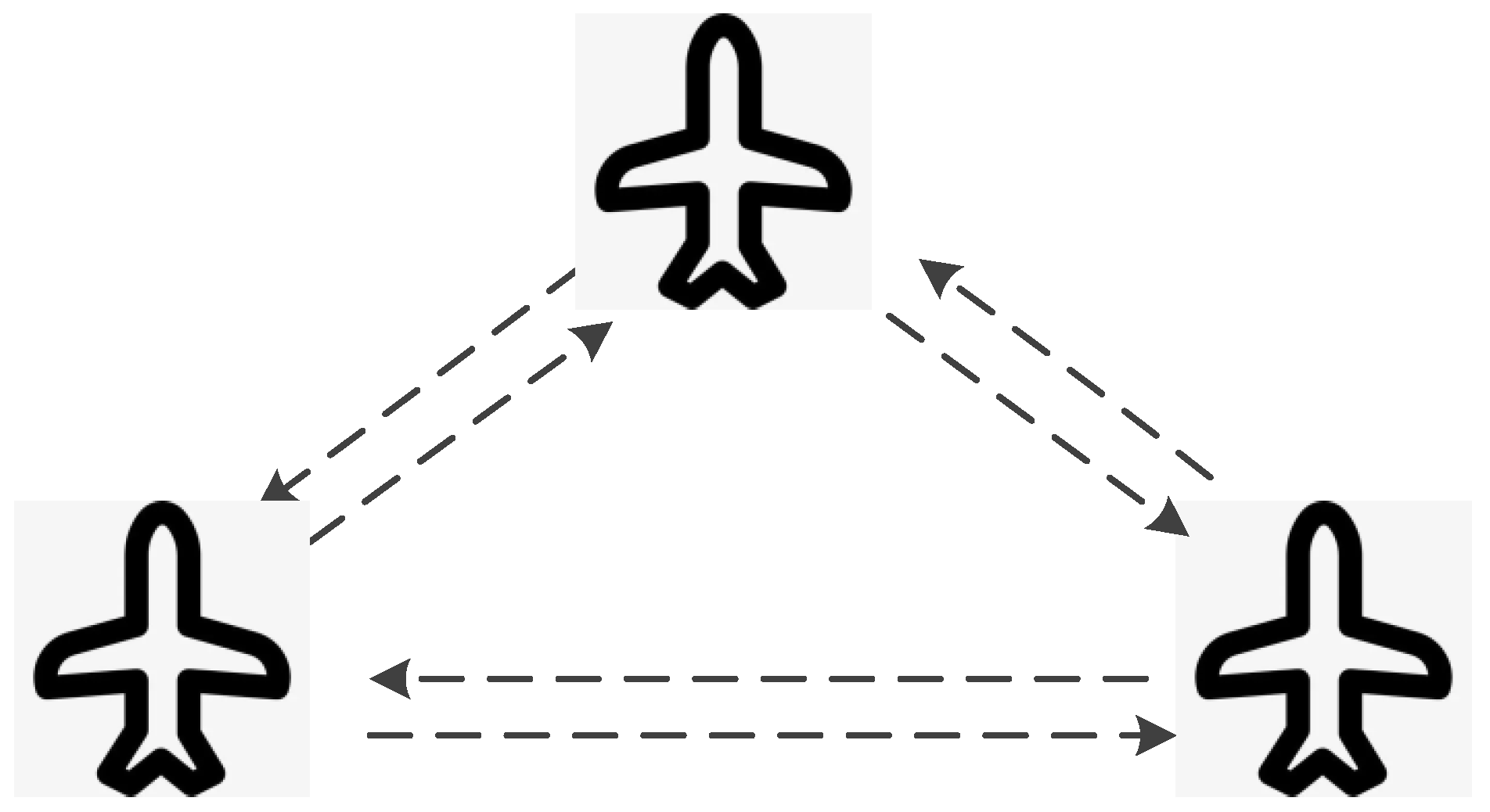
In a distributed control scheme, control actions and decision-making processes are spread across all UAVs in the swarm. Each UAV possesses a degree of autonomy but also collaborates closely with others, sharing information and making decisions that benefit the collective objective. The distributed control scheme is different from the decentralized scheme. In decentralized control, each UAV operates based on its local perception and predefined rules without necessarily collaborating with others. In contrast, distributed control involves a more collaborative approach, with UAVs working together to make decisions that reflect the collective interest. Decentralized control minimizes reliance on communication, focusing on local information. Distributed control, however, leverages extensive communication among UAVs to share information and make decisions based on a broader understanding of the environment and the mission. Distributed control typically requires more sophisticated communication infrastructure and computational resources than decentralized control, due to the need for continuous data exchange and collective processing. Figure 4 shows an example of a distributed control scheme, in which a UAV swarm is flying in formation by communicating with each other. The distributed control framework offers a more collaborative approach to UAV swarm management compared to decentralized control, emphasizing teamwork and shared decision-making. This approach is particularly advantageous in scenarios where the mission’s success depends on the collective use of detailed, shared information and where redundancy and resilience are paramount. Consensus-based formation control methods [27] often belong to the distributed control scheme.
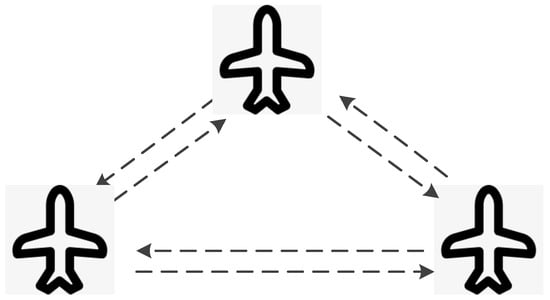
Figure 4.
An example of a distributed control scheme is a UAV swarm flying in formation by communicating with each other.
4. Conventional Strategy
Formation control methods of conventional strategy are often based on specific models. According to fundamental ideas of modeling, these methods can be broadly categorized into leader–follower methods, virtual structure methods, behavior-based methods, consensus-based methods, and APF methods.
4.1. Leader–Follower
The leader–follower method for formation control is a hierarchical approach used in UAV swarm operations, where one or several UAVs are designated as leaders, and the others follow these leaders based on predefined rules. The leaders navigate according to the mission’s objectives, while the followers maintain specific relative positions or distances from the leaders or other followers. This method simplifies the control logic by breaking down the formation task into manageable sub-tasks, where each follower only needs to focus on its immediate leaders, reducing the complexity of coordination. The leader–follower method is currently the most widely used and fundamental in UAV swarm formation control.
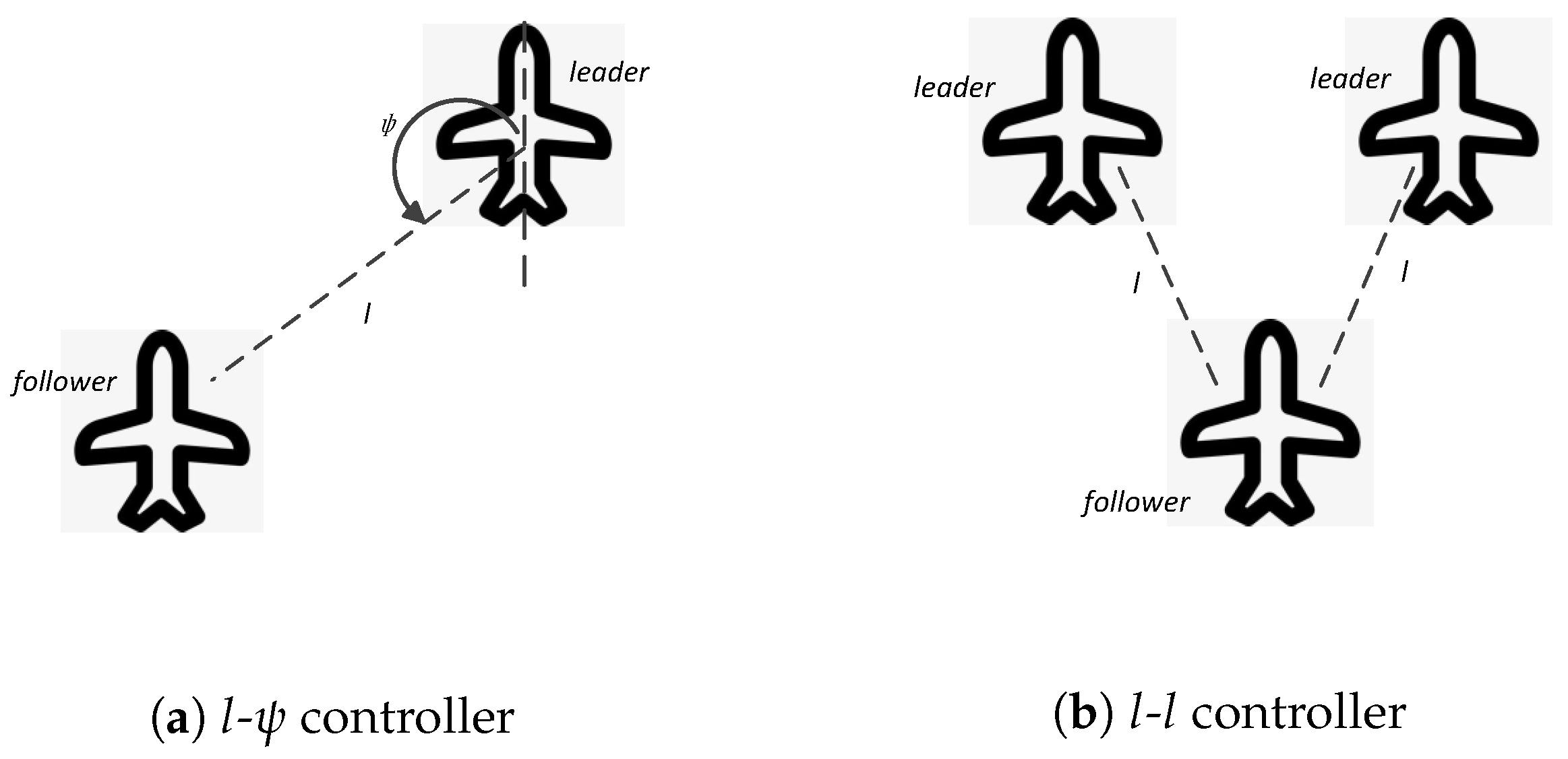
In the leader–follower method, the UAV swarm formation can be represented by graph-based models [18] as shown in Figure 1a. The leader–follower structure is naturally modeled by directed graphs, in which UAVs are viewed as vertexes and leader–follower relationships are represented by edges. If there is a directed edge from node to node , then is the leader of . The formation control in the leader–follower method can be divided into swarm leaders’ control and other followers’ control. The majority of work in the literature is based on the assumption of a single swarm leader. The swarm leader is controlled autonomously or controlled by some other external source such as a human operator with a predefined or dynamically generated path; the others are controlled by follower’s controllers with a cascade-type structure. Jaydev et al. [18] proposed two feedback controllers for followers: controller and controller. The control objective in the controller is to retain the length l and the relative angle at the desired values relative to one leader as shown in Figure 5a, while the control objective in the controller is to retain the length l relative to two leaders at the desired values as shown in Figure 5b. The controller and controller are mainly used for formation keeping, while the controller is also discussed for keeping relative distance to obstacles [18]. Formation switching can be achieved by the transition of graphs representing UAV swarms [22].
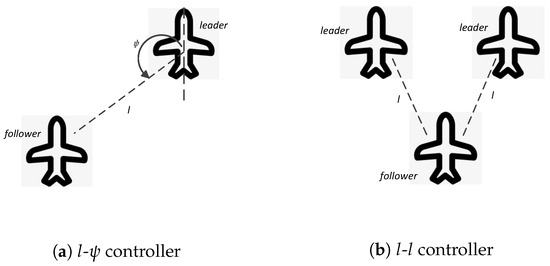
Figure 5.
Two examples of controllers for followers: (a) controller aiming to retain the length l and the relative angle at the desired values relative to one leader; (b) controller aiming to retain the length l relative to two leaders at the desired values.
Most research on the leader–follower method focuses on the design and evaluation of follower controllers for formation keeping, collision avoidance, and obstacle avoidance. Some of the literature discusses the design of follower controllers based on different ideas, such as feedback linearization [18], backstepping techniques [28,29,30], sliding mode control [31,32], model predictive control [24], control [33], hybrid methods [34], the cascade-type guidance method [35], and so on. Some other research focuses on the implementation and testing of follower control laws with actual drones [36,37,38].
Some research discusses formation control under different leadership structures, such as multiple leaders [39], implicit or virtual leaders [40,41], and leaders for groups [42]. Some others discuss complex scenarios and constraints, such as time-varying formation [43,44], GPS-denied environments [45,46], uncertainties dynamics and external disturbances [47], and communication constraints [48].
The leader–follower method demonstrates high flexibility and is suitable for various complex scenarios. In practical applications, it is necessary to consider the impact of communication delays, data loss, and other practical issues on formation control, and design corresponding robust control strategies. This approach relies on the stability and reliability of the leader, and if the leader experiences a communication interruption, the entire formation may be affected. In a multi-leader structure, coordinating the behavior of different leaders is challenging. When dealing with complex scenarios and constraints, existing control strategies may not meet all requirements and require further research and improvement.
4.2. Virtual Structure
The virtual structure method for formation control in UAV swarms organizes the swarm as if it is a virtual structure, with each UAV assigned a specific position within this structure. This method involves creating a geometric pattern or formation, in which the UAVs collectively move as a unified entity. Each UAV maintains its relative position within the virtual structure as the swarm navigates through the environment, effectively translating, rotating, or scaling the entire formation as needed to adapt to mission objectives or to navigate around obstacles. This approach allows for precise control over the formation’s shape and offers a straightforward mechanism for altering formations in response to dynamic conditions.
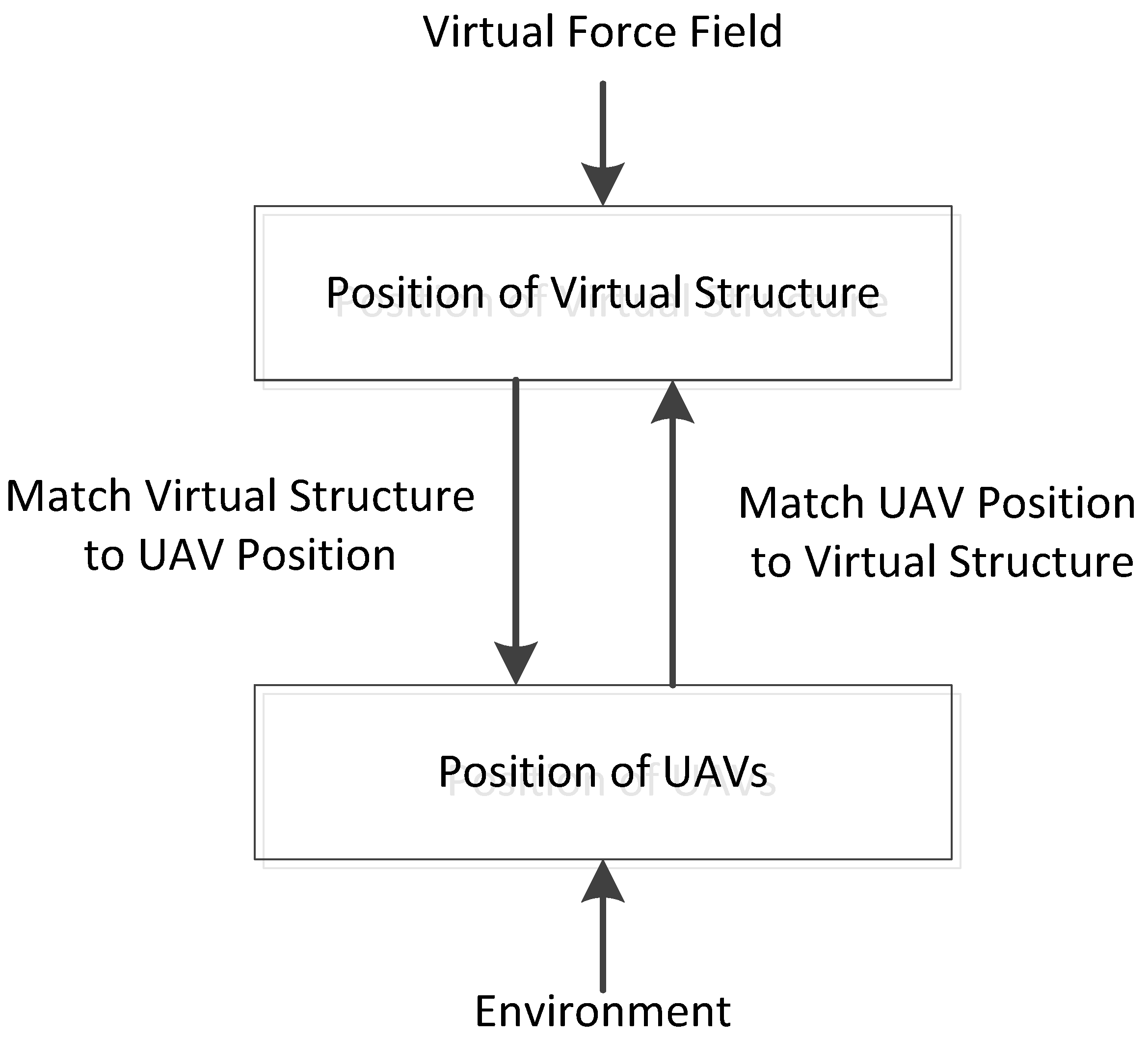
In this method, the UAV swarm formation can be represented by virtual structures, which maintain a rigid geometric relationship to each other [19]. The UAV swarm formation control in the virtual structure method can be divided into the control of the virtual structure and the control of UAVs. The control of the virtual structure focuses on the movement of the entire formation, while the control of UAVs focuses on how each UAV maintains its position within the virtual structure. This decomposition makes the control strategy more modular, making it easier to design and implement. Controlling the trajectory of a formation by controlling the virtual forces acting on the virtual structure is an intuitive and effective method. This method allows for smooth and continuous control of the formation’s motion while considering the interaction and constraints between UAVs. The virtual structure method provides a simple and effective mechanism for generating, maintaining, and changing formations. By adjusting the position and shape of the virtual structure, it is easy to achieve translation, rotation, and scaling of the formation. In addition, by attempting to match UAVs with virtual structures and bypass obstacles, collision and obstacle avoidance can be achieved.
Tan et al. [19,23] proposed a bidirectional flow of formation control for virtual structure methods. Figure 6 illustrates the basic idea: the virtual structure’s position is controlled by the positions of the UAVs, while the positions of the UAVs are controlled by the position of the virtual structure. The trajectory control of the formation is achieved by controlling the virtual forces acting on the virtual structure. Formation generation, formation keeping, and obstacle avoidance are achieved by trying to match UAVs with the virtual structure and bypassing obstacles, and formation switching can be achieved by altering the virtual structure.
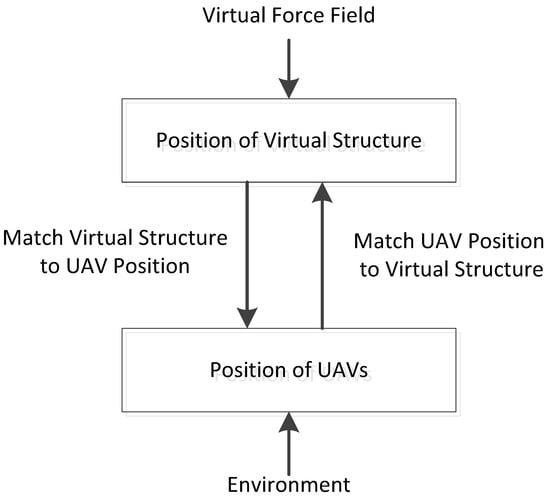
Figure 6.
A bidirectional flow of formation control for virtual structure methods.
To enhance the stability, robustness, and responsiveness of formation maintenance in the virtual structure methods, some techniques are proposed, such as feedback mechanism [49,50], motion synchronization [51], the Lyapunov technique [52], nonlinear guidance logic [53], and dynamic adjustments methods [54]. Some other research focuses on solving collision and obstacle avoidance problems during formation flying and formation change, e.g., deconfliction techniques [55], and multiple layered potential field methods [56]. Ren et al. [57] discussed decentralized schemes for virtual structure methods. Recently, Jiandong et al. [58] introduced an approach for controlling UAV formations without the need for constant real-time data communication between the UAVs. In summary, many innovative control strategies have emerged in virtual structure methods. These strategies not only improve the stability and flexibility of the formation but also enhance the coordination and cooperation between UAVs.
Although virtual structure methods have many advantages, they also have some limitations. For example, when there are a large number of UAVs, maintaining the stability and accuracy of virtual structures may become difficult. In addition, if the virtual structure is severely disturbed or damaged, the entire formation may lose control. Future research can further explore how to combine virtual structure methods with advanced perception, decision-making, and communication technologies to improve the autonomy, adaptability, and robustness of UAV formations. Meanwhile, it is also possible to study how to apply virtual structure methods to more complex task scenarios and a wider range of UAV types.
4.3. Behavior-Based
The behavior-based formation control in UAV swarms relies on defining simple, local interaction rules for individual UAVs, which collectively lead to the emergence of complex global behaviors, such as formation generation and keeping. Each UAV makes decisions based on its local perception of the environment and the state of its neighboring UAVs, following basic behavioral rules like cohesion (staying close to neighbors), separation (avoiding collisions), and alignment (moving in the same direction as neighbors). This decentralized approach is inspired by natural systems, such as flocks of birds or schools of fish [9], and does not require a central controller or complex communication protocols. The behavior-based method is scalable and adaptable, making it effective for operating in dynamic environments and responding to changes or disturbances within the swarm.
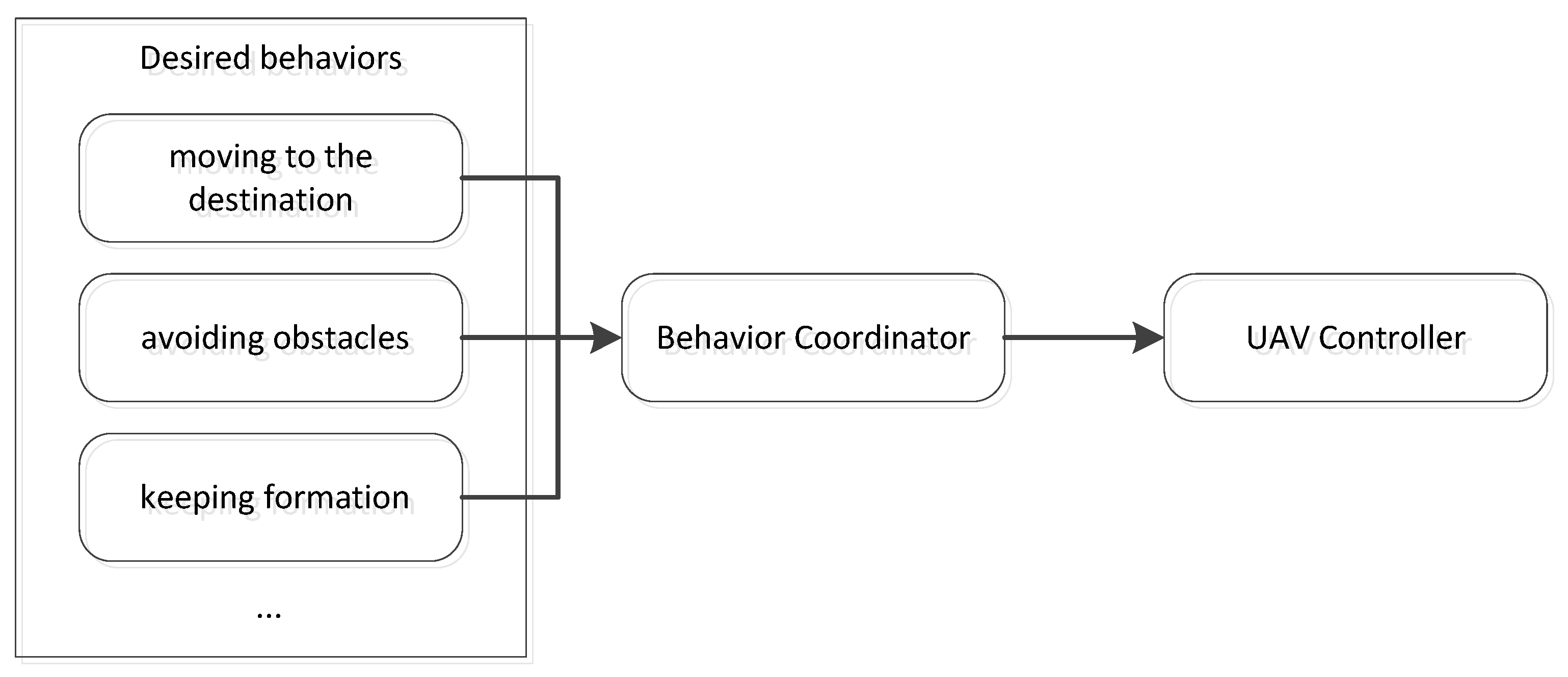
The formation can be represented by the UAV’s relative position to others in behavior-based methods. In the behavior-based control method, the basic idea is that the control action for each UAV is defined by a weighted average of the control corresponding to each desired behavior for the UAV. As shown in Figure 7, desired behaviors (e.g., moving to the destination, avoiding obstacles, keeping formation) are coordinated as input for the UAV controller. Specifically speaking, multiple objectives including trajectory tracking, formation generation, formation keeping, and obstacle avoidance are used to generate the control corresponding to each desired behavior, and a behavior coordinator is implemented to compute the weighted average of the control variables.
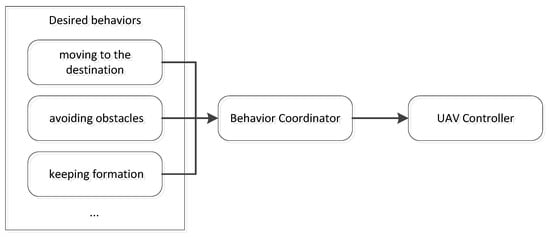
Figure 7.
The basic idea of the behavior-based method with desired behaviors (e.g., moving to the destination, avoiding obstacles, keeping formation) coordinated as input for the UAV controller.
Most behavior-based methods integrate multiple goal-oriented behaviors into controllers. For example, avoid static obstacles, avoid robots, move to a goal, and maintain formation in [25]; trajectory control and position control in [59]; formation control, trajectory tracking, and obstacle/collision avoidance in [60]; target tracking, obstacle avoidance, dynamic wall following, and avoid robots in [61]. To further improve the performance of behavior-based methods, some research introduces advanced techniques into behavior controllers, such as dynamical systems theory methods [62], genetic algorithms for parameter selecting [63], the coupled dynamics control methods [64], feedback linearization and optimization techniques [65,66,67], the null-space-based behavioral control method [68,69,70], and the predictive null-space-based behavior control method [71]. Some other research discusses both formation generation and formation maintenance with obstacle avoidance with behavior-based methods [72,73].
A significant advantage of behavior-based formation control methods is decentralization. This method does not require a central controller or complex communication protocols, reducing the risk of a single point of failure and improving the robustness of the system. In addition, decentralization also makes the system more flexible and able to adapt to different environments and task requirements. Due to each UAV making decisions based on local information and simple rules, behavior-based methods have good scalability. When the number of UAVs increases, it is only necessary to ensure that each UAV can correctly perceive its adjacent UAVs and environment to achieve the expansion of the formation. In addition, due to the fact that UAVs interact with each other through simple rules, the system also has strong adaptability and can cope with environmental changes and interference within the swarm. However, this method also faces some technical challenges that require further research and exploration. Future work can focus on optimizing local interaction rules, improving communication efficiency and reliability, and implementing more intelligent and adaptive formation control strategies.
4.4. Consensus-Based
Consensus-based formation control in UAV swarms involves distributed algorithms that enable the UAVs to agree on specific parameters such as position, velocity, or direction, making the swarm move cohesively as a unit. Each UAV in the swarm updates its state based on information shared by neighboring UAVs, striving to reach a consensus on the desired state across the entire swarm. This method allows for distributed decision-making, reducing the need for a central controller and enhancing the robustness of the formation control against individual UAV failures. Consensus algorithms are key for achieving synchronized movements and alignments in the swarm, facilitating dynamic adaptation to environmental changes and collaborative task execution. The effectiveness of this approach relies on reliable inter-UAV communication and the ability to converge on consensus quickly.
In the consensus-based method, the UAV swarm formation can be represented by graphs. Graph connections play a crucial role in managing the dynamics and coordination within the swarm. Each UAV in the swarm is considered a node in a graph. Edges between nodes represent communication links or sensing relationships, indicating which UAVs can directly share information or sense each other’s state (position, velocity, etc.). The structure of the graph affects how information flows through the swarm and how decisions are propagated.
Ren et al. [27] applied variants of some consensus algorithms to tackle formation control problems by appropriately choosing information states on which consensus is reached. They show that many existing leader–follower, virtual structure, and behavior-based approaches can be thought of as special cases of consensus-based strategies. Shihua et al. [74] proposed finite-time position consensus algorithms and incorporated gradient terms from collision avoidance and connectivity maintenance functions into the consensus algorithms. Wenbo et al. [75] leveraged consensus theory for the design of a UAV swarm formation control protocol. Fabricio et al. [76] presented a study focusing on the impact of network topology on the formation control of UAVs using a distributed consensus approach. Some techniques are combined with consensus algorithms to solve the formation control problem, such as the feedback linearization method [77,78], failure detection algorithms [78], artificial potential strategies [79], distributed Kalman filter [80], and decentralized model predictive control [81].
The consensus-based formation control method reduces the risk of single-point failures and improves the robustness of the system through distributed decision-making. Meanwhile, due to the absence of a central controller, the system can easily expand to accommodate more UAVs. However, the effectiveness of consensus algorithms highly depends on the communication quality between UAVs and the convergence speed of the algorithms. In complex dynamic environments, further research is needed on how to ensure the reliability and real-time performance of communication, as well as how to improve the convergence speed and stability of algorithms.
4.5. Artificial Potential Field
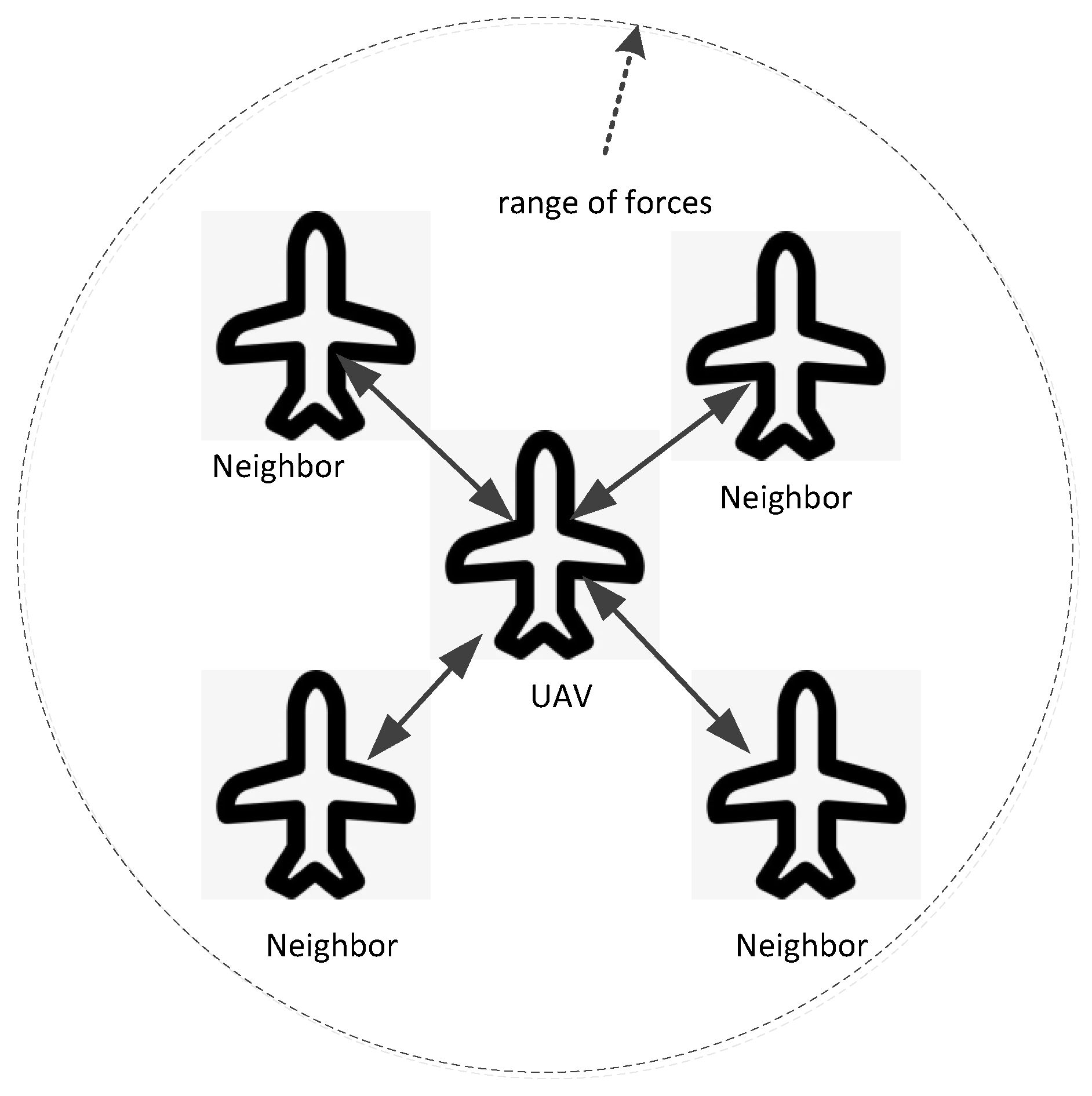
The artificial potential field or APF methods for formation control in UAV swarms use virtual forces to guide the UAVs into and maintain specific formations. Each UAV is influenced by attractive forces pulling it towards a target position or other UAVs within the formation, and repulsive forces pushing it away from obstacles or to avoid collisions with other UAVs. Figure 8 illustrates the basic idea with the circle representing the range of forces, in which each UAV detects the states of its neighbors by sensors or communication and is controlled by an artificial potential field function with the neighbors’ state as input.
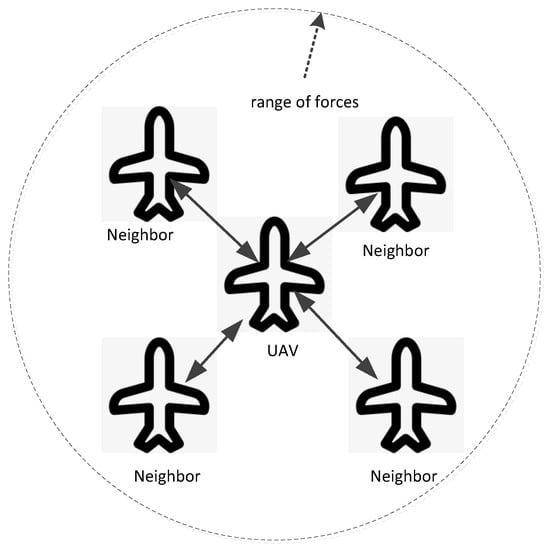
Figure 8.
The basic idea of the artificial potential field method with the circle representing the range of forces.
This method conceptualizes the formation control problem in terms of potential fields, where each UAV seeks to minimize its potential energy by adjusting its position relative to the others and environmental features. The APF approach is particularly useful for dynamically adapting formations in response to changing environments and for obstacle avoidance, providing a balance between maintaining formation integrity and ensuring the safety of individual UAVs. Its intuitive nature makes it widely applicable, although care must be taken to avoid local minima where UAVs could become stuck.
Oussama et al. [26] introduced a real-time obstacle avoidance method using the artificial potential field concept, which creates attractive and repulsive forces to guide robot movement. This concept allows for real-time adjustments to robot trajectories and ensures collision-free navigation. Naomi et al. [82] introduced a framework for coordinating multiple autonomous vehicles through artificial potentials and virtual leaders. These virtual leaders act as moving reference points and influence nearby vehicles with additional artificial potential. Thus, it enables group maneuvers and direction control. Tobias et al. [83] explored the application of three-dimensional potential fields for coordinating the flight of UAVs in formation. Jiayi et al. [84] presented an approach to collision avoidance and trajectory planning for UAVs using an optimized APF algorithm. Yuanchen et al. [85] proposed a method for controlling the formation of UAVs and enhancing their ability to avoid obstacles using an improved version of the APF algorithm. He et al. [86] introduced a method for controlling the formation of multiple UAVs and tracking targets using APF algorithms.
The APF method allows UAVs to adjust their trajectory in real time based on environmental changes, making it particularly suitable for dynamic formation control and obstacle avoidance. In complex environments, UAVs can quickly respond and make corresponding adjustments to ensure the stability and safety of the formation. The APF method can provide a balance between maintaining formation integrity and ensuring the safety of individual UAVs. By defining appropriate potential field functions, UAVs can maintain their formation while avoiding collisions with obstacles or other drones. One of the main challenges of the APF method is how to avoid drones becoming stuck in local minima. In some cases, UAVs may remain in positions with low potential energy that are not globally optimal, leading to a loss of stability in the formation.
4.6. Comparison
The comparison of leader–follower, virtual structure, behavior-based, consensus-based, and APF methods is shown in Table 1.

Table 1.
Comparison of conventional strategy methods.
The main advantages of the leader–follower method are simplicity, predictability, simplified path planning, and hierarchies. This method is easy to implement and the movements are highly predictable based on the leader’s behavior. In this method, only the leader needs to engage in path planning for obstacles and navigation. The UAVs can also be controlled hierarchically in the leader–follower method. The main disadvantages of this method are leader bottlenecks and limited flexibility. If the leader is lost or disabled, the entire formation may struggle to maintain coherence, especially if there is no mechanism to quickly designate a new leader. Formation shape and behavior are constrained by the leader’s actions, limiting adaptability to changing circumstances or mission requirements.
The main advantages of the virtual structure method are flexible shape, simplified path planning, and flexible formation change. In the virtual structure method, UAV swarms can form flexible formation shapes. By managing the formation as a whole, virtual structure methods also simplify path planning and can dynamically adjust the formation shape. The disadvantages of the method include communication dependency and limited adaptability. The method relies on accurate and consistent communication between UAVs to maintain the virtual structure. The predefined virtual structure may lack adaptability in highly dynamic environments.
The advantages of the behavior-based method include simplicity and scalability. Compared to other methods, behavior-based approaches can be simpler to implement and understand. This approach is generally scalable to large numbers of agents since each agent operates independently based on local sensory information and predefined behaviors. The disadvantages of the behavior-based method include coordination challenges, emergent complexity, limited global optimization, and dependency on sensory inputs. Coordinating the behaviors of multiple agents to achieve a desired formation can be challenging, especially for complex formations or in dynamically changing environments. As the number of agents and behaviors increases, emergent complexity may arise, making it difficult to predict or understand the collective behavior of the system. Behavior-based methods may prioritize local optimization of individual behaviors over global optimization of the formation as a whole. This can lead to suboptimal formations or inefficient use of resources, especially in scenarios where global coordination is essential for achieving specific performance metrics. The effectiveness of behavior-based methods relies heavily on accurate and reliable sensory inputs from the environment.
The advantages of the consensus-based method include guaranteed convergence and global optimization. Consensus-based methods guarantee convergence to a common formation among agents, ensuring that all agents reach an agreement on their positions and velocities over time. This can lead to stable and coordinated formations even in the presence of disturbances or uncertainties. By explicitly seeking consensus among agents, this method can achieve global optimization of the formation shape and configuration. The disadvantages of the consensus-based method include design complexity, communication dependency, and limited adaptability. Designing consensus algorithms and associated control laws can be complex, especially for large-scale formations or formations with intricate shapes. Consensus-based methods rely heavily on inter-agent communication to exchange information and reach a consensus state. While consensus-based methods excel in achieving agreement among agents, they may lack adaptability to dynamic changes in the environment or mission requirements.
The advantages of the APF method include simple implementation and obstacle avoidance. APF is relatively easy to implement as it requires agents to respond to simple forces derived from their environment. This straightforward computational model makes it accessible and quick to deploy. One of the key strengths of APF is its inherent capability for obstacle avoidance. Agents are repelled by obstacles through repulsive forces, naturally integrating collision avoidance into their navigation toward the formation’s goals. The disadvantages of the APF method include local minimum problems, tuning complexity, and lack of coordination. A well-known limitation of APF is its susceptibility to local minima, where an agent becomes stuck at a point that is not the global goal due to conflicting forces. This can prevent the system from reaching the desired target or maintaining the correct formation. While the basic implementation is straightforward, tuning the parameters of the potential fields (like the strength and range of forces) to achieve optimal performance can be complex and scenario-dependent. For more complex formation shapes or behaviors, APF might struggle without additional coordination mechanisms. It primarily ensures agents do not conflict with each other, rather than enforcing a precise geometric pattern or formation behavior.
5. AI Strategy
In recent years, several popular AI algorithms, such as ANN [16] and DRL [17], have gained prominence due to their effectiveness in solving various complex problems across different domains. AI algorithms have the potential to play an important role in enhancing the capabilities and effectiveness of UAV swarm formation control. In this section, the application of AI algorithms in formation control is reviewed from the perspectives of ANN-based methods and DRL-based methods.
5.1. ANN-Based
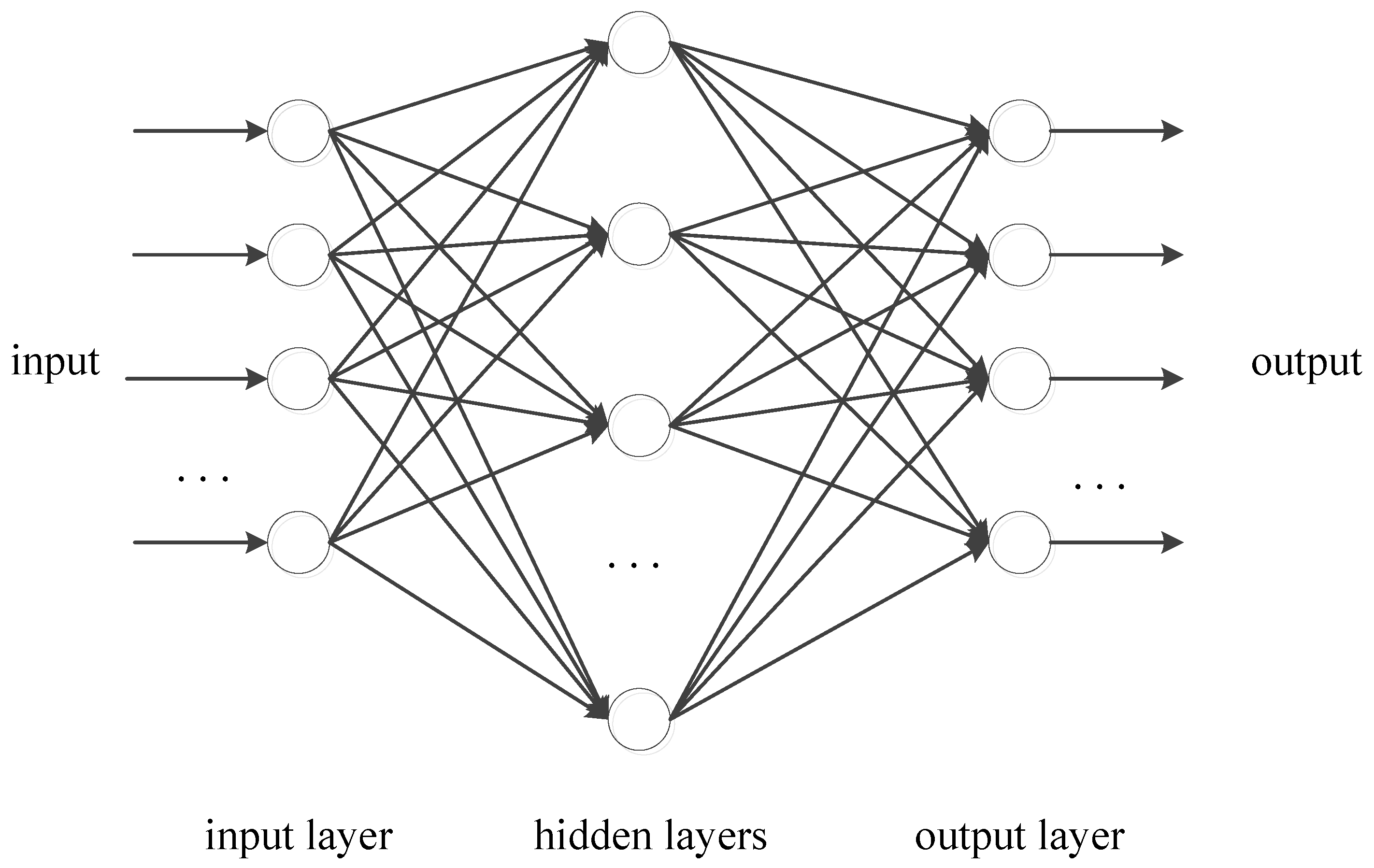
An ANN is a computational model inspired by the structure of the brain’s neural networks. The basic units of a neural network are neurons. These are simple processors that receive input, process it, and generate output based on the input and activation functions. The common activation functions include sigmoid, tanh, ReLU, and so on. Neurons are organized in layers and three main types of layers are the input layer, hidden layers, and output layer as shown in Figure 9. The input layer is the first layer that receives the input data; hidden layers perform most of the computational heavy lifting through their neurons and a neural network can have one or multiple hidden layers; the output layer is the last layer that produces the output of the network based on the information learned from the hidden layers.
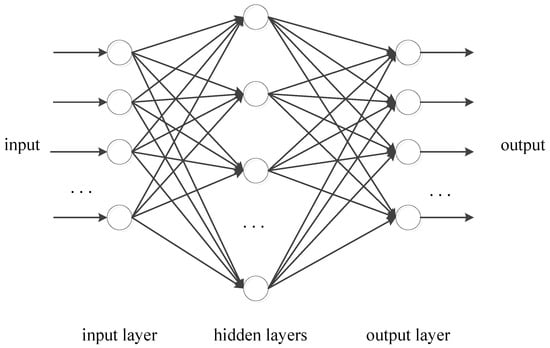
Figure 9.
The structure of neural networks with one input layer, one or multiple hidden layers, and one output layer.
ANNs, especially deep neural networks [87], have become a cornerstone of modern AI due to their ability to learn from data, generalize from previous experiences, and improve their accuracy over time without being explicitly programmed to perform specific tasks. ANNs are playing an increasingly important role in the development and enhancement of UAV swarm formation control systems. These networks provide the computational architecture needed to handle the complex dynamics and autonomous decision-making processes required for effective swarm operations. Some typical ANNs being applyied to UAV swarm formation control include radial basis function neural networks [88], Chebyshev neural networks [89], recurrent neural networks [90], and convolutional neural networks [91].
5.1.1. Radial Basis Function Neural Network
A radial function neural network is a type of ANN that uses radial basis functions as activation functions. It is structured similarly to other types of neural networks and consists of an input layer, one hidden layer, and an output layer. The unique aspect of a radial function neural network is its use of radial basis functions in the hidden layer, which enables it to perform certain types of classification and function approximation tasks very effectively. These features are used to approximate uncertain dynamics in the UAV formation control law.
Long et al. [92] designed a control strategy for scenarios where all follower agents needed to adjust their state based on a leading agent’s state, which may vary over time. The leader provides a reference state that all following agents aim to track. The approach uses a radial function neural network to approximate the dynamics of agents that may not be precisely known or may change over time. This neural network helps adapt the control signals to the agents’ dynamics. Xiaomei et al. [93] introduced a radial basis function neural networks strategy for managing the formation of multi-agent systems in constrained spaces where direct path planning may face challenges due to unknown obstacles and environment constraints. The work highlights the potential of neural networks in enhancing control systems’ adaptability and robustness. Shiqi et al. [94] adopted a radial basis function neural network to approximate the completely unknown nonlinearities.
5.1.2. Chebyshev Neural Network
Chebyshev neural networks are a type of neural network that utilizes Chebyshev polynomials as activation functions in the hidden layers [89]. Unlike traditional neural networks that often use sigmoid, tanh, or ReLU activation functions, Chebyshev neural networks leverage the properties of Chebyshev polynomials to enhance their representational capacity and improve learning performance. Chebyshev polynomials are a family of orthogonal polynomials that have desirable properties for function approximation, such as minimax approximation. By using Chebyshev polynomials as activation functions, Chebyshev neural networks can approximate complex nonlinear functions more efficiently and accurately. These features are used to approximate uncertain dynamics and unknown functions in the UAV formation control law, similar to the radial basis function neural network.
An-Min et al. [95,96,97,98] proposed some adaptive controllers with Chebyshev neural networks. These controllers aim to enable a group of agents, like drones or robots, to move in a swarm while maintaining a specific geometric formation, even in the presence of unknown dynamics and external disturbances. Chebyshev neural networks are used to approximate unknown nonlinearities in the system dynamics. Yang et al. [99] developed a formation control strategy for multi-agent systems with the adaptive dynamic sliding mode control and integrate a Chebyshev neural network. The Chebyshev neural network is employed to estimate nonlinear functions related to the system model with less computation burden and higher learning speed.
5.1.3. Recurrent Neural Network
Recurrent neural networks [90] are a class of neural networks designed specifically for processing sequential data. They excel at tasks where the input data are temporally dependent, such as language processing, speech recognition, and time series forecasting. RNNs are distinguished by their ability to maintain a hidden state or memory, which captures information about what has been processed so far in the sequence. This feature allows them to exhibit dynamic temporal behavior and handle inputs of varying lengths. Recurrent neural networks can be used for model prediction in UAV formation control.
Yunpeng et al. [100] addressed the problem of achieving optimal formation, which refers to organizing a multi-robot system into a desired configuration that minimizes the overall movement from their initial positions. The problem is transformed into an optimization issue where constraints such as orientation, scale, and the permissible range of the formation are considered. Recurrent neural networks are used due to their ability to handle parallel computations and solve nonsmooth optimization problems effectively. Chia-Wei et al. [101] explored the application of recurrent neural networks for intelligent leader-following consensus control in small-size unmanned helicopters. Recurrent neural networks are utilized to capture the dynamic behavior of the leader helicopter and facilitate the follower helicopters in maintaining the desired formation. Boyang et al. [102] introduced a distributed hierarchical control system consisting of translation and rotational subsystems, each managed by a specific model predictive controller that incorporates recurrent neural networks for enhanced predictive modeling. The recurrent neural networks are utilized to predict future states in the model predictive control framework, providing dynamic adjustments based on real-time data.
5.1.4. Convolutional Neural Network
Convolutional neural networks [91] are specialized for processing structured grid data, such as images. They consist of convolutional layers that apply filters to gain features from input data, followed by pooling layers to reduce dimensionality. Convolutional neural networks have achieved state-of-the-art performance in tasks like image classification and object detection. These features make them have significant potential in vision-based formation control.
Yanlin et al. [103] proposed an approach for adaptive leader–follower formation control and obstacle avoidance. The methodology separates vision-based control into two modules: perception and control. The system includes a convolutional neural network for vision-based localization. The convolutional neural network is used to accurately determine the robot’s position relative to its environment.
5.1.5. Other ANNs
In addition to the above-discussed ANNs, there are also some other ANNs used for formation control. Travis et al. [104,105,106] developed some neural network-based frameworks for quadrotor UAV formation control. A two-layer neural network with the robust integral of the sign of the error feedback is introduced to approximate dynamic uncertainties in both the follower and the leader robots in real time. The two-layer neural network consists of one layer of randomly assigned constant weights in the input layer and one layer of tunable weights in the output layer. Yang et al. [107] proposed a neural network-based formation controller that utilizes a three-layer neural observer to estimate uncertainties and manage actuator saturation effects. The neural network is used for better approximation of unknown functions in the control system. Xiaohua et al. [108] introduced a control strategy that incorporates a dual-mode approach to manage UAV formations: a safe mode for obstacle-free environments and a danger mode for situations with potential collisions or obstacles. A modified Grossberg neural network algorithm [109] is used to generate the obstacle-free optimal path in danger mode for obstacle or collision avoidance.
5.2. DRL-Based
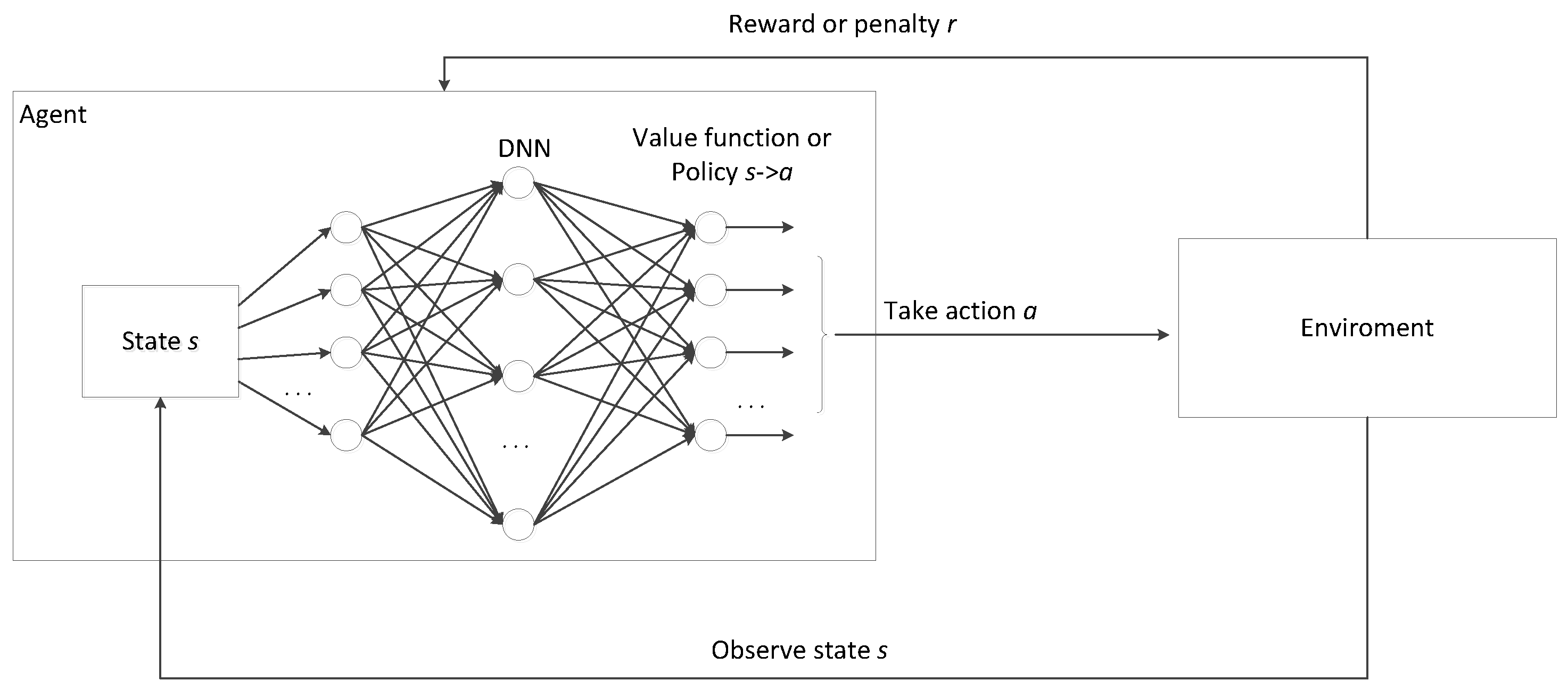
Reinforcement learning is a type of machine learning where an agent learns to make decisions by interacting with an environment. The agent takes actions in the environment and receives feedback in the form of rewards or penalties based on the actions taken. The goal of the agent is to learn a value function or a policy that maximizes the cumulative reward over time. Reinforcement learning has a relatively long history in the integration with multi-agent systems and forms an independent research direction, called multi-agent reinforcement learning (MARL) [110]. In recent years, deep reinforcement learning [17] has attracted great attention, which combines reinforcement learning techniques with deep neural networks (DNNs). In DRL, deep neural networks are used to approximate the value function, policy, or both in reinforcement learning algorithms, which enables agents to handle high-dimensional input spaces. The structure of DRL is shown in Figure 10. Each agent observes the state from the environment and takes action based on its value function or policy aiming to maximize the rewards. The value function or policy is learned by a DNN. After taking action, the agent is granted rewards or penalties from the environment. The value function or policy is updated by the rewards or penalties.
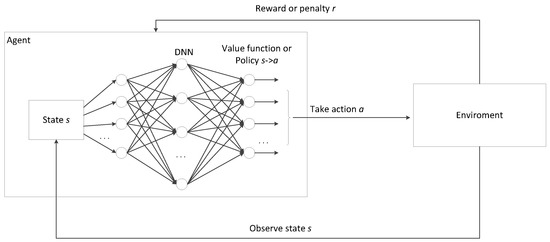
Figure 10.
The structure of deep reinforcement learning combined reinforcement learning techniques with deep neural networks.
The application of DRL in UAV formation control represents a significant advancement in autonomous UAV swarms. By leveraging DRL techniques, UAVs can autonomously coordinate their movements to maintain desired formation patterns while ensuring collision avoidance and adapting to dynamic environments. DRL enables UAVs to learn optimal control policies through interactions with the environment, which can lead to more efficient and robust formation control strategies compared to traditional methods. Overall, the application of DRL in UAV formation control holds great promise for enhancing the capabilities and effectiveness of UAV in various real-world scenarios [111,112,113,114]. Popular algorithms including deep Q-Network algorithm, momentum policy gradient algorithm, deep deterministic policy gradient algorithm, and multi-agent deep deterministic policy gradient algorithm are utilized in the UAV swarm formation control.
5.2.1. Deep Q-Network
The deep Q-network (DQN) algorithm combines deep learning with Q-learning, a classic reinforcement learning algorithm, enabling learning directly from high-dimensional sensory inputs [17]. In a DQN, a neural network, typically a convolutional neural network, is used to approximate the Q-function, which predicts the expected cumulative reward for taking a particular action in a given state. The network takes the state as input and outputs Q-values for each possible action. During training, the network parameters are updated iteratively to minimize the difference between predicted Q-values and target Q-values, which are obtained from a target network. Overall, DQNs have been successfully applied to formation control for autonomous navigation demonstrating their effectiveness in learning optimal policies from high-dimensional input spaces.
Yilan et al. [115,116] proposed the implementation of a system that employs the DQN algorithm as a means to tackle the difficulties associated with autonomous waypoint planning for multi-rotor UAVs. In the DQN-based waypoint planning approach, the entire 3D environment is divided into grids and each UAV chooses the next grid adjacent to its current grid with the DQN algorithm at every time step. The system incorporates the DQN algorithm to achieve optimal waypoint planning. The primary objectives of this algorithm are to minimize control energy expenditure and effectively navigate around obstacles within a specified area. Federico et al. [117] addressed the need for efficient coordination among UAVs to explore unknown areas, and monitor targets with minimal movement. They introduced a DQN-based algorithm within a MARL framework, which aimed for efficient area exploration and surveillance. The UAVs share observations through a communication channel, which helps avoid collisions and encourages cooperative behavior. Xiuxia et al. [118] proposed a DQN-based multi-UAV formation transformation method. The UAV formation transformation problem in this paper focuses on planning the position and route of each UAV in the target formation according to certain constraints according to the initial and the target formation. The formation transformation problem of multiple UAVs is modeled as a Markov decision process and the good practicability of this algorithm is verified by the formation transformation. Zhijun et al. [119] presented an approach to the formation control of leader–follower UAVs using DRL, specifically through a DQN algorithm. The effectiveness of the DQN-based method is validated through numerical simulations, showing potential for enhancing the cooperative control capabilities of UAVs in complex environments.
5.2.2. Momentum Policy Gradient
The momentum policy gradient (MPG) algorithm combines the concept of momentum from optimization algorithms with policy gradient methods [17]. Momentum, which is commonly used in optimization algorithms like stochastic gradient descent, helps accelerate convergence by accumulating gradients over time and smoothing out updates. In the context of reinforcement learning, MPG applies momentum to the policy updates, allowing the agent to build up momentum towards promising regions of the policy space. This helps the agent explore more efficiently, especially in environments with sparse rewards or complex action spaces.
Yanlin et al. [103] proposed an approach for adaptive leader–follower formation control and obstacle avoidance. The MPG-based algorithm is used for solving leader-following problems with regular and irregular leader trajectories. They experimentally proved MPG’s convergence and proved that the proposed algorithm can be extended to solve the collision avoidance and formation control problems by simply modifying the reward function.
5.2.3. Deep Deterministic Policy Gradient
The deep deterministic policy gradient (DDPG) algorithm combines ideas from both deep learning and policy gradient methods to learn complex policies directly from high-dimensional observations. DDPG is an actor–critic algorithm [120], meaning it learns both a policy (the actor) and a value function (the critic) simultaneously. The DDPG algorithm is suited for solving continuous action space problems.
For the UAV landing maneuver problem, Rodriguez-Ramos et al. [121] introduced a DDPG algorithm as a solution to the problem of executing UAV landing operations on a mobile platform. Numerous simulations have been conducted under diverse settings, encompassing simulated and actual fights, thereby establishing the broad applicability of the methodology.
5.2.4. Multi-Agent Deep Deterministic Policy Gradient
The multi-agent deep deterministic policy gradient (MADDPG) is an extension of the DDPG algorithm, adapted specifically for environments where multiple agents are interacting simultaneously. This approach is particularly useful in scenarios where agents must learn to cooperate, compete, or coexist in a shared environment. MADDPG takes advantage of centralized training with a decentralized execution paradigm. The key idea behind MADDPG is to extend the actor–critic method by using a centralized critic for each agent that can see the actions of all agents along with the global state. This makes it particularly powerful for complex multi-agent environments where agents must learn to navigate inter-agent interactions to achieve their goals.
Xu et al. [122] introduced a modified version of the MADDPG algorithm, addressing challenges like learning efficiency, collision avoidance, and cooperative behavior enhancement within UAV clusters. The paper proposes centralized training with a decentralized execution approach using an actor–critic network. Key improvements include a more precise calculation of Q-values, incorporation of collision avoidance mechanisms, and adjustments to the reward mechanism to foster better cooperative capabilities among UAVs.
5.3. Comparison
The comparison of the advantages and disadvantages of the ANN-based method and DRL-based method is shown in Table 2.

Table 2.
Comparison of different methods in the AI strategy.
The advantages of ANN-based methods include function approximation, generalization, real-time response, and parallel processing. ANNs can approximate complex nonlinear functions, making them suitable for modeling the dynamics of formation control systems. Trained ANNs can generalize their learned behaviors to unseen scenarios, allowing for adaptability in various environments. Once trained, ANNs can provide real-time responses, enabling swift adaptation to changes in the environment or mission requirements. ANNs can perform parallel processing, potentially leading to faster computation times and improved efficiency in formation control. The disadvantages of ANN-based methods include training data requirements, overfitting, and black box nature. ANNs typically require large amounts of labeled training data to learn effective formation control strategies, which can be costly and time-consuming to obtain. There is a risk of overfitting the model to the training data. Trained ANNs may lack transparency, making it challenging to interpret or understand the reasoning behind their decisions or behaviors.
The advantages of DRL-based methods include learning from interaction, complex decision-making, optimization of long-term rewards, and adaptability. DRL algorithms learn through trial-and-error interactions with the environment, enabling autonomous adaptation and improvement over time. DRL can handle complex decision-making tasks and high-dimensional state spaces, making them suitable for formation control in dynamic and uncertain environments. DRL algorithms can optimize for long-term rewards, allowing for the discovery of optimal formation control policies that maximize mission objectives. DRL algorithms can adapt to changes in the environment or mission requirements without explicit programming, enhancing flexibility in formation control. The disadvantages of DRL-based methods include sample inefficiency, training instability, hyperparameter tuning, and safety concerns. DRL algorithms can be sample inefficient, requiring a large number of interactions with the environment to learn effective policies, which can be time-consuming and resource-intensive. Training DRL algorithms can be unstable, with learning progress subject to fluctuations and challenges such as reward sparsity or function approximation errors. DRL algorithms often involve tuning numerous hyperparameters, such as learning rates and exploration strategies, which can be challenging and require expertise. There may be safety concerns during the learning process, as DRL algorithms explore different actions, potentially leading to undesirable behaviors or collisions in real-world applications.
In summary, ANN-based AI algorithms offer function approximation, generalization, real-time response, and parallel processing but may require extensive training data, risk overfitting, and lack transparency. On the other hand, DRL-based AI algorithms provide learning from interaction, complex decision-making, optimization of long-term rewards, and adaptability but can be sample-inefficient, prone to training instability, require hyperparameter tuning, and raise safety concerns during learning. The choice between these approaches depends on factors such as the specific requirements of the formation control task, available data, computational resources, and safety considerations.
6. Discussion
The comparison of different methods based on conventional strategy and AI strategy is shown in Table 3. The main advantages of conventional methods include well-understood principles, less computational requirements, and reliability. Most conventional methods such as leader–follower, virtual structure, and behavior-based often have simple and well-understood principles. These methods generally have less computational requirements, enabling real-time performance even on less capable hardware. Having been extensively tested and applied in various settings, these methods provide a level of reliability that is well documented. The main disadvantage of conventional strategy methods is the limited adaptability. Conventional methods may struggle with dynamic environments or unexpected scenarios not explicitly programmed into the system. Designing these systems can become especially challenging for complex formations or dynamic tasks.

Table 3.
Comparison of formation control strategies.
The main advantages of AI methods include high adaptability and generalization. AI algorithms excel in environments that require adaptation to new or changing conditions without human intervention. Trained AI models can generalize their learned behaviors to unseen scenarios or environments, reducing the need for extensive retraining or tuning when deploying formation control systems in different contexts. The main disadvantages of AI methods include data and training dependence, interpretability, computational complexity, robustness, and safety issues. AI algorithms typically require large amounts of training to learn effective formation control strategies, especially for complex multi-agent systems operating in diverse environments. Some AI algorithms can be challenging to interpret or understand how they arrive at certain decisions or behaviors. Training and running AI algorithms can be computationally intensive. This may limit their applicability in real-time formation control systems or resource-constrained environments. AI algorithms may be vulnerable to adversarial attacks. Ensuring robustness and safety of AI-based formation control systems requires thorough testing and mitigation of potential failure modes.
Although significant progress has been made in the formation control of UAV swarms with both conventional methods and AI methods, this research field still faces many challenges. Firstly, as the number of UAVs in a swarm increases, the complexity of coordination and communication grows exponentially. Managing large-scale swarms requires sophisticated algorithms capable of scaling efficiently while maintaining robustness in dynamic environments. Secondly, UAV swarms must adapt to dynamic environmental conditions, such as wind disturbances, obstacles, and varying terrain. Robust control algorithms capable of dynamically adjusting formation geometry and trajectory planning based on real-time sensory inputs are essential for maintaining desired performance levels under changing circumstances. Thirdly, UAV swarms may consist of heterogeneous agents with diverse capabilities and roles. Coordinating such swarms to accomplish complex missions, such as surveillance, search and rescue, or infrastructure inspection, requires algorithms that can accommodate different objectives, constraints, and task allocations efficiently. To address these challenges, fully leveraging the advantages of the two kinds of methods to solve the challenges of UAV swarm formation control is a worthwhile research topic.
7. Conclusions
In this paper, we provide a thorough examination of the state-of-the-art research in UAV swarm formation control, encompassing both conventional and AI-based methodologies. This review highlights the significant progress made in leveraging various techniques to address the challenges inherent in coordinating swarms of UAV flying formation.
Conventional methods such as leader–follower, virtual structure, behavior-based, consensus-based, and APF offer established frameworks for formation control, each with its unique strengths and limitations. Leader–follower systems provide simplicity and predictability but may lack adaptability in dynamic environments. Virtual structure methods offer flexibility but are sensitive to communication dependencies. Behavior-based approaches prioritize simplicity and scalability but may face challenges in coordination and emergent complexity. Consensus-based methods ensure convergence and global optimization but may be complex to design and depend on communication. APF methods offer simplicity and obstacle avoidance but may struggle with local minima and lack coordination in complex formations.
In contrast, AI-based methods, particularly those based on ANNs and DRL, present promising avenues for enhancing formation control capabilities. ANNs offer function approximation and generalization, while DRL enables autonomous adaptation and complex decision-making. However, both AI approaches require careful consideration of training data, computational resources, and safety concerns.
The future development of UAV formation control technology faces multiple challenges (e.g., real-time algorithm). With the expansion of cluster size and the increase in task complexity, the limitations of traditional strategies in adaptability and flexibility are gradually becoming apparent. Meanwhile, the computational demand increases with the complexity of the formation and the number of UAVs in the swarm, especially for real-time algorithms. Although AI strategies have strong potential, they also face challenges such as data dependence, computing resource requirements, security, and reliability. In addition, the effectiveness of communication latency and collaborative strategies is crucial for maintaining the cluster. Meanwhile, UAVs also require strong environmental awareness and fast and accurate decision-making abilities to cope with complex and ever-changing environments and tasks. In order to overcome these challenges, future research and technological innovation will be devoted to improving algorithm performance, optimizing collaborative mechanisms, and enhancing environmental awareness and decision-making capabilities for both conventional and AI methods, thereby promoting the further development and widespread application of UAV formation control technology.
Overall, this comprehensive review underscores the importance of interdisciplinary collaboration and innovative approaches in advancing UAV swarm formation control. By addressing the identified challenges and leveraging the strengths of conventional and AI-based methodologies, researchers can unlock the full potential of UAV swarm technology for the benefit of society.
Author Contributions
Conceptualization, Y.B. and Y.Y. (Ye Yan); methodology, Y.Y. (Yueneng Yang); investigation, Y.B.; writing—original draft preparation, Y.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The Support Program of Young Talents of Huxiang, grant number No. 2019RS2029, and Chinese Postdoctoral Science Foundation, grant number No. 47661.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| UAV | Unmanned Aerial Vehicles |
| MAS | Multi-agent System |
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| DRL | Deep Reinforcement Learning |
| APF | Artificial Potential Field |
| MARL | Multi-agent Reinforcement Learning |
| DNN | Deep Neural Networks |
| DQN | Deep Q-network |
| MPG | Momentum Policy Gradient |
| DDPG | Deep Deterministic Policy Gradient |
| MADDPG | Multi-agent Deep Deterministic Policy Gradient |
References
- Kozera Cyprian, A. Military Use of Unmanned Aerial Vehicles—A Historical Study. Saf. Def. 2018, 4, 17–21. [Google Scholar]
- Kim, J.; Kim, S.; Ju, C.; Son, H.I. Unmanned Aerial Vehicles in Agriculture: A Review of Perspective of Platform, Control, and Applications. IEEE Access 2019, 7, 105100–105115. [Google Scholar] [CrossRef]
- Lyu, M.; Zhao, Y.; Huang, C.; Huang, H. Unmanned Aerial Vehicles for Search and Rescue: A Survey. Remote Sens. 2023, 15, 3266. [Google Scholar] [CrossRef]
- Guimarães, N.; Pádua, L.; Marques, P.; Silva, N.; Peres, E.; Sousa, J.J. Forestry Remote Sensing from Unmanned Aerial Vehicles: A Review Focusing on the Data, Processing and Potentialities. Remote Sens. 2020, 12, 1046. [Google Scholar] [CrossRef]
- Peng, K.; Du, J.; Lu, F.; Sun, Q.; Dong, Y.; Zhou, P.; Hu, M. A Hybrid Genetic Algorithm on Routing and Scheduling for Vehicle-Assisted Multi-Drone Parcel Delivery. IEEE Access 2019, 7, 49191–49200. [Google Scholar] [CrossRef]
- Chen, W.; Liu, J.; Guo, H.; Kato, N. Toward Robust and Intelligent Drone Swarm: Challenges and Future Directions. IEEE Netw. 2020, 34, 278–283. [Google Scholar] [CrossRef]
- Shakeri, R.; Al-Garadi, M.A.; Badawy, A.; Mohamed, A.; Khattab, T.; Al-Ali, A.K.; Guizani, M. Multiple UAV Systems: A Survey. Unmanned Syst. 2020, 8, 149–169. [Google Scholar]
- Chung, S.J.; Paranjape, A.A.; Dames, P.; Shen, S.; Kumar, V. A Survey on Aerial Swarm Robotics. IEEE Trans. Robot. 2018, 34, 837–855. [Google Scholar] [CrossRef]
- Craig, W.R. Flocks, Herds, and Schools: A Distributed Behavioral Model. In Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, Anaheim, CA, USA, 27–31 July 1987; pp. 25–34. [Google Scholar]
- Do, H.T.; Hua, H.T.; Nguyen, M.T.; Nguyen, C.V.; Nguyen, H.T.; Nguyen, H.T.; Nguyen, N.T. Formation Control Algorithms for Multiple-UAVs: A Comprehensive Survey. EAI Endorsed Trans. Ind. Netw. Intell. Syst. 2021, 8, e3. [Google Scholar] [CrossRef]
- Ouyang, Q.; Wu, Z.; Cong, Y.; Wang, Z. Formation Control of Unmanned Aerial Vehicle Swarms: A Comprehensive Review. Asian J. Control 2023, 25, 570–593. [Google Scholar] [CrossRef]
- Oh, K.K.; Park, M.C.; Ahn, H.S. A Survey of Multi-Agent Formation Control. Automatica 2015, 53, 424–440. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; He, Z.; Li, Z.; Zhang, Q.; Ding, Z. A Survey of Multi-Agent Systems on Distributed Formation Control. Unmanned Syst. 2023, 1–14. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, Y.; Jin, Y.; Wang, T.; Nie, X.; Yan, T. A Survey of An Intelligent Multi-Agent Formation Control. Appl. Sci. 2023, 13, 5934. [Google Scholar] [CrossRef]
- Saffre, F.; Hildmann, H.; Karvonen, H. The Design Challenges of Drone Swarm Control. In Proceedings of the International Conference on Human-Computer Interaction, Washington DC, USA, 29 June–4 July 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 408–421. [Google Scholar]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in Artificial Neural Network Applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef]
- François-Lavet, V.; Henderson, P.; Islam, R.; Bellemare, M.G.; Pineau, J. An Introduction to Deep Reinforcement Learning. Found. Trends Mach. Learn. 2018, 11, 219–354. [Google Scholar]
- Desai, J.P.; Ostrowski, J.; Kumar, V. Controlling Formations of Multiple Mobile Robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Leuven, Belgium, 16–20 May 1998; Volume 4, pp. 2864–2869. [Google Scholar]
- Tan, K.H.; Lewis, M.A. Virtual Structures for High-Precision Cooperative Mobile Robotic Control. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Osaka, Japan, 4–8 November 1996; pp. 132–139. [Google Scholar]
- Huang, S.; Teo, R.S.H.; Tan, K.K. Collision Avoidance of Multi Unmanned Aerial Vehicles: A review. Annu. Rev. Control 2019, 48, 147–164. [Google Scholar] [CrossRef]
- Yasin, J.N.; Mohamed, S.A.; Haghbayan, M.H.; Heikkonen, J.; Tenhunen, H.; Plosila, J. Unmanned Aerial Vehicles (UAVs): Collision Avoidance Systems and Approaches. IEEE Access 2020, 8, 105139–105155. [Google Scholar] [CrossRef]
- Desai, J.P.; Ostrowski, J.P.; Kumar, V. Modeling and Control of Formations of Nonholonomic Mobile Robots. IEEE Trans. Robot. Autom. 2001, 17, 905–908. [Google Scholar] [CrossRef]
- Lewis, M.A.; Tan, K.H. High Precision Formation Control of Mobile Robots Using Virtual Structures. Auton. Robot. 1997, 4, 387–403. [Google Scholar] [CrossRef]
- Turpin, M.; Michael, N.; Kumar, V. Trajectory Design and Control for Aggressive Formation Flight with Quadrotors. Auton. Robot. 2012, 33, 143–156. [Google Scholar] [CrossRef]
- Balch, T.; Arkin, R.C. Behavior-Based Formation Control for Multirobot Teams. IEEE Trans. Robot. Autom. 1998, 14, 926–939. [Google Scholar] [CrossRef]
- Khatib, O. Real-Time Obstacle Avoidance for Manipulators and Mobile Robots. Int. J. Robot. Res. 1986, 5, 90–98. [Google Scholar] [CrossRef]
- Ren, W. Consensus Strategies for Cooperative Control of Vehicle Formations. IET Control. Theory Appl. 2007, 1, 505–512. [Google Scholar] [CrossRef]
- Li, X.; Xiao, J.; Cai, Z. Backstepping Based Multiple Mobile Robots Formation Control. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 887–892. [Google Scholar]
- Roldão, V.; Cunha, R.; Cabecinhas, D.; Silvestre, C.; Oliveira, P. A Leader-Following Trajectory Generator with Application to Quadrotor Formation Flight. Robot. Auton. Syst. 2014, 62, 1597–1609. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, J.; Zhang, P. Multi-UAV Formation Control Based on a Novel Back-Stepping Approach. IEEE Trans. Veh. Technol. 2020, 69, 2437–2448. [Google Scholar] [CrossRef]
- Mercado, D.A.; Castro, R.; Lozano, R. Quadrotors Flight Formation Control Using a Leader-Follower Approach. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 3858–3863. [Google Scholar]
- Yang, K.; Dong, W.; Tong, Y.; He, L. Leader-Follower Formation Consensus of Quadrotor UAVs Based on Prescribed Performance Adaptive Constrained Backstepping Control. Int. J. Control Autom. Syst. 2022, 20, 3138–3154. [Google Scholar] [CrossRef]
- Jasim, W.; Gu, D. Robust Team Formation Control for Quadrotors. IEEE Trans. Control Syst. Technol. 2017, 26, 1516–1523. [Google Scholar] [CrossRef]
- Ali, Z.A.; Zhangang, H. Multi-Unmanned Aerial Vehicle Swarm Formation Control Using Hybrid Strategy. Trans. Inst. Meas. Control 2021, 43, 2689–2701. [Google Scholar] [CrossRef]
- No, T.S.; Kim, Y.; Tahk, M.J.; Jeon, G.E. Cascade-Type Guidance Law Design for Multiple-UAV Formation Keeping. Aerosp. Sci. Technol. 2011, 15, 431–439. [Google Scholar] [CrossRef]
- Gu, Y.; Seanor, B.; Campa, G.; Napolitano, M.R.; Rowe, L.; Gururajan, S.; Wan, S. Design and Flight Testing Evaluation of Formation Control Laws. IEEE Trans. Control Syst. Technol. 2006, 14, 1105–1112. [Google Scholar] [CrossRef]
- Campa, G.; Gu, Y.; Seanor, B.; Napolitano, M.R.; Pollini, L.; Fravolini, M.L. Design and Flight-testing of Non-linear Formation Control Laws. Control Eng. Pract. 2007, 15, 1077–1092. [Google Scholar] [CrossRef]
- Yun, B.; Chen, B.M.; Lum, K.Y.; Lee, T.H. Design and Implementation of a Leader-Follower Cooperative Control System for Unmanned Helicopters. J. Control Theory Appl. 2010, 8, 61–68. [Google Scholar] [CrossRef]
- Sorensen, N.; Ren, W. A Unified Formation Control Scheme with a Single or Multiple Leaders. In Proceedings of the American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 5412–5418. [Google Scholar]
- He, L.; Bai, P.; Liang, X.; Zhang, J.; Wang, W. Feedback Formation Control of UAV Swarm with Multiple Implicit Leaders. Aerosp. Sci. Technol. 2018, 72, 327–334. [Google Scholar] [CrossRef]
- Sadowska, A.; den Broek, T.V.; Huijberts, H.; van de Wouw, N.; Kostić, D.; Nijmeijer, H. A Virtual Structure Approach to Formation Control of Unicycle Mobile Robots using Mutual Coupling. Int. J. Control. 2011, 84, 1886–1902. [Google Scholar] [CrossRef]
- Hao, C.H.E.N.; Xiangke, W.A.N.G.; Lincheng, S.H.E.N.; Yirui, C.O.N.G. Formation Flight of Fixed-Wing UAV Swarms: A Group-based Hierarchical Approach. Chin. J. Aeronaut. 2021, 34, 504–515. [Google Scholar]
- Dong, X.; Li, Y.; Lu, C.; Hu, G.; Li, Q.; Ren, Z. Time-Varying Formation Tracking for UAV Swarm Systems with Switching Interaction Topologies. In Proceedings of the 35th Chinese Control Conference, Chengdu, China, 27–29 July 2016; pp. 7658–7665. [Google Scholar]
- Zhou, S.; Dong, X.; Li, Q.; Ren, Z. Time-Varying Formation Tracking for UAV Swarm Systems with Switching Directed Topologies. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 3674–3685. [Google Scholar]
- Saska, M.; Baca, T.; Thomas, J.; Chudoba, J.; Preucil, L.; Krajnik, T.; Kumar, V. System for Deployment of Groups of Unmanned Micro Aerial Vehicles in GPS-denied Environments Using Onboard Visual Relative Localization. Auton. Robot. 2017, 41, 919–944. [Google Scholar] [CrossRef]
- Fu, X.; Pan, J.; Wang, H.; Gao, X. A Formation Maintenance and Reconstruction Method of UAV Swarm Based on Distributed Control. Aerosp. Sci. Technol. 2020, 104, 105981. [Google Scholar] [CrossRef]
- Liang, Y.; Qi, D.O.N.G.; Yanjie, Z.H.A.O. Adaptive Leader-Follower Formation Control for Swarms of Unmanned Aerial Vehicles with Motion Constraints and Unknown Disturbances. Chin. J. Aeronaut. 2020, 33, 2972–2988. [Google Scholar] [CrossRef]
- Li, N.; Wang, H.; Luo, Q.; Zheng, W. Distributed Formation Control for Multiple Quadrotor UAVs Based on Distributed Estimator and Singular Perturbation System. Int. J. Control. Autom. Syst. 2024, 22, 1349–1359. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R. Virtual Structure Based Spacecraft Formation Control with Formation Feedback. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002; p. 4963. [Google Scholar]
- Ren, W.; Beard, R.W. Formation Feedback Control for Multiple Spacecraft via Virtual Structures. IEE Proc.-Control Theory Appl. 2004, 151, 357–368. [Google Scholar] [CrossRef]
- Li, N.H.; Liu, H.H. Formation UAV Flight Control Using Virtual Structure and Motion Synchronization. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 1782–1787. [Google Scholar]
- Mehrjerdi, H.; Ghommam, J.; Saad, M. Nonlinear Coordination Control for a Group of Mobile Robots Using a Virtual Structure. Mechatronics 2011, 21, 1147–1155. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, Y.; Lu, Y. Formation Control for UAVs Based on the Virtual Structure Idea and Nonlinear Guidance Logic. In Proceedings of the 2021 6th International Conference on Automation, Control and Robotics Engineering (CACRE), Dalian, China, 15–17 July 2021; pp. 135–139. [Google Scholar]
- Askari, A.; Mortazavi, M.; Talebi, H.A. UAV Formation Control via the Virtual Structure Approach. J. Aerosp. Eng. 2015, 28, 04014047. [Google Scholar] [CrossRef]
- Lalish, E.; Morgansen, K.A.; Tsukamaki, T. Formation Tracking Control Using Virtual Structures and Deconfliction. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 5699–5705. [Google Scholar]
- Zhou, D.; Wang, Z.; Schwager, M. Agile Coordination and Assistive Collision Avoidance for Quadrotor Swarms Using Virtual Structures. IEEE Trans. Robot. 2018, 34, 916–923. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W. Decentralized Scheme for Spacecraft Formation Flying via the Virtual Structure Approach. J. Guid. Control Dyn. 2004, 27, 73–82. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Z.; Song, Y.; Yang, C.; Liang, C. Research on Multi-UAV Formation and Semi-Physical Simulation with Virtual Structure. IEEE Access 2023, 11, 126027–126039. [Google Scholar] [CrossRef]
- Giulietti, F.; Innocenti, M.; Pollini, L. Formation Flight Control-A Behavioral Approach. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Montreal, QC, Canada, 6–9 August 2001; p. 4239. [Google Scholar]
- Wang, J.; Xin, M. Integrated Optimal Formation Control of Multiple Unmanned Aerial Vehicles. IEEE Trans. Control Syst. Technol. 2012, 21, 1731–1744. [Google Scholar] [CrossRef]
- Hacene, N.; Mendil, B. Behavior-based Autonomous Navigation and Formation Control of Mobile Robots in Unknown Cluttered Dynamic Environments with Dynamic Target Tracking. Int. J. Autom. Comput. 2021, 18, 766–786. [Google Scholar] [CrossRef]
- Monteiro, S.; Bicho, E. A Dynamical Systems Approach to Behavior-based Formation Control. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No. 02CH37292), Washington, DC, USA, 11–15 May 2002; Volume 3, pp. 2606–2611. [Google Scholar]
- Cao, Z.; Tan, M.; Wang, S.; Fan, Y.; Zhang, B. The Optimization Research of Formation Control for Multiple Mobile Robots. In Proceedings of the 4th World Congress on Intelligent Control and Automation, Shanghai, China, 10–14 June 2002; pp. 1270–1274. [Google Scholar]
- Lawton, J.R.; Beard, R.W.; Young, B.J. A Decentralized Approach to Formation Maneuvers. IEEE Trans. Robot. Autom. 2003, 19, 933–941. [Google Scholar] [CrossRef]
- Kim, S.; Kim, Y. Three Dimensional Optimum Controller for Multiple UAV Formation Flight Using Behavior-based Decentralized Approach. In Proceedings of the 2007 International Conference on Control, Automation and Systems, Seoul, Republic of Korea, 17–20 October 2007; pp. 1387–1392. [Google Scholar]
- Kim, S.; Kim, Y.; Tsourdos, A. Optimized Behavioural UAV Formation Flight Controller Design. In Proceedings of the 2009 European Control Conference (ECC), Budapest, Hungary, 23–26 August 2009; pp. 4973–4978. [Google Scholar]
- Kim, S.; Kim, Y. Optimum Design of Three-Dimensional Behavioural Decentralized Controller for UAV Formation Flight. Eng. Optim. 2009, 41, 199–224. [Google Scholar] [CrossRef]
- Arrichiello, F.; Chiaverini, S.; Fossen, T.I. Formation Control of Marine Surface Vessels Using the Null-Space-Based Behavioral Control. In Group Coordination and Cooperative Control; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–19. [Google Scholar]
- Arrichiello, F.; Chiaverini, S.; Fossen, T.I. Formation Control of Underactuated Surface Vessels Using the Null-Space-Based Behavioral Control. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–13 October 2006; pp. 5942–5947. [Google Scholar]
- Antonelli, G.; Arrichiello, F.; Chiaverini, S. Experiments of Formation Control with Multirobot Systems Using the Null-Space-Based Behavioral Control. IEEE Trans. Control Syst. Technol. 2009, 17, 1173–1182. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, J.; Tian, G.; Chen, Y. Integrated Planning and Control for Formation Reconfiguration of Multiple Spacecrafts: A Predictive Behavior Control Approach. Adv. Space Res. 2023, 72, 2007–2019. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, X.; Zhu, Z.; Chen, C.; Yang, P. Behavior-Based Formation Control of Swarm Robots. Math. Probl. Eng. 2014, 2014, 205759. [Google Scholar] [CrossRef]
- Lee, G.; Chwa, D. Decentralized Behavior-Based Formation Control of Multiple Robots Considering Obstacle Avoidance. Intell. Serv. Robot. 2018, 11, 127–138. [Google Scholar] [CrossRef]
- Li, S.; Wang, X. Finite-time Consensus and Collision Avoidance Control Algorithms for Multiple AUVs. Automatica 2013, 49, 3359–3367. [Google Scholar] [CrossRef]
- Suo, W.; Wang, M.; Zhang, D.; Qu, Z.; Yu, L. Formation Control Technology of Fixed-Wing UAV Swarm Based on Distributed Ad Hoc Network. Appl. Sci. 2022, 12, 535. [Google Scholar] [CrossRef]
- Souza, F.C.; Dos Santos, S.R.B.; de Oliveira, A.M.; Givigi, S.N. Influence of Network Topology on UAVs Formation Control Based on Distributed Consensus. In Proceedings of the 2022 IEEE International Systems Conference (SysCon), Virtual, 25 April–23 May 2022; pp. 1–8. [Google Scholar]
- Seo, J.; Ahn, C.; Kim, Y. Controller Design for UAV Formation Flight Using Consensus based Decentralized Approach. In Proceedings of the AIAA Infotech Aerospace Conference and AIAA Unmanned Unlimited Conference, Seattle, WA, USA, 6–9 April 2009; p. 1826. [Google Scholar]
- Seo, J.; Kim, Y.; Kim, S.; Tsourdos, A. Consensus-based Reconfigurable Controller Design for Unmanned Aerial Vehicle Formation Flight. J. Aerosp. Eng. 2012, 226, 817–829. [Google Scholar] [CrossRef]
- Kuriki, Y.; Namerikawa, T. Consensus-based Cooperative Formation Control with Collision Avoidance for a Multi-UAV System. In Proceedings of the 2014 American Control Conference, Portland, ON, USA, 4–6 June 2014; pp. 2077–2082. [Google Scholar]
- Nägeli, T.; Conte, C.; Domahidi, A.; Morari, M.; Hilliges, O. Environment-independent Formation Flight for Micro Aerial Vehicles. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 1141–1146. [Google Scholar]
- Kuriki, Y.; Namerikawa, T. Formation Control with Collision Avoidance for a Multi-UAV System Using Decentralized MPC and Consensus-Based Control. SICE J. Control Meas. Syst. Integr. 2015, 8, 285–294. [Google Scholar] [CrossRef]
- Leonard, N.E.; Fiorelli, E. Virtual Leaders, Artificial Potentials and Coordinated Control of Group. In Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, FL, USA, 4–7 December 2001; pp. 2968–2973. [Google Scholar]
- Paul, T.; Krogstad, T.R.; Gravdahl, J.T. Modelling of UAV Formation Flight Using 3D Potential Field. Simul. Model. Pract. Theory 2008, 16, 1453–1462. [Google Scholar] [CrossRef]
- Sun, J.; Tang, J.; Lao, S. Collision Avoidance for Cooperative UAVs with Optimized Artificial Potential Field Algorithm. IEEE Access 2017, 5, 18382–18390. [Google Scholar] [CrossRef]
- Zhao, Y.; Jiao, L.; Zhou, R.; Zhang, J. UAV Formation Control with Obstacle Avoidance Using Improved Artificial Potential Fields. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 6219–6224. [Google Scholar]
- Song, H.; Hu, S.; Jiang, W.; Guo, Q.; Zhu, M. Artificial Potential Field-Based Multi-UAV Formation Control and Target Tracking. Int. J. Aerosp. Eng. 2022, 2022, 4253558. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Montazer, G.A.; Giveki, D.; Karami, M.; Rastegar, H. Radial Basis Function Neural Networks: A Review. Comput. Rev. J. 2018, 1, 52–74. [Google Scholar]
- Lee, T.T.; Jeng, J.T. Chebyshev Polynomials Based (CPB) Unified Model Neural Networks for Function Approximation. IEEE Trans. Syst. Man Cybern. 1998, 28, 925–935. [Google Scholar]
- Schuster, M.; Paliwal, K.K. Bidirectional Recurrent Neural Networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A Survey of Convolutional Neural Networks: Analysis, Applications, and Prospects. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6999–7019. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Hou, Z.G.; Tan, M.; Lin, Y.; Zhang, W. Neural-Network-Based Adaptive Leader-Following Control for Multiagent Systems with Uncertainties. IEEE Trans. Neural Netw. 2010, 21, 1351–1358. [Google Scholar] [CrossRef]
- Liu, X.; Ge, S.S.; Goh, C.H. Neural-Network-Based Switching Formation Tracking Control of Multiagents with Uncertainties in Constrained Space. IEEE Trans. Syst. Man Cybern. Syst. 2017, 49, 1006–1015. [Google Scholar] [CrossRef]
- Zheng, S.; Shi, P.; Wang, S.; Shi, Y. Adaptive Neural Control for a Class of Nonlinear Multiagent Systems. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 763–776. [Google Scholar] [CrossRef]
- Zou, A.M.; Kumar, K.D. Adaptive Output Feedback Control of Spacecraft Formation Flying Using Chebyshev Neural Networks. J. Aerosp. Eng. 2011, 24, 361–372. [Google Scholar] [CrossRef]
- Zou, A.M.; Kumar, K.D. Neural Network-Based Adaptive Output Feedback Formation Control for Multi-Agent Systems. Nonlinear Dyn. 2012, 70, 1283–1296. [Google Scholar] [CrossRef]
- Zou, A.M.; Kumar, K.D. Neural Network-Based Distributed Attitude Coordination Control for Spacecraft Formation Flying with Input Saturation. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1155–1162. [Google Scholar] [PubMed]
- Zou, A.M.; Kumar, K.D.; Hou, Z.G. Distributed Consensus Control for Multi-Agent Systems Using Terminal Sliding Mode and Chebyshev Neural Networks. Int. J. Robust Nonlinear Control 2013, 23, 334–357. [Google Scholar] [CrossRef]
- Fei, Y.; Shi, P.; Lim, C.C. Neural Network Adaptive Dynamic Sliding Mode Formation Control of Multi-Agent Systems. Int. J. Syst. Sci. 2020, 51, 2025–2040. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, L.; Hou, Z.G.; Yu, J.; Tan, M. Optimal Formation of Multirobot Systems Based on a Recurrent Neural Network. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 322–333. [Google Scholar] [CrossRef] [PubMed]
- Kuo, C.W.; Tsai, C.C.; Lee, C.T. Intelligent Leader-Following Consensus Formation Control Using Recurrent Neural Networks for Small-Size Unmanned Helicopters. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 1288–1301. [Google Scholar] [CrossRef]
- Zhang, B.; Sun, X.; Liu, S.; Deng, X. Recurrent Neural Network-Based Model Predictive Control for Multiple Unmanned Quadrotor Formation Flight. Int. J. Aerosp. Eng. 2019, 2019, 1–18. [Google Scholar] [CrossRef]
- Zhou, Y.; Lu, F.; Pu, G.; Ma, X.; Sun, R.; Chen, H.Y.; Li, X. Adaptive Leader-Follower Formation Control and Obstacle Avoidance via Deep Reinforcement Learning. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 4273–4280. [Google Scholar]
- Dierks, T.; Jagannathan, S. Neural Network Control of Mobile Robot Formations Using RISE Feedback. IEEE Trans. Syst. Man Cybern. 2008, 39, 332–347. [Google Scholar] [CrossRef] [PubMed]
- Dierks, T.; Jagannathan, S. Neural Network Control of Quadrotor UAV Formations. In Proceedings of the 2009 American Control Conference, St. Louis, MI, USA, 10–12 June 2009; pp. 2990–2996. [Google Scholar]
- Travis, D.; Sarangapani, J. Neural Network Output Feedback Control of Robot Formations. IEEE Trans. Syst. Man Cybern. 2009, 40, 383–399. [Google Scholar]
- Fei, Y.; Shi, P.; Lim, C.C. Neural-Based Formation Control of Uncertain Multi-Agent Systems with Actuator Saturation. Nonlinear Dyn. 2022, 108, 3693–3709. [Google Scholar] [CrossRef]
- Wang, X.; Yadav, V.; Balakrishnan, S.N. Cooperative UAV Formation Flying with Obstacle/Collision Avoidance. IEEE Trans. Control Syst. Technol. 2007, 15, 672–679. [Google Scholar] [CrossRef]
- Grossberg, S. Nonlinear Neural Networks: Principles, Mechanisms, and Architectures. Neural Networks 1988, 1, 17–61. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, Z.; Başar, T. Multi-Agent Reinforcement Learning: A Selective Overview of Theories and Algorithms. In Handbook of Reinforcement Learning and Control; Springer: Berlin/Heidelberg, Germany, 2021; pp. 321–384. [Google Scholar]
- Oroojlooy, A.; Hajinezhad, D. A Review of Cooperative Multi-Agent Deep Reinforcement Learning. Appl. Intell. 2022, 53, 13677–13722. [Google Scholar] [CrossRef]
- Sui, Z.; Pu, Z.; Yi, J.; Wu, S. Formation Control with Collision Avoidance Through Deep Reinforcement Learning. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar]
- Sui, Z.; Pu, Z.; Yi, J.; Wu, S. Formation Control with Collision Avoidance Through Deep Reinforcement Learning Using Model-Guided Demonstration. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 2358–2372. [Google Scholar] [CrossRef] [PubMed]
- Pu, Z.; Zhang, T.; Ai, X.; Qiu, T.; Yi, J. A Deep Reinforcement Learning Approach Combined with Model-Based Paradigms for Multiagent Formation Control with Collision Avoidance. IEEE Trans. Syst. Man, Cybern. Syst. 2023, 53, 4189–4204. [Google Scholar] [CrossRef]
- Li, Y.; Eslamiat, H.; Wang, N.; Zhao, Z.; Sanyal, A.K.; Qiu, Q. Autonomous Waypoints Planning and Trajectory Generation for Multi-rotor UAVs. In Proceedings of the Workshop on Design Automation for CPS and IoT, Naples, Italy, 25–28 June 2019; pp. 31–40. [Google Scholar]
- Eslamiat, H.; Li, Y.; Wang, N.; Sanyal, A.K.; Qiu, Q. Autonomous Waypoint Planning, Optimal Trajectory Generation and Nonlinear Tracking Control for Multi-Rotor UAVs. In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 2695–2700. [Google Scholar]
- Venturini, F.; Mason, F.; Pase, F.; Chiariotti, F.; Testolin, A.; Zanella, A.; Zorzi, M. Distributed Reinforcement Learning for Flexible and Efficient UAV Swarm Control. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 955–969. [Google Scholar] [CrossRef]
- Yang, X.; Gao, H.; Wang, C.; Jiang, Z.; Yu, H.; Wu, X. Formation Change Strategy of Multiple UAVs Based on Improved DQN. In International Conference on Guidance, Navigation and Control; Springer: Singapore, 2022; pp. 4632–4642. [Google Scholar]
- Liu, Z.; Li, J.; Shen, J.; Wang, X.; Chen, P. Leader-Follower UAVs Formation Control Based on A Deep Q-network Collaborative Framework. Sci. Rep. 2024, 14, 4674. [Google Scholar] [CrossRef]
- Konda, V.; Tsitsiklis, J. Actor-Critic Algorithms. Adv. Neural Inf. Process. Syst. 1999, 12, 1008–1014. [Google Scholar]
- Rodriguez-Ramos, A.; Sampedro, C.; Bavle, H.; De La Puente, P.; Campoy, P. A Deep Reinforcement Learning Strategy for UAV Autonomous Landing on a Moving Platform. J. Intell. Robot. Syst. 2019, 93, 351–366. [Google Scholar] [CrossRef]
- Xu, D.; Chen, G. Autonomous and Cooperative Control of UAV Cluster with Multi-Agent Reinforcement Learning. Aeronaut. J. 2022, 126, 932–951. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).