Abstract
A folding wing vertical take-off and landing (VTOL) UAV is capable of transitioning between quadrotor and fixed-wing modes, but significant alterations occur in its dynamics model and maneuvering mode during the transformation process, thereby imposing greater demands on the adaptability of its control system. In this paper, a multi-level switching control scheme based on dynamic allocation is proposed for the deformation stage. Firstly, according to the physical characteristics of the wing folding mechanism, a dynamic model is established. The influence of the incoming flow on the rotors is considered, and the dynamic coupling characteristics in its transition process are analyzed. Secondly, by inverting the changes in rotor position and axial direction, a dynamic allocation algorithm for the rotors is designed. Then, the quadrotor controller and the fixed-wing controller are switched and mixed in multiple loops to form a multi-level switching control scheme. Finally, the simulation results show that the designed multi-level switching control scheme is effective and robust in forward and backward deformation processes, and its anti-interference ability is stronger compared with that of the control scheme without dynamic allocation.
1. Introduction
Thanks to continuous technological progress, UAVs have become flexible, efficient, and diverse tools with broad application prospects, and are now used in fields such as military reconnaissance, disaster survey, agricultural plant protection [1,2], and relay communications [3,4,5,6]. In recent years, there has been a rapid increase in the types of UAVs, and among these, VTOL UAVs have been attracting the attention of many researchers [7], as they combine the advantages of both fixed-wing and multi-rotor vehicles [8] and are capable of both VTOL and long-distance cruising.
Common vertical take-off and landing UAVs fall into four categories based on their structural characteristics: hybrid [9], tailsitter [10], tilt-rotor [11,12], and tilt-wing [13,14]. Hybrid UAVs have a simple structure and easy-to-design control algorithms, but their lift and thrust systems act as deadweights to each other, which impairs their loading capacity [15]. The tailsitter UAV can change its flight mode by adjusting the fuselage attitude without the need for other tilt actuators, but its hovering stability is compromised by a large windward area [16,17]. Tilt-rotor UAVs share a common rotor system in different modes, which solves the deadweight problem, but nonlinear time-varying aerodynamic interference between the rotor and the wing is easily generated [18] and affects the stability of the UAV [19]. The relative positions of the rotor and the wing of the tilt-wing UAV are fixed, and the aerodynamic interference between the rotor and the wing can be effectively reduced through the optimized design [20], but there are also additional tilt actuators, which increase the complexity of the controller design [21]. All of the above-mentioned UAV models can realize the VTOL function, because their cruise flight generally requires the wing to provide lift, but this key component leads to the VTOL UAV occupying a larger space than that of the multi-rotor UAV with the same wheelbase, which makes it difficult to complete a VTOL mission in a narrow space or platform [22]. At the same time, better flight performance and efficiency in cruise conditions usually require a larger wing area and aspect ratio [23], which further increases the space requirement for VTOL UAVs.
Designed to meet the demands for vertical take-off and landing in confined space and to increase flexibility, a new type of UAV, the folding wing VTOL UAV, has been attracting the attention of researchers in recent years. The folding wing VTOL UAV can switch between fixed-wing and multi-rotor modes by folding its wings [24,25,26]. It can hover and cruise rapidly and offers the advantages of requiring less space for take-off and landing and increasing flexibility [27]. This feature makes it suitable for deployment and take-off on ship and truck decks with limited platform space.
Although folding wing UAVs reduce the space requirements for landing and take-off, compared with hybrid and tailsitter VTOL UAVs, the folding wing increases the complexity of the dynamics of the UAV in the transition phase. In particular, the characteristics of the propulsion system undergo significant change, including in the orientation and position of the rotor relative to the fuselage, as well as a change in the efficiency of the aileron rudders, which puts higher requirements on the adaptability of the control system and its robustness to parameter regression. Compared with traditional tilt-rotor and tilt-wing UAVs, folding wing UAVs tend to have a larger lateral windward area in hovering and transition modes, which makes them more susceptible to cross-side wind interference, which is very dangerous for the transition phase of the flight; therefore, their control systems need to have better lateral anti-interference ability and robustness.
Researchers have carried out work related to the design of a control system for variant VTOL UAVs. For tilt-rotor [28] or tilt-wing UAVs [29], a transition strategy was formulated based on the dynamic characteristics, and a deformation controller was designed based on genetic algorithm adaptive control and other methods. Unified controllers for VTOL UAVs are also receiving increasing research attention. For example, references [30,31,32] took control methods such as INDI and PID as their basis and considered the deformation amount as an active control input, so as to change the UAV morphology adaptively according to the mission requirements. This approach eliminates the necessity of designing a deformation process for the UAVs. A multi-segment folding wing UAV was designed in reference [25] to accomplish the switching of modes by setting the attitude and airspeed conditions for the transition. A transition controller based on backstepping was designed for a folding wing VTOL UAV in reference [24]. In reference [26], a UAV similar to that in reference [25] was designed. Its aerodynamic characteristics were analyzed, and a control strategy for the transition process based on the critical airspeed and the critical pitch angle was designed so that the UAV could undertake mode switching similarly to the tailsitter. However, most studies on the control of deformable VTOL UAVs do not consider the effect of incoming flow on rotor dynamics. Additionally, many papers overlook the impact of rotor position variation on multi-rotor controllers. The inflexibility of wing folding mechanisms constrains unified control algorithms, and transverse heading perturbations on the deformation process remain largely unexplored in the existing literature.
Therefore, in order to address the issues mentioned above, a multi-level switching control scheme based on dynamic allocation is proposed. Specifically, the main contributions of this paper are as follows:
- A dynamic model containing the full modal state of the UAV is developed, which takes into account the influence of incoming flow on the rotor dynamics to bring the model closer to the real physical model.
- On the basis of the established rotor model and dynamic model, the rotor dynamics and aileron aerodynamic characteristics during the deformation process are analyzed. Based on the conclusions drawn from the analysis, a dynamic allocation algorithm of rotor control variables is designed to improve the lateral stability of the folding wing UAV during deformation.
- In analyzing the dynamic model, a deformation control strategy with multi-level switching containing the dynamic allocation algorithm is designed, and a hybrid transition strategy for two sets of maneuvering mechanisms is designed according to the changes in the maneuvering characteristics of rotors and rudders.
The structure of this paper is organized as follows: Section 2 introduces the folding wing UAV and establishes its mathematical model; Section 3 analyzes the dynamic characteristics of the UAV; Section 4 lays out the design of the control strategy; Section 5 shows the experiments carried out to validate the performance of the controller; and Section 6 concludes the paper and presents future prospects.
2. Problem Statement
In this section, we will introduce a folding wing UAV, build coordinate systems, and establish a kinematic model of the UAV’s position and attitude on this basis. Section 3 and Section 4 will outline the UAV’s dynamic characterization and the design of the control strategy based on this model, respectively.
The research object of this paper is a newly designed VTOL UAV that can change rotor pull direction by folding its wings, meaning that the UAV can switch between quadrotor mode and fixed-wing mode. This deformable feature gives the UAV both vertical take-off and landing ability and fast cruise capabilities. The basic structure and deformation process of the folding wing UAV are shown in Figure 1.
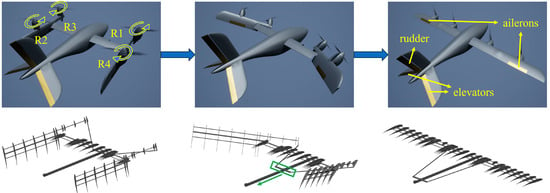
Figure 1.
Schematic of the folding wing UAV structure and its deformation process.
Inside the folding wing UAV, there is a rail with a slider on it, which has two rods attached to it that push and pull the wings to fold them. The movement of the slider is driven by a brushless motor. When the wings are folded, the UAV will be in quadrotor mode, where it can perform vertical take-off and landing; when the wings are unfolded, the UAV is in fixed-wing mode, which means it can carry out long endurance flight missions. The main physical parameters of this folding wing UAV are shown in Table 1.

Table 1.
Folding wing UAV parameter table.
Remark 1.
This folding wing UAV structure significantly reduces the space requirement for vertical take-off and landing and placement, decreasing aerodynamic interference between the rotor and the wing. This feature enhances its versatility. However, its distinctive deformation also complicates the maneuvering characteristics and controller design.
2.1. Coordinate System
In order to establish the motion model of the folding wing UAV, this study took the fixed-wing mode as the reference to establish the coordinate systems, as shown in Figure 2.
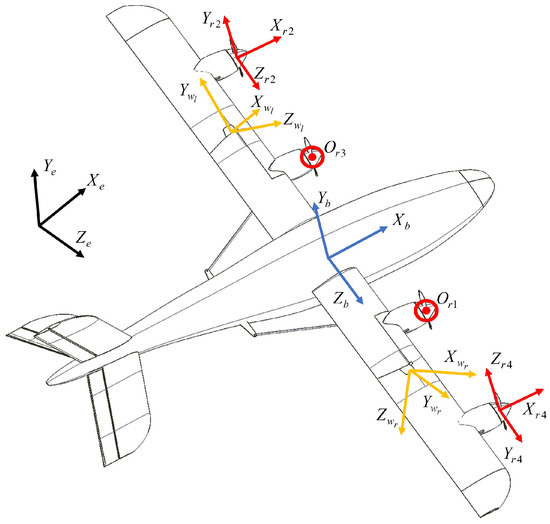
Figure 2.
Coordinate systems.
These systems include the inertial coordinate system , body coordinate system , rotor coordinate system , left wing coordinate system , and right wing coordinate system . Here, is the center of mass of the UAV in quadrotor mode; and are the centers of the wing-folding axes; and is the center of the propeller. The transformation relationship of each coordinate system is as follows:
where is the transformation matrix from the body coordinate system to the inertial coordinate system; and are the transformation matrices from the left and right wing coordinate systems to the body coordinate system; , is the transformation matrix from the rotor coordinate system to the wing coordinate system; s and c represent sin and cos, respectively; is the roll angle; is the pitch angle; is the yaw angle; and are the angular constants, which are determined by the folding structure of the wings; and is the folding angle of the wings, for the fixed-wing mode, and for the quadrotor mode.
The wing coordinate system is obtained by rotating the body coordinate system by a sequence of intrinsic rotations. The left wing coordinate system is obtained when the corresponding rotation angles are , , and . The right wing coordinate system is obtained when the rotation angles are , , and . Folding is accomplished by rotating the wing around the and axes.
Remark 2.
The wing coordinate system established in this way is solidly connected to the foldable part of the wing; and are the constant value matrices, and only the angular value γ changes during the deformation process, which reduces the computational effort.
To facilitate a representation of the rotor tension and moment on the left and right wings, the transformation matrix from the rotor coordinate system to the airframe coordinate system is unified as
2.2. Positional Kinematic Model
The main forces acting on a folding wing UAV during flight are rotor tension, aerodynamic forces, and gravity. The rotor tension can be expressed in the airframe coordinate system as
where is the normalized rotor speed, where , and the maximum rotation speed is 10,000 rpm; is the forward ratio of the rotor, and is the airspeed perpendicular to the plane of the propeller disk; and is the rotor pull coefficient, and it varies with . This is because this study considered the effects of incoming flow on the propulsion system, which is usually neglected in most VTOL vehicle models [33,34,35]. In this paper, a second-order polynomial is used to fit the propeller tension data at different forward ratios, and the data are obtained from the official APC propeller website. The curve of versus is , as shown in Figure 3.
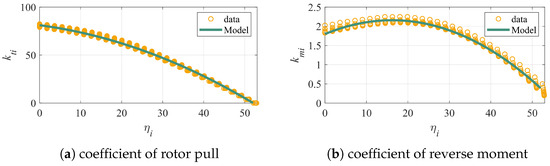
Figure 3.
Variation curve of propeller coefficients.
The aerodynamic forces on the folding wing UAV are
where is the atmospheric density; v is the airspeed; S is the reference area; , , and are the axial, normal, and lateral aerodynamic coefficients, respectively, which are calculated from the aerodynamic simulation at different folding angles; and are the angle of attack and the sideslip angle, respectively; and are the rudder deflection angles.
According to Newton’s theorem, the positional motion of a folding wing UAV is modeled as
where and are the position coordinate and velocity of the folding wing UAV in the coordinate system , respectively; g is the gravitational acceleration; and is the mass of the folding wing UAV.
2.3. Attitude Kinematic Model
The moments applied to a folding wing UAV can be categorized into moments from the rotors and aerodynamic moments, and the former can be expressed as
where are the coordinates of each rotor tension center in the airframe coordinate system; and are the coordinates of the centers of the rotational axes of the wings on both sides in the airframe coordinate system; the superscript indicates that the value of this variable is taken at , where is easily measured and from which the position of the rotor centroid can be deduced for each folding angle; and is the coefficient of the reverse moment, which is similar to the coefficient , and it also varies with . In this paper, a second-order polynomial is fitted to the rotor reversing moment data at different forward ratios. The resulting variation curve of with is obtained as , as shown in Figure 3.
Remark 3.
Figure 3 demonstrates that the incoming flow exerts a significant impact on the propeller dynamic performance. The conventional approach of assuming constant values for rotor tension and reversing moment coefficients is inappropriate. In this study, the forward ratio is introduced to calculate the rotor dynamics more closely with regard to physical properties, and the model developed has a higher granularity.
The aerodynamic moment applied to the folding wing UAV can be expressed as
where , , and are the roll, yaw, and pitch moment coefficients, respectively, which are calculated by aerodynamic simulation, and b and are the wingspan length and average aerodynamic chord length, respectively.
According to Euler’s theorem, the attitude kinematic model of the folding wing UAV can be obtained as
where is the attitude Euler angle; is the body angular velocity; is the transformation matrix from the body angular velocity to the Euler angular velocity; and is the body inertia matrix.
3. Problem Analysis
In this section, the dynamics of the folding wing UAV during the deformation process will be analyzed, as well as the challenges of its special deformation mode in flight control, which will provide the basis for the design of the control scheme in Section 4.
During the deformation process, the wings will rotate around the axis, which not only allows the rotor orientation to switch between upward and forward, realizing modal change, but also folds the wings, reducing the occupied space. However, the tilted axis of rotation also poses the following problems:
- With regard to the effect of rotor dynamics, it should be noted that the direction of rotor pull does not change in a single plane during the deformation process. Furthermore, the positional distribution of the four rotors will be significantly altered, while the position of the center of mass of the airframe will be regulated. These changes will all impact the effect of rotor maneuvering on the airframe, and consequently the performance of the quadrotor controller.
- On the aerodynamic side, wing folding will change the aerodynamic configuration of the whole aircraft, and will especially cause changes in the aerodynamic characteristics of the ailerons, which will seriously affect the aerodynamic maneuvering characteristics of the UAV.
Each of these issues will be analyzed in detail below.
3.1. Rotor Dynamic Characterization
In order to investigate the distinction between rotor dynamic characteristics in the deformation mode and in the quadrotor mode, we analyzed the changes in rotor dynamic characteristics based on Equations (7) and (10). The position and attitude of the UAV are assumed to be fixed at 0. The rotational speeds of the four rotors are set to 5000 rpm, and the UAV is deformed from the fixed-wing mode to the quadrotor mode. In the airframe coordinate system, the variation in the unit vector representing the direction of the rotor pull is shown in Figure 4.
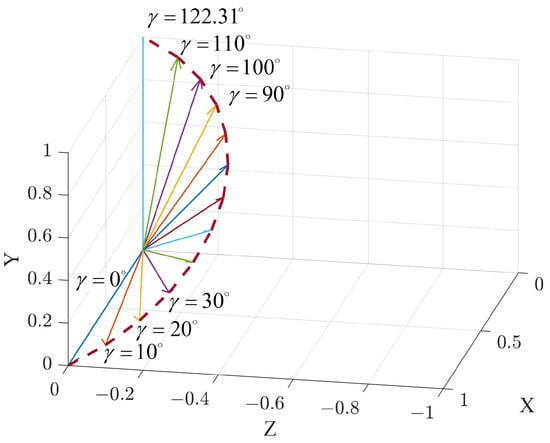
Figure 4.
Variations in orientation of rotor.
The changes in the tension and reversal moments of each rotor with the deformation angle are illustrated in Figure 5.
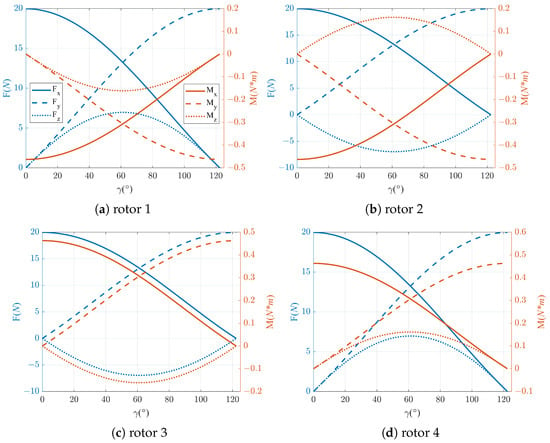
Figure 5.
Tension and reversal torque of the four rotors.
, , and are the components of the rotor tension force on each axis of the airframe coordinate system; , , and are the components of the rotor reversal moment on each axis of the airframe coordinate system. Figure 5 illustrates that the conversion from fixed-wing mode to quadrotor mode results in disparate changes in rotor tension and reversal moments for each rotor. However, notable alterations are observed in each of their components.
From the perspective of rotor tension, the tension of each rotor undergoes a gradual transition from the direction to the direction. However, unlike traditional tilt-rotor UAVs, each rotor will generate a split force in the direction, and at a rotational speed of 5000 rpm, the lateral component force generated will reach a maximum of 6.7 N, accounting for of the total tension at this time. Therefore, the rotational speed difference between the left and right rotors will significantly affect the lateral motion of the UAV, resulting in a coupling problem for position control. From the point of view of the rotor reversal moment, it will gradually transition from the direction to the direction and also generate a component in the direction, meaning that the rotor reversal moment will affect the roll, pitch, and yaw motions of the folding wing UAV at the same time. When using the maneuvering method in quadrotor mode, i.e., when controlling the yaw motion by virtue of the reversal moment, there will be a serious coupling phenomenon.
We further take into account the moment formed by the rotor pull force acting on the center of gravity. The variations in the center of gravity and inertia are shown in Figure 6. The variations in the tension force and moment generated by rotor 1 on the airframe are shown in Figure 7.
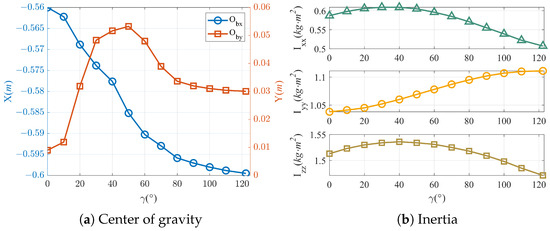
Figure 6.
Variation curves of center of gravity position and inertia.
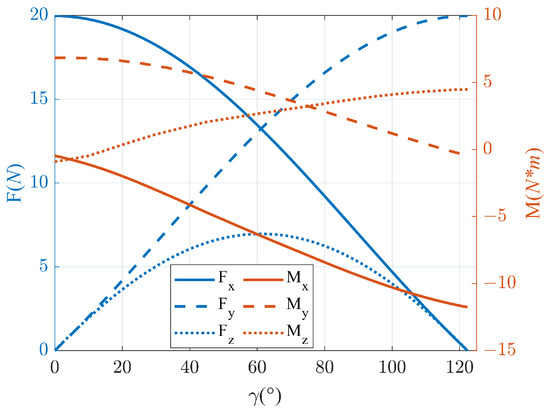
Figure 7.
Rotor tension and torque.
and are the center of gravity distances relative to the nose point; and , , and are the components of the rotor moment in each axis of the airframe coordinate system, respectively. From Figure 7, it can be seen that there is a substantial change in the components of in each axis during the deformation from a quadrotor to a fixed wing. The pitch and roll moments will decrease to near 0 when approaching the fixed-wing mode, and the yaw moment will even undergo a positive or negative polarity shift (from −0.5 N·m to 6.8 N·m).
The preceding analysis demonstrates that the rotor dynamic characteristics in the deformation mode of the folding wing UAV exhibit a considerable degree of variability, resulting in markedly disparate maneuvering characteristics when compared to those observed in the quadrotor mode. This is mainly reflected in the severe coupling of the maneuvering channels and the dynamic changes in the maneuvering characteristics. If the deformation process follows the quadrotor control distribution mode throughout, it will undoubtedly reduce the control efficiency, and may even lead to the reverse maneuvering of the actuator, which puts the vehicle in danger. Therefore, the static allocation method of rotor control in the quadrotor mode will no longer be applicable to the deformation mode.
3.2. Aerodynamic Characterization
In the deformation mode of the folding wing UAV, the position of the ailerons relative to the airframe is also changed, and the layout of the wing is changed significantly. As can be seen in Figure 1, during the deformation process, the ailerons will no longer be deflected around the axis, which results in a notable alteration to its aerodynamic maneuvering characteristics. In order to analyze the change in the ailerons’ aerodynamic characteristics, the ailerons were deflected by at different folding angles and angles of attack. The additional moment coefficients are shown in Figure 8.
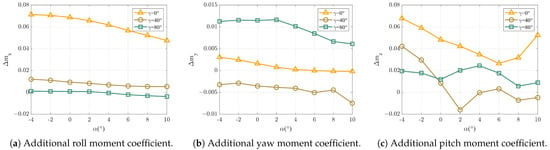
Figure 8.
Additional aerodynamic coefficients due to aileron deflection.
In Figure 8a, it can be seen that the roll maneuvering efficiency of the ailerons decreases substantially when the folding wing UAV transitions from a fixed-wing mode to a quadrotor mode, i.e., when the folding angle gradually increases. In taking the angle of attack as an example, the additional roll moment coefficient at is lower than that at . When , the aileron almost loses its roll control effect and even generates a reverse roll moment when . As can be seen from Figure 8b, the additional yaw moment coefficient decreases at the beginning of the deformation and occurs in reverse. However, the additional yaw moment coefficient starts to increase as the folding angle increases further. When and , the aileron deflection produces an additional yaw moment coefficient of , which already corresponds to of the yaw rudder effect at this point, indicating a large-maneuver coupling situation. As shown in Figure 8c, the additional pitching moment coefficient does not change much during the folding deformation process, and the maximum value does not exceed , indicating that the coupled maneuvering effect of the aileron deflection on the pitching channel is small.
The above analysis shows that the aileron maneuvering characteristics in the deformation mode are highly variable. As the folding angle increases, the roll maneuvering efficiency of the aileron will decrease sharply, and at , a large additional yaw moment will be generated, resulting in the coupling of the maneuvering channel. Therefore, in the process of deformation, the dynamic changes to the actuator maneuvering characteristics need to be taken into account, otherwise the uncontrolled phenomenon of the roll and yaw channels will occur.
4. Control Scheme Design
In this section, for the problems of quadrotor control coupling and drastic changes to actuator maneuvering characteristics during deformation, we establish the controllers in quadrotor mode and fixed-wing mode, respectively, and then design a dynamic allocation algorithm of rotor control and a hybrid transition strategy for the two controllers.
4.1. Non-Deforming Mode Controller Framework
The dynamic models and operation manners of the folding wing UAV are significantly different when in fixed-wing and quadrotor modes, and it is difficult to meet the full-state flight control requirements with a single fixed controller. In this study, the cascade controllers for quadrotor mode and fixed-wing mode were built separately, and the structures of the controllers for the two states are shown in Figure 9 and Figure 10, respectively, where the left superscript denotes the command value, denotes the control command outputted by the quadrotor controller, and denotes the control command outputted by the fixed-wing controller. The position control loop, velocity control loop, attitude control loop, and angular velocity control loop all employ the PID control method.

Figure 9.
Quadcopter controller structure.

Figure 10.
Fixed-wing controller structure.
The two controllers are similar in structure, but the main difference lies in the yaw angle control. The quadrotor controller takes the current speed command and converts it to the yaw command value, while the fixed-wing controller derives the yaw speed command according to the current roll and pitch angles and the flight speed to complete the banked turn, i.e.,
where is the yaw angle command of the quadrotor controller at the previous moment.
4.2. Dynamic Allocation Algorithm for Rotor Control
As demonstrated in Section 3, the rotor dynamics and maneuvering characteristics of the folding wing UAV exhibit significant variability. This may result in the irrational allocation of control commands by the quadrotor static mixer, which could negatively impact the control performance of the quadrotor controller. Therefore, in this paper, a rotor control dynamic allocation algorithm is proposed for the folding wing UAV model to improve the controller performance during the deformation process.
The actual physical meaning of rotor control distribution is the distribution of control signals to the various actuators, converting the control signals into direct drive variables for the actuators. For the control of a quadrotor UAV, this means the conversion of the control commands into rotation speed control commands for the four rotor motors. In this paper, the rotor control allocation algorithm is combined with the changes in rotor tension coefficients and rotor positions, so that the mixer changes dynamically according to the flight state to adapt to the current control requirements. The main block diagram of the algorithm is shown in Figure 11.
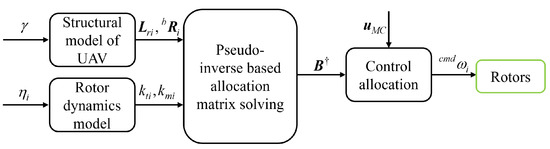
Figure 11.
Diagram of the allocation algorithm.
Firstly, Equations (7) and (10) are rewritten as
where denotes the element in the first row and first column of . and and similar. The combined force and moment exerted by the rotor on the airframe can be expressed as
where is the control efficiency matrix of the four rotors for the folding wing UAV. The pseudo-inverse that gives the rotor dynamic allocation matrix is the following:
Then, the control command can be converted into a rotational speed command for the four rotor motors through , i.e,
4.3. Multi-Level Switching Transition Control Scheme
For the transition phase control of VTOL UAV, the traditional hybrid transition control scheme only fuses or assigns the control variables and . It cannot realize switching at the level of the attitude angle command and angular velocity command. This may lead to function conflict between the two controllers. To illustrate, consider a case in which the UAV requires forward acceleration during deformation. In this instance, the quadrotor controller will generate a negative pitch angle command to create a rotor pull-forward component force. Conversely, the fixed-wing controller may issue a positive pitch angle command to maintain the flight altitude, thereby maintaining a positive angle-of-attack state. At this juncture, the two sets of actuators will execute conflicting control commands, thereby increasing the control energy loss.
In order to avoid the rotors and rudders executing opposite or uncoordinated control commands, this paper proposes a multi-level switching transition control scheme, and its overall structure is shown in Figure 12. Here, FW refers to fixed wing and MC refers to multi-rotor mode. The position manager can output different position commands according to the current flight mode. The attitude and throttle switcher will switch the attitude angle commands and throttle commands from different controllers. It will then transmit the desired attitude to the attitude angle control loops of the two controllers. Similarly, the angular velocity command switcher selects one of the two angular velocity commands and outputs it. The actuator mixer completes the control mixing of the rotor and rudder and then outputs signals to drive the rotor motors and rudder servos.
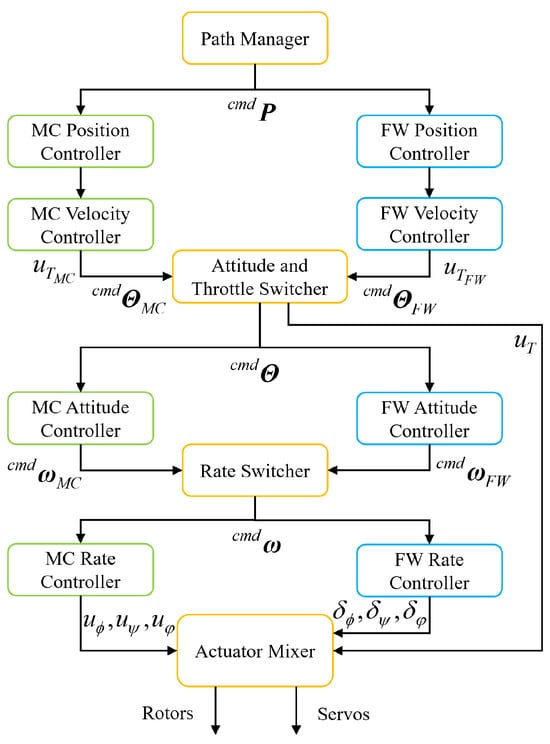
Figure 12.
Multi-level switching transition control scheme.
Next, the path manager and switcher strategies are designed for both forward deformation (MC to FM) and backward deformation (FM to MC) processes.
4.3.1. Forward Deformation
The folding wing UAV transitions from a quadrotor hovering mode to a fixed wing mode using the following hybrid transition scheme.
(1) Path manager
During the deformation process, the height change and lateral displacement are of greater significance than the forward displacement. It is anticipated that the UAV will fly at a fixed height and direction along the current heading to complete the deformation. Therefore, the expected values of vertical and lateral displacement have been set to 0.
(2) Attitude and throttle command switcher
This switcher needs to select the attitude angle command and the throttle command to be output. For the attitude angle command, at this stage, we elected to output the fixed-wing controller’s control command, i.e., . This is due to the fact that, during the deformation process, the UAV experiences a rapid acceleration as the rotor tilts forward. Consequently, the fixed-wing controller’s attitude angle command is directly related to the position control, particularly the pitch angle command. As the altitude of the flight decreases during the transition process, the fixed-wing speed controller increases the pitch angle command to enhance the lift, thereby maintaining altitude stabilization. For the throttle command, we chose to use the throttle command output from the quadrotor controller, i.e., . This is because can play a role in controlling the altitude throughout the whole deformation process. In the early stage of deformation, it mainly relies on the rotor upward tension to maintain the altitude. In the late stage of deformation, it mainly relies on the forward tension to increase the forward flight speed, thus increasing the lift to maintain the altitude. As a result, without designing other algorithms, the folding wing UAV can realize the automatic acceleration of the fixed height forward flight process.
(3) Rate command switcher
The speed of the UAV increases rapidly during the deformation process, and in order to maintain the flight stability, the yaw motion needs to be coordinated with the roll motion. This study therefore selected the fixed-wing attitude angular velocity command as .
(4) Actuator mixer
Due to the unique deformation of the folding wing UAV, the two sets of maneuvering mechanisms, the rotors and the rudders, need to complete the switching process during the deformation process. From the analysis in Section 3.1, it can be seen that in the process of changing the UAV from quadrotor mode to fixed-wing mode, when the folding angle is near 60°, the main tension direction of the rotor will change from upward to forward. The rotor manipulation mode of the UAV will change significantly at this time. The efficiency of the rudder surface will also rapidly improve during acceleration. This paper therefore proposes that the switching point of the manipulation mechanism should be set at . From the analysis in Section 3.2, it can be seen that the control efficiency of the rudder surface varies with the deformation angle, particularly for the aileron. During the intermediate deformation state, the aileron’s deflection generates a significant additional yaw moment, resulting in a notable coupling effect. Therefore, in order to ensure the stability of the UAV, the aileron rudder can only be enabled when the folding angle is small. As can be seen from Figure 8b, when the wing folding angle is , the yaw moment coefficient brought about by the aileron deflection is smaller; therefore, this paper chooses to start enabling the aileron rudder surface when . In summary, the rotor and rudder mixing strategy designed is as follows:
where , , and are the control mixing coefficients, and their variation curves with the wing folding angle are shown in Figure 13.
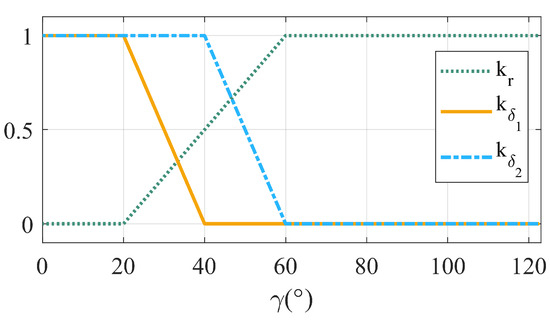
Figure 13.
Control mixing coefficient variation graph.
4.3.2. Backward Deformation
Here, the folding wing UAV transitions from the fixed-wing cruise mode to quadrotor mode, and the switching transition scheme is basically the same as that of forward deformation. The only difference lies in the pitch angle command. To prevent the airspeed from becoming excessively high when the UAV transitions to quadrotor mode, resulting in control difficulties, an adaptive law for the pitch angle command was designed to address the reverse deformation:
where and are the control coefficients; is the horizontal velocity of the UAV; is the horizontal acceleration of the UAV; and is the pitch angle command limit during reverse deformation. The main purpose of this adaptive variation law is to increase the pitch angle so that the folding wing UAV can decelerate during the reverse deformation process and obtain a lower airspeed before reaching quadrotor mode.
5. Simulation Experiments
In order to verify the feasibility, superiority, and robustness of the multi-level switching transition control scheme of the rotor control dynamic allocation, a comparative simulation and parameter perturbation simulation were conducted.
5.1. Flight Simulation Comparison Experiment
In this experiment, the folding wing UAV will forward-deform from a hovering state to a fixed-wing cruising state and will then perform a reverse deformation to quadrotor mode and then hover. We added lateral wind disturbances during forward and reverse deformation. The process of the task is shown schematically in Figure 14.

Figure 14.
Description of mission scenarios.
The simulation’s initial parameters were set as shown in Table 2. The simulation results of the forward deformation stage are shown in Figure 15, and the simulation results of the backward deformation stage are shown in Figure 16, where the red vertical lines represent the beginning or ending moments of deformation.

Table 2.
Simulation parameter settings.
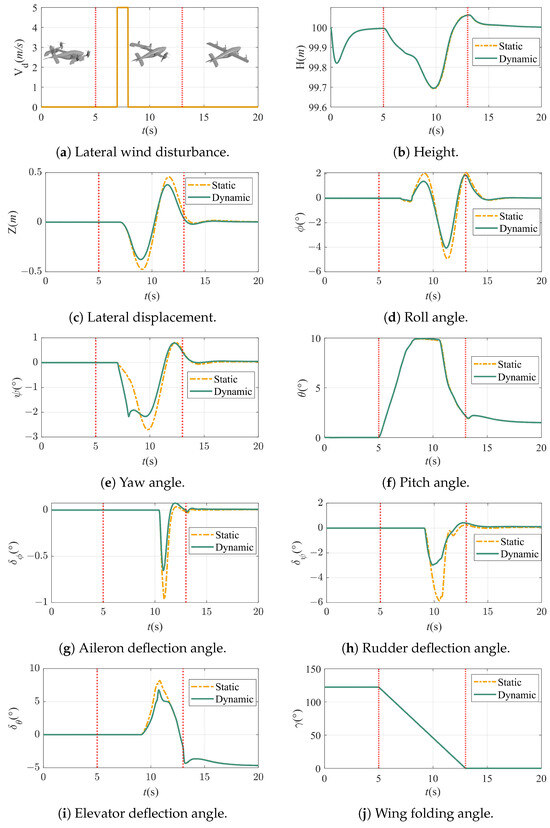
Figure 15.
Forward deformation simulation results.
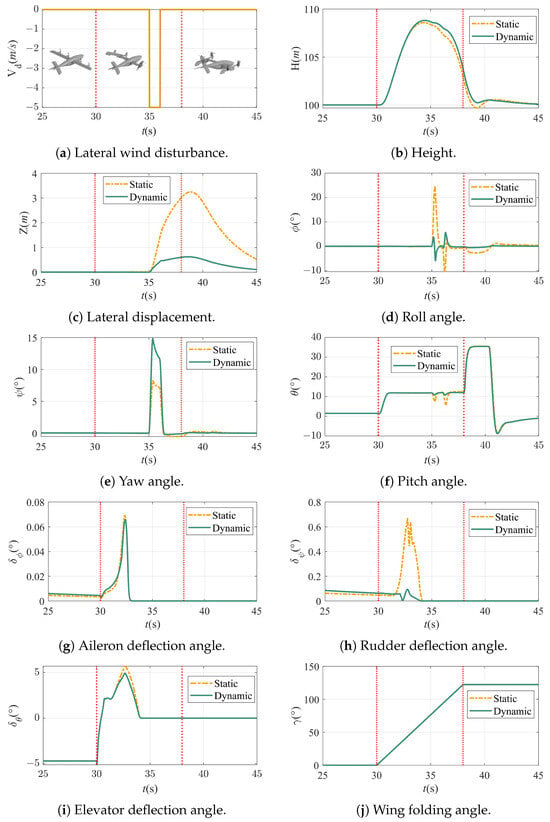
Figure 16.
Backward deformation simulation results.
As illustrated in Figure 15, the multi-level hybrid control scheme designed in this study can maintain the stability of the altitude during the forward deformation of the folding wing UAV. The maximum drop height is not more than 0.31 m under the two control allocation schemes. In terms of anti-disturbance, the lateral wind affects the lateral motion as well as the attitude angle of the UAV, but the controller based on the dynamic allocation scheme can control the lateral disturbance displacement within 0.38 m compared to 0.46 m under the static scheme. The roll angle fluctuation under the dynamic allocation scheme is in the range of compared to under the static scheme. Overall, the dynamic control allocation scheme reduced the displacement due to lateral disturbances by and the roll angle fluctuations by . This is because the quadrotor controller under the dynamic allocation can adjust the attitude faster and more accurately, allowing the heading to be adjusted rapidly and avoiding a large deviation from the course. This can also be seen in the yaw angle change curve. In terms of rudder usage, the rudder deflection is smaller under the dynamic allocation scheme, which also shows that the quadrotor controller is more sensitive under dynamic allocation.
As can be seen in Figure 16, in terms of height control, although the pitch angle adaptive law increases the angle of attack, causing the flight height to climb, this is safe and acceptable. In terms of anti-disturbance, similar to forward deformation, the lateral disturbance displacement under the dynamic allocation scheme is 0.5 m, while under the static allocation scheme, it is 3.2 m. At this time, due to the larger forward flight speed, the lateral wind will have a greater impact on the UAV’s attitude, and the roll angle under the static allocation scheme will already be close to , whereas the fluctuation of the roll angle under the dynamic allocation scheme will only be , which is in the safe range. In summary, the dynamic control allocation scheme reduced the displacement due to lateral disturbances by and the roll angle fluctuations by . It can also be seen from the change curves of the yaw angle and pitch angle that the attitude adjustment under the dynamic allocation scheme is more rapid, resulting in smaller fluctuations in the lateral disturbance displacement and roll angle of the UAV. In summary, the multi-level hybrid controller based on the dynamic allocation of rotor control is reasonable and feasible, and its anti-disturbance ability is stronger than that of the controller under the traditional static allocation scheme.
5.2. Simulation with Parameter Perturbations
In this study, in order to verify the robustness of the multi-level hybrid control scheme with the dynamic allocation of rotor control, the parameters of the folding wing UAV were subjected to a combination of perturbations, and the range of perturbations is shown in Table 3. The initial conditions and deformation moments of the flight simulation are the same as those of the previous experiment, and the results are shown in Figure 17. A visual simulation video based on the Rflysim [36] platform can be viewed at https://pan.baidu.com/s/1ruKs4zJ_j3uF3YZSPTPSEg?pwd=zqx6 (accessed on 7 June 2024).

Table 3.
Perturbation range table.
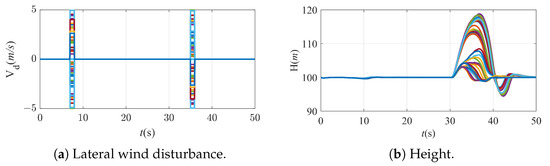
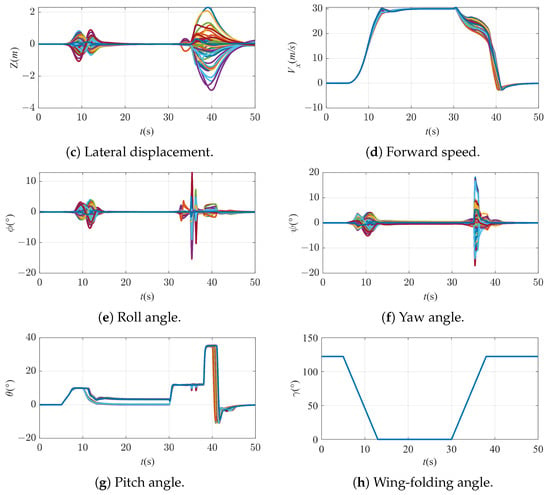
Figure 17.
Results of simulation with parameter perturbations.
As can be seen from Figure 17, when the folding wing UAV has uncertainties in its inertia parameters, the center of mass position, the body aerodynamic parameters, and external disturbances, etc., the UAV will still be able to realize the transition of folding deformation stably. During the simulation, the range of the UAV’s altitude drop was small, the lateral stability was satisfactory, the fluctuation of the roll angle and yaw angle was no more than , and the lateral displacement was no more than 3 m. This indicates that the rotor dynamic allocation algorithm and the multi-level switching transition control scheme are robust and have strong practicability.
6. Conclusions
With the aim of tackling the control problem of the folding wing UAV deformation transition process, a full-mode dynamic model was established, its dynamic characteristics were analyzed, and the control strategy was designed according to the model’s characteristics. In general, the main contributions of this paper are as follows:
- Based on the structural characteristics of the folding wing UAV, a dynamic and kinematic model including the influence of the incoming flow on the rotor dynamics was established.
- Through an analysis of rotor dynamic and aerodynamic maneuvering characteristics, the rotor coupling characteristics and the efficiency change characteristics of the aileron during the deformation process are obtained.
- According to the change rule of the rotor position relative to the airframe, the dynamic allocation algorithm of rotor control was designed to adapt to the folding angle of the folding wing UAV, which improves the resistance of the UAV to lateral interference in the deformation process.
- A multi-level switching control strategy was designed for the forward and reverse deformation processes of the folding wing VTOL UAV, and the two sets of maneuvering mechanisms are fused and transitioned; the experiment proves that the control algorithm has strong robustness.
In future research work, we will study the intelligent coordination strategy of deformation and flight in detail to improve the efficiency of mission execution and also design a flight control system based on advanced control algorithms to further enhance the performance of the vehicle and conduct complete deformation flight tests.
Author Contributions
Conceptualization, Z.L. and B.Y.; methodology, Z.L.; software, Z.L.; validation, Z.L., S.L. (Shuangxi Liu), and B.Y.; formal analysis, T.Z.; investigation, S.L. (Shaoyi Li); resources, B.Y.; data curation, Z.M.; writing—original draft preparation, Z.L. and S.L. (Shuangxi Liu); writing—review and editing, Z.L. and B.Y.; visualization, Z.L.; supervision, B.Y.; project administration, B.Y.; funding acquisition, B.Y. All authors have read and agreed to the published version of the manuscript.
Funding
The authors appreciate the financial support provided by the National Natural Science Foundation of China (NSFC) (grant no. 62173274).
Data Availability Statement
Some or all data, models, or code generated or used during the study are proprietary or confidential in nature and may only be provided with the following restriction: All data may be provided upon request, but codes are proprietary or confidential in nature.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ducard, G.J.; Allenspach, M. Review of designs and flight control techniques of hybrid and convertible VTOL UAVs. Aerosp. Sci. Technol. 2021, 118, 107035. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Khan, M.A.; Noor, F.; Ullah, I.; Alsharif, M.H. Towards the unmanned aerial vehicles (UAVs): A comprehensive review. Drones 2022, 6, 147. [Google Scholar] [CrossRef]
- Mahmood, A.; Vu, T.X.; Khan, W.U.; Chatzinotas, S.; Ottersten, B. Optimizing computational and communication resources for MEC network empowered UAV-RIS communication. In Proceedings of the 2022 IEEE Globecom Workshops (GC Wkshps), Rio de Janeiro, Brazil, 4–8 December 2022; pp. 974–979. [Google Scholar]
- Mahmood, A.; Vu, T.X.; Chatzinotas, S.; Ottersten, B. Joint optimization of 3D placement and radio resource allocation for per-UAV sum rate maximization. IEEE Trans. Veh. Technol. 2023, 72, 13094–13105. [Google Scholar] [CrossRef]
- Mahmood, A.; Vu, T.X.; Khan, W.U.; Chatzinotas, S.; Ottersten, B. Joint computation and communication resource optimization for beyond diagonal UAV-IRS empowered MEC networks. arXiv 2023, arXiv:2311.07199. [Google Scholar]
- Mahmood, A.; Vu, T.X.; Sharma, S.K.; Chatzinotas, S.; Ottersten, B. Multi-objective optimization for 3D placement and resource allocation in OFDMA-based multi-UAV networks. In Proceedings of the 2023 IEEE 97th Vehicular Technology Conference (VTC2023-Spring), Florence, Italy, 20–23 June 2023; pp. 1–6. [Google Scholar]
- Hu, J.; Wei, J.; Liu, K.; Yu, X.; Cao, M.; Qin, Z. Hybrid Mode: Routinization of the Transition Mode as the Third Common Mode for Compound VTOL Drones. Drones 2024, 8, 93. [Google Scholar] [CrossRef]
- Bauersfeld, L.; Spannagl, L.; Ducard, G.J.; Onder, C.H. MPC flight control for a tilt-rotor VTOL aircraft. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2395–2409. [Google Scholar] [CrossRef]
- Kikumoto, C.; Urakubo, T.; Sabe, K.; Hazama, Y. Back-transition control with large deceleration for a dual propulsion VTOL UAV based on its maneuverability. IEEE Robot. Autom. Lett. 2022, 7, 11697–11704. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, J.; Yuan, X.; Wang, X.; Kuang, M.; Shi, H. Dynamic characteristics analysis and robust transition control of tail-sitter VTOL UAVs. Aerosp. Sci. Technol. 2024, 145, 108868. [Google Scholar] [CrossRef]
- Tavoosi, J. Hybrid intelligent adaptive controller for tiltrotor UAV. Int. J. Intell. Unmanned Syst. 2021, 9, 256–273. [Google Scholar] [CrossRef]
- Willis, J.; Johnson, J.; Beard, R.W. State-dependent LQR control for a tilt-rotor UAV. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 4175–4181. [Google Scholar]
- Zhu, J.; Yang, Y.; Wang, X.; Yuan, X.; Yang, X. Attitude control of a novel tilt-wing UAV in hovering flight. Sci. China Inf. Sci. 2023, 66, 154201. [Google Scholar] [CrossRef]
- Takayama, T.; Uchiyama, K.; Masuda, K. Controller Design Using SDRE Method for Tilt-Wing UAV. In Proceedings of the 2020 11th International Conference on Mechanical and Aerospace Engineering (ICMAE), Athens, Greece, 14–17 July 2020; pp. 102–106. [Google Scholar]
- Rehan, M.; Akram, F.; Shahzad, A.; Shams, T.; Ali, Q. Vertical take-off and landing hybrid unmanned aerial vehicles: An overview. Aeronaut. J. 2022, 126, 2017–2057. [Google Scholar] [CrossRef]
- Saeed, A.S.; Younes, A.B.; Islam, S.; Dias, J.; Seneviratne, L.; Cai, G. A review on the platform design, dynamic modeling and control of hybrid UAVs. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 806–815. [Google Scholar]
- Lyu, X.; Zhou, J.; Gu, H.; Li, Z.; Shen, S.; Zhang, F. Disturbance Observer Based Hovering Control of Quadrotor Tail-Sitter VTOL UAVs Using H∞ Synthesis. IEEE Robot. Autom. Lett. 2018, 3, 2910–2917. [Google Scholar] [CrossRef]
- Huang, H.; Yu, L.; He, G.; Wang, X. Tilting Curve Design of a Novel Tilt-rotor UAV Based on Rotor/Wing Interference Model. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 2356–2361. [Google Scholar]
- Wang, Z.; Wang, Q.; Yu, H.; Duan, D.; Ding, Z.; Li, J. Trimming analysis method of quad tilt rotor based on aerodynamic interference model. J. Aircr. 2021, 58, 253–265. [Google Scholar] [CrossRef]
- Droandi, G.; Zanotti, A.; Gibertini, G. Aerodynamic interaction between rotor and tilting wing in hovering flight condition. J. Am. Helicopter Soc. 2015, 60, 042011. [Google Scholar] [CrossRef]
- Hartmann, P.; Meyer, C.; Moormann, D. Unified velocity control and flight state transition of unmanned tilt-wing aircraft. J. Guid. Control. Dyn. 2017, 40, 1348–1359. [Google Scholar] [CrossRef]
- Garg, P. Characterisation of Fixed-Wing Versus Multirotors UAVs/Drones. J. Geomat. 2022, 16, 152–159. [Google Scholar] [CrossRef]
- Kretov, A.; Tiniakov, D. Evaluation of the mass and aerodynamic efficiency of a high aspect ratio wing for prospective passenger aircraft. Aerospace 2022, 9, 497. [Google Scholar] [CrossRef]
- Patel, T.; Kumar, M.; Abdallah, S. Control of Hybrid Transitioning Morphing-wing VTOL UAV. IFAC-PapersOnLine 2022, 55, 554–559. [Google Scholar] [CrossRef]
- D’Sa, R.; Papanikolopoulos, N. Design and experiments for multi-section-transformable (MIST)-UAV. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 1878–1883. [Google Scholar]
- Chen, Q.; Shi, Z.; Zhan, W.; Yao, L.; Tong, S. Aerodynamic layout and control strategy design and flight verification of a wing-foldable variant VTOL aircraft. Acta Aeronaut. Astronaut. Sin. 2024, 45, 155–172. [Google Scholar]
- Vourtsis, C.; Rochel, V.C.; Müller, N.S.; Stewart, W.; Floreano, D. Wind defiant morphing drones. Adv. Intell. Syst. 2023, 5, 2200297. [Google Scholar] [CrossRef]
- Hegde, N.T.; George, V.; Nayak, C.G.; Kumar, K. Transition flight modeling and robust control of a VTOL unmanned quad tilt-rotor aerial vehicle. Indones. J. Electr. Eng. Comput. Sci. 2020, 18, 1252–1261. [Google Scholar]
- Yildiz, Y.; Unel, M.; Demirel, A.E. Nonlinear hierarchical control of a quad tilt-wing UAV: An adaptive control approach. Int. J. Adapt. Control Signal Process. 2017, 31, 1245–1264. [Google Scholar] [CrossRef]
- Milz, D.; Looye, G. Tilt-wing control design for a unified control concept. In Proceedings of the AIAA Scitech 2022 Forum, San Diego, CA, USA, 7 January 2022; p. 1084. [Google Scholar]
- Lin, Z.; Liu, Q.; Liu, S.; Yan, B. Transition Controller Design of Tilt-Rotor UAV Based on Incremental Nonlinear Dynamic Inversion. In Proceedings of the IECON 2023-49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 16–19 October 2023; pp. 1–6. [Google Scholar]
- Allenspach, M.; Ducard, G.J.J. Nonlinear model predictive control and guidance for a propeller-tilting hybrid unmanned air vehicle. Automatica 2021, 132, 109790. [Google Scholar] [CrossRef]
- Suiçmez, E.; Kutay, A.T. Full envelope nonlinear flight controller design for a novel electric VTOL (eVTOL) air taxi. Aeronaut. J. 2024, 128, 966–993. [Google Scholar] [CrossRef]
- Kong, L.; Reis, J.; He, W.; Silvestre, C. Comprehensive nonlinear control strategy for VTOL-UAVs with windowed output constraints. IEEE Trans. Control Syst. Technol. 2023, 31, 2673–2684. [Google Scholar] [CrossRef]
- Durán-Delfín, J.; García-Beltrán, C.; Guerrero-Sánchez, M.; Valencia-Palomo, G.; Hernández-González, O. Modeling and Passivity-Based Control for a convertible fixed-wing VTOL. Appl. Math. Comput. 2024, 461, 128298. [Google Scholar] [CrossRef]
- Dai, X.; Ke, C.; Quan, Q.; Cai, K.Y. RFlySim: Automatic test platform for UAV autopilot systems with FPGA-based hardware-in-the-loop simulations. Aerosp. Sci. Technol. 2021, 114, 106727. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).