An Integrated Geometric Obstacle Avoidance and Genetic Algorithm TSP Model for UAV Path Planning

Abstract

In this paper, we propose an innovative approach for the path planning of Uninhabited Aerial Vehicles (UAVs) that combines an advanced Genetic Algorithm (GA) for optimising missions in advance and a geometrically based obstacle avoidance algorithm (QuickNav) for avoiding obstacles along the optimised path. The proposed approach addresses the key problem of determining an optimised trajectory for UAVs that covers multiple waypoints by enabling efficient obstacle avoidance, thus improving operational safety and efficiency. The study highlights the numerous challenges for UAV path planning by focusing on the importance of both global and local path planning approaches. To find the optimal routes, the GA utilises multiple methods of selection to optimise trajectories using the Cartesian Coordinate System (CCS) data transformed from a motion capture system. The QuickNav algorithm applies linear equations and geometric methods to detect obstacles, guaranteeing the safe navigation of UAVs and preventing real-time collisions. The proposed methodology has been proven useful in reducing the total distance travelled and computing times and successfully navigating UAVs across different scenarios with varying numbers of waypoints and obstacles, as demonstrated by simulations and real-world UAV flights. This comprehensive approach provides advantageous perspectives for real-world applications in a variety of operational situations and improves UAV autonomy, safety, and efficiency.

1. Introduction

Modern technological developments have made UAVs a part of contemporary human culture. UAV technology has developed significantly in recent decades and is currently utilised extensively in military and civilian applications. UAV autonomous flight systems with obstacle avoidance received attention from scholars worldwide, becoming a topic of research in UAVs [1]. The future evolution of UAVs will inevitably include autonomous mission performance and one of the most essential developments to enhance UAV autonomy and guarantee flight safety is path planning [2,3]. The successful deployment of UAVs at their designated mission site relies on effective path planning, which serves as the fundamental aspect of the flight towards the mission location [4].

Several sectors, including the military, farming, industry, and academics, have long been interested in UAV route planning [5,6,7]. Path planning is an essential method for UAVs, encompassing two main components: global path planning (offline) and local path planning (online) [8,9,10]. Global planning, also known as static path planning, involves determining the path when complete environmental information is available. In circumstances in which the environment is uncertain or just partially understood, local planning methods are used for path planning. Local planning can be considered as a form of dynamic path planning [11,12].

The challenges of path planning involve determining the optimal sequence of valid routes for travel to achieve strategic objectives while reducing expenses, such as the total length of the trip. This technique has traditionally been associated with addressing the Travelling Salesmen Problem (TSP), in which the cost of travel is determined by the distance between consecutive sites on the road [13]. Although UAV routes are significantly more complex, such an approach supports generic optimisation, which shares a similar difficulty with UAV path planning [14].

Moreover, UAVs are progressively being employed for gathering data in inaccessible regions through the use of Wireless Sensor Networks (WSNs) [15,16]. In these situations, UAVs are required to travel to specified waypoints in order to acquire data. This represents a challenge for solving the TSP as it involves optimising journey distance and minimising operational time [17,18]. Furthermore, in precision agriculture, it is important to have effective path planning for UAVs to navigate specific locations that have been identified by images or data analysis, especially for tasks like targeted pesticide application for controlling weeds [19]. Aligning the optimisation of these paths of flight with the aims of TSP optimisation requires ensuring complete coverage while minimising the expenditure of time [20].

Numerous studies have been conducted on path planning and obstacle avoidance algorithms, leading to the development of different study methodologies. The path planning algorithms can be categorised into two groups: classic optimisation methods and new intelligence algorithms. Conventional optimisation algorithms contain the steepest descent approach, optimal control technique, and derivative connection approach. The most prevalent instances of modern intelligence algorithms are Genetic Algorithms, Artificial Neural Networks, and Ant Colony Optimisation (ACO) [21,22].

Several conventional optimisation algorithms possess notable limitations, including inadequate adaptability, stability, and a tendency to become trapped in local optimisation, rendering them unsuitable for UAV path planning. On the other hand, the GA promotes the principles of survival and competition, subsequently selecting the most favourable outcome through the inheritance execution, continuously converging towards the optimal solution [23]. The study entitled “Comparison of Parallel Genetic Algorithm and Particle Swarm Optimisation for Real-Time UAV Path Planning” examines and establishes that the GA outperforms the Particle Swarm Algorithm in trajectory planning [24]. Nevertheless, the GA discussed in this paper has inadequate optimisation accuracy and is susceptible to local optimisation, rendering it inefficient for solving current path planning problems. On the other hand, the process of ACO necessitates a substantial quantity of information to identify the most efficient solution. Its iteration speed is inefficient, leading to a significantly greater amount of simulation time and rendering it inappropriate for the path planning problem [25,26]. Yang et al. proposed an alternative method for path optimisation combining a basic rapidly exploring random tree (RRT) algorithm and ACO [27]. However, the level of unpredictability in the RRT method is excessive, making it difficult to achieve an effective solution. Lin et al. presented a map-based offline path planning technique to construct an initial path and trajectory waypoints for fight guiding [28]. To perceive the environment, an onboard camera captures monocular images during navigation. A collision avoidance system is proposed, employing vision-based obstacle identification using optical flow. However, they achieve low success rates for multiple obstacles due to the optical flow field’s inability to effectively distinguish between objects and the surroundings. Pehlivanoglu et al. introduced artificial intelligence methods combined with a GA, ACO, Voronoi diagram, and clustering approaches to tackle the path planning problem of autonomous UAV in target coverage challenges [29]. Regardless, the presence of altitude restrictions can make the resulting trajectories hazardous and therefore devoid of significance, as they may lead to collisions with the terrain surface. Hu et al. used deep reinforcement learning and the Proximal Policy Optimisation (PPO) method to improve the navigation of autonomous Unmanned Aerial Systems (UASs) in continuous state and action spaces [30]. The limitation of this method is its inability to model intruders as agents or incorporate teamwork across multiple aircraft. Furthermore, it failed to incorporate learning difficulties related to both stationary and moving obstacles through the combination of reward functions. In another paper, AlRaslan et al. proposed the Parallel Genetic Algorithm (PGA) models and explained the way the recommended path planner can be used in parallel on multi-core processors with OpenMP [31]. However, as the number of threads increased, the parallel implementation failed to accelerate at a sustainable rate. Several hybrid intelligence algorithms that combine various methods may exhibit superior performance. However, the algorithms do not take into account the influence of obstacles on the TSP [32,33].

Heuristic search algorithms provide appealing features for UAV path planning, particularly in unpredictable circumstances because of their efficient exploration and flexibility [34]. Nevertheless, their dependence on well-crafted rules and the computational expense linked to complex surroundings can result in less-than-ideal solutions or limit real-time efficiency, especially for those solving the TSP [35]. This research acknowledges the limitations of heuristic search algorithms like A* in addressing the minimal time TSP issue, despite their effectiveness in changing circumstances with real-time modifications [36]. Although A* effectively navigates across the search area and adjusts to dynamic circumstances, its reliance on a carefully designed heuristic function might result in less-than-optimal solutions, particularly in sophisticated situations with an extensive number of waypoints [37]. Moreover, the expense of expanding the search tree might be substantial for TSP examples on a large scale, impeding real-time performance in time-sensitive situations [38].

This study introduces a unique method that combines an enhanced Genetic Algorithm (GA) with a geometrically based obstacle avoidance algorithm titled QuickNav in order to address UAV path planning with obstacle avoidance. Although previous research has examined this topic using different optimisation strategies, this approach offers a new and innovative solution. This integration aims to overcome the obstacles that have been identified in prior solutions. In this section, we delineate the key contributions of this research:

• Hybrid Optimisation for Path Planning Efficiency: This study presents a new hybrid strategy that combines the advantages of Genetic Algorithms (GAs) and geometric-based methodologies. Genetic Algorithms (GAs) are highly proficient in swiftly navigating through the search space to determine the most effective paths. On the other hand, the QuickNav algorithm guarantees obstacle avoidance that prioritises safety by utilising the CCS data transformed from a motion capture system. This integrated methodology seeks to overcome the drawbacks of exclusively depending on GAs, such as their vulnerability to getting stuck in local optimal solutions and the high computational cost of some linear path planning techniques.
• Decreased Path Planning Time for Obstacle Avoidance: The integration of QuickNav significantly improves the efficiency of computing for planning routes throughout obstacle avoidance, utilising an effective approach for faster computation times. The enhanced efficiency is particularly crucial for urgent emergency operations that necessitate rapid path optimisation with minimal delay.
• Validation Across Diverse Scenarios: The proposed GA-QuickNav combination has been tested extensively to prove its reliability and effectiveness in various scenarios. This has been accomplished by conducting simulations in environments with variable obstacle densities. The method has been evaluated in scenarios with varying numbers and configurations of obstacles to determine its effectiveness in different obstacle environments. Furthermore, real UAV flight data have been included to assess the approach’s practicality and verify its performance in real-life scenarios.

2. Materials and Methods

This study employs an improved GA to solve the path planning problem in a TSP model and a geometric-based algorithm (QuickNav) is used for both detection and avoidance to find an optimised path for a specific set of waypoints in a two-dimensional environment. The GA generates the optimal linear trajectory by utilising specified locations obtained from a motion capture system (optitrack) data in the latitude–longitude–altitude form. For indoor experiment purposes, in the Cartesian Coordinate System (CCS), these three parameters can be denoted as x, y, and z alternatively. The flight controller is responsible for executing motion control and navigation operations. Figure 1 represents the flight situation for TSP path planning. The figure depicts a possible version of the TSP specifically designed for UAVs. The map displays 13 waypoints labelled as “Waypoint”. The UAV is required to visit these waypoints in the most efficient sequence. The objective is to identify the most efficient path that covers all places and returns to the initial location, minimising flight distance and avoiding obstacles between waypoints.

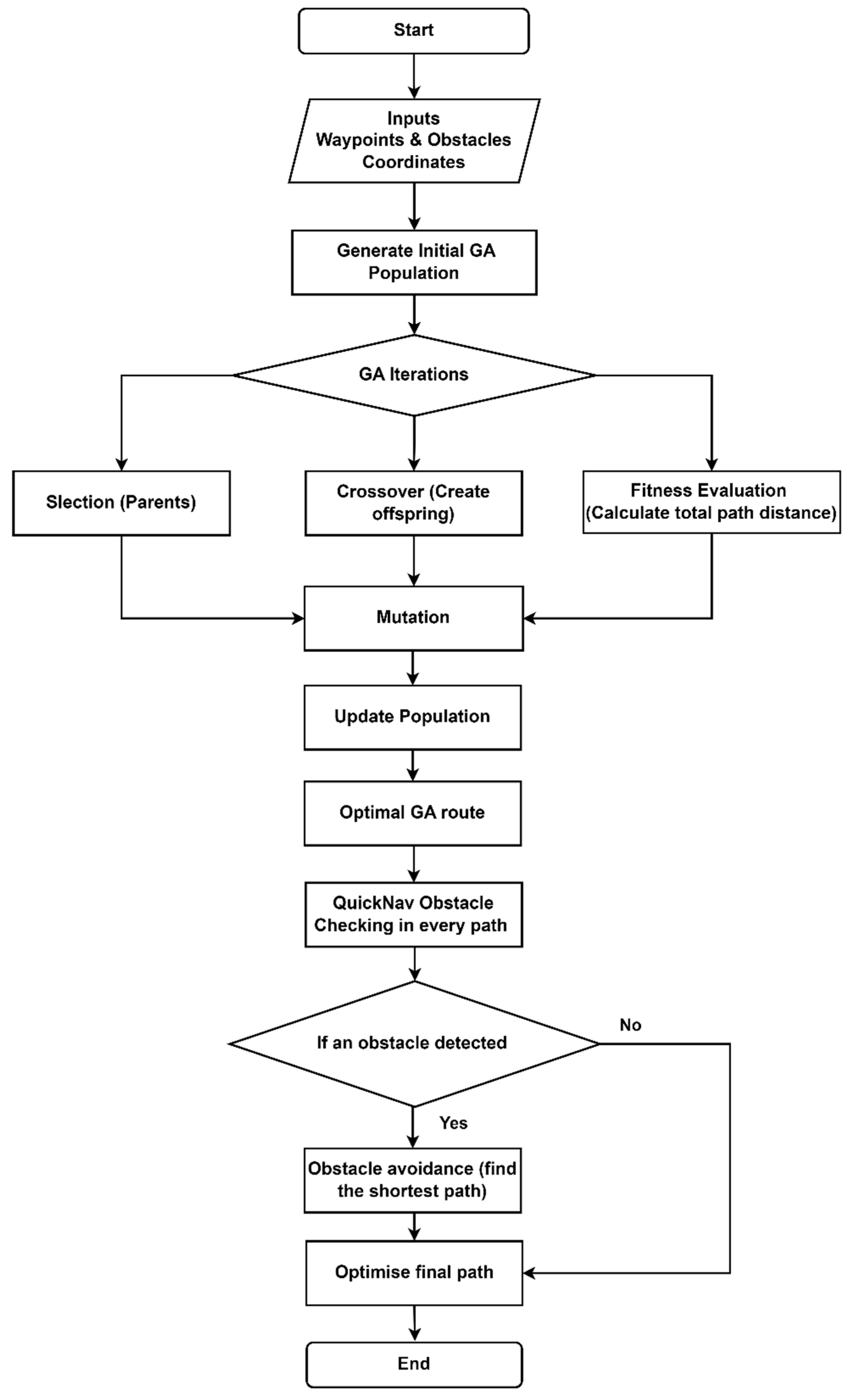
The primary purpose of the path planning module is to generate a sequence of pre-determined optimised waypoints in the shortest amount of time for the flight controller to navigate. Since the experimentation method selected is based on an indoor GPS-denied flight area with a cartesian localisation motion capture system, we express the TSP problem using the CCS data transformed from the motion capture system coordinates. Parameter z, in this case, denotes the vertical dimension, specifically the height or altitude, which holds significant importance in the process of 3D path planning. Nevertheless, this study specifically examines the process of planning a two-dimensional course and operates under the assumption that the UAV maintains a constant altitude. This assumption is especially advantageous for the specific applications of precision agriculture and Wireless Sensor Network monitoring. It ensures that the sensors can operate consistently and provide coverage by maintaining a constant altitude. Therefore, the calculation of the z component will be excluded. The route cost will be estimated by two variables: the distance that must be travelled and the travel duration. Initially, the GA is introduced as an enhanced algorithm for identifying the most efficient route. Subsequently, the geometrical-based algorithm (QuickNav) verifies this optimal route and checks every path for obstacle detection and avoidance. Finally, if any obstacles are encountered during the journey, the QuickNav algorithm navigates around them using the shortest feasible route. The complete process is illustrated in Figure 2.

In our improved GA, xy represents the matrix that contains the 2D coordinates of waypoints that we get from the motion capture system used as CGS form and d_ij represents the matrix that contains the distances calculated using the Euclidean distance formula:

$$d_{ij}=\sqrt{{(x_i-x_j)}^2+{{(y}_i-y_j)}^2}$$

(1)

In this context, d_ij represents the Euclidean distance between waypoints i and j in a two-dimensional environment. The GA is set up with a population of potential routes, where each route is represented as a permutation of waypoints. Here, the UAV used a Genetic Algorithm as a mechanism for the selection of the route outcome. The goal is to arrive at a conclusion that is either the same as or comparable to the solution of a problem. The present layout is built upon previous model solutions. The main method used in Genetic Algorithms for developing and enhancing solutions/offspring involves the cooperation of parent chromosomes. The crossover function configuration has a greater impact on the Genetic Algorithm’s outputs. First, in our advanced Genetic Algorithm, the UAV generates a population using the data from the TSP model obtained using the motion capture system shown in Figure 2. For instance, if the TSP model consists of six cities represented by the sequence [1 2 3 4 5 6], the algorithm generates the population by randomly permuting the sequence, resulting in population 1 (2 3 4 1 6 5). Subsequently, the algorithm computed the aggregate distance across all populations. Additionally, the duration of the iteration for resolving the problem in this algorithm was specified. In the population, the GA chooses twelve parents that are closest to a minimum distance and uses them to produce the next generation of offspring. The mutation process begins in the algorithm by employing sliding, swapping, and flipping operations across the cities of parent chromosomes until the iteration phase is finished. The crucial variables consist of the population size (Pop Size) and the maximum number of iterations (numIter). In this algorithm, the population size is assigned the number 12, and the iteration period for the algorithm is 1,000,000. The selection of a population size of 12 enables a sufficiently diverse genetic pool, allowing the searching of a wide range of possibilities while maintaining computational efficiency. This specific size is highly efficient in producing numerous offspring, allowing the algorithm to thoroughly explore different combinations of paths and significantly increasing the chances of avoiding suboptimal solutions. Moreover, by limiting the number of iterations to one million, the algorithm is able to thoroughly explore the solution space in a reasonable amount of time, which is essential for applications that involve efficient path planning. The large iteration count is essential for thoroughly refining the solution space, particularly when the dataset size expands and the complexity of the path planning challenge increases. The parameter configuration was selected after extensive testing, which demonstrated its ability to effectively generate optimal pathways under different conditions. This configuration is well-suited for rapid deployment in UAV applications, corresponding with operational requirements. Although these parameters were successful in our experiments, they can be modified to meet the specific needs of the operational environment, ensuring that the Genetic Algorithm remains flexible and adaptable to numerous conditions. The iterative GA procedure entails the evaluation of routes using a fitness function.

$$f\left(R\right)={\sum }_{k=1}^n{d}_{R_k{R}_{k+1}}$$

(2)

This function computes the cumulative distance of a given route R by considering the lengths between each succeeding waypoint. The population undergoes iterative application of selection, crossover, and mutation procedures, which introduce genetic variation.

The algorithm’s convergence is monitored by tracking the minimum attainable total distance (minDist).

$$minDist=\min \left\{{\sum }_{k=1}^n{d}_{R_k{R}_{k+1}}\right\}$$

(3)

In this context, the representation of R indicates a specific route, while d_RkR(k+1) denotes the distance between consecutive waypoints along that route. The symbol “min” represents the action of finding the smallest value among all the routes evaluated in a specific iteration of the GA. The goal is to identify the path that minimises the overall distance, and “minDist” represents the minimum value attained during the execution of the algorithm. The visualisation techniques encompass the act of graphically representing progress and exhibiting the ultimate optimised route. From the improved GA algorithm, we will obtain our optimised route. To evaluate the distance obtained by the enhanced GA with the distance collected from the TSP library database, a percentage is determined using Equation (4). The difference in trip lengths is then presented in result section.

$$Trip Distance Difference= \frac{TSP library outcome-GA outcome}{GA outcome}\times 100$$

(4)

The Genetic Algorithm requires the following steps, which are explained below.

• Evaluation.
• Crossover.
• Genetic mutation.

The GA employs a population of distinct entities, each with an associated measure of fitness, to advance towards a subsequent generation of the population. This algorithm is inspired by the principles of human evolution proposed by Darwin, as well as the occurrence of naturally occurring genetic processes such as crossover (recombination) and mutation. An individualised approach can be found for each member of the population to address a particular problem. GA aims to solve problems effectively and accurately by genetically reproducing a group of individuals.

Evaluation: The aspect of evolution is crucial in GA. Here, we employ the probabilistic permutation technique to evaluate the quality of a chromosome. The number of beginning chromosomes (parents) is determined based on the dimension of the population, and their overall distance is calculated.

Crossover: After the completion of the selection process, the chromosomes of the parents are merged to create new chromosomes. The next set of children is considered a new path here; the outcomes of searches may be significantly influenced by the combination and by the crossover system.

Mutation: The process of mutation enables the creation of an additional system. The method commences by selecting a parent chromosome according to the shortest distance from the population. An arbitrary location throughout the sequence is chosen and the element at that position is changed. The modified sequence is then copied to the following iteration. We selected the minimal distance value from the chromosomal site at random to mutate and alter its value. There exist numerous categories of mutation drivers. Three forms of mutation processes are employed here. The first type is the flip mutation, which is applicable exclusively to binary chromosomal representations. It involves flipping the chromosome from one place to another. The second process is the swap operation, which allows for the exchange of one place with another location within the chromosome. The final step is the sliding procedure, in which the chromosome is moved from one point to another to determine the route with the least distance for the TSP. This operation proceeds until the given number of iterations has been accomplished.

GA Algorithm 1 pseudocode is given below:

Algorithm 1: Enhanced Genetic Algorithm path planning pseudocode

Start or set up: a.  Waypoints: A collection of coordinates (x, y) that indicate specific destinations. b.  Max_iterations: The upper limit on the number of iterations that the Genetic Algorithm (GA) will perform. c.  Population size: The quantity of chromosomes (paths) present in each generation. Features: Distance: The function distance (p1, p2) computes the Euclidean distance between two waypoints. Fitness(chromosome): Computes the overall distance covered by the chromosome. Main iteration: 1.  Create the first population: Generate a set of chromosomes with a population size, where each chromosome represents a permutation of waypoint indices ranging from 1 to the total number of waypoints. 2.  Iterative Loop: Time: For every iteration i ranging from 1 to maximum iterations: Fitness Evaluation: ➢ For every chromosome c in the population: ➢ Determine the overall distance of the path using the fitness function (c). Selection: Choose a group of chromosomes (parents) for crossover based on their fitness (specifically, the shortest path length). Crossover: Utilise the crossover operator, such as single-point crossover, to produce offspring chromosomes containing rearranged waypoint sequences. Mutation: Randomly alter offspring by introducing mutations, such as switching waypoint indices, with a low chance. Updated: Merge the chromosomes of parents and kids to create the population of the following generation. 3.  Discover Optimal Route: Determine the chromosome in the final population that has the smallest path length. The output: Best chromosome: The chromosome that represents the most optimal route for the UAV without considering obstacle avoidance.

After obtaining the optimised path from the GA, we present a geometrical-based obstacle detection and avoidance (QuickNav) method that is fast-converging, extremely scalable, and operationally cost-effective. Following the completion of the optimal path, the GA generates this path as a series of waypoints. These waypoints are then used as one of the key inputs for the QuickNav algorithm. In addition to the optimised course, QuickNav also relies on the coordinates of known obstacles in order to carry out its role successfully. The incorporation of these two algorithms is essential for the path planning process. After GA finishes its computation by identifying the optimal sequence of waypoints, these data are inputted into QuickNav. The QuickNav algorithm uses data from both the GA-derived path and obstacle location to continuously alter the trajectory of the UAV. This ensures that the UAV avoids obstacles while still following the most efficient route. This process is performed off-board, allowing for comprehensive analysis and adjustment before the actual flight mission. The smooth transfer of data from the GA to QuickNav, as shown in Figure 2, demonstrates a systematic process of combining optimised route data. This process improves the operational safety and efficiency of the UAV. This approach is ideal for optimising a route at a fixed altitude. Figure 3 represents multiple obstacles together with a varying number of waypoints. In this example, the QuickNav algorithm employs square areas centred around each obstacle location coordinates to reduce the complexity of the route planning procedure. These square zones are assumed to cover the obstacles, despite their actual shapes or sizes. The UAV safely navigates across these square zones, avoiding direct contact with the enclosed obstacles. This method is especially efficient in regulated indoor environments where the size of obstacles is constant and can be predetermined.

The obstacles are identified as “O_n”, where n = 1, 2, 3… is the number of obstacles in a TSP model.

The suggested approach requires the use of a simulation or numerical technique to identify and overcome obstacles present in the surrounding TSP environment. To simplify the scenario, it is assumed that any obstacles that are visible here are in the form of square shapes and the size of the obstacle always remains inside of the square region. The dimensions of the obstacles are determined by the perimeter necessary for the UAV to navigate safely. A series of UAV waypoints and obstacle coordinates are obtained from the TSP model via a motion capture system. Figure 4 and Figure 5 show the obstacle detection process and geometric perspective in determining the avoided path between waypoints when an obstacle is identified.

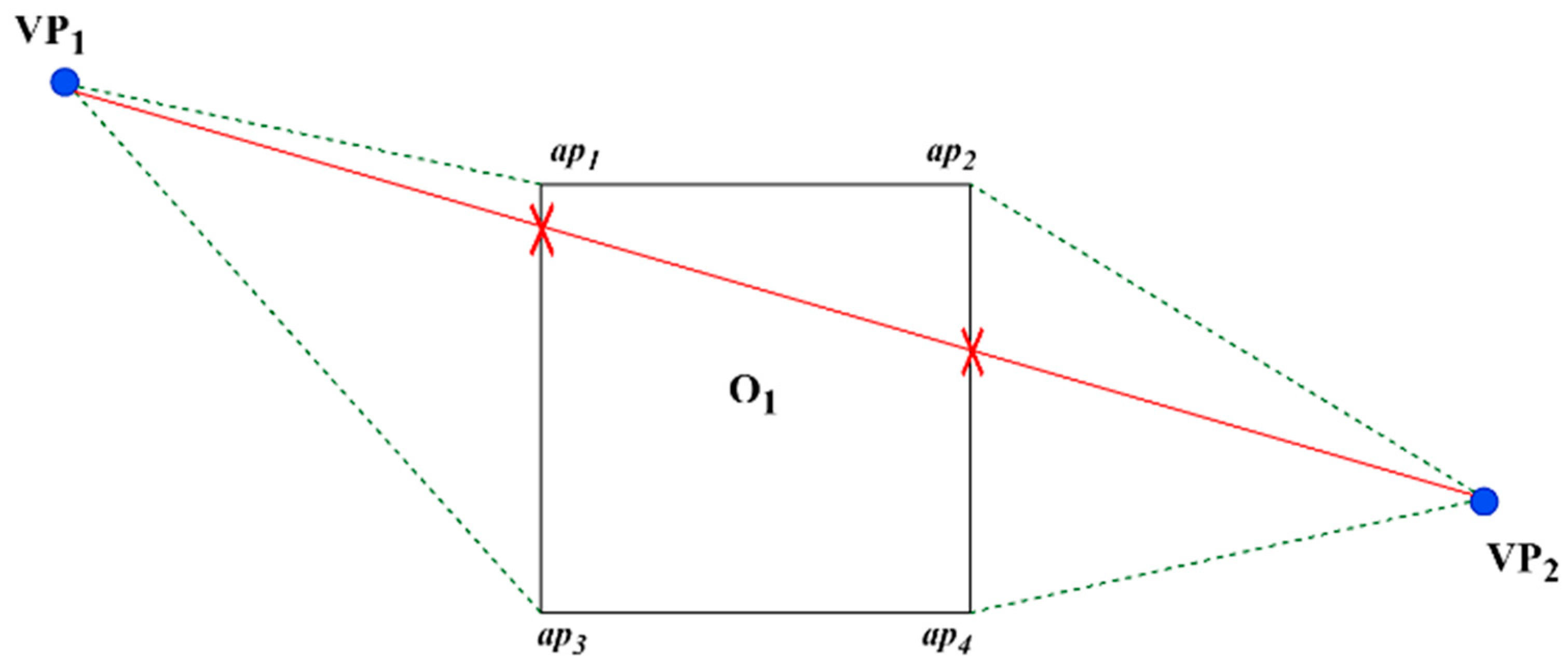
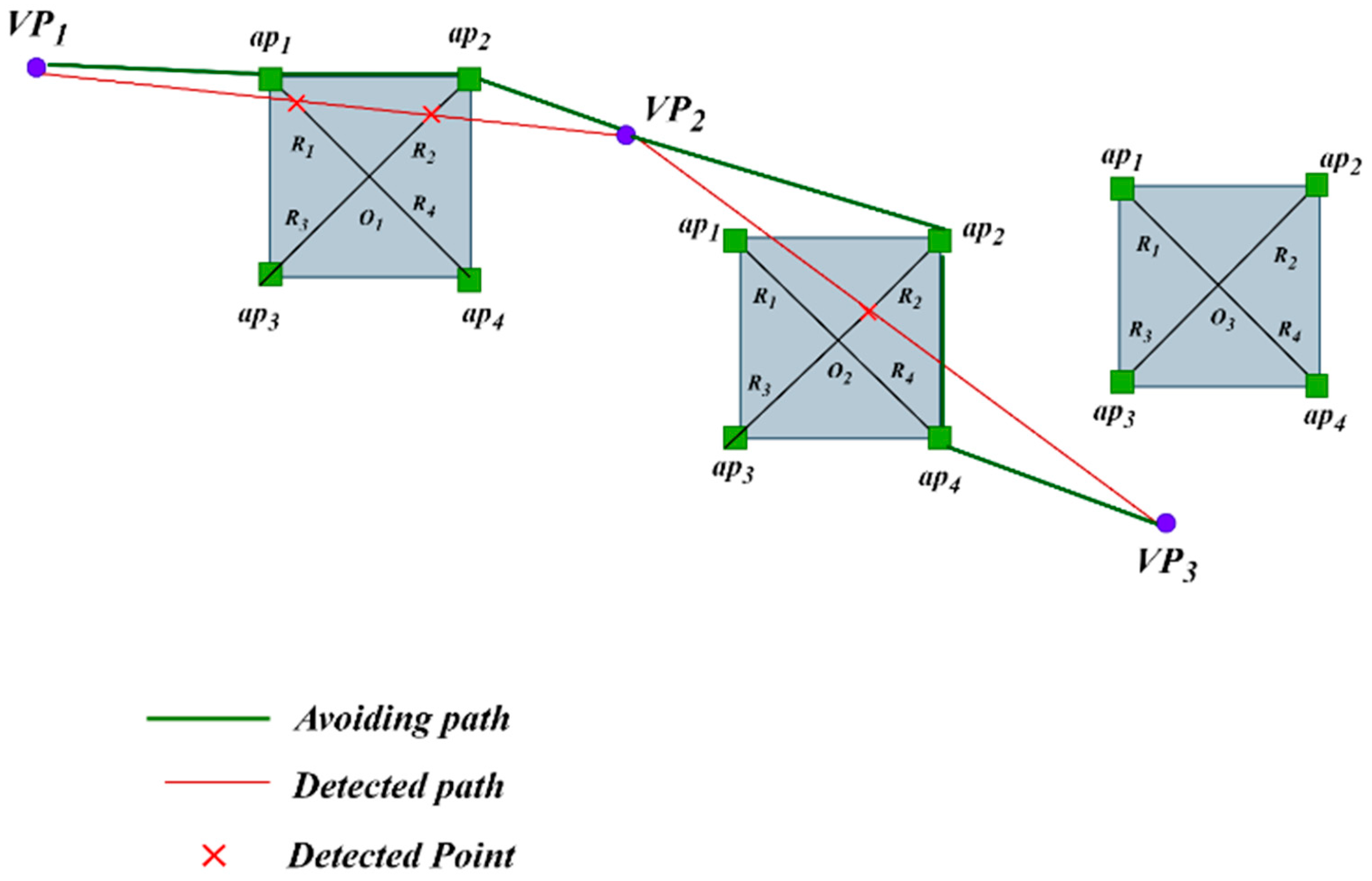
On the path between the two visiting waypoints (VP), the algorithm can encounter obstacle O₁, as shown in Figure 6. The presented detection approach employs linear equations to identify the path obstacle by determining the locations of intersections between the perimeters of the obstruction and the route lines. Any barriers encountered along the visiting points VP₁-VP₂ lines will be seen as obstacles and must be avoided. The inevitable trajectory is depicted as a linear, unbroken line, whereas the potential alternative courses are illustrated by dashed lines. In this situation, the avoidance strategy will involve at least two separate approaches to circumvent the obstruction O₁. These routes will be around the borders of the obstacle, which are designated as avoidable points (ap). Each obstacle will have four avoidable points, denoted as ap₁, ap₂, ap₃, and ap₄. The path VP₁-VP₂ intersects the fences over obstacle O₁, indicated by the red x. Therefore, there are at least two alternative routes that can be taken (shown by the dashed lines) in the form of VP₁–O₁ ap₁)–O₁(ap₂)–VP₂ and VP₁–O₁(ap₃)–O₁(ap₄)–VP₂. The shortest route from VP₁ to VP₂ is used as the requirement for selection. The shortest way in this example is VP₁–O₁(ap₁)–O₁(ap₂)–VP_2, and as such, it is chosen as the avoidable path.

The algorithm evaluates the trajectory and identifies obstacles for each path iteration, then estimates the path with the shortest length. By applying this methodology, we propose a detection method based on the intersection of two diagonal perpendicular lines at the centre point of an obstacle. Following that, we divide the two lines into four separate lines, each extending from the centre of the obstacles to each corner of the square, which we have specified as the locations that we want to avoid. The APs are extended from the obstacle point by a secure perimeter, which is described as r. Here, r represents the horizontal and vertical distance from the centre coordinate of the obstacle. For example, if the path crosses O_n(R₁), O_n(ap₁) will be the waypoint to avoid. By employing this technique, if a route intersects any of the four diagonal lines, the algorithm can promptly acknowledge the corresponding access points as the waypoints to avoid, as represented in Figure 7.

The algorithm accepts the optimised waypoints from the GA and the coordinates of the obstacle centres as inputs. A square zone is generated around the obstruction point, using the safe distance around the obstacle as the value of r. Four diagonal points are generated for each obstacle, creating a square zone that is shaded, as shown in Figure 7. The information is provided with the coordinates of the obstacle. Around the obstacle’s central point, O_n = (a, b), the safe flying perimeter around the obstacle centre point is r. The value of r represents the radius that determines the boundary of the safe flying area around the obstacle. It is determined based on the obstacle’s central point. The illustration depicts an obstacle, symbolised by a red irregular shape, positioned at a specific spot in Figure 8. The obstacle is encompassed by a red square box, with the width of the box (w) determined by the largest dimensions of the obstacle. The width of the flying perimeter is increased by adding a buffer zone (b) to ensure safety, resulting in r = w + b. The expanded buffer distance surrounding the obstruction results in the creation of a green square, which represents the safe zone. This ensures that the UAV can navigate from point A to point B without colliding with the obstacle. The purpose of this buffer is to accommodate any uncertainties in the dimensions of obstacles and the accuracy of UAV navigation, thus ensuring the safe execution of operations. The square zone approach is more efficient than other geofencing methods, such as circular or dynamic geofences. It simplifies computation by creating a uniform buffer around the obstacle, making implementation easier and computationally less challenging. This approach effectively ensures that the UAV stays at a safe distance from obstacles. As the UAV moves from point A to point B, it must stay inside the safe perimeter r. This perimeter includes the obstacle width (w) and the buffer (b). By following this clear path, the UAV can prevent collisions and stay within safe bounds while effectively avoiding obstacles.

The equation of a line connecting two points (x₁, y₁) and (x₂, y₂) can be expressed using the basic two-point form linear equation as follows:

$$\left(x-x_{1 }\right)=\frac{x_2-x_1}{y_2-y_1} \left(y-y_1\right)$$

(5)

The following equation gives the linear distance between all the waypoints.

$$D_{ij }=\sqrt{{\sum }_{k=1}^n{{\left(\right(x}_{ik }-x_{jk})}^2+{{(y}_{ik }-y_{jk})}^2}$$

(6)

In this equation, the variable n denotes the total number of optimised visiting waypoints (VP) from the TSP model, and the summing is conducted across all points ranging from 1 to n.

To establish the flight path between two coordinate visiting waypoints, VP_n (c, d) and VP_n+1(e, f), with reference to Figure 6, the following expression can be used:

$$R_{path }=\frac{f-d}{e-c} \left[\left(x-c\right)+d\right] Subject to \left\{c\le x\le e\right\}$$

(7)

By implementing the same principles, it can be performed to create four linear equations for each obstacle’s coordinate. These equations relate to the obstacle’s centre point, denoted as O_n(a, b), and four related avoidable path (AP) values: [ap₁, ap₂, ap₃, ap₄].

$$R_{1 }=-x+a+b ; Subject to \left\{\left(a-r\right)\le x\le a\right\}$$

(8)

$$R_2=x-a+b ; Subject to \left\{a\le x\le \left(a+r\right)\right\}$$

(9)

$$R_3=x-a+b ; Subject to \left\{\left(a-r\right)\le x\le a\right\}$$

(10)

$$R_{4 }=-x+a+b ; Subject to \{\left(a\le x\le \left(a+r\right)\right\}$$

(11)

The decision to avoid obstacles in path planning is required to conform to the following equations.

Lemma 1: 

A flight trajectory between visiting waypoint VP_n and another visiting waypoint VP_n+1 is considered to intersect with an obstacle if there exists at least one point of intersection between any line associated with the obstruction.

$$R_{path}=R_{1 };Subject to \left\{\left(a-r\right)\le x\le a\right\}$$

(12)

$$R_{path}=R_{2 }; Subject to \left\{a\le x\le \left(a+r\right)\right\}$$

(13)

$$R_{path }=R_{3 }; Subject to \left\{\left(a-r\right)\le x\le a\right\}$$

(14)

$$R_{path}=R_{4 }; Subject to \left\{a\le x\le \left(a+r\right)\right\}$$

(15)

Lemma 2: 

During each iteration, if Lemma 1 holds true, the algorithm must repeat the step to ensure that a new route does not intersect with any obstacle’s line after avoidance has occurred. The final avoidable path will be determined by the line that connects the edges of obstacles without intersecting any other lines.

The solution for identifying a new avoidable path (AP) when the trajectory intersects with any obstacle lines is given below:

$$AP={\sum }_{l=1}^{l=n}{VP}_l R_{path }{\sum }_{k=1}^{k=n}{O}_{k }\left(R_{1 }, R_{2 },R_{3 },R_{4 }\right)$$

(16)

The value is constrained by the limit specified in Equations (8)–(11) above.

The procedure for solving the given equations is described in Algorithm 2.

In certain circumstances, the act of avoiding one obstacle may result in the avoidance path intersecting with another obstacle. The program will then recalculate in successive iterations until there is no interception for any waypoint in this case. The algorithm compares the current travel line with the lines representing obstacles within the square area defined by two visiting points, such as VP₁ and VP₂, or VP₂ and VP₃, as shown in Figure 9. First, the route linking VP₁ and VP₂ intersects with the O₁(R₁) line. Given that the path intersects O₁(R₁), a new destination point, O₁(ap₁) is designated. A new route has been established connecting VP₁ and O₁(ap₁). Subsequently, the trajectory originating from O₁(ap₁) intersects with the line O₁(R₂), resulting in the emergence of O₁(ap₂) as a novel point that must be avoided before reaching VP₂. Similarly, while transitioning from VP₂ to VP₃, it intersects with the O₂(R₂) line, causing O₂(ap₂) to become a point that can be avoided. Then, as it moves from O₂(ap₂) towards VP₃, though it collided only once during the journey, it will go through another safest path to make sure that it will not collide with the same obstacle again. In this scenario, it will go to O₂(ap₄) before moving to destination point VP₃. Hence, the ultimate avoided route is the route that links VP₁-O₁(ap₁)-O₁(ap₂)-VP₂-O₂(ap₂)-O₂(ap₄)-VP₃, as seen by the bold green line in Figure 9. The QuickNav algorithm in Figure 9 ensures that the UAV safely navigates through the safe zone locations, which are defined by the square zones surrounding obstacles. Despite the seemingly shorter distance between O₂-(ap₂) and VP₃, the algorithm requires that the UAV must first go from VP₂ to (ap₂), then to (ap₄), and lastly to VP₃. This trajectory ensures that the UAV remains at a secure distance from the obstacle while following the safety limitations set by the specified square areas. QuickNav is specially designed to navigate via a minimum of two secure areas if it detects obstacles along any route, significantly improving the safety of the UAV. The approach focuses an emphasis on avoiding collisions and assuring safety. It ensures that the UAV effectively navigates around objects while maintaining a distance to prevent collisions.

Algorithm 2: Geometrically based obstacle detection and avoidance algorithm (QuickNav) pseudocode

Initialise input Optimise Visiting points VPn (c, d), where n = 1,2,3… input obstacle coordinate, 0n (a, b), where n = 1,2,3… input safe flying perimeter r, define starting visiting point = [VP1] define destination visiting point = [VP2] define starting path = [Rpath] (between starting visiting point and destination visiting point) formulate four functions for every obstacle, On{R1, R2, R3, R4 } define current path = starting path define current visiting point = starting visiting point Main while collision detected! Check     if <current path intercepts R1 >       update {next visiting point candidate} = ap1     else if <current path intercepts R2 >       update {next visiting point candidate} = ap2       else if <current path intercepts R3 >         update {next visiting point candidate} = ap3         else if <current path intercepts R4>           update {next visiting point candidate} = ap4 break; find the nearest distance between {next visiting point candidate} and     [current visiting point]  update [nearest {candidate next visiting point}] = [current visiting point] end if while no collision was detected! do    update [current visiting point] = [destination visiting point] //move to the next path    update [destination visiting point] = destination visiting point ++    update avoiding waypoint = {starting visiting point,… end visiting points} end

This method continues until all the routes on each waypoint are free of any intersections with the obstacle lines. After the process finishes, the avoided path is graphed for presentation. The following chapter will evaluate the algorithm’s effectiveness in terms of reducing the distance and demonstrate it in various scenarios. Furthermore, we calculate the travel time and the durations of the alternative paths. In this study, we define r as equivalent to 0.6 units. Therefore, the distance between the obstacle point and the horizontal and vertical boundaries is precisely 0.6 units for each.

3. Results

To evaluate the efficiency of our proposed enhanced Genetic Algorithm, we conducted experiments using four scenarios sourced from the TSP database [39]. Each scenario in the dataset presented a distinct level of complexity. We utilised TSP examples from the TSP database package to evaluate the performance of our GA-QuickNav algorithm. The TSP database offers a comprehensive set of sample examples for the TSP and related issues, which have gained significant popularity in the area. In general, a combination of exact and heuristic methods is used to find answers to these problems. The branch-and-cut algorithm is commonly utilised for the solutions. This method utilises the ideas of branch-and-bound, along with cutting planes, to progressively enhance the solution space until the optimal solution is achieved. Furthermore, the Concorde TSP Solver, known for its effectiveness and precision, has been applied to solve numerous TSP database problems that have demonstrated optimality. By utilising well-established, optimal solutions, the comparisons used in our study provide an efficient foundation to assess the performance of our proposed method.

Table 1. Listed problems from the TSP library.

Name of the Problem	Total Number of Waypoints
BAYG29	29
EIL101	101
GR202	202
PA561	561

displays a comprehensive list of difficulties together with their corresponding total location points. The TSP library contains a set of TSP problems together with their optimal solutions, allowing for comparison and evaluation. The items in Table 1 were chosen according to the level of intricacy. The naming convention of the problems specifies the name of a city and the number of waypoints. For instance, BAYG29 is a specific route within the city of BAYG that includes a total of 29 cities.

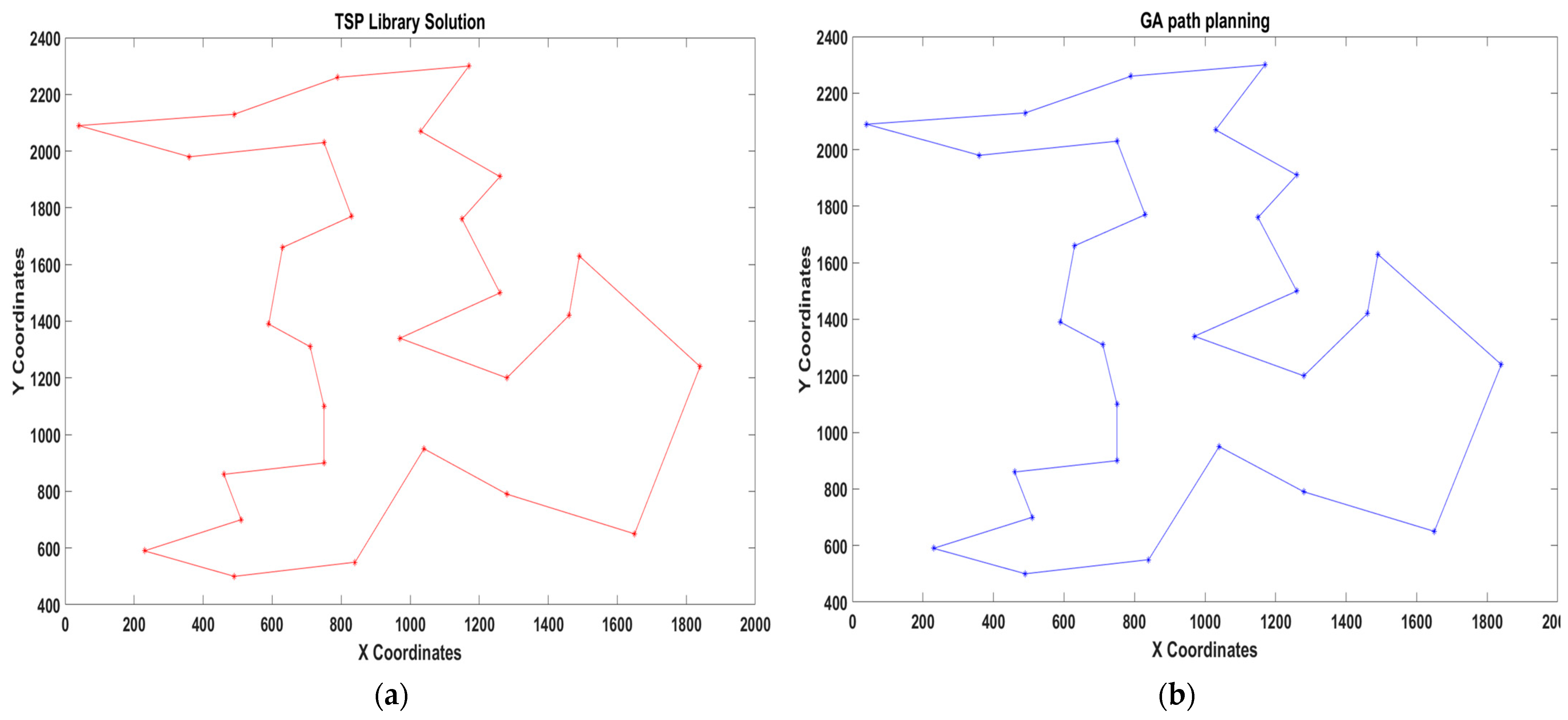
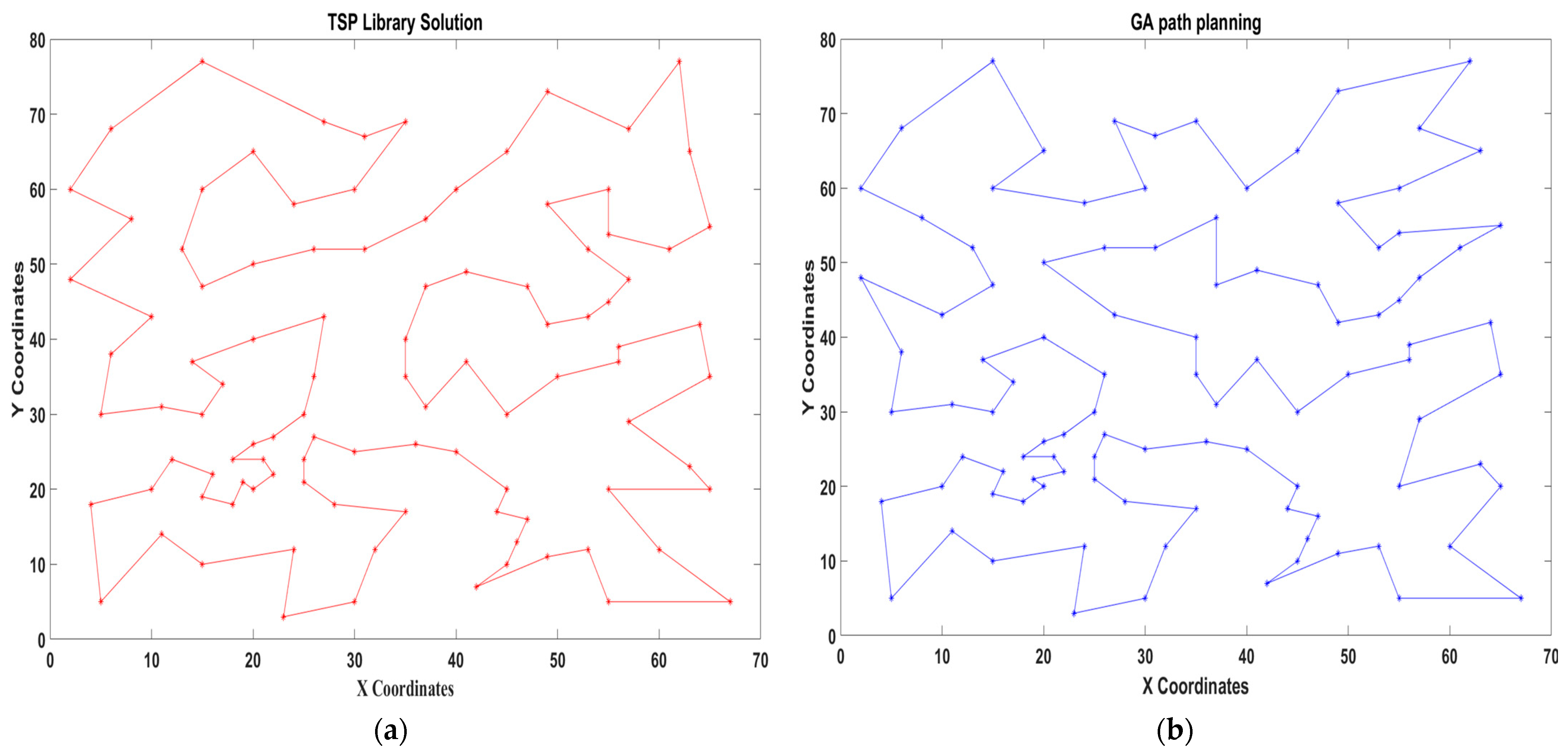
The location of points data are uploaded into the GA for optimisation purposes, based on the selected problem from Table 1. The result obtained using GA is depicted in Figure (10-13)b for each problem, throughout the images from Figure 10, Figure 11, Figure 12 and Figure 13. Figure 10 shows identical results for BAYG29 with a distance of 9073 m using both the TSP library and the GA. The second one is named the EIL101 area scenario, and the provided result is 629 m. As seen on the right side of Figure 11b, the GA calculates a total distance of 639 m. In the next scenario, the scenario is identified as GR202, and the result is 547 m. 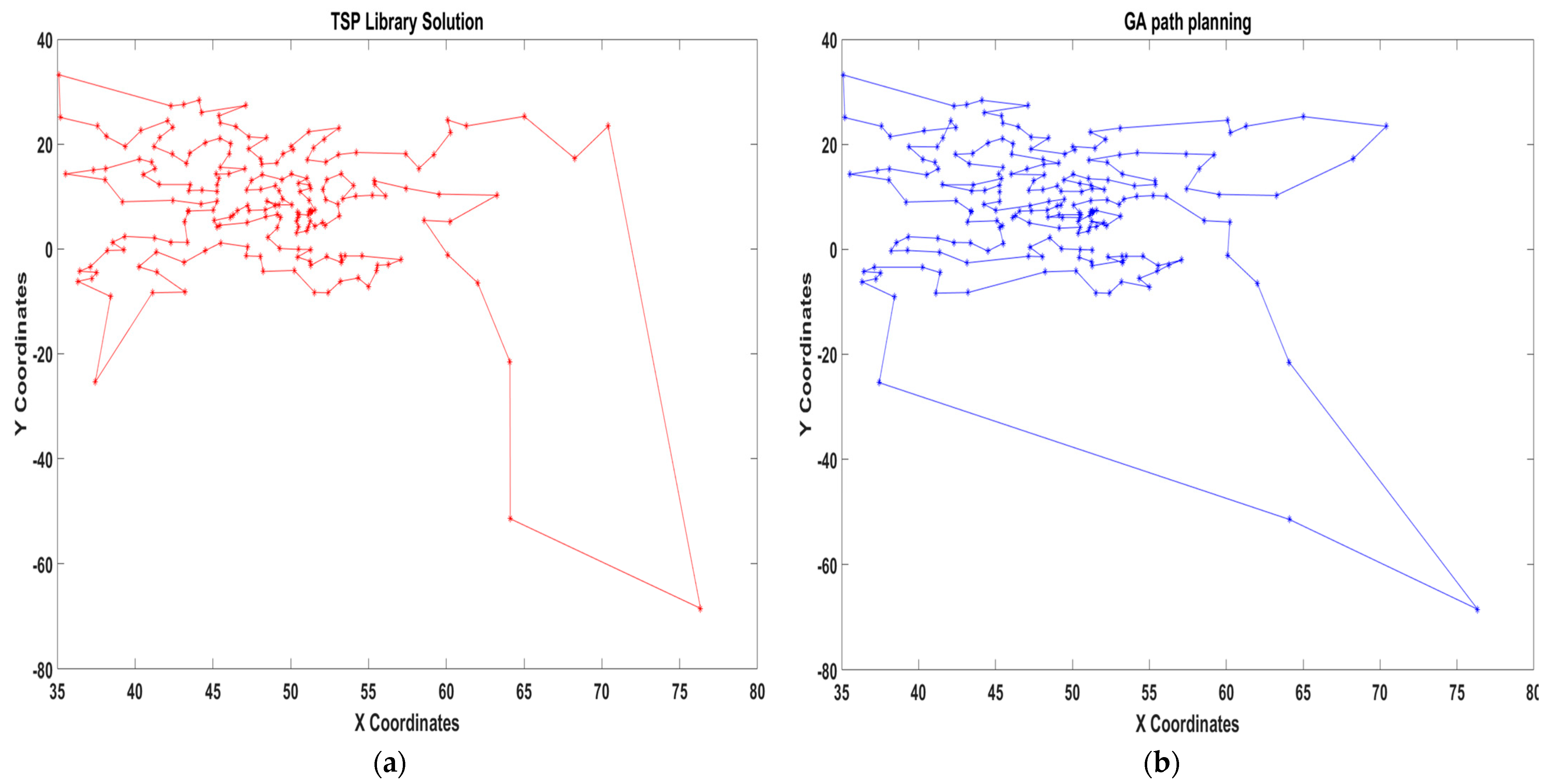The GA obtains an outcome of 490 m for the scenario depicted in Figure 12. The outcome of the GA demonstrates that the algorithms produce better outcomes compared to the solution provided by the TSP library. In the last test, there is a selection of 561 cities available, and a specific answer has been provided for this, reaching 19,311 m. 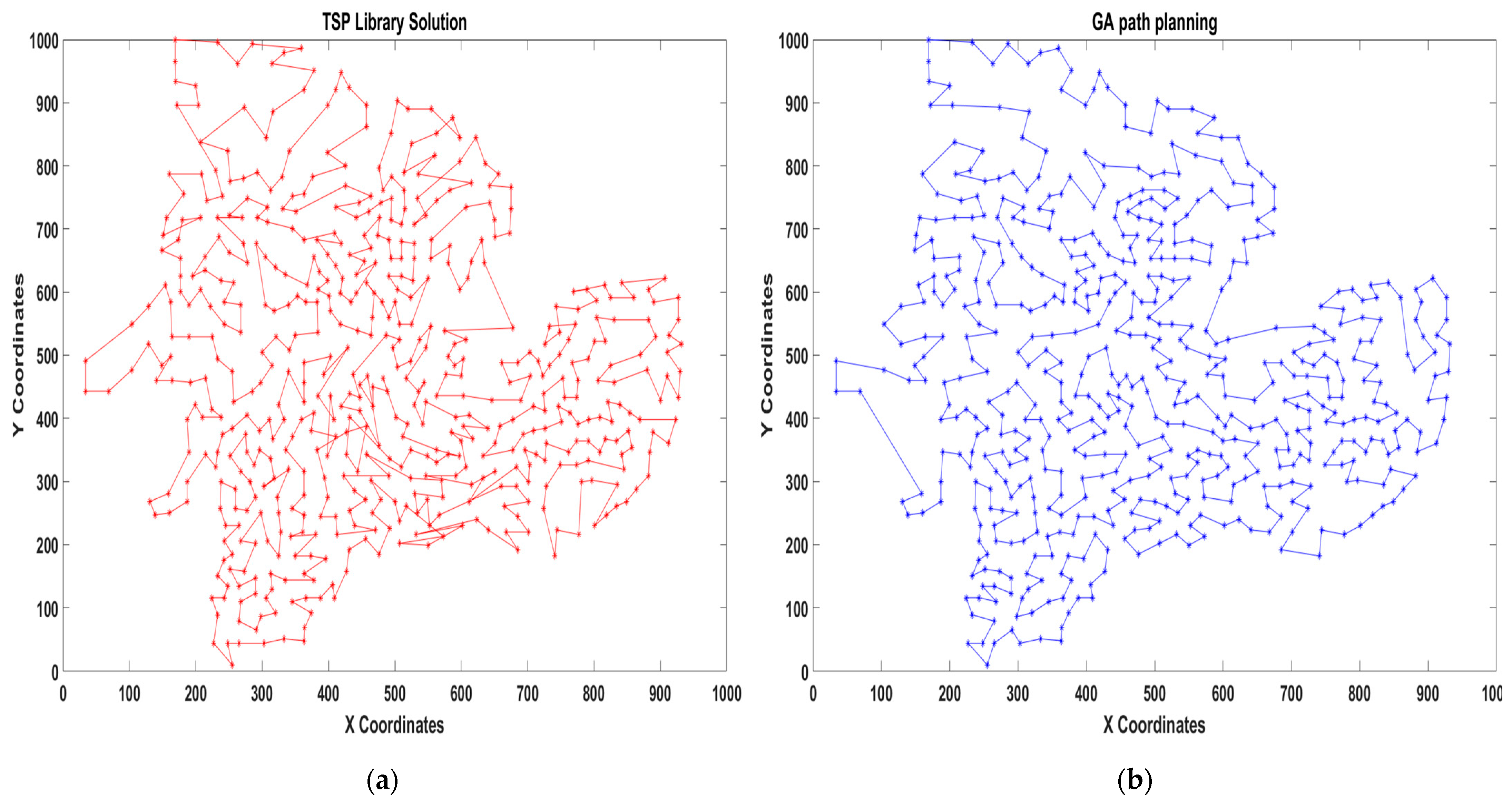As illustrated in Figure 13, the GA computes the final distance of 15,928 m in a more efficient manner compared to the provided distance. In this situation, the result is more effective than the solution provided by the TSP library because of the utilisation of the GA. Figure 13a displays many intersections at the corresponding points of the TSP library approach whereas the GA offers an enhanced and optimal solution by ensuring that there is no overlap or crossover within location points in the process.

As shown in

Table 2. Comparative analysis of the outcomes obtained using the TSP library and the GA (positive sign indicates that the GA trip length is better than the TSP library).

TSP Problem Name	TSP Library Result	GA Result	GA Outcome Time (s)	Trip Distance Difference (%)
	Trip Distance (m)	Shortest Trip Distance (m)
BAYG29	9073	9073	3.03	0
EIL101	629	639	38.85	−1.59
GR202	54 7	490	41.66	10.42
PA561	19,311	15,928	90.42	17.51

, all the obtained outcomes are measured against the results collected from the TSP database. The trip distance difference illustrates the proximity of the GA to the outcome of the TSP library data. Positive numbers indicate that the GA solution performs better than the results produced by the TSP Library, showing its greater effectiveness. Conversely, negative numbers indicate situations where the GA solution performs less optimally than the solution provided by the TSP Library. The solutions to the problem BAYG29, both GA and TSP results, are identical, and their percentage levels correspond to those displayed in Table 2. The GA solution required a total of 3.03 s. Table 2 also demonstrates that the EIL101 GA problem obtains outcomes that are nearly identical to those achieved using the TSP library, with a trip distance difference percentage approaching 0 per cent in just 38.85 s. Other problems, including GR202 and PA561, have GA outcomes that are up to 10.42% and 17.51% higher than TSP database answers, respectively, and both GA results need less than two minutes to resolve the problem.

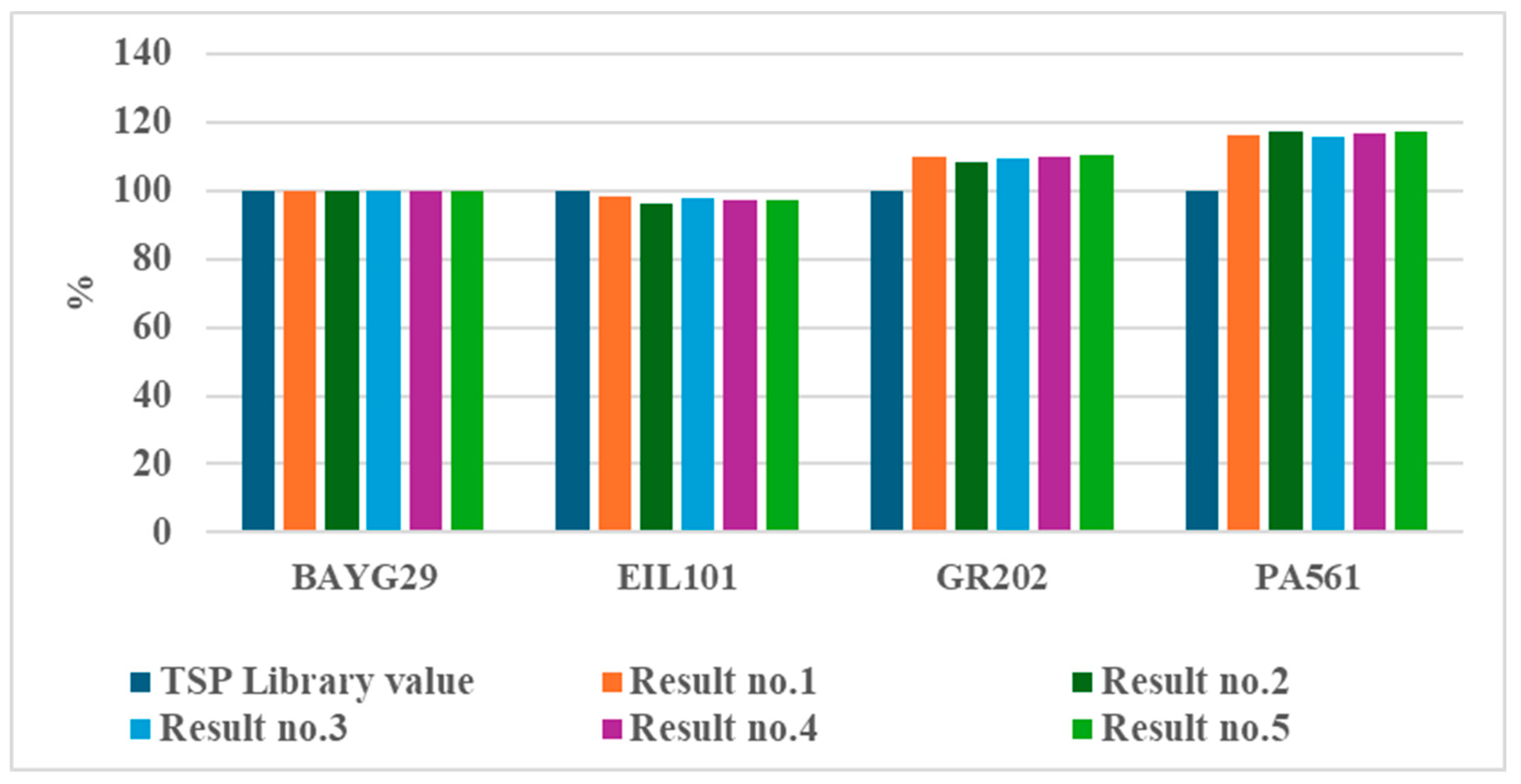
In order to assess the precision and consistency of the GA results, we analyse not only Table 2 but also five GA results for every scenario, as represented in Figure 14 (results no. 1 to 5). Based on the GA outcomes, it can be concluded that BAYG29 shows a high level of consistency. Specifically, BAYG29 exhibits perfect accuracy with a zero percentage of trip distance difference between the solutions. The percentage values for EIL101 in the TSP collection were highly comparable to other values, and the percentage levels for EIL101 were also near the reference value. On each occasion this problem was executed, it consistently exhibited a trip distance difference rate of approximately 4%. Remarkably, the GA demonstrates outstanding efficiency in solving the GR202 and PA561 problems, exceeding the results obtained using the TSP lib by around 10%.

Table 3. Statistical analysis for TSP library problem using GA trip distance outcome.

TSP Problem Name	Result no. 1	Result no. 2	Result no. 3	Result no. 4	Result no. 5	Mean	Standard Deviation	95% CI Lower	95% CI Upper
BAYG29	9073	9073	9073	9073	9073	9073	0	9073	9073
EIL101	639	653	642	647	648	645.8	5.45	639	652.6
GR202	492	502	497	493	490	494.8	4.764	488.9	500.7
PA561	16,192	15,977	16,300	16,108	15,928	16,101	152.7	15,911	16,291

provides an extensive overview of the distances travelled for specific TSP problems. In the case of the BAYG29 problem, all five outcomes consistently produced a value of 9073. This resulted in a mean of 9073 and a standard deviation of 0, suggesting that there was no variability in the results. Additionally, the 95% confidence intervals (CIs) for both the lower and upper bounds were also 9073, highlighting the algorithm’s stability in this situation. Conversely, the EIL101 problem showed little variation, with outcomes ranging from 639 to 653. The average value was 645.8, while the standard deviation was 5.45. The 95% confidence interval for EIL101 ranges from 639 to 652.6, indicating minor variations over iterations. The GR202 problem demonstrated consistent results despite the modest variability, with values ranging from 490 to 502. The mean is 494.8, while the standard deviation is 4.764. The PA561 problem displayed variations, with outcomes varying from 15,928 to 16,300. The mean value was 16101, and the standard deviation was 152.7. These results illustrate how the algorithm responds to different levels of scenario complexity and emphasise the difficulty presented by this more detailed TSP scenario.

Table 4. Statistical analysis for TSP library problem using GA computation time outcome.

TSP Problem Name	Result no. 1 (s)	Result no. 2 (s)	Result no. 3 (s)	Result no. 4 (s)	Result no. 5 (s)	Mean (s)	Standard Deviation	95% CI Lower	95% CI Upper
BAYG29	3.03	3.03	3.04	3.06	3.03	3.038	3.022	3.054	0.01304
EIL101	38.85	39.11	38.87	39.01	39.06	38.98	38.84	39.12	0.1153
GR202	41.89	43.06	42.99	42.36	41.66	42.39	41.61	43.18	0.631
PA561	91.46	90.66	91.55	91.02	90.42	91.02	90.41	91.63	0.4909

presents a comprehensive examination of the time required to conduct calculations for the same set of TSP problems. It demonstrates the performance of the GA under various computational requirements. For the BAYG29 problem, computation times were extremely consistent, with a mean of 3.038 s and a very low standard deviation of 0.01304. This demonstrates how well the method works for this scenario. A narrow 95% confidence interval (CI) of 3.022 to 3.054 s indicates predictable and reliable computation times. EIL101 computation times are also efficient, with a mean of 38.98 s and a standard deviation of 0.1153, showing minor fluctuation. This problem’s 95% CI is 38.84 to 39.12 s, demonstrating the algorithm’s robustness in slightly challenging environments. Computation times varied substantially for the more complex GR202 problem, with a mean of 42.39 s and a standard deviation of 0.631. The 95% CI for this problem, 41.61 to 43.18 s, demonstrates a greater computational time range due to its complexity and processing requirements. The PA561 problem, which is significantly more challenging, has a mean computation time of 91.02 s and a standard deviation of 0.4909. The 95% CI ranges from 90.41 to 91.63 s, suggesting that the method performs well even in particularly complicated circumstances, despite increased computation times.

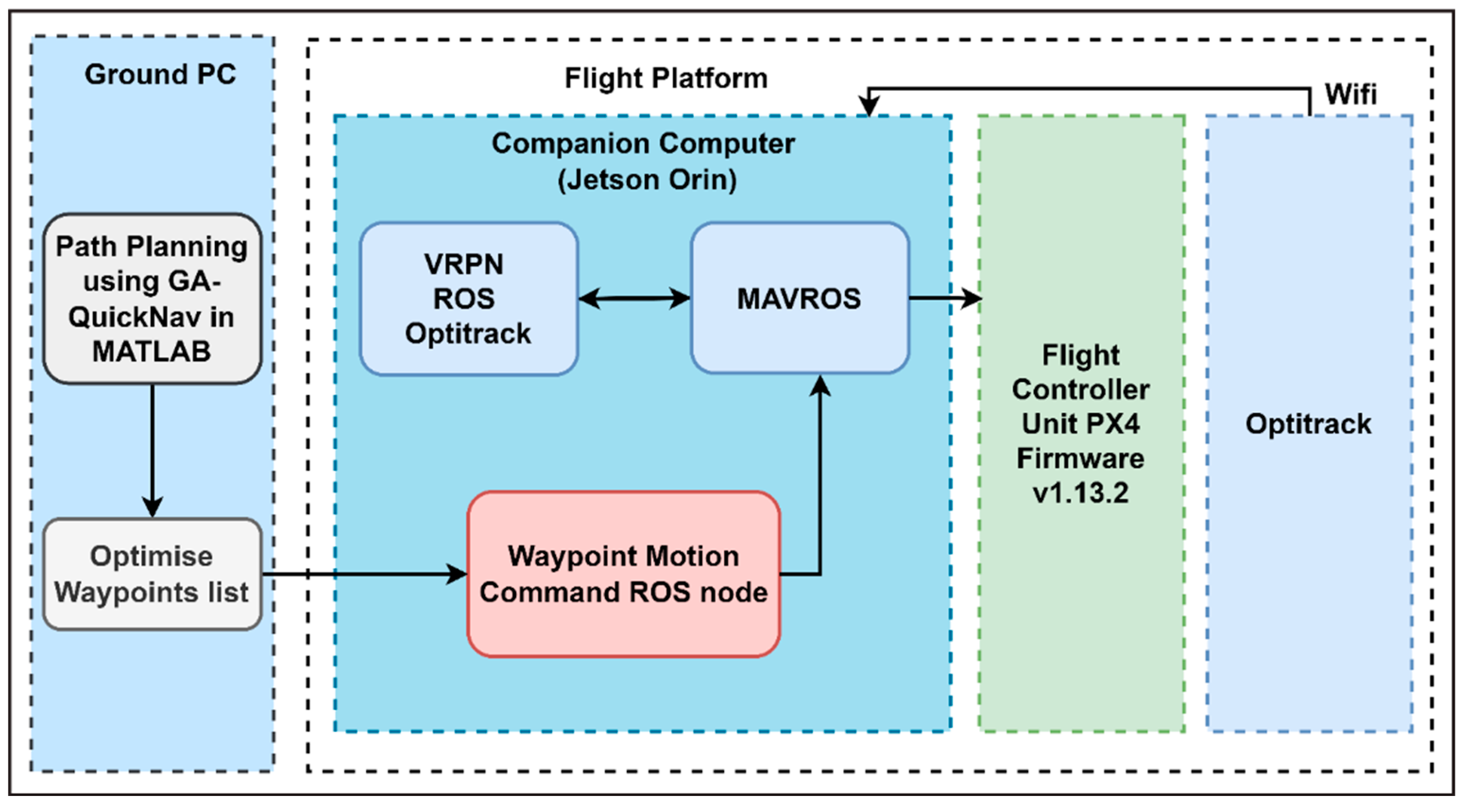
The performance of the GA-QuickNav algorithm, which combines a Genetic Algorithm (GA) with the QuickNav algorithm, was evaluated using four different TSP scenarios of increasing levels of complexity. We utilised MATLAB for simulations and the Robot Operating System (ROS) platform for conducting real-time flight testing with a UAV. The system architecture is shown in Figure 15.

Flight testing was conducted in real time using the following setup:

• Flight Platform: A Holybro X500 V2 multi-rotor system with 2216 KV920 motors and 1045 propellers (10″/254 mm length, 4.5″/114.3 mm pitch) utilised as the UAV frame shown in Figure 16. The UAV is controlled by a Holybro Pixhawk 6C autopilot running the PX4 firmware. Holybro 915 MHz telemetry radios enabled communication. The 500 × 215 × 1440 mm UAV has a 1-kilogram payload capacity. A four-cell 5000 mAh LiPo battery gave it 8 min of flight autonomy with a payload [40].
• Onboard Computing: The onboard computer for path planning execution used an NVIDIA Jetson Orin Nano developer kit, which consisted of an NVIDIA Ampere architecture featuring 1024 CUDA cores and 32 Tensor cores. It also included a 6-core Arm Cortex-A78AE v8.2 64-bit CPU and 8GB of LPDDR5 DRAM.
• Software Environment: The companion computer is equipped with Ubuntu 20.04, a 64-bit Linux-based operating system (OS). The ROS Noetic version enabled communication between the VRPN-optitrack system, MAVROS, and a waypoint motion command ROS node. To control the UAV, the open-source PX4 firmware version 1.13.2 is used.
• Testing Location: The real-world flight experiments were carried out within an indoor environment at QUT O-134, which has a motion capture system (optitrack) facility for safety and millimetre precision localisation.
• Flight Execution: The GA-QuickNav produces an output flight path as a sequence of waypoints and time for each waypoint. This flight path is then executed by an ROS node communicating with the PX4 firmware through MAVROS an ROS wrapper of the Micro Air Vehicle Link (MAVLink) protocol.
• Indoor Localisation: Optitrack system for localisation connected to the UAV companion computer via WiFi. The companion computer runs a Virtual-Reality Peripheral Network (VRPN) server to obtain the UAV pose in the flight area local frame. This is then transmitted to the Flight Controller Unit (FCU) using ROS and mavros for proper localisation in a GPS-denied environment.

Performance criteria:

• Path Optimisation: The algorithm’s efficacy in optimising the path is assessed by comparing the total distance covered before and after obstacle avoidance through real-time motion capture system data.
• Computational Time: The GA-QuickNav algorithm’s total computational time for processing each scenario was measured.

The outcomes of the simulation flight tests are shown in Table 3.

Table 5. TSP simulation flight test outcomes using GA-QuickNav.

TSP Problem	Number of Waypoints	Number of Obstacles	Detected Obstacles	Initial Distance (m)	Final Distance (m)	Time (s)
1	10	5	3	45.48	28.01	2.99
2	12	6	1	52.66	29.84	2.36
3	7	7	5	32.09	25.60	2.35
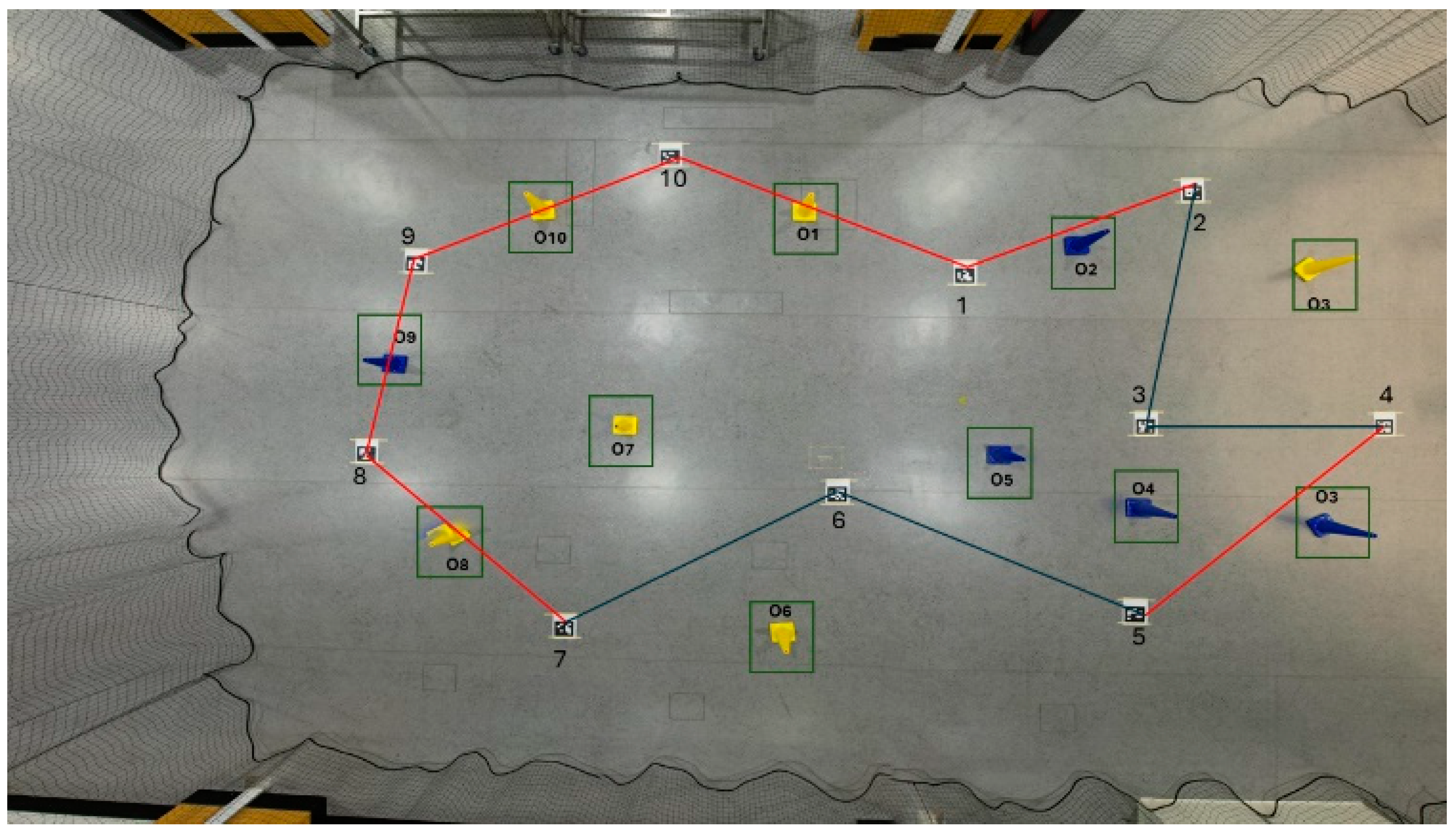
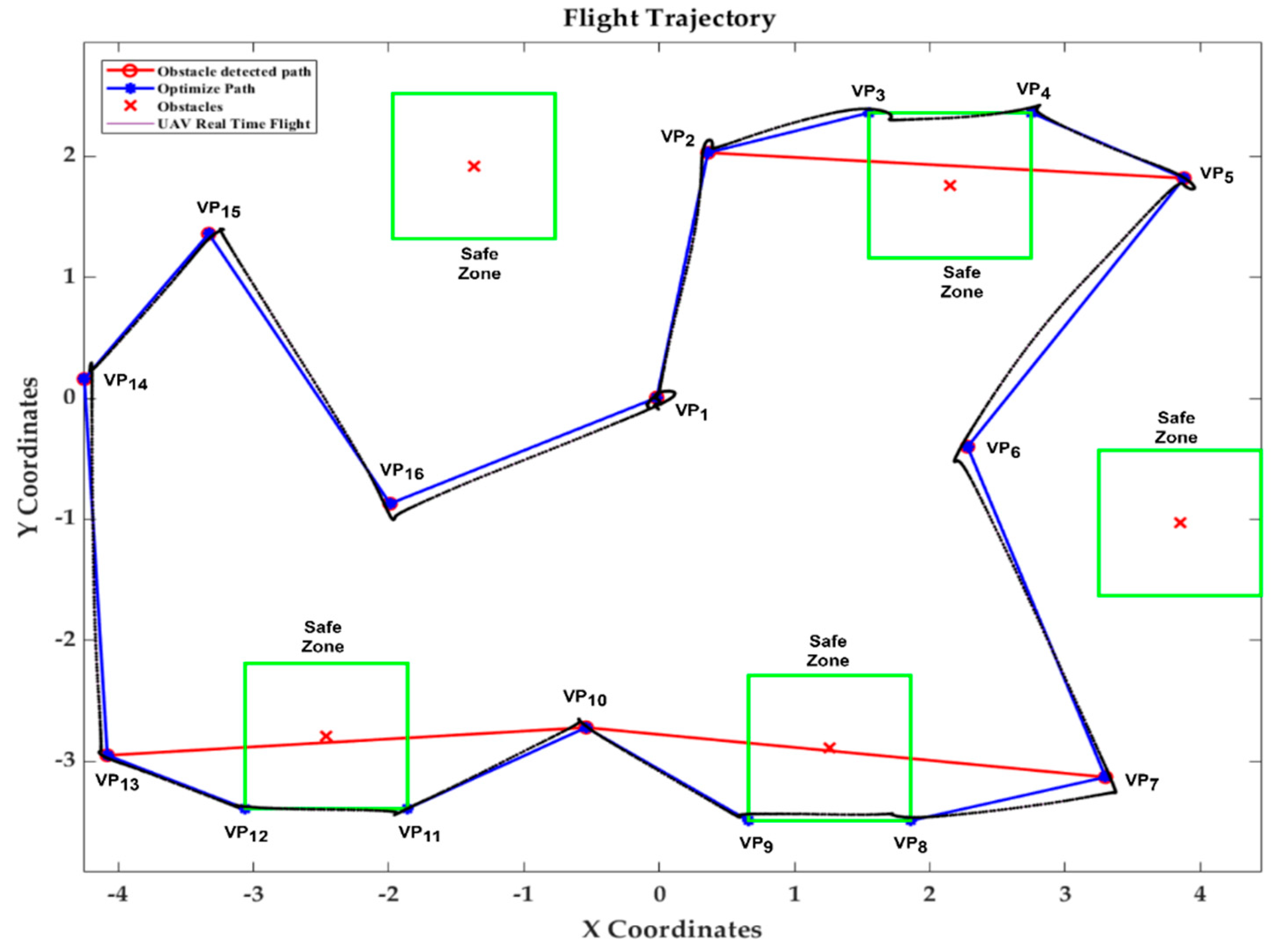
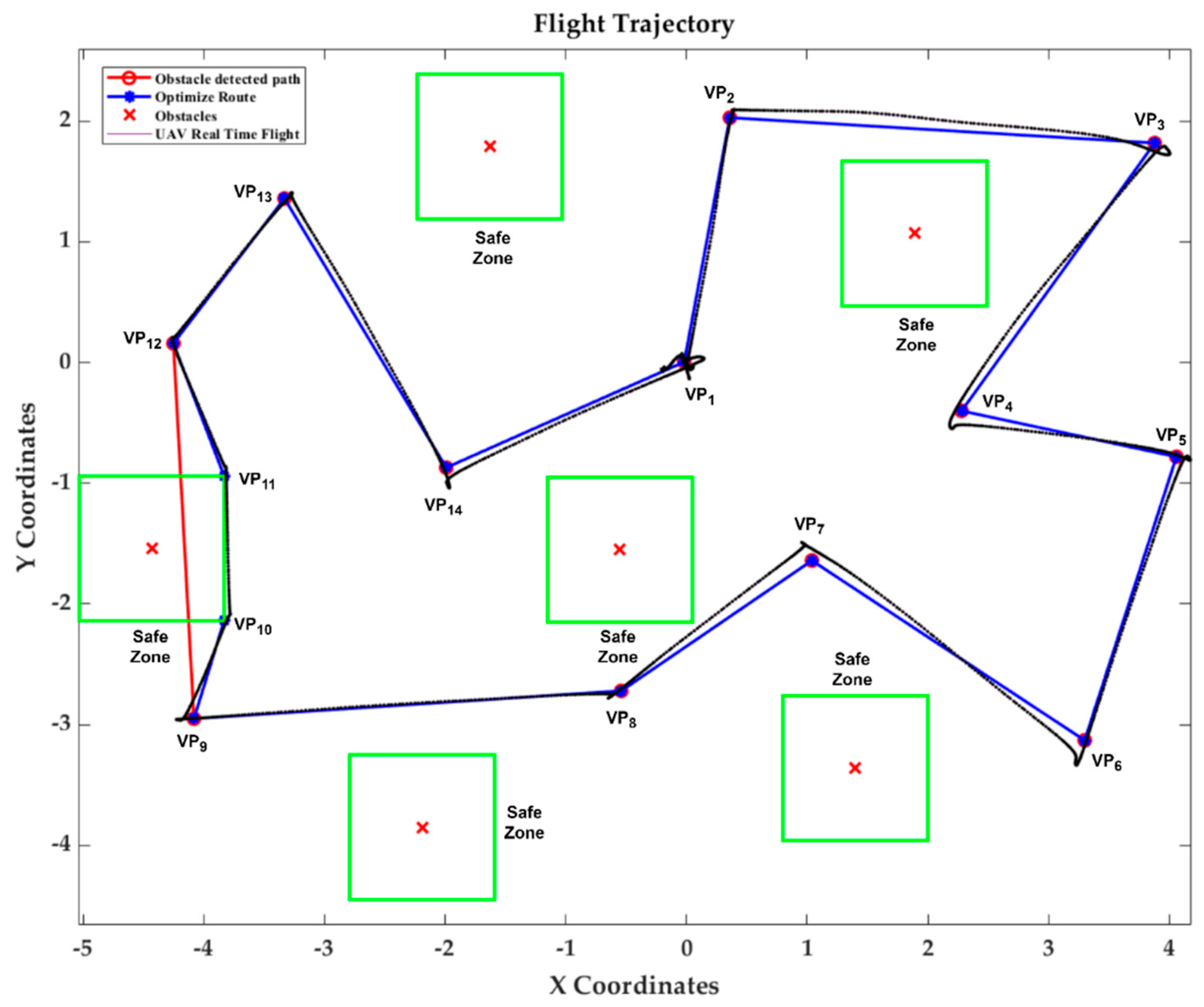
4	4	8	6	17.75	21.94	2.46

presents the outcomes of a comprehensive study focused on the TSP across several scenarios involving visiting waypoints (VPs) and obstacles. The algorithm was able to detect three of the obstacles in the optimised path during the first experiment, which consisted of ten visiting waypoints and five obstacles. This resulted in a significant reduction from the initial distance of 45.48 m, which was before path optimisation, to the final distance of 28.01 m of the optimised path in a short amount of time, 2.99 s, which is shown in Figure 17. 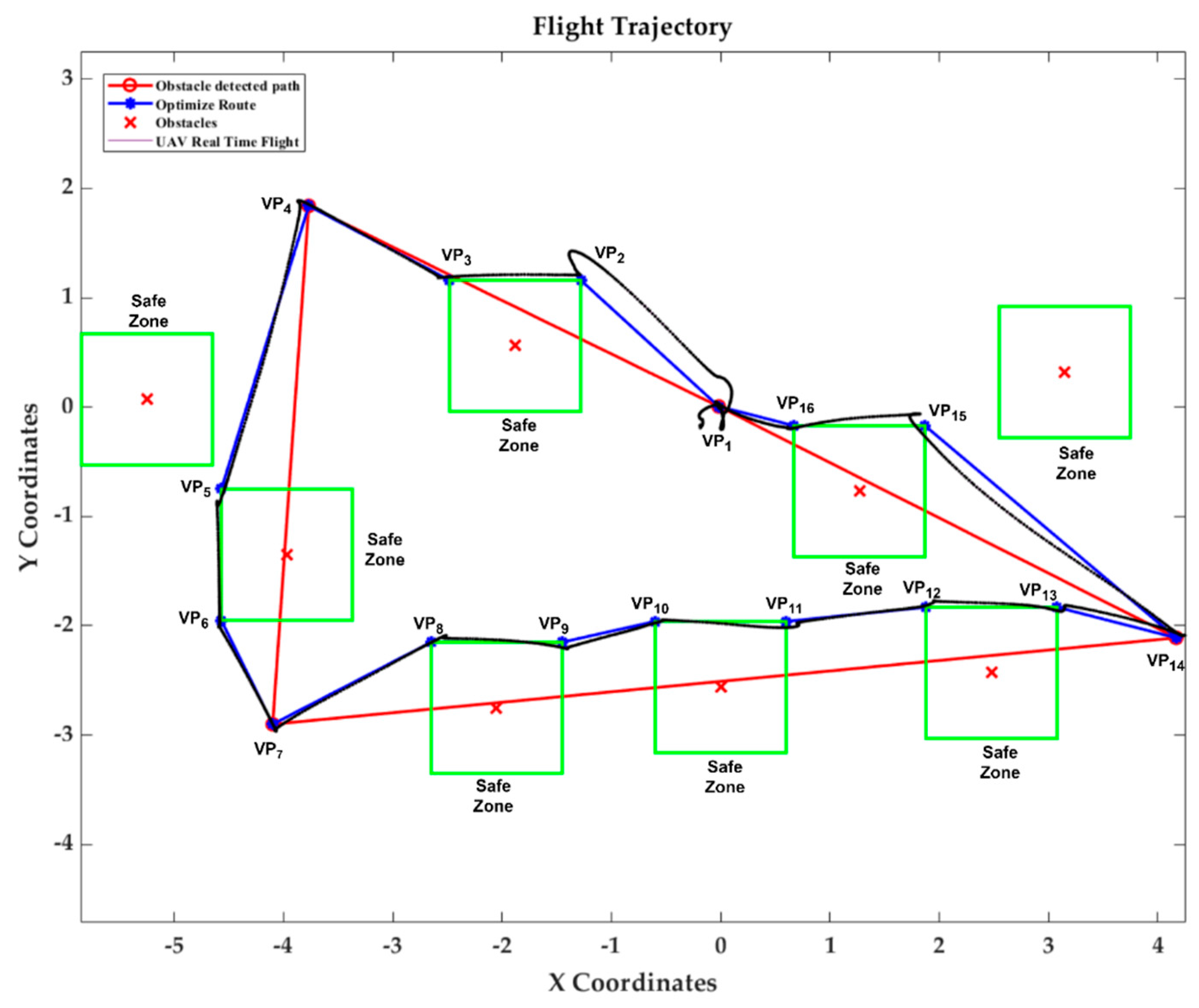During the second case, which included twelve VPs and six obstacles, the effectiveness of the approach was demonstrated by the fact that the starting distance of 52.66 m was reduced to 29.84 m after optimisation, and the estimated amount of time required for the computation was 2.36 s, as shown in Figure 18. During the third experiment, which consisted of seven VPs and seven obstacles, it was discovered that the optimum route contained five obstacles. The starting distance was 32.09 m, and the final distance was 25.60 m. It took 2.35 s to perform the computations. In Figure 19, the flight path is displayed. According to the results of the last experiment, which consisted of four VPs and eight obstacles, the optimal path was found to have six obstacles. The initial distance was 17.75 m, and after six obstacles were found in the optimum route, the final distance was 21.94 m. The entire processing time was 2.46 s. The flight path is depicted in Figure 20. A video demonstration of the UAV flight test can be accessed at https://bit.ly/UAV-test-video (accessed on 10 May 2024).

The following

Table 6. Comparison between TSP simulation flight test trip distance outcomes.

TSP Problem	Number of Waypoints	GA-QuickNav Final Distance (m)	A* Final Distance (m)	NN Final Distance (m)
1	10	28.01	32.48	40.95
2	12	29.84	39.79	38.95
3	7	25.60	26.99	43.58
4	4	21.94	21.93	30.54

presents a comparison of the final distances achieved by the three different path planning algorithms, GA-QuickNav, A*, and Nearest Neighbour (NN), across four different TSP problems with different numbers of waypoints.

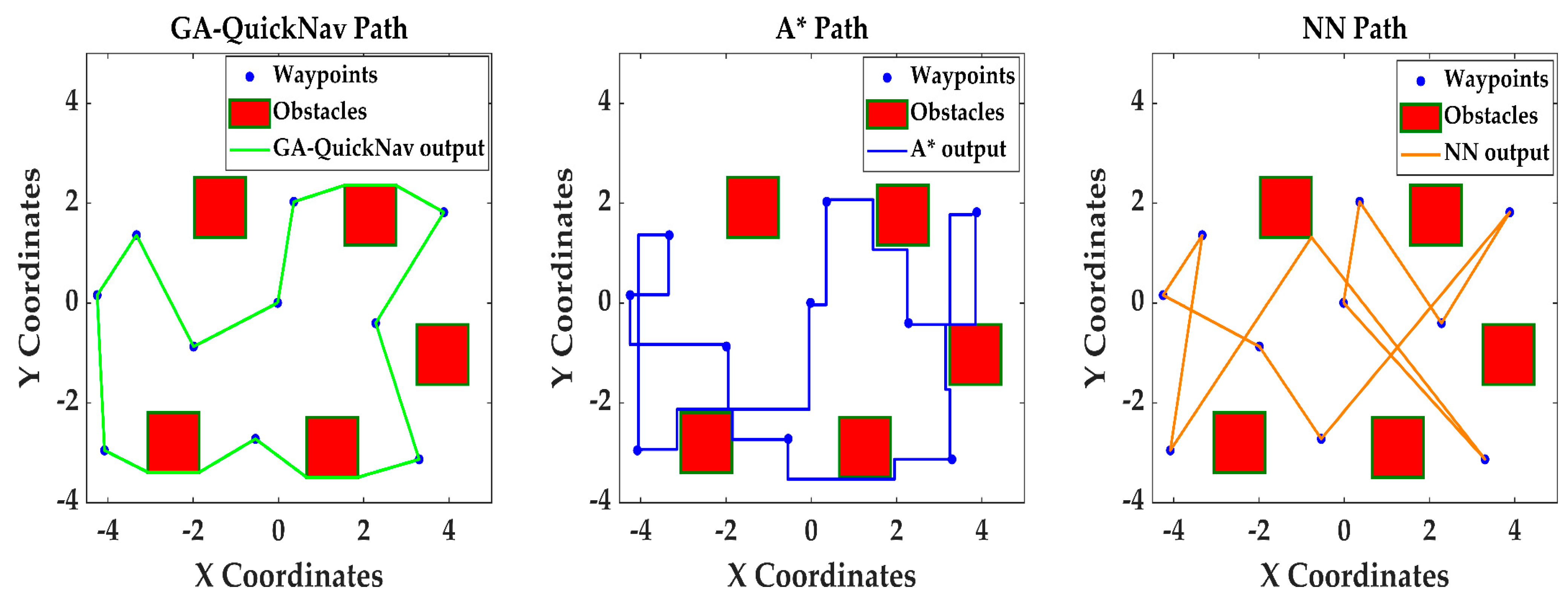
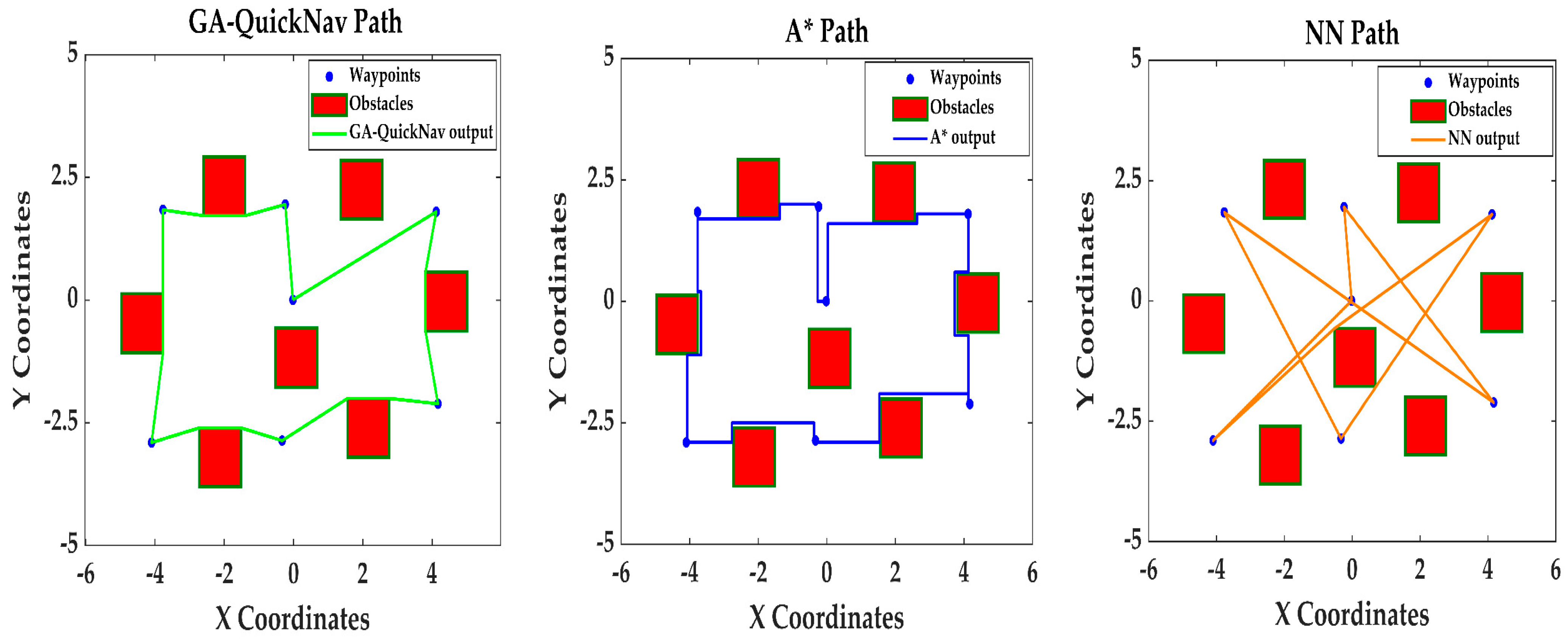
The GA-QuickNav algorithm outperformed both the A* algorithm and the NN algorithm in solving TSP problem 1, which included 10 waypoints. It reached a final distance of 28.01 m, while the A* algorithm resulted in a final distance of 32.48 m and the NN algorithm had a maximum final distance of 40.95 m. The findings are visually represented in Figure 21, which demonstrates the efficiency of the GA-QuickNav algorithm in this scenario. For TSP problem 2, consisting of 12 waypoints, the GA-QuickNav algorithm exceeded the A* algorithm and the NN algorithm. 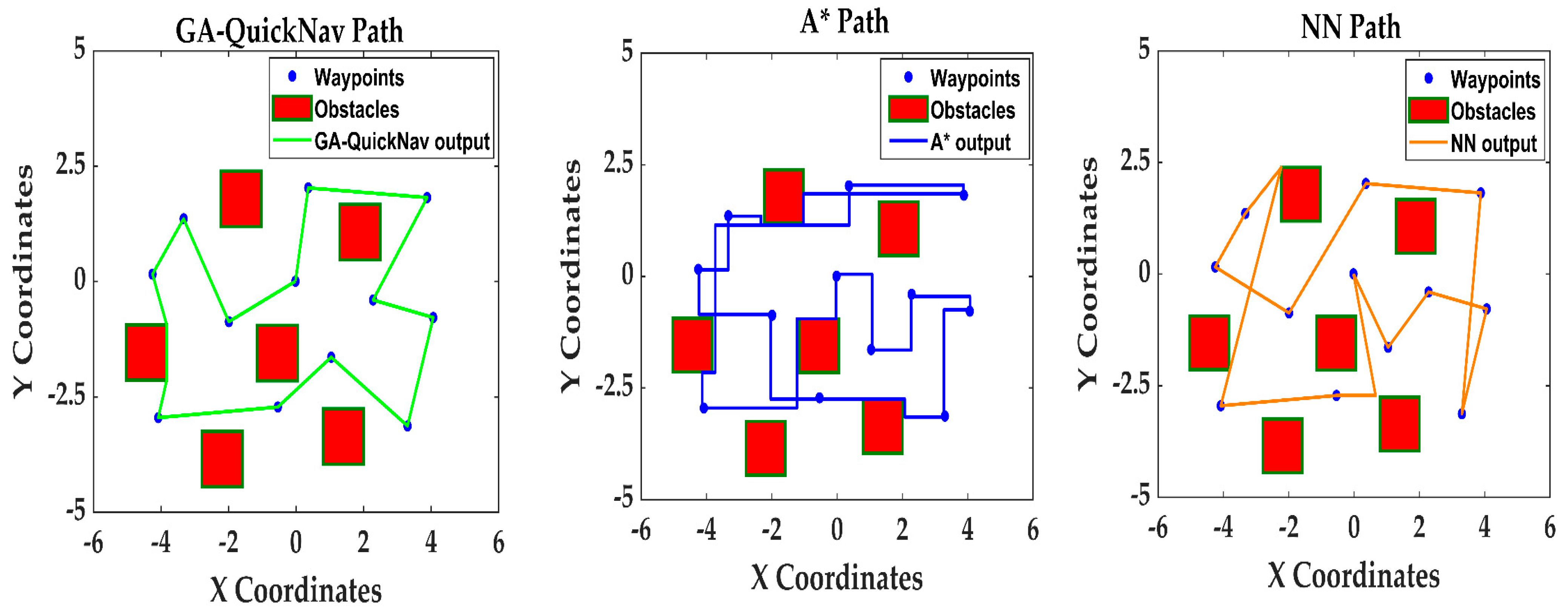It achieved a final distance of 29.84 m, while the A* algorithm and the NN algorithm achieved distances of 39.79 m and 38.95 m, respectively shown in Figure 22. The GA-QuickNav algorithm calculated 25.60 m for TSP problem 3. The obtained result was close to that of the A* algorithm, which achieved 26.99 m, and notably superior to that of the NN method, which achieved 43.58 m. The results are displayed in Figure 23. Regarding TSP problem 4, which involved four waypoints, both the GA-QuickNav and A* algorithms produced comparable final distances of 21.94 m and 21.93 m, respectively. Nevertheless, the NN method showed lower efficiency, resulting in a final distance of 30.54 m. Figure 24 illustrates the outcomes, showing that GA-QuickNav and A* performed similarly in this situation. However, the NN algorithm was unable to navigate around multiple obstacles in a single path, resulting in an inefficient route. In summary, the table and figures demonstrate that the GA-QuickNav algorithm consistently achieves shorter travel distances compared to the A* and NN algorithms in various scenarios with different numbers of waypoints. These results indicate that the GA-QuickNav algorithm is effective and reliable in path planning for UAVs.

The proposed combination of the GA-QuickNav approach proved the ability to efficiently optimise paths across a variety of scenarios requiring visiting waypoints and obstacles, according to the thorough results provided in the study. Nevertheless, numerous obstacles and significant discoveries arose from the thorough validation process. The algorithm demonstrated strong performance in optimising pathways while assuring the avoidance of obstacles, as seen by the substantial reductions in total travel distances achieved after integrating the QuickNav module in all test situations (Table 5). In Scenario 1, the starting distance of 45.48 m was decreased to 28.01 m after optimisation and obstacle avoidance, when there were 10 waypoints and 5 obstacles. The algorithm showed its effectiveness in path optimisation when crossing dense areas with obstacles, as seen by the significant reductions that were also noted in the other instances. In addition to four waypoints and eight obstacles, Scenario 4 was a significant challenge, as the ultimate distance of 21.94 m was larger than the initial distance of 17.75 m. This outcome includes a thorough explanation, specifically regarding the connections between the GA and the QuickNav obstacle avoidance system. At first, the GA identified the optimal route by only evaluating the shortest distance between waypoints, without considering any possible obstacles. After this optimisation, QuickNav executed its obstacle identification and avoidance procedure. During this stage, QuickNav identified three obstacles located along the GA’s first optimised path shown in Figure 20. To ensure safe navigation, the UAV needed to effectively manoeuvre around these obstructions by following designated safe zones. Particularly, the UAV navigated the shortest path found involving waypoints VP₇ through VP₁₄, effectively avoiding the obstacles while following the safe flying perimeter established for each of them. As a result of this diversion, the UAV ended up travelling through additional areas that were not initially part of the straight route, thereby increasing the total amount of distance travelled. The situation where there are many obstacles compared to the number of waypoints demonstrates the inherent compromise between minimising journey distance and assuring the safe avoidance of obstacles. The algorithm prioritised safety by intentionally diverting from the shortest path in order to effectively navigate around various obstacles. Regardless of this limitation, the suggested method consistently showed its ability to create optimal paths involving visiting waypoints and obstacles across all scenarios assessed, as shown by the representations of the paths (Figure 17, Figure 18, Figure 19 and Figure 20). Although the algorithm has shown strong performance in tested circumstances, its ability to handle bigger and more complex real-world scenarios has to be further examined. The main focus of the present study was on indoor scenarios with predetermined obstacle layouts, which may not fully represent the complexity found in large open environments. Expanding the algorithm to include additional circumstances presents difficulties, including enhanced computational requirements caused by larger amounts of data and more intricate path computations. In order to address these problems, future implementations may employ distributed computing approaches to improve processing capabilities. Furthermore, in order to efficiently handle dynamic obstacles in extensive and complex situations, the algorithm needs to be capable of adjusting to a three-dimensional operational environment. This includes travelling across various heights and addressing aerial obstacles that do not exist in two-dimensional scenarios. These improvements are crucial for maintaining the effectiveness and efficiency of the GA-QuickNav algorithm as the complexity of the task environment increases. These developments are essential for expanding the usefulness of our technique in situations like urban navigation and disaster response operations, where it is necessary to avoid dynamic obstacles and quickly optimise the course. The UAV successfully executed the optimised paths while avoiding obstacles based on real-time localisation data from the motion capture system, further validating the algorithm’s practical applicability in real-world flight tests conducted in a GPS-denied indoor environment. Additionally, the incorporation of QuickNav significantly improved computational efficiency, with execution times varying from 2.35 to 2.99 s throughout the scenarios. This computational efficiency is essential for real-world applications, especially time-sensitive situations, which require swift path optimisation with minimal latency while maintaining obstacle avoidance and safety. Overall, the extensive testing procedure emphasised the algorithm’s strength, effectiveness, and practicality for planning routes for scenarios that involve travelling to waypoints and avoiding obstacles. This presents the combination of GA-QuickNav as an appealing approach for improving the autonomy and safety of UAVs in real-world operations.

4. Conclusions

This research presents an innovative combined approach for offline path planning and obstacle avoidance for UAV operations, addressing the key challenges encountered in applications such as Wireless Sensor Networks (WSNs) and precision agriculture. The proposed approach combines an advanced GA with a geometrically based obstacle avoidance algorithm, QuickNav, to optimise mission trajectories and ensure safe and efficient UAV missions. The GA efficiently improves the optimisation of trajectories by generating a population of potential routes and using iterative selection processes to find the most optimal trajectory for visiting multiple predetermined waypoints. Concurrently, the QuickNav algorithm employs linear equations and geometric methods to identify and avoid obstacles along the optimised path, providing collision-free navigation. The integrated GA-QuickNav approach has been extensively evaluated through comprehensive simulations on assessed TSP scenarios and real-world UAV flight tests conducted in an indoor GPS-denied environment using a motion capture system for localisation. The proposed algorithm consistently proved its efficacy in reducing overall travel distances, successfully navigating UAVs through complex environments, and adhering to safety constraints across diverse scenarios with different waypoint combinations and obstacle densities. Using real-world testing to systematically evaluate and validate the proposed method gives this research credibility and practical relevance. The comprehensive testing conducted in various environments provides significant insights into the algorithm’s capabilities, strengths, and potential areas for further improvement. This study assumes that the UAV maintains a constant altitude, which simplifies the problem to a two-dimensional path planning scenario. This assumption is in line with the special requirements of interior environments or fields such as precision agriculture and WSN monitoring. In these cases, having a consistent altitude helps ensure the accuracy and dependability of data gathering. To guarantee consistent coverage, it is necessary for the UAV to maintain a steady elevation, which allows for optimised sensor operations. Nevertheless, we recognise that this assumption limits the relevance of the findings to dynamic outdoor scenarios with large height variations caused by diverse topography and aerial obstructions. However our results are limited in their applicability, this also highlights the opportunity to expand this research into further complex scenarios. Also, the present approach of the QuickNav algorithm involves enclosing obstacles within uniform square zones. This facilitates navigation, but it is specifically designed for environments that have predictable and consistent obstacle configurations. Future improvements can focus on modifying this approach to a wider range of diverse and constantly evolving scenarios, improving the algorithm’s usefulness and resilience. Although the proposed method has shown encouraging outcomes in offline path planning and obstacle avoidance, further research could investigate the incorporation of dynamic obstacle detection and avoidance capabilities. This would allow the algorithm to adjust to rapidly changing environments while executing a mission. Moreover, extending the approach to three-dimensional path planning and including additional constraints, such as energy efficiency and environmental considerations, could further enhance its applicability in various operational scenarios. This research provides a substantial contribution to the field of UAV path planning by introducing an innovative and effective solution that resolves the key problems of optimising missions, avoiding obstacles, and ensuring operational safety in applications like WSN and precision agriculture. The proposed integrated method not only enhances the theoretical underpinnings of path planning algorithms but also positions itself as a promising option for enabling efficient, secure, and autonomous UAV operations in numerous real-world applications.