Optimizing AoI in IoT Networks: UAV-Assisted Data Processing Framework Integrating Cloud–Edge Computing
Abstract
1. Introduction
- To ensure the freshness of information in the IoT, we develop a multi-UAV-enabled cloud–edge hierarchical data processing framework to minimize the AAoI and PAoI. It can be achieved by jointly optimizing the uploading order, service associations, and UAVs’ trajectories, while making informed computation offloading decisions considering UAVs’ operational endurance constraints.
- Building on the above framework, we devise an SN clustering model that considers SN geo-distributions and minimal uploading time to determine the optimal uploading order of SNs and the HPs. In addition, we develop an HP clustering scheme to dynamically adjust HP-UAV service associations, taking into account the processing time and energy consumption required for UAV task completion.
- According to the HPs and the service association on HP-UAV, we propose an intelligent multi-objective strategy by improving the gray wolf optimization algorithm, which explores the better UAVs’ flight trajectories at every HP cluster to further optimize the AAoI and PAoI.
- Simulation results demonstrate that our proposed AODP is able to efficiently accomplish data collection and processing under various parameter settings; it also has superiority in optimizing PAoI and AAoI and ensuring the energy saving of UAVs compared with four mainstream algorithms.
2. System Model and Problem Definition
2.1. System Model
2.2. Communication Model
2.3. AoI Model
2.4. Energy Usage Model
2.5. Problem Definition
3. Solution Design
3.1. Joint SN Clustering and HP Exploration Scheme Using the Affinity Propagation (AP) Algorithm
3.2. Improved Expectation-Maximization Algorithm for Gaussian Mixture Models-Based HP-UAV Association Scheme
| Algorithm 1 JSCHE: Joint SN Clustering and HP Exploration Scheme based on AP Algorithm |
|
| Algorithm 2 HUAEM: HP-UAV Association Optimization Scheme based on IEM Algorithm |
|
3.3. AoI-Oriented Multi-Objective Gray Wolf Optimization for Path Planing
| Algorithm 3 PMGWO-based multi-UAV Path Planning |
|
3.4. AODP: An AoI Optimization Data Processing Framework
| Algorithm 4 AODP: AoI Optimization Data Processing |
|
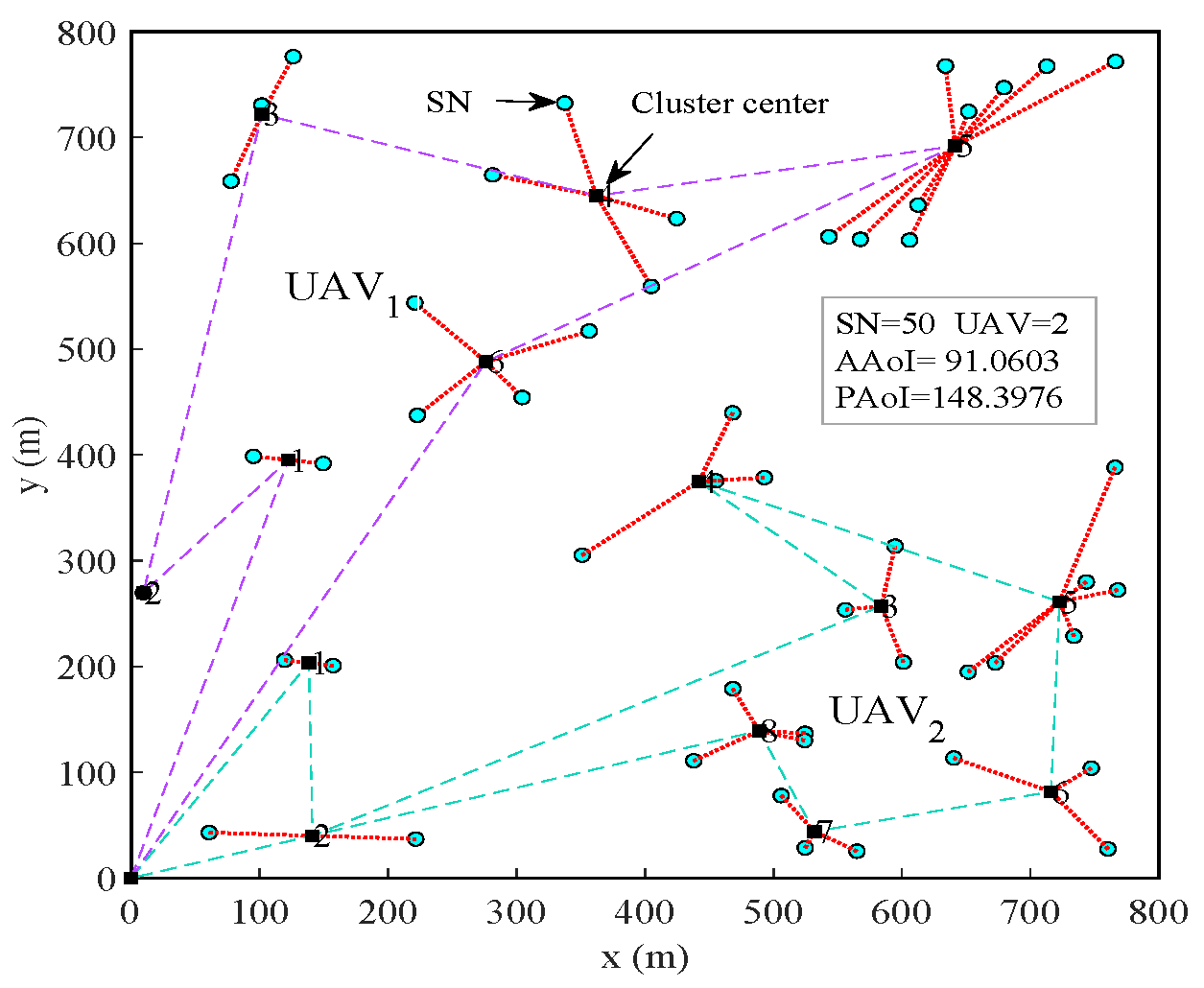
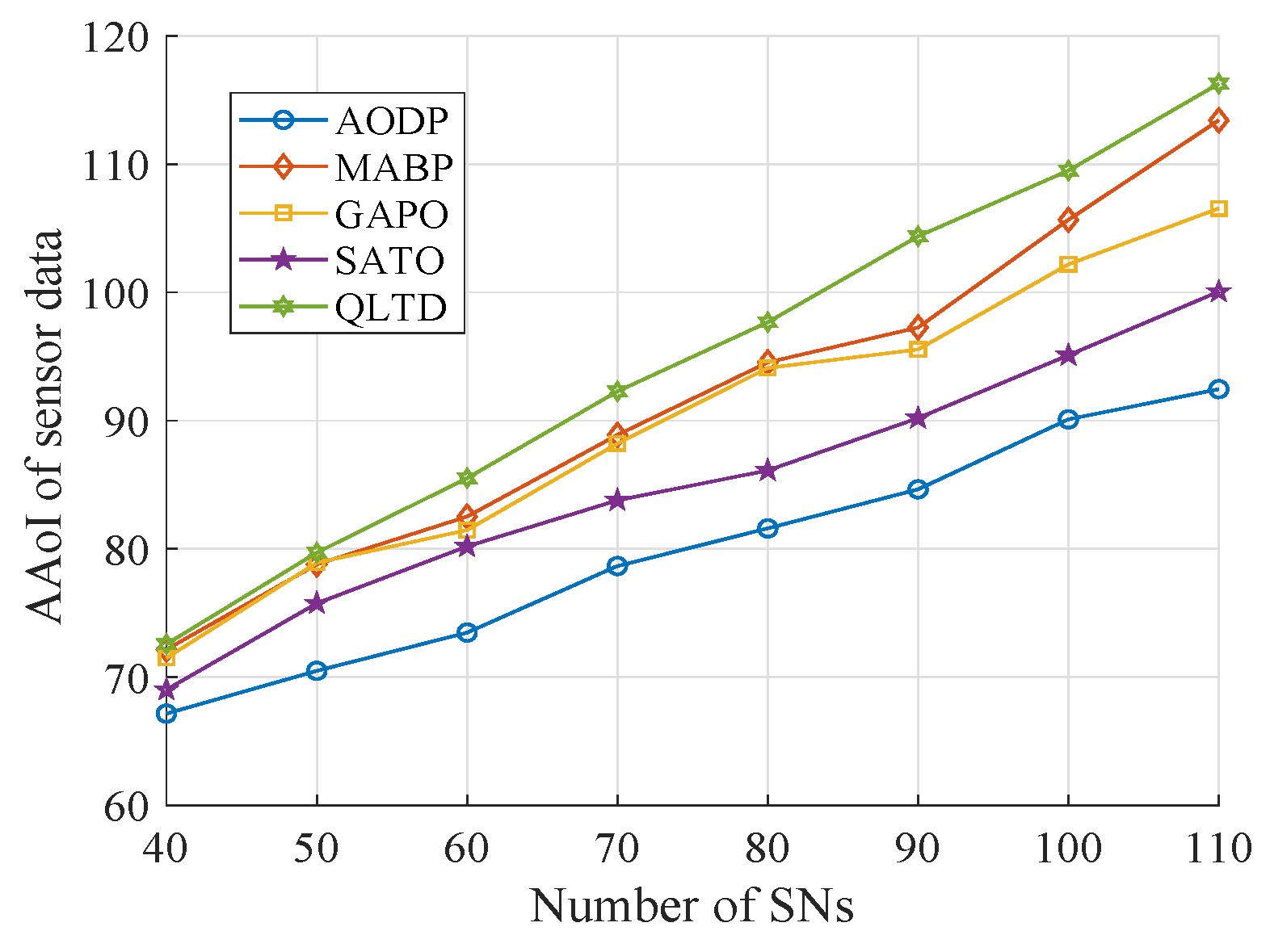
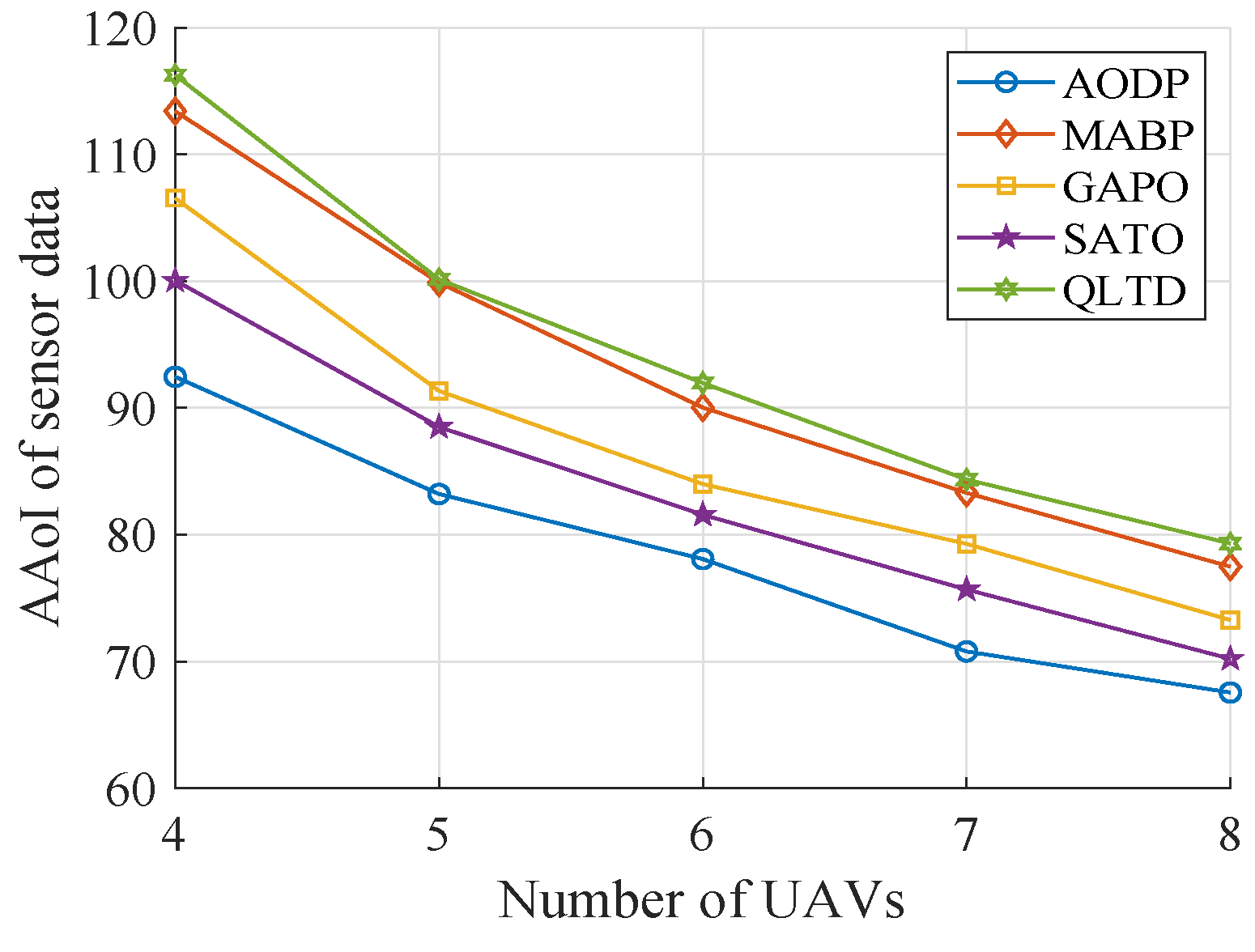
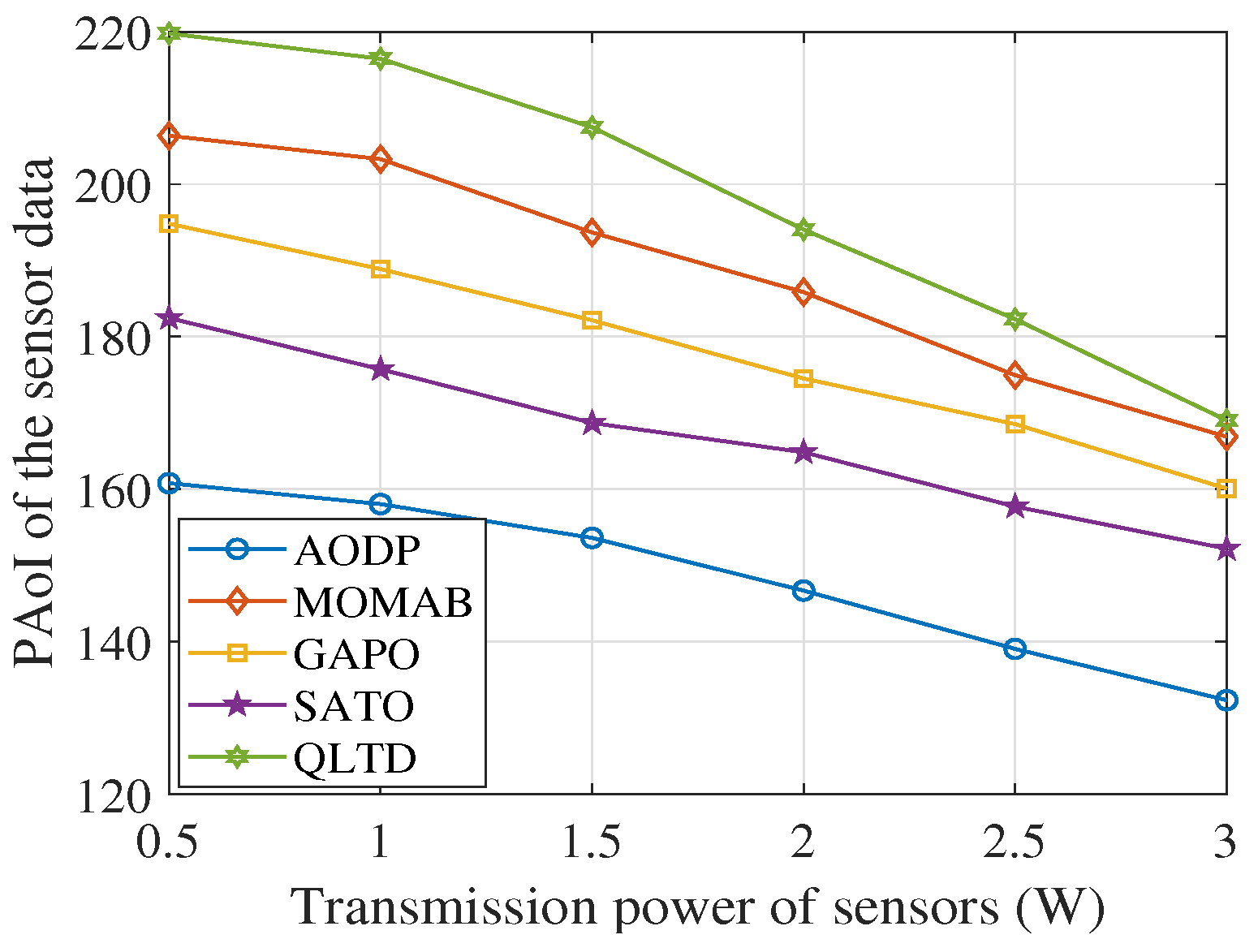
4. Simulation Evaluation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khadka, G.; Nemati, M.; Zhou, X.; Choi, J. Index Modulation in Backscatter Communication for IoT Sensor Based Applications: A Review. IEEE Sens. J. 2022, 22, 21445–21461. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, G.; Wang, Y.; Wang, Z. A Load-Aware Energy-Efficient Clustering Algorithm in Sensor-Cloud. J. Grid Comput. 2023, 21, 50. [Google Scholar] [CrossRef]
- Chawla, D.; Mehra, P.S. A roadmap from classical cryptography to post-quantum resistant cryptography for 5G-enabled IoT: Challenges, opportunities and solutions. Internet Things 2023, 24, 100950. [Google Scholar] [CrossRef]
- Zhu, A.; Zeng, Z.; Guo, S.; Lu, H.; Ma, M.; Zhou, Z. Game-theoretic robotic offloading via multi-agent learning for agricultural applications in heterogeneous networks. Comput. Electron. Agric. 2023, 211, 108017. [Google Scholar] [CrossRef]
- Wan, X. Dynamic Resource Management in MEC Powered by Edge Intelligence for Smart City Internet of Things. J. Grid Comput. 2024, 22, 29. [Google Scholar] [CrossRef]
- Borkowski, A.S. Low-Cost Internet of Things Solution for Building Information Modeling Level 3B—Monitoring, Analysis and Management. J. Sens. Actuator Netw. 2024, 13, 19. [Google Scholar] [CrossRef]
- Bhambri, P.; Rani, S.; Gupta, G.; Khang, A. Cloud and fog Computing Platforms for Internet of Things; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Ghandour, O.; El Kafhali, S.; Hanini, M. Computing Resources Scalability Performance Analysis in Cloud Computing Data Center. J. Grid Comput. 2023, 21, 61. [Google Scholar] [CrossRef]
- Zhu, A.; Ma, M.; Guo, S.; Yang, Y. Adaptive Access Selection Algorithm for Multi-Service in 5G Heterogeneous Internet of Things. IEEE Trans. Netw. Sci. Eng. 2022, 9, 1630–1644. [Google Scholar] [CrossRef]
- Zhu, A.; Ma, M.; Guo, S.; Yu, S.; Yi, L. Adaptive multi-access algorithm for multi-service edge users in 5G ultra-dense heterogeneous networks. IEEE Trans. Veh. Technol. 2021, 70, 2807–2821. [Google Scholar] [CrossRef]
- Jin, X.; Hua, W.; Wang, Z.; Chen, Y. A survey of research on computation offloading in mobile cloud computing. Wirel. Netw. 2022, 28, 1563–1585. [Google Scholar] [CrossRef]
- Sofla, M.S.; Kashani, M.H.; Mahdipour, E.; Mirzaee, R.F. Towards effective offloading mechanisms in fog computing. Multimed. Tools Appl. 2022, 81, 1997. [Google Scholar] [CrossRef] [PubMed]
- Wen, X.; Sun, H.M. Parking Cooperation-Based Mobile Edge Computing Using Task Offloading Strategy. J. Grid Comput. 2024, 22, 8. [Google Scholar]
- Naouri, A.; Wu, H.; Nouri, N.A.; Dhelim, S.; Ning, H. A novel framework for mobile-edge computing by optimizing task offloading. IEEE Internet Things J. 2021, 8, 13065–13076. [Google Scholar] [CrossRef]
- Li, M.; Lei, H.; Guo, H.; Sulaiman, R.; Deebani, W.; Shutaywi, M. Efficient data offloading using markovian decision on state reward action in edge computing. J. Grid Comput. 2023, 21, 25. [Google Scholar] [CrossRef]
- Hu, S.; Xiao, Y. Design of cloud computing task offloading algorithm based on dynamic multi-objective evolution. Future Gener. Comput. Syst. 2021, 122, 144–148. [Google Scholar] [CrossRef]
- Liu, J.; Guo, S.; Wang, Q.; Pan, C.; Yang, L. Optimal multi-user offloading with resources allocation in mobile edge cloud computing. Comput. Netw. 2023, 221, 109522. [Google Scholar] [CrossRef]
- Guo, K.; Zhang, R. Fairness-oriented computation offloading for cloud-assisted edge computing. Future Gener. Comput. Syst. 2022, 128, 132–141. [Google Scholar] [CrossRef]
- Qu, X.; Wang, H. Emergency task offloading strategy based on cloud-edge-end collaboration for smart factories. Comput. Netw. 2023, 234, 109915. [Google Scholar] [CrossRef]
- Du, R.; Liu, C.; Gao, Y.; Hao, P.; Wang, Z. Collaborative cloud-edge-end task offloading in NOMA-enabled mobile edge computing using deep learning. J. Grid Comput. 2022, 20, 14. [Google Scholar] [CrossRef]
- Chen, S.; Chen, J.; Miao, Y.; Wang, Q.; Zhao, C. Deep reinforcement learning-based cloud-edge collaborative mobile computation offloading in industrial networks. IEEE Trans. Signal Inf. Process. Over Netw. 2022, 8, 364–375. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, Z.; Cheng, N.; Zeng, D.; Fan, P. Stackelberg-Game-Based Computation Offloading Method in Cloud—Edge Computing Networks. IEEE Internet Things J. 2022, 9, 16510–16520. [Google Scholar] [CrossRef]
- Zhu, A.; Lu, H.; Guo, S.; Zeng, Z.; Ma, M.; Zhou, Z. SyRoC: Symbiotic robotics for QoS-aware heterogeneous applications in IoT-edge-cloud computing paradigm. Future Gener. Comput. Syst. 2024, 150, 202–219. [Google Scholar] [CrossRef]
- Zhu, A.; Lu, H.; Guo, S.; Zeng, Z.; Zhou, Z. CollOR: Distributed collaborative offloading and routing for tasks with QoS demands in multi-robot system. Ad Hoc Netw. 2024, 152, 103311. [Google Scholar] [CrossRef]
- Ma, M.; Wang, Z. Distributed Offloading for Multi-UAV Swarms in MEC-Assisted 5G Heterogeneous Networks. Drones 2023, 7, 226. [Google Scholar] [CrossRef]
- Liu, Z. A Multi-joint Optimisation Method for Distributed Edge Computing Resources in IoT-Based Smart Cities. J. Grid Comput. 2023, 21, 58. [Google Scholar] [CrossRef]
- Zhu, A.; Lu, H.; Ma, M.; Zhou, Z.; Zeng, Z. DELOFF: Decentralized Learning-Based Task Offloading for Multi-UAVs in U2X-Assisted Heterogeneous Networks. Drones 2023, 7, 656. [Google Scholar] [CrossRef]
- Sun, Y.; Kadota, I.; Talak, R.; Modiano, E. Age of Information: A New Metric for Information Freshness; Springer Nature: Berlin, Germany, 2022. [Google Scholar]
- Aoki, S.; Yonezawa, T.; Kawaguchi, N.; Steenkiste, P.; Rajkumar, R.R. Time-Sensitive Cooperative Perception for Real-Time Data Sharing over Vehicular Communications: Overview, Challenges, and Future Directions. IEEE Internet Things Mag. 2022, 5, 108–113. [Google Scholar] [CrossRef]
- Fu, R.; Ren, X.; Li, Y.; Wu, Y.; Sun, H.; Al-Absi, M.A. Machine-Learning-Based UAV-Assisted Agricultural Information Security Architecture and Intrusion Detection. IEEE Internet Things J. 2023, 10, 18589–18598. [Google Scholar] [CrossRef]
- Niu, Z.; Yang, H.; Zhou, L.; Farag Taha, M.; He, Y.; Qiu, Z. Deep learning-based ranging error mitigation method for UWB localization system in greenhouse. Comput. Electron. Agric. 2023, 205, 107573. [Google Scholar] [CrossRef]
- Liu, K.; Zheng, J. UAV trajectory optimization for time-constrained data collection in UAV-enabled environmental monitoring systems. IEEE Internet Things J. 2022, 9, 24300–24314. [Google Scholar] [CrossRef]
- Diao, X.; Yang, W.; Yang, L.; Cai, Y. Uav-relaying-assisted multi-access edge computing with multi-antenna base station: Offloading and scheduling optimization. IEEE Trans. Veh. Technol. 2021, 70, 9495–9509. [Google Scholar] [CrossRef]
- Hernández-Rojas, D.L.; Fernández-Caramés, T.M.; Fraga-Lamas, P.; Escudero, C.J. Design and Practical Evaluation of a Family of Lightweight Protocols for Heterogeneous Sensing through BLE Beacons in IoT Telemetry Applications. Sensors 2018, 18, 57. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, H.N.; Wang, Q.; Imran, M.; Guizani, N. Wireless powering Internet of Things with UAVs: Challenges and opportunities. IEEE Netw. 2022, 36, 146–152. [Google Scholar] [CrossRef]
- Zhang, Z.; Chang, Q.; Yang, S.; Xing, J. Sensing-Communication Bandwidth Allocation in Vehicular Links Based on Reinforcement Learning. IEEE Wirel. Commun. Lett. 2023, 12, 11–15. [Google Scholar] [CrossRef]
- Zhou, W.; Fan, L.; Zhou, F.; Li, F.; Lei, X.; Xu, W.; Nallanathan, A. Priority-aware resource scheduling for uav-mounted mobile edge computing networks. IEEE Trans. Veh. Technol. 2023, 72, 9682–9687. [Google Scholar] [CrossRef]
- Wang, W.; Qu, R.; Liao, H.; Wang, Z.; Zhou, Z.; Wang, Z.; Mumtaz, S.; Guizani, M. 5G MEC-Based Intelligent Computation Offloading in Power Robotic Inspection. IEEE Wirel. Commun. 2023, 30, 66–74. [Google Scholar] [CrossRef]
- Kang, H.; Chang, X.; Mišić, J.; Mišić, V.B.; Fan, J.; Liu, Y. Cooperative UAV Resource Allocation and Task Offloading in Hierarchical Aerial Computing Systems: A MAPPO Based Approach. IEEE Internet Things J. 2023, 10, 10497–10509. [Google Scholar] [CrossRef]
- Zhang, H.; Liao, K.; Tai, Y.; Ma, W.; Cao, G.; Sun, W.; Xu, L. Decentralized and Fault-Tolerant Task Offloading for Enabling Network Edge Intelligence. IEEE Syst. J. 2024, 18, 1459–1470. [Google Scholar] [CrossRef]
- Gong, X.; Chen, M.; Li, D.; Cao, Y. Delay-Optimal Distributed Computation Offloading in Wireless Edge Networks. IEEE/ACM Trans. Netw. 2024, 1–16. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, J.; Zhang, R. Energy minimization for wireless communication with rotary-wing UAV. IEEE Trans. Wirel. Commun. 2019, 18, 2329–2345. [Google Scholar] [CrossRef]
- Ait-Saadi, A.; Meraihi, Y.; Soukane, A.; Ramdane-Cherif, A.; Benmessaoud Gabis, A. A novel hybrid Chaotic Aquila Optimization algorithm with Simulated Annealing for Unmanned Aerial Vehicles path planning. Comput. Electr. Eng. 2022, 104, 108461. [Google Scholar] [CrossRef]
- Zhou, P.; Zhao, W.; Li, J.; Li, A.; Du, W.; Wen, S. Massive Maritime Path Planning: A Contextual Online Learning Approach. IEEE Trans. Cybern. 2021, 51, 6262–6273. [Google Scholar] [CrossRef] [PubMed]
- Indu; Singh, R.P.; Choudhary, H.R.; Dubey, A.K. Trajectory Design for UAV-to-Ground Communication With Energy Optimization Using Genetic Algorithm for Agriculture Application. IEEE Sens. J. 2021, 21, 17548–17555. [Google Scholar] [CrossRef]
- Chang, J.; Dong, N.; Li, D.; Ip, W.H.; Yung, K.L. Skeleton Extraction and Greedy-Algorithm-Based Path Planning and its Application in UAV Trajectory Tracking. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4953–4964. [Google Scholar] [CrossRef]















| Ref. | Objective | Strengths | Environment | Contribution | Metrics |
|---|---|---|---|---|---|
| [16] | Minimize execution time with energy constraint | Enhanced offloading for terminals | Cloud only | A theoretical basis for offloading | No AoI metrics |
| [17] | Minimize time and energy | Consideration of the multi-user competition | Edge only | Addresses the constraints of mobility and limited resources | No AoI focus |
| [18] | Reduce response time | Consideration of trade-offs in resource allocation | Cloud–edge | Optimization of data transmission and cloudâedge cooperation | No AoI metrics |
| [19] | Reduce execution time | Prioritization for the key tasks’ offloading | Cloud–edge | Optimization of task execution during emergencies | No AoI metrics |
| [23] | Improve system performance | Consideration of muti-robot task execution | Cloud–edge | Proposal of optimal data transmission solution | No AoI metrics |
| [25] | Minimize time and energy | Use of UAVs | UAV-assisted edge | Realize cost-effective transmission and offloading | No AoI metrics |
| [26] | Minimize time and energy | Collaborative UAVs | UAV-assisted cloud–edge | Ensuring optimal task scheduling and energy efficiency | No AoI metrics |
| [28] | Ensure real-time data processing | Analyze AoI | Not specified | Highlighting AoI importance | No UAVs |
| [29] | Reduce data processing time | Timely data transmission | Cloud–edge | Studying the cooperative data perception solution | No UAVs |
| Ours | Minimize AAoI and PAoI, optimize energy usage | Collaborative UAVs and timely data processing | Comprise UAV, cloud and edge layers | Study the optimal data transmission, trajectory planning and offloading solution | AoI focus |
| Symbol | Values | Symbol | Values |
|---|---|---|---|
| (m) | 30 | (W) | 0.5 |
| (m) | 30 | (W) | 10 |
| (MHz) | 0.5 | (MHz) | 10 |
| (dBm) | −110 | −110 | |
| (dB) | 3 | (dB) | 23 |
| 9.61 | 0.16 | ||
| (Mbits) | [20, 30] | (cycles/bit) | 1000 |
| (GHz) | [1, 2] | (GHz) | [2, 3] |
| (GHz) | 2 | (kg/m3) | 1.225 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, M.; Wang, Z. Optimizing AoI in IoT Networks: UAV-Assisted Data Processing Framework Integrating Cloud–Edge Computing. Drones 2024, 8, 401. https://doi.org/10.3390/drones8080401
Ma M, Wang Z. Optimizing AoI in IoT Networks: UAV-Assisted Data Processing Framework Integrating Cloud–Edge Computing. Drones. 2024; 8(8):401. https://doi.org/10.3390/drones8080401
Chicago/Turabian StyleMa, Mingfang, and Zhengming Wang. 2024. "Optimizing AoI in IoT Networks: UAV-Assisted Data Processing Framework Integrating Cloud–Edge Computing" Drones 8, no. 8: 401. https://doi.org/10.3390/drones8080401
APA StyleMa, M., & Wang, Z. (2024). Optimizing AoI in IoT Networks: UAV-Assisted Data Processing Framework Integrating Cloud–Edge Computing. Drones, 8(8), 401. https://doi.org/10.3390/drones8080401





