Cooperative Target Fencing Control for Unmanned Aerial Vehicle Swarm with Collision, Obstacle Avoidance, and Connectivity Maintenance

Abstract

This paper investigates the target fencing control problem of fixed-wing Unmanned Aerial Vehicle (UAV) swarms with collision avoidance and connectivity maintenance in obstacle environments. A distributed cooperative fencing scheme for maneuvering targets is proposed without predefined accurate formation. Firstly, considering that not all states of the target can be obtained by UAVs, a differential state observer is developed to estimate the target’s unknown speed and control input. Secondly, by constructing potential functions with fewer parameter adjustments, corresponding negative gradient terms are calculated to guarantee the flight safety and communication connectivity of the swarm. A distributed cooperative controller is designed using the self-organized theory and consensus control. Additionally, the stability of the closed-loop system with the controller is analyzed based on Lyapunov stability theory. Finally, numerical simulations are performed to illustrate the effectiveness of the proposed scheme.

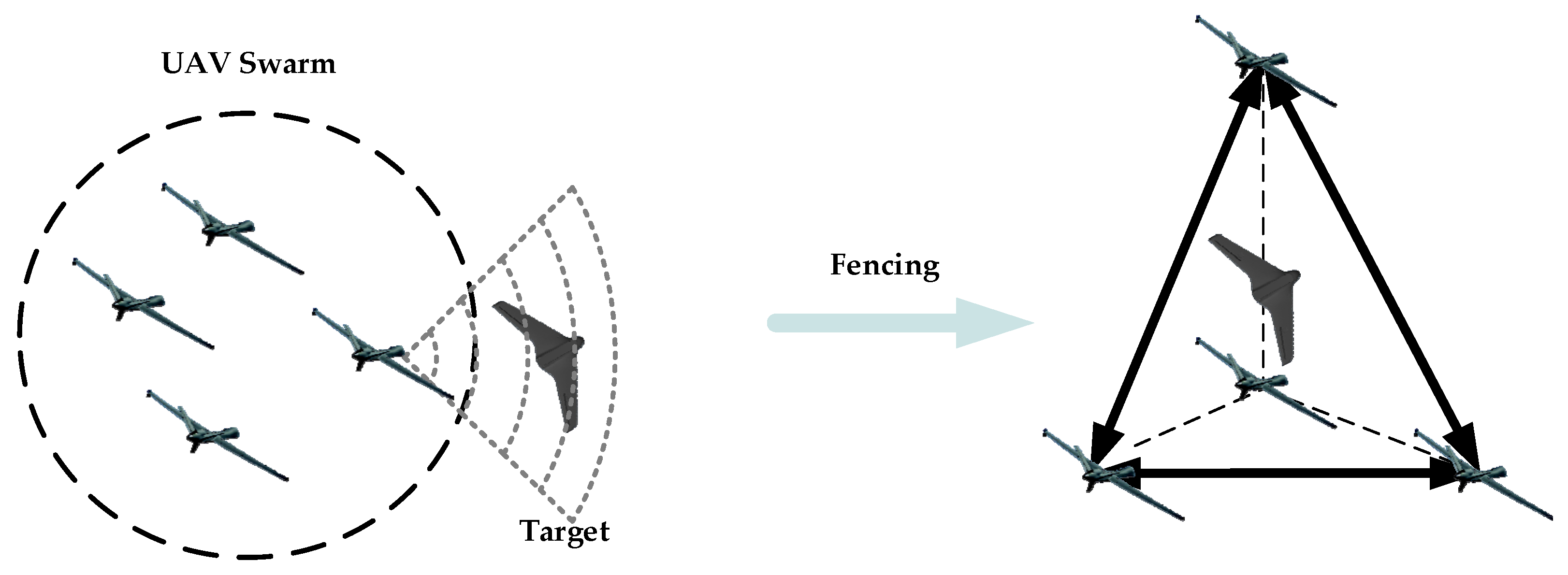
1. Introduction

UAVs have been endowed with stronger autonomous decision-making and response capabilities through artificial intelligence technology. Nevertheless, the intricacy of flight airspace and the constraints of onboard sensors pose challenges for a single UAV in executing complex tasks. The UAV swarm effectively mitigates these limitations by leveraging cooperative capabilities. They are often applied to high-risk and easily exposed tasks such as target tracking [1,2], target fencing [3,4], and area searching [5]. Consequently, they have received widespread attention from scholars [6,7].

Target fencing control aims to design a cooperative controller for a group of UAVs to enclose the target within their flight convex hull [8]. The design of the fencing strategy focuses on four main aspects. The first aspect involves how to obtain the target’s unknown state. In practical tracking or fencing scenarios, the target is typically uncooperative, implying that its speed and control input are not directly accessible. Several studies assume that the target’s states were partially or entirely known by UAVs. In [9], a high-order sliding mode observer was designed to estimate the unmeasurable linear velocity of the target, enabling UAVs to enclose the target in the desired formation. In [10], the target’s state can be obtained by certain UAVs and transmitted to their neighbors through the network for distributed estimation within each formation form. An adaptive extended state observer was constructed in [11] which can simultaneously estimate the leader’s maneuvers and external disturbances.

The second aspect involves designing an appropriate control scheme for fencing. To address the problem of fencing control, various relevant controllers were designed [12,13,14,15]. In [12], a formation controller was designed to ensure that followers gradually converge to the moving convex hull formed by leaders. Based on a disturbance observer, a formation controller was designed in [13] to achieve fencing control for unmanned surface vehicle swarms containing uncertainty and external disturbance. In [14,15], a distributed circular formation controller was introduced to fence the target by guiding agents toward a fixed-distance circle centered on the target. Most existing fencing control studies, including the aforementioned literature, require pre-designing desired orientations or distances centered around the target. However, in practical applications, defining appropriate parameter values becomes challenging due to complex flight environments of UAV swarms. To overcome this, a cooperative controller for fencing the target with a constant speed was presented in [16], eliminating preset formation parameters. Building upon [16], cooperative controllers for fencing targets were further developed for mobile robot systems and UAV swarms in [17,18].

The third aspect involves the security control of the target fencing process. Safety requirements, including collision avoidance and obstacle avoidance, are fundamental for the successful swarm execution of target fencing, as well as prerequisites for other tasks [19]. Therefore, the problem of swarm cooperative control with a security mechanism is studied. Currently, there exist three methods to ensure swarm security control. The first is the widely used artificial potential field (APF) method [20,21,22,23,24]. In [20], a safety overtaking controller for multi-unmanned ground vehicles in dynamic environments was designed based on APF. In [21], an adaptive controller that combines repulsive potential function and sliding manifold was proposed to achieve the fixed-time convergence of agent formation. To address the secure area control in second-order agent systems, an exponential control obstacle function was introduced in [22] to ensure internal collision avoidance and the external obstacle avoidance of agents. In [23,24], collision avoidance in formation and trajectory tracking were solved based on the consensus term and collision avoidance term, respectively. Additionally, distributed model predictive control (DMPC) also serves as an effective method for ensuring swarm security control. In [25], DMPC was introduced to avoid collision in the formation navigation control of unmanned underwater vehicles. In [26], the MPC method was utilized to eliminate collision risks during the formation reconstruction of the robot system. In [27], a combined soft/hard constraint-based MPC scheme was designed to tackle both collision avoidance and obstacle avoidance challenges encountered by UAV swarms. The stability and feasibility of MPC for collision and obstacle avoidance in multi-agent systems were analyzed in [28]. The third approach to achieve security control is the online optimization method. In [29], the collision-free global path of a multi-robot system was calculated based on the motion planning method. Deep reinforcement learning-based methods were proposed in [30,31] to address collision avoidance in uncertain dynamic environments by planning the optimal paths. It should be noted that APF-based methods provide an explicit security controller related to distance, endowing the swarm with real-time collision and obstacle avoidance capabilities [32]. As noted in [20,21,22,23,24], the agent was treated as a particle when designing potential functions. Nevertheless, during the collision avoidance process, the body radius of UAVs cannot be ignored. The DMPC method and online optimization method are capable of overcoming model constraints and addressing control challenges in complex systems. However, they demand substantial computational resources, which may potentially compromise real-time performance, particularly when dealing with large numbers of agents or high-dimensional systems.

The fourth aspect involves effectively maintaining connectivity within the swarm during the target fencing process. Incorporating collision avoidance and obstacle avoidance terms into the cooperative controller may result in a distance between UAVs that exceeds the sensing range of onboard sensors, leading to a loss of connectivity among the swarm. Therefore, it is crucial to investigate the connectivity maintenance of the swarm system. In [33,34], the authors focused on connectivity maintenance and collision avoidance within a fixed communication topology. A decentralized adaptive output feedback formation tracking controller was proposed in [35]. However, due to its communication structure limitations, it only guaranteed connectivity between the leader and follower. In [36], a prescribed performance method was proposed to guarantee agent connectivity but failed to consider security control in obstacle avoidance environments. Despite widespread attention given to multi-agent system connectivity, several limitations as described in [33,34,35,36] remain. Furthermore, fewer research studies consider collision avoidance, obstacle avoidance, and connectivity maintenance simultaneously for swarms in complex flight environments.

Motivated by the aforementioned discussion, this paper investigates the cooperative target fencing control problem of UAV swarms with collision, obstacle avoidance, and connectivity maintenance. A distributed control scheme is proposed based on swarm self-organization theory and consensus control. Specifically, the controller comprises three primary functionalities. The navigation control term drives the swarm toward the target. The repulsive and attractive terms between UAVs are used for collision avoidance and connectivity maintenance, respectively. The obstacle avoidance term ensures the flight safety of the swarm. In comparison with existing research, the main contributions of this paper are as follows.

• A distributed cooperative fencing control scheme for UAV swarms is proposed, comprising a target state observer and a distributed cooperative fencing controller. Compared with most existing fencing or containment schemes [12,13,14,15], the proposed control strategy directly fences a target instead of forming a formation based on preset orientations or distances and subsequently guiding the swarm around it.
• Compared to [16,17], which only applies to fencing a target with constant speed, we design a differential state observer to estimate the unknown speed and control input of the target based on measurable position information, thus enabling cooperative fencing of a maneuvering target.
• Different from [18], which primarily focuses on defining the separation and attraction rules, we further improve the swarm self-organized behaviors during the process of fencing a target. Within a dynamic network topology, collision, obstacle avoidance, and connectivity maintenance control mechanisms are introduced for the swarm based on local interaction information, ensuring effective target fencing in complex environments while meeting security requirements.

2. Problem Formulation

2.1. Modeling of UAV Swarm

In this paper, the nonlinear model in [37] that satisfies the relevant assumptions is used to describe the motion of the fixed-wing UAV swarm. The related variables are defined under the inertial frame $\left(x_E,y_E,z_E\right)$ in Figure 1.

Considering a system composed of $n$ UAVs in 3D space, the mathematical model of the $i-\mathrm{th}$ UAV is described as follows:

$$\left\{\begin{array}{l}{\dot{x}}_i\left(t\right)=V_i\left(t\right)\cos \left({\gamma }_i\left(t\right)\right)\cos \left({\psi }_i\left(t\right)\right)\\ {\dot{y}}_i\left(t\right)=V_i\left(t\right)\cos \left({\gamma }_i\left(t\right)\right)\sin \left({\psi }_i\left(t\right)\right)\\ {\dot{z}}_i\left(t\right)=V_i\left(t\right)\sin \left({\gamma }_i\left(t\right)\right)\\ {\dot{V}}_i\left(t\right)=\frac{T_i\left(t\right)-D_i\left(t\right)}{m_i}-g\sin \left({\gamma }_i\left(t\right)\right)\\ {\dot{\gamma }}_i\left(t\right)=\frac{g}{V_i\left(t\right)}\left(n_i\left(t\right)\cos \left({\varphi }_i\left(t\right)\right)-\cos \left({\gamma }_i\left(t\right)\right)\right)\\ {\dot{\psi }}_i\left(t\right)=\frac{L_i\left(t\right)\sin \left({\varphi }_i\left(t\right)\right)}{m_i{V}_i\left(t\right)\cos \left({\gamma }_i\left(t\right)\right)}\end{array}\right.$$

(1)

where $i=1,2,\cdots ,n$ is the index of the UAVs, and $p_i\left(t\right)={\left[x_i\left(t\right),y_i\left(t\right),z_i\left(t\right)\right]}^{\mathrm{T}}$, $V_i\left(t\right)$, ${\gamma }_i\left(t\right)$, and ${\psi }_i\left(t\right)$ represent the position, speed, flight-path angle, and heading angle of the $i$-th UAV, respectively. $m_i$, $g$, $L_i\left(t\right)$, and $D_i\left(t\right)$ represent the mass, gravitational acceleration, lift, and drag, respectively. The actual control vector $u_{ic}\left(t\right)={\left[T_i\left(t\right),n_i\left(t\right),{\varphi }_i\left(t\right)\right]}^{\mathrm{T}}$ represents the thrust, g-load, and banking angle. Moreover, the constraints on the relevant variables are as follows: $T_{\min }\le T_i\left(t\right)\le T_{\max }$, $n_{\min }\le n_i\left(t\right)\le n_{\max }$, ${\varphi }_{\min }\le {\varphi }_i\left(t\right)\le {\varphi }_{\max }$, $V_{\min }\le V_i\left(t\right)\le V_{\max }$, ${\psi }_{\min }\le {\psi }_i\left(t\right)\le {\psi }_{\max }$, and ${\gamma }_{\min }\le {\gamma }_i\left(t\right)\le {\gamma }_{\max }$.

To facilitate the controller design, the component of $V_i\left(t\right)$ along the coordinate axis is defined as $q_i\left(t\right)={\left[\dot{x}\left(t\right),\dot{y}\left(t\right),\dot{z}\left(t\right)\right]}^{\mathrm{T}}$, and the virtual control vector along the coordinate axis is defined as $u_i\left(t\right)={\left[u_{ix}\left(t\right),u_{iy}\left(t\right),u_{iz}\left(t\right)\right]}^{\mathrm{T}}$. The relationships between $u_i\left(t\right)$ and $u_{ic}\left(t\right)$ are given as follows:

$$\left\{\begin{array}{l}{T}_i\left(t\right)=\left[\cos \left({\gamma }_i\left(t\right)\right)\left(u_{xi}\left(t\right)\cos \left({\psi }_i\left(t\right)\right)+u_{yi}\left(t\right)\sin \left({\psi }_i\left(t\right)\right)\right)+\left(u_{zi}\left(t\right)+g\right)\sin \left({\gamma }_i\left(t\right)\right)\right]m_i+D_i\left(t\right)\hfill \\ n_i\left(t\right)=\frac{\left[\left(u_{zi}\left(t\right)+g\right)\cos \left({\gamma }_i\left(t\right)\right)-\sin \left({\gamma }_i\left(t\right)\right)\left(u_{xi}\left(t\right)\cos \left({\psi }_i\left(t\right)\right)+u_{yi}\left(t\right)\sin \left({\psi }_i\left(t\right)\right)\right)\right]}{g\cos \left({\varphi }_i\left(t\right)\right)}\hfill \\ {\varphi }_i\left(t\right)={\tan }^{-1}\left[\frac{u_{yi}\left(t\right)\cos \left({\psi }_i\left(t\right)\right)-u_{xi}\left(t\right)\sin \left({\psi }_i\left(t\right)\right)}{\left(u_{zi}\left(t\right)+g\right)\cos \left({\gamma }_i\left(t\right)\right)-\left(u_{xi}\left(t\right)\cos \left({\psi }_i\left(t\right)\right)+u_{yi}\left(t\right)\sin \left({\psi }_i\left(t\right)\right)\right)\sin \left({\gamma }_i\left(t\right)\right)}\right]\hfill \end{array}\right.$$

(2)

The flight-path angle ${\gamma }_i\left(t\right)$ and the heading angle ${\psi }_i\left(t\right)$ are computed by $\sin {\gamma }_i\left(t\right)=\frac{{\dot{z}}_i\left(t\right)}{V_i\left(t\right)}$ and $\tan {\psi }_i\left(t\right)=\frac{{\dot{y}}_i\left(t\right)}{{\dot{x}}_i\left(t\right)}$.

We denote the flight convex hull formed by the UAV swarm as $co\left(p\right)$, that is

$$co\left(p\right)=\left\{{\displaystyle \sum _{i=1}^n{w}_i{p}_i:w_i\ge 0,\forall i \mathrm{and} {\displaystyle \sum _{i=1}^n{w}_i=1}}\right\}$$

(3)

Let

$$H\left(p\right)=\underset{r\in co\left(p\right)}{\min }‖p_T-r‖$$

(4)

be the distance between the target and $co\left(p\right)$ and

$$h\left(p\right)=\arg \underset{r\in co\left(p\right)}{\min }‖p_T-r‖$$

(5)

be the point in $co\left(p\right)$ that has distance from the target, where $p_T$ represents the target’s position vector. It is obvious that $p_T\in co\left(p\right)$ if and only if $H\left(p\right)=0$. The target fencing diagram is shown in Figure 2.

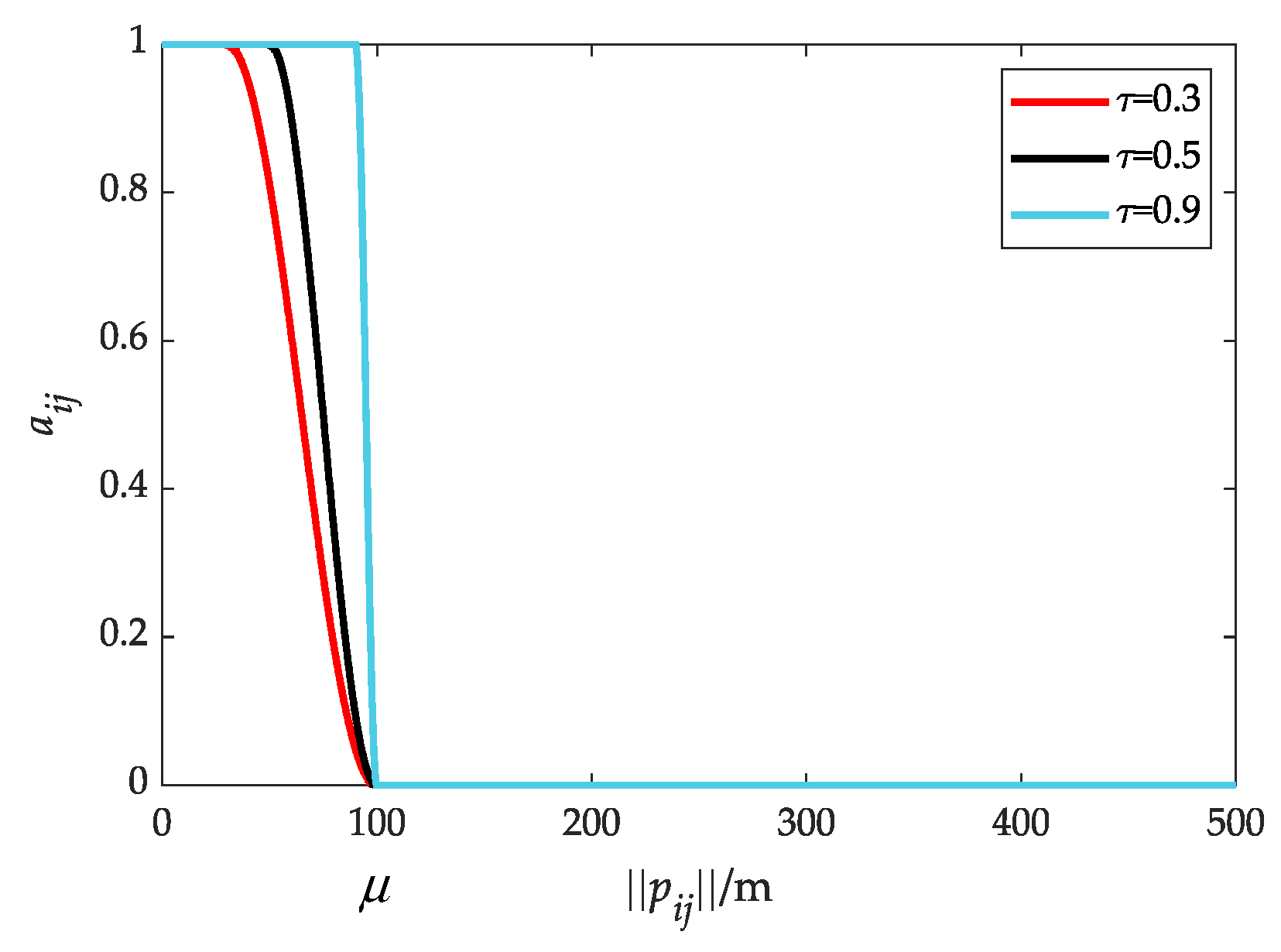
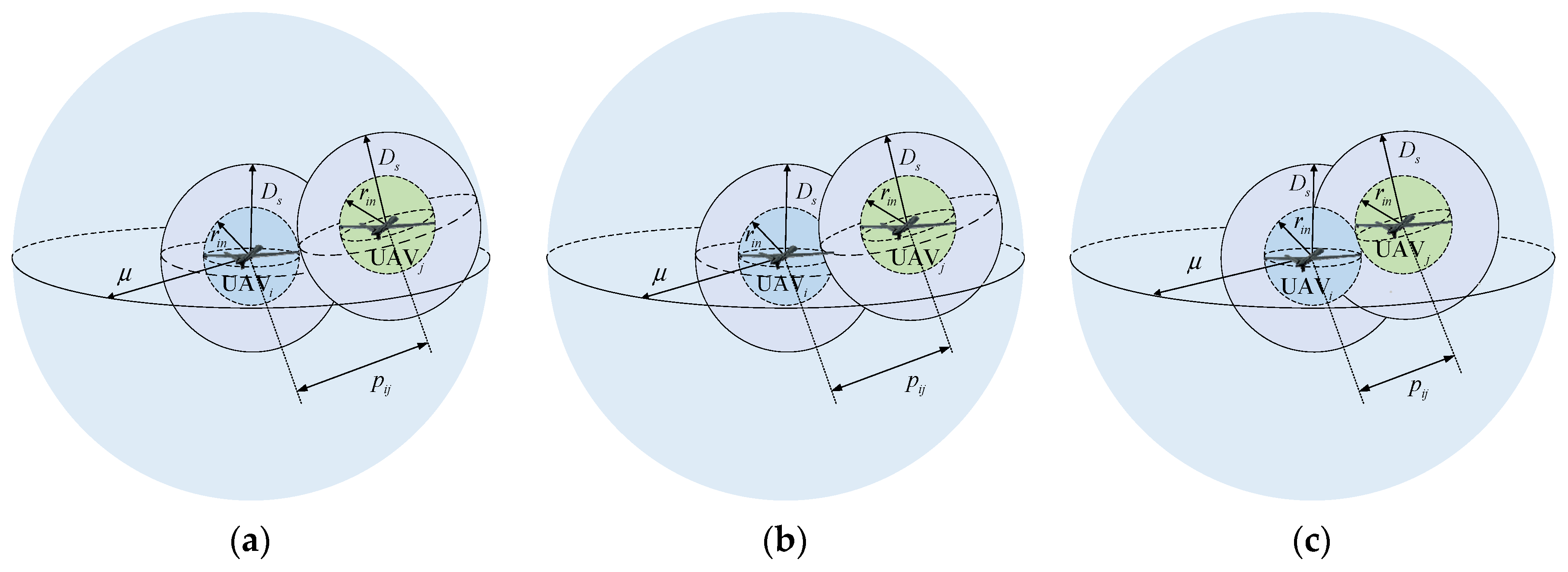
2.2. Dynamic Communication Topology

The interaction between UAVs can be described by graph $G=\left\{v,\epsilon ,A\right\}$, where $v=\left\{1,2,\cdots ,n\right\}$ is the set of nodes and $\epsilon \subseteq v\times v$ is the set of edges. The weighted adjacency matrix of $G$ is denoted as $A=\left[a_{ij}\right]\in {\mathrm{R}}^{n\times n}$. If the $i$-th UAV can obtain the information from the $j$-th UAV, $a_{ij}>0$; otherwise, $a_{ij}=0$. We define the Laplacian matrix of $G$ as $L=D-A$, where $D=\mathrm{diag}\left\{d_1,d_2,\cdots ,d_n\right\}$ and $d_i={\displaystyle {\sum }_{j=1}^n{a}_{ij}},\forall i\in v$.

Notice that the position distribution of the swarm is dynamically changing in accordance with the planned trajectory, and the UAV with sensing range is continually moving in 3D space. Therefore, the neighbor set of each UAV is constantly updated, resulting in a dynamic communication topology. We define the time-varying neighbor set of the $i$-th UAV as follows:

$$M_i\left(t\right)=\left\{j\in \left\{1,2,\cdots ,n\right\},‖p_{ij}‖\le \mu ,j\ne i\right\}$$

(6)

where $‖p_{ij}‖=‖p_i-p_j‖$ represents the Euclidean distance between the $i$-th UAV and the $j$-th UAV.

Remark 1.

In this paper, we assume that each UAV is equipped with the same onboard sensors and the $j$-th UAV can be observed by the $i$-th UAV if $‖p_{ij}‖\le \mu$. Thus, graph $G$ is undirected and the Laplacian matrix $L$ is semi-positive definite.

In practical applications, the performance of sensors is related to the distance between UAVs. Therefore, combined with the dynamic topology, the communication weight based on relative distance is defined as follows.

$$a_{ij}\left(‖p_{ij}‖\right)=\left\{\begin{array}{ll}1,\hfill & ‖p_{ij}‖\in \left[0,\tau \mu \right)\hfill \\ \frac{1}{2}\left[1+\cos \left(\pi \left(\frac{‖p_{ij}‖}{\mu }-\tau \right)/\left(1-\tau \right)\right)\right],\hfill & ‖p_{ij}‖\in \left[\tau \mu ,\mu \right]\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(7)

where $0<\tau <1$ is the communication decay rate. Figure 3 shows the evolution of the $a_{ij}$ for different $\tau$. It is obvious that $a_{ij}$ smoothly varies from 1 to 0 by designing (7).

2.3. Control Objective

In specific mission scenarios, UAVs are required to cooperatively fence or capture high-value flying targets. To ensure the safety of the swarm, UAVs should possess autonomous collision and obstacle avoidance capabilities. Furthermore, the behaviors associated with collision or obstacle avoidance may lead to significant separation distances, resulting in losing connectivity between UAVs once $‖p_{ij}‖>\mu$. Hence, maintaining connectivity within the swarm holds crucial significance. Additionally, given the limitations of onboard sensors, the speed and control input of the target may not always be directly measurable, requiring the estimation of both. In the target fencing mission, our primary concern is the dynamic changes in the position and velocity of the UAV swarm relative to the target in 3D space. Consequently, in formulating the control law, we prioritize the virtual position $p_i$ and speed $q_i$ of the UAVs as the principal control variables. Combining the above analysis, the control objective can be expressed as follows.

(C1) The target’s speed and control input can be estimated within a fixed time, i.e., $\underset{t\to T_i}{\lim }{\hat{V}}_T^i\left(t\right)=V_T\left(t\right)$ and $\underset{t\to T_i}{\lim }{\hat{u}}_T^i\left(t\right)=u_T\left(t\right)$, where $V_T\left(t\right)$ represents target’s speed vector, and ${\hat{V}}_T^i\left(t\right)$ and ${\hat{u}}_T^i\left(t\right)$ represent the estimation of the target’s speed and control input for the $i$-th UAV, respectively.

(C2) The target can be fenced by the UAV swarm, and each UAV’s speed converges to the target’s speed eventually, i.e., $\underset{t\to \infty }{\lim }H\left(p\left(t\right)\right)=0$ and $\underset{t\to \infty }{\lim }{q}_i\left(t\right)=\underset{t\to \infty }{\lim }{q}_j\left(t\right)=V_T\left(t\right)$.

(C3) Collision avoidance and connectivity maintenance: $2r_{in}<‖p_{ij}\left(t\right)‖\le \mu ,\forall t>0$, where $r_{in}$ represents the body radius of the $i-\mathrm{th}$ UAV.

(C4) Obstacle avoidance: $‖p_{i,o_{\overline{k}}}\left(t\right)‖=‖p_i\left(t\right)-o_{\overline{k}}‖>r_{in}+r_{o_{\overline{k}}},\forall t>0,\overline{k}=1,2,\cdots ,l$, where $o_{\overline{k}}$ represents the position vector of the $\overline{k}-\mathrm{th}$ obstacle, and $‖p_{i,o_k}\left(t\right)‖$ represents the Euclidean distance between the $i-\mathrm{th}$ UAV and the $\overline{k}-\mathrm{th}$ obstacle.

Remark 2.

(C2) means that there exists a flight trajectory $p^{\ast }\left(t\right)=p\left(t\right)+1_n\otimes \left[p_T\left(t\right)-h\left(p\left(t\right)\right)\right]$, which enables the swarm to constantly fence the target, i.e., $H\left(p^{\ast }\left(t\right)\right)=\underset{r\in co\left(p\right)}{\min }‖p_T-r‖=0$ and the trajectory $p\left(t\right)$ of the UAVs converges $p^{\ast }\left(t\right)$, where $\otimes$ represents the Kronecker product [16].

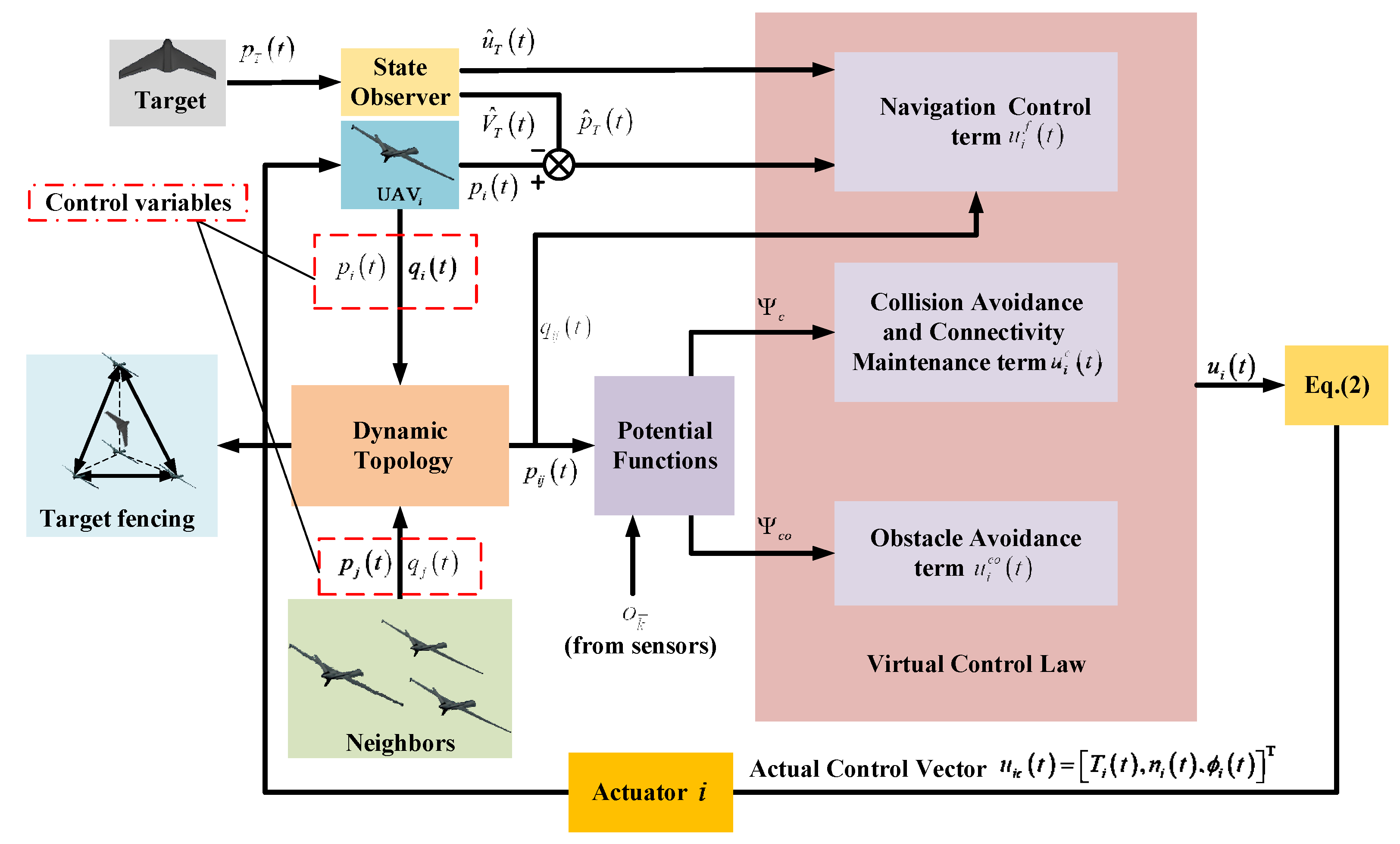
3. Main Results

3.1. Differential State Observer

In the uncooperative scenarios, the UAVs and the target have a competitive relationship. Therefore, it is unreasonable for the UAVs to obtain $V_T\left(t\right)$ and $u_T\left(t\right)$. Assuming that the target’s position can be measured by the UAVs through onboard sensors, we design a fixed-time state observer (8) to estimate $V_T\left(t\right)$ and $u_T\left(t\right)$.

$$\left\{\begin{array}{c}{\dot{z}}_1^i\left(t\right)=z_2^i\left(t\right)-{\kappa }_1^i{\left|z_1^i\left(t\right)-p_T\left(t\right)\right|}^{{\alpha }_1^i}\mathrm{sgn}\left(z_1^i\left(t\right)-p_T\left(t\right)\right)\\ -{\overline{\kappa }}_1^i{\left|z_1^i\left(t\right)-p_T\left(t\right)\right|}^{{\beta }_1^i}\mathrm{sgn}\left(z_1^i\left(t\right)-p_T\left(t\right)\right)\\ {\dot{z}}_2^i\left(t\right)=z_3^i\left(t\right)-{\kappa }_2^i{\left|z_1^i\left(t\right)-p_T\left(t\right)\right|}^{{\alpha }_2^i}\mathrm{sgn}\left(z_1^i\left(t\right)-p_T\left(t\right)\right)\\ -{\overline{\kappa }}_2^i{\left|z_1^i\left(t\right)-p_T\left(t\right)\right|}^{{\beta }_2^i}\mathrm{sgn}\left(z_1^i\left(t\right)-p_T\left(t\right)\right)\\ {\dot{z}}_3^i\left(t\right)=-{\kappa }_3^i{\left|z_1^i\left(t\right)-p_T\left(t\right)\right|}^{{\alpha }_3^i}\mathrm{sgn}\left(z_1^i\left(t\right)-p_T\left(t\right)\right)\hfill \\ -{\overline{\kappa }}_3^i{\left|z_1^i\left(t\right)-p_T\left(t\right)\right|}^{{\beta }_3^i}\mathrm{sgn}\left(z_1^i\left(t\right)-p_T\left(t\right)\right)\end{array}\right.$$

(8)

where $z_k^i\left(t\right),k=1,2,3$ represents the estimation of $p_T^{\left(k-1\right)}\left(t\right)$ (i.e., $p_T\left(t\right)$, $V_T\left(t\right)$, and $u_T\left(t\right)$) for the $i-\mathrm{th}$ UAV. ${\alpha }_k^i\in \left(0,1\right)$ satisfies ${\alpha }_k^i=k{\alpha }^i-\left(k-1\right)$ and ${\alpha }^i$ belongs to $\left(1-{\epsilon }_1,1\right)$ for a sufficiently small ${\epsilon }_1>0$. ${\beta }_k^i>1$ satisfies ${\beta }_k^i=k{\beta }^i-\left(k-1\right)$ and ${\beta }^i$ belongs to $\left(1,1+{\epsilon }_2\right)$ for a sufficiently small ${\epsilon }_2>0$. Observer gains ${\kappa }_k^i$ and ${\overline{\kappa }}_k^i$ are selected such that the polynomials $s^3+{\kappa }_1^i{s}^2+{\kappa }_2^{i}s+{\kappa }_3^i=0$ and $s^3+{\overline{\kappa }}_1^i{s}^2+{\overline{\kappa }}_2^{i}s+{\overline{\kappa }}_3^i=0$ are Hurwitz.

Theorem 1.

Based on the observer (8), $V_T\left(t\right)$ and $u_T\left(t\right)$ can be estimated within a fixed time

$$T_i\le \frac{{\lambda }_{\max }^{2-{\alpha }^i}\left({\tilde{P}}^i\right)}{\left(1-{\alpha }^i\right){\lambda }_{\min }\left({\tilde{Q}}^i\right)}+\frac{{\lambda }_{\max }\left({\tilde{P}}_1^i\right)}{\left({\beta }^i-1\right){\lambda }_{\min }\left({\tilde{Q}}_1^i\right)}{\lambda }_{\min }^{1-{\beta }^i}\left({\tilde{P}}_1^i\right)$$

(9)

where ${\tilde{Q}}^i$ and ${\tilde{Q}}_1^i$ are the symmetric positive definite matrix. ${\tilde{P}}^i={\left({\tilde{P}}^i\right)}^{\mathrm{T}}>0$ and ${\tilde{P}}_1^i={\left({\tilde{P}}_1^i\right)}^{\mathrm{T}}>0$ satisfy the Lyapunov equation ${\tilde{P}}^i{\tilde{A}}^i+{\left({\tilde{A}}^i\right)}^{\mathrm{T}}{\tilde{P}}^i=-{\tilde{Q}}^i$ and ${\tilde{P}}_1^i{\tilde{A}}_1^i+{\left({\tilde{A}}_1^i\right)}^{\mathrm{T}}{\tilde{P}}_1^i=-{\tilde{Q}}_1^i$, respectively, where ${\tilde{A}}^i=\left[\begin{array}{ccc}-{\kappa }_1^i& 1& 0\\ -{\kappa }_2^i& 0& 1\\ -{\kappa }_3^i& 0& 0\end{array}\right]$ and ${\tilde{A}}_1^i=\left[\begin{array}{ccc}-{\overline{\kappa }}_1^i& 1& 0\\ -{\overline{\kappa }}_2^i& 0& 1\\ -{\overline{\kappa }}_3^i& 0& 0\end{array}\right]$ are Hurwitz.

Proof of Theorem 1.

We denote the observer error as ${\xi }^i\left(t\right)={\xi }_1^i\left(t\right)=p_T\left(t\right)-z_1^i\left(t\right)$ and its derivatives ${\xi }_k^i\left(t\right)=p_T^{\left(k-1\right)}\left(t\right)-z_k^i\left(t\right)$ take the form

$$\left\{\begin{array}{l}{\dot{\xi }}_1^i\left(t\right)={\xi }_2^i\left(t\right)-{\kappa }_1^i{\left|{\xi }^i\left(t\right)\right|}^{{\alpha }_1^i}\mathrm{sgn}\left({\xi }^i\left(t\right)\right)-{\overline{\kappa }}_1^i{\left|{\xi }^i\left(t\right)\right|}^{{\beta }_1^i}\mathrm{sgn}\left({\xi }^i\left(t\right)\right)\\ {\dot{\xi }}_2^i\left(t\right)={\xi }_3^i\left(t\right)-{\kappa }_2^i{\left|{\xi }^i\left(t\right)\right|}^{{\alpha }_2^i}\mathrm{sgn}\left({\xi }^i\left(t\right)\right)-{\overline{\kappa }}_2^i{\left|{\xi }^i\left(t\right)\right|}^{{\beta }_2^i}\mathrm{sgn}\left({\xi }^i\left(t\right)\right)\\ {\dot{\xi }}_3^i\left(t\right)=-{\kappa }_3^i{\left|{\xi }^i\left(t\right)\right|}^{{\alpha }_3^i}\mathrm{sgn}\left({\xi }^i\left(t\right)\right)-{\overline{\kappa }}_3^i{\left|{\xi }^i\left(t\right)\right|}^{{\beta }_3^i}\mathrm{sgn}\left({\xi }^i\left(t\right)\right)\end{array}\right.$$

(10)

Furthermore, (10) is rewritten as

$$\left\{\begin{array}{l}{\dot{\xi }}_1^i\left(t\right)={\dot{\zeta }}_1^i\left(t\right)+{\dot{\varsigma }}_1^i\left(t\right)\\ ={\zeta }_2^i\left(t\right)-{\kappa }_1^i{\left|{\xi }^i\left(t\right)\right|}^{{\alpha }_1^i}\mathrm{sgn}\left({\xi }^i\left(t\right)\right)+{\varsigma }_2^i\left(t\right)-{\overline{\kappa }}_1^i{\left|{\xi }^i\left(t\right)\right|}^{{\beta }_1^i}\mathrm{sgn}\left({\xi }^i\left(t\right)\right)\\ {\dot{\xi }}_2^i\left(t\right)={\dot{\zeta }}_2^i\left(t\right)+{\dot{\varsigma }}_2^i\left(t\right)\\ ={\zeta }_3^i\left(t\right)-{\kappa }_2^i{\left|{\xi }^i\left(t\right)\right|}^{{\alpha }_2^i}\mathrm{sgn}\left({\xi }^i\left(t\right)\right)+{\varsigma }_3^i\left(t\right)-{\overline{\kappa }}_2^i{\left|{\xi }^i\left(t\right)\right|}^{{\beta }_2^i}\mathrm{sgn}\left({\xi }^i\left(t\right)\right)\\ {\dot{\xi }}_3^i\left(t\right)={\dot{\zeta }}_3^i\left(t\right)+{\dot{\varsigma }}_3^i\left(t\right)\\ =-{\kappa }_3^i{\left|{\xi }^i\left(t\right)\right|}^{{\alpha }_3^i}\mathrm{sgn}\left({\xi }^i\left(t\right)\right)-{\overline{\kappa }}_3^i{\left|{\xi }^i\left(t\right)\right|}^{{\beta }_3^i}\mathrm{sgn}\left({\xi }^i\left(t\right)\right)\end{array}\right.$$

(11)

Since $\tilde{A}$ and ${\tilde{A}}_1$ are Hurwitz, the systems ${\dot{\zeta }}^i\left(t\right)={\tilde{A}}^i{\zeta }^i\left(t\right)$ and ${\dot{\varsigma }}^i\left(t\right)={\tilde{A}}_1^i{\varsigma }^i\left(t\right)$ are asymptotically stable.

For the function $V_o^i={\left({\zeta }^i\right)}^{\mathrm{T}}{\tilde{P}}^i{\zeta }^i+{\left({\varsigma }^i\right)}^{\mathrm{T}}{\tilde{P}}_1^i{\varsigma }^i$, its time derivative yields

$$\begin{array}{l}{\dot{V}}_o^i={\left({\dot{\zeta }}^i\right)}^{\mathrm{T}}{\tilde{P}}^i{\zeta }^i+{\left({\dot{\varsigma }}^i\right)}^{\mathrm{T}}{\tilde{P}}_1^i{\varsigma }^i\\ ={\left({\zeta }^i\right)}^{\mathrm{T}}\left({\tilde{P}}^i{\tilde{A}}^i+{\left({\tilde{A}}^i\right)}^{\mathrm{T}}{\tilde{P}}^i\right){\zeta }^i+{\left({\varsigma }^i\right)}^{\mathrm{T}}\left({\tilde{P}}_1^i{\tilde{A}}_1^i+{\left({\tilde{A}}_1^i\right)}^{\mathrm{T}}{\tilde{P}}_1^i\right){\varsigma }^i\\ =-\left({\left({\zeta }^i\right)}^{\mathrm{T}}{\tilde{Q}}^i{\zeta }^i+{\left({\varsigma }^i\right)}^{\mathrm{T}}{\tilde{Q}}_1^i{\varsigma }^i\right)<0\end{array}$$

(12)

We define an energy function

$$V_g^i={\left({\Theta }^i\right)}^{\mathrm{T}}{\tilde{P}}^i{\Theta }^i+{\left({\Lambda }^i\right)}^{\mathrm{T}}{\tilde{P}}_1^i{\Lambda }^i$$

(13)

where ${\Theta }^i=\left[{\left({\zeta }^i\right)}^{\frac{1}{{\vartheta }_1^i}},{\left({\zeta }^i\right)}^{\frac{1}{{\vartheta }_2^i}},{\left({\zeta }^i\right)}^{\frac{1}{{\vartheta }_3^i}}\right]$, ${\Lambda }^i=\left[{\left({\varsigma }^i\right)}^{\frac{1}{{\sigma }_1^i}},{\left({\varsigma }^i\right)}^{\frac{1}{{\sigma }_2^i}},{\left({\varsigma }^i\right)}^{\frac{1}{{\sigma }_3^i}}\right]$, ${\vartheta }_k^i=\left(k-1\right){\alpha }^i-\left(k-2\right)$, and ${\sigma }_k^i=\left(k-1\right){\beta }^i-\left(k-2\right)$.

Based on [38], if ${\alpha }^i\in \left(1-{\epsilon }_1,1\right),{\beta }^i\in \left(1,1+{\epsilon }_2\right)$, $V_g^i$ is the Lyapunov function for the error system (11). In view of (12), it implies that ${\dot{V}}_g^i<0$ and

$${\dot{V}}_g^i\le -\frac{{\lambda }_{\min }\left({\tilde{Q}}^i\right)}{{\lambda }_{\max }\left({\tilde{P}}^i\right)}{\left({\left({\dot{\zeta }}^i\right)}^{\mathrm{T}}{\tilde{P}}^i{\zeta }^i\right)}^{1+{\eta }_1}-\frac{{\lambda }_{\min }\left({\tilde{Q}}_1^i\right)}{{\lambda }_{\max }\left({\tilde{P}}_1^i\right)}{\left({\left({\dot{\varsigma }}^i\right)}^{\mathrm{T}}{\tilde{P}}_1^i{\varsigma }^i\right)}^{1+{\eta }_2}$$

(14)

As noted in [38,39], the observer error converges to 0 within a fixed time, i.e., $\underset{t\to T_i}{\lim }{\hat{V}}_T^i\left(t\right)=V_T\left(t\right)$ and $\underset{t\to T_i}{\lim }{\hat{u}}_T^i\left(t\right)=u_T\left(t\right)$. The convergence time $T_i$ is bounded by (9). Thus, (C1) is proved. □

Remark 3.

In [18], assuming a consistently connected communication topology, a network-based observer was designed to estimate the target’s state. In this paper, we address the challenge of maintaining connectivity within a dynamic topology and propose a differential state observer capable of simultaneously estimating the target’s velocity and control input, laying the foundation for UAV swarms to accurately fence a maneuvering target. Prior to commencing their tasks, the observer algorithm can be pre-integrated into the onboard computer, enabling real-time computation of speed and control input once the target’s position is acquired or detected.

3.2. Cooperative Fencing Controller

In this section, the cooperative target fencing controller designed for UAV swarms consists of three components: a navigation control term $u_i^f\left(t\right)$, a collision avoidance and connectivity maintenance term $u_i^c\left(t\right)$, and an obstacle avoidance term $u_i^{co}\left(t\right)$. The schematic diagram of the cooperative target fencing control is illustrated in Figure 4.

3.2.1. Navigation Control Term

Given that the primary objective of the UAV swarm is to fence the target, it is imperative to guide each UAV towards the target using the navigation control term. Moreover, each UAV must maintain a consistent flight speed that aligns with the target’s speed to preserve a stable convex hull and ensure continuous target fencing. To fulfill these requirements, $u_i^f\left(t\right)$ is designed, as follows:

$$u_i^f\left(t\right)={\hat{u}}_T^i\left(t\right)-c_1\left(p_i\left(t\right)-p_T\left(t\right)\right)-c_2\left(q_i\left(t\right)-{\hat{V}}_T\left(t\right)\right)-c_3{\displaystyle \sum _{j\in M_i\left(t\right)}{a}_{ij}\left(t\right)\left(q_i\left(t\right)-q_j\left(t\right)\right)}$$

(15)

where the control gains $c_1,c_2$ and $c_3$ are positive constants.

Remark 4.

In (15), $u_i^f\left(t\right)$ introduces a feedback term $-c_1\left(p_i\left(t\right)-p_T\left(t\right)\right)$ about the relative distance between the $i-\mathrm{th}$ UAV and the target, serving solely as an attractive term to drive the UAVs towards the target, rather than directing them to converge to the target’s position. The collision avoidance term in Section 3.2.2 ensures that the relative distance between each UAV is automatically maintained, thus guaranteeing the existence of the convex hull and enabling the swarm to fence the target.

3.2.2. Collision Avoidance and Connectivity Maintenance Term

To facilitate real-time collision avoidance, we propose a modified potential field method that incorporates the physical radius of each UAV into the design of the potential function, in contrast to previous studies [21,22,23,24,25], where the agent was treated as a particle.

Assume that the collision avoidance radius of each UAV is $D_s$. To ensure collision avoidance and connectivity maintenance among UAVs, each UAV should be encompassed by both attractive and repulsive potential fields. As described in Figure 5a, when the relative distance $‖p_{ij}\left(t\right)‖=r_{in}+D_s$ between UAVs, they are positioned at a safe distance and the repulsive force remains $F_{r_{ij}}=0$. In Figure 5b, as they continue to approach, that is, $‖p_{ij}\left(t\right)‖<r_{in}+D_s$, the $i-\mathrm{th}$ UAV triggers the repulsive potential field of the $j-\mathrm{th}$ UAV, resulting in the repulsion between them. In Figure 5c, $‖p_{ij}\left(t\right)‖=2r_{in}$ represents the minimum safe distance between them and the corresponding repulsive force $F_{r_{ij}}=\infty$.

Moreover, due to the movement of the $i-\mathrm{th}$ UAV and the repulsive force, it is possible for the $j-\mathrm{th}$ UAV to be positioned outside of the sensing range, that is, $‖p_{ij}\left(t\right)‖>\mu$, resulting in a loss of connectivity between them. To address this problem, we construct an attractive potential field and constrain their relative distance within $\mu$.

In summary, the $i-\mathrm{th}$ UAV and the $j-\mathrm{th}$ UAV exhibit repulsive behavior when $‖p_{ij}\left(t\right)‖\in \left(2r_{in},r_{in}+D_s\right)$, while exhibiting attractive behavior when $‖p_{ij}\left(t\right)‖\in \left(r_{in}+D_s,\mu \right]$. Based on the above analysis, the potential function including collision avoidance and connectivity maintenance is defined as follows:

$${\Psi }_c\left(‖p_{ij}\left(t\right)‖\right)={\displaystyle {\int }_{r_{in}+D_s}^{‖p_{ij}\left(t\right)‖}{\phi }_c\left(‖p_{ij}\left(t\right)‖\right)}d‖p_{ij}\left(t\right)‖$$

(16)

$${\phi }_c\left(‖p_{ij}\left(t\right)‖\right)=\left\{\begin{array}{ll}{e}^{-\left(\frac{\left(‖p_{ij}\left(t\right)‖-\left(r_{in}+D_s\right)\right)\left(‖p_{ij}\left(t\right)‖-\mu \right)}{{\left(‖p_{ij}\left(t\right)‖-2r_{in}\right)}^2}\right)}-1,\hfill & ‖p_{ij}\left(t\right)‖\in \left(2r_{in},\mu \right]\hfill \\ 0,\hfill & ‖p_{ij}\left(t\right)‖\in \left(\mu ,\infty \right)\hfill \end{array}\right.$$

(17)

Remark 5.

Given that collision avoidance and connectivity maintenance rely on the constraint of relative distance between UAVs, we draw inspiration from [40] to design a potential field function for achieving these two functionalities. Although target fencing control with a collision avoidance strategy has been investigated in [16,17,18], these studies generally assume that the topology between UAVs is consistently connected with time-invariant communication weights. However, in practical scenarios, it is difficult to meet these idealized conditions.

Considering the neighbor set $M_i\left(t\right)$ and the time-variant communication weights, the potential-based control term is formulated as

$$u_i^c\left(t\right)=-{\displaystyle \sum _{j\in M_i\left(t\right)}{a}_{ij}\left(t\right)k_c{\nabla }_{p_i}{\Psi }_c\left(‖p_{ij}\left(t\right)‖\right)}$$

(18)

where $k_c>0$ is the control gain and ${\nabla }_{p_i}{\Psi }_c\left(‖p_{ij}\left(t\right)‖\right)$ represents the gradient of ${\Psi }_c\left(‖p_{ij}\left(t\right)‖\right)$ along $p_i\left(t\right)$.

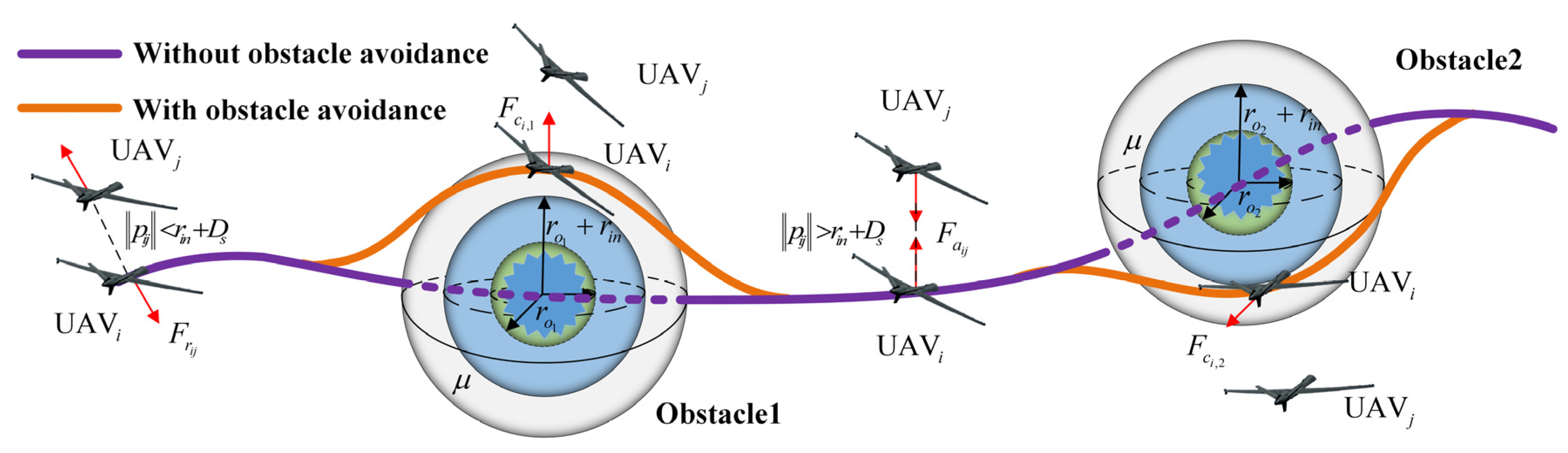
3.2.3. Obstacle Avoidance Term

Assumption 1.

The flight trajectory of the target is ideal under $u_T\left(t\right)$, that is, no problems of obstacle avoidance arise with the target.

The obstacle avoidance potential field is defined similarly to Section 3.2.2, with the exception that the attractive term is omitted. Consider that an obstacle is surrounded by a sphere with a radius of $r_{o_{\overline{k}}}$, and set the safe obstacle avoidance distance as $\chi r_{in}+r_{o_{\overline{k}}}$, where $\chi \ge 1$ represents the obstacle avoidance margin parameter. When the UAV detects the obstacle within its sensing range $\mu$, it actively maneuvers away from the obstacle under the repulsive force $F_{c_{i,o_{\overline{k}}}}$.

To further illustrate the obstacle avoidance process of the swarm, a schematic diagram of the obstacle avoidance potential field is shown in Figure 6. It is noteworthy that this paper distinguishes itself from others solely focused on obstacle avoidance by also considering collision avoidance and connectivity maintenance among UAVs within the context of obstacle avoidance.

The obstacle avoidance potential function ${\Psi }_{co}\left(‖p_{i,o_{\overline{k}}}\left(t\right)‖\right)$ can be designed as follows:

$${\Psi }_{co}\left(‖p_{i,o_{\overline{k}}}\left(t\right)‖\right)={\displaystyle {\int }_{\mu }^{‖p_{i,o_{\overline{k}}}\left(t\right)‖}{\phi }_{co}\left(‖p_{i,o_{\overline{k}}}\left(t\right)‖\right)}d‖p_{i,o_{\overline{k}}}\left(t\right)‖$$

(19)

$${\phi }_{co}\left(‖p_{i,o_{\overline{k}}}\left(t\right)‖\right)=\left\{\begin{array}{ll}{e}^{\left(\frac{‖p_{i,o_{\overline{k}}}\left(t\right)‖-\mu }{‖p_{i,o_{\overline{k}}}\left(t\right)‖-\left(\chi r_{in}+r_{o_{\overline{k}}}\right)}\right)}-1,& ‖p_{i,o_{\overline{k}}}\left(t\right)‖\in \left(\chi r_{in}+r_{o_{\overline{k}}},\mu \right]\\ 0,& ‖p_{i,o_{\overline{k}}}\left(t\right)‖\in \left(\mu ,\infty \right)\end{array}\right.$$

(20)

Then, the control term $u_i^{co}\left(t\right)$ is

$$u_i^{co}\left(t\right)=-{\varpi }_i{\displaystyle \sum _{\overline{k}=1}^l{k}_{o_{\overline{k}}}{\nabla }_{p_{i,o_{\overline{k}}}}{\Psi }_{co}\left(‖p_{i,o_{\overline{k}}}\left(t\right)‖\right)}$$

(21)

where $k_{o_{\overline{k}}}>0$ is the control gain, ${\varpi }_i>0$ is designed later, and ${\nabla }_{p_{i,o_{\overline{k}}}}{\Psi }_{co}\left(‖p_{i,o_{\overline{k}}}\left(t\right)‖\right)$ represents the gradient of ${\Psi }_{co}\left(‖p_{i,o_{\overline{k}}}\left(t\right)‖\right)$ along $p_{i,o_{\overline{k}}}\left(t\right)$.

Remark 6.

In (19), UAVs have the capability to obtain obstacle positions, with obstacle detection being performed through airborne sensing equipment. For instance, the UAV utilizes visual and laser sensors to perceive the flight environment and measure the relative distance to obstacles, thereby calculating control commands required to avoid obstacles.

Combined with the above analysis, we have developed a cooperative fencing controller (22) for UAV swarms:

$$\begin{array}{l}{u}_i\left(t\right)=u_i^f\left(t\right)+u_i^c\left(t\right)+u_i^{co}\left(t\right)\\ ={\hat{u}}_T^i\left(t\right)-c_1\left(p_i\left(t\right)-p_T\left(t\right)\right)-c_2\left(q_i\left(t\right)-{\hat{V}}_T^i\left(t\right)\right)-c_3{\displaystyle \sum _{j\in M_i\left(t\right)}{a}_{ij}\left(t\right)\left(q_i\left(t\right)-q_j\left(t\right)\right)}\\ -{\displaystyle \sum _{j\in M_i\left(t\right)}{a}_{ij}\left(t\right)k_c{\nabla }_{p_i}{\Psi }_c\left(‖p_{ij}\left(t\right)‖\right)}-{\varpi }_i{\displaystyle \sum _{\overline{k}=1}^l{k}_{o_{\overline{k}}}{\nabla }_{p_{i,o_{\overline{k}}}}{\Psi }_{co}\left(‖p_{i,o_{\overline{k}}}\left(t\right)‖\right)}\end{array}$$

(22)

Remark 7.

This paper adopts the method of the segmented design of potential fields to address collision, obstacle avoidance, and connectivity maintenance problems simultaneously. Compared to the traditional APF methods, the potential functions in this paper exhibit smooth variability, which avoids the saltation phenomenon of the controller. When obstacle avoidance and connectivity maintenance are not considered, the controller (19) can also be effectively applied to solve the target fencing control problem in [18].

3.3. Stability Analysis

Assumption 2.

The initial state of the $i-\mathrm{th}$ UAV is chosen to satisfy $‖p_i\left(0\right)-o_{\overline{k}}‖>\chi r_{in}+r_{o_{\overline{k}}}$, $‖p_i\left(0\right)-p_j\left(0\right)‖\le \mu$, and $‖p_i\left(0\right)-p_j\left(0\right)‖>2r_{in}$.

Theorem 2.

Supposing that Assumptions 1–2 hold and the control parameters satisfy the aforementioned requirements, the fixed-wing UAV swarm is capable of effectively fencing a maneuvering target under the control law (22). Moreover, the control law facilitates collision, obstacle avoidance, and connectivity maintenance throughout the target fencing process.

Proof of Theorem 2.

According to Theorem 1, the target’s speed and control input can be observed by UAVs within a fixed time, i.e., $\underset{t\to T_i}{\lim }{\hat{V}}_T^i\left(t\right)=V_T\left(t\right)$ and $\underset{t\to T_i}{\lim }{\hat{u}}_T^i\left(t\right)=u_T\left(t\right)$. Thus, the controller (22) can be transformed into

$$\begin{array}{l}{u}_i\left(t\right)=u_T\left(t\right)-c_1\left(p_i\left(t\right)-p_T\left(t\right)\right)-c_2\left(q_i\left(t\right)-V_T\left(t\right)\right)\\ -c_3{\displaystyle \sum _{j\in M_i\left(t\right)}{a}_{ij}\left(t\right)\left(q_i\left(t\right)-q_j\left(t\right)\right)}\\ -{\displaystyle \sum _{j\in M_i\left(t\right)}{a}_{ij}\left(t\right)k_c{\nabla }_{p_i}{\Psi }_c\left(‖p_{ij}\left(t\right)‖\right)}-{\varpi }_i{\displaystyle \sum _{\overline{k}=1}^l{k}_{o_{\overline{k}}}{\nabla }_{p_{i,o_{\overline{k}}}}{\Psi }_{co}\left(‖p_{i,o_{\overline{k}}}\left(t\right)‖\right)}\end{array}$$

(23)

The control objectives (C2)–(C4) will be proved in four steps. The first part is to prove the system stability without obstacles.

Step 1: Proof of target fencing stability

For convenience, we denote ${\tilde{p}}_i\left(t\right)=p_i\left(t\right)-p_T\left(t\right)$ as the position error between the $i-\mathrm{th}$ UAV and the target, $\overline{p}\left(t\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\tilde{p}}_i\left(t\right)}$ as the average position error, ${\tilde{q}}_i\left(t\right)=q_i\left(t\right)-V_T\left(t\right)$ as the speed error between the $i-\mathrm{th}$ UAV and the target, and $\overline{q}\left(t\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\tilde{q}}_i\left(t\right)}$ as the average speed error.

The time derivative of $\overline{p}\left(t\right)$ yields

$$\dot{\overline{p}}\left(t\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\dot{\tilde{p}}}_i\left(t\right)}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\tilde{q}}_i\left(t\right)}$$

(24)

Then, differentiating $\dot{\overline{p}}\left(t\right)$,

$$\begin{array}{l}\ddot{\overline{p}}\left(t\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left({\dot{q}}_i\left(t\right)-{\dot{V}}_T\left(t\right)\right)}\\ =\frac{1}{n}{\displaystyle \sum _{i=1}^n\left(-c_1{\tilde{p}}_i\left(t\right)-c_2{\tilde{q}}_i\left(t\right)-c_3\right.{\displaystyle \sum _{j\in M_i\left(t\right)}{a}_{ij}\left(t\right)\left(q_i\left(t\right)-q_j\left(t\right)\right)}}\\ \left.-{\displaystyle \sum _{j\in M_i\left(t\right)}{a}_{ij}\left(t\right)k_c{\nabla }_{p_i}{\Psi }_c\left(‖p_{ij}\left(t\right)‖\right)}\right)\end{array}$$

(25)

Based on the definition of a dynamic network in Section 2.2, which states that the communication between UAVs is undirected, it is implied that $p_{ij}=-p_{ji}$ and $q_{ij}=-q_{ji}$. We have ${\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j\in M_i\left(t\right)}{a}_{ij}\left(t\right)\left(q_i\left(t\right)-q_j\left(t\right)\right)}}=0$ and ${\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j\in M_i\left(t\right)}{a}_{ij}\left(t\right)k_c{\nabla }_{p_i}{\Psi }_c\left(‖p_{ij}\left(t\right)‖\right)}}=0$.

Thus, (25) can be transformed into the following system

$$\ddot{\overline{p}}\left(t\right)+c_1\dot{\overline{p}}\left(t\right)+c_2\overline{p}\left(t\right)=0$$

(26)

Due to $c_1>0,c_2>0$, it is obvious that (26) is stable. $\overline{p}\left(t\right),\dot{\overline{p}}\left(t\right)$ and $\ddot{\overline{p}}\left(t\right)$ exponentially converge to zero as $t\to \infty$. It implies that $\overline{p}\left(t\right)\in co\left(p\right)$ and $\underset{t\to \infty }{\lim }H\left(p\right)=0$, i.e., the target is fenced by the swarm.

Step 2: Proof of convergence for UAVs’ speed

We denote the following Lyapunov function candidate as

$$V_s\left(t\right)=\frac{1}{2}{\displaystyle \sum _{i=1}^n\left({\tilde{q}}_i^T\left(t\right){\tilde{q}}_i\left(t\right)+c_1{\tilde{p}}_i^T\left(t\right){\tilde{p}}_i\left(t\right)\right)}$$

(27)

The time derivative of (27) is

$$\begin{array}{ll}{\dot{V}}_s\left(t\right)& ={\displaystyle \sum _{i=1}^n\left[{\tilde{q}}_i^{\mathrm{T}}\left(t\right)\left(-c_1{\tilde{p}}_i\left(t\right)-c_2{\tilde{q}}_i\left(t\right)-c_3{\displaystyle \sum _{j\in M_i\left(t\right)}{a}_{ij}\left(t\right)\left({\tilde{q}}_i\left(t\right)-{\tilde{q}}_j\left(t\right)\right)}\right)+c_1{\tilde{p}}_i^{\mathrm{T}}\left(t\right){\tilde{q}}_i\left(t\right)\right]}\\ & ={\displaystyle \sum _{i=1}^n\left(-c_2{\tilde{q}}_i^{\mathrm{T}}\left(t\right){\tilde{q}}_i\left(t\right)-c_3{\tilde{q}}_i^{\mathrm{T}}\left(t\right){\displaystyle \sum _{j\in M_i\left(t\right)}{a}_{ij}\left(t\right)\left({\tilde{q}}_i\left(t\right)-{\tilde{q}}_j\left(t\right)\right)}\right)}\\ & =-c_2{\tilde{q}}^{\mathrm{T}}\left(t\right)\left(I_n\otimes I_3\right)\tilde{q}\left(t\right)-c_3{\tilde{q}}^{\mathrm{T}}\left(t\right)\left(L\otimes I_3\right)\tilde{q}\left(t\right)\\ & =-{\tilde{q}}^{\mathrm{T}}\left(t\right)\left[\left(c_{3}L+c_2{I}_n\right)\otimes I_3\right]\tilde{q}\left(t\right)\end{array}$$

(28)

where $\tilde{q}\left(t\right)={\left[{\tilde{q}}_1\left(t\right),{\tilde{q}}_2\left(t\right),\cdots ,{\tilde{q}}_n\left(t\right)\right]}^{\mathrm{T}}$. Since the Laplacian matrix $L$ is positive semi-definite, $I_n$ is positive definite, and $c_2>0,c_3>0$, it follows that matrix $c_{3}L+c_2{I}_n$ is positive definite. Hence, ${\dot{V}}_s\left(t\right)\le 0$ indicates $V_s\left(t\right)\le V_s\left(t_0\right)=c,\forall t\ge t_0$. Combined with Theorem 1 in [40], it can be shown that $\Omega =\left\{\left(\tilde{p}\left(t\right),\tilde{q}\left(t\right)\right):V_s\left(t\right)\le c\right\}$ is an invariant set and all solutions starting from $\Omega$ for Equation (29) will converge to the largest invariant set $\overline{\Omega }=\left\{\left(\tilde{p}\left(t\right),\tilde{q}\left(t\right)\right):V_s\left(t\right)=0\right\}$.

$${\dot{V}}_s\left(t\right)=-{\tilde{q}}^{\mathrm{T}}\left(t\right)\left[\left(c_{3}L+c_2{I}_n\right)\otimes I_3\right]\tilde{q}\left(t\right)=0$$

(29)

Therefore, $\tilde{q}\left(t\right)=0$, i.e., $q_1\left(t\right)=q_2\left(t\right)=\cdots =q_n\left(t\right)=V_T\left(t\right)$, which means that the speeds of each UAV can consistently converge to the target’s speed. With this, the control objective (C2) is proved.

Step 3: Proof of collision avoidance and connectivity maintenance

To prove (C3), the Lyapunov function $V_c\left(X\left(t\right)\right)$ is constructed as follows

$$\begin{array}{ll}{V}_c\left(X\left(t\right)\right)& =\frac{1}{2}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j\in M_i\left(t\right)}{a}_{ij}\left(t\right)k_c{\Psi }_c\left(‖p_{ij}\left(t\right)‖\right)}}\\ & +\frac{c_1}{2}{\displaystyle \sum _{i=1}^n{‖p_i\left(t\right)-p_T\left(t\right)‖}^2}+\frac{1}{2}{\displaystyle \sum _{i=1}^n{‖q_i\left(t\right)-V_T\left(t\right)‖}^2}\end{array}$$

(30)

where vectors $X\left(t\right)={\left[p^{\mathrm{T}}\left(t\right),q^{\mathrm{T}}\left(t\right),p_T^{\mathrm{T}}\left(t\right),V_T^{\mathrm{T}}\left(t\right)\right]}^{\mathrm{T}}$, $p\left(t\right)={\left[p_1\left(t\right),p_2\left(t\right),\cdots ,p_n\left(t\right)\right]}^{\mathrm{T}}$, and $q\left(t\right)={\left[q_1\left(t\right),q_2\left(t\right),\cdots ,q_n\left(t\right)\right]}^{\mathrm{T}}$.

Taking the derivatives of $V_c\left(X\left(t\right)\right)$ gives

$$\begin{array}{ll}\frac{d{V}_c\left(X\left(t\right)\right)}{dt}& ={\displaystyle \sum _{i=1}^n\frac{\partial V_c\left(X\left(t\right)\right)}{\partial p_i^{\mathrm{T}}\left(t\right)}}{\dot{p}}_i\left(t\right)+{\displaystyle \sum _{i=1}^n\frac{\partial V_c\left(X\left(t\right)\right)}{\partial q_i^{\mathrm{T}}\left(t\right)}}{\dot{q}}_i\left(t\right)+{\displaystyle \sum _{i=1}^n\frac{\partial V_c\left(X\left(t\right)\right)}{\partial p_T^{\mathrm{T}}\left(t\right)}{\dot{p}}_T\left(t\right)}+{\displaystyle \sum _{i=1}^n\frac{\partial V_c\left(X\left(t\right)\right)}{\partial V_T^{\mathrm{T}}\left(t\right)}}{\dot{V}}_T\left(t\right)\\ & ={\displaystyle \sum _{i=1}^n\left[{\left(-u_i^c\left(t\right)\right)}^{\mathrm{T}}+\left(c_1{\left(p_i\left(t\right)-p_T\left(t\right)\right)}^{\mathrm{T}}\right)\right]}{q}_i\left(t\right)\\ & +{\displaystyle \sum _{i=1}^n\left(-c_1{\left(p_i\left(t\right)-p_T\left(t\right)\right)}^{\mathrm{T}}\right)}{V}_T\left(t\right)+{\displaystyle \sum _{i=1}^n{\left(q_i\left(t\right)-V_T\left(t\right)\right)}^{\mathrm{T}}{u}_i\left(t\right)}\\ & +{\displaystyle \sum _{i=1}^n\left(-{\left(q_i\left(t\right)-V_T\left(t\right)\right)}^{\mathrm{T}}\right)u_T\left(t\right)}\end{array}$$

(31)

Substituting (23) into (31), we have

$$\begin{array}{ll}\frac{d{V}_c\left(X\left(t\right)\right)}{dt}& ={\displaystyle \sum _{i=1}^n\left[{\left(-u_i^c\left(t\right)\right)}^{\mathrm{T}}{q}_i\left(t\right)+c_1{\left(p_i\left(t\right)-p_T\left(t\right)\right)}^{\mathrm{T}}\left(q_i\left(t\right)-V_T\left(t\right)\right)\right.}\\ & \left.+{\left(q_i\left(t\right)-V_T\left(t\right)\right)}^{\mathrm{T}}\left(u_i\left(t\right)-u_T\left(t\right)\right)\right]\\ & =-c_2{\displaystyle \sum _{i=1}^n{‖q_i\left(t\right)-V_T\left(t\right)‖}^2}-{\displaystyle \sum _{i=1}^n\left(-u_i^c\left(t\right)\right)V_T^{\mathrm{T}}\left(t\right)}\\ & -c_3{\displaystyle \sum _{i=1}^n{\left(q_i\left(t\right)-V_T\left(t\right)\right)}^{\mathrm{T}}{\displaystyle \sum _{j\in M_i\left(t\right)}{a}_{ij}\left(t\right)\left(q_i\left(t\right)-q_j\left(t\right)\right)}}\\ & =-c_2{\displaystyle \sum _{i=1}^n{‖q_i\left(t\right)-V_T\left(t\right)‖}^2}-c_3{\tilde{q}}^{\mathrm{T}}\left(t\right)\left(L\otimes I_3\right)\tilde{q}\left(t\right)\le 0\end{array}$$

(32)

In view of (30) and (32), it is derived that

$$\begin{array}{c}{a}_{ij}\left(t\right)k_c{\Psi }_c\left(‖p_{ij}\left(t\right)‖\right)\le V_c\left(X\left(t\right)\right)=\\ V_c\left(X\left(0\right)\right)+{\displaystyle {\int }_0^t\frac{d{V}_c\left(X\left(t\right)\right)}{dt}dt}\le V_c\left(X\left(0\right)\right)<\infty \end{array}$$

(33)

If $‖p_{ij}\left(t\right)‖=2r_{in}$, then ${\Psi }_c\left(2r_{in}\right)=-{\displaystyle {\int }_{2r_{in}}^{r_{in}+D_s}{\phi }_c\left(‖p_{ij}\left(t\right)‖\right)}d‖p_{ij}\left(t\right)‖=\infty$, which contradicts Equation (33). Hence, $‖p_{ij}\left(t\right)‖>2r_{in},\forall i\ne j$, that is, collision avoidance can be achieved between UAVs.

Note that, according to the potential field function defined in (16), if $‖p_{ij}\left(t\right)‖\in \left(2r_{in},r_{in}+D_s\right)$, UAVs are affected by repulsive force, leading to an increase in the inter-UAV distance. As the distance extends to $‖p_{ij}\left(t\right)‖\in \left(r_{in}+D_s,\mu \right]$, UAVs are impacted by the attractive force, leading to a decrease in the inter-UAV distance. By appropriately designing the potential field gain $k_c$, the connectivity within the swarm is maintained. The control objective (C3) is proved.

Step 4: Proof of obstacle avoidance

We choose a Lyapunov function candidate $V_{i,o_{\overline{k}}}\left(t\right)$ as

$$V_{i,o_{\overline{k}}}\left(t\right)=\frac{1}{2}{p}_{i,o_{\overline{k}}}^{\mathrm{T}}\left(t\right)p_{i.o_{\overline{k}}}\left(t\right)+\frac{1}{2}{q}_i^{\mathrm{T}}\left(t\right)q_i\left(t\right)$$

(34)

Differentiating $V_{i,o_{\overline{k}}}\left(t\right)$ with respect to time, we have

$$\begin{array}{ll}{\dot{V}}_{i,o_{\overline{k}}}\left(t\right)& =p_{i,o_{\overline{k}}}^{\mathrm{T}}\left(t\right)q_i\left(t\right)+q_i^{\mathrm{T}}\left(t\right)\left[u_T\left(t\right)-c_1\left(p_i\left(t\right)-p_T\left(t\right)\right)-c_2\left(q_i\left(t\right)-V_T\left(t\right)\right)\right.\\ & -c_3{\displaystyle \sum _{j\in M_i\left(t\right)}{a}_{ij}\left(t\right)\left(q_i\left(t\right)-q_j\left(t\right)\right)}-{\displaystyle \sum _{j\in M_i\left(t\right)}{a}_{ij}\left(t\right)k_c{\nabla }_{p_i}{\Psi }_c\left(‖p_{ij}\left(t\right)‖\right)}\\ & \left.-{\varpi }_i{\displaystyle \sum _{\overline{k}=1}^l{k}_{o_{\overline{k}}}{\nabla }_{p_{i,o_{\overline{k}}}}{\Psi }_{co}\left(‖p_{i,o_{\overline{k}}}\left(t\right)‖\right)}\right]\end{array}$$

(35)

Given that the dwell time of the $i-\mathrm{th}$ UAV in ${\Omega }_o=\left\{p_i\left|‖p_{i,o_{\overline{k}}}‖\le \mu \right.\right\}$ is finite, the terms in (35) are bounded except $-{\varpi }_i{q}_i^{\mathrm{T}}\left(t\right){\displaystyle \sum _{\overline{k}=1}^l{k}_{o_{\overline{k}}}{\nabla }_{p_{i,o_{\overline{k}}}}{\Psi }_{co}\left(‖p_{i,o_{\overline{k}}}\left(t\right)‖\right)}$. From the definition of the obstacle avoidance potential field function, if $‖p_{i,o_{\overline{k}}}\left(t\right)‖\to r_{in}+r_{o_{\overline{k}}}$, then ${\nabla }_{p_{i,o_{\overline{k}}}}{\Psi }_{co}\left(‖p_{i,o_{\overline{k}}}\left(t\right)‖\right)\to \infty$. As the $i-\mathrm{th}$ UAV approaches the obstacle, we can derive the following inequality.

$$\begin{array}{l}-{\varpi }_i{q}_i^{\mathrm{T}}\left(t\right){\displaystyle \sum _{\overline{k}=1}^l{k}_{o_{\overline{k}}}{\nabla }_{p_{i,o_{\overline{k}}}}{\Psi }_{co}\left(‖p_{i,o_{\overline{k}}}\left(t\right)‖\right)}\\ >\frac{1}{2}{\varpi }_i{p}_{i,o_{\overline{k}}}^{\mathrm{T}}\left(t\right)p_{i.o_{\overline{k}}}\left(t\right)+\frac{1}{2}{\varpi }_i{q}_i^{\mathrm{T}}\left(t\right)q_i\left(t\right)\\ -p_{i,o_k}^{\mathrm{T}}\left(t\right)q_i\left(t\right)-q_i^{\mathrm{T}}\left(t\right)\left[u_T\left(t\right)-c_1\left(p_i\left(t\right)-p_T\left(t\right)\right)-c_2\left(q_i\left(t\right)-V_T\left(t\right)\right)\right.\\ \left.-c_3{\displaystyle \sum _{j\in M_i\left(t\right)}{a}_{ij}\left(t\right)\left(q_i\left(t\right)-q_j\left(t\right)\right)}-{\displaystyle \sum _{j\in M_i\left(t\right)}{a}_{ij}\left(t\right)k_c{\nabla }_{p_i}{\Psi }_c\left(‖p_{ij}\left(t\right)‖\right)}\right]\end{array}$$

(36)

Substituting (23) into (31), we have ${\dot{V}}_{i,o_{\overline{k}}}\left(t\right)>{\varpi }_i{V}_{i,o_{\overline{k}}}\left(t\right)$. And the following inequality

$${‖p_{i,o_{\overline{k}}}\left(t\right)‖}^2>2e^{{\varpi }_i\left(t-t_0\right)}{V}_{i,o_{\overline{k}}}\left(0\right)-{‖q_i\left(t\right)‖}^2$$

(37)

holds, where ${‖q_i\left(t\right)‖}^2$ is bounded in ${\Omega }_o$. Hence, we design the parameter ${\varpi }_i$ appropriately such that ${‖p_{i,o_{\overline{k}}}\left(t\right)‖}^2>2e^{{\varpi }_i\left(t-t_0\right)}{V}_{i,o_{\overline{k}}}\left(0\right)-{‖q_i\left(t\right)‖}^2>{\left(r_{in}+r_{o_{\overline{k}}}\right)}^2$. As a consequence, no collision occurs between UAVs and obstacles throughout the target fencing process.

It is worth noting that through Steps 1–3, we have demonstrated the stability of the system outside of ${\Omega }_o$. Therefore, we do not need to prove the stability of the system during the obstacle avoidance process, and it is only necessary to illustrate that under the action of the obstacle avoidance potential function, each UAV can avoid collision with obstacles. The control objective (C4) is proved.

In summary, the target fencing with collision, obstacle avoidance, and connectivity maintenance is achieved. The proof of Theorem 2 is completed. □

4. Numerical Simulation

In this section, we conduct two simulations to verify the effectiveness of the cooperative target fencing control strategy by the MATLAB R2020a platform. In the first scenario, the cooperative fencing of a target moving with a constant speed in a UAV swarm in an obstacle-free flight environment is validated. In the second scenario, it verifies that the same UAV swarm can fence a maneuvering target cooperatively in the presence of obstacles.

The parameters of the UAV model are selected from [37]. $L_i\left(t\right)$ and $D_i\left(t\right)$ are calculated by (38).

$$\left\{\begin{array}{l}{L}_i\left(t\right)=m_{i}g{n}_i\left(t\right)\\ D_i\left(t\right)=\frac{1}{2}\rho V_i^2\left(t\right)S_w{C}_{D0}+\frac{2k_d{k}_n^2{n}_i^2\left(t\right)m_i^2}{\rho S_w{V}_i\left(t\right)}\end{array}\right.$$

(38)

where $\rho =1.225\mathrm{kg}/{\mathrm{m}}^3$, $S_w=1.37{\mathrm{m}}^2$, and $C_{D0}=0.02$ represent the atmospheric density, the wing area, and the zero-lift drag coefficient, respectively. The rest of the parameters in the model are the include coefficient $k_d=0.1$, the load-factor effectiveness $k_n=1$, and the weight of the UAV $m_i=20\mathrm{kg}$. The constraints on the actual control variables are $10N\le T_i\le 125N$, $-1.5\le n_i\le 2.0$, and $-{80}^{°}\le {\varphi }_i\le {80}^{°}$. Moreover, the body radius of each UAV is set to $r_{in}=10\mathrm{m}$ and sensing range is $\mu =100\mathrm{m}$.

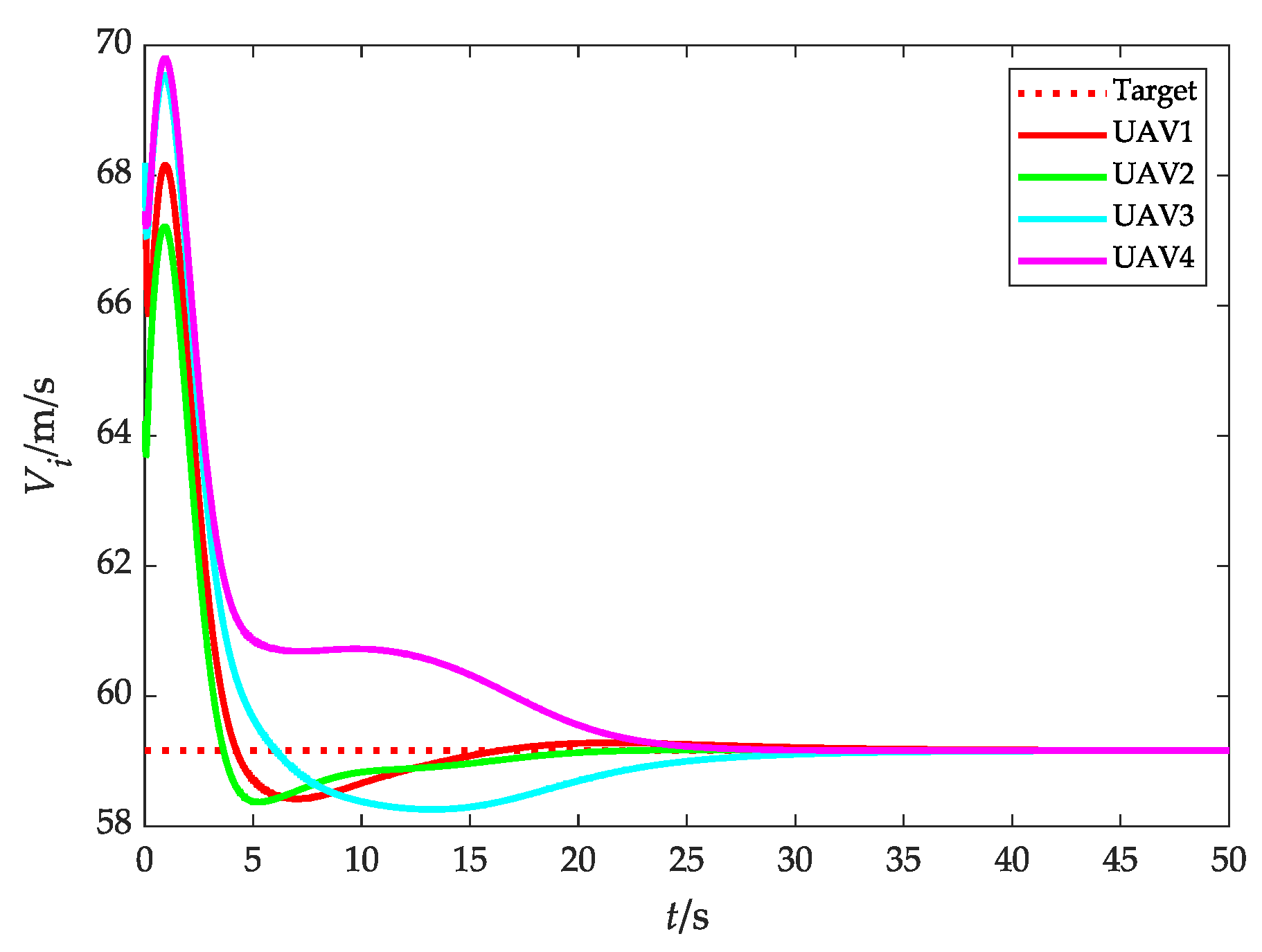
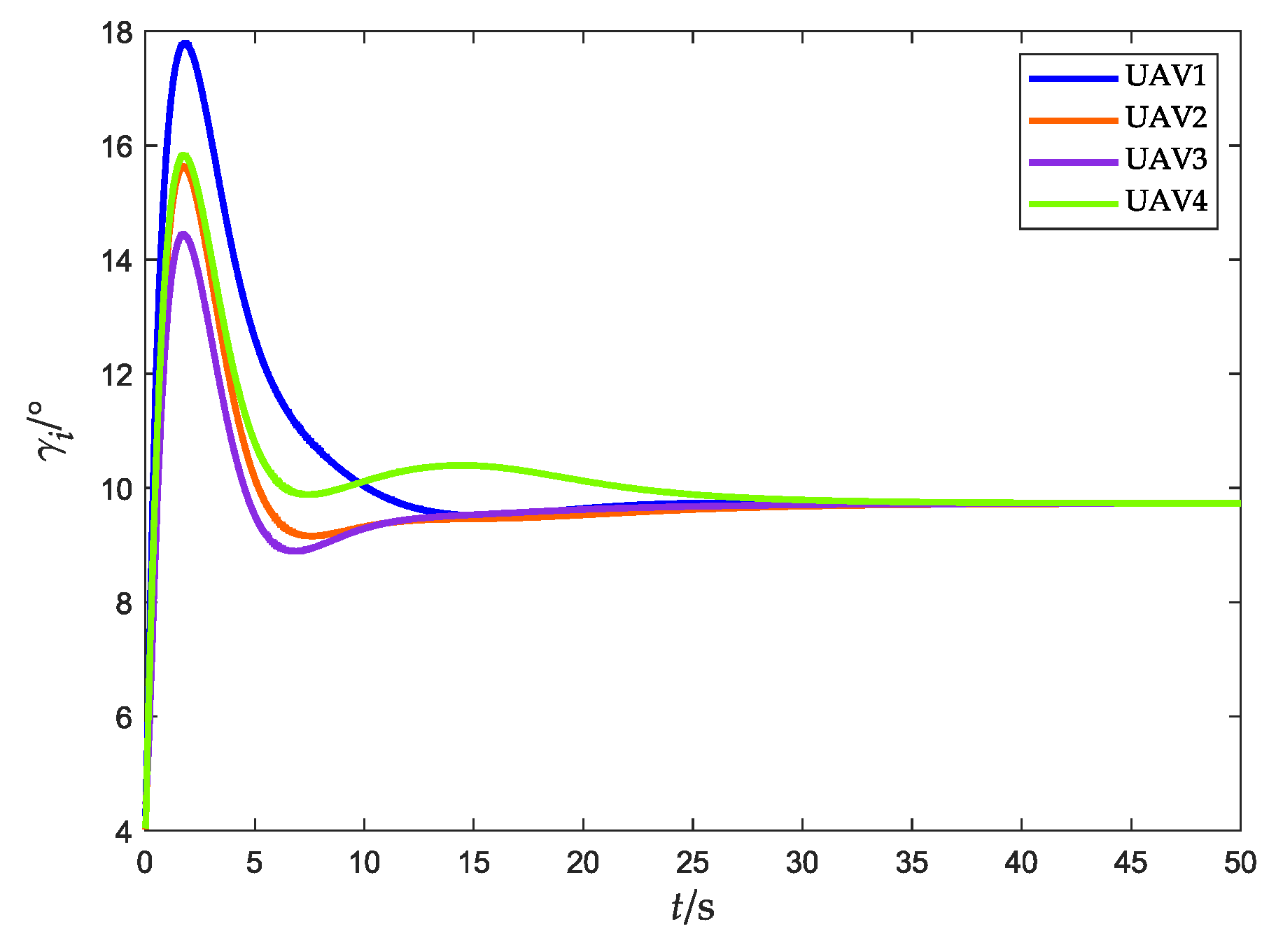
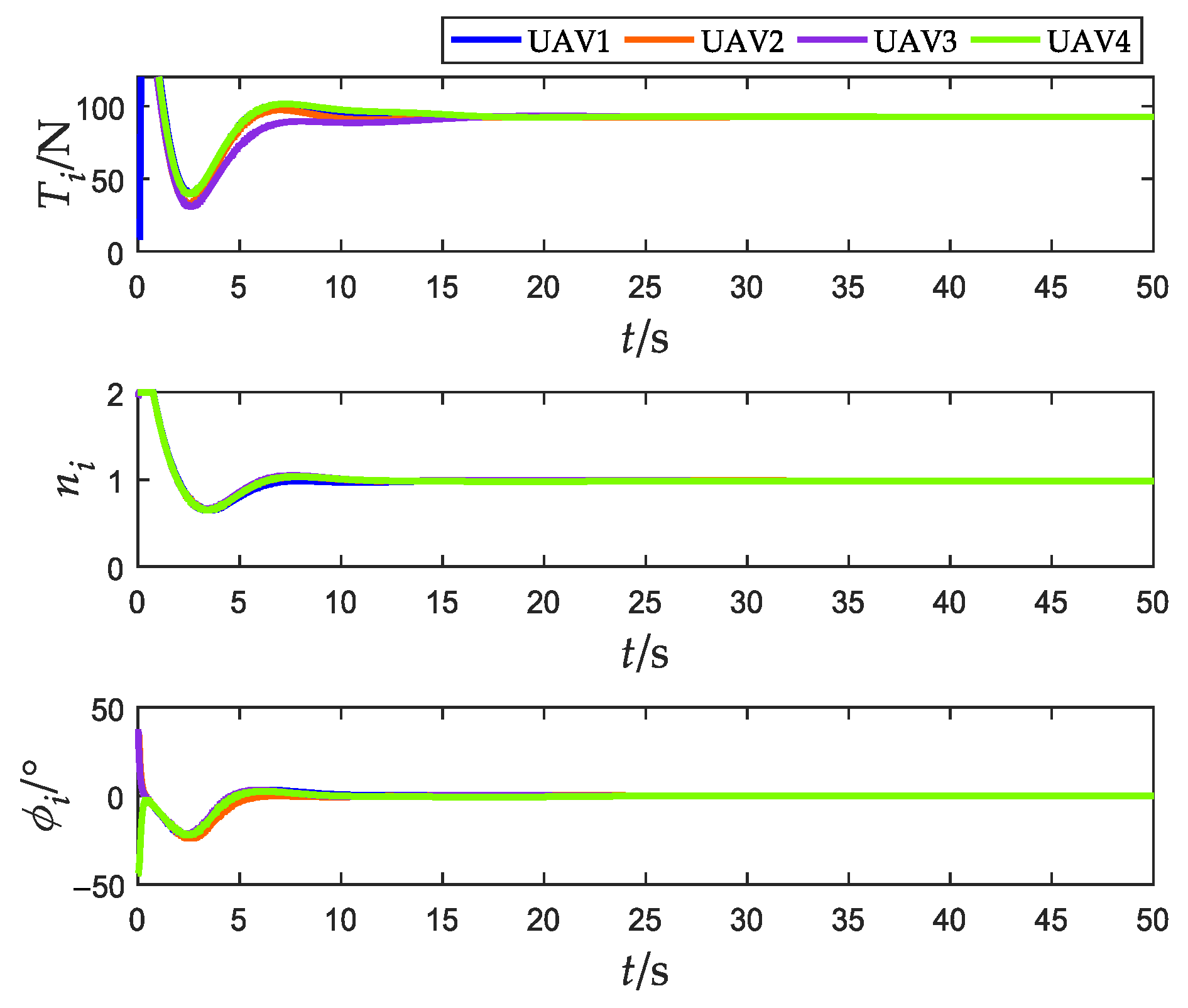
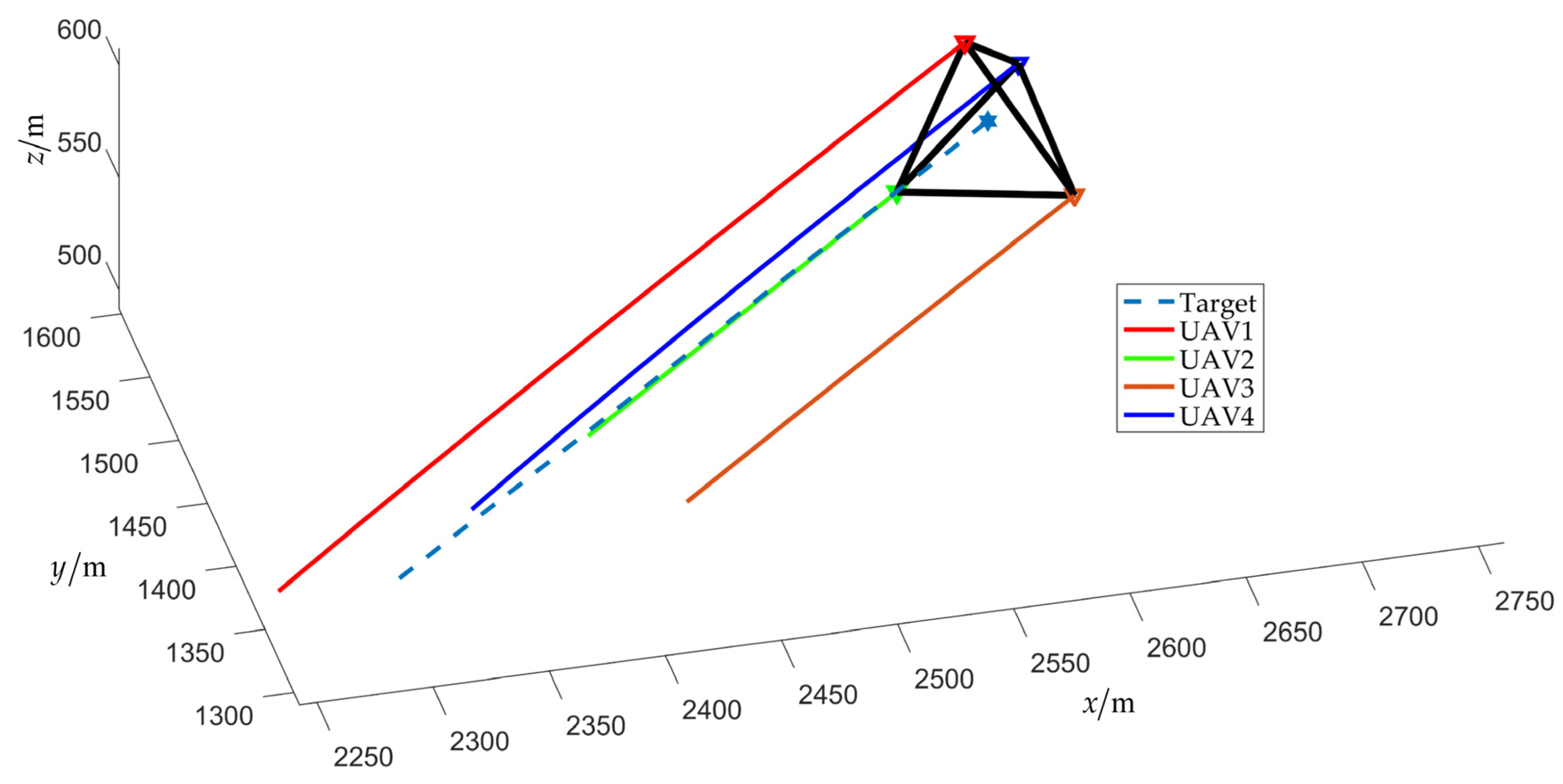
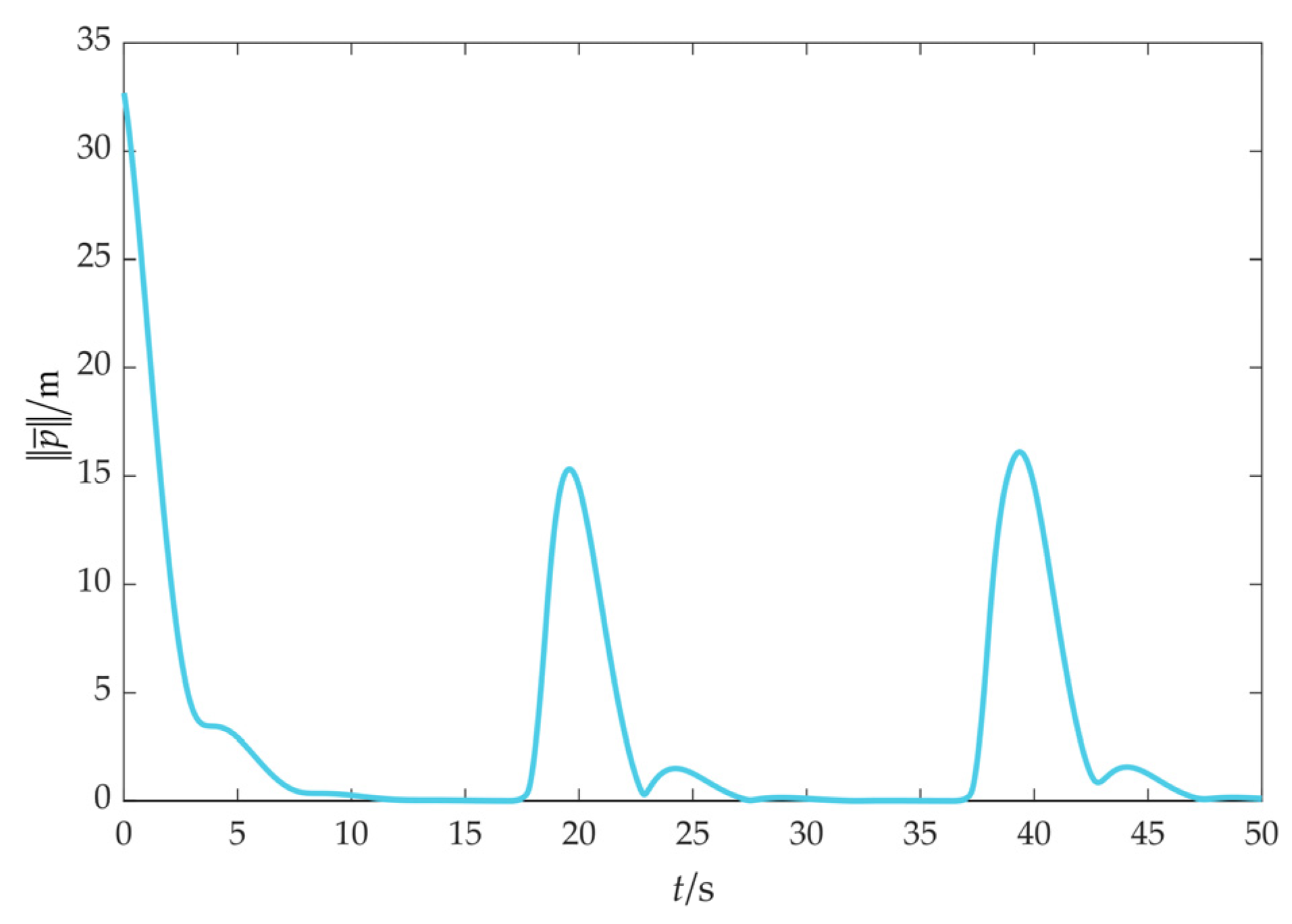
4.1. Scenario 1: Fencing a Target with a Constant Speed without Obstacles

Consider fencing the target with four UAVs. The initial speed of the UAV is randomly chosen from $\left[60,75\right]\mathrm{m}/\mathrm{s}$. The controller parameters are selected as follows: $c_1=0.7$, $c_2=2.5$, and $c_3=1$. The communication decay rate is set as $\tau =0.5$. The parameters of the potential field are $k_c=0.001$, ${\varpi }_i=1.5$, and $\chi =2$.

The simulation results of scenario 1 are shown in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15. Among them, Figure 7 and Figure 8 plot the target fencing trajectories and the final state of the UAV swarm under the controller (22), where the hexagram and triangle represent the target and the UAVs, respectively.

As depicted in Figure 9, the fencing error converges to 0, which means that the UAV swarm can fence the target, indicating that the effectiveness of the cooperative fencing strategy based on the flight convex hull is demonstrated.

Figure 10 illustrates the relative distance between UAVs, and it is obvious that $‖p_{ij}‖\in \left(2r_{in},\mu \right)$ is consistently upheld during the fencing process, that is, UAVs can avoid collision and maintain the connectivity under the potential function (16).

Figure 11 and Figure 12 show the relative distance $‖{\tilde{p}}_i‖$ and flight speed, and each UAV maintains a fixed distance from the target while moving at a consistent speed. Combined with Figure 10, it can be seen that the UAV swarm is capable of achieving a stable flight convex hull configuration and fence the target, which further explains Remark 4 in Section 3.2.1.

Figure 13 and Figure 14 show the calculated heading angle and flight-path angle. Figure 15 plots the time evolution of actual control variables $T_i$, $n_i$, and ${\varphi }_i$ under the imposed constraints.

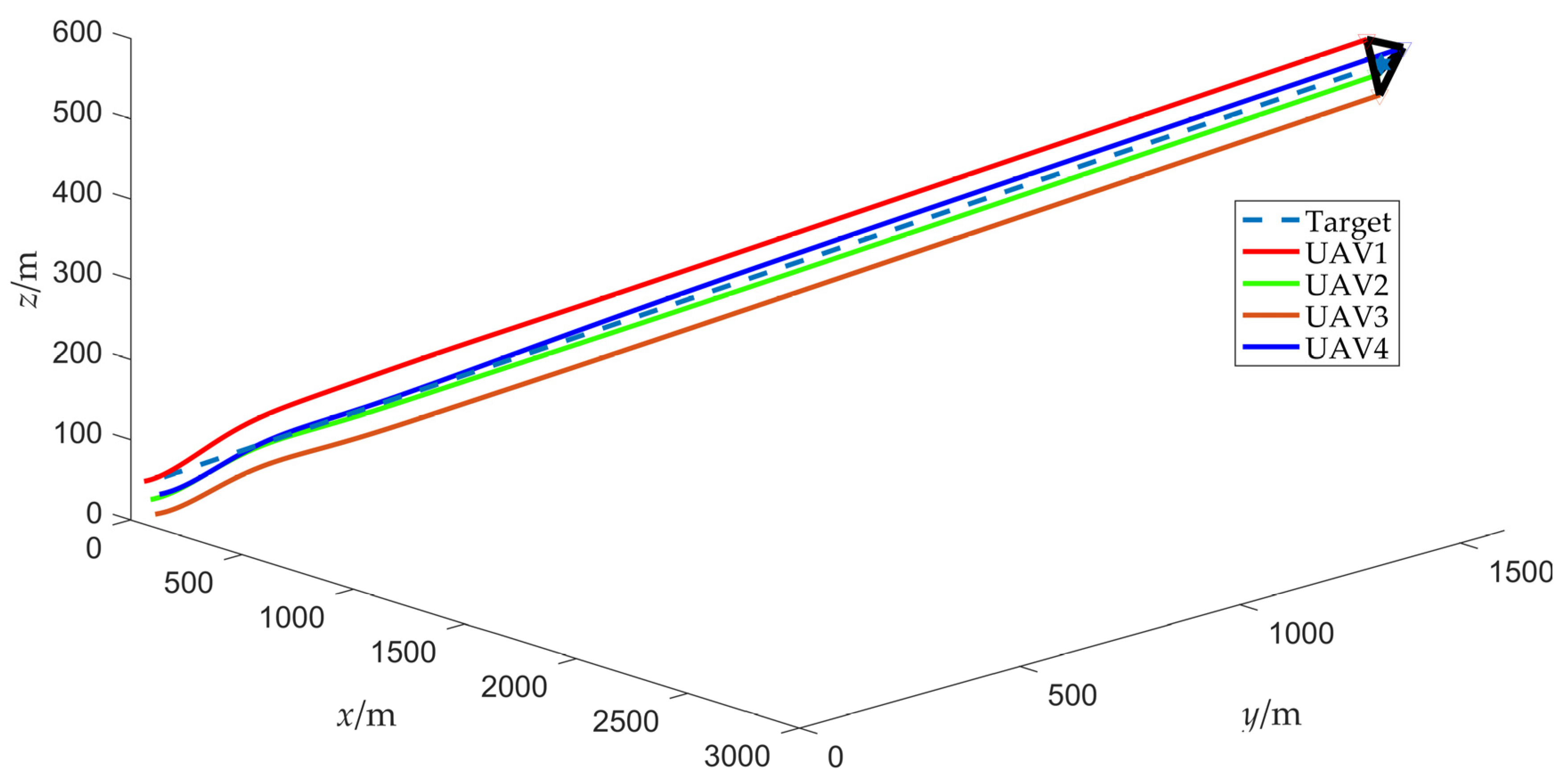
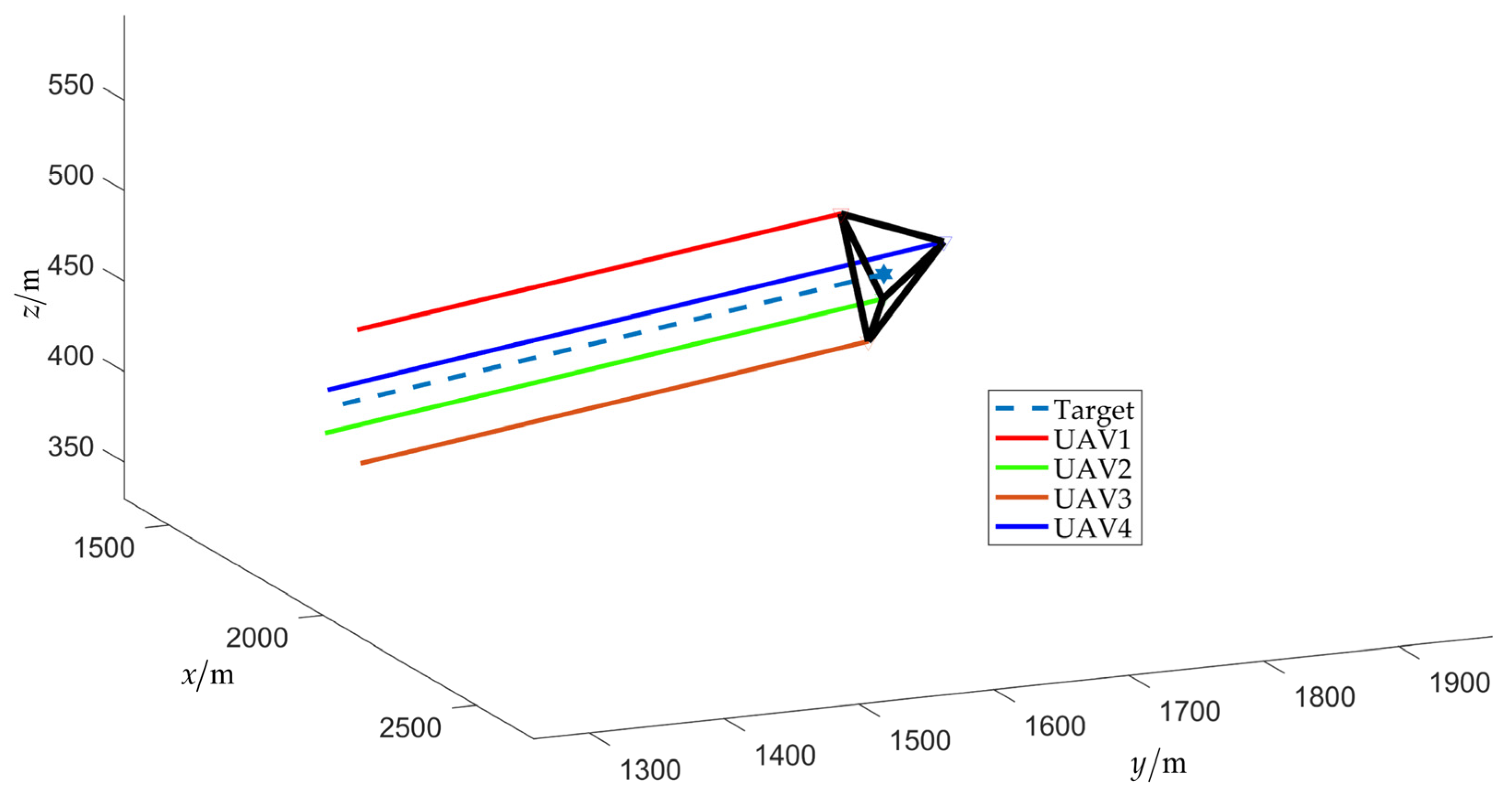
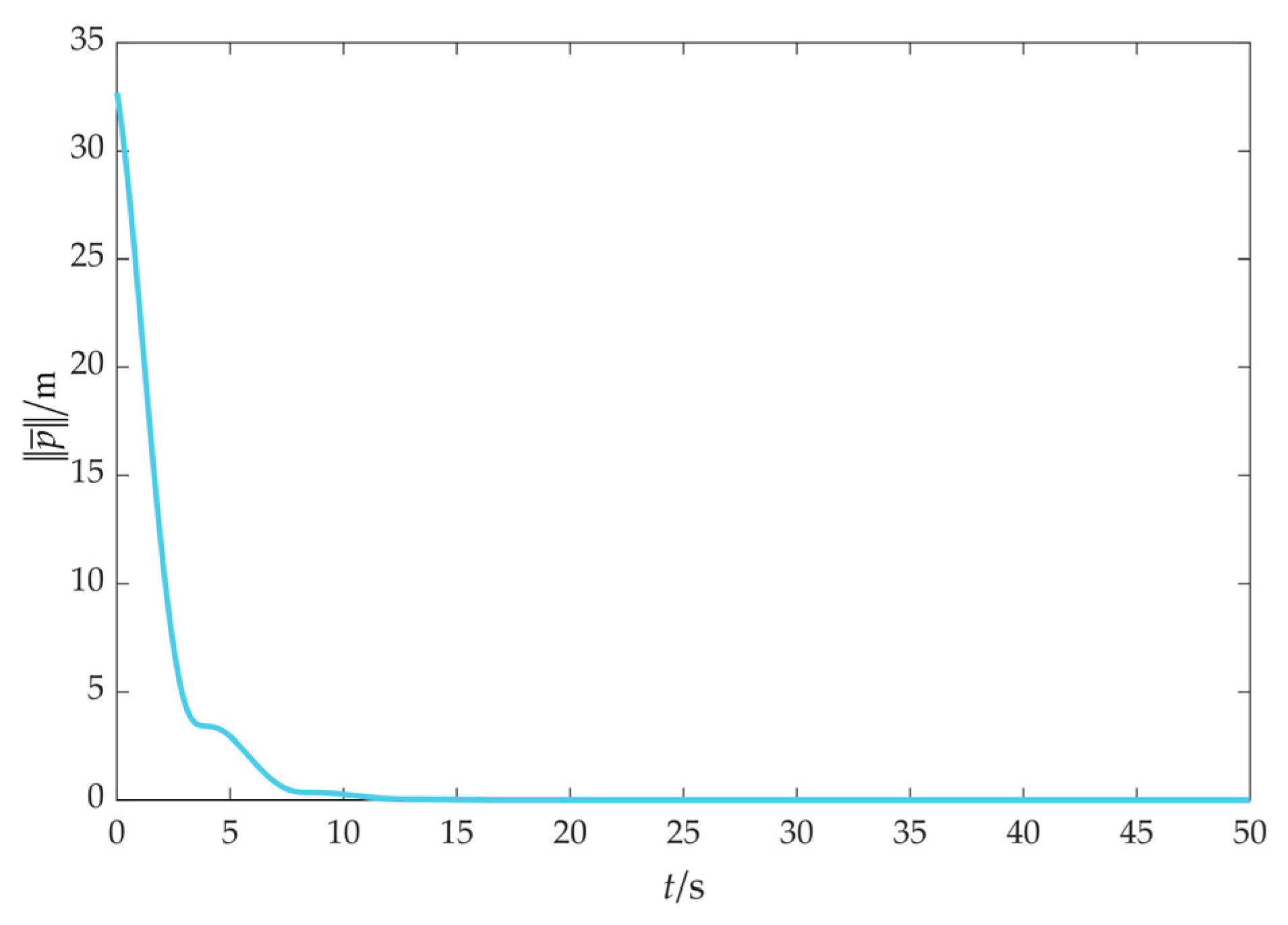
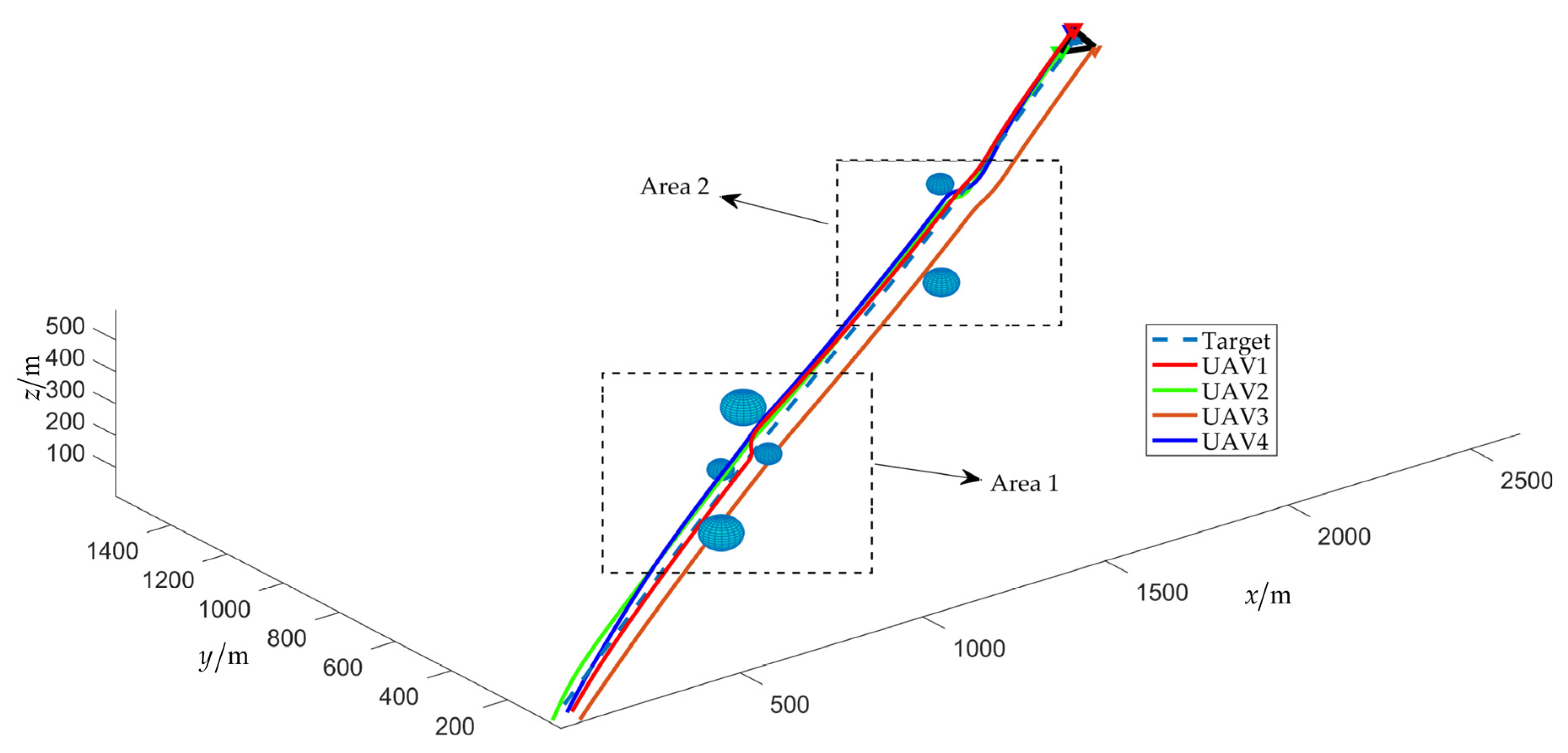
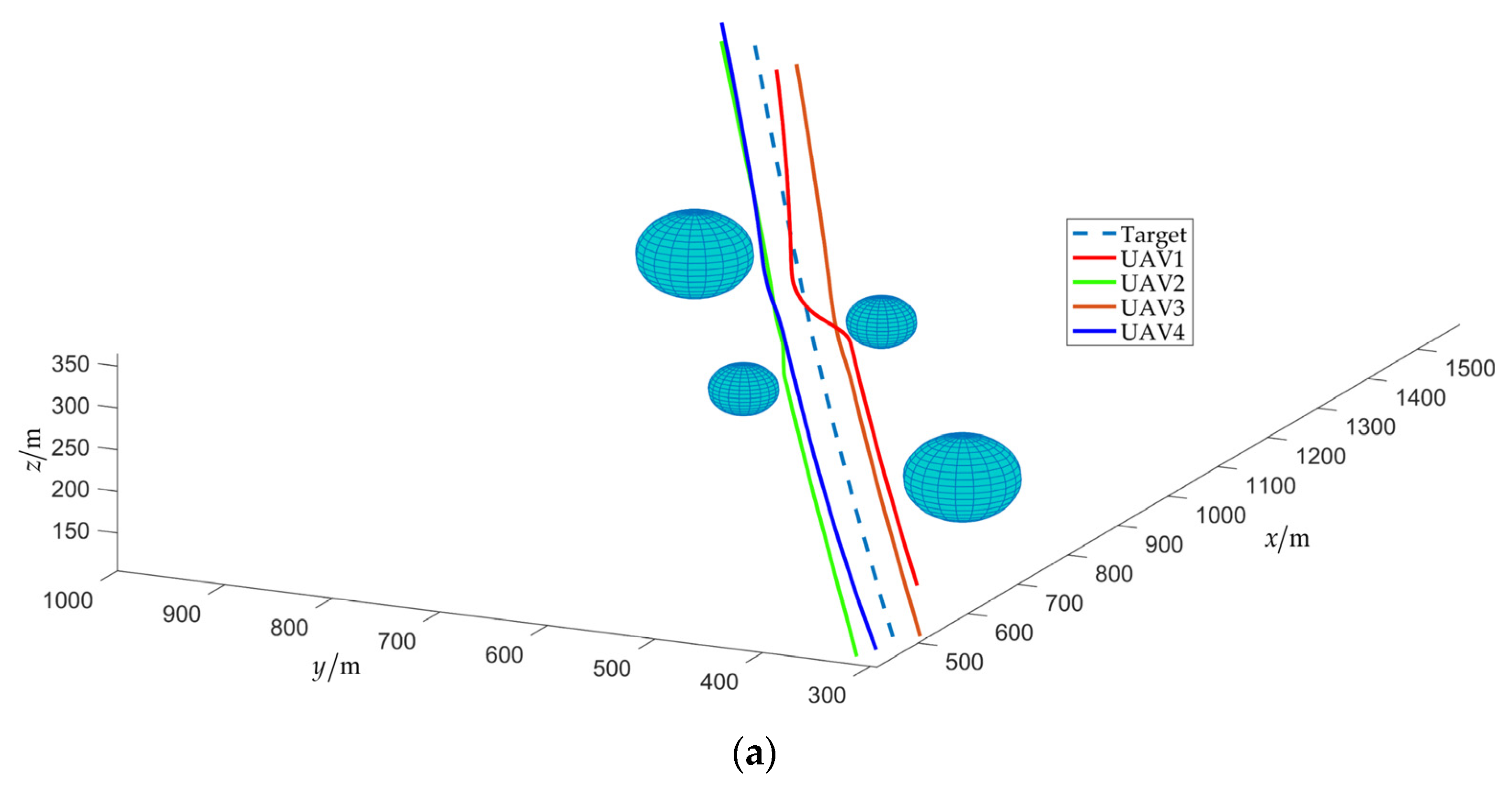
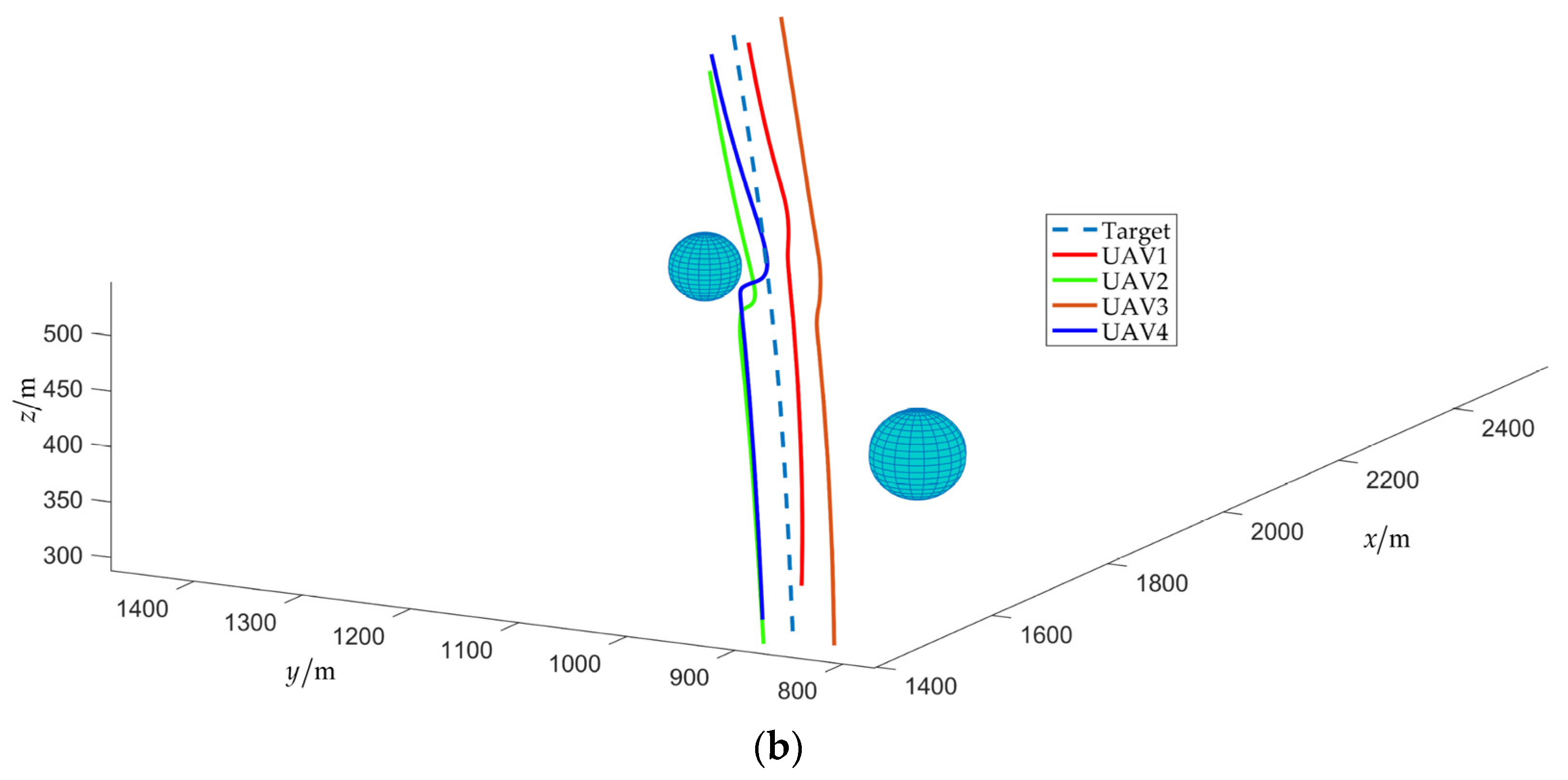
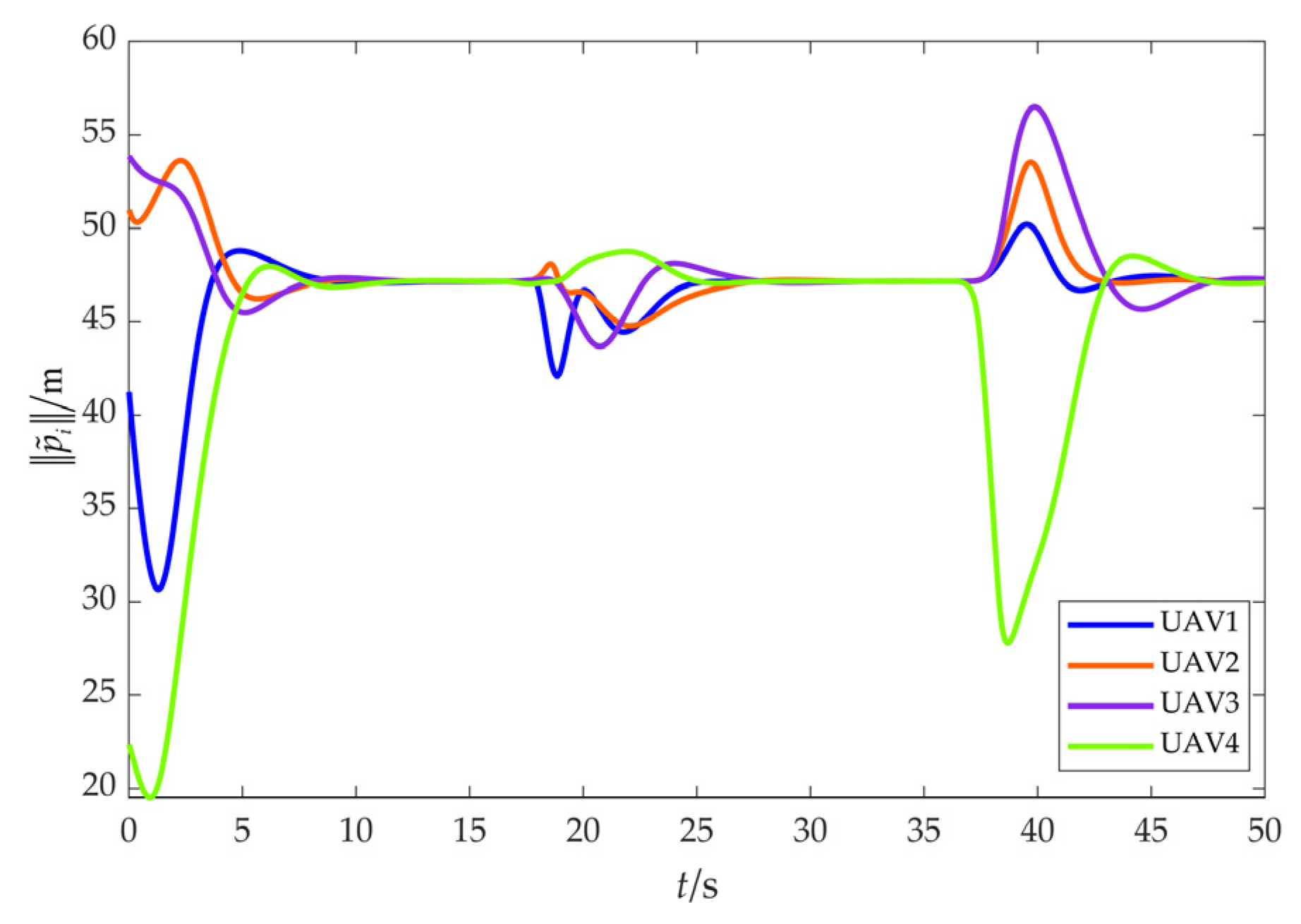
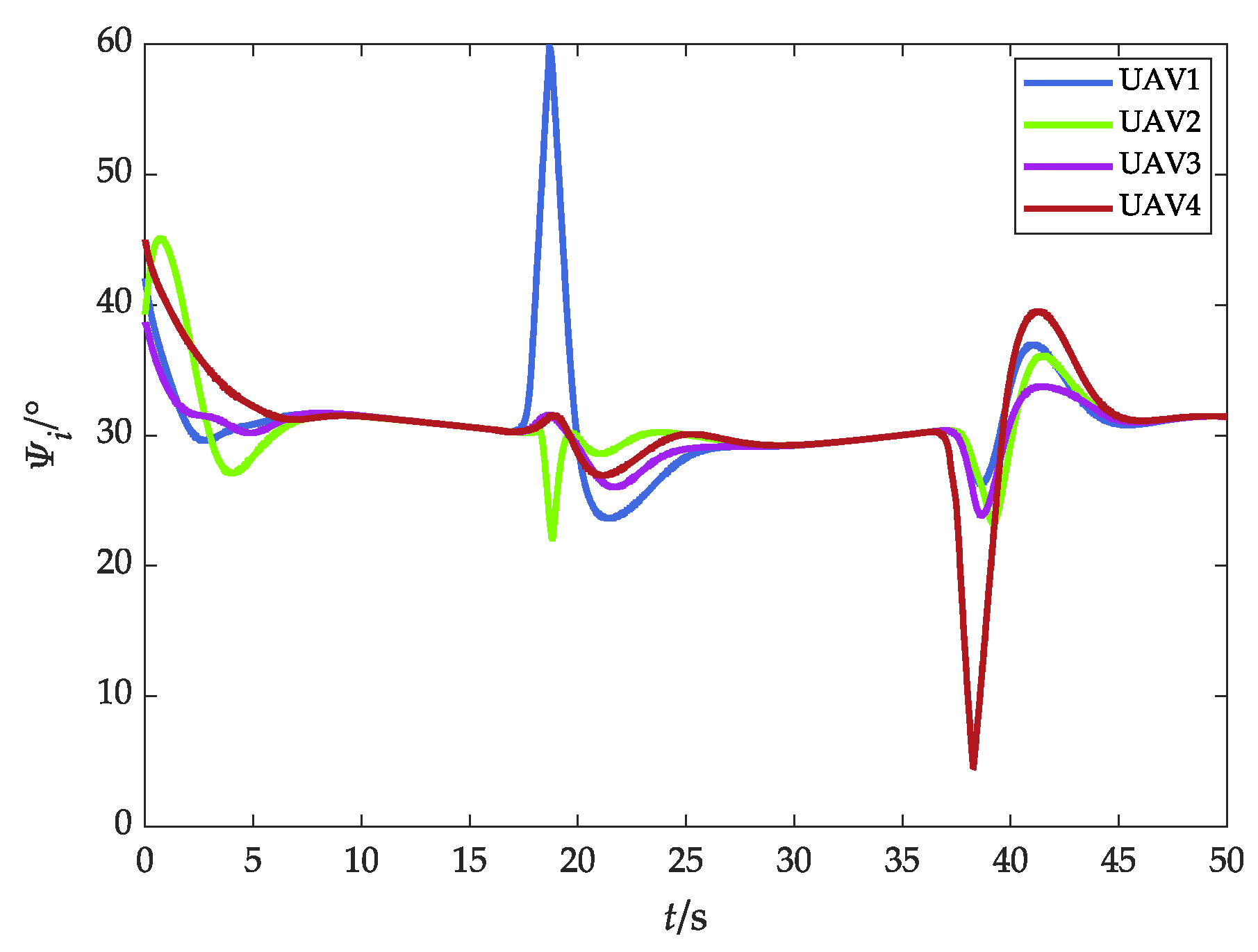
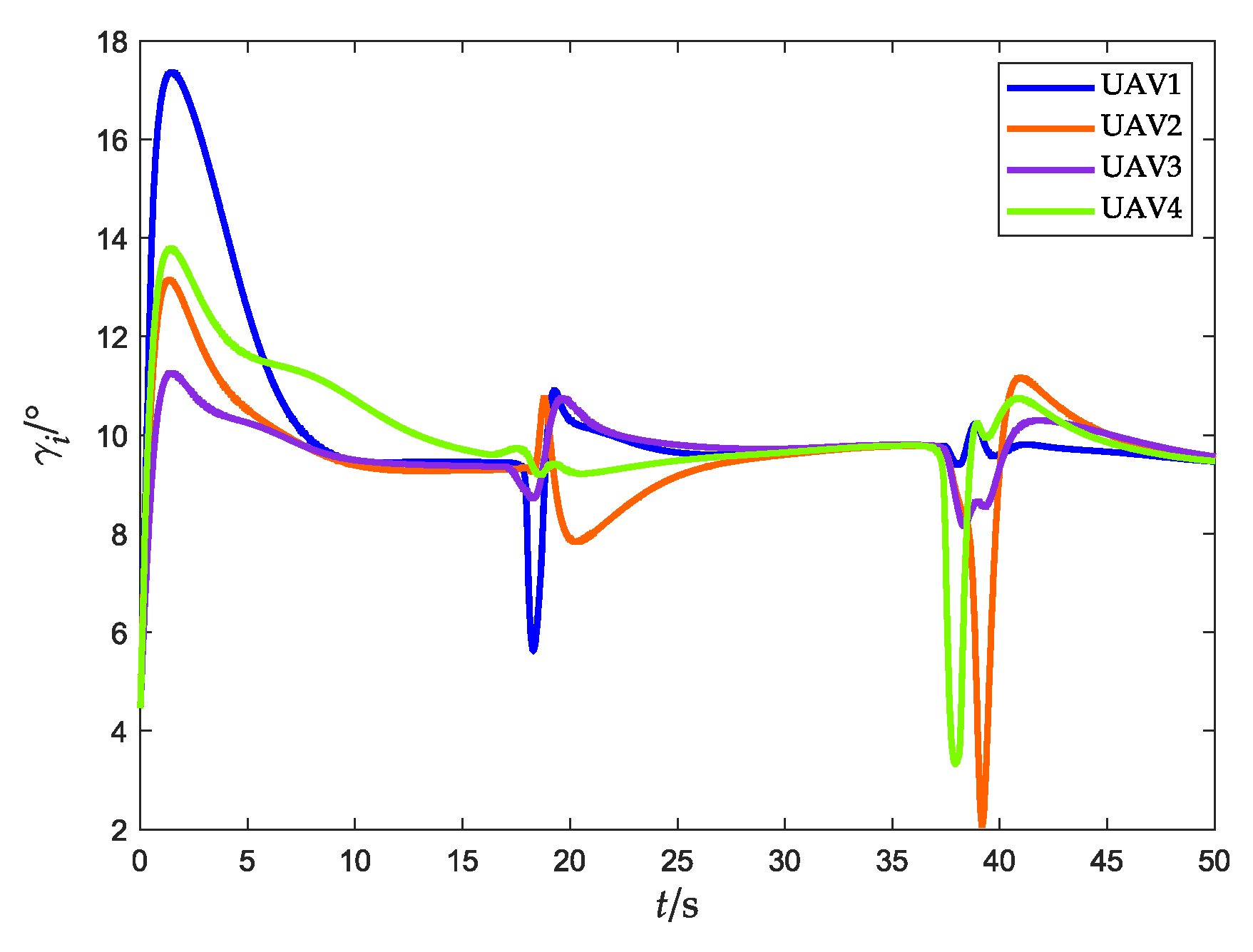
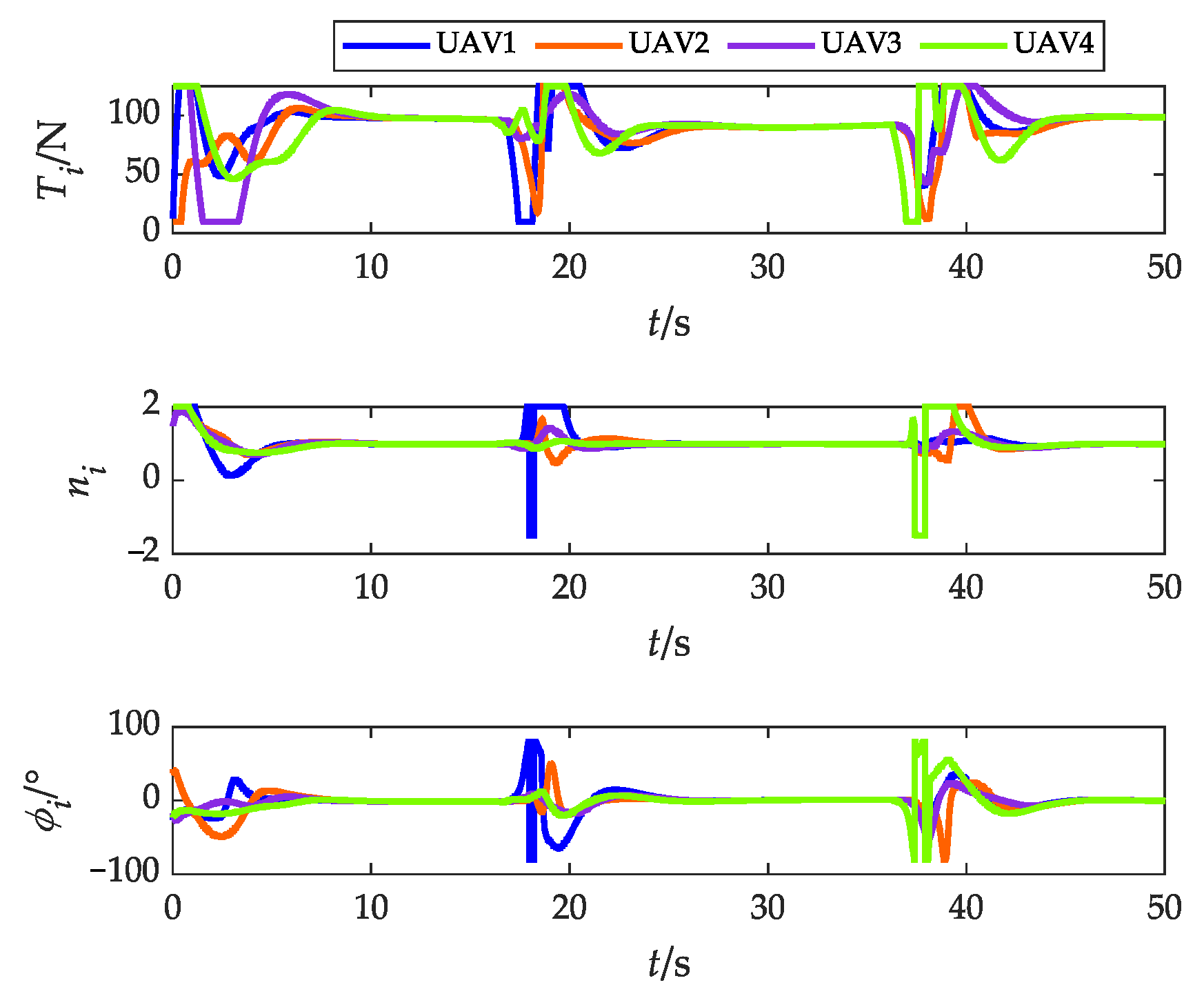
4.2. Scenario 2: Fencing a Maneuvering Target with Obstacle Avoidance

This section mainly demonstrates the effectiveness of the control law for fencing a maneuvering target considering obstacle avoidance. The target’s control input is set as $u_t\left(t\right)={\left[0.2\sin \left(0.05\pi t\right),0.2\cos \left(0.05\pi t\right),0.01\sin \left(0.2\pi t\right)\right]}^{\mathrm{T}}$, which is unknown to the UAVs. The controller parameters are $c_1=0.7$, $c_2=0.5$, and $c_3=1$. Other parameters are the same as those in Section 4.1.

The simulation results of scenario 2 are shown in Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24 and Figure 25. Among them, Figure 16, Figure 17 and Figure 18 demonstrate that a maneuvering target remains to be fenced by the UAV swarm within an obstacle environment. Despite that the cooperative fencing error temporarily increases during obstacle avoidance, it can still rapidly converge to 0.

Figure 19 shows a partial schematic of the obstacle avoidance process, and it is obvious that $‖p_i-o_{\overline{k}}‖>\chi r_{in}+r_{o_{\overline{k}}}$ is consistently upheld during the fencing process, that is, the UAV can avoid obstacles under the potential field (19).

Figure 20 shows the time evolution of the relative distance between UAVs under two cases: with or without the attractive potential field. As depicted in Figure 20a, $‖p_{ij}‖$ is consistently maintained within the range of $\left(2r_{in},\mu \right)$, indicating that UAVs can avoid collision and maintain connectivity during the obstacle avoidance process. In Figure 20b, UAVs are propelled away from obstacles by the repulsive force of obstacle avoidance, but due to the absence of inter-UAV attraction, the maximum relative distance exceeds $\mu$. This indicates a disruption in network connectivity, leading to the impairment of the communication link.

Figure 21 depicts the relative distance $‖{\tilde{p}}_i‖$. It is shown that there are significant fluctuations in the evolution curve of $‖{\tilde{p}}_i‖$ during the obstacle avoidance process, but it still consistently converges to a constant value, which means that UAVs can form a stable convex to fence the target.

Figure 22, Figure 23, Figure 24 and Figure 25 show the time evolution of actual states $V_i$, ${\psi }_i$, and ${\gamma }_i$ and actual control variables $T_i$, $n_i$, and ${\varphi }_i$.

5. Conclusions

In this paper, a distributed cooperative target fencing strategy for UAV swarms with collision, obstacle avoidance, and connectivity maintenance is proposed. A differential state observer is constituted to simultaneously estimate the unknown speed and control input of the target. Collision, obstacle avoidance, and connectivity maintenance potential functions are constructed to guarantee flight safety. Based on the differential state observer and the gradient control terms, a controller without a predefined formation is designed to actualize the cooperative target fencing by combining swarm self-organized theory and consensus theory. Simulation results demonstrate the effectiveness of the proposed controller in fencing a target within an obstacle-laden environment. Future research aims to extend this study to address safety control challenges under interference and node failure conditions and to explore distributed control in a large-scale UAV swarm.