A Novel UAV Air-to-Air Channel Model Incorporating the Effect of UAV Vibrations and Diffuse Scattering
Abstract
1. Introduction
1.1. Related Works
1.2. Motivations
1.3. Contributions
- A novel A2A channel model combining LoS, specular reflection, and diffuse components is proposed. The channel properties are characterized in the presence of large-scale path loss and small-scale fading. Additionally, the proposed model can capture the effects of both large-scale and small-scale mobilities of UAVs. The former refers to UAVs’ flight, while the latter describes UAVs’ random vibrations caused by propeller rotation and engine operation at both ends of the link.
- We derive a closed-form expression that jointly describes the zenith and azimuth angles of diffuse rays as the function of the UAV’s location and the dispersion of scatterers. The power of the diffuse rays is calculated by taking into account various factors, such as the path loss, reflection coefficient, and scattering radiation pattern. This is determined based on the grazing angles of impinging rays and the electrical properties and roughness of the reflective materials.
- Key statistics incorporating the spatial-temporal CCF, Doppler PSD, and coherence time are derived. The impacts of model parameters on channel statistics are presented, including the UAV’s altitude and the scattering lobe width, as well as the amplitude, direction, and frequency of UAV vibration. We show that the random vibration of UAVs can reduce the temporal correlation and coherence time of the channel and induce extra Doppler frequency components. The influences of UAV vibrations become more pronounced as the carrier frequency increases.
2. The 3D A2A MIMO Channel Model
2.1. LoS Component
- •
- accounts for the phase shift due to the initial propagation distance .
- •
- is the phase shift due to the relative locations of in the Tx array.
- •
- is the phase shift due to the relative locations of in the Rx array.
- •
- is the phase shift due to the large-scale movements of the UAVs in specific directions.
- •
- is the phase shift stemming from the random vibration of the Tx antennas
- •
- is the phase shift due to the random vibrations of the Rx antennas.
2.2. Specular and Diffuse Components
2.2.1. Lengths and Angles of the Rays
2.2.2. Powers of the Rays
3. Spatial and Temporal Correlation Characteristics
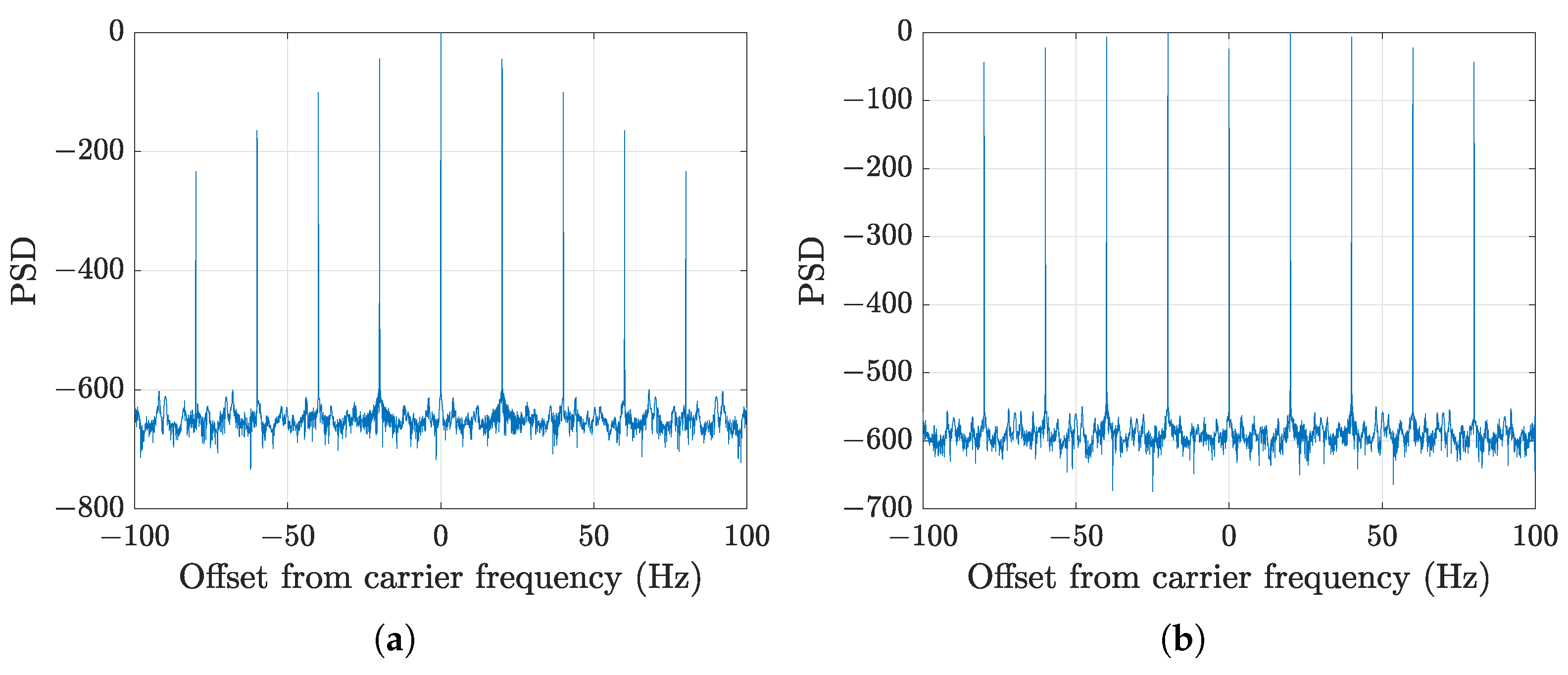
4. Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, C.X.; You, X.; Gao, X.; Zhu, X.; Li, Z.; Zhang, C.; Wang, H.; Huang, Y.; Chen, Y.; Haas, H.; et al. On the road to 6G: Visions, requirements, key technologies, and testbeds. IEEE Commun. Surveys Tuts. 2023, 25, 905–974. [Google Scholar] [CrossRef]
- Yan, C.; Fu, L.; Zhang, J.; Wang, J. A Comprehensive survey on UAV communication channel modeling. IEEE Access 2019, 7, 107769–107792. [Google Scholar] [CrossRef]
- Chang, H.; Bian, J.; Wang, C.X.; Bai, Z.; Zhou, W.; Aggoune, e.H.M. A 3D non-stationary wideband GBSM for low-altitude UAV-to-ground V2V MIMO channels. IEEE Access 2019, 7, 70719–70732. [Google Scholar] [CrossRef]
- Chang, H.; Wang, C.X.; Bian, J.; Feng, R.; He, Y.; Chen, Y.; Aggoune, E.H.M. A novel 3D beam domain channel model for UAV massive MIMO communications. IEEE Trans. Wireless Commun. 2023, 22, 5431–5445. [Google Scholar] [CrossRef]
- Mao, K.; Zhu, Q.; Qiu, Y.; Liu, X.; Song, M.; Fan, W.; Kokkeler, A.B.J.; Miao, Y. A UAV-aided real-time channel sounder for highly dynamic nonstationary A2G scenarios. IEEE Trans. Instrum. Meas. 2023, 72, 1–15. [Google Scholar] [CrossRef]
- Lian, Z.; Su, Y.; Wang, Y.; Ji, P.; Jin, B.; Zhang, Z.; Xie, Z. A novel geometry-based 3-D wideband channel model and capacity analysis for IRS-assisted UAV communication systems. IEEE Trans. Wireless Commun. 2023, 22, 5502–5517. [Google Scholar] [CrossRef]
- Bian, J.; Wang, C.X.; Liu, Y.; Tian, J.; Qiao, J.; Zheng, X. 3D non-stationary wideband UAV-to-ground MIMO channel models based on aeronautic random mobility model. IEEE Trans. Veh. Technol. 2021, 70, 11154–11168. [Google Scholar] [CrossRef]
- Bai, L.; Huang, Z.; Cheng, X. A non-stationary 6G UAV channel model with 3D continuously arbitrary trajectory and self-rotation. IEEE Trans. Wireles Commun. 2022, 21, 10592–10606. [Google Scholar] [CrossRef]
- Hua, B.; Ni, H.; Zhu, Q.; Wang, C.X.; Zhou, T.; Mao, K.; Bao, J.; Zhang, X. Channel modeling for UAV-to-ground communications with posture variation and fuselage scattering effect. IEEE Trans. Commun. 2023, 71, 3103–3116. [Google Scholar] [CrossRef]
- Ma, Z.; Ai, B.; He, R.; Wang, G.; Niu, Y.; Yang, M.; Wang, J.; Li, Y.; Zhong, Z. Impact of UAV rotation on MIMO channel characterization for air-to-ground communication systems. IEEE Trans. Veh. Technol. 2020, 69, 12418–12431. [Google Scholar] [CrossRef]
- Banagar, M.; Dhillon, H.S.; Molisch, A.F. Impact of UAV wobbling on the air-to-ground wireless channel. IEEE Trans. Veh. Technol. 2020, 69, 14025–14030. [Google Scholar] [CrossRef]
- Dabiri, M.T.; Rezaee, M.; Yazdanian, V.; Maham, B.; Saad, W.; Hong, C.S. 3D channel characterization and performance analysis of UAV-assisted millimeter wave links. IEEE Trans. Wireless Commun. 2021, 20, 110–125. [Google Scholar] [CrossRef]
- Ma, Z.; Ai, B.; He, R.; Wang, G.; Zhong, Z.; Yang, M.; Wang, J.; Li, Y. Impact of UAV rotation on MIMO channel space-time correlation. In Proceedings of the IEEE 92nd Vehicular Technology Conference (VTC2020-Fall), Victoria, BC, Canada, 18 November–16 December 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Al-Mashhadani, M.A. Random vibrations in umanned aerial vehicles, mathematical analysis and control methodology based on expectation and probability. J. Low Freq. Noise Vib. Act. Control 2019, 38, 143–153. [Google Scholar] [CrossRef]
- Hoffmann, F.; Ritchie, M.; Fioranelli, F.; Charlish, A.; Griffiths, H. Micro-Doppler based detection and tracking of UAVs with multistatic radar. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, Z.; Jiang, H.; Qian, Y.; Liu, K.; Dang, J.; Wu, L. Measurement-based characterization and modeling for low-altitude UAV air-to-air channels. IEEE Access 2019, 7, 98832–98840. [Google Scholar] [CrossRef]
- Ede, B.; Kaplan, B.; Kahraman, i.; Kesir, S.; Yarkan, S.; Ekti, A.R.; Baykaş, T.; Görçin, A.; Çırpan, H.A. Measurement-based large scale statistical modeling of air-to-air wireless UAV channels via novel time-frequency analysis. IEEE Wireless Commun. Lett. 2022, 11, 136–140. [Google Scholar] [CrossRef]
- Zhou, L.; Yang, Z.; Zhao, G.; Zhou, S.; Wang, C.X. Propagation characteristics of air-to-air channels in urban environments. In Proceedings of the IEEE Global Communications (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Mao, X.; Wang, C.X.; Chang, H. A 3D non-stationary geometry-based stochastic model for 6G UAV air-to-air channels. In Proceedings of the International Conference on Wireless Communications and Signal Processing (WCSP), Changsha, China, 20–22 October 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Y.; Ji, Z.; Lin, K.; He, Z. A three-dimensional geometry-based stochastic model for air-to-air UAV channels. In Proceedings of the IEEE Conference on Vehicular Technology (VTC), Victoria, BC, Canada, 18 November–16 December 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Ma, Z.; Ai, B.; He, R.; Wang, G.; Niu, Y.; Zhong, Z. A wideband non-stationary air-to-air channel model for UAV communications. IEEE Trans. Veh. Technol. 2020, 69, 1214–1226. [Google Scholar] [CrossRef]
- Degli-Esposti, V.; Fuschini, F.; Vitucci, E.M.; Falciasecca, G. Measurement and modelling of scattering from buildings. IEEE Trans. Antennas Propag. 2007, 55, 143–153. [Google Scholar] [CrossRef]
- Hanssens, B.; Kshetri, S.R.; Tanghe, E.; Plets, D.; Hoebeke, J.; Karaağaç, A.; Haxhibeqiri, J.; Gaillot, D.P.; Liénard, M.; Oestges, C.; et al. Measurement-based analysis of dense multipath components in a large industrial warehouse. In Proceedings of the European Conference on Antennas and Propagation (EuCAP), London, UK, 9–13 April 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Rashdan, I.; Unterhuber, P.; de Ponte Müller, F.; Sand, S.; Caire, G. Diffuse multipath analysis of vehicle-to-vulnerable road user channel in urban environment. In Proceedings of the European Conference on Antennas and Propagation (EuCAP), Dusseldorf, Germany, 22–26 March 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Virk, U.T.; Haneda, K.; Wagen, J.F. Dense multipath components add-on for COST 2100 channel model. In Proceedings of the European Conference on Antennas and Propagation (EuCAP), Lisbon, Portugal, 13–17 April 2015; pp. 1–5. [Google Scholar]
- Mao, K.; Zhu, Q.; Song, M.; Li, H.; Ning, B.; Pedersen, G.F.; Fan, W. Machine-learning-based 3-D channel modeling for U2V mmWave communications. IEEE Internet Things J. 2022, 9, 17592–17607. [Google Scholar] [CrossRef]
- Xia, W.; Rangan, S.; Mezzavilla, M.; Lozano, A.; Geraci, G.; Semkin, V.; Loianno, G. Generative neural network channel modeling for millimeter-wave UAV communication. IEEE Trans. Wireless Commun. 2022, 21, 9417–9431. [Google Scholar] [CrossRef]
- Tian, Y.; Li, H.; Zhu, Q.; Mao, K.; Ali, F.; Chen, X.; Zhong, W. Generative network-based channel modeling and generation for air-to-cround Communication scenarios. IEEE Commun. Lett. 2024, 28, 892–896. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, Q.; Lin, Z.; Wu, Q.; Huang, Y.; Cai, X.; Zhong, W.; Zhao, Y. Sparse Bayesian learning-based 3-D radio environment map construction—Sampling optimization, scenario-dependent dictionary construction, and sparse recovery. IEEE Trans. Cogn. Commun. Netw. 2024, 10, 80–93. [Google Scholar] [CrossRef]
- Hou, X.; Wang, J.; Jiang, C.; Zhang, X.; Ren, Y.; Debbah, M. UAV-enabled covert federated learning. IEEE Trans. Wireless Commun. 2023, 22, 6793–6809. [Google Scholar] [CrossRef]
- Wang, Y.; Su, Z.; Zhang, N.; Benslimane, A. Learning in the air: Secure federated learning for UAV-assisted crowdsensing. IEEE Trans. Netw. Sci. Eng. 2021, 8, 1055–1069. [Google Scholar] [CrossRef]
- Rappaport, T.S. Wireless Communications: Principles and Practice, 2nd ed.; Pearson Education: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Khuwaja, A.A.; Chen, Y.; Zhao, N.; Alouini, M.S.; Dobbins, P. A survey of channel modeling for UAV communications. IEEE Commun. Surveys Tuts. 2018, 20, 2804–2821. [Google Scholar] [CrossRef]
- Kilgore, I.M.; Kabiri, S.A.; Kane, A.W.; Steer, M.B. The effect of chaotic vibrations on antenna characteristics. IEEE Antennas Wireless Propag. Lett. 2016, 15, 1242–1244. [Google Scholar] [CrossRef]
- Bian, J.; Wang, C.X.; Gao, X.; You, X.; Zhang, M. A general 3D non-stationary wireless channel model for 5G and beyond. IEEE Trans. Wireless Commun. 2021, 20, 3211–3224. [Google Scholar] [CrossRef]
- Colton, D.; Kress, R. Inverse Acoustic and Electromagnetic Scattering Theory, 2nd ed.; Springer: New York, NY, USA, 1998. [Google Scholar]
- Oestges, C.; Clerckx, B. MIMO Wireless Communications: From Real-World Propagation to Space-Time Code Design, 1st ed.; Academic Press: London, UK, 2010. [Google Scholar]
- Quitin, F.; Oestges, C.; Bellens, F.; van Roy, S.; Horlin, F.; De Doncker, P. Extracting specular-diffuse clusters from MIMO channel measurements. In Proceedings of the International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Toronto, ON, Canada, 11–14 September 2011; pp. 940–944. [Google Scholar] [CrossRef]
- Santos, T.; Tufvesson, F.; Molisch, A.F. Modeling the ultra-wideband outdoor channel: Model specification and validation. IEEE Trans. Wireless Commun. 2010, 9, 1987–1997. [Google Scholar] [CrossRef]
- Andrade, A.; Covarrubias, D. Radio channel spatial propagation model for mobile 3G in smart antenna systems. IEICE Trans. Commun. 2003, E86-B, 213–220. [Google Scholar]
- Kelner, J.M.; Ziólkowski, C. Adjustment of the gaussian scatterer density model to different mobile radio propagation environment. In Proceedings of the 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016; pp. 1–5. [Google Scholar]
- Zaixue, W.; Qipeng, T. Analytical RS-GBSM-based nonstationary low-altitude air-to-air channel modeling over open area. Int. J. Antennas Propag. 2022, 2022, 1–18. [Google Scholar] [CrossRef]
- Wei, Z.; Geng, J. Time-variant PDFs of AODs and AOAs for ground scattering in low-altitude air-to-air communication over open area. IEEE Commun. Lett. 2021, 25, 701–705. [Google Scholar] [CrossRef]
- Mani, F.; Quitin, F.; Oestges, C. Accuracy of depolarization and delay spread predictions using advanced ray-based modeling in indoor scenarios. J. Wireless Com. Netw. 2011, 2011, 11. [Google Scholar] [CrossRef]
- Pascual-García, J.; Molina-García-Pardo, J.M.; Martínez-Inglés, M.T.; Rodríguez, J.V.; Saurín-Serrano, N. On the importance of diffuse scattering model parameterization in indoor wireless channels at mm-wave frequencies. IEEE Access 2016, 4, 688–701. [Google Scholar] [CrossRef]
- Va, V.; Heath, R.W. Basic relationship between channel coherence time and beamwidth in vehicular channels. In Proceedings of the Conference on Vehicular Technology (VTC), Boston, MA, USA, 6–9 September 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Goddemeier, N.; Wietfeld, C. Investigation of air-to-air channel characteristics and a UAV specific extension to the rice model. In Proceedings of the Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–5. [Google Scholar] [CrossRef]
- ITU-R P.527; Electrical Characteristics of the Surface of the Earth. ITU-R: Geneva, Switzerland, 2021.
- Egido, A.; Paloscia, S.; Motte, E.; Guerriero, L.; Pierdicca, N.; Caparrini, M.; Santi, E.; Fontanelli, G.; Floury, N. Airborne GNSS-R polarimetric measurements for soil moisture and above-ground biomass estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1522–1532. [Google Scholar] [CrossRef]
- DJI Website. Available online: https://www.dji.com/hk-en/e5000 (accessed on 5 April 2024).
- IEEE Std 802.11n TM-2009; Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications-Amendment 5: Enhancements for Higher Throughput. IEEE 802.11 Working Group: New York, NY, USA, 2009.
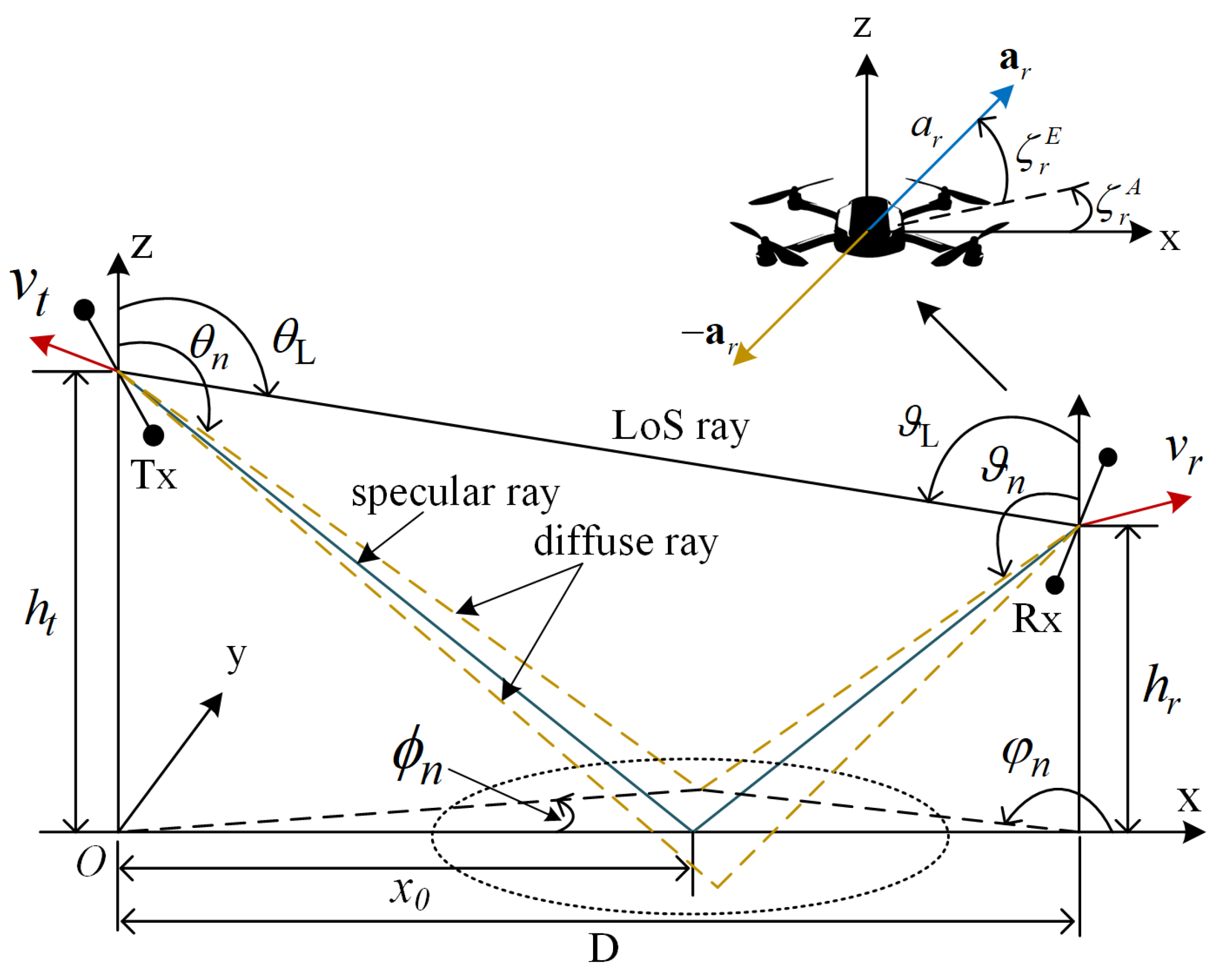











| Parameter | Definition |
|---|---|
| O | The origin of coordinates |
| Numbers of Tx and Rx antennas, respectively | |
| The pth Tx and the qth Rx antennas, respectively | |
| Tilt angles of Tx and Rx arrays in the horizontal plane, respectively | |
| Spacings between adjacent antennas at the Tx and Rx arrays, respectively | |
| Heights of the Tx and Rx, respectively | |
| D | Horizontal separation between Tx and Rx centers |
| Distance from O to the specular reflection point | |
| ZoD, ZoA, AoD, and AoA of the nth ray | |
| Incident angle of the nth ray | |
| Lengths of the LoS and the nth ray, respectively | |
| Speeds of the Tx and Rx, respectively | |
| Angles of motion of the Tx and Rx, respectively | |
| , | Vibration displacement vectors of the Tx and Rx antennas, respectively |
| Vibration frequencies of the Tx and Rx antennas, respectively | |
| , | Vibration amplitudes of the Tx and Rx antennas, respectively |
| , | Vibration elevation and azimuth angles of the Tx and Rx antennas, respectively |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, W.; Bian, J.; Wang, Z.; Liu, W. A Novel UAV Air-to-Air Channel Model Incorporating the Effect of UAV Vibrations and Diffuse Scattering. Drones 2024, 8, 194. https://doi.org/10.3390/drones8050194
Qi W, Bian J, Wang Z, Liu W. A Novel UAV Air-to-Air Channel Model Incorporating the Effect of UAV Vibrations and Diffuse Scattering. Drones. 2024; 8(5):194. https://doi.org/10.3390/drones8050194
Chicago/Turabian StyleQi, Wenzhe, Ji Bian, Zili Wang, and Wenzhao Liu. 2024. "A Novel UAV Air-to-Air Channel Model Incorporating the Effect of UAV Vibrations and Diffuse Scattering" Drones 8, no. 5: 194. https://doi.org/10.3390/drones8050194
APA StyleQi, W., Bian, J., Wang, Z., & Liu, W. (2024). A Novel UAV Air-to-Air Channel Model Incorporating the Effect of UAV Vibrations and Diffuse Scattering. Drones, 8(5), 194. https://doi.org/10.3390/drones8050194







