Channel Knowledge Map Construction Based on a UAV-Assisted Channel Measurement System
Abstract
1. Introduction
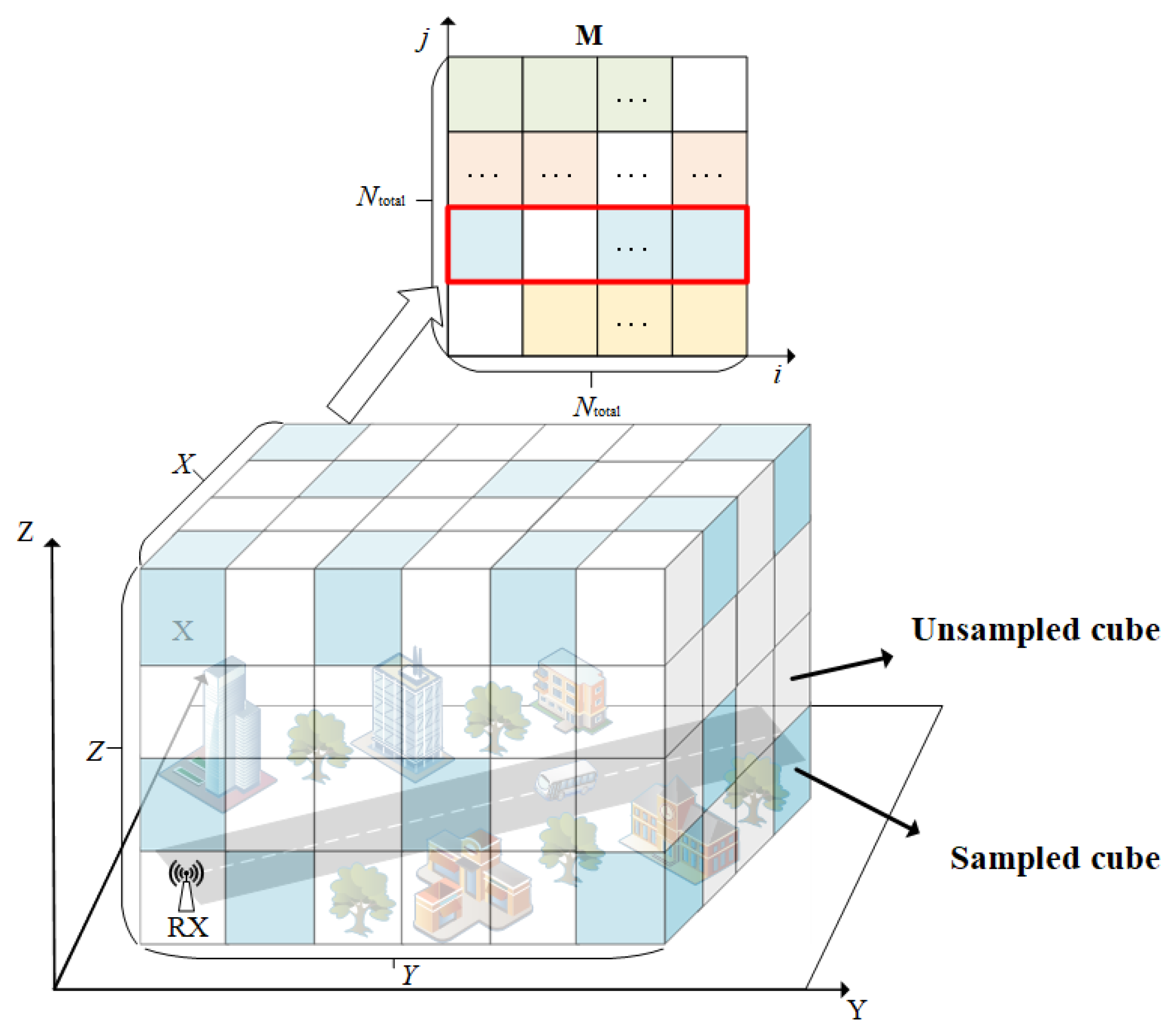
- A three-dimensional (3D) channel knowledge construction scheme in real-world scenarios is provided and implemented. The measurement scenario is divided into a 3D grid region and the CKM can be expressed by a 3D matrix. The channel knowledge along the flight trajectories is obtained by a self-developed channel measurement system. Then, the sparse CKM matrix is completed based on the spatial correlation of the channel characteristics.
- An algorithm for extracting and completing channel knowledge is proposed. The time-domain channel measurement idea is adopted to obtain the channel impulse response (CIR). An adaptive dynamic noise threshold approach is proposed based on the constant false alarm rate (CFAR) to improve the extraction accuracy in real-world scenarios. Due to the limitation of measurement time and cost, the CIR and channel knowledge are only measured along the UAV trajectories. The channel knowledge in other positions is completed by a 3D Kriging interpolation approach.
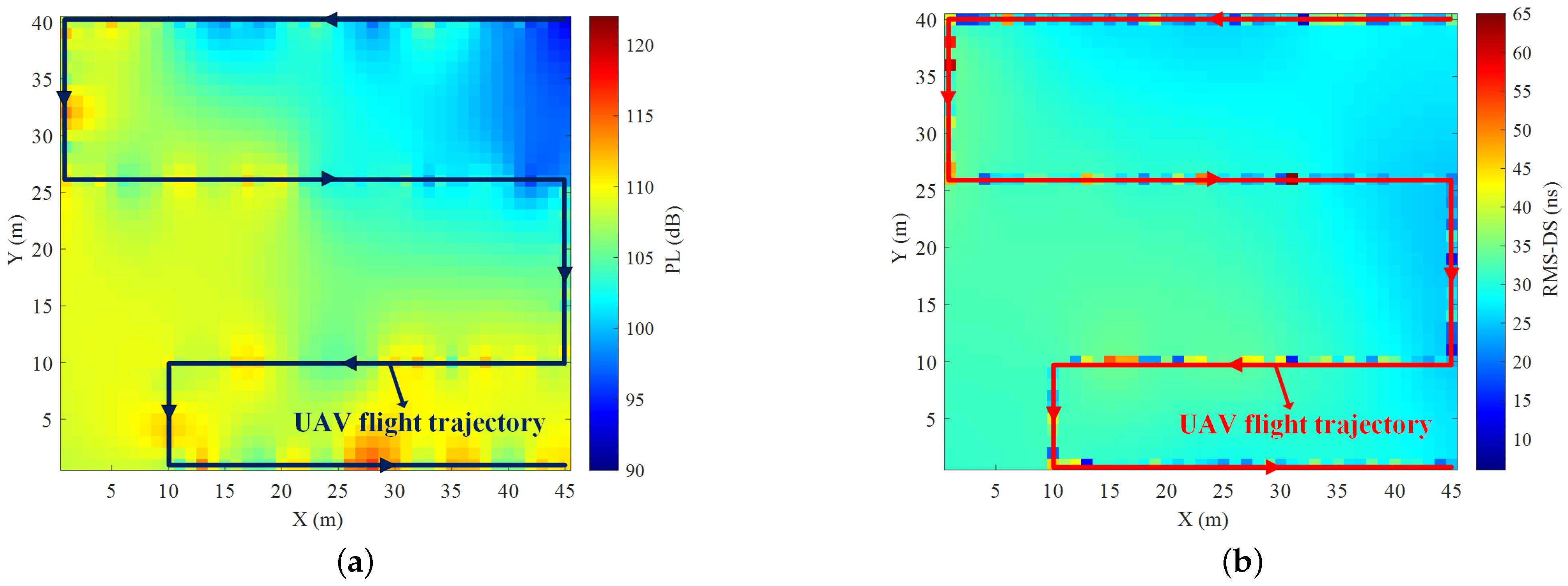
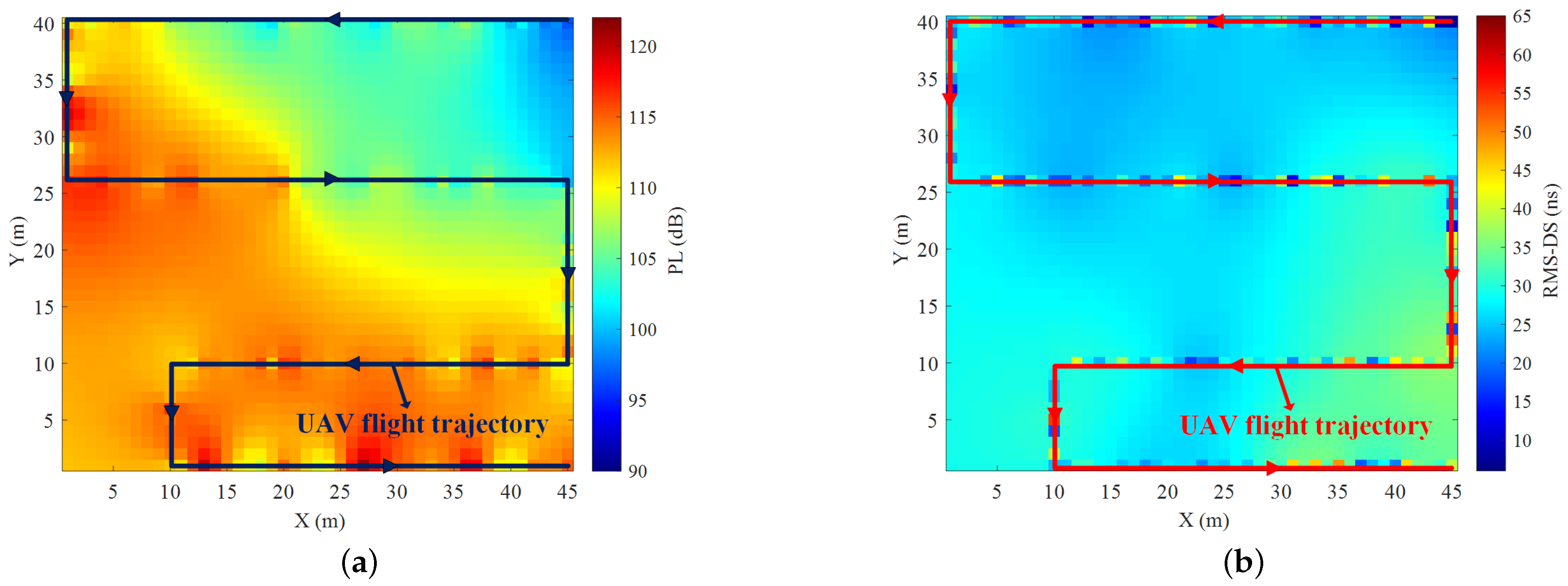
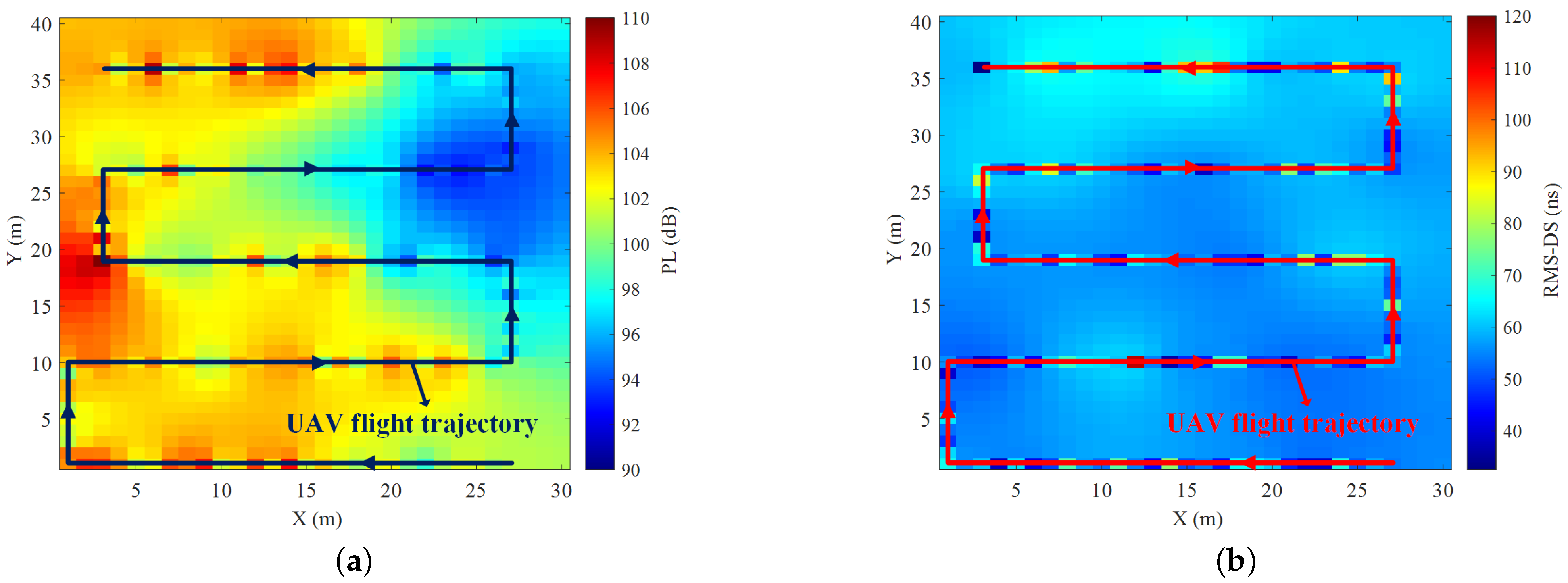
- A UAV-assisted channel measurement system is developed and applied to measure the CKMs in the real-world scenarios. The system consists of a UAV transmitting unit and a ground receiving unit. CKM measurement campaigns are conducted in two typical scenarios of campus and farmland, and CKMs of PL and RMS-DS at two different heights under these two scenarios are constructed. The accuracy of the constructed CKMs is verified by the root mean square error (RMSE).
2. 3D Channel Knowledge Mapping
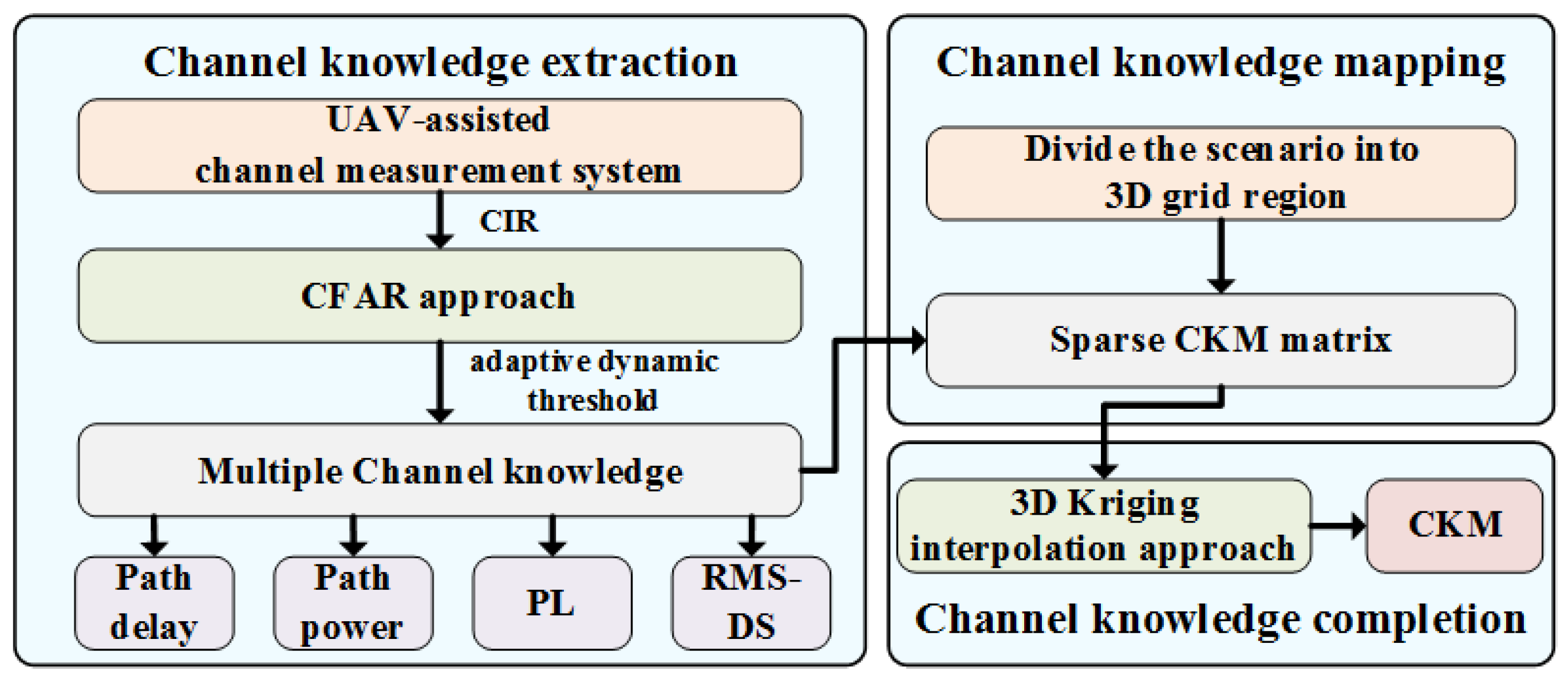
3. Channel Knowledge Extraction and Completion
3.1. Channel Impulse Response Extraction
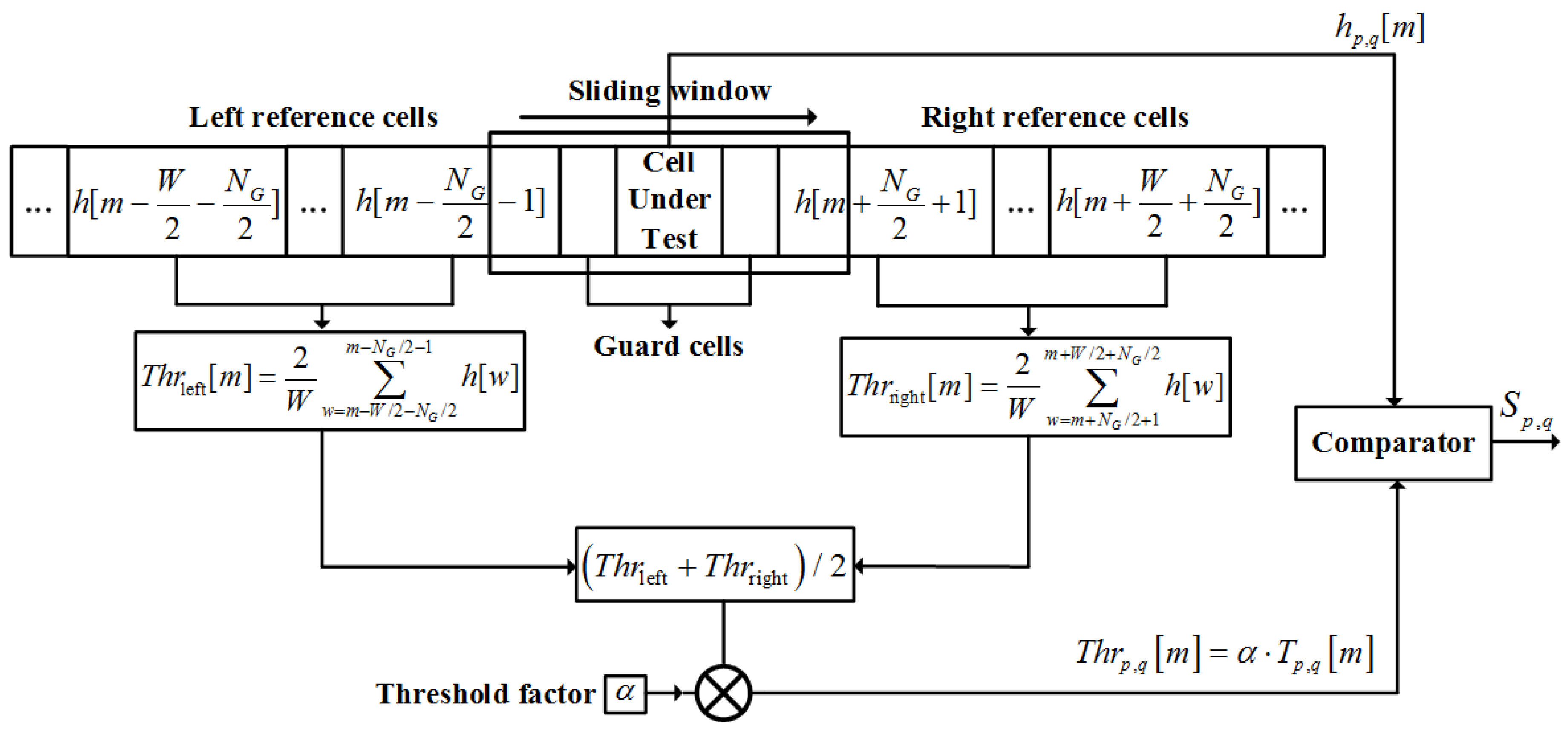
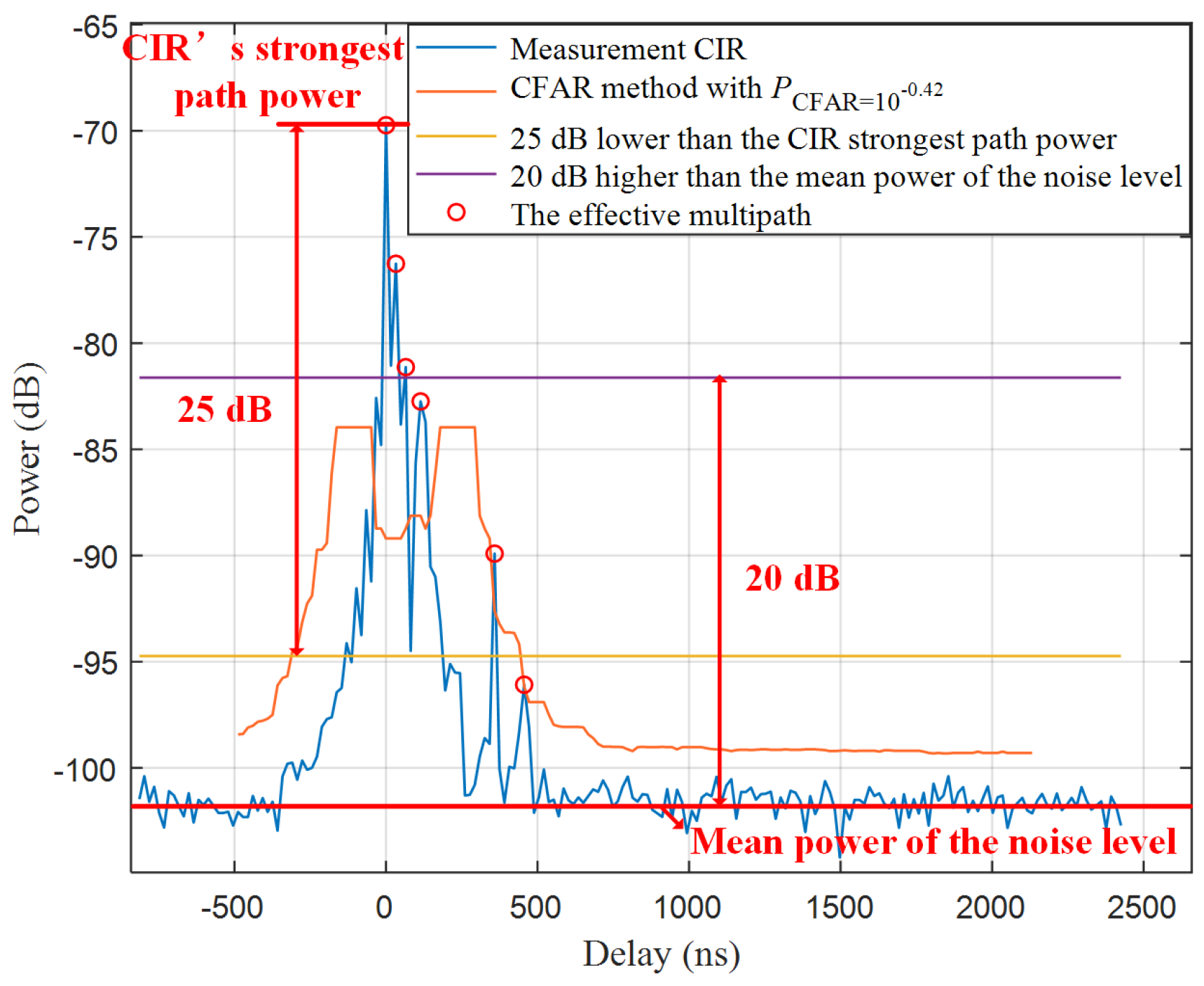
3.2. Channel Knowledge Extraction
3.3. Channel Knowledge Completion and Prediction
4. CKM Measurement Results and Analysis
4.1. Measurement System and Campaign
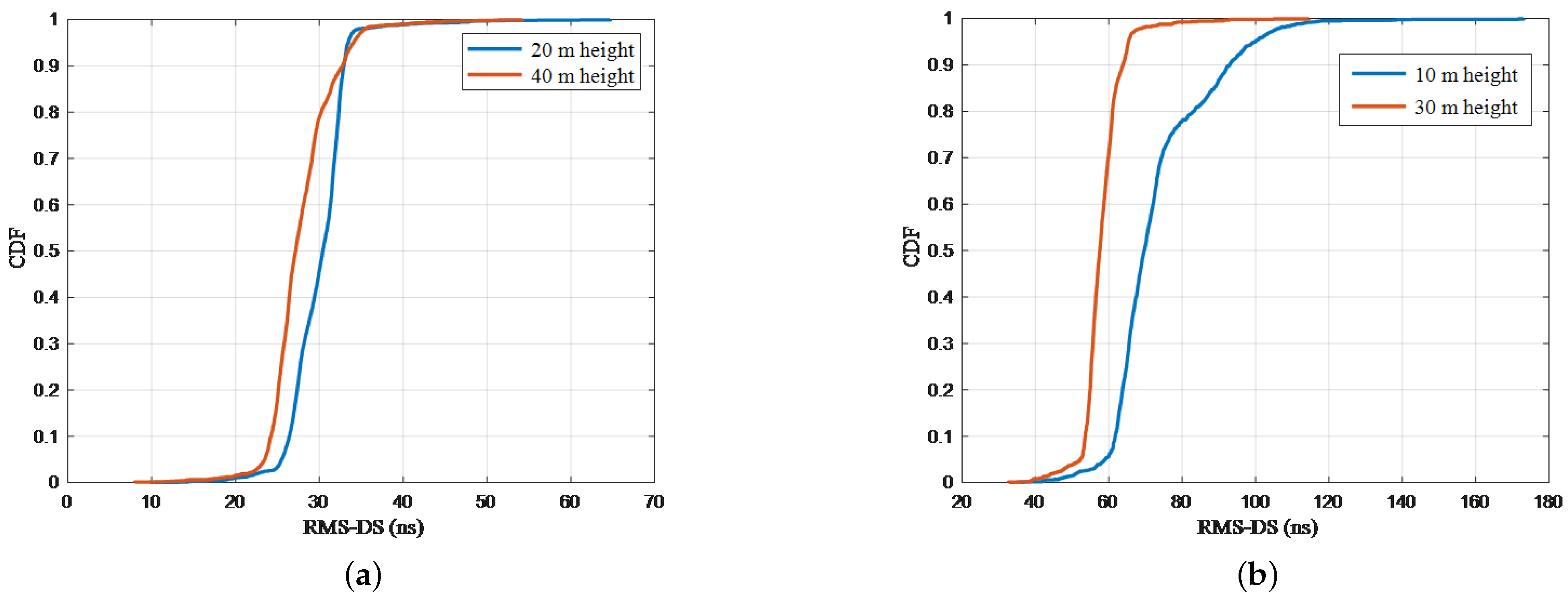
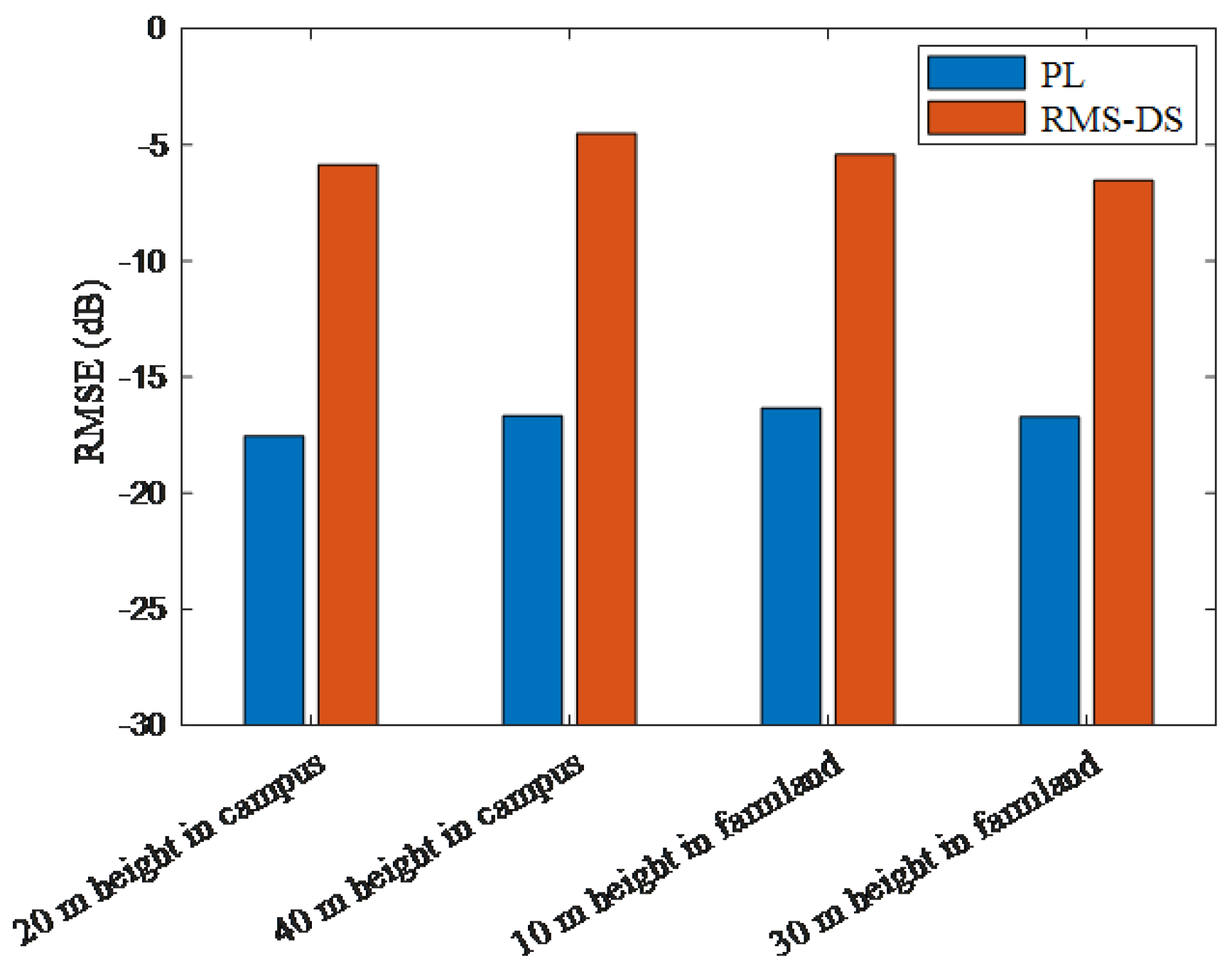
4.2. CKM Construction and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mozaffari, M.; Saad, W.; Bennis, M.; Nam, Y.-H.; Debbah, M. A Tutorial on UAVs for Wireless Networks: Applications, Challenges, and Open Problems. IEEE Commun. Surveys Tuts. 2019, 21, 2334–2360. [Google Scholar] [CrossRef]
- Huang, Y.; Cui, H.; Hou, Y.; Hao, C.; Wang, W.; Zhu, Q.; Li, J.; Wu, Q.; Wang, J. Space-Based Electromagnetic Spectrum Sensing and Situation Awareness. Space Sci Technol. 2024, 4, 0109. [Google Scholar] [CrossRef]
- Xiao, Z.; Dong, H.; Bai, L.; Wu, D.O.; Xia, X.-G. Unmanned Aerial Vehicle Base Station (UAV-BS) Deployment With Millimeter-Wave Beamforming. IEEE Internet Things J. 2020, 21, 1336–1349. [Google Scholar] [CrossRef]
- Shi, M.; Yang, K.; Niyato, D.; Yuan, H.; Zhou, H.; Xu, Z. The Meta Distribution of SINR in UAV-Assisted Cellular Networks. IEEE Trans. Commun. 2023, 71, 1193–1206. [Google Scholar] [CrossRef]
- Zeng, Y.; Wu, Q.; Zhang, R. Accessing From the Sky: A Tutorial on UAV Communications for 5G and Beyond. Proc. IEEE 2019, 107, 2327–2375. [Google Scholar] [CrossRef]
- Na, Z.; Liu, Y.; Shi, J.; Liu, C.; Gao, Z. UAV-Supported Clustered NOMA for 6G-Enabled Internet of Things: Trajectory Planning and Resource Allocation. IEEE Internet Things J. 2021, 8, 15041–15048. [Google Scholar] [CrossRef]
- Hua, B.; Ni, H.; Zhu, Q.; Wang, C.-X.; Zhou, T.; Mao, K.; Bao, J.; Zhang, X. Channel Modeling for UAV-to-Ground Communications with Posture Variation and Fuselage Scattering Effect. IEEE Trans. Commun. 2023, 71, 3103–3116. [Google Scholar] [CrossRef]
- Pan, J.; Ye, N.; Yu, H.; Hong, T.; Al-Rubaye, S.; Mumtaz, S.; Al-Dulaimi, A.; Chih-Lin, I. AI-Driven Blind Signature Classification for IoT Connectivity: A Deep Learning Approach. IEEE Trans. Wireless Commun. 2022, 21, 6033–6047. [Google Scholar] [CrossRef]
- Ding, X.; Zhou, K.; Li, G.; Yang, K.; Gao, X.; Yuan, J.; An, J. Customized Joint Blind Frame Synchronization and Decoding Methods for Analog LDPC Decoder. IEEE Trans. Commun. 2024, 72, 756–770. [Google Scholar] [CrossRef]
- Lyu, Y.; Wang, W.; Sun, Y.; Yue, H.; Chai, J. Low-Altitude UAV Air-to-Ground Multilink Channel Modeling and Analysis at 2.4 and 5.9 GHz. IEEE Antennas Wireless Propag. Lett. 2023, 22, 2135–2139. [Google Scholar] [CrossRef]
- Lyu, Y.; Wang, W.; Rashdan, I. Measurement-based Fading Characteristics Analysis and Modeling of UAV to Vehicles Channel. Veh. Commun. 2024, 45, 100707. [Google Scholar] [CrossRef]
- Fuschini, F.; Barbiroli, M.; Vitucci, E.M.; Semkin, V.; Oestges, C.; Strano, B.; Degli-Esposti, V. An UAV-Based Experimental Setup for Propagation Characterization in Urban Environment. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Y.; Cosmas, J.; Jawad, N.; Li, W.; Muller, R.; Jiang, T. mmWave Indoor Channel Measurement Campaign for 5G New Radio Indoor Broadcasting. IEEE Trans. Broadcast. 2022, 68, 331–344. [Google Scholar] [CrossRef]
- Quimby, J.T.; Williams, D.F.; Remley, K.A.; Ribeiro, D.; Sun, R.; Senic, J. Millimeter-Wave Channel-Sounder Performance Verification Using Vector Network Analyzer in a Controlled RF Channel. IEEE Trans. Antennas Propag. 2021, 69, 7867–7875. [Google Scholar] [CrossRef] [PubMed]
- Mbugua, A.W.; Fan, W.; Olesen, K.; Cai, X.; Pedersen, G.F. Phase-Compensated Optical Fiber-Based Ultrawideband Channel Sounder. IEEE Trans. Microw. Theory Tech. 2019, 68, 636–647. [Google Scholar] [CrossRef]
- Lyu, Y.; Kyösti, P.; Fan, W. Sub-Terahertz Channel Sounder: Review and Future Challenges. China Commun. 2023, 20, 26–48. [Google Scholar] [CrossRef]
- Mao, K.; Zhu, Q.; Qiu, Y.; Liu, X.; Song, M.; Fan, W.; Kokkeler, A.B.J.; Miao, Y. A UAV-Aided Real-Time Channel Sounder for Highly Dynamic Non-Stationary A2G Scenarios. IEEE Trans. Instrum. Meas. 2023, 72, 1–15. [Google Scholar]
- Zeng, Y.; Xu, X. Toward Environment-Aware 6G Communications via Channel Knowledge Map. IEEE Wireless Commun. 2021, 28, 84–91. [Google Scholar] [CrossRef]
- Xia, X.; Wang, Y.; Xu, K.; Xu, Y. Toward Digitalizing the Wireless Environment: A Unified A2G Information and Energy Delivery Framework Based on Binary Channel Feature Map. IEEE Trans. Wireless Commun. 2022, 21, 6448–6463. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhu, Q.; Lin, Z.; Guo, L.; Wu, Q.; Wang, J.; Zhong, W. Temporal Prediction for Spectrum Environment Maps with Moving Radiation Sources. IET Commun. 2022, 17, 539–548. [Google Scholar] [CrossRef]
- Ruan, T.; Huang, Y.; Zhu, Q.; Hao, C.; Wu, Q. Multi-Stage RF Emitter Search and Geolocation With UAV: A Cognitive Learning-Based Method. IEEE Trans. Veh. Technol. 2023, 72, 6349–6362. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, R. Radio Map-Based 3D Path Planning for Cellular-Connected UAV. IEEE Trans. Wireless Commun. 2021, 20, 1975–1989. [Google Scholar] [CrossRef]
- Wu, D.; Zeng, Y.; Jin, S.; Zhang, R. Environment-Aware Hybrid Beamforming by Leveraging Channel Knowledge Map. IEEE Trans. Wireless Commun. 2023, 23, 4990–5005. [Google Scholar] [CrossRef]
- Ding, D.; Wu, D.; Zeng, Y.; Jin, S.; Zhang, R. Environment-Aware Beam Selection for IRS-Aided Communication with Channel Knowledge Map. In Proceedings of the 2021 IEEE Globecom Workshops (GC Wkshps), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar]
- Li, H.; Li, P.; Cheng, G.; Xu, J.; Chen, J.; Zeng, Y. Channel Knowledge Map (CKM)-Assisted Multi-UAV Wireless Network: CKM Construction and UAV Placement. J. Commun. Inf. Netw. 2023, 8, 256–270. [Google Scholar] [CrossRef]
- Li, H.; Li, P.; Xu, J.; Chen, J.; Zeng, Y. Derivative-Free Placement Optimization for Multi-UAV Wireless Networks with Channel Knowledge Map. In Proceedings of the 2022 IEEE International Conference on Communications Workshops (ICC Workshops), Seoul, Republic of Korea, 16–20 May 2022; pp. 1029–1034. [Google Scholar]
- Claussen. Efficient modelling of channel maps with correlated shadow fading in mobile radio systems. In Proceedings of the 2005 IEEE 16th International Symposium on Personal, Indoor and Mobile Radio Communications, Berlin, Germany, 11–14 September 2005; pp. 512–516. [Google Scholar]
- Dall’Anese, E.; Kim, S.-J.; Giannakis, G.B. Channel Gain Map Tracking via Distributed Kriging. IEEE Trans. Veh. Technol. 2011, 60, 1205–1211. [Google Scholar] [CrossRef]
- Mao, D.; Shao, W.; Qian, Z.; Xue, H.; Lu, X.; Wu, H. Constructing Accurate Radio Environment Maps with Kriging Interpolation in Cognitive Radio Networks. In Proceedings of the 2018 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference (CSQRWC), Xuzhou, China, 21–24 July 2018; pp. 1–3. [Google Scholar]
- Chen, J.; Yatnalli, U.; Gesbert, D. Learning Radio Maps for UAV-Aided Wireless Networks: A Segmented Regression Approach. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Zhu, Q.; Zhao, Y.; Huang, Y.; Lin, Z.; Wang, L.H.; Bai, Y.; Lan, T.; Zhou, F.; Wu, Q. An UAV-based 3D Spectrum Real-time Mapping System. In Proceedings of the IEEE INFOCOM 2022—IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), New York, NY, USA, 2–5 May 2022; pp. 1–2. [Google Scholar]
- Wang, J.; Zhu, Q.; Lin, Z.; Wu, Q.; Huang, Y.; Cai, X.; Zhong, W.; Zhao, Y. Sparse Bayesian Learning-Based 3D Radio Environment Map Construction—Sampling Optimization, Scenario-Dependent Dictionary Construction and Sparse Recovery. IEEE Trans. Cogn. Commun. Netw. 2024, 10, 80–93. [Google Scholar] [CrossRef]
- Qiu, Y.; Chen, X.; Mao, K.; Ye, X.; Zhao, Y.; Ge, Y.; Zhong, W.; Zhu, Q. Channel Knowledge Extraction and Completion Methods for 3D CKM Construction. In Proceedings of the International Conference in Communications, Signal Processing, and Systems, Singapore, 12–15 July 2023; pp. 275–283. [Google Scholar]
- Zhu, Q.; Mao, K.; Song, M.; Chen, X.; Hua, B.; Zhong, W.; Ye, X. Map-Based Channel Modeling and Generation for U2V mmWave Communication. IEEE Trans. Veh. Technol. 2022, 71, 8004–8015. [Google Scholar] [CrossRef]
- Mao, K.; Zhu, Q.; Song, M.; Li, H.; Ning, B.; Pedersen, G.F.; Fan, W. Machine-Learning-Based 3D Channel modeling for U2V mmWave communications. IEEE Internet Things J. 2022, 9, 17592–17607. [Google Scholar] [CrossRef]
- Jiang, H.; Xiong, B.; Zhang, H.; Basar, E. Hybrid Far- and Near-Field Modeling for Reconfigurable Intelligent Surface Assisted V2V Channels: A Sub-Array Partition Based Approach. IEEE Trans. Wireless Commun. (Early Access) 2023, 22, 8290–8303. [Google Scholar] [CrossRef]
- Zhang, D.; Ai, B.; Fei, D.; Chen, Z. Comparison of Different Sounding Waveforms for a Wideband Correlation Channel Sounder. In Proceedings of the 5th International Conference on Electrical Engineering and Information Technologies for Rail Transportation (EITRT), Qingdao, China, 22–24 October 2021; pp. 119–126. [Google Scholar]
- An, H.; Guan, K.; Li, W.; Zhang, J.; He, D.; Zhu, F.; Chen, L. Measurement and Ray-Tracing for UAV Air-to-Air Channel Modeling. In Proceedings of the 2022 IEEE 5th International Conference on Electronic Information and Communication Technology (ICEICT), Hefei, China, 21–23 August 2022; pp. 1–6. [Google Scholar]
- Gomez-Ponce, J.; Choi, T.; Abbasi, N.A.; Adame, A.; Alvarado, A.; Bullard, C.; Shen, R.; Daneshgaran, F.; Dhillon, H.S.; Molisch, A.F. Air-to-Ground Directional Channel Sounder With Drone and 64-antenna Dual-polarized Cylindrical Array. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]
- Khawaja, W.; Ozdemir, O.; Erden, F.; Guvenc, I.; Matolak, D.W. Ultra-Wideband Air-to-Ground Propagation Channel Characterization in an Open Area. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4533–4555. [Google Scholar] [CrossRef]
- Cui, Z.; Briso, C.; Guan, K.; Matolak, D.W.; Calvo-Ramírez, C.; Ai, B.; Zhong, Z. Low-Altitude UAV Air-Ground Propagation Channel Measurement and Analysis in a Suburban Environment at 3.9 GHz. IET Microw. Antennas Propag. 2019, 13, 1503–1508. [Google Scholar] [CrossRef]
- Santoso, T.B.; Huda, M.; Mahmudah, H. Performance Evaluation of CFAR Detector for Delay Spread Analysis of Underwater Acoustic Channel. In Proceedings of the 2015 International Electronics Symposium (IES), Surabaya, Indonesia, 29–30 September 2015; pp. 173–177. [Google Scholar]
- Ovchinnikov, V.V.; Ryabova, N.V.; Elsukov, A.A. Adaptive HF Signal Detection Algorithm CFAR and Its Verification By Means of SDR Based Digital Ionosonde with USRP Platform. In Proceedings of the 2018 Systems of Signal Synchronization, Generating and Processing in Telecommunications (SYNCHROINFO), Minsk, Belarus, 4–5 July 2018; pp. 1–5. [Google Scholar]
- Ferreira, S.; Gonsioroski, L.; Santos, A.d.; Batista, J.; Matos, L.; Castellanos, P.G.; Silva, R.M.L.; Oliveira, C.H.R. Power Delay Profile Filtering Technique Using Artificial Neural Networks. In Proceedings of the 2020 IEEE Latin-American Conference on Communications (LATINCOM), Santo Domingo, Dominican Republic, 18–20 November 2020; pp. 1–6. [Google Scholar]
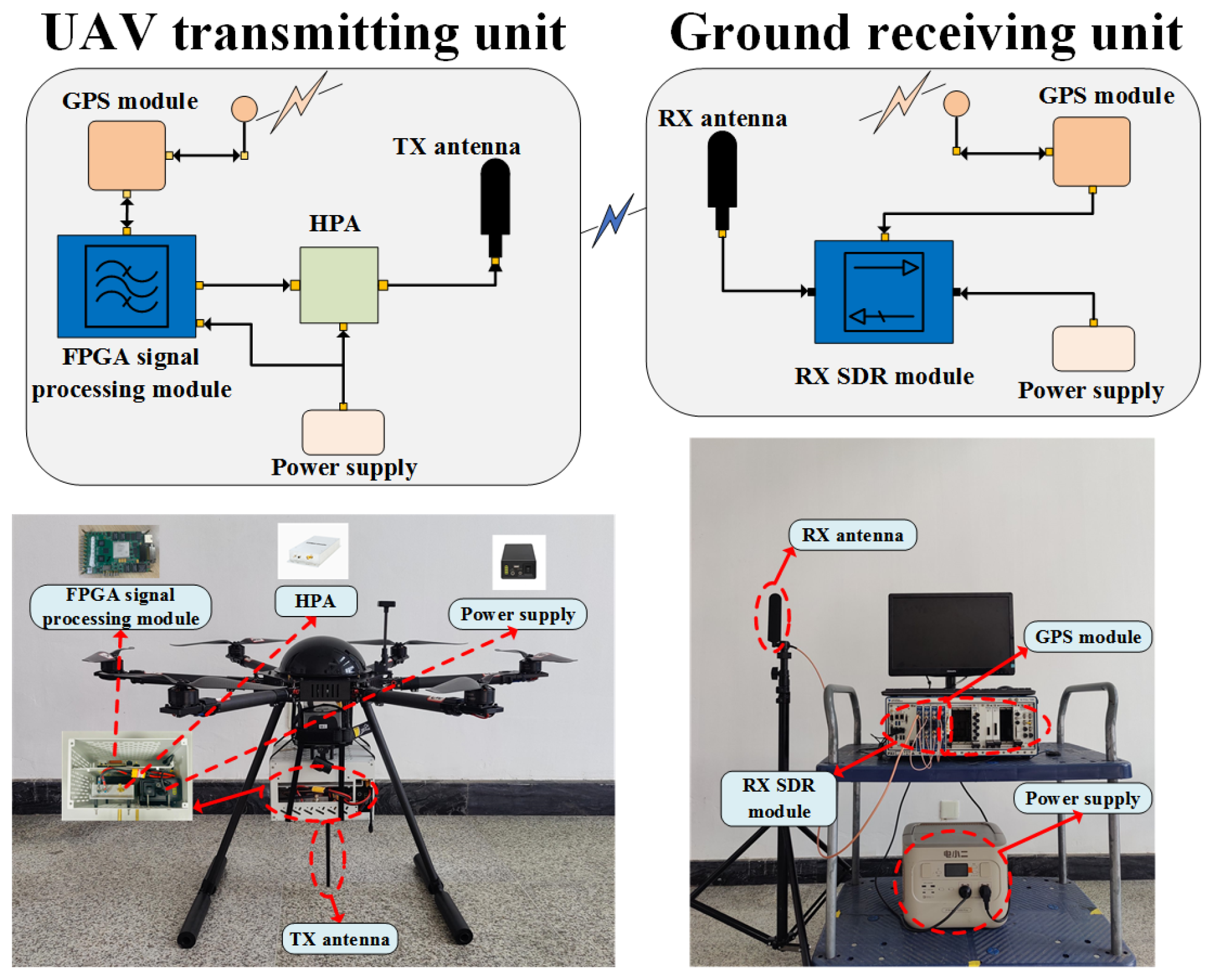


| Types | Features |
|---|---|
| TX/RX antenna | Frequency range: 3.2 GHz–3.9 GHz Gain: 3 dBi |
| FPGA signal processing module | Frequency range: 500 MHz–6 GHz Bandwidth: 61.44 MHz |
| RX SDR module | Frequency range: 1 GHz–4 GHz Bandwidth: 100 MHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, Y.; Chen, X.; Mao, K.; Ye, X.; Li, H.; Ali, F.; Huang, Y.; Zhu, Q. Channel Knowledge Map Construction Based on a UAV-Assisted Channel Measurement System. Drones 2024, 8, 191. https://doi.org/10.3390/drones8050191
Qiu Y, Chen X, Mao K, Ye X, Li H, Ali F, Huang Y, Zhu Q. Channel Knowledge Map Construction Based on a UAV-Assisted Channel Measurement System. Drones. 2024; 8(5):191. https://doi.org/10.3390/drones8050191
Chicago/Turabian StyleQiu, Yanheng, Xiaomin Chen, Kai Mao, Xuchao Ye, Hanpeng Li, Farman Ali, Yang Huang, and Qiuming Zhu. 2024. "Channel Knowledge Map Construction Based on a UAV-Assisted Channel Measurement System" Drones 8, no. 5: 191. https://doi.org/10.3390/drones8050191
APA StyleQiu, Y., Chen, X., Mao, K., Ye, X., Li, H., Ali, F., Huang, Y., & Zhu, Q. (2024). Channel Knowledge Map Construction Based on a UAV-Assisted Channel Measurement System. Drones, 8(5), 191. https://doi.org/10.3390/drones8050191







