Kinodynamic Model-Based UAV Trajectory Optimization for Wireless Communication Support of Internet of Vehicles in Smart Cities

Abstract

Unmanned aerial vehicles (UAVs) are utilized for wireless communication support of Internet of Intelligent Vehicles (IoVs). Intelligent vehicles (IVs) need vehicle-to-vehicle (V2V) and vehicle-to-everything (V2X) wireless communication for real-time perception knowledge exchange and dynamic environment modeling for safe autonomous driving and mission accomplishment. UAVs autonomously navigate through dense urban areas to provide aerial line-of-sight (LoS) communication links for IoVs. Real-time UAV trajectory design is required for minimum energy consumption and maximum channel performance. However, this is multidisciplinary research including (1) dynamic-aware kinematic (kinodynamic) planning by considering UAVs’ motion and nonholonomic constraints; (2) channel modeling and channel performance improvement in future wireless networks (i.e., beyond 5G and 6G) that are limited to beamforming to LoS links with the aid of reconfigurable intelligent surfaces (RISs); and (3) real-time obstacle-free crash avoidance 3D trajectory optimization in dense urban areas by modeling obstacles and LoS paths in convex programming. Modeling and solving this multilateral problem in real-time are computationally prohibitive unless extensive computational and overhead processing costs are imposed. To pave the path for computationally efficient yet feasible real-time trajectory optimization, this paper presents UAV kinodynamic modeling. Then, it proposes a convex trajectory optimization problem with the developed linear kinodynamic models. The optimality and smoothness of the trajectory optimization problem are improved by utilizing model predictive control and quadratic state feedback control. Simulation results are provided to validate the methodology.

1. Introduction

Civilian applications benefit from the great aerial mobility and flexibility of unmanned aerial vehicles (UAVs) in areas such as surveillance [1], tracking [2], smart agriculture [3], and wildfire detection [4]. Wireless communication networks (WCNs) and sensor networks of the Internet of Things (IoTs) are among the popular areas in which UAVs play problem-solving and other key roles [5,6]. UAVs are utilized as on-demand airborne base stations (BSs) when the terrestrial cellular network is congested in social events or when they are damaged in natural disasters [7]. Additionally, UAVs can support IoTs in remote areas where terrestrial cellular networks are not available [8]. Moreover, UAV networks can be utilized for mobile edge computing to power IoTs [9,10,11]. Path planning for maximizing the coverage area and quality of service (QoS) is a common research topic [12,13].

Nevertheless, the most recent application of UAVs for future WCNs is providing reliable, low latency, and stable aerial wireless communication services for mobile nodes [14], mobile sensor networks [15], and intelligent vehicles [16,17]. Intelligent vehicles (IVs) are designed for autonomous driving in the context of smart cities and intelligent transportation systems, which is a trending research topic [18]. For autonomous driving, IVs require capabilities such as perception (localization), path planning, and path tracking (control). For perception and localization, IVs use various inputs such as visual data, LiDAR, and radar sensors to monitor the environment and create a map for path planning [19]. Visual place recognition and localization in a map, or simultaneous localization and mapping (SLAM) are popular research topics in the robotics community [20]. For these tasks, IVs need wireless communication [21] for vehicle-to-vehicle (V2V) [22] and vehicle-to-everything (V2X) [23] communication to exchange perception knowledge; create accurate maps of dynamic environments, including other vehicles, pedestrians, etc.; and ensure safe driving and crash avoidance.

However, the increased data rate in wireless communication of smart cities [24] has raised bandwidth requirements, thus necessitating higher carrier frequencies in WCNs. This has led to the deployment of the beyond fifth-generation (B5G) and sixth-generation (6G) WCNs with millimeter-wave (mmWave) communication [25]. Beamforming through multi-input multi-output (MIMO) BSs, limited to line-of-sight (LoS) communication, is likely the main feature of future WCNs [13] for transmitting stronger signals. Furthermore, passive reconfigurable intelligent surfaces (RISs) [26] are adopted to reduce the complexity of future WCNs and enhance network sustainability by reducing energy consumption in beamforming [27]. RISs are effective in reflecting electromagnetic waves and covering blind spots in the network [26], a critical advantage in dense urban environments where LoS paths between BSs and users are obstructed by buildings and skyscrapers [28].

Utilizing UAVs is effective in providing aerial LoS wireless channels for the Internet of Intelligent Vehicles (IoVs) [29,30] for autonomous driving and accomplishing civilian and municipal services in smart cities [31]. Here, trajectory design and wireless communication control of UAVs are critical, as UAVs may act as active BSs, active relays, or passive reflectors equipped with RIS [32,33]. However, for mobile IoVs, time is an extra crucial factor that brings the UAV speed into the optimal path-planning formulation that converts the problem to path-plus-speed, i.e., trajectory optimization. Furthermore, UAV navigation for IoVs in dense urban areas and urban canyons, where buildings pose significant obstacles, requires crash avoidance trajectory optimization. Therefore, by taking UAV speed as an optimization variable as well as considering obstacle-free navigation, UAV dynamics and kinematic motion constraints should be considered in the trajectory design [14], which has been overlooked in the wireless communication community. While the concept of no-fly zones has been considered in the trajectory design in a few works [34], it has not been addressed in the context of obstacle-free navigations with motion constraints.

Although obstacle-free path planning has been studied in the robotics community, the channel performance and specific trajectory optimization required for WCNs still need more consideration. Notably, optimality and autonomy are two key concepts. The optimality of the UAV trajectory refers to an energy-efficient minimum path with optimal speed planning, which indicates that time is an important factor due to the movement of IVs that are under aerial LoS wireless services. Also, the designed trajectory should provide a path that maximizes channel performance and QoS. This makes a significant change compared with robotics literature in which the starting and goal points are known with no stress on the time. Also, the extra objectives make the conventional path planning more complicated with higher time complexity of nonconvex constraints. On the other hand, from the autonomous navigation perspective, real-time trajectory design is crucial for autonomous navigation, in which the UAV does not depend on external resources, such as memories, processors, and controllers for navigation. Therefore, regarding the size and cost of the overhead package, the onboard controller should be able to implement the optimization independently. This requires a linearized kinematic model with convexified objectives and constraints to develop a computationally tractable trajectory optimization problem.

1.1. Importance of the Study

In general, UAV path planning methods fall into three categories, as follows:

(1)

Short distances with high agility (e.g., in cluttered indoor areas [35]), for which dynamics-aware kinematic (kinodynamic) trajectory is required. This ensures the dynamic feasibility of motions in relation to the dynamics of quadrotors [36]. Normally, control signals are generated by the trajectory planning algorithm [37], in which the dynamics and kinematics of the UAV are taken into account.

(2)

Medium distance with a medium level of agility (e.g., urban areas), in which kinematic trajectory planning is considered by focusing on motion and nonholonomic (i.e., rate of heading change) constraints [38].

(3)

Long-distance sparse environment with no stress on agility and obstacles [39], in which only an optimal energy-efficient path is considered at a constant speed [40], which is almost the case in the wireless communication community [41,42]. The approach taken for path planning determines the 2D coordinates of the UAV path in a global (Earth) reference frame (with a fixed altitude) where an extra controller is required to follow the trajectory.

The UAV navigation for IoVs falls into the first or second class depending on the density of the environment where a kinodynamic smooth trajectory is optimally determined. Although the rotational dynamics of the UAV can be ignored, the trajectory should be smooth to be dynamically feasible in practice. Furthermore, the navigation goals and safety measures (i.e., obstacle-aware collision-free flight) must be considered. Therefore, motion and nonholonomic constraints are critical for UAV navigation, which increases the time complexity of the trajectory design problem. In this sense, the time complexity for satisfying problem constraints is prohibitively high for real-time trajectory optimization. This issue has been considered in only a few works in the wireless communication community. For instance, in addition to kinodynamic constraints in [14], the conversion efficiency of electric motors associated with quadrotors was considered in [43]. However, a generic approach is required with a linear kinodynamic model and constraints for computationally efficient and real-time trajectory optimization for autonomous navigation applications.

The main difference between UAV trajectory design with path planning techniques in the robotics community is as follows. UAVs do not have a specific goal point, and the optimal trajectory varies over time depending on the IoVs’ trajectories. By contrast, in most robotic navigation or autonomous vehicles, a minimum path is developed to reach a goal point. For instance, in sampling-based methods such as rapidly exploring random trees (RRT) [31,44] and A* search [45], at each sampling, a part of the path is set on the basis of the distance between the current state and the goal considering motion constraints. However, in UAV navigation, all the possible trajectories should be explored to find the global optimal trajectory. For example, hovering without 2D horizontal movement can be a candidate for optimal trajectory.

To facilitate navigation design, it is performed for a given receding time interval (e.g., 30 s), which in turn is discretized into several samples (e.g., with a sampling time of a few seconds). So, by optimizing the UAV trajectory at the initial time samples, the planner loses a degree of freedom for the final time samples to reach positions where admissible QoS can be achieved. Adopting the model predictive control (MPC) technique with a finite receding horizon [17] can be a solution, but it imposes prohibitive computational costs and preferably requires a linear kinematic model. Moreover, since the endpoint of the trajectory is uncertain (depending on the IoV trajectories and the shape of the environment), dynamic programming is also inefficient. Furthermore, the validity of LoS links should be checked for each random sample. Therefore, the time complexity of the UAV trajectory design is significantly high and prohibitive for sampling techniques.

1.2. Summary of the Methodology

In this paper, we discuss UAV motion modeling by developing dynamic-aware kinematic equations for path-plus-speed (trajectory) optimization in the context of future wireless networks. The methodology of the paper is summarized as follows:

(1)

The paper studies the principles of UAV (notably quadrotors) motion and dynamics and develops two generic linear kinodynamic motion models ($\mathcal{K}\mathcal{M}1$ and $\mathcal{K}\mathcal{M}2$) in the state space domain that can be used for trajectory optimization or in a sensor fusion algorithm like the Kalman filter for position estimation.

(2)

A systematic UAV trajectory optimization problem is presented ($\mathcal{P}1$) by utilizing the proposed kinodynamic models.

(3)

The optimality issue of the optimization problem ($\mathcal{P}1$) is discussed. The optimization problem is modified to be used in the finite receding horizon MPC optimization ($\mathcal{P}2$) to achieve a more optimal solution. Required formulations and appropriate matrix dimensions are presented.

(4)

A trajectory smoothing technique is proposed ($\mathcal{P}3$) to ensure that the discrete-time trajectory becomes dynamically feasible in continuous time.

(5)

Although communication channel modeling is not considered in this paper, the methodology is valid. Because it is the case in most of the relevant works that use sequential convex programming, in which the trajectory optimization and channel performance objectives are solved consecutively by relaxing other objectives and constraints [16].

(6)

Simulation results are provided to evaluate the crash-avoidance performance and the running time of the proposed trajectory optimization and are compared with sampling-based techniques.

1.3. Contributions of the Paper

The contributions of this paper are outlined as follows:

(1)

A closed-form kinodynamic-aware UAV trajectory optimization is proposed for IoVs in future wireless communication networks in $\mathcal{P}1$ and $\mathcal{P}2$.

(2)

A convex relaxation technique is proposed (through Lemma 1) for the nonconvex constraint associated with heading change (highlighted in Remark 2) to make the optimization problem computationally feasible for real-time applications.

(3)

The proposed trajectory smoothing technique includes quadratic objective functions utilizing elasticity and the smoothing concepts in $\mathcal{P}3$.

(4)

The smoothing technique is based on state feedback control in which the state feedback gain matrix is optimized to make the trajectory smooth, which is modeled by the linear state space kinematic motion model. The significant advantage is that the proposed smoothing technique can be used with generated motion primitives by the trajectory optimization and without the requirement of a trajectory tracking controller, thanks to the developed kinematic model and the proposed optimization technique.

2. UAV Motion Model

2.1. Quadrotors

A quadrotor is a vertical take-off and landing (VTOL) vehicle with four propellers. Compared with fixed-wing UAVs, which possess some limitations in hovering [46], quadrotors are more popular UAVs for wireless communication of IoVs in dense urban areas thanks to their agility, hovering capability, and maneuverability. Therefore, we briefly studied and reviewed quadrotor motion principles for developing kinodynamic models for path planning and trajectory optimization.

2.2. Quadrotor Motion Principle

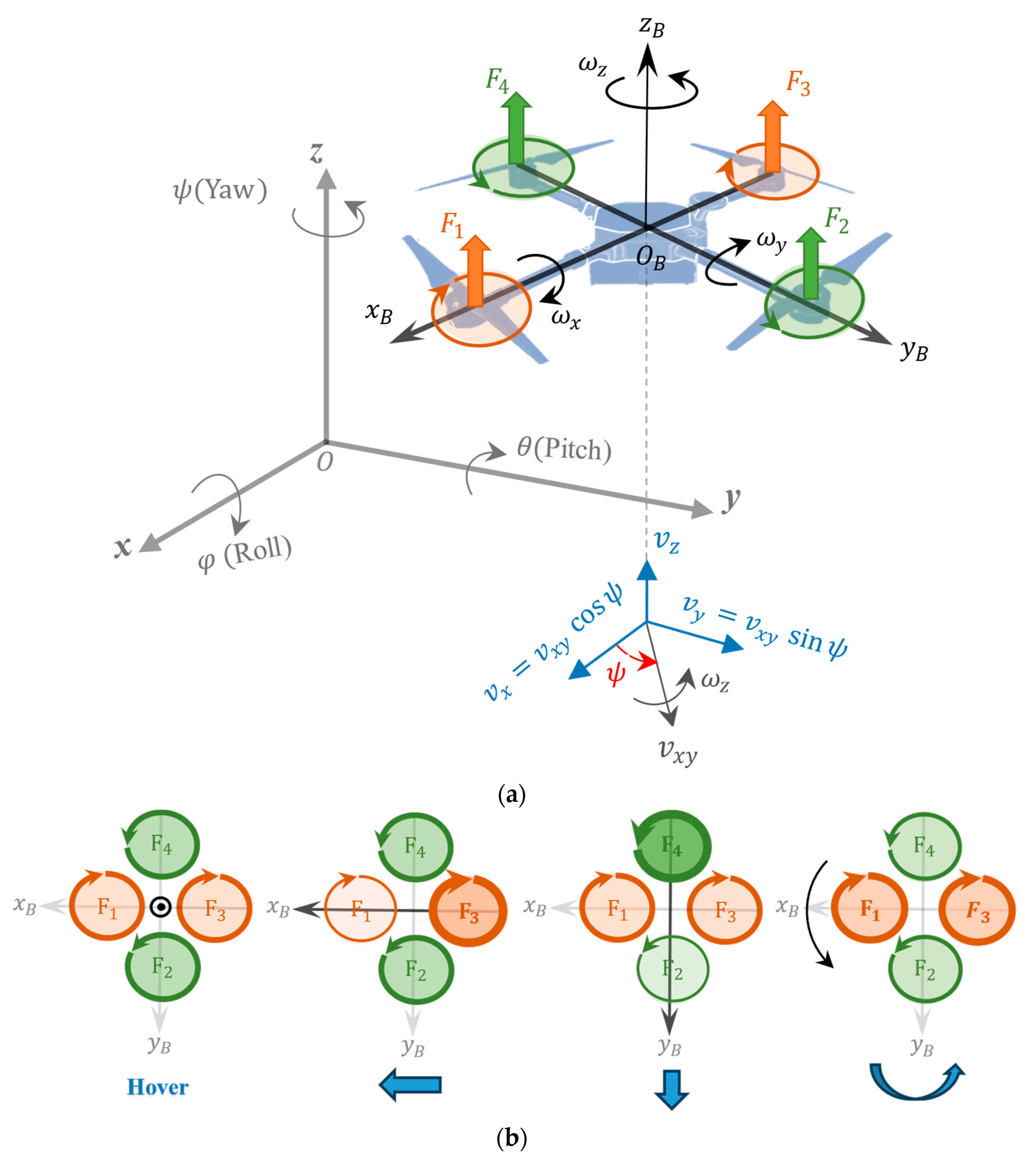
The motion principles of the quadrotor are illustrated in Figure 1, in which opposite propellers (1, 3) and (2, 4) are paired and rotate in opposite clockwise and counterclockwise directions to cancel out rotational torques. By controlling the speeds of rotors, motions in various directions can be achieved [47], as shown in Figure 1b, in which (from left to right) (1) increasing/decreasing four propellers with the same speed results in a vertical motion; (2) the difference in the speeds of the propeller pair (1, 3) results in changes in the pitch angle (around the y-axis) and thus movement along the x-axis; (3) the difference in the speeds of the propeller pair (2, 4) results in changes in the roll angle (around the x-axis) and thus movement along the y-axis; and (4) the difference in the speeds of propeller pair (1, 3) with pair (2, 4) results in counter-torque between pairs and thus changes in the yaw angle (around the z-axis), leading to a rotation around the z-axis.

2.3. Quadrotor Kinodynamic Model

The quadrotor’s linear/angular transition, speed, and acceleration are correlated as follows:

$$\underset{acceleration}{\underbrace{\left[\begin{array}{c}a\left\{\begin{array}{c}{a}_x\\ a_y\\ a_z\end{array}\right.\\ \varphi \left\{\begin{array}{c}{a}_{\phi }\\ a_{\theta }\\ a_{\psi }\end{array}\right.\end{array}\right]}}={\displaystyle \frac{d}{dt}}\left(\underset{\begin{array}{c}linear and angular\\ velocities\end{array}}{\underbrace{\left[\begin{array}{c}v\left\{\begin{array}{c}{v}_x\\ v_y\\ v_z\end{array}\right.\\ \omega \left\{\begin{array}{c}{\omega }_x\\ {\omega }_y\\ {\omega }_z\end{array}\right.\end{array}\right]}}\right)={\displaystyle \frac{d^2}{d{t}^2}}\left(\underset{\begin{array}{c}linear and angular\\ transitions\end{array}}{\underbrace{\left[\begin{array}{c}\xi \left\{\begin{array}{c}x\\ y\\ z\end{array}\right.\\ \mathcal{E}\left\{\begin{array}{c}\phi \\ \theta \\ \psi \end{array}\right.\end{array}\right]}}\right)$$

(1)

which should be determined for trajectory optimization based on inputs to the UAV navigation system that adjusts the propellers’ speeds.

Propeller $i$, which rotates with angular velocity ${\varpi }_i$, produces vertical force $F_i$ and horizontal moment $M_i$, both proportional to the square of angular velocity [35]:

$$F_i=k_F{\varpi }_i^2;M_i=k_M{\varpi }_i^2$$

(2)

where $k_F$ and $k_M$ are positive parameters based on the quadrotor design [48].

Therefore, based on Figure 1b and Equation (2), the input $u\in {\mathbb{R}}^4$ to the UAV motion model is obtained as:

$$u=\left[\begin{array}{c}{u}_1\\ u_2\\ \begin{array}{c}{u}_3\\ u_4\end{array}\end{array}\right]=\left[\begin{array}{ccc}{k}_F& k_F& \begin{array}{cc}{k}_F& k_F\end{array}\\ 0& -L{k}_F& \begin{array}{cc}0& L{k}_F\end{array}\\ \begin{array}{c}L{k}_F\\ k_M\end{array}& \begin{array}{c}0\\ -k_M\end{array}& \begin{array}{cc}\begin{array}{c}-L{k}_F\\ k_M\end{array}& \begin{array}{c}0\\ -k_M\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}{\varpi }_1^2\\ {\varpi }_2^2\\ \begin{array}{c}{\varpi }_3^2\\ {\varpi }_4^2\end{array}\end{array}\right]$$

(3)

where $L$ denotes the distance from the axis of rotation of the rotors to the center of the quadrotor; $u_1$ is the total force produced by propellers; $u_{\mathrm{2,3}}$ are input forces that result in angular (rotational) velocity (${\omega }_x$ and ${\omega }_y$) around the vehicle body along the x- and y-axes, respectively, which result in movement in 2D $(x-y)$ space in the Earth reference frame; and $u_4$ denotes the counter-toque, which results in angular velocity ${\omega }_z$ around the vehicle body along the z-axis, which results in heading change in 2D $(x-y)$ space in the Earth reference frame.

Remark 1. 

The angular velocity ${\varpi }_i$ of rotor i for $i=1~4$ can be obtained from $u_{1~4}$, given in Equation (3). Therefore, if $u_{1~4}$ are available from the trajectory optimization technique; rotor speeds and thus desired UAV motion can be obtained without the requirement of a trajectory tracking controller.

The dynamics of the rotational rates around the vehicle body (angular velocities) are obtained as:

$$J\dot{\omega }=-\omega \times J\omega +{\left[\begin{array}{ccc}{u}_2& u_3& u_4\end{array}\right]}^{\top }$$

(4)

where superscript $\mathrm{\top }$ denotes matrix transpose; $\omega ={\left[\begin{array}{ccc}{\omega }_x& {\omega }_y& {\omega }_z\end{array}\right]}^{\top }$; $J\in {\mathbb{R}}^{3\times 3}$ is the inertia matrix with respect to the center of mass along the $x_B-y_B-z_B$ axes; and $\times$ denotes the cross-product operator. The vehicle’s transition dynamic model ($\mathcal{D}\mathcal{M})$ in the Earth frame is given as:

$$\mathcal{D}\mathcal{M}:=\left\{\begin{array}{c} \dot{\xi }=v \\ \begin{array}{c}\mathcal{m}\dot{v}=-\mathcal{m}\mathrm{g}\overrightarrow{\mathrm{z}}+\mathcal{R}\overrightarrow{\mathrm{z}}{u}_1\\ \dot{\mathcal{R}}=\mathcal{R}\widehat{\omega } \end{array}\end{array}\right.$$

(5)

where $\xi ={\left[\begin{array}{ccc}x& y& z\end{array}\right]}^{\top }\in {\mathbb{R}}^3$ denotes the UAV 3D transition in the Earth reference frame; $v={\left[\begin{array}{ccc}{v}_x& v_y& v_z\end{array}\right]}^{\top }\in {\mathbb{R}}^3$ denotes the UAV linear velocity in the Earth reference frame; $\overrightarrow{z}={\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^{\top }$ is the unit vector of the z-axis; $\mathcal{m}$ [$\mathrm{k}\mathrm{g}$] is the vehicle mass and g [${\displaystyle \frac{N{m}^2}{{kg}^2}}$] is the gravitational constant; $\widehat{\omega }$ is the skew-symmetric matrix such that:

$$\widehat{\omega }v=\omega \times v, \mathrm{and} {\widehat{\omega }}^{\top }=-\widehat{\omega }.$$

$$\widehat{\omega }=\left[\begin{array}{ccc}0& -{\omega }_z& {\omega }_y\\ {\omega }_z& 0& -{\omega }_x\\ {-\omega }_y& {\omega }_x& 0\end{array}\right],$$

(6)

and $\mathcal{R}$ denotes the rotation matrix based on $\mathcal{E}={\left[\begin{array}{ccc}\phi & \theta & \psi \end{array}\right]}^{\top }\in {\mathbb{R}}^3$ denoting Euler’s roll ($\phi$), pitch ($\theta$), and yaw ($\psi$) angles with respect to the $x-y-z$ axes, respectively, as:

$$\mathcal{R}=\left[\begin{array}{ccc}\mathcal{c}\theta \mathcal{c}\psi & \mathrm{s}\phi \mathrm{s}\theta \mathcal{c}\psi -\mathcal{c}\phi \mathrm{s}\psi & \mathrm{s}\phi \mathrm{s}\psi +\mathcal{c}\phi \mathrm{s}\theta \mathcal{c}\psi \\ \mathcal{c}\theta \mathrm{s}\psi & \mathrm{s}\phi \mathrm{s}\theta \mathrm{s}\psi +\mathcal{c}\phi \mathcal{c}\psi & \mathcal{c}\phi \mathrm{s}\theta \mathrm{s}\psi -\mathrm{s}\phi \mathcal{c}\psi \\ -\mathrm{s}\theta & \mathrm{s}\phi \mathcal{c}\theta & \mathcal{c}\phi \mathcal{c}\theta \end{array}\right];$$

(7)

where $\mathcal{c}$ and $\mathrm{s}$ denote shorthand forms of the cosine and sine functions, respectively. The state space model of the quadrotor can be developed by plugging $\widehat{\omega }$ and $\mathcal{R}$ into $\mathcal{D}\mathcal{M}$, [47,49]. Various dynamics-aware UAV trajectory optimization algorithms have been proposed in the literature [35,37,50]. However, as mentioned earlier, it is not computationally efficient to use complicated models for trajectory design when the sampling time is larger than the UAV motion dynamics. Therefore, it is preferable to use linear kinodynamic models.

3. UAV Kinodynamic Models

We introduce two linear kinodynamic models, $\mathcal{K}\mathcal{M}1$ and $\mathcal{K}\mathcal{M}2$, which can be used in the trajectory optimization problem based on the UAV application and density of the WCN.

3.1. Kinodynamic Model 1

The first kinodynamic motion model ($\mathcal{K}\mathcal{M}1)$ is derived from the popular nonlinear but simple motion model that is used for fixed-wing UAVs [51,52], as follows:

$$\mathcal{K}\mathcal{M}1≔\left\{\begin{array}{l}\hspace{1em}\dot{x}\left(t\right)=v_{xy}\left(t\right)\cos \psi \left(t\right)\\ \hspace{1em}\dot{y}\left(t\right)=v_{xy}\left(t\right)\sin \psi \left(t\right)\\ \mathcal{m}\dot{z}\left(t\right)=u_z\left(t\right)-\mathcal{m}\mathrm{g}\\ \hspace{1em}\dot{\psi }\left(t\right)={\omega }_z\left(t\right)\end{array}\right.$$

(8)

where the notation of parameters is the same as the earlier formulation in the paper; to recap, $v_{xy}$ and $u_z$ denote horizontal and vertical linear input speeds, and ${\omega }_z$ is the angular velocity that specifies the UAV heading $\psi$ in 2D horizontal space. Through the following analogy, $\mathcal{K}\mathcal{M}1$ can be used for quadrotors:

$$u :\left\{ \begin{array}{l}{u}_1=u_z\\ u_2=v_{xy}\sin \psi =v_y \\ u_3=v_{xy}\cos \psi =v_x\\ u_4={\omega }_z\end{array}\right.$$

(9)

with $\left\{ \begin{array}{c}{v}_{xy}={‖u_2,u_3‖}_2 \\ \psi ={\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(u_2/u_3\right) \end{array}\right.$ where the operator ${‖ .‖}_2$ denotes the Euclidean (${\mathcal{L}}_2$) norm. The transitional and angular accelerations as well as the dynamics of rotational velocities are ignored, which is reasonable because of the use of high bandwidth controllers with very fast responses (considering the sampling time). However, this model is still nonlinear, making computationally efficient real-time trajectory optimization challenging, particularly for long-receding horizon MPC optimization [17]. The linearized form of $\mathcal{K}\mathcal{M}1$ in discrete time with sampling time $h$ is presented as:

$$\mathcal{D}\mathcal{K}\mathcal{M}1:=\left\{ \underset{\dot{X_1[k+1]}}{\underbrace{\xi [k+1]}}=\underset{G_1}{\underbrace{\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]}}\underset{X_1\left[k\right[}{\underbrace{\xi \left[k\right]}}+h\underset{H_1}{\underbrace{\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1/\mathcal{m}\end{array}\right]}}\left(\underset{\mathfrak{U}\left[k\right]}{\underbrace{\left[\begin{array}{c}{u}_3\left[k\right]\\ u_2\left[k\right]\\ u_1\left[k\right]\end{array}\right]-\left[\begin{array}{c}0\\ 0\\ \mathcal{m}\mathrm{g}\end{array}\right]}}\right)\right.$$

(10)

where $\xi ={\left[\begin{array}{ccc}x& y& z\end{array}\right]}^{\top }\in {\mathbb{R}}^3$ denotes the 3D coordinates (position) of the UAV; $X_1\in {\mathbb{R}}^3$ denotes state vector (3D coordinates), $G_1\in {\mathbb{R}}^{3\times 3}$ denotes discrete state matrix, and $H_1\in {\mathbb{R}}^{3\times 3}$ denotes discrete input matrix.

Remark 2. 

$u_4={\omega }_z$, associated with the UAV lateral movement (i.e., turning around the z-axis), is eliminated in the input vector, as it does not impact the linear motion [53] and the quadrotor’s heading change is controlled by controlling horizontal speeds in x and y directions ($v_x and v_y$). Nevertheless, we add a rate of heading change (i.e., nonholonomic) constraint to the trajectory optimization problem, with appropriate convexification presented in Lemma 1.

The rate of heading change constraint is modeled as:

$$\overrightarrow{\psi }\left[k\right]=\left({\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left({\displaystyle \raisebox{1ex}{$v_y\left[k\right]$}\!\left/ \!\raisebox{-1ex}{$v_x\left[k\right]$}\right.}\right)-{\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left({\displaystyle \raisebox{1ex}{$v_y[k-1]$}\!\left/ \!\raisebox{-1ex}{$v_x[k-1]$}\right.}\right)\right)<{\displaystyle \raisebox{1ex}{$\left(h\ast {\psi }_{max}\right)$}\!\left/ \!\raisebox{-1ex}{$\left(1+\gamma v_{xy}\right)$}\right.}$$

(11)

where ${\psi }_{max}$ denotes the maximum heading change that can be achieved in rad/s, and $\gamma$ is a hyperparameter to limit heading change based on horizontal speed. For example, if the horizontal speed is zero (i.e., the quadrotor is hovering) the maximum heading change can be achieved, but by increasing the horizontal speed, its heading change is limited for a stable maneuver. However, embedding the rate of the heading change constraint to model nonholonomic limitations makes the optimization problem non-convex.

3.2. Kinodynamic Model 2

The rotational rates of the UAV around its rigid body and its time constant on horizontal movement in 2D space can be ignored regarding the sampling time of the trajectory design [50,53]. Therefore, with the notation of (1), $\mathcal{D}\mathcal{M}$ in (5) can be written in the following forms in the state space domain [36]:

$$\mathcal{K}\mathcal{M}{2}_1:=\left\{ \underset{{\dot{X}}_2}{\underbrace{\left[\begin{array}{c}\dot{\xi }\\ \dot{v}\end{array}\right]}}=\underset{A_2}{\underbrace{\left[\begin{array}{cc}{0}_3& I_3\\ 0_3& 0_3\end{array}\right]}}\underset{X_2}{\underbrace{\left[\begin{array}{c}\xi \\ v\end{array}\right]}}+\underset{B_2}{\underbrace{\left[\begin{array}{c}{0}_3\\ H_1\end{array}\right]}}\left(\underset{\mathfrak{U}}{\underbrace{\left[\begin{array}{c}{u}_3\\ u_2\\ u_1\end{array}\right]-\left[\begin{array}{c}0\\ 0\\ \mathcal{m}\mathrm{g}\end{array}\right]}}\right)\right.$$

(12)

$$\mathcal{K}\mathcal{M}{2}_2:=\left\{ \underset{{\dot{X}}_3}{\underbrace{\left[\begin{array}{c}\dot{\xi }\\ \dot{v}\\ \dot{a}\end{array}\right]}}=\underset{A_3}{\underbrace{\left[\begin{array}{ccc}{0}_3& I_3& 0_3\\ 0_3& 0_3& I_3\\ 0_3& 0_3& 0_3\end{array}\right]}}\underset{X_3}{\underbrace{\left[\begin{array}{c}\xi \\ v\\ a\end{array}\right]}}+\underset{B_3}{\underbrace{\left[\begin{array}{c}{0}_3\\ 0_3\\ H_1\end{array}\right]}}\left(\underset{\mathfrak{U}}{\underbrace{\left[\begin{array}{c}{u}_3\\ u_2\\ u_1\end{array}\right]-\left[\begin{array}{c}0\\ 0\\ \mathcal{m}\mathrm{g}\end{array}\right]}}\right)\right.$$

(13)

where $0_3\in {\mathbb{R}}^{3\times 3}$ and $I_3\in {\mathbb{R}}^{3\times 3}$ are 3-by-3 zero and identity matrices, respectively; $X_2\in {\mathbb{R}}^6$ and $X_3\in {\mathbb{R}}^9$ denote state vectors; $A_2\in {\mathbb{R}}^{6\times 6}$ ($A_3\in {\mathbb{R}}^{9\times 9}$) and $B_2\in {\mathbb{R}}^{6\times 3}$ ($B_3\in {\mathbb{R}}^{9\times 3}$) denote state and input matrices, respectively; and $\mathfrak{U}\in {\mathbb{R}}^3$ is the control input that determines motion primitives (jerks) to the UAV navigation system. Compared with $\mathcal{K}\mathcal{M}{2}_1,$ $\mathcal{K}\mathcal{M}{2}_2$ is better suited for denser, obstructed environments with obstacles (e.g., cluttered indoor environments) where more agility, i.e., more frequent changes in the velocity, is required, and thus acceleration is crucial and should be bounded. The solution to the state space model $\mathcal{K}\mathcal{M}2$ including first-order differential equations that specify states and thus system dynamics is obtained as:

$$X\left(t\right)=X\left(0\right)e^{At}+{\int }_0^t{e}^{A\left(t-\tau \right)}B\mathfrak{U}\left(\tau \right)d\tau$$

(14)

where $X\left(0\right)$ denotes the initial state. Since state matrix A is singular, the discrete form of the kinodynamic model can be obtained utilizing the Tayor series expansion, with sampling time $h$ as follows:

$$\mathcal{D}\mathcal{K}\mathcal{M}{2}_1≔\left\{ \underset{X_2[k+1]}{\underbrace{\left[\begin{array}{c}\xi [k+1]\\ v[k+1]\end{array}\right]}}=\underset{G_2\left(h\right)}{\underbrace{\left[\begin{array}{cc}{\mathrm{I}}_3& I_{3}h\\ 0_3& {\mathrm{I}}_3\end{array}\right]}}\underset{X_2\left[k\right]}{\underbrace{\left[\begin{array}{c}\xi \left[k\right]\\ v\left[k\right]\end{array}\right]}}+\underset{H_2\left(h\right)}{\underbrace{\left[\begin{array}{c}{\mathrm{I}}_3{h}^2/2\\ {hH}_1\end{array}\right]}}\mathfrak{U}[k]\right.$$

(15)

$$\mathcal{D}\mathcal{K}\mathcal{M}{2}_2≔\left\{ \underset{X_3[k+1]}{\underbrace{\left[\begin{array}{c}\xi [k+1]\\ v[k+1]\\ a[k+1]\end{array}\right]}}=\underset{G_3\left(h\right)}{\underbrace{\left[\begin{array}{ccc}{\mathrm{I}}_3& {\mathrm{I}}_{3}h& 0.5{\mathrm{I}}_3{h}^2\\ 0& {\mathrm{I}}_3& {\mathrm{I}}_{3}h\\ 0& 0& {\mathrm{I}}_3\end{array}\right]}}\underset{X_3\left[k\right]}{\underbrace{\left[\begin{array}{c}\xi \left[k\right]\\ v\left[k\right]\\ a\left[k\right]\end{array}\right]}}+\underset{H_3\left(h\right)}{\underbrace{\left[\begin{array}{c}{\mathrm{I}}_3{h}^3/6\\ {\mathrm{I}}_3{h}^2/2\\ {hH}_1\end{array}\right]}}\mathfrak{U}[k]\right.$$

(16)

where $G_2\left(h\right)\in {\mathbb{R}}^{6\times 6}$ ($G_3\left(h\right)\in {\mathbb{R}}^{9\times 9}$) and $H_2\left(h\right)\in {\mathbb{R}}^{6\times 3}$ ($H_3\left(h\right)\in {\mathbb{R}}^{9\times 3}$) denote the discretized state and input matrices, respectively. Similar to $\mathcal{D}\mathcal{K}\mathcal{M}$, the UAV heading is obtained on the basis of linear horizontal speed along the $x$-axis and $y$-axis as $\psi ={\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(v_y/v_x\right)$.

4. Trajectory Optimization Problem

A UAV may work as an airborne BS (UAV-BS) to provide aerial wireless communication for intelligent vehicles, or it may be equipped with RIS (RISeUAV [38]) for the reflection of the communication signals in the sky toward intelligent vehicles (see Figure 2). This scenario is practical in future 6G wireless networks (that are limited to LoS communication links) in smart cities where intelligent vehicles require V2V and V2X wireless communication and supportive stable wireless communication links for autonomous driving and autonomous mission accomplishment (e.g., in a natural disaster or traffic congestions). Therefore, the trajectory design is needed for the UAV to navigate through a path that is energy-efficient (for navigation endurance) and provides maximum support for the wireless communication of IoVs. Furthermore, the kinodynamic motion and crash avoidance constraints must be satisfied, leading to the trajectory design problem. We introduce the following trajectory optimization problem ($\mathcal{P}1$), for which both linear kinodynamic motion models $\mathcal{D}\mathcal{K}\mathcal{M}1$ and $\mathcal{D}\mathcal{K}\mathcal{M}2$ can be used. Also, $\mathcal{P}1$ is formulated to be computationally feasible to be solved in real time for the autonomous navigation of the UAV.

The navigation time interval of interest $\mathcal{T}$ is discretized with sampling time $h$ into $K=⌈\mathcal{T}/h⌉$ sampling slots in the set $\mathcal{K}=\left\{1, 2,\dots ,K\right\}$, where $⌈ .⌉$ denotes the ceiling operator. The optimization problem $\mathcal{P}1$ is solved for every sampling time consecutively. For example, by solving $\mathcal{P}1$ for step time $k$, the input at step time $k$ ($\mathfrak{U}\left[k\right]$) is determined. Then, using $\mathfrak{U}\left[k\right]$, the UAV’s waypoint at $k+1$ is calculated on the basis of the motion model and is used for the next time step. Velocity and acceleration can be calculated and bounded by constraints if $\mathcal{D}\mathcal{K}\mathcal{M}$2 is used.

$\mathcal{P}1:$
$\mathrm{O}\mathrm{F}1.$	$\underset{\mathfrak{U}\left[k\right]}{\mathrm{m}\mathrm{i}\mathrm{n}} \underset{{\mathrm{O}\mathrm{F}1}_1}{\underbrace{{\mathcal{w}}_{1_1}{‖\mathfrak{U}\left[k\right]‖}_2^2}}+{\mathcal{w}}_{1_2}\underset{{\mathrm{O}\mathrm{F}1}_2}{\underbrace{\sum _{n=1}^N{‖\xi \left[k\right]-p_n\left[k\right]‖}_2^2}}$
s. t.
${\mathrm{C}1}_1.$	$X\left[k+1\right]=GX\left[k\right]+H\mathfrak{U}\left[k\right]$;
${\mathrm{C}1}_2.$	$\xi \left[k\right]\cap {\mathbb{P}}_{\mathrm{O}\mathrm{b}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{c}\mathrm{l}\mathrm{e}}=\varnothing$;
${\mathrm{C}1}_3.$	$Z_{min}\le z\left[k\right]\le Z_{max}$;
${\mathrm{C}1}_4.$	${{ v}_{xy}\left[k\right]=‖v_x\left[k\right],v_y\left[k\right]‖}_2\le V_{max}, { u}_z\left[k\right]\le \left(U_{max}-{\gamma }_1{v}_{xy}\left[k\right]\right);$
${\mathrm{C}1}_5.$	${ ‖a‖}_2\le {\mathcal{A}}_{max};$
${\mathrm{C}1}_6.$	$\left[\begin{array}{c}{v}_x\left[k\right]\\ v_y\left[k\right]\end{array}\right]-\left(1+{\displaystyle \frac{{\gamma }_2}{V_{max}}}\right)\left[\begin{array}{c}{v}_x\left[k-1\right]\\ v_y\left[k-1\right]\end{array}\right]<0$;
${\mathrm{C}1}_7.$	$\left[\begin{array}{c}{v}_x\left[k\right]\\ v_y\left[k\right]\end{array}\right]-\left(1-{\displaystyle \frac{{\gamma }_2}{V_{max}}}\right)\left[\begin{array}{c}{v}_x\left[k-1\right]\\ v_y\left[k-1\right]\end{array}\right]>0$;

where ${\mathcal{w}}_{1_1}$ and ${\mathcal{w}}_{1_2}$ are weighting coefficients; $\mathfrak{U}={\left[\begin{array}{ccc}{u}_3& u_2& u_1\end{array}\right]}^{\top }={\left[\begin{array}{ccc}{v}_x& v_y& u_z\end{array}\right]}^{\top }\in {\mathbb{R}}^3$ denotes control input effort; $p_n\left[k\right]\in {\mathbb{R}}^3$ denotes the 3D coordinates of the $n^{th}$ vehicle at sample time $k$; $N$ denotes the number of vehicles in the IoVs; ${\mathbb{P}}_{\mathrm{O}\mathrm{b}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{c}\mathrm{l}\mathrm{e}}$ denotes the set of coordinates associated with obstacles; $\varnothing$ indicates an empty set; $Z_{min}$ and $Z_{max}$ denote minimum and maximum permitted altitudes; $V_{max}$ and $U_{max}$ denote maximum linear horizontal and vertical velocities; ${\mathcal{A}}_{max}$ denotes maximum reachable acceleration; and ${\gamma }_1$ and ${\gamma }_2$ are hyperparameters to control the vertical speed based on the horizontal speed and the rate of change of the horizontal speed, respectively.

Objective function ${\mathrm{O}\mathrm{F}1}_1$ minimizes the input effort as an indicator of minimizing energy consumption by propellers, and ${\mathrm{O}\mathrm{F}1}_2$ minimizes the average Euclidean distances between the UAV and vehicles in the IoVs. Constraint ${\mathrm{C}1}_1$ models the linearized kinematic motion model (where $\mathcal{D}\mathcal{K}\mathcal{M}1$ and $\mathcal{D}\mathcal{K}\mathcal{M}2$ can be used) to be plugged into ${\mathrm{O}\mathrm{F}1}_2$ and for calculating motion variables used in other constraints; ${\mathrm{C}1}_2$ satisfies obstacle-free trajectory planning for crash avoidance navigation; ${\mathrm{C}1}_{\mathrm{3,4},5}$impose altitude, speed, and acceleration constraints (note that ${\mathrm{C}1}_5$ is valid if $\mathcal{D}\mathcal{K}\mathcal{M}2$ is used to calculate accelerations); and ${\mathrm{C}1}_{\mathrm{6,7}}$linearize nonholonomic (rate of heading change) constraints as per the convex relaxation technique proposed in Lemma 1.

Lemma 1. 

The rate of heading change of the UAV in the 2D horizontal space can be bounded by applying the following constraints, ${CL1}_{\mathrm{1,2}}$, that limit the lower bounds and upper bounds of the $v_x$ and $v_y$ terms of the horizontal linear speed.

$$\begin{gathered} {CL1}_1≔\left\{\begin{array}{c}{v}_x\left[k\right]-v_x\left[k-1\right]<{\displaystyle \frac{\gamma v_x\left[k-1\right]}{V_{max}}}\\ v_y\left[k\right]-v_y\left[k-1\right]<{\displaystyle \frac{\gamma v_x\left[k-1\right]}{V_{max}}}\end{array}\right. \\ {CL1}_2≔\left\{\begin{array}{c}{v}_x\left[k\right]-v_x\left[k-1\right]>-{\displaystyle \frac{\gamma v_x\left[k-1\right]}{V_{max}}}\\ v_y\left[k\right]-v_y\left[k-1\right]>-{\displaystyle \frac{\gamma v_y\left[k-1\right]}{V_{max}}}\end{array}\right. \end{gathered}$$

(17)

Proof of Lemma 1. 

In the horizontal 2D space, the velocity and heading are obtained as $v_{xy}={‖v_x,v_y‖}_2$ and $\psi ={\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(v_y/v_x\right)$. The rate of heading change is obtained by taking the first derivative of the heading, as follows:

$$d\psi ={\displaystyle \frac{v_x}{{v_x}^2+{v_y}^2}}d{v}_y-{\displaystyle \frac{v_y}{{v_x}^2+{v_y}^2}}d{v}_x;$$

(18)

which indicates that the heading rate is proportional to changes in velocity terms in the $x$ and $y$ directions. By limiting the lower/upper bounds of $v_{x,y}$ in discrete time, as $∆v_{x,y}=v_{x,y}\left[k\right]-v_{x,y}\left[k-1\right]$, $∆\psi$ is linearly bounded. For this purpose, the upper bounds of $v_{x,y}\left[k\right]$ can be constrained by limiting the difference between consecutive slots by ${CL1}_1$, assuming that the largest possible value for linear horizontal speed is $V_{max}$, which is modeled by ${\mathrm{C}1}_6$. Similarly, ${CL1}_2$ limits lower bound of $v_{x,y}$, which is modeled by ${\mathrm{C}1}_7$. Therefore, ${\mathrm{C}1}_{\mathrm{6,7}}$ limit rapid heading change. □

The optimization problem $\mathcal{P}1$ is an energy-efficient trajectory optimization in which the UAV kinematic model with motion (speed and nonholonomic) constraints is considered. Objectives and constraints associated with channel performance are not considered here. However, channel modeling adds more computational costs to trajectory optimization, such as power transmission, RIS phase shift control, and the maximization of channel performance, which are listed as future works in the Conclusion Section below. Nevertheless, there are some points related to solving $\mathcal{P}1$ that are highlighted in the following Remarks.

Remark 3. 

$\mathcal{P}1$ is convex except in ${C1}_2$, which is nonconvex in 3D space with obstacles (e.g., buildings and skyscrapers in dense urban environments), which makes $\mathcal{P}1$ an NP-hard optimization problem. However, it can be relaxed through an iterative method, as given in Algorithm 1.

Algorithm 1 Solution to $\mathcal{P}1$
1.	Choose kinodynamic model (i.e., $\mathcal{D}\mathcal{K}\mathcal{M}1$ or $\mathcal{D}\mathcal{K}\mathcal{M}2$) based on the context.
2.	Take input data (e.g., $Z_{min}$, $Z_{max}$, $V_{max},$${\mathcal{A}}_{max}$, ${\mathbb{P}}_{\mathrm{O}\mathrm{b}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{c}\mathrm{l}\mathrm{e}}$, ${\gamma }_{\mathrm{1,2}}$, ${\mathcal{w}}_{1_{\mathrm{1,2}}})$
3.	Relax ${\mathrm{C}1}_2$ (then $\mathcal{P}1$is a quadratically-constrained convex quadratic optimization problem)
4.	Solve $\mathcal{P}1$ using standard convex programming technique (e.g., interior point method)
5.	Take the generated path from step 4.
6.	Obviate obstacles using Benders cut [38] (or mixed-integer programming [54])
7.	end

Remark 4. 

Future wireless networks will be limited to LoS channels, particularly for intelligent vehicles that need reliable communication channels for V2V and V2X communication for information exchange and environment modeling. Therefore, LoS communication becomes crucial for safe autonomous driving. In dense urban areas and urban canyons, LoS must be considered in path planning and trajectory optimization. It is not reliable to use probabilistic LoS modeling [55], and spots where LoS paths between the UAV and vehicles are obstructed can be regarded as factious obstacles that must be avoided. However, modeling LoS paths, such as vehicle-to-UAV-to-vehicle or vehicle-to-UAV-to-BS, is an NP-hard problem in convex programming and is an open research question.

4.1. Model Predictive Control (MPC) Optimization

In addition to time complexities associated with 3D obstacle-free trajectory design with valid LoS to IoVs, there is another factor that makes the trajectory optimization problem challenging. Since the goal point of the AV trajectory is uncertain, the solution to $\mathcal{P}1$ can be suboptimal. The reason is that $\mathcal{P}1$ is solved for each sample time, where the solutions of the receding time steps depend on the solution of the preceding time steps. This implies that after each time step, as the UAV moves to a new position, it loses a degree of freedom to explore the global optimal trajectory because the UAV trajectory is restricted to motion constraints. Figure 3 shows a naive illustration for two consecutive time slots. Suppose that $X_{opt}\left[k+2\right]$ is a waypoint of the global optimum trajectory indicated by the green trajectory. On the other hand, the solution to $\mathcal{P}1$ at sample time $\left[k+1\right]$ is denoted by $X[k+1]$, which can be an energy-efficient and optimal solution. However, $\mathcal{P}1$ cannot converge $X[k+1]$ to $X_{opt}\left[k+2\right]$ due to the speed/acceleration as well as the heading change constraints, so the solution lands upon $X[k+2]$. This results in the divergence of the trajectory from the global optimum trajectory after each sampling time. Therefore, the whole trajectory including all sample times should be optimized at the same time. To this end, the trajectory optimization problem can be modeled as a finite horizon MPC optimization where the UAV trajectory across all sample times is optimized in one step so that global optimization is achieved.

The MPC optimization can be formulated as $\mathcal{P}2$ in the following.

$\mathcal{P}2:$
$\mathrm{O}\mathrm{F}2.$	$\underset{\mathfrak{U}\left[k\right] \forall k\in \mathcal{K}}{\mathrm{m}\mathrm{i}\mathrm{n}} {\displaystyle \sum _{k=1}^K}\left(\underset{{\mathrm{O}\mathrm{F}2}_1}{\underbrace{{\mathcal{w}}_{2_1}{‖\mathfrak{U}\left[k\right]‖}_2^2}}+{\mathcal{w}}_{2_2}\underset{{\mathrm{O}\mathrm{F}2}_2}{\underbrace{{\displaystyle \sum _n^N}{‖\xi \left[k\right]-p_n\left[k\right]‖}_2^2}}\right)$
s. t.
${\mathrm{C}2}_1.$	$X\left[k+1\right]=G X\left[k\right]+H \mathfrak{U}\left[k\right]$;	$\forall k\in \mathcal{K}$
${\mathrm{C}2}_2.$	$X\left[k+1\right]={\mathcal{G}}_k X\left[0\right]+{\mathcal{H}}_k\mathbb{U}\left[k\right],$	$\forall k\in \mathcal{K}$
${\mathrm{C}2}_3.$	$\mathbb{X}=\mathbb{G}X\left[0\right]+\mathbb{H}\mathbb{U}\left[K-1\right],$
${\mathrm{C}2}_4.$	${\mathrm{C}1}_{1~7}.$	$\forall k\in \mathcal{K}$

where, e.g., for $\mathcal{D}\mathcal{K}\mathcal{M}1$ in terms of matrix dimensions, we have:

$$\mathbb{X}=X\left[1~K\right]={\left[X^{\top }\left[1\right], X^{\top }\left[2\right],\dots ,X^{\top }\left[K\right]\right]}^{\top }\in {\mathbb{R}}^{3K\times 1};$$

(19)

$$\mathbb{U}\left[k\right]={\left[{\mathfrak{U}}^{\top }\left[0\right], {\mathfrak{U}}^{\top }\left[1\right], {\mathfrak{U}}^{\top }\left[2\right],\dots ,{\mathfrak{U}}^{\top }\left[k\right]\right]}^{\top }\in {\mathbb{R}}^{3(k+1)\times 1};$$

(20)

$${\mathcal{G}}_k=G^{k+1}\in {\mathbb{R}}^{3\times 3};$$

(21)

$$\mathbb{G}={\left[G^1, G^2,\dots ,G^K\right]}^{\top }\in {\mathbb{R}}^{3K\times 3};$$

(22)

$${\mathcal{H}}_k={\left[G^{k}H, G^{k-1}H,\dots ,GH,H\right]}^{\top }\in {\mathbb{R}}^{3(k+1)\times 3};$$

(23)

$$\mathbb{H}=\left[\begin{array}{ccc}\begin{array}{cc}H& 0\\ \begin{array}{c}GH\\ G^{2}H\end{array}& \begin{array}{c}H\\ GH\end{array}\end{array}& \cdots & \begin{array}{c}\begin{array}{cc}0& 0\end{array}\\ \begin{array}{c}\begin{array}{cc}0& 0\end{array}\\ \begin{array}{cc}0& 0\end{array}\end{array}\end{array}\\ ⋮& \ddots & ⋮\\ \begin{array}{cc}{G}^{K-1}H& G^{K-2}H\end{array}& \cdots & \begin{array}{cc}GH& H\end{array}\end{array}\right]\in {\mathbb{R}}^{3K\times 3K}.$$

(24)

${\mathrm{C}2}_1$ is the same as ${\mathrm{C}1}_1$, which models the linearized motion and state transition in consecutive time slots; through ${\mathrm{C}2}_2$, the state of the system can be obtained from the initial position $X\left[0\right]$ (start point) by having $\mathbb{U}\left[k\right]$, which provides motion inputs from the initial state to state $k+1$. Lastly, using ${\mathrm{C}2}_3$, all states of the system $\left(\mathbb{X}\right)$, i.e., UAV consecutive positions/velocity and accelerations, are obtained from the initial point up to the last sample time, provided that $\mathbb{U}\left[K-1\right]$ (i.e., all inputs from $k=0~K-1$) are given.

Remark 5. 

Despite the advantage of MPC optimization in obtaining the global optimal trajectory, it imposes a greater computation cost, particularly when the number of samples increases in the finite receding horizon to achieve more optimality. Furthermore, obstacle-free navigation as well as the validation of UAV−IoVs LoS links to maximize communication performance are extra concerns that are not considered in $\mathcal{P}2$ in this work. Therefore, the current paper considers $\mathcal{P}2$ a basic MPC optimization problem that can be completed by embedding objectives and constraints associated with the wireless communication performance and proposing a solution considering crash-avoidance navigation. Hence, we will not evaluate the performance of MPC optimization in the simulation results in this paper, as this requires an appropriate solution, which can be considered to extend the research.

Remark 6. 

The rotational dynamics are disregarded in the trajectory optimization problems $\mathcal{P}1$ and $\mathcal{P}2$, which may result in a sharp transition in the vehicle states after each sampling. Although heading change has been limited, using input jerks $\mathfrak{U}\left[k\right]$ as real motion primitives may not adequately satisfy rotational dynamics. To make the generated trajectory dynamically feasible, smoothing the trajectory is required, which is addressed in the next subsection.

4.2. Dynamically Feasible Trajectory

To smooth the trajectory obtained after solving the optimization problems $\mathcal{P}1$ or $\mathcal{P}2$, we use state feedback control. It should be noted that the solutions to both $\mathcal{P}1$ and $\mathcal{P}2$ are motion primitives, so both can be used in the following trajectory smoothing technique based on a feedback control loop. The state feedback gain matrix is determined by solving a quadratic optimization problem in $\mathcal{P}3$. To this end, each sampling interval $h$, i.e., the point-to-point (p2p) trajectory, is discretized into $\mathfrak{K}$ sub-sampling slots by sub-sampling time $\delta \ll h$, where $\mathfrak{K}=⌈h/\delta ⌉$. From the trajectory optimizations $\mathcal{P}\mathrm{1,2}$ we obtain $\mathfrak{U}\left[k\right], \forall k\in \mathcal{K}$. Then, for sub-sampling slots between $\left[k~\left(k+1\right)\right]h$, we define the following state transition model with state feedback gain matrix $\mathsf{\Gamma }$ (we consider $\mathcal{D}\mathcal{K}\mathcal{M}{2}_1$ with subscript 2, e.g., $X_2$ and ${\mathsf{\Gamma }}_2$):

$$X_2\left[kh+\left(\kappa +1\right)\delta \right]=\underset{G_2^{\prime }}{\underbrace{\left(G_2-H_2{\mathsf{\Gamma }}_2\left[kh+\kappa \delta \right]\right)}}{X}_2\left[kh+\kappa \delta \right]+\left(\underset{H_2^{\prime }}{\underbrace{H_2/\left({\displaystyle \frac{h}{\delta }}\right)}}\right)\mathfrak{U}\left[kh\right];$$

(25)

where ${\mathsf{\Gamma }}_2\left[kh+\kappa \delta \right]\in {\mathbb{R}}^{3\times 6}$ denotes the state feedback matrix, which is defined by solving the following quadratic optimization problem $\left(\mathcal{P}3\right)$:

$\mathcal{P}3:$
$\mathrm{O}\mathrm{F}3.$	$\underset{\begin{array}{c}{\mathsf{\Gamma }}_2\left[\kappa \right]\\ \forall k,\kappa \end{array}}{\mathrm{m}\mathrm{i}\mathrm{n}} \left({\mathcal{w}}_{3_1}\underset{{\mathrm{O}\mathrm{F}3}_1}{\underbrace{{‖X_2\left[kh+\left(\kappa +1\right)\delta \right]-X_2^{dis}\left[kh+\left(\kappa +1\right)\delta \right]‖}_2^2}}+{\mathcal{w}}_{3_2}\underset{{\mathrm{O}\mathrm{F}3}_1}{\underbrace{{‖X_2\left[kh+\left(\kappa +1\right)\delta \right]-X_2\left[\left(k+2\right)h\right]‖}_2^2}}\right)$
s. t.
${\mathrm{C}3}_1.$	${\mathrm{C}1}_{2~7}$,       $\forall k, \forall \kappa \in \mathfrak{K}.$

where ${\mathcal{w}}_{3_1}$ and ${\mathcal{w}}_{3_2}$ are weighting coefficients, and $X_2^{dis}\left[kh+\left(\kappa +1\right)\delta \right]$ denotes the state at step time $kh+\left(\kappa +1\right)\delta$ on the original linearly discretized p2p trajectory between sampling time $\left[k~\left(k+1\right)\right]h$ (see Figure 4 for an illustration).

${\mathrm{O}\mathrm{F}3}_1$ acts as an elastic rubber band between the next state (e.g., assume the next waypoint) in the tentative smooth p2p trajectory and the next waypoint in the linearly discretized original p2p trajectory. In other words, ${\mathrm{O}\mathrm{F}3}_1$ ensures that the smooth p2p trajectory stays close to the original p2p trajectory by approaching (by minimizing the distance between) the next waypoint $X_2\left[kh+\left(\kappa +1\right)\delta \right]$ of the p2p trajectory to the next waypoint $X_2^{dis}\left[kh+\left(\kappa +1\right)\delta \right]$ of the linearly discretized original p2p trajectory. ${\mathrm{O}\mathrm{F}3}_1$, which acts as another rubber band, gives some flexibility to the p2p trajectory to be smooth by approaching (by minimization) the next waypoint $X_2\left[kh+\left(\kappa +1\right)\delta \right]$ of the p2p trajectory to the second next waypoint $X_2\left[\left(k+2\right)h\right]$ of the original trajectory. By tuning the weighting coefficients ${\mathcal{w}}_{3_{\mathrm{1,2}}}$ (i.e., tuning of elasticity of rubber bands), the elasticity and smoothness of the method can be adjusted. The smoothing principle is illustrated in Figure 4 and presented in Algorithm 2.

Algorithm 2 Smoothing Technique
1.	$\mathbf{Take} \mathfrak{U}\left[kh\right],$ $\forall k\in \mathcal{K}$ $\mathrm{from} \mathrm{the} \mathrm{solutions} \mathrm{to} \mathcal{P}1$
2.	${for}_1$ $k=1:\mathcal{K}$
	$⋮$
	$\mathrm{for} \mathrm{time} \mathrm{step} \left[kh\right] ~ \left[kh+h\right]$ with sample time $h$, use $\mathfrak{U}\left[kh\right]$;
3.	${for}_2$ $\kappa =1:\mathfrak{K}$                                                 $⋮$
4.	$\mathrm{for} \mathrm{time} \mathrm{slot} \left[kh+\kappa \delta \right]~ \left[kh+\left(\kappa +1\right)\delta \right]$ with sample time $\delta$
5.	Do:
6.	$\mathrm{Plug} X_2\left[kh+\left(\kappa +1\right)\delta \right]$ $\mathrm{from} \left(25\right) \mathrm{into} \mathrm{O}\mathrm{F}2$ $\mathrm{in} \mathcal{P}3$
7.	$\mathrm{Solve} \mathcal{P}2$ $\mathrm{and} \mathrm{determine} {\mathsf{\Gamma }}_2\left[kh+\kappa \delta \right]$
8.	$\mathrm{Use} {\mathsf{\Gamma }}_2\left[kh+\kappa \delta \right]\mathrm{in} \left(25\right) \mathrm{to} \mathrm{calculate} X_2\left[kh+\left(\kappa +1\right)\delta \right]$                                                 $⋮$
9.	$end {for}_2$ $⋮$
10.	$end {for}_1$

5. Numerical and Simulation Results

Numerical results via computer simulations are provided to evaluate the proposed trajectory optimization technique. For the simulations, trajectory optimization is considered for one UAV that provides aerial wireless communication for IoVs including four IVs. The navigation time interval of interest is discretized into 10 time steps with a sampling time of 5 s, i.e., a total time of 50 s. The maximum horizontal and vertical speeds are 10 m/s and 8 m/s, respectively.

A 3D occupancy map of a typical urban area is simulated in the MATLAB platform, as shown in Figure 5a. Also, the map routes of four IVs are illustrated in a 2D plot of the occupancy map in Figure 5b, where IVs move in the arrow directions.

We assessed the results of the optimization algorithm and its running time using the developed linear kinematic model. Also, we compared it with the sampling-based RRT-like technique that is used in complex situations. Computations were performed on a laptop computer with the following processor: Intel(R) Core(TM) i7-8665U CPU @ 1.90GHz, 2112 MHz, 4 Core(s), 8 Logical Processor(s).

5.1. The Performance of the Proposed Technique

The simulation is run for five consecutive time intervals of interest (5 × 50 s) with the same IoV map routes to see if the trajectory planner can generate a kinodynamic-aware path for the UAV satisfying motion constraints. The starting point is $\xi \left[0\right]={\left[\begin{array}{ccc}0& 0& 0\end{array}\right]}^{\top }\measuredangle \psi =0$. To obviate obstacles, the Benders cut method was used [38].

In the first scenario, the minimum UAV altitude limit is lower than the height of the building ($Z_{min}=30$, $Z_{max}=150$) to evaluate the crash avoidance performance of the trajectory optimization technique. The output results of the trajectory optimization problem are shown in Figure 5c,d through 3D and 2D plots. The proposed optimization technique generates kinematics-aware paths where the motion constraints, i.e., the speed and rate of heading change (nonholonomic) constraints, have been satisfied.

In the second scenario, to narrow the navigation space, the UAV’s maximum altitude is also limited to be lower than the average height of a tall building ($Z_{max}=100$) so that the solution space does not include multiple different homotopies. The results are shown in Figure 6, indicating that the navigation objective, i.e., the kinodynamic-aware crash avoidance trajectory design, is achieved. However, it may end up with a less optimal solution due to the imposed motion constraints. The performance of the proposed smoothing technique is shown in Figure 7.

According to the MATLAB $tic-toc$ function, the running time of the method is 9.3 s on average plus 3 s for smoothing for each time interval of 50 s. The results indicate that the optimizer has sufficient time for real-time trajectory optimization. For example, while the UAV follows the trajectory of the current time interval, it has 50 s to solve the trajectory optimization problem for the next 50 s time interval.

5.2. The Performance of the Sampling RRT Technique

We used an RRT-like technique to generate random paths for a time interval of interest of 25 s with five time slots, each lasting 5 s, and the results are shown in Figure 8. We took three random samples for the first step (sampling) time. The number of random samples increased exponentially with $3^k$ for the coming sampling times. The problem objectives and constraints should be checked for all samples and validated. It takes more than 150 s for RRT to generate random samples with valid obstacle-free paths that satisfy motion constraints as well as calculate problem objectives, i.e., the energy-efficient path with the minimum distance between the UAV and vehicles. The running time indicates that RRT is computationally prohibitive (153.546 s) in such a complex environment. Specifically, since the navigation time interval of interest is 25 s, the running time of RRT is significantly higher, implying that it cannot be used for real-time applications, i.e., less than 25 s.

6. Discussion

The proposed kinodynamic-aware obstacle-free trajectory optimization technique revealed promising performance for real-time trajectory optimization, which is necessary for the autonomous navigation of the UAV. It should be noted that, in this paper, by real-time optimization, we did not mean dynamics or high-frequency (e.g., sensor) rate time scales. Rather, we meant formulating and solving the optimization problem in the time frame of a few seconds to ten seconds, which the overhead controller requires to plan the motion primitives for the receding time horizon.

The developed kinematic model is linear, and thus the proposed trajectory optimization can be easily modified for receding horizon MPC optimization. Although MPC imposes more of a computational burden, more efficient results can be achieved. This is because the optimization problem for the whole step times in the time interval is solved in one go, which converges the solution to the global path. However, modeling obstacle-free paths and LoS channels in the context of MPC requires more research.

Furthermore, channel modeling is required in the context of UAV-enabled aerial wireless communication for mobile IoVs to be incorporated in trajectory optimization. However, including the channel models with LoS paths in the convex programming imposes a greater computational cost. In this paper, we relaxed channel performance in the path planner and considered the performance of the proposed trajectory optimization technique for kinodynamic navigation exposed to motion constraints, which was verified through simulation results. It is a common procedure in relevant multi-objective optimizations utilizing sequential convex programming that problem objectives are optimized one by one to tackle the computational complexity and nonconvexity of the optimization problem.

Therefore, in the simulation results section, quantitative and statistics results, which are meaningful when communication performance is considered, were not provided. Furthermore, effective solutions are needed to make the modeling and solving of the trajectory optimization computationally tractable, which maximizes the wireless communication performance and satisfies the QoS index. This issue will be studied in future works in which UAV-enabled RIS-assisted channel modeling will be incorporated into the UAV trajectory optimization problem.

7. Conclusions

In this paper, the autonomous UAV navigation perspective of UAV-enabled wireless communication for IoVs was studied. It was indicated that, for autonomous navigation, real-time UAV trajectory optimization is required, which must be computationally tractable. However, satisfying problem objectives, such as obstacle-free kinodynamic-aware navigation in dense urban areas and urban canyons, imposes a computational burden on the overhead controller, where channel modeling and wireless communication performance are extra concerns. Therefore, in this paper, only kinodynamic-aware trajectory generation was considered. We first studied the motion principles and dynamics of quadrotors, the most popular UAVs for dense environments. Then, linear state-space kinodynamic models were developed to be used in the convex optimization for real-time trajectory generation. A systematic trajectory optimization problem was introduced with some convex relaxation techniques. The optimization variables are motion primitives that satisfy motion constraints, such as speed, acceleration, and heading change, which can be directly used without a path-tracking controller. To make the trajectory dynamically feasible, to satisfy quadrotor rotational rates, a trajectory smoothing technique was also proposed. The smoothing technique was based on state feedback, and thus motion primitives produced by the trajectory optimization can still be used without an extra controller.

Future works will study appropriate channel modeling for UAV-enabled RIS-assisted communication for IoVs. The developed model will be used to modify the trajectory optimization problem and discuss its computational complexities with possible solutions and research topics. Nevertheless, uncertainties in IoVs and users’ positions, channel state information in dynamic environments, and randomly blocked LoS paths make UAV path planning a probabilistic problem, which can be used to extend the research.