Flight Plan Optimisation of Unmanned Aerial Vehicles with Minimised Radar Observability Using Action Shaping Proximal Policy Optimisation
Abstract
1. Introduction
2. Related Work
2.1. Heuristic-Based Path Planning Approaches
2.2. Reinforcement Learning-Based Path Planning
2.3. Contributions
- A novel path-planning approach based on the PPO algorithm and an action-shaping mechanism that accelerates learning and avoids radar detection.
- A radar warning zone switching criteria is developed based on the Neyman–Pearson Criteria to improve the action selection in both warning and non-warning radar detection zones.
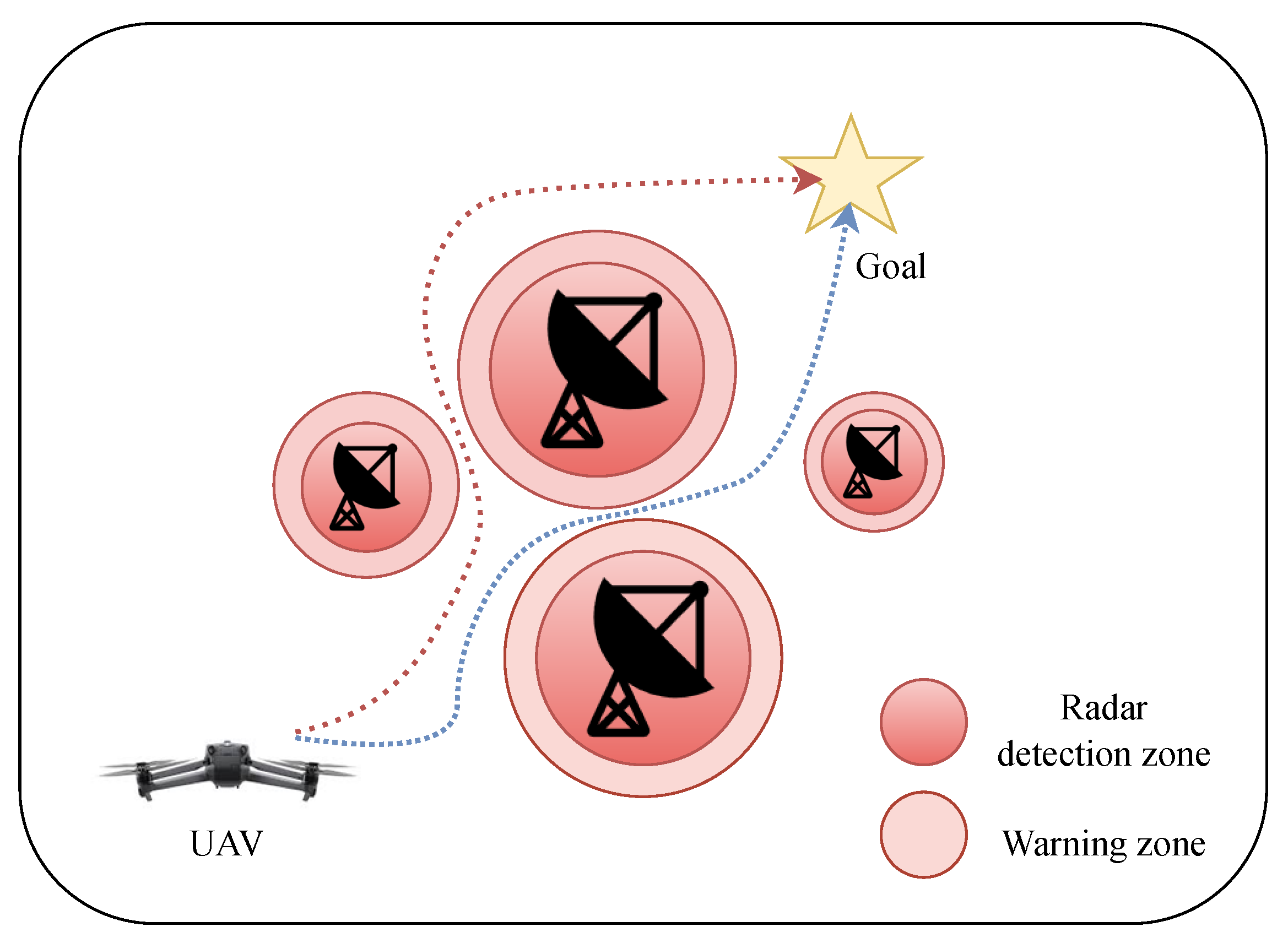
3. Problem Formulation
3.1. UAV Model
3.2. Technical and Theoretical Concepts
3.2.1. Radar Detection
3.2.2. Neyman–Pearson Criterion
- Signal-to-Noise Ratio (SNR): The SNR is a measure of the signal strength relative to the background noise. In the radar context, it helps to determine how easily a target can be detected by the radar. A higher SNR means better detectability of the target. SNR is calculated based on the distance between the UAV and the radar. The SNR decreases with the fourth power of the distance, i.e.,
- Eigenvalues of the Correlation matrix: The correlation matrix represents how similar or correlated the signals received by the radar are across different pulses or measurements. Suppose a radar transmits a series of pulses, and for each pulse, it receives a signal that may or may not contain the reflected signal from a target like a UAV. If the radar transmits N pulses, the signals it receives can be represented as a vector, where each entry corresponds to the received signal for one pulse. For a radar with N pulses and correlation , the eigenvalues of the correlation matrix are
- Detection threshold: The detection threshold is obtained by specifying the false alarm probability as [19]
- Detection probability: the detection probability is calculated by adding the contributions from each pulse while accounting for the SNR and the detection threshold, i.e.,
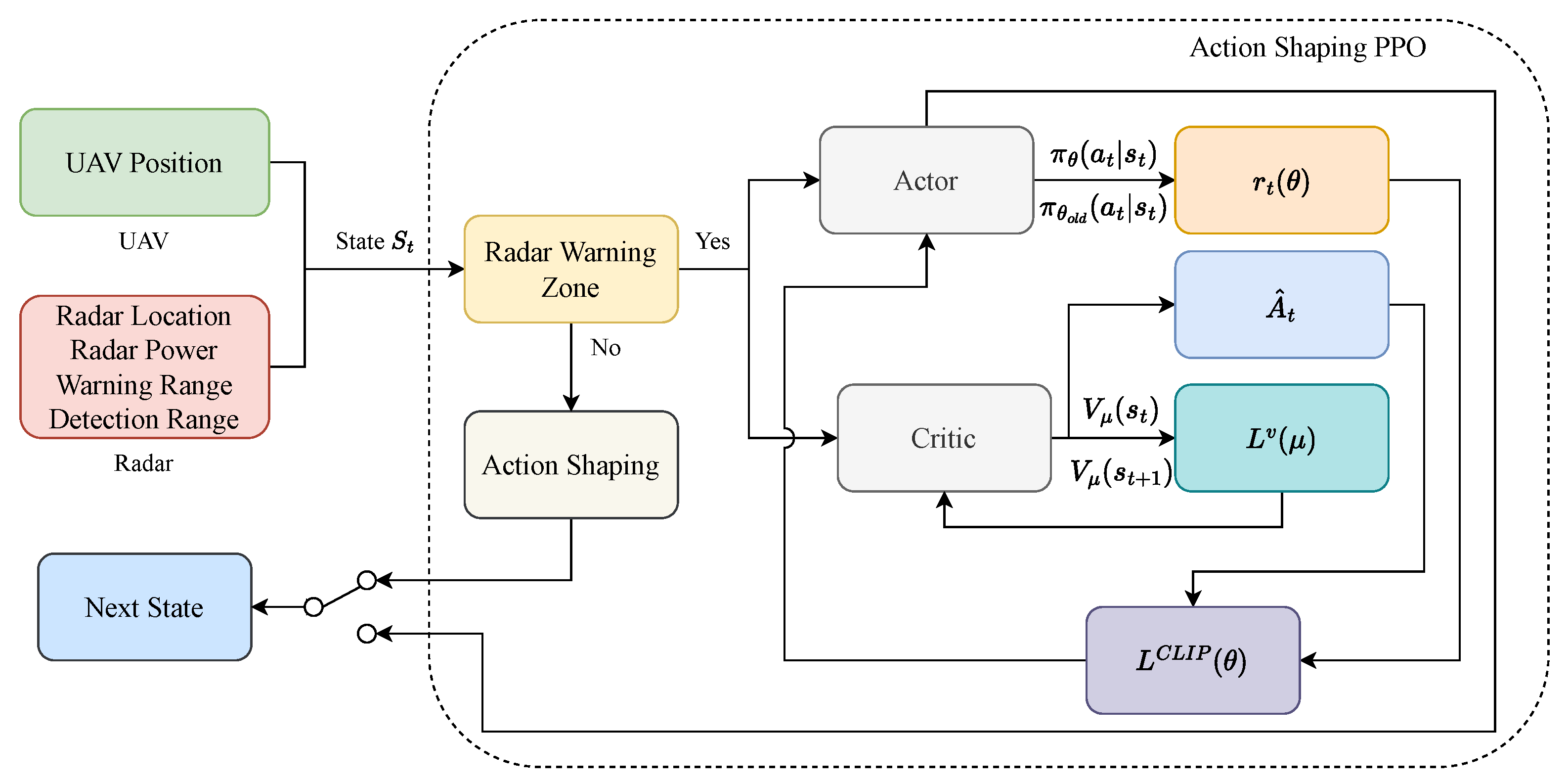
4. Methodology
- UAV and Radar State Information: these blocks provide the necessary information regarding both the locations of the UAV and radar, as well as the radar power, warning and detection ranges. This information plays a pivotal role in the decision-making process for action selection and manoeuvrability.
- Radar Warning: in this block, the state is analysed to verify if the UAV is within a radar’s warning zone. If the UAV is within a warning zone, then the PPO algorithm is applied for detection avoidance. Otherwise, it applies an action-shaping mechanism to select actions that drive the UAV towards the target location.
- Action-shaping mechanism: this mechanism is used only when the UAV is not within a radar’s warning range. Here, the action-shaping consists of reducing the action-space of the UAV to move only in the direction of the target goal and avoid using actions that may produce unnecessary movements.
- Actor-Critic PPO Module: this module consists of two main elements,
- Actor Network: which is responsible for the action selection based on a parametrised policy with parameters .
- Critic Network: which evaluates the value function with parameter that enables to improvement of the actor policy.
Both the actor and critic networks are updated using mini-batches of experiences collected from the environment–UAV interaction. - Reward function and policy update: the PPO algorithm uses a clipped objective function to prevent large and unstable updates. In the action-shaping implementation, the restricted action space complementary works with the clipped updates to stabilise the algorithm training and accelerate its convergence. The PPO updates the policy using a clipped objective based on the advantage estimate .The reward is designed to penalise actions leading to radar detection. This encourages the UAV to avoid those penalising paths, whilst moving towards to the location goal.
- Action and policy iteration: based on the reward and value function updates, the actor selects the next action that the UAV will apply to reach a new state that is not within the detection range of the radars. This process is repeated until the goal is reached or if a terminal condition is met (e.g., the maximum number of steps is reached).
4.1. Proximal Policy Optimisation (PPO)
4.2. Action Shaping PPO
| Algorithm 1 Action shaping mechanism |
|
- Restricted Movement Integration: The action space is reduced based on the UAV’s position relative to the target goal and the radar warning zone. The UAV’s movement options are dynamically adjusted during training. Depending on its environment, the action space can be narrowed or expanded, ensuring the UAV avoids unnecessary movements that would lead to the exploration of suboptimal paths.
- Actor-Critic Structure: The use of separate actor and critic networks allows for more stable learning in environments with complex dynamics.
- Adaptive Action Selection: The model adapts the action space depending on whether the UAV is in a radar warning area, improving efficiency and safety.
- Faster Convergence: By limiting the action space to strategic movements, the model converges faster, requiring fewer training steps.
- Enhanced Safety: The restricted movement prevents the UAV from making large, unpredictable moves, ensuring it stays within safe zones during both training and deployment.
- If the UAV is in a non-detection zone, that is, the action-shaping mechanism is applied then the reward is where is the position of the UAV and is the position of the target goal.
- If the UAV moves to a previous visited state, then it is penalised with a reward of .
- If the UAV moves to a position that reduces the distance to the target, then a positive reward of is given.
- If the UAV enters into the radar detection range and exceeds a threshold of 0.2, then it is penalised by a reward of .
- If the UAV is within the radar range, then it is penalised by a reward of .
- If the UAV reaches the target then a positive reward of is given; otherwise, it is penalised with a reward of .
4.3. Modified Sparse Algorithm
- Total distance: this term accounts for the cumulative distance travelled. This term accounts for the cumulative distance travelled along the current path. The algorithm aims to minimise the overall distance, which aligns with operational efficiency and fuel conservation.
- Distance to Goal: This heuristic guides the path toward the goal. It is the Euclidean distance between the current node and the goal. This term encourages the UAV to move closer to the target in a straight line when possible.
- Cumulative Radar Detection Probability: It considers the cumulative radar detection probability encountered along the path. Lower detection probabilities are preferred, so paths that keep this metric low are favoured. The radar detection probability is computed using a Neyman–Pearson criterion-based model that accounts for factors like signal-to-noise ratio (SNR), and the characteristics of the radar (e.g., pulse number, correlation).
- Height Difference: This term measures the altitude change between consecutive nodes. Large altitude changes are undesirable due to aircraft performance limits, energy consumption, or increased radar visibility. For 2D environments, it can be set to zero.
- Immediate Radar Detection Probability: This term considers the radar detection probability at the current node. It ensures that paths moving into high-risk areas (high detection probability) are heavily penalised.
5. Results
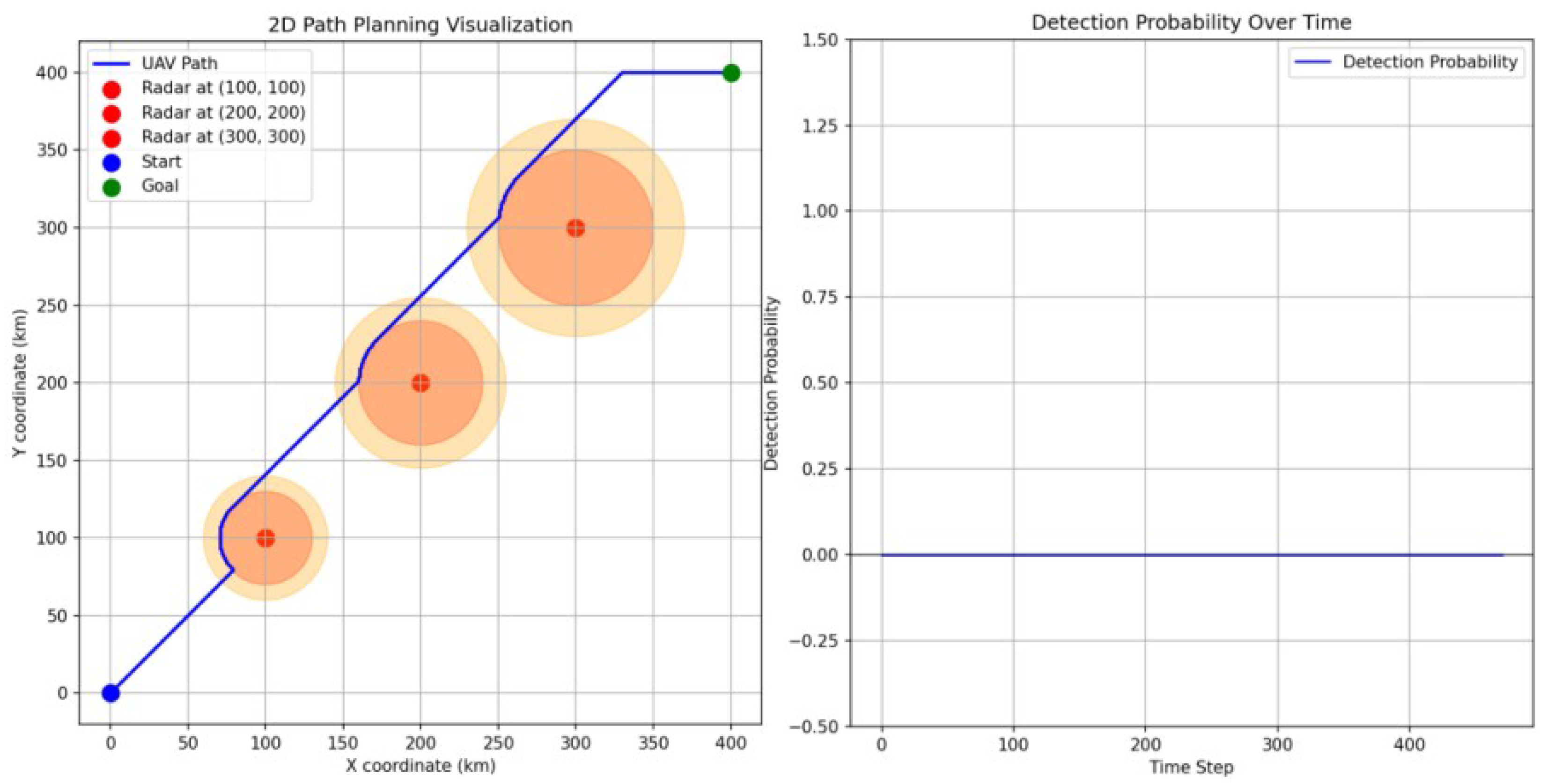
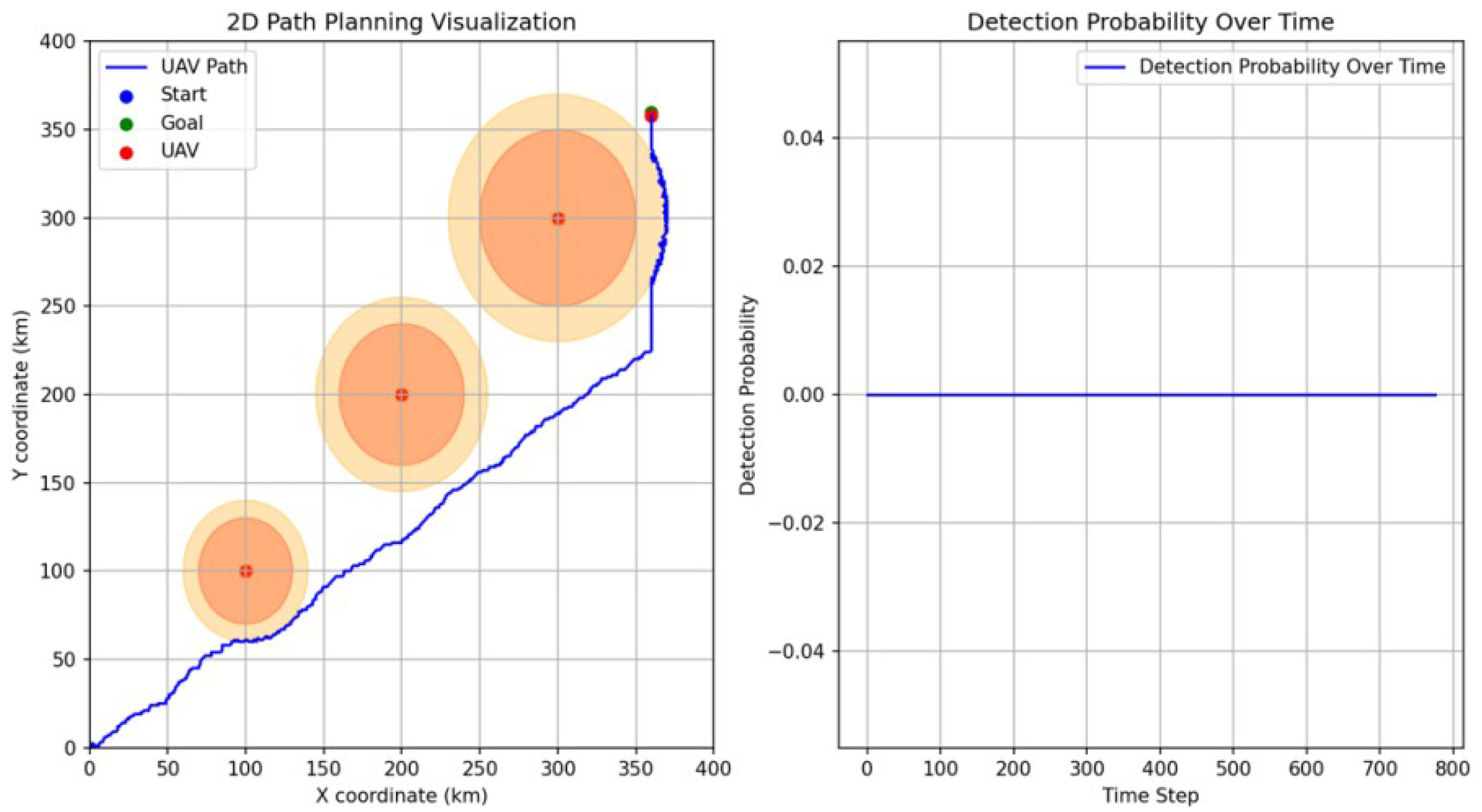
5.1. Comparison against Traditional PPO
- Efficiency: the UAV using the action-shaping PPO reaches the goal much faster compared with the UAV using the standard PPO. This means that the action-shaping mechanism provides an effective tool to guide the UAV towards the goal without applying unnecessary actions.
- Detection probability: the cumulative detection probability is notably reduced which is critical for this particular implementation to ensure the survivability of the UAV.
- Path smoothness: as previously discussed, the path of the standard PPO is not smooth due to the random selection of actions in zones without radar detectability. In contrast, the proposed approach overcomes this issue such that the PPO is only applied in the coverage area of the radar.
- Distance travelled: this is a key benefit of the proposed approach since the UAV is capable of reaching the goal in less number of steps which directly affects the travel distance that is a critical element when the UAV resources are limited, e.g., battery time or fuel.
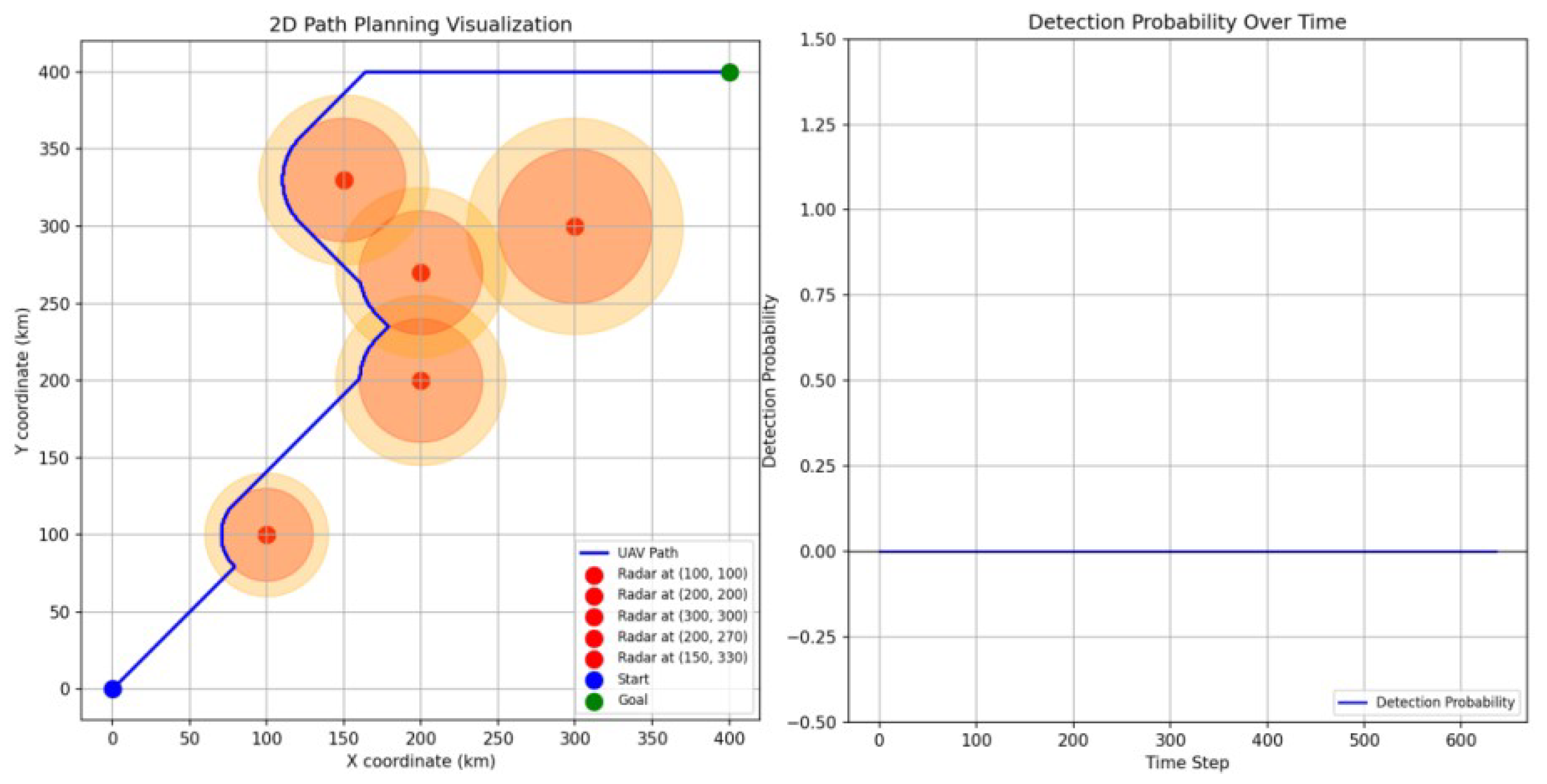
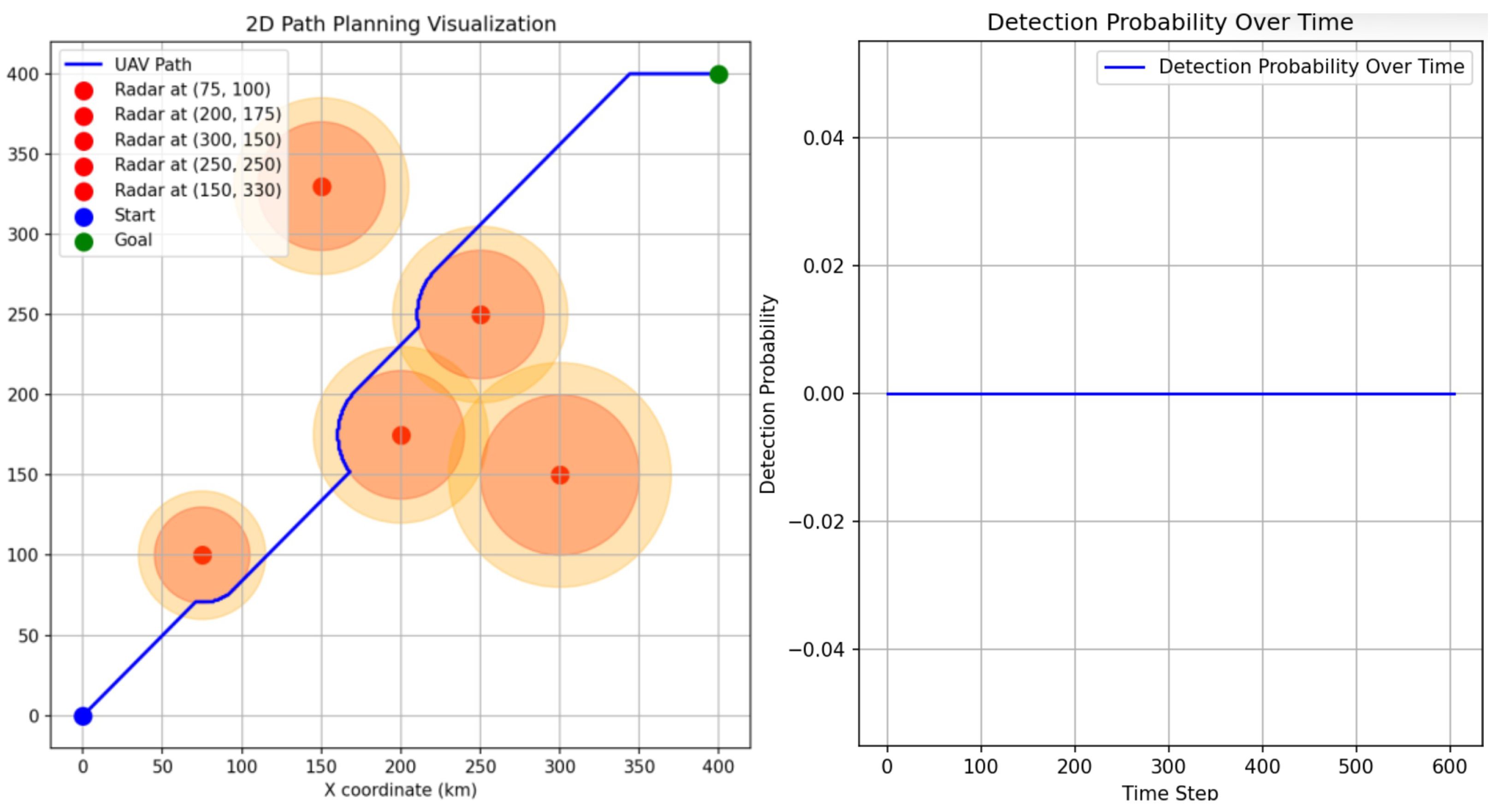
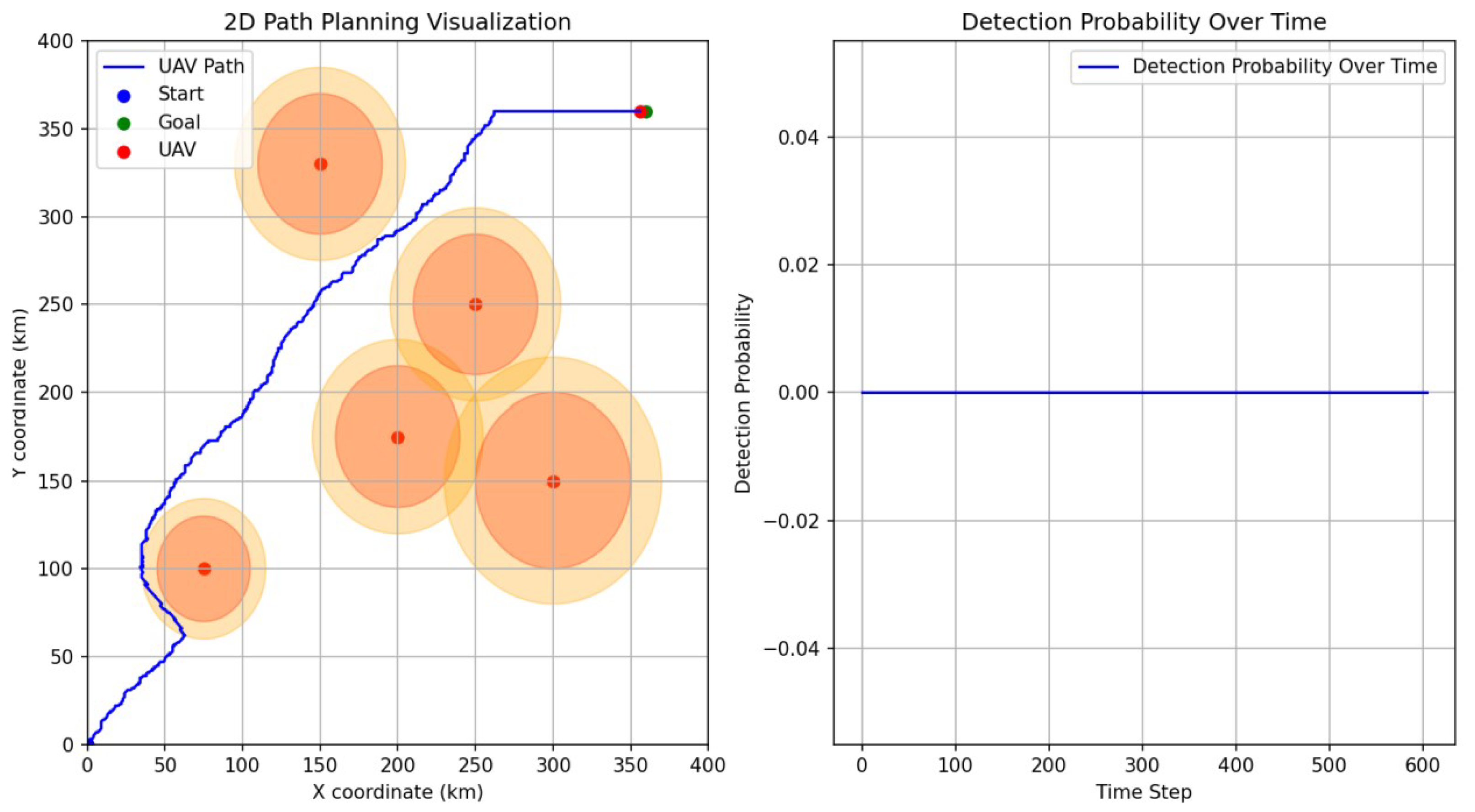
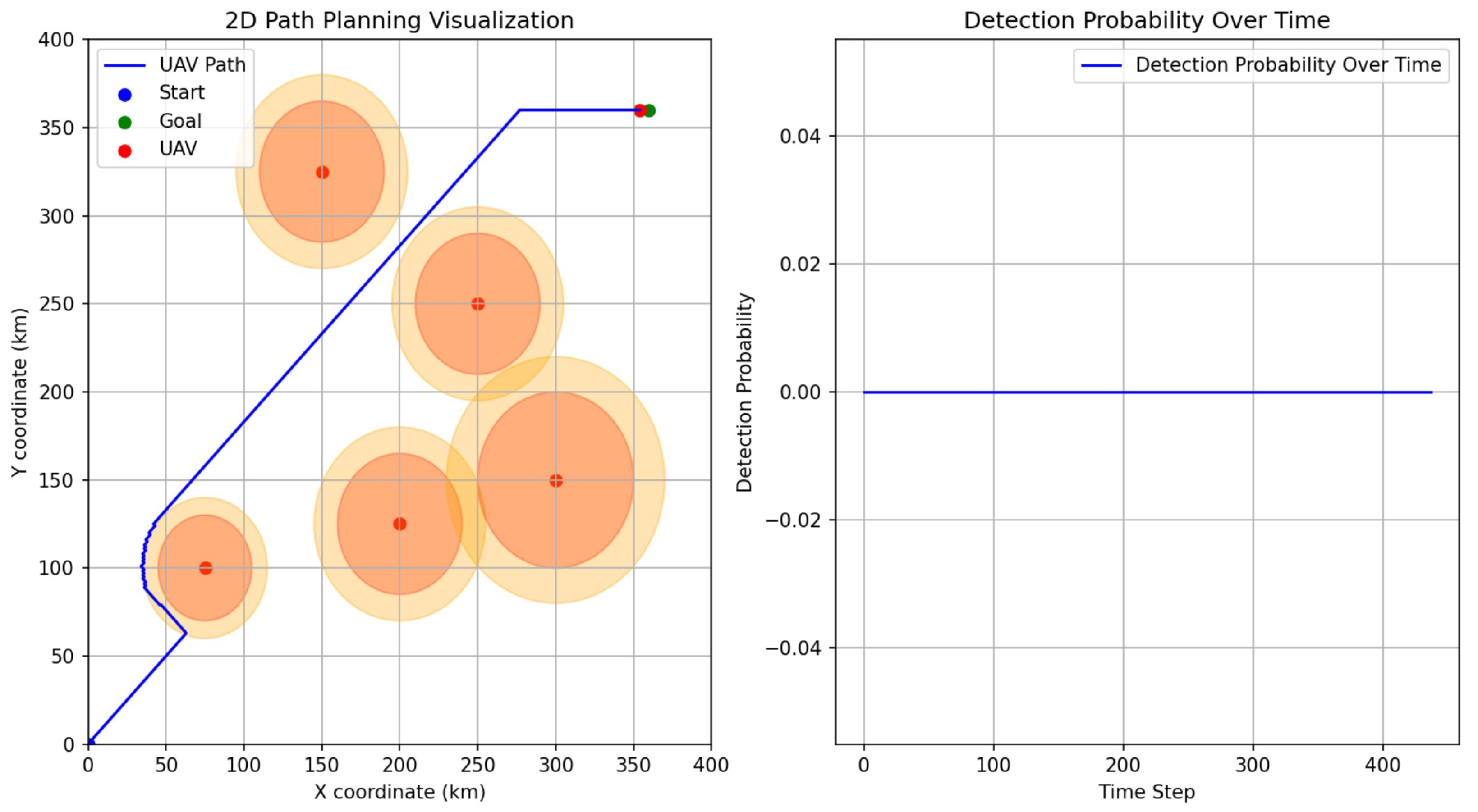
5.2. Scenario 1
5.3. Scenario 2
5.4. Scenario 3
5.5. Improvement of the Action-Shaping PPO
5.6. Limitations and Future Work
- Geometric Data of the Aircraft: this includes the dimensions of the aircraft such as its length, wingspan, height, and overall shape. In addition, the surface materials for the absorption of radar waves, and the panel configuration are critical aspects that affect the RCS.
- Data on Stealth Features: this covers the design features (e.g., edge alignment, RAM coating, cooling techniques) and operational profiles (e.g., typical flights and angles that the aircraft operates) that play important roles in the performance of the RCS.
- Radar Characteristics:
- -
- Radar frequencies that interact differently with the aircraft’s surface. Higher frequencies (shorter wavelengths) are more sensitive to smaller details on the aircraft’s surface, while lower frequencies (longer wavelengths) interact more with the overall shape.
- -
- Polarisation of the radar signal (vertical, horizontal, or circular) can affect how the radar waves interact with the aircraft. The RCS can vary depending on the polarisation of the incoming radar signal.
- -
- Incident Angle where the radar waves hit the aircraft is critical. RCS is highly dependent on the aspect angle, and the orientation of the aircraft relative to the radar source.
- Environmental Conditions: include both atmospheric conditions (e.g., humidity, temperature and pressure) and background noise which can reduce the radar signal strength and/or the radar readings.
- Radar Cross-section Data: such as monostatic and bistatic RCS. Here, the monostatic RCS is a measurement taken when the radar transmitter and receiver are at the same location. It is the most common method and provides a direct measure of how much energy is reflected back to the radar source. On the other hand, the bistatic RCS is the measurement taken when the radar transmitter and receiver are at different locations. These data help in understanding how radar waves are scattered in different directions, not just back towards the radar source.
- Computational Simulations:
- -
- Electromagnetic Modelling to predict the RCS, electromagnetic modelling techniques like the Method of Moments (MoM), Finite Element Method (FEM), or Finite Difference Time Domain (FDTD) are used. These simulations require detailed geometric and material data of the aircraft.
- -
- Simulation Parameters such as frequency range, incident angles, and polarisation settings, which need to align with the actual measurement conditions.
- Historical RCS Data: which consists of data from previous tests or from similar aircraft models used for comparison. This helps to understand the effectiveness of the stealth features and identify areas for improvement.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
DURC Statement
Conflicts of Interest
Abbreviations
| DC | Discretize continuous actions |
| DQN | Deep Q-Networks |
| FDTD | Finite Difference Time Domain |
| FEM | Finite Element Method |
| LSTM | Long Short-Term Memory |
| MoM | Method of Moments |
| PD | Probability Distribution |
| PPO | Proximal Policy Optimisation |
| RCS | Radar Cross section |
| RA | Removing actions |
| RL | Reinforcement Learning |
| RPP | Real Path Planning |
| UAV | Unmanned Air Vehicle |
References
- Wang, N. “A Success Story that Can Be Sold”?: A Case Study of Humanitarian Use of Drones. In Proceedings of the 2019 IEEE International Symposium on Technology and Society (ISTAS), Medford, MA, USA, 15–16 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Cui, Y.; Osaki, S.; Matsubara, T. Autonomous boat driving system using sample-efficient model predictive control-based reinforcement learning approach. J. Field Robot. 2021, 38, 331–354. [Google Scholar] [CrossRef]
- Amendola, J.; Miura, L.S.; Costa, A.H.R.; Cozman, F.G.; Tannuri, E.A. Navigation in restricted channels under environmental conditions: Fast-time simulation by asynchronous deep reinforcement learning. IEEE Access 2020, 8, 149199–149213. [Google Scholar] [CrossRef]
- Thombre, S.; Zhao, Z.; Ramm-Schmidt, H.; García, J.M.V.; Malkamäki, T.; Nikolskiy, S.; Hammarberg, T.; Nuortie, H.; Bhuiyan, M.Z.H.; Särkkä, S.; et al. Sensors and AI techniques for situational awareness in autonomous ships: A review. IEEE Trans. Intell. Transp. Syst. 2020, 23, 64–83. [Google Scholar] [CrossRef]
- Fraser, B.; Perrusquía, A.; Panagiotakopoulos, D.; Guo, W. A Deep Mixture of Experts Network for Drone Trajectory Intent Classification and Prediction Using Non-Cooperative Radar Data. In Proceedings of the 2023 IEEE Symposium Series on Computational Intelligence (SSCI), Mexico City, Mexico, 5–8 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Gasparetto, A.; Boscariol, P.; Lanzutti, A.; Vidoni, R. Path planning and trajectory planning algorithms: A general overview. In Motion and Operation Planning of Robotic Systems: Background and Practical Approaches; Springer International Publishing: Cham, Switzerland, 2015; pp. 3–27. [Google Scholar]
- Gruffeille, C.; Perrusquía, A.; Tsourdos, A.; Guo, W. Disaster Area Coverage Optimisation Using Reinforcement Learning. In Proceedings of the 2024 International Conference on Unmanned Aircraft Systems (ICUAS), Chania, Crete, Greece, 4–7 June 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 61–67. [Google Scholar]
- Vagale, A.; Bye, R.T.; Oucheikh, R.; Osen, O.L.; Fossen, T.I. Path planning and collision avoidance for autonomous surface vehicles II: A comparative study of algorithms. J. Mar. Sci. Technol. 2021, 26, 1307–1323. [Google Scholar] [CrossRef]
- Bildik, E.; Tsourdos, A.; Perrusquía, A.; Inalhan, G. Swarm decoys deployment for missile deceive using multi-agent reinforcement learning. In Proceedings of the 2024 International Conference on Unmanned Aircraft Systems (ICUAS), Chania, Crete, Greece, 4–7 June 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 256–263. [Google Scholar]
- Li, G.; Hildre, H.P.; Zhang, H. Toward time-optimal trajectory planning for autonomous ship maneuvering in close-range encounters. IEEE J. Ocean. Eng. 2019, 45, 1219–1234. [Google Scholar] [CrossRef]
- Shaobo, W.; Yingjun, Z.; Lianbo, L. A collision avoidance decision-making system for autonomous ship based on modified velocity obstacle method. Ocean Eng. 2020, 215, 107910. [Google Scholar] [CrossRef]
- El Debeiki, M.; Al-Rubaye, S.; Perrusquía, A.; Conrad, C.; Flores-Campos, J.A. An Advanced Path Planning and UAV Relay System: Enhancing Connectivity in Rural Environments. Future Internet 2024, 16, 89. [Google Scholar] [CrossRef]
- Lyu, D.; Chen, Z.; Cai, Z.; Piao, S. Robot path planning by leveraging the graph-encoded Floyd algorithm. Future Gener. Comput. Syst. 2021, 122, 204–208. [Google Scholar] [CrossRef]
- Hameed, R.; Maqsood, A.; Hashmi, A.; Saeed, M.; Riaz, R. Reinforcement learning-based radar-evasive path planning: A comparative analysis. Aeronaut. J. 2022, 126, 547–564. [Google Scholar] [CrossRef]
- Tang, G.; Tang, C.; Claramunt, C.; Hu, X.; Zhou, P. Geometric A-star algorithm: An improved A-star algorithm for AGV path planning in a port environment. IEEE Access 2021, 9, 59196–59210. [Google Scholar] [CrossRef]
- Kang, H.I.; Lee, B.; Kim, K. Path planning algorithm using the particle swarm optimization and the improved Dijkstra algorithm. In Proceedings of the 2008 IEEE Pacific-Asia Workshop on Computational Intelligence and Industrial Application, Wuhan, China, 19–20 December 2008; IEEE: Piscataway, NJ, USA, 2008; Volume 2, pp. 1002–1004. [Google Scholar]
- Luo, M.; Hou, X.; Yang, J. Surface optimal path planning using an extended Dijkstra algorithm. IEEE Access 2020, 8, 147827–147838. [Google Scholar] [CrossRef]
- Yang, R.; Ma, Y.; Tao, Z.; Yang, R. A stealthy route planning algorithm for the fourth generation fighters. In Proceedings of the 2017 International Conference on Mechanical, System and Control Engineering (ICMSC), St. Petersburg, Russia, 19–21 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 323–327. [Google Scholar]
- Guan, J.; Huang, J.; Song, L.; Lu, X. Stealth Aircraft Penetration Trajectory Planning in 3D Complex Dynamic Environment Based on Sparse A* Algorithm. Aerospace 2024, 11, 87. [Google Scholar] [CrossRef]
- Meng, B.b. UAV path planning based on bidirectional sparse A* search algorithm. In Proceedings of the 2010 International Conference on Intelligent Computation Technology and Automation, Changsha, China, 11–12 May 2010; IEEE: Piscataway, NJ, USA, 2010; Volume 3, pp. 1106–1109. [Google Scholar]
- Zhaoying, L.; Ruoling, S.; Zhao, Z. A new path planning method based on sparse A* algorithm with map segmentation. Trans. Inst. Meas. Control 2022, 44, 916–925. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Panov, A.I.; Yakovlev, K.S.; Suvorov, R. Grid path planning with deep reinforcement learning: Preliminary results. Procedia Comput. Sci. 2018, 123, 347–353. [Google Scholar] [CrossRef]
- Yang, Y.; Xiong, X.; Yan, Y. UAV Formation Trajectory Planning Algorithms: A Review. Drones 2023, 7, 62. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Lei, X.; Zhang, Z.; Dong, P. Dynamic path planning of unknown environment based on deep reinforcement learning. J. Robot. 2018, 2018, 5781591. [Google Scholar] [CrossRef]
- Bae, H.; Kim, G.; Kim, J.; Qian, D.; Lee, S. Multi-robot path planning method using reinforcement learning. Appl. Sci. 2019, 9, 3057. [Google Scholar] [CrossRef]
- Tascioglu, E.; Gunes, A. Path-planning with minimum probability of detection for auvs using reinforcement learning. In Proceedings of the 2022 Innovations in Intelligent Systems and Applications Conference (ASYU), Antalya, Turkey, 7–9 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–5. [Google Scholar]
- Qi, C.; Wu, C.; Lei, L.; Li, X.; Cong, P. UAV path planning based on the improved PPO algorithm. In Proceedings of the 2022 Asia Conference on Advanced Robotics, Automation, and Control Engineering (ARACE), Qingdao, China, 26–28 August 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 193–199. [Google Scholar]
- Wang, H.; Lu, B.; Li, J.; Liu, T.; Xing, Y.; Lv, C.; Cao, D.; Li, J.; Zhang, J.; Hashemi, E. Risk assessment and mitigation in local path planning for autonomous vehicles with LSTM based predictive model. IEEE Trans. Autom. Sci. Eng. 2021, 19, 2738–2749. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, Y.; Zheng, L.; Yang, Q.; Shi, G.; Wu, Y. Real-time UAV path planning based on LSTM network. J. Syst. Eng. Electron. 2024, 35, 374–385. [Google Scholar] [CrossRef]
- Ma, H.; Luo, Z.; Vo, T.V.; Sima, K.; Leong, T.Y. Highly efficient self-adaptive reward shaping for reinforcement learning. arXiv 2024, arXiv:2408.03029. [Google Scholar]
- Chu, K.; Zhu, X.; Zhu, W. Accelerating Lifelong Reinforcement Learning via Reshaping Rewards. In Proceedings of the 2021 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Melbourne, Australia, 17–20 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 619–624. [Google Scholar]
- Kliem, J.; Dasgupta, P. Reward Shaping for Improved Learning in Real-Time Strategy Game Play. arXiv 2023, arXiv:2311.16339. [Google Scholar]
- Zare, M.; Kebria, P.M.; Khosravi, A.; Nahavandi, S. A survey of imitation learning: Algorithms, recent developments, and challenges. IEEE Trans. Cybern. 2024, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Ke, J.; Wu, A. Inverse reinforcement learning with the average reward criterion. Adv. Neural Inf. Process. Syst. 2024, 36. [Google Scholar]
- Perrusquía, A.; Guo, W.; Fraser, B.; Wei, Z. Uncovering drone intentions using control physics informed machine learning. Commun. Eng. 2024, 3, 36. [Google Scholar] [CrossRef]
- Singh, U.; Suttle, W.A.; Sadler, B.M.; Namboodiri, V.P.; Bedi, A.S. PIPER: Primitive-Informed Preference-Based Hierarchical Reinforcement Learning via Hindsight Relabeling. arXiv 2024, arXiv:2404.13423. [Google Scholar]
- Kanervisto, A.; Scheller, C.; Hautamäki, V. Action space shaping in deep reinforcement learning. In Proceedings of the 2020 IEEE Conference on Games (CoG), Osaka, Japan, 24–27 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 479–486. [Google Scholar]
- Zahavy, T.; Haroush, M.; Merlis, N.; Mankowitz, D.J.; Mannor, S. Learn what not to learn: Action elimination with deep reinforcement learning. Adv. Neural Inf. Process. Syst. 2018, 31, 3566–3577. [Google Scholar]
- Zhuang, J.Y.; Zhang, L.; Zhao, S.Q.; Cao, J.; Wang, B.; Sun, H.B. Radar-based collision avoidance for unmanned surface vehicles. China Ocean Eng. 2016, 30, 867–883. [Google Scholar] [CrossRef]
- Safa, A.; Verbelen, T.; Keuninckx, L.; Ocket, I.; Hartmann, M.; Bourdoux, A.; Catthoor, F.; Gielen, G.G. A low-complexity radar detector outperforming OS-CFAR for indoor drone obstacle avoidance. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9162–9175. [Google Scholar] [CrossRef]
- Scott, C.; Nowak, R. A Neyman–Pearson approach to statistical learning. IEEE Trans. Inf. Theory 2005, 51, 3806–3819. [Google Scholar] [CrossRef]
- Li, S.E. Deep reinforcement learning. In Reinforcement Learning for Sequential Decision and Optimal Control; Springer: Berlin/Heidelberg, Germany, 2023; pp. 365–402. [Google Scholar]
- Zhou, L.; Ye, X.; Yang, X.; Shao, Y.; Liu, X.; Xie, P.; Tong, Y. A 3D-Sparse A* autonomous recovery path planning algorithm for Unmanned Surface Vehicle. Ocean Eng. 2024, 301, 117565. [Google Scholar] [CrossRef]





| Symbol | Meaning |
|---|---|
| → | Forward |
| ↑ | Upward |
| ↓ | Downward |
| ↗ | Forward-upward |
| ↘ | Forward-downward |
| ← | Backward |
| ↖ | Backward-upward |
| ↙ | Backward-downward |
| No | Radar Detection | Warning Range | Radar Power | Pulse | Correlation | False Alarm |
|---|---|---|---|---|---|---|
| 1 | 30 | 40 | 5 × 10−5 | 5 | 0.5 | 1 × 10−6 |
| 2 | 40 | 55 | 1 × 10−4 | 10 | 0.5 | 1 × 10−6 |
| 3 | 50 | 70 | 3.9063 × 10−3 | 15 | 0.5 | 1 × 10−6 |
| No | Radar Detection | Weights |
|---|---|---|
| 1 | 30 | (0, 1 × 10−4 , 0.8, 0, 0) |
| 2 | 40 | (1 × 10−6, 1 × 10−4, 8, 0, 1 × 102) |
| 3 | 50 | (1 × 10−9, 1 × 10−4, 8, 0, 9.5) |
| Methods | Time Steps | Cum. Probability | Dist. Travelled |
|---|---|---|---|
| PPO | 74,879 | 49.99 | 86,048.72 km |
| Action-shaping PPO | 887 | 15.99 | 1504.12 km |
| Methods | Time Steps | Cum. Probability | Dist. Travelled |
|---|---|---|---|
| Modified sparse | 470 | 0.0 | 613.32 km |
| Action-shaping PPO | 778 | 0.0 | 1394.76 km |
| Methods | Time Steps | Cum. Probability | Dist. Travelled |
|---|---|---|---|
| Modified sparse | 636 | 0.0 | 767.72 km |
| Action-shaping PPO | 681 | 0.0 | 1323.03 km |
| Methods | Time Steps | Cum. Probability | Dist. Travelled |
|---|---|---|---|
| Modified sparse | 472 | 0.0 | 615.31 km |
| Action-shaping PPO | 609 | 0.0 | 1197.18 km |
| Methods | Time Steps | Cum. Probability | Dist. Travelled |
|---|---|---|---|
| Modified sparse | 472 | 0.0 | 615.31 km |
| Action-shaping PPO | 609 | 0.0 | 1197.18 km |
| Improved Action-shaping PPO | 444 | 0.0 | 1100.53 km |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, A.M.; Perrusquía, A.; Guo, W.; Tsourdos, A. Flight Plan Optimisation of Unmanned Aerial Vehicles with Minimised Radar Observability Using Action Shaping Proximal Policy Optimisation. Drones 2024, 8, 546. https://doi.org/10.3390/drones8100546
Ali AM, Perrusquía A, Guo W, Tsourdos A. Flight Plan Optimisation of Unmanned Aerial Vehicles with Minimised Radar Observability Using Action Shaping Proximal Policy Optimisation. Drones. 2024; 8(10):546. https://doi.org/10.3390/drones8100546
Chicago/Turabian StyleAli, Ahmed Moazzam, Adolfo Perrusquía, Weisi Guo, and Antonios Tsourdos. 2024. "Flight Plan Optimisation of Unmanned Aerial Vehicles with Minimised Radar Observability Using Action Shaping Proximal Policy Optimisation" Drones 8, no. 10: 546. https://doi.org/10.3390/drones8100546
APA StyleAli, A. M., Perrusquía, A., Guo, W., & Tsourdos, A. (2024). Flight Plan Optimisation of Unmanned Aerial Vehicles with Minimised Radar Observability Using Action Shaping Proximal Policy Optimisation. Drones, 8(10), 546. https://doi.org/10.3390/drones8100546








