Abstract
Drones are an ecological tool used increasingly in shark research over the past decade. Due to their high-resolution camera and GPS systems, they have been used to estimate the sizes of animals using drone-based photogrammetry. Previous studies have used drone altitude to measure the target size accuracy of objects at the surface; however, target depth and its interaction with altitude have not been studied. We used DJI Mavic 3 video (3960 × 2160 pixel) and images (5280 × 3960 pixel) to measure an autonomous underwater vehicle of known size traveling at six progressively deeper depths to assess how sizing accuracy from a drone at 10 m to 80 m altitude is affected. Drone altitudes below 40 m and target depths below 2 m led to an underestimation of size of 76%. We provide evidence that accounting for the drone’s altitude and the target depth can significantly increase accuracy to 5% underestimation or less. Methods described in this study can be used to measure free-swimming, submerged shark size with accuracy that rivals hand-measuring methods.
1. Introduction
Uncrewed aerial vehicles, or UAVs, have become a popular ecological tool in monitoring and surveilling sharks in nearshore environments. To date, they have been used to study hunting behaviors in sharks [1,2], predation avoidance behaviors [1,3], nearshore movements and distributions [4,5,6,7,8], overlap with humans at beach locations [8], the effects of ecotourism on shark behavior [9,10], swimming kinematics and speeds [2,4,7,11], human–shark interactions [12], and as an early warning system for human safety [13,14,15,16]. However, the ability to accurately estimate the size of submerged marine life has proven to be challenging. Accurate estimates of shark size from UAV images or videos are important for providing water safety personnel with safety information and scientists with critical data used for quantifying population dynamics.
The most accurate measurements of shark size come from direct measures when a specimen is captured, restrained, and physically measured. Typical errors are less than 1% using these methods; however, these methods require capture and handling and can be linked to fishing-related animal mortality [17,18,19], handling stress [20,21], or size or species bias based on the fishing gear used [22,23]. Underwater or from the air, size estimates can also be made using calibrated stereoscopic cameras [24,25], and submerged parallel lasers [26,27]. However, in the absence of some frame of reference, visual estimates of size are prone to much larger errors. Sequira, Thums, Brooks, and Meekan (2016) [25], identified a significant, negative linear relationship for visual size estimates and shark body size, leading to an underestimation of 3 m for their largest observed whale sharks, Rhincodon typus.
UAV videos and images also suffer from this challenge if there is nothing of known size within the field of view at the time a shark is in the frame. While studies do exist that measure elasmobranch size using UAVs, these generally focus on surface-associated animals such as juvenile white sharks, whale sharks, and manta rays [4,28,29,30]. Traditional photogrammetry makes measuring mid-water column or demersal animals largely inaccurate.
Traditional UAV photogrammetry uses the UAV’s altitude, camera sensor width, and the frame’s pixel width to convert the individual pixels into an “actual” length, or ground sample distance (GSD), to measure distances [31]. In essence, the total distance between the target to be measured and the UAV is used to calibrate the image size. As a result, accurate altitude measurements are paramount to accurate size measurements. Unger et al. (2018) found that the internal barometric sensor onboard typical commercial UAVs can overestimate their altitude by 1.4 m even at low altitudes of 15 m [32]. Furthermore, UAVs, upon start-up, calibrate their launching altitude as 0. So, if they are launched from a pilot’s hands, a berm, a vessel, or any other unaccounted-for height above ground or sea level, this will lead to inaccurate altitude measurements. A calibration tool such as a floating meter stick can be placed in the field of view of the UAV to disregard altitude measurements, in which the calibration tool is measured in pixels and converted to a length within the frame of the UAV’s image to create a GSD [28,29]. However, this does not allow for changes in altitude while operating the UAV. This also has limited functionality for potentially dangerous species, long-distance flights in remote areas, and this also does not address the issue of target (animal) depth. Depth increases the shark’s actual distance from the UAV camera which can create bias in size measurements just as readily as inaccurate altitude measurements.
The varying target depth creates a unique issue when measuring submerged aquatic animals. Multiple studies have shown that properly identifying or even spotting sharks at deeper depths is difficult during UAV surveys [15,33,34,35] (Figure 1B,D). Surface conditions such as high turbidity due to recent rainfall, swell, or wind chop can also affect the operator’s ability to spot sharks, which is often compounded by the depth of the shark [14,35,36,37] (Figure 1C,D). Furthermore, wave swell or wind chop can break up or occlude the outline of a submerged shark being measured, leading to increased human error or bias during the image processing step of measuring. Snell’s Law also demonstrates that the difference in refractive index at the air–water interface alters the apparent size of observed objects. Due to the heterogeneity and random nature of sea surface movement, this can unpredictably refract light when observing objects across the air–water interface [38]. Without quantifying the magnitude of UAV image-based measurement errors associated with the distortion of a shark’s image based on its depth and the UAV’s altitude, the measurement of free-swimming sharks without the use of a calibration tool may remain inaccurate.

Figure 1.
Examples of sharks at varying depths from the surface and under varying conditions. (A) indicates a shark at the surface, with favorable body posture and environmental conditions for measurement. (B) depicts the same shark under the same environmental conditions at depth, where the caudal fin is nearly invisible. (C) depicts a shark in turbid waters, where despite being close to the surface, it is hard to see the complete silhouette. (D) depicts the effects of turbid water and depth. One shark may or may not be close to the surface but turbid waters show it is unclear how deep the shark is. The second shark is nearly invisible due to depth and turbid water.
Determining submerged depth of target is a measurement challenge that is unique for aquatic species that are not air breathers. Drone photogrammetry has been successfully used to accurately size air-breathing marine mammals [39,40,41,42,43]. Krause et al. (2011) [39], found a ~1–2% size error when estimating the leopard seal (Hydrurga leptonyx) size, for example. However, their air-breathing requirements force them to the surface where they can more easily be photographed. They also use terrestrial areas as haul-outs and resting areas, which allows for the length measurement without the impact of depth on the photogrammetry process. While aerial photogrammetry has shown to be successful in this field, there is still an unknown error that requires quantification for this method to be successful to measure the length of free-swimming sharks.
The primary goal of this study was to quantify the error associated with UAV-based shark size measurement based on the altitude of the UAV calibrated to varying depths of a shark proxy—an autonomous underwater vehicle (AUV). We aimed to quantify the magnitude of error across multiple image sources, e.g., still shots (photo mode) versus frame grabs from 4k video, associated with shark proxy depth ranging from the surface to 3 m depth and UAV altitudes ranging from 10 m to 80 m. We hypothesized that both increased target depth and increased UAV altitude would decrease the measurement accuracy. The goal of this study was to quantify the magnitude of overall error with this method, determine whether this error could be methodologically corrected, and determine the best methods for estimating free swimming sharks without an in-frame measurement reference.
2. Methods
2.1. Study Site
Data were collected offshore of Belmont Shore, Long Beach California, United States of America (33.747934319183, −118.132995506648) from 09:15 to 10:30 on 5 September 2023 (Figure 2) known as a former juvenile white shark aggregation site [43]. Wind speed was light, 1.3 m/s (NOAA meteorological weather buoy 9,410,665 J, Los Angeles Pier, California, 33.733164, −118.185491, 6 min resolution) so there was little to no wind chop. Belmont Shore is protected by large jetties due to its proximity to the Los Angeles Harbor so there was no swell during field data collection. Cloud cover was 99.2%, with 22.9 km of visibility (Visual Crossing Weather Data [44]). We conducted this study during the calmest and clearest possible conditions to determine the error during the best possible visibility for measurement conditions.
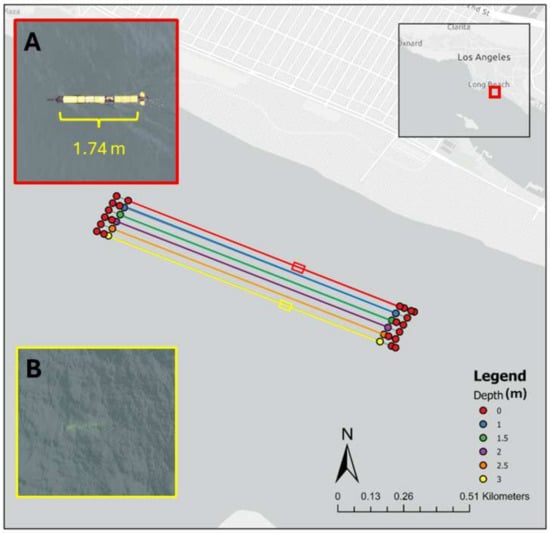
Figure 2.
A map of the study site and transect path of the AUV. (A) depicts the AUV at the surface at a UAV altitude of 10 m, as well as the measured length of the AUV. (B) depicts the AUV at a depth of 3 m at a UAV altitude of 10 m to show the difficulty in accurate measurements at depth. Each straight line represents a separate transect at subsequently deeper depths taken by the AUV. Colored symbols indicate GPS points of the AUV at separate depths. The AUV can only attain GPS at the surface, and each start and end of the transect indicate GPS points where the AUV is then programmed to dive or surface to the indicated depth.
2.2. Data Collection
The shark target proxy was a 2.14 m Iver 3 I3XO Ecomapper autonomous underwater vehicle (AUV) (YSI Integrated Systems and Services, St. Petersburg, FL, USA) (Figure 2, inset A; Figure 3). The AUV was used because it could mimic a free-swimming shark target, while also programmable to operate at known depths to account for the depth of the AUV during measurements. Although there was significant cloud cover, the bright yellow coloration (1.74 m long) on the vehicle made it easier to observe at the surface and at depth (Figure 2A,B). The vehicle was programmed to operate at 1.5 m/s in six separate 965 m straight-line transects in a “lawnmower” fashion. The first transect was programmed with the AUV at the surface, but the AUV operated each subsequent transect at progressively deeper depths (e.g., 0 m, 1 m, 1.5 m, 2 m, 2.5 m, and 3 m) (Figure 2 and Figure 3). Multiple studies have shown that sharks and shark decoys are rarely visible during aerial surveys when below 2–2.5 m [33,34,36,45]. Southern California also generally has turbid water, occluding the view of submerged marine life deeper than 3 m. To represent actual aerial surveys in similar areas or conditions, we did not test depths below 3 m. Marine life may be visible below 3 m in less turbid waters such as tropical, oligotrophic water, but that did not accurately represent the study site. In total, the programmed AUV mission covered 6570 m in 1 h and 12 min.
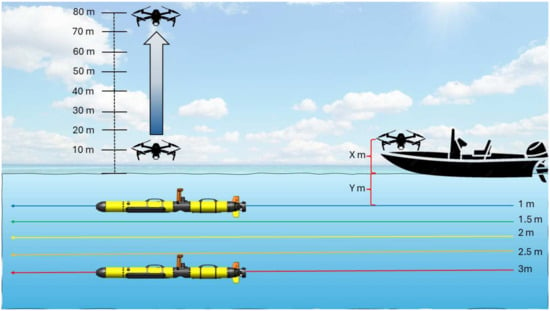
Figure 3.
A simplified representation of data collection. Each colored horizontal line represents an individual AUV transect. Colder colors represent earlier transects and warmer colors representing later transects. Altitudes listed next to the drone represent altitudes included in this study. The red brackets “X” and “Y” meters represent potentially unknown separation between the drone and the AUV, and potential sources of error. Images and videos were taken while the drone was directly above the AUV while moving (see Supplementary Materials Figures S1–S8 for examples).
We simultaneously manually flew a Mavic 3 (Da-Jiang Innovation Technology, Shenzhen, China) over the AUV maintaining an orthogonal camera position with the AUV in the center of the frame during each mission leg (Figure 2 and Figure 3; Supplementary Materials Figures S1–S8). The Mavic 3 was started and launched from the same location on the bow of a boat at the start of each transect, which placed the UAV 0.77 m above the sea surface upon start-up. Both photos and videos were taken to compare the measurement accuracy performance across both settings for the UAV. Both images and videos were tested because the UAV camera sensor operates at different pixel aspect ratios for still images and videos. Still images (photo mode) captured by the Mavic 3 contain 21 megapixels (5280 × 3956 pixels) while 4k videos captured by the Mavic 3 contains 8 megapixels (3840 × 2160 pixels) per frame representing ~2.5 times more pixels in still images recorded in photo mode. We captured 30 still images in a row, followed by 30 s of 4k video (30 fps) while the UAV was directly above the AUV. To make the still image and video data comparable, we took video frame grabs once a second throughout the 30 s video using VLC video processing software (VideoLan, v. 3.0.19) which retains the resolution of the original video in the frame grab. Of the 30 still images and video frame grabs taken, we used the best 15 images where the AUV was clearly visible, there was no motion blur, and minimal disruption of the AUV outline. This process was repeated for each altitude included in the study which represents 10–80 m in 10 m increments (Supplementary Materials Figures S1–S8 showcase data collected. Stills represent altitude differences with the AUV at the surface). Although the United States Federal Aviation Administration regulations allow for UAV flights up to 120 m above take-off elevation, we used 80 m as the ceiling for this study. Altitudes higher than 80 m made it difficult to properly discern the 1.74 m AUV within the UAV’s camera frame. In particular, when the UAV was at the surface, it only measured ~75 pixels for still images and ~55 pixels for video frame grabs. At higher altitudes we were not confident that the AUV would be visible, nor would accurate measurements be possible.
Current research on whether drone flight sound affects the behavior of elasmobranch is limited; however, there is limited evidence that flight altitudes as low as 5 m do not effect elasmobranch behavior [46]. A flight altitude of 10 m is not expected to impact the natural behavior of free-swimming elasmobranchs. Altitudes less than 10 m, however, make it very hard to track a large free-swimming shark, so 10 m was the floor for drone flights for this study to represent in situ data collection methods.
2.3. Image Processing
Images were processed using the ImageJ image processing software (NIH, v. 1.54d). Once pulled into ImageJ, the image was calibrated using pix4D’s ground sampling distance (GSD) calculator (https://support.pix4d.com/hc/en-us/articles/202560249. (accessed on 5 September 2023)) to determine the corresponding size of each pixel within the frame. GSD was calculated by inputting the camera sensor width (17.3 mm), the focal length (12.3 mm), the image height and width in pixels, and the altitude of the UAV from when the image was taken. The straight segment tool within ImageJ was then used to make the measurements. The length of the measurement in pixels was then multiplied by the GSD to obtain a full measured length. Due to the linear nature of the shark proxy used in this study, only the straight segment tool within ImageJ was used. Free-swimming sharks may have a curved body position, in which the segmented line tool within ImageJ would be used. This allows for the placement of individual measurement sections to be placed over the curvature of the dorsal surface of the shark to encompass the entire total length of the animal. Measurements in this fashion sum the measurement between all sections into one length representing the shark’s total length. The images were recalibrated separately for every set of images for each separate altitude and each image source. To ensure comparability between shots where the AUV may be less visible due to increased depth, only the distance between the start and end of the yellow portion of the AUV (1.74 m) was used for length measurements (Figure 2A,B). The AUV was not visible at a depth of 3 m when the UAV was flown at the lowest trial altitude (10 m) while capturing video due to a combination of general low visibility of an object at that depth, and glare at that altitude obscuring the AUV. As a result, those measurement data were excluded from the analyses.
2.4. Data Processing
Measurements of the AUV length at different depths were compared for still images and video frames using a two-way ANOVA from the statistics package in R studio (CRAN, v. 2024.4.0.735). The measured value was our continuous dependent variable and AUV depth, UAV altitude, the interaction between these two variables, and the image source (still image or video frames) were independent categorical variables. AUV depth and UAV altitude were controlled and were treated as categorical.
Size measurement accuracy was determined by calculating the relative error of each measurement. Predominantly, this is calculated by subtracting measured values from the true value and dividing them by the true value. We calculated relative error by subtracting measured values from the actual length of the AUV and dividing them by the measured values. This better reflects real-world scenarios where the “actual length” of a shark is an unknown variable. As a result, this allows us to calculate the relative error as a function of the measured size to help determine a potential correction factor for each measurement. Due to the non-linear, non-parametric, large dataset, presence of outliers, and heterogeneity in the variance of the data, relative error and measured size were plotted and modeled using a local regression fitting (loess) spline to assess how values change across depth and UAV altitude.
We repeated all the above processes for each of our three UAV altitude correction treatments. The first used the UAVs barometric estimate of launch altitude, uncorrected for actual altitude above sea level. The second treatment added the UAV’s altitude at image/video capture plus the UAVs launch altitude (launch elevation above the sea surface (UAV’s altitude +0.77 m)) to account for the separation of the UAV from the sea surface. This altered the GSD which was multiplied by the pixel measurement from ImageJ to attain a new measurement value. The third treatment added the UAV’s altitude at image/video capture plus the launch height off the sea surface and the depth of the AUV at image/video capture (UAV’s altitude + 0.77 m + AUV depth). This, again, altered the GSD which was then multiplied by the pixel measurement to attain a new measurement value and accommodated the entire distance between the UAV and the AUV.
3. Results
3.1. Overall Size Measurement Accuracy
Over 1445 AUV measurements were made across all AUV depths and UAV altitudes with size measurements ranging from 0.68 m to 2.39 m. The median was 1.5 m (first quartile 1.38, third quartile 1.58), with a mean of 1.46 m, representing a significant underestimation of size relative to the actual length of the AUV at 1.74 m. Measurements from still images and video frames showed a logarithmic increase in measurement accuracy with UAV altitude. Measurements taken at the lowest UAV altitudes performed the worst with the greatest underestimation of actual length and error. The only exception to this was measurements performed when the AUV was at the surface, and the UAV was at 10 m using still images (Figure 4A). Measurement accuracy exponentially increased until 30 to 40 m UAV altitude (depending on AUV depth) whereafter the measurements approach asymptote but still underestimated the actual AUV length (Figure 4A).
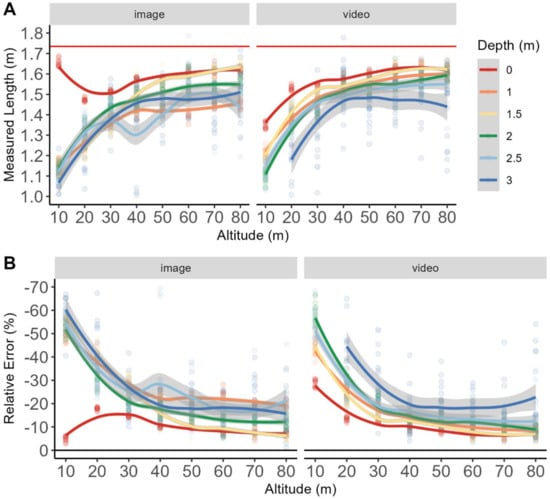
Figure 4.
Loess spline modeled measurement accuracy for both images and video for all raw data. (A) shows the raw measurements compared to the actual length of the AUV, indicated by the red line at 1.74 m across all depths. Raw data are shown as points. (B) depicts the relative error of each measurement to compare the accuracy of each measurement across all depths. All measurements were underestimations so relative error is negative.
AUV depth also had a significant effect on the accuracy of the measurement. In general, accuracy decreased with depth for both still images and video frames (Figure 4A). Video frame measurements seemed to share similar logarithmic increase accuracy rates between AUV depths, but deeper AUV depths had lower y-intercepts, and asymptotes were farther from the actual length of the AUV than the shallower depths (Figure 4A). For instance, when the AUV was at the surface, we observed the most accurate estimates of length for video frames, while when the AUV was at 3 m depth, we observed the least accurate estimates of AUV length for video frames. Still images, however, had less consistency in the logarithmic rate of increase in accuracy across AUV depths. For example, we observed the most accurate measurements when the AUV was at the surface, but accuracy decreased with increasing AUV depth (Figure 4A). There was also a significant drop in accuracy for measurements made with the UAV at 40 m altitude and the AUV at 2.5 m depth (Figure 4A). Variability in measurement estimates also increased significantly with depth for both still image and video frame measurements, likely due to the inability to accurately identify the AUV outline at depth (Figure 3 inset B for visual example; Figure 4A). For instance, with the UAV at 80 m altitude and the AUV at the surface, measurements ranged from 1.59 m to 1.63 m estimated length for video frames. When the UAV was at 80 m and the AUV was at 3 m, however, measurements ranged from 1.12 m to 2.31 m for video frames. This highlights the inaccuracy of making measurements of targets (e.g., sharks) at unknown depths. UAV altitude, AUV depth, the interaction between altitude and depth, and the image source all significantly affected the measurement accuracy (ANOVA, df = 7, 5, 35, and 1 respectively, F = 276.17, 109.95, 74.01, and 16.40, respectively, p < 0.05). Overall, video frame measurements seem to perform better and more consistently than still image measurements when the AUV was at any depth other than the surface.
Relative error data follow the same trends as the measurement data but allow for the quantification of the magnitude of error observed. For instance, the maximum relative error observed for this study was −76.4% ± 7.5% when the AUV was at 2.5 m depth and a UAV altitude of 40 m for still images (Table 1). Despite relative error peaking at a different UAV altitude, measurement accuracy was the least accurate when the UAV was at 10 m for both still images and video frames (Figure 4B and Table 1). A UAV altitude of 10 m relative error was significantly greater than any other UAV altitude for the same image source and AUV depth (Figure 4B and Table 1). The only exception to this was when the AUV was at 3 m and the UAV was at 20 m for video frames. This represented the maximum video frame relative error (−59.9% ±33.3%) observed in this study, but this is likely because the 3 m AUV depth and 10 m UAV altitude data could not be used in this study.

Table 1.
Relative error for every measurement across all depths, all altitudes, both sources, across all treatments. Values are the mean and standard deviation of the relative error.
3.2. Boat Height Corrected Measurement Accuracy
Correcting for launch height off the water (UAV altitude +0.77 m) significantly decreased the underestimation error of AUV length (Figure 5A,B). The maximum relative error for still images observed was when the AUV was at 2.5 m depth with the UAV at 40 m altitude with an error of 42.5% ± 2.4%, but this represents a 45% reduction in error for this combination of altitude and depth. Still images from the UAV at 10 m altitude still represent the greatest range in relative error ranging from 1.3% ± 1.1% with the AUV at the surface to an underestimation of −36% ± 5.2% with the AUV at 3 m depth. This resulted in a 37% difference in estimated size of the AUV between 0 m and 3 m depth with the UAV at 10 m altitude (Table 1). As a result, while accounting for the UAV launch height above the sea surface reduced relative error, still images performed worse than video frames. While the relative error was comparable at higher altitudes, low altitude measurement accuracy was inconsistent across depths and significantly worse when the AUV was at 3 m.
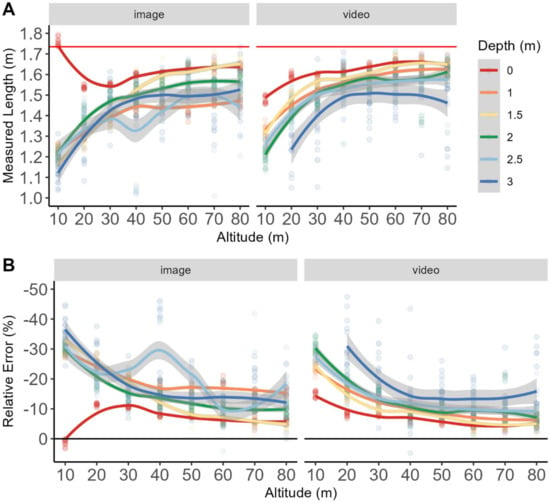
Figure 5.
Loess spline modeled measurement accuracy for both images and videos for data where the boat’s bow height was added to the UAV’s altitude to generate the GSD. (A) shows the raw measurements compared to the true length of the AUV, indicated by the red line at 1.74 m across all depths. Raw data are shown as points. (B) depicts the relative error of each measurement to compare the accuracy of each measurement across all depths.
Video frames had significantly lower relative error than still images in this treatment, where the boat’s height off the water is accounted for. (Figure 5). Twenty-two of the forty-eight depth and altitude combinations had ≤15% relative underestimation error (Table 1). Error peaked (−32.8% ± 11%) with the AUV at 3 m depth and the UAV at 20 m altitude, which represents a 54% reduction in relative underestimation error compared to non-corrected launch altitude. Furthermore, measurement accuracy still decreased with AUV depth, but the observed relative error was significantly reduced by accounting for the boat’s height off the sea surface across both image source datasets. (Figure 5 and Table 1).
3.3. Correction for Total Distance between UAV and AUV
Correction for the total distance between the UAV and the AUV (UAV’s altitude + 0.77 m + AUV depth at time of image capture) significantly increased accuracy for both still images and video frames across all depths. The only exception was the measurements when the AUV was at the surface, which remained unchanged (Figure 6 and Table 1). The maximum observed relative error was for still images when the AUV was at 2.5 m and the UAV was at 40 m altitude with an error of −38.9% ± 2.6% (Table 1). This represents an error reduction of 49% for this altitude and depth combination compared to uncorrected data (Table 1). This is the only treatment where a 10 m UAV altitude and 3 m AUV depth did not represent the highest relative error for still images. At 10 m UAV altitude and 1.5 m AUV depth, there was a −22.8% ± 2.2% error for still images while 10 m UAV altitude at 3 m AUV depth had a relative error of −18.3% ± 6.7% for still images (Table 1). Correcting for the entire distance between the UAV and AUV reduced the relative error for video frame data significantly more than the still image data.
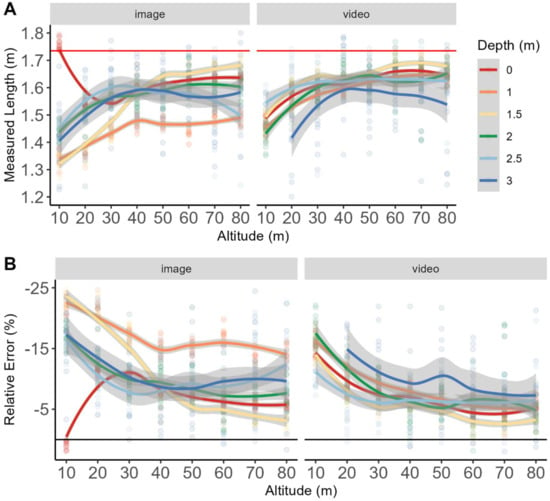
Figure 6.
Loess spline modeled measurement accuracy for both images and video for data where the boat’s bow height and the AUV depth were added to the UAV’s altitude to generate the GSD. (A) shows the raw measurements compared to the true length of the AUV, indicated by the red line at 1.74 m across all depths. Raw data are shown as points. (B) depicts the relative error of each measurement to compare the accuracy of each measurement across all depths.
Video frame data had significantly less relative error by accounting for the entire distance between the UAV and the AUV; only 8 of the 48 depth and altitude combinations retained an error greater than 10%, while 11 of the 48 altitude and depth combinations had <5% relative error for video frame data (Table 1). Every depth and altitude combination for UAV altitude > 40 m had less than 10% relative error for video frame data. This represents a maximum measurement discrepancy of 0.17 m between the actual length and UAV-based image measurements at UAV altitudes of 40 m or greater using this method. Furthermore, error can be as little as 0.08 m for UAV altitudes and depths where the error is less than 5%. Video frame data relative error still peaked at 23% ± 12.6% at a UAV altitude of 20 m and AUV depth of 3 m: (Table 1).
This treatment decreased the observed relative error between measurements taken when the AUV was at the surface and when it was at deeper depths. (Figure 6A,B). There was no significant difference between the 1.5 m, 2 m, and 3 m depths for still images and there was no significant difference between every single depth besides 3 m for video-sourced images (ANOVA, df = 5, F = 32.740 p > 0.05). While it did reduce observed relative error across all depths, it did not remove it completely. In fact, the only AUV depth and UAV altitude combination that approaches the actual length of the AUV were measurements taken when the UAV was at 10 m and the AUV was at the surface (Figure 6A,B). While error was still present, this treatment also highlights those methods that improve accuracy the most; almost all AUV depth and UAV altitude measurements from above 40 m were within 8 cm of the actual length of the AUV.
4. Discussion
This is the first study to identify the accuracy of UAV-based image length measurements of submerged aquatic targets without using an in-frame size reference. This is also the first study to identify how depth, and the interaction of depth and altitude, may lead to a significant underestimation of the length of measurements of a shark or other submerged aquatic species. Measurement underestimation can reach 76% if no corrective measures are taken. This study identifies previously undescribed measurement error sources, and provides alternatives, both during and after data collection, to increase measurement accuracy to within 5% of the actual length of a free-swimming shark assuming its depth is known.
4.1. The Effect of Altitude on UAV-Based Measurement Accuracy
Altitude significantly affected the accuracy of measurements, but, contrary to our hypotheses, the worst measurement estimates were at the lowest altitudes. At a UAV altitude <20 m, target measurement error increased by nearly ten-fold for still images and around six-fold for video frames for uncorrected UAV-based barometric calibration. This is contrary to other studies that have similarly assessed how altitude affects UAV-based image length measurements. For instance, Ramos et al. (2022) compared the size measurements of DJI Mavic 2 video frame (3840 × 2160, 24 frames per second) length measurements of captive manatees to actual measured lengths [41]. They observed a quadratic relationship between altitude and relative error, where low (30 m) UAV altitudes overestimated manatee body lengths by 15 cm and high (70 m) UAV altitudes overestimated lengths by 25 cm. The most overestimation they observed, however, was when the drone was at 50 m and they observed an overestimation of 35 cm [41]. Interestingly, they also only observed overestimation instead of underestimation as observed in our study. Multiple studies have also observed no significant difference between measurement accuracy or relative error and UAV altitude. Aubert et al. (2024) observed no significant difference between crocodilian proxy targets ranging in size from 13.7 cm, 27.3 cm, and 40.8 cm and measured them at 20 m, 30 m, and 40 m UAV altitude, with a maximum relative error of 4.4% [47]. Putch (2017) observed a maximum error of 1.14% error when measuring the distances between targets (11.8 m, 14.9 m, and 30.4 m) on a rooftop across 20 m, 30 m, 60 m, and 120 m UAV altitude [48]. It is important to note that these studies differed significantly from our methods by using a 1 m × 0.25 m polystyrene in-frame reference object [41], combining transect survey images into an orthomosaic map to make measurements of land-based targets [47], or used ground control points at known distances apart within the frame to calibrate images [48]. While this significantly reduces the error for measurements, these methods are not often feasible for highly mobile aquatic animals like sharks. One source of error within our study likely stems from the lack of accurate altitude of the UAV.
UAV altitude is often internally calculated during flight using a barometric altimeter, which can contribute a source of error. Although Unger et al. (2018) identified the potential for UAV barometers to overestimate their altitude by 1.4 m, this is likely not the case for our study [32]. GSD increases with altitude [42,47,49], so an overestimation of altitude would lead to an overestimation in the measurement values for surface targets. Matyja, Stanik, and Kubik (2022) [50] identified both an overall trend for underestimation of altitude and significant drift over time in the accuracy of barometric pressure sensors as they warm operational use [50]. For each transect within our data collection, we collected the lowest UAV altitude data first and collected data at progressively higher UAV altitudes. It is possible that the UAV altimeter underestimated UAV altitude at the beginning of the flight (10 m data collection) and as the UAV began to heat up throughout the transect it potentially corrected for the altitude underestimation and counteracted inherent drift over time. Combined with the stated 0.5 m vertical error in altitude DJI describes for the Mavic 3, this could explain the logarithmic underestimation trends with increasing altitude of flight. Low altitudes were exponentially higher in target length underestimation compared to higher altitudes. At 10 m UAV altitude, a 1 m altitude underestimation is a 10% bias, while at 80 m UAV altitude, a difference of 1 m only accounts for 1.25% of the altitude. Because the altitude of the UAV was not measured to assess accuracy, if there is any inaccuracy in the internal barometric altimeters it would affect low UAV measurements more than higher altitude UAV measurements. Furthermore, most UAVs use two systems to estimate their altitude: barometric altimeters and GNSS GPS trilateration. Albieri et al. (2017) identified that GNSS GPS trilateration performs significantly worse below 70 m altitude due to environmental noise [51]. This also provides evidence for why in this study, correcting the UAV’s altitude by adding the launch height (0.77 m) significantly improved the performance of our measurement accuracy. Even this small correction in altitude helps reduce potential underestimation based on data collected from the UAV’s onboard barometric altimeter.
The physical limitations of using UAV photogrammetry introduce another source of error along with altitude estimations. Light passes through a convex lens before it reaches the digital sensor to capture images with any UAV camera, which can distort straight lines within the image that are not present in the environment. This distortion propagates radially from the center of the image, where objects in the center have little to no observed distortion, while distortion increases at the periphery of the image [52,53,54]. At low altitudes (<20 m), the AUV takes up significantly more of the center of the image and approaches the edges of the image potentially being affected by this distortion. At high altitudes, the proportionately small AUV in the center of the frame is unaffected by this lens distortion. Bierlich et al. (2021) found that UAV-based length measurement uncertainty decreases exponentially with UAV altitude which may also reflect this distortion-related error [42]. Due to these sources of error, using low altitude (<40 m) still images or video frames for targets (>2 m) may introduce substantial underestimation error.
4.2. The Effect of Depth on Measurement Accuracy
This study highlights the need to account for the depth of the target when measuring the length of an animal using UAV-based images. We observed an order of magnitude more relative error associated with a 3 m depth vs. surface measurements for still images and up to a three-fold increase in relative error for video-sourced images. This highlights the importance of measuring targets that are near the surface unless depth is a known variable. We observed the largest standard deviations for measurements at the 2.5 m and 3 m depths across both still images and video-sourced images. This is likely due to image processing errors due to poor image resolution for the AUV’s outline at depth. Despite the yellow, high-contrast finish on the AUV, it remained difficult to accurately measure the AUV when it was below 2 m due to poor water clarity or surface ripples obscuring edges of the AUV. This aligns with previous aerial survey studies that suggested shark and proxy targets were significantly harder to spot below 2 m [15,33,34,35]. Color contrast captured by RGB visible light spectrum cameras decreases exponentially from the surface to 5 m depth, which indicates that silhouettes of targets at depth may no longer be distinguishable from their backgrounds [55].
Using images to measure lengths can increase human error. Bierlich et al.’s 2021 study found that a “blooming” effect along the edges of measured targets can occur which makes it unclear which pixels contain the edge of the target and which are superfluous [42]. This effect is increased with altitude, which decreases the pixel resolution for the target to be measured [42]. In our study, we observed that this effect was amplified with target depth, further increasing the likelihood of image processing error within measurements. This accentuates the issue of measuring live sharks at unknown depths. We used an AUV with a clear, high-contrast color finish to identify the error under the best visual circumstances. In the field, morphological features such as the tip of the caudal fin, which have low contrast and are visually nondescript when viewed from above, would not be visible at depths < 2 m. This would compound image processing errors for length measurements. As a result, it is clear that depth alters the appearance of the size of submerged targets or sharks and should always be accounted for in UAV-based length measurements.
Accounting for the depth of the target being measured in this study highlights the magnitude of error associated with target depth and the need to introduce methods to determine an animal’s depth. Even if the target depth is unknown, collecting data when the shark is closest to the surface and adding an estimated 1 m depth into the UAV’s altitude will increase measurement accuracy (Figure 5A,B and Figure 6). This highlights a potential source of error for studies that utilize a calibration tool at the surface but measure aquatic animals that are submerged. Calibration tools use an object of known length to convert each pixel into a known size. However, if there is a discrepancy between the plane at which the calibration tool sits and the target (e.g., shark) being measured, this will lead to inaccuracies. There is also no way to correct this during the data collection process or image processing since the distance between the UAV and the target is no longer a variable in the pixel-to-length conversion process. This severely limits the applicability of this method for sharks that spend a vast amount of time near the surface such as whale sharks and manta rays [28,29]. Regardless of the presence of a calibration tool or not, it is paramount to know or estimate the depth of an animal for proper measurement accuracy. While not present in current, cheap, commercially available UAVs, green laser LiDAR can be used to estimate depth and bathymetry [56]. Utilizing a two-camera system in the future, in which a high-resolution RGB camera captures images of the animal and a green-laser LiDAR camera estimates depth, we predict measurement accuracy could reach within 1% of the actual length. Artificial intelligent machine learning algorithms can certainly also be used to automate the measurement processes. These algorithms require being trained on thousands of images that account for the highly variable image quality attributed to varying water conditions and shark depth. Furthermore, machine learning algorithms struggle significantly to detect cryptic silhouettes, such as sharks at depth, which means any target not at the surface may not accurately be measured. Methods such as those discussed in this study can be immediately implemented and widely used, so even though artificial intelligence may eventually prove to be significantly powerful, presently these methods are less time-consuming while remaining accurate if performed correctly.
4.3. Best Methods for Accurate Size Measurement and Impacts
Our data show that uncorrected measurements using this method substantially underestimate the actual size of submerged targets. However, using the following methods, an accuracy of <5% can be achieved with very little methodological data collection alterations. We suggest that the UAV be started up and taken off from a known distance above the sea surface. This height should be added to the altitude of the UAV during data collection to correct for the unaccounted-for distance between the UAV and the shark. We suggest that data should be collected by taking videos at the highest resolution (3840 × 2160) at 30 fps. While 60 fps can be used to reduce blur between frames and increase the likelihood of capturing a usable frame within the video for size measurement, it requires more memory. Grabbing frames from a video also allows for the opportunity to film shark behaviors during the data collection process, while also observing the shark for opportunities to take frames when the shark is closest to the surface. We suggest that data be collected at ~40 m altitude, but this is dependent on the size of the sharks to be measured. Low altitudes have higher error rates and altitudes higher than 40 m or 50 m increase the “bloom” effect, thus increasing image processing error during the measurement process, with no significant increase in accuracy. Once the video has been taken, we suggest using a program like VLC to pull frames from the video to retain the original resolution of the video within the still extracted. Once the frames are extracted, we suggest only using images where the shark is closest to the surface and then adding an estimated depth to the altitude of the UAV. If sufficiently close to the surface, simply adding 1 m to the UAV’s altitude to account for the shark’s depth is sufficient. Lastly, we suggest using the Pix4D GSD calculator using these corrections to determine an accurate GSD. The final step is to measure the shark’s length in pixels and multiply it by the GSD. UAVs combining standard light-based video cameras and green Lidar cameras may provide a tool for estimating the depth of the shark, as Lidar can penetrate seawater and return an estimated depth of a target.
5. Conclusions
This study highlights the necessity for proper testing and identification of error source and error magnitude for the implementation of technology in new methods, such as UAV image-based shark size measurement. Estimates of UAV altitude and aquatic animal depth, if uncorrected, will lead to inaccurate measurements despite high-resolution images or video frame grabs. However, some of these effects can easily be corrected methodologically to accurately measure free-swimming sharks when at the surface without handling or disturbing the animals. The greatest challenge for applying corrections is determining the depth of the shark in the water; however, combining technologies such as Lidar and light-based cameras may allow estimates of depth of target. While future comparisons to images with a calibration tool in the frame are needed, this study is the first of its kind to correct for a known, yet previously unquantified, error source in the field.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/drones8100547/s1, Figures S1–S8.
Author Contributions
Conceptualization, P.T.R. and C.G.L.; methodology, P.T.R., K.J.A., R.E.P. and C.G.L., formal analysis, P.T.R., K.J.A., R.E.P. and C.G.L., writing—original draft preparation, P.T.R.; writing—review and editing, P.T.R., K.J.A., R.E.P. and C.G.L.; administration, C.G.L., funding acquisition, C.G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the State of California—Shark Beach Safety Program and the authors do not declare any conflicts of interest.
Data Availability Statement
Data can be publicly accessed through the OSF data repository found here: https://doi.org/10.17605/OSF.IO/PZ2C6.
Conflicts of Interest
The authors do not declare any conflicts of interest.
References
- Doan, M.D.; Kajiura, S.M. Adult blacktip sharks (Carcharhinus limbatus) use shallow water as a refuge from great hammerheads (Sphyrna mokarran). J. Fish Biol. 2020, 96, 1530–1533. [Google Scholar] [CrossRef] [PubMed]
- Tucker, J.P.; Colefax, A.P.; Santos, I.R.; Kelaher, B.P.; Pagendam, D.E.; Butcher, P.A. White shark behaviour altered by stranded whale carcasses: Insights from drones and implications for beach management. Ocean Coast. Manag. 2021, 200, 105477. [Google Scholar] [CrossRef]
- Towner, A.V.; Kock, A.A.; Stopforth, C.; Hurwitz, D.; Elwen, S.H. Direct observation of killer whales preying on white sharks and evidence of a flight response. Ecology 2023, 104, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Colefax, A.P.; Kelaher, B.P.; Pagendam, D.E.; Butcher, P.A. Assessing White Shark (Carcharodon carcharias) Behavior Along Coastal Beaches for Conservation-Focused Shark Mitigation. Front. Mar. Sci. 2020, 7, 268. [Google Scholar] [CrossRef]
- López, N.A. Spatial and temporal characterization of a recur rent scalloped hammerhead shark Sphyrna lewini aggregation using drones. ICES J. Mar. Sci. 2023, 80, 2356–2367. [Google Scholar] [CrossRef]
- Colefax, A.P.; Butcher, P.A.; Pagendam, D.E.; Kelaher, B.P. Comparing distributions of white, bull, and tiger sharks near and away from the surf break using three tech-based methods. Ocean Coast. Manag. 2020, 198, 105366. [Google Scholar] [CrossRef]
- Anderson, J.M.; Spurgeon, E.; Stirling, B.S.; May, J.; Rex, P.T.; Hyla, B.; McCullough, S.; Thompson, M.; Lowe, C.G. High resolution acoustic telemetry reveals swim speeds and inferred field metabolic rates in juvenile white sharks (Carcharodon carcharias). PLoS ONE 2022, 17, e0268914. [Google Scholar] [CrossRef]
- Rex, P.T.; May, J.H.; Pierce, E.K.; Lowe, C.G. Patterns of overlapping habitat use of juvenile white shark and human recreational water users along southern California beaches. PLoS ONE 2023, 18, e0286575. [Google Scholar] [CrossRef]
- Séguigne, C.; Mourier, J.; Vignaud, T.; Buray, N.; Clua, É. Effects of a COVID-19 lockdown-induced pause and resumption of artificial provisioning on blacktip reef sharks (Carcharhinus melanopterus) and pink whiprays (Pateobatis fai) in French Polynesia (East-Pacific). Ethology 2022, 128, 119–130. [Google Scholar] [CrossRef]
- Gayford, J.H.; Pearse, W.D.; De La Parra Venegas, R.; Whitehead, D.A. Quantifying the behavioural consequences of shark ecotourism. Sci. Rep. 2023, 13, 12938. [Google Scholar] [CrossRef]
- Porter, M.E.; Ruddy, B.T.; Kajiura, S.M. Volitional swimming kinematics of blacktip sharks, Carcharhinus limbatus, in the wild. Drones 2020, 4, 78. [Google Scholar] [CrossRef]
- Pirotta, V.; Hocking, D.P.; Iggleden, J.; Harcourt, R. Drone Observations of Marine Life and Human–Wildlife Interactions off Sydney, Australia. Drones 2022, 6, 75. [Google Scholar] [CrossRef]
- Engelbrecht, T.; Kock, A.; Waries, S.; O’Riain, M.J. Shark Spotters: Successfully reducing spatial overlap between white sharks (Carcharodon carcharias) and recreational water users in False Bay, South Africa. PLoS ONE 2017, 12, e0185335. [Google Scholar] [CrossRef]
- Hernández, C.; Mitchell, J.D.; Scott-Holland, T.B.; Butcher, P.A. Factors Affecting Shark Detection from Drone Patrols in Southeast Queensland, Eastern Australia. Biology 2022, 11, 1552. [Google Scholar] [CrossRef]
- Butcher, P.A.; Piddocke, T.P.; Colefax, A.P.; Hoade, B.; Peddemors, V.M.; Borg, L.; Cullis, B.R.; Butcher, P.A.; Piddocke, T.P.; Colefax, A.P.; et al. Beach safety: Can drones provide a platform for sighting sharks? Wildl. Res. 2019, 46, 701–712. [Google Scholar] [CrossRef]
- Sheridan, K.; Justin O’Riain, M.; Needham, M.D. Recreationist perceptions of lethal and non-lethal management of sharks in two of South Africa’s marine areas. Mar. Policy 2021, 132, 104633. [Google Scholar] [CrossRef]
- Musyl, M.K.; Brill, R.W.; Curran, D.S.; Fragoso, N.M.; McNaughton, L.M.; Nielsen, A.; Kikkawa, B.S.; Moyes, C.D. Postrelease survival, vertical and horizontal movements, and thermal habitats of five species of pelagic sharks in the central Pacific Ocean. Fish. Bull. 2011, 109, 341–368. [Google Scholar] [CrossRef]
- Benson, J.F.; Jorgensen, S.J.; O’Sullivan, J.B.; Winkler, C.; White, C.F.; Garcia-Rodriguez, E.; Sosa-Nishizaki, O.; Lowe, C.G. Juvenile survival, competing risks, and spatial variation in mortality risk of a marine apex predator. J. Appl. Ecol. 2018, 55, 2888–2897. [Google Scholar] [CrossRef]
- Gulak, S.J.B.; de Ron Santiago, A.J.; Carlson, J.K. Hooking mortality of scalloped hammerhead Sphyrna lewini and great hammerhead Sphyrna mokarran sharks caught on bottom longlines. Afr. J. Mar. Sci. 2015, 37, 267–273. [Google Scholar] [CrossRef]
- Mohan, J.A.; Jones, E.R.; Hendon, J.M.; Falterman, B.; Boswell, K.M.; Hoffmayer, E.R.; David Wells, R.J. Capture stress and post-release mortality of blacktip sharks in recreational charter fisheries of the Gulf of Mexico. Conserv. Physiol. 2020, 8, coaa041. [Google Scholar] [CrossRef]
- Bowlby, H.D.; Benoît, H.P.; Joyce, W.; Sulikowski, J.; Coelho, R.; Domingo, A.; Cortés, E.; Hazin, F.; Macias, D.; Biais, G.; et al. Beyond Post-release Mortality: Inferences on Recovery Periods and Natural Mortality From Electronic Tagging Data for Discarded Lamnid Sharks. Front. Mar. Sci. 2021, 8, 325. [Google Scholar] [CrossRef]
- Roskar, G.; McCallister, M.P.; Ajemian, M.J. Performance of Two Survey Gears Targeting Elasmobranchs in a Shallow, Subtropical Estuary. Mar. Coast. Fish. 2020, 12, 50–63. [Google Scholar] [CrossRef]
- Hannan, K.M.; Fogg, A.Q.; Driggers, W.B.; Hoffmayer, E.R.; Ingram, G.W.; Grace, M.A. Size selectivity and catch rates of two small coastal shark species caught on circle and J hooks in the northern Gulf of Mexico. Fish. Res. 2013, 147, 145–149. [Google Scholar] [CrossRef]
- Delacy, C.R.; Olsen, A.; Howey, L.A.; Chapman, D.D.; Brooks, E.J.; Bond, M.E. Affordable and accurate stereo-video system for measuring dimensions underwater: A case study using oceanic whitetip sharks Carcharhinus longimanus. Mar. Ecol. Prog. Ser. 2017, 574, 75–84. [Google Scholar] [CrossRef]
- Sequeira, A.M.M.; Thums, M.; Brooks, K.; Meekan, M.G. Error and bias in size estimates of whale sharks: Implications for understanding demography. R. Soc. Open Sci. 2016, 3, 150668. [Google Scholar] [CrossRef]
- Boube, T.; Azam, C.S.; Guilbert, A.; Huveneers, C.; Papastamatiou, Y.P.; Mourier, J.; Trujillo, J.E.; Femmami, N.; Kunovsky, A.; Bersani, F.; et al. First insights into the population characteristics and seasonal occurrence of the great hammerhead shark, Sphyrna mokarran (Rüppell, 1837) in the Western Tuamotu archipelago, French Polynesia. Front. Mar. Sci. 2023, 10, 1234059. [Google Scholar] [CrossRef]
- O’Connell, C.P.; Payne, M.; Payne, S.; Eller, L.J.; Shaw, J.; McGregor, A.; Rerekura, A.; Stewart, M.; Fox, A. Observations of Multiple Young-of-the-Year to Juvenile White Sharks (Carcharodon carcharias) within South-West Australian Waters and Its Implications for a Potential Nursery Area(s). J. Mar. Sci. Eng. 2023, 11, 563. [Google Scholar] [CrossRef]
- Whitehead, D.A.; Ayres, K.A.; Gayford, J.H.; Ketchum, J.T.; Galván-Magana, F.; Christiansen, F. Aerial photogrammetry of whale sharks (Rhincodon typus) in the Bay of La Paz, using an unoccupied aerial vehicle. Mar. Biol. 2022, 169, 94. [Google Scholar] [CrossRef]
- Setyawan, E.; Stevenson, B.C.; Izuan, M.; Constantine, R.; Erdmann, M.V. How Big Is That Manta Ray? A Novel and Non-Invasive Method for Measuring Reef Manta Rays Using Small Drones. Drones 2022, 6, 63. [Google Scholar] [CrossRef]
- McCauley, D.J.; Parsons, J.K.; Braman, C.A.; Anderson, J.M.; Caselle, J.E.; Critchley, E.J.; Glina, A.; Joyce, F.H.; Lowe, C.G.; Mladjov, S.; et al. Temporal and oceanographic factors differentially affect two size classes of white shark at a Southern California aggregation site. Mar. Ecol. Prog. Ser. 2024, 744, 101–114. [Google Scholar] [CrossRef]
- Tu, Y.H.; Phinn, S.; Johansen, K.; Robson, A.; Wu, D. Optimising drone flight planning for measuring horticultural tree crop structure. ISPRS J. Photogramm. Remote Sens. 2020, 160, 83–96. [Google Scholar] [CrossRef]
- Unger, D.; Hung, I.-K.; Kulhavy, D.; Zhang, Y.; Busch-Petersen, K. Accuracy of Unmanned Aerial System (Drone) Height Measurements. Int. J. Geospat. Environ. Res. 2018, 5, 6. [Google Scholar]
- Robbins, W.D.; Peddemors, V.M.; Kennelly, S.J. Assessment of Shark Sighting Rates by Aerial Beach Patrols. 2012. Available online: https://www.dpi.nsw.gov.au/ (accessed on 19 August 2022).
- Robbins, W.D.; Peddemors, V.M.; Kennelly, S.J.; Ives, M.C. Experimental Evaluation of Shark Detection Rates by Aerial Observers. PLoS ONE 2014, 9, e83456. [Google Scholar] [CrossRef] [PubMed]
- Benavides, M.T.; Fodrie, F.J.; Johnston, D.W. Shark detection probability from aerial drone surveys within a temperate estuary. J. Unmanned Veh. Syst. 2020, 8, 44–56. [Google Scholar] [CrossRef]
- Kelaher, B.P.; Colefax, A.P.; Tagliafico, A.; Bishop, M.J.; Giles, A.; Butcher, P.A. Assessing variation in assemblages of large marine fauna off ocean beaches using drones. Mar. Freshw. Res. 2019, 71, 68–77. [Google Scholar] [CrossRef]
- Monteforte, K.I.P.; Butcher, P.A.; Morris, S.G.; Kelaher, B.P. The Relative Abundance and Occurrence of Sharks off Ocean Beaches of New South Wales, Australia. Biology 2022, 11, 1456. [Google Scholar] [CrossRef]
- Alterman, M.; Schechner, Y.Y.; Perona, P.; Shamir, J. Detecting motion through dynamic refraction. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 245–251. [Google Scholar] [CrossRef]
- Krause, D.J.; Hinke, J.T.; Perryman, W.L.; Goebel, M.E.; LeRoi, D.J. An accurate and adaptable photogrammetric approach for estimating the mass and body condition of pinnipeds using an unmanned aerial system. PLoS ONE 2017, 12, e0187465. [Google Scholar] [CrossRef]
- Fudala, K.; Bialik, R. Breeding Colony Dynamics of Southern Elephant. Remote Sens. 2020, 12, 2964. [Google Scholar] [CrossRef]
- Ramos, E.A.; Landeo-Yauri, S.; Castelblanco-Martínez, N.; Arreola, M.R.; Quade, A.H.; Rieucau, G. Drone-based photogrammetry assessments of body size and body condition of Antillean manatees. Mamm. Biol. 2022, 102, 765–779. [Google Scholar] [CrossRef]
- Bierlich, K.C.; Schick, R.S.; Hewitt, J.; Dale, J.; Goldbogen, J.A.; Friedlaender, A.S.; Johnston, D.W. Bayesian approach for predicting photogrammetric uncertainty in morphometric measurements derived from drones. Mar. Ecol. Prog. Ser. 2021, 673, 193–210. [Google Scholar] [CrossRef]
- Anderson, J.M.; Burns, E.S.; Meese, E.N.; Farrugia, T.J.; Stirling, B.S.; White, C.F.; Logan, R.K.; O’Sullivan, J.; Winkler, C.; Lowe, C.G. Interannual Nearshore Habitat Use of Young of the Year White Sharks Off Southern California. Front. Mar. Sci. 2021, 8, 238. [Google Scholar] [CrossRef]
- Weather Data Services. Visual Crossing. Available online: https://www.visualcrossing.com/weather/weather-data-services (accessed on 4 April 2024).
- Colefax, A.P.; Butcher, P.A.; Pagendam, D.E.; Kelaher, B.P. Reliability of marine faunal detections in drone-based monitoring. Ocean Coast. Manag. 2019, 174, 108–115. [Google Scholar] [CrossRef]
- Bourke, E.; Raoult, V.; Williamson, J.E.; Gaston, T.F. Estuary Stingray (Dasyatis fluviorum) Behaviour Does Not Change in Response to Drone Altitude. Drones 2023, 7, 164. [Google Scholar] [CrossRef]
- Aubert, C.; Le Moguédec, G.; Velasco, A.; Combrink, X.; Lang, J.W.; Griffith, P.; Pacheco-Sierra, G.; Pérez, E.; Charruau, P.; Villamarín, F.; et al. Estimating Total Length of Partially Submerged Crocodylians from Drone Imagery. Drones 2024, 8, 115. [Google Scholar] [CrossRef]
- Putch, A. Linear Measurement Accuracy of DJI Drone Platforms and Photogrammetry. 2017, pp. 1–17. Available online: https://dronedeploy-www.cdn.prismic.io/dronedeploy-www%2F46e720cd-fb03-41ec-a6a3-09b424d674b8_linear+measurement+accuracy+of+dji+drone+platforms+and+cloud-based+photogrammetry-v11.pdf (accessed on 5 September 2024).
- Oleksyn, S.; Tosetto, L.; Raoult, V.; Williamson, J.E. Drone-based tracking of the fine-scale movement of a coastal stingray (Bathytoshia brevicaudata). Remote Sens. 2021, 13, 40. [Google Scholar] [CrossRef]
- Matyja, T.; Kubik, A.; Stanik, Z. the Mems-Based Barometric Altimeter Inaccuracy and Drift Phenomenon. Sci. J. Silesian Univ. Technol. Ser. Transp. 2022, 116, 141–162. [Google Scholar] [CrossRef]
- Albéri, M.; Baldoncini, M.; Bottardi, C.; Chiarelli, E.; Fiorentini, G.; Raptis, K.G.C.; Realini, E.; Reguzzoni, M.; Rossi, L.; Sampietro, D.; et al. Accuracy of flight altitude measured with low-cost GNSS, radar and barometer sensors: Implications for airborne radiometric surveys. Sensors 2017, 17, 1889. [Google Scholar] [CrossRef]
- Ricolfe-Viala, C.; Sánchez-Salmerón, A.J. Robust metric calibration of non-linear camera lens distortion. Pattern Recognit. 2010, 43, 1688–1699. [Google Scholar] [CrossRef]
- Yahyanejad, S.; Misiorny, J.; Rinner, B. Lens distortion correction for thermal cameras to improve aerial imaging with small-scale UAVs. In Proceedings of the 2011 IEEE International Symposium on Robotic and Sensors Environments (ROSE), Montreal, QC, Canada, 17–18 September 2011; pp. 231–236. [Google Scholar] [CrossRef]
- Dallaire, X.; Buquet, J.; Roulet, P.; Parent, J.; Konen, P.; Lalonde, J.-F.; Thibault, S. Enhancing learning-based computer vision algorithms accuracy in sUAS using navigation wide-angle cameras. In Proceedings of the Artificial Intelligence and Machine Learning in Defense Applications III, Online, 13–18 September 2021; Volume 11870, pp. 12–20. [Google Scholar] [CrossRef]
- Sabbah, S.; Gray, S.M.; Hawryshyn, C.W. Radiance fluctuations induced by surface waves can enhance the appearance of underwater objects. Limnol. Oceanogr. 2012, 57, 1025–1041. [Google Scholar] [CrossRef]
- Szafarczyk, A.; Toś, C. The Use of Green Laser in LiDAR Bathymetry: State of the Art and Recent Advancements. Sensors 2023, 23, 292. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).