Drone Multiline Light Detection and Ranging Data Filtering in Coastal Salt Marshes Using Extreme Gradient Boosting Model
Abstract
1. Introduction
2. Methodology
2.1. Architecture Overview
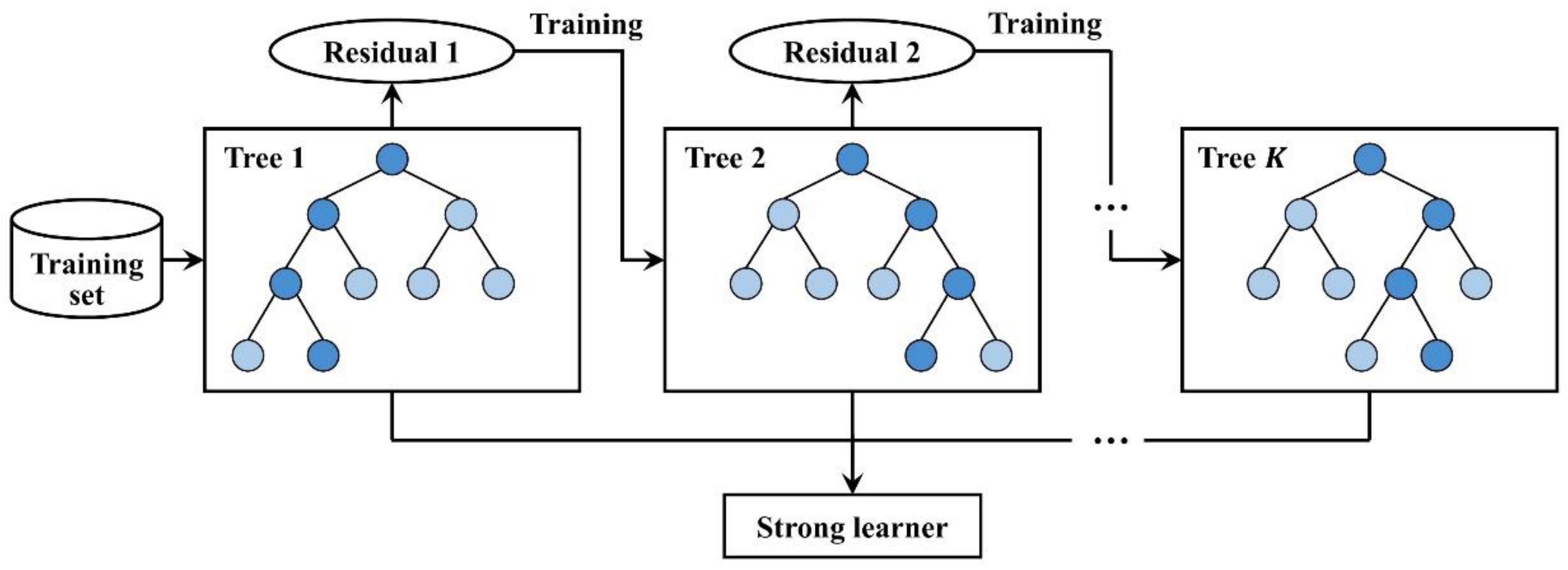
2.2. XGBoost Algorithm
2.3. Feature Selection and Derivation
2.3.1. Feature Selection
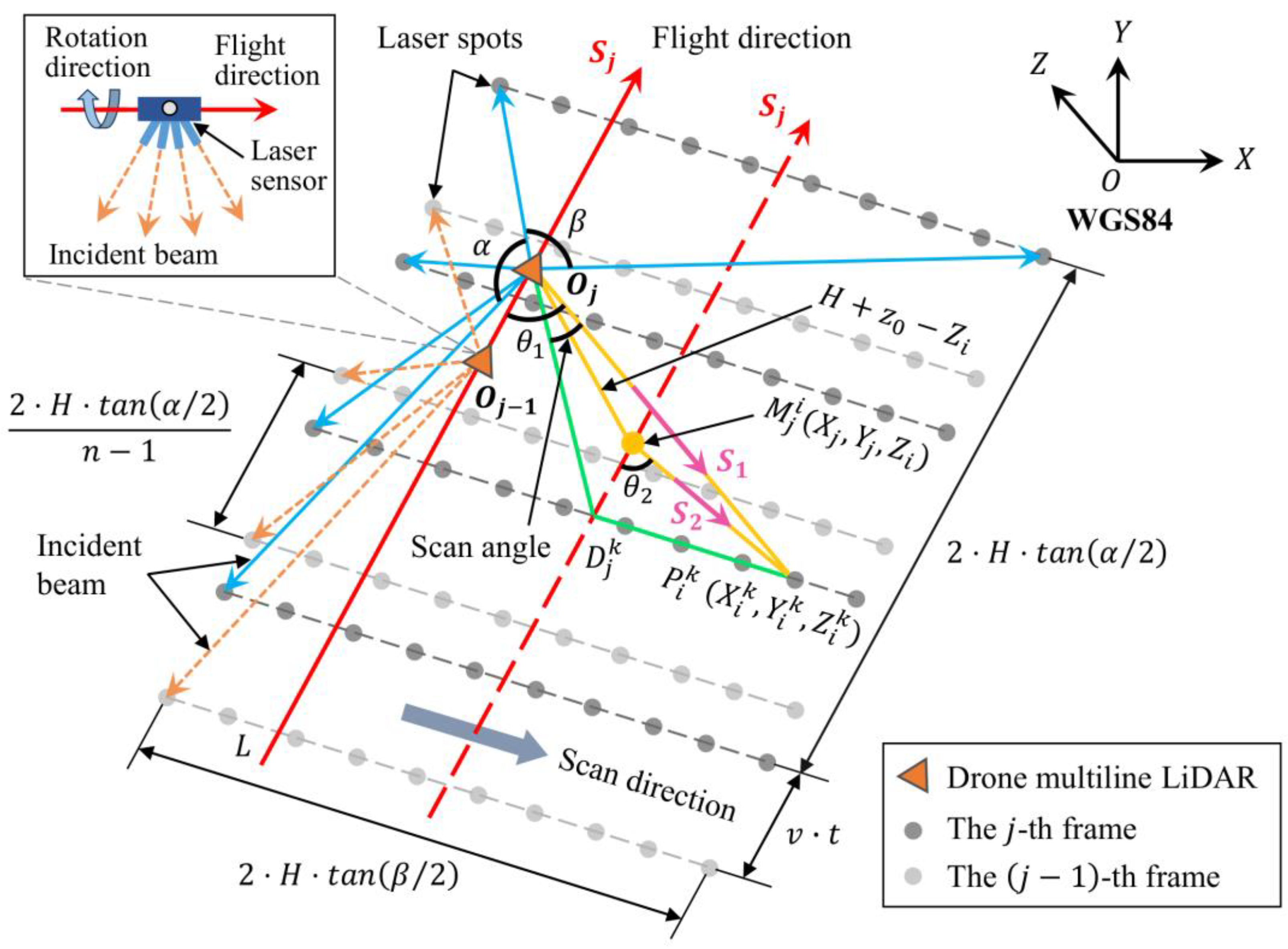
2.3.2. Derivation of Scan Angle and Distance
2.4. Accuracy Evaluation
3. Experiments and Results
3.1. Data and Materials
3.2. Model Training and Testing Results
3.3. Model-Validation Results
3.4. Separating Results of the Entire Study Site
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Noujas, V.; Thomas, K.V.; Badarees, K.O. Shoreline management plan for a mudbank dominated coast. Ocean Eng. 2016, 112, 47–65. [Google Scholar] [CrossRef]
- Yan, J.F.; Zhao, S.Y.; Su, F.Z.; Du, J.X.; Feng, P.F.; Zhang, S.X. Tidal flat extraction and change analysis based on the RF-W model: A case study of Jiaozhou Bay, East China. Remote Sens. 2021, 13, 1436. [Google Scholar] [CrossRef]
- Macreadie, P.I.; Anton, A.; Raven, J.A.; Beaumont, N.; Connolly, R.M.; Friess, D.A.; Kelleway, J.J.; Kennedy, H.; Kuwae, T.; Lavery, P.S.; et al. The future of Blue Carbon science. Nat. Commun. 2019, 10, 13. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.M.; Sanders, C.J.; Santos, I.R.; Tang, J.W.; Schuerch, M.; Kirwan, M.L.; Kopp, R.E.; Zhu, K.; Li, X.Z.; Yuan, J.C.; et al. Global blue carbon accumulation in tidal wetlands increases with climate change. Nat. Sci. Rev. 2021, 8, 11. [Google Scholar] [CrossRef] [PubMed]
- Rolando, J.L.; Hodges, M.; Garcia, K.D.; Krueger, G.; Williams, N.; Carr, J.C.; Robinson, J.; George, A.; Morris, J.; Kostka, J.E. Restoration and resilience to sea level rise of a salt marsh affected by dieback events. Ecosphere 2023, 14, 16. [Google Scholar] [CrossRef]
- Paul, M.; Bischoff, C.; Koop-Jakobsen, K. Biomechanical traits of salt marsh vegetation are insensitive to future climate scenarios. Sci. Rep. 2022, 12, 21272. [Google Scholar] [CrossRef] [PubMed]
- Kulawardhana, R.W.; Popescu, S.C.; Feagin, R.A. Fusion of lidar and multispectral data to quantify salt marsh carbon stocks. Remote Sens. Environ. 2014, 154, 345–357. [Google Scholar] [CrossRef]
- White, S.M.; Madsen, E.A. Tracking tidal inundation in a coastal salt marsh with Helikite airphotos: Influence of hydrology on ecological zonation at Crab Haul Creek, South Carolina. Remote Sens. Environ. 2016, 184, 605–614. [Google Scholar] [CrossRef]
- Tang, Y.N.; Ma, J.; Xu, J.X.; Wu, W.B.; Wang, Y.C.; Guo, H.Q. Assessing the impacts of tidal creeks on the spatial patterns of coastal salt marsh vegetation and its aboveground biomass. Remote Sens. 2022, 14, 1839. [Google Scholar] [CrossRef]
- Jin, C.; Gong, Z.; Shi, L.; Zhao, K.; Tinoco, R.O.; San Juan, J.E.; Geng, L.; Coco, G. Medium-term observations of salt marsh morphodynamics. Front. Mar. Sci. 2022, 9, 13. [Google Scholar] [CrossRef]
- Kang, Y.; Ding, X.; Xu, F.; Zhang, C.; Ge, X. Topographic mapping on large-scale tidal flats with an iterative approach on the waterline method. Estuar. Coast. Shelf Sci. 2017, 190, 11–22. [Google Scholar] [CrossRef]
- Gao, W.L.; Shen, F.; Tan, K.; Zhang, W.G.; Liu, Q.X.; Lam, N.S.N.; Ge, J.Z. Monitoring terrain elevation of intertidal wetlands by utilising the spatial-temporal fusion of multi-source satellite data: A case study in the Yangtze (Changjiang) Estuary. Geomorphology 2021, 383, 12. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, C.; Schwarz, C.; Tian, B.; Jiang, W.; Wu, W.; Garg, R.; Garg, P.; Aleksandr, C.; Mikhail, S.; et al. Mapping three-dimensional morphological characteristics of tidal salt-marsh channels using UAV structure-from-motion photogrammetry. Geomorphology 2022, 407, 108235. [Google Scholar] [CrossRef]
- Yang, B.; Ali, F.; Zhou, B.; Li, S.; Yu, Y.; Yang, T.; Liu, X.; Liang, Z.; Zhang, K. A novel approach of efficient 3D reconstruction for real scene using unmanned aerial vehicle oblique photogrammetry with five cameras. Comput. Electr. Eng. 2022, 99, 107804. [Google Scholar] [CrossRef]
- Taddia, Y.; Pellegrinelli, A.; Corbau, C.; Franchi, G.; Staver, L.W.; Stevenson, J.C.; Nardin, W. High-resolution monitoring of tidal systems using UAV: A case study on poplar island, MD (USA). Remote Sens. 2021, 13, 1364. [Google Scholar] [CrossRef]
- Wang, X.X.; Xiao, X.M.; Zou, Z.H.; Chen, B.Q.; Ma, J.; Dong, J.W.; Doughty, R.B.; Zhong, Q.Y.; Qin, Y.W.; Dai, S.Q.; et al. Tracking annual changes of coastal tidal flats in China during 1986-2016 through analyses of Landsat images with Google Earth Engine. Remote Sens. Environ. 2020, 238, 15. [Google Scholar] [CrossRef]
- Xu, N.; Ma, Y.; Yang, J.; Wang, X.H.; Wang, Y.J.; Xu, R. Deriving tidal flat topography using ICESat-2 laser altimetry and Sentinel-2 imagery. Geophys. Res. Lett. 2022, 49, 10. [Google Scholar] [CrossRef]
- Chen, C.P.; Zhang, C.; Tian, B.; Wu, W.T.; Zhou, Y.X. Tide2Topo: A new method for mapping intertidal topography accurately in complex estuaries and bays with time-series Sentinel-2 images. ISPRS-J. Photogramm. Remote Sens. 2023, 200, 55–72. [Google Scholar] [CrossRef]
- Brunetta, R.; Duo, E.; Ciavola, P. Evaluating short-term tidal flat evolution through UAV surveys: A case study in the Po Delta (Italy). Remote Sens. 2021, 13, 2322. [Google Scholar] [CrossRef]
- Xie, W.M.; Guo, L.C.; Wang, X.Y.; He, Q.; Dou, S.T.; Yu, X. Detection of seasonal changes in vegetation and morphology on coastal salt marshes using terrestrial laser scanning. Geomorphology 2021, 380, 10. [Google Scholar] [CrossRef]
- Zhou, W.; Chen, F.L.; Guo, H.D.; Hu, M.Y.; Li, Q.; Tang, P.P.; Zheng, W.W.; Liu, J.A.; Luo, R.P.; Yan, K.K.; et al. UAV Laser scanning technology: A potential cost-effective tool for micro-topography detection over wooded areas for archaeological prospection. Int. J. Digit. Earth 2020, 13, 1279–1301. [Google Scholar] [CrossRef]
- Kim, H.; Kim, Y.; Lee, J. Tidal creek extraction from airborne LiDAR data using ground filtering techniques. KSCE J. Civ. Eng. 2020, 24, 2767–2783. [Google Scholar] [CrossRef]
- Sun, X.B.; Wang, S.K.; Liu, M. A novel coding architecture for multi-line LiDAR point clouds based on clustering and convolutional LSTM network. IEEE Trans. Intell. Transp. Syst. 2022, 23, 2190–2201. [Google Scholar] [CrossRef]
- Tao, P.J.; Tan, K.; Ke, T.; Liu, S.; Zhang, W.G.; Yang, J.R.; Zhu, X.J. Recognition of ecological vegetation fairy circles in intertidal salt marshes from UAV LiDAR point clouds. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 9. [Google Scholar] [CrossRef]
- Li, H.F.; Ye, C.M.; Guo, Z.X.; Wei, R.L.; Wang, L.X.; Li, J. A fast progressive TIN densification filtering algorithm for airborne LiDAR data using adjacent surface information. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 12492–12503. [Google Scholar] [CrossRef]
- Zhang, K.Q.; Chen, S.C.; Whitman, D.; Shyu, M.L.; Yan, J.H.; Zhang, C.C. A progressive morphological filter for removing nonground measurements from airborne LIDAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef]
- Vosselman, G. Slope based filtering of laser altimetry data. Int. Arch. Photogramm. Remote Sens. 2000, 33, 935–942. [Google Scholar]
- Zhang, W.M.; Qi, J.B.; Wan, P.; Wang, H.T.; Xie, D.H.; Wang, X.Y.; Yan, G.J. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Tan, K.; Chen, J.; Qian, W.W.; Zhang, W.G.; Shen, F.; Cheng, X.J. Intensity data correction for long-range terrestrial laser scanners: A case study of target differentiation in an intertidal zone. Remote Sens. 2019, 11, 331. [Google Scholar] [CrossRef]
- Errington, A.F.C.; Daku, B.L.F. Temperature compensation for radiometric correction of terrestrial LiDAR intensity data. Remote Sens. 2017, 9, 356. [Google Scholar] [CrossRef]
- Tan, K.; Cheng, X.J. Correction of incidence angle and distance effects on TLS intensity data based on reference targets. Remote Sens. 2016, 8, 251. [Google Scholar] [CrossRef]
- Sanchiz-Viel, N.; Bretagne, E.; Mouaddib, E.; Dassonvalle, P. Radiometric correction of laser scanning intensity data applied for terrestrial laser scanning. ISPRS-J. Photogramm. Remote Sens. 2021, 172, 1–16. [Google Scholar] [CrossRef]
- Poullain, E.; Garestier, F.; Levoy, F.; Bretel, P. Analysis of ALS intensity behavior as a function of the incidence angle in coastal environments. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 313–325. [Google Scholar] [CrossRef]
- Zhao, J.H.; Chen, M.Y.; Zhang, H.M.; Zheng, G. A hovercraft-borne LiDAR and a comprehensive filtering method for the topographic survey of mudflats. Remote Sens. 2019, 11, 1646. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef]
- Sheykhmousa, M.; Mahdianpari, M.; Ghanbari, H.; Mohammadimanesh, F.; Ghamisi, P.; Homayouni, S. Support vector machine versus random forest for remote sensing image classification: A meta-analysis and systematic review. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 6308–6325. [Google Scholar] [CrossRef]
- Zhong, L.H.; Hu, L.N.; Zhou, H. Deep learning based multi-temporal crop classification. Remote Sens. Environ. 2019, 221, 430–443. [Google Scholar] [CrossRef]
- Liu, S.; Tan, K.; Tao, P.J.; Yang, J.R.; Zhang, W.G.; Wang, Y.J. Rigorous density correction model for single-scan TLS point clouds. IEEE Trans. Geosci. Remote Sens. 2023, 61, 18. [Google Scholar] [CrossRef]
- Chen, T.Q.; Guestrin, C.; Assoc Comp, M. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Nguyen, M.H.; de la Torre, F. Optimal feature selection for support vector machines. Pattern Recognit. 2010, 43, 584–591. [Google Scholar] [CrossRef]
- Yan, W.Y.; Shaker, A. Radiometric correction and normalization of airborne LiDAR intensity data for improving land-cover classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7658–7673. [Google Scholar]
- Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare-Earth extraction from airborne laser scanning point clouds. ISPRS-J. Photogramm. Remote Sens. 2004, 59, 85–101. [Google Scholar] [CrossRef]
- Lusted, L.B. Decision-making studies in patient management. N. Engl. J. Med. 1971, 284, 416–424. [Google Scholar] [CrossRef] [PubMed]
- Bradley, A.P. The use of the area under the roc curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- He, H.; Garcia, E.A. Learning from imbalanced data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar]

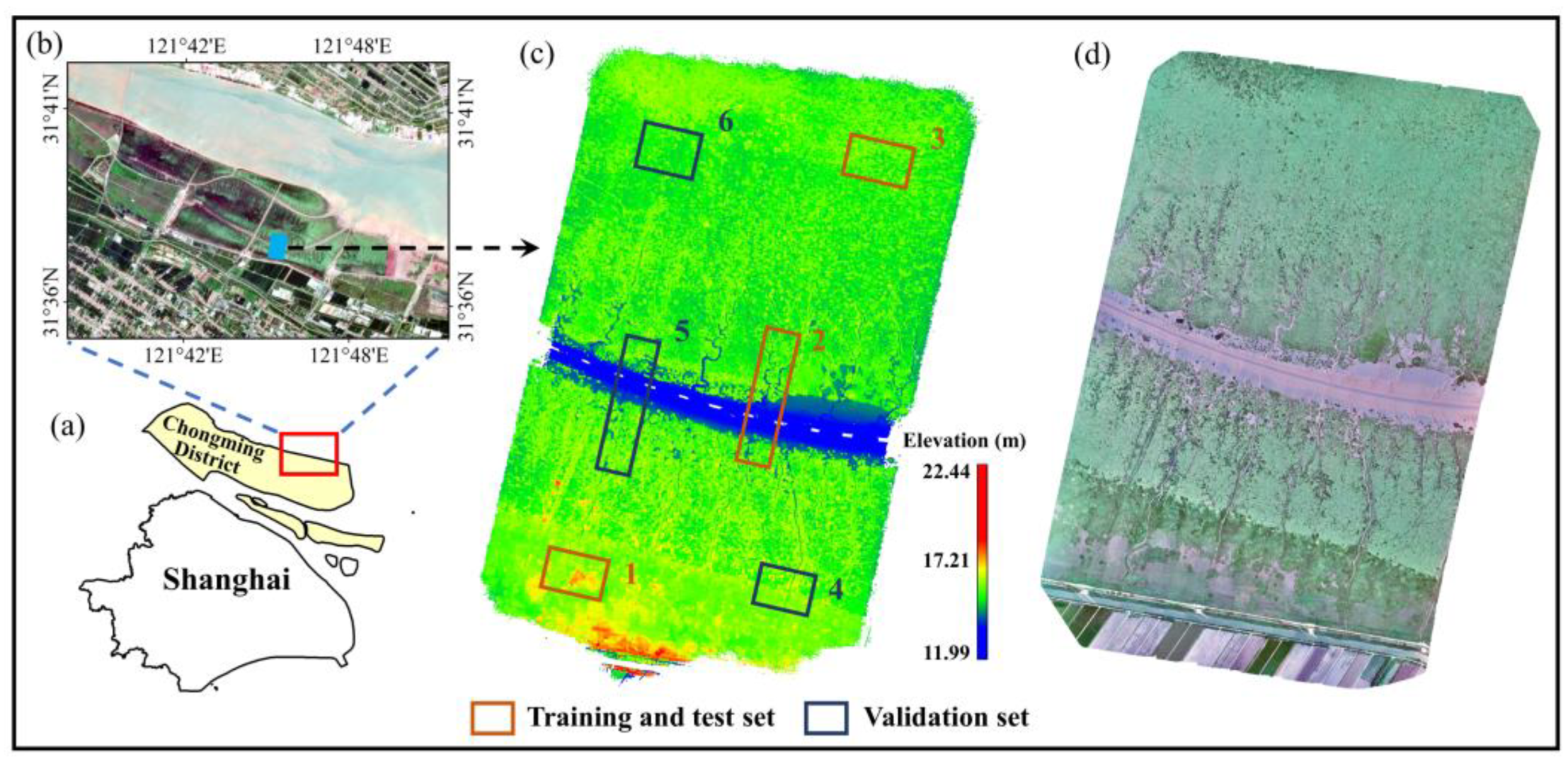







| Dataset | Point Number | Size | Features | |
|---|---|---|---|---|
| Training and test set | 1 | 5,410,276 | 250 × 160 m | (1) Vegetation: PA, SA, and SM, highly dense (2) Several intertidal creeks |
| 2 | 5,260,976 | 130 × 510 m | (1) Vegetation: SA and SM, relatively dense (2) Multiple intertidal creeks and a small part of bare mudflat | |
| 3 | 5,201,640 | 260 × 170 m | (1) Vegetation: SA, highly dense (2) No intertidal creek | |
| Validation set | 4 | 4,780,134 | 250 × 180 m | (1) Vegetation: PA and SA, relatively dense (2) Several intertidal creeks |
| 5 | 4,700,965 | 120 × 490 m | (1) Vegetation: SA and SM, relatively dense (2) Multiple intertidal creeks and a small part of bare mudflat | |
| 6 | 5,147,804 | 240 × 195 m | (1) Vegetation: SA, relatively dense (2) No intertidal creek |
| Region 4 | Region 5 | Region 6 | |
|---|---|---|---|
| AUC | 0.9191 | 0.9535 | 0.8607 |
| G-mean | 0.9158 | 0.9534 | 0.8496 |
| Region 4 | Region 5 | Region 6 | ||||
|---|---|---|---|---|---|---|
| AUC | G-Mean | AUC | G-Mean | AUC | G-Mean | |
| XGBoost | 0.9191 | 0.9158 | 0.9535 | 0.9534 | 0.8607 | 0.8496 |
| RF | 0.9069 | 0.9023 | 0.9551 | 0.9550 | 0.8554 | 0.8433 |
| AdaBoost | 0.9032 | 0.8984 | 0.9516 | 0.9515 | 0.8124 | 0.7911 |
| CatBoost | 0.9136 | 0.9098 | 0.9549 | 0.9548 | 0.8363 | 0.8204 |
| PMF | 0.7350 | 0.7226 | 0.8019 | 0.7986 | 0.7232 | 0.7157 |
| SF | 0.6495 | 0.6169 | 0.7301 | 0.7296 | 0.7017 | 0.6829 |
| CSF | 0.7366 | 0.7251 | 0.6820 | 0.6819 | 0.5627 | 0.5588 |
| CIF | 0.6876 | 0.6237 | 0.7639 | 0.7361 | 0.5209 | 0.5092 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Tan, K.; Liu, S.; Wang, F.; Tao, P.; Wang, Y.; Cheng, X. Drone Multiline Light Detection and Ranging Data Filtering in Coastal Salt Marshes Using Extreme Gradient Boosting Model. Drones 2024, 8, 13. https://doi.org/10.3390/drones8010013
Wu X, Tan K, Liu S, Wang F, Tao P, Wang Y, Cheng X. Drone Multiline Light Detection and Ranging Data Filtering in Coastal Salt Marshes Using Extreme Gradient Boosting Model. Drones. 2024; 8(1):13. https://doi.org/10.3390/drones8010013
Chicago/Turabian StyleWu, Xixiu, Kai Tan, Shuai Liu, Feng Wang, Pengjie Tao, Yanjun Wang, and Xiaolong Cheng. 2024. "Drone Multiline Light Detection and Ranging Data Filtering in Coastal Salt Marshes Using Extreme Gradient Boosting Model" Drones 8, no. 1: 13. https://doi.org/10.3390/drones8010013
APA StyleWu, X., Tan, K., Liu, S., Wang, F., Tao, P., Wang, Y., & Cheng, X. (2024). Drone Multiline Light Detection and Ranging Data Filtering in Coastal Salt Marshes Using Extreme Gradient Boosting Model. Drones, 8(1), 13. https://doi.org/10.3390/drones8010013







