Dynamic Analysis and Experiment of Multiple Variable Sweep Wings on a Tandem-Wing MAV
Abstract
:1. Introduction
- (1)
- The multiple variable sweep design can reduce the additional inertia forces and moments and weaken the dynamic coupling between longitudinal and lateral motion during morphing;
- (2)
- The tandem-wing MAV can morph symmetrically for pitch control and asymmetrically for roll control and fly without traditional aileron and elevator.
2. Design of the Tandem-Wing MAV and Aerodynamic Characteristics
2.1. Design of the Tandem-Wing MAV
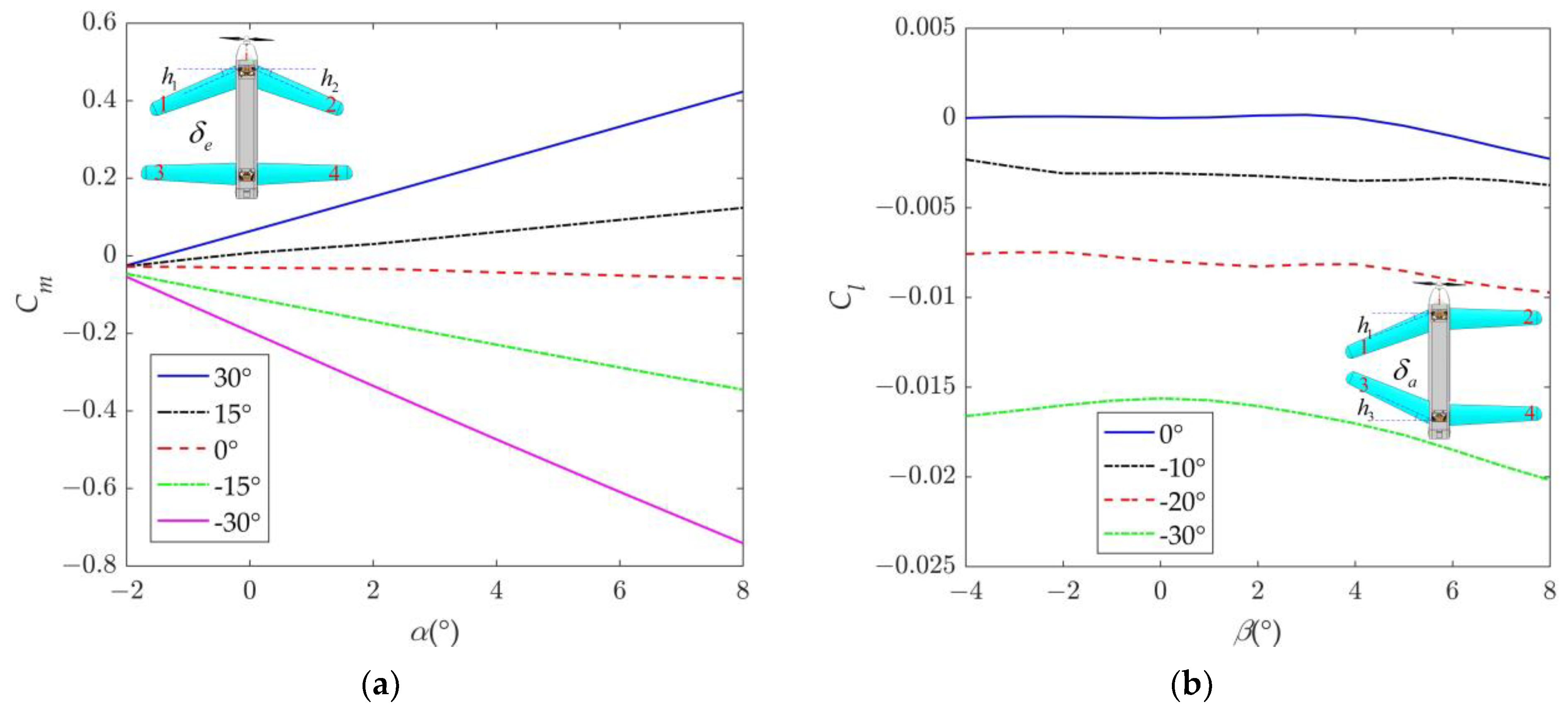
2.2. Aerodynamic Characteristics with Morphing
3. Modeling and Dynamic Analysis
3.1. Longitudinal Dynamic Analysis with Symmetric Morphing
3.1.1. Model Simplification of Longitudinal Motion
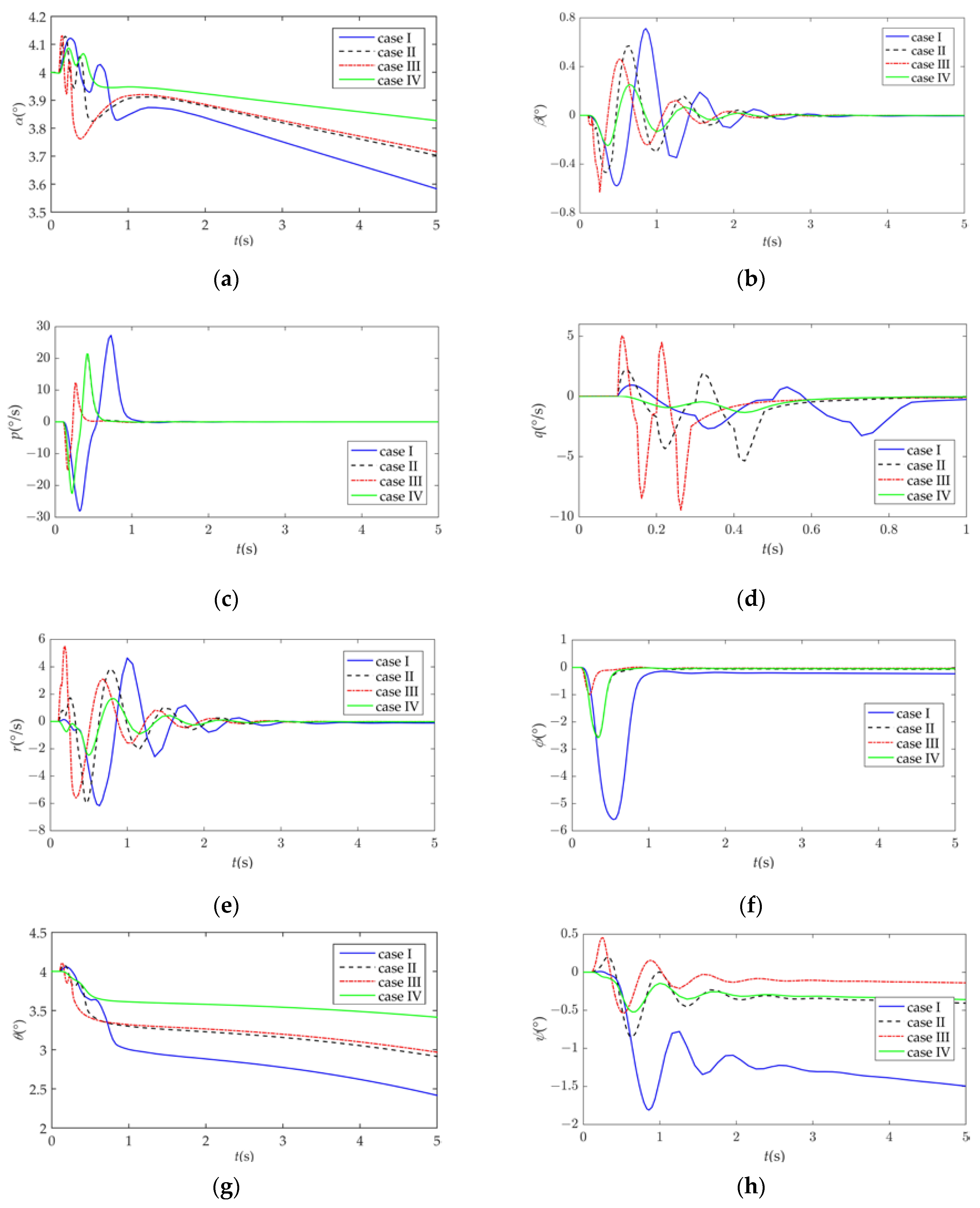
3.1.2. Dynamic Response Analysis of Symmetric Morphing
3.2. Lateral Dynamic Analysis with Asymmetric Morphing
3.2.1. Model Simplification of Lateral Motion
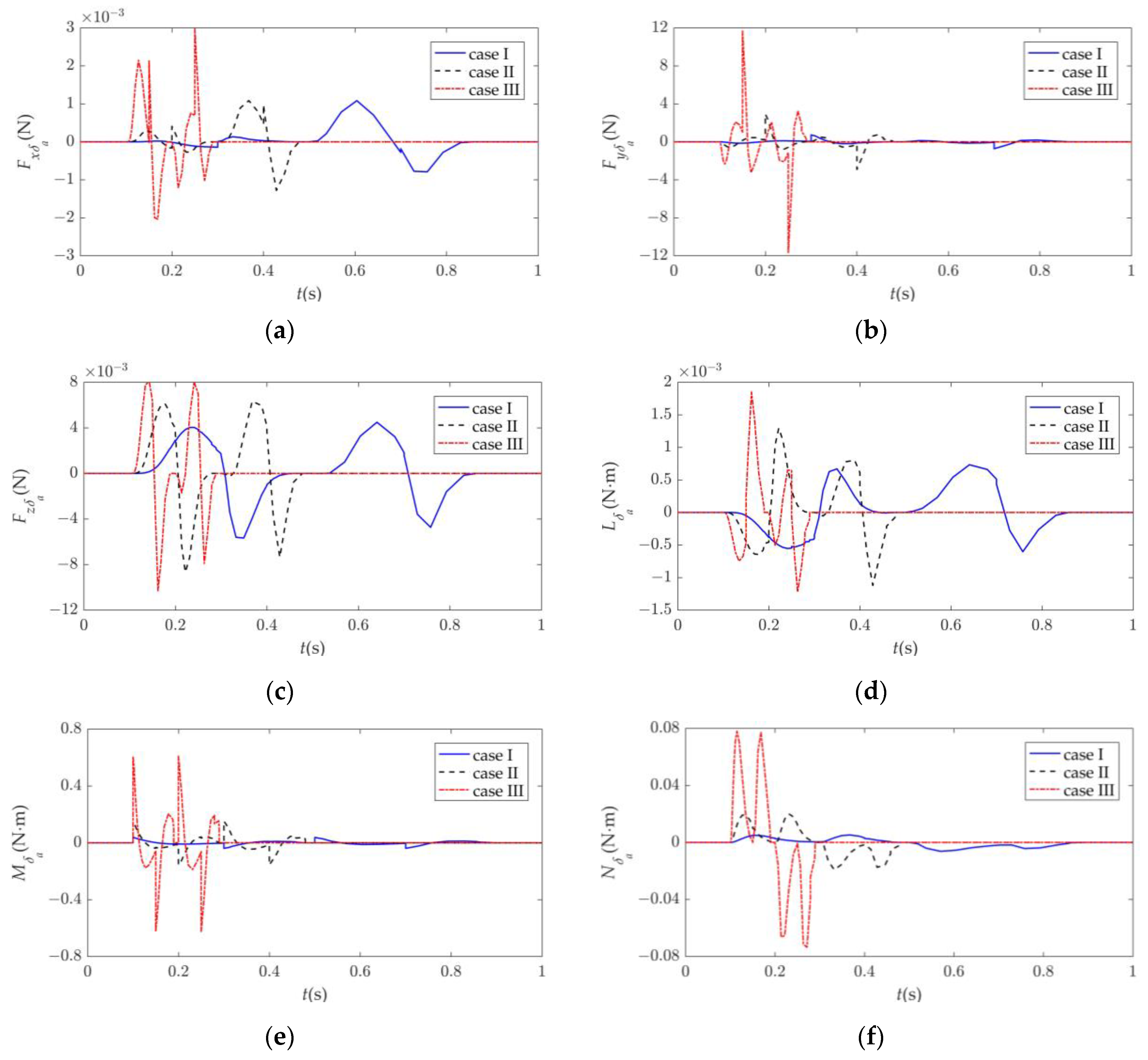
3.2.2. Dynamic Response Analysis of Asymmetric Morphing
4. Experiments
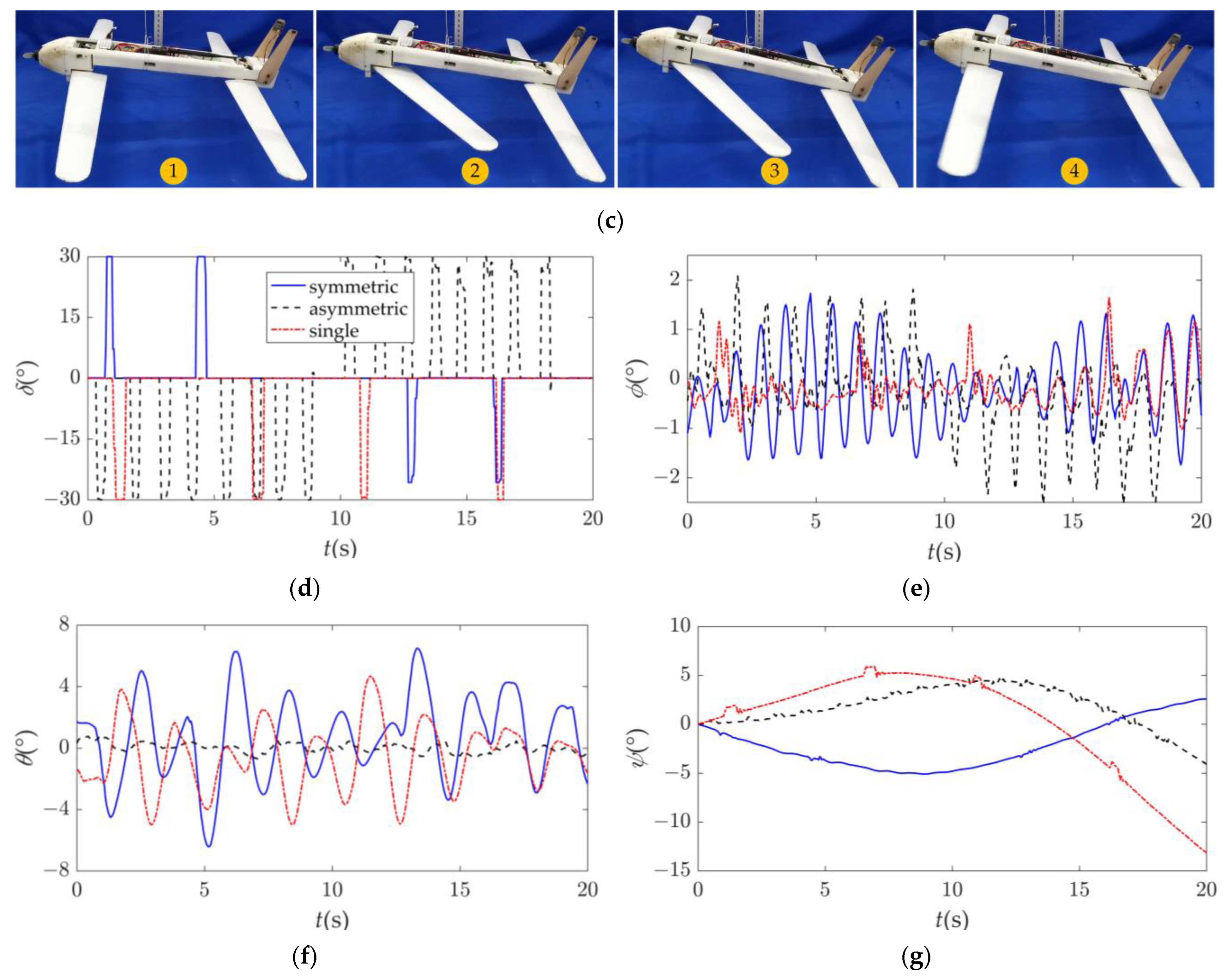
4.1. Dynamic Response Experiments
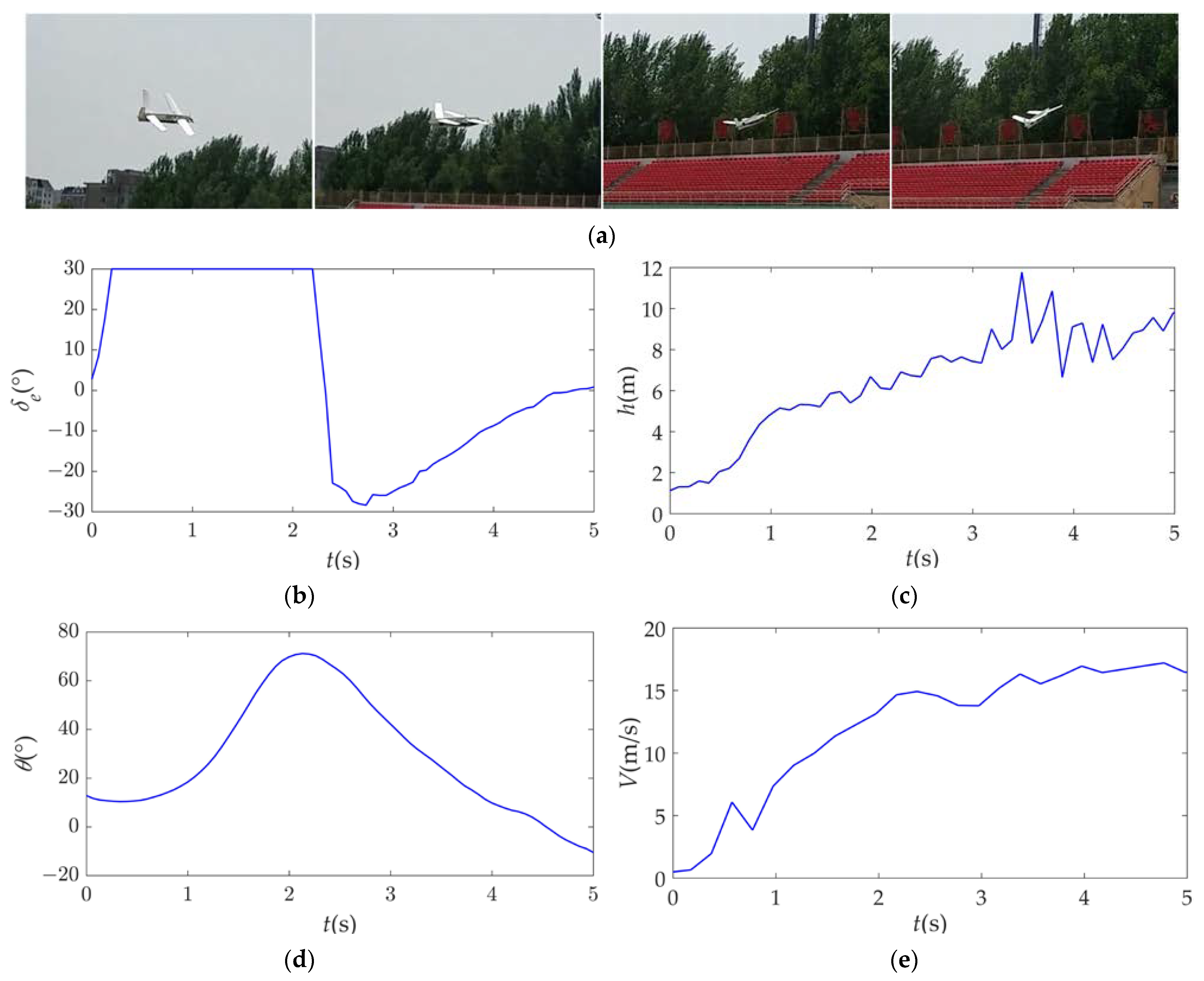
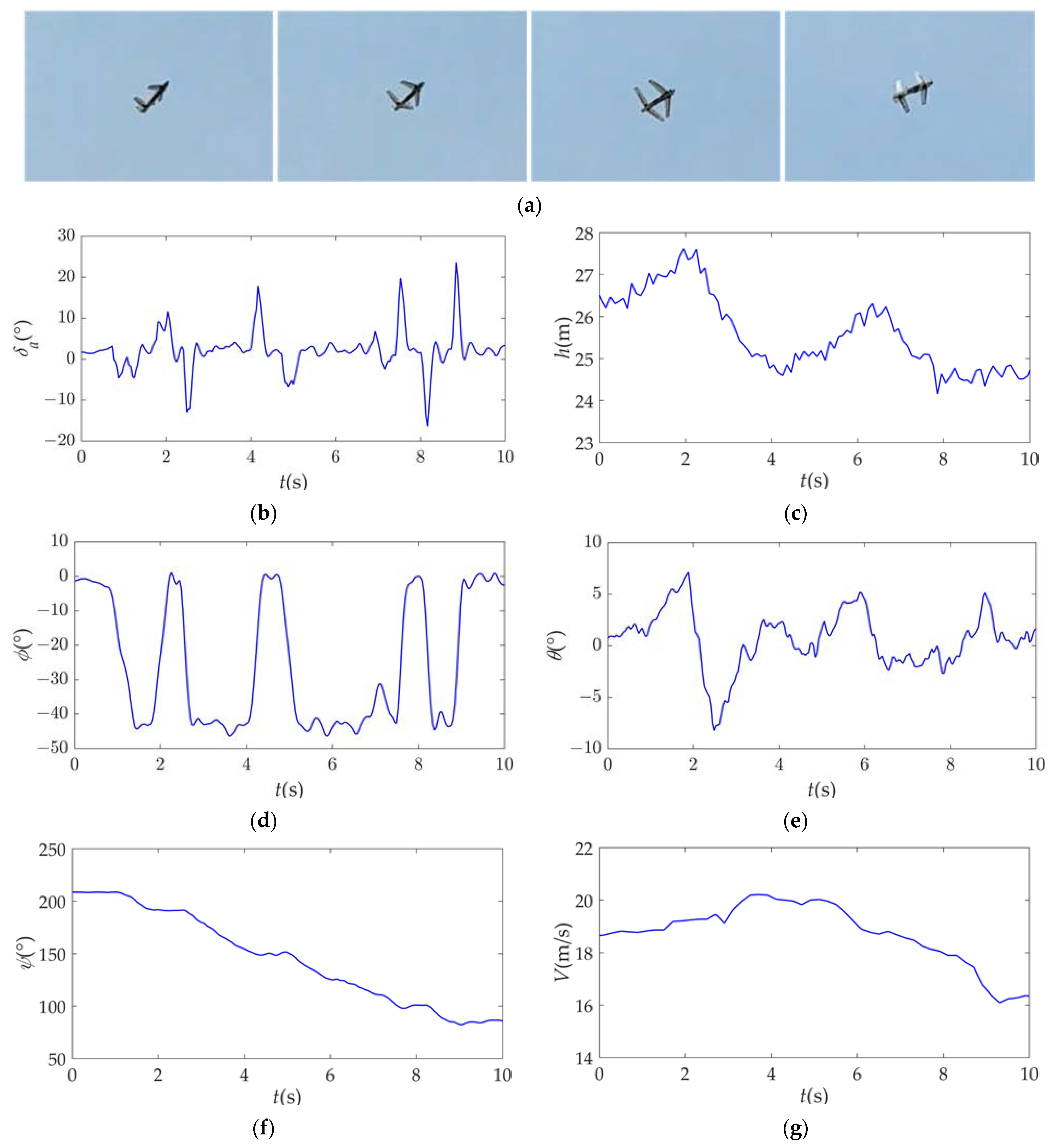
4.2. Flight Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| δe | command of symmetric morphing |
| δa | command of asymmetric morphing |
| hi | sweep angle of each airfoil |
| α | attack angle |
| β | sideslip angle |
| m | mass of the entire MAV |
| ma | mass of a single airfoil |
| u | flight velocity in the xb-axis |
| v | flight velocity in the yb-axis |
| w | flight velocity in the zb-axis |
| ϕ | roll angle |
| θ | pitch angle |
| ψ | yaw angle |
| p | roll angular velocity |
| q | pitch angular velocity |
| r | yaw angular velocity |
| V | flight velocity |
| L | lift |
| Y | side force |
| D | drag |
| P | thrust |
| L | roll moment |
| M | pitch moment |
| N | yaw moment |
| Fx | forces in the xb-axis |
| Fy | forces in the yb-axis |
| Fz | forces in the zb-axis |
| Δxcg | shift of gravity center in the xb-axis |
| Δycg | shift of gravity center in the yb-axis |
| H | height |
Appendix A
References
- Darvishpoor, S.; Roshanian, J.; Raissi, A.; Hassanalian, M. Configurations, flight mechanisms, and applications of unmanned aerial systems: A review. Prog. Aerosp. Sci. 2020, 121, 100694. [Google Scholar] [CrossRef]
- Lentink, D.; Müller, U.; Stamhuis, E.; de Kat, R.; van Gestel, W.; Veldhuis, L.L.M.; Veldhuis, P.; Veldhuis, A.; Veldhuis, J.J.; Veldhuis, J.L. How swifts control their glide performance with morphing wings. Nature 2007, 446, 1082–1085. [Google Scholar] [CrossRef] [PubMed]
- Dai, P.; Feng, D.; Zhao, J.; Cui, J.; Wang, C. Asymmetric integral barrier Lyapunov function-based dynamic surface control of a state-constrained morphing waverider with anti-saturation compensator. Aerosp. Sci. Technol. 2022, 131, 107975. [Google Scholar] [CrossRef]
- Xu, W.F.; Li, Y.H.; Pei, B.B.; Yu, Z.L. A nonlinear programming-based morphing strategy for a variable-sweep morphing aircraft aiming at optimizing the cruising efficiency. Aerospace 2023, 10, 49. [Google Scholar] [CrossRef]
- Dai, P.; Yan, B.; Huang, W.; Zhen, Y.; Wang, M.; Liu, S. Design and aerodynamic performance analysis of a variable-sweep-wing morphing waverider. Aerosp. Sci. Technol. 2020, 98, 105703. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Gao, L.; Liu, B.; Zhu, Y.; Zeng, X.; Zhao, J.; Cai, H. Bioinspired drone actuated using wing and aileron motion for extended flight capabilities. IEEE Robot. Autom. Lett. 2022, 7, 11197–11204. [Google Scholar] [CrossRef]
- Ameduri, S.; Concilio, A. Morphing wings review: Aims, challenges, and current open issues of a technology. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 1–19. [Google Scholar] [CrossRef]
- Chakravarthy, A.; Grant, D.; Lind, R. Time-varying dynamics of a micro air vehicle with variable-sweep morphing. J. Guid. Control Dyn. 2012, 35, 890–903. [Google Scholar] [CrossRef]
- Kim, W. Investigating the Use of Wing Sweep for Pitch Control of a Small Unmanned Air Vehicle. Ph.D. Thesis, University of California, San Diego, CA, USA, 2011. [Google Scholar]
- Siddall, R.; Ancel, A.O.; Kovac, M. Wind and water tunnel testing of a morphing aquatic micro air vehicle. Interface Focus 2017, 7, 20160085. [Google Scholar] [CrossRef]
- Greatwood, C.; Waldock, A.; Richardson, T. Perched landings manoeuvres with a variable sweep wing UAV. Aerosp. Sci. Technol. 2017, 71, 510–520. [Google Scholar] [CrossRef]
- Tong, L.; Ji, H. Multi-body dynamic modelling and flight control for an asymmetric variable sweep morphing UAV. Aeronaut. J. 2014, 118, 683–706. [Google Scholar] [CrossRef]
- Ajaj, R.; Jankee, G. The transformer aircraft: A multimission unmanned aerial vehicle capable of symmetric and asymmetric span morphing. Aerosp. Sci. Technol. 2018, 76, 512–522. [Google Scholar] [CrossRef]
- Vos, R.; Gürdal, Z.; Abdalla, M. Mechanism for warp-controlled twist of a morphing wing. J. Aircr. 2010, 47, 450–457. [Google Scholar] [CrossRef]
- Vos, R.; Barrett, R. Pressure adaptive honeycomb: A new adaptive structure for aerospace applications. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systemsm, San Diego, CA, USA, 31 March 2010. [Google Scholar]
- Bishay, P.L.; Aguilar, C. Parametric study of a composite skin for a twist-morphing wing. Aerospace 2021, 8, 259. [Google Scholar] [CrossRef]
- Obradovic, B.; Subbarao, K. Modeling of flight dynamics of morphing-wing aircraft. J. Aircr. 2011, 48, 391–402. [Google Scholar] [CrossRef]
- Han, M.W.; Rodrigue, H.; Kim, H.I.; Song, S.H.; Ahn, S.H. Shape memory alloy/glass fiber woven composite for soft morphing winglets of unmanned aerial vehicles. Compos. Struct. 2016, 140, 202–212. [Google Scholar] [CrossRef]
- Monner, H.P. Realization of an optimized wing camber by using formvariable flap structures. Aerosp. Sci. Technol. 2001, 5, 445–455. [Google Scholar] [CrossRef]
- Popov, A.V.; Grigorie, L.T.; Botez, R.M.; Mamou, M.; Mébarki, Y. Real time morphing wing optimisation validation using wind-tunnel tests. J. Aircr. 2010, 47, 1346–1355. [Google Scholar] [CrossRef]
- Li, D.C.; Guo, S.J.; Aburass, T.O.; Yang, D.Q.; Xiang, J.W. Active control design for an unmanned air vehicle with a morphing wing. Aircr. Eng. Aerosp. Technol. 2016, 88, 168–177. [Google Scholar] [CrossRef]
- Ajanic, E.; Feroskhan, M.; Mintchev, S.; Noca, F.; Floreano, D. Bioinspired wing and tail morphing extends drone flight capabilities. Sci. Robot. 2020, 5, eabc2897. [Google Scholar] [CrossRef]
- Grant, D.; Lind, R. Effects of time-varying inertias on flight dynamics of an asymmetric variable-sweep morphing aircraft. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Hilton Head, SC, USA, 23–27 August 2007. [Google Scholar]
- Xia, F.; Jing, B.; Xu, W. Analysis of the short-term dynamics of morphing aircraft caused by shape change based on the open-loop response and the reachable set theory. Aerospace 2023, 10, 448. [Google Scholar] [CrossRef]
- Yan, B.; Dai, P.; Liu, R.; Xing, M.; Liu, S. Adaptive super-twisting sliding mode control of variable sweep morphing aircraft. Aerosp. Sci. Technol. 2019, 92, 198–210. [Google Scholar] [CrossRef]
- Harvey, C.; Baliga, V.B.; Wong, J.C.M.; Altshuler, D.L.; Inman, D.J. Birds can transition between stable and unstable states via wing morphing. Nature 2022, 603, 648–653. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Yu, S.C.M. Unsteady aerodynamics of a morphing tandem-wing unmanned aerial vehicle. J. Aircr. 2012, 49, 1315–1323. [Google Scholar] [CrossRef]
- Cheng, H.; Shi, Q.; Wang, H.; Shan, W.; Zeng, T. Flight dynamics modeling and stability analysis of a tube-launched tandem wing aerial vehicle during the deploying process. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2021, 236, 262–280. [Google Scholar] [CrossRef]
- Gao, L.; Zhu, Y.; Liu, Y.; Zhang, J.; Liu, B.; Zhao, J. Analysis and control for the mode transition of tandem-wing aircraft with variable sweep. Aerospace 2022, 9, 463. [Google Scholar] [CrossRef]
- Gao, L.; Jin, H.; Zhao, J.; Cai, H.; Zhu, H. Flight dynamics modeling and control of a novel catapult launched tandem-wing micro aerial vehicle with variable sweep. IEEE Access 2018, 6, 42294–42308. [Google Scholar] [CrossRef]
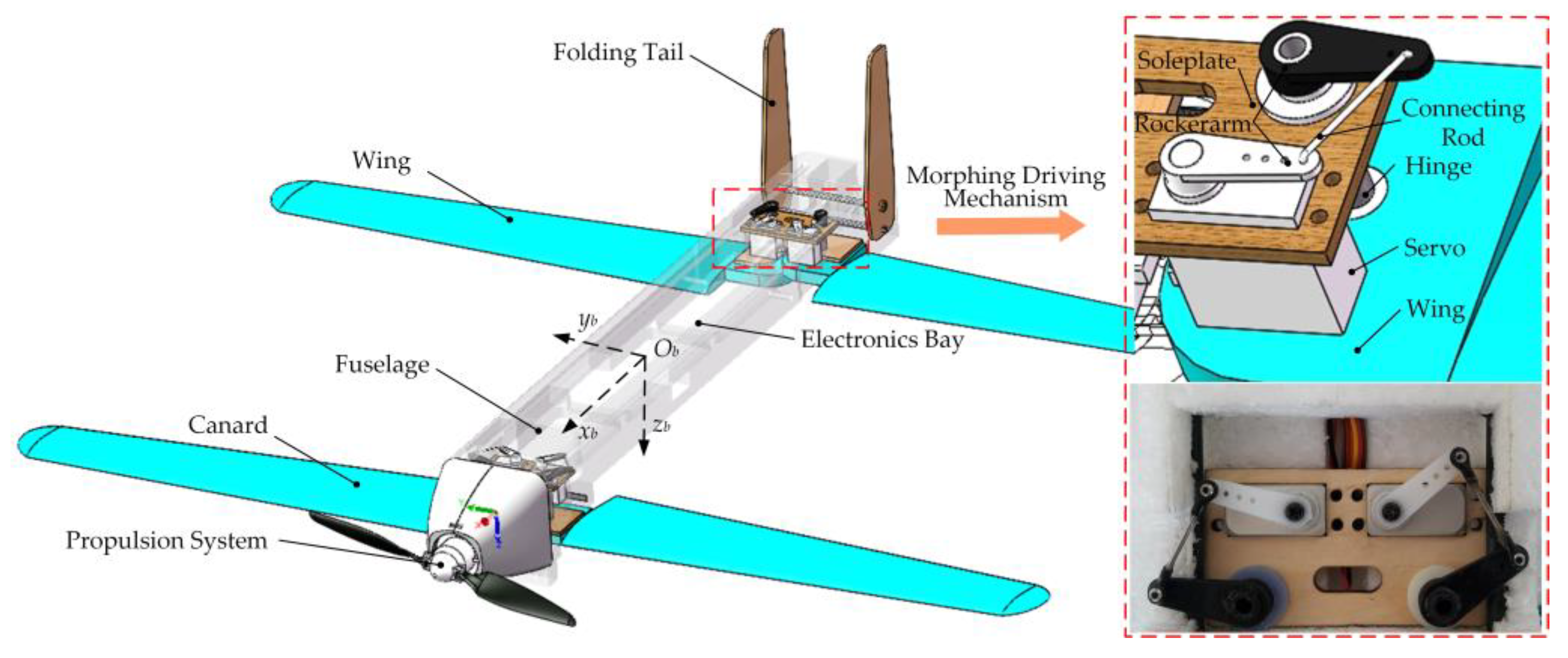





| Parameter | Unit | Value |
|---|---|---|
| Length of fuselage, lf | m | 0.72 |
| Span, b | m | 0.893 |
| Mass of the MAV, m | kg | 1.67 |
| Stagger between canard and wing, St | m | 0.42 |
| Mean aerodynamic chord, cA | m | 0.077 |
| Reference area, S | m2 | 0.135 |
| Design flight velocity, V | m·s−1 | 20–30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Zhu, Y.; Zang, X.; Zhang, J.; Chen, B.; Li, L.; Zhao, J. Dynamic Analysis and Experiment of Multiple Variable Sweep Wings on a Tandem-Wing MAV. Drones 2023, 7, 552. https://doi.org/10.3390/drones7090552
Gao L, Zhu Y, Zang X, Zhang J, Chen B, Li L, Zhao J. Dynamic Analysis and Experiment of Multiple Variable Sweep Wings on a Tandem-Wing MAV. Drones. 2023; 7(9):552. https://doi.org/10.3390/drones7090552
Chicago/Turabian StyleGao, Liang, Yanhe Zhu, Xizhe Zang, Junming Zhang, Boyang Chen, Liyi Li, and Jie Zhao. 2023. "Dynamic Analysis and Experiment of Multiple Variable Sweep Wings on a Tandem-Wing MAV" Drones 7, no. 9: 552. https://doi.org/10.3390/drones7090552
APA StyleGao, L., Zhu, Y., Zang, X., Zhang, J., Chen, B., Li, L., & Zhao, J. (2023). Dynamic Analysis and Experiment of Multiple Variable Sweep Wings on a Tandem-Wing MAV. Drones, 7(9), 552. https://doi.org/10.3390/drones7090552









