Aerial Torsional Work Utilizing a Multirotor UAV with Add-on Thrust Vectoring Device
Abstract
1. Introduction
- The presentation of the mechanical design of a add-on thrust vectoring system for torsional work.
- The design and evaluation of a passive landing mechanism for valve manipulation.
- The modeling and control allocation of the aerial platform in its general case and its transition between modes.
- The evaluation of the torque capabilities of the system in real life experiments from flight to the operation of an industrial grade valve.
2. Valve Turning Problem and Design Constraints
- 1.
- Valve’s location and orientation;
- 2.
- Fastening/gripping method;
- 3.
- Torque source and control of the manipulator.
Thrust and Torque Relation
- Collinearly oriented propellers (COP): All the propellers have the same orientation, thus their resultant thrust vectors points in the same direction.
- Non-collinearly oriented propellers (NCOP): One or more than one of the propellers are positioned in different orientations, having their resultant thrust vectors pointing at different directions.
- 1.
- Torsional work on objects located above and below the airframe such as horizontal valves [10,11,12,13] often rely on the UAV’s yaw, but are limited to low torsional magnitudes. To solve this situation other methods use custom frames such as non-collinearly oriented propeller (NCOP) systems, which are able to produce higher torque magnitudes as shown in [9,12].
- 2.
- 3.
- Vertical valves present their own particular set of challenges due to their axis of rotation with respect to the UAV. Although collinearly oriented propeller (COP) multirotors can produce higher torsional magnitudes in their pitch and roll rotations. These torques are coupled to the movement and flight of the UAV, which complicates their use for valve manipulation tasks.
3. System Description
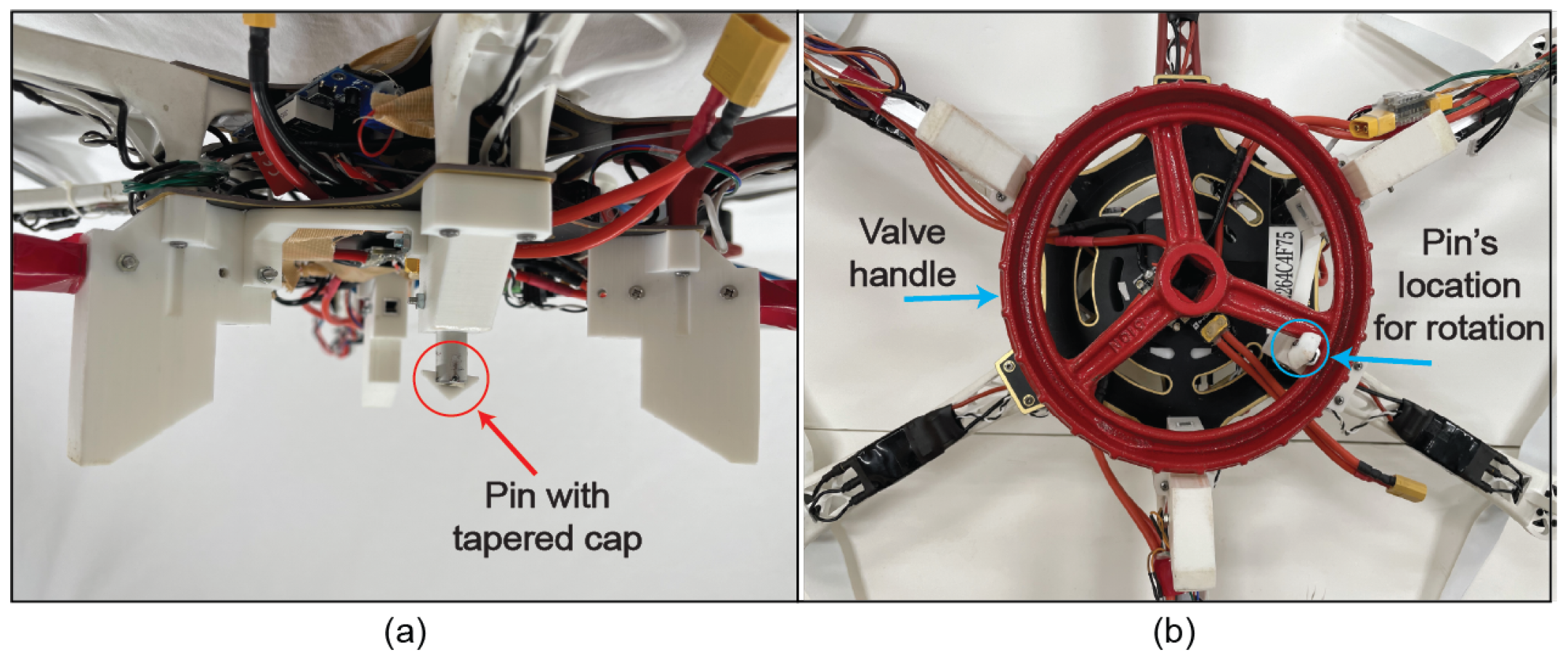
4. Passive Landing Mechanism
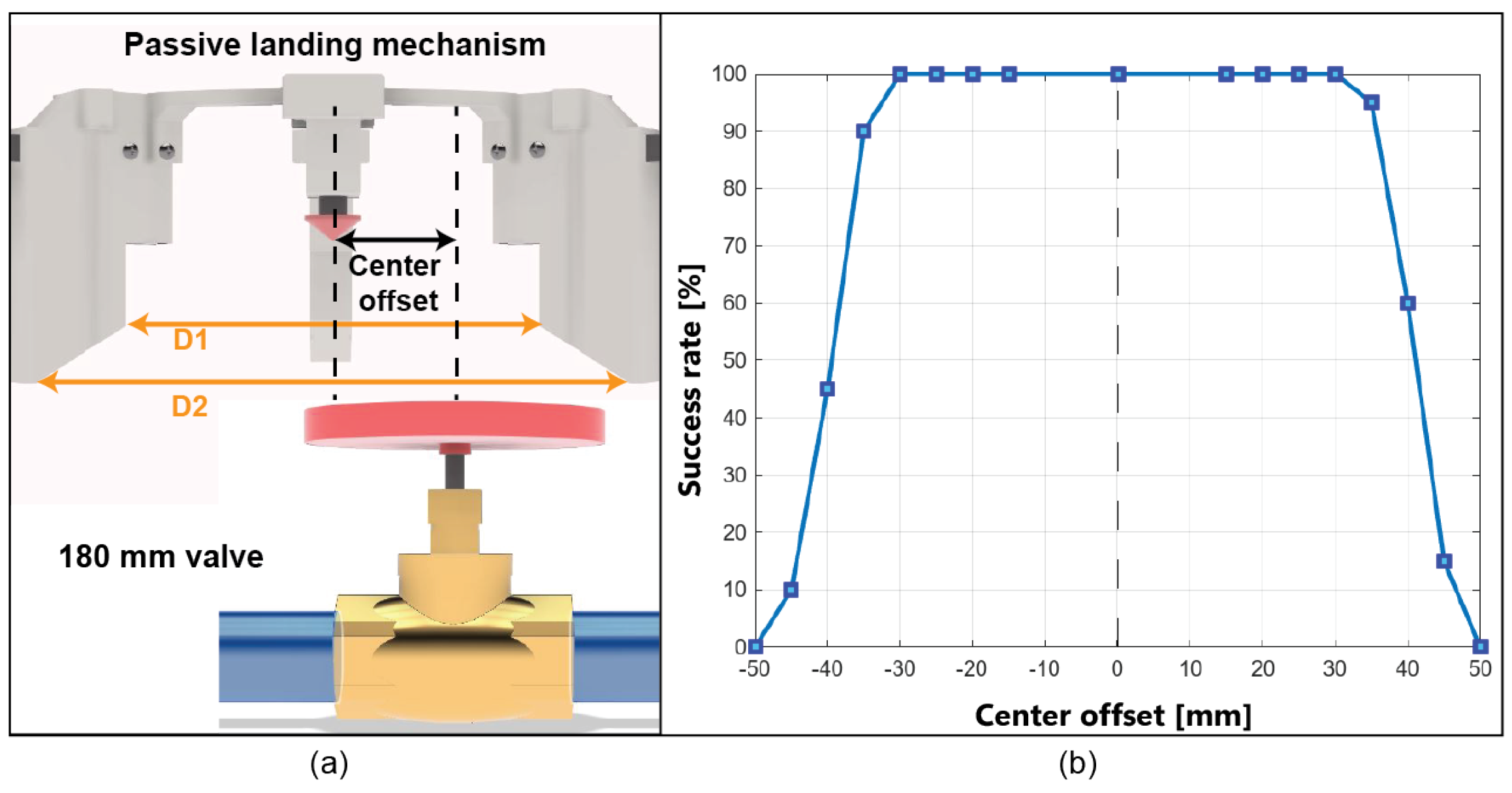
Passive Landing Mechanism Tolerance
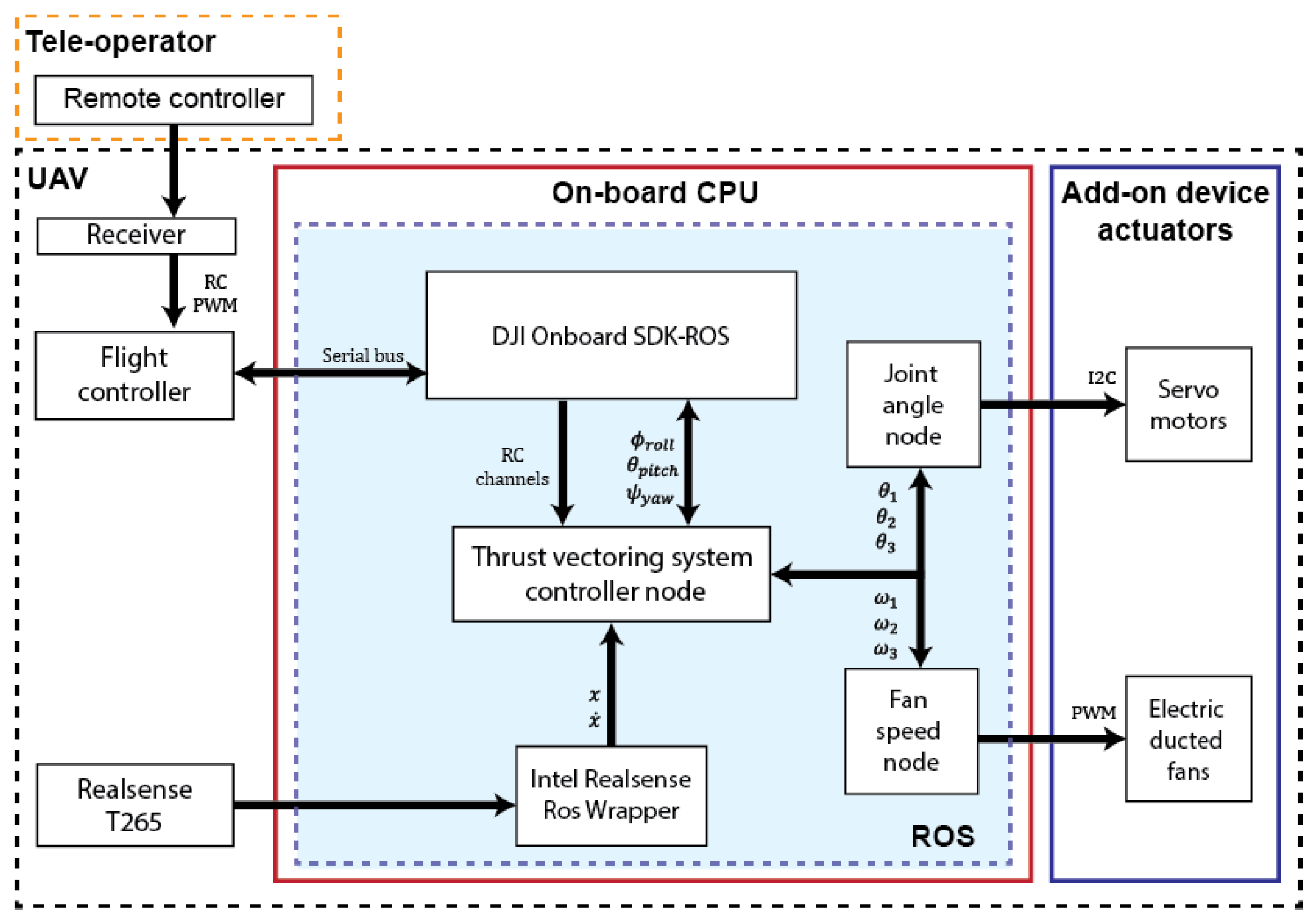
5. Thrust Vectoring Control Framework
- 1.
- Translational flight mode: This configuration follows the control framework expressed in our previous research [16]. The EDFs are positioned as follows:As shown in Figure 8a, this causes the thrust vectors to be collinear to the direction vector from the CoG to each respective frame. This produces a 0 net torque in . The only remaining components are the thrust forces, which allow for planar motion and forces. Based on the odometry information provided by the tracking camera module, the system is capable of holding its current position controlling the EDFs’ thrust vectors.
- 2.
- Torsional work configuration: Assisted by the passive landing mechanism the system can land on the valve and transition to this mode. The propellers are disarmed, and EDFs are controlled to apply the required torque . The EDFs must be oriented so that the thrust vectors are perpendicular to their respective distance vector . Figure 8b correspond to the negative torque configuration with:Figure 8c corresponds to the positive torque configuration with:
6. Experimental Results
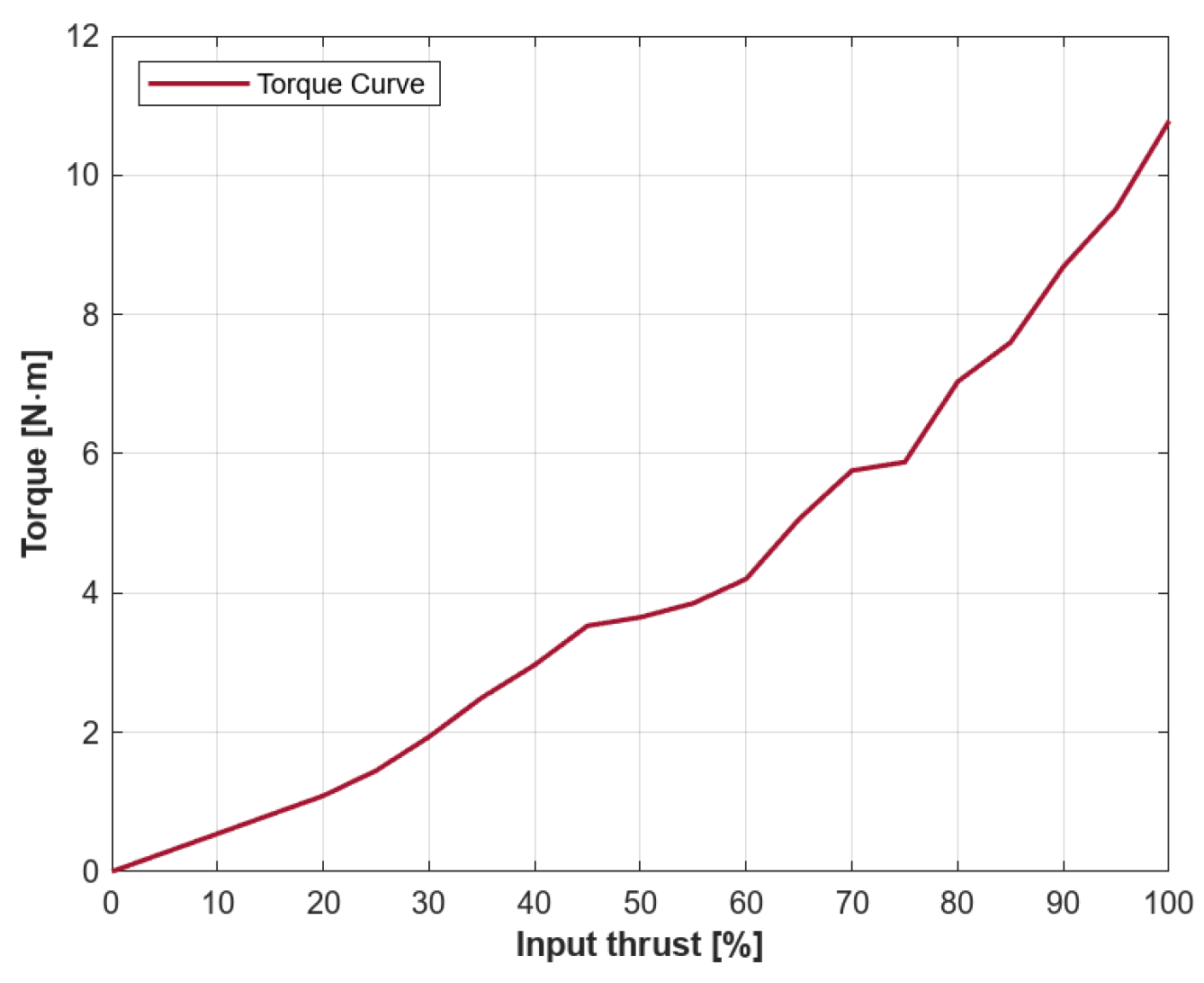
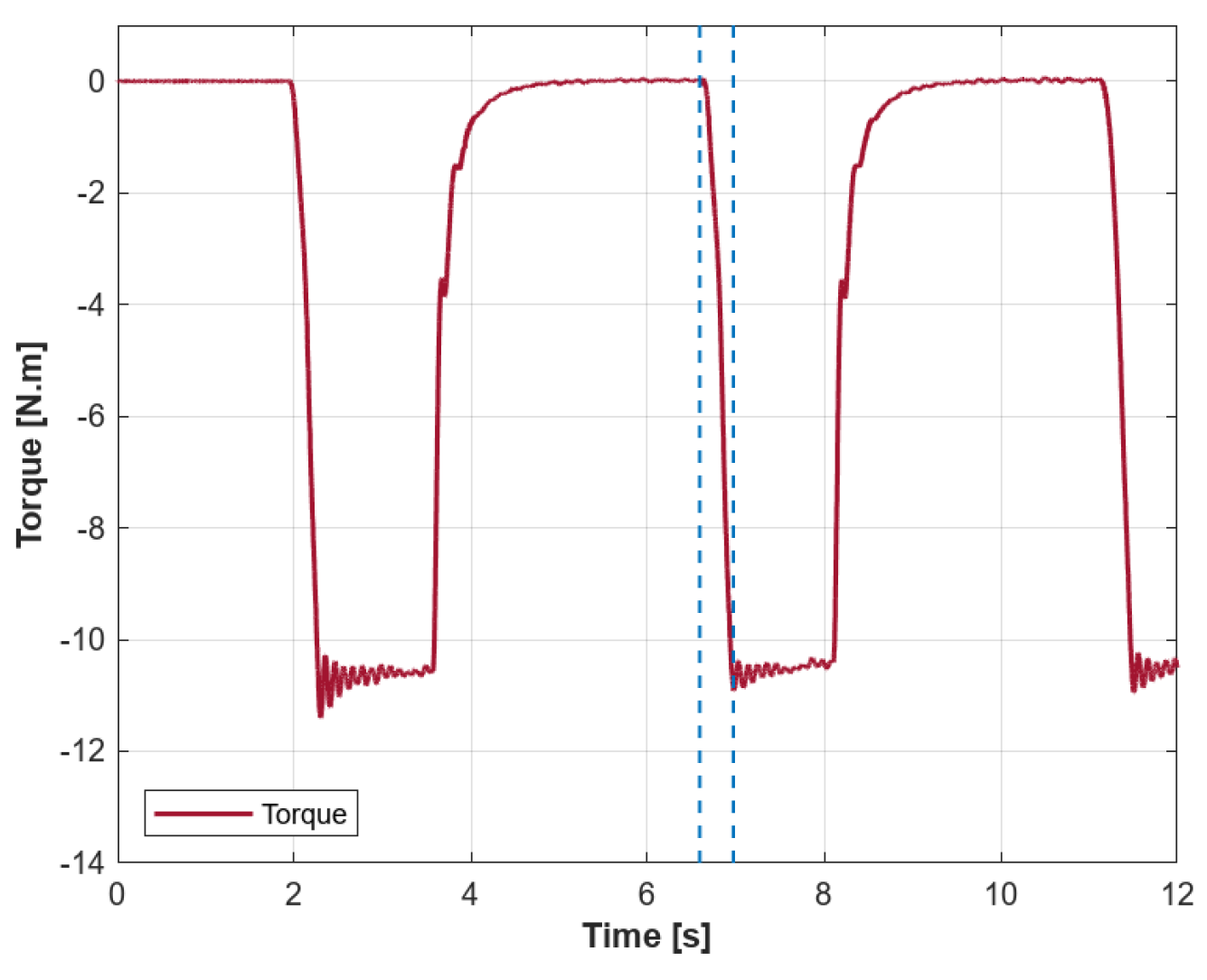
6.1. Torque Evaluation
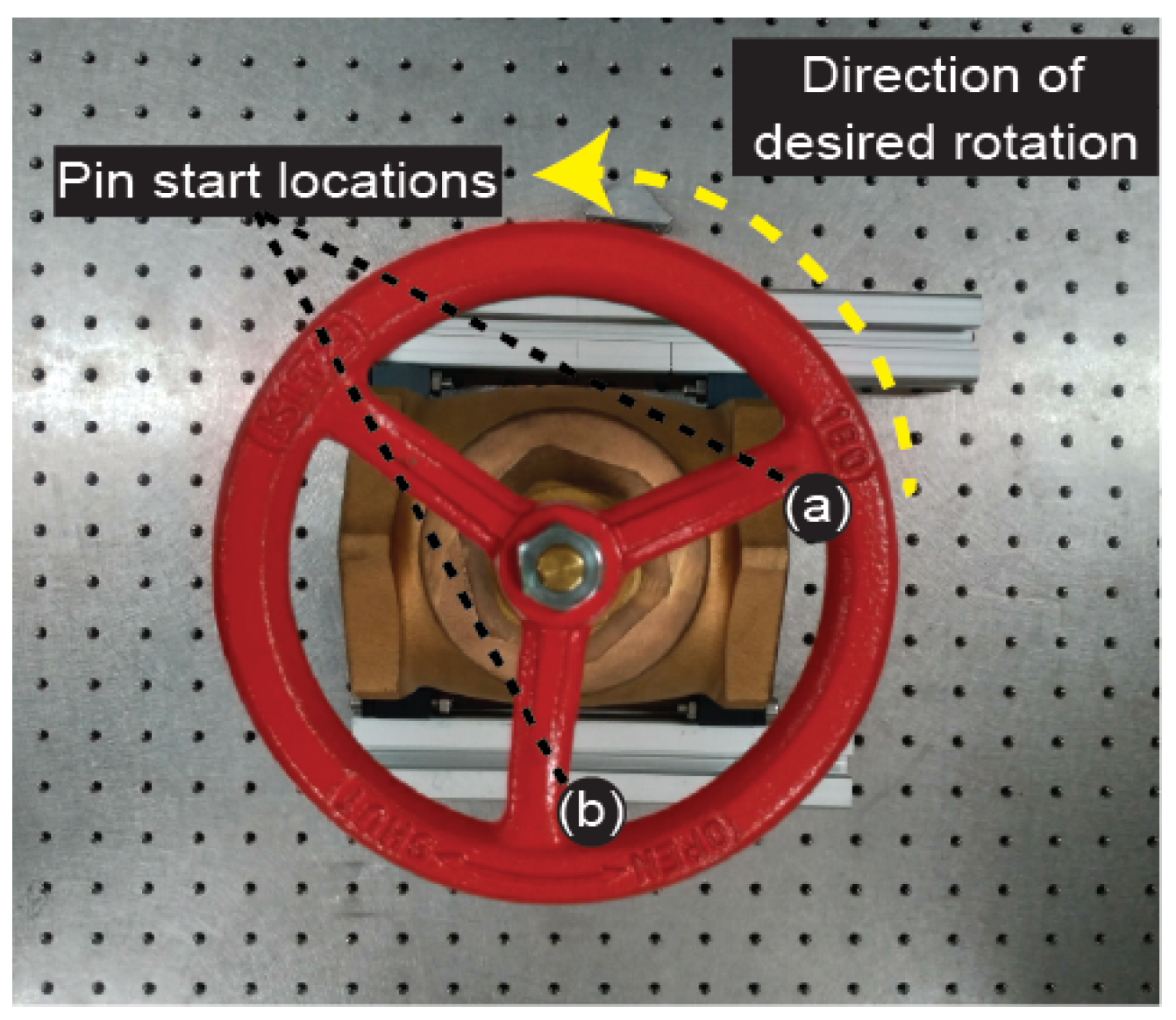
6.2. Pre-Flight Valve Rotation Evaluation
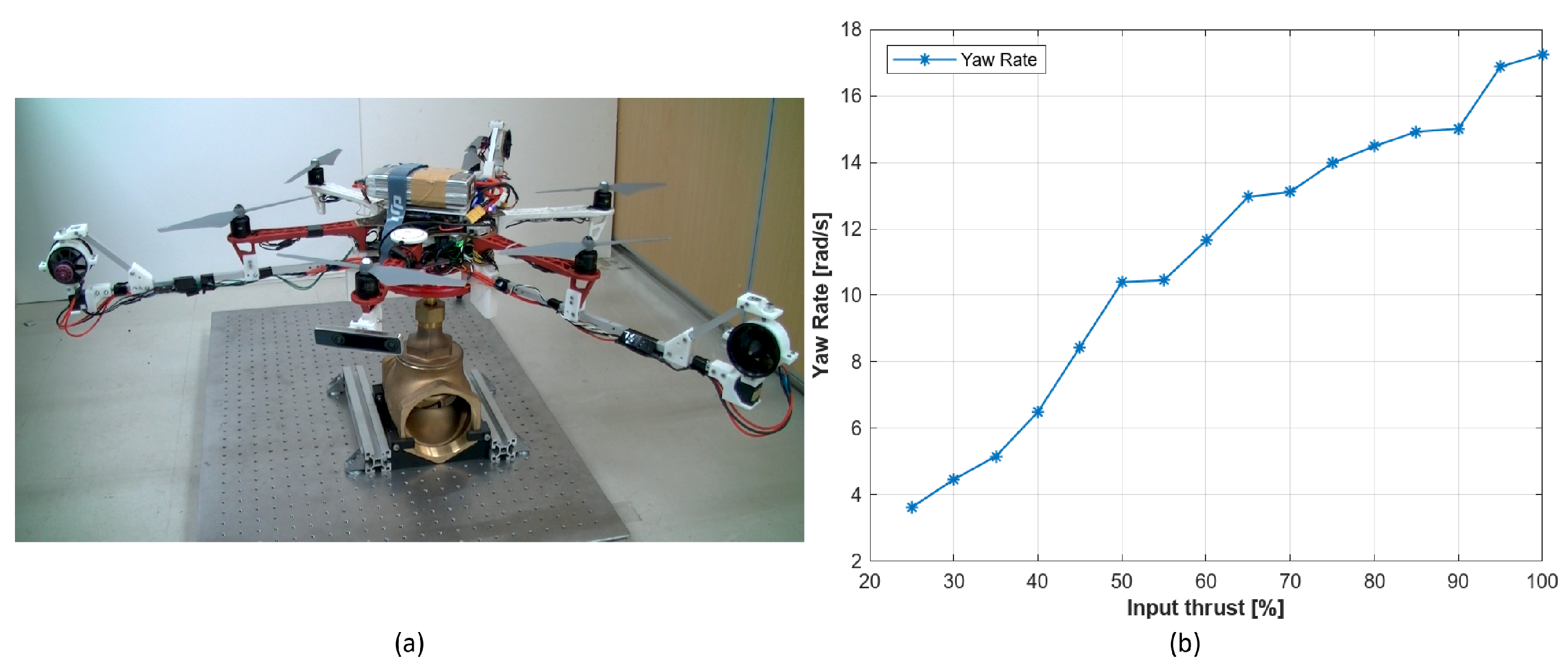
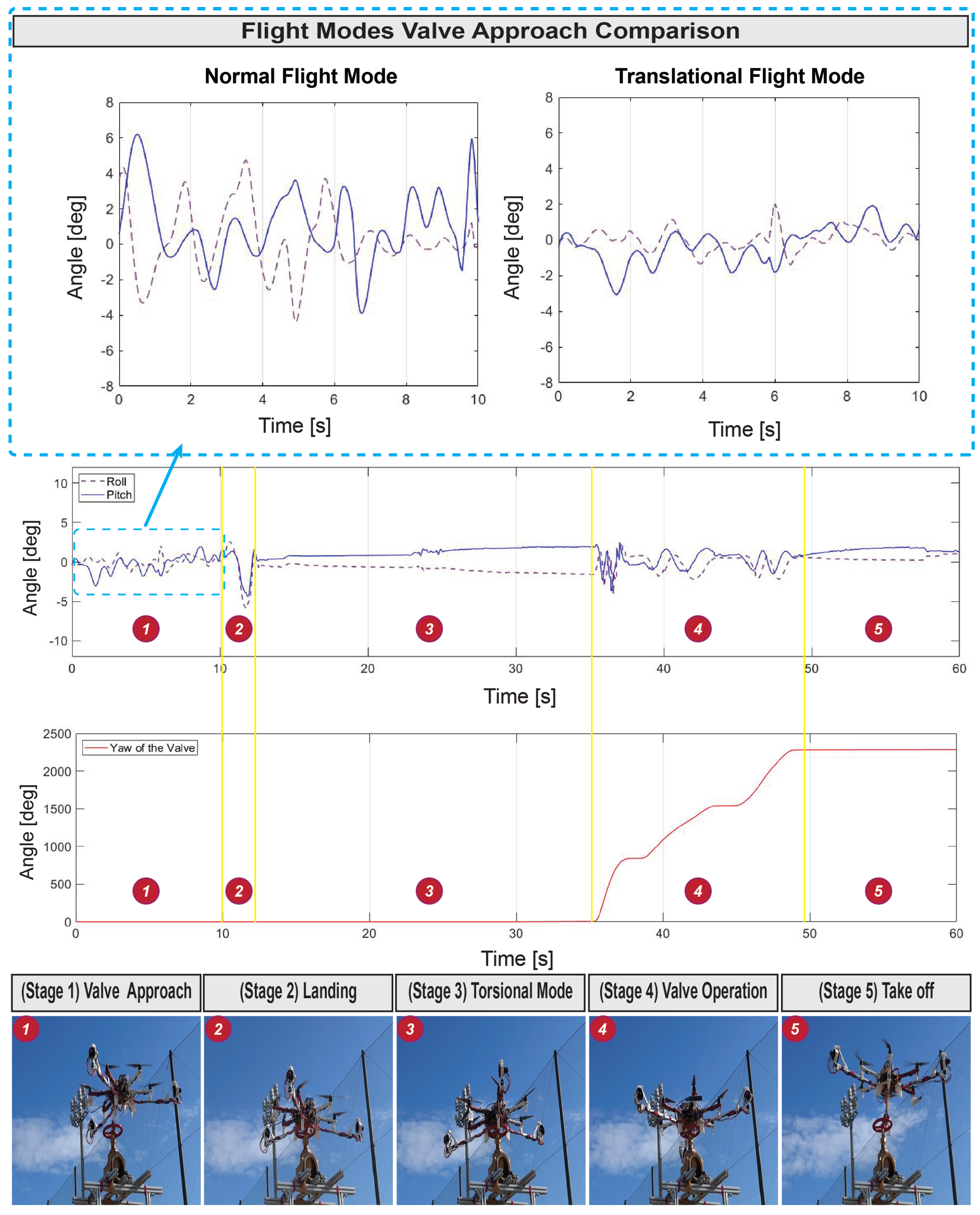
6.3. Flying Task Experiment Mode Evaluation
7. Discussion
8. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AUV | Autonomous Underwater Vehicles |
| CoG | Center of Gravity |
| COP | Collinearly Oriented Propellers |
| DOF | Degree of Freedom |
| EDF | Electric Ducted Fan |
| IMU | Inertial Measurement Unit |
| NCOP | Non-Collinearly Oriented propellers |
| UAV | Unmanned Aerial Vehicles |
| UVG | Unmanned Ground Vehicles |
References
- Ruggiero, F.; Lippiello, V.; Ollero, A. Aerial Manipulation: A Literature Review. IEEE Robot. Autom. Lett. 2018, 3, 1957–1964. [Google Scholar] [CrossRef]
- Suarez, A.; Vega, V.M.; Fernandez, M.; Heredia, G.; Ollero, A. Benchmarks for Aerial Manipulation. IEEE Robot. Autom. Lett. 2020, 5, 2650–2657. [Google Scholar] [CrossRef]
- Shimahara, S.; Leewiwatwong, S.; Ladig, R.; Shimonomura, K. Aerial torsional manipulation employing multi-rotor flying robot. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 1595–1600. [Google Scholar] [CrossRef]
- Rastegarpanah, A.; Ner, R.; Stolkin, R.; Marturi, N. Nut Unfastening by Robotic Surface Exploration. Robotics 2021, 10, 107. [Google Scholar] [CrossRef]
- Zhao, Y.; Gao, F.; Hu, Y. Novel method for six-legged robots turning valves based on force sensing. Mech. Mach. Theory 2019, 133, 64–83. [Google Scholar] [CrossRef]
- Newman, W.; Chong, Z.H.; Du, C.; Hung, R.T.; Lee, K.H.; Ma, L.; Ng, T.W.; Swetenham, C.E.; Tjoeng, K.K.; Wang, W. Autonomous valve turning with an Atlas humanoid robot. In Proceedings of the 2014 IEEE-RAS International Conference on Humanoid Robots, Madrid, Spain, 8–20 November 2014; pp. 493–499. [Google Scholar] [CrossRef]
- Ajoudani, A.; Lee, J.; Rocchi, A.; Ferrati, M.; Hoffman, E.M.; Settimi, A.; Caldwell, D.G.; Bicchi, A.; Tsagarakis, N.G. A manipulation framework for compliant humanoid COMAN: Application to a valve turning task. In Proceedings of the 2014 IEEE-RAS International Conference on Humanoid Robots, Madrid, Spain, 8–20 November 2014; pp. 664–670. [Google Scholar] [CrossRef]
- Konno, A.; Hwang, Y.; Tamada, S.; Uchiyama, M. Working postures for humanoid robots to generate large manipulation force. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 2548–2553. [Google Scholar] [CrossRef]
- Yang, H.; Park, S.; Lee, J.; Ahn, J.; Son, D.; Lee, D. LASDRA: Large-Size Aerial Skeleton System with Distributed Rotor Actuation. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 7017–7023. [Google Scholar] [CrossRef]
- Orsag, M.; Korpela, C.; Bogdan, S.; Oh, P. Dexterous Aerial Robots—Mobile Manipulation Using Unmanned Aerial Systems. IEEE Trans. Robot. 2017, 33, 1453–1466. [Google Scholar] [CrossRef]
- Ramon-Soria, P.; Arrue, B.C.; Ollero, A. Grasp planning and visual servoing for an outdoors aerial dual manipulator. Engineering 2020, 6, 77–88. [Google Scholar] [CrossRef]
- Nguyen, H.; Alexis, K. Forceful Aerial Manipulation Based on an Aerial Robotic Chain: Hybrid Modeling and Control. IEEE Robot. Autom. Lett. 2021, 6, 3711–3719. [Google Scholar] [CrossRef]
- Zhao, M.; Nagato, K.; Okada, K.; Inaba, M.; Nakao, M. Forceful Valve Manipulation With Arbitrary Direction by Articulated Aerial Robot Equipped With Thrust Vectoring Apparatus. IEEE Robot. Autom. Lett. 2022, 7, 4893–4900. [Google Scholar] [CrossRef]
- Carrera, A.; Palomeras, N.; Hurtós, N.; Kormushev, P.; Carreras, M. Learning multiple strategies to perform a valve turning with underwater currents using an I-AUV. In Proceedings of the OCEANS 2015, Genova, Italy, 18–21 May 2015; pp. 1–8. [Google Scholar] [CrossRef]
- Administration, U. Water Supply Systems and Evaluation Methods; Volume I: Water Supply System Concepts; Fema: Washington, DC, USA, 2008. [Google Scholar]
- Miyazaki, R.; Paul, H.; Shimonomura, K. Development of Add-On Planar Translational Driving System for Aerial Manipulation with Multirotor Platform. Appl. Sci. 2021, 11, 1462. [Google Scholar] [CrossRef]
- Council, I.C. 2018 IPC, International Plumbing Code; International Code Council: Nappanee, IN, USA, 2018. [Google Scholar]
- Council, I.C. 2021 IFGC, International Fuel Gas Code; International Code Council: Nappanee, IN, USA, 2021. [Google Scholar]
- Brescianini, D.; D’Andrea, R. Design, modeling and control of an omni-directional aerial vehicle. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 3261–3266. [Google Scholar] [CrossRef]
- Ollero, A.; Heredia, G.; Franchi, A.; Antonelli, G.; Kondak, K.; Sanfeliu, A.; Viguria, A.; Martinez-de Dios, J.R.; Pierri, F.; Cortes, J.; et al. The AEROARMS Project: Aerial Robots with Advanced Manipulation Capabilities for Inspection and Maintenance. IEEE Robot. Autom. Mag. 2018, 25, 12–23. [Google Scholar] [CrossRef]
- Bodie, K.; Brunner, M.; Pantic, M.; Walser, S.; Pfändler, P.; Angst, U.; Siegwart, R.; Nieto, J.I. An Omnidirectional Aerial Manipulation Platform for Contact-Based Inspection. arXiv 2019, arXiv:1905.03502. [Google Scholar]
- Kamel, M.; Verling, S.; Elkhatib, O.; Sprecher, C.; Wulkop, P.; Taylor, Z.; Siegwart, R.; Gilitschenski, I. Voliro: An Omnidirectional Hexacopter With Tiltable Rotors. arXiv 2018, arXiv:1801.04581. [Google Scholar]
- Miwa, M.; Uemura, S.; Imamura, A. Arbitrary Attitude Hovering Control of Quad Tilt Rotor Helicopter. J. Robot. Mechatronics 2016, 28, 328–333. [Google Scholar] [CrossRef]
- Hasegawa, N.; Suzuki, S.; Kawamura, T.; Shimizu, T.; Ueno, H.; Murakami, H. Independent Attitude and Position Control of Non-planer Multi-rotor Helicopter. J. Robot. Soc. Jpn. 2020, 38, 192–198. [Google Scholar] [CrossRef]
- Shankarpure, M.R.; Patil, D.D. A Comprehensive Survey on Methods and Techniques for Automated Fruit Plucking. Int. J. Intell. Syst. Appl. Eng. 2023, 11, 156–168. [Google Scholar]


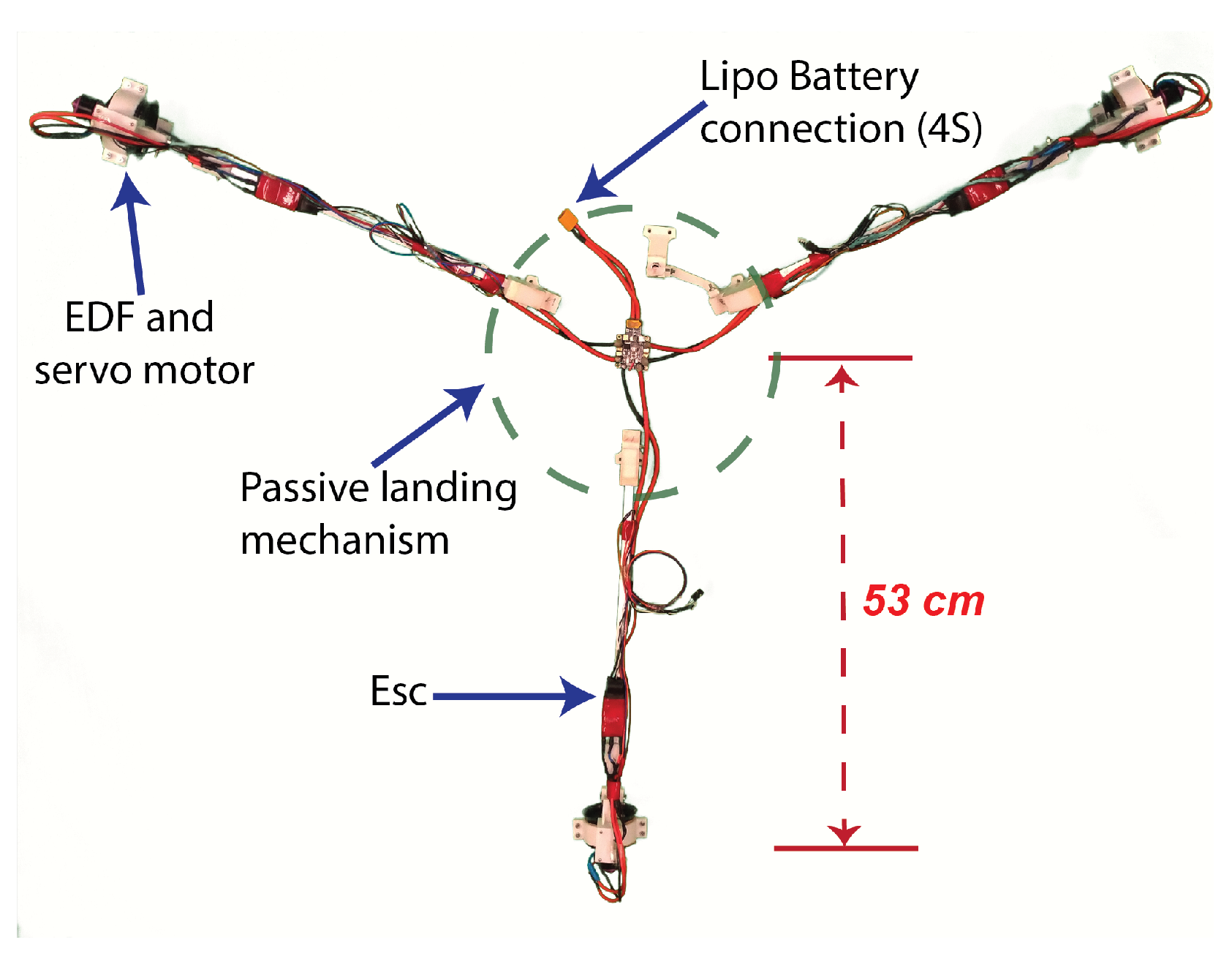


| Gross weight | 1.01 kg without battery |
| Distance to EDF from center | 53 cm |
| Number of EDFs | 3 |
| EDF characteristics | Powerfun EDF mm/4300 KV |
| Max thrust | 9.31 (N) for each ducted fan |
| Servomotors characteristics | Dynamixel XL330 (0.228 N · m) |
| EDFs range of motion | ±360° |
| Symbol | Description |
|---|---|
| Resultant forces acting on the center of gravity () | |
| Resultant moments acting on the center of gravity | |
| Thrust force vector generated by the EDFs () | |
| Distance vector from the CoG to each EDFs’s frame () | |
| Angular position of the EDFs | |
| Angular velocity of the EDFs | |
| Vector of squared angular velocities | |
| Lift force coefficient | |
| k | Aerodynamic drag coefficient |
| and |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martinez, R.R.; Paul, H.; Shimonomura, K. Aerial Torsional Work Utilizing a Multirotor UAV with Add-on Thrust Vectoring Device. Drones 2023, 7, 551. https://doi.org/10.3390/drones7090551
Martinez RR, Paul H, Shimonomura K. Aerial Torsional Work Utilizing a Multirotor UAV with Add-on Thrust Vectoring Device. Drones. 2023; 7(9):551. https://doi.org/10.3390/drones7090551
Chicago/Turabian StyleMartinez, Ricardo Rosales, Hannibal Paul, and Kazuhiro Shimonomura. 2023. "Aerial Torsional Work Utilizing a Multirotor UAV with Add-on Thrust Vectoring Device" Drones 7, no. 9: 551. https://doi.org/10.3390/drones7090551
APA StyleMartinez, R. R., Paul, H., & Shimonomura, K. (2023). Aerial Torsional Work Utilizing a Multirotor UAV with Add-on Thrust Vectoring Device. Drones, 7(9), 551. https://doi.org/10.3390/drones7090551







