Trust–Region Nonlinear Optimization Algorithm for Orientation Estimator and Visual Measurement of Inertial–Magnetic Sensor
Abstract
:1. Introduction
- 1.
- We propose a novel nonlinear optimization algorithm for improving the bearing estimation of inexpensive airborne inertial–magnetic sensors. The proposed algorithm utilizes the Huber robust kernel to suppress maneuvering acceleration interference of the drone and a trust-region strategy to optimize positioning precision. The experiments indicate that our algorithm has significant advantages in orientation accuracy under high–dynamic conditions.
- 2.
- We propose a method for measuring orientation with a monocular camera based on nonlinear optimization and evaluate the measurement error of the proposed method in depth.
- 3.
- We evaluate the accuracy and robustness of the proposed estimator, complementary filtering algorithms, and typical implementations of Kalman filtering algorithms relative to visual reference orientation under low– and high–dynamic conditions on the ARM platform. In addition, we assess the operational effectiveness of the aforementioned algorithms on the X86–64 and ARM platforms, which can serve as a reference for airborne multimodal fusion units.
2. Related Work
2.1. Trust–Region Optimization Algorithm
2.2. Perspective–n–Point Algorithm
2.3. ArUco Marker
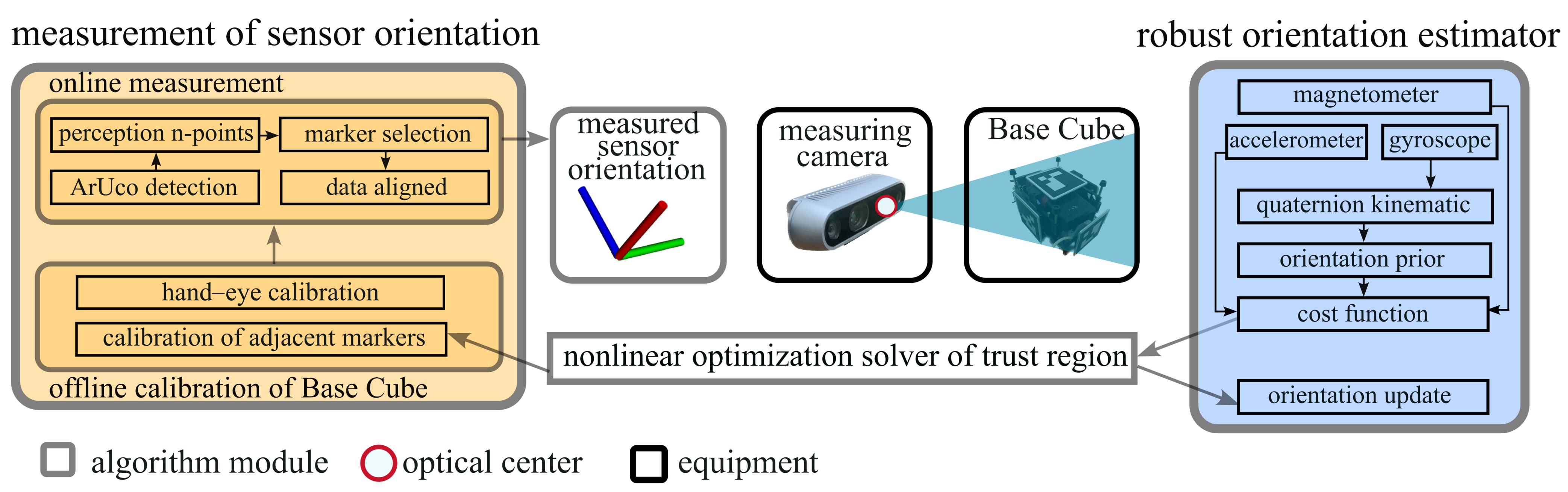
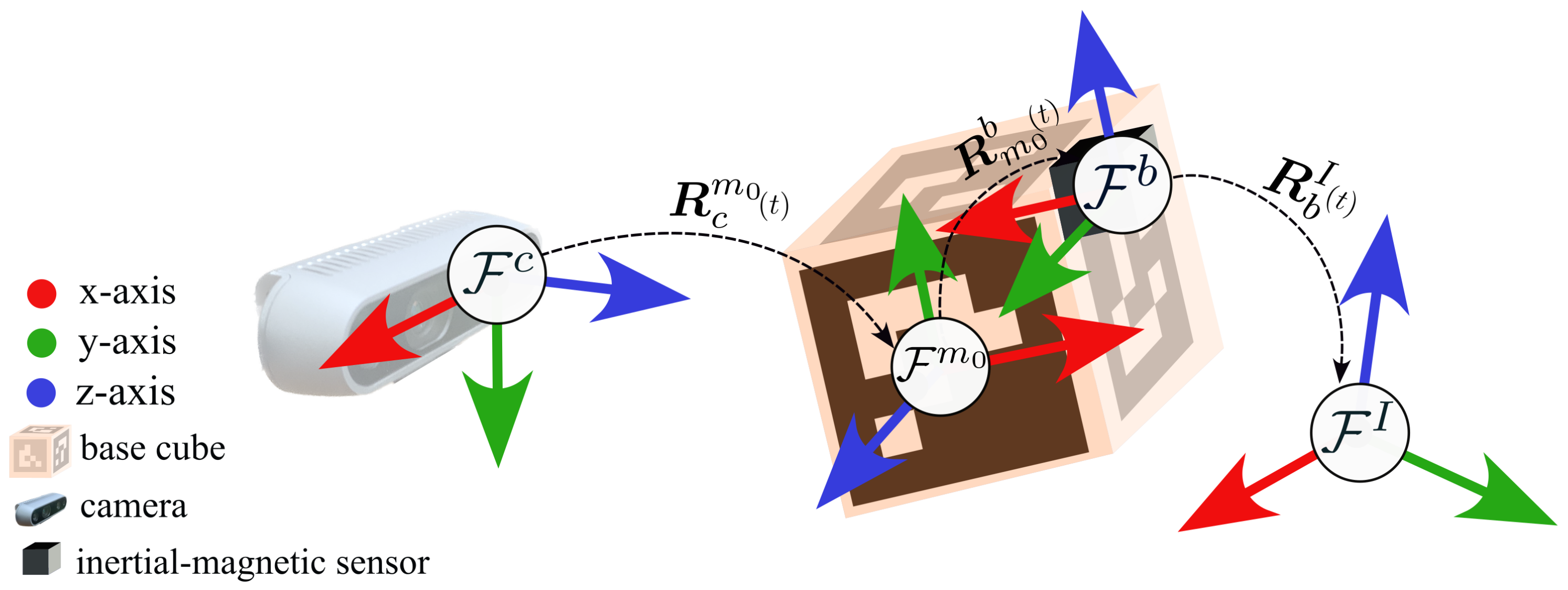
3. Overview of Proposed Algorithm
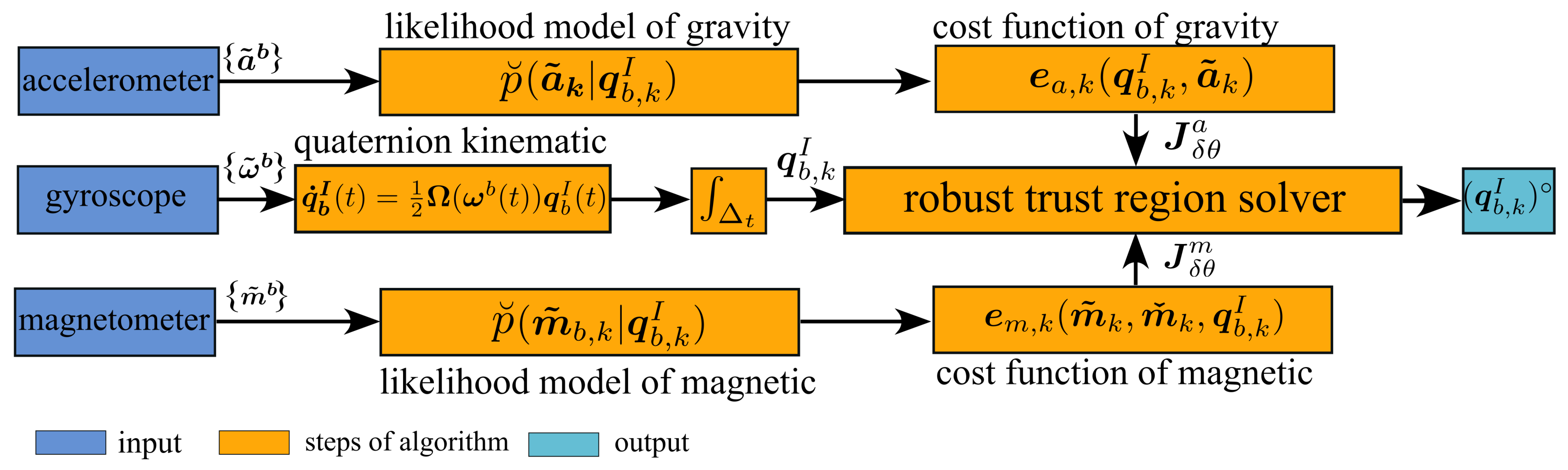
4. Proposed Robust Orientation Estimator
4.1. Quaternion Kinematic
4.2. Cost Function of Field Measurement
4.3. Robust Trust-Region Solver
5. Proposed Method for Orientation Measurement Based on Vision
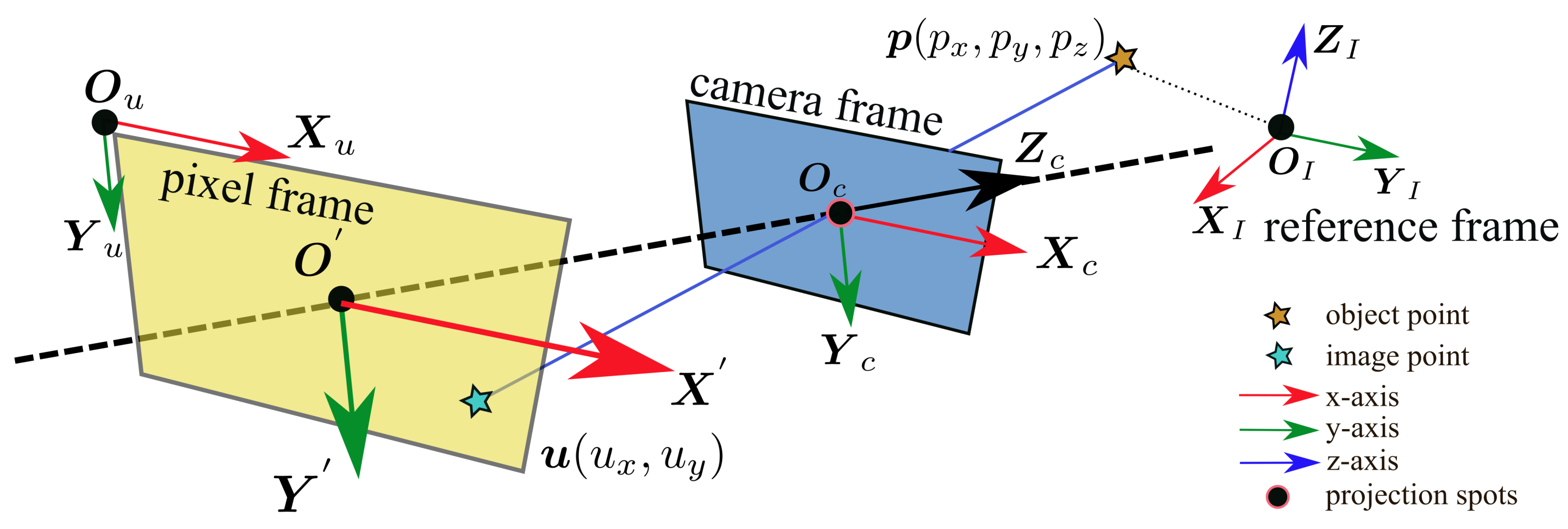
5.1. Pinhole Camera Model and Re–Projection Error
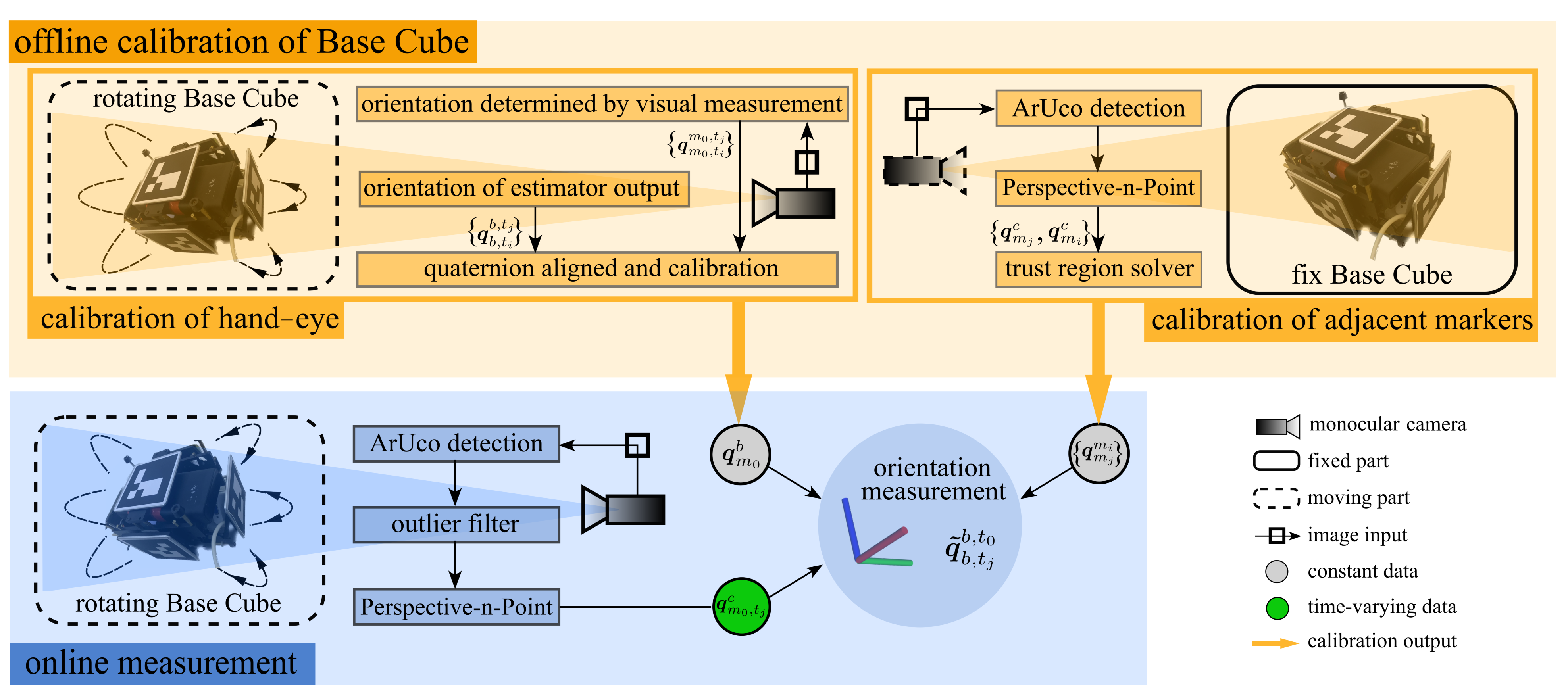
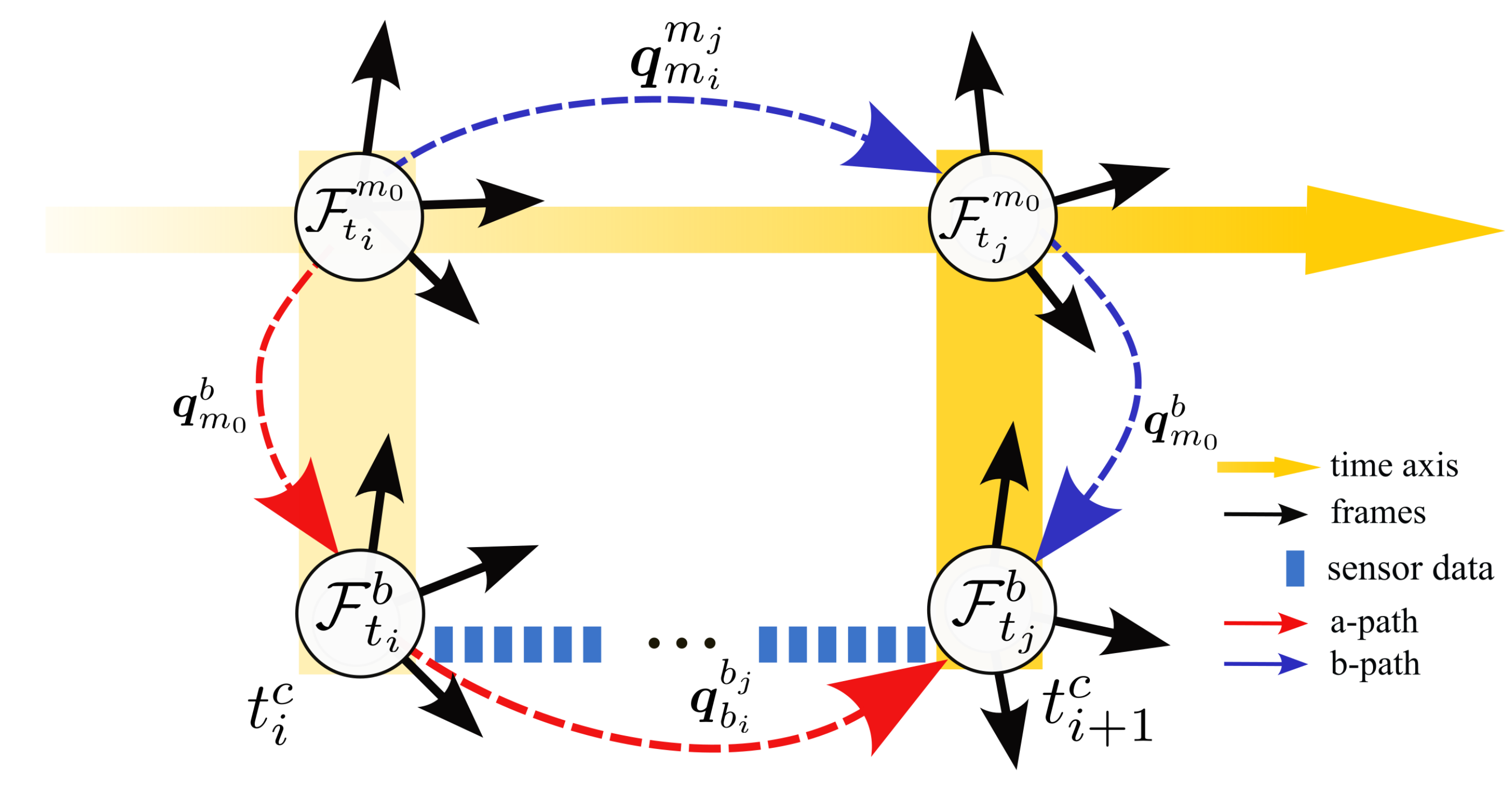
5.2. Calibration of Adjacent Markers
5.3. Calibration of Hand–Eye
6. Experiment and Discussion
6.1. Environment of Experiments
6.2. Experiment of Calibration for Base Cube
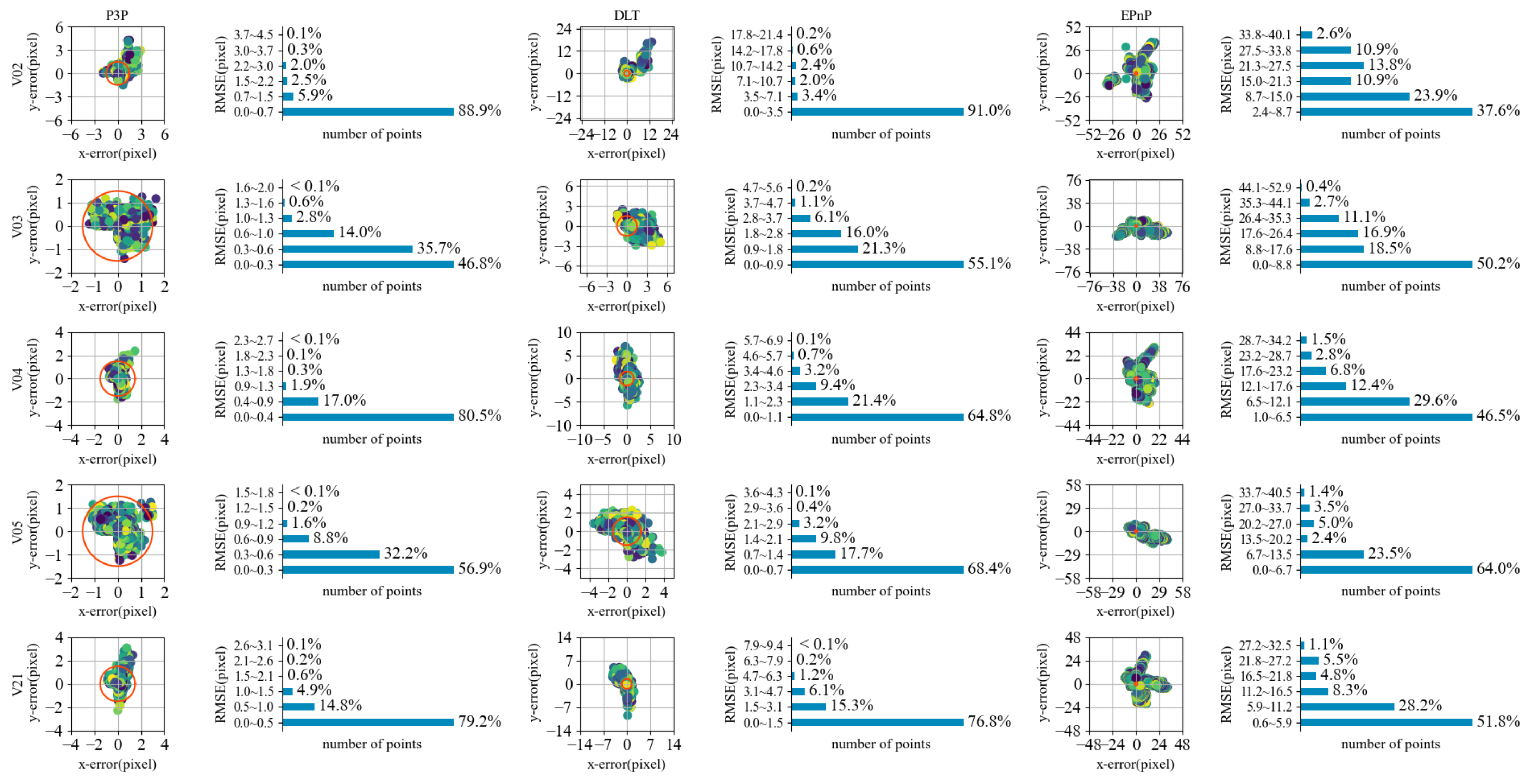
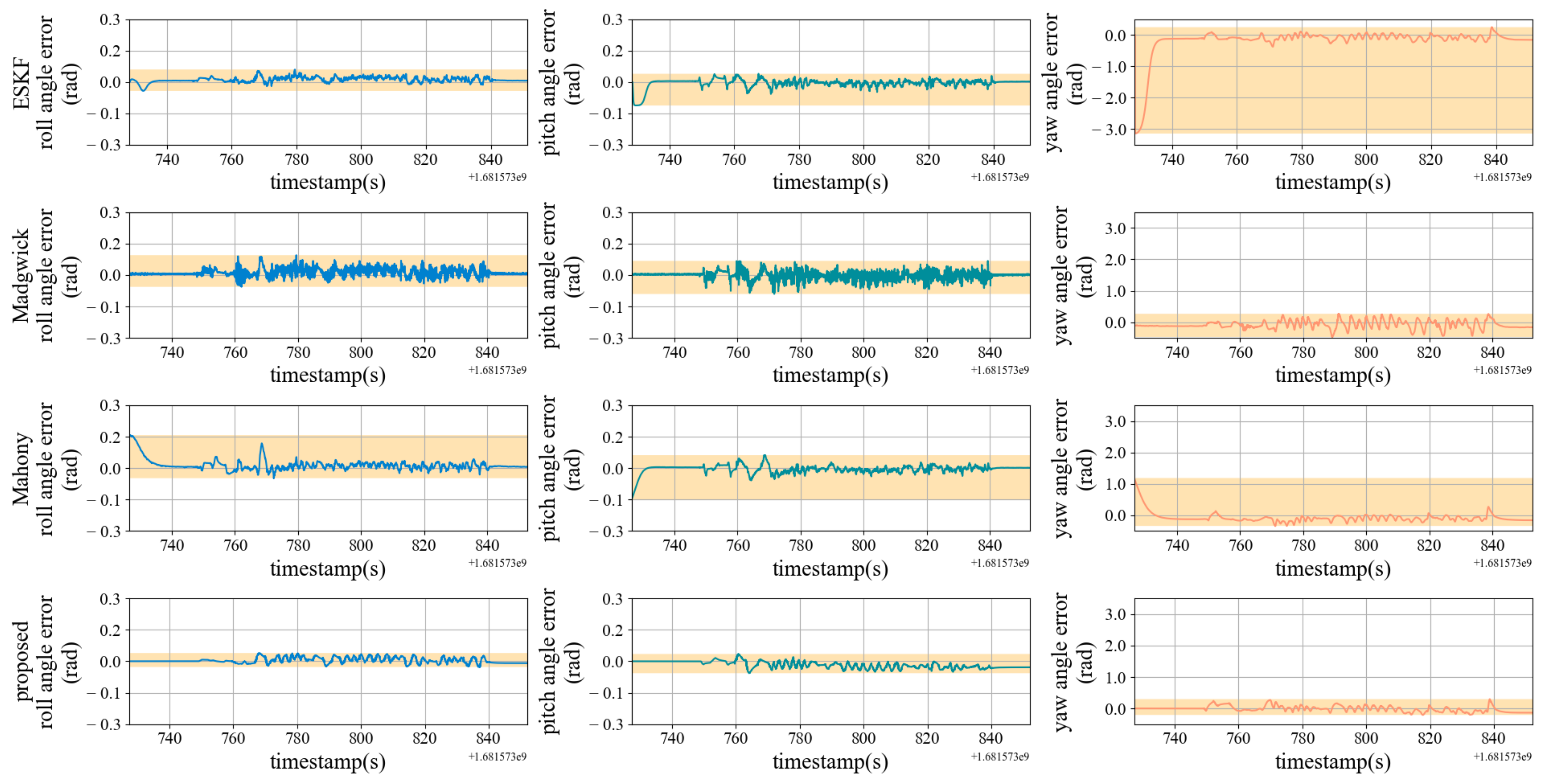
6.3. Experiment of Orientation Measurement Accuracy
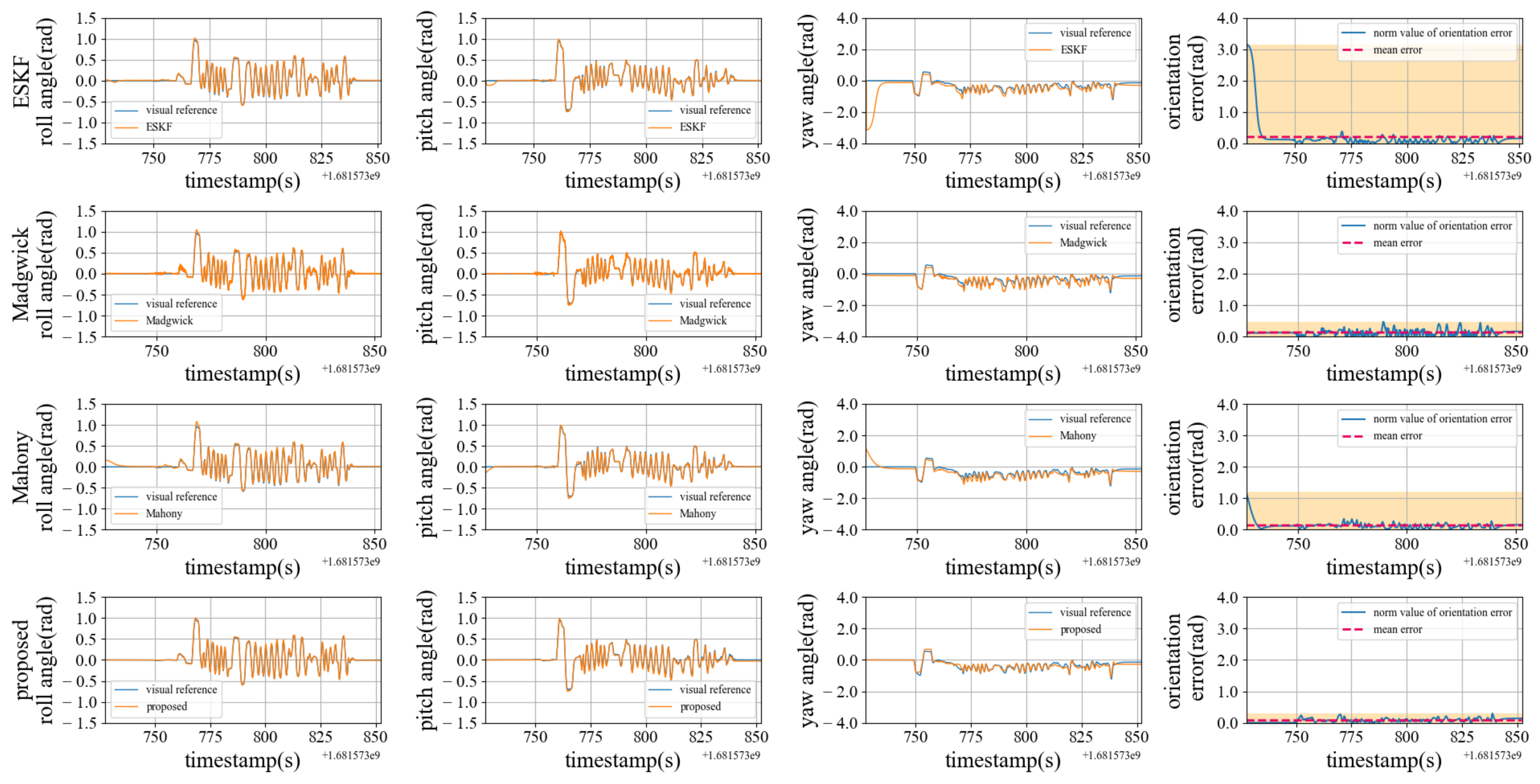
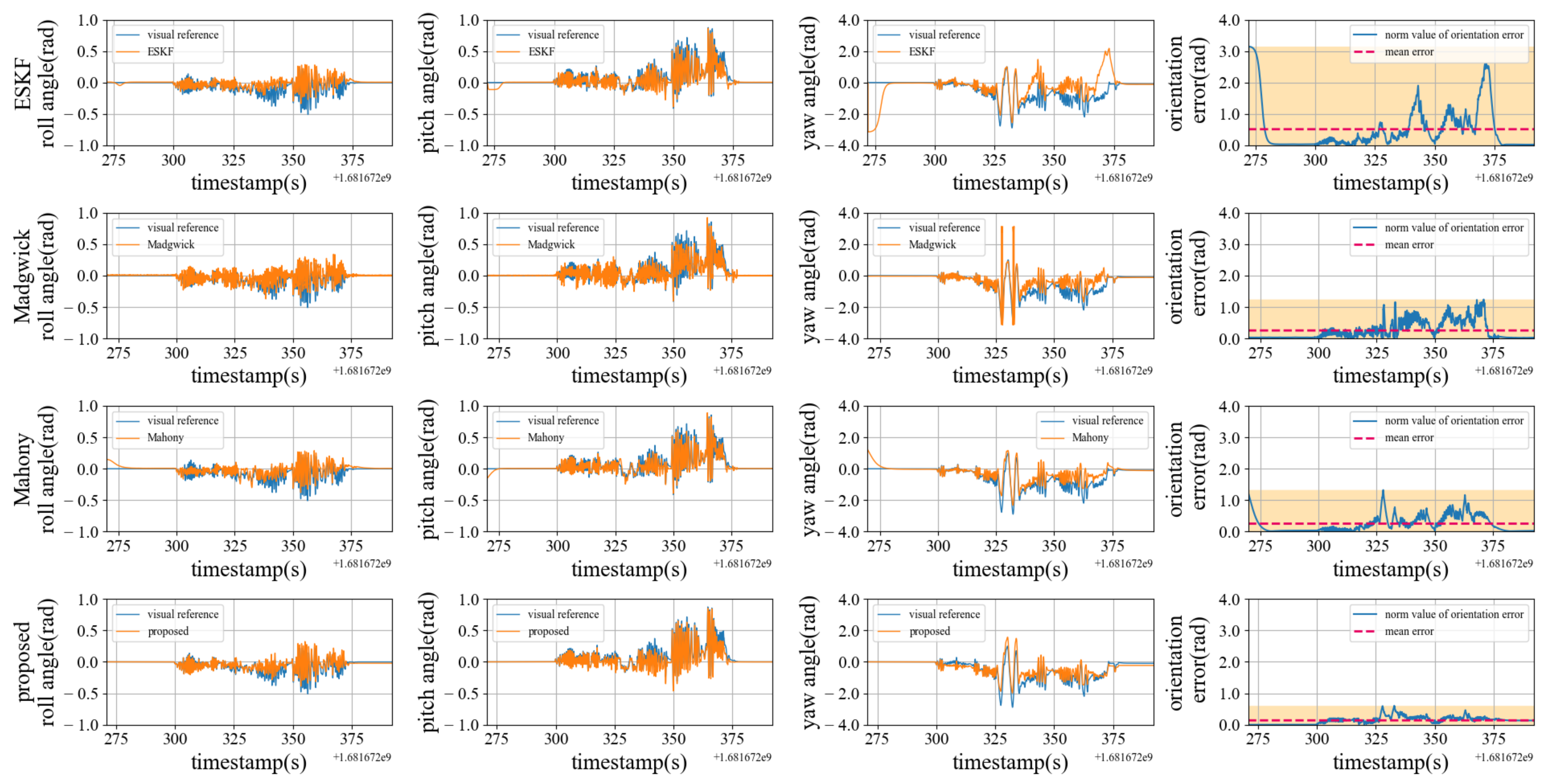
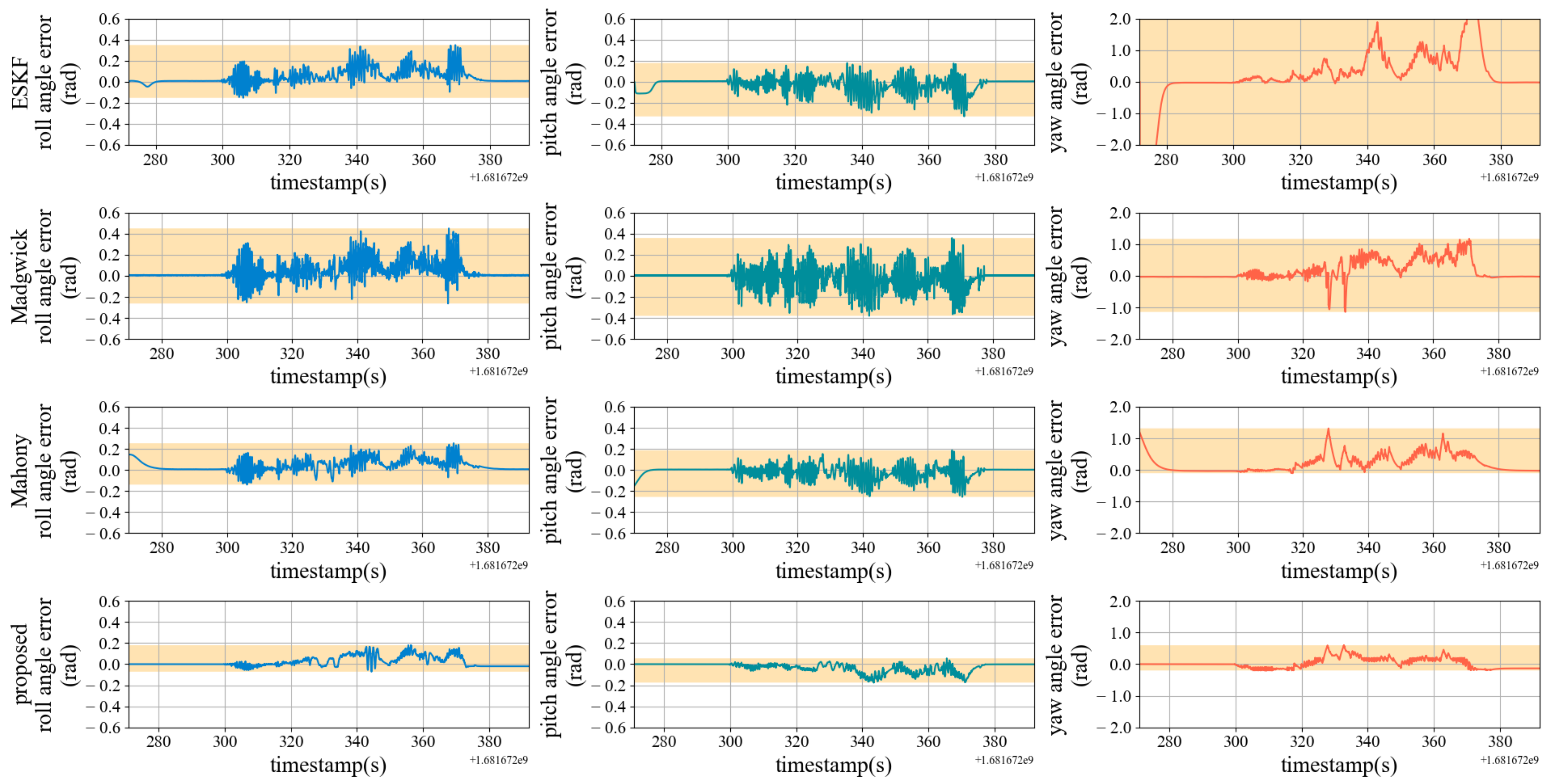
6.4. Experiment of Orientation Estimation Precision
6.5. Efficiency Test of Orientation Estimation Algorithm
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ARM | Advanced RISC Machine |
| ArUco | Augmented Reality University of Cordoba |
| CPU | Central processing unit |
| DL | Dogleg algorithm |
| EKF | Extended Kalman filter |
| ENU | East-North-Upper |
| ESKF | Error-state Kalman filter |
| ID | Identity document |
| IMU | Inertial measurement unit |
| I2C | Inter-integrated Circuit |
| LM | Levenberg–Marquardt |
| MEMS | Micro electrical system |
| PI | proportional and integral |
| PnP | Perspective-n-Point |
Appendix A
Appendix B
References
- Alteriis, G.; Conte, C.; Moriello, R.S.L.; Accardo, D. Use of consumer-grade MEMS inertial sensors for accurate attitude determination of drones. In Proceedings of the 2020 IEEE 7th International Workshop on Metrology for AeroSpace, Pisa, Italy, 22–24 June 2020. [Google Scholar]
- Kuevor, P.E.; Ghaffari, M.; Atkins, E.M.; Cutler, J.W. Fast and Noise-Resilient Magnetic Field Mapping on a Low-Cost UAV Using Gaussian Process Regression. Sensors 2023, 23, 3897. [Google Scholar] [CrossRef]
- Karam, S.; Nex, F.; Chidura, B.T.; Kerle, N. Microdrone-Based Indoor Mapping with Graph SLAM. Drones 2022, 6, 352. [Google Scholar] [CrossRef]
- George, A.; Koivumäki, N.; Hakala, T.; Suomalainen, J.; Honkavaara, E. Visual-Inertial Odometry Using High Flying Altitude Drone Datasets. Drones 2023, 7, 36. [Google Scholar] [CrossRef]
- He, Z.; Gao, W.; He, X.; Wang, M.; Liu, Y.; Song, Y.; An, Z. Fuzzy intelligent control method for improving flight attitude stability of plant protection quadrotor UAV. Int. J. Agric. Biol. Eng. 2019, 12, 110–115. [Google Scholar]
- Flores, D.A.; Saito, C.; Paredes, J.A.; Trujillano, F. Aerial photography for 3D reconstruction in the Peruvian Highlands through a fixed-wing UAV system. In Proceedings of the IEEE International Conference on Mechatronics (ICM), Akamatsu, Japan, 6–9 August 2017.
- Nazarahari, M.; Rouhani, H. Sensor fusion algorithms for orientation tracking via magnetic and inertial measurement units: An experimental comparison survey. Inf. Fusion 2021, 76, 8–23. [Google Scholar] [CrossRef]
- Li, X.; Xu, Q.; Shi, Q.; Tang, Y. Complementary Filter for orientation Estimation Based on MARG and Optical Flow Sensors. J. Phy. Conf. Ser. 2021, 2010, 012160. [Google Scholar] [CrossRef]
- Park, S.; Park, J.; Park, C.G. Adaptive orientation estimation for low-cost MEMS IMU using ellipsoidal method. IEEE Trans. Instrum. Meas. TTM 2020, 9, 7082–7091. [Google Scholar] [CrossRef]
- Mahony, R.; Hamel, T.; Pflimlin, J.M. Nonlinear complementary filters on the special orthogonal group. IEEE Trans. Autom. Control TAC 2008, 5, 1203–1218. [Google Scholar] [CrossRef]
- Madgwick, S.O.; Harrison, A.J.; Vaidyanathan, R. Estimation of IMU and MARG orientation using a gradient descent algorithm. In Proceedings of the IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011. [Google Scholar]
- Sabatini, A.M. Quaternion-based extended Kalman filter for determining orientation by inertial and magnetic sensing. IEEE Trans. Biomed. Eng. 2006, 53, 1346–1356. [Google Scholar] [CrossRef]
- Vitali, R.V. McGinnis, R.S. and Perkins, N.C., Robust error-state Kalman filter for estimating IMU orientation. IEEE Sens. J. 2020, 3, 3561–3569. [Google Scholar]
- Sola, J. Quaternion kinematics for the error-state Kalman filter. arXiv 2017, arXiv:1711.02508. [Google Scholar]
- Soliman, A.; Ribeiro, G.A.; Torres, A.; Rastgaar, M. Error-state Kalman filter for online evaluation of ankle angle. In Proceedings of the International Conference on Advanced Intelligent Mechatronics (AIM), Sapporo, Japan, 11–15 July 2022. [Google Scholar]
- Kam, H.C.; Yu, Y.K.; Wong, K.H. An improvement on aruco marker for pose tracking using kalman filter. In Proceedings of the 19th IEEE/ACIS International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing, Busan, Republic of Korea, 27–29 June 2018. [Google Scholar]
- Marut, A.; Wojtowicz, K.; Falkowski, K. ArUco markers pose estimation in UAV landing aid system. In Proceedings of the IEEE 5th International Workshop on Metrology for AeroSpace, Trento, Italy, 19–21 June 2019. [Google Scholar]
- Lu, X.X. A Review of Solutions for Perspective-n-Point Problem in Camera Pose Estimation. J. Phys. Conf. Ser. 2018, 5, 052009. [Google Scholar] [CrossRef]
- Qin, T.; Li, P.; Shen, S. Vins-mono: A robust and versatile monocular visual-inertial state estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Westman, E.; Hinduja, A.; Kaess, M. Feature-based SLAM for imaging sonar with under-constrained landmarks. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018. [Google Scholar]
- Yuan, Y.X. Recent advances in trust region algorithms. Math. Program. 2015, 151, 249–281. [Google Scholar] [CrossRef]
- Jafari, H.; Shahmiri, F. Examination of Quadrotor Inverse Simulation Problem Using Trust-Region Dogleg Solution Method. J. Aerosp. Sci. Technol. 2019, 12, 39–51. [Google Scholar]
- iplimage, P3P. Available online: http://iplimage.com/blog/p3p-perspective-point-overview/ (accessed on 5 April 2023).
- Gao, X.S.; Hou, X.R.; Tang, J.; Cheng, H.F. Complete solution classification for the perspective-three-point problem. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 930–943. [Google Scholar]
- Li, S.; Xu, C. A stable direct solution of perspective-three-point problem. Int. J. Pattern Recognit. Artif. Intell. 2011, 25, 627–642. [Google Scholar] [CrossRef]
- Hesch, J.A.; Roumeliotis, S.I. A Direct Least-Squares (DLS) method for PnP. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Lepetit, V.; Moreno-Noguer, F.; Fua, P. EPnP: Efficient Perspective-n-Point Camera Pose Estimation. Int. J. Comput. Vis. 2009, 81, 155–166. [Google Scholar] [CrossRef]
- Penate-Sanchez, A.; Andrade-Cetto, J.; Moreno-Noguer, F. Exhaustive linearization for robust camera pose and focal length estimation. IEEE Trans. Pattern Anal. Mach. Intell. TPAMI 2013, 10, 2387–2400. [Google Scholar] [CrossRef]
- Garrido-Jurado, S.; Muñoz-Salinas, R.; Madrid-Cuevas, F.J.; Medina-Carnicer, R. Generation of fiducial marker dictionaries using mixed integer linear programming. Pattern Recognit. 2016, 51, 481–491. [Google Scholar] [CrossRef]
- Romero-Ramirez, F.J.; Muñoz-Salinas, R.; Medina-Carnicer, R. Speeded up detection of squared fiducial markers. Image Vis. Comput. 2018, 76, 38–47. [Google Scholar] [CrossRef]
- Filus, K.; Sobczak, Ł; Domańska, J.; Domański, A.; Cupek, R. Real-time testing of vision-based systems for AGVs with ArUco markers. In Proceedings of the IEEE International Conference on Big Data, Osaka, Japan, 17–20 December 2022. [Google Scholar]
- Kalaitzakis, M.; Carroll, S.; Ambrosi, A.; Whitehead, C.; Vitzilaios, N. Experimental Comparison of Fiducial Markers for Pose Estimation. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Nagoya, Japan, 23–25 March 2020. [Google Scholar]
- MacTavish, K.; Barfoot, T.D. At all Costs: A Comparison of Robust Cost Functions for Camera Correspondence Outliers. In Proceedings of the Conference on Computer and Robot Vision, Halifax, UK, 3–5 June 2015. [Google Scholar]
- Kümmerle, R.; Grisetti, G.; Strasdat, H.; Konolige, K.; Burgard, W. g2o: A general framework for graph optimization. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar]
- Ceres Solver. Available online: https://github.com/ceres-solver/ceres-solver (accessed on 2 April 2023).
- Furgale, P.; Rehder, J.; Siegwart, R. Unified Temporal and Spatial Calibration for Multi-Sensor Systems. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–8 November 2013. [Google Scholar]
- Hartley, R.; Zisserman, A. Numerical Method. In Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2003; p. 412. [Google Scholar]
- InvenSense MPU9250. Available online: https://invensense.tdk.com/products/motion-tracking/9-axis/mpu-9250/ (accessed on 2 April 2023).
- Pi-4-model-b. Available online: https://www.raspberrypi.com/products/raspberry-pi-4-model-b/ (accessed on 2 April 2023).
- Intel Realsense D435i. Available online: https://www.intelrealsense.com/depth-camera-d435i/ (accessed on 2 April 2023).









| Symbols | Description |
|---|---|
| Bold capital letters represent matrices | |
| Bold lowercase letters represent vectors | |
| x | Scalar |
| Measurement value of sensor | |
| Probability | |
| Normalized quaternion | |
| The imaginary part of a quaternion | |
| Optimal value | |
| Coordinate system |
| Test Sets | Algorithm | () | () | |
|---|---|---|---|---|
| V02 | P3P + LM | 0.14 | 0.12 | |
| P3P + DL | 0.14 | 0.05 | ||
| DLT + LM | 0.52 | 0.09 | ||
| DLT + DL | 0.52 | 0.08 | ||
| V03 | P3P + LM | 0.27 | 0.13 | |
| P3P + DL | 0.27 | 0.06 | ||
| DLT + LM | 0.51 | 0.15 | ||
| DLT + DL | 0.51 | 0.08 | ||
| V04 | P3P + LM | 0.53 | 0.32 | |
| P3P + DL | 0.53 | 0.06 | ||
| DLT + LM | 1.22 | 0.21 | ||
| DLT + DL | 1.22 | 0.08 | ||
| V05 | P3P + LM | 0.54 | 0.09 | |
| P3P + DL | 0.54 | 0.08 | ||
| DLT + LM | 1.14 | 0.15 | ||
| DLT + DL | 1.14 | 0.24 | ||
| V21 | P3P + LM | 0.38 | 0.09 | |
| P3P + DL | 0.38 | 0.06 | ||
| DLT + LM | 1.23 | 0.31 | ||
| DLT + DL | 1.23 | 0.09 |
| Algorithm | ||||||||
|---|---|---|---|---|---|---|---|---|
| ESKF | 3.141 | 0.205 | 0.059 | 0.011 | 0.038 | 0.005 | 0.241 | 0.188 |
| Madgwick | 0.470 | 0.130 | 0.094 | 0.013 | 0.067 | 0.001 | 0.266 | 0.081 |
| Mahony | 1.205 | 0.136 | 0.158 | 0.016 | 0.062 | 0.004 | 1.185 | 0.076 |
| Proposed | 0.299 | 0.076 | 0.039 | 0.004 | 0.034 | 0.016 | 0.296 | 0.015 |
| Algorithm | ||||||||
|---|---|---|---|---|---|---|---|---|
| ESKF | 3.141 | 0.514 | 0.347 | 0.046 | 0.177 | 0.027 | 2.598 | 0.198 |
| Madgwick | 5.995 | 0.299 | 0.450 | 0.044 | 0.359 | 0.014 | 1.169 | 0.168 |
| Mahony | 1.324 | 0.253 | 0.254 | 0.044 | 0.187 | 0.016 | 1.317 | 0.217 |
| proposed | 0.600 | 0.138 | 0.179 | 0.021 | 0.055 | 0.030 | 0.598 | 0.029 |
| Test Data | Algorithm | (ms) | (ms) | (ms) | (ms) |
|---|---|---|---|---|---|
| Low dynamics | ESKF | 0.913 | 24.998 | 0.164 | 0.276 |
| Madgwick | 0.007 | 0.626 | <0.001 | 0.018 | |
| Mahony | 0.081 | 3.938 | 0.105 | 0.102 | |
| Proposed | 9.781 | 53.269 | 0.102 | 0.109 | |
| High dynamics | ESKF | 0.864 | 13.737 | 0.167 | 0.393 |
| Madgwick | 0.008 | 1.231 | <0.001 | 0.008 | |
| Mahony | 0.078 | 3.842 | 0.011 | 0.041 | |
| Proposed | 22.468 | 78.200 | 2.678 | 9.815 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, N.; Wei, Z.; Li, B. Trust–Region Nonlinear Optimization Algorithm for Orientation Estimator and Visual Measurement of Inertial–Magnetic Sensor. Drones 2023, 7, 351. https://doi.org/10.3390/drones7060351
Jia N, Wei Z, Li B. Trust–Region Nonlinear Optimization Algorithm for Orientation Estimator and Visual Measurement of Inertial–Magnetic Sensor. Drones. 2023; 7(6):351. https://doi.org/10.3390/drones7060351
Chicago/Turabian StyleJia, Nan, Zongkang Wei, and Bangyu Li. 2023. "Trust–Region Nonlinear Optimization Algorithm for Orientation Estimator and Visual Measurement of Inertial–Magnetic Sensor" Drones 7, no. 6: 351. https://doi.org/10.3390/drones7060351
APA StyleJia, N., Wei, Z., & Li, B. (2023). Trust–Region Nonlinear Optimization Algorithm for Orientation Estimator and Visual Measurement of Inertial–Magnetic Sensor. Drones, 7(6), 351. https://doi.org/10.3390/drones7060351







