A Safety-Assured Semantic Map for an Unstructured Terrain Environment towards Autonomous Engineering Vehicles
Abstract
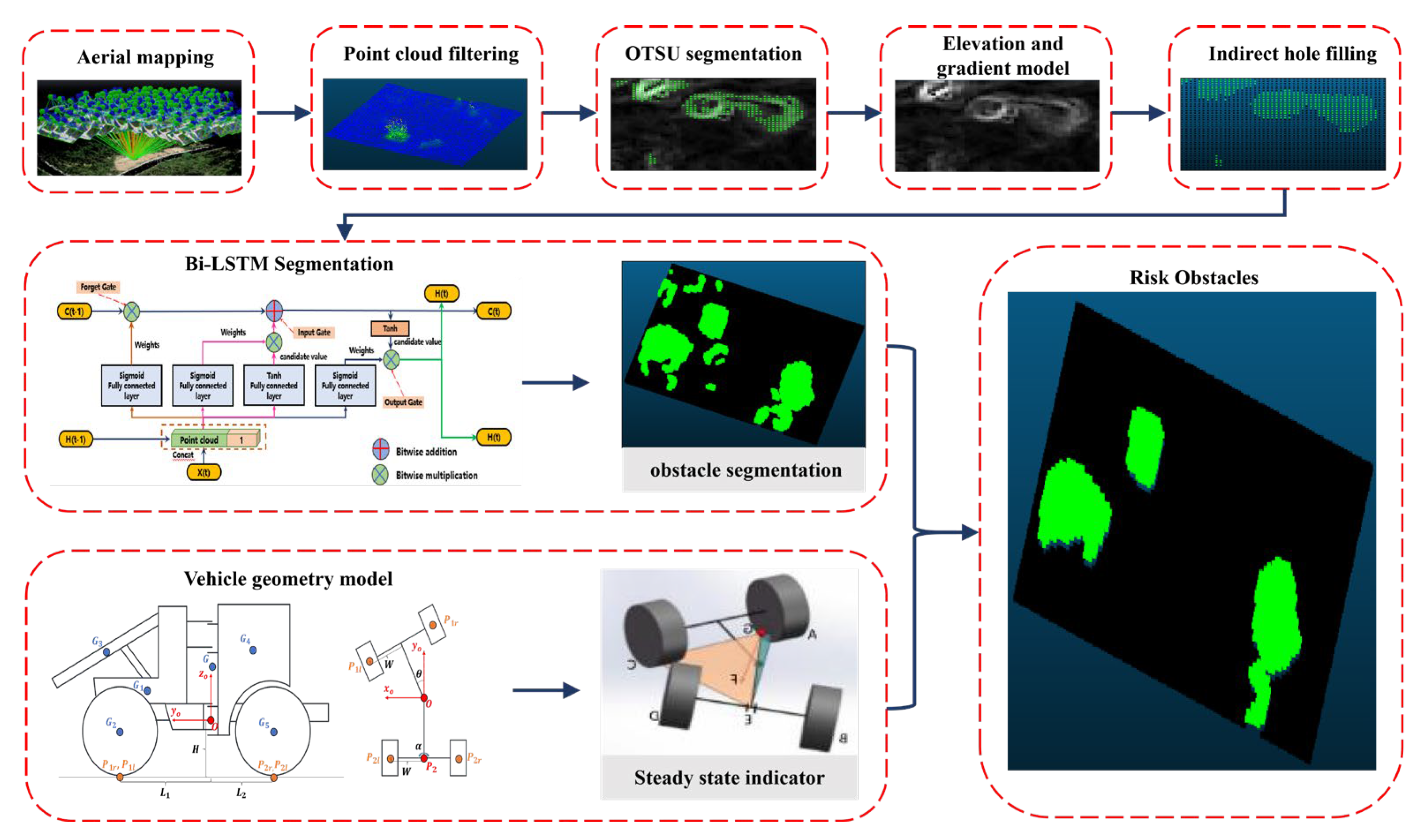
:1. Introduction
- Point cloud filtering algorithms that employ geometric and color spaces to filter outliers and refine unstructured scene point cloud models;
- Introducing the Sobel-G operator to build a digital gradient model. The reverse hole-filling method is designed to address point cloud model defects, and the OTSU segmentation algorithm is employed for further marking of hazardous obstacles;
- Innovative application of a bidirectional long short-term memory (Bi-LSTM) neural network to train point cloud features, facilitating faster and more accurate semantic segmentation of hazardous obstacles in similar unstructured environments;
- Accurate extraction of hazardous obstacles that impact the safe driving of vehicles by leveraging the vehicle-terrain model.
2. Methods
2.1. Experimental Equipment and Site
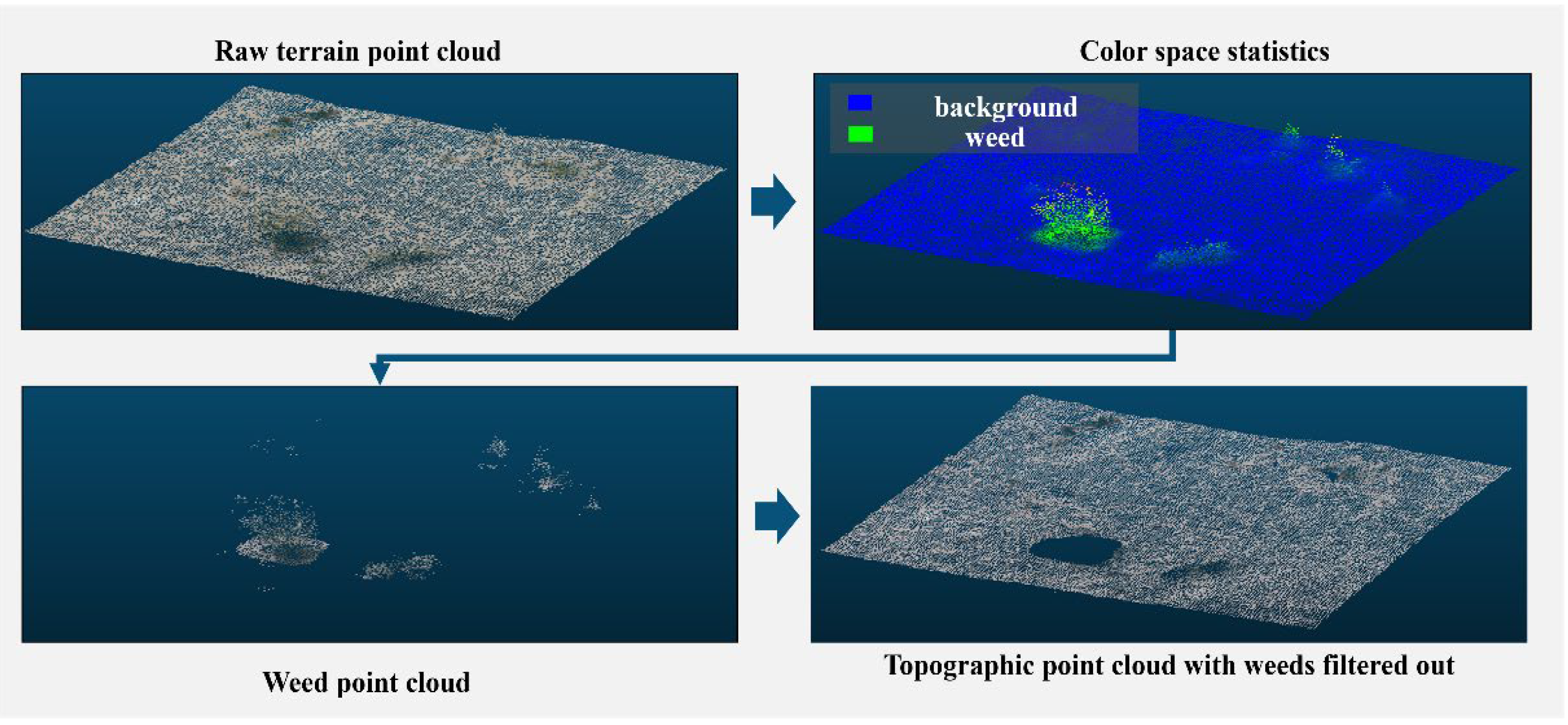
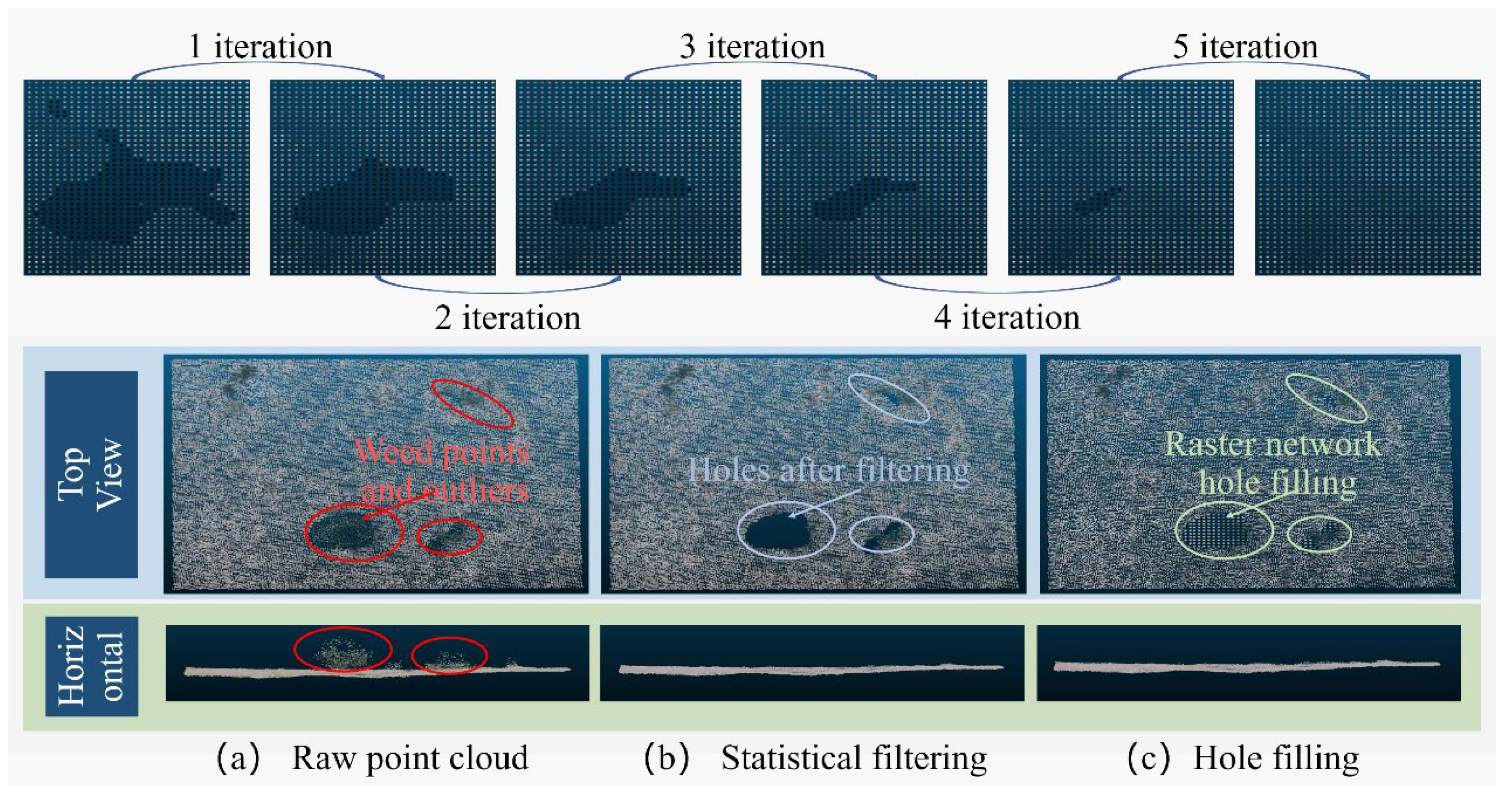
2.2. Terrain Point Cloud Filtering and Hole Completion
- Geostatistical filtering on outliers
- Color space statistical filtering on surface weed
- Hole-filling of filtered point clouds
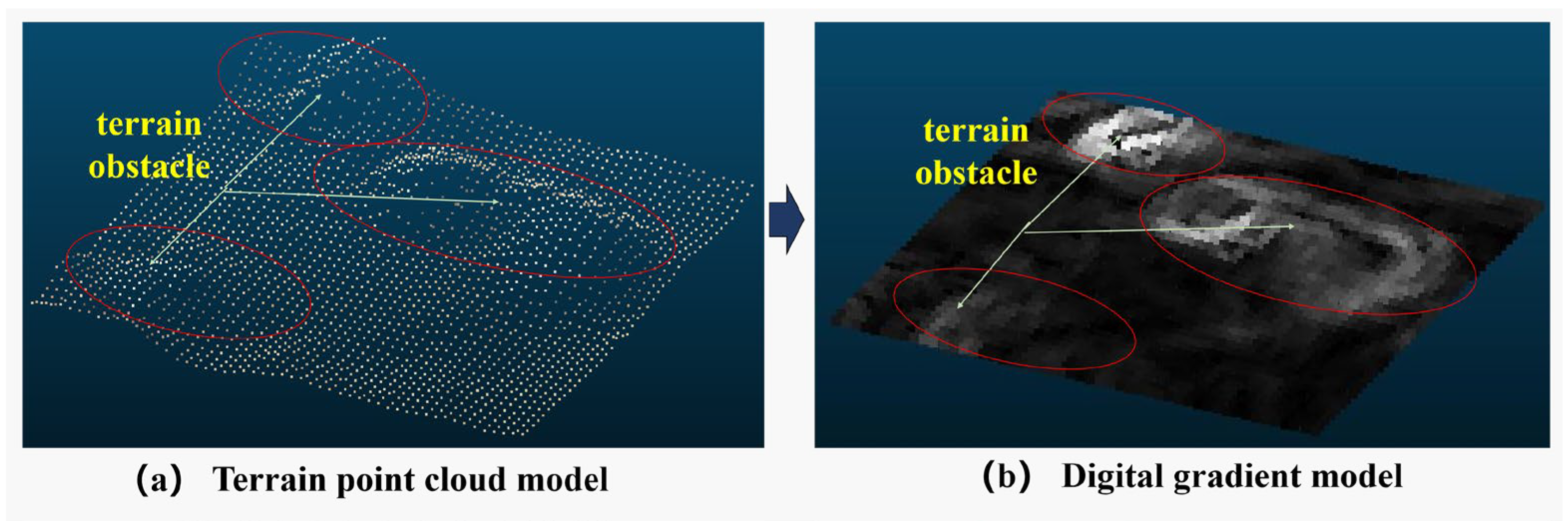
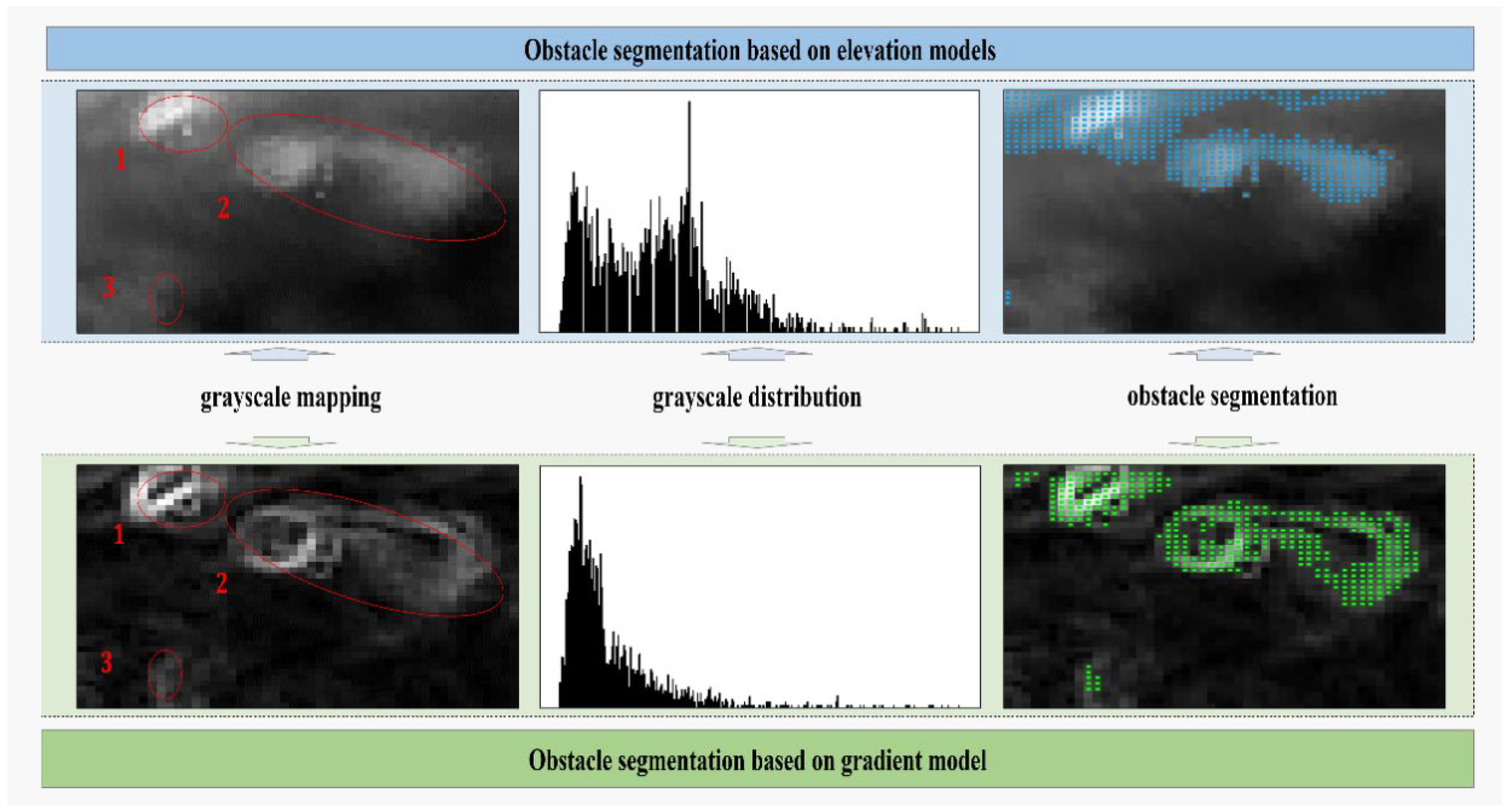
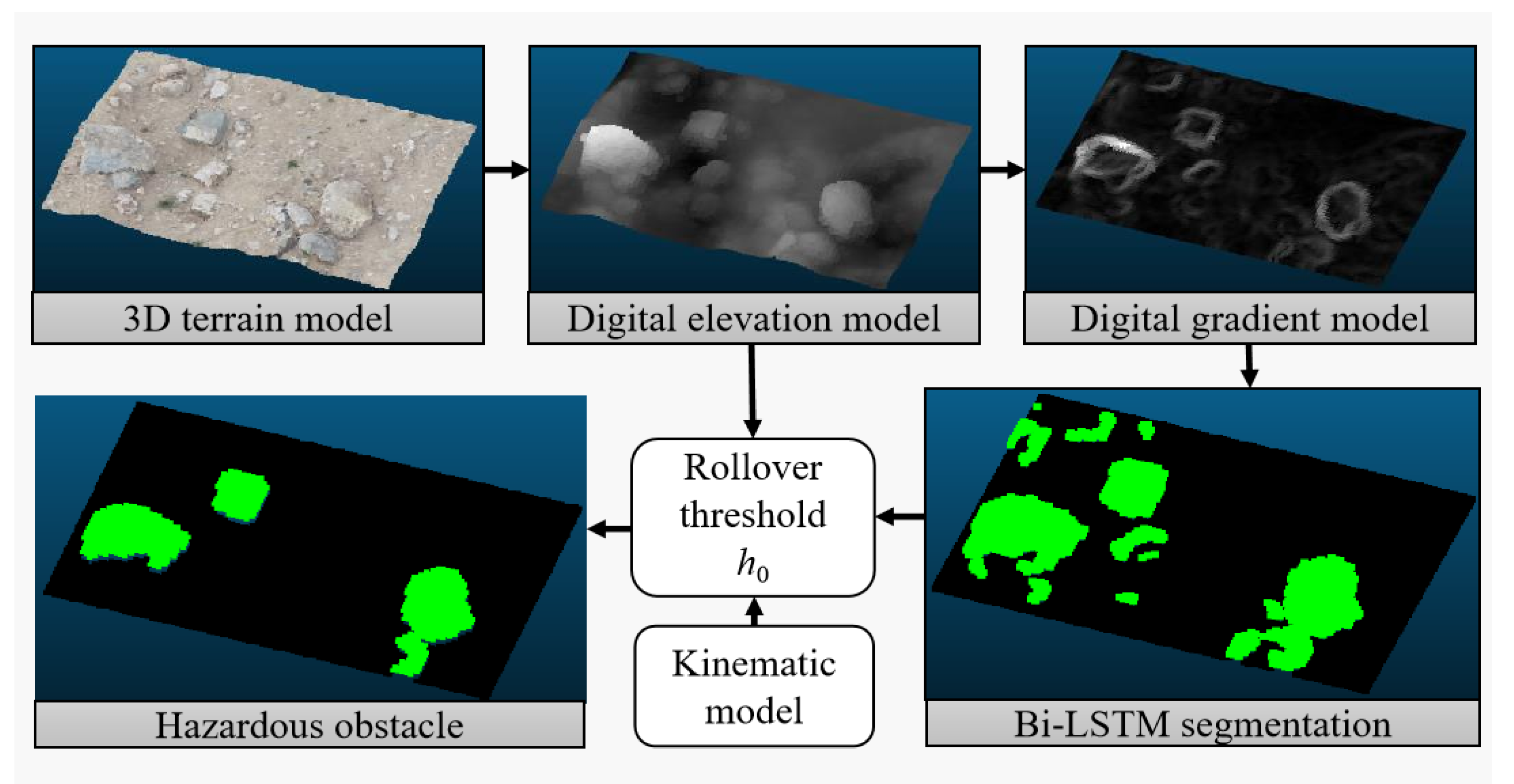
2.3. Segmentation of Primary Obstacles Based on a Digital Gradient Model
- Digital Gradient Model Construction and Obstacle Semantic Labeling Based on the Sobel-G Operator
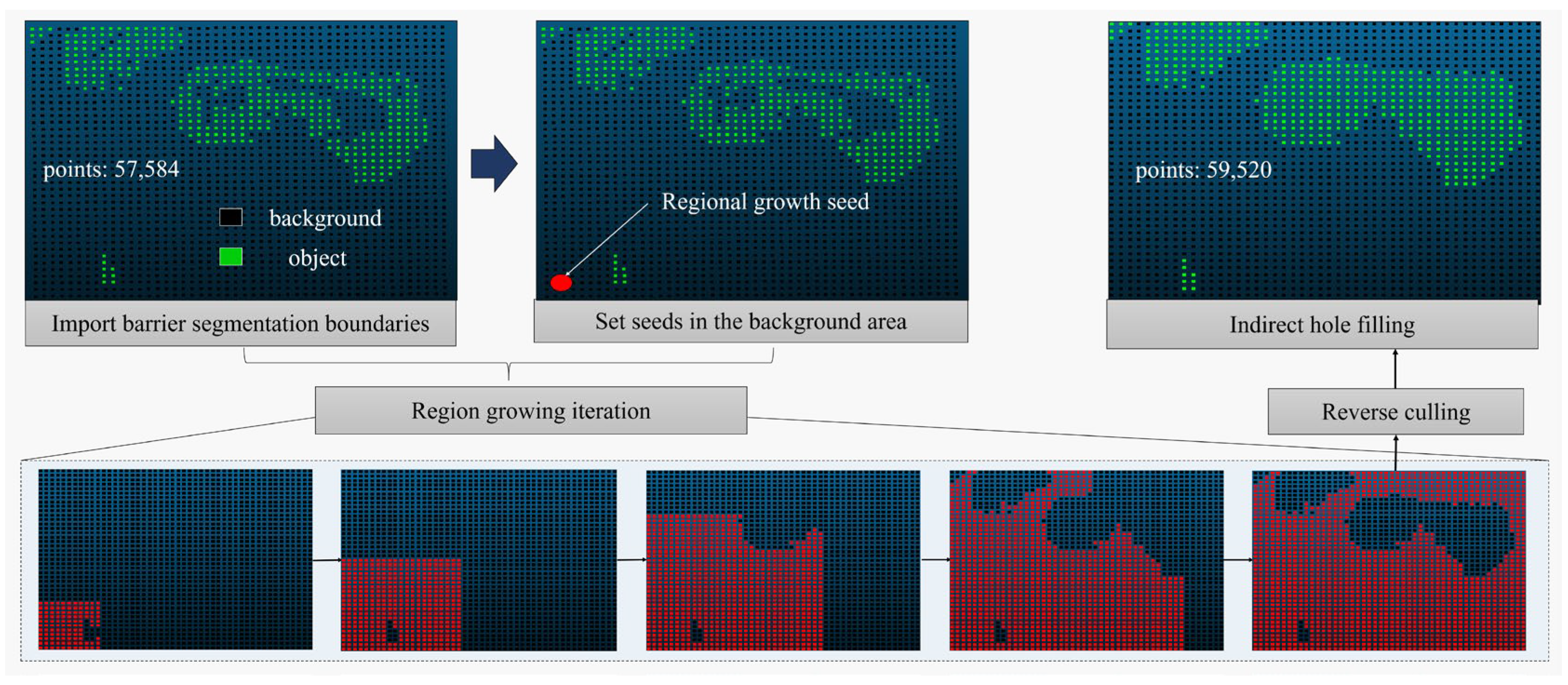
- Indirect hole filling based on background region culling
| Algorithm 1 Indirect hole filling for obstacles in boundary models |
Input: Obstacle_Boundary_Model(OB) Output: Obstacle_Model(O) Start:
End |
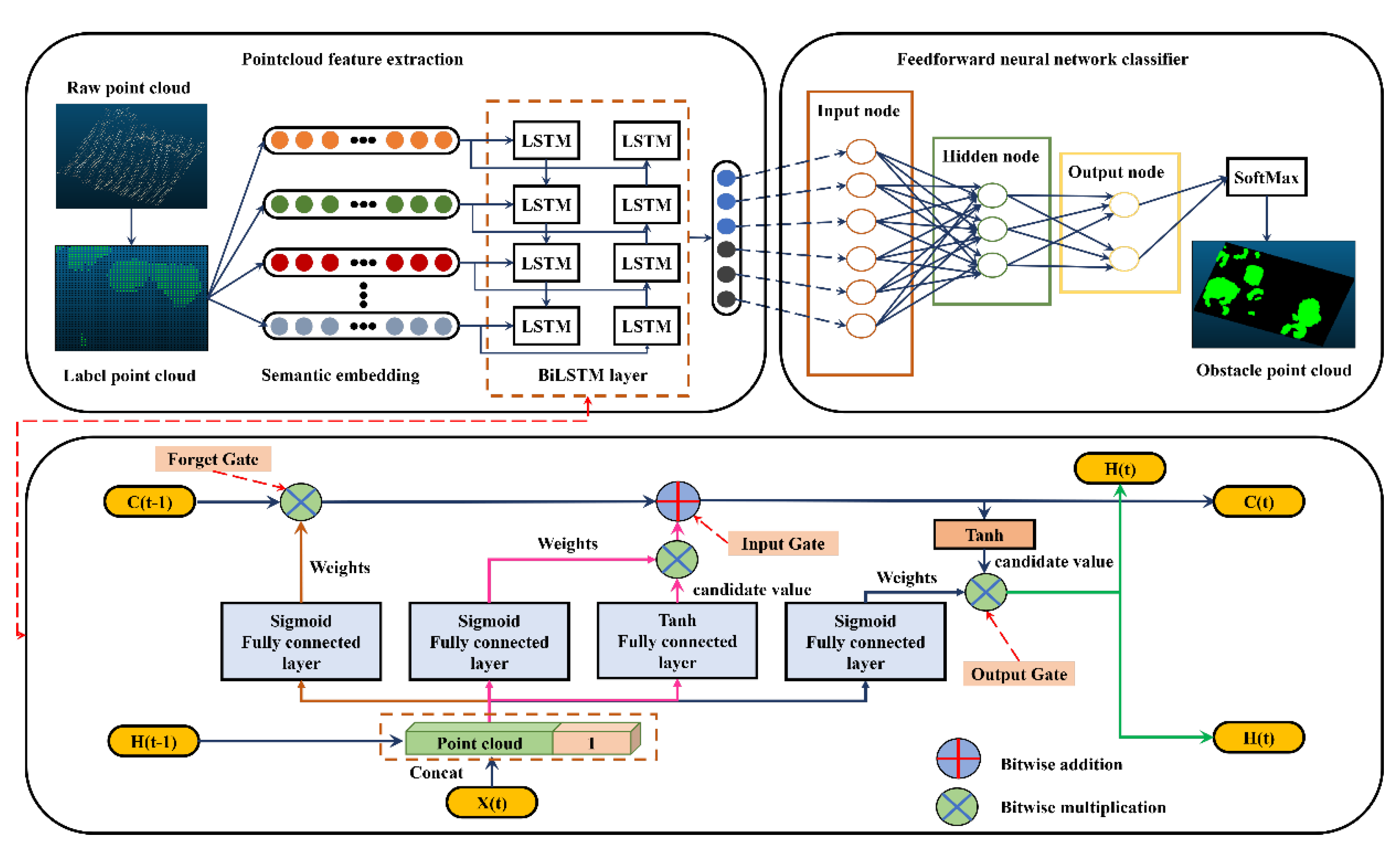
2.4. Point Cloud Segmentation Based on Bi-LSTM Neural Network
- The deep learning network framework for point cloud tuning
- Implementation process for applicable point clouds
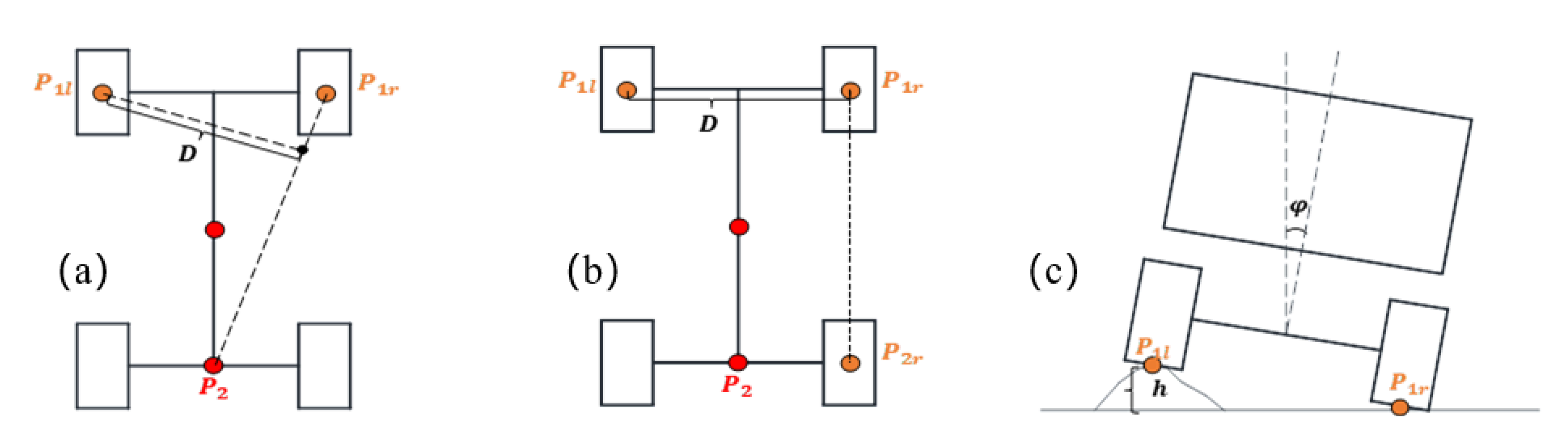
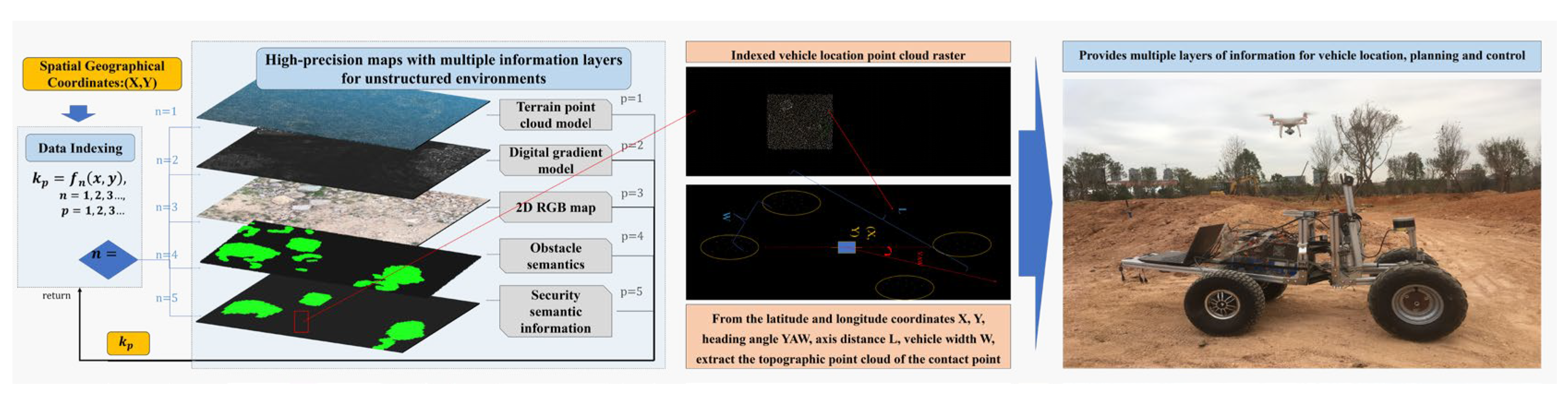
2.5. Semantic Segmentation of Hazardous Obstacles Based on Vehicle-Terrain Model
3. Experiment and Result Analysis
3.1. Datasets and Evaluation Metrics
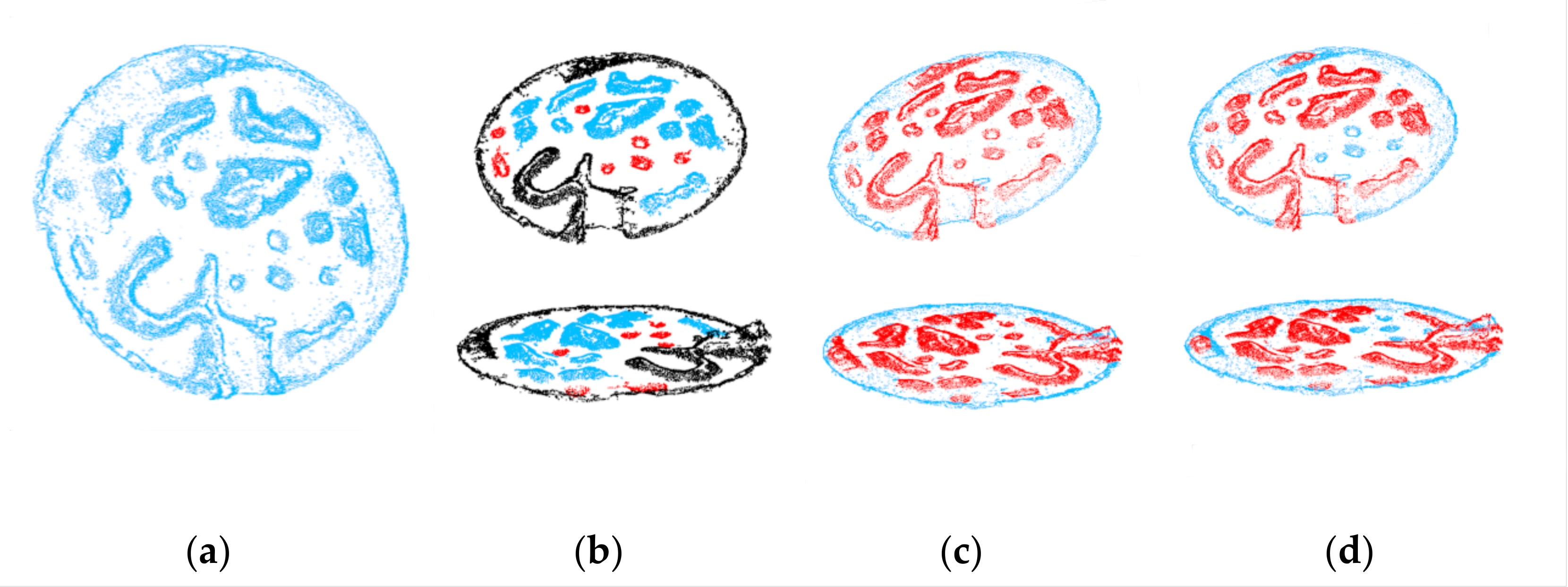
3.2. Obstacle Detection Results of the Image Point Cloud
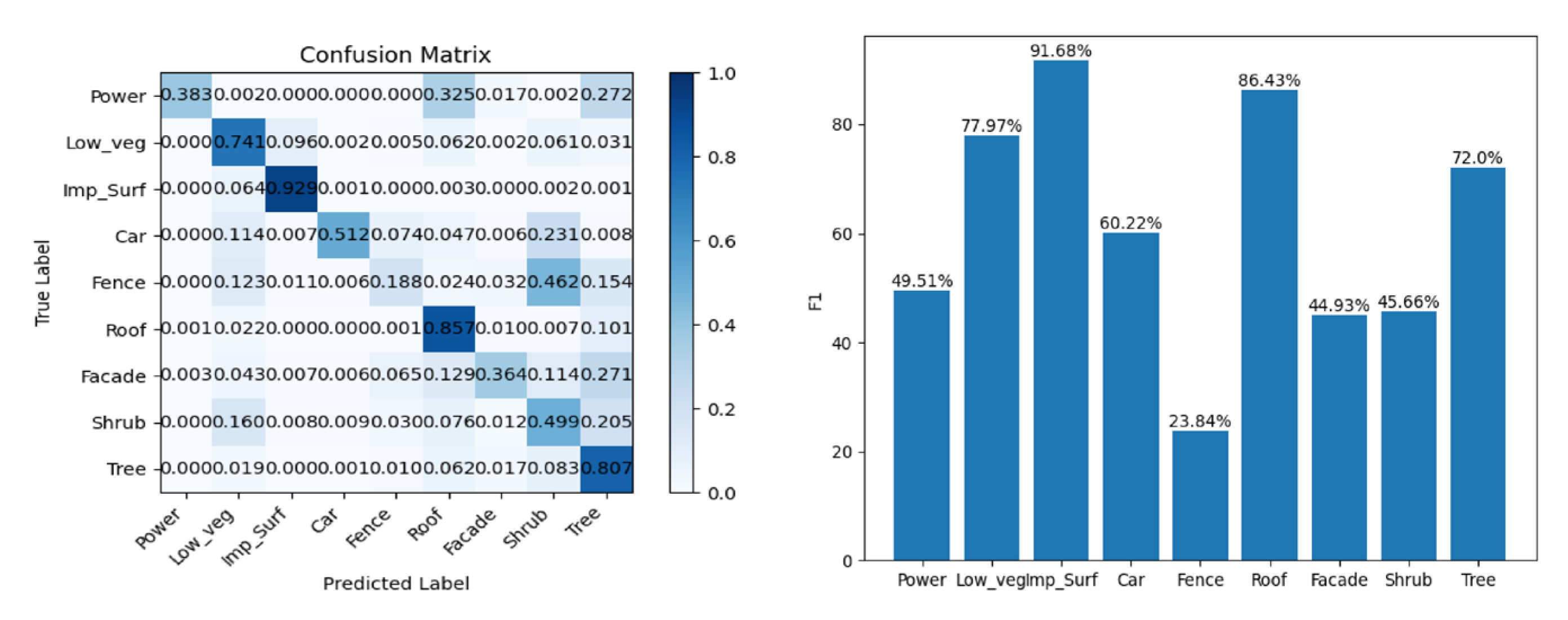
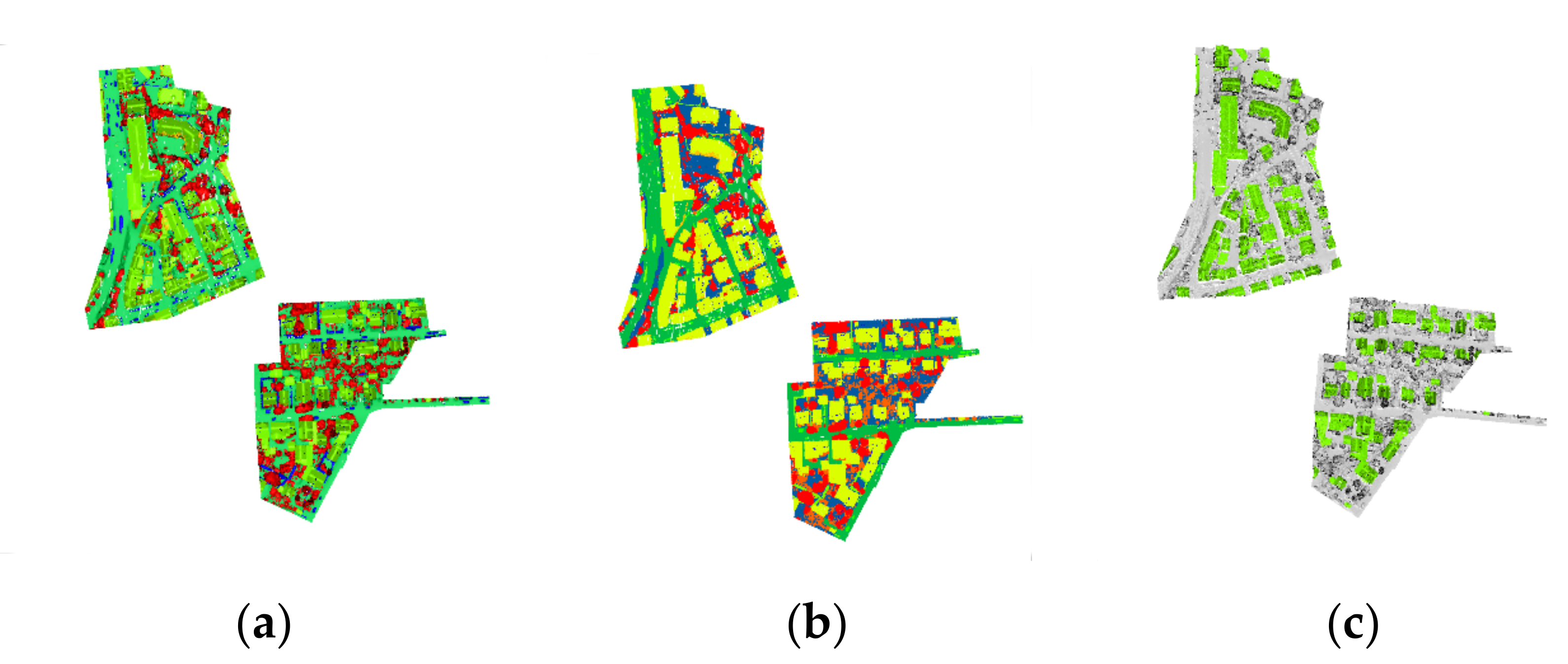
3.3. Classification Results of the ISPRS 3D Semantic Labeling Contest Dataset
3.4. Classification Results of the Canadian Planetary Emulation Terrain 3D Mapping Dataset
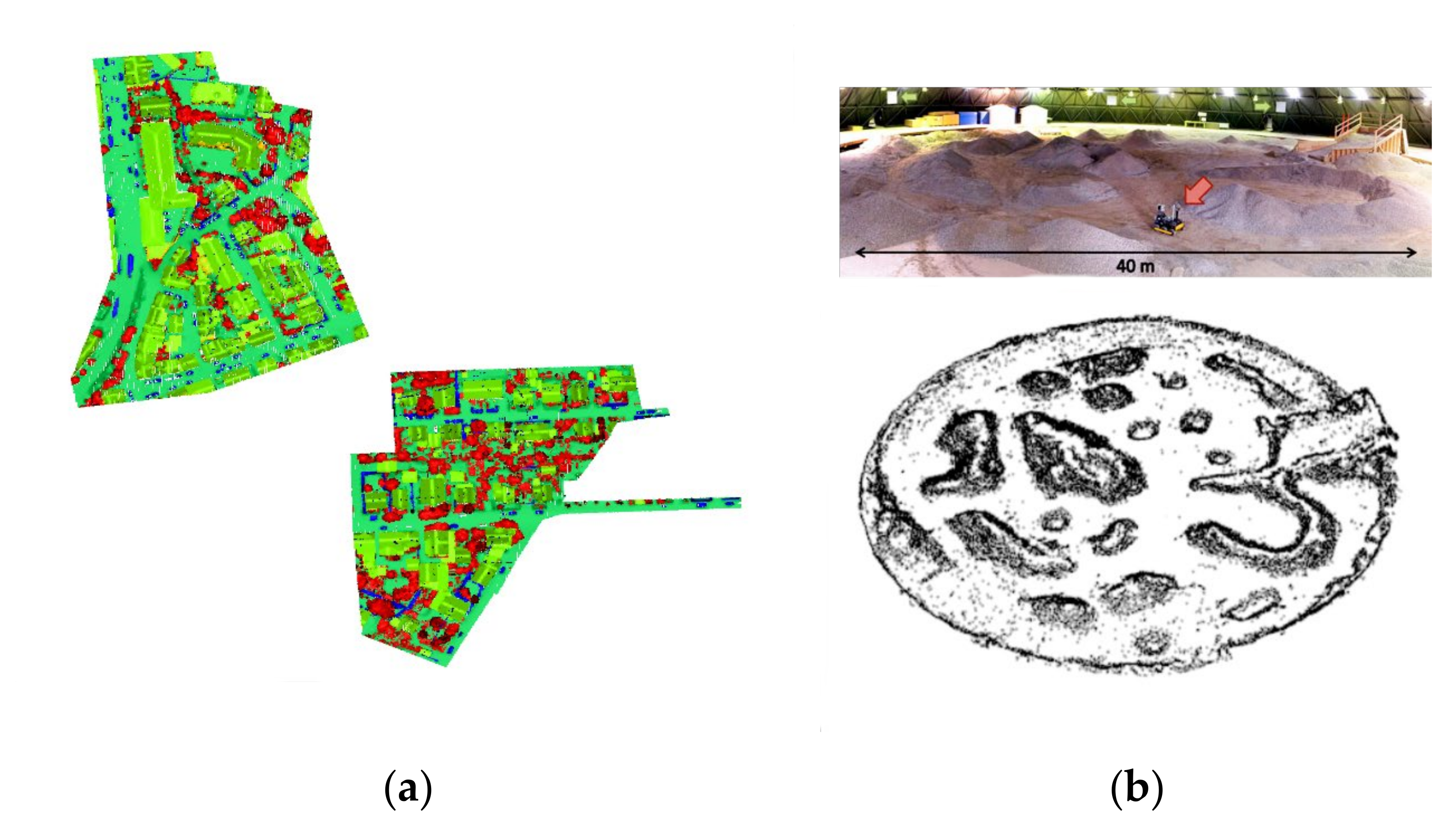
3.5. Engineering Applications of the Hazardous Obstacle Detection Framework
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, L.; Zhao, J.; Long, P.; Wang, L.; Qian, L.; Lu, F.; Song, X.; Manocha, D. An autonomous excavator system for material loading tasks. Sci. Robot. 2021, 6, 55. [Google Scholar] [CrossRef] [PubMed]
- Ha, Q.P.; Yen, L.; Balaguer, C. Robotic autonomous systems for earthmoving in military applications. Autom. Constr. 2019, 107, 102934. [Google Scholar] [CrossRef]
- Sharma, K.; Zhao, C.; Swarup, C.; Pandey, S.K.; Kumar, A.; Doriya, R.; Singh, K.U.; Singh, T. Early detection of obstacle to optimize the robot path planning. Drones 2022, 6, 10. [Google Scholar] [CrossRef]
- Bai, Y.; Fan, L.; Pan, Z.; Chen, L. Monocular outdoor semantic mapping with a multi-task network. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 4–8 November 2019; pp. 1992–1997. [Google Scholar]
- Jiang, K.; Yang, D.; Liu, C.; Zhang, T.; Xiao, Z. A flexible multi-layer map model designed for lane-level route planning in autonomous vehicles. Engineering 2019, 5, 305–318. [Google Scholar] [CrossRef]
- Ebadi, K.; Chang, Y.; Palieri, M.; Stephens, A.; Hatteland, A.; Heiden, E.; Thakur, A.; Funabiki, N.; Morrell, B.; Wood, S.; et al. LAMP: Large-scale autonomous mapping and positioning for exploration of perceptually-degraded subterranean environments. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 80–86. [Google Scholar]
- Pan, Y.; Xu, X.; Ding, X.; Huang, S.; Wang, S.; Xiong, R. GEM: Online globally consistent dense elevation mapping for unstructured terrain. IEEE Trans. Instrum. Meas. 2021, 70, 1–13. [Google Scholar] [CrossRef]
- Matthies, L.; Maimone, M.; Johnson, A.; Cheng, Y.; Willson, R.; Villalpando, C.; Goldberg, S.; Huertas, A.; Stein, A.; Angelova, A. Computer vision on Mars. Int. J. Comput. Vis. 2007, 75, 67–92. [Google Scholar] [CrossRef]
- Cheng, Y.; Maimone, M.W.; Matthies, L. Visual odometry on the Mars exploration rovers-a tool to ensure accurate driving and science imaging. IEEE Robot. Autom. Mag. 2006, 13, 54–62. [Google Scholar] [CrossRef]
- Ma, J.; Bajracharya, M.; Susca, S.; Matthies, L.; Malchano, M. Real-time pose estimation of a dynamic quadruped in GPS-denied environments for 24-hour operation. Int. J. Robot. Res. 2016, 35, 631–653. [Google Scholar] [CrossRef]
- Bernuy, F.; del Solar, J.R. Semantic mapping of large-scale outdoor scenes for autonomous off-road driving. In Proceedings of the IEEE International Conference on Computer Vision Workshops(ICCVW), Santiago, Chile, 11–18 December 2015; pp. 35–41. [Google Scholar]
- Sock, J.; Kim, J.; Min, J.; Kwak, K. Probabilistic traversability map generation using 3D-LIDAR and camera. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 5631–5637. [Google Scholar]
- Jamali, A.; Anton, F.; Rahman, A.A.; Mioc, D. 3D indoor building environment reconstruction using least square adjustment, polynomial kernel, interval analysis and homotopy continuation. In Proceedings of the 3rd International GeoAdvances Workshop/ISPRS Workshop on Multi-dimensional and Multi-Scale Spatial Data Modeling, Istanbul, Turkey, 16–17 October 2016; pp. 103–113. [Google Scholar]
- Milella, A.; Cicirelli, G.; Distante, A. RFID-assisted mobile robot system for mapping and surveillance of indoor environments. Ind. Robot. 2008, 35, 143–152. [Google Scholar] [CrossRef]
- Xia, X.; Meng, Z.; Han, X.; Li, H.; Tsukiji, T.; Xu, R.; Zheng, Z.; Ma, J. An automated driving systems data acquisition and analytics platform. Transp. Res. Pt. C-Emerg. Technol. 2023, 151, 104120. [Google Scholar] [CrossRef]
- Shan, T.; Englot, B. LeGO-LOAM: Lightweight and ground-optimized lidar odometry and mapping on variable terrain. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4758–4765. [Google Scholar]
- Le Gentil, C.; Vayugundla, M.; Giubilato, R.; Stürzl, W.; Vidal-Calleja, T.; Triebel, R. Gaussian process gradient maps for loop-closure detection in unstructured planetary environments. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 1895–1902. [Google Scholar]
- Casella, V.; Franzini, M. Modelling steep surfaces by various configurations of nadir and oblique photogrammetry. In Proceedings of the 23rd ISPRS Congress, Prague, Czech Republic, 12–19 July 2016; Volume 3, pp. 175–182. [Google Scholar]
- Ren, J.; Chen, X.; Zheng, Z. Future prospects of UAV tilt photogrammetry technology. In IOP Conference Series: Materials Science and Engineering; IOP: Bristol, UK, 2019; Volume 612, p. 032023. [Google Scholar]
- Liu, Y.; Zheng, X.; Ai, G.; Zhang, Y.; Zuo, Y. Generating a high-precision true digital orthophoto map based on UAV images. ISPRS Int. J. Geo-Inf. 2018, 7, 333. [Google Scholar] [CrossRef]
- Liu, J.; Xu, W.; Guo, B.; Zhou, G.; Zhu, H. Accurate mapping method for UAV photogrammetry without ground control points in the map projection frame. IEEE Trans. Geosci. Remote Sens. 2021, 5, 9673–9681. [Google Scholar] [CrossRef]
- Li, X.; Wu, Y.; Zhou, W.; Yao, Z. Study on roll instability mechanism and stability index of articulated steering vehicles. Math. Probl. Eng. 2016, 2016, 7816503. [Google Scholar] [CrossRef]
- Zhu, Q.; Chen, W.; Hu, H.; Wu, X.; Xiao, C.; Song, X. Multi-sensor based attitude prediction for agricultural vehicles. Comput. Electron. Agric. 2019, 156, 24–32. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Q.; Liu, J.; Zhu, Q.; Hu, H. Using gyro stabilizer for active anti-rollover control of articulated wheeled loader vehicles. Proc. Inst. Mech. Eng. Part I-J. Syst Control Eng. 2021, 235, 237–248. [Google Scholar] [CrossRef]
- Ghotbi, B.; González, F.; Kövecses, J.; Angeles, J. Vehicle-terrain interaction models for analysis and performance evaluation of wheeled rovers. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Algarve, Portugal, 7–12 October 2012; pp. 3138–3143. [Google Scholar]
- Choi, Y.; Kim, H. Convex hull obstacle-aware pedestrian tracking and target detection in theme park applications. Drones 2023, 7, 279. [Google Scholar] [CrossRef]
- Meng, Z.; Xia, X.; Xu, R.; Liu, W.; Ma, J. Hydro-3d: Hybrid object detection and tracking for cooperative perception using 3d lidar. IEEE T Intell. Veh. 2023, 1–13. [Google Scholar] [CrossRef]
- Qi, C.; Su, H.; Mo, K.; Guibas, L. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Liu, X.Q.; Chen, Y.M.; Li, S.Y.; Cheng, L.; Li, M.C. Hierarchical Classification of Urban ALS Data by Using Geometry and Intensity Information. Sensors 2019, 19, 4583. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.B.; Liu, Z.W.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph cnn for learning on point clouds. ACM Trans. Graph. 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Winiwarter, L.; Mandlburger, G.; Schmohl, S.; Pfeifer, N. Classification of ALS Point Clouds Using End-to-End Deep Learning. PFG-J. Photogramm. Remote Sens. Geoinf. Sci. 2019, 87, 75–90. [Google Scholar] [CrossRef]
- Wen, P.; Cheng, Y.L.; Wang, P.; Zhao, M.J.; Zhang, B.X. HA-GCN: An als point cloud classification method based on height-aware graph convolution network. In Proceedings of the 13th International Conference on Graphics and Image Processing (ICGIP), Yunnan Univ, Kunming, China, 18–20 August 2022; p. 12083. [Google Scholar]
- Hu, Q.; Ang, B.; Xie, L.; Rosa, S.; Markham, A. RandLA-Net: Efficient semantic segmentation of large-scale point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 11108–11117. [Google Scholar]
- Chen, W.; Liu, Q.; Hu, H.; Liu, J.; Wang, S.; Zhu, Q. Novel laser-based obstacle detection for autonomous robots on unstructured terrain. Sensors 2020, 20, 18. [Google Scholar] [CrossRef]
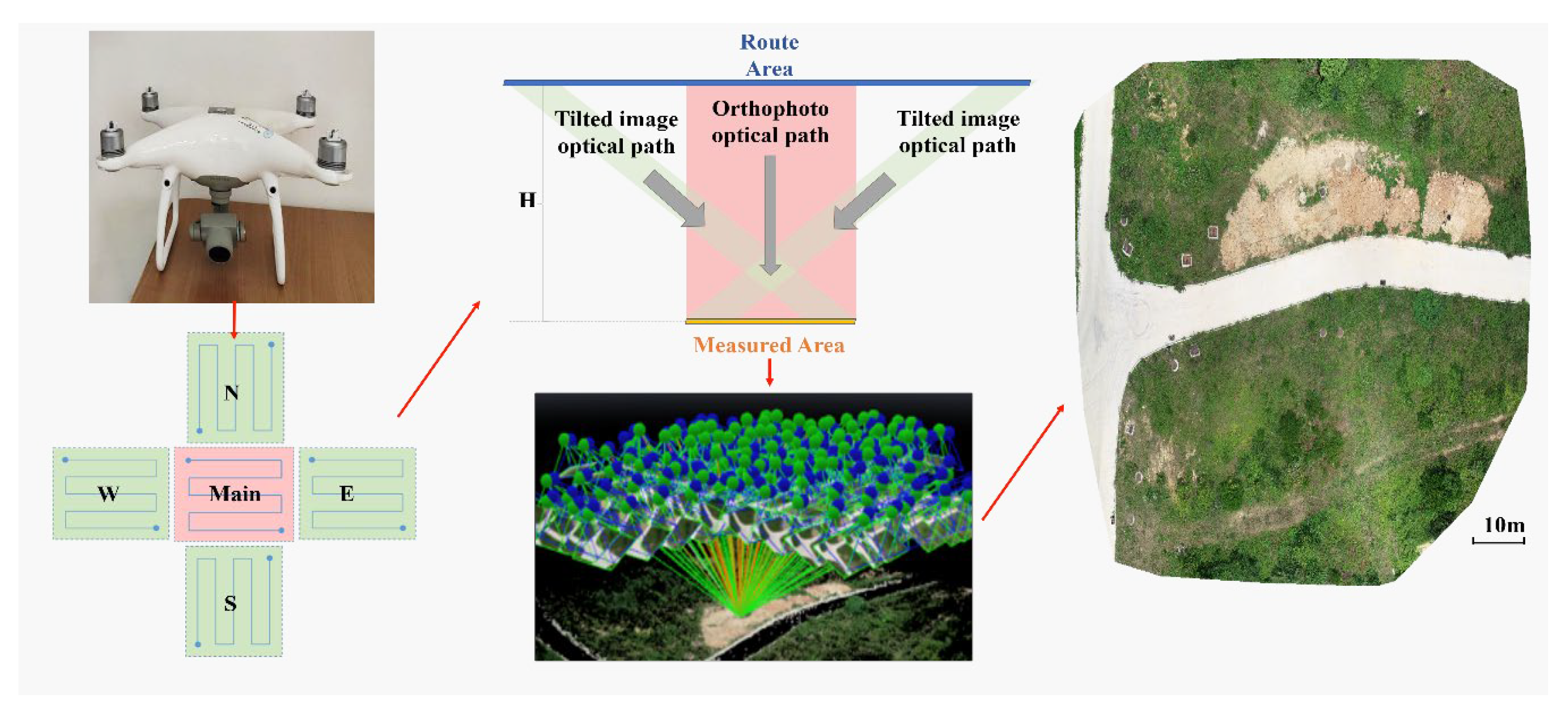





| DJI Phantom 4 Pro | |||
|---|---|---|---|
| Photosensitive device area | 1 inch CMOS | Angle of view | 84° |
| Effective pixels | 20 MP | Aperture | f/2.8–f/11 |
| Focal length | 35 mm equivalent | Shutter speed | 8–1/8000 s |
| Focusing distance | 1 m–infinity | IOS | 100–12,800 |
| Weight | 1375 g | Flight duration | 30 min |
| Vertical retention accuracy | ± 0.1 m | Horizontal preservation accuracy | ± 0.3 m |
| Gimbal pitch angle | 30°–90° | Gimbal angle jitter | ± 0.02° |
| Hazardous Obstacle | Ground | Precision | Recall | F1 | |
|---|---|---|---|---|---|
| Hazardous obstacle | 11,639 | 1416 | 93.99% | 89.15% | 91.51% |
| Ground | 743 | 27,160 | 95.04% | 97.34% | 96.18% |
| Power | Low_veg | Imp_Surf | Car | Fence | Roof | Facade | Shrub | Tree | |
|---|---|---|---|---|---|---|---|---|---|
| Power | 230 | 1 | 0 | 0 | 0 | 195 | 10 | 1 | 163 |
| Low_veg | 0 | 73,154 | 9471 | 190 | 497 | 6114 | 212 | 6002 | 3050 |
| Imp_Surf | 0 | 6542 | 94,725 | 130 | 8 | 307 | 14 | 207 | 53 |
| Car | 0 | 421 | 27 | 1899 | 276 | 174 | 23 | 857 | 31 |
| Fence | 0 | 911 | 82 | 48 | 1398 | 176 | 240 | 3427 | 1140 |
| Roof | 64 | 2441 | 53 | 3 | 127 | 93,402 | 1123 | 793 | 11,042 |
| Façade | 31 | 478 | 73 | 68 | 727 | 1447 | 4083 | 1276 | 3041 |
| Shrub | 0 | 3981 | 202 | 227 | 742 | 1879 | 307 | 12,386 | 5094 |
| Tree | 4 | 1038 | 26 | 34 | 532 | 3379 | 938 | 4490 | 43,785 |
| Precision (%) | 69.91 | 82.23 | 90.51 | 73.07 | 32.46 | 87.23 | 58.75 | 42.07 | 64.96 |
| Recall (%) | 38.33 | 74.13 | 92.88 | 51.21 | 18.84 | 85.65 | 36.38 | 49.91 | 80.75 |
| F1 (%) | 49.51 | 77.97 | 91.68 | 60.22 | 23.84 | 86.43 | 44.93 | 45.66 | 72.00 |
| Method | Power | Low_veg | Imp_Surf | Car | Fence | Roof | Facade | Shrub | Tree | Avg. F1 |
|---|---|---|---|---|---|---|---|---|---|---|
| PointNet [28] | 0.526 | 0.700 | 0.832 | 0.112 | 0.075 | 0.748 | 0.078 | 0.246 | 0.454 | 0.419 |
| DT+GMM [29] | 0.018 | 0.653 | 0.746 | 0.333 | 0.144 | 0.818 | 0.287 | 0.348 | 0.732 | 0.453 |
| DGCNN [30] | 0.446 | 0.712 | 0.810 | 0.420 | 0.118 | 0.938 | 0.643 | 0.464 | 0.817 | 0.597 |
| alsNet [31] | 0.701 | 0.805 | 0.902 | 0.457 | 0.076 | 0.931 | 0.473 | 0.347 | 0.745 | 0.604 |
| HA-GCN [32] | 0.303 | 0.866 | 0.903 | 0.765 | 0.370 | 0.957 | 0.377 | 0.582 | 0.827 | 0.694 |
| RandLA-Net [33] | 0.690 | 0.801 | 0.914 | 0.731 | 0.362 | 0.937 | 0.584 | 0.458 | 0.827 | 0.701 |
| Ours | 0.495 | 0.780 | 0.917 | 0.602 | 0.238 | 0.864 | 0.449 | 0.457 | 0.720 | 0.614 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, S.; Huang, T.; Li, C.; Shao, G.; Gao, Y.; Zhu, Q. A Safety-Assured Semantic Map for an Unstructured Terrain Environment towards Autonomous Engineering Vehicles. Drones 2023, 7, 550. https://doi.org/10.3390/drones7090550
Song S, Huang T, Li C, Shao G, Gao Y, Zhu Q. A Safety-Assured Semantic Map for an Unstructured Terrain Environment towards Autonomous Engineering Vehicles. Drones. 2023; 7(9):550. https://doi.org/10.3390/drones7090550
Chicago/Turabian StyleSong, Shuang, Tengchao Huang, Chenyang Li, Guifang Shao, Yunlong Gao, and Qingyuan Zhu. 2023. "A Safety-Assured Semantic Map for an Unstructured Terrain Environment towards Autonomous Engineering Vehicles" Drones 7, no. 9: 550. https://doi.org/10.3390/drones7090550
APA StyleSong, S., Huang, T., Li, C., Shao, G., Gao, Y., & Zhu, Q. (2023). A Safety-Assured Semantic Map for an Unstructured Terrain Environment towards Autonomous Engineering Vehicles. Drones, 7(9), 550. https://doi.org/10.3390/drones7090550






