Joint Resource Slicing and Vehicle Association for Drone-Assisted Vehicular Networks †
Abstract
:1. Introduction
1.1. Related Works
1.2. Contributions and Organization
- We construct an optimization framework for resource slicing and vehicle association, which takes into account DSC deployment, traffic statistics, inter-DSC interference, and QoS requirements. We formulate a network utility maximization problem using the logarithmic function to determine spectrum slicing ratios and vehicle association patterns. We transform the joint optimization problem into a tractable biconcave maximization problem.
- We develop a convex search algorithm that iteratively solves the transformed problem for vehicle association patterns and spectrum partition with reduced complexity. The algorithm converges to a set of partial optimal solutions. Simulation results demonstrate that the proposed solution outperforms two other resource slicing baseline schemes regarding resource utilization and network throughput.
2. System Model
2.1. Resource Slicing Framework
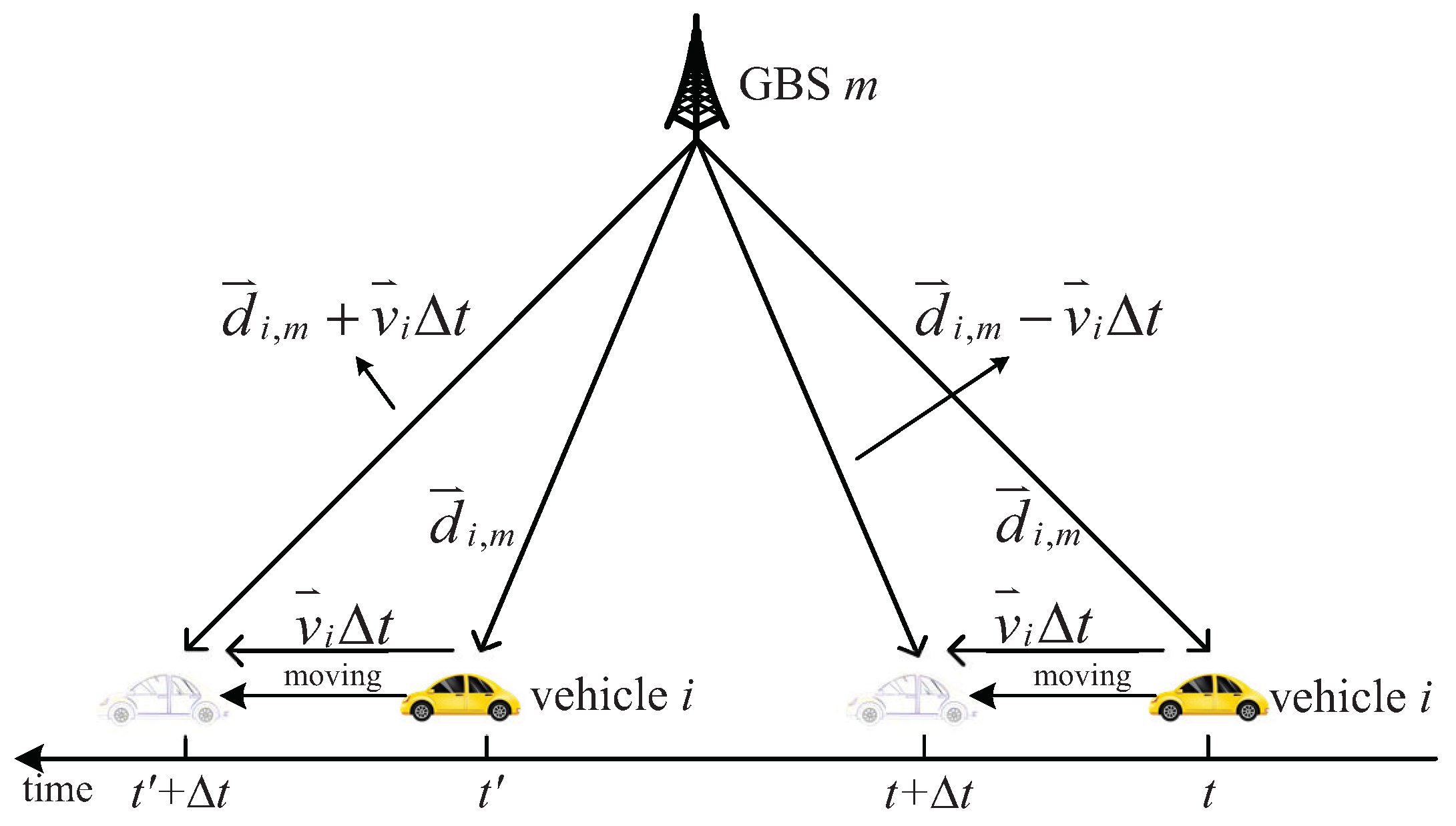
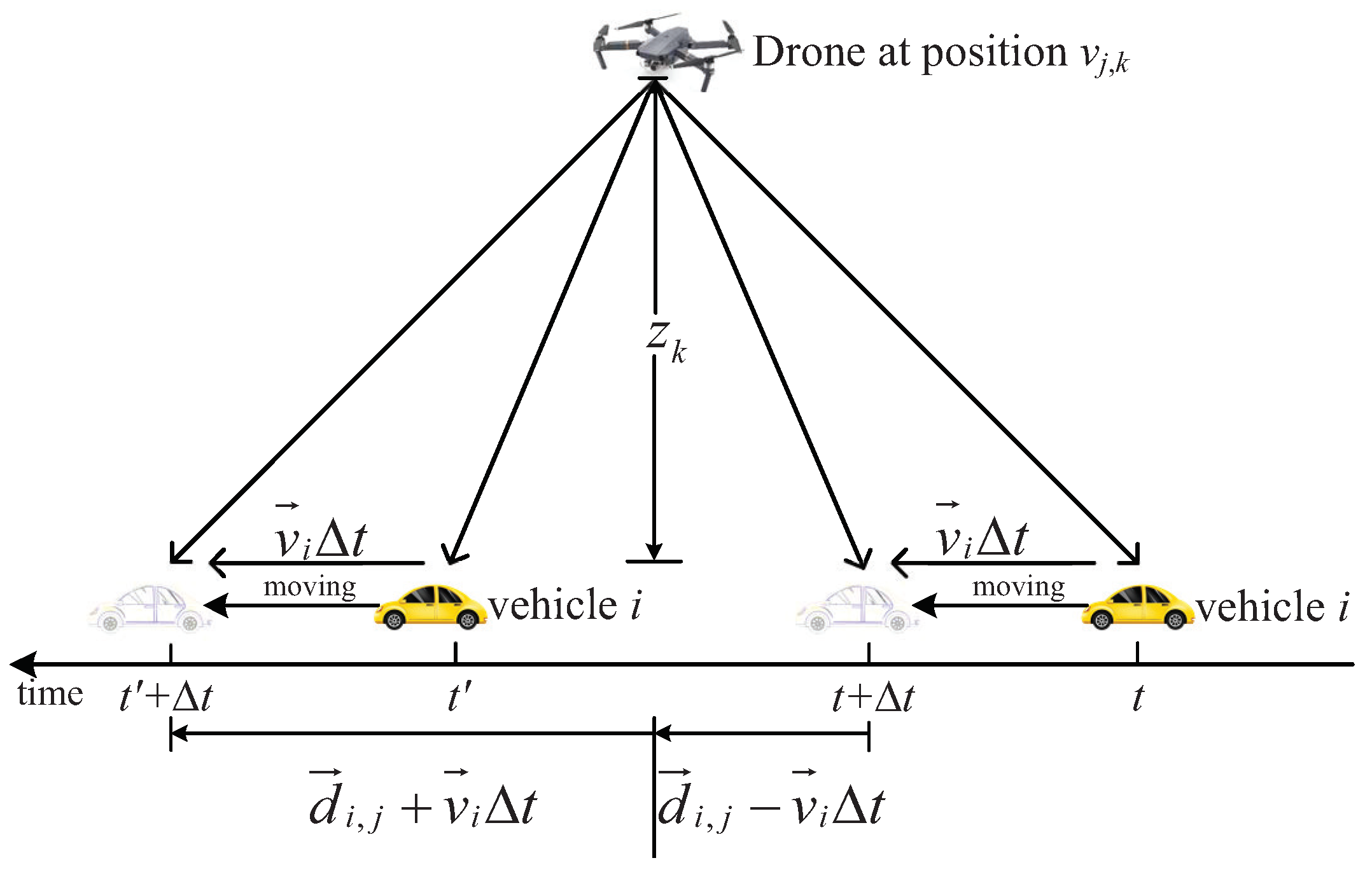
2.2. Communication Model
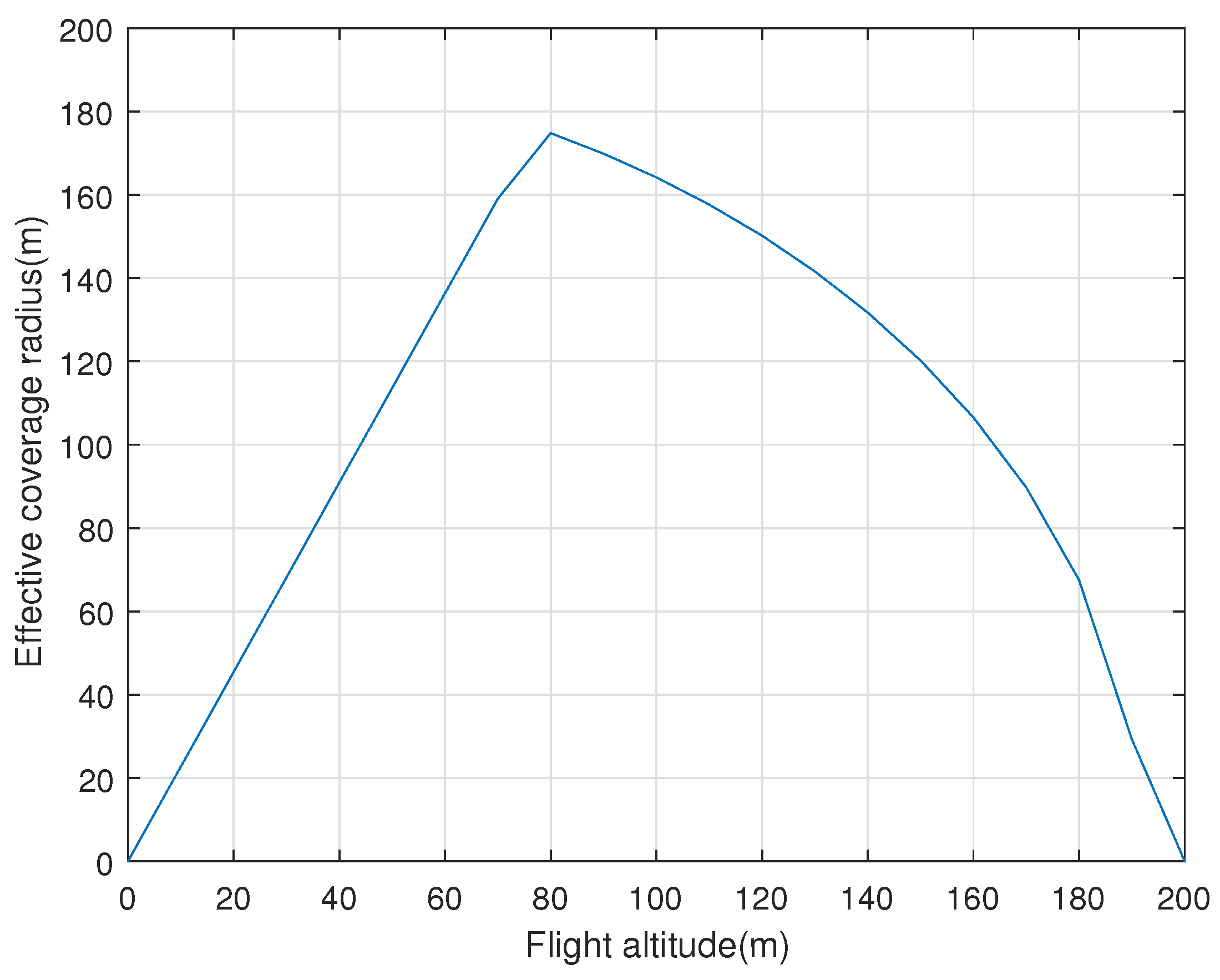
2.3. DSC Coverage Model
2.4. Traffic Model
3. Problem Formulation
4. Solution to 1
4.1. Problem Approximation
4.2. Problem Transformation
4.3. Algorithm Design
| Algorithm 1: Alternate_search_algorithm |
 |
5. Performance Evaluation
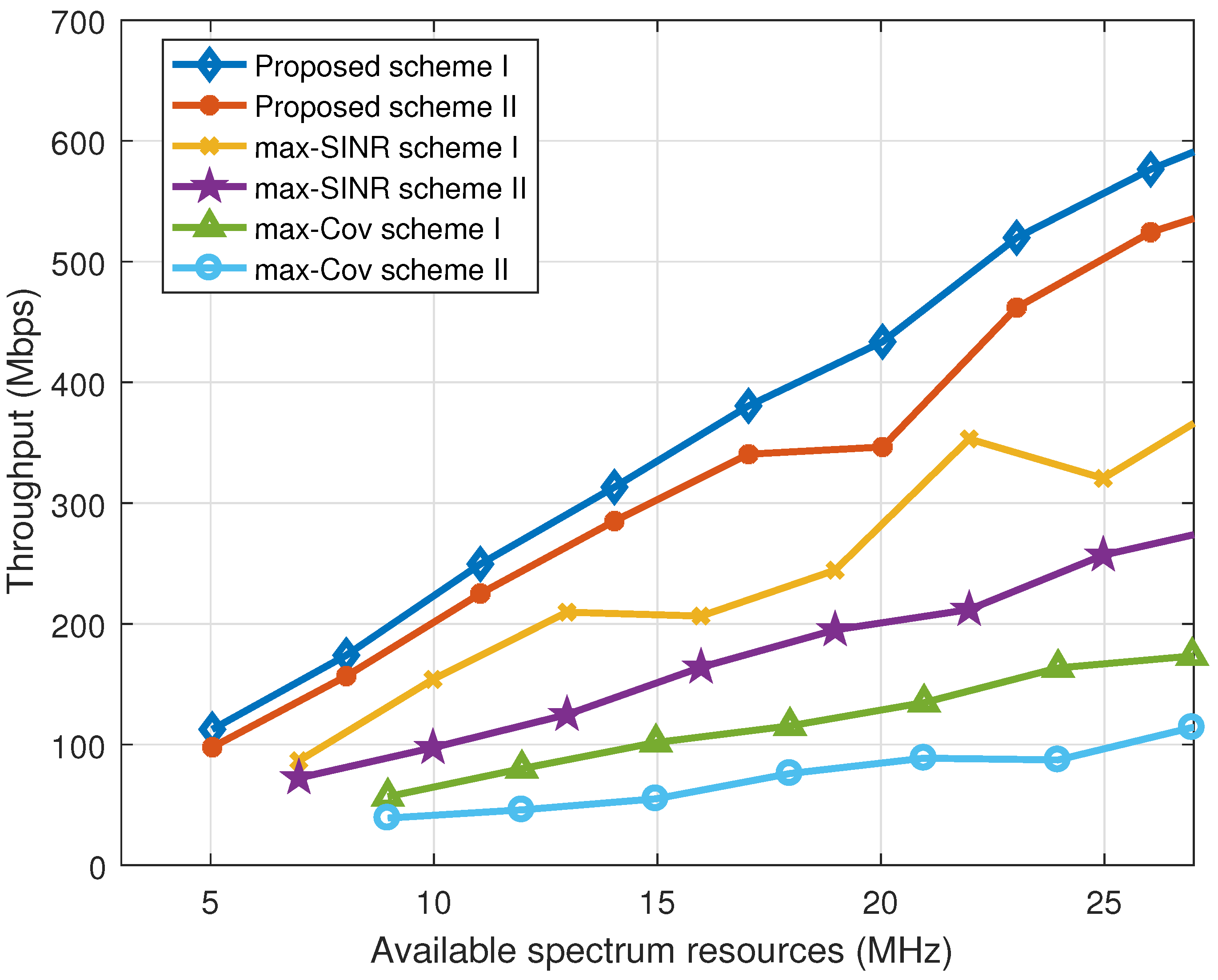
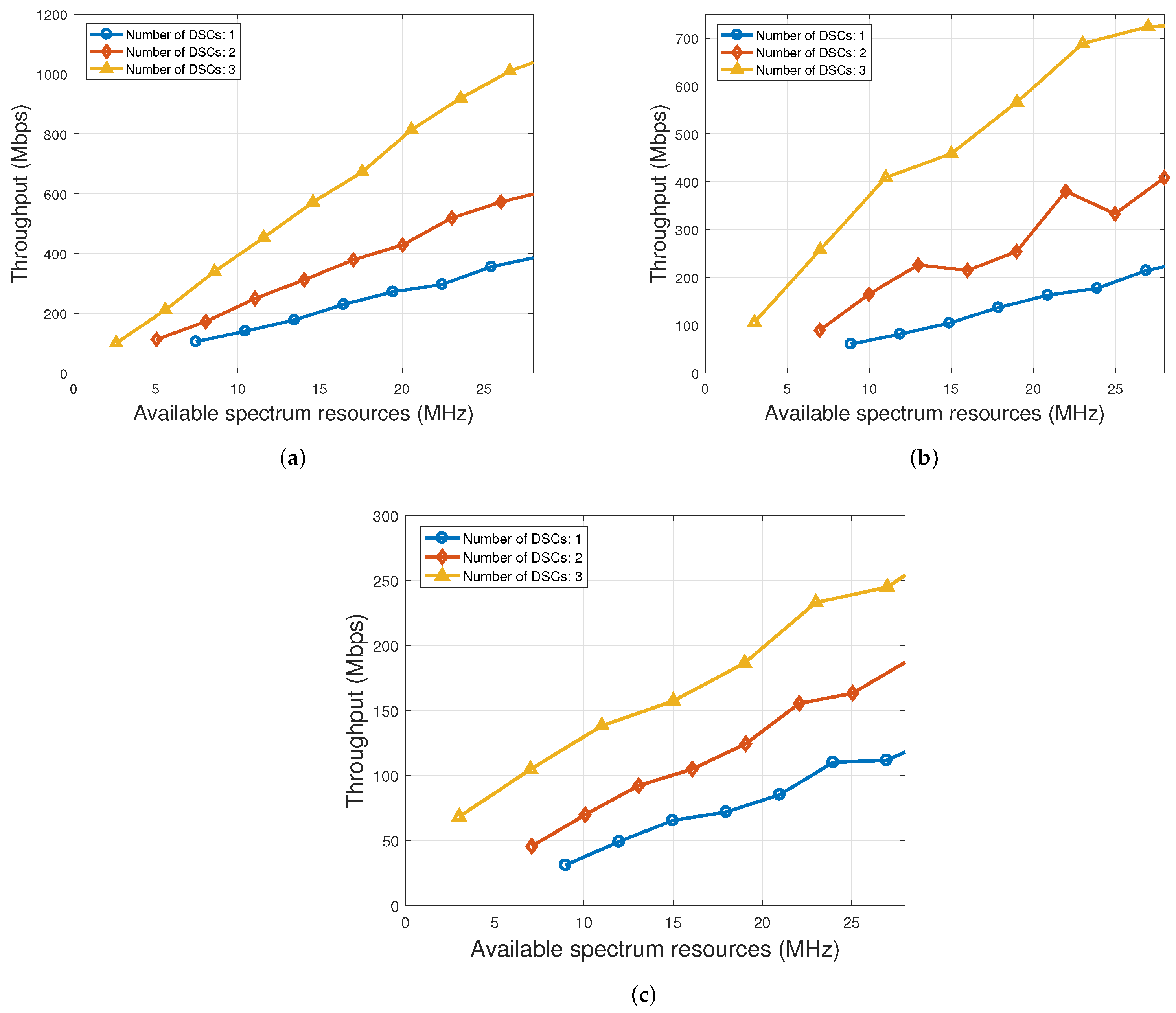
5.1. Impact of Available Spectrum Resources
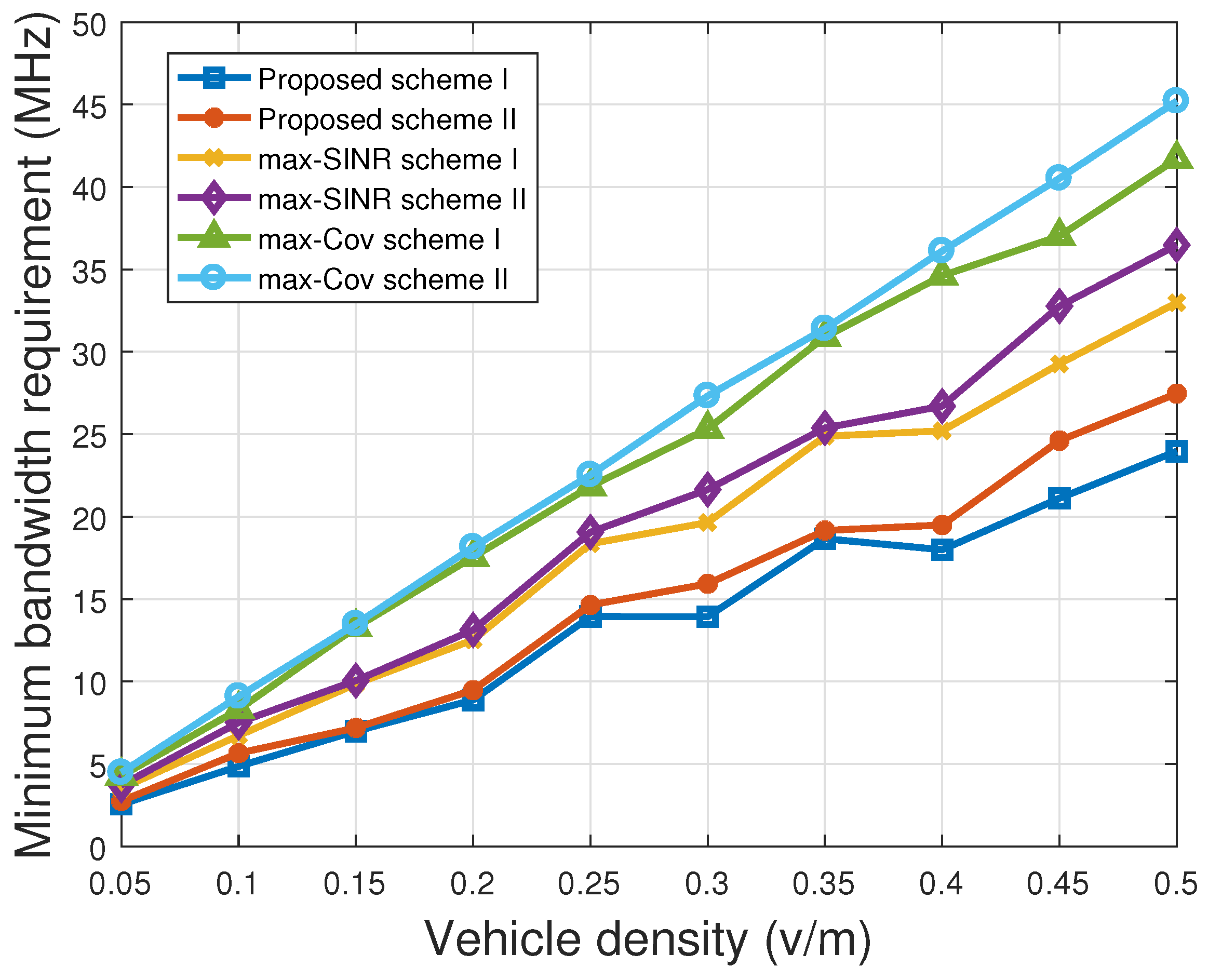
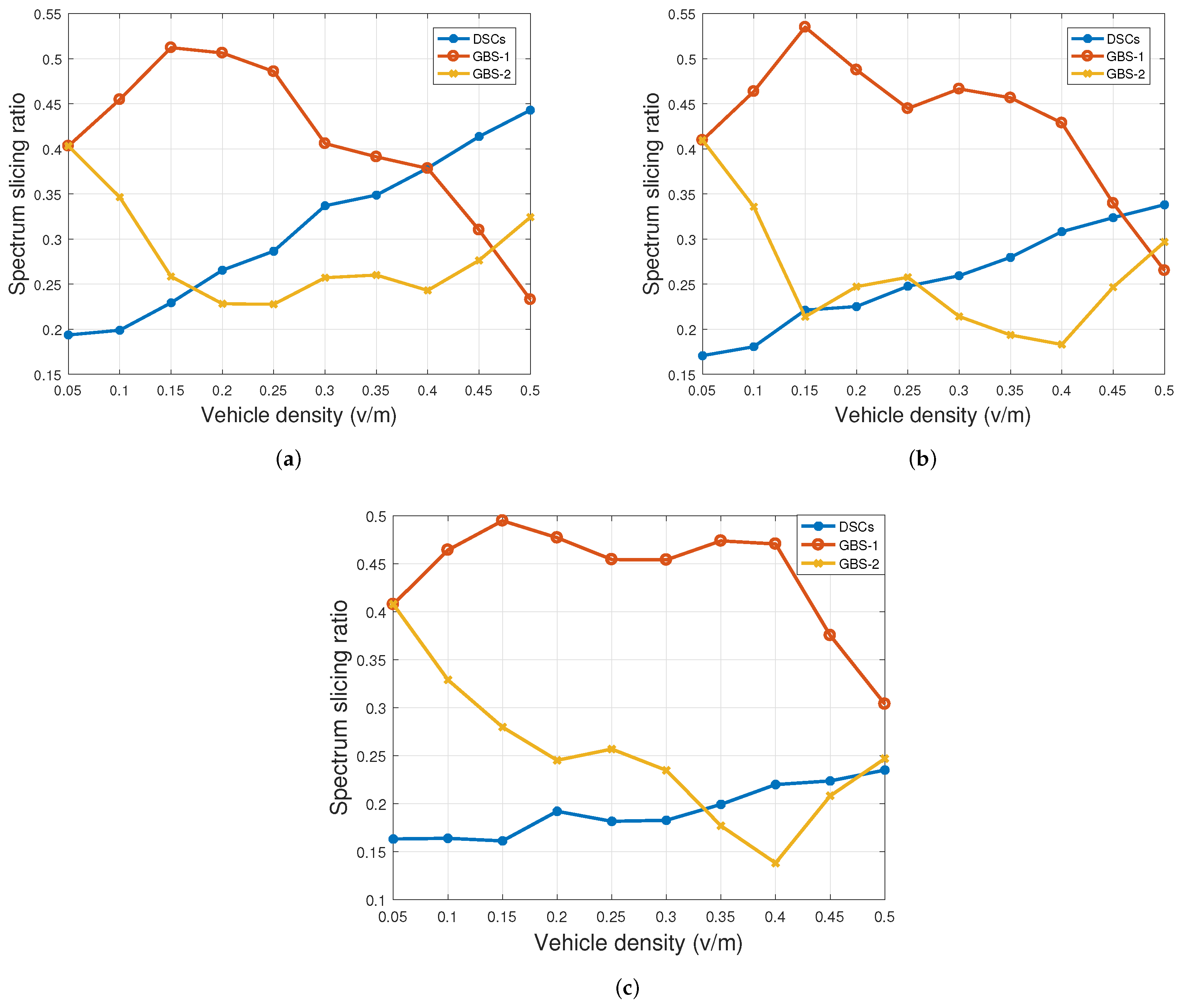
5.2. Impact of Vehicle Density
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Proposition 1
Appendix A.2. Proof of Proposition 2
Appendix A.3. Proof of Corollary 1
Appendix A.4. Proof of Corollary 2
References
- Zhuang, W.; Ye, Q.; Lyu, F.; Cheng, N.; Ren, J. SDN/NFV-Empowered Future IoV with Enhanced Communication, Computing, and Caching. Proc. IEEE 2020, 108, 274–291. [Google Scholar] [CrossRef]
- Chen, S.; Hu, J.; Shi, Y.; Zhao, L.; Li, W. A Vision of C-V2X: Technologies, Field Testing, and Challenges with Chinese Development. IEEE Internet Things J. 2020, 7, 3872–3881. [Google Scholar] [CrossRef]
- Shen, X.; Gao, J.; Wu, W.; Lyu, K.; Li, M.; Zhuang, W.; Li, X.; Rao, J. AI-assisted network-slicing based next-generation wireless networks. IEEE Open J. Veh. Technol. 2020, 1, 45–66. [Google Scholar] [CrossRef]
- Shi, W.; Li, J.; Cheng, N.; Lyu, F.; Shen, X. Multi-Drone 3D Trajectory Planning and Scheduling in Drone Assisted Radio Access Networks. IEEE Trans. Veh. Technol. 2019, 68, 8145–8158. [Google Scholar] [CrossRef]
- Liu, J.; Kato, N. A Markovian analysis for explicit probabilistic stopping-based information propagation in postdisaster ad hoc mobile networks. IEEE Trans. Wirel. Commun. 2015, 15, 81–90. [Google Scholar] [CrossRef]
- Peng, H.; Ye, Q.; Shen, X. Spectrum Management for Multi-Access Edge Computing in Autonomous Vehicular Networks. IEEE Trans. Intell. Transp. Syst. 2020, 21, 3001–3012. [Google Scholar] [CrossRef]
- Peng, H.; Shen, X. Multi-Agent Reinforcement Learning Based Resource Management in MEC- and UAV-Assisted Vehicular Networks. IEEE J. Sel. Areas Commun. 2021, 39, 131–141. [Google Scholar] [CrossRef]
- Ye, Q.; Shi, W.; Qu, K.; He, H.; Zhuang, W.; Shen, X. Joint RAN slicing and computation offloading for autonomous vehicular networks: A learning-assisted hierarchical approach. IEEE Open J. Veh. Technol. 2021, 2, 272–288. [Google Scholar] [CrossRef]
- Riggio, R.; Bradai, A.; Harutyunyan, D.; Rasheed, T.; Ahmed, T. Scheduling wireless virtual networks functions. IEEE Trans. Netw. Serv. Manag. 2016, 13, 240–252. [Google Scholar] [CrossRef]
- Yi, B.; Wang, X.; Li, K.; Huang, M. A comprehensive survey of network function virtualization. Comput. Netw. 2018, 133, 212–262. [Google Scholar] [CrossRef]
- Shen, X.; Gao, J.; Wu, W.; Li, M.; Zhou, C.; Zhuang, W. Holistic Network Virtualization and Pervasive Network Intelligence for 6G. IEEE Commun. Surv. Tutor. 2022, 24, 1–30. [Google Scholar] [CrossRef]
- Zarandi, S.; Tabassum, H. Delay minimization in sliced multi-cell mobile edge computing (MEC) systems. IEEE Commun. Lett. 2021, 25, 1964–1968. [Google Scholar] [CrossRef]
- Yan, Z.; Tabassum, H. Reinforcement Learning for Joint V2I Network Selection and Autonomous Driving Policies. arXiv 2022, arXiv:2208.02249. [Google Scholar]
- Sun, X.; Ansari, N. Jointly optimizing drone-mounted base station placement and user association in heterogeneous networks. In Proceedings of the IEEE ICC, Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Shi, W.; Li, J.; Xu, W.; Zhou, H.; Zhang, N.; Zhang, S.; Shen, X. Multiple drone-cell deployment analyses and optimization in drone assisted radio access networks. IEEE Access 2018, 6, 12518–12529. [Google Scholar] [CrossRef]
- Li, Y.; Cai, L. UAV-assisted dynamic coverage in a heterogeneous cellular system. IEEE Netw. 2017, 31, 56–61. [Google Scholar] [CrossRef]
- Cheng, N.; Lyu, F.; Quan, W.; Zhou, C.; He, H.; Shi, W.; Shen, X. Space/Aerial-Assisted Computing Offloading for IoT Applications: A Learning-Based Approach. IEEE J. Sel. Areas Commun. 2019, 37, 1117–1129. [Google Scholar] [CrossRef]
- Shen, H.; Ye, Q.; Zhuang, W.; Shi, W.; Bai, G.; Yang, G. Drone-Small-Cell-Assisted Resource Slicing for 5G Uplink Radio Access Networks. IEEE Trans. Veh. Technol. 2021, 70, 7071–7086. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, S.; Yang, P.; Alhussein, O.; Shen, X. Software Defined Space-Air-Ground Integrated Vehicular Networks: Challenges and Solutions. IEEE Commun. Mag. 2017, 55, 101–109. [Google Scholar] [CrossRef]
- He, Y.; Zhai, D.; Jiang, Y.; Zhang, R. Relay Selection for UAV-Assisted Urban Vehicular Ad Hoc Networks. IEEE Wirel. Commun. Lett. 2020, 9, 1379–1383. [Google Scholar] [CrossRef]
- Wu, H.; Chen, J.; Zhou, C.; Shi, W.; Cheng, N.; Xu, W.; Zhuang, W.; Shen, X.S. Resource Management in Space-Air-Ground Integrated Vehicular Networks: SDN Control and AI Algorithm Design. IEEE Wirel. Commun. 2020, 27, 52–60. [Google Scholar] [CrossRef]
- Lyu, F.; Yang, P.; Wu, H.; Zhou, C.; Ren, J.; Zhang, Y.; Shen, X. Service-Oriented Dynamic Resource Slicing and Optimization for Space-Air-Ground Integrated Vehicular Networks. IEEE Trans. Intell. Transp. Syst. 2022, 23, 7469–7483. [Google Scholar] [CrossRef]
- Han, R.; Wen, Y.; Bai, L.; Liu, J.; Choi, J. Age of Information Aware UAV Deployment for Intelligent Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2021, 23, 2705–2715. [Google Scholar] [CrossRef]
- Kishk, M.; Bader, A.; Alouini, M.S. Aerial base station deployment in 6G cellular networks using tethered drones: The mobility and endurance tradeoff. IEEE Veh. Technol. Mag. 2020, 15, 103–111. [Google Scholar] [CrossRef]
- Azimi, Y.; Yousefi, S.; Kalbkhani, H.; Kunz, T. Energy-Efficient Deep Reinforcement Learning Assisted Resource Allocation for 5G-RAN Slicing. IEEE Trans. Veh. Technol. 2022, 71, 856–871. [Google Scholar] [CrossRef]
- Duan, Q.; Ansari, N.; Toy, M. Software-defined network virtualization: An architectural framework for integrating SDN and NFV for service provisioning in future networks. IEEE Netw. 2016, 30, 10–16. [Google Scholar] [CrossRef]
- Ye, Q.; Zhuang, W.; Zhang, S.; Jin, A.L.; Shen, X.; Li, X. Dynamic radio resource slicing for a two-tier heterogeneous wireless network. IEEE Trans. Veh. Technol. 2018, 67, 9896–9910. [Google Scholar] [CrossRef]
- Al-Hourani, A.; Kandeepan, S.; Lardner, S. Optimal LAP altitude for maximum coverage. IEEE Wirel. Commun. Lett. 2014, 3, 569–572. [Google Scholar] [CrossRef]
- Al-Hourani, A.; Gomez, K. Modeling Cellular-to-UAV Path-Loss for Suburban Environments. IEEE Wirel. Commun. Lett. 2018, 7, 82–85. [Google Scholar] [CrossRef]
- Gorski, J.; Pfeuffer, F.; Klamroth, K. Biconvex sets and optimization with biconvex functions: A survey and extensions. Math. Methods Oper. Res. 2007, 66, 373–407. [Google Scholar] [CrossRef]



| Symbols | Definition |
|---|---|
| Association indicator for vehicle i with the DSC at | |
| Association indicator for vehicle i with GBS m | |
| Achievable rates of vehicle i associated with the DSC at | |
| Achievable rate at vehicle i from the DSC at for | |
| Achievable rate at vehicle i from GBS m | |
| Achievable rate at the DSC at from GBS m for vehicle i | |
| Minimum rate for a bounded delay violation probability | |
| Euclidean distance between vehicle i and GBS m | |
| Horizontal distance between vehicle i and the DSC at | |
| Amount of spectrum allocated to vehicle i (out of ) from the DSC at | |
| Amount of spectrum allocated to vehicle i from GBS m | |
| Amount of spectrum allocated to vehicle i from GBS m | |
| Channel gain from GBS m to vehicle i | |
| Channel gain from the DSC at to vehicle i | |
| Channel gain from GBS m to the DSC at | |
| / | Set/Num. of candidate DSC positions covered by GBS m |
| / | Set/Num. of vehicles covered by the DSC at |
| / | Set/Num. of vehicles covered by GBS m |
| / | Set/Num. of plane position indexes in the coverage of GBS m |
| W | Available amount of radio spectrum resources to the system |
| / | Transmit power on GBS m/the DSC at |
| Spectrum efficiency at vehicle i from GBS m | |
| Spectrum efficiency at vehicle i from the DSC at for | |
| Spectrum efficiency at the DSC at from GBS m | |
| Effective ground coverage radius of the DSC at altitude | |
| Candidate DSC position | |
| / | Spectrum slicing ratio for GBS 1/GBS 2 |
| Spectrum slicing ratio for each DSC | |
| Fraction of spectrum resources from for G2V links | |
| Fraction of resources from allocated to the DSC at | |
| Arrival rate of the delay-sensitive packet | |
| LoS probability threshold for D2V links | |
| Free space path-loss threshold |
| Parameters | Values |
|---|---|
| GBS altitude m () | 10 m |
| Coverage radius of each GBS () | 800 m |
| Transmit power of GBS m () | 46 dBm |
| Transmit power of the DSC at () | 24 dBm |
| Urban environment parameter (/) | 4.88/0.43 |
| Excess path-loss scalar/angle scalar(/) | −23.29/4.14 |
| Additional loss for LoS/NLoS links (/) | 0.1/21 |
| Terrestrial path-loss exponent () | 3.04 |
| Angle offset () | 3.61 |
| Excess path-loss offset () | 20.7 |
| Carrier frequency (f) | 3.5 GHz |
| LoS probability threshold for D2V links () | 0.5 |
| Free space path-loss threshold () | 89 dB |
| Packet arrival rate () | 4 pkt/s |
| Packet length () | 1048 bit |
| Packet delay bound () | 0.001 s |
| Delay bound violation probability () | |
| Stop criterion () | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, H.; Wang, T.; Heng, Y.; Bai, G. Joint Resource Slicing and Vehicle Association for Drone-Assisted Vehicular Networks. Drones 2023, 7, 534. https://doi.org/10.3390/drones7080534
Shen H, Wang T, Heng Y, Bai G. Joint Resource Slicing and Vehicle Association for Drone-Assisted Vehicular Networks. Drones. 2023; 7(8):534. https://doi.org/10.3390/drones7080534
Chicago/Turabian StyleShen, Hang, Tianjing Wang, Yilong Heng, and Guangwei Bai. 2023. "Joint Resource Slicing and Vehicle Association for Drone-Assisted Vehicular Networks" Drones 7, no. 8: 534. https://doi.org/10.3390/drones7080534
APA StyleShen, H., Wang, T., Heng, Y., & Bai, G. (2023). Joint Resource Slicing and Vehicle Association for Drone-Assisted Vehicular Networks. Drones, 7(8), 534. https://doi.org/10.3390/drones7080534






