Abstract
In order to solve the problem of multiple aircraft formation transformation to a designated formation, a distributed formation transformation algorithm that decomposes the formation transformation problem into target-matching problems and trajectory-planning problems was studied. According to the actual formation transformation requirements, the target allocation index was proposed, and the improved genetic algorithm which is 23% better than other algorithms was used to achieve target matching. The adaptive cross-mutation probability was designed, and the population was propagated without duplicates by the hash algorithm. The multi-objective algorithm of distributed model predictive control was used to design smooth and conflict-free trajectories for the UAVs in formation transformation, and the trajectory-planning problem was transformed into a quadratic programming problem under inequality constraints. Finally, point-to-point collision-free offline trajectory planning was realized by simulation.
1. Introduction
UAV formation is a flexible and effective UAV management and organization mode, including formation maintenance, formation change, and mission organization planning execution. In the current advancement of multi-UAV formation research, centralized communication-based multi-UAV formation has yielded significant theoretical outcomes and practical applications in the domains of formation maintenance and cooperative obstacle avoidance [1,2,3,4,5]. However, due to the growing demand for larger formation sizes, the traditional centralized formation approach is inadequate in meeting the requirements of large-scale formation control. With advancements in electronic information technology and network communication, and by harnessing the benefits demonstrated by the distributed formation control method, integrating distributed UAV formation with consistency theory shows promising prospects for future research [6,7].
A well-designed information interaction mechanism is crucial for achieving rapid convergence to the desired formation during multi-UAV operations. It facilitates maintaining formation accuracy, expanding formation size, and enhancing overall redundancy. Currently, three mainstream formation communication strategies exist: distributed [8,9,10], centralized [11,12], and decentralized [13]. In the distributed strategy, each UAV communicates with its neighboring nodes, eliminating the need for a central node within the formation [14].
Formation control is a crucial aspect of formation algorithms, complementing formation communication. The consistency algorithm, leveraging graph theory, is a widely employed strategy for formation control. For instance, Ren Wei introduced the concept of consistent formation, where information exchange with neighboring nodes ensures consensus among machines on specific cooperative state variables, enabling large-scale distributed cooperative formation [15,16,17]. Wang et al. proposed an adaptive distributed formation protocol using time-varying gain, obviating the need for a global communication topology map [18]. Deng et al. proposed a multi-step particle swarm optimization algorithm based on swarm intelligence consistency theory for UAV formation trajectory planning, yielding smooth trajectories and broad applicability [19]. Kuriki et al. developed a distributed model predictive control mechanism aligned with the consistency algorithm, enabling cooperative formation with collision avoidance capabilities [20]. Najm et al. proposed an enhanced consistency algorithm for quad-rotor formations utilizing a master–slave communication topology, with the algorithm’s controls being fine-tuned using genetic algorithms [21]. The consistency algorithm finds applications in diverse fields such as multi-UAV time-varying formations, sensor networks, and formation task decision making due to its scalability, self-healing properties, and ease of implementation in UAV formation groups.
The purpose of this study is to propose a novel method for UAV formation transformation, which combines an improved genetic algorithm for target matching and a distributed model predictive control strategy for trajectory planning. The significance of this research lies in its potential to provide an effective solution for the challenging and crucial task of UAV formation transformation in various applications of multi-UAV systems, including military reconnaissance, rescue and disaster relief, environmental monitoring, traffic management, and more. This task necessitates the coordination and cooperation of multiple UAVs, considering factors such as communication topology, obstacle avoidance, and control input constraints. Existing methods for UAV formation transformation exhibit limitations, such as high computational complexity, low convergence speed, and duplicate solutions.
The paper presents a novel method for UAV formation transformation that integrates an improved genetic algorithm for target matching and a distributed model predictive control strategy for trajectory planning. An adaptive genetic algorithm is devised to dynamically adjust the crossover probability and variation probability based on the fitness value of individuals, and a hash algorithm is employed to eliminate duplicate solutions. Furthermore, this paper applies an enhanced genetic algorithm in conjunction with a distributed model predictive control strategy to address UAV formation transformation. The feasibility of this approach is then confirmed through simulation and semi-physical experiments.
The rest of the paper is organized as follows: In Section 2, we present the optimization of the target matching using an improved genetic algorithm. In Section 3, we describe the use of distributed model predictive control (DMPC) for collision-free trajectory planning. Section 4 presents simulation results in various scenarios. Section 5 outlines the shortcomings and presents a summary.
2. Objective Assignment Based on Improved Genetic Algorithm
There are two ways to obtain the optimal eye-matching solution from initial to target formation during formation transformation: constructing an exact mathematical model of the UAS and using metaheuristic algorithms. Although most metaheuristic algorithms do not guarantee optimality, they simplify computational effort compared to the exact mathematical model approach and find relatively optimal solutions through finite iterations. Additionally, using metaheuristic algorithms eases deployment and implementation on embedded system boards, making it a common strategy in engineering.
It is possible to turn the target-matching problem into an optimization problem by establishing metrics for time and distance optimization. Optimization problems are a classical application area for genetic algorithms due to their suitability in finding global optimization solutions in large-scale problems containing discrete variables. This approach is faster and provides better quality results than conventional methods. To solve the target point matching, an improved genetic algorithm is used, which includes genetic coding, fitness function calculation, selection, crossover, variation, and outputting an optimal match through a specified number of iterations while meeting set conditions.
2.1. Genetic Operator Coding Design
Selecting the appropriate encoding method for a genetic algorithm is crucial and should depend on the specific problem and solution. Binary and symbolic coding methods are appropriate for solving the target point matching problem. Binary coding offers simple coding and decoding operations, crossover, and easy implementation of mutation operations. Here, each point of the current and desired formations is labeled as 1, 2, 3, ⋯, n, and a feasible solution is represented by a two-dimensional matrix. The current queue number serves as the column number while the desired queue number acts as the row number. Each column has a separate match for each row, where the matrix element for the matching row position is 1, and the rest of the row elements in that column are 0. Ten UAVs are arranged in formation as shown in Figure 1.
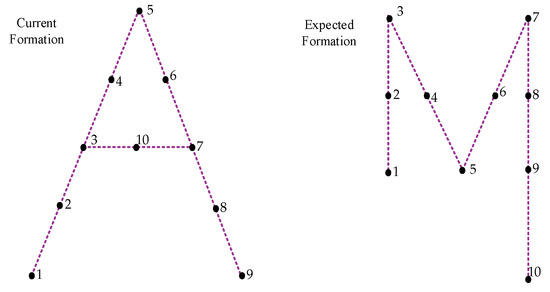
Figure 1.
Current formation and desired formation of the aircraft formation.
Assuming that the set of matches corresponding to 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 is 7, 3, 2, 8, 9, 4, 1, 10, 6, 5, the corresponding binary code can be expressed in the form of a two-dimensional matrix as follows:
The symbolic encoding in this problem is a direct encoding using each UAV number in the formation 1, 2, 3, ⋯, n to construct a numeric string-based genetic operator as a feasible solution. Taking the formation transformation shown as an example, assuming that the set of matches corresponding to 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 is 7, 3, 2, 8, 9, 4, 1, 10, 6, 5, the corresponding symbolic encoding can be expressed in the form of a row vector as follows:
A2 = [7 3 2 8 9 1 10 6 5]; the implicit left-to-right indexes in the row vector match the values corresponding to the indexes, forming a set of target null point matches.
Both of the above encoding methods can be implemented in the formation transformation to solve the target airspace point matching problem, but considering the engineering problem of the actual algorithm, the space used for two-dimensional matrix storage is larger. Assuming that the number of populations in the genetic algorithm is m and the number of formation UAVs is n, the storage space occupied by a single genetic operator with binary encoding is n2 and the overall space complexity is O(mn2); the storage space occupied by a single genetic operator with symbolic encoding is n and the overall space complexity is O(mn). Considering the small storage space of the embedded chip SDRAM, the symbolic encoding method is more convenient for the deployment of the algorithm on the embedded system board, which is conducive to the engineering of the algorithm, and the symbolic encoding method is more intuitive for the subsequent cross-variance operation, so the symbolic encoding method is chosen for this problem.
2.2. Adaptation Function Analysis
Given that the genetic algorithm is a stochastic global search and optimization method that mimics the evolutionary mechanism of organisms in nature, it is crucial to establish evaluation metrics to score individuals in the population and implement survival of the fittest. In this problem, a fitness function is constructed using the total distance metric for formation transformation, as well as time and the number of trajectory crossings as optimization objectives.
- (1)
- Formation change flight distance constraint
In the process of formation transformation, the total distance from the current formation to the desired formation is the metric that we need to optimize, and the smaller the distance sum, the better. Suppose there are n UAVs, the position of the UAV in the current formation is (xi, yi, zi), the corresponding matching target point in the desired formation is marked as (ai, bi, ci), and the total distance cost is dsum; then, we have the following equation:
- (2)
- UAV maximum flight time constraint
Assuming that each UAV has the same speed v during the formation change, the time to complete the formation change depends on the UAV that takes the longest time to reach the specified position, and the maximum flight time is recorded as tmax, the distance from each UAV to the corresponding matching point is recorded as di, and the following equations are obtained:
- (3)
- Constraint on the number of trajectory crossings
To subsequently reduce the difficulty of the collision avoidance algorithm, target matching with the lowest possible number of trajectory crossings should be considered as much as possible. Suppose the two position points of the current formation are A and C, and the expected transformed position points are B and D. Let the coordinates of the four points A, B, C, and D be (x1, y1, z1), (x2, y2, z2), (x3, y3, z3), and (x4, y4, z4). The parametric equations of the line segments AB and CD are
where t ∈ [0, 1] The parametric equation of the line CD is t′ ∈ [0, 1]. Now, the question of whether the two trajectories intersect translates into whether there exists t1, t2 ∈ [0, 1] such that the following system of equations holds:
Equation (5) can be expressed in matrix form as follows:
When aTa is invertible, at which point there is an intersection or dissimilarity of the two line segments, solving the system of equations using the least squares method yields
where A11A22 – A12A21 ≠ 0. After solving for t1, t2, determine if its value is within the interval [0, 1], and then further determine if the following equation holds:
where eps is the set tolerance; if (9) holds, then the line segment AB intersects the line segment CD; otherwise, the line segment AB is opposite to CD. When aTa is not invertible, then the two line segments are parallel, and the trajectories do not have the possibility of intersection.
Using the above derivation, we can determine whether the assigned trajectories are crossed or not, and we can achieve the statistics of the number of crossings for all trajectories with the time complexity of O(n2), and the number of crossings is mcross. Considering the above optimization indexes, the following cost function can be constructed:
where k is the bounding value constant, v is the formation transformation UAV flight speed, a1 is the total distance scaling factor, a2 is the maximum time scaling factor, the scaling factor a3 is used to maintain uniform order of magnitude for the medium distance cost, the maximum time cost, and the trajectory crossing number cost. stores the coordinates 1, 2, 3, ⋯, n corresponding to the current numbered queue. stores the coordinates 1, 2, 3, ⋯, n corresponding to the desired numbered queue. chrom is a set of feasible symbolic encoding solutions. can be adjusted based on the matching information provided by chrom, resulting in a two-dimensional matrix that stores the corresponding matched coordinates. This matrix is denoted as . To solve dsum, the Euclidean distance between the corresponding rows of and is calculated individually and then accumulated.
Fitness (cur, tar, v, chrom) = k − a1dsum − a2tmax − a3mcorss
2.3. Selection Operator and Hash De-Duplication Design
The selection strategy used in this paper utilizes the roulette selection algorithm. Firstly, the fitness of individuals in the population is calculated. Then, individuals are selected at random based on their fitness, using a proportional range to determine the likelihood of selection. As a result, individuals with higher fitness levels are more likely to be selected and retained during the evolutionary iteration process.
If an individual is denoted as i and its fitness is fi, the probability that it will be selected is expressed as
High-fitness individuals are more likely to be selected. The retention method for elite individuals is utilized in the initial selection strategy, where the top 5% of high-fitness individuals in the population are retained, and the remaining individuals are randomly selected using the roulette algorithm.
After the roulette strategy selection, some individuals with higher fitness will be selected repeatedly, which may lead to the individuals with higher fitness occupying the population rapidly in the subsequent iterative solution process, resulting in the local optimal solution at the initial iteration stage. Therefore, steady-state selection without a repeat string should be realized. In this section, the Rabin–Karp string hashing algorithm is used to realize the non-repeated string judgment of genetic operators. Let the symbolic code of each feasible solution be chrom; chrom is a sequence consisting of numbers a0, a1, a2, ⋯, an−1, which can be treated as a max{ai} + 1 progressive number, and then the corresponding value of this sequence can be calculated by the following equation:
Considering that the hash value obtained from the calculation will be very large, it is necessary to mold the result of the calculation f(chrom) on a large prime number P and map this value to the int range. Two different genetic operators will have different encoding values before modulo, but the encoding values may be the same after modulo, because the hash encoding method is not single-shot, and there is a possibility of hash collision. However, according to the birthday paradox, there is a high probability of collision when a sequence of numbers is generated randomly, so the modulus can be set as large as possible to avoid collision. So, the actual hash function is modified as follows:
The Rabin–Karp string hashing algorithm can be employed to eliminate duplicate genetic operators in the roulette wheel selection strategy. Subsequently, the excluded genetic operators can be replenished by randomly initializing new genetic operators.
2.4. Crossover and Variational Operator Design
A crossover operation involves permuting and reconstructing the local structure of two parent operators to create new individuals. In the iterative process of a genetic algorithm, a crossover operation has a probability of producing new and improved individuals.
In this section, we utilize partial cross-matching. The following Figure 2 and Figure 3 depicts the encoding pre- and post-exchange.
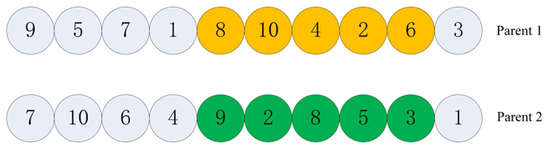
Figure 2.
Pre-crossover coding.
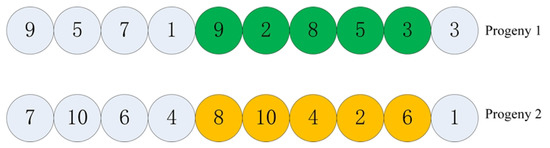
Figure 3.
Post-crossover coding.
The operator crossover generation strategy is specific to the following steps: Firstly, we save the numbers in the sequence for each genetic operator using a hash table. Then, we perform a two-point crossover for the genetic operator. Next, we traverse the number sequence for the other genetic operator, removing numbers from the corresponding hash table if present and marking the corresponding number in the genetic operator as visited. Finally, we traverse the exchanged fragment of the genetic operator and sequentially remove and replace the data in the hash table of the genetic operator with the data removed from the unvisited position in the hash table. The resulting modified operator is shown in Figure 4.
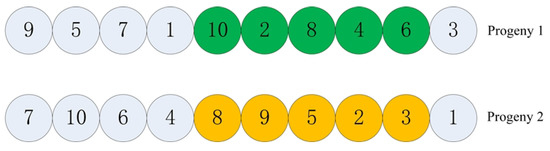
Figure 4.
Modified crossover operator.
The variation operation often accompanies the selection and crossover operations to prevent the genetic algorithm from converging to a local optimum too early in the iterative process. Variation is carried out on a single chromosome; we employ the reversal variation, depicted in Figure 5.

Figure 5.
Variational operator.
The operator crossover probability Pc and variance probability Pm are fixed values in conventional genetic algorithms, and these two parameters directly affect the convergence of the algorithm. Based on this, an adaptive genetic algorithm is proposed that can dynamically modify the crossover probability Pc and the variation probability Pm. For individuals whose fitness is higher than the average fitness value of the population, Pc and Pm with smaller probability values are constructed so that the individuals have a higher probability of being retained.
where fmax is the maximum fitness value in the population; favg is the average fitness value of the population per generation; f′ is the larger fitness value of the two individuals to be crossed; f is the fitness value of the individual to be mutated; and Pc1, Pc2, Pm1, and Pm2 are constants. The Figure 6 is the overall flow chart of the improved genetic algorithm.
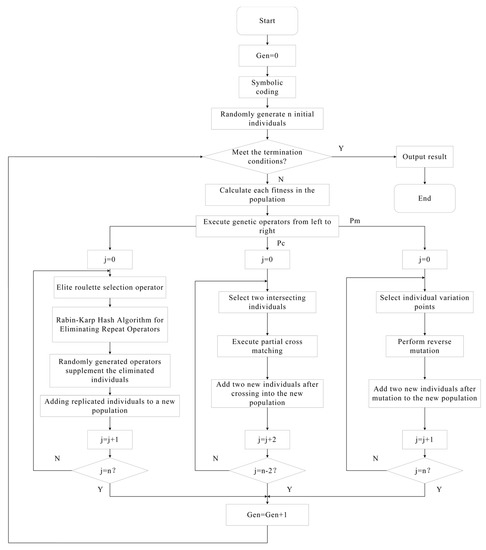
Figure 6.
Overall flow chart of the improved genetic algorithm.
3. Design of Trajectory-Planning Strategy Based on Distributed Model Prediction
3.1. The Basic Principle of MPC Algorithm
The model predictive control (MPC) algorithm is a model to predict the performance of the system in a future time period for optimal control, mostly used for digit control, and is a discrete state space expression.
Suppose the following discrete state space expression is available:
x(k + 1) = Ax(k) + Bu(k)
Let the predicted system input at time k for the system at time k + i be denoted as u(k = i|k) and the predicted system state vector k be denoted as x(k = i|k). The prediction horizon of the system is N. Considering the initial state of the system as xk, the following recursive equation can be obtained:
Let Xk be the column vector consisting of the system state variables at N + 1 moments and Uk be the column vector consisting of the system predicted input variables at N moments; the above equation can be written in the following matrix form:
where , , , xk is the initial state variables, and .
Xk = Mxk + CUk
For model predictive control, the commonly used optimization strategy is quadratic programming (QP). The general form of quadratic programming is as follows:
where ZTQZ is quadratic and CTZ is linear for the model predictive control algorithm in which the cost function needs to be reduced to a general quadratic form for optimal control. To simplify the derivation, this paper treats the reference state quantity as 0, so the error state quantity is the system state quantity, so the following cost function can be obtained:
where Q, R, and F are diagonal matrices. The above cost function can be written in the following form:
where and . Substituting Formula (20) into the previous Equation (21), we can further expand it, resulting in the following:
f = ZTQZ + CTZ
Let be G, be E, and be H, so the above equation can be reduced to
This transforms the optimization problem of model predictive control into a quadratic programming problem.
3.2. Single UAV Prediction Modeling
An improved genetic algorithm can be implemented to determine the optimal target matching during the formation transformation process and determine the destination point of each UAV. In this section, we conduct conflict-free trajectory planning to solve the UAV point-to-point transformation problem. For trajectory generation, we employ a distributed model predictive control (DMPC)-based multi-objective algorithm.
The UAV uses a second-order integrator model. Assume that at time step k, the position vectors in the three directions of x, y, z for UAVi are represented as di[k]3×1, the velocity vector is represented as vi[k]3×1, and the acceleration vector is represented as ai[k]3×1. If the acceleration is used as the system input and the discretization step is s, then the dynamic model of the UAVi is as follows:
At each discretized time slice, an optimal input sequence can be obtained based on the controlled object’s model, within the given prediction interval. The resulting first input is applied to the actual system, and the current system state variables are measured to initiate the optimal control problem in the subsequent moment. This approach enables rolling control optimization. Considering the current discrete time slice sequence as the first kt, UAVs are deployed in a distributed manner, iteratively optimizing trajectory generation by sharing predicted state sequences with neighboring UAVs. Each UAV calculates the optimal input sequence considering collision possibilities, system constraints, and motion model parameters. The first input of the obtained sequence is applied to the UAV, followed by a collective movement to the next time step while sharing state variables. The prediction model of the UAVi is as follows:
By choosing acceleration as the model input, the above equation can be reduced to the following form:
where , , , and . The state of the system at time is as follows:
where , , , , ,, and .
3.3. Establishment of the Cost Function of the DMPC Algorithm
The goal of optimal control is to minimize the cost function. In this section, the cost function primarily comprises error tracking, control input, and input variation terms. Our aim is to find the optimal input sequence that minimizes the cost function.
- (1)
- Error tracking term
The error tracking term is used to better track the reference trajectory. The smaller the error tracking, the better the actual flight fits the target planning curve. The form of the error tracking term is as follows:
where do,i is the final desired target location point and is the discretization step from K to . Using (23), the error tracking term can be written in the following quadratic form:
where is a positive definite diagonal matrix and the elements on the diagonal indicate the error weights corresponding at each sampling point, when , corresponding to ; Q is also a positive definite diagonal matrix, . The larger is, the more drastically the UAV moves toward the target point and may appear to overshoot at the end point.
- (2)
- Control input items
The smaller the input control term, the smaller the overall energy consumption of the system. Based on the derivation in the previous section, the term can be written in the following quadratic form:
where is a positive definite diagonal matrix; the elements on the diagonal represent the corresponding input weights at each sampling point; and , , and R are also positive definite diagonal matrices.
- (3)
- Input change items
The smaller the input variation term, the smoother the control will be, and no violent oscillations or large changes in trajectory will occur. The cost expression of the input variation term is as follows:
The above expression can be rewritten as the following quadratic form:
where is a positive definite diagonal array, and the elements on the diagonal represent the weights of the input variables corresponding to , , and at each sampling point, and summing the above three surrogate values gives the final cost function:
3.4. Collision Avoidance Constraints and Physical Constraint Design
We can use the prediction property of DMPC to detect collision trajectories and impose constraints to avoid collisions. The constraint condition for UAV to avoid collision with UAV j at time step kC,i is as follows:
denotes the minimum distance between the UAVi and the UAVj in the xy plane. denotes the scaling matrix, which is expanded in the following form:
Generally, take , ; thus, the minimum distance constraint required at the axis is . The solution time is at , and each UAV has only the information of other UAVs at the time of ; then, the collision prediction occurs at the time of , and the set of collision constraints is
If a collision is detected, a new input sequence must be calculated by including a collision constraint. Considering that the optimization problem can sometimes be infeasible, a relaxed obstacle avoidance constraint is developed as follows:
where is a relaxation factor less than 0. We can use the first-order Taylor expansion at of the UAVi to make an approximation to the above equation, with the expansion point taken as , and the approximate expansion process is as follows: let ; the column vector parametrization is defined as , . The partial derivative of gives the following results:
Taking the independent variable as and the expansion point as , by Taylor expansion, we have the following:
It can be inferred from (34) that
Substituting the above equation into (39) yields
It can be inferred from (37) that
Substituting into the above equation, we obtain
Further simplification yields
Obtain
where . As physical constraints, this paper considers acceleration as well as position sequences, and the following constraints can be obtained: and . Expressing them in matrix form, we have
By listing all the constraints for the prediction interval and rewriting them in matrix form, the final inequality constraint is obtained as follows:
In order to transform the collision constraint into an affine function of the decision variables, we expand the previously obtained formula by introducing column vectors, , and denoting the number of neighboring UAVs within the collision radius, and can be expressed as follows:
where , , , and . Listing the above inequalities in order by and writing them in matrix form yields.
where ; the final cost function with obstacle avoidance information is as follows:
where and .
4. Simulation Results and Analysis
4.1. Target Assignment Algorithm Simulation Verification
According to simulation comparison results in Figure 7, the improved genetic algorithm demonstrates the smallest total distance traveled. In terms of solving time, the Hungarian algorithm experiences slower solving speed due to the increasing matrix dimension with a growing number of UAVs, while the improved genetic algorithm becomes faster. Additionally, regarding the number of trajectory crossings, the improved genetic algorithm maintains fewer crossings compared to the ordinary genetic algorithm and the Hungarian algorithm, which do not consider this element and result in more random trajectory crossings. In conclusion, the proposed improved genetic algorithm exhibits excellent performance in solving the queue transformation goal assignment problem.
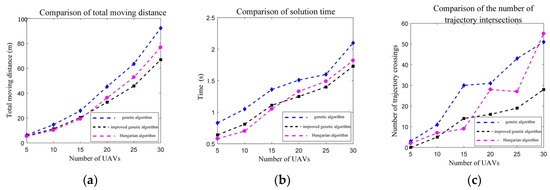
Figure 7.
(a) Description of comparison of total moving distance; (b) description of comparison of solution times; (c) description of comparison of the number of trajectory intersections.
The target-matching results of the Hungarian algorithm and the improved genetic algorithm are shown in Figure 8.
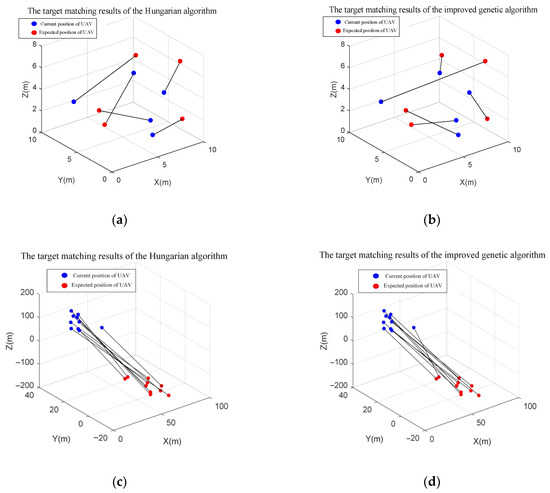
Figure 8.
(a) Description of Hungarian algorithm target-matching results for 5 UAVs; (b) Description of improved genetic algorithm target-matching results for 5 UAVs; (c) Description of Hungarian algorithm target-matching results for 10 UAVs; (d) Description of improved genetic algorithm target-matching results for 10 UAVs.
The two comparison experiments above reveal that with a small number of UAVs in the formation transformation, trajectories rarely intersect. However, as the number of UAVs increases, the Hungarian algorithm, which does not consider trajectory crossover, generates more crossovers in its optimal solution compared to the improved genetic algorithm.
4.2. Simulation Verification of Formation Transformation Collision Avoidance Constraints
This subsection examines the impact of collision avoidance constraints in the trajectory-planning algorithm to demonstrate that collision-free arrival at the target position is possible during the formation transformation. We set the initial formation of four UAVs as a rectangle to necessitate trajectory crossover during the transformation process. The crossover transformation is then applied to the diagonal vertices within the 2D plane. The coordinates of UAVs 1–4 are set as (0, 0), (50, 50), (50, 0), and (0, 50), respectively, and the simulation results are presented in Figure 9, Figure 10, Figure 11 and Figure 12.
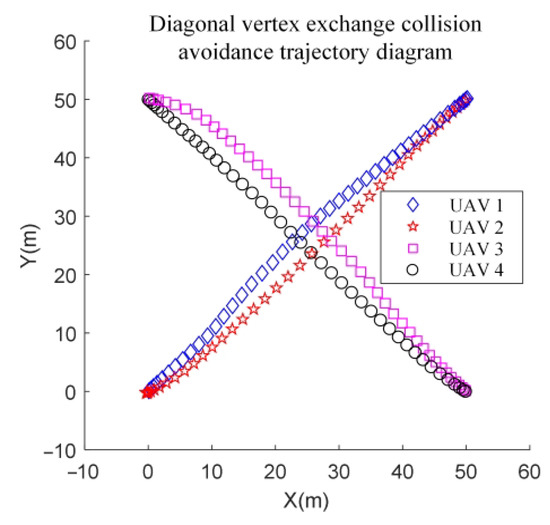
Figure 9.
Diagonal vertex exchange collision avoidance trajectory diagram.
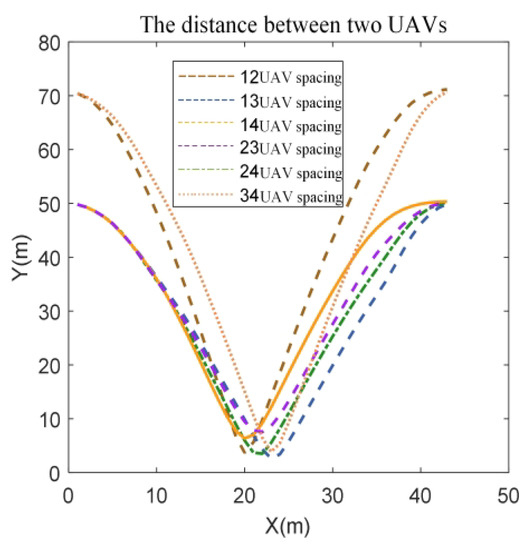
Figure 10.
Distance between two UAVs.
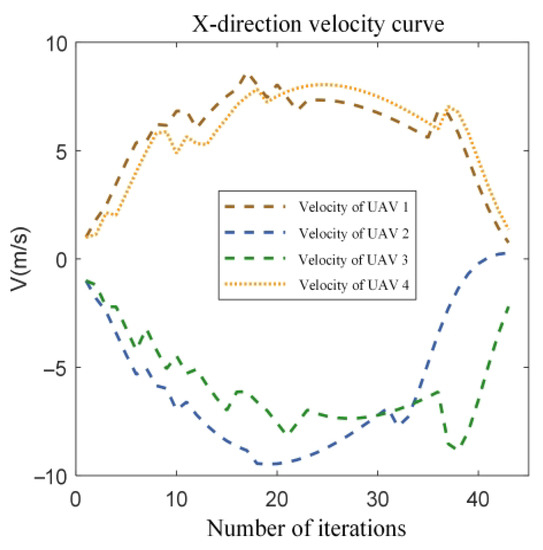
Figure 11.
The x-direction velocity curves for 4 UAVs.
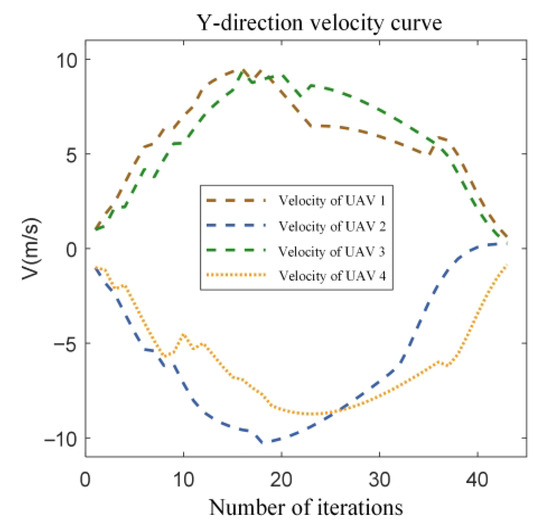
Figure 12.
The y-direction velocity curves for 4 UAVs.
It can be seen from the figure that in the diagonal vertex exchange process, collision avoidance constraint plays a role in trajectory planning; when UAV 1 and UAV 2 are exchanged in position, the UAV 1 trajectory is shifted, avoiding the situation of head-on collision with UAV 2.
4.3. Simulation and Verification of Trajectory-Planning Algorithm
We independently simulated transformation scenarios for distance-sparse and distance-dense formations to gauge the efficacy of the trajectory planner. Firstly, we defined the following simulation conditions for the distance sparse formation:
The current formation of 13 UAVs is set as the letter “N”, the desired formation is set as the letter “A”, and the compactness factor of the formation is set as ktight. The larger the ktight is, the thinner the formation is. For this simulation, ktight = 10; the specific coordinates of formation “N” and formation “A” are presented in Table 1.

Table 1.
Initial and desired formation coordinate settings for 13 UAVs.
Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 depict the initial state diagrams of formation transformation and the corresponding target-matching results.
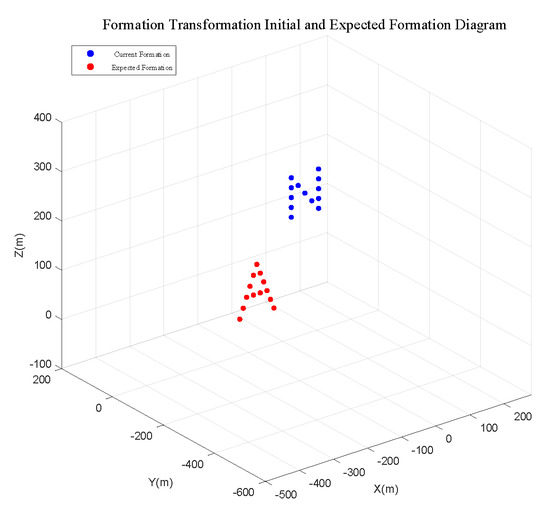
Figure 13.
Initial state of 13-UAV sparse formation transformation.
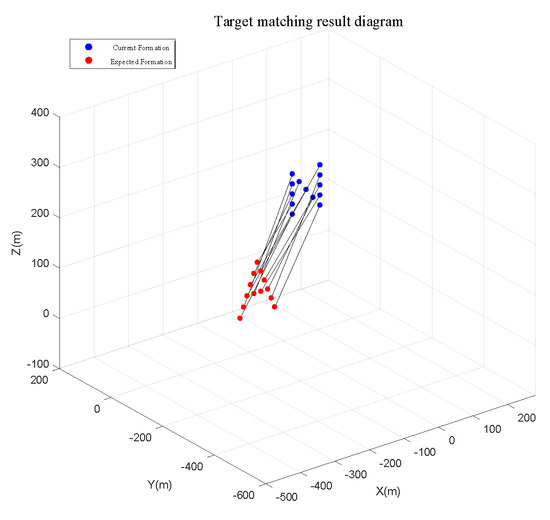
Figure 14.
Improved genetic algorithm target-matching results for 13 UAVs.
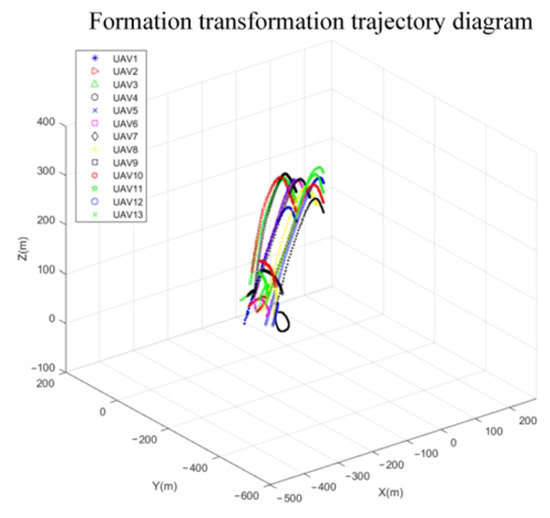
Figure 15.
Sparse formation transformation trajectory-planning diagram for 13 UAVs.
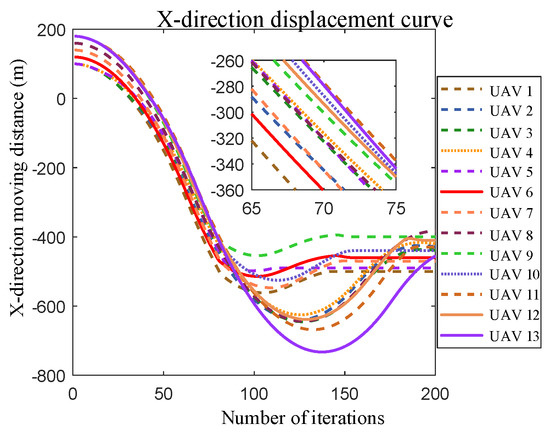
Figure 16.
Sparse formation transformation x-direction displacement curve for 13 UAVs.
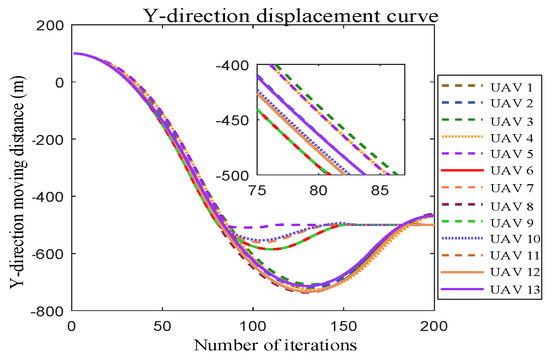
Figure 17.
Sparse formation transformation y-direction displacement curve for 13 UAVs.
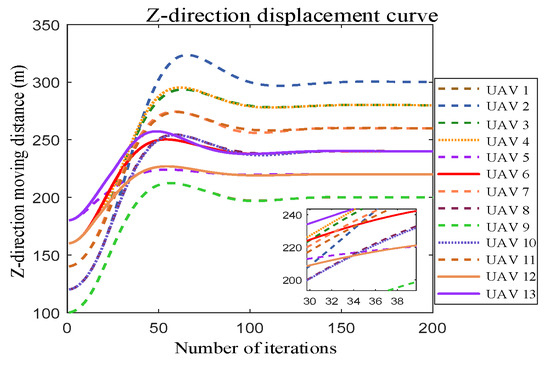
Figure 18.
Sparse formation transformation z-directional displacement curve for 13 UAVs.
In the simulation of compact formation transformation, the formation compactness factor ktight was set to 2, and the rest of the conditions were set to be consistent with the sparse formation transformation; the simulation results are presented in Figure 19, Figure 20, Figure 21 and Figure 22.
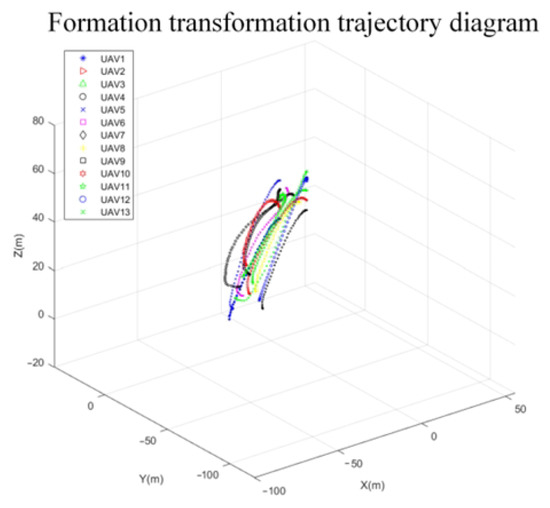
Figure 19.
Compact formation transformation trajectory diagram for 13 UAVs.
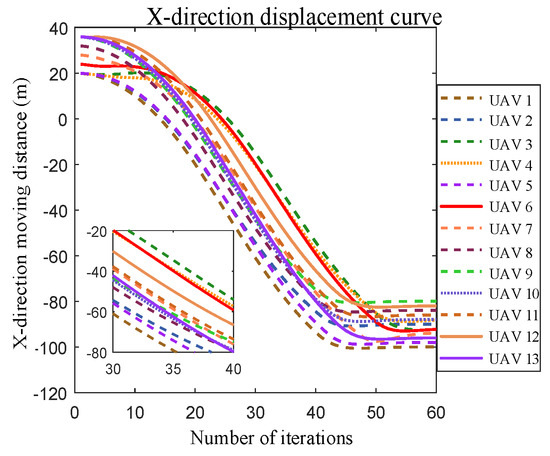
Figure 20.
Compact formation transformation x-direction displacement curve for 13 UAVs.
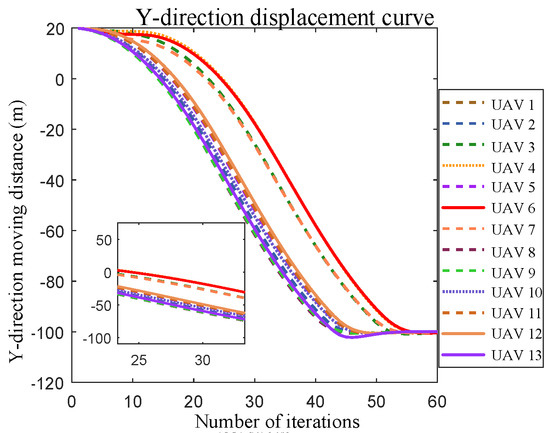
Figure 21.
Compact formation transformation y-direction displacement curve for 13 UAVs.
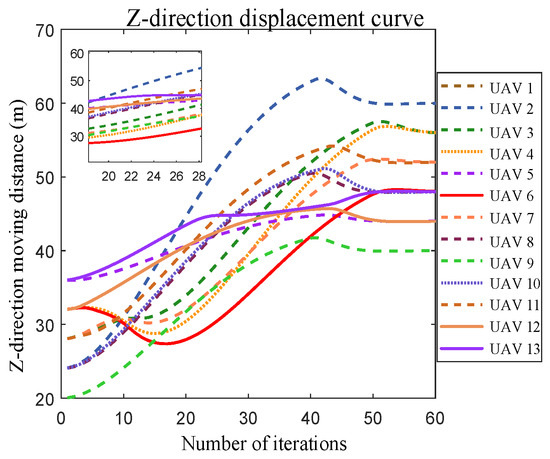
Figure 22.
Compact formation transformation z-directional displacement curve for 13 UAVs.
From the simulation results, Figure 14 shows that the improved genetic algorithm successfully performs the UAV formation position assignment. Figure 15 shows the path diagram of 13 UAVs planned from their own starting point to the end point, from which it can be seen that the trajectories of individual UAVs do not cross each other. Figure 16, Figure 17 and Figure 18 show the displacement curves of each UAV in the x, y, z directions with time during the formation transformation. From the final end coordinates, the x-axis coordinates of the 13 drones are concentrated in the range of −500 m to −400 m, while the y-axis coordinates are concentrated around −500 m. In the z-axis direction, two drones converge at a height of 200 m, two at 220 m, four at 240 m, two at 280 m, and one at 300 m. The actual simulation results are consistent with the expected results set in the experiment. Therefore, the trajectories planned by the UAVs can ensure the smooth transformation of each aircraft from the current formation to the desired formation.
When the formation spacing was decreased, the single-axis distance between UAVs ranged between 2 m and 4 m. Simulation results indicate that collision-free trajectory planning can still be achieved with smooth convergence from the current formation “N” to the desired formation “A”, as shown in Figure 20, Figure 21 and Figure 22.
4.4. Semi-Physical Simulation Results and Analysis
The formation transformation algorithm was previously verified by Matlab simulation. In order to further verify the effectiveness of the proposed algorithm in real engineering applications, semi-physical simulations were performed using Airsim Unreal Engine in conjunction with the Ardupilot flight control and distributed networking data transmission.
The goal of the simulation was to change the 13 UAVs from the initial “M” formation to the “A” formation, and the initial and final formations of UAV 1 to UAV 13 are shown in Figure 23.
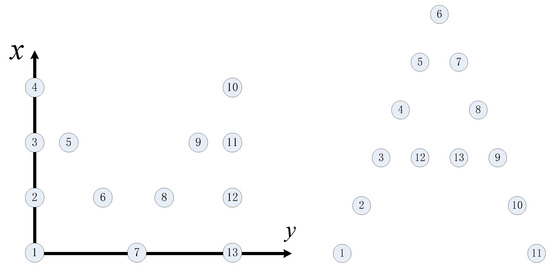
Figure 23.
Formation transition diagram.
The initial coordinates of UAVs 1–13 are (0, 0, 10), (6, 0, 10), (12, 0, 10), (18, 0, 10), (12, 3, 10), (6, 6, 10), (0, 9, 10), (6, 12, 10), (12, 15, 10), (18, 18, 10), (12, 18, 10), (6, 8, 10), and (0, 18, 10). The coordinates of the final formation are (60, 60, 50), (64, 63, 50), (68, 66, 50), (72, 69, 50), (76, 72, 50), (80, 75, 50), (76, 78, 50), (72, 81, 50), (68, 84, 50), (64, 87, 50), (60, 90, 50), (68, 69, 50), and (68, 72, 50). The simulation results are plotted in Figure 24, Figure 25, Figure 26 and Figure 27.

Figure 24.
Initial formation.
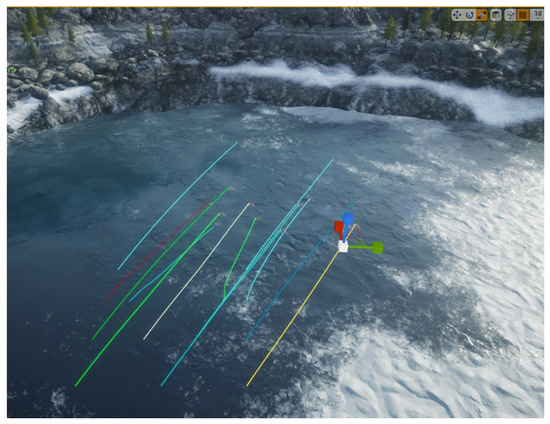
Figure 25.
Initial trajectory.

Figure 26.
Final formation.

Figure 27.
Overall trajectory diagram.
From the simulation diagram, it can be seen that each UAV flies according to the target position point assigned by the improved genetic algorithm, there is no cross-collision in the trajectory of the formation transformation, and there is an error of about 2 m in the composition of “A”, but the transformed formation is basically maintained.
5. Conclusions
When designing a formation transformation algorithm, the possibility of failure in planning trajectories using distributed model predictive control algorithms for overly compact formations should be acknowledged. Moreover, further discussions should be conducted regarding collision avoidance constraints to address the formation transformation problem under more compact conditions.
This paper primarily addresses the formation transformation problem, which involved decomposing it into target-matching and trajectory-planning problems. The target-matching algorithm adopts the improved genetic algorithm, designs the adaptive cross-mutation probability, and realizes the population reproduction without a repeated string using a hash algorithm, and the improved genetic algorithm is combined with the distributed model predictive control strategy to achieve the formation transformation. The feasibility of the engineering of the method was verified by simulation as well as semi-physical experiments.
Author Contributions
Conceptualization, G.C.; methodology, C.Z.; software, S.Z., X.W. and H.G.; validation, G.C., C.Z. and S.Z.; writing—review, G.C., C.Z., X.W., S.Z. and H.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cai, Z.; Wang, L.; Zhao, J.; Wu, K.; Wang, Y. Virtual target guidance-based predictive control for formation control of multiple UAVs. Chin. J. Aeronaut. 2020, 33, 1037–1056. [Google Scholar] [CrossRef]
- Luis, C.E.; Schoellig, A.P. Trajectory generation for multiagent point-to-point transitions via distributed model predictive control. IEEE Robot. Autom. Lett. 2019, 4, 375–382. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Mayne, D.Q.; Diehl, M. Model Predictive Control: Theory, Computation, and Design; Nob Hill Publishing: Madison, WI, USA, 2017. [Google Scholar]
- Liu, C.-H. Centralized control-based formation of multiple unmanned aerial vehicles. J. Huazhong Univ. Sci. Technol. Nat. Sci. Ed. 2015, 43, 481–485. [Google Scholar]
- Zhou, L.; Li, S. Distributed model predictive control for multi-agent flocking via neighbor screening optimization. Int. J. Robust Nonlinear Control 2017, 27, 1690–1705. [Google Scholar] [CrossRef]
- Shao, Z.; Yan, F.; Zhou, Z.; Zhu, X. Path planning for multi-UAV formation rendezvous based on distributed cooperative particle swarm optimization. Appl. Sci. 2019, 9, 2621. [Google Scholar] [CrossRef]
- Cai, Z.; Zhou, H.; Zhao, J.; Wu, K.; Wang, Y. Formation control of multiple unmanned aerial vehicles by event-triggered distributed model predictive control. IEEE Access 2018, 6, 55614–55627. [Google Scholar] [CrossRef]
- Christofides, P.D.; Scattolini, R.; de la Peña, D.M.; Liu, J. Distributed model predictive control: A tutorial review and future research directions. Comput. Chem. Eng. 2013, 51, 21–41. [Google Scholar] [CrossRef]
- Wang, T.-M.; Zhang, Y.-C.; Liang, J.-H.; Chen, Y.; Wang, C.-L. Multi-UAV collaborative system with a feature fast matching algorithm. Front. Inf. Technol. Electron. Eng. 2020, 21, 1695–1712. [Google Scholar] [CrossRef]
- Chen, R.; Yang, B.; Zhang, W. Distributed and collaborative localization for swarming UAVs. IEEE Internet Things J. 2020, 8, 5062–5074. [Google Scholar] [CrossRef]
- Brandão, A.S.; Sarcinelli-Filho, M. On the Guidance of Multiple UAV using a Centralize Formation Control Scheme and Delaunay Triangulation. J. Intell. Robot. Syst. 2016, 84, 397–413. [Google Scholar] [CrossRef]
- Xiao, H.; Chen, C.L.P. Incremental updating multirobot formation using nonlinear model predictive control method with general projection neural network. IEEE Trans. Ind. Electron. 2018, 66, 4502–4512. [Google Scholar] [CrossRef]
- Zhang, J.; Meng, F.; Zhou, Y.; Lu, G.; Zhong, Y. Decentralized Formation Control of Multi-UAV Systems Under wind Disturbances. In Proceedings of the 2015 34th Chinese Control Conference, Hangzhou, China, 28–30 July 2015; pp. 7392–7397. [Google Scholar]
- Azam, A.; Dey, S.; Mittelmann, H.D.; Ragi, S. Decentralized UAV Swarm Control for Multitarget Tracking using Approximate Dynamic Programming. In Proceedings of the 2021 IEEE World AI IoT Congress (AIIoT), Virtual, 10–13 May 2021; pp. 0457–0461. [Google Scholar] [CrossRef]
- Ren, W. Consensus Based Formation Control Strategies for Multi-Vehicle Systems. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 6–16. [Google Scholar]
- Ren, W.; Sorensen, N. Distributed Coordination Architecture for Multi-Robot Formation Control. Robot. Auton. Syst. 2008, 56, 324–333. [Google Scholar] [CrossRef]
- Ren, W.; Peeld, R.W. Distributed Consistency in Collaborative Control of Multimarine Bodies; Wu, X.F., Translator; Electronic Industry Press: Beijing, China, 2014; pp. 5–7. [Google Scholar]
- Wang, P.; Liu, C. Distributed formation control of second-order nonlinear multi-intelligent body systems. Unmanned Syst. Technol. 2021, 4, 26–31. [Google Scholar] [CrossRef]
- Gou, Z.; Wu, Y.; Deng, J.N. Research on a full process flight path planning method for UAV formation based on swarm intelligence-consistency theory. Control. Decis. Mak. 2023, 38, 1464–1472. [Google Scholar] [CrossRef]
- Kuriki, Y.; Namerikawa, T. Formation Control with Collision Avoidance for a Multi-UAV System using Decentralized MPC and Consensus-Based Control. In Proceedings of the European Control Conference, Linz, Austria, 15–17 July 2015; pp. 3079–3084. [Google Scholar]
- Najm, A.A.; Ibraheem, I.K.; Azar, A.T.; Humaidi, A.J. Genetic Optimization-Based Consensus Control of Multi-Agent 6-DoF UAV System. Sensors 2020, 20, 3576. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).