Integrating Commercial-Off-The-Shelf Components into Radiation-Hardened Drone Designs for Nuclear-Contaminated Search and Rescue Missions
Abstract
1. Introduction
Literature Review
2. Methodology
3. Demonstration Case
3.1. Scenario Description
3.2. Assumptions and Simplifications
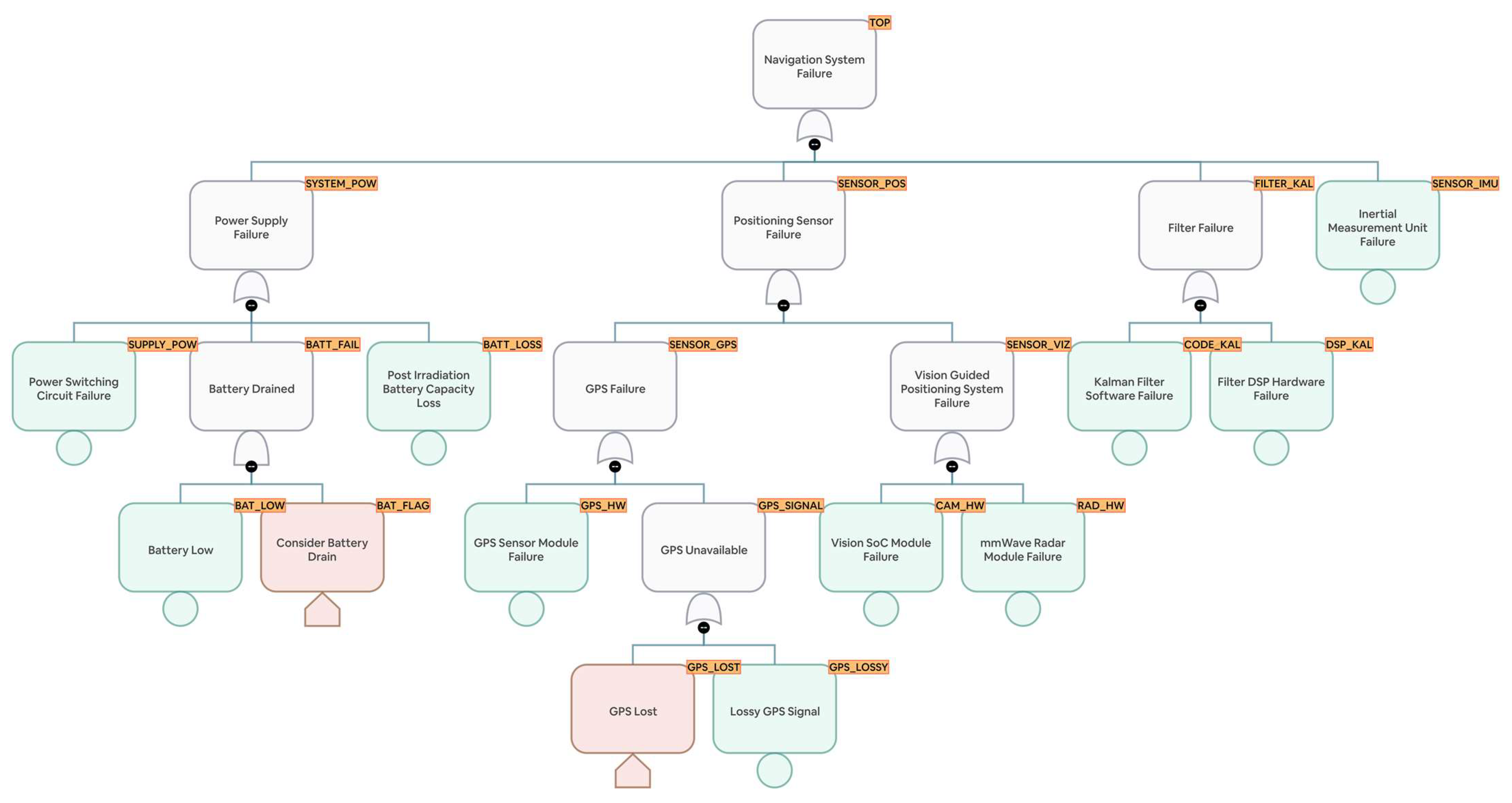
3.3. Navigation System Fault Tree
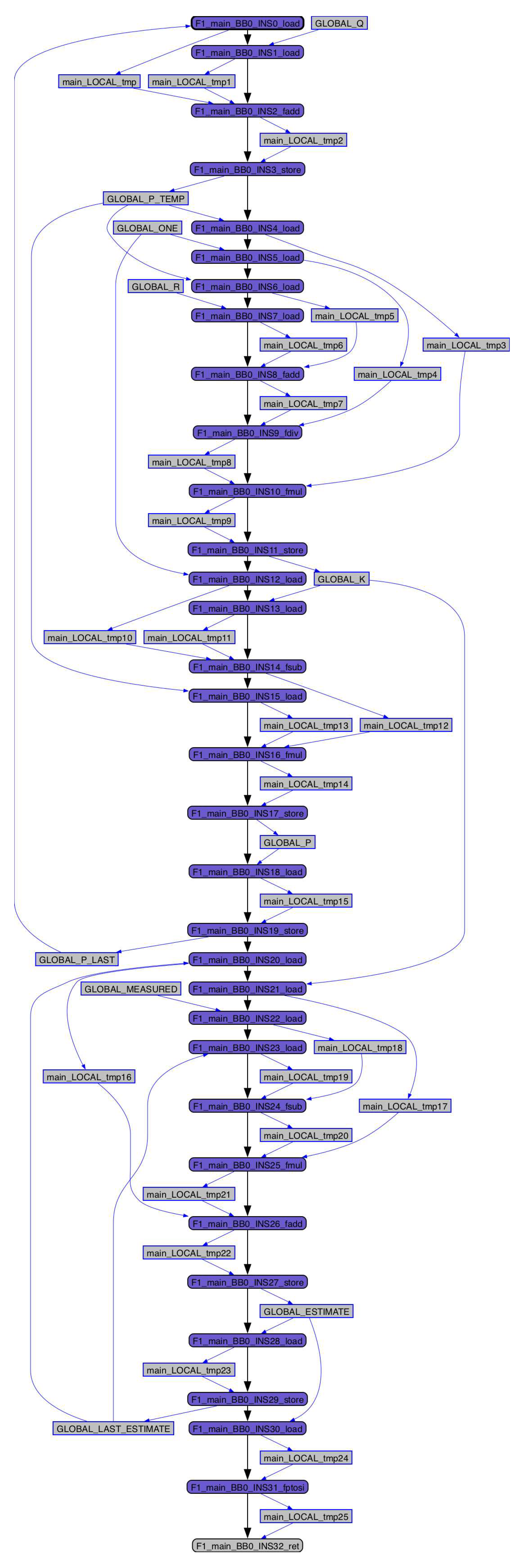
3.4. Modeling Kalman Filter Software Failures Using Dual-Graph Error Propagation Method (DEPM)
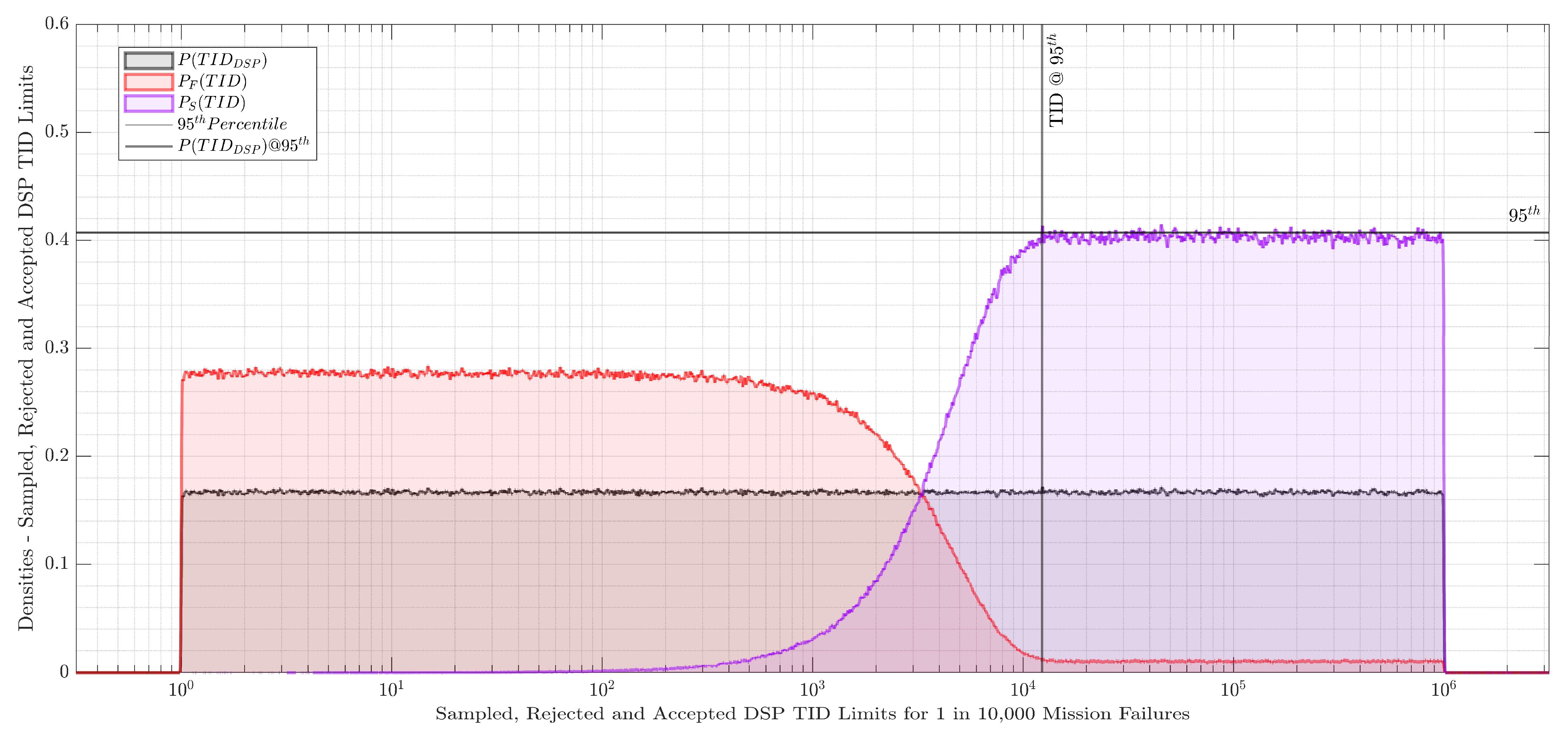
3.5. Modeling Total Ionizing Dose Limits for Electronic Hardware
4. Results and Discussion
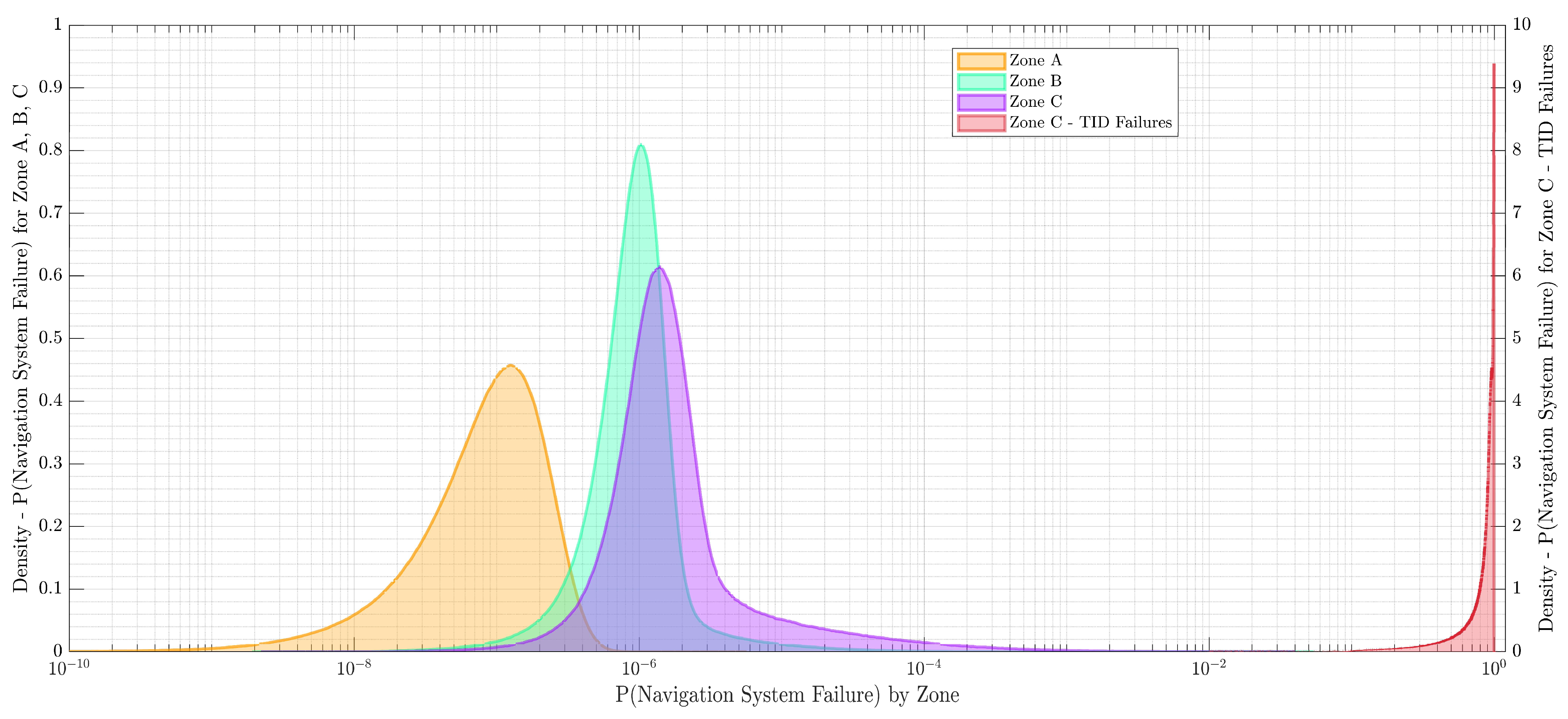
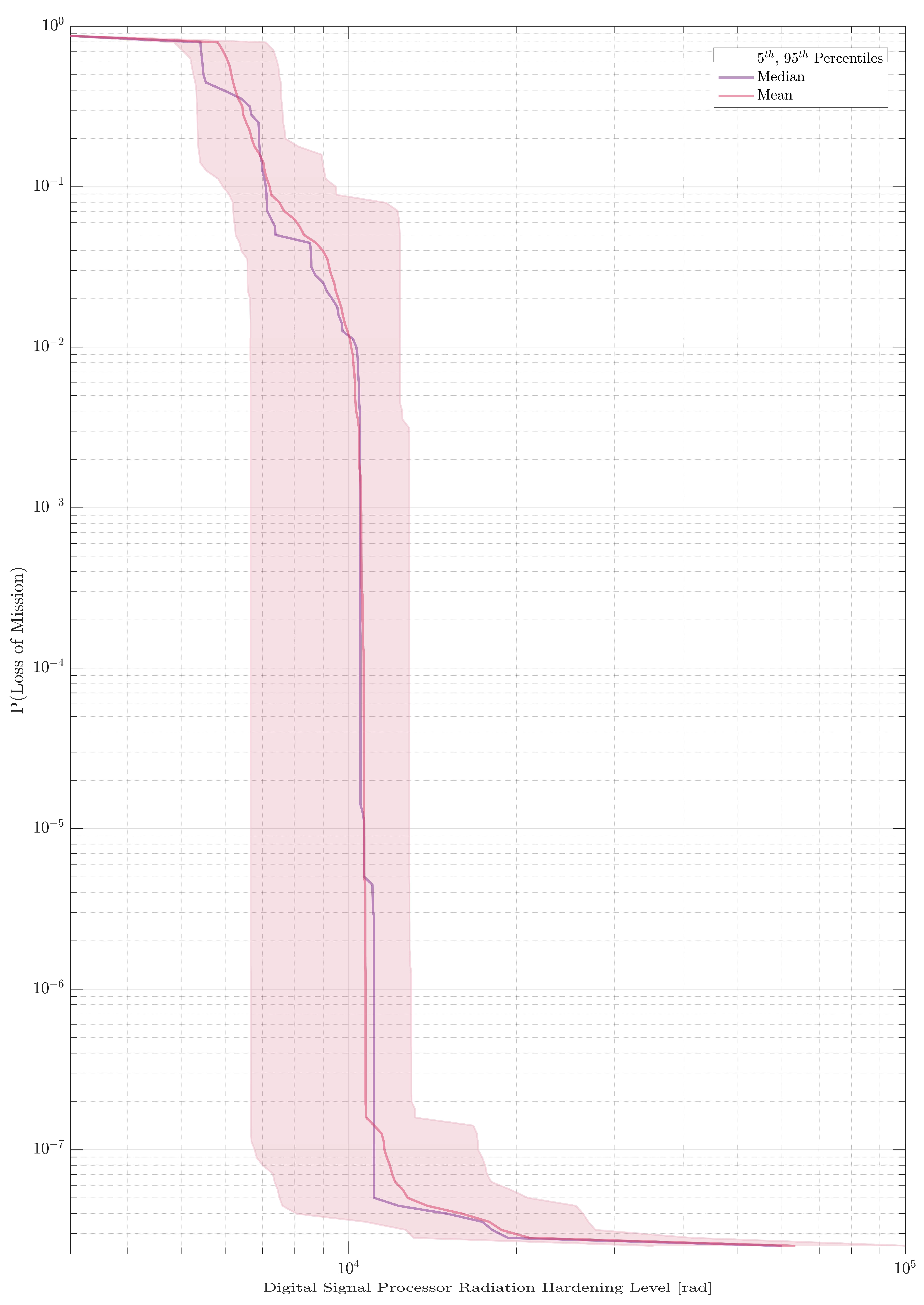
4.1. Probability of Loss of Mission (LOM) Using Commercial Off-The-Shelf (COTS) Components
4.2. Selective Radiation-Hardening Using Mission Success Criteria
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahmad, M.I.; Rahim, M.H.A.; Nordin, R.; Mohamed, F.; Abu-Samah, A.; Abdullah, N.F. Ionizing Radiation Monitoring Technology at the Verge of Internet of Things. Sensors 2021, 21, 7629. [Google Scholar] [CrossRef]
- Pinto, L.R.; Vale, A.; Brouwer, Y.; Borbinha, J.; Corisco, J.; Ventura, R.; Silva, A.M.; Mourato, A.; Marques, G.; Romanets, Y. Radiological Scouting, Monitoring and Inspection Using Drones. Sensors 2021, 21, 3143. [Google Scholar] [CrossRef] [PubMed]
- Murphy, R.R.; Tadokoro, S.; Kleiner, A. Disaster Robotics. In Springer Handbook of Robotics; Siciliano, B., Khatib, O., Eds.; Springer Handbooks; Springer International Publishing: Cham, Switzerland, 2016; pp. 1577–1604. [Google Scholar] [CrossRef]
- Fleetwood, D.M.; Winokur, P.S.; Dodd, P.E. An overview of radiation effects on electronics in the space telecommunications environment. Microelectron. Reliab. 2000, 40, 17–26. [Google Scholar] [CrossRef]
- Normand, E. Single event upset at ground level. IEEE Trans. Nucl. Sci. 1996, 43, 2742–2750. [Google Scholar] [CrossRef]
- Dodd, P.E.; Shaneyfelt, M.R.; Schwank, J.R.; Felix, J.A. Current and Future Challenges in Radiation Effects on CMOS Electronics. IEEE Trans. Nucl. Sci. 2020, 57, 1747–1763. [Google Scholar] [CrossRef]
- Winokur, P.S.; Lum, G.K.; Shaneyfelt, M.R.; Sexton, F.W.; Hash, G.L.; Scott, L. Use of COTS microelectronics in radiation environments. IEEE Trans. Nucl. Sci. 1999, 46, 1494–1503. [Google Scholar] [CrossRef]
- Privat, A.; Barnaby, H.J.; Adell, P.C.; Tolleson, B.S.; Wang, Y.; Han, X.; Davis, P.; Rax, B.R.; Buchheit, T.E. Multiscale Modeling of Total Ionizing Dose Effects in Commercial-off-the-Shelf Parts in Bipolar Technologies. IEEE Trans. Nucl. Sci. 2019, 66, 190–198. [Google Scholar] [CrossRef]
- Ladbury, R.; Bay, M.; Zinchuk, J. Threats to Resiliency of Redundant Systems Due to Destructive SEEs. IEEE Trans. Nucl. Sci. 2021, 68, 970–979. [Google Scholar] [CrossRef]
- Apostolakis, G. The Concept of Probability in Safety Assessments of Technological Systems. Science 1990, 250, 1359–1364. [Google Scholar] [CrossRef] [PubMed]
- Modarres, M.; Kaminskiy, M.; Krivtsov, V. Reliability Engineering and Risk Analysis: A Practical Guide, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Kripke, S.A. Semantical Considerations on Modal Logic. Acta Philos. Fenn. 1963, 16, 83–94. Available online: http://saulkripkecenter.org/wp-content/uploads/2019/03/Semantical-Considerations-on-Modal-Logic-PUBLIC.pdf (accessed on 1 June 2023).
- Kwiatkowska, M.; Norman, G.; Parker, D. Stochastic Model Checking. In Formal Methods for Performance Evaluation; Bernardo, M., Hillston, J., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4486, pp. 220–270. [Google Scholar] [CrossRef]
- Baier, C.; Katoen, J.-P. Principles of Model Checking; The MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Schneider, K. Verification of Reactive Systems: Formal Methods and Algorithms; Texts in theoretical computer science; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Rabin, M.O.; Scott, D. Finite Automata and Their Decision Problems. IBM J. Res. Dev. 1959, 3, 114–125. [Google Scholar] [CrossRef]
- Garrick, B.J. Quantifying and Controlling Catastrophic Risks; Academic Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Vesely, W.E.; Goldberg, F.F.; Roberts, N.H.; Haasl, D.F. NUREG-0492, ‘Fault Tree Handbook’. 1981. Available online: https://www.nrc.gov/docs/ML1007/ML100780465.pdf (accessed on 1 June 2023).
- Diaconeasa, M.A.; Mosleh, A. The ADS-IDAC Dynamic Platform with Dynamically Linked System Fault Trees. In Proceedings of the International Topical Meeting on Probabilistic Safety, Pittsburgh, PA, USA, 24–28 September 2017. [Google Scholar]
- Morozov, A.; Janschek, K. Dual Graph Error Propagation Model for Mechatronic System Analysis. IFAC Proc. Vol. 2011, 44, 9893–9898. [Google Scholar] [CrossRef]
- Vidineev, V.; Yusupova, N.; Ding, K.; Morozov, A.; Janschek, K. Improved Stochastic Control Flow Model for LLVM-Based Software Reliability Analysis. Industry 4.0 2018, Volume 3. pp. 172–174. Available online: https://stumejournals.com/journals/i4/2018/4/172 (accessed on 2 August 2022).
- Ding, K.; Ding, S.; Morozov, A.; Fabarisov, T.; Janschek, K. On-Line Error Detection and Mitigation for Time-Series Data of Cyber-Physical Systems using Deep Learning Based Methods. In Proceedings of the 2019 15th European Dependable Computing Conference (EDCC), Naples, Italy, 17–20 September 2019; IEEE: New York, NY, USA, 2019; pp. 7–14. [Google Scholar] [CrossRef]
- Marques-silva, J. Practical applications of boolean satisfiability. In Workshop on Discrete Event Systems (WODES); IEEE Press: New York, NY, USA, 2008. [Google Scholar]
- Bryant, R.E.; Heule, M.J. Generating extended resolution proofs with a BDD-based SAT solver. In International Conference on Tools and Algorithms for the Construction and Analysis of Systems; Springer: Berlin/Heidelberg, Germany, 2021; pp. 76–93. [Google Scholar]
- Vetter, K. The Institute of Resilient Communities. In Resilience: A New Paradigm of Nuclear Safety; Ahn, J., Guarnieri, F., Furuta, K., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 207–218. [Google Scholar] [CrossRef]
- Vetter, K. Multi-sensor radiation detection, imaging, and fusion. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2016, 805, 127–134. [Google Scholar] [CrossRef]
- Medvedevs, G.U. JPRS Report, Soviet Union: Economic Affairs (‘Chernobyl Notebook’), Soviet Union: Economic Affairs, JPRS-UEA-89-034. 1989. Available online: https://apps.dtic.mil/sti/pdfs/ADA335076.pdf (accessed on 19 June 2023).
- OpenPRA Community, OpenPRA Initiative. 2019. Available online: https://openpra.org/ (accessed on 17 January 2022).
- Earthperson, A.; Otani, C.M.; Nevius, D.; Prescott, S.R.; Diaconeasa, M.A. A combined strategy for dynamic probabilistic risk assessment of fission battery designs using EMRALD and DEPM. Prog. Nucl. Energy 2023, 160, 104673. [Google Scholar] [CrossRef]
- Texas Instruments—Reliability Testing, Texas Instruments Quality & Reliability. Available online: https://www.ti.com/support-quality/reliability/reliability-testing.html (accessed on 10 January 2022).
- mbsa-tud, mbsa-tud/LLVMPars. 2021. Available online: https://github.com/mbsa-tud/LLVMPars (accessed on 25 July 2023).
- GSFC Radiation Data Base. Available online: https://radhome.gsfc.nasa.gov/radhome/RadDataBase/RadDataBase.html (accessed on 16 June 2023).
- Bazzano, G.; Ampollini, A.; Cardelli, F.; Fortini, F.; Nenzi, P.; Palmerini, G.; Picardi, L.; Piersanti, L.; Ronsivalle, C.; Surrenti, V.; et al. Radiation testing of a commercial 6-axis MEMS inertial navigation unit at ENEA Frascati proton linear accelerator. Adv. Space Res. 2021, 67, 1379–1391. [Google Scholar] [CrossRef]
- Qiu, J.; He, D.; Sun, M.; Li, S.; Wen, C.; Hattrick-Simpers, J.; Zheng, Y.F.; Cao, L. Effects of neutron and gamma radiation on lithium-ion batteries. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2015, 345, 27–32. [Google Scholar] [CrossRef]
- Markgraf, M.; Montenbruck, O. Total Ionizing Dose Testing of the Orion and Phoenix GPS Receivers, German Space Operations Center (GSOC), TN. 2004. Available online: https://www.dlr.de/rb/Portaldata/38/Resources/dokumente/GSOC_dokumente/RB-RFT/TN_0401.pdf (accessed on 1 June 2023).
- Rezzak, N.; Wang, J.-J.; Huang, C.-K.; Nguyen, V.; Bakker, G. Total Ionizing Dose Characterization of 65 nm Flash-Based FPGA. In Proceedings of the 2014 IEEE Radiation Effects Data Workshop (REDW), Paris, France, 13–17 July 2014; IEEE: New York, NY, USA, 2014; pp. 1–5. [Google Scholar] [CrossRef]
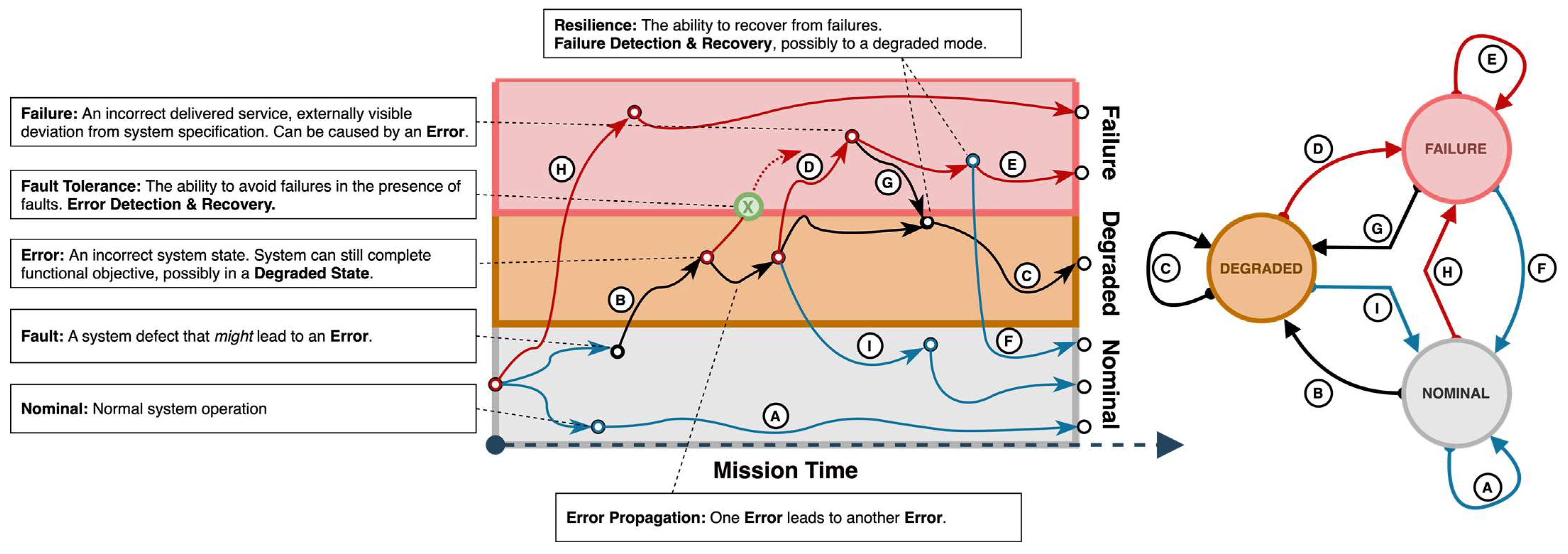
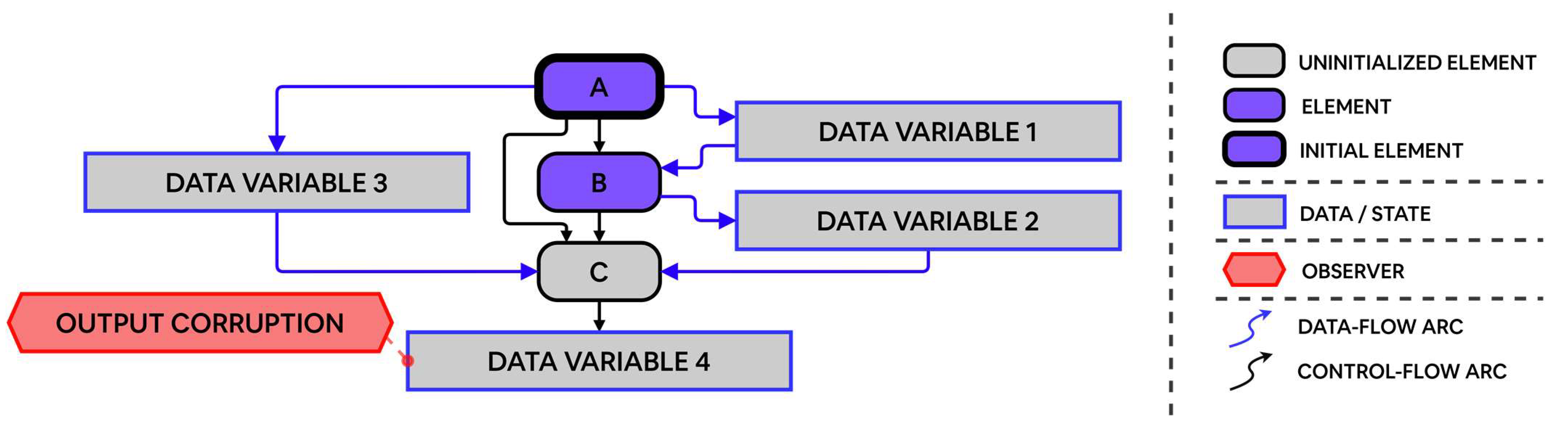
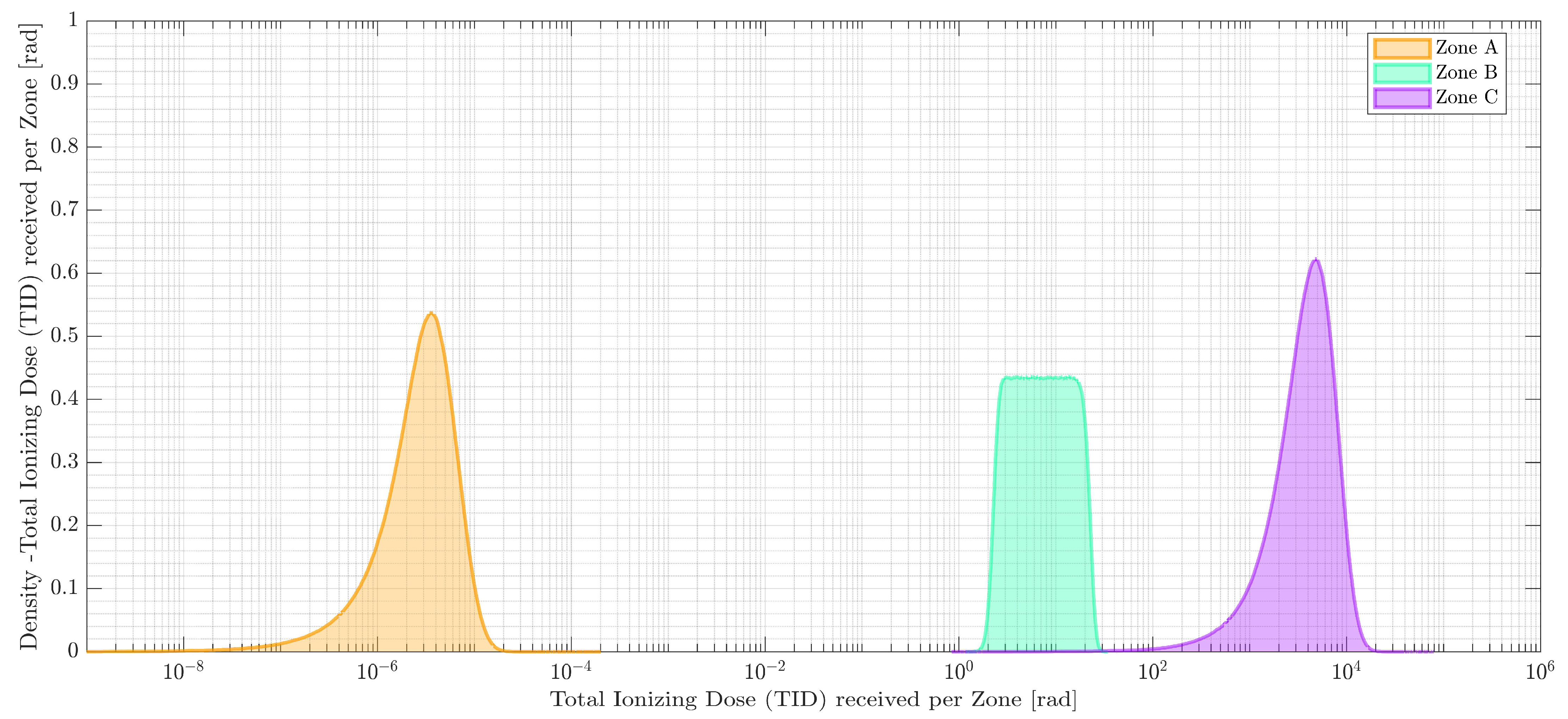
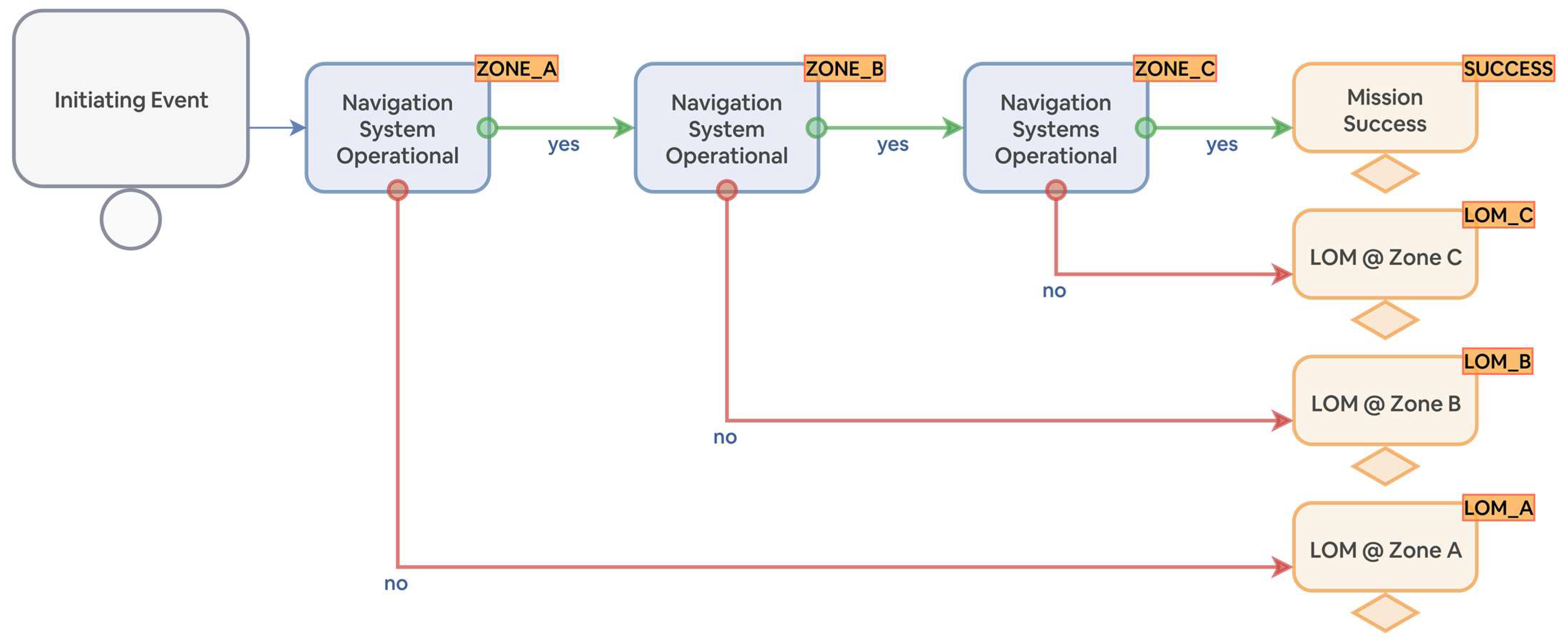
| Term | Definition | Description |
|---|---|---|
| A set of possible states. | ||
| The initial state, which is nominal. | ||
| A mapping or transition relation, where is left-total (if the source set equals the domain, is left-total), and is fully connected. |
| Regular Expression | Term | Description |
|---|---|---|
| A+ | Ideal/Perfect System | No errors, faults, or failures occur. |
| B | Fault | A fault is a weakness that can potentially lead to errors. |
| E+|C+ | Error Propagation | A move from an initial error state leads to a subsequent one. |
| D|H | Failure | System fails from either a degraded or a nominal state. |
| I|G|F | Recoverable System | Move from higher to lower degradation. |
| B(C*|I) | Fault-Tolerant | Avoid transition to failure, given a fault. |
| A+|(B(C*|I)) | Failure-Avoidant | No failures occur. |
| G|F | Resilient System | Recover from a failure, either fully or partially. |
| B(C*|D(E*|G))|(H(E*|G)) | Irrecoverable System | Neither completely fails, nor returns to nominal. |
| BC*(ϵ|DE*) | Permanently Failed | System remains irrecoverable forever. |
| Term | Definition |
|---|---|
| A set of elements, always non-empty. | |
| A set of optional data terms. | |
| An edge-list representing control flows. | |
| An edge-list representing data flows. | |
| A list of conditional expressions, which apply to the element set . |
| Element | Conditional Expressions |
|---|---|
| A | always: with P(0.8): DATA VARIABLE 1, DATA VARIABLE 2 = error with P(0.2): DATA VARIABLE 1, DATA VARIABLE 2 = ok |
| B | if DATA VARIABLE 1 = error, then: with P(0.9): DATA VARIABLE 2 = ok with P(0.1): DATA VARIABLE 2 = error else: with P(1.0): DATA VARIABLE 2 = ok |
| C | if DATA VARIABLE 2 & DATA VARIABLE 3 = ok, then: with P(1.0): DATA VARIABLE 4 = ok else: with P(0.2): DATA VARIABLE 4 = ok with P(0.8): DATA VARIABLE 4 = error |
| Zone | Dose Rate [rad/hour] | Elapsed Time [minute] | Total Received Dose [rad] |
|---|---|---|---|
| A | |||
| B | |||
| C |
| Basic Event | Part Number | Component Type | Derated Failure Rate |
|---|---|---|---|
| SENSOR_IMU | TI-MSP430 Series | MEMS IMU | |
| CAM_HW | TI-TDA4AL-Q1 | Vision SoC + DSP | |
| RAD_HW | TI-IWR1642AQAGABL | mmWave Radar + DSP | |
| DSP_KAL | TI-TMS320C6678 | Kalman Filter DSP |
| Basic Event | Basic Event Description | Failure Rate |
|---|---|---|
| SENSOR_IMU | Inertial Measurement Unit Failure | |
| CAM_HW | Vision System-on-Chip Module Failure | |
| RAD_HW | mmWave Radar Module Failure | |
| DSP_KAL | Filter DSP Hardware Failure | |
| CODE_KAL | Kalman Filter Software Failure | DEPM, see section on Page 11 |
| GPS_HW | GPS Sensor Module Failure | |
| GPS_LOSSY | Lossy GPS Signal | |
| SUPPLY_POW | Switching Power Supply Circuit Failure | |
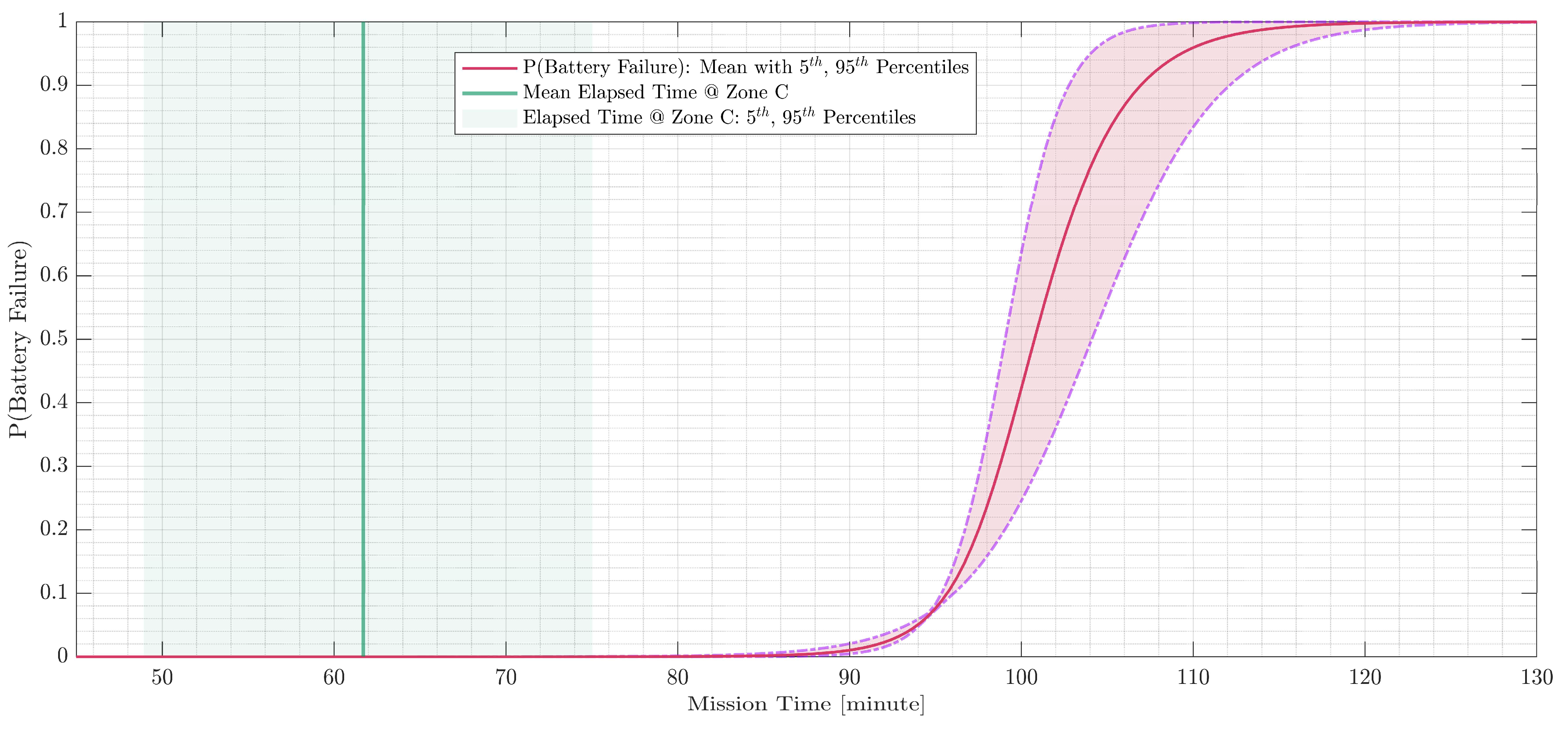
| BATT_LOW | Battery Low | Time-dependent; see Figure 6 |
| BATT_LOSS | Post-Irradiation Battery Capacity Loss | P = 1 as TID approaches TID limit |
| /** * Kalman Filter (single variable) * Assume the input is in register R0 * Assume the initial state estimate is in register R1 * Assume the initial error covariance is in register R2 * Assume the process noise variance is in register R3 * Assume the measurement noise variance is in register R4 **/ Initialization
|
| Component | Commercial Off-The-Shelf (COTS) |
|---|---|
| Inertial Measurement Unit | |
| Power Switching Circuit | |
| Lithium Ion Battery | |
| GPS Sensor Module | |
| Vision SoC Module | |
| mmWave Radar Module | |
| Filter DSP Hardware |
| End State | End State Description | P (End State) |
|---|---|---|
| LOM_A | Loss of Mission in Zone A | |
| LOM_B | Loss of Mission in Zone B | |
| LOM_C | Loss of Mission in Zone C | |
| SUCCESS | Mission Success |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Earthperson, A.; Diaconeasa, M.A. Integrating Commercial-Off-The-Shelf Components into Radiation-Hardened Drone Designs for Nuclear-Contaminated Search and Rescue Missions. Drones 2023, 7, 528. https://doi.org/10.3390/drones7080528
Earthperson A, Diaconeasa MA. Integrating Commercial-Off-The-Shelf Components into Radiation-Hardened Drone Designs for Nuclear-Contaminated Search and Rescue Missions. Drones. 2023; 7(8):528. https://doi.org/10.3390/drones7080528
Chicago/Turabian StyleEarthperson, Arjun, and Mihai A. Diaconeasa. 2023. "Integrating Commercial-Off-The-Shelf Components into Radiation-Hardened Drone Designs for Nuclear-Contaminated Search and Rescue Missions" Drones 7, no. 8: 528. https://doi.org/10.3390/drones7080528
APA StyleEarthperson, A., & Diaconeasa, M. A. (2023). Integrating Commercial-Off-The-Shelf Components into Radiation-Hardened Drone Designs for Nuclear-Contaminated Search and Rescue Missions. Drones, 7(8), 528. https://doi.org/10.3390/drones7080528







