Multi-UAV Cooperative Obstacle Avoidance of 3D Vector Field Histogram Plus and Dynamic Window Approach

Abstract

In this paper, we propose a fusion algorithm that integrates the 3D vector field histogram plus (VFH+) algorithm and the improved dynamic window approach (DWA) algorithm. The aim is to address the challenge of cooperative obstacle avoidance faced by multi-UAV formation flying in unknown environments. First, according to the navigation evaluation function of the standard DWA algorithm, the target distance is introduced to correct the azimuth. Then, aiming at the problem that the fixed weight mechanism in standard DWA algorithm is unreasonable, we combine the A* algorithm and introduce variable weight factors related to azimuth to improve the target orientation ability in local path planning. A new rotation cost evaluation function is added to improve the obstacle avoidance ability of two-dimensional UAV. Then, 3D VFH+ algorithm is introduced and integrated with improved DWA algorithm to design a distributed cooperative formation obstacle avoidance control algorithm. Simulation validation suggests that compared with the traditional DWA algorithm, the improved collaborative obstacle avoidance control algorithm can greatly optimize the obstacle avoidance effect of UAVs’ formation flight.

1. Introduction

Owing to their cost-effectiveness, advanced functionalities, and ability to be reused, UAVs have garnered escalating popularity within the domain of reconnaissance and monitoring [1,2,3,4]. Over the past years, the operational landscape has witnessed a rise in complexity, thereby amplifying the demand for UAV implementation in these specific missions. Yet, a single UAV can hardly meet its actual task requirements when operating independently [5,6], as its sensor’s range of view may be easily blocked, limiting its ability to accomplish tasks. Cooperative efforts made by UAVs can significantly mitigate the risk of target loss [7,8,9], thus leading to the adoption of multi-UAV collaboration [10,11] in trajectory planning for moving target tracking purposes.

Currently, the research hotspots in cooperative formation algorithms encompass communication strategies, formation control strategies, formation transformation trajectory planning, and cooperative obstacle avoidance. Formation transformation and cooperative obstacle avoidance have yielded significant and fruitful outcomes following extensive years of research. Muhammad Umer Farooq proposed a novel nonlinear quadcopter probabilistic roadmap (PRM) navigation method [12], specifically designed to address the challenge of formation reconstruction for quadcopter formations after dynamic obstacle avoidance. Li J et al. [13] conducted an investigation into collective obstacle avoidance algorithms for both first-order kinematic agents and second-order dynamic agents. They introduced an obstacle avoidance algorithm that eliminates the need for velocity measurements in agents with first-order kinematics. This algorithm is particularly beneficial when only a fixed proportion of agents can perceive obstacle information. Okechi Onuoha delved into the study of affine formation maneuver control for multi-agent systems with triple integrator dynamics, considering both continuous time and sampled data settings [14]. As a result, the research demonstrated the effectiveness of maneuver-based formation transformations in facilitating obstacle avoidance.

Most cooperative obstacle avoidance strategies use the artificial potential field (APF) method. The APF method [15,16,17] is extensively employed in UAV formation obstacle avoidance. The algorithm relies on establishing gravitational and repulsive fields to calculate the resultant force that guides path planning at each moment. However, the APF algorithm can fall into a local optimal solution if the field function design is unreasonable. Moreover, the algorithm lacks consideration for the dynamic motion constraints of UAVs, making it challenging to track the planned path in real-time.

DWA was proposed in 1997 [18]. The algorithm considers the limitation of velocity and acceleration of a moving body and employs an evaluation function to select the most favorable trajectory. Nonetheless, the algorithm exhibits several limitations, including the inherent challenge of designing a suitable evaluation function, a tendency towards a conservative speed window, and a propensity to converge towards suboptimal positions within a localized context. Reference [19] proposes the collision avoidance dynamic window approach (CADWA) algorithm, which addresses problems such as collision avoidance failure and improper evaluation function weighting. Furthermore, reference [20] introduces an additional evaluation factor of direction change, which mitigates issues related to the contradiction between heading and speed factors in DWA, such as untimely obstacle avoidance and frequent direction changes on certain road conditions, resulting in smoother trajectories.

Additionally, an effective improvement direction involves merging the DWA algorithm with other algorithms, such as the A* algorithm first proposed by Hart in 1968 [21]. Extracting the key points of path planning by the improved A* algorithm as temporary target points of DWA algorithm, achieving the fusion of the improved A* and DWA algorithm on the basis of global optimization, thus realizing dynamic path planning in complex environments has been realized by reference [22]. In reference [23], the traditional A* algorithm’s drawbacks, such as non-optimal path and many redundant points, were addressed by expanding its search neighborhood to remove the limitation of motion direction and combining it with the DWA’s improved speed evaluation function for temporary obstacle avoidance. Reference [24] tested the hybrid path planning algorithm of A* and DWA on four typical Turlebot2 mobile robot terrains. The experiment demonstrated that the hybrid algorithm outperforms the individual algorithms by offering efficient obstacle avoidance and a faster path-finding process.

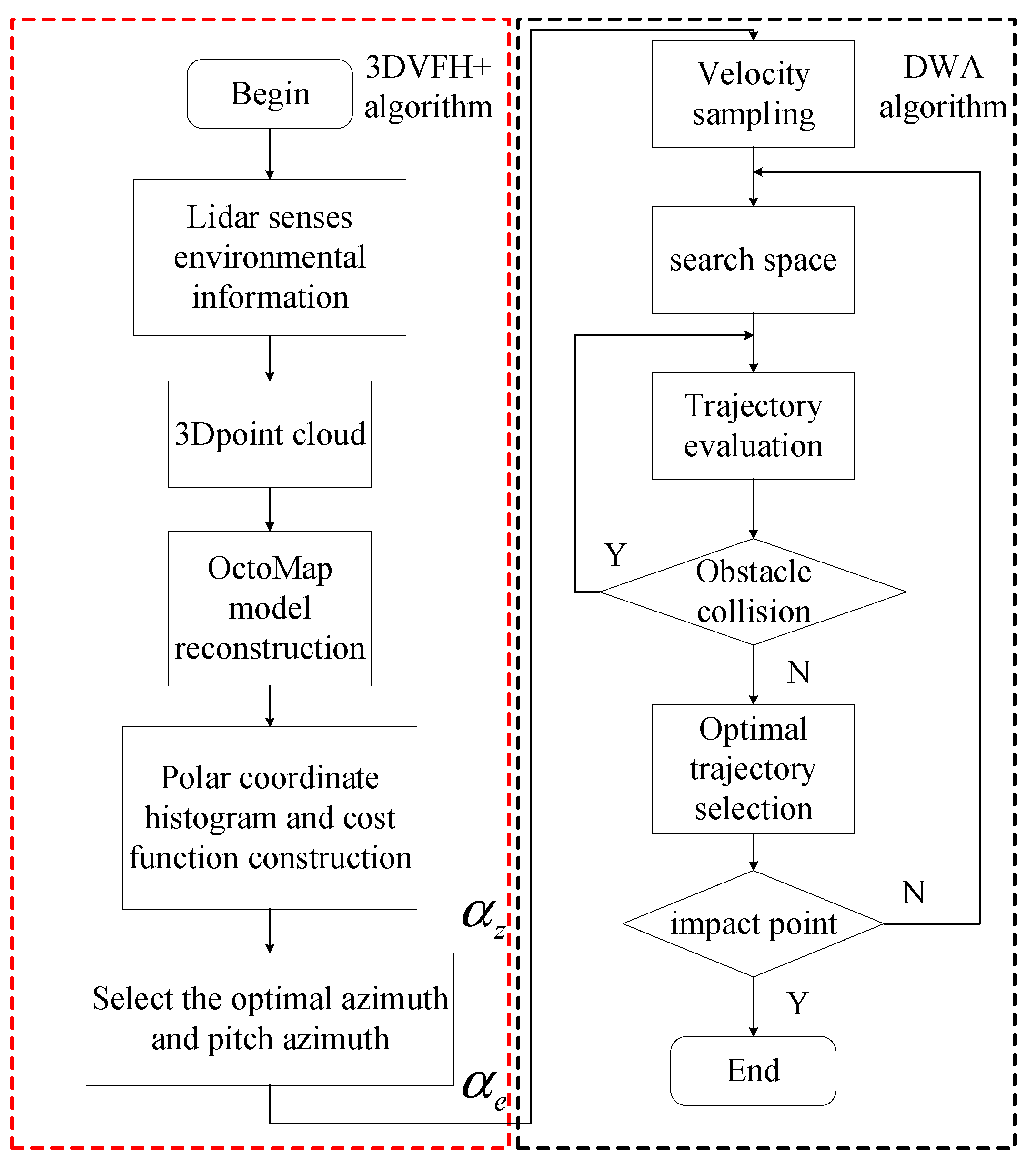
This paper introduces a novel algorithm for UAV Formation Control, specifically designed to enable efficient task completion by multi-UAV formations operating in complex environments that include a variety of obstacles. The proposed algorithm comprehensively considers the sensor measurement range and the kinematic constraints of UAVs, effectively tackling the challenge of maintaining formation integrity in the presence of disturbances and navigating obstacles. The key contributions of this paper can be summarized as follows.

We propose an enhanced version of the traditional DWA algorithm, with a specific focus on improving the navigation evaluation function. To achieve this, we incorporate the concept of target distance, which serves to correct the azimuth angle. Additionally, we integrate the A* algorithm to address the limitations of the fixed weight mechanism and enhance the overall efficiency of the process. Furthermore, we introduce a novel rotation evaluation function to constrain large rotation angles, thereby further improving the search efficiency. The ultimate goal of these enhancements is to bolster the obstacle avoidance capability of two-dimensional planar UAVs.

Combined with the 3D VFH + algorithm and improved DWA, it improves the obstacle avoidance ability of two-dimensional plane UAV and solves the obstacle avoidance problem of multi-aircraft formation in three-dimensional space.

The rest of this paper is organized as follows. Section 2 describes the improved DWA algorithm. Section 3 describes the algorithm design for 3D VFH+. Section 4 introduces the UAV formation control fusion algorithm. Section 5 verifies and analyzes our algorithm. Finally, concluding remarks are provided in Section 6.

2. Design of Improved DWA

2.1. Basic Principle of Standard DWA

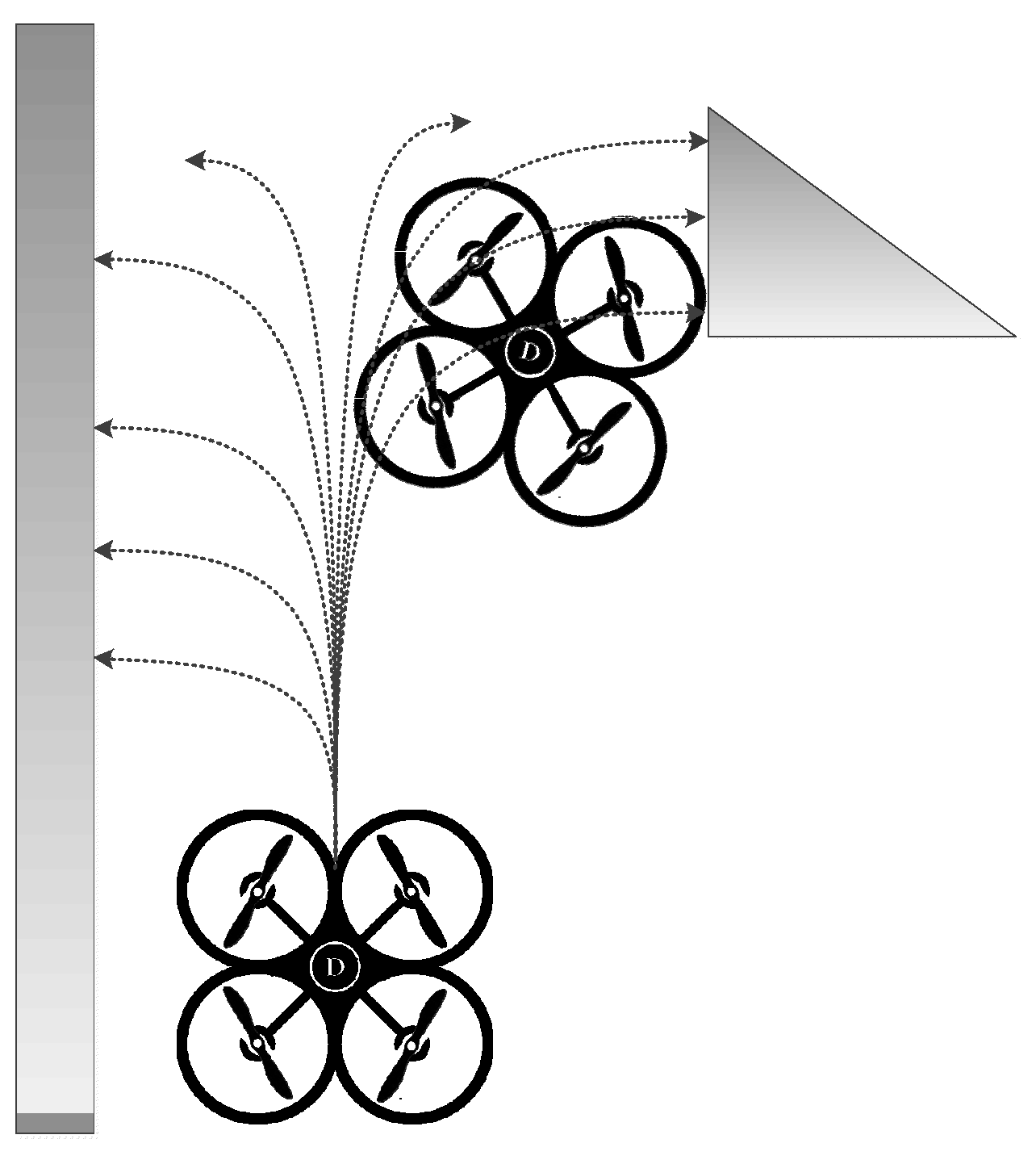
The DWA algorithm primarily samples within the two-dimensional velocity space $(v,\omega )$ and identifies a constrained set of velocity combinations that fulfill predetermined criteria. After this step, the method determines the optimal speed at the current time through the utilization of an evaluation function.

Firstly, due to the limitation of its own hardware, the moving body has the constraint of linear velocity in kinematics:

$$V_m=\left\{\nu \in \left[{\nu }_{\min },{\nu }_{\max }\right],\omega \in \left[{\omega }_{\min },{\omega }_{\max }\right]\right\}$$

(1)

Secondly, there is a maximum acceleration constraint:

$$V_n=\left\{(v,\omega )|v\in \left[v_c-{\dot{v}}_d\Delta t,v_c+{\dot{v}}_a\Delta t\right]^\omega \in \left[{\omega }_c-{\dot{\omega }}_d\Delta t,{\omega }_c+{\dot{\omega }}_a\Delta t\right]\right\}$$

(2)

$v_c$ indicates the linear velocity of current motion, ${\omega }_c$ indicates the angular velocity of current motion, ${\dot{v}}_d$ indicates the minimum linear acceleration of current motion, ${\dot{v}}_a$ indicates the maximum linear acceleration of current motion, ${\dot{\omega }}_d$ indicates the minimum angular acceleration of current motion, ${\dot{\omega }}_a$ indicates the maximum angular acceleration of current motion, and the sampling interval, represented as “$\Delta t$”, remains consistent without any alterations.

Finally, there is an obstacle constraint:

$$V_o=\left\{(v,\omega )|v\le \sqrt{2\ast dist(v,\omega )\ast {\dot{v}}_d}^\omega \le \sqrt{2\ast dist(v,\omega )\ast {\dot{\omega }}_d}\right\}$$

(3)

where $dist(v,\omega )$ denotes the closest distance between the moving body and the obstacle.

Through the utilization of the DWA, it becomes feasible to simulate a multitude of prospective paths within the given map, as shown in Figure 1.

Then, the current optimal speed combination is selected according to the velocity evaluation function of (4).

$$C\left(v,\omega \right)=\lambda \left[\alpha ·heading(v,\omega )+\beta ·obdist(v,\omega )+\gamma ·vel(v,\omega )\right]$$

(4)

In the equation, $heading(v,\omega )$ represents the azimuth evaluation function, which guides the motion of the object towards the target direction. The $obdist(v,\omega )$ represents the obstacle avoidance evaluation function to guide the motion of the object away from the obstacle. The $vel(v,\omega )$ denotes the kinematic body linear velocity evaluation function to stimulate its rapid passage; $\alpha ,\beta ,\gamma$ are the fixed weights of the evaluation function and $\lambda$ is the normalization coefficient.

2.2. Improving the DWA

(1) Introduction of target distance

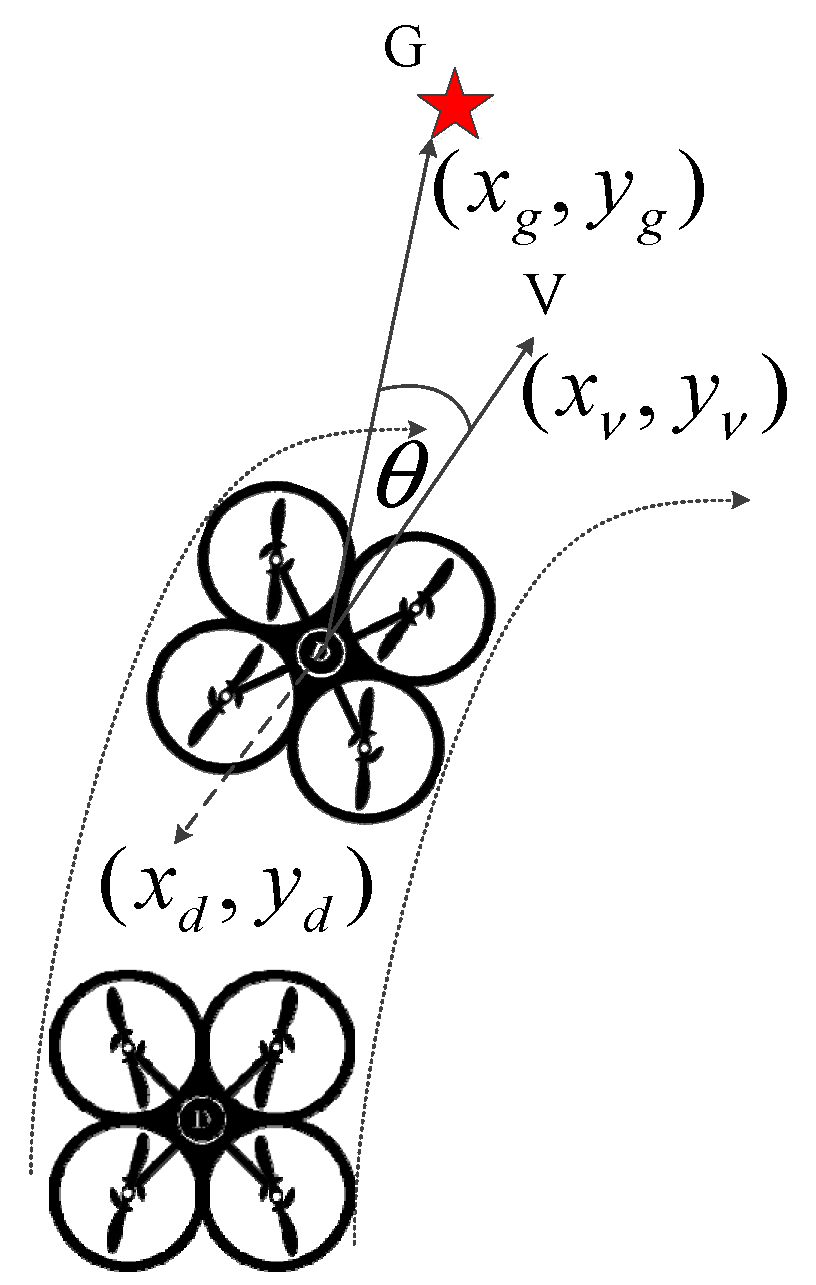
The azimuth evaluation function in the standard DWA is shown as:

$$heading\left(v,\omega \right)={180}^{\circ }-\theta$$

(5)

where $\theta$ is the angle between the velocity vector and the vector connecting the current position of the moving object to the target point. The smaller the value of $\theta$, the higher the evaluation score. Given that the current position of the moving object is denoted as D:$(x_d,y_d)$, the position of the velocity trajectory’s endpoint is denoted as V:$(x_{\nu },y_{\nu })$, and the position of the target point is denoted as G:$(x_g,y_g)$, Equation (6) can be derived as shown in the Figure 2.

$$\cos \theta =\frac{\overrightarrow{DG}·\overrightarrow{DV}}{\left|DG\right|\left|DV\right|}=\frac{(x_g-x_d)(x_{\nu }-x_d)+(y_g-y_d)(y_{\nu }-y_d)}{\sqrt{{(x_g-x_d)}^2+{(y_g-y_d)}^2}\sqrt{{(x_{\nu }-x_d)}^2+{(y_{\nu }-y_d)}^2}}$$

(6)

Combining (5) with (6) yields:

$$heading\left(v,\omega \right)={180}^{\circ }-\arccos \frac{(x_g-x_d)(x_{\nu }-x_d)+(y_g-y_d)(y_{\nu }-y_d)}{\sqrt{{(x_g-x_d)}^2+{(y_g-y_d)}^2}\sqrt{{(x_{\nu }-x_d)}^2+{(y_{\nu }-y_d)}^2}}$$

(7)

Under the action of (7), as the moving object approaches the target point, the angle $\theta$ experiences rapid expansion, resulting in oscillations of the moving object at the target point. Therefore, the introduction of target distance is employed as a constraint to mitigate this issue, as shown in (8):

$$heading\_new\left(v,\omega \right)=\frac{{180}^{\circ }-\theta }{\sqrt{{(x_{\nu }-x_d)}^2+{(y_{\nu }-y_d)}^2}}$$

(8)

(2) Dynamic weights of the fusion A* algorithm

The A* algorithm is usually used for global path planning. By rasterizing the global map and identifying a number of nodes to be expanded, the raster point with the lowest current cost can be selected according to the cost function as shown in (9), denoted as A:$(x_a,y_a)$.

$$f\left(n\right)=g(n)+h(n)$$

(9)

where $g(n)$ represents the distance cost from the starting point to the current grid point, while $h(n)$ represents the distance cost from the current grid point to the target point. The global path coordinates obtained from the A* algorithm is merged with the final coordinates of the velocity trajectory obtained from the DWA algorithm. By utilizing the cosine relationship, the dynamic weight $\mu$ for the azimuth evaluation function can be obtained as shown in (10).

$$\mu =\frac{(x_a-x_d)(x_v-x_d)+(y_a-y_d)(y_v-y_d)}{\sqrt{{(x_a-x_d)}^2+{(y_a-y_d)}^2}\sqrt{{(x_v-x_d)}^2+{(y_v-y_d)}^2}}$$

(10)

The introduction of dynamic weights improves navigation efficiency.

(3) New $twirling(v,\omega )$ function

Considering that large turning angles affect the actual following result of the path by the moving body, the $twirling(v,\omega )$ function is added to the evaluation function of the DWA algorithm. This function will compensate for the large rotation angle, so as to avoid the large rotation angle of the moving body in path planning. The evaluation function is shown as:

$$twirling\left(v,\omega \right)=-(1-\mu )(\left|x_a-x_v\right|+\left|y_a-y_v\right|)$$

(11)

where $\mu$ is the dynamic weight in the evaluation function. The final improved DWA evaluation function obtained is shown as:

$$C\left(v,\omega \right)=\lambda \left[\mu ·heading\_new(v,\omega )+\beta ·obdist(v,\omega )+\gamma ·vel(v,\omega )+twirling(v,\omega )\right]$$

(12)

The introduction of a new rotation cost function improves the DWA algorithm curve smoothness in path planning, allowing for better tracking of actual body movements. In the upcoming section, we will examine effective approaches for vertical obstacle avoidance.

3. Algorithm Design for 3D VFH+

3.1. OctoMap Build Map and Search

During a cooperative obstacle avoidance operation, the UAV will obtain point cloud data using its sensors. Nevertheless, since the limitation of UAVs computational power and sensor measurement range, it may not have explored all surrounding spatial points in an obstacle filled environment. To alleviate the resultant computational load, this section adopts the OctoMap data structure to compress point cloud data and build a map.

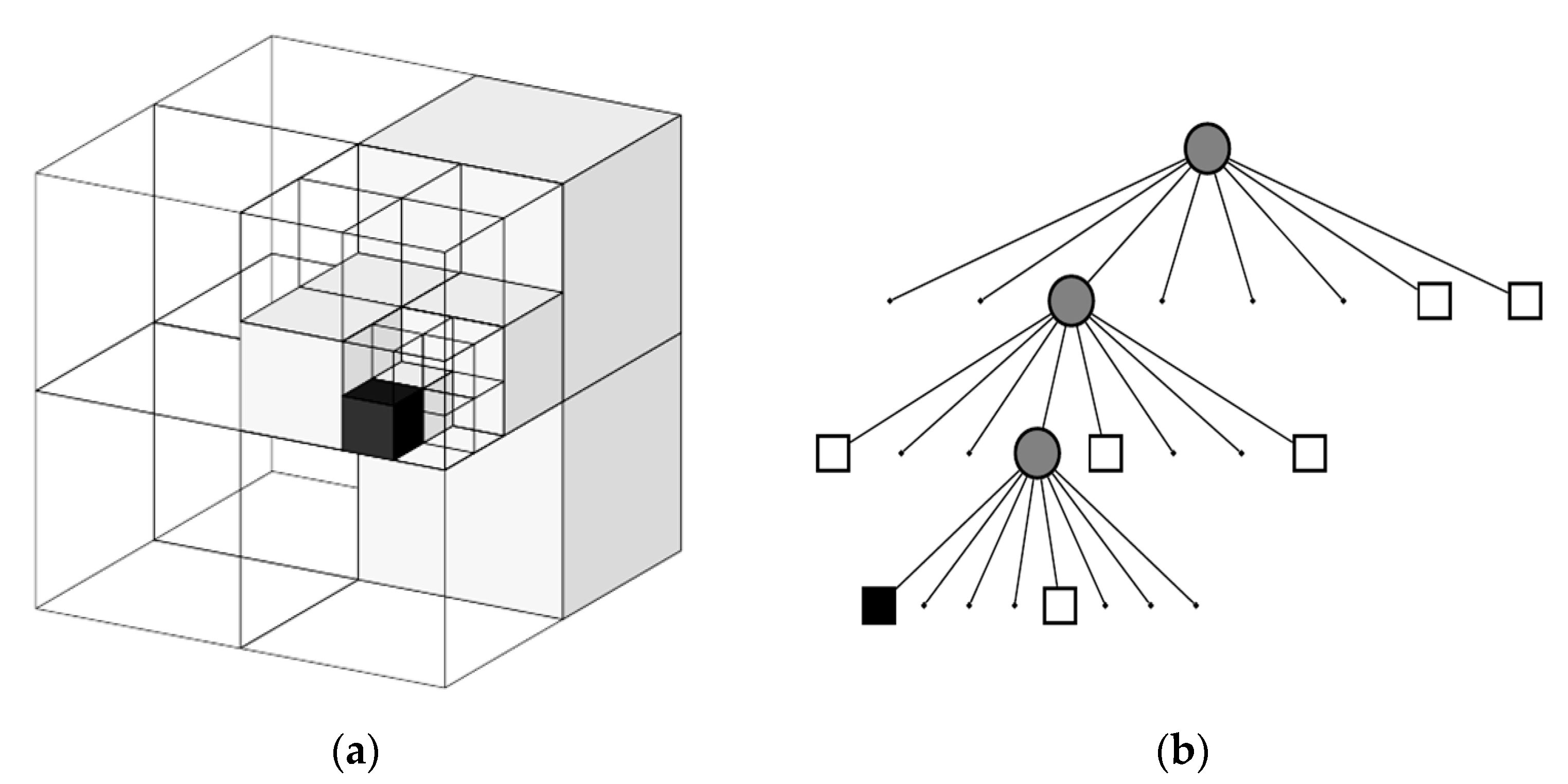
OctoMap is a 3D map generation software based on octree, which can display full 3D images including features that are not mapped or overlaid and can estimate the fusion of sensor data through multiple measurements within the grid. The system is characterized by high resolution, compressed data, and small storage space. The octree structure is a spatial partitioning method which has been explored in various operations since the 1980s. It divides the three-dimensional space into eight quadrants wherein each quadrant represents a node in the octree. The octree starts from the root node and when this node is located in an empty three-dimensional space, it is referred to as an empty node. When located in the same dimension, it is known as a black node. Otherwise, it is called a gray node. It is divided into 2 × 2 × 2 sub-nodes based on the orientation of each coordinate axis. This process continues recursively until a node is either empty, or the stereoscopic space in which it is located is homogeneous or reaches a predetermined minimum scale. Figure 3 shows examples of a simple object represented in an octree, illustrating the octree in terms of a three-dimensional raster structure and a tree structure.

In general, the value 0 is used to indicate non-occupation, 1 indicates occupation, and the floating-point number between 0 and 1 indicates the probability of occupation at that specific time. A higher floating-point number indicates a higher probability of the node being occupied by an obstacle. Because the spatial structure description is transformed into octree representation, it can be pruned quickly for three special states: 0, 0.5, and 1 node, thus achieving the purpose of saving space.

3.2. Construction of Two-Dimensional Principal Pole Histogram

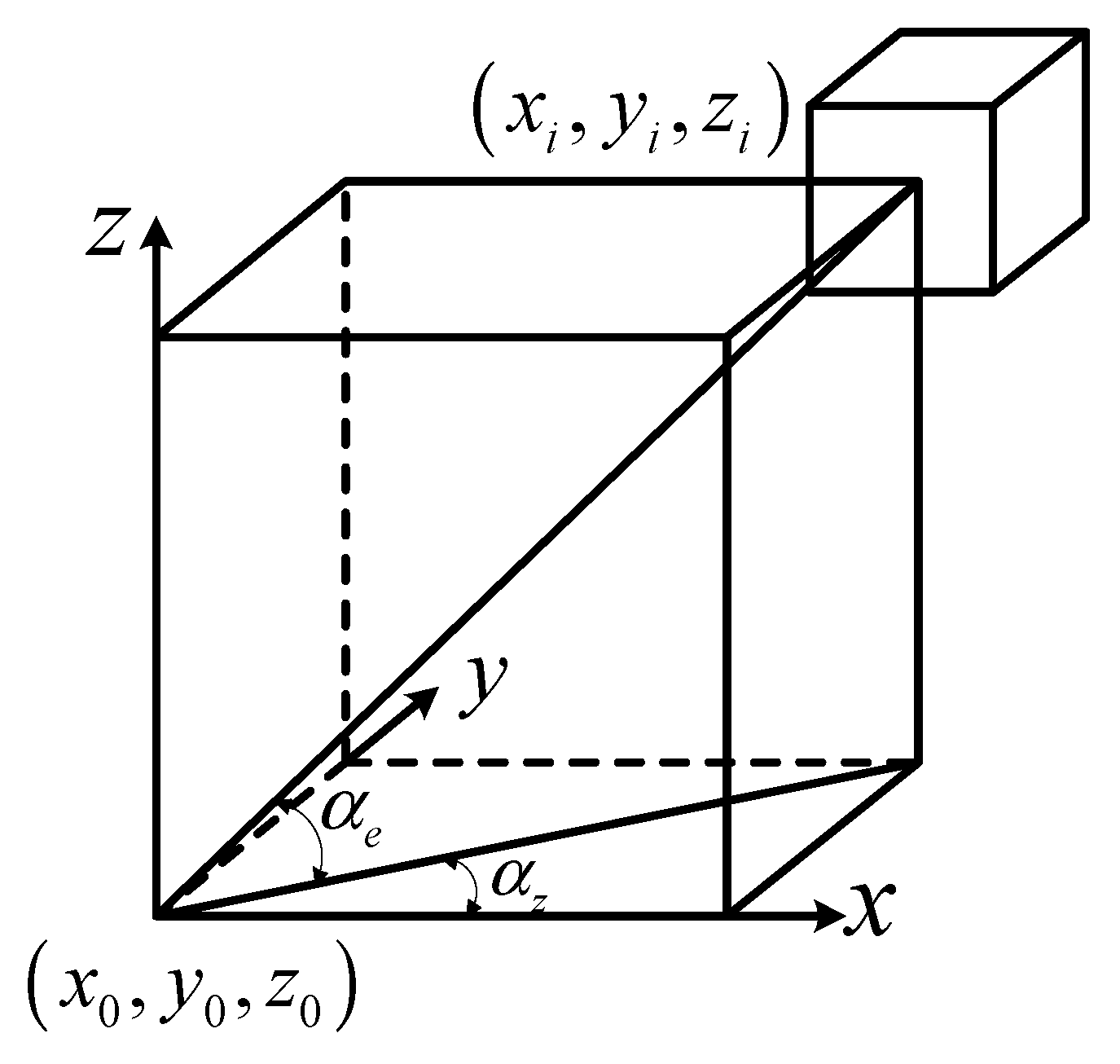
The OctoMap introduced in the previous section can divide the environmental space into cubes, and this section will calculate the respective weights for each cube to construct a two-dimensional main polar histogram. The UAV’s current location is the center and $d_{i,j,k}$ is the radius to build a UAV’s exploration range. Only some of the cubes on the surface of the sphere are involved in the construction of the 2D main polar histogram. When the UAV is the center, the coordinates of each cube on the surface of the sphere constructed by the UAV can be determined by two angles. The coordinates of the center of a cube $i$ on the surface of the sphere is $\left(x_i,y_i,z_i\right)$, the angle between the projection of the cube and the center of the UAV in the $xoy$ plane and the $x$ axis is ${\alpha }_z$, which is the azimuth angle. The angle between the cube and the center of the UAV and its projection in the $xoy$ plane is ${\alpha }_e$, which is the pitch angle. The horizontal coordinates ${\beta }_z$ and vertical coordinates ${\beta }_e$ of the two-dimensional main polar histogram can be obtained by making certain factor transformations, as Figure 4, Figure 5 and Figure 6 show.

According to Figure 6, the equations for calculating the azimuth and the x-axis coordinates of the two-dimensional main polar histogram are as follows:

$${\alpha }_z=⌊\arctan \frac{x_i-x_0}{y_i-y_0}⌋$$

(13)

$${\beta }_z=\frac{1}{\alpha }{\alpha }_z$$

(14)

The equations for calculating the pitch azimuth and the y-axis coordinates of the two-dimensional main polar histogram are as follows:

$${\alpha }_e=⌊\arctan \frac{z_i-z_0}{\sqrt{{\left(x_i-x_0\right)}^2+{\left(y_i-y_0\right)}^2}}⌋$$

(15)

$${\beta }_e=\frac{1}{\alpha }{\alpha }_e$$

(16)

The transformation factor, denoted by 1/α, is used to convert azimuth and pitch angles into the coordinates of the 2D main polar histogram. The size of the UAV is not taken into consideration during the calculation process. The 3DVFH+ algorithm compensates for it by increasing the size of the cube segmented by OctoMap. Additionally, the algorithm determines the maximum and minimum angles of the cube using the calculated compensation factor. 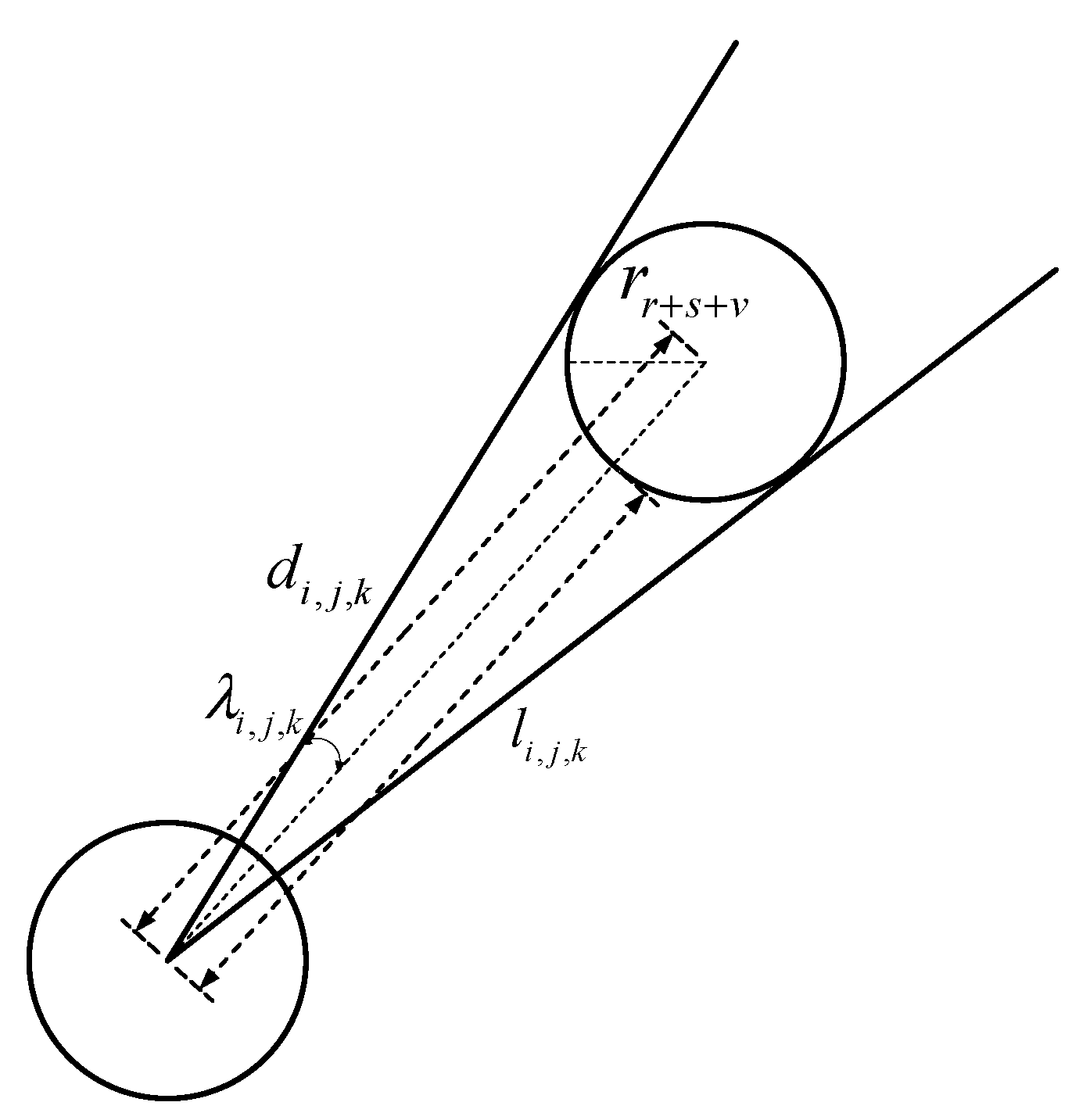The expanded cube size is depicted in Figure 7.

For cube expansion, the main considerations are the drone size $r_r$, the safety radius $r_s$, the cube size $r_v$, and the final expanded radius:

$$r_{r+s+v}=r_r+r_s+r_v$$

(17)

The compensation factor ${\lambda }_{i,j,k}$ is calculated as follows:

$${\lambda }_{i,j,k}=⌊\frac{1}{\alpha }\arcsin \frac{r_{r+s+v}}{d_{i,j,k}}⌋$$

(18)

where $d_{i,j,k}$ is the distance between the center of UAV and the center of cube. From Figure 8 above, we can get:

$$l_{i,j,k}=d_{i,j,k}-r_{r+s+v}$$

(19)

The weight of each cube mapped to the two-dimensional principal pole histogram is calculated as follows:

$$H_{z,e}^p={\displaystyle \sum _{i,j,k\in C_a}\left\{\begin{array}{l}{\left(o_{i,j,k}\right)}^2\left(a-b{l}_{i,j,k}\right)\hspace{1em}e\in \left[{\beta }_e-\frac{\lambda }{\alpha },{\beta }_e+\frac{\lambda }{\alpha }\right]\&\&\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} z\in \left[{\beta }_z-\frac{\lambda }{\alpha },{\beta }_z+\frac{\lambda }{\alpha }\right]\\ 0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} otherwise\end{array}\right.}$$

(20)

where $C_a$ is a collection of spherical surface cubes constructed by UAV exploration space, $a$ and $b$ are constants that satisfy the following relations:

$$a-b{\left(\frac{d_{i,j,k}-1}{2}\right)}^2=1$$

(21)

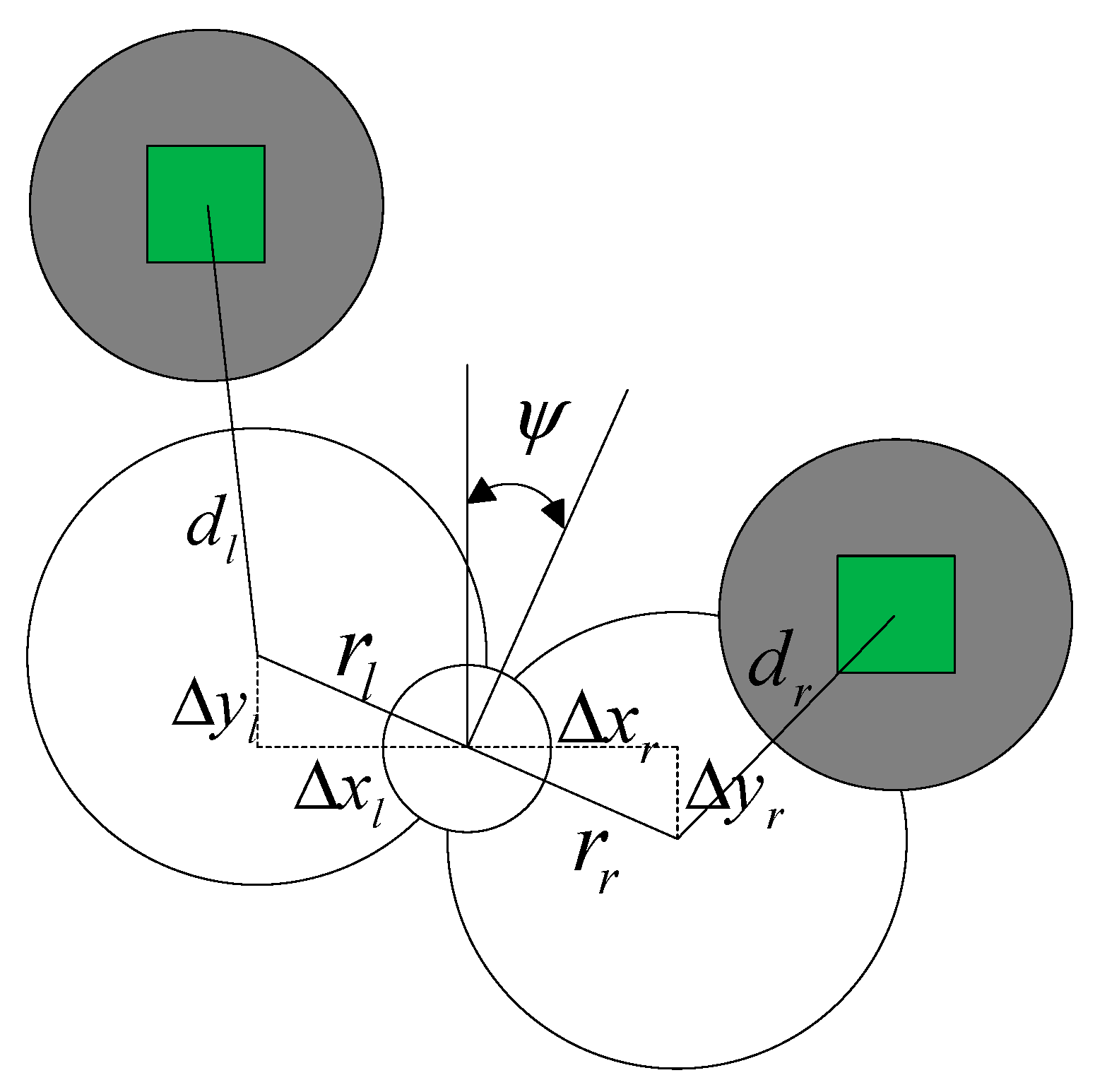
3.3. Kinematic Constraint Design

This section focuses on the kinematic constraints of UAV during obstacle avoidance. The $xoy$ plane turn obstacle avoidance model, which is established in the VFH+ algorithm, is shown in Figure 8.

$$\left\{\begin{array}{l}\Delta x_r=r_r\cos \psi \hspace{1em}\hspace{1em}\hspace{1em}\Delta y_r=r_r\sin \psi \\ \Delta x_l=r_l\cos \psi \hspace{1em}\hspace{1em}\hspace{1em}\Delta y_l=r_l\sin \psi \end{array}\right.$$

(22)

The distance from the center of the drone to the two cubes is as follows:

$$d_r=\sqrt{{\left(\Delta x_r-\Delta x_i\right)}^2+{\left(\Delta y_r-\Delta y_j\right)}^2}$$

(23)

$$d_l=\sqrt{{\left(\Delta x_l-\Delta x_i\right)}^2+{\left(\Delta y_l-\Delta y_j\right)}^2}$$

(24)

when the possible turning circles of the UAV intersect the occupied cube, the left and right limiting angles ${\phi }_l$ and ${\phi }_r$ are obtained, and initialization season ${\phi }_l={\phi }_r=\pi +\psi$:

$$\left\{\begin{array}{l}{d}_r<r_r+r_{r+s+v}\\ d_l<r_l+r_{r+s+v}\end{array}\right.$$

(25)

If the drone meets $\psi <{\alpha }_z<{\phi }_r$ at this time, update ${\phi }_r={\alpha }_z$ if it does. If the drone meets ${\phi }_l<{\alpha }_z<\psi$ at this time, update ${\phi }_l={\alpha }_z$.

Considering the limited climb speed of the quadrotor, a limit is placed on the UAV pitch azimuth. Firstly, the turning distance to the obstacle is calculated using the arc length formula $dist$, then the altitude difference is divided with $dist$ to calculate the altitude direction climbing motion coefficient $f$.

$$\left\{\begin{array}{l}dist=\frac{2\pi r{\alpha }_z}{360}\\ f=\frac{z_i-z_0}{dist}\end{array}\right.$$

(26)

The max azimuth difference is ${\phi }_r-{\phi }_l$ and the maximum turning distance $dis{t}_{\max }$ and the maximum height $z_{az}$ for each cube are as follows:

$$dis{t}_{\max }=\frac{2\pi r\left({\phi }_r-{\phi }_l\right)}{360}$$

(27)

$$z_{\max }=fdis{t}_{\max }$$

(28)

The final formula for calculating the maximum achievable pitch azimuth is as follows:

$${\alpha }_{e,\max }=\frac{1}{\alpha }\arctan \left(\frac{z_{\max }}{\sqrt{r^4-2r^2\cos \left(270-{\alpha }_z\right)}}\right)$$

(29)

3.4. Path Detection and Selection

The weights corresponding to each cube in the environment space were calculated in the previous section, and the two-dimensional principal-pole histogram was constructed, and the azimuth upper and lower limits of $xoy$ plane $\left[{\phi }_l,{\phi }_r\right]$ and the maximum limits of pitch azimuth ${\alpha }_{e,\max }$ in $z$ direction were given considering the kinematic constraints. In this section, we will select the cube cell with the lowest path weight value from the constructed histogram as the moving trajectory in three-dimensional space. We use evaluation functions to determine the current optimal azimuth and pitch azimuth angles.

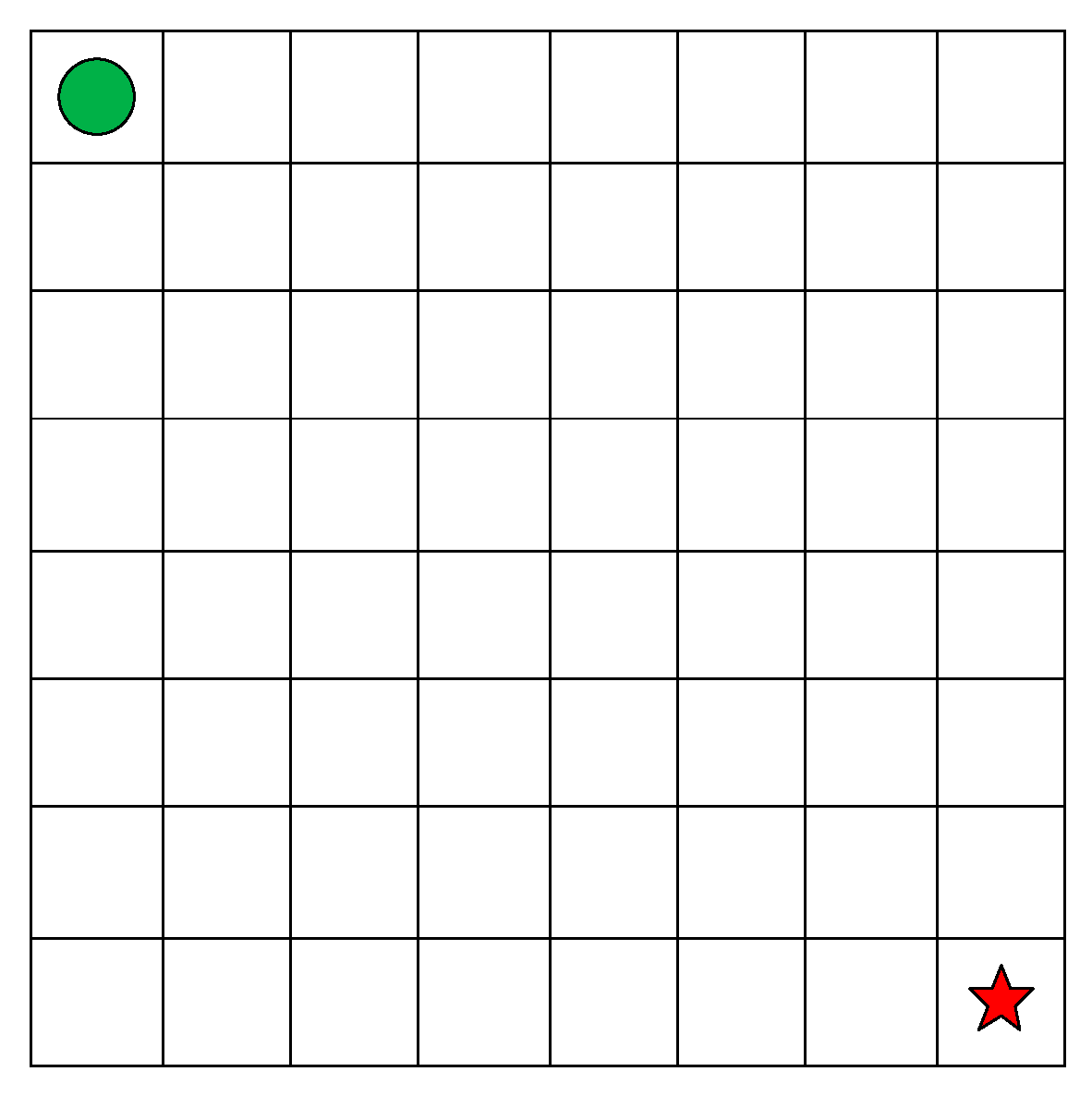
Let us begin our journey starting at the top-left corner and reaching the destination at the bottom-right, as depicted in Figure 9. We are permitted to move in the top, bottom, left, and right directions, excluding top-left, which moves in the opposite direction. As a result, only the bottom-right corner yields two possible moves. For this reason, each element in the first row of the grid can only be accessed by moving right from the top-left element. Similarly, each element in the first column can only be reached by moving down from the top-left element. During this time, the path becomes unique, and hence the minimum path sum corresponding to each element is the sum of the numbers on the corresponding path. For elements not present in the first row and first column, an adjacent element above each can be reached by moving down by one step, while an adjacent element left of it can be reached by moving right by one step. The minimum path sum corresponding to the element is equal to either the minimum path sum corresponding to the adjacent element above it or the element left of it plus the value of the current element, whichever yields the smallest value. Since each minimum path sum is related to its adjacent elements, dynamic programming can be employed to solve this problem using the subsequent recursive equation:

$$dp\left[i\right]\left[j\right]=\min \left(dp\left[i-1\right]\left[j\right],dp\left[i\right]\left[j-1\right]\right)+grid\left[i\right]\left[j\right]$$

(30)

where $dp\left[i\right]\left[j\right]$ denotes the minimum path sum from the upper left corner to the position of $\left(i,j\right)$. The transition from the previous historical state to the current state exists only in two cases $dp\left[i-1\right]\left[j\right]$ and $dp\left[i\right]\left[j-1\right]$, and the minimum is taken plus the current grid weight. The azimuth and pitch azimuth in each grid are selected by the following cost function for the smaller surrogate value.

$$k_i={\mu }_1\Delta \left(v_z,k_t\right)+{\mu }_2\Delta \left(v_e,\psi \right)+{\mu }_3\Delta \left(v_{z,e},k_{i-1}\right)$$

(31)

The first coefficient is determined based on the difference between the pitch azimuth of the line from the current position to the target point $k_t$ and the pitch azimuth of the candidate direction $v_z$. The second coefficient is calculated as the difference between the yaw angle of the UAV $\psi$ and the azimuth of the candidate direction $v_e$. Finally, the third coefficient represents the difference between the direction selected in the last historical moment and the currently considered candidate direction v. These three coefficients can be employed to adjust the direction of inclined climbing or horizontal turning motion as selected.

4. Cooperative Obstacle Avoidance by Fusing Improved DWA and 3D VFH+

The dynamic window method is applicable to two-dimensional space avoidance, which can obtain the current optimal velocity $v_{x,y}$ and yaw angle ${\psi }_1$. The 3D VFH+ algorithm can obtain the current optimal azimuth ${\alpha }_z$ and pitch azimuth ${\alpha }_e$ by constructing histogram and cost function. The algorithm can provide pitch azimuth $z$, thus the two-dimensional DWA algorithm can be extended to three-dimensional space avoidance. The design idea of the hybrid algorithm is to take the average of the optimal yaw angle ${\psi }_c$ of the current UAV, and calculate the directional velocity $z$ based on the pitch angle ${\alpha }_e$ and the forward velocity $v_{x,y}$ of the current UAV. The details are as follows:

$$\left\{\begin{array}{l}{v}_x=v_{x,y}\cos {\psi }_c,v_y=v_{x,y}\sin {\psi }_c,v_z=v_{x,y}\tan {\alpha }_e\\ {\psi }_c=\frac{{\psi }_1+{\alpha }_z}{2},{\phi }_l\le {\alpha }_z\le {\phi }_r,-{\alpha }_{e,\max }\le {\alpha }_e\le {\alpha }_{e,\max }\end{array}\right.$$

(32)

The design flow chart of the fusion algorithm is shown in Figure 10 below:

5. Simulation and Analysis of Cooperative Formation Obstacle Avoidance

5.1. Static Obstacle Avoidance

This section presents the simulation and validation results of the proposed improved dynamic window method for cooperative obstacle avoidance in formation flight using UAVs. The initial parameters of the simulation are shown in

Table 1. Initialization of system parameters.

Serial Number	Parameters Name	Parameter Value
1	UAV1 starting position	(−5 m, 0 m, 1 m)
2	UAV2 starting position	(−10 m, 0 m, 1m)
3	UAV3 starting position	(0 m, −5 m,1 m)
4	UAV4 starting position	(0 m, −10 m,1 m)
5	UAV5 starting position	(0 m, 0 m, 1 m)
6	Obstacle 1 starting position	(18 m, 23 m, 24 m)
7	Obstacle 2 starting position	(9 m, 19 m, 20 m)
8	Obstacle 3 starting position	(15 m, 15 m, 15 m)
9	Obstacle 4 starting position	(19 m, 14 m, 20 m)
10	Obstacle 5 starting position	(23 m, 13 m, 24 m)
11	Number of UAVs N	5
12	Number of Obstacles N	5
13	Obstacle radius	1.5 m

below:

The conventional DWA combined with artificial potential field method for 3D cooperative obstacle avoidance is compared with the fused DWA and 3DVFH+ cooperative obstacle avoidance algorithm proposed in this chapter, and the simulation results are as follows:

According to the trajectory shown in Figure 11 and Figure 12, it can be seen that when no obstacles are encountered, the formation is maintained in a “right-angle” shape. After encountering obstacles, each unit in the formation can smoothly avoid them by working together with the obstacle avoidance algorithm. At this time, the original formation shape is temporarily abandoned, and the obstacle avoidance algorithm accounts for a large proportion in the output. Figure 13 shows that the improved DWA algorithm is smoother in speed, with less speed oscillation, and more suitable for actual formation flight.

5.2. Dynamic Obstacle Avoidance

This section of the simulation sets the same conditions as those in Section 5.1, except that some obstacles are added to the motion conditions. Dynamic obstacles are set to green ball, red ball, black ball; where the green ball is along $x$ axis direction in the range of 16–23 m with 1 m/s speed back and forth, the red ball along $z$ axis direction in the range of 15–25 m with 0.6 m/s speed up and down, the black ball along $x,y,z$ three axis direction in the range of 12–18 m with 1.5 m/s speed back and forth, blue ball, purple ball for static obstacles, the final target point to (30,30,30). The UAV detects the obstacle radius of 1.5 m. The simulation results are as follows.

Figure 14 illustrates a 3D spatial trajectory diagram indicating smooth obstacle avoidance by the five UAVs. In the absence of obstacles, the UAVs moved in a “right-angle” formation.

From Figure 15, it can be observed that in the absence of obstacles, the speed of the UAVs in the x, y, and z directions are maintained at 1.3 m/s. After detecting obstacles and with the improved DWA algorithm in effect, resampling in three-dimensional velocity space shows an increase of varying degrees in the positive speed directions of the UAVs x, y, and z axes in order to avoid the obstacles. The combined speed direction drives the UAVs to move away from the direction of the obstacles. Once the obstacles are passed, the output control of cooperative obstacle avoidance accounted for 0 percent, and after each UAV returns to its desired position, the whole formation will converge to the same speed.

Figure 16 displays the shortest distance between each UAV and five moving obstacles: UAV 1 was 1.93 m, UAV 2 was 1.89 m, UAV 3 was 1.8 m, UAV 4 was 1.72 m, and UAV 5 was 1.7 m. These results demonstrate that no collisions occurred between the UAVs and obstacles, indicating the successful achievement of the cooperative obstacle avoidance formation.

5.3. Semi-Physical Simulation

In this section, the fusion algorithm proposed in this paper is verified by semi-physical dynamic obstacle avoidance on AirSim physical engine simulation platform. The initial parameters of the simulation are shown in

Table 2. Initialization of system parameters.

Serial Number	Parameters Name	Parameter Value
1	UAV1 starting position	(3 m, 3 m, 15 m)
2	UAV2 starting position	(6 m, 6 m, 15 m)
3	UAV3 starting position	(6 m, −6 m, 15 m)
4	UAV4 starting position	(3 m, −3 m, 15 m)
5	UAV5 starting position	(−3 m, −3 m, 15 m)
6	UAV6 starting position	(−3 m, 3 m, 15 m)
7	UAV7 starting position	(−6 m, 6 m, 15 m)
8	UAV8 starting position	(−6 m, −6 m, 15 m)
9	UAV9 starting position	(0 m, 0 m, 15 m)
10	Formation speed	(2 m/s, 0, 0)
11	Obstacle 1 starting position	(45 m, −77 m, 15 m)
12	Obstacle 1 speed	(0, 3 m/s, 0)
13	Obstacle 2 starting position	(58 m, −26 m, 15 m)
14	Obstacle 2 speed	(−3 m/s, 3 m/s, 0)
15	Obstacle 3 starting position	(187 m, −127 m, 139 m)
16	Obstacle 3 speed	(−4 m/s, 4 m/s, 4 m/s)
17	Obstacle 4 starting position	(187 m, −121 m, 139 m)
18	Obstacle 4 speed	(−4 m/s, 4 m/s, 4 m/s)
19	Obstacle 5 starting position	(184 m, −124 m, 139 m)
20	Obstacle 5 speed	(−4 m/s, 4 m/s, 4 m/s)
21	Number of UAVs N	9
22	Number of Obstacles N	5

below:

The final simulation results are shown in the following Figure 17:

According to the simulation results of dynamic obstacle avoidance, the initial formation is set to “X” shape, and the dynamic obstacles are set to five UAVs that cross the predetermined trajectory of the formation; Obstacle No. 2 will first conflict with the predetermined motion trajectory of UAV No. 2. Therefore, under the influence of this obstacle, UAV No. 2 will have an operation to modify its own motion trajectory to avoid obstacles, as shown in Figure 17b. In the middle of the rightmost green curve, the zigzag part occurs. At this time, UAV No. 2 first flies to the upper right corner of three-dimensional space, and quickly accelerates back to the original formation position in the upper left corner after avoiding obstacles. Then, UAV No. 5 in the formation may collide with the obstacle No. 1. In this simulation, the UAV No. 5 accelerates first and then decelerates under the action of the cooperative obstacle avoidance algorithm, avoiding the obstacles that originally crashed into itself horizontally and returning to the original formation position, as shown in Figure 17c.

The set dynamic obstacles No. 3–5 also conflict with the motion trajectories of No. 1, No. 4, No. 5, and No. 9 UAV in Figure 17c, so the blue trajectory corresponding to No. 1 UAV moves first from the lower right to the upper left, the pink trajectory corresponding to No. 4 UAV moves first from the lower right to the upper left, the gray trajectory corresponding to No. 5 UAV moves first from the lower left to the upper right, and the green trajectory corresponding to No. 9 UAV moves first from the lower left to the upper right. Figure 17d shows the formation maintenance after finally reaching the destination. It can be seen that the formation can still maintain the original formation after being disturbed by dynamic obstacles, but there are also certain position errors. For example, the pink trajectory and gray trajectory corresponding to UAV No. 4 and UAV No. 5 do not coincide at this time, but there is a distance in the axial direction, which indicates that there is position error when the original formation is restored after dynamic obstacle avoidance.

Based on the simulation results of dynamic obstacle avoidance mentioned above, the control output calculated by the cooperative obstacle avoidance algorithm can ensure a good obstacle avoidance trajectory planning in actual four-rotor formation flight, which has practical engineering value.

6. Conclusions and Future Research

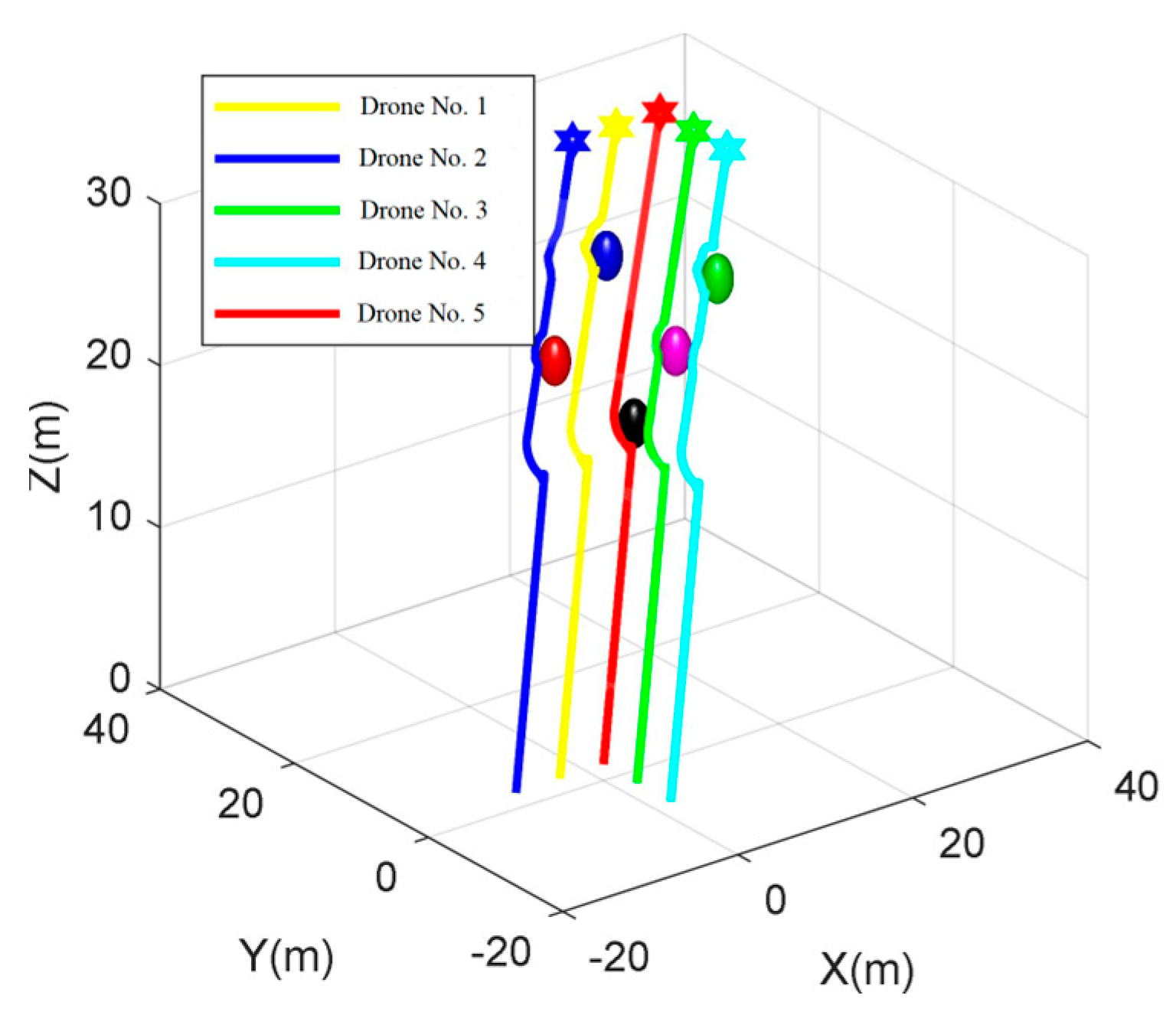
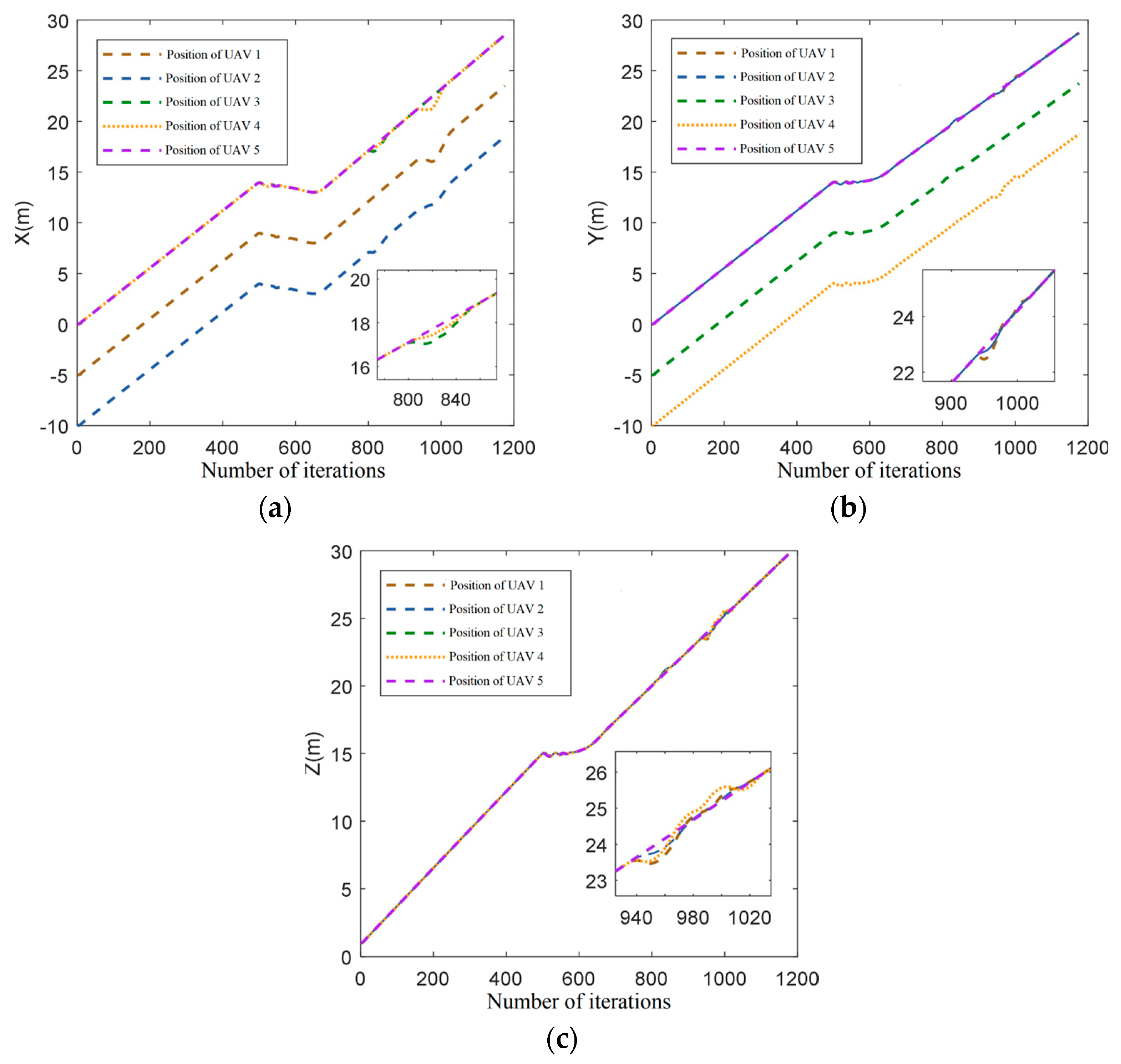
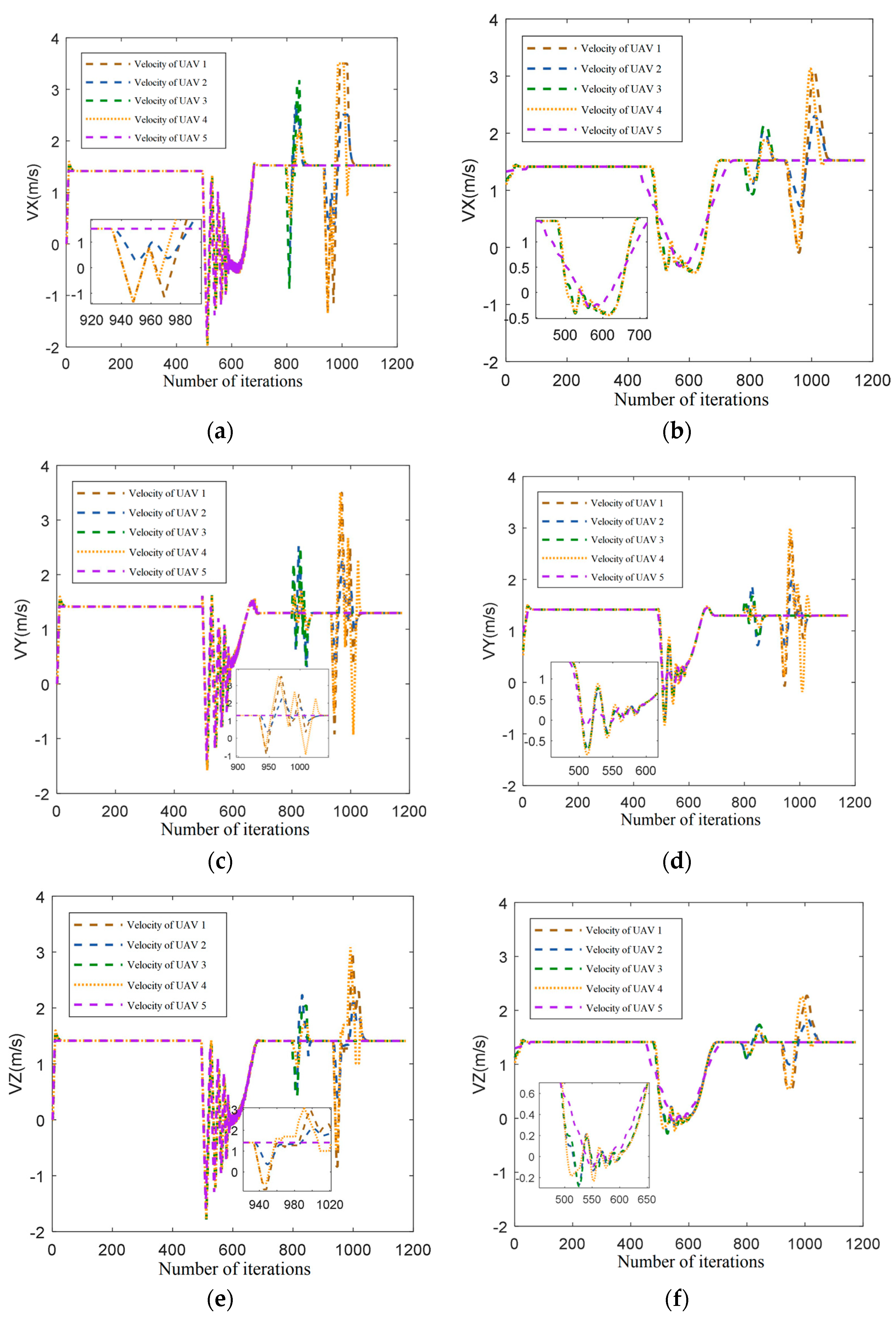
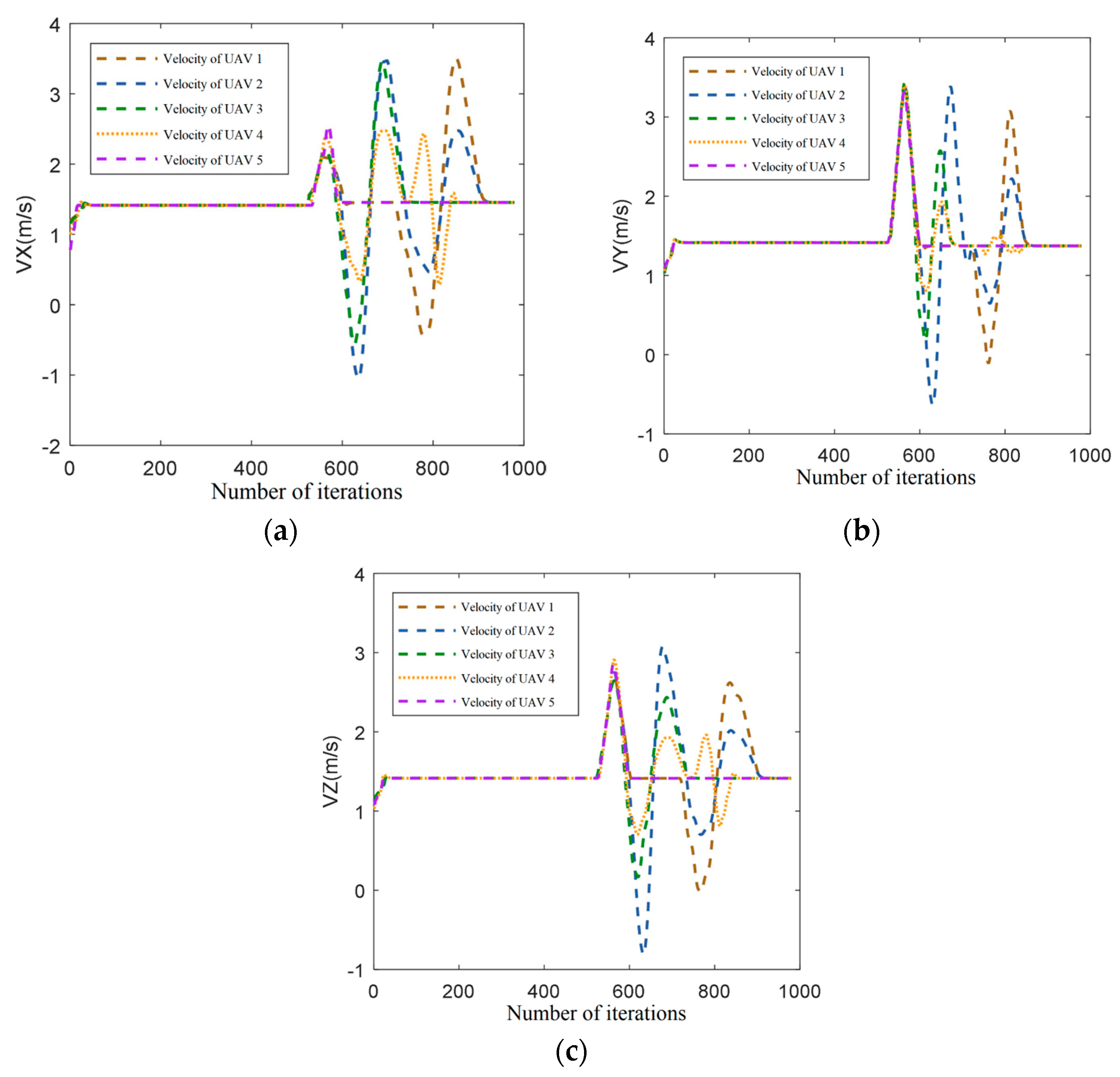
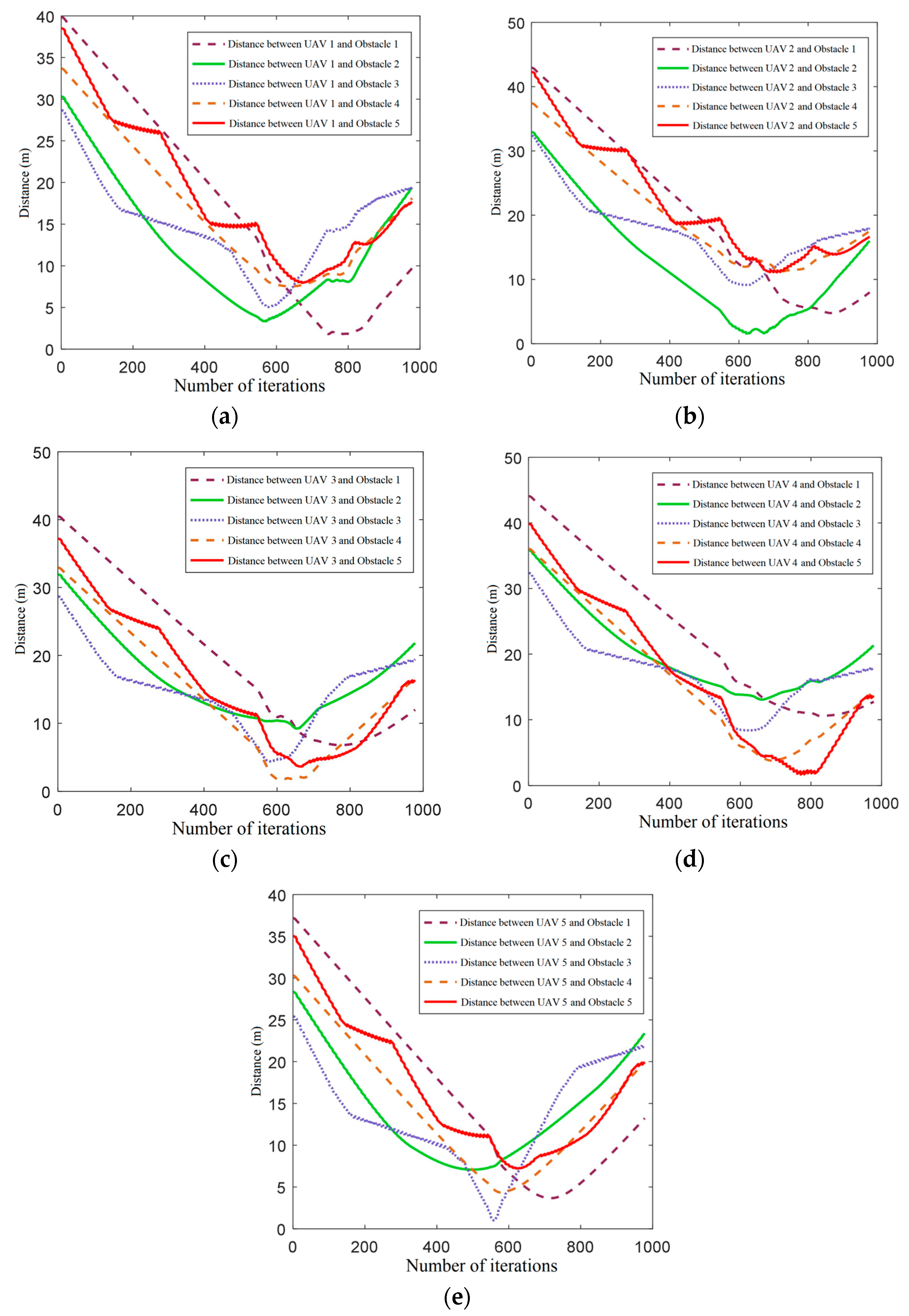
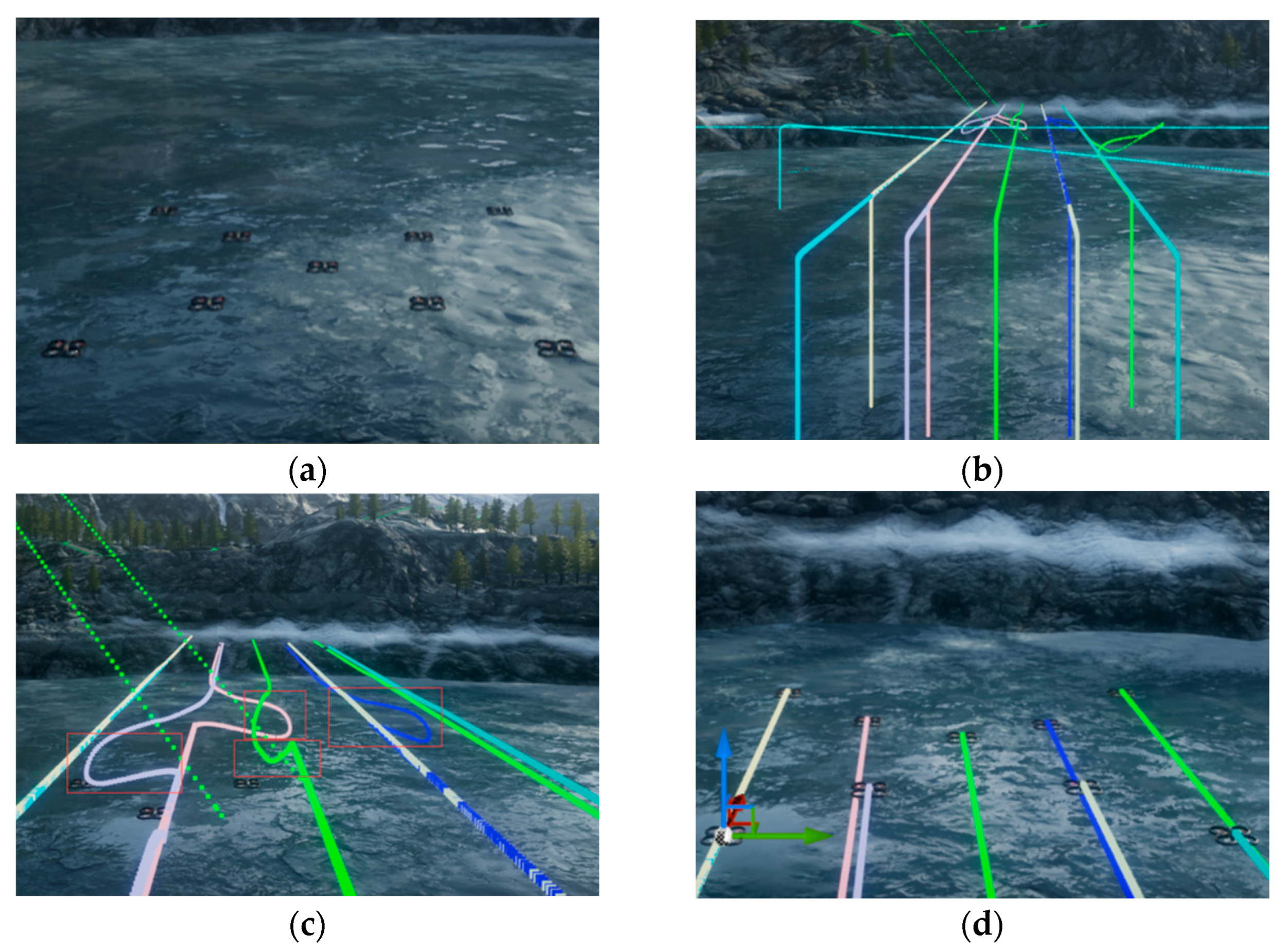
This paper introduces an improved DWA algorithm that optimizes obstacle avoidance for UAVs. Firstly, the azimuth evaluation function in the DWA algorithm is optimized by introducing the target distance. Additionally, the A* algorithm is integrated to replace the fixed weights in the azimuth evaluation function, thereby improving the search efficiency of the DWA algorithm. A rotation cost function is introduced into the evaluation function, which effectively smoothens the path and resolves the two-dimensional plane formation obstacle avoidance problem for UAVs by constraining large-angle rotation frequency. Moreover, the 3DVFH+ algorithm is incorporated to efficiently acquire the pitch azimuth and extend the cooperative obstacle avoidance function for two-dimensional plane formation to three-dimensional space formation. Simulation results demonstrate the effectiveness of this approach in multi-aircraft formation obstacle avoidance path planning.

This paper presents a fusion algorithm for multi-UAV cooperative formation obstacle avoidance path planning. The algorithm’s effectiveness is verified through simulation, yielding favorable results. However, the current research process has certain limitations. Notably, when dealing with dynamic obstacles, the speed of both moving obstacles and the advancing UAV formation is insufficient, necessitating further consideration for obstacle avoidance with medium- and high-speed obstacles. In future research, introducing more improvement strategies can enhance the algorithm’s performance. Additionally, physical simulation in a real environment will be explored to further verify the algorithm’s effectiveness.