Performance Analysis of Multi-Hop Flying Mesh Network Using Directional Antenna Based on β-GPP
Abstract
1. Introduction
- The spatial distribution of the UAVs was modeled as -GPP, and the UAVs were equipped with directional antennas to reduce signal self-interference. The repulsive parameter describes different application environments with tunability. Different values of describe the UAVs’ deployment in different environments, which makes our model more practical;
- We considered the information transmission performance of a certain instantaneous snapshot. By ignoring small-scale fading of interfering links and using random geometry tools, an approximate expression for the coverage probability of multi hop relay systems was obtained, thereby obtaining the traversal capacity. Then, according to the diagonal approximate matrix property of -GPP, we derived the approximate expression of the coverage probability. The above analysis results can better predict the performance of FlyMesh in different environments;
- Based on the theoretical expressions obtained, we analyzed the effects of various parameters on the performance of FlyMesh in different environments. The simulation results verified the correctness of the theoretical expression. We also adjusted the beam width and the number of relay hops N, to achieve the best network performance according to the repulsive parameter .
2. Related Work
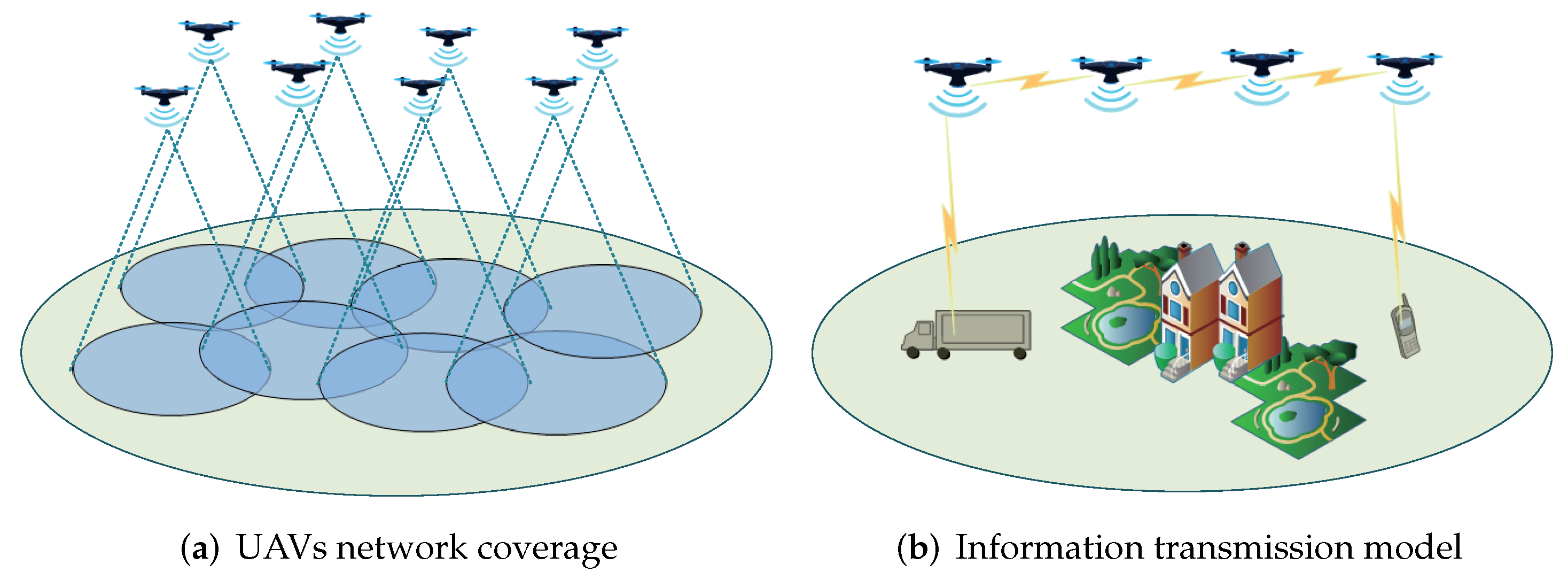
3. Mathematical Preliminaries and System Model
3.1. -GPP Model
- (1)
- K is a symmetric integral operator with upper and lower bounds, whose kernel is defined as ;
- (2)
- The spectrum of K belongs to ;
- (3)
- K is a local mapping of tracking classes.
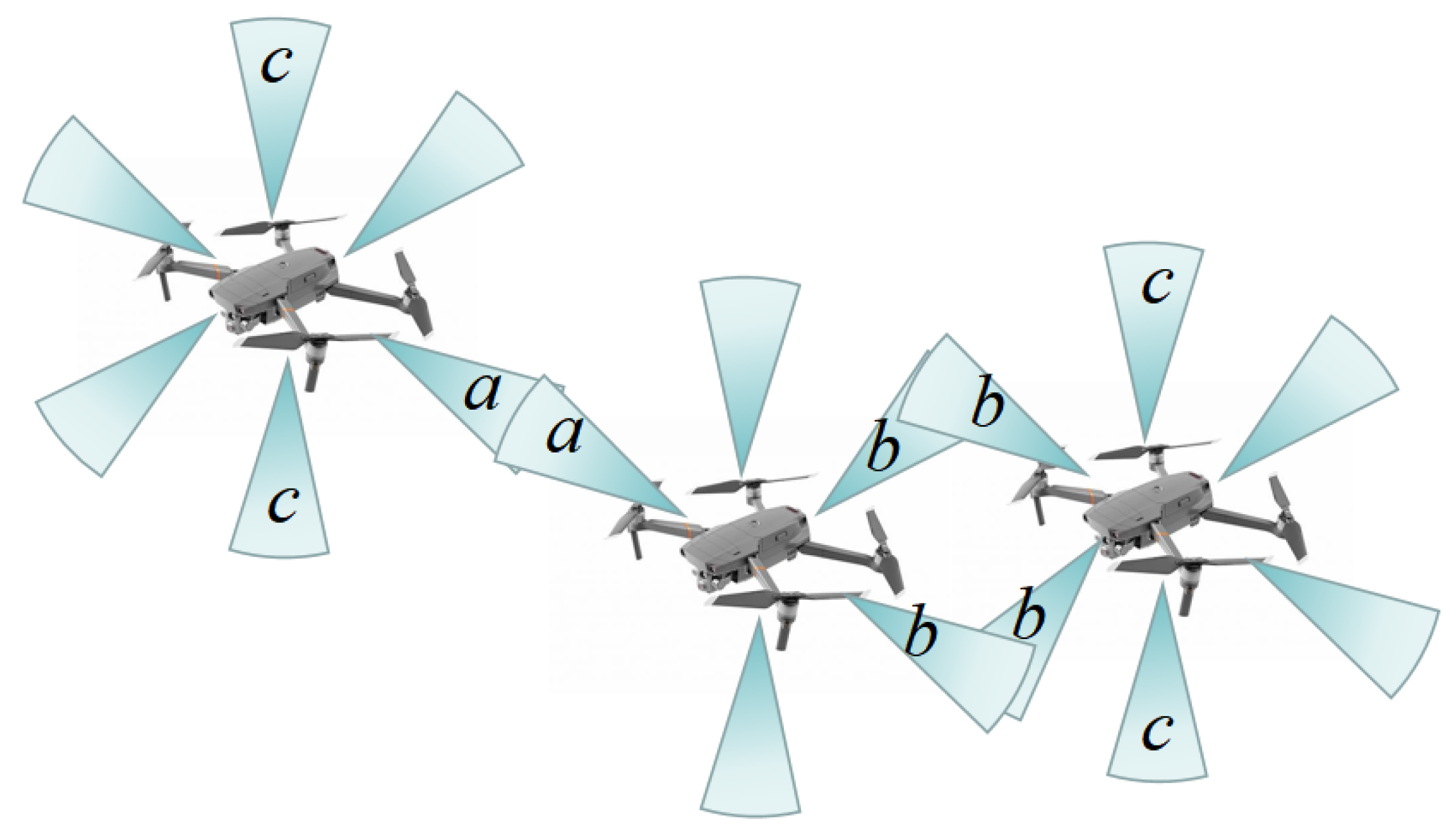
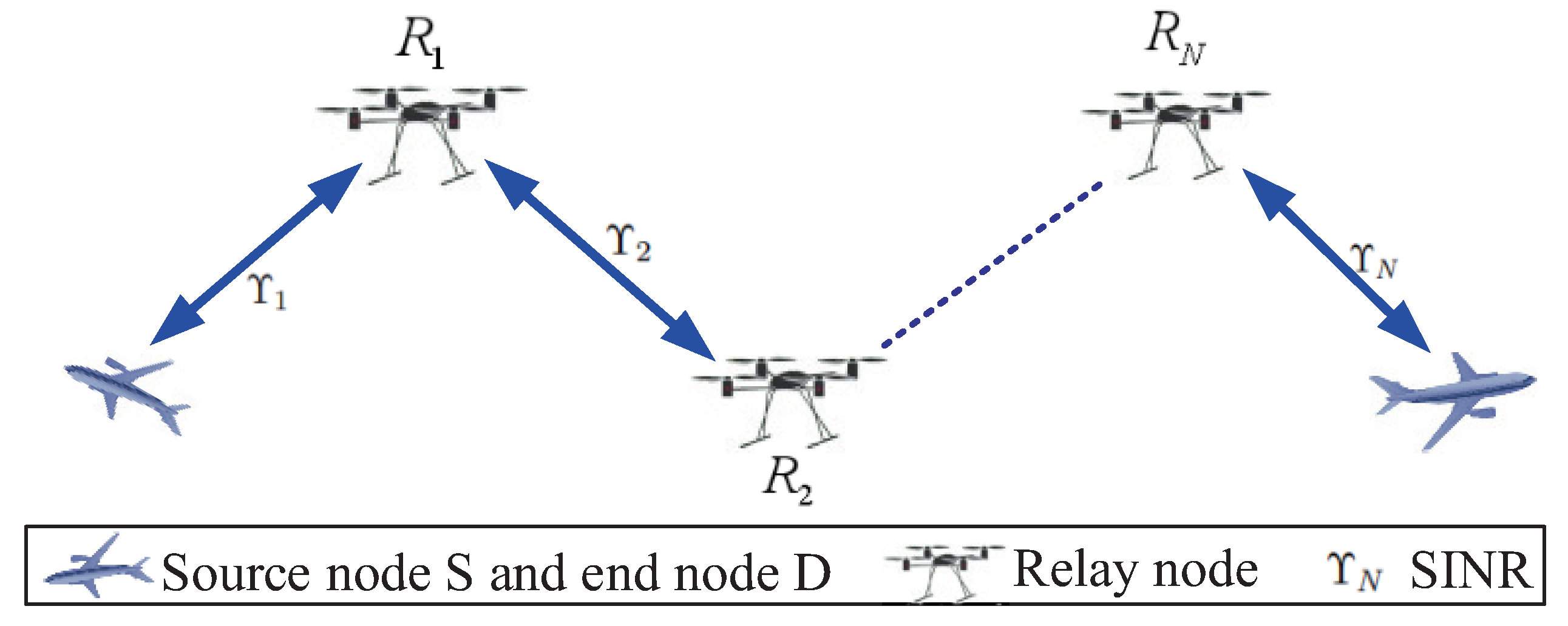
3.2. FlyMesh System Model
4. Performance Probability Analysis
4.1. Connection Probability
4.2. Ergodic Capacity
4.3. Coverage Probability
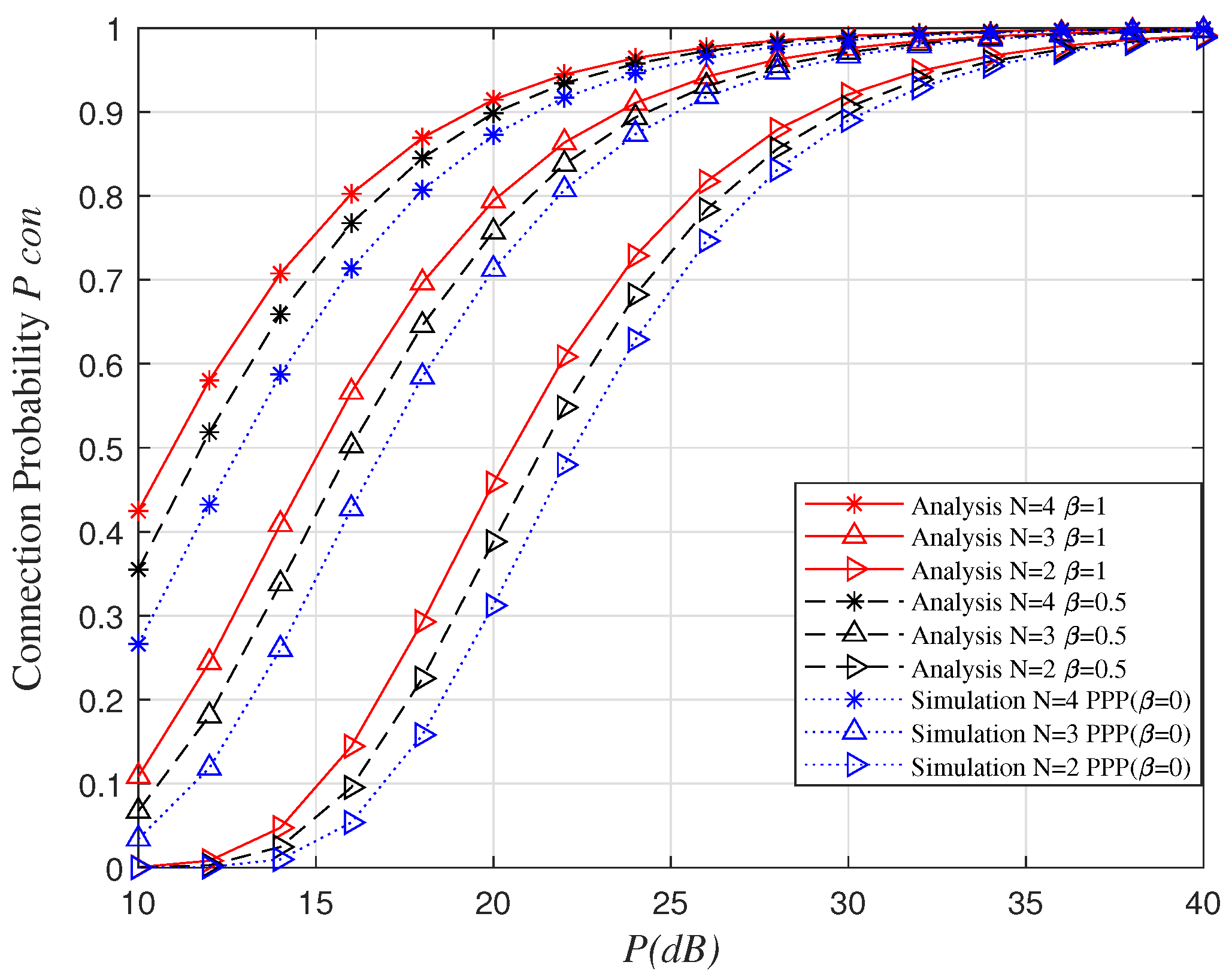
5. Numerical Results
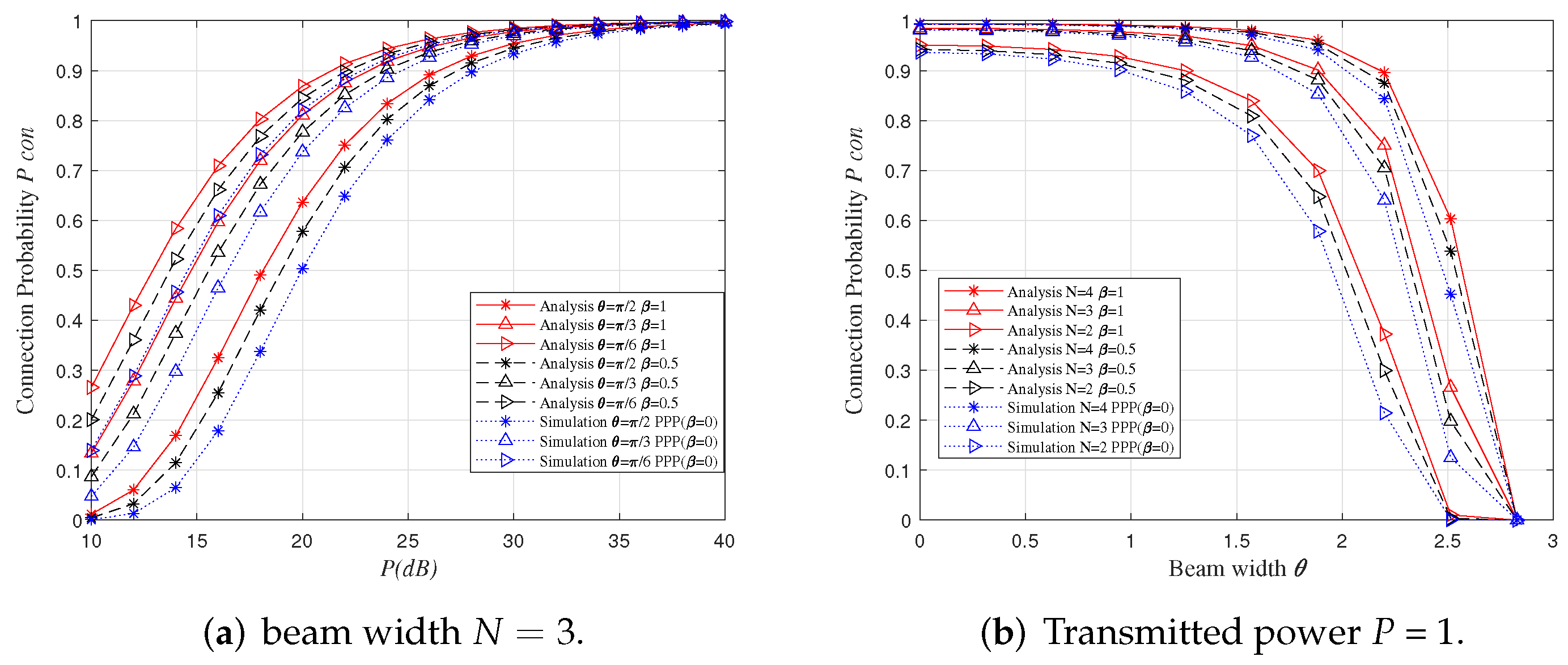
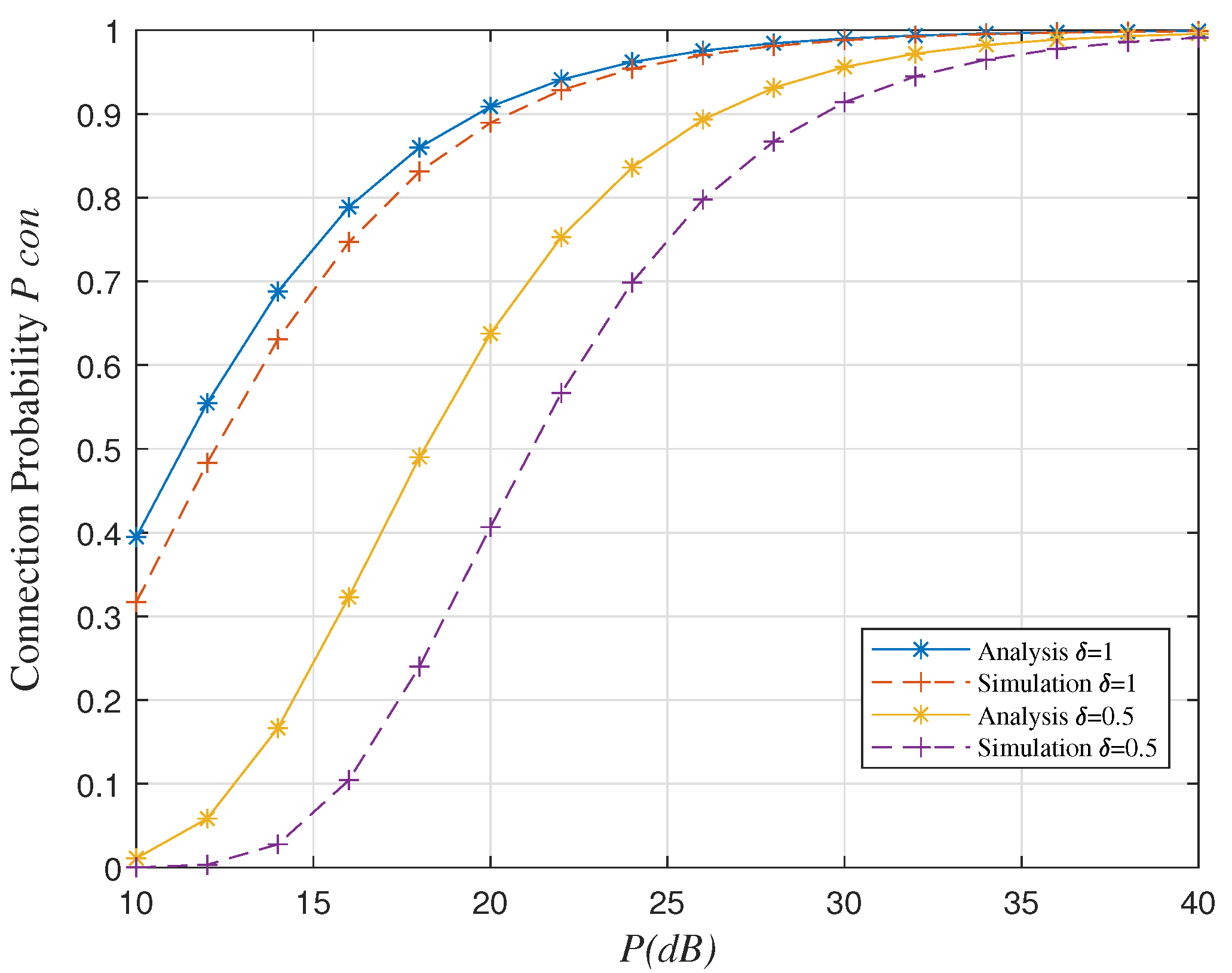
5.1. Connection Probability Verification
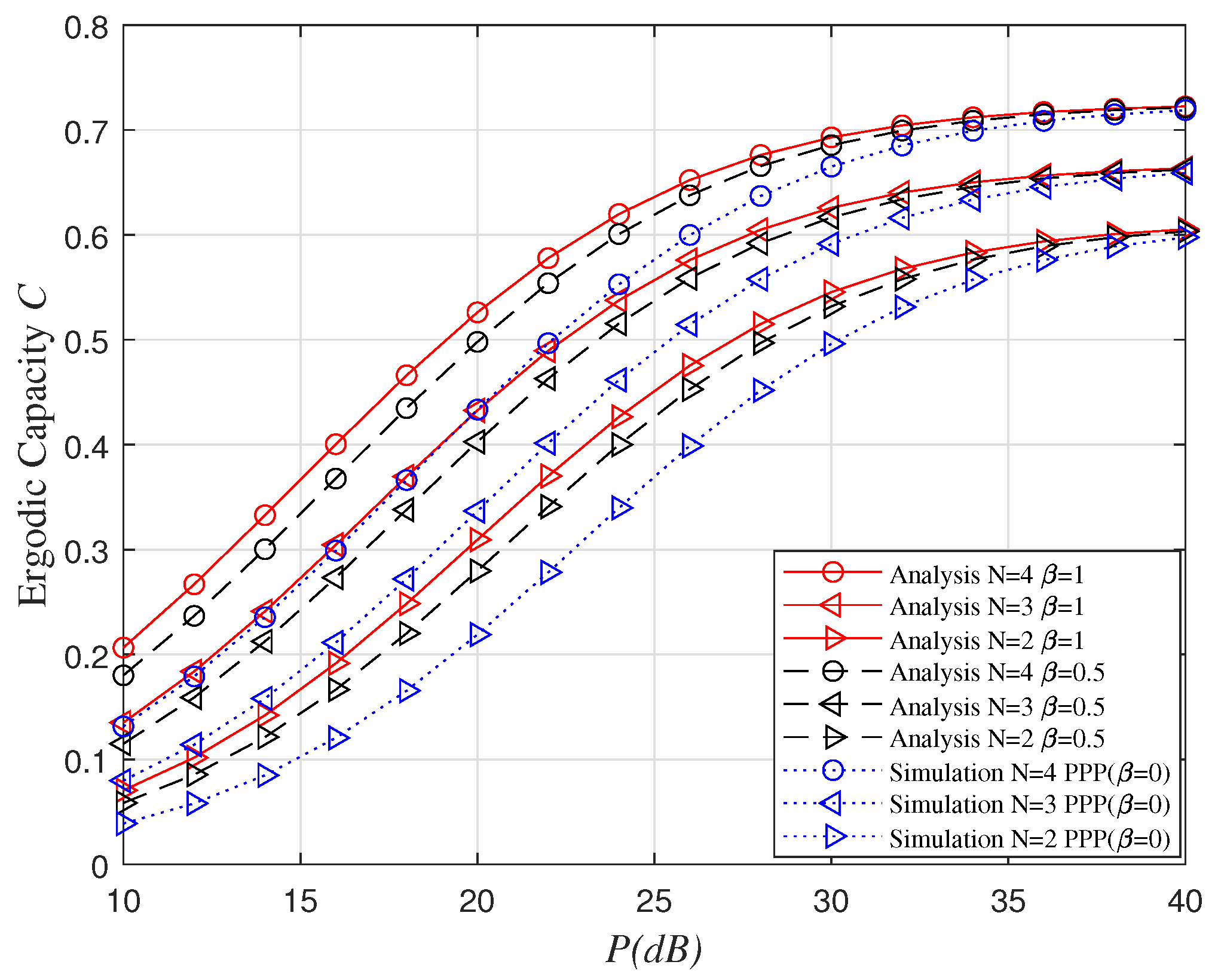
5.2. Ergodic Capacity Verification
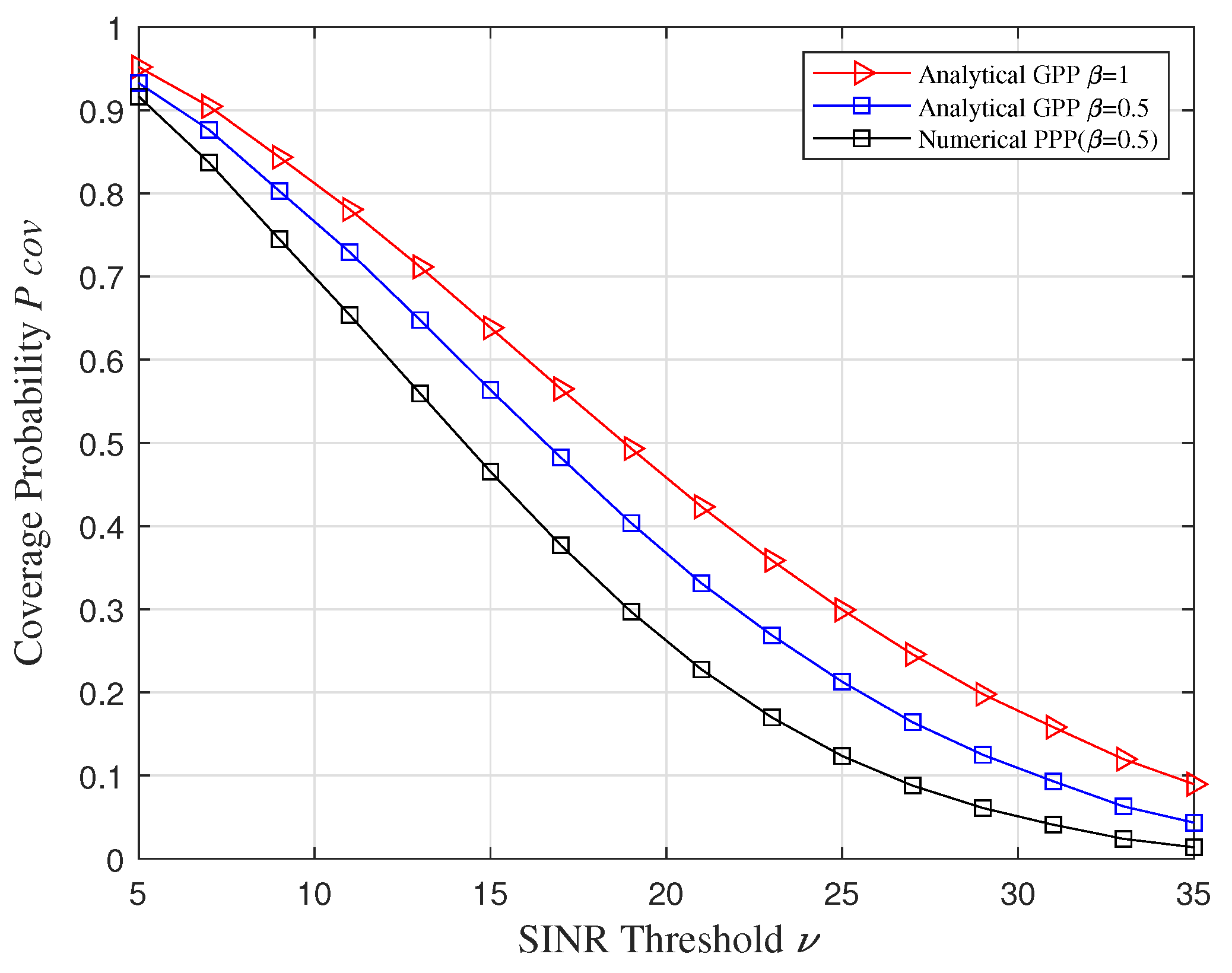
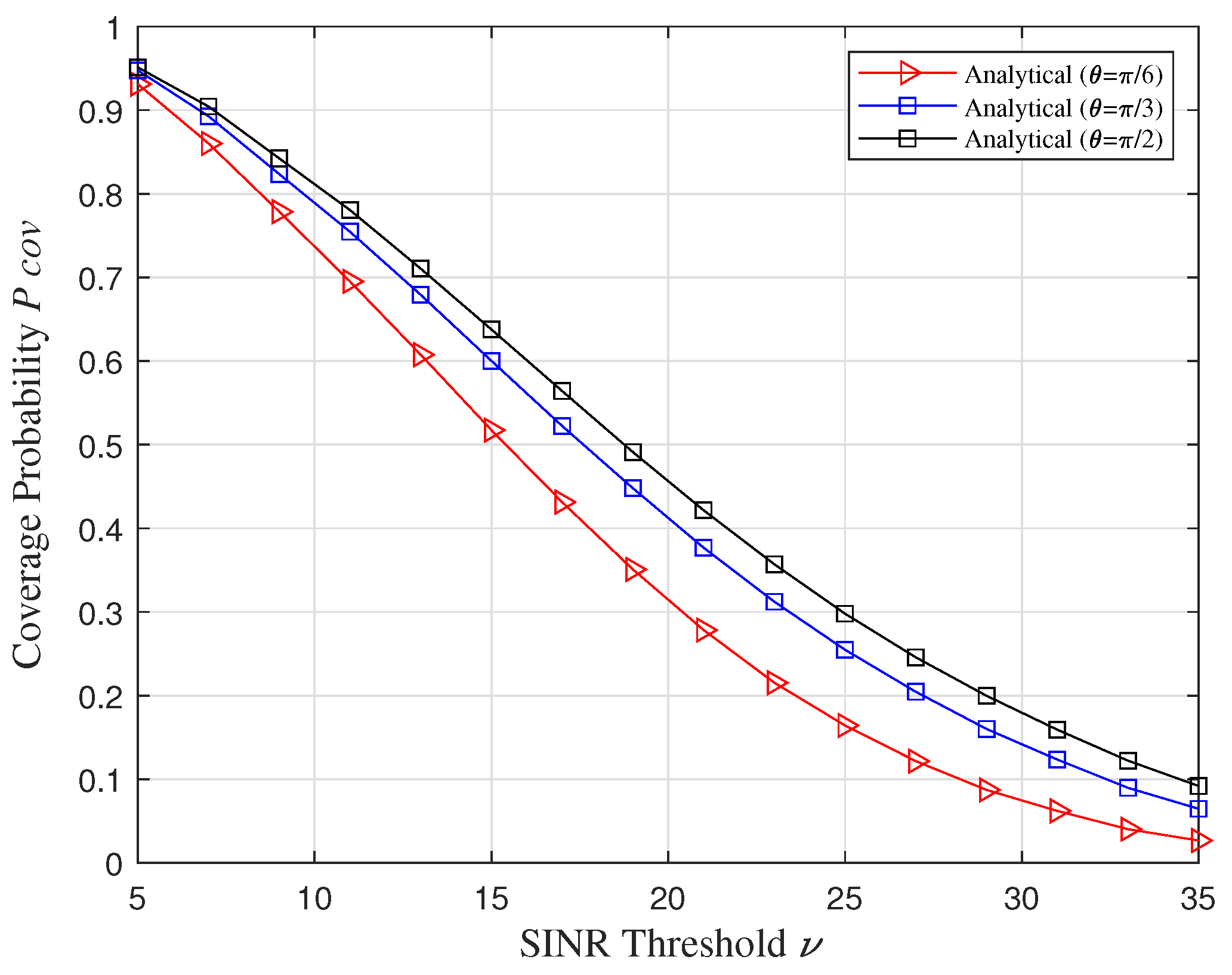
5.3. Coverage Probability Verification
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAVs | Unmanned aerial vehicles |
| IoT | Internet of Things |
| FlyMesh | flying mesh network |
| -GPP | -Ginibre point process |
| PPP | Poisson point process |
| IPPP | inhomogeneous Poisson point process |
| DPP | deterministic point process |
| FBS | flying base station |
| FMT | flying mobile terminal |
| GMT | ground mobile terminal |
| DF | decode-and-forward |
| SINR | signal-to-interference-plus-noise ratio |
References
- Huang, H.; Savkin, A.V. Deployment of heterogeneous UAV base stations for optimal quality of coverage. IEEE Internet Things J. 2022, 9, 16429–16437. [Google Scholar] [CrossRef]
- Ding, R.; Chen, J.; Wu, W.; Liu, J.; Gao, F.; Shen, X. Packet routing in dynamic multi-hop UAV relay network: A multi-agent learning approach. IEEE Trans. Veh. Technol. 2022, 71, 10059–10072. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, N.; Ding, Z.; Alouini, M.-S. Multiple UAVs as Relays: Multi-Hop Single Link Versus Multiple Dual-Hop Links. IEEE Trans. Wirel. Commun. 2018, 17, 6348–6359. [Google Scholar] [CrossRef]
- Izydorczyk, T.; Berardinelli, G.; Mogensen, P.; Ginard, M.M.; Wigard, J.; Kovács, I.Z. Achieving High UAV Uplink Throughput by Using Beamforming on Board. IEEE Access 2020, 8, 82528–82538. [Google Scholar] [CrossRef]
- Bekmezci, I.; Sahingoz, O.K.; Temel, Ş. Flying ad-hoc networks (FANETs): A survey. Ad Hoc Netw. 2013, 11, 1254–1270. [Google Scholar] [CrossRef]
- Haenggi, M. Stochastic Geometry for Wireless Networks; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Lahmeri, M.-A.; Kishk, M.A.; Alouini, M.-S. Laser-Powered UAVs for Wireless Communication Coverage: A Large-Scale Deployment Strategy. IEEE Trans. Wirel. Commun. 2023, 22, 518–533. [Google Scholar] [CrossRef]
- Goldman, A. The Palm measure and the Voronoi tessellation for the Ginibre process. Ann. Appl. Probab. 2010, 20, 90–128. [Google Scholar] [CrossRef]
- Matracia, M.; Kishk, M.A.; Alouini, M.-S. Coverage analysis for UAV-assisted cellular networks in rural areas. IEEE Open J. Veh. Technol. 2021, 2, 194–206. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Unmanned aerial vehicle with underlaid device-to-device communications: Performance and tradeoffs. IEEE Trans. Wirel. Commun. 2016, 15, 3949–3963. [Google Scholar] [CrossRef]
- Choi, C.-S.; Baccelli, F.; Veciana, G.D. Modeling and analysis of data harvesting architecture based on unmanned aerial vehicles. IEEE Trans. Wirel. Commun. 2019, 19, 1825–1838. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhang, Y.; Lim, W.Y.B.; Kang, J.; Niyato, D.; Leung, C.; Miao, C. UAV-assisted wireless energy and data transfer with deep reinforcement learning. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 85–99. [Google Scholar] [CrossRef]
- Ng, J.S.; Ng, W.C.; Lim, W.Y.B.; Xiong, Z.; Niyato, D.; Leung, C.; Miao, C. UAV-assisted Wireless Power Charging for Efficient Hybrid Coded Edge Computing Network. In Proceedings of the ICC 2022-IEEE International Conference on Communications, Seoul, Republic of Korea, 16–20 May 2022; pp. 4037–4042. [Google Scholar]
- Wei, X.; Cai, L.; Wei, N.; Zou, P.; Zhang, J.; Subramaniam, S. Joint UAV Trajectory Planning, DAG Task Scheduling, and Service Function Deployment based on DRL in UAV-empowered Edge Computing. IEEE Internet Things J. 2023. [Google Scholar] [CrossRef]
- Armeniakos, C.K.; Kanatas, A.G. Performance Comparison of Wireless Aerial 3D Cellular Network Models. IEEE Commun. Lett. 2022, 26, 1779–1783. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, C.; Yu, F.; Chen, H. Coverage analysis for UAVassisted mmwave cellular networks using Poisson hole process. IEEE Trans. Veh. Technol. 2022, 71, 3171–3186. [Google Scholar] [CrossRef]
- Lavancier, F.; Møller, J.; Rubak, E. Determinantal point process models and statistical inference. J. Roy. Stat. Soc. B (Stat. Methodol.) 2015, 77, 853–877. [Google Scholar] [CrossRef]
- Kong, H.B.; Flint, I.; Wang, P.; Niyato, D.; Privault, N. Exact performance analysis of ambient RF energy harvesting wireless sensor networks with Ginibre point process. IEEE J. Sel. Areas Commun. 2016, 34, 3769–3784. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, F.; Wang, Z.; Lyu, G. Performance Analysis of Clustered Wireless-Powered Ad Hoc Networks via β-Ginibre Point Processes. IEEE Trans. Wirel. Commun. 2021, 20, 7475–7489. [Google Scholar] [CrossRef]
- Deng, N.; Zhou, W.; Haenggi, M. The Ginibre point process as a model for wireless networks with repulsion. IEEE Trans. Wirel. Commun. 2015, 14, 107–121. [Google Scholar] [CrossRef]
- Kong, H.-B.; Wang, P.; Niyato, D. Performance Analysis of Multihop Relaying Systems in an α-Ginibre Field of Interferers. IEEE Trans. Veh. Technol. 2017, 66, 7573–7577. [Google Scholar] [CrossRef]
- Kong, H.-B.; Wang, P.; Niyato, D. Performance analysis of wireless sensor networks with ginibre point process modeling. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Guo, J.; Walk, P.; Jafarkhani, H. Optimal Deployments of UAVs With Directional Antennas for a Power-Efficient Coverage. IEEE Trans. Commun. 2020, 68, 5159–5174. [Google Scholar] [CrossRef]
- Tyrovolas, D.; Tegos, S.A.; Diamantoulakis, P.D.; Karagiannidis, G.K. Synergetic UAV-RIS Communication With Highly Directional Transmission. IEEE Wirel. Commun. Lett. 2022, 11, 583–587. [Google Scholar] [CrossRef]
- Peng, J.; Tang, W.; Zhang, H. Directional Antennas Modeling and Coverage Analysis of UAV-Assisted Networks. IEEE Wirel. Commun. Lett. 2022, 11, 2175–2179. [Google Scholar] [CrossRef]
- Chen, S.; Sun, S.; Xu, G.; Su, X.; Cai, Y. Beam-Space Multiplexing: Practice, Theory, and Trends, From 4G TD-LTE, 5G, to 6G and Beyond. IEEE Trans. Commun. 2020, 27, 162–172. [Google Scholar]
- Shirai, T.; Takahashi, Y. Random point fields associated with certain Fredholm determinants I: Fermion, poisson and boson point processes. J. Funct. Anal. 2003, 205, 414–463. [Google Scholar] [CrossRef]
- Miyoshi, N.; Shirai, T. A cellular network model with Ginibre configured base stations. Adv. Appl. Probab. 2014, 46, 832–845. [Google Scholar] [CrossRef]
- Georgiou, O.; Wang, S.; Bocus, M.Z.; Dettmann, C.P.; Coon, J.P. Directional antennas improve the link-connectivity of interference limited ad hoc networks. In Proceedings of the 2015 IEEE 26th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Hong Kong, China, 30 August–2 September 2015; pp. 1311–1316. [Google Scholar]
- Huang, C.; Zhang, R.; Cui, S. Throughput Maximization for the Gaussian Relay Channel with Energy Harvesting Constraints. IEEE J. Sel. Areas Commun. 2013, 31, 1469–1479. [Google Scholar] [CrossRef]
- Li, Y.; Baccelli, F.; Dhillon, H.S.; Andrews, J.G. Statistical modelling and probabilistic analysis of cellular networks with determinantal point processes. IEEE Trans. Wirel. Commun. 2015, 63, 3405–3422. [Google Scholar] [CrossRef]
- Ali, A.; Vesilo, R. Interference Modelling in Cellular Networks with beta-Ginibre Point Process Deployed Base Stations. In Proceedings of the 2017 IEEE 85th Vehicular Technology Conference (VTC Spring), Sydney, NSW, Australia, 4–7 June 2017; pp. 1–6. [Google Scholar]


| Definition | Parameters | Values |
|---|---|---|
| End-to-end distance | d | |
| Interference power coefficient | k | |
| Transmission power coefficient | P | |
| Effective signal coefficient | , | 1 |
| Threshold value | Q | 1 |
| Background noise | 1 | |
| Length coefficient | L | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, S.; Peng, L.; Xu, R.; Wei, X.; Wei, X.; Jiang, D. Performance Analysis of Multi-Hop Flying Mesh Network Using Directional Antenna Based on β-GPP. Drones 2023, 7, 335. https://doi.org/10.3390/drones7050335
Qin S, Peng L, Xu R, Wei X, Wei X, Jiang D. Performance Analysis of Multi-Hop Flying Mesh Network Using Directional Antenna Based on β-GPP. Drones. 2023; 7(5):335. https://doi.org/10.3390/drones7050335
Chicago/Turabian StyleQin, Shenghong, Laixian Peng, Renhui Xu, Xianglin Wei, Xingchen Wei, and Dan Jiang. 2023. "Performance Analysis of Multi-Hop Flying Mesh Network Using Directional Antenna Based on β-GPP" Drones 7, no. 5: 335. https://doi.org/10.3390/drones7050335
APA StyleQin, S., Peng, L., Xu, R., Wei, X., Wei, X., & Jiang, D. (2023). Performance Analysis of Multi-Hop Flying Mesh Network Using Directional Antenna Based on β-GPP. Drones, 7(5), 335. https://doi.org/10.3390/drones7050335





