A Deep Learning Approach for Wireless Network Performance Classification Based on UAV Mobility Features
Abstract
1. Introduction
2. Materials and Methods
2.1. Mobility Model
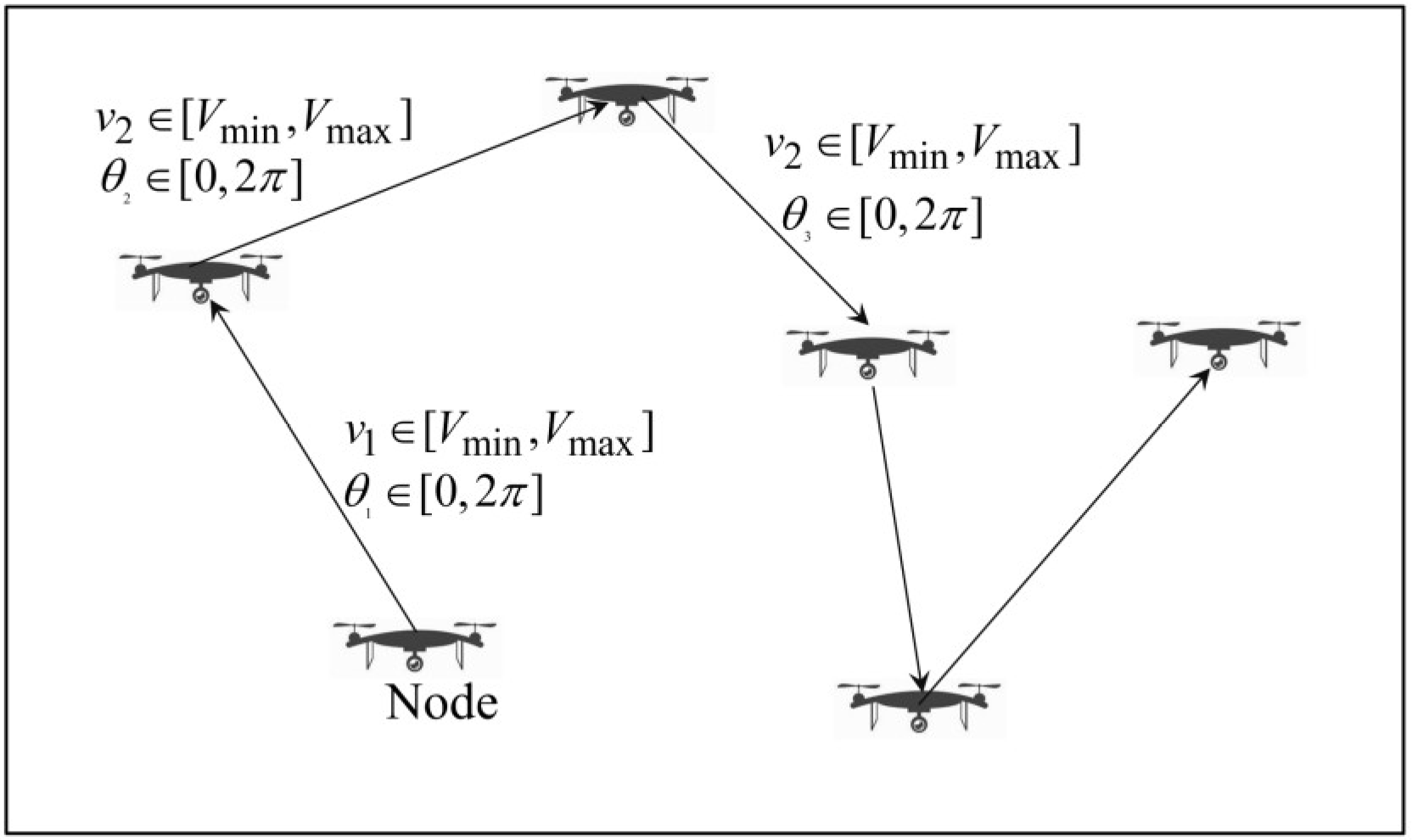
2.1.1. Random Waypoint Mobility Model
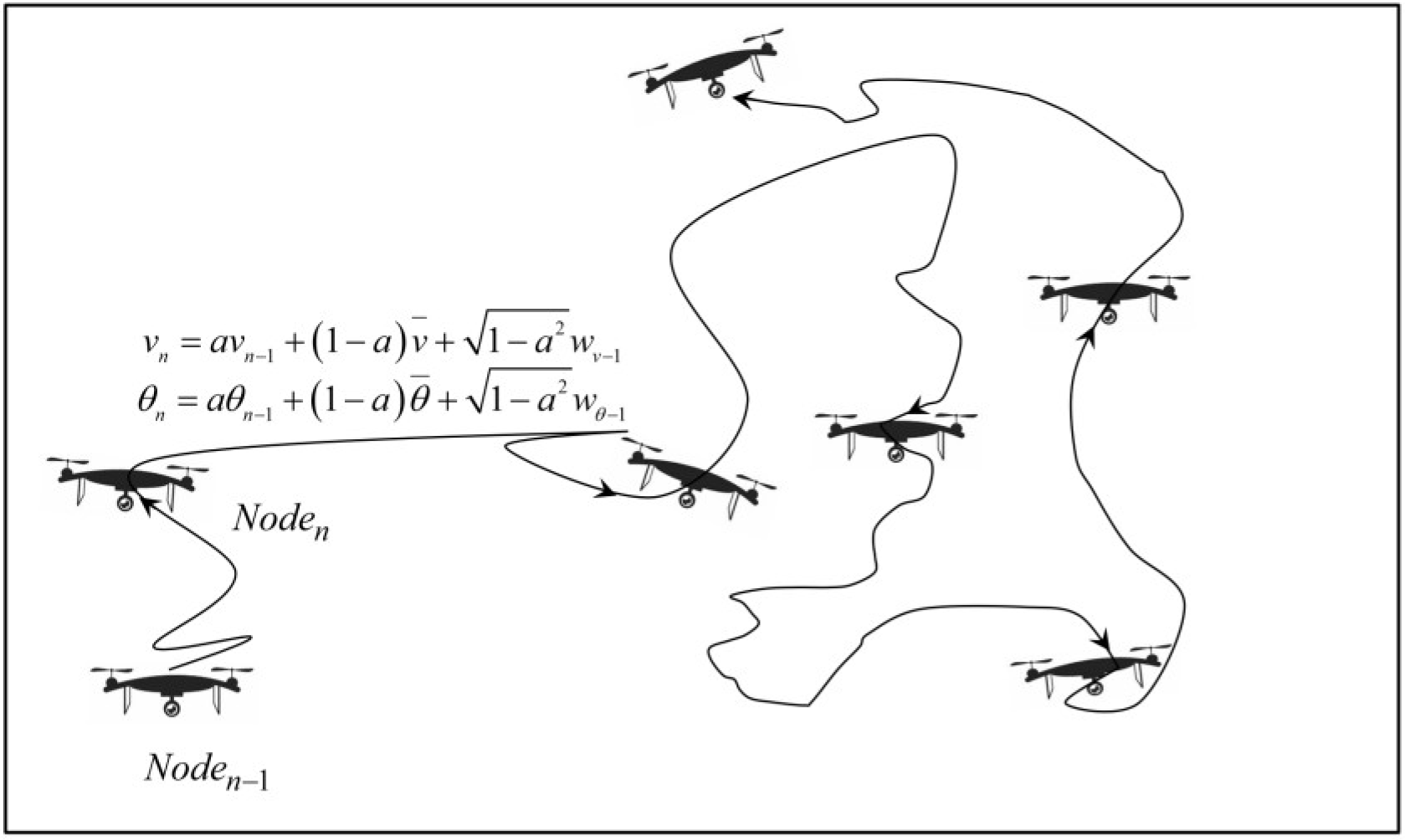
2.1.2. Gaussian–Markov Mobility Model
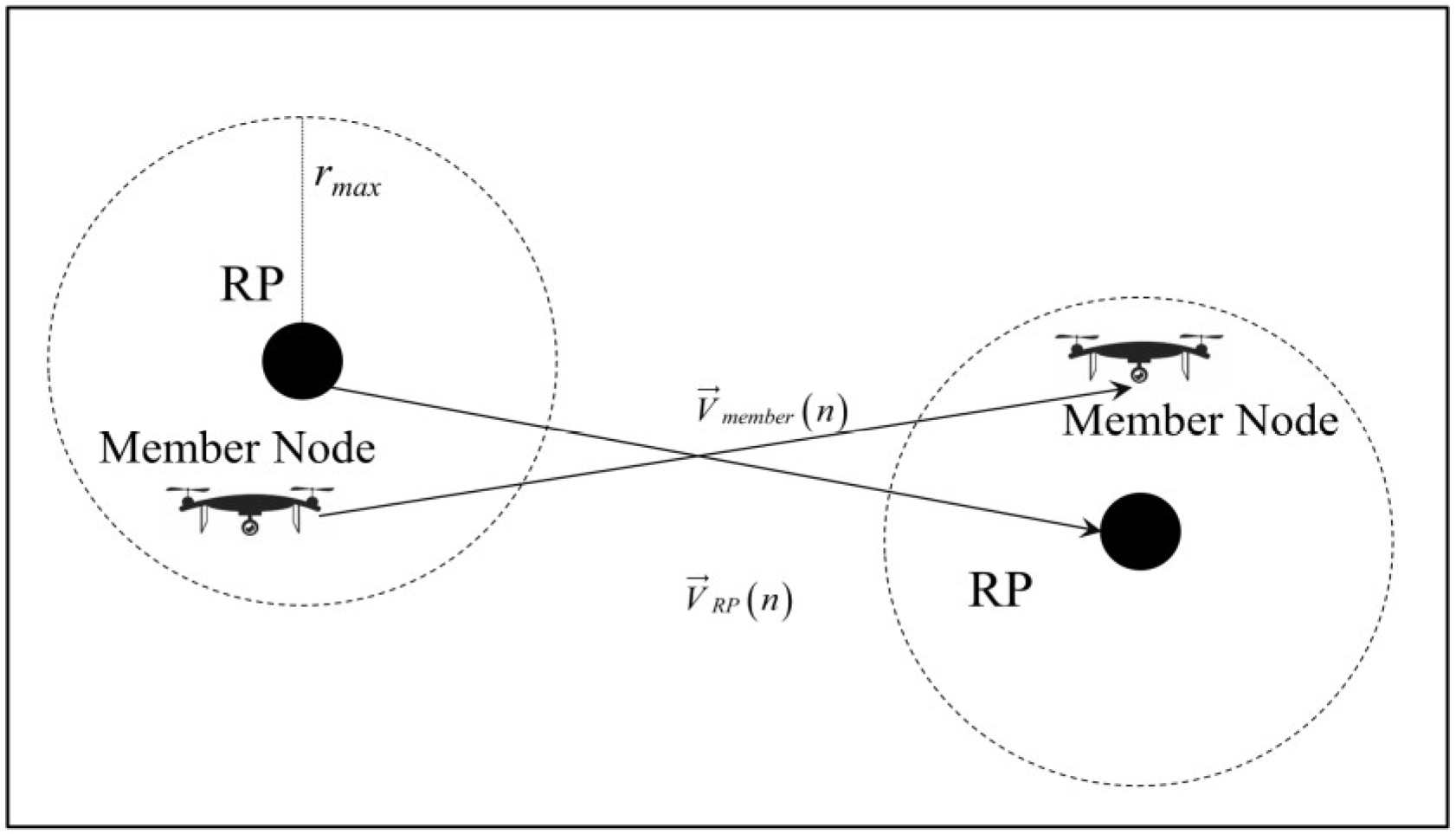
2.1.3. Reference Point Group Mobility Model
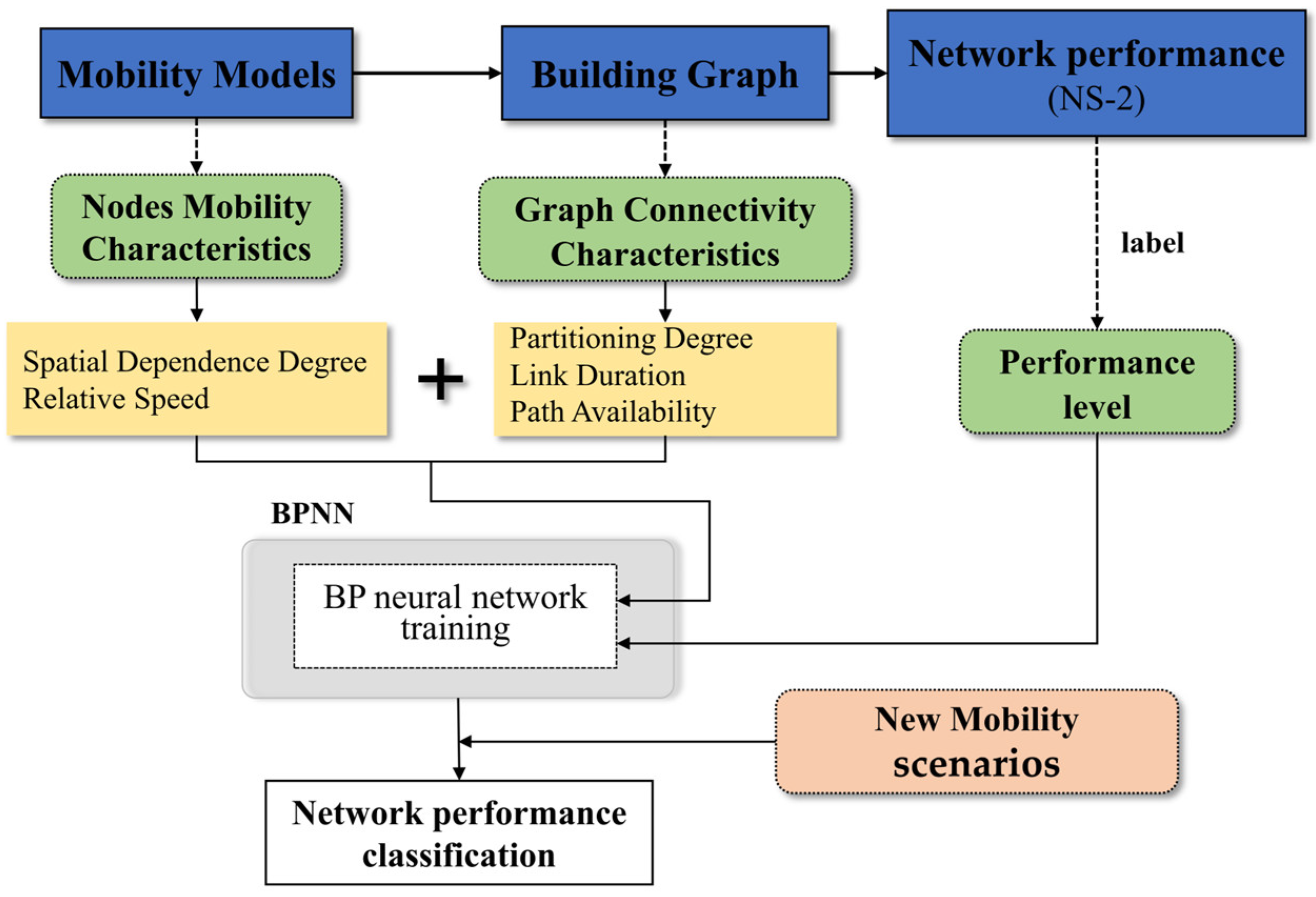
2.2. Mobility Indicator Design
- Node s is the source node, node d is the destination node for forwarding, and R is the communication radius of the node.
- indicates the Euclidean distance between node x and node y at time t.
- represents the velocity vector of node x at time t; and represents the velocity value of node x at time t.
- represents the x coordinate of node x at time t; and represents the y coordinate of node x at time t.
- : the relative direction (RD), or cosine of the angle between two velocity vectors, calculated by .
- : the velocity ratio (VR) between two vectors, calculated by .
- N: number of mobile nodes.
- T: time of nodes motion duration.
2.2.1. Spatial Dependency
2.2.2. Partitioning Degree
2.2.3. Link Duration
2.2.4. Relative Speed
2.2.5. Path Availability
2.3. Neural Network Architecture
3. Experiments and Settings
3.1. Experimental Settings and Data Preparation
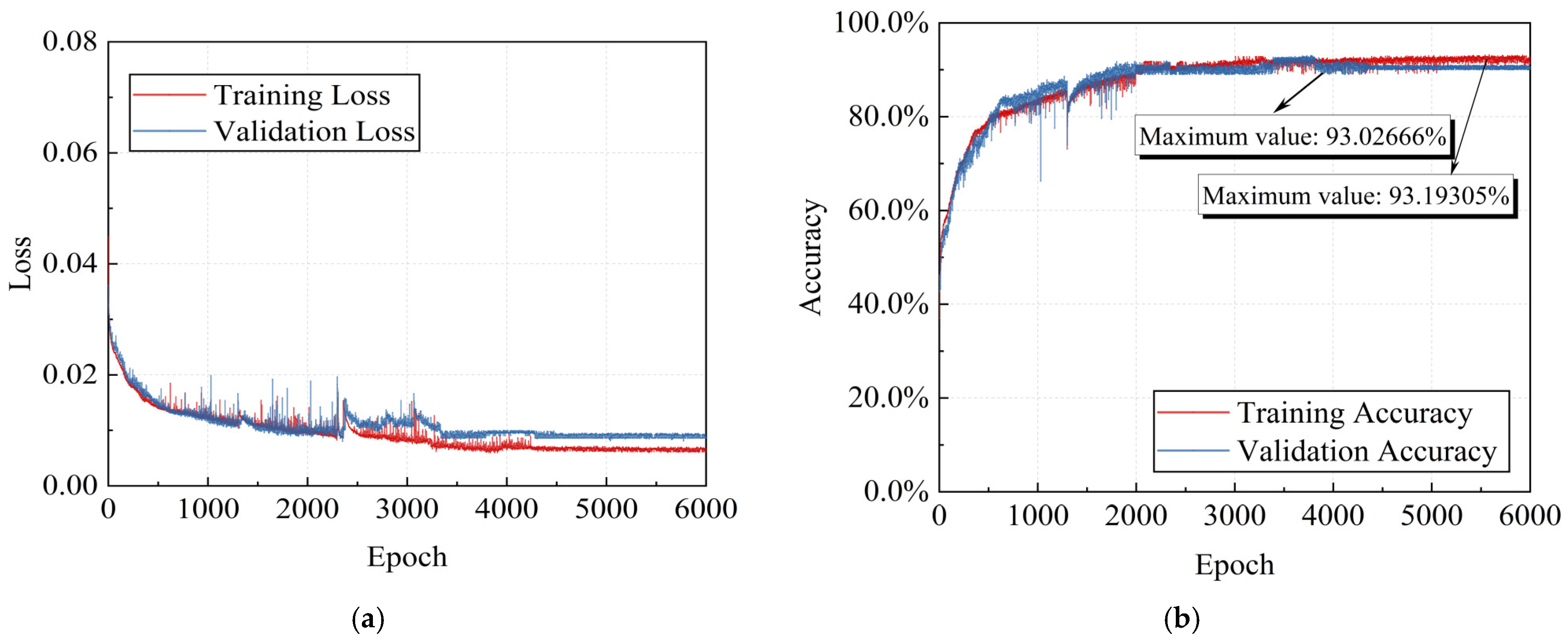
3.2. Training the Network
| Algorithm 1 The proposed BPNN-based algorithm for the mobility model and network performance evaluation method. |
| 1. Initialization of neural network: random initialize weights and bias; set batch size = 32 and learning rate = 0.004. |
| 2. Input sample data with five features, , and calculate the output for each layer, . |
| 3. Calculate loss: . |
4. Calculate loss signals for each layer:
|
5. Adjusting the weight values of each layer:
|
| 6. At the end of the iteration, save the optimal neural network parameters; otherwise, continue with Step 2. |
| 7. End. |
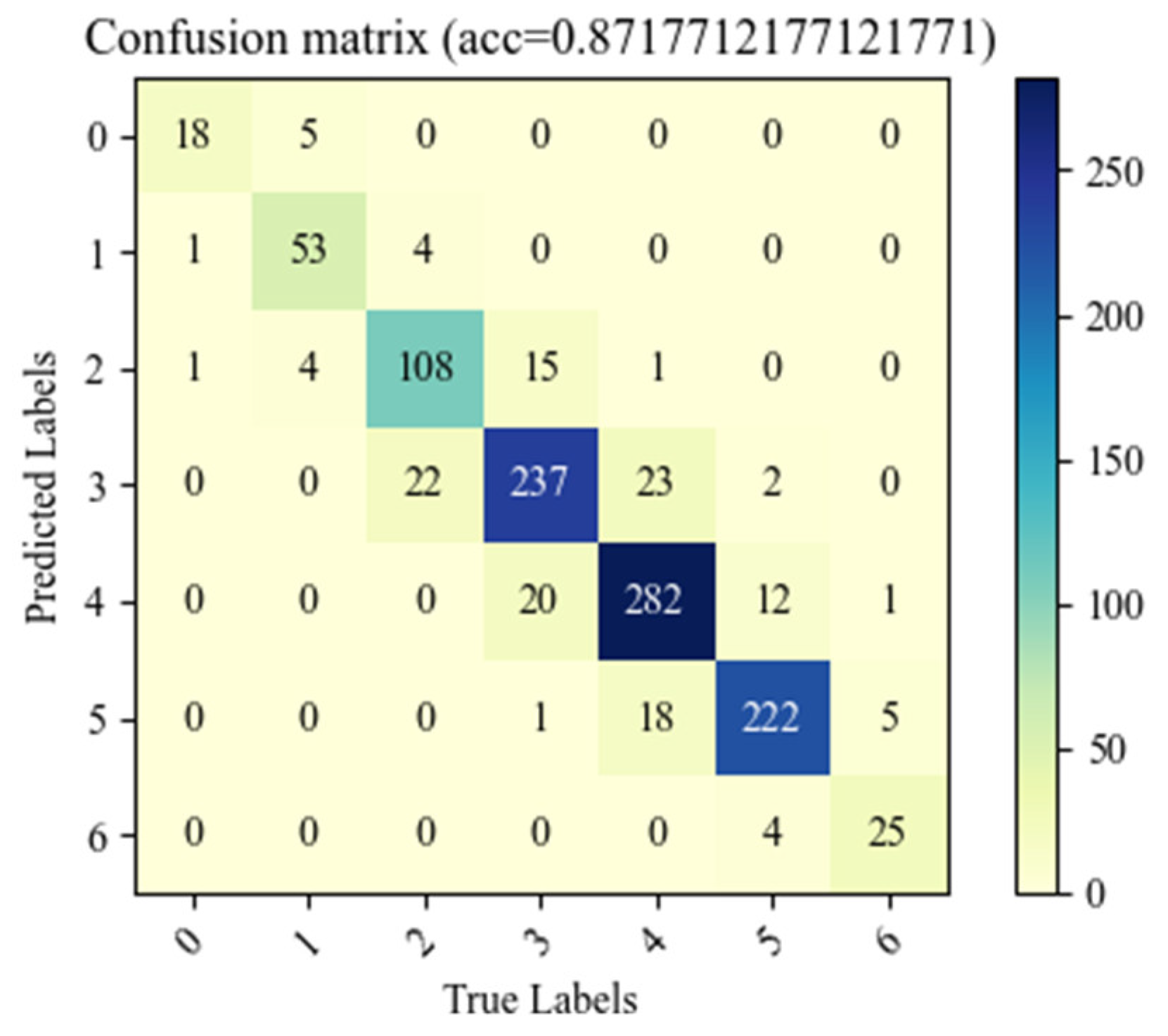
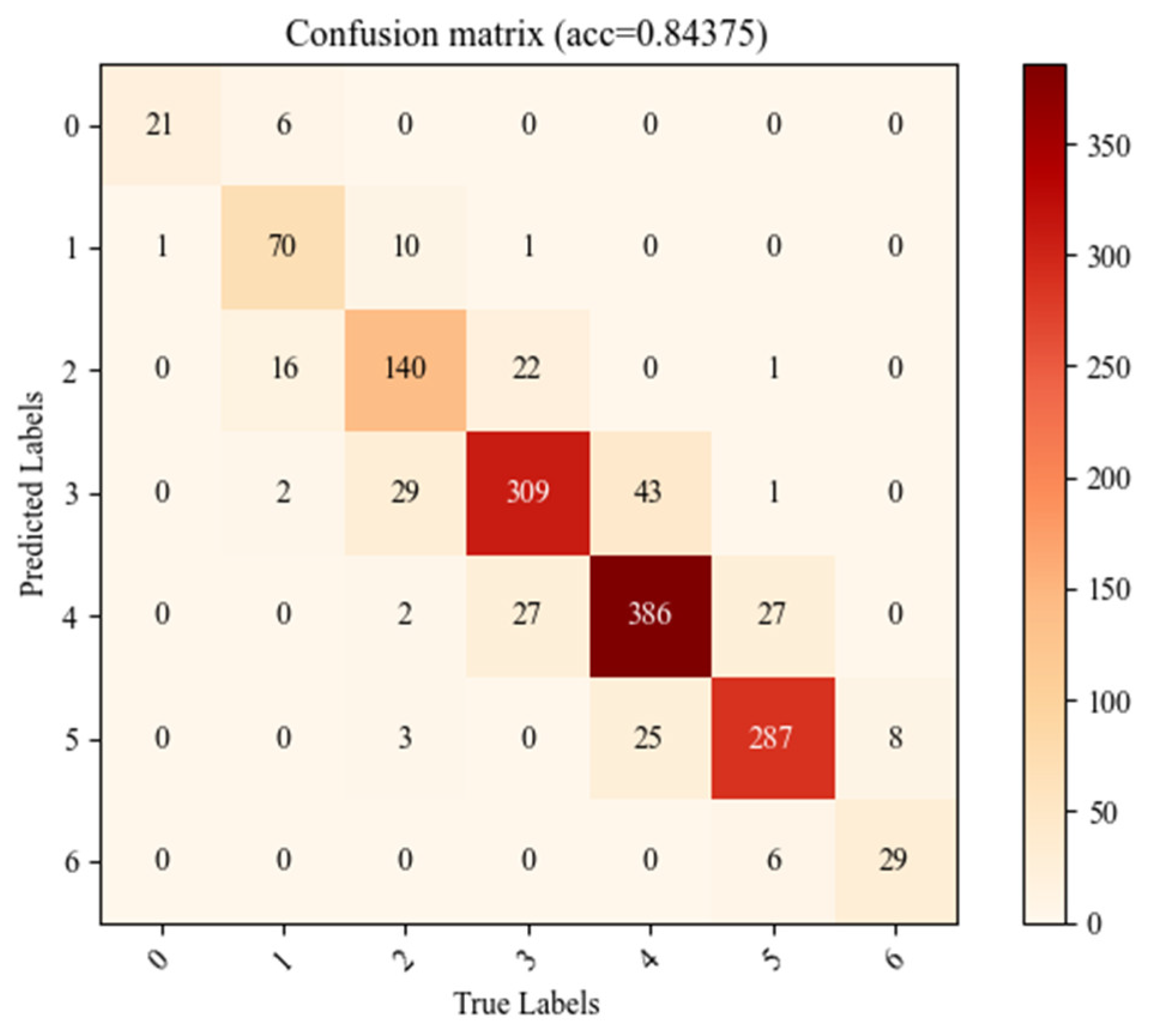
4. Results and Analysis
- Precision: the ratio of the number of samples correctly identified as P to the total number of samples identified as P. In terms of the determined results, this parameter can serve as a basis for determining classification accuracy, reflecting the ability of the neural network to “find the right” positive samples.
- Recall: the ratio of the number of samples correctly classified as P to the total number of real P-class samples. In terms of real samples, this parameter can determine the comprehensiveness of neural networks in sample classification.
- Specificity: the proportion of samples classified to be correct among all negative samples, which measures the neural network’s ability to recognize negative samples.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Toh, C.K. Ad Hoc Mobile Wireless Networks: Protocols and Systems; Pearson Education: New York, NY, USA, 2001. [Google Scholar]
- Khan, M.A.; Safi, A.; Qureshi, I.M.; Khan, I.U. Flying ad-hoc networks (FANETs): A review of communication architectures, and routing protocols. In Proceedings of the First International Conference on Latest Trends in Electrical Engineering and Computing Technologies (INTELLECT), Karachi, Pakistan, 15–16 November 2017; pp. 1–9. [Google Scholar]
- Kumari, K.; Sah, B.; Maakar, S. A survey: Different mobility model for FANET. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2015, 5. [Google Scholar]
- Camp, T.; Boleng, J.; Davies, V. A survey of mobility models for ad hoc network research. Wirel. Commun. Mob. Comput. 2002, 2, 483–502. [Google Scholar] [CrossRef]
- Sun, Y.; Belding-Royer, E.M.; Perkins, C.E. Internet connectivity for ad hoc mobile networks. Int. J. Wirel. Inf. Netw. 2002, 9, 75–88. [Google Scholar] [CrossRef]
- Ye, Y.; Wandong, C.; Guangli, T. Research on the link topology lifetime of mobility model in ad hoc network. In Proceedings of the International Conference on Networks Security, Wireless Communications and Trusted Computing, Wuhan, China, 25–26 April 2009; pp. 103–107. [Google Scholar]
- Johnson, D.B.; Maltz, D.A. Dynamic source routing in ad hoc wireless networks. Mob. Comput. 1996, 353, 153–181. [Google Scholar]
- Lassila, P.; Hyytiä, E.; Koskinen, H. Connectivity properties of random waypoint mobility model for ad hoc networks. In Challenges in Ad Hoc Networking; Springer: Cham, Switzerland, 2006; pp. 159–168. [Google Scholar]
- Gu, X.; Feng, H. Connectivity analysis for a wireless sensor network based on percolation theory. In Proceedings of the 2010 International Computer Application and System Modeling (ICCASM), Taiyuan, China, 22–24 October 2010; pp. V5–V203. [Google Scholar]
- Sheng, M.; Shi, Y.; Tian, Y.; Li, J.D.; Zhou, E.H. On the k-connectivity in mobile ad hoc networks. Acta Electron. Sin. 2008, 36, 1857. [Google Scholar]
- Guo, L.; Xu, H.; Harfoush, K. The node degree for wireless ad hoc networks in shadow fading environments. In Proceedings of the 2011 6th IEEE Conference on Industrial Electronics and Applications, Beijing, China, 21–23 June 2011; pp. 815–820. [Google Scholar]
- Sarker, I.H. Deep learning: A comprehensive overview on techniques, taxonomy, applications and research directions. SN Comput. Sci. 2021, 2, 420. [Google Scholar] [CrossRef] [PubMed]
- Mahesh, B. Machine learning algorithms—A review. Int. J. Sci. Res. 2020, 9, 381–386. [Google Scholar]
- Pan, J.; Ye, N.; Yu, H.; Hong, T.; Al-Rubaye, S.; Mumtaz, S.; Al-Dulaimi, A.; Chin-Lin, I. AI-driven blind signature classification for IoT connectivity: A deep learning approach. IEEE Trans. Wirel. Commun. 2022, 21, 6033–6047. [Google Scholar] [CrossRef]
- Wu, H.; Li, X.; Deng, Y. Deep learning-driven wireless communication for edge-cloud computing: Opportunities and challenges. J. Cloud Comput. 2020, 9, 1–14. [Google Scholar] [CrossRef]
- Bi, S.; Ho, C.K.; Zhang, R. Wireless powered communication: Opportunities and challenges. IEEE Commun. Mag. 2015, 53, 117–125. [Google Scholar] [CrossRef]
- Sangeetha, S.K.B.; Dhaya, R. Deep learning era for future 6G wireless communications—Theory, applications and challenges. Artif. Intell. Tech. Wirel. Commun. Netw. 2022, 8, 105–119. [Google Scholar]
- Chander, B. Approaches for Intelligent Wireless Sensor Networks. In Machine Learning and Deep Learning Techniques in Wireless and Mobile Networking Systems; CRC Press: Boca Raton, FL, USA, 2021; pp. 11–40. [Google Scholar]
- Mozaffari, M.; Saad, W.; Bennis, M.; Nam, Y.-H.; Debbah, M. A tutorial on UAVs for wireless networks: Applications, challenges, and open problems. IEEE Commun. Surv. Tutor. 2019, 21, 2334–2360. [Google Scholar] [CrossRef]
- Hecht-Nielsen, R. Theory of the backpropagation neural network. In Neural Networks for Perception; Academic Press: Cambridge, MA, USA, 1992; pp. 65–93. [Google Scholar]
- Liang, B.; Haas, Z.J. Predictive distance-based mobility management for PCS networks. In Proceedings of the IEEE INFOCOM’99. Conference on Computer Communications. Proceedings. Eighteenth Annual Joint Conference of the IEEE Computer and Communications Societies. The Future is Now (Cat. No. 99CH36320), New York, NY, USA, 21–25 March 1999; Volume 3, pp. 1377–1384. [Google Scholar]
- Hong, X.; Gerla, M.; Pei, G.; Chiang, C.C. A group mobility model for ad hoc wireless networks. In Proceedings of the 2nd ACM International Workshop on Modeling, Analysis and Simulation of Wireless and Mobile Systems, New York, NY, USA, 1 August 1999; pp. 53–60. [Google Scholar]
- Davies, V.A. Evaluating mobility models within an ad hoc network. Mines Theses Diss. 2000. [Google Scholar]
- Hyytiä, E.; Koskinen, H.; Lassila, P.; Penttinen, J.; Roszik, J.; Virtamo, J. Random waypoint model in wireless networks. Netw. Algorithms Complex. Phys. Comput. Sci. 2005, 6, 16–19. [Google Scholar]
- Navidi, W.; Camp, T. Stationary distributions for the random waypoint mobility model. IEEE Trans. Mob. Comput. 2004, 3, 99–108. [Google Scholar] [CrossRef]
- Bujari, A.; Palazzi, C.E.; Ronzani, D. FANET application scenarios and mobility models. In Proceedings of the 3rd Workshop on Micro Aerial Vehicle Networks, Systems, and Applications, New York, NY, USA, 23 June 2017; pp. 43–46. [Google Scholar]
- Bai, F.; Sadagopan, N.; Helmy, A. IMPORTANT: A framework to systematically analyze the Impact of Mobility on Performance of RouTing protocols for Adhoc NeTworks. In Proceedings of the INFOCOM 2003. Twenty-Second Annual Joint Conference of the IEEE Computer and Communications, San Francisco, CA, USA, 30 March 2003–3 April 2003. [Google Scholar]
- Anthony, M.; Bartlett, P.L.; Bartlett, P.L. Neural Network Learning: Theoretical Foundations; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Aschenbruck, N.; Ernst, R.; Gerhards-Padilla, E.; Schwamborn, M. Bonnmotion: A mobility scenario generation and analysis tool. In Proceedings of the 3rd International ICST Conference on Simulation Tools and Techniques, Institute for Computer Sciences, Social-Informatics and Telecommunications Engineering, Brussels, Belgium, 16 May 2010. [Google Scholar]
- (Ns-2, 2005) “The Network Simulator HomePage”. Available online: http://www.isi.edu/nsnam/ns/ (accessed on 16 April 2023).
- Perkins, C.; Belding-Royer, E.; Das, S. Ad Hoc On-Demand Distance Vector (AODV) Routing; 2003. Available online: https://datatracker.ietf.org/doc/rfc3561/ (accessed on 16 April 2023).
- Bai, F.; Helmy, A. A survey of mobility models. Wirel. Adhoc Netw. Univ. South. Calif. USA 2004, 206, 147. [Google Scholar]
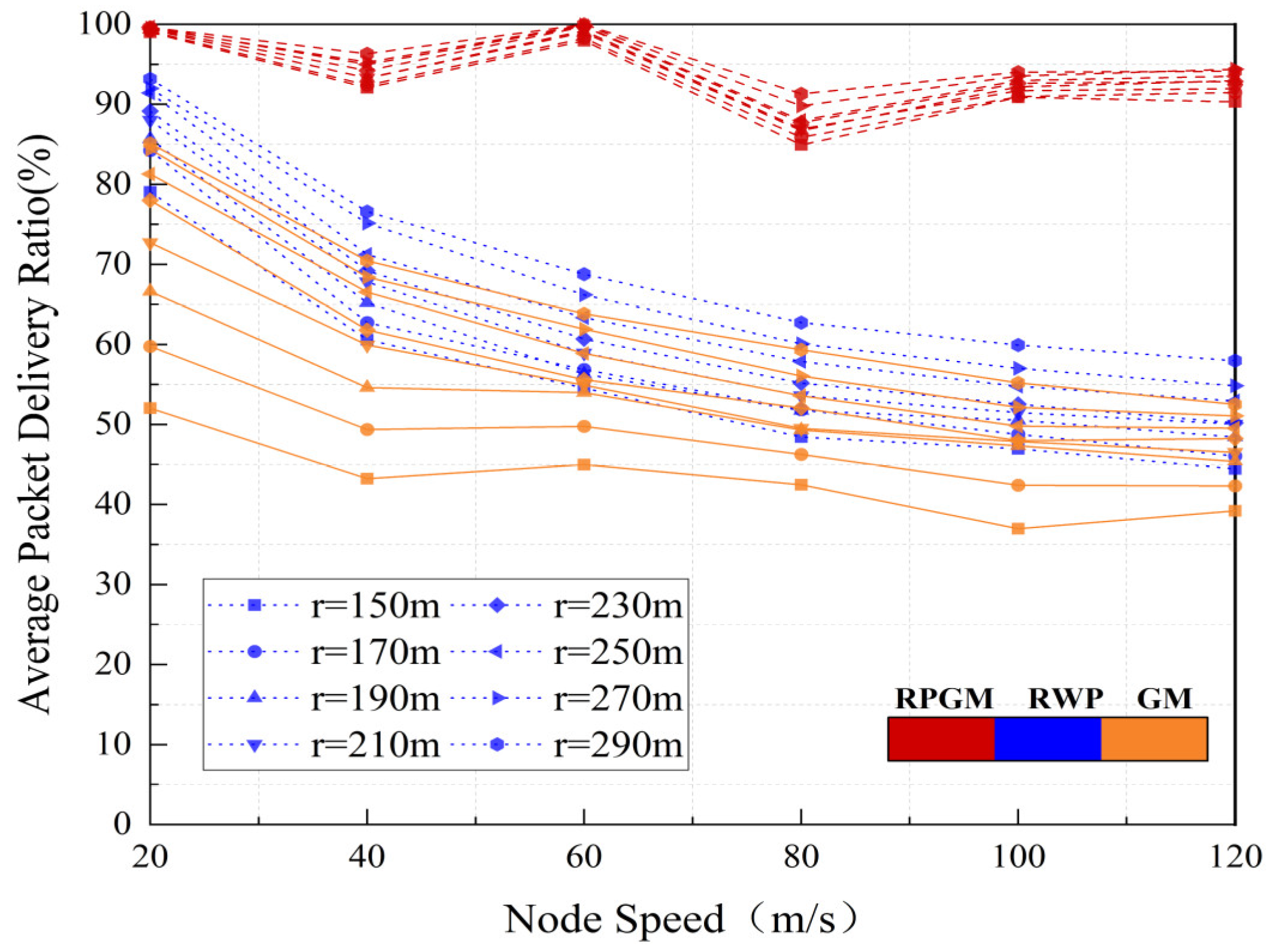
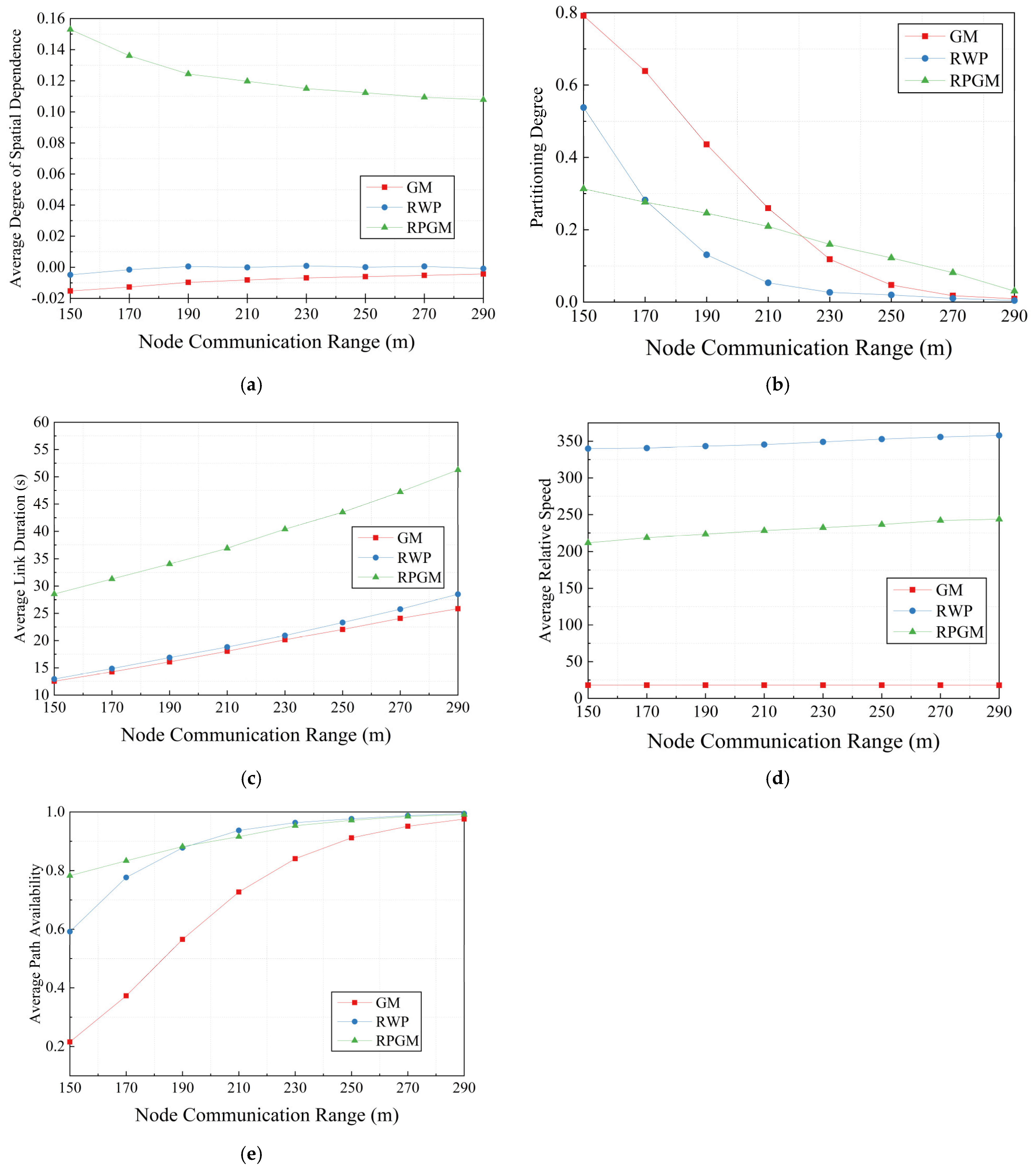

| Mobility Models | R | Spatial Dependency | Partitioning Degree | Link Duration | Relative Speed | Path Availability |
|---|---|---|---|---|---|---|
| GM | 150 m | −0.015215 | 0.79171 | 12.54591 | 17.91827 | 0.215451 |
| 170 m | −0.012723 | 0.63871 | 14.25538 | 17.92939 | 0.3729329 | |
| 190 m | −0.009718 | 0.43584 | 16.08956 | 17.91865 | 0.5653631 | |
| 210 m | −0.008186 | 0.25967 | 18.04655 | 17.89447 | 0.7269393 | |
| 230 m | −0.006838 | 0.11843 | 20.15201 | 17.88892 | 0.8405965 | |
| 250 m | −0.006032 | 0.04717 | 22.04167 | 17.89431 | 0.9115855 | |
| 270 m | −0.005227 | 0.01758 | 24.07127 | 17.88145 | 0.9512641 | |
| 290 m | −0.004291 | 0.00908 | 25.84114 | 17.8526 | 0.975736 | |
| RWP | 150 m | −0.004837 | 0.5379 | 12.94823 | 339.91358 | 0.5918288 |
| 170 m | −0.001533 | 0.28228 | 14.86327 | 340.65322 | 0.7765334 | |
| 190 m | 0.0005551 | 0.13087 | 16.88473 | 343.33133 | 0.8776451 | |
| 210 m | −6.69 × 10−5 | 0.05339 | 18.81895 | 345.42728 | 0.9371746 | |
| 230 m | 0.0008916 | 0.02679 | 20.92555 | 349.1127 | 0.9635666 | |
| 250 m | 0.0001047 | 0.01976 | 23.31782 | 352.91237 | 0.9766939 | |
| 270 m | 0.0006109 | 0.01021 | 25.76445 | 355.74068 | 0.9875341 | |
| 290 m | −0.000827 | 0.0042 | 28.50262 | 358.01649 | 0.9942976 | |
| RPGM | 150 m | 0.1529827 | 0.31306 | 28.54253 | 211.58224 | 0.7826548 |
| 170 m | 0.1360633 | 0.27617 | 31.30638 | 218.66965 | 0.8334138 | |
| 190 m | 0.1243506 | 0.24576 | 34.05127 | 223.39237 | 0.8820463 | |
| 210 m | 0.1196804 | 0.20896 | 36.91552 | 228.24037 | 0.9156089 | |
| 230 m | 0.1149647 | 0.15945 | 40.39146 | 232.21462 | 0.9529495 | |
| 250 m | 0.1122537 | 0.12214 | 43.50398 | 236.51875 | 0.9714706 | |
| 270 m | 0.1093957 | 0.08126 | 47.21895 | 242.02399 | 0.9846366 | |
| 290 m | 0.107786 | 0.03047 | 51.25484 | 243.77849 | 0.990941 |
| Simulation Parameter | Value |
|---|---|
| Transmitter range | 150 m–290 m |
| Bandwidth | 2 Mbps |
| Simulation time | 500 s |
| Number of nodes | 40 |
| Speed | 0 m/s–140 m/s |
| Environment size | 1000 m × 1000 m |
| Traffic type | constant bit rate |
| Packet rate | 4 packets/s |
| Packet size | 64 bytes |
| Number of flows | 10 |
| Propagation model | Friis loss model |
| Transmit power | 7.5 dBm |
| Actual Result | Predicted Result | |
|---|---|---|
| Positive | Negative | |
| Positive | TP | FN |
| Negative | FP | TN |
| Network Performance Label | Precision | Recall | Specificity |
|---|---|---|---|
| 0 | 0.783 | 0.9 | 0.995 |
| 1 | 0.914 | 0.855 | 0.995 |
| 2 | 0.837 | 0.806 | 0.978 |
| 3 | 0.835 | 0.868 | 0.942 |
| 4 | 0.895 | 0.87 | 0.957 |
| 5 | 0.902 | 0.925 | 0.972 |
| 6 | 0.806 | 0.806 | 0.996 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.; Yu, D.; Zhang, X.; Chai, M.; Liu, G.; Du, J.; Wang, L. A Deep Learning Approach for Wireless Network Performance Classification Based on UAV Mobility Features. Drones 2023, 7, 377. https://doi.org/10.3390/drones7060377
Bai Y, Yu D, Zhang X, Chai M, Liu G, Du J, Wang L. A Deep Learning Approach for Wireless Network Performance Classification Based on UAV Mobility Features. Drones. 2023; 7(6):377. https://doi.org/10.3390/drones7060377
Chicago/Turabian StyleBai, Yijie, Daojie Yu, Xia Zhang, Mengjuan Chai, Guangyi Liu, Jianping Du, and Linyu Wang. 2023. "A Deep Learning Approach for Wireless Network Performance Classification Based on UAV Mobility Features" Drones 7, no. 6: 377. https://doi.org/10.3390/drones7060377
APA StyleBai, Y., Yu, D., Zhang, X., Chai, M., Liu, G., Du, J., & Wang, L. (2023). A Deep Learning Approach for Wireless Network Performance Classification Based on UAV Mobility Features. Drones, 7(6), 377. https://doi.org/10.3390/drones7060377





