Estimating Effective Leaf Area Index of Winter Wheat Based on UAV Point Cloud Data
Abstract
1. Introduction
2. Materials and Methods
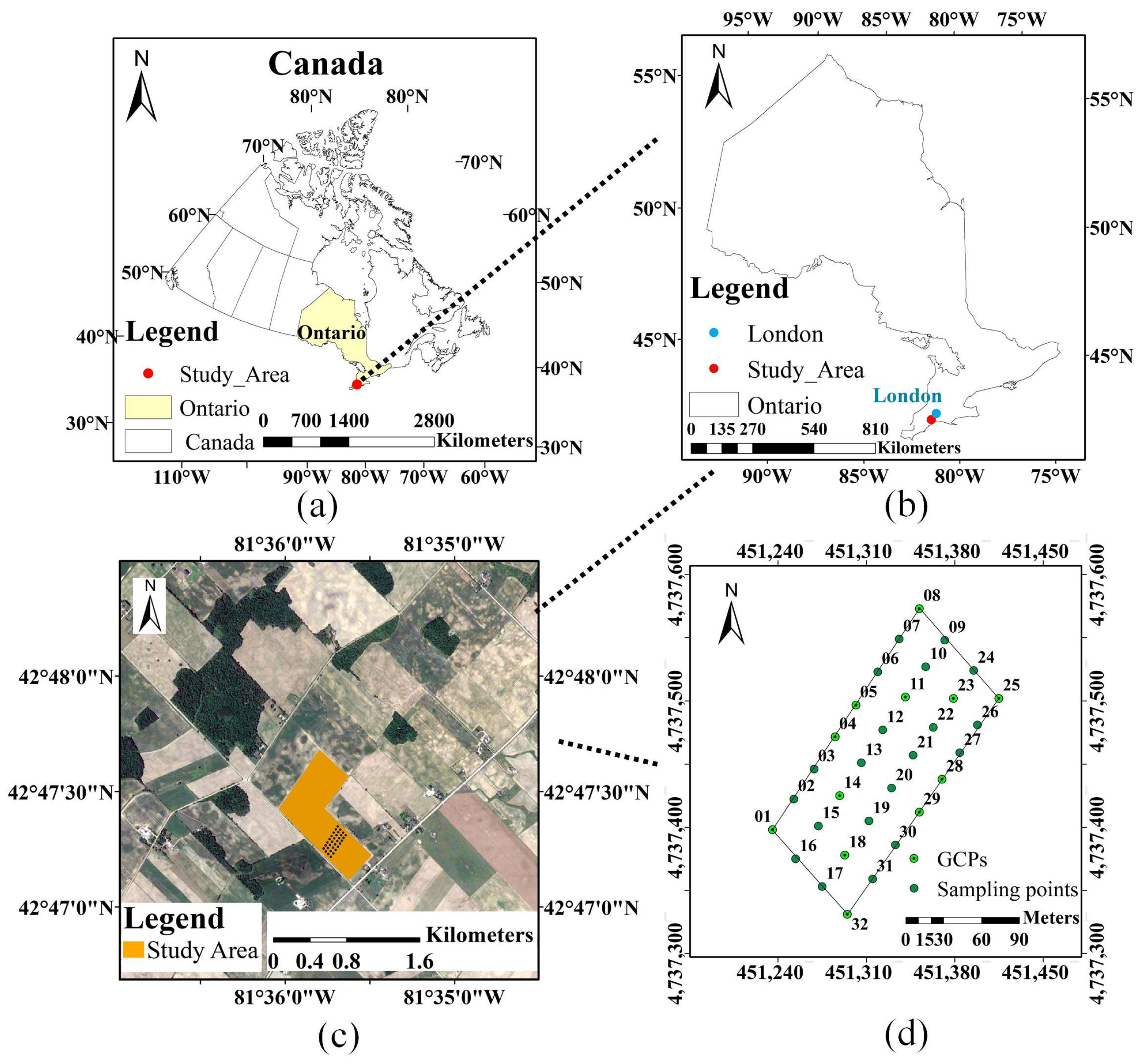
2.1. Site Description
2.2. Field Measurements
2.3. UAV Data Acquisition and Processing
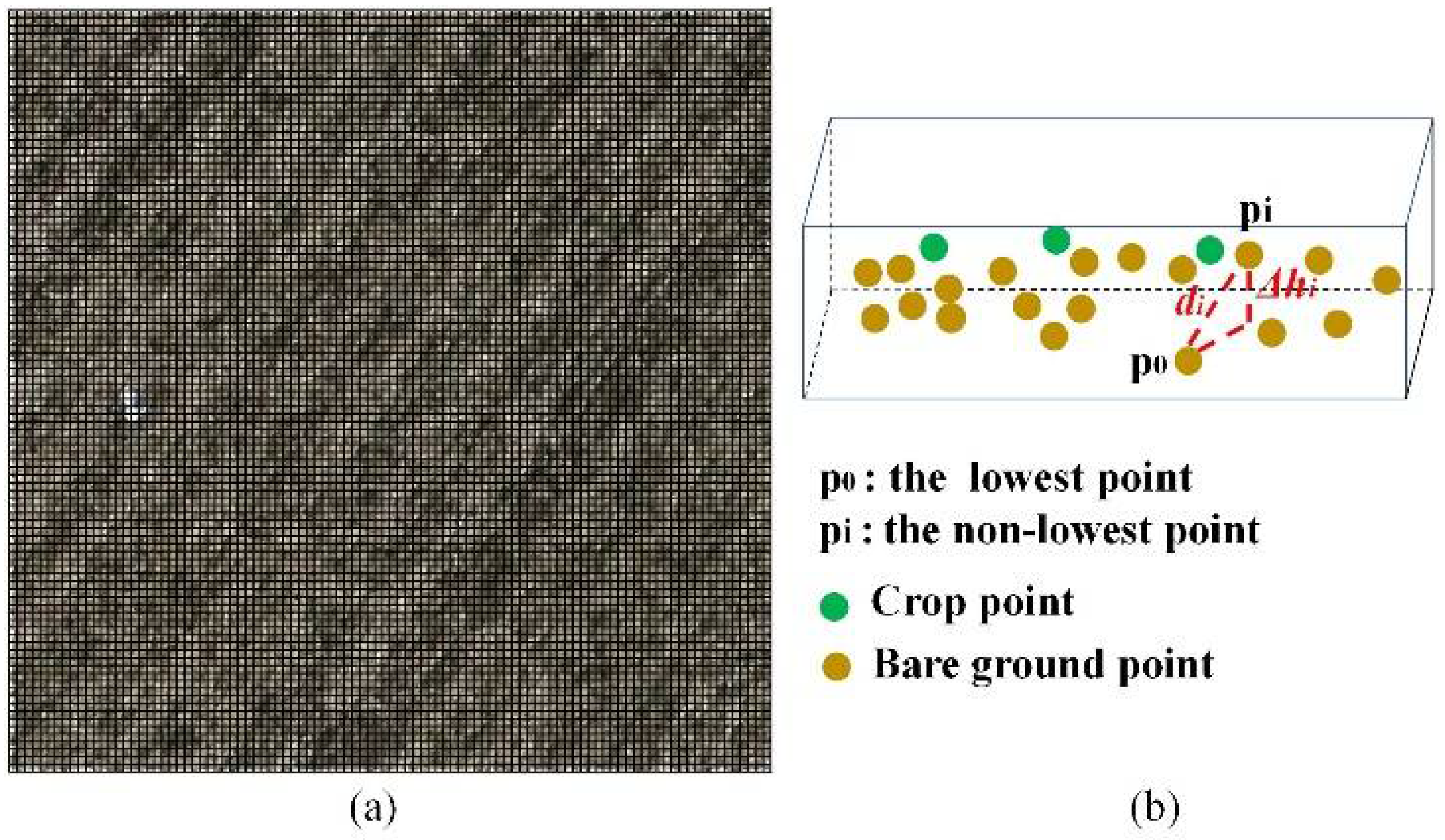
2.4. Point Cloud Data Filtering
2.5. Projection of Spherical Point Cloud onto a Plane
2.6. LAIe Estimation Using Gap Fraction
2.7. Methods Assessment
3. Results
3.1. Point Cloud Filtering
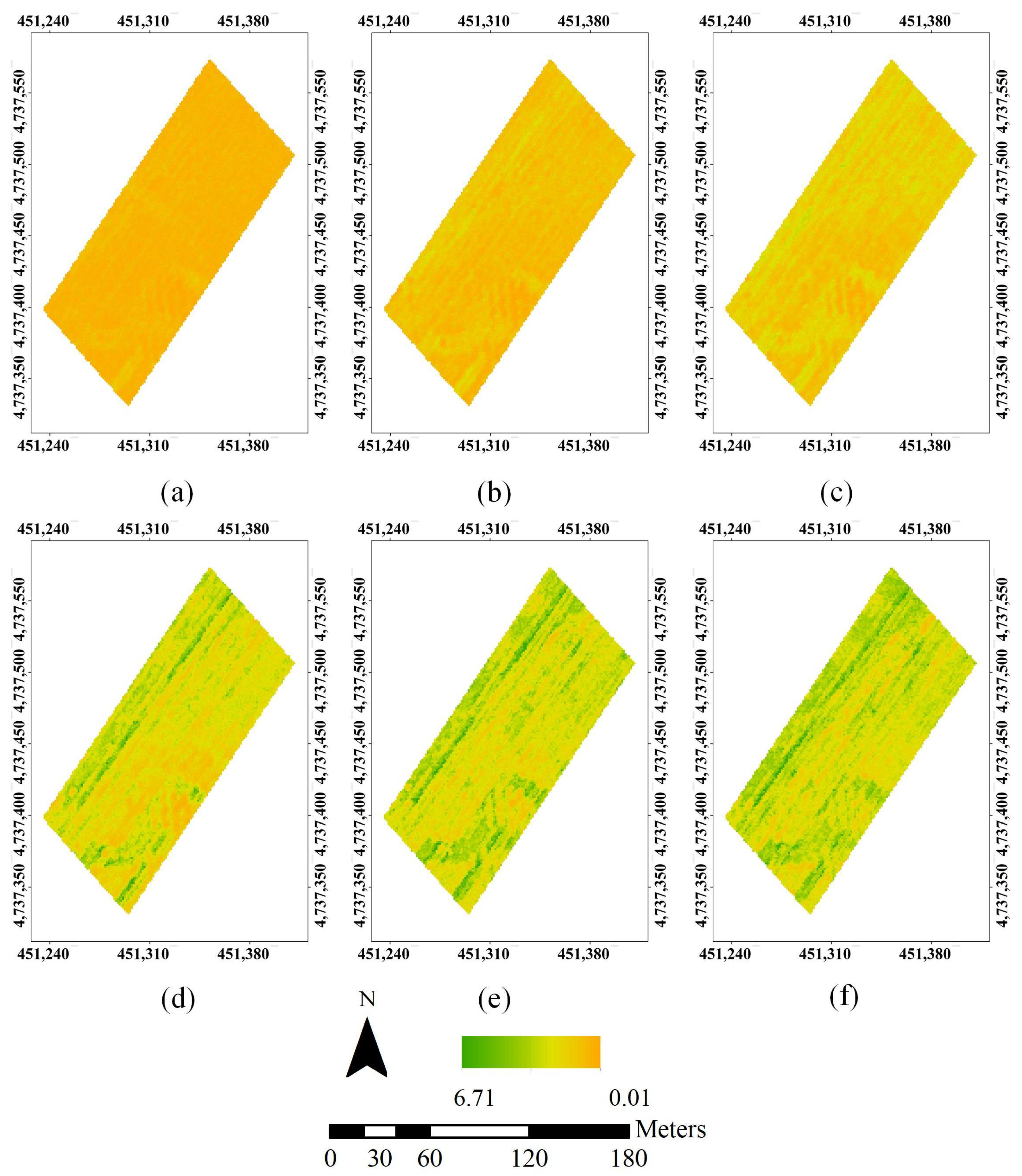
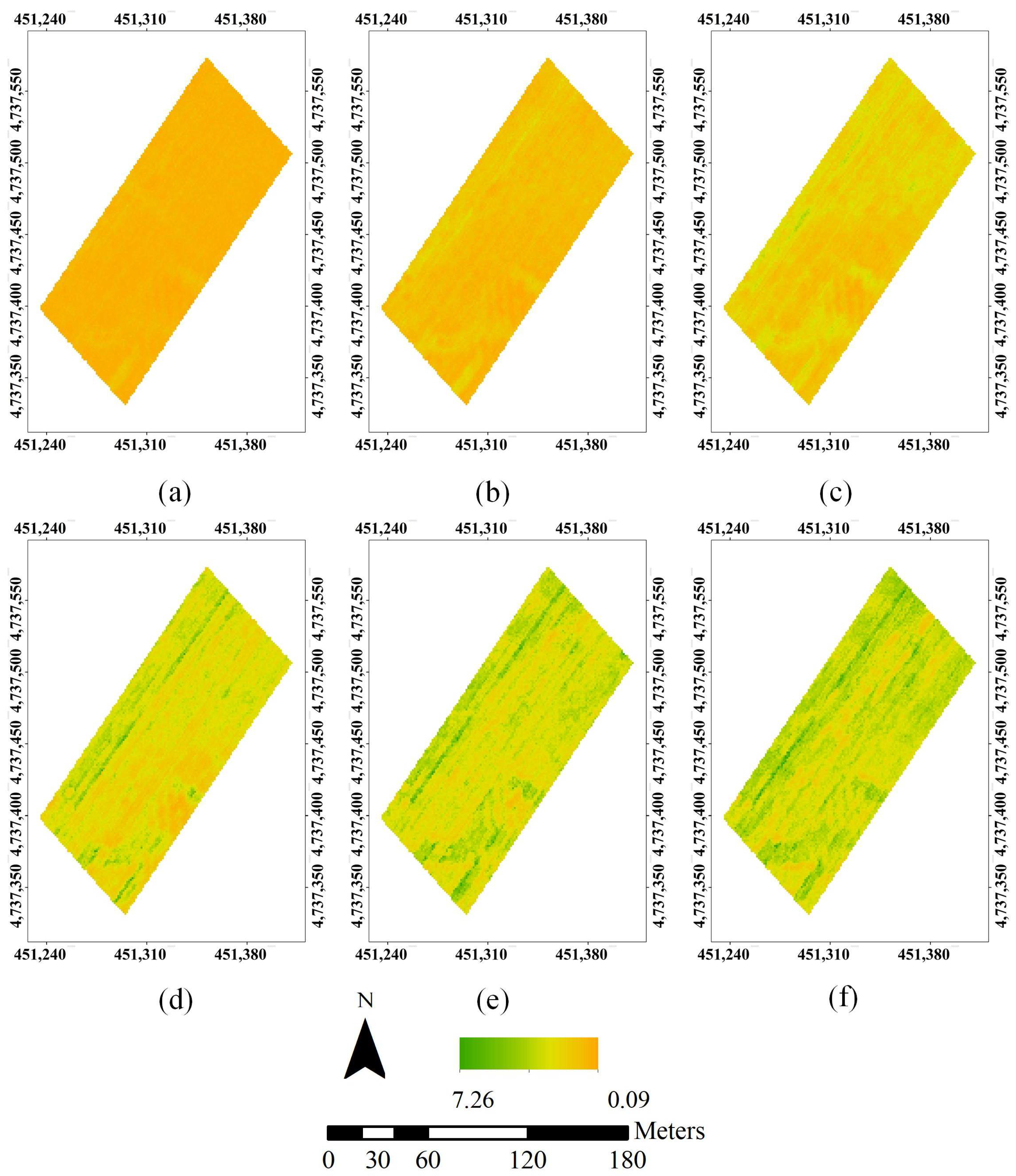
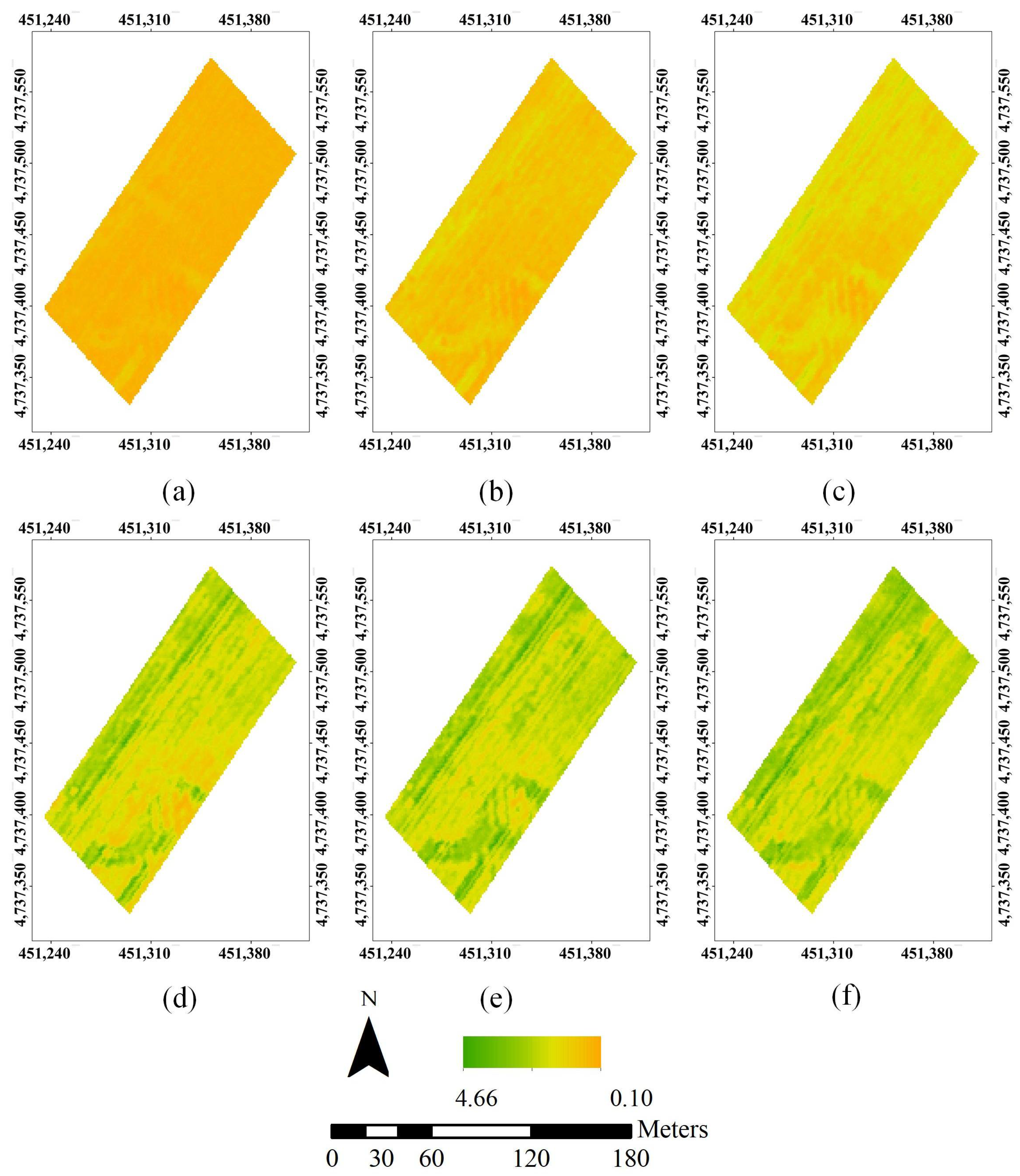
3.2. Hemispherical Image of Point Cloud Data
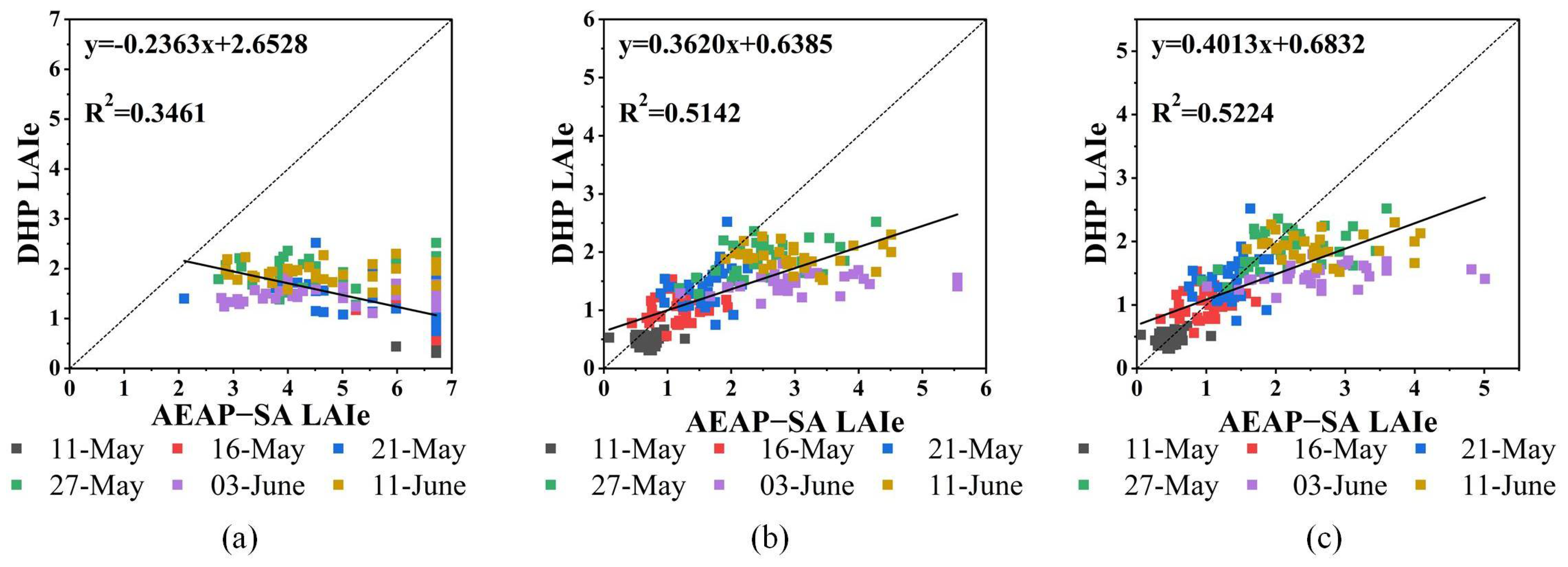
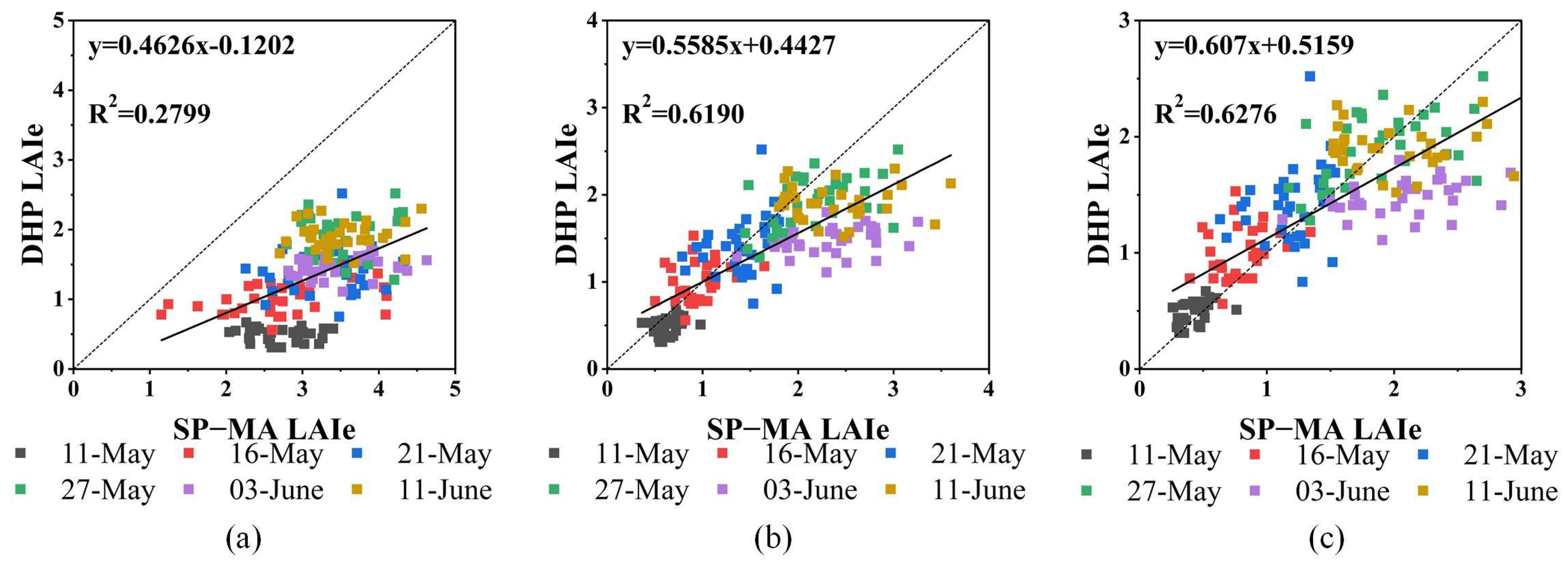
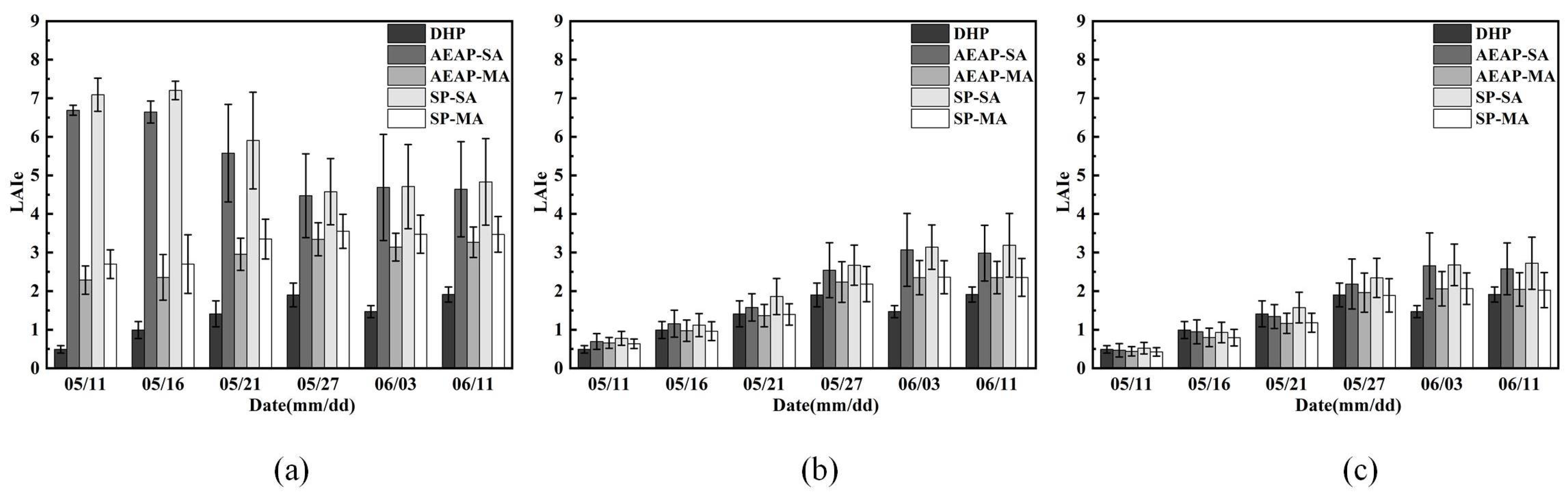
3.3. LAIe Inversion Results
4. Discussion
4.1. Accuracy Comparison of LAIe Estimation by Filtering Methods
4.2. Assessment of Four Methods for LAIe Estimation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Weiss, M.; Baret, F.; Smith, G.; Jonckheere, I.; Coppin, P. Review of methods for in situ leaf area index (LAI) determination: Part II. Estimation of LAI, errors and sampling. Agric. For. Meteorol. 2004, 121, 37–53. [Google Scholar] [CrossRef]
- Fang, H.L.; Baret, F.; Plummer, S.; Schaepman-Strub, G. An Overview of Global Leaf Area Index (LAI): Methods, Products, Validation, and Applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar] [CrossRef]
- Luisa, E.M.; Frederic, B.; Marie, W. Slope correction for LAI estimation from gap fraction measurements. Agric. For. Meteorol. 2008, 148, 1553–1562. [Google Scholar] [CrossRef]
- Nackaerts, K.; Coppin, P.; Muys, B.; Hermy, M. Sampling methodology for LAI measurements with LAI-2000 in small forest stands. Agric. For. Meteorol. 2000, 101, 247–250. [Google Scholar] [CrossRef]
- Denison, R.F.; Russotti, R. Field estimates of green leaf area index using laser-induced chlorophyll fluorescence. Field Crops Res. 1997, 52, 143–149. [Google Scholar] [CrossRef]
- Denison, R. Minimizing errors in LAI estimates from laser-probe inclined-point quadrats. Field Crops Res. 1997, 51, 231–240. [Google Scholar] [CrossRef]
- Garrigues, S.; Shabanov, N.V.; Swanson, K.; Morisette, J.T.; Baret, F.; Myneni, R.B. Intercomparison and sensitivity analysis of Leaf Area Index retrievals from LAI-2000, AccuPAR, and digital hemispherical photography over croplands. Agric. For. Meteorol. 2008, 148, 1193–1209. [Google Scholar] [CrossRef]
- Jiapaer, G.; Yi, Q.X.; Yao, F.; Zhang, P. Comparison of non-destructive LAI determination methods and optimization of sampling schemes in Populus euphratica. Urban For. Urban Green. 2017, 26, 114–123. [Google Scholar] [CrossRef]
- Yan, G.J.; Hu, R.H.; Luo, J.H.; Weiss, M.; Jiang, H.L.; Mu, X.H.; Xie, D.H.; Zhang, W.M. Review of indirect optical measurements of leaf area index: Recent advances, challenges, and perspectives. Agric. For. Meteorol. 2019, 265, 390–411. [Google Scholar] [CrossRef]
- Kussner, R.; Mosandl, R. Comparison of direct and indirect estimation of leaf area index in mature Norway spruce stands of eastern Germany. Can. J. For. Res. 2000, 30, 440–447. [Google Scholar] [CrossRef]
- Rhoads, A.G.; Hamburg, S.P.; Fahey, T.J.; Siccama, T.G.; Kobe, R. Comparing direct and indirect methods of assessing canopy structure in a northern hardwood forest. Can. J. For. Res. 2004, 34, 584–591. [Google Scholar] [CrossRef]
- Jay, S.; Maupas, F.; Bendoula, R.; Gorretta, N. Retrieving LAI, chlorophyll and nitrogen contents in sugar beet crops from multi-angular optical remote sensing: Comparison of vegetation indices and PROSAIL inversion for field phenotyping. Field Crops Res. 2017, 210, 33–46. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Z.; Tao, F.L. Improving regional winter wheat yield estimation through assimilation of phenology and leaf area index from remote sensing data. Eur. J. Agron. 2018, 101, 163–173. [Google Scholar] [CrossRef]
- Zhang, P.; Anderson, B.; Tan, B.; Huang, D.; Myneni, R. Potential monitoring of crop production using a new satellite-Based Climate-Variability Impact Index. Agric. For. Meteorol. 2005, 132, 344–358. [Google Scholar] [CrossRef]
- Huang, J.X.; Tian, L.Y.; Liang, S.L.; Ma, H.Y.; Becker-Reshef, I.; Huang, Y.B.; Su, W.; Zhang, X.D.; Zhu, D.H.; Wu, W.B. Improving winter wheat yield estimation by assimilation of the leaf area index from Landsat TM and MODIS data into the WOFOST model. Agric. For. Meteorol. 2015, 204, 106–121. [Google Scholar] [CrossRef]
- Song, Y.; Wang, J.F.; Shan, B. Estimation of winter wheat yield from UAV-based multi-temporal imagery using crop allometric relationship and SAFY model. Drones 2021, 5, 78. [Google Scholar] [CrossRef]
- Luo, S.Z.; Chen, J.M.; Wang, C.; Gonsamo, A.; Xi, X.H.; Lin, Y.; Qian, M.J.; Peng, D.L.; Nie, S.; Qin, H.M. Comparative performances of airborne LiDAR height and intensity data for leaf area index estimation. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2017, 11, 300–310. [Google Scholar] [CrossRef]
- Maki, M.; Homma, K. Empirical Regression Models for Estimating Multiyear Leaf Area Index of Rice from Several Vegetation Indices at the Field Scale. Remote Sens. 2014, 6, 4764–4779. [Google Scholar] [CrossRef]
- Liu, K.; Zhou, Q.B.; Wu, W.B.; Xia, T.; Tang, H.J. Estimating the crop leaf area index using hyperspectral remote sensing. J. Integr. Agric. 2016, 15, 475–491. [Google Scholar] [CrossRef]
- Yuan, H.H.; Yang, G.J.; Li, C.C.; Wang, Y.J.; Liu, J.G.; Yu, H.Y.; Feng, H.K.; Xu, B.; Zhao, X.Q.; Yang, X.D. Retrieving Soybean Leaf Area Index from Unmanned Aerial Vehicle Hyperspectral Remote Sensing: Analysis of RF, ANN, and SVM Regression Models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef]
- Tang, H.; Brolly, M.; Zhao, F.; Strahler, A.H.; Schaaf, C.L.; Ganguly, S.; Zhang, G.; Dubayah, R. Deriving and validating Leaf Area Index (LAI) at multiple spatial scales through lidar remote sensing: A case study in Sierra National Forest, CA. Remote Sens. Environ. 2014, 143, 131–141. [Google Scholar] [CrossRef]
- Duan, B.; Liu, Y.T.; Gong, Y.; Peng, Y.; Wu, X.T.; Zhu, R.S.; Fang, S.H. Remote estimation of rice LAI based on Fourier spectrum texture from UAV image. Plant Methods 2019, 15, 124. [Google Scholar] [CrossRef] [PubMed]
- Qi, J.; Kerr, Y.H.; Moran, M.S.; Weltz, M.; Huete, A.R.; Sorooshian, S.; Bryant, R. Leaf Area Index Estimates Using Remotely Sensed Data and BRDF Models in a Semiarid Region. Remote Sens. Environ. 2000, 73, 18–30. [Google Scholar] [CrossRef]
- Tian, Y.; Huang, H.; Zhou, G.; Zhang, Q.; Tao, J.; Zhang, Y.; Lin, J. Aboveground mangrove biomass estimation in Beibu Gulf using machine learning and UAV remote sensing. Sci.Total Environ. 2021, 781, 146816. [Google Scholar] [CrossRef]
- Tian, J.Y.; Wang, L.; Li, X.J.; Gong, H.L.; Shi, C.; Zhong, R.F.; Liu, X.M. Comparison of UAV and WorldView-2 imagery for mapping leaf area index of mangrove forest. Int. J. Appl. Earth Observation GeoInf. 2017, 61, 22–31. [Google Scholar] [CrossRef]
- Li, S.Y.; Yuan, F.; Ata-UI-Karim, S.T.; Zheng, H.B.; Cheng, T.; Liu, X.J.; Tian, Y.C.; Zhu, Y.; Cao, W.X.; Cao, Q. Combining Color Indices and Textures of UAV-Based Digital Imagery for Rice LAI Estimation. Remote Sens. 2019, 11, 1763. [Google Scholar] [CrossRef]
- Liu, S.B.; Jin, X.; Nie, C.W.; Wang, S.Y.; Yu, X.; Cheng, M.H.; Shao, M.C.; Wang, Z.X.; Tuohuti, N.; Bai, Y.; et al. Estimating leaf area index using unmanned aerial vehicle data: Shallow vs. deep machine learning algorithms. Plant Physiol. 2021, 187, 1551–1576. [Google Scholar] [CrossRef]
- Duan, S.B.; Li, Z.L.; Wu, H.; Tang, B.H.; Ma, L.L.; Zhao, E.Y.; Li, C.R. Inversion of the PROSAIL model to estimate leaf area index of maize, potato, and sunflower fields from unmanned aerial vehicle hyperspectral data. Int. J. Appl. Earth Obs. GeoInf. 2014, 26, 12–20. [Google Scholar] [CrossRef]
- Pascu, I.; Dobre, A.; Badea, O.; Tanase, M. Estimating forest stand structure attributes from terrestrial laser scans. Sci. Total Environ. 2019, 691, 205–215. [Google Scholar] [CrossRef]
- dos Santos, L.M.; Ferraz, G.A.E.S.; Barbosa, B.D.D.; Diotto, A.V.; Maciel, D.T.; Xavier, L.A.G. Biophysical parameters of coffee crop estimated by UAV RGB images. Precis. Agric. 2020, 21, 1227–1241. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Malenovsky, Z.; Turner, D.; Vopenka, P. Assessment of forest structure using two UAV techniques: A comparison of airborne laser scanning and structure from motion (SfM) point clouds. Forests 2016, 7, 62. [Google Scholar] [CrossRef]
- Arno, J.; Escola, A.; Valles, J.M.; Llorens, J.; Sanz, R.; Masip, J.; Palacin, J.; Rosell-Polo, J.R. Leaf area index estimation in vineyards using a ground-based LiDAR scanner. Precis. Agric. 2013, 14, 290–306. [Google Scholar] [CrossRef]
- Comba, L.; Biglia, A.; Aimonino, D.R.; Tortia, C.; Mania, E.; Guidoni, S.; Gay, P. Leaf Area Index evaluation in vineyards using 3D point clouds from UAV imagery. Precis. Agric. 2020, 21, 881–896. [Google Scholar] [CrossRef]
- Yin, T.G.; Qi, J.B.; Cook, B.D.; Morton, D.C.; Wei, S.S.; Gastellu-Etchegorry, J.-P. Modeling small-footprint airborne LiDAR-derived estimates of gap probability and leaf area index. Remote Sens. 2019, 12, 4. [Google Scholar] [CrossRef]
- Ross, C.W.; Loudermilk, E.L.; Skowronski, N.; Pokswinski, S.; Hiers, J.K.; O’Brien, J. LiDAR Voxel-Size Optimization for Canopy Gap Estimation. Remote Sens. 2022, 14, 1054. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M.; Kim, S.-H. Retrieval of Effective Leaf Area Index in Heterogeneous Forests With Terrestrial Laser Scanning. IEEE Trans. Geosci. 2013, 51, 777–786. [Google Scholar] [CrossRef]
- Hancock, S.; Essery, R.; Reild, T.; Carle, J.; Baxter, R.; Rutter, N.; Huntley, B. Characterising forest gap fraction with terrestrial lidar and photography: An examination of relative limitations. Agric. For. Meteorol. 2014, 189, 105–114. [Google Scholar] [CrossRef]
- Danson, F.M.; Hetherington, D.; Morsdorf, F.; Koetz, B.; Allgower, B. Forest canopy gap fraction from terrestrial laser scanning. IEEE Geosci. Remote Sens. Lett. 2007, 4, 157–160. [Google Scholar] [CrossRef]
- Song, Y.; Wang, J.F.; Shang, J.L. Estimating effective leaf area index of winter wheat using simulated observation on unmanned aerial vehicle-based point cloud data. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2020, 13, 2874–2887. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Vosselman, G. Slope based filtering of laser altimetry data. IAPRS 2000, 18, 935–942. [Google Scholar]
- Zhang, K.Q.; Chen, S.C.; Whitman, D.; Shyu, M.L.; Yan, J.H.; Zhang, C.C. A progressive morphological filter for removing nonground measurements from airborne LIDAR data. IEEE Trans. Geosci. Remote Sens. Environ. 2003, 41, 872–882. [Google Scholar] [CrossRef]
- Herbert, T.J. Calibration of fisheye lenses by inversion of area projections. Appl. Opt. 1986, 25, 1875–1876. [Google Scholar] [CrossRef] [PubMed]
- Jonckheere, I.; Fleck, S.; Nackaerts, K.; Muys, B.; Coppin, P.; Weiss, M.; Baret, F. Review of methods for in situ leaf area index determination: Part I. Theories, sensors and hemispherical photography. Agric. For. Meteorol. 2004, 121, 19–35. [Google Scholar] [CrossRef]
- Herbert, T.J. Area projections of fisheye photographic lenses. Agric. For. Meteorol. 1987, 39, 215–223. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M. Computational-Geometry-Based Retrieval of Effective Leaf Area Index Using Terrestrial Laser Scanning. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3958–3969. [Google Scholar] [CrossRef]
- Heiskanen, J.; Korhonen, L.; Hietanen, J.; Pellikka, P. Use of airborne lidar for estimating canopy gap fraction and leaf area index of tropical montane forests. Int. J. Remote Sens. 2015, 36, 2569–2583. [Google Scholar] [CrossRef]
- Chen, J.M.; Menges, C.H.; Leblanc, S.G. Global mapping of foliage clumping index using multi-angular satellite data. Remote Sens. Environ. 2005, 97, 447–457. [Google Scholar] [CrossRef]






| STD | RMSE | MAE | R2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | II | III | I | II | III | I | II | III | I | II | III | |
| 11-May | 0.13 | 0.20 | 0.17 | 6.20 | 0.30 | 0.18 | 6.20 | 0.25 | 0.14 | |||
| 16-May | 0.29 | 0.35 | 0.31 | 5.66 | 0.40 | 0.33 | 5.65 | 0.33 | 0.28 | |||
| 21-May | 1.26 | 0.35 | 0.31 | 4.40 | 0.43 | 0.39 | 4.16 | 0.34 | 0.31 | |||
| 27-May | 1.09 | 0.71 | 0.65 | 2.79 | 0.88 | 0.62 | 2.57 | 0.69 | 0.46 | |||
| 3-June | 1.38 | 0.94 | 0.85 | 3.48 | 1.83 | 1.43 | 3.22 | 1.60 | 1.21 | |||
| 11-June | 1.23 | 0.72 | 0.67 | 2.99 | 1.30 | 0.96 | 2.73 | 1.07 | 0.74 | |||
| Overall | 1.37 | 1.09 | 0.99 | 4.45 | 1.02 | 0.78 | 4.09 | 0.71 | 0.52 | 0.35 | 0.51 | 0.52 |
| STD | RMSE | MAE | R2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | II | III | I | II | III | I | II | III | I | II | III | |
| 11-May | 0.37 | 0.14 | 0.12 | 1.83 | 0.22 | 0.13 | 1.81 | 0.19 | 0.10 | |||
| 16-May | 0.59 | 0.28 | 0.24 | 1.48 | 0.30 | 0.33 | 1.36 | 0.24 | 0.24 | |||
| 21-May | 0.42 | 0.29 | 0.26 | 1.63 | 0.40 | 0.45 | 1.55 | 0.33 | 0.36 | |||
| 27-May | 0.43 | 0.53 | 0.51 | 1.53 | 0.55 | 0.43 | 1.44 | 0.40 | 0.31 | |||
| 3-June | 0.36 | 0.44 | 0.44 | 1.72 | 0.98 | 0.73 | 1.67 | 0.88 | 0.61 | |||
| 11-June | 0.40 | 0.42 | 0.43 | 1.41 | 0.63 | 0.48 | 1.36 | 0.49 | 0.40 | |||
| Overall | 0.60 | 0.78 | 0.74 | 1.61 | 0.57 | 0.46 | 1.53 | 0.42 | 0.34 | 0.35 | 0.61 | 0.61 |
| STD | RMSE | MAE | R2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | II | III | I | II | III | I | II | III | I | II | III | |
| 11-May | 0.43 | 0.18 | 0.15 | 6.62 | 0.34 | 0.15 | 6.60 | 0.30 | 0.11 | |||
| 16-May | 0.24 | 0.30 | 0.27 | 6.22 | 0.33 | 0.28 | 6.21 | 0.28 | 0.23 | |||
| 21-May | 1.25 | 0.47 | 0.40 | 4.72 | 0.69 | 0.52 | 4.49 | 0.53 | 0.39 | |||
| 27-May | 0.86 | 0.52 | 0.51 | 2.84 | 0.90 | 0.62 | 2.68 | 0.78 | 0.50 | |||
| 3-June | 1.09 | 0.58 | 0.54 | 3.41 | 1.77 | 1.33 | 3.24 | 1.67 | 1.21 | |||
| 11-June | 1.12 | 0.83 | 0.68 | 3.14 | 1.54 | 1.08 | 2.92 | 1.27 | 0.85 | |||
| Overall | 1.42 | 1.08 | 0.97 | 4.73 | 1.08 | 0.78 | 4.36 | 0.80 | 0.55 | 0.46 | 0.55 | 0.58 |
| STD | RMSE | MAE | R2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | II | III | I | II | III | I | II | III | I | II | III | |
| 11-May | 0.37 | 0.12 | 0.11 | 2.24 | 0.19 | 0.13 | 2.20 | 0.17 | 0.11 | |||
| 16-May | 0.76 | 0.24 | 0.22 | 1.84 | 0.27 | 0.32 | 1.71 | 0.22 | 0.24 | |||
| 21-May | 0.52 | 0.28 | 0.24 | 2.02 | 0.36 | 0.42 | 1.94 | 0.28 | 0.34 | |||
| 27-May | 0.44 | 0.46 | 0.43 | 1.74 | 0.48 | 0.37 | 1.65 | 0.38 | 0.27 | |||
| 3-June | 0.49 | 0.43 | 0.41 | 2.06 | 0.98 | 0.70 | 2.01 | 0.89 | 0.60 | |||
| 11-June | 0.47 | 0.50 | 0.46 | 1.63 | 0.68 | 0.49 | 1.56 | 0.52 | 0.40 | |||
| Overall | 0.63 | 0.78 | 0.72 | 1.93 | 0.56 | 0.44 | 1.84 | 0.41 | 0.33 | 0.28 | 0.62 | 0.63 |
| AEAP-SA Method | AEAP-MA Method | SP-SA Method | SP-MA Method | |
|---|---|---|---|---|
| AEAP-SA method | ||||
| AEAP-MA method | 0.003 | |||
| SP-SA method | 0.816 | 0.001 | ||
| SP-MA method | 0.003 | 0.962 | 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Xing, M.; Tan, Q.; Shang, J.; Song, Y.; Ni, X.; Wang, J.; Xu, M. Estimating Effective Leaf Area Index of Winter Wheat Based on UAV Point Cloud Data. Drones 2023, 7, 299. https://doi.org/10.3390/drones7050299
Yang J, Xing M, Tan Q, Shang J, Song Y, Ni X, Wang J, Xu M. Estimating Effective Leaf Area Index of Winter Wheat Based on UAV Point Cloud Data. Drones. 2023; 7(5):299. https://doi.org/10.3390/drones7050299
Chicago/Turabian StyleYang, Jie, Minfeng Xing, Qiyun Tan, Jiali Shang, Yang Song, Xiliang Ni, Jinfei Wang, and Min Xu. 2023. "Estimating Effective Leaf Area Index of Winter Wheat Based on UAV Point Cloud Data" Drones 7, no. 5: 299. https://doi.org/10.3390/drones7050299
APA StyleYang, J., Xing, M., Tan, Q., Shang, J., Song, Y., Ni, X., Wang, J., & Xu, M. (2023). Estimating Effective Leaf Area Index of Winter Wheat Based on UAV Point Cloud Data. Drones, 7(5), 299. https://doi.org/10.3390/drones7050299










