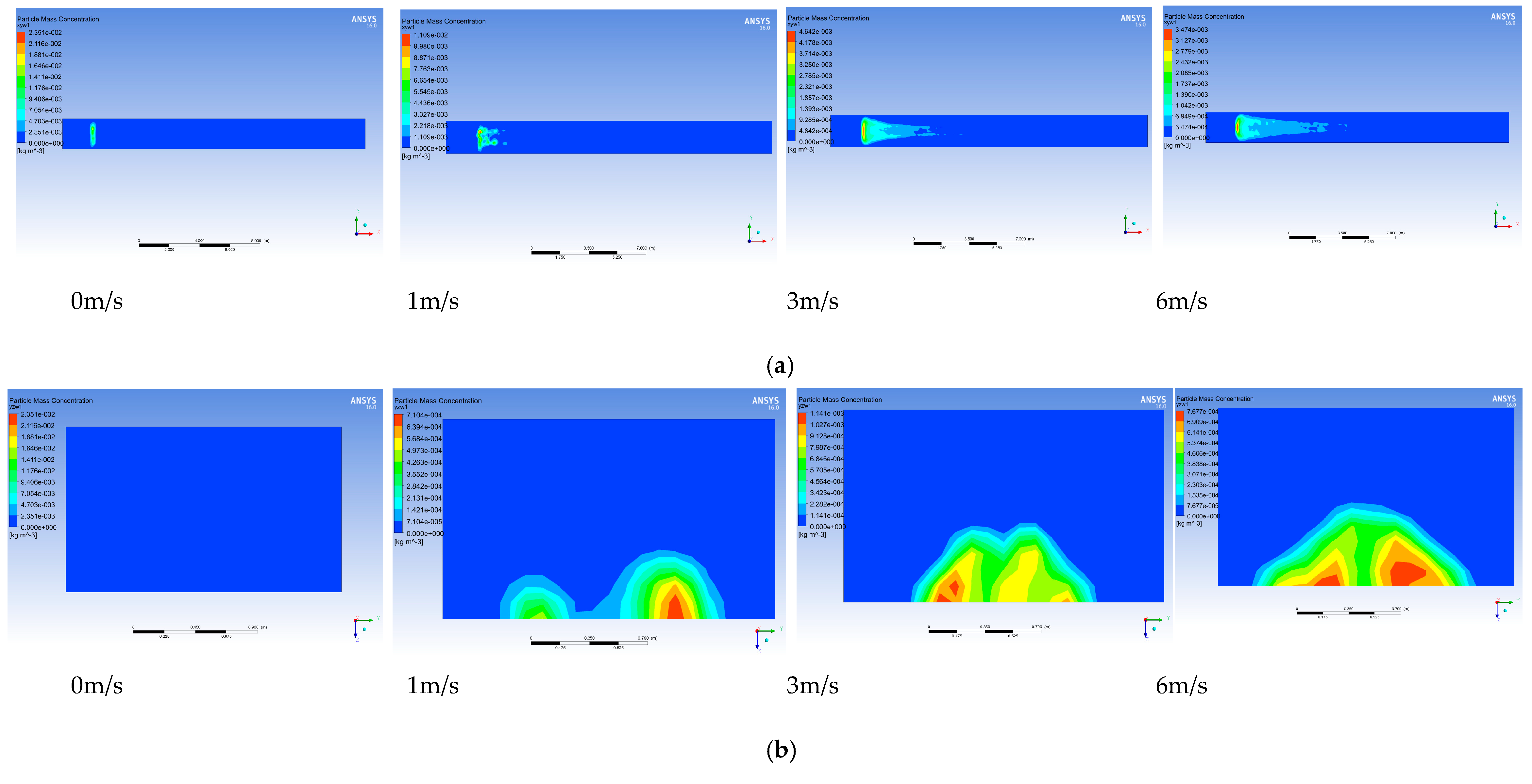
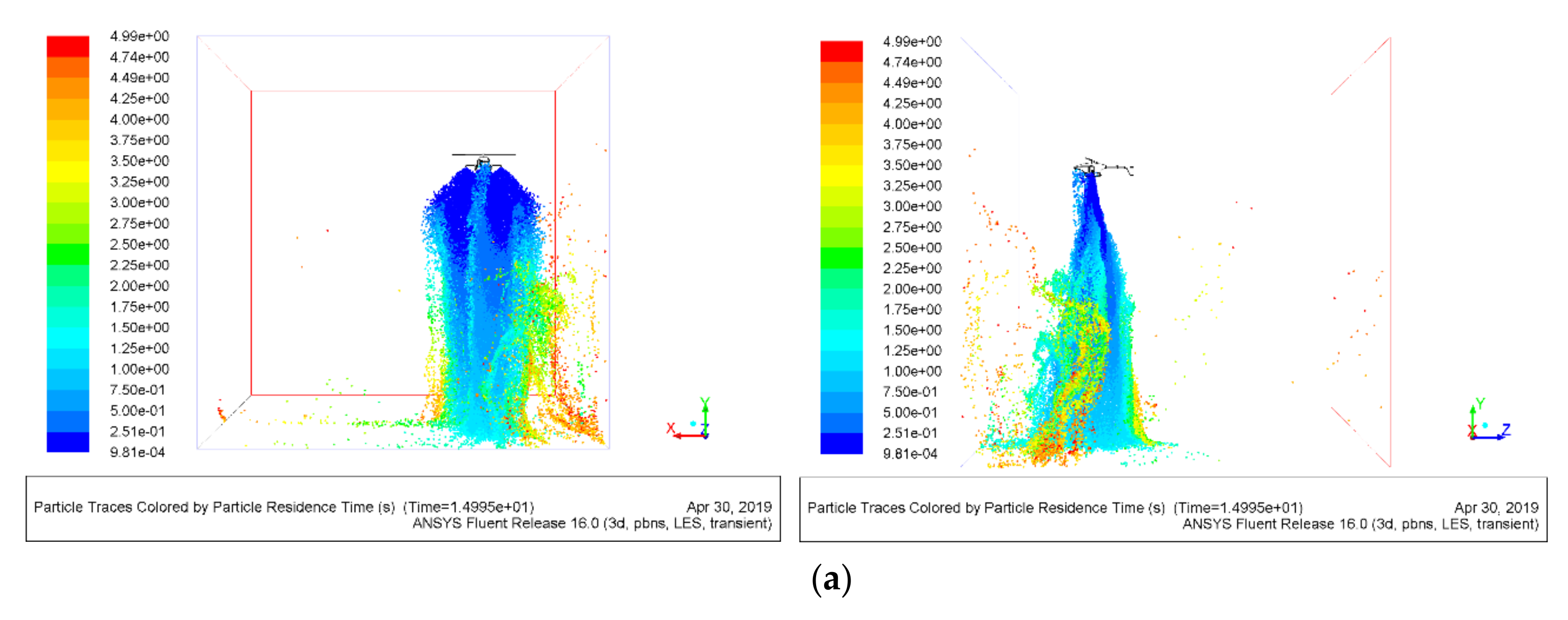
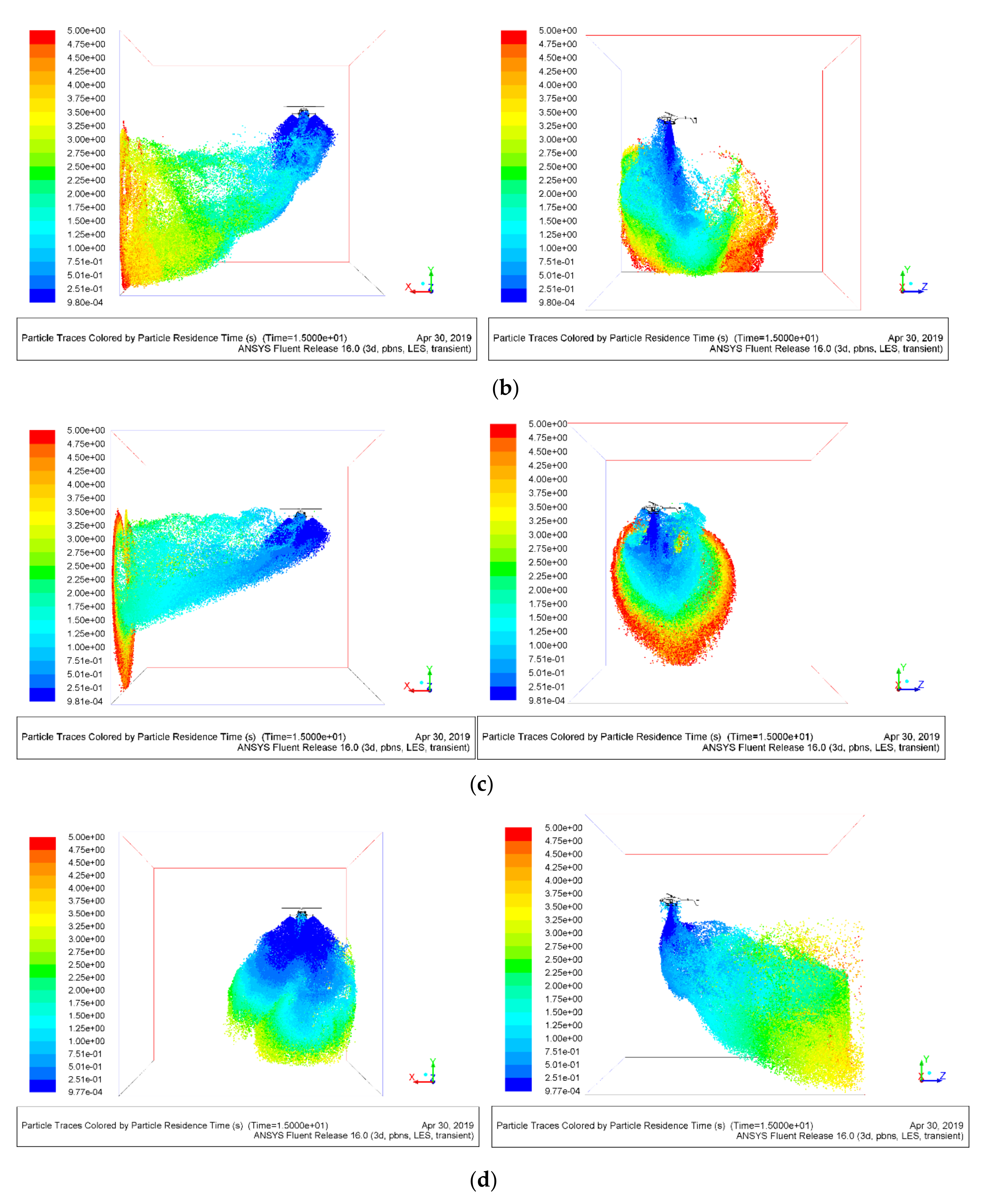
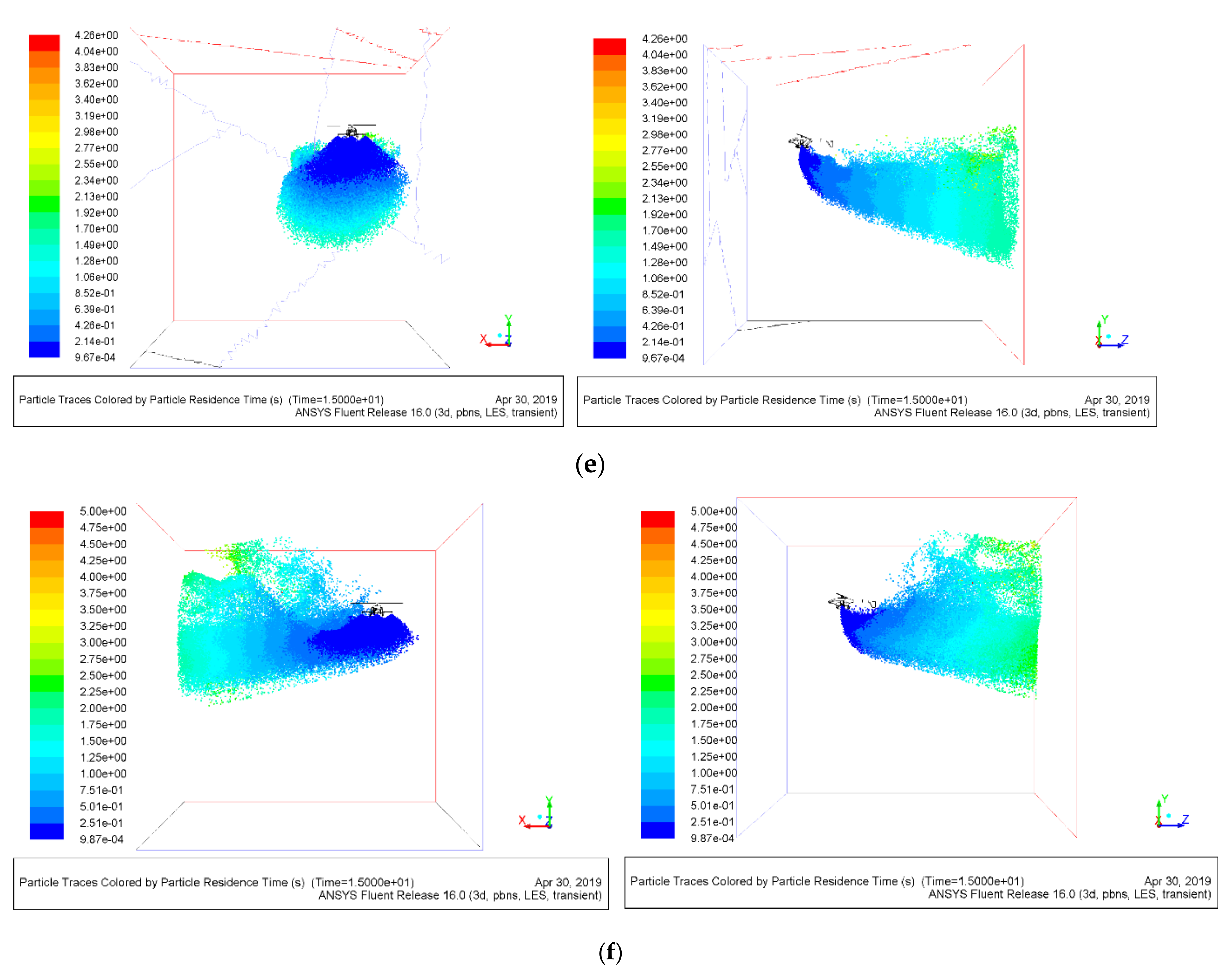
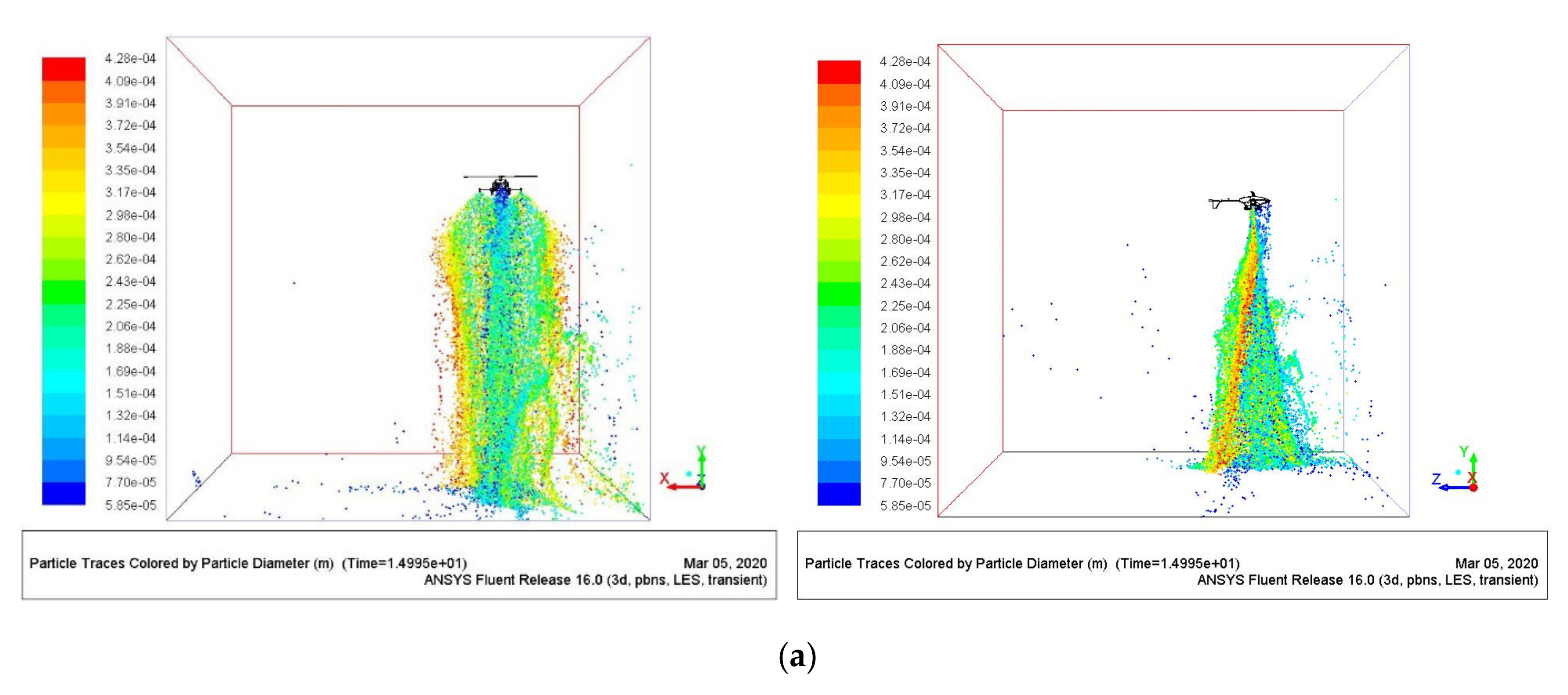
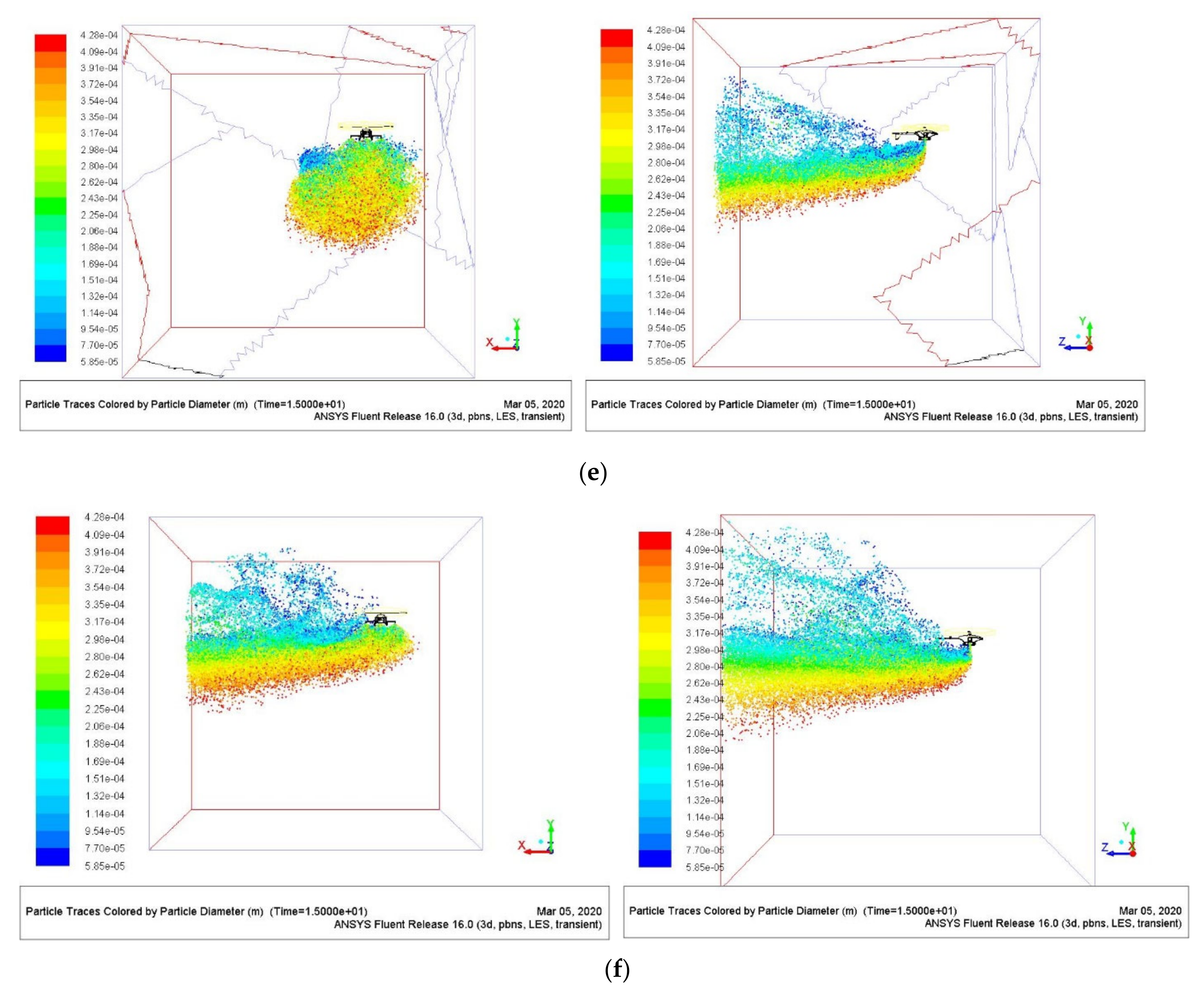
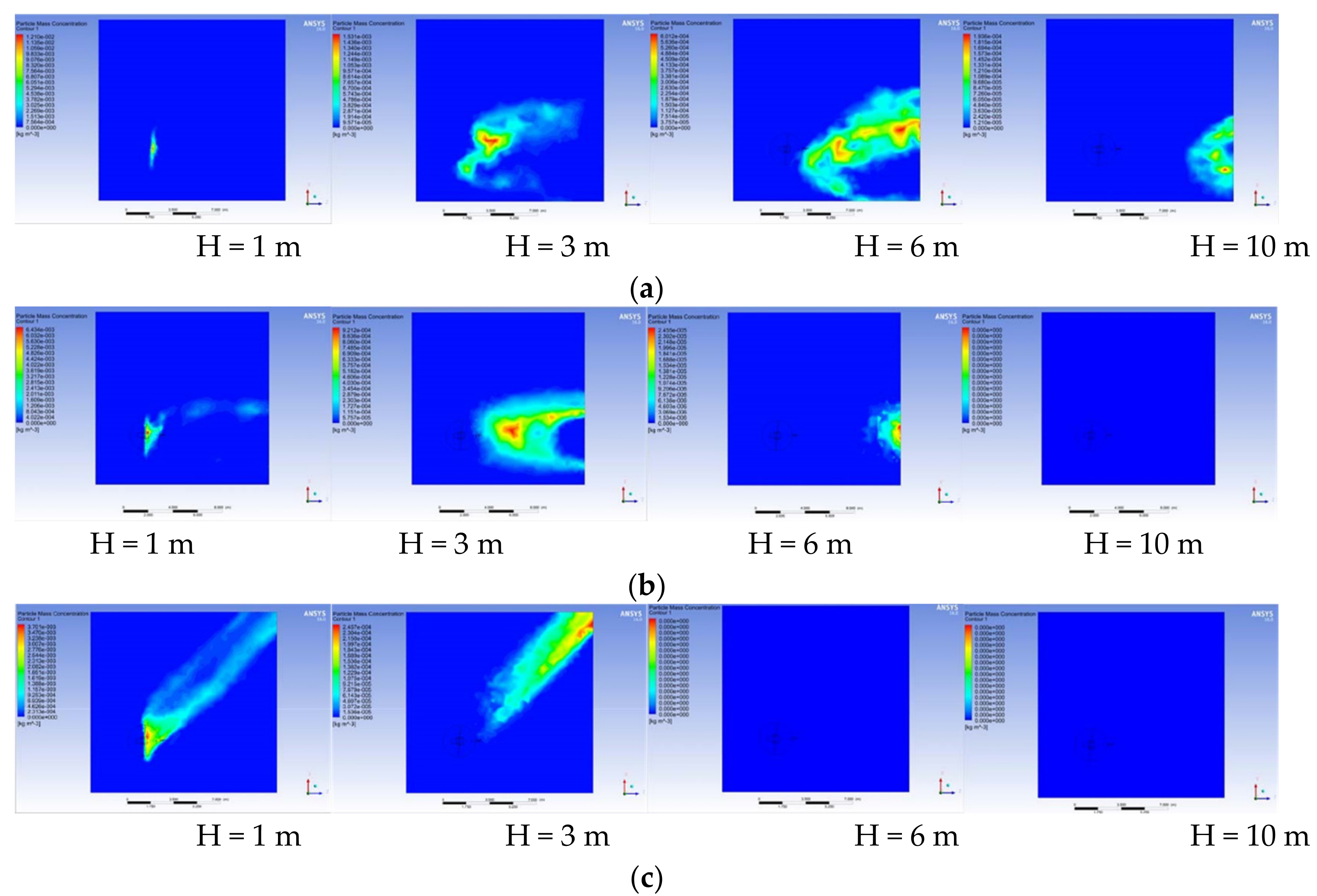
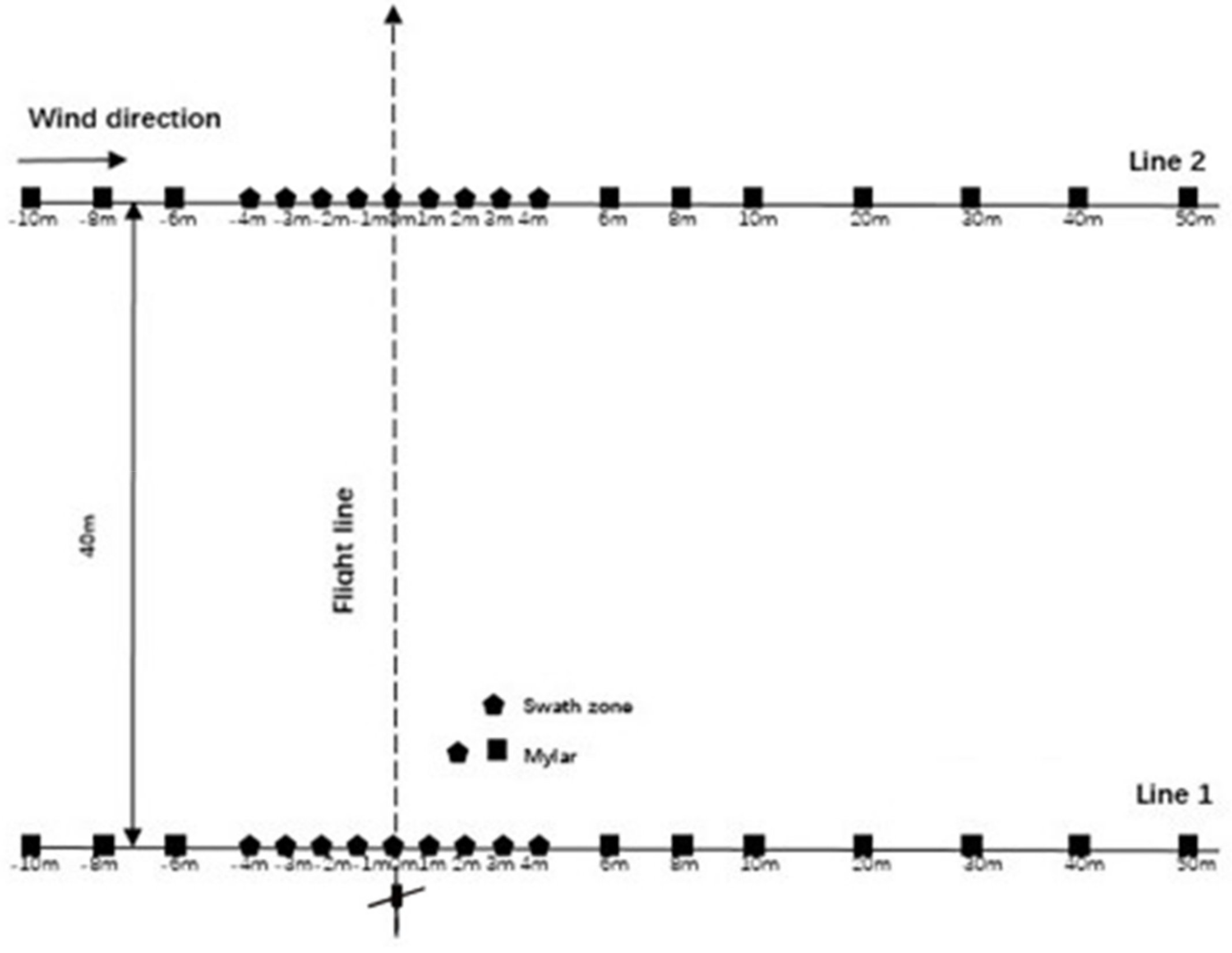
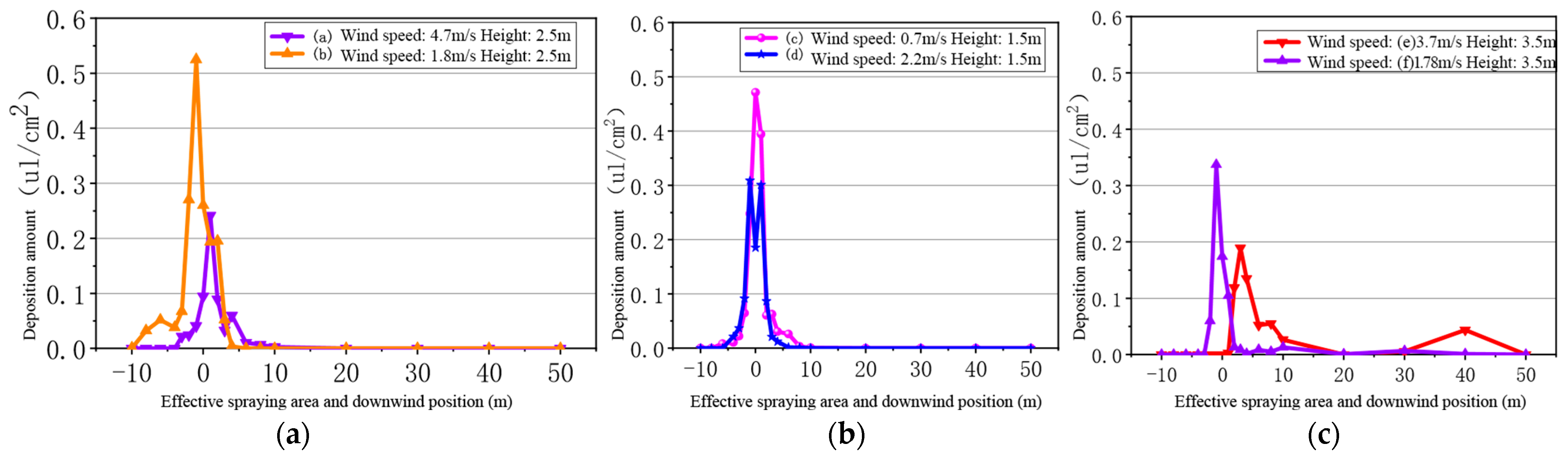
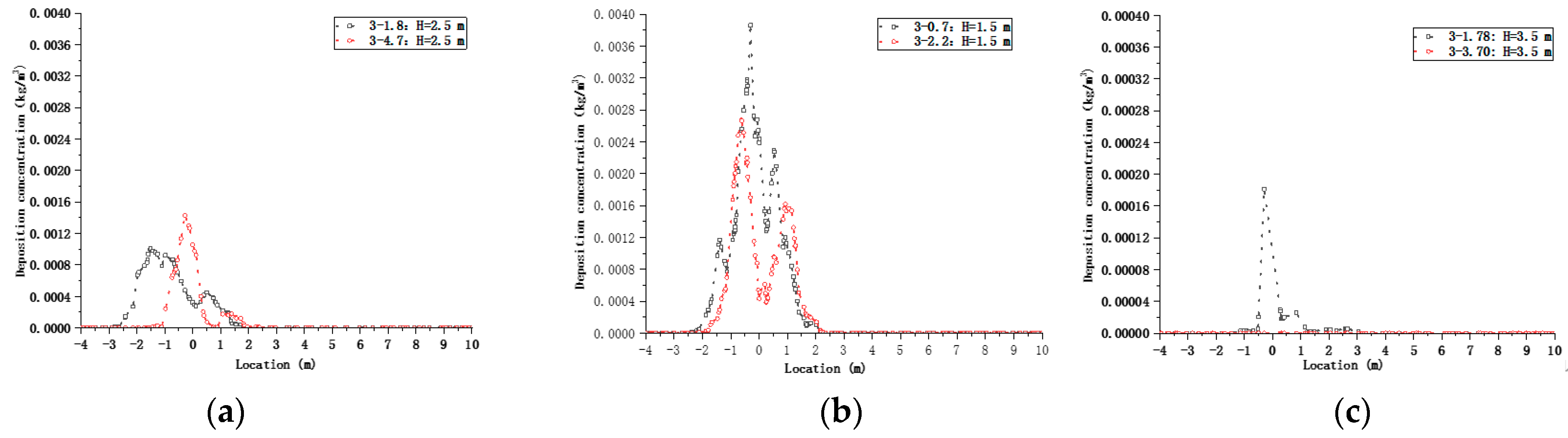
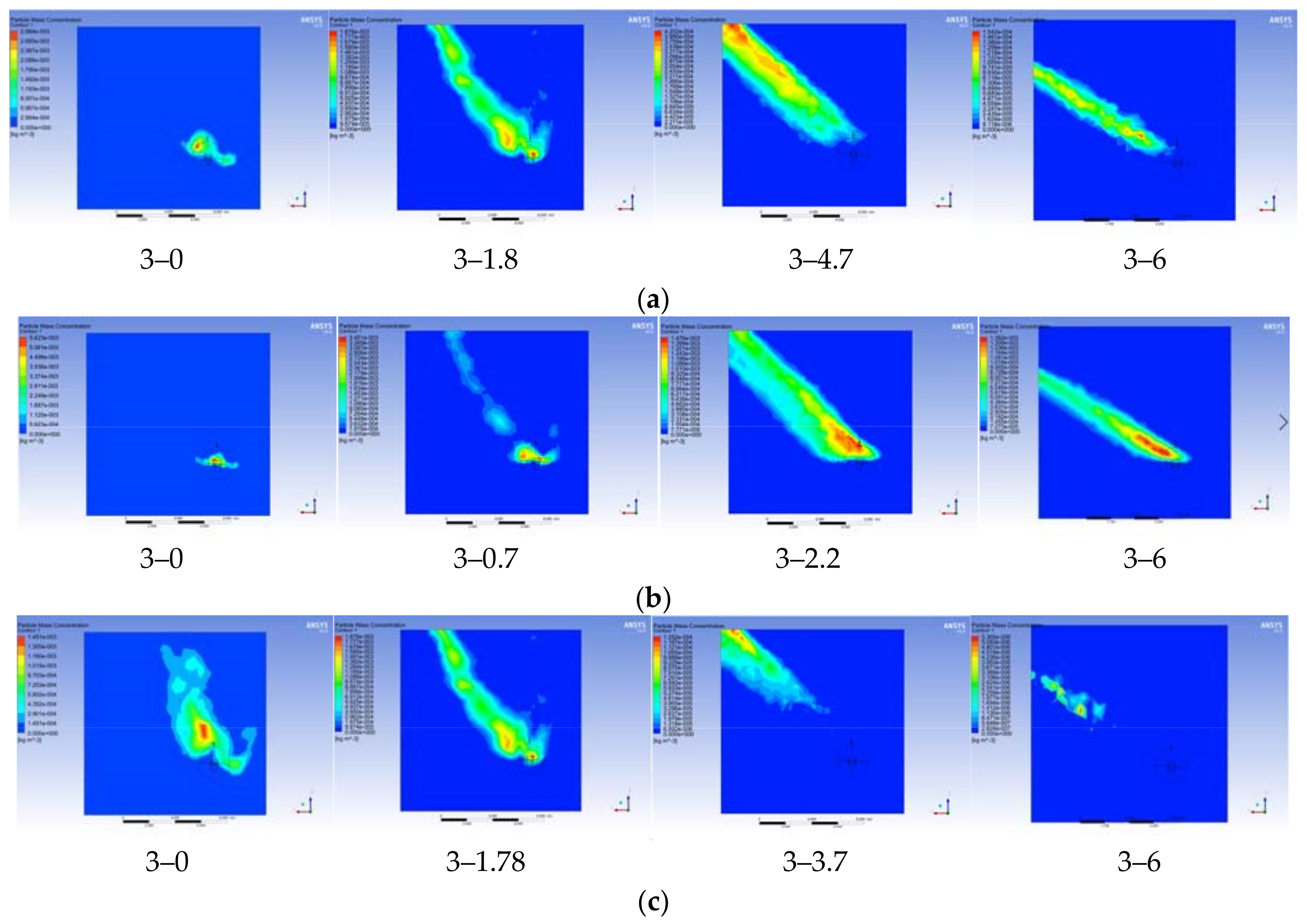
1. Introduction
Application is an important part of the plant growth and development process, and the application methods are mostly of the manual backpack type, ground machinery, and aerial application [
1,
2]. In the 1970s, as manned fixed-wing aircraft and helicopter applications became globally widespread, NASA and the U.S. Air Force developed a manned aircraft droplet drift prediction model based on Lagrangian equations and Gaussian models [
3,
4]. In China and other Southeast Asian countries, due to the small land area and complex terrain, ground machinery and fixed-wing aircraft have been difficult to apply on many occasions. China mainly used manual backpack sprayers and ground application machinery for a long period of time [
5,
6,
7]. Since 2016, plant protection drones have started to play a big role in China’s plant protection sector with advantages such as high efficiency, low cost, and suitability for applications in complex terrain [
8,
9,
10]. According to the latest data from the China Agricultural Technology Center, the number of plant protection drones in China was about 4000 in 2016, and by 2021, the plant protection drones of professional pest control service organizations alone exceeded 120,000, with an operational area of more than 1.07 billion mu, and more than 200,000 flyers active in fields [
11]; drones have become an important supplement to traditional application methods on some occasions [
12]. Under the influence of policy and demand, the agricultural unmanned aerial vehicle (UAV) market in China is expected to grow further in the next decade [
13]. Distinguished by the number of rotors, plant protection UAVs can be divided into two categories: single-rotor plant protection UAVs and multi-rotor plant protection UAVs [
14]. Single-rotor UAVs have the following advantages: they have a high load capacity, they have a longer stable endurance, and the wind field formed by a single rotor can blow the leaf surface to improve canopy penetration and effectively control the drifting problem of spraying chemicals [
15,
16,
17]. Single-rotor UAVs are now very widely used in plant protection operations. Japan was the first country to develop plant protection UAVs, and its representative model, the Yamaha Rmax series, is a single-rotor plant protection UAV [
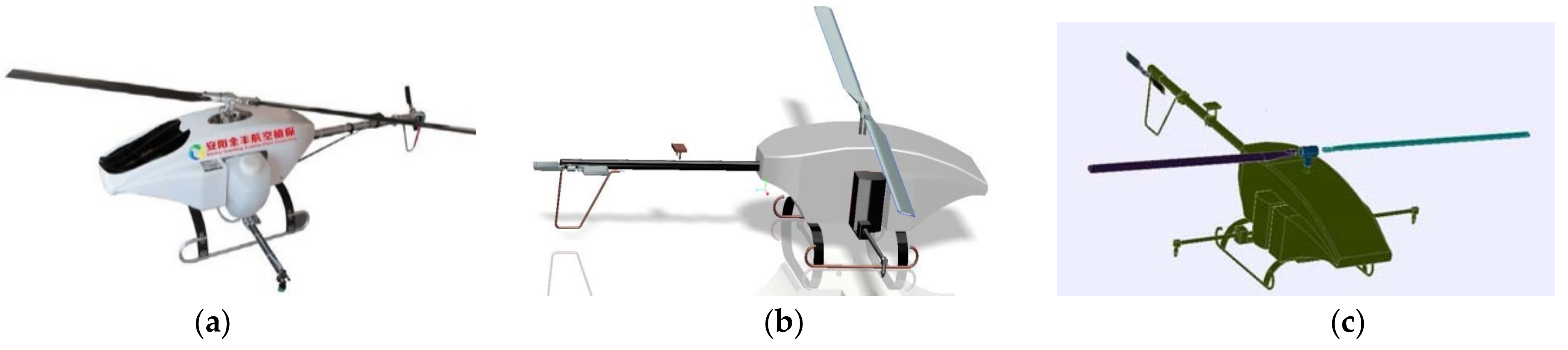
18]. The 3WQF120-12 produced by Quanfeng Aviation is the representative model of a domestic single-rotor plant protection UAV, and its common nozzle model is Lu120-015 (Lechler Lechler Ltd., Metzingen, Germany). Researchers have published many studies on the 3WQF120-12. Wang et al. [
16] experimentally studied the spraying effect of 3WQF120-12 on betel nut trees at different altitudes. Meng et al. [
19] experimentally studied the crop coverage of 3WQF120-12 with its spraying droplets under different flight parameters. Chen et al. [
20] evaluated the effective spray width of the 3WQF120-12 plant protection UAV through image analysis of the droplets on the acquisition card. However, there is still a lack of research regarding the mechanism of droplet deposition and drift during the spraying process of the 3WQF120-12 plant protection UAV. Due to the explosive growth in plant protection UAV applications, the need for application efficiency, application quality, and the assessment of potential risks of environmental pollution is increasingly prominent, while the simulation of droplet deposition drift started late and faces great research difficulties, and the number and accumulation of related studies is much lower than that of fixed-wing manned aircraft applications, which cannot meet the rapid growth of needs in time. The field environment where plant protection UAVs are applied is complex, with different growth characteristics of crops, and the heights of low crops and tall crops vary greatly. It is time-consuming and inefficient to study the spraying mechanism only using large-field experiments. Therefore, in this paper, we propose investigating key technologies and validation methods for the numerical simulation of droplet deposition and the drift of existing plant protection UAVs and to construct a spraying model by conducting a CFD simulation of the spraying mechanism of droplet application in the spraying process of 3WQF120-12 plant protection UAVs. The spray nozzle wind tunnel spraying model and the UAV spraying model were constructed and combined with a field test to observe the deposition pattern of droplets at different heights, ambient wind speeds, and flight parameters and to provide theoretical and data support for the movement pattern of droplets in the crop canopy.
Researchers in Western countries have constructed models for UAV spray droplet spraying after years of field trials and accumulating basic data. Among them, the FSCGB model established by Dumbauld et al. [
21] using the Gaussian method is suitable for predicting long-range drift and simulating the effect of atmospheric stability, but not for studying the deposition and drift of spray droplets. The AGDISP model proposed by Teske et al. [
22,
23,
24] is mainly based on the Lagrangian method for predicting the equations of the motion of spray droplets, including aircraft wake, aircraft fuselage, and environment turbulence effects generated during interactions with the environment. The AgDRIFT [
25] model, developed by the American Spray Drift Research Group and other organizations based on the AGDISP model, covers conditions such as aircraft model, aircraft vortex, nozzle type, and weather factors. However, ADGISP and AgDRIFT do not have pesticide drift prediction models for small UAVs, and the two models do not apply to droplet drift and deposition for common UAV types in China.
In contrast, computational fluid dynamics (CFD) techniques can isolate the effects of variables such as wind field and particle size on droplet drift and deposition. This method can accurately capture the flow details of the spraying process, bridging the gap between the AGDISP and AgDRIFT models in UAV spraying. Zhang et al. [
26] used computational fluid dynamics (CFD) techniques to predict the velocity field and subsequent motion trajectory of droplets in the wake stream of a Painted Maid 510 G aircraft. They compared the droplet deposition with the AGDISP prediction with good agreement, which proved the correctness of the CFD model. The application of this droplet motion model was refined and gradually accepted in plant protection spraying, and CFD is currently a robust design tool in agriculture [
27]. Initially, researchers used CFD techniques to simulate the spraying process of air-assisted sprayers in orchards [
28,
29]. In recent years, many CFD simulation applications have been devoted to investigating the effects of droplet size, wind speed, turbulence intensity, initial droplet velocity, droplet release height, and temperature on droplet displacement [
30,
31] and collection efficiency in wind tunnels. CFD simulations have been well used in the field of aerial spraying [
32,
33]. Ryan [
34] performed a 3D near-field wake vortex for AT-802 air tractor simulations, and the results clearly reveal that the droplets flowing out of the aircraft wingtip vortex had a significant entrainment effect, where the droplets were lifted upward by the wingtip vortex and moved outward at the same time. Yang et al. [
35] simulated the pesticide drift of the AGRAS MG-1 eight-rotor plant protection UAV spraying operation, and the results obtained have some significance for practical production.
There are many conditions affecting droplet drift, such as spraying height, flight speed, and side wind speed conditions. Wang et al. [
36,
37] measured UAV flight parameters by Beidou satellite positioning and conducted field trials combined with the spatial mass balance method and other methods to verify that the flight altitude, flight speed, and side wind speed conditions had significant effects on the drift of droplet deposition for UAV applications. Many researchers have studied the effects of the above factors on the spraying effect of plant protection UAVs. Yang et al. [
38] analyzed the dynamic development pattern and distribution characteristics of the downwash airflow of an SLK-5 six-rotor agricultural UAV at different altitudes. They studied the droplet drift characteristics of a multi-rotor UAV. Zhang et al. [
39] analyzed the four-rotor UAV’s downwash flow field distribution characteristics at different flight speeds. Grant et al. [
40] from the USA studied the drift characteristics of free-hovering UAV sprays in a wind tunnel at different wind speeds.
To study the pesticide spraying mechanism of the 3WQF120-12 plant protection UAV, in this study, the nozzle spraying model of the UAV was established by combining CFD and wind tunnel experiments, and the nozzle’s set points and geometric parameters were added to the UAV model. Subsequently, simulations of the droplets’ drift in the wind field below generated by the single-rotor plant protection UAV were performed under different spraying heights, flight speeds, and side wind conditions. The droplet particle size distribution, droplet duration variation law, and droplet deposition concentration cloud maps were obtained via the simulation to analyze the three-dimensional distribution of droplets and their variation laws. The results of the analysis were also verified in field tests.